完备剩余格上的蕴涵闭包算子
带蕴涵算子的N元格蕴涵代数不等式的解

带蕴涵算子的N元格蕴涵代数不等式的解龙希庆【摘要】The N-inequality with implication operator was studied in the lattice implication algebra.The necessary and sufficient conditions for existence of solution for the N-inequality will be presented respectively.In the case,that b is an irreducible element of L,the all maximal elements of solutions and detailed solution sets are given.%在格蕴涵代数中研究了带蕴涵算子的N元格蕴涵代数不等式,得到其有解的充分必要条件,同时还在b是L交既约元的情况下,找出该不等式的所有极大解,进而给出其具体解集.【期刊名称】《宜宾学院学报》【年(卷),期】2012(000)006【总页数】4页(P1-4)【关键词】格蕴涵代数;格蕴涵代数不等式;交既约元;极大元【作者】龙希庆【作者单位】宜宾学院数学学院,四川宜宾644000【正文语种】中文【中图分类】O1531993年,徐扬[1]在研究多值逻辑及逻辑公式的真值取于格上的逻辑系统时,提出格蕴涵代数的概念.随后,胡长流[2]等人研究了有余格的相关性质,Xu [3]、白利军[4]研究了格蕴涵代数的性质及基于格蕴涵代数的格值逻辑系统.赖家俊[5]等提出了格蕴涵代数不等式的概念,并讨论了几类简单格蕴涵代数不等式的解及其解集的若干性质.由于格蕴涵代数不等式作为格蕴涵代数的一个分支在研究格值逻辑公式的归结问题时具有重要的理论意义,特别是对归结域的研究多数都可转化为格蕴涵代数不等式的研究,因此,在详细深入地研究了一元和二元格蕴涵代数不等式的解集及其性质[6-8]、随后又研究了N元格蕴涵代数不等式有解的判别条件及解集的性质[9],笔者继续深入研究格蕴涵代数不等式特别是带蕴涵算子的N元格蕴涵代数不等式的解及其解集,得到该格蕴涵代数不等式有解的充要条件及其解集的性质,特别在b是L交既约元的情况下找出该不等式的所有极大解,进而给出其具体解集.定义 1.1[1]设(L,∧,∨,')是一有泛界 0,I的有余格,≤是L上的偏序关系,若映射→:L×L→L满足,对任意的 x,y,z∈L,(1)x→(y→z)=y→(x→z);(2)x→x=I;(3)若x→y=y→x=I,则 x=y;(4)x→y=y'→x';(5)(x→y)→y=(y→x)→x;则称(L,∧,∨,',→O,I)是一个拟格蕴涵代数.若它还满足:(6)(x∨y)→z=(x→z)∧(y→z);(7)(x∧y)→z=(x→z)∨(y→z).则称(L,∧,∨,',→)是一个格蕴涵代数.若对所有的x,y,z∈L 还满足x∨y∨[(x∧y)→z]=I,则(L,∧,∨,',→)称为格H蕴涵代数.定义1.2[2]设 L 是一个格,对任意的 x,y∈L,如果b=x∧y蕴涵着x=b或y=b,则称b为格L的交既约元.注:在下文中,对任意的自然数n,n 均表示集合{1,2,由定理2.6知,若M≠Ø,则M恒O(零)解,因此下面在b是L的交既约元的情况下去找出该方程的最大解或是极大解,进而由定理2.5和2.6知,则可以得到(ai→xi)≤b的所有解.定理2.7 如果b是L的交既约元,则M≠Ø⇔∃i∈n,使得a'i≤b.证明由定理2.3知,定理2.11 如果M≠Ø且b是L的交既约元,L是完备格蕴涵代数,则M的每个极大元都具有形式:由定理2.8知,M有|G'(b)|个极大元.由定理2.5、定理2.6及定理2.11直接可证以下定理2.12 成立.定理2.12 如果M≠Ø且b是L的交既约元,L是完备格蕴涵代数,则【相关文献】[1]徐扬.格蕴涵代数[J].西南交通大学学报,1993(1):20 -27.[2]胡长流,宋振明.格论基础[M].开封:河南大学出版社,1990.[3] Xu Y,Ruan D,Qin K Y,et ttice - valued logic[M].New York:Springer-Verlag Berlin Heidelberg,2003.[4]白利军.格蕴涵代数的对偶性质[J].宜宾学院学报,2011,11(6):11-13.[5]赖家俊,徐扬.格蕴涵代数不等式[J].江南大学学报,2007,6(3):366-370.[6]龙希庆.格蕴涵代数中-化子和不等式的研究[D].成都:西南交通大学研究生硕士学位论文,2007.[7]龙希庆.两类简单格蕴涵代数不等式的解[J].宜宾学院学报,2010,10(12):10 -12. [8]龙希庆.格蕴涵代数不等式的解[J].内江师范学院学报,2011,26(2):8 -10.[9]龙希庆.N元格蕴涵代数不等式的解I[J].绵阳师范学院学报,2011,30(2):6 -8. [10]Birkhoff ttice theory(Vol.XXV)[M].3rd ed.Providence,R I:A-merican Mathematical Society Colloquium Publications,1967.。
σ-完备向量格中算子方程组解的存在唯一性定理

Ex s e c nd Un q e e s Th o e s o o u i n o y t m s i t n e a i u n s e r m f S l to s f r S s e o e a o u to s i f Op r t r Eq a i n n Co p e e Ve t r La tc ・ m l t c o ti e
摘 要 : 用 半 序 的方 法 在 不 具 有 连 续 性 和 紧性 的条 件 下 , 论 了 一 备 向量 格 中 一 类 非 线 性 算 子 方程 组 的解 利 讨 完 的存 在 唯 一 性 及 迭 代 收 敛 性 , 给 出 了此 迭 代 的误 差 估 计 . 并 关 键 词 : 子 方 程 组 ; 序方 法 ; 一 备 向量 格 ;迭 代 序 列 算 半 完
f ( )一 U A “,
.
() 1
I , )一 “ B( “
得到 了其解 的存 在唯 一性 , 但这 些研究 基本 上都 是 在 B n c a a h空 间 中进 行 的. 本文将 在 d一 r 完备 向量 格 中
研 究算 子方 程组 ( ) 由于此 空 间只有 半序 结构 没有 拓扑结 构 , 1, 并且 不用对 锥加 正规 的条件 , 没有用 到 也
通 常 的 范 数 , 是 引 入 了一 个 新 的范 数 一 范 数 , 此 不 同 于 以往 的 研 究 . 而 格 因 首先 给出一 些相 关 的概念 .
定义 I E为 序 向量 空 间 , c E称为 向量 格 ( 又称 R ez is 空间 或半序 线性 空 间) 若对 任意 的 z, , Y∈E,
D e .2 0 c O1
【国家自然科学基金】_fuzzy蕴涵代数_基金支持热词逐年推荐_【万方软件创新助手】_20140802
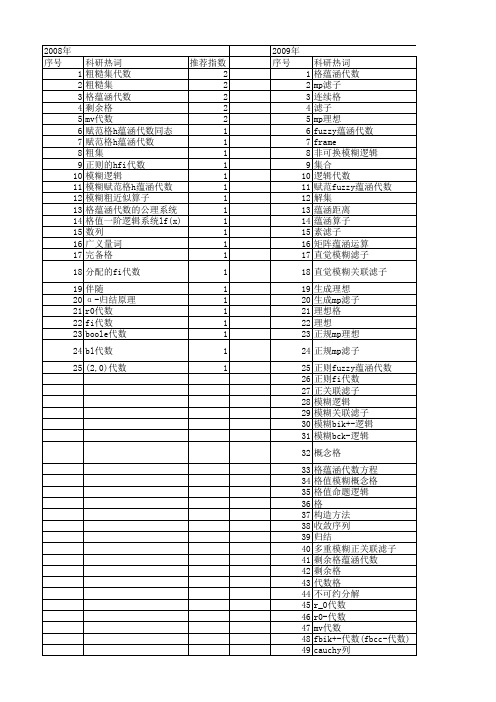
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42
科研热词 推荐指数 格蕴涵代数 6 模糊逻辑 5 同态 3 区间值模糊集 3 蕴涵理想 2 粗糙集代数 2 正关联)滤子 2 模糊滤子 2 商代数 2 t-模 2 fuzzy蕴涵代数 2 £-模 1 随机信息 1 语言值模糊集 1 语言值模糊聚类 1 语言值模糊矩阵 1 语言值模糊相似矩阵 1 蕴涵同态 1 自然语言 1 结合滤子 1 粗糙集 1 粗糙滤子 1 生成mp滤子 1 滤子 1 模糊滤子格 1 模糊信息 1 对合滤子 1 多重模糊结合滤子 1 双重不确定性信息 1 区间值£-模糊(关联 1 区间值t-模糊(关联 1 区间值(j)-模糊(关联、正关联)滤子 1 剩余格蕴涵代数 1 交换mp滤子 1 wbro-代数 1 wbr0-代数 1 swbro-代数 1 swbr0-代数 1 pfi代数 1 mp滤子 1 heyting代数 1 (正)关联mp滤子 1
2012年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33
科研热词 推荐指数 模糊逻辑 3 格蕴涵代数 3 直积 2 逻辑代数 1 连续性 1 语言值 1 蕴涵算子 1 正则可换双剩余格 1 正则fi-代数 1 模糊粗糙集 1 模糊滤子 1 格 1 度量空间 1 库存管理 1 同余关系 1 双剩余格 1 剩余格 1 关联mp滤子 1 公理系统 1 交换mp滤子 1 不确定性信息 1 ∈ⅴq)-模糊格蕴涵子代数 1 ⅳ-模糊集 1 ⅳ-(∈,∈∨q) -模糊格蕴涵子代数 1 wbr0-代数ห้องสมุดไป่ตู้1 rbr0-代数 1 mp滤子 1 iv-模糊集 1 iv-(∈ 1 fuzzy蕴涵代数 1 fi代数 1 fi-代数 1 fbr0-代数 1
完备格上正则蕴涵算子的研究

Th e u a m p i a i n n c m p e e a tc e r g l r i l to s o o c l t d l tie
L n IYa
( hax V ct n n ehia C lg , i n7 0 0 , h a S ani oa oa a dT cnc o ee X 1 10 C i ) i l l l a n
2 )
( )= ( Y z Y )¥ ;
3 }1 = ; )
4 l≤ ,1 Y ≤ ) 2 木 2 Y 半 ;
基金项 目: 陕西省 自然科学基金 资助项 目( 0 7 2 2 0 A1 ) 作者简 介: 李艳 , , 女 陕西商 洛人 , 从事基础数学及数学理论研究 。
完 备 格 上 正 则 蕴 涵 算 子 的 研 究
李 艳
( 陕西职业技术学 院 基础课部 , 陕西 西安 700 ) 1 10
摘要 : 目的
将 正则 蕴涵 算子 的概念推 广 到 完备格 上 。方 法
利 用定 义及 基 本 性质 。 结果
研 究
了完备格 上正 则蕴 涵算 子的性 质 以及与 一 些重要 的逻 辑代数 之 间的 关 系。结 论
子的概念 推广 到完 备格 上 。
1 ≤ Y ) 木 ; y 2 Y ≤ y )( ) ; 3 ) 4 )
5 )Βιβλιοθήκη 1 完 备 格 上 的正 则 蕴 涵 算 子
定 义 1 设 是完 备格 , : 一 £ 若满 足 一 ,
1 V Y z∈L, ) , , 3 V ∈L1 ) , ( Y = ; )=Y ( z; )
的三角模 构 成 伴 随 , 国俊 教 授 在 文 献 [ ] 王 1 中将 这
模糊完备格上的模糊同余关系

模糊完备格上的模糊同余关系刘敏;赵彬【摘要】在模糊完备格中引入模糊完备格同余关系的概念,讨论了模糊完备格同余与模糊闭包算子之间的关系.证明了一个模糊完备格上的模糊同余关系之集构成的模糊偏序集模糊序同构于其上的模糊闭包算子之集构成的模糊偏序集.给出了模糊完备格同余的商的概念,证明了任一模糊完备格满同态的像都模糊序同构于由该模糊完备格同态所诱导的同余关系的商.%The concept of fuzzy complete lattice congruence relation on fuzzy complete lattice is defined, and the relation between fuzzy complete lattice congruence and fuzzy closure operator is discussed. It is proved that in a fuzzy complete lattice, the fuzzy poset of fuzzy complete lattice congruence relations is fuzzy order isomorphic to the fuzzy poset of fuzzy closure operators. The quotient of a fuzzy complete lattice congruence relation is defined. It is also proved that the image of a fuzzy complete lattice under a surjective fuzzy complete lattice morphism is fuzzy order isomorphic to the quotient of the fuzzy complete lattice congruence relation induced by the fuzzy complete lattice morphism.【期刊名称】《陕西师范大学学报(自然科学版)》【年(卷),期】2013(041)001【总页数】5页(P5-9)【关键词】模糊偏序集;模糊完备格;模糊完备格同余;模糊闭包算子【作者】刘敏;赵彬【作者单位】陕西师范大学数学与信息科学学院,陕西西安 710062;陕西师范大学数学与信息科学学院,陕西西安 710062【正文语种】中文【中图分类】O159偏序集理论在数学以及相关学科领域有广泛的应用.但由于分明偏序仅能刻画元素之间的大小关系而不能反映其相对大或小的程度,因此自从Zadeh提出模糊集的概念以来许多学者致力于将分明的序关系推广到多值的情形.近年来,由于Ω-范畴理论[1-5]、量化Domain理论[6-10]的发展,一种新的模糊偏序[6,8,11]被提出.分明偏序集理论中的许多重要概念与结论,相继被推广到模糊偏序集的框架之下.完备格同余关系是偏序集理论中的一个重要概念,它与偏序集上的闭包算子、闭包系统等概念有密切的关系.因此,在模糊偏序集的理论框架下能否引入模糊完备格同余关系,它与模糊偏序集中已有的闭包算子等概念之间是否存在如分明情形下的关系是一个值得研究的问题.基于以上情况,本文在模糊完备格中引入模糊完备格同余关系,并进一步讨论它与模糊闭包算子之间的关系.1 预备知识文中L均表示一个Frame[12].用1、0分别表示L的最大元与最小元.为了统一概念,下面回顾有关模糊偏序集的概念和结论.相关内容来自文献[6-11].定义1[6-7,11]设X是一个集合,称映射e:X×X→L为X上的模糊偏序,如果e满足:(E1)∀x∈X,e(x,x)=1;(E2)∀x、y、z∈X,e(x,y)∧e(y,z)≤e(x,z);(E3)∀x、y∈X,e(x,y)=e(y,x)=1蕴含x=y,此时,称序对(X,e)为一个模糊偏序集.设(X,e)是一个模糊偏序集,定义X上的二元关系≤e为x≤ey当且仅当e(x,y)=1,则(X,≤e)是一个偏序集.通常记由模糊偏序集(X,e)诱导的偏序集(X,≤e)为X0.记X0中的并交运算为∨,∧.例1 下面给出本文将要用到的模糊偏序集的例子:(1)定义eL:L×L→L为∀α、β∈L,eL(α,β)=α→β,则(L,eL)是模糊偏序集;(2)设(X,e)是模糊偏序集,Y⊆X,则(Y,e|Y×Y)也是模糊偏序集,称为X的子模糊偏序集,简记为(Y,e);(3)设X是一个集合,(Y,eY)是一个模糊偏序集,记X到Y的所有映射之集为YX.定义sub:YX×YX→L为:∀f、g∈YX,sub(f,g)g(x)),则(YX,sub)是模糊偏序集.定义2[8]设(X,e)是一个模糊偏序集,A∈LX,a∈X,(1)称a是A的上确界,记作a=A,如果:(ⅰ)∀x∈X,A(x)≤e(x,a);(ⅱ)∀y∈X(A(x)→e(x,y))≤e(a,y).(2)称a是A的下确界,记作a=A,如果:(ⅰ)∀x∈X,A(x)≤e(a,x);(ⅱ)∀y∈X(A(x)→e(y,x))≤e(y,a).由(E3)可知,若上确界(或下确界)存在则必唯一.注1[8]设(X,e)是一个模糊偏序集,A∈LX,a∈X,则(1)a=A当且仅当∀y∈X,e(a,y)=(A(x)→e(x,y));(2)a=A当且仅当∀y∈X,e(y,a(A(x)→e(y,x));(3)定义↓A∈LX为:∀x∈X,(↓A)(x)=(A(y)∧e(x,y)),则A存在当且仅当↓A存在,此时定义3[8,10]设(X,e)是一个模糊偏序集,若∀A∈LXA和A存在,则称X是模糊完备格.注2[7,10]设(X,e)是一个模糊偏序集,则以下条件等价:(1)(X,e)是模糊完备格;(2)∀A∈LXA存在;(3)∀A∈LXA存在.易证,若(X,e)是模糊完备格,则X0是完备格.∀A⊆X0,∨A=χA,χA:X→L是A的特征函数,当x∈A时χA(x)=1;当x∉A时χA(x)=0.设f:X→Y是集合X到Y的一个映射,定义fL→:LX→LY为∀A∈LX,y∈Y,fL→ (A)(y)=∨{A(x)|x∈X,f(x)=y}.定义4 设f:X→Y是模糊偏序集(X,eX)、(Y,eY)之间的映射:(1)如果∀a、b∈X,eX(a,b)≤eY(f(a),f(b)),则称映射f保模糊序;(2)如果∀a、b∈X,eX(a,b)=eY(f(a),f(b)),则称映射f是模糊序嵌入;(3)如果f是满的模糊序嵌入,则称f是模糊序同构,此时称X和Y是同构的,记作X≅Y;(4)如果∀A∈LX,f(A)=fL→(A)则称f保模糊并.注3 设f:X→Y是模糊偏序集(X,eX)、(Y,eY)之间的映射:(1)若f保模糊序,则f:X0→Y0是保序映射;(2)若f保模糊并,则f保模糊序且f:X0→Y0是保并映射.定义5[3]设(X,e)是一个模糊偏序集,(1)称X是tensor完备的,如果∀x∈X,α∈L,存在α⊗x∈X,使得∀y∈X,e(α⊗x,y)=α→e(x,y);(2)称X是cotensor完备的,如果∀x∈X,α∈L,存在αx∈X,使得∀y∈X,e(y,αx)=α→e(y,x).设x∈X,α∈L,用xα表示从X到L将x映为α,其余映为0的映射.由定义可知,α⊗x=xα,α x=xα.因此,完备的模糊偏序集是tensor完备和cotensor完备的.若(X,e)是一个模糊完备格,则∀A∈LX,A=(A(X)⊗x);∀{xi|i∈I}⊆X,y∈X,e(xi,y).有关tensor完备和cotensor完备的模糊偏序集的进一步的性质可参考文献[3,5].定义6[13-14]设f:X→X是模糊偏序集(X,e)上保模糊序的映射,如果∀x∈X,e(x,f(x))=e(f(f(x)),f(x))=1,则称f是模糊闭包算子.记模糊偏序集(X,e)上的全体模糊闭包算子之集为COL(X).若f是模糊偏序集(X,e)上的模糊闭包算子,则f是X0上的闭包算子,且∀x、y∈X,e(x,f(y))=e(f(x),f(y)).2 模糊完备格上的模糊同余关系下面引入模糊完备格同余关系的概念,并讨论它与模糊闭包算子的关系.定义7[11]设X是一个非空集合,R:X×X→L是X上的L-关系,若对任意的x、y、z∈X,R满足:(1)R(x,x)=1;(2)R(x,y)=R(y,x);(3)R(x,y)∧R(y,z)≤R(x,z),则称R是X上的一个L-等价关系.定义8 设(X,e)是一个模糊完备格,R:X×X→L是X上的一个L-等价关系,若对任意的x、y、z∈X,R满足:(1)R(R(x,_),y)=R(x,y);(2)e(x,y)∧R(x,z)≤R(y,y∨z),则称R是X上的一个模糊完备格同余关系.记模糊完备格(X,e)上的全体模糊完备格同余关系之集为CRL(X).命题1 设f:X→Y是模糊完备格(X,eX)和(Y,eY)之间保模糊并的映射.定义Rf:X×X→L为:∀a、b∈X,Rf(a,b)=eY(f(a),f(b))∧eY(f (b),f(a)),则Rf是模糊完备格同余.证明由定义容易验证Rf是L-等价关系.(1)由于∀x∈X、t∈Y,因此,f(x)所以对任意的x、z∈X,Rf(Rf(x,_),z)=eY(f(Rf(x,_)),f(z))∧eY(f(z),f(Rf(x,_)))=eY(f(x),f(z))∧eY(f(z),f(x))=Rf(x,z).(2)∀a、b、c∈X,eX(a,b)∧Rf(a,c)≤eY(f(a),f(b))∧(eY (f(a),f(c))∧eY(f(c),f(a)))≤eY(f(c),f(b))∧ey(f (b),f(b))=ey(f(b)∨f(c),f(b))=eY(f(b∨c),f(b))∧eY(f(b),f(b∨c))=Rf(b,b∨c).因此Rf是模糊完备格同余.命题2 设j:X→X是模糊完备格(X,e)上的一个模糊闭包算子.定义Rj:X×X→L为:∀x、y∈X,Rj(x,y)=e(j(x),j(y))∧e(j(y),j (x)),则Rj是X上的模糊完备格同余关系.证明(1)容易验证Rj是L-等价关系.(2)因为∀y∈X,Rj(x,y)=e(j(x),j(y))∧e(j(y),j(x))≤e (y,j(x)),并且所以j(x)=Rj(x,_).因此对任意的x、y∈X,有Rj(Rj(x,_),y)=Rj(j(x),y)=e(jj(x),j(y))∧e(j(z),jj(x))=Rj(x,y).(3)∀x、y、z∈X,e(x,y)∧Rj(x,z)=e(x,y)∧e(j(x),j(z))∧e(j(z),j(x))≤e(j(x),j(y))∧e(j(z),j(x))≤e(j(z),j (y))=e(y,j(y))∧e(z,j(y))≤e(y∨z,j(y))=e(j(y∨z),j (y))=Rj(y,y∨z).由(1)—(3)可见Rj是模糊完备格同余.命题3 设(X,e)是一个模糊完备格,R∈CRL(X),定义映射jR:X→X为:∀x∈X,jR(x)=R(x,_),则jR是模糊闭包算子.证明对任意的x、y、z∈X,有由上知jR是模糊闭包算子.引理1 设(X,e)是模糊完备格,则(1)映射φ:CRL(X)→COL(X)(R jR)保模糊序;(2)映射ψ:COL(X)→CRL(X)(j Rj)保模糊序.证明(1)设R1、R2∈CRL(X),则(2)设j1、j2∈COL(X),则定理1 设(X,e)是模糊完备格,j∈COL(X),R∈CRL(X),则(1)jRj=j;(2)RjR=R.证明(1)由命题2的证明可知∀x∈X,(2)∀x∈X,一方面:另一方面:所以,RjR=R.定理2 设(X,e)是模糊完备格,则COL(X)≅CRL(X).证明由引理1和定理1可以证明.3 模糊完备格同余的商下面引入模糊完备格同余的商概念,并讨论它的有关性质.命题4 设R是模糊完备格(X,e)上的模糊同余关系.记X/R={R(x,_)|x∈X}.定义映射(1)(X/R,eR)是模糊完备格,对于A∈LX/R,其中(2)投射p:X→X/R(x R(x,_))保模糊并.证明(1)易知eR满足(E1)和(E2),下面证明eR满足(E3):设eR(R (x,_),R(y,_))=eR(R(y,_),R(x,_))=1,则jR(x)=jR(y).从而对任意的z∈X,所以eR是模糊序.设A∈LX/R,记R(x,_)),则对任意的z∈X,因此,A=R(a,_).(2)设A∈LX.由于p(A)=R(A,_),pL→(A)=R(a,_),其中为了证明,只需证明R(aA)=1.一方面,由于∀y∈X,A(y)≤e(y,A)≤e(jR(y),jR(A)),因此e(a,jR(A))=1.另一方面,由于∀t∈X,因此,∀x∈X,A(x)≤e(x,R(a,_)).所以,e(A,jR(a))=1.从而,R(a,A)=RjR(a,A)=e(jR(a),jR(A))∧e(jR(A),jR(a))=1.称(X/R,eR)是模糊完备格X模同余关系R的商,简称为同余关系R的商.定理3 设f:X→Y是模糊完备格(X,eX)和(Y,eY)之间保模糊并的满射,则(X/Rf,eRf)≅(Y,eY).证明定义映射φ:X/Rf→Y(Rf(x,_)f(x)),则(1)φ是良定的:若Rf(a,_)=Rf(b,_),则1=Rf(a,b)=eY(f (a),f(b))∧eY(f(b),f(a)),因此f(a)=f(b).(2)φ是满射:由f是满射可知φ是满射.(3)φ是模糊序嵌入:∀a、b∈X,一方面:另一方面:定理4 设j:X→X是模糊完备格(X,e)上的模糊闭包算子,则(j(X),e)≅(X/Rj,eRj).证明定义映射φ:X/Rj→j(X)(Rj(x,_)j(x)),则可验证φ是模糊序同构.4 结语本文给出了模糊完备格同余的概念,并讨论了它与模糊闭包算子的关系.研究了模糊完备格同余的商的性质.这为进一步讨论模糊完备格的其他性质提供了工具.有时人们将模糊偏序集定义在更一般的完备剩余格上,因而当L是完备剩余格时如何恰当地定义模糊完备格同余,以及它的相关应用有待进一步研究.参考文献:[1]Wagner K R.Solving recursive domain equations with enriched categories[D].Pittsburgh:Carnegie-Mellon University,School of Computer Science,1994.[2]Wagner K R.Liminf convergence inΩ-categories[J].Theoretical Computer Science,1997,184(1/2):61-104.[3]Lai Hongliang,Zhang Dexue.Many-valued complete distributivity [DB/OL].(2006-05-12)[2012-01-02].http://arxiv.org/abs/math/0603590.[4]Lai Hongliang,Zhang Dexue.Complete and directed completeΩ-categories[J].Theoretical Computer Science,2007,388(1/3):1-25.[5]赖洪亮.Ω-范畴序结构性质的研究[D].成都:四川大学数学学院,2007.[6]Fan Lei.A new approach to quantitative domain theory[J].Electronic Notes in Theoretical Computer Science 2001,45:77-87.[7]Yao Wei.Quantitative domains via fuzzy sets:Part I:continuity of fuzzy directed complete posets[J].Fuzzy Sets and Systems,2010,161(7):983-987.[8]Zhang Qiye,Fan Lei.Continuity in quantitative domains [J].Fuzzy Sets and Systems,2005,154(1):118-131.[9]樊磊.Domain理论中若干问题的研究[D].北京:首都师范大学数学科学学院,2001.[10]Zhang Qiye,Xie Weixian,Fan Lei.Fuzzy complete lattices [J].Fuzzy Sets and Systems,2009,160(16):2275-2291.[11]Bělohláve k R.Fuzzy relational systems:Foundations and principles [M].New York:Kluwer Academic Publishers,Plenum Publishers,2002:203-213.[12]郑崇友,樊磊,崔宏斌.Frame与连续格[M].北京:首都师范大学出版社,1994:84-91.[13]Yao Wei,Lu Lingxia.Fuzzy Galois connections on fuzzy posets [J].Mathematical Logic Quarterly,2009,55(1):105-112.[14]Guo Lankun,Zhang Guoqiang,Li Qingguo.Fuzzy closure systems on L-ordered sets[J].Mathematical Logic Quarterly,2011,57(3):281-291.。
【国家自然科学基金】_模糊算子_基金支持热词逐年推荐_【万方软件创新助手】_20140801

科研热词 直觉模糊集 模糊控制器 蕴涵算子 模糊逻辑 非线性规划 边缘检测 粗糙集 模糊集 模糊推理 模糊划分 集合 逻辑代数 近似算子 自适应 聚类算法 综合评价 直觉模糊数 熵权 泛逼近性 模糊物元 模糊层次分析法 模糊 梯形模糊数 格 插值式 学习算法 多目标规划 多属性决策 三角模 三i算法 r0-代数 鲁棒性 高木-关野模糊模型 非线性逼近 集结算子 集结 隶属度 阶跃型边缘 闭包 进化算法 近似空间 运动目标检测 运动参数估计 边缘增强 轮廓提取 跟踪 超分辨率重构 诱导梯形模糊有序加权平均算子 误差预测 语义web 设计方案 记忆克隆
107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160
计算智能 观测模型 覆盖 范畴嵌入 范畴同构 自重构 自定义数据类型 自学习算法 群决策 网络安全 网格计算 缺陷模型 结构元素 级别特征值 粒计算 类近似算子 管理域 算子分裂 稳定性 神经元模型 知识化制造系统 相对 相位中心偏置天线 直觉模糊集合 直觉模糊蕴涵算子 直觉模糊奇异集合 直觉模糊关系 直觉模糊值测度 直觉模糊值sugeno积分 直觉模糊s-粗集 直方图 目标规划模型 电热老化 理想点 理想格 混沌优化 浮游植物 油纸绝缘 水质评价 水平集 正则化 模糊集合 模糊逻辑控制 模糊赋值 模糊识别 模糊规划 模糊覆盖 模糊蕴涵算子 模糊蕴涵 模糊聚类 模糊联想记忆网络 模糊综 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106
完备格上正则蕴涵算子的研究

完备格上正则蕴涵算子的研究李艳【期刊名称】《西北大学学报(自然科学版)》【年(卷),期】2011(041)004【摘要】Aim Generalizing the regular implications to completed lattice. Methods The concept and the basic properties are used to study. Results The properties of the regular implications on completed lattice are studied. Meanwhile the relationships between the regular implications and some important logic algebras are studied. Conclusion Because of the close relations, the regular implication is the key point for studying logic algebras.%目的将正则蕴涵算子的概念推广到完备格上.方法利用定义及基本性质.结果研究了完备格上正则蕴涵算子的性质以及与一些重要的逻辑代数之间的关系.结论完备格上的正则蕴涵算子与逻辑代数关系密切,是研究逻辑代数的基础.【总页数】4页(P569-571,576)【作者】李艳【作者单位】陕西职业技术学院基础课部,陕西西安710100【正文语种】中文【中图分类】O141.1【相关文献】1.完备格上伪t-模与蕴涵算子的限制和诱导 [J], 廖大见;刘才贵;乔庆荣;翟余华2.完备格上的拟t-模与蕴涵算子 [J], 廖大见3.完备格上的拟-t-模及蕴涵算子的直积和直积分解 [J], 翟余华;廖大见4.基于蕴涵算子上的模糊强正则子半群 [J], 姜雪;廖祖华;刘春芝;曹姝;张扬5.完备格Brouwer上伪t-模与蕴涵算子的注记(II)(英文) [J], 王住登因版权原因,仅展示原文概要,查看原文内容请购买。
【国家自然科学基金】_模糊同余关系_基金支持热词逐年推荐_【万方软件创新助手】_20140802
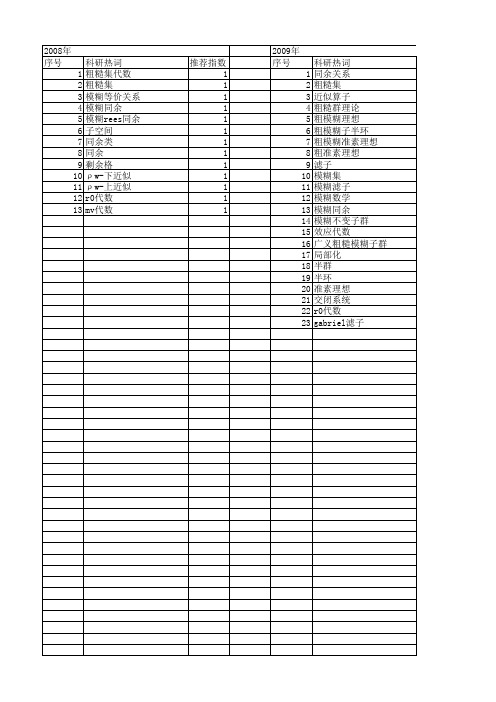
科研热词 同余关系 粗糙集 近似算子 粗糙群理论 粗模糊理想 粗模糊子半环 粗模糊准素理想 粗准素理想 滤子 模糊集 模糊滤子 模糊数学 模糊同余 模糊不变子群 效应代数 广义粗糙模糊子群 局部化 半群 半环 准素理想 交闭系统 r0代数 gabriel滤子
推荐指数 3 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
科研热词 同态 蕴涵理想 模糊逻辑 商代数 同余 粗糙集 滤子 模糊闭包算子 模糊滤子 模糊完备格同余 模糊完备格 模糊同余关系 模糊偏序集 概率转移矩阵 概率有限状态自动机 同构 剩余格 伪准相等 交换 wbro-代数 wbr0-代数 swbro-代数 swbr0-代数 mtl-代数 leibniz代数
2012年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
科研热词 模糊滤子 格 素理想 粗素理想 粗糙模糊子格 滤子 模糊子格 模糊同余关系 模糊关系同态 极大理想 效应代数 同余关系 同余 fi代数
推荐指数 2 2 1 1 1 1 1 1 1 1 1 1 1 1
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
2010年 序号 1 2 3 4 5 6 7
科研热词 同余 模糊强φ -同余对 模糊强φ -同余 模糊强(p)-同余对 模糊强(p)-同余 φ -反演半群 (p)-反演半群
推荐指数 2 1 1 1 1 1 1
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
2011年 科研热词 模糊理想 模糊滤子 模糊子坡代数 模糊同余关系 蕴涵格 素滤子定理 等价刻画 直觉模糊有限自动机 直觉模糊变换半群 模糊逻辑 模糊等价关系 拓扑范畴 子完备格 同构 同态 同余关系 剩余格 t-模糊滤子 t-模糊同余 s-滤子 mp-滤子 mp*-滤子 推荐指数 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
L-偏序集上闭包算子和内部算子的等价刻画

可 以看作 文 献 13 - 中所 研究 的 闭 包 系统 和 内部 系统 5
的简 化 和推 广.结 果 表 明 , ,偏 序集 上 的 L 一闭包 工
当且 仅 当 ≤ Y— .
L 一系统 ( L 一内部 L 一系统 ) L 一 和 闭包 算子 ( x L 一内 部 算 子 ) 间存 在 一一 对应 关 系. 之
第 38 卷 第 8期
2 1 0 1 年 8 月
湖
南 大 学 学
报 (自 然 科 学 版 )
Vo . 8 NO 8 13 , .
A u . 2 1 g 0 1
J u n lo n n Un v r iy Na u a ce c s o r a f Hu a i e st ( t r l in e ) S
闭包 算 子 和 闭包 系统在 许 多数 学分 支 中起着 重
要作 用 .经 典偏 序 集上 的闭包算 子 和 闭包 系统 已被
1 LK 一闭包 算 子 和 LK 一内部 算 子
本文 取 完 备 剩 余 格 为 真 值 结 构.称 L 一 ( L, ^,V, , , ,)为一 个完 备剩 余 格 ,如 果 满足 o 一 01
文 章 编 号 :6 42 7 (0 1 0—0 60 1 7—9 4 2 1 )80 7—3
工 厂偏 序 集 上 闭 包 算 子 和 内 部 算 子 的 等 价 刻 画
郭兰坤 , 庆 国 李
( 南 大学 数 学 与 计 量 经 济 学 院 , 南 长 沙 湖 湖 408) 1 0 2
十 讯 联 系 人 , - i l ig u l a o .on c 通 E mal in g oi lq @y h o c r.n
基于9种常用蕴涵算子上的模糊强正则子半群

基于9种常用蕴涵算子上的模糊强正则子半群模糊强正则子半群是一种基于蕴涵算子的集合。
它由一系列的模糊子半群组成,它们根据正则正规语言的一些性质,通过强正则的结构,形成了一种新的集合结构。
1、谓语蕴涵算子它表示x隶属于Y,也叫属性蕴涵算子,运用论证来表述。
2、范畴蕴涵算子它代表两个元素之间关系,是类论证的基本结构。
3、逆蕴涵算子它表示一个集合,它的逆运算与蕴涵相对,表达一个事实,即不满足蕴涵算子的元素都在集合内。
4、交蕴涵算子它在论证中扮演着一种因素的联系作用,把不同的因素归结为一类。
5、和蕴涵算子它把具有不同属性的元素联系起来,组成一个具有规律性的集合。
6、联结蕴涵算子它表示一个集合内元素与另一个集合内元素之间的关系,即两个集合之间的连接关系。
7、否定蕴涵算子它实际上是一个简单的否定,表示被蕴涵元素A不属于蕴涵元素B。
8、超蕴涵算子它表示元素A是元素B的超集,即元素A包含了元素B,并且元素A还包含其他元素。
9、集合蕴涵算子它指明一个集合A是另一个集合B的子集,这样,在集合B中没有元素与集合A中有元素相互可比性。
由以上九种蕴涵算子组成的模糊强正则子半群具有一定的性质。
首先,他们具有单调性,这意味着某一性质的变化会影响另一性质,因此可以通过增加或减少某一元素来改变子半群的整体性质。
其次,他们具有分层性和重叠性,这意味着子半群中的元素可以划分成不同的层,而每一层可以由不同取值的多个元素组成,因此可以调节所有元素的属性。
最后,他们具有稳定性,因此只有当系统的一部分发生变化时,系统的整体性质才会发生变化。
模糊强正则子半群的优越性在于他们可以以较弱的整体性质来应对不同的行为变化,同时他们可以运用于不同的应用领域,即研究者使用这种结构来描述和处理不同的系统行为、方法和技术,并进行有效的系统研究,从而探索出更好的结构和解决方案。
同时,此种结构能够有效地识别出系统之间的连接关系,并能够以可控制的方式进行变化,从而更好地支持其他系统的发展,可以在智能化系统领域中得以应用。
偏序集拟阵间的PO映射和开映射

逆 序对 合 对应. 于任意 对
P, 记 = { ) ( I
0 引言
拟 阵是 图 、 阵 、 矩 向量 相 关 关 系 等 概 念 的抽
∈X} 同时将 “ ( 和 ( )看 作是 同义 的 )
如 果没有 特 别说 明 , 文所 提及 的偏 序集 均 该
象 和推 广 , 组合 优化 、 数规 划 、 在 整 网络 流及 电网 理论 中有着 广 泛 的应 用 . 目前 为 止 , 阵 的 概 到 拟
1 预 备 知 识
定 义 11 . 设 ( ≤) 偏序 集. : 尸 P, 是 P一 是 P到 自身 的映射 , 如果 是 对 合对 应 ( 即对 于 任意 的 a∈ P, ( ) = a ( a ) )且 是 逆 序 对 应
收稿 日期 :0 1—0 21 9—1 8 ¥陕 西 省教 育 厅专 项 科 研 计 划项 目( J 0 8 ) 1 44 iK
y, )存在 B 使得 B ∈ 则称 是 P 上 的偏 序集 拟阵基 族 , 中的成员 叫偏 序集拟 阵
基. P上 的偏序 集 拟阵基 族 的全体 记作 B P) 该 ( . 文用 M = ( )来记 J 的一个偏 序集 拟 阵. P, P上
( )设 P是 有 限 偏 序 集 , ,c F lP)一 2 若 i ( { j 满足 : (} 2 (1 , ( i P) )中的下集 . I) 是 Fl , ( (2 1 )若 X, Y∈, I l<I , , 存在 Y∈ 且 l则 l
射 , 论 了它 与 已有 偏 序 集 拟 阵 间映 射 的关 系 , 讨 最后 指 出 了它在这 种 映射 下 的几种 不 变 性 等 , 这
些结果 为 进一 步 研 究 偏 序 集 拟 阵 的范 畴性 质 奠
【国家自然科学基金】_完备格_基金支持热词逐年推荐_【万方软件创新助手】_20140730
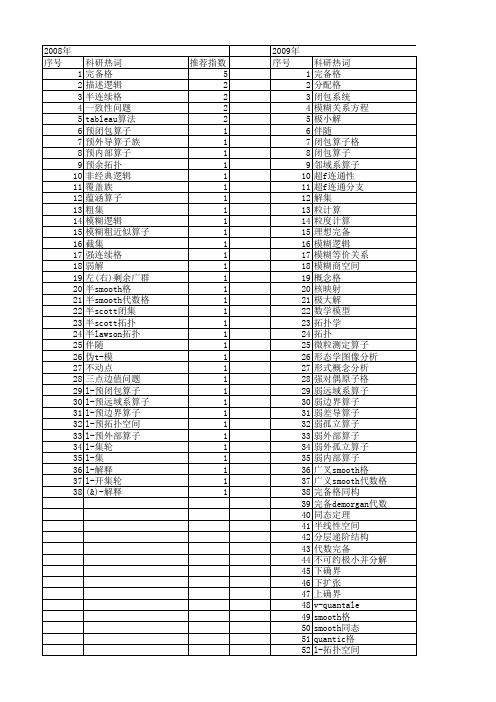
科研热词 完备格 quantale 滤子 拓扑范畴 基 同余 半连续格 预girard quantale 闭映射 闭包算子 连续映射 超因子元 超因子 蕴涵 网 线性逻辑 算法 算子 笛卡儿闭 稠密子集 特征 模糊滤子 权 有补模格 最小实现化 拟一致结构 形式概念分析 弱闭包算子 弱远域算子 弱边界算子 弱拓扑分子格 弱外部算子 弱内部算子 弱余拓扑 弱n-导算子确定 开映射 序收敛格 序拓扑 序半群 局部核映射 局部半基 对偶同构 完备de morgan代数 子基 子quantale 套代数 变精度概念 取值于完备格的同步机 反蕴涵 反heyting代数 双侧核映射 半素理想
2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38
科研热词 完备格 描述逻辑 半连续格 一致性问题 tableau算法 预闭包算子 预外导算子族 预内部算子 预余拓扑 非经典逻辑 覆盖族 蕴涵算子 粗集 模糊逻辑 模糊粗近似算子 截集 强连续格 弱解 左(右)剩余广群 半smooth格 半smooth代数格 半scott闭集 半scott拓扑 半lawson拓扑 伴随 伪t-模 不动点 三点边值问题 l-预闭包算子 l-预远域系算子 l-预边界算子 l-预拓扑空间 l-预外部算子 l-集轮 l-集 l-解释 l-开集轮 (&)-解释
53 coframe
推荐指数 8 3 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
泛函分析知识点总结

泛函分析知识点总结1.Baire定理定理(Baire纲定理)完备的距离空间是第⼆类型集。
解释:完备的距离空间(X,d),∀x∈X都是内点,因为X在X中是开集。
⼀个⽆处稠密(nowhere dense)的集合就是闭包不含内点的集合不会是整个X,即X不是第⼀类型集,所以只能是第⼆类型集。
注:完备的距离空间是第⼆类型集,那么它的闭包⾄少存在⼀个内点。
这个经常被⽤来证明。
例如,开映射定理、闭图像定理等。
2. 闭包和导集的区别根据定义,集合的闭包是集合的导集和集合的并。
导集是集合所有聚点组成的集合,不包含孤⽴点。
所以闭包是集合导集和孤⽴点组成的集合。
3.闭集在度量空间中,如果⼀个集合所有的极限点都是这个集合中的点,那么这个集合是闭集。
4.不动点定理压缩映射:设(X,d)是距离空间,T是X到X的映射,如果存在⼀个常数θ(0≤θ<1),对于所有的x,y∈X,满⾜下述不等式:d(Tx,Ty)<θd(x,y)则称T是X上的⼀个压缩映射。
不动点定理:设X是完备的距离空间,T是X到X的压缩映射,则T在X上有唯⼀的不动点x∗.即Tx∗=x∗是⽅程Tx=x在X上的唯⼀解。
5.施密特正交化将⼀个线性⽆关的集合{x n}进⾏施密特正交化。
e1=x1 ||x1||e2=x2−<x2,e1>e1 ||x2−<x2,e1>e1||e j+1=x j+1−j∑k=1<x j+1,e k>e k ||x j+1−j∑k=1<x j+1,e k>e k||注:本质上说就是让x j+1减去其在e k,k=0,…,j上的分量,就正交化了。
然后再除以对应范数,进⾏单位化。
6.Hilbert空间的同构n为的实(复)Hilbert空间与R n(C n)同构。
(保距离,保线性,保范数,保内积)⽆限维可分Hilbert空间与l2空间(L2[0,1])等距同构。
7.算⼦的连续性和有界性连续性:对于X中的任何收敛于x0的点列{x n},恒有Tx n→Tx0,n→=∞有界性:存在正常数M,使得对⼀切x∈X,有||Tx||≤M||x||⼀点连续,则处处连续:设X和Y是数域\textbf{F}上的线性赋范空间,T:X→Y是⼀个线性算⼦。
蕴涵算子族及其应用

TP 0 31
中 图法 分 a i n Ope a o s a e r App i a i n m le f I lc to r t r nd Th i lc to
orr d e。 。 R 『,) veutr dt ui p tRa。rr i ——。∈ 1 hesan s i r l eo 2 p tRn a n a L ( 1 ardlo a ss e a 7 i m n af g r - y —
t . C n e u n l t i WO o e a o s a e i e 1 Fi a l t e a p ia i n f L — — R。( ∈ y o s q e ty, h s t p r t r r d a . nl y, h p l t s o c o
iu — R [ ]wmndur ly R ‘,)d ndi 。 丢 ) eayssgr 。 ——。∈丢1 a n — ( . i c ui f ld L ∈ lisea L t ( [ ]n
trd 。 ——。∈ 1 w £r.hetdtt 。 kic heuf R 『,)ii一m T uicsanLawz esa i L ( 1 tt n s es ieh lus i 7 hs 。 r I a t y e n
第3 O卷
第 3期
计
算
机
学
报
维普资讯
Vo .3 NO I O .3
M a. 2 7 r 00
20 0 7年 3 月
CHI NES J E 0URNA L OF COM PUTERS
完备Brouwerlan格上有限@-Fuzzy关系方程有解的一个充要条件

完备Brouwerlan格上有限@-Fuzzy关系方程有解的一个充
要条件
王学平;李裕梅
【期刊名称】《工程数学学报》
【年(卷),期】2004(021)004
【摘要】本文在论域为有限集时讨论了完备Brouwerian格上@-Fuzzy关系方程(其中@表示inf-α合成),给出了@-Fuzzy关系方程有解的一个充要条件并构造出了方程的极大解,进一步确定了方程的解集.
【总页数】7页(P602-608)
【作者】王学平;李裕梅
【作者单位】四川师范大学数学与软件科学学院,成都,610066;四川师范大学数学与软件科学学院,成都,610066
【正文语种】中文
【中图分类】O159
【相关文献】
1.完备Brouwerian格上@-Fuzzy关系方程极大解的性质 [J], 夏嫦;蒲松
2.完备Brouwerian格上@-Fuzzy关系方程有唯一解的判别法 [J], 夏嫦
3.完备格上Fuzzy关系方程的解是极小元的一个充要条件 [J], 王学平
4.完备Brouwer格上有限sup-inf合成Fuzzy关系方程解集的一些性质 [J], 舒乾宇;夏嫦;王学平
5.完备Brouwerian格上Fuzzy关系方程极小解存在的一个充分条件 [J], 王学平;张三华;冯山
因版权原因,仅展示原文概要,查看原文内容请购买。
完备剩余格中的全蕴涵推理方法

完备剩余格中的全蕴涵推理方法
吴洪博;邵晓丽
【期刊名称】《数学进展》
【年(卷),期】2006(35)3
【摘要】三Ⅰ算法是王国俊教授提出的一种模糊推理方法,较之模糊控制理论中广泛采用的CRI算法更具有严谨性、合理性.本文在完备剩余格中给出了模糊推理RL-型全蕴涵α-MIFMP,α-MIFMT规则,并讨论了完备剩余格中的RL-型全蕴涵α-MI算法,得到了完备剩余格中RL-型全蕴涵α-MIFMP,α-MIFMT的计算公式,并将之应用于G(o)del逻辑系统,Lukasiewicz逻辑系统,Goguen逻辑系统和(-W)逻辑系统.特别是将结果应用于(-W)逻辑系统中得到了R0-型全蕴涵α-三Ⅰ算法计算公式,简化了原有的R0-型三Ⅰ算法的证明.
【总页数】12页(P303-314)
【作者】吴洪博;邵晓丽
【作者单位】陕西师范大学数学研究所,西安,陕西,710062;陕西师范大学数学研究所,西安,陕西,710062
【正文语种】中文
【中图分类】O141.1
【相关文献】
1.完备格上的伪t-模与剩余蕴涵的直积和直积分解 [J], 廖大见
2.完备剩余格上的蕴涵闭包算子 [J], 于海;詹婉荣
3.完备剩余格上的蕴涵闭包系统 [J], 于海;詹婉荣
4.完备剩余格中的上近似与下近似模糊推理方法 [J], 刘鹏惠;陈子春;秦克云
5.基于完备BR_0-代数的全蕴涵三I算法 [J], 吴洪博;王国俊;于鸿丽
因版权原因,仅展示原文概要,查看原文内容请购买。
完备剩余格上的蕴涵闭包算子

摘
要 : 用 蕴 涵 运 算 , 完备 剩 余 格 上 定 义 了 蕴 涵 闭 包 算子 , 出 了它 的 若 干等 价 刻 画及 其表 示 定 理 。 利 在 给
关键词 : 余格 ; 剩 完备 剩 余格 ; 包 算子 ; 涵 闭 包算 子 闭 蕴 DO :03 7 /i n1 0 —3 1 0 0 80 4 文章 编 号 :0 28 3 (0 0 2 —0 90 文献 标识 码 : 中 图 分 类 号 : 4 I1 .7 8 .s . 28 3 . 1 . .1 js 0 2 2 10 —3 1 2 1 )80 4 —2 A O1 1
Ema :u a 0 0 1 6cm — iyhi 0@ 2 . l 2 o
YU H ai ,ZHA N W a r ng.m plc i c o ur ope a or Ol o plt r sdua e n- o I iatve l s e r t s i c m ee e i t d l ti e . a tc sCom put r e Eng ne rng nd A p- i e i a
洛阳师范学院 数学科学学院 , 河南 洛 阳 4 12 702
Co l e leg of M ahe ai s n t m tc a d Sce e, oy ng inc Lu a Nor a Cole e, m l l g Luo ng, e n 71 2, ya H na 4 02 Chi na
p iai n , 0 0, 6 2 :9 5 . l t s 2 1 4 ( 8) 4 — 0 c o
A bsr t By m e ns f m plc to op r ton,m plc tve l s r o e ao s r d fn d o t ac : a o i i ai n eai i i a i c o u e p r t r a e e e i n c plt r sd td l tiesSom e om e e e iua e atc . e ui lnt ha a trz to a t r p e e ai t e r m a e i n. q va e c r ce i ai ns nd he e r s ntton h o e r g ve K e wor y ds: r sd td atc c m pl t e i ua e l ti e; l s r o r t r i plc tv cos e e i uae l tie; o ee r sd td atc c o u e pe a o ;m i ai e l ur op r t r e ao
原子闭包系统, 原子闭包算子和原子全蕴含系统

: A ⊆ F}。
2. 有限原子格的表示定理
本节我们讨论一个特殊的有限格的表示,即有限原子格的表示。 定义 3.1 在集合 S 上的原子闭包系统 (1) S ∈ ; (2) F1 , F2 ∈ 是一个集合系统并且满足下列条件:
⇒ F1 ∩ F2 ∈ ;
。 。实际上, ( , ∩) 是一个包含 S 的原子格,这就
0. 引言
在有限集合 S 上的闭包系统 的映射。 由 Caspard[1]和 Monjardet[6]知,当集合 S 是有限集时,闭包系统和闭包算子是一一对应 的,并且任一闭包系统 都是一个有限格,同时由 Monjarder[3]知,任一有限格都可以由一 个闭包系统表示。 那么对于有限原子格, 它所对应的闭包系统和闭包算子如何来刻画?在有 限集 S 上所有的闭包算子又有什么好的性质呢?这就是本文所讨论的。 同时本文还研究了原 子闭包算子和原子全蕴含系统之间的关系, 并讨论了有限原子格所生成的范畴和原子闭包系 统所生成的范畴之间的关系。 是 2 的一个子集并且满足有限交和 S ∈
2
命题 2.5 ([1])设 θ 是一闭包算子,那么
θ
:= {F ⊆ S : θ ( F ) = F } 是一闭包系统,并且
F1 ∧ F2 = F1 ∩ F2 , F1 ∨ F2 = θ ( F1 ∪ F2 ) 。
反之,给定 S 上的一闭包系统 ,存在一闭包算子 θ 并且 θ ( A) := ∩{F ∈
θ1 ≤ θ 2 当且仅当 θ1 ( X ) ⊆ θ 2 ( X ) (其中 X 为 S 中的任一子集) ,则, (θ K , ≤) 一个余原子格,
并且设 θi (i = 1, 2) 所对应的原子闭包系统分别为 证明:显然 (θ K , ≤) 是一个偏序集且是一个格。 设
多值置信的格值闭包算子及Galois联络

多值置信的格值闭包算子及Galois联络
方进明;张虎;褚晓清
【期刊名称】《中国海洋大学学报(自然科学版)》
【年(卷),期】2013(043)001
【摘要】在多值逻辑的环境下,为进一步完善格值闭包理论的置信化问题,提出多值置信滤子的概念和实例.以多值置信滤子为工具界定了置信格值闭包算子和置信格值Galois联络的概念,并得到它们的等价刻画条件.结果表明:多值置信滤子是十分有用的置信推理工具,其不但可以解决格值闭包算子的置信化问题,而且可以描述置信格值Galois联络现象.
【总页数】4页(P98-101)
【作者】方进明;张虎;褚晓清
【作者单位】中国海洋大学数学科学学院,山东青岛266100;中国海洋大学数学科学学院,山东青岛266100;中国海洋大学数学科学学院,山东青岛266100
【正文语种】中文
【中图分类】O189.13
【相关文献】
1.完备剩余格上的蕴涵闭包算子 [J], 于海;詹婉荣
2.格序群扭类与半单类之间的Galois联络 [J], 杨胜良
3.Banach空间中多值线性算子的集值度量广义逆 [J], 刘宏丽;王玉文
4.基于L*-格值逻辑上的直觉 I-fuzzy拓扑空间闭包及网收敛理论 [J], 张春芝;王瑞
英;姚尧
5.有限格,闭包系统和闭包算子 [J], 何霞辉;李庆国
因版权原因,仅展示原文概要,查看原文内容请购买。
2013-2014-2学年度 《泛函分析》期末试题1

大庆师范学院2013——2014学年第二学期《泛函分析》期末考试试卷院: 专业: 班级: 姓名: 学号:----------------------------------------------------------------------------------------------------------------------------------------- --------------------------------------装-----------------------------订---------------------------线----------------------------------大庆师范学院2011级数学与应用数学专业《泛函分析》期末考试试卷题号 一 二 三 四 五 总分 核分人得分--------------------------------------------一、填空题(每空1分,共5分)1.如果度量空间X 有一个可数的稠密子集,则称X 是可分空间. 2.离散度量空间X 可分的充要条件是X 是可数集. 3.'l 的共轭空间是 .4.当Y 是巴拿赫空间时,)(Y X →B 是 . 5.完备的度量空间上的 有唯一的不动点.二、单项选择题(每小题1分,共5分)1.设111(,)P x y ,222(,)P x y 是平面2R 上任意两点,则下列关系d 不是2R 上距离的为 ( ) A .22121212,)()()(P x x y y d P =-+- B .{}121212,)max ||,||(P x x y y d P =--C .2121212,)()(P x x y y d P =-+-D .121212||,)1||(x x P x x d P -=+-2.下列度量空间不是可分空间的有 ( )A .R nB .[,]C a b C .l ∞D .(0)p L p <<∞3.(2R )中,按下列定义不能构成赋范线性空间的有 ( )A .22y x P +=()2R y x P ∈⋅= B .y x P +=C .}{y x P ⋅=max D .xx P +=1三、判断题(每小题1分,共10分)1.完备度量空间的闭子空间是完备子空间. ( ) 2.离散度量空间是完备的度量空间. ( ) 3.有限维赋范线性空间都是巴拿赫空间. ( ) 4.赋范空间有限维子空间都是完备的. ( ) 5.(1)Ln i +1ln 2(2),0,1,2,24i k k ππ=++=±±L L .( )四、计算题( 共70分 )1.设)(31132R x x T x ∈∀⎥⎦⎤⎢⎣⎡=为2R 上算子,求T .得分 阅卷人得分 阅卷人得分 阅卷人得分 阅卷人。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
别是最小元和最大元。如果 L 上还有两个二元运算 ⊗ 和
基金项目: 河南省基础与前沿研究计划项目 (No.082300410270) ; 河南省教育厅自然科学基金资助项目 (No.2009A520019) 。 作者简介: 于海 (1979-) , 男, 助教, 研究领域: 不确定性推理和粗糙集理论; 詹婉荣 (1981-) , 女, 助教, 研究领域: 不确定性推理和粗糙集理论。 收稿日期: 2009-06-22 修回日期: 2009-08-03
C ( y) Ú y = x Ú y ® C ( y) £ C ( x Ú y) ® C (C ( y)) = C ( x Ú y) ® C ( y) 。
可知定理成立。证毕。 以上是从公理化形式给出蕴涵闭包算子的定义及其刻 画。下面给出蕴涵闭包算子的具体构造, 即下述的蕴涵闭包 算子的表示定理。 当存在集合 X = {zi Î L| i Î I } , 使得 定理 4 (表示定理) 映射 C:L ® L 是蕴涵闭包算子当且仅
C ( x ⊗ y ) 。证毕。
( x ® zi ) ⊗ (( x ® zi ) ® zi ) £ zi 由此可知 ( x ® y ) ⊗ (( x ® zi ) ® zi ) £ ( y ® zi ) ® zi 所以
iÎI
Ù
(( x ® y ) ⊗ (( x ® z ) ® z )) £ Ù (( y ® z ) ® z ) = C ( y )
*
(C*4)C ( x ) ⊗ C ( y ) £ C ( x ⊗ y ) 。
{
}
(C5)C ( x ® y ) £ C ( x ) ® C ( y ) 。 证明 连续利用两次 ( C4 ) , 得 C ( x ) ⊗ C ( y ) £ C ( x ⊗ C ( y )) £
C C ( x ⊗ y ) = C ( x ⊗ y ) 。 即(C*4)成 立 。 则 由(C*4)可 知 C ( x ) ⊗ C ( x ® y ) £ C ( x ⊗ ( x ® y )) £ C ( y ) C ( x ® y ) £ C ( x ) ® C ( y ) 。证毕。
(
)
定理 3 映射 C:L ® L 是蕴涵闭包算子当且仅当 C 满足 (C1)、 (C2)、 (C3)和(C*4)当 且 仅 当 C 满 足(C1)、 (C3)和 (C5) 。 证明 由定义 3、 定理 2 以及命题 3 可知, 只需证明 (C*4)Þ (C4) , (C5)Þ(C*2) 。事实上, 由
y ) £ iÙ ( x ⊗ yi) 。 (P9)x ⊗ (i Ù ÎI i ÎI
1
预备知识
定义 1[1] 设 L 是完备格,J:L ® L 是映射。如果对一切
x y Î L 以下条件成立:
(C1) 增值性:x £ J ( x ) 。 (C2) 保序性: 当 x £ y 时,J ( x ) £ J ( y ) 。 (C3) 幂等性:J ( J ( x)) = J ( x) 。 那么称 J 为 L 上的闭包算子。 定义 2
关键词: 剩余格; 完备剩余格; 闭包算子; 蕴涵闭包算子 DOI: 10.3778/j.issn.1002-8331.2010.28.014
20 世纪 40 年代以来, 序结构上的闭包算子得到了深入的 研究。偏序集上的闭包算子是基本的, 同时也是重要的概 念。尤其是定义在幂集格 ( P( X ) Í ) 上的闭包算子, 在很多领 域中都扮演着非常重要的角色, 如: 代数、 拓扑、 逻辑以及计算 机科学等。文献[1]系统地研究了完备格 L 上的闭包算子与闭 包系统, 并且很好地应用到逻辑学之中, 形成了完备格上的逻 辑学。而剩余格是与非经典逻辑, 特别是模糊逻辑密切相关 的代数结构, 是研究模糊逻辑的重要工具。比如, 近年来出现 的模糊逻辑形式系统 L 、 BL、 MTL 等均与特殊的剩余格相关 联。可以说剩余格已经成为模糊逻辑中相当理想的代数框 架。同时, 剩余格既具有代数结构又具有序结构, 因而成为多 个数学分支的研究课题。与格相比, 剩余格多了两个二元运 算⊗和®, 也就是说剩余格上的结构比格上的结构更为丰 富、 复杂。因此, 有必要研究剩余格上的闭包算子, 利用剩余 格上的蕴涵运算, 研究完备剩余格上的蕴涵闭包算子。
即 (C*2) 成立。在 (C*3) 中, 令 x = C ( y) , 有 C (C ( y )) £ C ( y ) 。 又 C (C ( y )) ³ C ( y ) , 所以 (C3) 成立。证毕。 接着, 给出蕴涵闭包算子的一个重要性质。 (C4)x ⊗ C ( y ) £ C ( x ⊗ y ) "x y Î L 。 命题 2 设 C:L ® L 是蕴涵闭包算子, 则 C 满足: 证明 由 (C1) 有 x ⊗ y £ C ( x ⊗ y) , 又由 (C*2) 和 (C3) 可 得 , x £ y ® C ( x ⊗ y) £ C ( y) ® C ( x ⊗ y) , 所 以 x ⊗ C ( y) £
x ⊗ C ( y) £ C ( x) ⊗ C ( y) £ C ( x ⊗ y) x ® y £ C ( x ® y) £ C ( x) ® C ( y)
下面给出蕴涵闭包算子的一个等价刻画。首先证明一个 引理。 引理 1 设 C:L ® L 是闭包算子, 则下面三个性质等价: (1)x ® y £ C ( x) ® C ( y) 。 (2)x ® C ( y) £ C ( x Ú y) ® C ( y) 。 (3)x ® C ( y) £ C ( x) ® C ( y) 。 证明 (1)Þ(2) 。由 (P7) 和 (1) 可知 x ® C ( y) £ x Ú y ®
C ( y) , 又由 (C1) 和 (P4) 可 知 x ® y £ x ® C ( y ) £ C ( x) ® C ( y ) ,
所以 x £ i Ù 即 x £ C ( x) 。 (C1) 成立。 ( x ® zi ) ® zi , ÎI ② "i Î I , 由 (P5) 得
(
)
( x ® y ) ⊗ (( x ® zi ) ® zi ) ⊗ ( y ® zi ) £
[2-4]
2
蕴涵闭包算子
若无特别说明, 以下 L 均为完备剩余格。 定义 3 设 C:L ® L 是映射, 若对任意 x y Î L 都有 (C1)x £ C ( x) ; (C*2)x ® y £ C ( x) ® C ( y) ;
设 ( L Ú Ù 0 1) 是一个有界格, 其中 0 和 1 分
50
2010, 46 (28) (C3)C (C ( x)) = C ( x) 。
Computer Engineering and Applications 计算机工程与应用 命题 3 设映射 C:L ® L 是蕴涵闭包算子, 则 C 满足:
则称 C 为 L 上的蕴涵闭包算子。 注 1 容易证明由 (C 2) 可以推出 (C2) , 所以蕴涵闭包算子 一定是闭包算子。但反之不成立, 例 如 取 L = 0, 1 , 3 ,1 , 4 4
C ( x) ® C ( y) 。证毕。
(
)
证明 (1) 充分性。假设 X = {zi Î L| i Î I } 已给定。证明由
C ( x) = i Ù ( x ® ® 的伴随性可知, 引理 1 中的 (3) 等价于 (C 3) ( x ® C ( y)) ⊗ C ( x) £ C ( y)
" x Î L C ( x ) = i Ù ( x ® zi ) ® zi ÎI
(2)Þ(3) 。由 (2) 、 (C2) 和 (P4) , 得 x ® C ( y) £ C ( x Ú y) ®
C ( y ) £ C ( x) ® C ( y ) 。
(3)Þ(1) 。由 (C1) 、 (P4) 和 (3) , 得 x ® y £ x ® C ( y) £
⊗ ® 分别为 Lukasiewicz 三角模和蕴涵算子。设 f (0) = 0 f ( 1 ) = 3 f ( 3 ) = 3 f (1) = 1 4 4 4 4 容易验证 f 为 L 上的闭包算子, 但不是蕴涵闭包算子。因为 1 ® 0 = 3 而 4 4 1 f ( ) ® f (0) = 1 4 4 * 不满足 (C 2) 。
*
(
)
定义的映射 C 是蕴涵闭包算子。 ①由 (P2) 可知,
" i Î I x £ ( x ® z i ) ® z i
定理 1 映射 C:L ® L 为蕴涵闭包算子当且仅当 C 满足 (C1) 和 (C*3) 。 证明 由定义 3 和引理 1 可知, 只需证明由 (C1) 和 (C*3) 能 推出 (C*2) 和 (C3) 。 事实上, 对任意 x y Î L , 由 (C*3) 可得 x ® C ( y) £ C ( x) ®
*
®, 且满足:
(1)( L ⊗ 1) 是以 1 为单位元的交换半群, 即 ⊗ 满足交 换律和结合律且 1 ⊗ x = x "x Î L ; (2)(⊗ ® ) 是伴随对, 即 x ⊗ y £ z 当且仅当 x £ y ® z ,
" x y z Î L 。
则称 ( L Ú Ù ⊗ ® 0 1) 为一个剩余格。 若剩余格 L 同时是完备格, 则 L 为完备剩余格。 命题 1[2-4] 设 ( L Ú Ù ⊗ ® 0 1) 是一个完备剩余格, 则 " x y z Î L , 有 (P1)x £ y 当且仅当 x ® y = 1 ; (P2)x = 1 ® x x ® ( y ® x) = 1 ,y £ ( y ® x) ® x ; (P3)x £ y ® z 当且仅当 y £ x ® z ; (P4) 若 x£y , 则 z ® x £ z ® y ,y ® z £ x ® z ; (P5)( x ® y) ⊗ ( y ® z) £ x ® z ; (P6) 若 x£y , 则 x⊗z£y⊗z ; (P7)x ® y £ ( x Ú z) ® ( y Ú z) ; (P8)(( x ® y) ® y) ® y = x ® y ;
