模拟高通、带通滤波器设计
模拟信号滤波器设计

模拟信号滤波器设计模拟信号在现代电子技术中占据着重要的地位,然而在很多应用场合中,模拟信号常常受到各种噪声或干扰的影响,这时就需要使用模拟信号滤波器来对信号进行处理,从而达到降噪或抗干扰的目的。
本文将介绍模拟信号滤波器设计的一些基本知识和方法。
一、模拟信号滤波器的分类根据滤波器的传输特性,模拟信号滤波器可以分为低通滤波器、高通滤波器、带通滤波器和带阻滤波器四种类型。
低通滤波器:可以让低于一定频率的信号通过,而对高于该频率的信号进行衰减,常用于滤除高频噪声或振荡。
高通滤波器:可以让高于一定频率的信号通过,而对低于该频率的信号进行衰减,常用于滤除低频噪声或直流分量。
带通滤波器:可以让一定范围内的频率信号通过,而对其他频率信号进行衰减,常用于保留一定频率范围内的信号。
带阻滤波器:可以让一定范围外的频率信号通过,而对该范围内的信号进行衰减,常用于滤除一定频率范围内的信号。
二、模拟信号滤波器的设计模拟信号滤波器的设计需要确定其传输特性和电路参数。
根据电路参数的不同,可以将模拟信号滤波器分为被动滤波器和有源滤波器。
被动滤波器指的是由电阻、电容和电感等被动元器件组成的滤波器,其缺点是带宽窄、增益小、稳定性差,适用于低频和中频信号的滤波。
有源滤波器指的是使用了运放等有源器件的滤波器,其优点是带宽宽、增益大、稳定性好,适用于高频信号的滤波。
有源滤波器的设计需要确定运放的电路结构和参数。
在具体的滤波器设计中,需要确定滤波器的截止频率、滤波器型号、电阻、电容、电感等电路元器件的值,以及电路的耦合方式和截止特性等。
还需要进行仿真和实验验证,以确保所设计的滤波器能够滤除目标噪声或干扰。
三、模拟信号滤波器的应用模拟信号滤波器在很多现代电子产品中都有广泛的应用,例如通信领域的信号处理、音频系统的去噪处理、传感器的信号处理等。
在工业自动化控制系统中,模拟信号滤波器也被广泛应用于模拟量的采集和处理中,以提高信号的稳定性和准确度。
模拟信号处理中的滤波器设计技巧

模拟信号处理中的滤波器设计技巧
在模拟信号处理中,滤波器设计是一项关键的技术,它可以帮助我们对信号进行处理和改善,使得我们可以更好地提取出有用的信息。
在设计滤波器时,有一些技巧是非常重要的,下面我将介绍一些常用的技巧和方法。
首先,我们需要了解滤波器的种类和特性。
常见的滤波器包括低通滤波器、高通滤波器、带通滤波器和带阻滤波器。
每种滤波器都有其特定的频率响应和传递函数,我们需要根据信号的特点和需求选择合适的滤波器类型。
其次,我们需要考虑滤波器的设计参数。
在设计滤波器时,我们需要确定滤波器的截止频率、通带波纹、阻带衰减等参数。
这些参数将直接影响滤波器的性能和效果,因此需要进行合理的选择和调整。
另外,我们还需要考虑滤波器的设计方法。
常用的滤波器设计方法包括脉冲响应不变法、双线性变换法和频率变换法等。
每种方法都有其优缺点,我们需要根据具体的应用需求选择合适的方法。
此外,在设计滤波器时,我们还需要考虑滤波器的稳定性和实现方法。
滤波器的稳定性是一个重要的性能指标,我们需要确保滤波器在所有频率下都是稳定的。
同时,我们还需要考虑如何实现所设计的滤波器,可以选择模拟电路、数字电路或者混合电路进行实现。
总的来说,滤波器设计是模拟信号处理中的重要技术,通过合理选择滤波器类型、设计参数、方法和实现方式,我们可以实现对信号的有效处理和改善。
希望以上介绍的技巧和方法能够对您在滤波器设计中有所帮助。
如果您对滤波器设计还有其他问题或者需要更深入的了解,请随时联系我,我会尽力为您提供帮助和支持。
LC带通滤波器的设计与仿真设计毕业设计(论文)

1.3.3 滤波器的前景....................................................7
1.3.4几种新型滤波器介绍..........................................8
●阻带滤波器:它的阻带限定在两个有限频率ƒ1与ƒ2之间,阻带两侧都有通带。
1.1.2 滤波器的种类
根据使用的波段和元件的不同,滤波器有很多种类,而且随着技术的发展,种类还在不断增加。总的来说,滤波器可分为两大类:无源滤波器和有源滤波器。
在无源滤波器中,所使用的是无源元件。他们在个体或组合的情况下,能够把一种形式的能量变换为另一种形式,并重新变回到原来的形式,换言之,它们必须是谐振性的。例如,在一个LC谐振电路中,在电容器的电场和电感线圈的磁场之间不断发生着能量的反复交换。因此,如果两个不同储能装置当相互偶合时,能够以很小的损耗实现能量的交换,它们就可以被利用为滤波器元件。
结束语.................................................................................43
致谢....................................................................................45
摘要
随着电子信息的发展,滤波器作为信号处理的不可缺少的部分,也得到了迅速的发展。LC滤波器作为滤波器的一个重要组成部分,它的应用相当的广泛。因此对于它的设计也受到人们的广泛关注。如何设计利用简单的方法设计出高性能的LC滤波器是人们一直研究的课题。
滤波器的多通道和多频带滤波器设计

滤波器的多通道和多频带滤波器设计滤波器在信号处理中起着至关重要的作用,可以帮助去除噪音,增强信号,提取所需频段等。
其中多通道和多频带滤波器是常见的滤波器类型,本文将针对这两种滤波器的设计进行详细讨论。
一、多通道滤波器设计多通道滤波器是指可以同时处理多个通道的滤波器,通常用于多声道音频处理、图像处理等领域。
以下是多通道滤波器设计的基本步骤:1. 确定滤波器类型:常见的滤波器类型包括低通、高通、带通和带阻。
根据实际需求选择适合的滤波器类型。
2. 设计滤波器参数:确定滤波器的截止频率、通带增益和阻带衰减等参数。
这些参数的选择需要根据具体的应用场景和信号特点。
3. 选择滤波器实现结构:常见的多通道滤波器结构包括并联结构和级联结构。
并联结构适合于通道之间没有相互干扰的情况,而级联结构则适用于通道之间存在相互干扰的情况。
4. 实现滤波器:根据选择的滤波器实现结构,设计滤波器的电路或算法,并进行实现。
可以通过模拟电路、数字滤波器算法等方式来实现多通道滤波器。
二、多频带滤波器设计多频带滤波器是指可以同时处理多个频带的滤波器,通常用于频谱分析、语音处理等领域。
以下是多频带滤波器设计的基本步骤:1. 确定频带数量和范围:根据实际需求确定需要处理的频带数量和每个频带的范围。
2. 设计滤波器参数:对每个频带进行滤波器参数的设计,包括截止频率、通带增益和阻带衰减等。
3. 选择滤波器实现结构:常见的多频带滤波器结构包括并行结构和串联结构。
并行结构适合于频带之间没有相互干扰的情况,而串联结构则适用于频带之间存在相互干扰的情况。
4. 实现滤波器:根据选择的滤波器实现结构,设计滤波器的电路或算法,并进行实现。
可以采用模拟电路、数字滤波器算法等方式来实现多频带滤波器。
总结:多通道滤波器和多频带滤波器在信号处理中起到了重要的作用。
通过合理的滤波器设计,可以满足不同应用场景中的信号处理需求。
在设计过程中,需要考虑滤波器类型、参数选择、实现结构等因素,并选择适合的实现方式。
高通滤波器设计及仿真

信息与电气工程学院电子电路仿真及设计CDIO三级项目设计说明书(2013/2014学年第二学期)题目:高通滤波器系统仿真及设计专业班级:通信工程班目录第一章文氏桥振荡器-------------------------------------------------1 1.1振荡器的设计及要求 ---------------------------------------------1 1.2系统工作原理 ---------------------------------------------------1 1.3电路设计原理图,实物图, 参数计算及仿真 --------------------------2第二章高通滤波器---------------------------------------------------6 2.1实际滤波器的基本参数--------------------------------------------6 2.2滤波器的设计目的------------------------------------------------6 2.3设计要求--------------------------------------------------------7 2.4系统的设计方案--------------------------------------------------7 2.5系统工作原理----------------------------------------------------7 2.6滤波器设计仿真,仿真结果,实物图,实测结果----------------------7 第三章合成电路----------------------------------------------------11 3.1合成电路仿真图-------------------------------------------------11 3.2焊接成品-------------------------------------------------------12 第四章心得体会----------------------------------------------------14 附录---------------------------------------------------------------14 参考文献-----------------------------------------------------------14第一章文氏桥振荡器1.1 振荡器的设计及要求(1)设计任务:根据文氏桥原理设计一正弦波振荡器。
带通滤波器设计 (2)

带通滤波器设计1. 引言在信号处理中,滤波器是一种重要的工具,用于去除或改变信号的特定频率成分。
带通滤波器是一种常用的滤波器,它可以传递一定范围内的频率成分,而抑制其他频率成分。
本文将介绍带通滤波器的基本原理和设计方法。
2. 带通滤波器的原理带通滤波器是一种频率选择性滤波器,它可以传递一定范围内的频率信号,而将其他频率信号抑制。
其基本原理是利用滤波器的频率响应特性,对输入信号进行滤波处理。
带通滤波器通常由一个低通滤波器和一个高通滤波器级联连接而成。
低通滤波器用于抑制高于截止频率的频率成分,而高通滤波器用于抑制低于截止频率的频率成分,从而实现带通滤波效果。
3. 带通滤波器的设计方法带通滤波器的设计通常包括以下几个步骤:在设计带通滤波器之前,需要确定滤波器的一些规格参数,包括中心频率、通带宽度、阻带宽度等。
这些参数决定了滤波器的性能和应用范围。
步骤二:选择滤波器的类型常见的带通滤波器类型包括巴特沃斯滤波器、切比雪夫滤波器、椭圆滤波器等。
根据具体的应用要求和设计指标,选择适合的滤波器类型。
步骤三:计算滤波器的阶数滤波器的阶数决定了滤波器的陡峭程度和相频特性。
根据设计要求和滤波器类型,计算滤波器的阶数。
步骤四:确定滤波器的传输函数根据滤波器的类型和阶数,使用滤波器设计方法计算滤波器的传输函数。
常用的设计方法包括频率折叠法、零极点法等。
根据滤波器的传输函数,采用模拟滤波器的设计方法,设计滤波器的电路结构和参数。
常用的设计方法包括电压法、电流法等。
步骤六:数字滤波器的设计对于数字信号处理系统,需要将模拟滤波器转换为数字滤波器。
常用的设计方法包括脉冲响应法、频率采样法等。
根据系统的采样率和滤波器的性能要求设计数字滤波器。
4. 带通滤波器的应用带通滤波器在信号处理领域有着广泛的应用。
例如,音频处理中常用带通滤波器对音频信号进行频率选择性处理,去除噪声和杂音。
图像处理中常用带通滤波器对图像进行频率域滤波,增强或抑制特定频率成分,实现图像增强、去噪等功能。
常用模拟滤波器的设计方法

常用模拟滤波器的设计方法设计模拟滤波器常用的方法有很多种,如巴特沃斯滤波器、切比雪夫滤波器、脉冲响应滤波器等。
这些方法各有特点,适用于不同的滤波器设计需求。
下面将逐步介绍常用模拟滤波器的设计方法。
1. 巴特沃斯滤波器的设计方法巴特沃斯滤波器是一种最常用的模拟滤波器,其主要特点是通频带的频率响应是平坦的,也就是说在通过的频率范围内的信号不会被衰减或增强。
巴特沃斯滤波器的设计方法包括以下步骤:1.1 确定滤波器类型首先,根据滤波器的设计需求,确定滤波器的类型,包括低通滤波器、高通滤波器、带通滤波器和带阻滤波器。
不同类型的滤波器在频率响应和陡度上有一些差异。
1.2 确定滤波器模型根据滤波器类型,选择相应的滤波器模型。
比如,低通滤波器通常选择Butterworth滤波器模型、Elliptic滤波器模型或者Chebyshev滤波器模型。
1.3 确定滤波器参数确定滤波器的相关参数,包括截止频率、阻带衰减和通带波纹等。
这些参数的选择需要根据特定的滤波器性能需求决定。
1.4 开始设计根据确定的滤波器模型和参数,开始进行滤波器的设计。
可以使用电路设计软件进行模拟,或者手动计算和画图设计。
1.5 仿真和优化设计完成后,对滤波器进行仿真,检查其频率响应和时域特性。
根据仿真结果,可以调整一些参数以优化滤波器的性能。
1.6 实际搭建和测试在电路板上搭建设计好的滤波器电路,并进行实际测试。
测试结果比较与设计要求进行评估和调整,最终得到满足要求的滤波器。
2. 切比雪夫滤波器的设计方法切比雪夫滤波器是一种在通频带内具有较窄的波纹和较快的过渡带的滤波器。
其设计方法如下:2.1 确定滤波器类型和阶数选择滤波器的类型和阶数,通常切比雪夫滤波器可以选择类型Ⅰ和类型Ⅱ。
阶数的选择取决于滤波器对波纹的要求和频率范围。
2.2 确定滤波器参数确定滤波器的相关参数,包括截止频率、阻带衰减、通带波纹和过渡带宽度等。
这些参数的选择需要根据特定的滤波器性能需求决定。
带通滤波器设计--模拟电子技术课程设计报告

带通滤波器设计--模拟电⼦技术课程设计报告模拟电⼦技术课程设计报告带通滤波器设计班级:⾃动化1202姓名:杨益伟学号:120900321⽇期:2014年7⽉2⽇信息科学与技术学院⽬录第⼀章设计任务及要求1、1设计概述------------------------------------31、2设计任务及要求------------------------------3 第⼆章总体电路设计⽅案2、1设计思想-----------------------------------42、2各功能的组成-------------------------------52、3总体⼯作过程及⽅案框图---------------------5 第三章单元电路设计与分析3、1各单元电路的选择---------------------------63、2单元电路软件仿真---------------------------8 第四章总体电路⼯作原理图及电路仿真结果4、1总体电路⼯作原理图及元件参数的确定---------94、2总体电路软件仿真---------------------------11 第五章电路的组构与调试5、1使⽤的主要仪器、仪表-----------------------125、2测试的数据与波形---------------------------125、3组装与调试---------------------------------145、4调试出现的故障及解决⽅法-------------------14 第六章设计电路的特点及改进⽅向6、1设计电路的特点及改进⽅向-------------------14 第七章电路元件参数列表7、1 电路元件⼀览表---------------------------15 第⼋章结束语8、1 对设计题⽬的结论性意见及改进的意向说明----168、2 总结设计的收获与体会----------------------16 附图(电路仿真总图、电路图)参考⽂献第⼀章设计任务及要求1、1设计概述:带通滤波器是指允许某⼀频率范围内的频率分量通过、其他范围的频率分量衰减到极低⽔平的滤波器。
二阶RC有源低通,高通,带阻滤波器的设计

电子技术课程设计报告(二阶RC有源滤波器的设计)目录第一章设计任务与要求 (3)1.1 设计任务 (3)1.2 设计要求 (3)第二章设计方案 (3)2.1 总方案设计 (3)2.1.1 方案框图 (3)2.1.2 子框图的作用 (3)2.1.3 方案选择 (4)第三章设计原理与电路 (6)3.1 单元电路的设计 (6)3.1.1 原理图设计 (6)3.1.2 滤波器的传输函数与性能参数 (8)3.2 元件参数的计算 (10)3.2.1 二阶低通滤波器 (10)3.2.2 二阶高通滤波器 (10)3.2.3 二阶带通滤波器 (10)3.2.4 二阶带阻滤波器 (11)3.2 元器件选择 (11)3.3 工作原理 (12)第四章电路的组装与调试 (12)4.1 MultiSim电路图 (13)4.2 MultiSim仿真分析 (15)第五章设计总结 (19)附录 (20)附录Ⅰ元件清单 (20)附录Ⅱ Protel原理图 (20)附录Ⅲ PCB图(正面) (21)附录Ⅳ PCB图(反面) (22)参考文献 (23)第一章 设计任务与要求1.1 设计任务1、学习RC 有源滤波器的设计方法;2、由滤波器设计指标计算电路元件参数;3、设计二阶RC 有源滤波器(低通、高通、带通、带阻);4、掌握有源滤波器的测试方法;5、测量有源滤波器的幅频特性。
1.2 设计要求1、分别设计二阶RC 低通、高通、带通、带阻滤波器电路,计算电路元件参数,拟定测试方案和步骤;2、在multisim 里仿真电路,测量并调整静态工作点;3、测量技术指标参数;4、测量有源滤波器的幅频特性;5、写出设计报告。
第二章 设计方案2.1 总方案设计2.1.1方案框图图2.1.1 RC 有源滤波总框图RC 网络反馈网络放大器2.1.2子框图的作用1 RC网络的作用在电路中RC网络起着滤波的作用,滤掉不需要的信号,这样在对波形的选取上起着至关重要的作用,通常主要由电阻和电容组成。
《模拟滤波器设计》课件

滤波器的频率响应
幅度频率响应
群时延频率响应
描述滤波器对不同频率信号的幅度增 益或衰减。
描述滤波器对不同频率信号的群时延 变化。
相位频率响应
描述滤波器对不同频率信号的相位偏 移。
滤波器的传递函数
一阶滤波器:具有一个极点和零点的传递函数。 高阶滤波器:具有多个极点和零点的传递函数。
二阶滤波器:具有两个极点和两个零点的传递函数。
频率等参数,可以使用 MATLAB等工具进行辅助设
计。
巴特沃斯滤波器的应用广泛, 如音频信号处理、图像增强等
。
切比雪夫滤波器设计
切比雪夫滤波器是一种具有等波纹特性的滤波 器,其幅度特性在通带和阻带内都是等波纹的 。
设计切比雪夫滤波器时,需要确定滤波器的阶 数、通带和阻带的波纹幅度等参数,可以使用 MATLAB等工具进行辅助设计。
ERA
模拟滤波器设计的挑战与机遇
挑战
随着信号处理技术的发展,对模拟滤波器的性能要求越来越高,如何提高滤波器的性能、减小其体积 和成本是当前面临的主要挑战。
机遇
随着新材料、新工艺的不断涌现,为模拟滤波器的设计提供了更多的可能性,同时也为解决上述挑战 提供了新的思路和方法。
未来发展方向与趋势
发展方向
切比雪夫滤波器的应用也较广泛,如雷达信号 处理、通信系统等。
椭圆滤波器设计
1
椭圆滤波器是一种具有最小相位特性的滤波器, 其幅度特性和相位特性都是线性的。
2
设计椭圆滤波器时,需要确定滤波器的阶数和截 止频率等参数,可以使用MATLAB应用相对较少,主要在一些特殊领 域如控制系统、信号处理等领域中使用。
测试结果的评价与改进
结果评价
根据测试数据,对模拟滤波器的性能进行客观评价,与设计要求进行对比,找出性能不足之处。
低通、高通、带通、带阻、全通、三运放差分滤波器
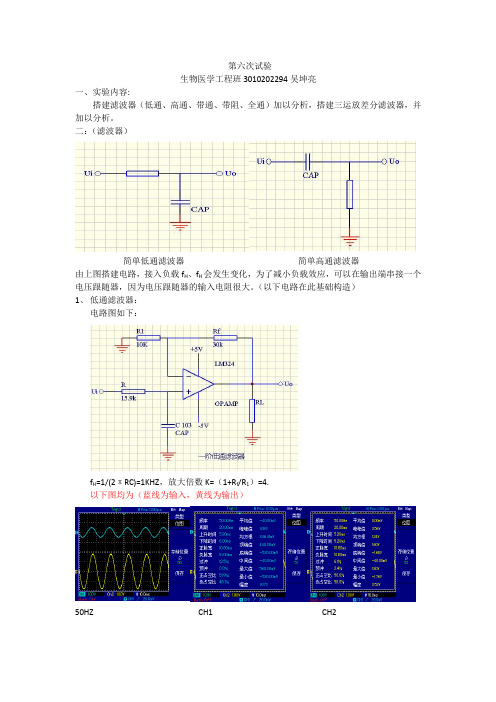
第六次试验生物医学工程班3010202294吴坤亮一、实验内容:搭建滤波器(低通、高通、带通、带阻、全通)加以分析,搭建三运放差分滤波器,并加以分析。
二:(滤波器)简单低通滤波器简单高通滤波器由上图搭建电路,接入负载f H、f H会发生变化,为了减小负载效应,可以在输出端串接一个电压跟随器,因为电压跟随器的输入电阻很大。
(以下电路在此基础构造)1、低通滤波器:电路图如下:f H=1/(2πRC)=1KHZ,放大倍数K=(1+R f/R1)=4.以下图均为(蓝线为输入,黄线为输出)50HZ CH1 CH2200HZ CH1 CH2500HZ CH1 CH2900HZ CH1 CH2 由以上波形比例可知,实验成功。
2、高通滤波器:f l=1/(2πRC)=1KHZ,放大倍数K=(1+R f/R1)=4.200HZ CH1 CH2500HZ CH1 CH21000HZ CH1 CH25KHZ CH1 CH230KHZ CH1 CH275KHZ(失真)CH1 CH2高通电路上限是有限制(不是很理解),正常增益内输入输出信号存在相移。
(以下带通、带阻可以通过低通带通的电路构造出来,我做了尝试误差较大,这里不再试用)3、带通滤波器:(中心频率)f o=1/(2πc(R1R2)1/2)=2022HZ,f BW=1/(R2C)=1000HZ(2.7HZ1.00vpp)数据图如下:4、带阻滤波器:它常用于通信和生物医学仪器中以清除无用的频率分量(如50HZ的电源频率等)f o=1/2πRC=4.423KHZ。
以下为不同频率下的波形:f=1KHZf=4.432KHZf=45KHZ实验测量数据如下:5、全通滤波器:输入信号所有无衰减地通过的一种滤波器。
但它对不同的频率分量提供不同的相移。
传输线(如电话线)常常会引起输入信号的相位移动,故全通滤波器称为相位校正器或延迟均衡器。
∠H(jw)=-2arctan(wRC)以下为调节R所得位移波形:R=834Ω R=19.57kΩR=26.9Ω相位移动明显二、三运放差分滤波器电路图如下:电路分析:差模增益:Avd=(R1+R2+R6)/R6*(R4/R3)=17共模增益:Avc=Rw/( R5+Rw)* (R3+R4)/ R3- R4/R3=0;(R w=16K)所以电路的共模抑制比CMRR为:CMRR= Avd/ Avc=[(R1+R2+Rw)/ Rw*(R4/R3)]/ [Rw/( R5+Rw )* (R3+R4)/ R3- R4/R3]=无穷大(理论上)1、首先调节共模抑制,使其简直最低方法(将两输入端接相同信号)(输入1KHZ、1vpp)(以下为输出波形和数据)R=24.1KR=19.6KR=16K(最好)R=11.96K (又开始变大)R=6.74K(可知R w=R4=16K,共模抑制比最大,实验与理论最大程度的吻合)以下为Vi1接正弦信号,Vi2接地2、输入50mvpp观察频率对其影响(以下为输出)f=50HZf=5KHZf=10.5KHZ(开始发生变化)f=50KHZf=500KHZf=1M(在示波器上显示为失真导出图片只是它的某一帧)3、5KHZ下不同伏值对其影响(蓝线为输入、黄线为输出)30mvpp(无放大)35mvpp40mvpp(很好)50mvpp(很好)160mvpp(失真)600mvpp8vpp以下图形为Vi1用手捏住做输入其他不变(娱乐):。
模拟信号处理中的滤波器设计实例

模拟信号处理中的滤波器设计实例在模拟信号处理中,滤波器是一种常用的工具,用于去除信号中的噪声或选择特定频率范围内的信号。
滤波器的设计是信号处理的重要环节,能够有效地改善信号质量,并使其更适合后续的分析或应用。
在设计滤波器时,需要考虑到信号的特性、系统的要求以及滤波器的类型。
常见的滤波器类型包括低通滤波器、高通滤波器、带通滤波器和带阻滤波器。
不同类型的滤波器在频域内有不同的频率响应特性,因此在实际应用中需要根据需要选择合适的滤波器类型。
以设计一个低通滤波器为例。
低通滤波器可以去除高频噪声或选择低频信号。
首先,我们需要确定设计要求,如截止频率、通带波动、阻带衰减等。
接着,选择合适的滤波器结构,如巴特沃斯滤波器、切比雪夫滤波器或椭圆滤波器。
不同的结构有不同的设计方法和性能指标。
在设计实例中,以巴特沃斯滤波器为例。
巴特沃斯滤波器是一种常见的低通滤波器,具有平坦的通带响应和快速的衰减特性。
设计流程如下:1. 确定设计要求:假设我们需要设计一个10阶的低通巴特沃斯滤波器,截止频率为1kHz,通带波动不超过0.1dB。
2. 计算滤波器参数:根据设计要求,可以计算出滤波器的截止频率下限、截止频率上限、归一化的通带频率、归一化的截止频率等参数。
3. 计算极点位置:根据设计参数和所选择的巴特沃斯滤波器类型,可以计算出滤波器的极点位置。
4. 数字化滤波器:利用双线性变换或频率响应不变法将模拟滤波器转换为数字滤波器,以便在数字信号处理系统中使用。
5. 仿真验证:通过仿真软件对设计的滤波器进行验证,检查设计是否符合要求。
通过以上步骤,设计出来的巴特沃斯滤波器可以满足低通滤波的需求。
在实际应用中,设计滤波器时需根据具体情况选择合适的滤波器类型和参数,以达到最佳的信号处理效果。
综上所述,滤波器设计是模拟信号处理中的重要环节,合理设计滤波器可以有效改善信号质量,使信号更适合后续处理或应用。
设计滤波器需要考虑信号特性、系统要求和滤波器类型,通过合理的设计方法和参数选择,可以得到满足需求的滤波器。
模拟高通带通滤波器设计

电路设计
设计滤波器电路结构
根据滤波器类型和电路元件选择,设计出合适的电路结构。
计算元件参数
根据设计目标和电路元件选择,计算出各元件的具体参数值。
绘制电路图
使用电路设计软件绘制出高通带通滤波器的电路图。
仿真验证
建立仿真模型
在仿真软件中建立高通带通滤波器的电路模型,并设 置适当的仿真参数。
进行仿真实验
群时延特性分析
总结词
群时延是衡量滤波器对信号畸变影响的指标,它反映了信号通过滤波器后的时间 延迟。
详细描述
高通带通滤波器的群时延特性在通带内应保持相对稳定,以保证信号的完整性。 在通带边缘和阻带,群时延特性会出现较大的波动,这可能会影响信号的相位特 性。
插入损耗分析
总结词
插入损耗是指滤波器接入电路后,输入信号的功与输出信 号的功率之比。
椭圆函数逼近法
利用椭圆函数来逼近理想 滤波器的频率响应特性, 设计出具有特定性能的高 通带通滤波器。
高通带通滤波器的设计难点
如何平衡阻带抑制与通带平坦度
在设计中需要权衡阻带抑制和通带平坦度,以确保滤波器性能达到 要求。
如何减小群时延波动
群时延是衡量滤波器对信号时间延迟的参数,需要在设计中尽量减 小群时延波动。
定义。
品质因数
衡量滤波器性能的一个 重要参数,与滤波器的 带宽和截止频率有关。
群时延
衡量滤波器对信号时间 延迟的参数,要求在通
带内保持恒定。
滤波器设计方法
01
02
03
切比雪夫逼近法
通过逼近理想滤波器的频 率响应特性,设计出具有 特定性能的高通带通滤波 器。
巴特沃斯逼近法
通过逼近理想滤波器的频 率响应特性,设计出具有 平坦幅频特性的高通带通 滤波器。
数字信号处理课程设计-用双线性变换法设计高通和带通数字滤波器

1、问号选择问、倒装问句末才用问,反问、追问、特指问每句都问,有疑问词非疑问句不用问。
2、顿号大并套小并,大并逗小并顿,集合词语连得紧,中间不必插入顿,概数约数不确切,中间也别带上顿。
并列词语有点长,顿号变逗不要忘。
书名号和引号多次出现,中间顿号可省略。
3、分号分号表并列,点在句句间。
分句内部用了逗,分句之间才用分。
4、冒号提示下文、总结上文要用冒,说在中间且一人说,说后不用冒,冒号的管辖范围,冒号注意不可套。
5、引号冒号、引号、引内句号是一套,引用部分能独立,句末标点引号里,引用之语不独立,句末标点引号尾。
括号表注解,句末符号不可写。
注释部分紧挨着,注释整体隔开着。
7、书名号报刊杂志、书名文章、法规文件、电影戏剧用书名号。
电视节目、画展、主题、杂志社则不可书名号。
8、几种不套用情况省略号“和”等等不套用,“是”和破折号不可套,冒号和“即”不套,破折号和括号不套。
1.非疑问句句末用问号。
2.倒装句问号未用于句末。
3.分句之间用顿号。
4.多层并列都用顿号。
5.表示概数时用顿号。
6.句中没有逗号直接用分号。
7.一句话中两个冒号套用。
8.“某某说”在引语中间,“说”后面用冒号。
9.滥用书名号。
10.引号与句末点号位置错误,括号与点号连用位置错误。
一、标点符号的作用(请分析下列各句中标点符号的使用方法)1、引出总括性的说明她的坚强,她的意志的纯洁,她的律已之严,她的客观,她的公正不阿的判断——所有这一切都难得地集中在一个人的身上。
2、表示突然转变话题你画得真好。
——你为什么这样勇敢,不怕他?3、突出语意转折让他一个人留在房里还不到两分钟,当我们进去的时候,便发现他在安乐椅上安静地睡着了——但已经永远地睡着了。
4、表示声音延长“嘎——”传过来一声水禽被惊动的鸣叫。
5、表示解释说明李时珍花了二十多年时间,才编成这部药学经典——《本草纲目》。
6、表示补充说明朦胧之中似乎胎孕着一个如花的笑——这么淡,那么淡的倩笑。
模拟滤波器设计及运放选择

模拟滤波器设计及运放选择滤波器是一种能够对信号进行频率选择和频率衰减的电路。
在电子系统中,滤波器广泛应用于音频处理、通信系统、控制系统等方面。
滤波器设计的目标是通过选择合适的电路元件和参数,使得滤波器能够满足特定的频率响应要求。
在滤波器设计中,常用的滤波器类型包括低通滤波器、高通滤波器、带通滤波器和带阻滤波器。
除了选择滤波器类型外,选择合适的滤波器阶数也是设计滤波器的关键。
滤波器阶数指的是滤波器中电子元件的数量,阶数越高,滤波器对信号的衰减能力越强。
当设计滤波器时,还需要选择合适的运放。
运放是一种放大器,可以将输入信号放大到合适的范围。
在滤波器中,运放的功能不仅限于放大信号,还可以提供一些额外的功能,比如放大增益、相位延迟等。
在选择运放时,需要考虑以下几个因素:1.噪声水平:运放的噪声水平对滤波器的性能有很大影响。
噪声水平越低,滤波器的信噪比就越高。
2.带宽:运放的带宽决定了滤波器能够传递的最高频率。
如果带宽不足,信号的高频分量将无法通过滤波器。
3.运放增益和稳定性:运放的增益和稳定性对于滤波器的放大系数和频率响应有很大影响。
因此,选择具有适当增益和高稳定性的运放是设计滤波器的重要考虑因素之一在实际的滤波器设计中,通常会先根据预设的频率响应要求选择合适的滤波器类型和阶数。
然后,根据滤波器的阻抗要求和电源电压等因素,选择合适的运放。
在选择运放时,可以参考运放的数据手册,了解其噪声水平、带宽、增益和稳定性等参数。
根据实际需求,结合数据手册中的参数,选择符合要求的运放。
总之,滤波器设计和运放选择是一项复杂的任务。
需要综合考虑滤波器的频率响应要求、阻抗要求以及运放的噪声水平、带宽、增益和稳定性等因素。
只有合理选择滤波器类型和阶数,并且选择适当的运放,才能设计出性能良好的滤波器。
有源滤波器Multisim 仿真 低通 高通 带通 带阻

有源一阶低通滤波器XSC1通带截止频率:假设R R 3=,,C C 1=H f RCπ1=2 通带电压放大倍数:f up R A R 1=1+有源二阶压控低通滤波器Rf R1品质因数:upQ A 1=3-,0.5≤Q ≤100,一般选取Q =1附近的值通带截止频率:假设R R R 32==,C C C 12==,H f RCπ1=2 通带电压放大倍数:f up R A R 1=1+有源二阶压控高通滤波器Rf R1通带电压放大倍数:f up R A R 1=1+通带截止频率:假设R R R 32==,C C C 12==,L f RCπ1=2 品质因数:upQ A 1=3-有源二阶压控带通滤波器Rf R110k Ω通带电压放大倍数:uf up ufA A A =3-。
f up R A R 1=1+应小于3,否则电路不能稳定工作。
通带中心频率:假设R R R R 234=2=2=2,C C C 12==,通带中心频率f RCπ01=2通带宽度:()H L uf BW f f A f 0=-=3-,()L uf f f A 0⎤=-3-⎦2,()H uf ff A 0⎤=+3-⎦2有源二阶压控带阻滤波器Rf R1f uf R A R 1=1+应小于2,否则电路不能稳定工作阻带宽度:()H L uf f BW f f A f Q 00=-=22-=,其中()uf Q A 1=22-,()L uf f A f 0⎤=-2-⎦,()H uf A f 0阻带中心频率:假设,C C C C 1232=2==2R R R R 342==2=,阻带中心频率f RCπ01=2 f ⎤=+2-⎦。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
p
c s
Ha(s)
q s C
低通归一化的系统函数G(p)
p 1 q
1
高通归一化的系统函数H(q)
模拟高通滤波器的设计步骤:
(1)确定高通滤波器的技术指标:通带下限频率 p ,阻 带上限频率 ,通带最大衰减 s
s
p ,阻带最小衰减
。
(2)确定相应低通滤波器的设计指标:将高通滤波器的 边界频率转换成低通滤波器的边界频率 ①低通滤波器通带截止频率
H ( s) G( p)
p
sB 2 s2 0
6.5 数字高通、带通和带阻滤波器的设计
数字滤波器的指标
2 1 tan T 2
H(Z) 双线性变换法 Ha(s) 转换 关系
模拟滤波器指标
ALF的指标
转换关系
低通归一化的系统函数G(p)
例6.5.1 设计一个数字高通滤波器,要求通带截止频 率ωp=0.8πrad,通带衰减不大于3dB,阻带截止频率 ωs=0.44πrad, 阻带衰减不小于15dB。希望采用巴特 沃斯型滤波器。 (1)数字高通的技术指标为 ωp=0.8πrad, αp=3dB;
0 l u,阻带宽度 B u l
2
lHale Waihona Puke ,上通带截止频率 u s1,阻带上限频率 s 2
它们相应的归一化边界频率为
s1 s 2 l s1 ,s 2 ,l B B B u 2 u ,0 l u B
以及通带最大衰减
p
和阻带最小衰减
将以上边界频率对带宽B归一化,得到
ηu=3.348, ηl=2.348; ηs2=4.608, ηs1=1.498; η0=2.804 (3) 模拟归一化低通滤波器技术指标:
归一化阻带截止频率
s22 02 s 2.902 s 2
归一化通带截止频率 λp=1 αp=3dB,αs=18dB
ωs=0.44πrad, αs=15dB (2) 模拟高通的技术指标
令T=1,则有
1 p 2 tan p 6.155rad / s, p 3dB 2 1 s 2 tan s 1.655rad / s, s 3dB 2
(3)转化为模拟低通滤波器的技术指标:
αp=3dB,αs=25dB。试设计巴特沃斯带阻滤波器。
Ω20=ΩlΩu=4π2×1000025,
B=Ωu Ωl=2π×200;
ηl=Ωl/B=4.525,
ηs1=Ωs1/B=4.9, η20=ηlηu=25
ηu=Ωu/B=5.525;
ηs2=5.1;
(2) 归一化低通的技术要求:
s 2 p 1, s 2 4.95, s 4.95 2 s1 0 p 3dB, s 25dB
N 3
④ 求模拟高通H(s):
3
G( p)
p 2p 2p 1
2
H ( s) G( p) 2 f
p
c s
s 3 2 2 3 s 2 c s 2 c s c
模拟带通filter的设计方法 带通滤波器的指标要求
s1 s1 / B,s 2 s 2 / B l l / B,u u / B 02 l u
2 s2
2 0
模拟带通filter的设计方法
模拟带通滤波器指标 转换关系
ALF的指标
Ha(s)
低通归一化的系统函数G(p)
2 q 2 0 p q
2 2 0
q=s/B
高通归一化的系统函数H(q)
s 2 l u p s ( u l ) H ( s) G( p)
H ( z ) H a ( s)
1 z 1 s 2 1 z 1
实际上(5)、(6)两步可合并成一步,即
H ( z ) G( s)
11 z 1 s 2 1 z 1
0.106(1 z 1 ) 2 0.0653(1 z 1 ) 2 H ( z) 1 2 1.624 1.947 z 0.566 z 1 1.199 z 1 0.349 z 2
p
c s
例 6.2.3 设计高通滤波器 ,fp=200Hz,fs=100Hz ,幅度特 性 单 调 下 降 , fp 处 最 大 衰 减 为 3dB , 阻 带 最 小 衰 减 αs=15dB。 ①高通技术要求: fp=200Hz, αp=3dB; fs=100Hz, αs=15dB
fs p 1, s 0.5, fc fc ②低通技术要求:
通带最大衰减仍为αp,阻带最小衰减亦为αs。
(3) 设计归一化低通G(p)。
(4) 直接将G(p)转换成带通H(s)。
模拟带通filter的设计方法
低通与带阻滤波器的频率变换
3) 低通到带阻的频率变换
通带中心频率
0 l u ,通带宽度 B u l
2
为低通到带阻的频率变换公式:
与以上边界频率对应的归一化边界频率如下:
s1 s 2 l s1 ,s 2 ,l B B B u 2 u ,0 l u B
(2) 确定归一化低通技术要求:
2 2 s22 0 s21 0 p 1, s , s s 2 s1
4.模拟滤波器的频率变换——模拟高通、带通、带阻滤波器的 设计
1) 低通到高通的频率变换
λ和η之间的关系为
1
如 果 已 知 低 通 G(jλ) , 高 通 H(jη)则用下式转换:
H ( j ) G ( j )
1
模拟高通filter的设计方法
H ( s) G( p)
转换关系 模拟高通滤波器指标 转换关系 ALF的指标
s 2 l u p s ( u l )
总结模拟带通的设计步骤: (1)确定模拟带通滤波器的技术指标,即: 带通上限频率
u ,带通下限频率 l
s1
2
下阻带上限频率
,上阻带下限频率
s 2
通带中心频率 0 通带最大衰减为
p
l u ,通带宽度 B u l
,阻带最小衰减为 s :
4.模拟滤波器的频率变换——模拟高通、带通、带阻滤波器
的设计
H ( s ) 需要设计的“实际 AF ”频响函数 s j 拉式复变量 实际AF 的归一化频率 q j 实际AF 的归一化拉式复变量 H ( j ) 实际AF 的归一化频响函数
G ( s) 低通AF 传输函数; s j 低通AF 拉式复变量 低通AF 归一化频率 p j 低通AF 归一化拉式复变量 G ( j ) 低通AF 归一化频响函数
s
。
(2) 确定归一化模拟低通技术要求,即:
s1 s 2 p 1, s 2 , s 2 2 2 s1 0 s 2 0
为
。 ,阻带最小衰减为 s p
取 λs 和 λs 的绝对值较小的 λs ;通带最大衰减
(3) 设计归一化模拟低通G(p)。 (4) 直接将G(p)转换成带阻滤波器H(s)。
2 2 0
p=jλ,并去归一化 s/B,可得
sB s ( u l ) p 2 2 2 s 0 s u l
上式是直接由归一化低通转换成带阻的频率变换公式。
H ( s) G( p)
p
sB 2 s 2 0
下面总结设计带阻滤波器的步骤: (1)确定模拟带阻滤波器的技术要求,即: 下通带截止频率 阻带下限频率 阻带中心频率
去归一化,将p=s/Ωc代入上式得到:
2 c G( s) 2 s 2 c s 2 c
(5) 将模拟低通转换成模拟高通。将G(s) 的变量换成1/s,得到模拟高通Ha(s):
2 1 2 s H a ( s ) G( ) 2 2 c s c s 2c s 1
(6)用双线性变换法将模拟高通H (s)转换成数字高 通H(z):
1 0.163rad / s, p 3dB 6.155 1 s 0.604 rad / s, s 15dB 1.655 p
将Ωp和Ωs对3dB截止频率Ωc归一化,这里Ωc=Ωp
s p 1, s 3.71 p
(4) 设计归一化模拟低通滤波器 G(p) 。模拟低通滤
(3)设计归一化低通滤波器G(p):
10 1 k sp 0.0562 0.1 s 10 1
0.1 p
s sp 4.95 p
N lg k sp lg sp 1.8, N 2
1 G( p) 2 p 2p 1
(4) 带阻滤波器的H(s)为
2 2 4 s 4 20 s 0 4 2 2 4 s 2 Bs2 ( B 2 20 ) s 2 2 B0 s 0
(4) 设计模拟低通滤波器:
10 p 1 k sp 0.127 0.1 s 10 1
0.1
s sp 2.902 p
B u l
带通滤波器频率特性是正负对称的,故 这个变换必须是一对二的映射,它应该 是Ω的二次函数
2 2 0
指标转换公式:边界频率转换成低通的边界频率。
2 2 0
λp对应ηu λs对应ηs2
2 2 u 0 1 p u l u
s s 2
通带内最大衰减αp=3dB,阻带内最小衰减αs=18dB。
(2) 模拟带通滤波器技术指标如下:
设T=1,则有
1 u 2 tan u 1.453rad / s 2 1 l 2 tan l 1.019 rad / s 2 1 s 2 2 tan s 2 2 rad / s 2 1 s1 2 tan s1 0.650rad / s 2 0 u l 1.217 rad / s (通带中心频率) B u l 0.434rad / s (带宽)
