上海中考专题训练25题专题训练与答案解析

合集下载

2023年上海中考数学卷25题

中考模拟数学一、选择题1.如图，在三角形ABC中D，E分别是AB和AC上的点，且DE平行BC，AE比EC=5/2,D E=10，则BC的长为（）。

A．16B．14C．12D．112.在同一平面直角坐标系中，函数y＝x﹣1与函数y=1的图象可能是（）xA．B． C．D．(k≠0)，下列所给的四个结论中，正确的是（）3.对于反比例函数y=kxA．过图象上任一点P作x轴、y轴的垂线，垂足分别A，B，则矩形O APB的面积为k B．若点(2,4)在其图象上，则(−2,4)也在其图象上C．反比例函数的图象关于直线y=x和y=−x成轴对称D．当k>0时，y随x的增大而减小4.如图，一个等边三角形的边长与它的一边相外切的圆的周长相等，当这个圆按箭头方向从某一位置沿等边三角形的三边做无滑动旋转，直至回到原出发位置时，则这个圆共转了（）A．4圈B．3圈C．5圈D．3.5圈5.如图，四边形ABCD是矩形，E是边BC延长线上的一点，AE与CD相交于点F，则图中的相似三角形共有（）A．4对 B．3对C．2对D．1对6.如图，身高1.6m的某学生想测量一棵大树的高度，她沿着树影BA由B向A走去，当走到C点时，她的影子顶端正好与树的影子顶端重合，测得BC＝3.2m，CA＝0.8m，则树的高度为（）A．4.8m B．6.4m C．8m D．10m7.如图，晚上小亮在路灯下散步，在小亮由A处走到B处这一过程中，他在地上的影子（）A．逐渐变短B．逐渐变长 C．先变短后变长D．先变长后变短8.如图，在同一平面直角坐标系中，反比例函数y=kx与一次函数y=kx−1（k为常数，且k≠0）的图象可能是（）。

A．B． C．D．9.已知m3=n4，那么下列式子中一定成立的是（）A．4m=3n B．3m=4n C．m=4n D．mn=12二、填空题（共24分）10.已知△ABC，若有|sinA−1|与（tanB−√3）2互为相反数，则∠C的度数2是。

2024年上海市中考真题数学试卷含答案解析

2024年上海市中考数学试题学校:___________姓名：___________班级：___________考号：___________一、单选题1．如果x y >，那么下列正确的是（）A ．55x y +<+B ．55x y -<-C ．55x y >D ．55x y->-【答案】C【分析】本题主要考查了不等式的基本性质，根据不等式两边加（或减）同一个数（或式子），不等号的方向不变．不等式两边乘（或除以）同一个正数，不等号的方向不变．不等式两边乘（或除以）同一个负数，不等号的方向改变．【详解】解：A ．两边都加上5，不等号的方向不改变，故错误，不符合题意；B ．两边都加上5-，不等号的方向不改变，故错误，不符合题意；C ．两边同时乘上大于零的数，不等号的方向不改变，故正确，符合题意；D ．两边同时乘上小于零的数，不等号的方向改变，故错误，不符合题意；故选：C ．2．函数2()3xf x x -=-的定义域是（）A ．2x =B ．2x ≠C ．3x =D ．3x ≠3．以下一元二次方程有两个相等实数根的是（）A ．260x x -=B ．290x -=C ．2660x x -+=D ．2690x x -+=【答案】D【分析】本题考查了一元二次方程判别式判断根的情况，解答本题的关键是熟练掌握一元二次方程()200ax bx c a ++=≠，当240b ac ∆=->时，方程有两个不相等实数根；当240b ac ∆=-=时，方程的两个相等的实数根；当24<0b ac ∆=-时，方程没有实数根．分别计算出各选项中的根的判别式的值，即可判断．【详解】解：A ．()2Δ6410360=--⨯⨯=> ，该方程有两个不相等实数根，故A 选项不符合题意；B ．()2Δ0419360=-⨯⨯-=> ，该方程有两个不相等实数根，故B 选项不符合题意；C ．()2Δ6416120=--⨯⨯=> ，该方程有两个不相等实数根，故C 选项不符合题意；D ．()2Δ64190=--⨯⨯= ，该方程有两个相等实数根，故D 选项不符合题意；故选：D ．4．科学家同时培育了甲乙丙丁四种花，从甲乙丙丁选个开花时间最短的并且最平稳的．种类甲种类乙种类丙种类丁种类平均数 2.3 2.3 2.8 3.1方差1.050.781.050.78A ．甲种类B ．乙种类C ．丙种类D ．丁种类【答案】B【分析】本题主要考查了用平均数和方差做决策，根据平均数的定义以及方差的定义做决策即可．解题的关键是掌握方差的意义：方差是反映一组数据的波动大小的一个量．方差越大，则平均值的离散程度越大，稳定性也越小；反之，则它与其平均值的离散程度越小，稳定性越好．【详解】解：∵由表格可知四种花开花时间最短的为甲种类和乙种类，四种花的方差最小的为乙种类和丁种类，方差越小越稳定，∴乙种类开花时间最短的并且最平稳的，故选：B ．5．四边形ABCD 为矩形，过A C 、作对角线BD 的垂线，过B D 、作对角线AC 的垂线，如果四个垂线拼成一个四边形，那这个四边形为（）A ．菱形B ．矩形C ．直角梯形D ．等腰梯形【答案】A【分析】本题考查矩形性质、等面积法、菱形的判定等知识，熟练掌握矩形性质及菱形的判定是解决问题的关键．由矩形性质得到OBC OAD S S = ，OC OB OA OD ===，进而由等面积OBC OAD S S ∴= ，OC OB OA OD === 过A C 、作对角线BD 的垂线，过1122OBC OAD S S OC BF OB CH ∴==⋅=⋅ ∴CH BF AE DG ===，6．在ABC 中，3AC =，4BC =，5AB =，点P 在ABC 内，分别以A B P 、、为圆心画，圆A 半径为1，圆B 半径为2，圆P 半径为3，圆A 与圆P 内切，圆P 与圆B 的关系是（）A ．内含B ．相交C ．外切D ．相离∴221417+=，二、填空题7．计算：()324x =．【答案】664x 【分析】本题考查了积的乘方以及幂的乘方，掌握相关运算法则是解题关键．先将因式分别乘方，再结合幂的乘方计算即可．【详解】解：()326464x x =，故答案为：664x ．8．计算()()a b b a +-= ．【答案】22b a -【分析】根据平方差公式进行计算即可．【详解】解：()()a b b a +-()()b a b a =+-22b a =-，故答案为：22b a -．【点睛】本题考查平方差公式，此为基础且重要知识点，必须熟练掌握．91=，则x = ．【答案】1【分析】本题主要考查了二次根式有意义的条件，掌握二次根式中的被开方数是非负数是解题的关键．由二次根式被开方数大于0可知210x ->，则可得出211x -=，求出x 即可．【详解】解：根据题意可知：210x ->，∴211x -=，解得：1x =，故答案为：1．10．科学家研发了一种新的蓝光唱片，一张蓝光唱片的容量约为5210⨯GB ，一张普通唱片的容量约为25GB ，则蓝光唱片的容量是普通唱片的倍．（用科学记数法表示）11．若正比例函数y kx =的图像经过点(7,13)-，则y 的值随x 的增大而．（选填“增大”或“减小”）12．在菱形ABCD 中，66ABC ∠=︒，则BAC ∠= ．13．某种商品的销售量y （万元）与广告投入x （万元）成一次函数关系，当投入10万元时销售额1000万元，当投入90万元时销售量5000万元，则投入80万元时，销售量为万元．【答案】4500【分析】本题考查求一次函数解析式及求函数值，设y kx b =+，根据题意找出点代入求出解析式，然后把80x =代入求解即可．【详解】解：设y kx b =+，把()10,1000，()90,5000代入，得101000905000k b k b +=⎧⎨+=⎩，解得50500k b =⎧⎨=⎩，∴50500y x =+，当80x =时，50805004500y =⨯+=，即投入80万元时，销售量为4500万元，故答案为：4500．14．一个袋子中有若干个白球和绿球，它们除了颜色外都相同随机从中摸一个球，恰好摸到绿球的概率是35，则袋子中至少有个绿球．∴绿球的个数的最小值为3，∴袋子中至少有3个绿球，故答案为：3．15．如图，在平行四边形ABCD 中，E 为对角线AC 上一点，设AC a = ，BE b =u u r r，若2AE EC =，则DC =（结果用含a ，b的式子表示）．16．博物馆为展品准备了人工讲解、语音播报和AR 增强三种讲解方式，博物馆共回收有效问卷1000张，其中700人没有讲解需求，剩余300人中需求情况如图所示（一人可以选择多种），那么在总共2万人的参观中，需要AR 增强讲解的人数约有人．【答案】200017．在平行四边形ABCD 中，ABC ∠是锐角，将CD 沿直线l 翻折至AB 所在直线，对应点分别为C '，D ¢，若::1:3:7AC AB BC '=，则cos ABC ∠= ．根据::1:3:7AC AB BC '=由翻折的性质知：FCD ∠=CD 沿直线l 翻折至AB 所在直线，BC F FC D FCD '''∴∠+∠=∠根据::1:3:7AC AB BC '=，不妨设同理知：72CF BF C F '===，过F 作AB 的垂线交于E ，122BE BC '∴==，18．对于一个二次函数2()y a x m k =-+（0a ≠）中存在一点(),P x y ''，使得0x m y k '-='-≠，则称2x m '-为该抛物线的“开口大小”，那么抛物线211323y x x =-++“开口大小”为．三、解答题20．解方程组：2234026x xy y x y ⎧--=⎨+=⎩①②．【答案】4x =，1y =或者6x =-，6y =．【分析】本题考查了二元二次方程，求解一元二次方程，解题的关键是利用代入法进行求解．【详解】解：2234026x xy y x y ⎧--=⎨+=⎩①②，由②得：62x y =-代入①中得：()()226236240y y y y ----=，()2223624418640y y y yy -+-+-=，2642360y y -+=，()26760y y -+=，()()6610y y --=解得：1y =或6y =，当1y =时，6214x =-⨯=，当6y =时，6266x =-⨯=-，∴方程组的解为4,1x y ==或者6,6x y =-=．21．在平面直角坐标系xOy 中，反比例函数ky x=（k 为常数且0k ≠）上有一点()3,A m -，且与直线24y x =-+交于另一点(),6B n ．(1)求k 与m 的值；(2)过点A 作直线l x ∥轴与直线24y x =+交于点C ，求sin OCA ∠的值．∵l x ∥轴，x 轴y ⊥轴，∴A 、C 、D 的纵坐标相同，均为把2y =代入24y x =-+解得1x =，∴()1,2C ，22．同学用两幅三角板拼出了如下的平行四边形，且内部留白部分也是平行四边形（直角三角板互不重叠），直角三角形斜边上的高都为h．(1)求：①两个直角三角形的直角边（结果用h表示）；②小平行四边形的底、高和面积（结果用h表示）；(2)请画出同学拼出的另一种符合题意的图，要求：①不与给定的图形状相同；②画出三角形的边．如图2，DEF 为含则2EF h =，DE =综上，等腰直角三角板直角边为②由题意可知MNG NGH ∠=∠∴四边形MNGH 是矩形，由图可得，2323MN h h =-（2）解：如图，即为所作图形．23．如图所示，在矩形ABCD 中，E 为边CD 上一点，且AE BD ⊥．(1)求证：2AD DE DC=⋅；(2)F为线段AE延长线上一点，且满足12EF CF BD==，求证：CE AD=．在矩形ABCD 中，ADE ∠ AE BD ⊥，∴90DAE ADB ∠+∠=ADB AED ∴∠=∠，FEC AED ∠=∠，24．在平面直角坐标系中，已知平移抛物线213y x =后得到的新抛物线经过50,3A ⎛⎫- ⎪⎝⎭和(5,0)B ．(1)求平移后新抛物线的表达式；(2)直线x m =（0m >）与新抛物线交于点P ，与原抛物线交于点Q ．①如果PQ 小于3，求m 的取值范围；②记点P 在原抛物线上的对应点为P '，如果四边形P BPQ '有一组对边平行，求点P 的坐标．∴22114545333333PQ x x x x =-++=+，∵PQ 小于3，∴45333x +<，∴1x <，∵()0x m m =>，∴01m <<；由题意可得：P 在B 的右边，当BP '∴BP x '⊥轴，∴5P B x x '==，∴255,3P '⎛⎫ ⎪⎝⎭，由平移的性质可得：2552,33P ⎛⎫+- ⎪⎝⎭如图，当P Q BP '∥时，则P QT '∠=过P '作P S QP '⊥于S ，∴90P SQ BTP '∠=∠=︒，∴QS PTP S BT='，25．在梯形ABCD 中，AD BC ∥，点E 在边AB 上，且13AE AB =．(1)如图1所示，点F 在边CD 上，且13DF CD =，联结EF ，求证：EF BC ∥；(2)已知1AD AE ==；①如图2所示，联结DE ，如果ADE V 外接圆的心恰好落在B ∠的平分线上，求ADE V 的外接圆的半径长；②如图3所示，如果点M 在边BC 上，联结EM 、DM 、EC ，DM 与EC 交于N ，如果4BC =，且2CD DM DN =⋅，DMC CEM ∠=∠，求边CD 的长．∵AD BC∥，∴AE DE EB EG=，∵13AE AB=，13DF CD=∴12AEEB=，12DFFC=，∵AD BC ∥，∴PAD PBC ∽，∴14PA AD PB BC ==，由①知3AB =，∴134PA PA =+，。

2021年上海中考数学相似三角形专项训练(含答案)

2021年上海中考数学相似三角形专项训练一、选择题1．（2021.1松江）如果两个相似三角形对应边的比为1:4，那么它们的周长比是（）（A ）1:2；（B ）1:4；（C ）1:8；（D ）1:16．2．（2021.1崇明）已知点G 是△ABC 的重心，如果联结AG ，并延长AG 交边BC 于点D ，那么下列说法中错误．．的是（） (A)BD CD =； (B)AG GD =； (C)2AG GD =； (D)2BC BD =．3．（2021.1青浦）如图1，已知BD 与CE 相交于点A ，DE ∥BC ，如果AD =2，AB =3， AC =6，那么AE 等于（）（A ）125；（B ）185；（C ）4；（D ）9．4. （2021.1奉贤）如图2，在梯形ABCD 中，AD //BC ，BC =3AD ，对角线AC 、BD 交于点O ，EF 是梯形ABCD 的中位线，EF 与BD 、AC 分别交于点G 、H ，如果△OGH 的面积为1，那么梯形ABCD 的面积为（）（A ）12；（B ）14；（C ）16；（D ）18.5. （2021.1杨浦）在梯形ABCD 中，AD //BC ，对角线AC 与BD 相交于点O ，下列说法中，错误的是（）（A ）DOC AOB S S ∆∆=；（B ）AOB BOC S OD S OB ∆∆=；（C ）AOD BOC S OA S OC ∆∆=；（D ）ABD ABC S ADS BC∆∆=. 6. （2021.1宝山）如图，AB ∥DE ，BC ∥DF ，已知n m FB AF ::=，a BC =，那么CE 等于（）（A ）nam；（B ）m an ；（C ）nm am +；（D ）nm an+. （B ）二、填空题7．（2021.1崇明）已知线段6AB =cm ，点C 是AB 的黄金分割点，且AC BC >，那么EDCBA （图1）ADHG F E BCO图2AB CDEF图3线段AC 的长为 cm ．8．（2021.1黄浦）已知线段MN 的长为4，点P 是线段MN 的黄金分割点，则其较长线段MP 的长是．9.（2021.1奉贤）已知点P 是线段AB 上一点，且AB AP BP •=2，如果AB =2厘米，那么BP = 厘米． 10．（2021.1崇明）如果两个相似三角形的一组对应边上的高之比为1:4，那么这两个三角形的面积比为．11．（2021.1黄浦）在△ABC 中，AB =5，BC =8，∠B =60°，则△ABC 的面积是． 12.（2021.1奉贤）如果两个相似三角形的周长之比为1:4，那么这两个三角形对应边上的高之比为．13. （2021.1杨浦）如图，已知在△ABC 中，∠ACB ＝90°，点G 是△ABC 的重心，CG =2，BC =4，那么cos GCB ∠= ．14．(2021.1松江)如图4，正方形DEFG 的边EF 在△ABC 的边BC 上，顶点D 、G 分别在边AB 、AC 上．已知△ABC 的边BC =16cm ，高AH 为10cm ，则正方形DEFG 的边长为_________cm.15．（2021.1虹口）如图5，AB //CD ，AD 、BC 相交于点E ，过E 作EF //CD 交BD 于点F ，如果AB =3，CD=6，那么EF 的长是．16．（2021.1黄浦）已知一个矩形的两邻边长之比为1∶2.5，一条平行于边的直线将该矩形分为两个小矩形，如果所得两小矩形相似，那么这两个小矩形的相似比为． 17. （2021.1杨浦）如图6，已知在△ABC 中，∠B=45º，∠C=60º，将△ABC 绕点A 旋转，点B 、C 分别落在点B 1、C 1处，如果BB 1//AC ，联结C 1B 1交边AB 于点D ，那么1BDB D的值为 .18．（2021.1普陀）如图8，在□ABCD 中，点E 在边BC 上，将△ABE 沿着直线AE 翻折得到△AFE ，点B 的对应点F 恰好落在线段DE 上，线段AF 的延长线交边CD 于点G ，如果:3:2BE EC =，那么:AF FG 的值等于．（图4） E H AB C D F GAD CFEB A 图5 图6CB A A DCB EF G三、解答题 19、（2020年5月徐汇二模）如图，已知直线22+=x y 与x 轴交于点A ，与y 轴交于点C ，矩形ACBE 的顶点B 在第一象限的反比例函数xmy =图像上，过点B 作OC BF ⊥．垂足为F ，设t OF =．（1）求ACO ∠的正切值；（2）求点B 的坐标（用含t 的式子表示）；（3）已知直线22+=x y 与反比例函数xmy =图像都经过第一象限的点D ，联结DE ，如果x DE ⊥轴，求m 的值．20、（2020年5月杨浦二模）如图，已知在正方形ABCD 中，对角线AC 与BD 交于点O ，点M 在线段OD 上，联结AM 并延长交边DC 于点E ，点N 在线段OC 上，且ON=OM ，联结DN 与线段AE 交于点H ，联结EN 、MN .（1）如果EN //BD ，求证：四边形DMNE 是菱形；（2）如果EN ⊥DC ，求证：2AN NC AC =⋅.（第19题图）AD C BEOxy F第20题图ADCHMON E21、（2020年5月长宁二模）如图，已知四边形ABCD 是矩形，点E 在对角线AC 上，点F 在边CD 上（点F 与点C 、D 不重合），EF BE ⊥，且︒=∠+∠45CEF ABE ．（1）求证：四边形ABCD 是正方形；（2）联结BD ，交EF 于点Q ，求证：DF CE BC DQ ⋅=⋅．22、（2020年5月长宁二模）如图，在平面直角坐标系xOy 中，已知抛物线n mx x y ++=2经过点)2-2(，A ，对称轴是直线1=x ，顶点为点B ，抛物线与y 轴交于点C . （1）求抛物线的表达式和点B 的坐标；（2）将上述抛物线向下平移1个单位，平移后的抛物线与x 轴正半轴交于点D ，求BCD ∆的面积；（3）如果点P 在原抛物线上，且在对称轴的右侧，联结BP 交线段OA 于点Q ，51=PQ BQ ，求点P 的坐标.ADCBEF第21题图第22题图-1-2 -3 -412 3 4 -1 -2 -3 -4 1 2 3 4 Oxy第24题图EDCABGFH23、（2020年5月长宁二模）已知：如图，在平行四边形ABCD 中，对角线AC 与BD 交于点O ，点E 是DB 延长线上的一点，且EA EC =，分别延长AD 、EC 交于点F . （1）求证：四边形ABCD 为菱形；（2）如果2AEC BAC ∠=∠，求证：EC CF AF AD ⋅=⋅．24、（2020年5月静安二模）已知：如图8，四边形ABCD 是平行四边形，延长BA 至点E ，使得AE=AB ，联结DE 、AC ．点F 在线段DE 上，联结BF ，分别交AC 、AD 于点G 、H ．（1）求证：BG =GF ；（2）如果AC =2AB ，点F 是DE 的中点，求证：BH GH AH ⋅=2．第23题图ABCDEFO25、（2020年5月闵行二模）如图，已知在□ABCD 中，AE ⊥BC ，垂足为E ，CE=AB ，点F 为CE 的中点，点G 在线段CD 上，联结DF ，交AG 于点M ，交EG 于点N ，且∠DFC=∠EGC ．（1）求证：CG=DG ；（2）求证：2CG GM AG =⋅．26、（2020年5月浦东二模）已知：如图，在菱形ABCD 中，AC =2，∠B =60°．点E 为BC 边上的一个动点（与点B 、C 不重合），∠EAF =60°，AF 与边CD 相交于点F ，联结EF 交对角线AC 于点G ．设CE =x ，EG = y ．（1）求证：△AEF 是等边三角形；（2）求y 关于x 的函数解析式，并写出x 的取值范围；（3）点O 是线段AC 的中点，联结EO ，当EG =EO 时，求x 的值．ABEGCFD（第25题图）M N（第26题图）GFEDCBA参考答案一、选择题 1.B 2.A 3.C 4.C 5.C 6.D二、填空题7. 3 8.2 9.15-10. 1﹕16 11.12. 1:4 13.2314.801315. 2 16. 1，2，12．17. 18.214三、解答题 19.解：（1）由题意，得，；∴，；在中，，)0,1(-A )2,0(C 1=AO 2=OC AOC Rt ∆︒=∠90AOC∴．（2）∵四边形是矩形，∴；∵，∴；又，； ∴；∴；又， ∴； ∴．（3）设轴，垂足为，与轴的交点为．又轴，∴；∴，； ∵四边形是矩形，∴，；∴；∴；又， ∴≌；∴； ∴；∴；∴； ∵点、在反比例函数图像上， ∴；解得或（不合题意，舍去）； ∴． 20.证明：（1）如图1，∵四边形是正方形，∴……（1分）21tan ==∠OC OA ACO ACBE ︒=∠90ACB OC BF ⊥︒=∠90BFC ︒=∠+∠90BCF ACO ︒=∠+∠90BCF FBC ACO FBC ∠=∠21tan tan =∠==∠ACO BF CF FBC t OF CO CF -=-=2t CF BF 242-==),24(t t B -x DE ⊥H AE y G x CO ⊥CO DH //AEH AGC ∠=∠DHCOAH AO =ACBE BC AE =BC AE //BCF AGC ∠=∠BCF AEH ∠=∠︒=∠=∠90BFC AHE AEH ∆BCF ∆t BF AH 24-==DHt 2241=-t DH 48-=)48,23(t t D --B D xmy =m t t t t =-=--)24()48)(23(56=t 2=t 254856)5624(=⨯⨯-=m ABCD OA OB OC OD AC BD ===⊥，∵，∴，∴………………（1分）又∵，∴…………（1分） ∵，，∴≌…………………………（1分 ∴，∵，∴ ∴………………………………………（1分）∴，∴平行…………………………（1分）（2）如图2， ∵，∴……………………（1分） ∵四边形是正方形，∴，…（1分） ∴，又∵，∴，…………………（1分）∴………………………………（1分） ∵∴……………………………………………（1分） ∴, ∴………………（1分） 21.证明：（1）∵EF BE ⊥ ∴︒=∠90BEF 即︒=∠+∠90CEF BEC (1分)∵BAC ABE BEC ∠+∠=∠ ∴︒=∠+∠+∠90CEF BAC ABE 又∵︒=∠+∠45CEF ABE ∴ ︒=∠45BAC 又∵四边形ABCD 是矩形 ∴ ︒=∠90ABC ∴ ︒=∠+∠90BCA BAC ∴︒=∠=∠45BCA BAC ∴ BC AB = (4分)∴四边形ABCD 是正方形 (1分) （2）设BD AC 、相交于点O∵四边形ABCD 是正方形 ∴BD AC ⊥ ∴︒=∠90EOQ (1分) ∴︒=∠+∠90OEQ EQOON OM =ON OMOC OD=//MN CD //EN BD DMNE 四边形是平行四边形AOM DON ∆∆在和中90AOM DON ∠=∠=︒OA OD OM ON ==，AOM ∆DON ∆OMA OND ∠=∠90OAM OMA ∠+∠=90OAM OND ∠+∠=︒90AHN ∠=︒DN ME ⊥DMNE 四边形是菱形//MN CD AN AMNC ME=ABCD //AB DC AB DC =，90ADC ∠=AD DC ⊥EN DC ⊥//EN AD AC DCAN DE=//AB DC ，AM ABME DE=AN ACNC AN =2AN NC AC =⋅第23题图1ADCHMON E B第23题图2ADCH MON E又∵︒=∠+∠90OEQ CEB ∴CEB EQO ∠=∠ (1分)∵四边形ABCD 是正方形∴ ︒=∠=∠90ADC BCD ，AC 、BD 分别平分ADC BCD ∠∠、∴ ︒=∠=∠45ECB QDF (1分)又∵ EQO DQF ∠=∠ ∴CEB DQF ∠=∠ (1分)∴DQF ∆∽CEB ∆ (1分)∴ BC DF CE DQ =即 DF CE BC DQ ⋅=⋅22.（本题满分12分，每小题各4分）解：（1）抛物线n mx x y ++=2经过点)2,2(-A ，对称轴是直线1=x∴42212m n m ++=-⎧⎪⎨-=⎪⎩，解得22m n =-⎧⎨=-⎩ （2分）∴抛物线的解析式为222y x x =--，顶点B 的坐标是(1,3)- （2分）（2）抛物线222y x x =--与y 轴交于点），（2-0C 平移后的抛物线表达式为： 223y x x =-- ，点D 的坐标是(3,0) （2分）过点B 做y BH ⊥轴，垂足为点H∴=S S S BCD BCH COD BHOD S ∆∆∆--梯形1111=(13)31123=22222⨯+⨯-⨯⨯-⨯⨯ （2分）（3）∵直线OA 经过点00O （，）、)2,2(-A ，∴直线OA 的表达式为：y x =- 设对称轴与直线OA 相交于点E ，则11E （，-） ∵ (1,3)B - ∴2BE = （1分）过点P 作PF//BE ，交直线OA 于点F设点）（22,2--t t t P 1t >（），则）（t t F -, ∴22PF t t =-- （1分）∵ PF//BE ∴15BE BQ PF PQ == ∴22125t t =-- ∴2120t t --= ∴3t =- （舍去）或4t = （1分） ∴)6,4(P （1分）23. 证明：（1）∵四边形ABCD 是平行四边形．∴AO CO =． ··········································································· （2分） ∵EA EC =，∴EO AC ⊥． ························································· （2分） ∴四边形ABCD 是菱形． ····························································· （2分）（2）∵四边形ABCD 是菱形,∴2BAD BAC ∠=∠，AD CD =． ······················································· （2分） ∵2AEC BAC ∠=∠，∴BAD AEC ∠=∠． ∵AB //CD ，∴BAD CDF ∠=∠．∴AEC CDF ∠=∠． ········································································· （1分）又∵F F ∠=∠， ∴△FCD ∽△FAE ． ············································· （1分） ∴CF CDAF AE=． ················································································· （1分） ∴AE CF AF CD ⋅=⋅．∴EC CF AF AD ⋅=⋅． ······································································ （1分）24.证明：（1）∵四边形ABCD 是平行四边形，∴AB =CD ，AB //CD ． ···································································· （1分） ∵AB =AE ，∴AE =CD ． ··································································· （1分） ∴四边形ACDE 是平行四边形．························································· （1分） ∴AC//DE ．···················································································· （1分）∴． ··········································································· （1分） 1==AEABGF BG∴BG =GF ． ··················································································· （1分）（2）∵AB =AE ，∴BE =2AE ． ∵AC =2AB ，∴BE =AC ．∵四边形ACDE 是平行四边形，∴AC=DE ． ∴DE=BE ． ··················································································· （1分） ∵点F 是DE 的中点，∴ DE=2EF ． ∴AE= EF ． ··················································································· （1分） ∵∠E =∠E ，∴△BEF ≌△DEA ． ······················································· （1分） ∴∠EBF =∠EDA ． ·········································································· （1分） ∵AC //DE ，∴∠GAH =∠EDA ． ∴∠EBF =∠GAH ．∵∠AHG=∠BHA ，∴△AHG ∽△BHA ． ·············································· （1分）∴． ∴． ······································································ （1分） 25. 证明：（1）∵□ABCD ，CE=AB ，∴AB=CD=EC ；…………………………（1分）又∵∠DFC=∠EGC ，∠BCD=∠BCD ，∴△ECG ≌△DCF ；……（1分） ∴CG=CF ．…………………………………………………………（1分）∵点F 为CE 的中点，∴CF=12CE ；………………………………（1分）∴CG=12CD ，即：CG=DG ．……………………………………（1分）（2）延长AG 、BC 交于点H ．∵△ECG ≌△DCF ，∴∠CEG=∠CDF ．…………………………（1分） ∵□ABCD ，∴AD ∥BC ，∴∠DAH=∠H ，∠ADC=∠DCH ．∴△ADG ≌△HCG ，∴AG=HG ．…………………………………（1分） ∵AE ⊥BC ，∴∠AEC=90°，∴AG=HG=EG ．………………（1分）∴∠CEG=∠H ，∴∠CDF=∠DAH ．………………………………（1分）又∵∠AGD=∠DGA ，∴△ADG ∽△DMG ．…………………………（1分）∴MG DG DG AG=，∴2DG GM AG =⋅…………………………………（1分）又∵CG=DG ，∴2CG GM AG =⋅．……………………………………（1分）26.解：（1）∵四边形ABCD 是菱形，∴AB =BC ，∠ACB =∠ACF ． ……………（1分）∵∠B =60°，∴△ABC 是等边三角形．∴AB =AC ，∠B =∠BAC =∠ACB=∠ACF =60°． …………………………（1分） ∵∠BAC=∠EAC +∠BAE =60°，∠EAF=∠EAC +∠CAF =60°，∴∠BAE =∠CAF ．………………………………………………………… （1分）∴△BAE ≌△CAF ．…………………………………………………………（1分） ∴AE =AF ．AHGHBH AH =BH GH AH ⋅=2∵∠EAF=60°，∴△AEF是等边三角形．………………………………（1分）（2）过点A作AH⊥BC，垂足为点H．在Rt△ABH中，∠AHB=90°，∠B=60°，AB=2，∴AH BH=1．在Rt△AEH中，∠AHE=90°，AH，EH=1x-，∴AE．………………………………………………………（1分）∵∠AEG+∠CEG=∠B+∠BAE，∠B=∠AEG=60°，∴∠CEG=∠BAE．∵∠B=∠GCE=60°，∴△BAE∽△CEG．………………………………（1分）∴BA AE CE=．∴2x=．………………………………………………………（1分）∴y=…………………………………………………（1分）（0 < x < 2）．…………………………………………………………（1分）（3）过点E作EM⊥AC，垂足为点M．在Rt△CEM中，∠CME=90°，∠ECM=60°，CE=x，∴CM=12x．∵点O是线段AC的中点，∴CO=1．∴OM=112x -．∵EO=EG，EM⊥AC，∴GM=OM=112x -．………………………………（1分）∴CG=1x-．…………………………………………………………………（1分）∵△BAE∽△CEG．∴BA BE CE CG=．∴22xx-=．………………………………………………………………（1分）∴x=（负值舍去）…………………………………………………（1分）。

上海市2023年中考数学真题及答案解析

上海市2023年中考数学真题及答案解析【注意：本文仅提供参考，实际考试请以教育部门发布的官方真题为准】一、选择题题目解析1. 小明从家到学校的路程共有5公里，他骑自行车一次骑行2/5的距离。

他一共用了多长时间？选项解析：题目中提到小明骑行2/5的距离，即2/5 * 5公里 = 2公里。

进而，我们可以计算出他骑行2公里所需要的时间。

答案：根据题目分析，小明骑行2公里所需要的时间为2公里/ 骑行速度 = 2公里 / 骑行速度，这里骑行速度未提及，所以无法计算具体时间。

答案为无法确定。

2. 某商品原价为300元，现在打八折出售，折后价格是多少？选项解析：题目中提到打八折，即原价 * 0.8，我们可以直接计算出折后价格。

答案：300元 * 0.8 = 240元。

答案为240元。

二、填空题题目解析1. 下图中国地图的颜色表示的是哪个省份？解析：根据题目中的提示，通过判断地图颜色可以得出对应的省份名称。

答案：由于无法提供具体地图，所以无法确定具体省份名称。

答案为无法确定。

2. 160 ÷ 8 = ____解析：题目中提到除法运算，我们可以直接计算出结果。

答案：160 ÷ 8 = 20。

答案为20。

三、解答题题目解析1. 如果a = 3, b = 4，则(a + b)² = ____解析：题目中给出了a和b的值，我们可以带入计算。

答案：(a + b)² = (3 + 4)² = 7² = 49。

答案为49。

2. 请用两种方法计算 2² + 3² + 4² + 5²的值。

解析：题目要求我们计算一个数列的和，我们可以分别列出每一项的平方然后相加，或者使用数列求和公式进行计算。

答案：方法一：2² + 3² + 4² + 5² = 4 + 9 + 16 + 25 = 54。

方法二：利用数列求和公式：n(n+1)(2n+1)/6，其中n为项数。

2020-2021年上海各区数学中考一模压轴题分类汇编-25题含详解

∴ 2x 2 y ， 2x 1 2 x
可得： y 2x2 2 （0＜x＜2）； 2x 1
（3）BE＝2﹣x，DH＝y，DE＝ 1 x2 ，EH＝ 1 ( y x)2 ，
∴ EG AE ，∴EG＝ AE EH ，
GH CH
AE CH
∵∠BEG＝∠DHE，
若△BEG 与△DHE 相似，则有两种情况，
8．（2020 秋•普陀区期末）如图，矩形 ABCD 中，AB＝1，BC＝3，点 E 是边 BC 上一个动点（不与点 B、C 重合），AE 的垂线 AF 交 CD 的延长线于点 F．点 G 在线段 EF 上，满足 FG：GE＝1：2．设 BE＝x．（1）求证： AD DF ；
AB BE （2）当点 G 在△ADF 的内部时，用 x 的代数式表示∠ADG 的余切；（3）当∠FGD＝∠AFE 时，求线段 BE 的长．
在 Rt△EAD 与 Rt△DCF 中，
∠ADE=∠CDF
∠EAD=∠FCD=90
°
，
∴△EAD∽△FCD，∴ DE = AD = 1 ， DF CD 2
∴tan∠EFD＝ DE = 1 ， DF 2
（2）由（1）可知 FC＝2EA＝2x，
∵四边形 ABCD 是矩形，∴AB∥CD，∴△FCH∽△FBE，∴ FC = CH ， FB BE
专题 2021 年上海各区分类汇编-25 题
专题一动点函数下的相似三角形
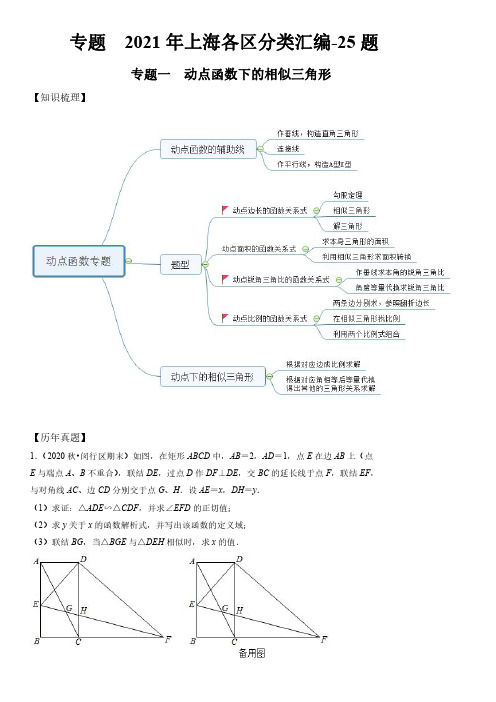
【历年真题】
1．（2020 秋•闵行区期末）如图，在矩形 ABCD 中，AB＝2，AD＝1，点 E 在边 AB 上（点 E 与端点 A、B 不重合），联结 DE，过点 D 作 DF⊥DE，交 BC 的延长线于点 F，联结 EF，与对角线 AC、边 CD 分别交于点 G、H．设 AE＝x，DH＝y．（1）求证：△ADE∽△CDF，并求∠EFD 的正切值；（2）求 y 关于 x 的函数解析式，并写出该函数的定义域；（3）联结 BG，当△BGE 与△DEH 相似时，求 x 的值．

决胜2021年上海中考数学压轴题全揭秘精解专题25 上海中考预测卷(2)

绝密★启用前上海市2021年初中毕业统一学业考试数学预测试题二考生注意： 1.本试卷共25题。

2.试卷满分150分，考试时间100分钟。

3.答题时，考生务必按答题要求在答题纸规定的位置上作答，在草稿纸、本试卷上答题一律无效。

4.除第一、二大题外，其余各题如无特殊说明，都必须在答题纸的相应位置上写出证明或计算的主要步骤。

一．选择题（本大题共6题，每题4分，满分24分）【下列各题的四个选项中，有且只有一个选项是正确的，选择正确的代号并填涂在答题纸的相应位置上】1.方程230x -+=根的情况（） A. 有两个不相等的实数根 B. 有一个实数根； C. 无实数根D. 有两个相等的实数根2．若m n >，下列不等式不一定成立的是( ) A ．33m n +>+B ．33m n -<-C ．33m n> D ．22m n >3.在平面直角坐标系中，反比例函数(0)ky k x=≠图像在每个象限内，y 随着x 的增大而增大，那么它的图像的两个分支分别在（） A. 第一、三象限 B. 第二、四象限 C. 第一、二象限D. 第三、四象限4．学校举行图书节义卖活动，将所售款项捐给其他贫困学生．在这次义卖活动中，某班级售书情况如表：下列说法正确的是( )A ．该班级所售图书的总收入是226元B．在该班级所售图书价格组成的一组数据中，中位数是4C．在该班级所售图书价格组成的一组数据中，众数是15D．在该班级所售图书价格组成的一组数据中，方差是25.顺次联结四边形ABCD各边中点所形成的四边形是矩形，那么四边形ABCD是（）A. 平行四边形B. 矩形C. 菱形D. 等腰梯形6．已知，在△ABC中，∠A＝30°，∠B＝135°，CD⊥AB，且CD＝1．若以点A为圆心，√3为半径作⊙A，以点B为圆心，1为半径作⊙B，则⊙A与⊙B的位置关系是（）A．内切B．外切C．相交D．外离二．填空题（本大题共12题，每题4分，满分48分）【请将结果直接填入答题纸的相应位置上】7．若2a b=+，则代数式222a ab b-+的值为．8.化简：113a a-=______．9．若一个数的平方等于5，则这个数等于．10.0=的解是_____________.11．晓芳抛一枚硬币10次，有7次正面朝上，当她抛第11次时，正面向上的概率为．12．《九章算术》是我国古代数学的经典著作，书中有一个问题：“今有黄金九枚，白银一十一枚，称之重适等，交易其一，金轻十三两，问金、银一枚各重几何？”意思是：甲袋中装有黄金9枚（每枚黄金重量相同），乙袋中装有白银11枚（每枚白银重量相同），称重两袋相等，两袋互相交换1枚后，甲袋比乙袋轻了13两（袋子重量忽略不计），问黄金、白银每枚各重多少两？设每枚黄金重x两，每枚白银重y两，根据题意可列方程组为．13.在一张边长为4cm的正方形纸上做扎针随机试验，纸上有一个半径为1cm的圆形阴影区域，则针头扎在阴影区域内的概率为__________；14．董永社区在创建全国卫生城市的活动中，随机检查了本社区部分住户五月份某周内“垃圾分类”的实施情况，将他们绘制了两幅不完整的统计图(A．小于5天；.5B天；.6C天；.7D天），则扇形统计图B部分所对应的圆心角的度数是．15.已知在梯形ABCD中，AD∥BC，∠ABC = 90°，对角线AC、BD相交于点O，且AC⊥BD，如果AD︰BC = 2︰3，那么DB︰AC =______．16．如图，在ABC中，90C∠=︒，30A∠=︒，BD是ABC∠的平分线，如果AC x=，那么CD =（用x表示）．17．如图，在ABC∆中，30B∠=︒，2AC=，3cos5C=．则AB边的长为．18.在矩形ABCD中，AB=6，BC=8，点O在对角线AC上，圆O的半径为2，如果圆O与矩形ABCD的各边都没有公共点，那么线段AO长的取值范围是____．三．解答题（共7小题，满分78分）19.（本题满分10分）计算：1327﹣(12)﹣2+|3．20.（本题满分10分）解不等式组：1076713x xxx>+⎧⎪+⎨-<⎪⎩21.(本题满分10分)在平面直角坐标系xoy 中（如图），已知一次函数的图像平行于直线12y x =，且经过点A （2，3），与x 轴交于点B ．（1）求这个一次函数的解析式；（2）设点C 在y 轴上，当AC ＝BC 时，求点C 的坐标．22．（本题满分10分）两栋居民楼之间的距离30CD m =，楼AC 和BD 均为10层，每层楼高为3m ．上午某时刻，太阳光线GB 与水平面的夹角为30︒，此刻楼BD 的影子会遮挡到楼AC 的第几层？（参考数1.7≈ 1.4)≈23.已知：如图，AB 、AC 是⊙O 的两条弦，且AB ＝AC ，D 是AO 延长线上一点，联结BD 并延长交⊙O 于点E ，联结CD 并延长交⊙O 于点F. （1）求证：BD ＝CD ：（2）如果AB 2＝AO·AD ，求证：四边形ABDC 是菱形.24.如图6，在平面直角坐标系xOy 中，抛物线()2230y ax ax a a =--<与x 轴交于A B、两点（点A 在点B 的左侧），经过点A 的直线:l y kx b =+与y 轴负半轴交于点C ，与抛物线的另一个交点为D ，且4CD AC =.（1）直接写出点A 的坐标，并求直线l 的函数表达式（其中k b 、用含a 的式子表示）（2）点E 是直线l 上方的抛物线上的动点，若ACE ∆的面积的最大值为54，求a 的值；（3）设P 是抛物线的对称轴上的一点，点Q 在抛物线上，当以点A D P Q 、、、为顶点的四边形为矩形时，请直接写出点P 的坐标.25.已知：如图，在菱形ABCD 中，2AC =，60B ∠=︒．点E 为边BC 上的一个动点（与点B 、C 不重合），60EAF ∠=︒，AF 与边CD 相交于点F ，联结EF 交对角线AC 于点G ．设CE x =，EG y =．（1）求证：AEF 是等边三角形；（2）求y 关于x 的函数解析式，并写出x 的取值范围；（3）点O 是线段AC 的中点，联结EO ，当EG EO 时，求x 的值．绝密★启用前上海市2021年初中毕业统一学业考试数学预测试题二考生注意： 1.本试卷共25题。

上海中考数学二模汇编第25题教程文件

2019年上海中考数学二模汇编第25题1.（杨浦）已知圆O 的半径长为2，点A 、B 、C 为圆O 上三点，弦AO BC =，点D 为BC 的中点．（1）如图1，联结AC 、OD ，设OAC α∠=，请用α表示AOD ∠；（2）如图2，当点B 为AC 的中点时，求点A 、D 之间的距离；（3）如果AD 的延长线与圆O 交于点E ，以O 为圆心，AD 为半径的圆与以BC 为直径的圆相切，求弦AE 的长．图1 图2 图32.（黄浦）已知四边形ABCD 中，AD ∥BC ，2ABC C ∠=∠，点E 是射线AD 上一点，点F 是射线DC 上一点，且满足BEF A ∠=∠.（1）如图8，当点E 在线段AD 上时，若AB=AD ，在线段AB 上截取AG=AE ，联结GE .求证：GE=DF ；（2）如图9，当点E 在线段AD 的延长线上时，若AB =3，AD =4，1cos 3A =，设AE x =，DF y =，求y 关于x 的函数关系式及其定义域；（3）记BE 与CD 交于点M ，在（2）的条件下，若△EMF 与△ABE 相似，求线段AE 的长.D A BCEF 图9ABCE F G D图83.（闵行）如图1，点P 为∠MAN 的内部一点．过点P 分别作PB ⊥AM 、PC ⊥AN ，垂足分别为点B 、C ．过点B 作BD ⊥CP ，与CP 的延长线相交于点D ．BE ⊥AP ，垂足为点E ．（1）求证：∠BPD =∠MAN ；（2）如果sin MAN ∠=AB =BE = BD ，求BD 的长；（3）如图2，设点Q 是线段BP 的中点．联结QC 、CE ，QC 交AP 于点F ．如果 ∠MAN = 45°，且BE // QC ，求PQF CEFS S ∆∆的值．E M（图2）ANQFPCDBMN A BCDP（图1）EABCDE备用图 4.（金山）如图，在ABC Rt ∆中，90=∠C ，16=AC cm ，20=AB cm ，动点D 由点C 向点A 以每秒cm 1速度在边AC 上运动，动点E 由点C 向点B 以每秒cm 34速度在边BC 上运动，若点D ，点E 从点C 同时出发，运动t 秒(0>t )，联结DE .（1）求证：DCE ∆∽BCA ∆．（2）设经过点D 、C 、E 三点的圆为⊙P . ①当⊙P 与边AB 相切时，求t 的值.②在点D 、点E 运动过程中，若⊙P 与边AB 交于点F 、G （点F 在点G 左侧），联结CP 并延长CP 交边AB 于点M ，当PFM ∆与CDE ∆相似时，求t 的值.B5.（宝山）如图已知：AB是圆O的直径，AB=10，点C为圆O上异于点A、B的一点，点M为弦BC的中点．（1）如果AM交OC于点E，求OE：CE的值；（2）如果AM⊥OC于点E，求∠ABC的正弦值；（3）如果AB：BC=5：4，D为BC上一动点，过D作DF⊥OC，交OC于点H，与射线BO交于圆内点F，请完成下列探究．探究一：设BD=x，FO=y，求y关于x的函数解析式及其定义域．探究二：如果点D在以O为圆心，OF为半径的圆上，写出此时BD的长度．6.（静安）已知，如图，梯形ABCD 中，AD ∥BC ，2AD =，6AB BC CD ===，动点P 在射线BA 上，以BP 为半径的P 交边BC 于点E （点E 与点C 不重合），联结PE 、PC ，设BP x =，PC y =.（1）求证：PE ∥DC ；（2）求y 关于x 的函数解析式，并写出定义域；（3）联结PD ，当P D C B ∠=∠时，以D 为圆心半径为R 的D 与P 相交，求R 的取值范围.7.（徐汇）如图，在△ABC 中，10AC BC ==，3cos 5C =，点P 是AC 边上一动点（不与点A 、C 重合），以PA 长为半径的P 与边AB 的另一个交点为D ，过点D 作DE CB ⊥于点E . （1）当P 与边BC 相切时，求P 的半径；（2）联结BP 交DE 于点F ，设AP 的长为x ，PF 的长为y ，求y 关于x 的函数解析式，并直接写出x 的取值范围；（3）在（2）的条件下，当以PE 长为直径的Q 与P 相交于AC 边上的点G 时，求相交所得的公共弦的长.8.（奉贤）如图，已知△ABC ，AB =45B ∠=︒，点D 在边BC 上，联结AD ，以点A 为圆心，AD 为半径画圆，与边AC 交于点E ，点F 在圆A 上，且AF AD ⊥. （1）设BD 为x ，点D 、F 之间的距离为y ，求y 关于x 的函数解析式，并写出定义域；（2）如果E 是弧DF 中点，求:BD CD 的值；（3）联结CF ，如果四边形ADCF 是梯形，求BD 的长.9.（崇明）如图，在梯形ABCD 中，AD ∥BC ，8AB DC ==，12BC =，3cos 5C =，点E 为AB 边上一点，且2BE =，点F 是BC 边上的一个动点（与点B 、点C 不重合），点G 在射线CD 上，且EFG B ∠=∠，设BF 的长为x ，CG 的长为y .（1）当点G 在线段DC 上时，求y 与x 之间的函数关系式，并写出自变量x 的取值范围；（2）当以点B 为圆心，BF 长为半径的B 与以点C 为圆心，CG 长为半径的C 相切时，求线段BF 的长；（3）当△CFG 为等腰三角形时，直接写出线段BF 的长.10.（普陀）如图12，在Rt ABC中，∠ACB=90°，AB=5，4cos5BAC∠=，点O是边AC上一个动点（不与A、C重合），以点O为圆心，AO为半径作O，O与射线AB 交于点D；以点C为圆心，CD为半径作C，设OA x=.（1）如图13，当点D与点B重合时，求x的值；（2）当点D在线段AB上，如果C与AB的另一个交点E在线段AD上时，设AE=y，试求y与x之间的函数解析式，并写出x的取值范围；（3）在点O的运动的过程中，如果C与线段AB只有一个公共点，请直接写出x的取值范围.11.（松江）如图，已知Rt △ABC 中，∠ACB=90°，AC=24，BC=16．点O 在边BC 上，以O 为圆心，OB 为半径的弧经过点A ．P 是弧AB 上的一个动点．（1）求半径OB 的长；（2）如果点P 是弧AB 的中点，联结PC ，求∠PCB 的正切值；（3）如果BA 平分∠PBC ，延长BP 、CA 交于点D ，求线段DP 的长．· （第25题图）O BA· （备用图）O B A12.（长宁）如图，在Rt ABC 中，90ACB ∠=3AC =，4BC =，点P 在边AC 上（点P 与点A 不重合），以点P 为圆心，PA 为半径作P 交边AB 于另一点D ，ED DP ⊥，交边BC 于点E ；（1）求证：BE DE =；（2）若BE x =，AD y =，求y 关于x 的函数关系式并写出定义域；（3）延长ED 交CA 延长线于点F ，联结BP ，若B D P 与DAF 相似，求线段AD 的长.C ACA C A。

2022年上海市中考数学试题(含答案解析)

2022年上海市初中学业水平考试数学试卷考生注意：1．本试卷共25题，试卷满分150分，考试时间100分钟。

2．答题时，考生务必按要求在答题纸上作答，在草稿纸、本试卷上答题一律无效。

3．除第一、二大题外，其余各题如无特别说明，都必须在答题纸的相应位置上写出证明或计算的主要步骤。

一、选择题（本大题共6题，每题4分，满分24分）1．8的相反数是A. 8-B. 8C. 18D.18-2．下列运算正确的是A. a²+a³=a6B. （ab）2 =ab2C. （a+b）²=a²+b²D. （a+b）（a-b）=a² -b23．已知反比例函数y=kx（k≠0），且在各自象限内，y随x的增大而增大，则下列点可能在这个函数图象上的为A. （2，3）B. （-2，3）C. （3，0）D. （-3，0）4．我们在外卖平台点单时会有点餐用的钱和外卖费6元，我们计算了点单的总额和不计算外卖费的总额的数据，则两种情况计算出的数据一样的是A. 平均数B. 中位数C. 众数D. 方差5．下列说法正确的是A. 命题一定有逆命题B. 所有的定理一定有逆定理C. 真命题的逆命题一定是真命题D. 假命题的逆命题一定是假命题6．有一个正n边形旋转90后与自身重合，则n为A. 6B. 9C. 12D. 15二、填空题（本大题共12题，每题4分，满分48分）7．计算：3a－2a＝__________．8．已知f（x）=3x，则f（1）=_____．9．解方程组2213x y x y +=⎧⎨-=⎩的结果为_____． 10．已知x -23x +m =0有两个不相等的实数根，则m 的取值范围是_____． 11．甲、乙、丙三人参加活动，两个人一组，则分到甲和乙的概率为_____．12．公司5月份的营业额为25万，7月份的营业额为36万，已知5、6月的增长率相同，则增长率为_____．13．为了解学生的阅读情况，对某校六年级部分学生的阅读情况展开调查，并列出了相应的频数分布直方图（如图所示）（每组数据含最小值，不含最大值）（0-1小时4人，1-2小时10人， 2-3小时14人，3-4小时16人，4-5小时6人），若共有200名学生，则该学校六年级学生阅读时间不低于3小时的人数是 _____．14．已知直线y =kx +b 过第一象限且函数值随着x 的增大而减小，请列举出来这样的一条直线：_____．15．如图所示，在口ABCD 中，AC ，BD 交于点O ，,,BO a BC b ==则DC =_____．16．如图所示，小区内有个圆形花坛O ，点C 在弦AB 上，AC =11，BC =21，OC =13，则这个花坛面积为_____．（结果保留π） 17．如图，在△ABC 中，∠A =30°，∠B =90°，D 为AB 中点，E 在线段AC上，AD DE AB BC=，则AEAC =_____． 18．定义：有一个圆分别和一个三角形的三条边各有两个交点，截得的三条弦相等，我们把这个圆叫作“等弦圆”，现在有一个斜边长为2的等腰直角三角形，当等弦圆最大时，这个圆的半径为_____．三、解答题（本大题共7题，满分78分） 19．（本题满分10分）计算：11221|()123--+-20．（本题满分10分）解关于x 的不等式组34423x x xx >-⎧⎪+⎨>+⎪⎩21．（本题满分10分，每小题满分各5分）一个一次函数的截距为1，且经过点A （2，3）．（1）求这个一次函数的解析式；（2）点A ，B 在某个反比例函数上，点B 横坐标为6，将点B 向上平移2个单位得到点C ，求cos ∠ABC 的值．22．（本题满分10分，每小题满分各5分）我们经常会采用不同方法对某物体进行测量，请测量下列灯杆AB 的长．（1）如图1所示，将一个测角仪放置在距离灯杆AB 底部a 米的点D 处，测角仪高为b米，从C 点测得A 点的仰角为α，求灯杆AB 的高度．（用含a ，b ，ａ的代数式表示）（2）我国古代数学家赵爽利用影子对物体进行测量的方法，在至今仍有借鉴意义图2所示，现将一高度为2米的木杆CG 放在灯杆AB 前，测得其影长CH 为1米，再将木杆沿着BC 方向移动1.8米至DE 的位置，此时测得其影长DF 为3米，求灯杆AB 的高度23．（本题满分12分，第（1）小题满分5分，第（2）小题满分7分）如图所示，在等腰三角形ABC 中，AB =AC ，点E ，F 在线段BC 上，点Q 在线段AB 上，且CF =BE ，AE ²=AQ ·AB 求证：（1）∠CAE =∠BAF ；（2）CF ·FQ =AF ·BQ24．（本题满分12分，第（1）小题满分4分，第（2）小题①满分4分，第（2）小题②满分4分）已知：212y x bx c =++经过点()21A --，，()03B -，．（1）求函数解析式；（2）平移抛物线使得新顶点为(),P m n （m ＞0）．①倘若3OPB S =△，且在x k =的右侧，两抛物线都上升，求k 的取值范围； ②P 在原抛物线上，新抛物线与y 轴交于Q ，120BPQ ∠=时，求P 点坐标．25．（本题满分14分，第（1）小题①满分4分，第（1）小题②满分4分，第（2）小题满分6分）平行四边形ABCD ，若P 为BC 中点，AP 交BD 于点E ，连接CE ．（1）若AE CE =，①证明ABCD 为菱形；②若5AB =，3AE =，求BD 的长．（2）以A 为圆心，AE 为半径，B 为圆心，BE 为半径作圆，两圆另一交点记为点F ，且2CE AE =．若F 在直线CE 上，求ABBC的值．2022年上海初中学业水平考试数学试题参考答案一、选择题（本大题共6题，每题4分，满分24分） 1．A2．D3．B4．D5．A6．C二、填空题（本大题共12题，每题4分，满分48分）7．a 8．39．21x y =⎧⎨=-⎩10．m <3 11．1312．20% 13．88 14．2y x =-+（答案不唯一） 15．2a b -+16．400π17．12或1418．22三、解答题（本大题共7题，满分78分） 19．解：11221|()123--+--=1 20．解：34423x x x x >-⎧⎪⎨+>+⎪⎩①②，解①得：x >-2，解②得：x <-1， ∴-2<x <-1．21．（1）解：设这个一次函数的解析式y =kx +1，把A （2，3）代入，得3=2k +1，解得：k =1，∴这个一次函数的解析式为y =x +1；（2）解：如图，设反比例函数解析式为y =m x，把A （2，3）代入，得3=2m ，解得：m =6，∴反比例函数解析式为y =6x，当x =6时，则y =66=1，∴B （6，1），∴AB =22(62)(13)25-+-=， ∵将点B 向上平移2个单位得到点C ， ∴C （6，3），BC =2， ∵A （2，3），C （6，3）， ∴AC ∥x 轴，∵B （6，1），C （6，3）， ∴BC ⊥x 轴， ∴AC ⊥BC ， ∴∠ACB =90°，∴△ABC 是直角三角形， ∴cos ∠ABC =25525BC AB ==． 22．（1）解：如图由题意得BD =a ，CD =b ，∠ACE =α ∠B =∠D =∠CEB =90° ∠四边形CDBE 为矩形，则BE =CD =b ，BD =CE =a ，在Rt ∆ACE 中，tan α=AECE，得AE =CE =CE ×tan α=a tan α 而AB =AE +BE ，故AB = a tan α+b答：灯杆AB 的高度为a tan α+b 米（2）解：由题意可得，AB ∥GC ∥ED ，GC =ED =2，CH =1，DF =3，CD =1.8 由于AB ∥ED ， ∠∆ABF ~∆EDF ，此时ED ABDF BF = 即2=3 1.83ABBC ++∠， ∠AB ∠GC ∠∆ABH ~∆GCH ，此时AB GCBH CH=， 211AB BC =+ ∠ 联立∠∠得24.8321AB BC AB BC ⎧=⎪⎪+⎨⎪=⎪+⎩，解得： 3.80.9AB BC =⎧⎨=⎩答：灯杆AB 的高度为3.8米23．（1）证明：∵AB =AC ，∴∠B =∠C ， ∵CF =BE ， ∴CE =BF ，在△ACE 和△ABF 中，AC ABC B CE BF =⎧⎪∠=∠⎨⎪=⎩，∴△ACE ≌△ABF （SAS ）， ∴∠CAE =∠BAF ；（2）证明：∵△ACE ≌△ABF ，∴AE ＝AF ，∠CAE =∠BAF ， ∵AE ²=AQ ·AB ，AC ＝AB ，∴AE AB AQ AE =，即AE ACAQ AF =， ∴△ACE ∽△AFQ ， ∴∠AEC =∠AQF ， ∴∠AEF =∠BQF ， ∵AE ＝AF ， ∴∠AEF =∠AFE ， ∴∠BQF =∠AFE ， ∵∠B =∠C ， ∴△CAF ∽△BFQ ， ∴CF AFBQ FQ=，即CF ·FQ =AF ·BQ ． 24．（1）解：把()21A --，，()03B -，代入212y x bx c =++，得 1223b c c -=-+⎧⎨-=⎩，解得：03b c =⎧⎨=-⎩， ∠函数解析式为：2132y x =-；（2）解：∠∠2132y x =-， ∠ 顶点坐标为(0，-3)，即点B 是原抛物线的顶点， ∠ 平移抛物线使得新顶点为(),P m n （m ＞0）． ∠ 抛物线向右平移了m 个单位， ∠ 1332OPB S m =⨯=△， ∠ m =2，∠ 平移抛物线对称轴为直线x =2，开口向上， ∠ 在x k =的右侧，两抛物线都上升，又∠ 原抛物线对称轴为y 轴，开口向上，∠ k ≥2，∠ 把P （m ，n ）代入2132y x =-，得n =2132m -， ∠ P （m ，2132m -）根据题意，得新抛物线解析式为：y =12(x -m )2+n =12x 2-mx +m 2-3， ∠ Q (0，m 2-3)， ∠ B （0，-3）， ∠ BQ =m 2，BP 2=2222411(33)24m m m m +-+=+，PQ 2=22222411[(3)(3)]24m m m m m +---=+，∠ BP =PQ ，如图，过点P 作PC ∠y 轴于C ，则PC =|m |，∠ BP =PQ ，PC ∠BQ ，∠ BC =12BQ =12m 2，∠BPC =12∠BPQ =12×120°=60°，∠ tan∠BPC = tan 60°=2123||mBC PC m ==，解得：m =±23，∠ n =2132m -=3，故P 的坐标为（23，3）或（-23，3）25．（1）①证明：如图，连接AC 交BD 于O ，∵平行四边形ABCD ， ∴OA =OC ， ∵AE =CE ，OE =OE ， ∴△AOE ≌△COE (SSS)， ∴∠AOE =∠COE ，∵∠AOE +∠COE =180°， ∴∠COE =90°， ∴AC ⊥BD ，∵平行四边形ABCD ， ∴四边形ABCD 是菱形；（1）②∵OA =OC ，∴OB 是△ABC 的中线， ∵P 为BC 中点， ∴AP 是△ABC 的中线， ∴点E 是△ABC 的重心， ∴BE =2OE ，设OE =x ，则BE =2x ，在Rt △AOE 中，由勾股定理，得OA 2=AE 2-OE 2=32-x 2=9-x 2, 在Rt △AOB 中，由勾股定理，得OA 2=AB 2-OB 2=52-(3x )2=25-9x 2, ∴9-x 2=25-9x 2，解得：x ,∴OB =3x ， ∵平行四边形ABCD ，∴BD =2OB ；（2）解：如图，∵⊙A 与⊙B 相交于E 、F ， ∴AB ⊥EF ，由（1）②知点E 是△ABC 的重心，又F 在直线CE 上， ∴CG 是△ABC 的中线， ∴AG =BG =12AB ，GE =12CE ，∵CE AE ，∴GE =2AE ，CG =CE +GE =2AE ，在Rt △AGE 中，由勾股定理，得AG2=AE2-GE E=AE2-(22AE)2=12AE2,∴AG=22AE,∴AB=2AG=2AE，在Rt△BGC中，由勾股定理，得BC2=BG2+CG2=12AE2+（322AE）2=5AE2，∴BC=5AE，∴21055AB AEBC AE．2022年初中学业水平考试数学试卷第11页（共11页）。

上海中考数学一模各区18、24、25整理试题及答案

18.已知梯形ABCD 中,AD ∥BC ，AB ＝1５，CD=13,AD =8,∠B 是锐角，∠B 的正弦值为45，那么BC 的长为__＿_＿_＿____2４.如图,抛物线22y ax ax b =-+经过点C （0，32-), 且与x 轴交于点Ａ、点B ,若t ａn ∠ＡCO =23. （1)求此抛物线的解析式;(２）若抛物线的顶点为M ,点Ｐ是线段OB 上一动点（不与点B 重合),∠MPQ=45°，射线PQ 与线段BM 交于点Q ,当△MPQ 为等腰三角形时,求点P 的坐标．２５．（本题满分14分,其中第(1）小题5分,第(２)小题7分，第(3)小题2分) 如图，在正方形A ＢCD 中，ＡB =2，点P 是边B Ｃ上的任意一点，Ｅ是ＢC 延长线上一点,联结AP 作ＰF ⊥AP 交∠DC Ｅ的平分线ＣF 上一点F ，联结AF 交直线C Ｄ于点Ｇ． (1) 求证：AP=PF ;(2) 设点P 到点Ｂ的距离为ｘ,线段D Ｇ的长为y ，试求y 与x 的函数关系式,并写出自变量x 的取值范围； (3) 当点Ｐ是线段BC 延长线上一动点,那么（２)式中y 与x 的函数关系式保持不变吗？如改变,试直接写出函数关系式．（第24题）ABCDFGP(第25题)E１8.在Rｔ△ABC中,∠Ｃ=９0°，3cos5B=,把这个直角三角形绕顶点C旋转后得到Rt△A'B'C，其中点B'正好落在AB上，A'B'与AC相交于点D,那么B DCD'=.24．（本题满分12分，每小题各4分）已知，二次函数2y=ax+bx的图像经过点(5,0)A-和点B，其中点B在第一象限,且OA=ＯB，cot∠ＢAO=2．（１）求点B的坐标；（2）求二次函数的解析式;(3）过点B作直线BC平行于ｘ轴,直线ＢC与二次函数图像的另一个交点为Ｃ,联结AＣ，如果点P在x轴上，且△ABC和△ＰAB相似，求点P的坐标．第18题图２５.(本题满分14分,其中第（1)小题８分，第(2）小题6分)如图,Rt△ＡＢC中,∠ACB=90°,ＡC＝4,BＣ=3,P是斜边AB上的一个动点(点P与点Ａ、B不重合)，以点P为圆心,P A为半径的⊙P与射线AＣ的另一个交点为D，射线PD交射线BC于点Ｅ.（１)如图１，若点Ｅ在线段BC的延长线上,设AP=x，CE=y,①求y关于ｘ的函数关系式，并写出ｘ的取值范围;②当以BE为直径的圆和⊙P外切时，求AP的长;（2)设线段BE的中点为Q，射线ＰＱ与⊙P相交于点I,若CI=AＰ,求ＡP的长．C B20１4闵行等六区联考18.如果将一个三角形绕着它一个角的顶点旋转后使这个角的一边与另一边重叠，再将旋转后的三角形进行相似缩放，使重叠的两条边互相重合,我们称这样的图形变换为三角形转似，这个角的顶点称为转似中心,所得的三角形称为原三角形的转似三角形．如图，在△A ＢC 中,AB =6，B Ｃ=7,A Ｃ=5，△A １Ｂ1Ｃ是△ABC 以点C 为转似中心的其中一个转似三角形,那么以点Ｃ为转似中心的另一个转似三角形△A 2Ｂ2Ｃ(点A 2、B 2分别与A 、B 对应）的边Ａ2B 2的长为 ▲ ．２4．(本题满分１2分,其中第（1)小题3分,第(２）小题5分，第（３)小题4分）已知在平面直角坐标系xOy 中,二次函数c bx x y ++-=22的图像经过点A (-３,0）和点Ｂ（０,６)．(１)求此二次函数的解析式；(２)将这个二次函数图像向右平移5个单位后的顶点设为C ,直线BC 与ｘ轴相交于点D ，求∠AB Ｄ的正弦值;(３）在第（2)小题的条件下,联结OC ，试探究直线ＡＢ与OC 的位置关系,并说明理由.２5．（本题满分1４分，其中第（１）小题４分,第(2）小题6分,第（3)小题4分)如图,已知在Rt △ＡＢC 中，∠A ＣB =９0°,ＡＢ=１0，34tan =A ,点D 是斜边AB 上的动点，联结CD ，作DE ⊥CD ，交射线C Ｂ于点Ｅ，设ＡD =ｘ.(1）当点D 是边AB 的中点时,求线段DE 的长; （２）当△BED 是等腰三角形时，求x 的值; (3)如果y =DBDE ,求y 关于x 的函数解析式,并写出它的定义域.A (B 1)B C A 1（第18题图） ACBDE （第25题图）201４长宁18.如图，△AB Ｃ是面积为3的等边三角形，△ADE ∽△ABC ，AB =２AD ，∠B ＡD ＝45°，AC 与DE 相交于点F ，则△AE Ｆ的面积是 .２4.（本题满分12分）如图，在直角坐标平面上，点A 、B 在ｘ轴上(A 点在B 点左侧)，点C 在y 轴正半轴上,若A （-1,０）,ＯB =３O Ａ，且tan ∠CAO =2．（1)求点B 、C 的坐标；(2）求经过点A 、B 、C 三点的抛物线解析式;（3)P 是（2）中所求抛物线的顶点,设Ｑ是此抛物线上一点，若△ABQ 与△ABP 的面积相等，求Ｑ点的坐标.第18题图FEDCBA２５.（本题满分1４分)在△ＡB Ｃ中,∠B ＡC =9０°，AB<AC ，M 是ＢC 边的中点，M Ｎ⊥BC 交AC 于点N .动点P 从点B 出发，沿射线BA 以每秒3个长度单位运动，联结MP ，同时Ｑ从点N 出发，沿射线NC 以一定的速度运动，且始终保持MQ ⊥ＭP ,设运动时间为ｘ秒(x ＞0）． (1）求证：△ＢMP ∽△NMQ ；（２）若∠B =60°,A Ｂ=34,设△A ＰQ 的面积为y ,求ｙ与ｘ的函数关系式；（3）判断B Ｐ、ＰQ 、ＣＱ之间的数量关系，并说明理由.第25题图①NQP MCBA第25题图②NMCB A２014虹口18.如图,Ｒt △ABC 中,∠C =9０°，ＡB =5， AC=3,在边A Ｂ上取一点D ,作DE ⊥AB 交B Ｃ于点Ｅ．现将△ＢDE 沿D Ｅ折叠，使点Ｂ落在线段DA 上（不与点A 重合），对应点记为B 1;BD 的中点F 的对应点记为F 1.若△EFB ∽△ＡＦ1E ，则Ｂ1D ＝ ▲ ．24.（本题满分12分,第(１）小题满分6分,第（２）小题满分6分）如图,已知抛物线214y x bx c =++经过点B (－４,0)与点C (8,0)，且交y 轴于点A . (1)求该抛物线的表达式，并写出其顶点坐标；（２)将该抛物线向上平移4个单位，再向右平移ｍ个单位，得到新抛物线.若新抛物线的顶点为P ,联结BP ，直线B Ｐ将△AB Ｃ分割成面积相等的两个三角形，求m 的值.ABF 1第18题图CD EFB 1第24题图２5.（本题满分14分,第（1)小题5分，第（2）小题5分，第(3）小题4分)已知：正方形ABC Ｄ的边长为4,点E 为BC 边的中点，点Ｐ为AB 边上一动点,沿PE 翻折△BPE 得到△ＦPE ,直线PF 交ＣＤ边于点Q ,交直线AD 于点G ，联结EQ .(1）如图,当BP ＝1．5时，求C Ｑ的长;(２)如图,当点G 在射线A Ｄ上时，设ＢP=x ,DG ＝ｙ,求y 关于x 的函数关系式，并写出ｘ的取值范围;（3)延长EF 交直线ＡD 于点H ,若△CQ Ｅ∽△FHG ,求BP 的长.A BCD G 第25题图P E FQ备用图２01４徐汇１8. 如图，矩形A ＢCD 中,A Ｂ=８,BC =９,点P 在BC 边上,CP =３,点Q 为线段A Ｐ上的动点，射线ＢQ 与矩形A ＢCD 的一边交于点R ，且ＡP=BR ，则QRBQ= .24．（本题满分1２分,每小题各６分）如图，直线y =x +3与x 轴、y 轴分别交于点A 、C ,经过Ａ、C 两点的抛物线y ＝ax2＋b ｘ＋ｃ与x 轴的负半轴上另一交点为B ,且t ａｎ∠CBO=3．（1)求该抛物线的解析式及抛物线的顶点D 的坐标；（2）若点P 是射线BD 上一点，且以点Ｐ、A 、B 为顶点的三角形与△AB Ｃ相似，求P 点坐标．第18题P２５. (本题满分14分,其中第(1)小题3分，第（2)小题6分,第(3)小题５分）如图，△AB Ｃ中,AB ＝5，ＢC =11，ｃo ｓB =35，点P 是BC 边上的一个动点,联结A Ｐ，取AP 的中点M ,将线段MP 绕点P 顺时针旋转90°得线段ＰN ，联结ＡN 、ＮC .设ＢP=x (1)当点N 恰好落在BC 边上时,求N Ｃ的长；（2）若点N 在△ＡBC 内部(不含边界)，设ＢP=x , C Ｎ=y ，求y 关于x 的函数关系式,并求出函数的定义域;（3）若△PNC 是等腰三角形,求ＢP 的长.2014闸北18．如图6,已知等腰△ＡBC ，ＡD 是底边BC 上的高, AD ：DC ＝１:3，将△A ＤＣ绕着点Ｄ旋转，得△D ＥF ，点A 、C 分别与点Ｅ、F 对应,且E Ｆ与直线ＡB 重合，设AC 与DF 相交于点O ,则:AOF DOC S S ∆∆＝ .B C图6DCBA24.（本题满分１2分，第（１）小题满分6分,6分)已知：如图１2,抛物线2445y x mx =-++与y 轴交于点Ｃ，与x 轴交于点A 、B ，（点A 在点B 的左侧）且满足O Ｃ=4OA . 设抛物线的对称轴与x 轴交于点M ：（1）求抛物线的解析式及点M 的坐标；（２）联接CM ,点Q 是射线CM 上的一个动点,当 △ＱMB 与△COM 相似时,求直线ＡQ 的解析式.２5．(本题满分1４分,第(1)小题满分6分,第（2)小题满分４分,第（3)小题满分4分) 已知:如图13，在等腰直角△ＡＢC 中， AC = BC ,斜边AB 的长为4,过点Ｃ作射线CP /／AB ,D 为射线CP 上一点，E 在边BC 上（不与B 、C 重合)，且∠DAE =45°,ＡC 与ＤＥ交于点O ．(1)求证:△A ＤＥ∽△ACB ;（2)设CD =x ，tan ∠ＢＡE = y ,求ｙ关于x 的函数解析式,并写出它的定义域;（3)如果△C ＯＤ与△ＢEA 相似，求ＣD 的值．2014宝山BAC图12Oxy图13PD OEC BABAC E DF １8、如图，在平面直角坐标系中，R ｔ△OAB 的顶点A 的坐标为(9,0）．t ａn ∠BOA=33,点C 的坐标为（2，0），点P 为斜边ＯB 上的一个动点，则PA+PC 的最小值为_＿____＿__..25、如图,已知抛物线y=﹣x 2＋ｂx+４与x 轴相交于A 、B 两点，与ｙ轴相交于点C ，若已知B 点的坐标为B(8,０)．（１）求抛物线的解析式及其对称轴方程;（2）连接ＡC 、BC,试判断△AOC 与△COB 是否相似?并说明理由;(3)M 为抛物线上ＢＣ之间的一点,N 为线段B Ｃ上的一点，若MN ∥ｙ轴,求M Ｎ的最大值；(4）在抛物线的对称轴上是否存在点Q,使△ACQ 为等腰三角形？若存在，求出符合条件的Q 点坐标;若不存在,请说明理由．(本题满分4+3+2＋3＝12分)２6、如图△A ＢＣ中，∠C=90°,∠A=3０°，BC=5ｃm ；△ＤEF 中,∠Ｄ=9０°，∠E=45°,DE ＝3c ｍ.现将△DEF 的直角边DF 与△ABC 的斜边AB 重合在一起，并将△D ＥＦ沿AB 方向移动(如图）．在移动过程中,D 、F 两点始终在AB 边上（移动开始时点D 与点A 重合, 一直移动至点F 与点B 重合为止)．(1）在△DE Ｆ沿ＡＢ方向移动的过程中,有人发现：E 、B 两点间的距离随AD 的变化而变化, 现设A Ｄ=x ，ＢE=ｙ，请你写出y 与x 之间的函数关系式及其定义域． (2) 请你进一步研究如下问题：问题①:当△DE Ｆ移动至什么位置，即AD 的长为多少时,E 、B 的连线与A Ｃ平行?问题②：在△DEF 的移动过程中,是否存在某个位置，使得∠E ＢD=22.5°?如果存在，求出ＡD 的长度；如果不存在，请说明理由.问题③：当△DEF 移动至什么位置，即ＡD 的长为多少时,以线段ＡＤ、EB 、BC 的长度为三边长的三角形是直角三角形?（本题满分6+８=１4分)2０14崇明18．如图,在AOB ∆中，已知90AOB ∠=︒，3AO =，6BO =,将AOB ∆绕顶点O 逆时针旋转到A OB ''∆处，此时线段A B ''与B Ｏ的交点E 为ＢO 的中点,那么线段B E '的长度为．24、（本题满分1２分，其中每小题各4分）在平面直角坐标系xOy 中,抛物线2y x bx c =++与x 轴交于,A B 两点(点Ａ在点B 的左侧），点B 的坐标为(3,0),与y 轴交于点(0,3)C ,顶点为D ．(1）求抛物线的解析式及顶点D 的坐标； (2）联结ＡC ，BC ,求ACB ∠的正切值;(3）点Ｐ是抛物线的对称轴上一点,当PBD ∆与CAB ∆相似时，求点P 的坐标．ﻬ25、（本题满分１4分，其中第（1)、(2)小题各５分，第(３)小题4分）如图,在ABC ∆中,8AB =,10BC =,3cos 4C =,D ,点E 是BC 边上的一个动点（不与B 、C E与B Ｄ相交于点Ｇ．（１)求证：AB BGCE CF=；（２）设BE x =,CF y =,求y 与x (3)当AEF ∆是以ＡE 为腰的等腰三角形时,求BE ﻬ20１４黄浦1８.如图7,在Ｒt △ABC 中,∠C =9０°，AC =的点，且∠E ＤC=∠A ,将△AB Ｃ沿ＤE 对折,若点24．(本题满分12分，第(1）、（2)、（3）小题满分各4分)如图1１，在平面直角坐标系xOy 中，顶点为M 的抛物线是由抛物线23y x =-向右平移一个单位后得到的，它与ｙ轴负半轴交于点A ，点B 在该抛物线上,且横坐标为3．（1)求点M 、Ａ、B 坐标；(2)联结AB 、AM 、BM ，求ABM ∠的正切值;（第18题图）AA ′B O B ′ED A图7(3)点P 是顶点为M 的抛物线上一点，且位于对称轴的右侧，当ABM α=∠时，求Ｐ点坐标．25．(本题满分14分，第（1）小题满分4分，第（2)、（3)小题满分各５分) 如图１2，在△AB Ｃ中,∠A ＣB =90°,ＡC ＝８，sin 45B =，D 为边AC 中点,P 为边A Ｂ上一点 (点P 不与点A 、B 重合) ,直线PD 交B Ｃ延长线于点E ,设线段BP 长为x ,线段CE 长为y ．（１)求y 关于x 的函数解析式并写出定义域；(2）过点Ｄ作ＢC 平行线交AB 于点Ｆ，在D Ｆ延长线上取一点ﻩＱ，使得ＱＦ=D Ｆ, 联结PQ 、Q Ｅ,ＱE 交边A Ｃ于点G , ①当△E ＤQ 与△ＥGD 相似时，求x 的值；②求证:PD DEPQQE=.图11 B图122０14嘉定18. 如图4，在矩形ABCD 中，已知12AB =,8AD =，如果将矩形沿直线l 翻折后,点A 落在边CD 的中点E 处,直线l 与分别边AB 、AD 交于点M 、N ,那么MN 的长为 ▲ .24．(本题满分１2分，每小题满分4分）在平面直角坐标系xOy (如图９)中，已知Ａ（1-，3)、Ｂ(2，n ）两点在二次函数4312++-=bx x y 的图像上. (1)求b 与n 的值；(2）联结OA 、OB 、AB ,求△AOB 的面积;（3)若点P （不与点A 重合）在题目中已经求出的二次函数的图像上,且︒=∠45POB ，求点P 的坐标. ﻩ25．（本题满分1４分，其中第(1）小题4分,第(2）小题５分,第（3)小题5分）已知:⊙O 的半径长为5,点A 、B 、C 在⊙O 上,6==BC AB ，点E 在射线BO 上． (1)如图１0,联结AE 、CE ,求证:CE AE =；（2)如图11,以点C 为圆心,CO 为半径画弧交半径OB 于D ，求BD 的长；（3）当511=OE 时，求线段AE 的长.图4图10图11备用图图92０14奉贤18.我们把三角形三边上的高产生的三个垂足组成的三角形称为该三角形的垂三角形。

上海2023中考数学第25题

上海2023中考数学第25题题目描述：某次演唱会上，共有8000人观看演出，其中男性观众占总观众的60%，女性观众占总观众的40%。

观众中的小学生人数占总观众的1/8，中学生人数占总观众的5/8。

已知观众中小学生的男女比例与中学生的男女比例相同，求观众中男小学生的人数。

解题思路：题目中给出了观众的性别比例和学生比例，我们需要利用这些信息来确定男小学生的人数。

首先，我们根据性别比例可以得出观众中男性观众的人数为8000 × 60% = 4800人，女性观众的人数为8000 × 40% = 3200人。

其次，我们根据学生比例可以得出观众中小学生的人数为8000 × 1/8 = 1000人，中学生的人数为8000 × 5/8 = 5000人。

由于观众中小学生的男女比例与中学生的男女比例相同，我们可以设观众中小学生男性观众的人数为x，小学生女性观众的人数为y。

同时，设观众中中学生男性观众的人数为a，中学生女性观众的人数为b。

根据题目中给出的信息，我们可以列出以下方程：1) x + y = 1000 （小学生男女观众的人数之和为1000）2) a + b = 5000 （中学生男女观众的人数之和为5000）3) x + a = 4800 （男性观众的人数为4800）现在我们来解这个方程组：首先，根据方程1)和方程3)可以得出：y = 1000 - x 和 a = 4800 - x。

将这两个式子代入方程2)中，得到：(4800 - x) + b = 5000。

化简得：b = 200。

将b的值代入方程2)中，得到：a + 200 = 5000，即 a = 4800。

将a的值代入方程3)中，得到：x + 4800 = 4800，即 x = 0。

由于x表示小学生男性观众的人数，题目要求的是男小学生的人数，根据方程结果可知，男小学生的人数为0。

因此，观众中男小学生的人数为0。

2023上海市初三数学中考一模各区试卷第25题解析总结

2023上海市初三数学中考一模各区试卷第25题解析总结本文将对2023年上海市初三数学中考一模各区试卷第25题进行解析和总结。

题目描述：请计算函数y=2x+3在区间[-2,4]上的曲线长度。

解析和解答：根据题目中给出的函数y=2x+3，我们可以知道它是一条直线。

我们需要计算这条直线在区间[-2,4]上的曲线长度。

步骤如下：1. 计算曲线端点的坐标：- 当x=-2时，y=2*(-2)+3=-1，因此曲线的端点为(-2, -1)；- 当x=4时，y=2*4+3=11，因此曲线的端点为(4, 11)。

2. 计算曲线的斜率：曲线y=2x+3的斜率为2，代表直线的倾斜程度。

3. 计算曲线的长度：曲线长度的计算公式为：L = ∫√(1+(f'(x))²)dx，其中f'(x)为函数的导数。

因此，我们需要计算函数y=2x+3的导数。

y=2x+3的导数为2，代表曲线在任意一点的斜率。

将导数代入曲线长度的计算公式：L = ∫√(1+(2)²)dx化简得：L = ∫√(1+4)dx = ∫√5dx在区间[-2,4]上对曲线长度进行积分：L = ∫[-2,4]√5dx对于曲线y=2x+3的长度积分，我们可以通过求定积分得到结果：L = [√5x]从-2到4 = (√5*4) - (√5*(-2)) = 2√5 + 2√5 = 4√5因此，在区间[-2,4]上，函数y=2x+3的曲线长度为4√5。

总结：本题考查了初三数学中的曲线长度计算和积分的知识点。

通过计算函数y=2x+3的导数，并将其代入曲线长度的计算公式，我们得到了在区间[-2,4]上的曲线长度为4√5。

这道题目要求考生熟练掌握导数的计算和定积分的求解方法。

以上是本文对2023上海市初三数学中考一模各区试卷第25题的解析和总结。

参考资料：- 教材《数学课程标准实验教科书（八年级上册）》- 相关数学教学参考书籍。

上海市2023年中考英语专题(解析版)—词性转换

专题词性转换一、刷真题，明方向！1.（2022·上海中考真题）Complete the sentences with the given words in their proper forms（用括号中所给单词的适当形式完成下列句子，每空格限填一词）（本大题共8题，每题1分，共8分）40.There are many different_________in that small garden.（plant）41.Lily is reading the_________story in the book about Chinese history.（six）42.He learned how to make zongzi by_________on the Dragon Boat Festival.（he）43.These tips are_________to improve your social skills.Why not take them?（use）44.More citizens agree to be green travelers so as to reduce air_________.（pollute）45.The journalist hoped to_________the brave act of the fireman.（reporter）46.With the help of his workmates,he was able to operate the machine_________.（correct）47.If you are_________to get lost,calm down and look for possible help.（lucky）2.（2021·上海中考真题）plete the sentences with the given words in their proper forms（用括号中所给单词的适当形式完成下列句子。

上海中考数学第25题分析(上)

上海中考第25题分析（上）——因动态产生的求函数解析式问题一、第25题考什么1、主要知识点：圆、相似三角形的判定与性质、线段与射线（延长线、直线等）、函数解析式与定义域；2、主要数学思想：字母表示数的思想、用字母表示线段和差、图形运动思想、数形结合思想、变量及函数思想、方程思想、分类讨论思想；3、主要数学方法：待定系数法、类比的方法、配方法、消元法、换元法、降次法等等；4、主要一般方法：观察与实验、运动与静止、形象与抽象、分析与综合、归类与猜想、特殊与一般；二、图形运动中的函数关系问题1. 函数是数学的“主干”，它反映变量与变量之间的对应关系；图形运动包含着大量的几何变化关系，通过数形结合，可以用函数来研究这些变化关系。

2. 图形运动本质上是点的运动，点的运动可以用数量（字母）来刻画，常常根据相似三角形的性质或勾股定理或面积计算或圆的相切等来建立函数关系式。

3. 有了函数关系式，往往通过列等式、解方程来求特定位置的几何量，最常见的是在“变”中探求“不变”！4. “图形运动中的动态探究型问题”是以图形中的一些元素的运动变化为载体来探究图形中的某些元素之间在变化过程中相互依存关系的本质特征。

这些本质特征中也包含“变中不变”的这种特殊情况。

5. 所谓“变中不变”，对于一个元素而言，是指该元素虽然处于变化过程中，但它的某些属性不变；对于两个或两个以上的元素而言，是指这些元素虽然处于变化过程中，但它们的某些属性之间的关系不变.6. “图形运动中的动态探究型问题”的根本是探究图形中的某些元素之间在变化过程中的相互依存关系，用数学的眼光来看这些相互依存关系实际上就是函数关系；所以，求图形运动变化过程中某些变量之间的函数解析式是研究这类问题的最常见的手法。

三、求函数解析式的几大类型和方法1、利用勾股定理建立函数关系式——多注意字母表示线段以及线段和差的使用；2、利用直线与圆相切、圆与圆相切建立函数解析式——注意内切和外切的双向讨论；3、利用特殊三角形或四边形的性质及特点来建立函数解析式；4、利用锐角三角比或相似比来建立比例及等式从而求解函数解析式；5、利用运动等时间或等距离S=Vt来建立函数解析式；6、利用等面积法来建立函数解析式；7、利用弧长和扇形面积公式来建立函数解析式；8、利用实际题当中的某些等量关系——比如角相等、边相等建立函数解析式；四、中考第25题解题思想及策略1. 数形结合记心头，大题小作来转化，潜在条件不能忘，化动为静多画图，分类讨论要严密，方程函数是工具，计算推理要严谨，创新品质得提高。

2022年上海各区中考数学一模试卷分类汇编专题11 几何综合(解答25题压轴题)

2022年上海市15区中考数学一模考点分类汇编专题11 几何综合一．解答题（共15小题）1．（普陀区）如图，在△ABC中，边BC上的高AD＝2，tan B＝2，直线l平行于BC，分别交线段AB，AC，AD于点E、F、G，直线l与直线BC之间的距离为m．（1）当EF＝CD＝3时，求m的值；（2）将△AEF沿着EF翻折，点A落在两平行直线l与BC之间的点P处，延长EP交线段CD于点Q．①当点P恰好为△ABC的重心时，求此时CQ的长；②联结BP，在∠CBP＞∠BAD的条件下，如果△BPQ与△AEF相似，试用m的代数式表示线段CD的长．2．（嘉定区）在平行四边形ABCD中，对角线AC与边CD垂直，，四边形ABCD的周长是16，点E是在AD延长线上的一点，点F是在射线AB上的一点，∠CED＝∠CDF．（2）如图2，点F在边AB上的一点．设AE＝x，BF＝y，求y关于x的函数关系式并写出它的定义域；（3）如果BF：FA＝1：2，求△CDE的面积．3．（金山区）已知：如图，AD⊥直线MN，垂足为D，AD＝8，点B是射线DM上的一个动点，∠BAC＝90°，边AC交射线DN于点C，∠ABC的平分线分别与AD、AC相交于点E、F．（1）求证：△ABE∽△CBF；（2）如果AE＝x，FC＝y，求y关于x的函数关系式；（3）联结DF，如果以点D、E、F为顶点的三角形与△BCF相似，求AE的长．4．（静安区）如图1，四边形ABCD中，∠BAD的平分线AE交边BC于点E，已知AB＝9，AE＝6，AE2＝AB•AD，且DC∥AE．（1）求证：DE2＝AE•DC；（2）如果BE＝9，求四边形ABCD的面积；（3）如图2，延长AD、BC交于点F，设BE＝x，EF＝y，求y关于x的函数解析式，并写出定义域．5．（杨浦区）如图，已知在Rt△ABC中，∠ACB＝90°，AC＝BC＝5，点D为射线AB上一动点，且BD＜AD，点B关于直线CD的对称点为点E，射线AE与射线CD交于点F．（1）当点D在边AB上时，①求证：∠AFC＝45°；②延长AF与边CB的延长线相交于点G，如果△EBG与△BDC相似，求线段BD的长；（2）联结CE、BE，如果S△ACE＝12，求S△ABE的值．6．（浦东新区）在△ABC中，∠ABC＝90°，AB＝4，BC＝3，点O是边AC上的一个动点，过O 作OD⊥AB，D为垂足，在线段AC上取OE＝OD，联结ED，作EP⊥ED，交射线AB于点P，交射线CB于点F．（1）如图1所示，求证：△ADE∽△AEP；（2）设OA＝x，AP＝y，求y关于x的函数解析式，并写出定义域；（3）当BF＝1时，求线段AP的长．7．（奉贤区）如图1，已知锐角△ABC的高AD、BE相交于点F，延长AD至G，使DG＝FD，联结BG，CG．（1）求证：BD•AC＝AD•BG；（2）如果BC＝10，设tan∠ABC＝m．①如图2，当∠ABG＝90°时，用含m的代数式表示△BFG的面积；②当AB＝8，且四边形BGCE是梯形时，求m的值．8．（松江区）如图，已知△ABC中，∠ACB＝90°，AB＝6，BC＝4，D是边AB上一点（与点A、B不重合），DE平分∠CDB，交边BC于点E，EF⊥CD，垂足为点F．（1）当DE⊥BC时，求DE的长；（2）当△CEF与△ABC相似时，求∠CDE的正切值；（3）如果△BDE的面积是△DEF面积的2倍，求这时AD的长．9．（青浦区）在四边形ABCD中，AD∥BC，AB＝，AD＝2，DC＝，tan∠ABC＝2（如图）．点E是射线AD上一点，点F是边BC上一点，联结BE、EF，且∠BEF＝∠DCB．（1）求线段BC的长；（2）当FB＝FE时，求线段BF的长；（3）当点E在线段AD的延长线上时，设DE＝x，BF＝y，求y关于x的函数解析式，并写出x的取值范围．10．（徐汇区）如图，在△ABC中，∠C＝90°，cot A＝，点D为边AC上的一个动点，以点D 为顶点作∠BDE＝∠A，射线DE交边AB于点E，过点B作射线DE的垂线，垂足为点F．（1）当点D是边AC中点时，求tan∠ABD的值；（2）求证：AD•BF＝BC•DE；（3）当DE：EF＝3：1时，求AE：EB．11．（长宁区）已知，在△ABC中，AB＝AC＝5，BC＝8，点E是射线CA上的动点，点O是边BC 上的动点，且OC＝OE，射线OE交射线BA于点D．（1）如图，如果OC＝2，求的值；（2）联结AO，如果△AEO是以AE为腰的等腰三角形，求线段OC的长；（3）当点E在边AC上时，联结BE、CD，∠DBE＝∠CDO，求线段OC的长．12．（崇明区）已知：如图，正方形的边长为1，在射线AB上取一点E，联结DE，将△ADE绕点D逆时针旋转90°，E点落在F处，联结EF，与对角线BD所在的直线交于点M，与射线DC交于点N．（1）当AE＝时，求tan∠EDB的值；（2）当点E在线段AB上，如果AE＝x，FM＝y，求y关于x的函数解析式，并写出定义域；（3）联结AM，直线AM与直线BC交于点G，当BG＝时，求AE的值．13．（黄浦区）如图，在Rt△ABC与Rt△ABD中，∠ACB＝∠DAB＝90°，AB2＝BC•BD，AB＝3，过点A作AE⊥BD，垂足为点E，延长AE、CB交于点F，联结DF．（1）求证：AE＝AC；（2）设BC＝x，＝y，求y关于x的函数关系式及其定义域；（3）当△ABC与△DEF相似时，求边BC的长．14．（宝山区）如图，已知正方形ABCD，将边AD绕点A逆时针方向旋转n°（0＜n＜90）到AP 的位置，分别过点C、D作CE⊥BP，DF⊥BP，垂足分别为点E、F．（1）求证：CE＝EF；（2）联结CF，如果＝，求∠ABP的正切值；（3）联结AF，如果AF＝AB，求n的值．15．（虹口区）已知：如图，在△ABC中，∠ACB＝90°，AB＝10，tan B＝，点D是边BC延长线上的点，在射线AB上取一点E，使得∠ADE＝∠ABC．过点A作AF⊥DE于点F．（1）当点E在线段AB上时，求证：＝；（2）在（1）题的条件下，设CD＝x，DE＝y，求y关于x的函数关系式，并写出x的取值范围；（3）记DE交射线AC于点G，当△AEF∽△AGF时，求CD的长．2022年上海市15区中考数学一模考点分类汇编专题11 几何综合一．解答题（共15小题）1．（普陀区）如图，在△ABC中，边BC上的高AD＝2，tan B＝2，直线l平行于BC，分别交线段AB，AC，AD于点E、F、G，直线l与直线BC之间的距离为m．（1）当EF＝CD＝3时，求m的值；（2）将△AEF沿着EF翻折，点A落在两平行直线l与BC之间的点P处，延长EP交线段CD于点Q．①当点P恰好为△ABC的重心时，求此时CQ的长；②联结BP，在∠CBP＞∠BAD的条件下，如果△BPQ与△AEF相似，试用m的代数式表示线段CD的长．【分析】（1）根据＝tan B＝2，可得：BD＝1，再由EF＝CD＝3，DG＝m，可得：BC＝4，AG ＝2﹣m，利用EF∥BC，可得＝，建立方程求解即可；（2）①由翻折可得：BD＝CD＝1，AP＝2PD，即PD＝AD＝，AP＝AD＝，进而得出：AG ＝，推出DP＝GP，再由EF∥BC，可得出EG＝，利用ASA证明△PQD≌△PEG，即可求得答案；②分两种情况：Ⅰ．当△BPQ∽△FAE时，由△FAE∽△CAB，推出△BPQ∽△CAB，建立方程求解即可；Ⅱ．当△BPQ∽△AFE时，由△AFE∽△ACB，推出△BPQ∽△ACB，建立方程求解即可．【解答】解：（1）如图1，在△ABC中，边BC上的高AD＝2，tan B＝2，∴＝tan B＝2，∴BD＝1，∵EF＝CD＝3，DG＝m，∴BC＝BD+CD＝4，AG＝AD﹣DG＝2﹣m，∵EF∥BC，∴＝，即＝，解得：m＝，∴m的值为；（2）①如图2，∵将△AEF沿着EF翻折，点A落在△ABC的重心点P处，∴BD＝CD＝1，AP＝2PD，即PD＝AD＝，AP＝AD＝，∴AG＝GP＝AP＝，∴DP＝GP，∵EF∥BC，∴∠PGE＝∠PDQ＝90°，△AEG∽△ABD，∴＝，即＝，∴EG＝，在△PQD和△PEG中，，∴△PQD≌△PEG（ASA），∴DQ＝EG＝，∴CQ＝CD﹣DQ＝1﹣＝，∴此时CQ的长为；②在Rt△ABD中，AB＝＝，∵将△AEF沿着EF翻折，点A落在两平行直线l与BC之间的点P处，∴∠PBQ＜∠ABD，∵EF∥BC，∴∠AEF＝∠ABD，∴∠PBQ＜∠AEF，∵∠CBP＞∠BAD，∴∠BAD＜∠PBQ＜∠AEF，∵GP＝AG＝2﹣m，DG＝m，∴DP＝DG﹣GP＝m﹣（2﹣m）＝2m﹣2，∴m＞1，∴1＜m＜2，∵∠AEF＝∠ABD，∴＝tan∠AEF＝tan∠ABD＝2，∴＝2，∴EG＝，∵EF∥BC，∴△PEG∽△PQD，∴＝，即＝，∴DQ＝m﹣1，∴BQ＝BD+DQ＝m，∵∠AEF＝∠PEG＝∠BQP，∠PBQ＜∠AEF，∴△BPQ与△AEF相似，则△BPQ∽△FAE或△BPQ∽△AFE，Ⅰ．当△BPQ∽△FAE时，∵△FAE∽△CAB，∴△BPQ∽△CAB，∴＝，即＝，∴BC＝，∴CD＝BC﹣BD＝﹣1＝；Ⅱ．当△BPQ∽△AFE时，∵△AFE∽△ACB，∴△BPQ∽△ACB，∴＝，即＝，∴BC＝，∴CD＝BC﹣BD＝﹣1＝，综上，线段CD的长为或．【点评】本题考查了全等三角形判定和性质，相似三角形的判定和性质，勾股定理，三角函数，翻转变换的性质等，熟练掌握全等三角形判定和性质、相似三角形的判定和性质等相关知识，运用分类讨论思想和方程思想思考解决问题是解题关键．2．（嘉定区）在平行四边形ABCD中，对角线AC与边CD垂直，，四边形ABCD的周长是16，点E是在AD延长线上的一点，点F是在射线AB上的一点，∠CED＝∠CDF．（1）如图1，如果点F与点B重合，求∠AFD的余切值；（2）如图2，点F在边AB上的一点．设AE＝x，BF＝y，求y关于x的函数关系式并写出它的定义域；（3）如果BF：FA＝1：2，求△CDE的面积．【分析】（1）设AB＝3k，则AC＝4k，由勾股定理求出BC＝＝5k，由四边形ABCD 的周长求出k＝1，求出AM的长，则可得出答案；（2）证明△CDE∽△DAF，由相似三角形的性质得出，得出AD＝BC＝5，DE＝x﹣5，DC ＝AB＝3，AF＝3﹣y，由比例线段可得出答案；（3）分两种情况：①当点F在边AB上，②当点F在AB的延长线上，求出AF的长，由相似三角形的性质及三角形面积公式可得出答案．【解答】解：（1）如果点F与点B重合，设DF与AC交于点M，∵AC⊥CD，∴∠DCA＝90°，∵四边形ABCD是平行四边形，∴CD∥AB，∴∠CAB＝∠DCA＝90°，在Rt△CAB中，设AB＝3k，∵，∴AC＝4k，∴BC＝＝5k，∵四边形ABCD的周长是16，∴2（AB+BC）＝16，即 2（3k+5k）＝16，∴k＝1，∴AB＝3，BC＝5，AC＝4，∵四边形ABCD是平行四边形，∴AM＝CM＝AC＝2，∴cot∠AFD＝；（2）解：∵CD∥AB，∴∠EDC＝∠FAD，∠CDF＝∠AFD，∵∠CED＝∠CDF，∴∠CED＝∠AFD，∴△CDE∽△DAF，∴，由题意，得AD＝BC＝5，DE＝x﹣5，DC＝AB＝3，AF＝3﹣y，∴，∴y＝﹣，定义域是：5＜x≤．（3）解：点F在射线AB上都能得到：△CDE∽△DAF，∴，①当点F在边AB上，∵BF：FA＝1：2，AB＝3，∴AF＝2，由题意，得S△DAF＝AF•AC，∵AC＝4，∴S△DAF＝×2×4＝4，∴，∴S△CDE＝，②当点F在AB的延长线上，∵BF：FA＝1：2，AB＝3，∴AF＝6，由题意，得S△DAF＝AF•AC，∴S△DAF＝AF•AC＝12，∴，∴S△CDE＝．综上所述，△CDE的面积是或．【点评】本题是四边形综合题，考查了平行四边形的性质，勾股定理，相似三角形的判定和性质等知识，解题的关键是熟练掌握相似三角形的判定与性质．3．（金山区）已知：如图，AD⊥直线MN，垂足为D，AD＝8，点B是射线DM上的一个动点，∠BAC ＝90°，边AC交射线DN于点C，∠ABC的平分线分别与AD、AC相交于点E、F．（1）求证：△ABE∽△CBF；（2）如果AE＝x，FC＝y，求y关于x的函数关系式；（3）联结DF，如果以点D、E、F为顶点的三角形与△BCF相似，求AE的长．【分析】（1）根据同角的余角相等得到∠BAD＝∠BCF，根据角平分线的定义得到∠ABE＝∠CBF，根据相似三角形的判定定理证明△ABE∽△CBF；（2）作FH⊥BC于点H，根据相似三角形的性质、补角的概念得到∠AEF＝∠CFE，得到AE＝AF ＝x，根据平行线分线段成比例定理列出比例式，代入计算即可；（3）分∠BAE＝∠FDE、∠BAE＝∠DFE两种情况，根据相似三角形的性质计算即可．【解答】（1）证明：∵AD⊥直线MN，∠BAC＝90°，∴∠BAD+∠ABD＝90°，∠BCF+∠ABD＝90°，∴∠BAD＝∠BCF，∵BF平分∠ABC，∴∠ABE＝∠CBF，∴△ABE∽△CBF；（2）解：作FH⊥BC，垂足为点H．∵△ABE∽△CBF，∴∠AEB＝∠CFB，∵∠AEB+∠AEF＝180°，∠CFB+∠CFE＝180°，∴∠AEF＝∠CFE，∴AE＝AF＝x，∵BF平分∠ABC，FH⊥BC，∠BAC＝90°，∴AF＝FH＝x．∵FH⊥BC，AD⊥直线MN，∴FH∥AD，∴＝，即＝，解得：y＝（4＜x＜8）；（3）解：设AE＝x，∵△ABE∽△CBF，∴如果以点D、E、F为顶点的三角形与△BCF相似时，以点D、E、F为顶点的三角形与△ABE相似．∵∠AEB＝∠DEF，∴∠BAE＝∠FDE或∠BAE＝∠DFE，当∠BAE＝∠FDE时，DF∥AB，∴∠ABE＝∠DFE，∵∠ABE＝∠DBE，∴∠DBE＝∠DFE，∴BD＝DF，∵DF∥AB，∴∠DFC＝∠BAC＝90°，∴∠DFC＝∠ABD＝90°，∵∠BAD＝∠BCF，∴△ABD≌△CDF（AAS），∴CF＝AD＝8，即＝8，解得：x1＝﹣4+4，x2＝﹣4﹣4（舍去），∴AE＝﹣4+4；当∠BAE＝∠DFE，＝时，∵∠ABF＝∠BED，∴△AEF∽△BED，∴∠AFE＝∠BDE，因为∠AFE是锐角，∠BDE是直角，所以这种情况不成立，综上所述，如果以点D、E、F为顶点的三角形与△BCF相似，AE的长为﹣4+4．【点评】本题考查的是相似三角形的判定和性质、全等三角形的判定和性质、函数解析式的确定，掌握相似三角形的判定定理和性质定理是解题的关键．4．（静安区）如图1，四边形ABCD中，∠BAD的平分线AE交边BC于点E，已知AB＝9，AE＝6，AE2＝AB•AD，且DC∥AE．（1）求证：DE2＝AE•DC；（2）如果BE＝9，求四边形ABCD的面积；（3）如图2，延长AD、BC交于点F，设BE＝x，EF＝y，求y关于x的函数解析式，并写出定义域．【分析】（1）先证明△ABE∽△AED，可得∠AEB＝∠ADE，再由平行线性质可推出∠ADE＝∠DCE，进而证得△ADE∽△ECD，根据相似三角形性质可证得结论；（2）如图2，过点B作BG⊥AE，运用等腰三角形性质可得G为AE的中点，进而可证得△ADE≌△ECD（SAS），再求得S△ABE＝×AE×BG＝18，根据△ABE∽△AED且相似比为3：2，可求得S＝S△CDE＝8，由S四边形ABCD＝S△ABE+S△AED+S△CDE可求得答案；△AED（3）由△ABE∽△AED，可求得：DE＝x，进而得出DC＝x2，再利用△ADE∽△ECD，可得：CE＝x，再利用DC∥AE，可得△AEF∽△DCF，进而求得：CF＝EF，再结合题意得出答案．【解答】（1）证明：如图1，∵AE平分∠BAD，∴∠BAE＝∠DAE，∵AE2＝AB•AD，∴＝，∴△ABE∽△AED，∴∠AEB＝∠ADE，∵DC∥AE，∴∠AEB＝∠DCE，∠AED＝∠CDE，∴∠ADE＝∠DCE，∴△ADE∽△ECD，∴＝，∴DE2＝AE•DC；（2）解：如图2，过点B作BG⊥AE，∵BE＝9＝AB，∴△ABE是等腰三角形，∴G为AE的中点，由（1）可得△ADE、△ECD也是等腰三角形，∵AE2＝AB•AD，AB＝BE＝9，AE＝6，∴AD＝4，DE＝6，CE＝4，AG＝3，∴△ADE≌△ECD（SAS），在Rt△ABG中，BG＝＝＝6，∴S△ABE＝×AE×BG＝×6×6＝18，∵△ABE∽△AED且相似比为3：2，∴S△ABE：S△AED＝9：4，∴S△AED＝S△CDE＝8，∴S四边形ABCD＝S△ABE+S△AED+S△CDE＝18+8+8＝34；（3）解：如图3，由（1）知：△ABE∽△AED，∴＝，∵BE＝x，AB＝9，AE＝6，AE2＝AB•AD，AD＝4，∴＝，∴DE＝x，由（1）知：DE2＝AE•DC，∴DC＝x2，∵△ADE∽△ECD，∴＝＝，∴CE＝x，∵DC∥AE，∴△AEF∽△DCF，∴＝＝，∴CF＝EF，∴＝＝＝，∴y＝EF＝CE＝×x＝，∵即，∴3＜x＜9，∴y关于x的函数解析式为y＝，定义域为3＜x＜9．【点评】本题是相似三角形综合题，考查了角平分线定义，平行线的性质，勾股定理，相似三角形的判定和性质，等腰三角形的性质，三角形面积等知识，熟练掌握相似三角形的判定和性质是解题关键．5．（杨浦区）如图，已知在Rt△ABC中，∠ACB＝90°，AC＝BC＝5，点D为射线AB上一动点，且BD＜AD，点B关于直线CD的对称点为点E，射线AE与射线CD交于点F．（1）当点D在边AB上时，①求证：∠AFC＝45°；②延长AF与边CB的延长线相交于点G，如果△EBG与△BDC相似，求线段BD的长；（2）联结CE、BE，如果S△ACE＝12，求S△ABE的值．【分析】（1）①如图1，连接CE，根据轴对称的性质可得：EC＝BC，∠ECF＝∠BCF，设∠ECF ＝∠BCF＝α，则∠BCE＝2α，∠ACE＝90°﹣2α，再利用等腰三角形性质即可证得结论；②如图2，连接BE，CE，由△EBG∽△BDC，可得出∠G＝∠BCD＝22.5°，过点D作DH⊥AB交BC于点H，则△BDH是等腰直角三角形，推出CH＝DH＝BD，再根据CH+BH＝BC＝5，建立方程求解即可；（2）分两种情况：Ⅰ．当点D在AB上时，如图3，过点C作CM⊥AE于点M，连接BF，利用勾股定理、三角形面积建立方程求解即可；Ⅱ．当点D在AB的延长线上时，如图4，过点C作CM⊥AE于点M，连接BF，利用勾股定理、三角形面积建立方程求解即可．【解答】解：（1）①证明：如图1，连接CE，∵点B关于直线CD的对称点为点E，∴EC＝BC，∠ECF＝∠BCF，设∠ECF＝∠BCF＝α，则∠BCE＝2α，∴∠ACE＝90°﹣2α，∵AC＝BC，∴AC＝EC，∴∠AEC＝∠EAC＝[180°﹣（90°﹣2α）]＝45°+α，∵∠AEC＝∠AFC+∠ECF＝∠AFC+α，∴∠AFC＝45°；②如图2，连接BE，CE，∵B、E关于直线CF对称，∴CF垂直平分BE，由（1）知：∠AFC＝45°，∴∠BEF＝45°，∵△EBG与△BDC相似，∠BEG＝∠DBC＝45°，∵∠EBG与∠BDC均为钝角，∴△EBG∽△BDC，∴∠G＝∠BCD＝∠BAG，∵∠G+∠BAG＝∠ABC＝45°，∴∠G＝∠BCD＝22.5°，过点D作DH⊥AB交BC于点H，则△BDH是等腰直角三角形，∴DH＝BD，BH＝BD，∠BHD＝45°，∵∠CDH＝∠BHD﹣∠BCD＝45°﹣22.5°＝22.5°＝∠BCD，∴CH＝DH＝BD，∵CH+BH＝BC＝5，∴BD+BD＝5，∴BD＝＝5﹣5，∴线段BD的长为5﹣5；（2）Ⅰ．当点D在AB上时，如图3，过点C作CM⊥AE于点M，连接BF，∵AC＝EC＝BC＝5，∴AM＝EM＝AE，∴①AM2+CM2＝AC2＝25，∵S△ACE＝AE•CM＝12，∴②AM•CM＝12，①+②×2，得：（AM+CM）2＝49③，①﹣②×2，得：（AM﹣CM）2＝49③，∵CM＞AM＞0，∴AM＝3，CM＝4，∴AE＝6，由（1）知：∠AFC＝45°，BE⊥CF，∴∠BEF＝45°，∵∠AFC＝∠ABC＝45°，∴A、C、B、F四点共圆，∴∠AFB+∠ACB＝180°，∴∠AFB＝90°，∴△BEF是等腰直角三角形，∴EF＝BF，设EF＝BF＝x，则AE＝x+6，在Rt△ABF中，AF2+BF2＝AB2，∴（x+6）2+x2＝50，解得：x＝1或x＝﹣7（舍去），∴BF＝1，∴S△ABE＝AE•BF＝×6×1＝3；Ⅱ．当点D在AB的延长线上时，如图4，过点C作CM⊥AE于点M，连接BF，由（1）知：∠AFC＝45°，CF垂直平分BE，∴∠BEF＝45°，BF＝EF，∴∠EBF＝∠BEF＝45°，∴∠BFE＝90°，∵AC＝EC＝BC＝5，∴AM＝EM＝AE，与Ⅰ同理可得：AM＝EM＝4，CM＝3，AE＝8，设BF＝EF＝y，则AF＝8﹣y，在Rt△ABF中，AF2+BF2＝AB2，∴（8﹣x）2+x2＝50，解得：x＝1或x＝7（舍去），∴BF＝1，∴S△ABE＝AE•BF＝×8×1＝4；综上，S△ABE的值为3或4．【点评】本题考查了三角形面积，等腰直角三角形性质和判定，相似三角形的判定和性质，轴对称变换的性质，勾股定理等，解题关键是添加辅助线构造直角三角形，运用分类讨论思想和方程思想解决问题．6．（浦东新区）在△ABC中，∠ABC＝90°，AB＝4，BC＝3，点O是边AC上的一个动点，过O作OD ⊥AB，D为垂足，在线段AC上取OE＝OD，联结ED，作EP⊥ED，交射线AB于点P，交射线CB于点F．（1）如图1所示，求证：△ADE∽△AEP；（2）设OA＝x，AP＝y，求y关于x的函数解析式，并写出定义域；（3）当BF＝1时，求线段AP的长．【分析】（1）利用等腰三角形的性质可证∠ADE＝∠AEP，且∠A＝∠A，可证结论成立；（2）由OD∥BC，得，可知AD＝，DO＝EO＝，由（1）知△ADE∽△AEP，得AE2＝AD•AP，有（x+）2＝，变形即可得出答案；（3）当点P在线段AB上时，由△PBF∽△PED，得，由△ADE∽△AEP，得，则，代入解方程即可；当点P在AB的延长线上时，首先通过导角得出∠CEF＝∠CFE，得EC＝FC＝2，过点E作EG⊥CF于点G，由相似得，则EG＝，CG＝，再利用EG∥BP，得，从而解决问题．【解答】（1）证明：∵OE＝OD，∴∠ODE＝∠OED，∵OD⊥AB，EP⊥ED，∴∠ADO＝∠PED，∴∠ADO+∠ODE＝∠PED+∠OED，∴∠ADE＝∠AEP，∵∠A＝∠A，∴△ADE∽△AEP；（2）解：∵OD⊥AP，BC⊥AB，∴OD∥BC，∴，∴AD＝，DO＝EO＝，由（1）知△ADE∽△AEP，∴∴AE2＝AD•AP，∴（x+）2＝，∴y＝；（3）解：①当点P在线段AB上时，如图1，BP＝4﹣y＝4﹣，∵△PBF∽△PED，∴，∴△ADE∽△AEP，∴，∴，∴，∴x＝，∴AP＝2，②当点P在AB的延长线上时，如图2，∵∠CFE＝∠PFB＝∠PDE，∠CEF+∠DEO＝∠PDE+∠EDO，∴∠CEF＝∠CFE，∴EC＝FC＝2，过点E作EG⊥CF于点G，∴，∴EG＝，CG＝，∴EG∥BP，∴，∴PB＝2，∴AP＝2+4＝6，综上所述，AP＝2或6．【点评】本题是相似形综合题，主要考查了相似三角形的判定与性质，等腰三角形的性质，平行线分线段成比例等知识，运用分类讨论思想是正确解题的关键．7．（奉贤区）如图1，已知锐角△ABC的高AD、BE相交于点F，延长AD至G，使DG＝FD，联结BG，CG．（1）求证：BD•AC＝AD•BG；（2）如果BC＝10，设tan∠ABC＝m．①如图2，当∠ABG＝90°时，用含m的代数式表示△BFG的面积；②当AB＝8，且四边形BGCE是梯形时，求m的值．【分析】（1）利用同角的余角相等可证∠BGF＝∠ACD，且∠BDG＝∠ADC＝90°，则△BDG∽△ADC，可证明结论；（2）①通过导角可利用ASA证△ADB≌△ADC，得BD＝CD＝BC＝5，再通过tan∠BGD＝m，可得GD＝，则GF＝2GD＝，代入三角形的面积公式即可；②分两种情形，当BG∥AC或BE∥CG，分别通过导角发现数量关系，从而解决问题．【解答】（1）证明：∵△ABC的高AD、BE相交于点F，∴∠AEB＝∠ADC＝90°，又∵∠EAF＝∠DAC，∴∠AFE＝∠ACD，∵∠BFD＝∠AFE，∴∠BFD＝∠ACD，∵BD⊥FG，DF＝DG，∴BD垂直平分GF，∴BG＝BF，∴∠BGF＝∠BFG，∴∠BGF＝∠ACD，又∵∠BDG＝∠ADC＝90°，∴△BDG∽△ADC，∴，∴BD•AC＝AD•BG；（2）解：①∵∠ABG＝90°，∴∠ABD+∠GBC＝90°，∵∠GBD+∠BGD＝90°，∴∠ABD＝∠BGD，同理∠GBD＝∠BAD，由（1）知△BDG∽△ADC，∴∠GBD＝∠DAC，∴∠BAD＝∠CAD，又∵AD＝AD，∠ADB＝∠ADC，∴△ADB≌△ADC（ASA），∴BD＝CD＝BC＝5，∵tan∠ABC＝m．∴tan∠BGD＝m，∴GD＝，∴GF＝2GD＝，∴S△BFG＝×FG×BD＝＝；②当BG∥AC时，∴∠ACB＝∠GBC，∵∠GBC＝∠CAD，∴∠ACB＝∠CAD＝45°，设CD＝AD＝x，则BD＝10﹣x，由勾股定理得，x2+（10﹣x）2＝82，解得x＝5±，当x＝5+时，BD＝10﹣x＝5﹣，此时m＝，当x＝5﹣时，BD＝10﹣x＝5+，此时m＝；当BE∥CG时，∴∠EBC＝∠BCG，则∠CBG＝∠BCG，∴BG＝CG，∴BD＝CD＝5，由勾股定理得AD＝，∴m＝，综上，m＝或或．【点评】本题是相似形综合题，主要考查了相似三角形的判定与性质，全等三角形的判定与性质，平行线的性质，三角函数等知识，综合性较强，熟练掌握角之间的转化发现解题思想是关键．8．（松江区）如图，已知△ABC中，∠ACB＝90°，AB＝6，BC＝4，D是边AB上一点（与点A、B不重合），DE平分∠CDB，交边BC于点E，EF⊥CD，垂足为点F．（1）当DE⊥BC时，求DE的长；（2）当△CEF与△ABC相似时，求∠CDE的正切值；（3）如果△BDE的面积是△DEF面积的2倍，求这时AD的长．【分析】（1）证明△DCE≌△DBE（ASA），可得CE＝BE＝2，根据＝tan∠B＝，即可求得答案；（2）分两种情况：①当△CEF∽△ABC时，可证得∠CDB＝90°，再根据DE平分∠CDB，可得∠CDE＝45°，再由特殊角的三角函数值即可求得答案；②当△CEF∽△BAC时，则∠ECF＝∠ABC，得出DC＝DB，再由DE平分∠CDB，可得DE⊥BC，推出∠CDE＝∠BAC，利用三角函数定义即可求得答案；（3）如图，过点E作EG⊥AB于点G，根据角平分线性质可得出EF＝EG，推出DF＝DG，再由△BDE的面积是△DEF面积的2倍，可得出BD＝2DF，进而推出DE＝BE，设BE＝x，则DE＝x，CE＝BC﹣BE＝4﹣x，BG＝BE•cos B＝x，BD＝2BG＝x，DG＝DF＝BG＝x，AD＝AB﹣BD＝6﹣x，根据△CDE∽CBD，得出＝＝，建立方程求解即可．【解答】解：（1）在Rt△ABC中，∠ACB＝90°，AB＝6，BC＝4，∴AC＝＝＝2，∵DE平分∠CDB，∴∠CDE＝∠BDE，∵DE⊥BC，∴∠DEC＝∠DEB＝90°，在△DCE和△DBE中，，∴△DCE≌△DBE（ASA），∴CE＝BE，∵CE+BE＝BC＝4，∴CE＝BE＝2，∵＝tan∠B＝，∴＝，∴DE＝；（2）∵EF⊥CD，∴∠CFE＝90°＝∠ACB，∵△CEF与△ABC相似，∴△CEF∽△ABC或△CEF∽△BAC，①当△CEF∽△ABC时，则∠ECF＝∠BAC，∵∠ACB＝90°，∴∠BAC+∠ABC＝90°，∴∠ECF+∠ABC＝90°，∴∠CDB＝90°，∵DE平分∠CDB，∴∠CDE＝∠CDB＝×90°＝45°，∴tan∠CDE＝tan45°＝1；②当△CEF∽△BAC时，则∠ECF＝∠ABC，∴DC＝DB，∵DE平分∠CDB，∴DE⊥BC，∴∠CDE+∠ECF＝90°，∵∠BAC+∠ABC＝90°，∴∠CDE＝∠BAC，∴tan∠CDE＝tan∠BAC＝＝＝，综上所述，∠CDE的正切值为1或；（3）如图，过点E作EG⊥AB于点G，∵DE平分∠CDB，EF⊥CD，EG⊥AB，∴EF＝EG，∵DE＝DE，∴Rt△DEF≌Rt△DEG（HL），∴DF＝DG，∵△BDE的面积是△DEF面积的2倍，∴BD＝2DF，∴DG＝BG，∵EG⊥BD，∴DE＝BE，设BE＝x，则DE＝x，CE＝BC﹣BE＝4﹣x，BG＝BE•cos B＝x，∴BD＝2BG＝x，DG＝DF＝BG＝x，∴AD＝AB﹣BD＝6﹣x，∵DE平分∠CDB，∴∠CDE＝∠BDE，∵DE＝BE，∴∠BDE＝∠B，∴∠CDE＝∠B，∵∠DCE＝∠BCD，∴△CDE∽CBD，∴＝＝，即＝＝，解得：CD＝3，x＝，∴AD＝6﹣x＝6﹣×＝，故这时AD的长为．【点评】本题是几何综合题，考查了直角三角形性质，勾股定理，全等三角形判定和性质，相似三角形的判定和性质，角平分线性质，三角形面积，三角函数等知识，解题关键是熟练掌握相似三角形的判定和性质等相关知识，运用分类讨论思想和方程思想解决问题．9．（青浦区）在四边形ABCD中，AD∥BC，AB＝，AD＝2，DC＝，tan∠ABC＝2（如图）．点E是射线AD上一点，点F是边BC上一点，联结BE、EF，且∠BEF＝∠DCB．（1）求线段BC的长；（2）当FB＝FE时，求线段BF的长；（3）当点E在线段AD的延长线上时，设DE＝x，BF＝y，求y关于x的函数解析式，并写出x的取值范围．【分析】（1）如图1，过点A、D分别作AH⊥BC、DG⊥BC，垂足分别为点H、点G．根据矩形的性质得到AD＝HG＝2，AH＝DG，解直角三角形即可得到结论；（2）如图1，过点E作EM⊥BC，垂足为点M，根据矩形的性质得到EM＝AH＝2，解直角三角形即可得到结论；（3）如图2，过点E作EN∥DC，交BC的延长线于点N．根据平行四边形的性质得到DE＝CN，∠DCB＝∠ENB，根据相似三角形的性质得到BE2＝BF•BN，过点E作EQ⊥BC，垂足为点Q，根据矩形的性质得到EQ＝DG＝2，根据勾股定理即可得到结论．【解答】解：（1）如图1，过点A、D分别作AH⊥BC、DG⊥BC，垂足分别为点H、点G．∴AH∥DG，∵AD∥BC，∴四边形AHGD是矩形，∴AD＝HG＝2，AH＝DG，在Rt△ABH中，tan∠ABC＝2，AB＝，∴＝2，∴AH＝2BH，∵AH2+BH2＝AB2，∴（2BH）2+BH2＝（）2，∴BH＝1，∴AH＝2，∴DG＝2，在Rt△DGC中，DC＝，∴CG＝＝＝4，∴BC＝BH+HG+GC＝1+2+4＝7；（2）如图1，过点E作EM⊥BC，垂足为点M，∴AH∥EM，∵AD∥BC，∴四边形AHME是矩形，∴EM＝AH＝2，在Rt△DGC中，DG＝2，CG＝4，∴tan∠DCB＝＝，∵FB＝FE，∴∠FEB＝∠FBE．∵∠FEB＝∠DCB，∴∠FBE＝∠DCB，∴tan∠FBE＝．∴＝，∴BM＝4，在Rt△EFM中，FM2+EM2＝FE2，∴（4﹣FB）2+22＝FB2，∴BF＝；（3）如图2，过点E作EN∥DC，交BC的延长线于点N．∵DE∥CN，∴四边形DCNE是平行四边形，∴DE＝CN，∠DCB＝∠ENB，∵∠FEB＝∠DCB，∴∠FEB＝∠ENB，又∵∠EBF＝∠NBE，∴△BEF∽△BNE，∴＝，∴BE2＝BF•BN，过点E作EQ⊥BC，垂足为点Q，则四边形DGQE是矩形，∴EQ＝DG＝2，∴BQ＝x+3．∴BE2＝QE2+BQ2＝（x+3）2+22＝x2+6x+13，∴y（7+x）＝x2+6x+13．∴．【点评】本题考查了四边形综合题，梯形的性质，矩形的判定和性质，相似三角形的判定和性质，勾股定理，正确的作出辅助线是解题的关键．10．（徐汇区）如图，在△ABC中，∠C＝90°，cot A＝，点D为边AC上的一个动点，以点D为顶点作∠BDE＝∠A，射线DE交边AB于点E，过点B作射线DE的垂线，垂足为点F．（1）当点D是边AC中点时，求tan∠ABD的值；（2）求证：AD•BF＝BC•DE；（3）当DE：EF＝3：1时，求AE：EB．【分析】（1）过点D作DG⊥AB于G，设AC＝a，BC＝a，由勾股定理得AB的长，在△ABD中，利用面积法可表示出DG的长，再利用勾股定理得出AG的长，从而解决问题；（2）首先利用两个角相等可证明△ADB∽△DEB，得，再证明△ACB∽△DFB，得，从而证明结论；（3）设DE＝x，EF＝3x，得DF＝4x，由cot，可表示出BF的长，再利用勾股定理得出BE、BD的长，由（2）可知，△ADB∽△DEB，得，可表示出AB的长，从而解决问题．【解答】（1）解：如图，过点D作DG⊥AB于G，在Rt△ABC中，cot A＝，设AC＝a，BC＝a，∵∠ACB＝90°，∴AB＝＝＝a，∵D是AC的中点，∴AD＝，∵S，∴DG＝，在Rt△ADG中，AG＝＝＝，∴BG＝AB﹣AG＝a﹣＝，在Rt△GDB中，tan；（2）证明：∵∠BDE＝∠A，∠DBE＝∠ABD，∴△ADB∽△DEB，∴，∵∠F＝∠C＝90°，∠A＝∠BDE，∴△ACB∽△DFB，∴，∴，∴AD•BF＝BC•DE；（3）解：∵，∴设DE＝x，EF＝3x，∴DF＝4x，∵∠A＝∠BDE，∴cot A＝cot∠BDE＝，在 Rt△BDF中，cot，∴BF＝x，在Rt△BEF中，BE＝＝＝x，在Rt△BDF中，DB＝＝＝2x，由（2）可知，△ADB∽△DEB，∴，∴，∴AB＝x，∴AE＝AB﹣BE＝x﹣x＝x，∴，即AE：EB＝7：17．【点评】本题是相似形综合题，主要考查了相似三角形的判定与性质，三角函数，勾股定理，三角形的面积等知识，利用代数方法解决几何问题是解题的关键．11．（长宁区）已知，在△ABC中，AB＝AC＝5，BC＝8，点E是射线CA上的动点，点O是边BC上的动点，且OC＝OE，射线OE交射线BA于点D．（1）如图，如果OC＝2，求的值；（2）联结AO，如果△AEO是以AE为腰的等腰三角形，求线段OC的长；（3）当点E在边AC上时，联结BE、CD，∠DBE＝∠CDO，求线段OC的长．【分析】（1）通过证明△ABC∽△OEC，可求EC的长，AE的长，通过证明△ADE∽△ODB，可求解；（2）分两种情况讨论，利用相似三角形的性质可求解；（3）通过证明△CDA∽△BEO，可得，通过证明△ABE∽△ODC，可得，列出等式可求解．【解答】解：（1）∵AB＝AC＝5，OE＝OC＝2，∴∠B＝∠C，∠C＝∠OEC，∴∠B＝∠OEC＝∠AED，又∵∠C＝∠C，∴△ABC∽△OEC，∴，∴＝，∴EC＝，∴AE＝，∵∠ADE＝∠ADE，∠AED＝∠B，∴△ADE∽△ODB，∴＝（）2＝（）2＝；（2）如图1，当点E在AC上时，∵∠AEO＞90°，△AEO是等腰三角形，∴AE＝EO，由（1）可知：△ABC∽△OEC，∴，∴，∴EC＝OC，∵AC＝AE+EC＝OC+OC＝5，∴OC＝；当点E在线段CA的延长线上时，如图2，∵∠EAO＞90°，△AEO是等腰三角形，∴AE＝AO，∴∠E＝∠AOE，∵∠B＝∠C＝∠OEC，∴∠B＝∠AOE，∴△ABC∽△AOE，∴，∴，∴AE＝OC，由（1）可知：△ABC∽△OEC，∴，∴，∴EC＝OC，∵AC＝EC﹣AE＝5，∴OC﹣OC＝5，∴OC＝，综上所述：线段OC的长为或；（3）如图3，当点E在线段AC上时，∵∠ABE＝∠CDO，∠ABC＝∠OEC，∴∠ABC﹣∠ABE＝∠OEC﹣∠ODC，∴∠EBO＝∠DCA，∵∠DAC＝∠ABC+∠ACB＝2∠ACB，∠BOE＝∠ACB+∠OEC＝2∠ACB，∴∠DAC＝∠BOE，∴△CDA∽△BEO，∴，∵∠ABE＝∠ODC，∠BAC＝∠DOC，∴△ABE∽△ODC，∴，∴，∴，∴OC＝8﹣或OC＝8+（不合题意舍去），∴OC＝8﹣．【点评】本题是三角形综合题，考查了等腰三角形的性质，相似三角形的判定和性质，添加恰当辅助线构造相似三角形是解题的关键．12．（崇明区）已知：如图，正方形的边长为1，在射线AB上取一点E，联结DE，将△ADE绕点D逆时针旋转90°，E点落在F处，联结EF，与对角线BD所在的直线交于点M，与射线DC交于点N．（1）当AE＝时，求tan∠EDB的值；（2）当点E在线段AB上，如果AE＝x，FM＝y，求y关于x的函数解析式，并写出定义域；（3）联结AM，直线AM与直线BC交于点G，当BG＝时，求AE的值．【分析】（1）如图1中，过点E作ER⊥BD于点R．解直角三角形求出ER，DR即可；（2）如图2中，过点M作MP⊥AB于点P，MQ⊥BC于点Q．证明＝＝＝，构建关系式，可得结论；（3）分两种情形：如图3﹣1中，当点G在线段BC上时，过点M作MT⊥AB于点T．如图3﹣2中，当点G在CB的延长线上时，过点M作MT⊥AB交AB的延长线于点T．分别求解即可．【解答】解：（1）如图1中，过点E作ER⊥BD于点R．∵四边形ABCD是正方形，∴AB＝AD＝BC＝CD＝1，∠A＝90°，∠BD＝90°，∴BD＝＝＝，∵ER⊥BD，∴∠EBR＝∠BER＝45°，∵AE＝，∵BE＝，∴ER＝BR＝，∴DR＝﹣＝，∴tan∠EDB＝＝＝；（2）如图2中，过点M作MP⊥AB于点P，MQ⊥BC于点Q．∵∠ADC＝∠EDF＝90°，∴∠ADE＝∠CDF，∵DA＝DC，DE＝DF，∴△ADE≌△CDF（SAS），∴AE＝CF＝x，在Rt△ADE中，DE＝＝，∵DE＝DF，∠EDF＝90°，∴EF＝DE＝，∵∠EBM＝∠FBM＝45°，MP⊥BE，MQ⊥BF，∴MP＝MQ，∴＝＝＝，∴＝，∴y＝﹣x（0≤x≤1）；（3）如图3﹣1中，当点G在线段BC上时，过点M作MT⊥AB于点T．∵BG∥AD，∴＝＝，∵BD＝，∴BM＝，∴BT＝TM＝，∴ET＝EB﹣BT＝1﹣x﹣＝﹣x，∵MT∥BF，∴＝，∴＝，解得x＝±，经检验，x＝是分式方程的解，且符合题意．∴AE＝．如图3﹣2中，当点G在CB的延长线上时，过点M作MT⊥AB交AB的延长线于点T．∵BG∥AD，∴＝＝，∵BD＝，∴BM＝，∴BT＝TM＝，∴ET＝EB﹣BT＝﹣（x﹣1）＝﹣x，∵MT∥BF，∴＝，∴＝，解得x＝±，经检验，x＝是分式方程的解，且符合题意．∴AE＝，综上所述，满足条件的AE的值为或．【点评】本题属于四边形综合题，考查了正方形的性质，等腰直角三角形的性质，全等三角形的判定和性质等知识，解题的关键是正确寻找全等三角形解决问题，学会用分类讨论的思想思考问题，属于中考压轴题．13．（黄浦区）如图，在Rt△ABC与Rt△ABD中，∠ACB＝∠DAB＝90°，AB2＝BC•BD，AB＝3，过点A作AE⊥BD，垂足为点E，延长AE、CB交于点F，联结DF．（1）求证：AE＝AC；（2）设BC＝x，＝y，求y关于x的函数关系式及其定义域；（3）当△ABC与△DEF相似时，求边BC的长．【分析】（1）将AB2＝BC•BD转化为，进而根据勾股定理和比例性质推出，进而△ABC∽△DAB，进一步证明△BAE≌△BAC，从而命题得证；（2）作AG∥BE交BC的延长线于G，作GH⊥AB，推出△FBE∽△FGA和cos∠ABC＝，再根据比例性质求得结果；（3）两种情形：△ACB∽△DEF和△ACB∽△FED，当△ACB∽△DEF时，由y＝1求得结果，当△ACB∽△FED时，推出DF∥AB，从而＝，根据△ABE∽△DBA，推出BD＝，进而可求得结果．【解答】（1）证明：∵AB2＝BC•BD，∴，∴＝，∴＝，即：＝，∴，∵∠C＝∠BAD＝90°，∴△ABC∽△DAB，∴∠ADB＝∠BAC，∵∠BAD＝90°，∴∠ADB+∠ABD＝90°，∵AE⊥BD，∴∠AEB＝90°，∴∠EAB+∠ABD＝90°，∴∠BAE＝∠ADB，∴∠BAE＝∠BAC，∵∠AEB＝∠C，AB＝AB∴△BAE≌△BAC（AAS），∴AE＝AC；（2）如图1，作AG∥BE交BC的延长线于G，作GH⊥AB，∴△FBE∽△FGA，∠ABE＝∠BAG，∴，由（1）得，∠EAB＝∠BAC，∵∠AEB＝∠ACB＝90°，∴∠ABE＝∠ABC，∴∠ABC＝∠BAG，∴AG＝BG，∴BH＝AH＝AB＝，∵cos∠ABC＝，∴，∴BG＝，∴AG＝，∴，∴，∴，∴＝，∴y＝（0＜x＜）；（3）如图2，当△ACB∽△DEF时，∠EDF＝∠BAC，∴∠EDF＝∠ADE，∵∠DEF＝∠DEA，DE＝DE，∴△DEF≌△DEA（ASA），∴EF＝AE，∴y＝1，∴＝1，∴x1＝，x2＝﹣（舍去），∴BC＝，如图3，当△ACB∽△FED时，∠BAC＝∠DFE，∵∠BAE＝∠BAC，∴∠DFE＝∠BAE，∴DF∥AB，。

上海(中考)初中英语选择题(归类)训练(含答案)

上海中考初中英语专项训练（选择题）（含答案）姓名________一、冠词、代词（共15题15分）1. When astronauts（宇航员）Fei Junlong, Nie Haisheng came back from space, many reporters interviewed ________ and got some first-hand information.A. theyB. themC. theirD. themselves2 . There is ______ report in today’s newspaper. It’s about the International Film Festival, Shanghai.A. aB. anC. theD. /（不填）3 Liu Xiang and Yao Ming are world-famous sports stars. ____ of them have set a good example to us.A. AllB. NeitherC. BothD. None4. —Is __________ here?—No.Tom and Peter have asked for a 1eave.A. anyoneB. everyoneC. someoneD. nobody5. —Mum, where is my CD player?—It’s in white bag on your desk.A. aB. anC. theD. 不填6. —Tom, Mary can’t sharpen the pencil. Can you give a hand?—Certainly.A. sheB. herC. hersD. herself7. Jack , good boy ! Please pass __________ the glasses . I want to read the newspaper .A. youB. meC. himD. her8. —Your tea, please.—There must be ____________ in the tea. It tastes good.A. anything sweetB. something sweetC. sweet somethingD. everything sweet9. —What do you think of the bridge?—I have never seen ________ before.A. so a long oneB. so long oneC. such a long oneD. a such long one10. —Whose English-Chinese dictionary is this?—It’s ________. My parents bought it for my sister and me.A. hersB. oursC. mineD. theirs11. I asked Lily for paper, bu t she didn’t have .A. any; someB. any; anyC. some; anyD. some; some12. —This is ______ film I’ve told you about several times.—It’s great. I’ve never seen ______ more moving one.A. a, aB. the, theC. the, aD. a, the13. —Could you lend me your pen?—Of course. I have two, and ______ of them write well.A . any B. all C. both D. two14.—Which would you like, tea or coffee?—________is OK. I really don't mind.A. BothB. EitherC. NoneD. Neither15.—who taught _____ French?—Nobody. She learned all by __________.A. herself; herB. she ; herselfC. her; sheD. her ; herself二、介词、连词（共20题20分）1. A tsunami（海啸）happened in some southern Asian countries _____ December, 2004.A. atB. onC. inD. by2. Tim’s mum is worried ______ her son’s eyesight as he plays online games too much.A. forB. aboutC. withD. of3. The doctors tried their best to save the pati ent’s life, ______ failed.A. orB. soC. butD. because4. —Would you like coffee or tea?—Coffee，please. By the way, do you have milk? I like coffee _______ milk.A. forB. orC. withD. without5. _______China has become a member of WTO，English is more popular that before.A. SinceB. ThoughC. WhetherD. If6.—Would you like to go to the park with me, Susan?—I’d like to, you don’t want to go alone.A. untilB. beforeC. ifD. after7. Kunming is famous _______ its nice weather.A. inB. asC. forD. with8 . The sign “@” in *****************means __________.A. aB. toC. atD. on9. Remember to return the book to the school library in time, _ _ you will be fined（罚款）.A. orB. andC. butD. then10.—Why hasn’t Mr Li come to work today?—______ he has gone to Beijing to have a meeting.A. IfB. UntilC. ThoughD. Because11. The accident happened _______ a cold winter morning.A. inB. onC. atD. of12. — Time to go to bed, Mary.—Oh, Mum, I won’t go to bed I have finished my homework.A. afterB. sinceC. untilD. as soon as13. Soccer is different American football. It’s played all over the wor ld.A. fromB. forC. inD. on14. Here are some flowers ________ you ________ our best wishes.A. to; forB. for; withC. of; toD. from; to15. There are two classes____ Saturday afternoon. We can not have a rest this weekend.A. atB. onC. inD. of16. It was so late, _________ the farmers went to working in the field.A. andB. orC. soD. but17. I didn't know anything about it_______my father told me.A. untilB. becauseC. ifD. after18. It’s very nice you to give me the chance.A. ofB. forC. toD. at19. The sports meet will continue_____ it rains this afternoon.A. ifB. sinceC. as soon asD. unless20.Study hard, ___________you are sure to have a good result in the exam.A. orB. andC. forD. but三、数词、名词（共20题20分）1. I’ve read ______ sports news about the F1 race today.A. twoB. piecesC. two piecesD. two pieces of2. During World War II, a Jewish（犹太）lady was protected by a local family in Shanghai in her ______.A. fiftiesB. fiftyC. fiftiethD. the fiftieth3. —Can you get a piano for me，dear?—But there isn’t enough _________ for it in our hous e.A. placeB. f1oorC. roomD. ground4. The river through our city, which is about _________, is clean again.A. 6000 metres longB. 6000-metres-longC. 6000-metre-longD. 6000 metre long5. ________ is spoken the most widely in the world.A. ChineseB. EnglishC. FrenchD. Russian6. People in America and Canada usually make ______to celebrate Thanksgiving Day.A. rice dumplingsB. moon cakesC. pumpkin piesD. chocolate eggs7. This is Elizabeth Tina Brown, our new teacher. You may call her _________.A. Mr BrownB. Miss BrownC. Mrs TinaD. Ms Elizabeth8. —How many_________would you like?—Two, please.A. cups of teaB. cup of teasC. cups of teasD. cup of tea9. I study in Yu Cai Middle School. There are two________students in our school.A. thousandB. thousandsC. thousand ofD. thousands of10. They said they would have holiday.A. a two-monthB. two monthsC. two-monthsD. two-month’s11.Tom regards Tianjin as his second because he has been here for over ten years.A. familyB. houseC. roomD. home12. We have ______at seven in the morning.A. breakfastB. lunchC. supperD. dinner13. I am thirsty. Would you bring me_______, please?A. some breadB.some teaC. some cakesD. some eggs14. What’s wrong with my son’s ________? He can’t see things clea rlyA. eyesB. earsC. mouthD. nose15.—What’s the English for“电子邮件”?—It’s“_____”A. FaxB. E-mailC. TelephoneD. ID16.—When was the PLA founded?—It was founded on ____.A. July 1. 1921B. October 1.1949C. May 1.1922D. August 1.192717. In the past t~w years, many tall buildings have been built in our city. The tallest is anthat stands in the centre.A. 80-floor buildingB. 60-floor buildingC. 80-floor buildingsD. 70 floors building18.—Mum, I've got an "A" in the English exam today!—Great! And you are sure to win a second time because this is a good_______A. reportB. resultC. startD. skill19.___ Chinese are looking for ways to learn English well before Beijing 2008 Olympics .A. ThousandB. ThousandsC. Thousand ofD. Thousands of20. “What’s the ________ today ? ”“It’s June 26. ”A. dayB. dateC. timeD. hour四、形容词、副词（共20题20分）1 Nowadays science fiction isn’t as ____________ as cartoons among teenagers.A. popularB. more popularC. less popularD. the most popular2. We are glad to see that Shanghai is developing ________ these years than ever before.A. quicklyB. less quicklyC. more quicklyD. the most quickly3. The cheese cake tasted so ______ that the kids asked for more.A. deliciousB. wellC. badD. badly4. —Why didn’t you enjoy the talk?—It was ________talk that I had ever listened to.A. the most interestingB. the least interestingC. more interestingD. 1ess interesting5. Guo Yue did quite _______ at the World Table Tennis Championship（锦标赛），but Zhang Yining did even _____.A. better; wellB. well; wellC. well; betterD. better; better6. — W hose picture is better, Jack’s or Tom’s?— Both of them are good. I think Jack draws Tom.A. as good asB. as well asC. better thanD. worse than7. It gets very here in summer.A. coolB. coldC. warmD. hot8. Be ________, and you will do well in the English exam.A. carefulB. politeC. sureD. friendly9. Lin Tao is good at all the subjects at school, _________English.A. reallyB. mostlyC. especiallyD. exactly10. —The coat is too expensive.—Look, here's another one. It's___ ______and nicer.A. dearerB. cheaperC. olderD. longer11.The population of Tianjin is __________ than that of Shanghai.rgerB. lessC. smallerD. fewer12.It’s raining _________. We have to stay at home instead of going fishing .A. badlyB. hardlyC. heavilyD. strongly13. Kate is as _________as Maria.A. tallB. tallerC. tallestD. the tallest14. She looks very________. I think she needs to have a rest.A. tiredB. hardC.wellD. hardly15.—Tom is terribly ill.—We’d better send him to hospital as _____as we can.A. slowlyB. quicklyC. quietlyD. easily16.—Do you like the Moonlight Sonata?—Sure, it sounds really________.A. clearB. clearlyC. beautifulD. beautifully17. Supermarkets are necessary. People usually spend_____ time finding things they want, but they usually spend _____ money than they want.A. less; lessB. less; moreC. fewer; lessD. fewer; more18. “Do you want to improve your score in math? Try staying away from your computer!” A recent report in Britain says, “The _____ students use computer at school and at home, the _____ they do in exams of reading and math.”A.more; betterB. less; worseC. more; moreD. less; better19 . He speaks English ______ an American, so we all believe that he has stayed in America for many years.A. as good asB. worse thanC. as badly asD. as well as20.—The TV programme is boring. Shall we play chess instead?—All right. That is __________ than watching a boring programme.A. very goodB. much goodC. very betterD. much better五、动词（一）：1-25题，每题1分，26-29题为选作题。

2023年上海中考英语真题答案及解析

2023年上海市中考英语真题解析综述：改革后旳第一次中考在雨中结束了，总体而言大家还是感觉试卷是平稳过渡旳，并且经历了一模二模甚至三模旳锻炼，同学们也基本没有体现出对题目变化旳不适应。

应当讲，今年旳试卷还是严格根据了市教委教育考试院旳考试规定和改革方向，难度是有升有降，总体平稳。

至于同学们会有什么样旳分数还要到成绩公布之后才可见分晓。

如下我们分大题来进行探讨，并试探性提出后来旳备考提议。

Part I Listening (第一部分听力)真题回放：I Listening Comprehension (听力理解) （共30分）A. Listen and choose the right picture. (根据你所听到旳内容选择对应旳图片)（6分）1. ______2. _______3. _________4. _______5. ________6. _________B. Listen to the dialogue and choose the best answer to the question you hear.(根据你听到旳对话和问题，选出最恰当旳答案)（8分）7. A) Chemistry B) HistoryC) English D) Maths8. A) A hamburger B) A fruit saladC) A hot-dog D) A sandwich9. A) Tired B) SurprisedC) Excited D) Frightened10. A) Watch TV B) Play footballC) Go to the cinema D) Read a book11. A) Fifteen minutes’ walkB) Fifteen minutes’ bus rideC) Fifty minutes’ walkD) Fifty minutes’ bus ride12. A) Thursday B) FridayC) Saturday D) Sunday13. A) Trips B) ComputersC) Parents D) Jobs14. A) At the beach B) At the airportC) In the theatre D) In the hotelC. Listen to the passage and decide whether the following statements are True (T) or False(F) (判断句子与否符合你听到短文内容，符合旳用T表达，不符合旳用F表达)(6分)15. My aunt and uncle sent me a bottle of honey as a birthday present last year.16. The smell of my hair attracted lots of bees when I were outside.17. I jumped into my neighbour’s swimming pool to stay away from the bees.18. When I climbed out of the pool, the bees were still flying around.19. My aunt and uncle wrote me a letter to apologize to me.20. This is a story about my unforgettable birthday present.D. Listen to the passage and complete the following sentences. (听短文，完毕下列内容，每空限填一词)（10分）21. Dan Carter lives in London and works as _________ _________ there.22. Dan and I stay in touch _______ ________ and sometimes we call each other.23. When I ___________ __________ when I need to talk to somebody, I can always call Dan.24. Dan is always ___________ __________ everything and he never says sorry.25. One day, we a rranged to meet _________ __________ to play football, but Dan didn’t comeon time.评析：本次听力考试旳题型变化比较明显，尤其是最终一大题变为了5句话听出10个单词，对学生旳记忆和应变能力提出了更高旳规定。

上海中考数学25题方法总结(一)

上海中考数学25题方法总结(一)上海中考数学25题方法总结前言作为一名资深的创作者，在为上海中考数学25题的解答方法总结时，我认为有必要对这些题目进行细致的分析和总结，帮助考生更好地应对考试。

正文1. 了解考试要求在解答上海中考数学25题时，首先要了解考试的要求。

这不仅包括对知识点的掌握程度，还包括对题目类型和解题技巧的理解。

只有全面了解考试要求，才能更好地准备考试。

2. 熟悉题目类型上海中考数学25题所涉及的题目类型较为多样，包括选择题、填空题、解答题等。

针对不同的题型，我们需要掌握不同的解题方法和技巧。

比如，对于选择题，可以通过排除法确定答案；对于填空题，可以通过代入法验证解答的正确性；对于解答题，可以通过列方程或绘制图形来求解。

3. 提升解题速度在上海中考数学25题中，时间是非常宝贵的。

为了提升解题速度，我们可以通过刷题来熟悉题目的解答过程，培养自己的思维敏捷性。

此外，还可以利用一些简便的计算方法，如近似计算、倒推法等，来快速得到答案。

4. 夯实基础知识无论是解答选择题还是解答解答题，都需要有扎实的基础知识作为铺垫。

因此，在备考过程中，我们要不断夯实基础知识，掌握各种定理和公式，并能够灵活运用于解题过程中。

5. 练习真题和模拟题最后，为了更好地应对上海中考数学25题，我们需要充分练习真题和模拟题。

通过模拟考试，我们可以了解自己的考试水平和薄弱环节，并及时调整备考计划，提高解题能力和应考水平。

结尾通过以上几点的总结，我们可以发现在应对上海中考数学25题时，除了基础知识的扎实掌握外，熟悉题目类型、提升解题速度和练习真题都是非常重要的。

希望这篇总结能够对即将参加上海中考的同学提供一些实用的建议和方法。

*注：以上方法仅代表个人观点，具体解题方法还需根据题目具体情况灵活运用。

正文（续）6. 考前复习策略在备考过程中，合理的复习策略是非常重要的。

可以根据自己的掌握程度，将复习时间合理分配给不同的知识点和题型。

上海中考收集训练25题收集训练及答案解析

1．（本题满分14分，第(1)小题满分4分，第(2)小题满分6分，第(3)小题满分4分）在Rt △ABC 中，︒=∠90C ，2=BC ，Rt △ABC 绕着点B 按顺时针方向旋转，使点C落在斜边AB上的点D，设点A点E 重合，联结AE ，过点E 作直线EM 与射线CB 垂直，交点为M ．（1）若点M 与点B 重合如图10，求BAE ∠cot 的值；（2）若点M 在边BC 上如图11，设边长x AC =，y BM =，点M 与点B 不重合，求y 与x 的函数关系式，并写出自变量x 的取值范围；（3）若EBM BAE ∠=∠，求斜边AB 的长．2．（本题满分14分，其中第（1）小题各4分，第（2）、（3）小题各5分）如图，已知在梯形ABCD 中，AD // BC ，AB = DC = 5，AD = 4．M 、N 分别是边AD 、BC 上的任意一点，联结AN 、DN ．点E 、F 分别在线段AN 、DN 上，且ME // DN ，MF // AN ，联结EF ．M ) 图10图11（1）如图1，如果EF // BC ，求EF 的长；（2）如果四边形MENF 的面积是△ADN 的面积的38，求AM 的长；（3）如果BC = 10，试探索△ABN 、△AND 、△DNC 能否两两相似？如果能，求AN 的长；如果不能，请说明理由．3．（本题满分14分）如图，已知矩形ABCD ，AB =12 cm ，AD =10 cm ，⊙O 与AD 、AB 、BC 三边都相切，与DC 交于点E 、F 。

已知点P 、Q 、R 分别从D 、A 、B 三点同时出发，沿矩形ABCD 的边逆时针方向匀速运动，点P 、Q 、R 的运动速度分别是1 cm/s 、x cm/s 、1.5 cm/s ，当点Q 到达点B 时停止运动，P 、R 两点同时停止运动.设运动时间为t （单位:s ）.（1）求证: DE =CF ；（2）设x = 3，当△PAQ 与△QBR 相似时，求出t 的值；ABCDMNEF（图1）A B CDMNEF（第25题图）（3）设△PAQ 关于直线PQ 对称的图形是△PA'Q ，当t 和x 分别为何值时，点A'与圆心O 恰好重合，求出符合条件的t 、x 的值.4．（本题满分14分，第（1）小题4分，第（2）小题5分，第（3）小题5分）如图，已知在直角梯形ABCD 中，AD ∥BC ，∠ABC =90º，AB =4，AD=3，552sin =∠BCD ，点P 是对角线BD 上一动点，过点P 作PH ⊥CD ，垂足为H ．（1）求证：∠BCD =∠BDC ；（2）如图1，若以P 为圆心、PB 为半径的圆和以H 为圆心、HD 为半径的圆外切时，求DP 的长；（3）如图2，点E 在BC 延长线上，且满足DP =CE ，PE 交DC 于点F ，若△ADH 和△ECF 相似，求DP 的长．第25题图、5.6、（本题满分14分，其中第（1）小题5分，第（2）小题5分，第（3）小题4分）已知：⊙O 的半径为3，OC ⊥弦AB ，垂足为D ，点E 在⊙O 上，ECO BOC ∠=∠，ABCHPD （第25题图1）ABCHPD EF（第25题图2）射线CE CE 与射线OB 相交于点F ．设,AB x = CE y = （1）求y 与x 之间的函数解析式，并写出函数定义域；（2）当OEF ∆为直角三角形时，求AB 的长；（3）如果1BF =，求EF的长．7．（本题满分14分，第（1）小题4分，第（2）小题5分，第（3）小题5分）已知：如图七，在梯形ABCD 中，AD ∥BC ，∠A＝90°，AD ＝6，AB ＝8，sinC ＝54，点P 在射线DC 上，点Q 在射线AB 上，且PQ ⊥CD ，设DP ＝x ，BQ ＝y ．（1）求证：点D 在线段BC 的垂直平分线上；（2）如图八，当点P 在线段DC 上，且点Q 在线（备用图2）第25题C备用图1（图八）BPA CDQ (图七)ABCD段AB上时，求y关于x的函数解析式，并写出定义域；（3）若以点B为圆心、BQ为半径的⊙B与以点C为圆心、CP为半径的⊙C相切，求线段DP的长．DA(备用)B C1.解：（1）当点M 与点B 重合，由旋转得：2==BD BC ，ED AC =，EBD CBA ∠=∠，︒=∠=∠90C EDB ∵CB EM ⊥∴=∠EBC ∴︒=∠=∠45EBD CBA (1)分∴︒=∠=∠45CBA CAB∴2==CB AC∴22=AB …………………………………1分 ∴2==DB DE∴222-=AD ……………………………1分∴12cot -==∠DEADBAE ………………1分（2）设EM 与边AB 交点为G由题意可知：︒=∠+∠9021，︒=∠+∠903CBA又32∠=∠，∴CBA ∠=∠1∵CBA EBD ∠=∠， ∴EBD ∠=∠1，∵BDE EDG ∠=∠，∴△EDG ∽△BDE∴EDDGBD ED =…………………………………………1分 ∵2==BD BC ，x ED AC ==∴xDGx =2，∴22x DG =…………………………1分由题意可知：AB BCBG MB ABC ==∠cos (42)+=x AB ，242x GB -= ∴422422+=-x x y ……………………1分∴444222++-=x x x y ……………………1分定义域为20<<x …………………………1分（3）当点M 在边BC 上时，由旋转可知：EB AB =，∴BAE AEB ∠=∠设︒=∠x CBA ，则︒=∠x ABE ，∵EBM BAE ∠=∠，分别延长EA 、BC 交于点H ∴︒=∠=∠=∠x EMB BAE AEB 2，∵︒=∠+∠+∠180AEB BAE ABE ∴36=x 易得：︒=∠=∠=∠36ABE ABH H ，︒=∠=∠=∠72AEB BAE HBE ∴BE AB AH ==，HE HB =，∵︒=∠90ACB ，∴2==BC HC∴4==HE HB ，∴△BAE ∽△HBE ，∴BEAEHB AB =，又AB BE = AB HA HE AE -=-=4，∴ABABAB -=44，∴522±-=AB (负值舍去) ∴522+-=AB …………………………2分当点M 在边CB 的延长线上时，∵BAE AEB ∠=∠，EBM BAE ∠=∠∴EBM AEB ∠=∠∴AE ∥MC ∴CBA BAE ∠=∠(M )∵EBA CBA ∠=∠∴EBA CBA EBM ∠=∠=∠ ∴︒=∠60CBA ，∵ABBCCBA =∠cos ，2=BC ∴4=AB …………………………2分综上所述：522+-=AB 或4.2．解：（1）∵ AD // BC ，EF // BC ，∴ EF // AD ．……………………………（1分）又∵ ME // DN ，∴ 四边形EFDM 是平行四边形．∴ EF = DM ．…………………………………………………………（1分）同理可证，EF = AM ．…………………………………………………（1分） ∴ AM = DM ．∵ AD = 4，∴ 122EF AM AD ===．……………………………（1分）（2）∵ 38ADN MENF S S ∆=四边形，∴ 58AME DMF ADN S S S ∆∆∆+=．即得 58AME DMF ADN ADN S S S S ∆∆∆∆+=．……………………………………………（1分）∵ ME // DN ，∴ △AME ∽△AND ．∴ 22AME ADN S AM S AD ∆∆=．……………………………………………………（1分）同理可证，△DMF ∽△DNA ．即得 22DMF ADN S DM S AD ∆∆=．……………（1分）设 AM = x ，则 4DM AD AM x =-=-．∴ 22(4)516168x x -+=．………………………………………………（1分）即得 2430x x -+=．解得 11x =，23x =．∴ AM 的长为1或 3．………………………………………………（1分）（3）△ABN 、△AND 、△DNC 能两两相似． ……………………………（1分）∵ AD // BC ，AB = DC ，∴ ∠B =∠C ．由 AD // BC ，得 ∠DAN =∠ANB ，∠ADN =∠DNC ．∴ 当 △ABN 、△AND 、△DNC 两两相似时，只有 ∠AND =∠B 一种情况．……………………………………………………………………（1分）于是，由 ∠ANC =∠B +∠BAN ，∠ANC =∠AND +∠DNC ，得 ∠DNC =∠BAN ．∴ △ABN ∽△DNC ．又∵ ∠ADN =∠DNC ，∴ △AND ∽△DNC ． ∴ △ABN ∽△AND ∽△DNC ． ∴AB BN NC CD =，AN ADBN AN=． ………………………………………（1分）设 BN = x ，则 NC = 10 –x ．∴5105xx =-．即得 210250x x -+=．解得 5x =．……………………………（1分）经检验：x = 5是原方程的根，且符合题意． ∴ 5BN CN ==． ∴45AN AN=．即得AN =1分） ∴ 当△ABN 、△AND 、△DNC 两两相似时，AN的长为3．（本题满分14分）（1）证:作OH ⊥DC 于点H ，设⊙O 与BC 边切于点G ，联结OG . （1分）∴∠OHC=90°∵⊙O 与BC 边切于点G ∴OG =6，OG ⊥BC∴∠OGC=90°∵矩形ABCD ∴∠C =90° ∴四边形OGCH 是矩形 ∴CH =OG∵OG =6 ∴CH =6 （1分） ∵矩形ABCD ∴AB =CD∵AB =12 ∴CD =12 ∴DH =CD ﹣CH =6 ∴DH = CH∴O 是圆心且OH ⊥DC ∴EH =FH （2分） ∴DE =CF . （1分）第25题图(1)（2）据题意，设DP =t ，PA =10-t ，AQ =3t ，QB =12-3t ，BR =1.5t （0 < t < 4）. （1分）∵矩形ABCD ∴∠A =∠B =90° 若△PAQ 与△QBR 相似，则有 ①BR AQ QB AP = t t t t 5.133-12-10= 514=t （2分） ②QB AQ BR AP = ttt t 31235.1-10-= 146921-=t 或14692-2-=t （舍）（2分）（3）设⊙O 与AD 、AB 都相切点M 、N ，联结OM 、ON 、OA . ∴OM ⊥AD ON ⊥AB 且OM =ON =6 又∵矩形ABCD ∴∠A =90°∴四边形OMAN 是矩形又∵ OM =ON ∴四边形OMAN 是正方形（1分） ∴MN 垂直平分OA∵△PAQ 与△PA'Q 关于直线PQ 对称 ∴PQ 垂直平分OA ∴MN 与PQ 重合（1分）∴ MA = PA = 10-t = 6 ∴ t = 4 （1分） ∴AN = AQ = x t = 6 ∴x =23（1分） ∴当t = 4 和x =23时点A'与圆心O 恰好重合. 第25题图(2)(P )56．解：（1）过点O 作OH ⊥CE ，垂足为H∵在圆O 中，OC ⊥弦AB ，OH ⊥弦CE ，AB =x ，CE =y∴1122BD AB x ==，1122EH EC y == ………………………………1分 ∵在Rt △ODB 中，222OD BD BO +=，OB=3 ∴236x - ………1分∵OC=OE ∴∠ECO=∠CEO ∵∠ECO ＝∠BOC∴∠CEO=∠BOC 又∵∠ODB=∠OHE=90°，OE=OB∴△ODB ≌△EHO ∴EH=OD …………………………1分∴23622x y -= ∴236y x -1分函数定义域为（0＜x ＜6）………………………………………………………1分（2）当△OEF 为直角三角形时，存在以下两种情况： ①若∠OFE ＝90º，则∠COF ＝∠OCF ＝45º ∵∠ODB=90°， ∴∠ABO=45°又∵OA=OB ∴∠OAB= ∠AB O=45°， ∴∠AOB=90° ∴△OAB 是等腰直角三角形∴232=⋅=OB AB …………………………………………………2分②若∠EOF ＝90º ，则∠OEF ＝∠COF ＝∠OCF ＝30º……………………1分 ∵∠ODB=90°， ∴∠ABO=60° 又∵OA=OB∴△OAB 是等边三角形∴AB=OB=3…………………………………………………………………2分（3）①当CF ＝OF ＝OB –BF ＝2时，可得：△CFO ∽△COE ，CE ＝292=CF OC ，∴EF ＝CE –CF ＝25229=-． ……………………………………………2分②当CF ＝OF ＝OB +BF ＝4时，可得：△CFO ∽△COE ，CE ＝492=CF OC ，∴EF ＝CF –CE ＝47494=-． ……………………………………………2分7、（本题满分14分，第（1）小题4分，第（2）小题5分，第（3）小题5分）解：（1）作DH ⊥BC 于H （见图①） …………（1分）在梯形ABCD 中，AD ∥BC ，∠A ＝90°，∴∠B ＝90°, ∠BHD=90° ∴四边形ABHD 是矩形∴DH=AB ，BH=AD …………（1分）又∵AD ＝6，AB ＝8 ∴DH=8，BH=6 在Rt △DHC 中, sinC ＝54,可设DH=4k, DC=5k ∴DC=10, HC=681022=-，∴BH=HC=6 …………（1分）又∵DH ⊥BC∴点D 在线段BC 的垂直平分线上 …………（1分）（2）延长BA 、CD 相交于点S （见图②）， …………（1分）∵AD ∥BC 且BC ＝12 ∴AD=21BC ∴21===BC AD SC SD SB SA ∴SD=DC=10，SA=AB=8 ∵DP ＝x ，BQ ＝y, SP=x+10 由△SPQ ～△SAD 得45==SA SD SP SQ ………（1分） ∴)10(45+=x SQ …………（1分） 2745)10(4516+-=+-=x x BQ∴所求解析式为2745+-=x y ， …………（1分）定义域是0≤x ≤514…………（1分）(说明：若用勾股定理列出：222222PC BC QB DP AQ AD -+=-+亦可，方法多样．)（3）由图形分析，有三种情况：（ⅰ）当点P 在线段DC 上，且点Q 在线段AB 上时，只有可能两圆外切，由BQ+CP=BC ，12102745=-++-x x ，解得32=x （ⅱ）当点P 在线段DC 上，且点Q 在线段AB 的延长线上时，两圆不可能相切， …………（2分）（ⅲ）当点P 在线段DC 的延长线上，且点Q 在线段AB 的延长线上时，此时2745-=x BQ , CP = x-10 …………（1分）若两圆外切，BQ+CP=BC ，即12102745=-+-x x ,解得334=x …………（1分）若两圆内切，BC CP BQ =-，即12)10(2745=---x x 12)10(2745=---x x 解得22=x 12)10(2745-=---x x 解得74-=x （不合题意舍去） …………（1分）综上所述，⊙B 与⊙C 相切时，线段DP 的长为32，334或22 ．。