光在晶体中的传播方向

合集下载

第五章光的偏振晶体内o光和e光

（2）由先到达界面的B点作另一条边缘光线的垂线BA，它就是入射的波面；求出光从A点到达C点所需时间，t＝ AC/c，令t＝AC/c＝1。
(3)对于方解石晶体
A
ne 1.486 no 1.658
B
C
空气
晶体
e no 1.658 . o ne 1.486
光轴
以B为圆心，以ot＝1.486为
o光和e光的子波面在光轴方向上相切；在垂直光轴方向
上，两波面相距最远。
❖正晶体和负晶体
在垂直于光轴的方向上：
若： e＜ o(或ne＞no)， e光的波面在o光波面内，称
为正晶体，如石英、冰等。
正晶体是球面包椭球面。
若： e＞ o （或ne＜no ）， e光的波面在o光波面外，
称为负晶体，如如方解石、红宝石等。
本节结束
（1）光轴垂直于晶体
表面，并平行于入射面。 o光和e光沿同一
空气
方向传播，传播速度
晶体
相同，所以o和e光波面重合。
光轴 o o
不发生双折射！
ee
（2）光轴平行于晶体表（2）面，并平行于入射面。
（3）光轴平行于晶体表光轴面，并垂直于入射面。
（2）、（3）两种情况， o光和e光沿同一方向传播，
则对o光来说其折射率为：
e光一般情况下不满足折射定律，其传播速度与方向有关。
no

c
o
但是当e光垂直于光轴方向传播时，e光的传播方向与其波面垂直，因此不论入射角为何值，总是满足：
sin i1 c
sin i2e e

光轴
A
B
C 空气
晶体

o

光子晶体中的光子禁带与传输特性

光子晶体中的光子禁带与传输特性光子晶体是一种具有周期性结构的材料，通过调控其结构可以有效地控制光的传输和操控。

其中一个重要的特性就是光子禁带，它在光子晶体中起到了关键的作用。

一、光子禁带的概念和原理光子禁带是指在光子晶体中存在一个频率范围，在这个范围内光的传播是被禁止的。

这意味着光子晶体能够对特定的波长光进行选择性的反射或吸收，同时允许其他波长的光通过。

这种禁带效应是由于光子晶体的周期性结构导致的。

光子晶体的周期性结构可以被理解为一系列的光子波导，它们之间的相位差会产生干涉效应。

当干涉效应导致波的幅值彼此相消时，禁带就形成了。

通俗地说，可以将光子禁带类比为一个光的“高速公路”，只有特定的车辆（特定波长的光）能够通过，其他车辆则被拦截。

二、光子禁带的应用1. 光子晶体光纤光子禁带的应用之一就是光子晶体光纤。

光纤是一种用于光信号传输的高效率导光介质，而光子晶体光纤在此基础上进一步实现了对光波在特定频率范围内的引导和控制。

通过光子晶体光纤，可以实现光信号的高速传输和低损耗，同时具备了较宽的传输带宽。

这使得光子晶体光纤在通信领域有着广阔的应用前景。

2. 光子晶体光子器件光子禁带还可以被用于设计和实现各种光子器件。

光子晶体中的禁带产生的光子态密度变化可以导致光的散射、反射和单向传输等效应。

通过调控光子晶体的结构，可以实现各种功能性器件，比如光子晶体滤波器、光子晶体光调制器等。

这些器件在光通信、激光器设计、光子计算等领域发挥着重要作用。

三、光子晶体中的光子传输特性光子禁带不仅影响着光子在光子晶体中的传输，还对其传输特性产生了重要的影响。

1. 禁带宽度和传输带宽光子晶体的禁带宽度决定了能通过的波长范围，而在禁带宽度之外的波长则被禁止传输。

禁带宽度的大小取决于光子晶体的周期性结构和材料参数，可通过调节这些参数来实现对禁带宽度的控制。

传输带宽则是指光子晶体中能够通过的波长范围，它取决于禁带宽度和其他非完美性质（如材料吸收和散射）的影响。

2_3 光波在声光晶体中的传播

声波
x 声波阵面
y
超声波），声光互作用长度小
s
入射光
L
L0
ns2 4
光波阵
面
静止的“平面相位光栅”
衍射光
sin m
m ks ki
m s
L
拉曼-纳斯衍射图
衍射特征：各级衍射光对称地分布在零级衍射光两侧，且同级次衍射光的强度相等.
2.3 光波在声光晶体中的传播
第2章光辐射的传播
2. 布喇格（Bragg）衍射
对光波而言，运动的“声
s
光栅”可视为静止。
n n n0
2.3 光波在声光晶体中的传播
第2章光辐射的传播
声波在介质中的传播分为行波和驻波两种形式。设声波的角频率为s，波矢为 k s ，则沿x方向传播的声
波方程为 a(x,t) Asin(st ks x)
可近似认为，介质折射率的变化正比于介质质点沿x方向位
第2章光辐射的传播
衍射光场强度各项取极大值的条件为
x ks
cos-1l
ki sin mks 0 (m 整数 0) +q/2 ki
-q/2
y
各级衍射的方位角为
d=xl -L/2 +L/2
sin m
m ks ki
m
s
(m 0, 1, 2, )
各级衍射光的强度为
Im
J
2 m
(v),
v
(n)ki L
—介质密度；vs—声速；S —应变幅值
超声强度：
Is
Ps HL
n 1 n3P 2
2Is
vs3
衍射效率
s
I1 Ii
sin 2
L

光的双折射解析

o光：双折射的两束折射光中，一束遵循折射定律，传播速度v o沿各个方向都相同，折射率n o=si n i/si n t o=c/v o=常量，称作寻常光，记为o光。

e光：通常不遵循折射定律，折射方向通常在入射面之外，传播速度随传播方向而改变，si n i/si n t e≠常量，称作非寻常光，记为e光o光和e光都是传播光线在双折射晶体内部定义的，双折射晶体外没有o光和e光光轴：晶体中的一个方向，光沿此方向传播不发生双折射，且折射光遵循折射定律光轴仅代表一个特殊的方向，凡平行于此方向的直线均为光轴只有一个光轴方向的晶体称作单轴晶体，有两个光轴方向的晶体称作双轴晶体在单轴晶体内，光线的传播方向与晶体光轴构成的平面称作该光线的主平面o主平面：光轴+o光线e主平面：光轴+e光线主截面：光轴+晶体表面法线。

入射面：入射光+晶体表面在入射点处的法线o光和e光都是线偏振光o光的电矢量垂直于o主平面，振动方向始终与光轴垂直。

e光的电矢量平行于e主平面，振动方向平行于e主平面通常e光不在入射面内，即e光和o光不共面。

只有当光轴在入射面内(也即入射光在主截面内)时，入射面、主截面、o主平面和e主平面四个面重合，此时o光和e光都在入射面内。

若入射光与光轴重合，则不再发生双折射。

若入射光与光轴共面但不重合，则有折射角t e≠t o，sin t e≠si n t o，发生双折射在双折射晶体中，o光沿各个方向传播的速度相同，o光的波面为半径为球面，o光的传播方向始终垂直于波面。

e光沿各个方向的传播速度不同，e光的波面为椭球面，传播方向仅在椭球的长短轴处垂直于波面。

o光和e光沿光轴方向的传播速度相同，沿垂直于光轴的方向传播速度相差最大n e称作晶体的主折射率。

n o为恒量，n e定义为e光沿垂直于光轴方向的折射率，其数学表达式中的v e也为同一方向的传播速度n e=cv e n o=cv o正晶体和负晶体：满足v o>v e→n o<n e的称作正晶体，e光波面在o光波面之内，椭球面内切于球面，切点为长轴(2v o t)的顶点，长轴方向即光轴，短轴(2v e t)。

晶体光学一、二

4、光性正负、与一轴晶光性正负的确定有所不同，二轴晶光性正负取决于：当Ng－Nm ＞Nm－Np （＋）。此时Nm 比较接近Np ，两个圆切面靠近Np ，光轴则接近Ng 。所以Ng 为 Bxa 、Np 为 Bxo 。当Ng－Nm ＜Nm－Np （－）。此时Ng为Bxo。Np为Bxa。
无法显示图像。计算机可能没有足够的内存以打开该图像，也可能是该图像已损坏。请重新启动计算机，然后重新打开该文件。如果仍然显示红色 “x” ，则可能需要删除该图像，然后重新将其插入。
无论光性如何，无论光性如何， ⊥Bxa 切面的双折率总是小于 ⊥Bxo 切面上的双折率。双折率。证明：（＋） Ng－Nm ＞ Nm－Np （⊥Bxo）（⊥Bxa）（－） Ng－Nm ＜ Nm－Np Bxa Bxo （⊥Bxa）（⊥Bxo）（5）斜交切面：即不垂直主轴，也不垂直光轴。 a、半任意斜切面（垂直于一个主轴面的斜交切面），椭圆，有一个半径为主轴。另一个为Ng’或Np’，比较重要的是⊥NgNp 面（AP）的切面。含Nm。 b、任意斜交切面，椭圆，半径为Ng’、Np’，双折率介于 O 与Ng－Np 之间。
2、一轴晶光率体的主要切面
岩矿鉴定中常应用的是晶体不同方向上的切面（薄片切面）。所以必须对光率体几种主要切面的形状和切面半径所表示的折射率值十分熟悉。
（1）⊥OA切面：不发生双折射，不改变特点。圆，半径为Ne ，一轴晶仅有一个。（过球心，⊥Z轴）（2）∥OA切面：分解为两种偏光，平行两个半径。椭圆：（＋）长半径为Ne，短No , （－）长半径为No，短Ne，双折率为（Ne－No）,为最大双折率。（3）斜交光轴切面（最常见）：分解成两种偏光。椭圆，（＋）长Ne＇，短No , （－）长No, 短Ne＇，双折率为No与Ne＇之差，大小介于0与（Ne－No）之间。小结：初步可知，应用光率体，可以确定光波在晶体中的传播方向（波法线方向）、振动方向及相应折射率值之间的关系。⊥OA方向的切面；圆，不发生双折射，非⊥OA 方向，双折射。椭圆，椭圆半径方向为振动方向。长度表示n值，二者差为双折率。

光的偏振和双折射

1晶体的光轴在晶体内有一个方向光沿此方向入射时不发生双折射此方向称为晶体的光轴在光轴方向上oe相同n相同2单晶体具有一个光轴方向的晶体方解石石英3正晶体和负晶体在晶体中波所到达的各点都是一个新的子波波源在各向异性的晶体中每个子波源发出二个子波晶体对e光的折射率在垂直光轴方向上主折射率19正晶体光轴以下都是以单轴负晶体为例讨论204入射面
或
将各方向的 E 投影到二个任意互相垂直的方向上，由于在所有可能的方向上 E 完全相等，所以在
任二个互相垂直的方向上光矢量的分量的和相等。自然光也可以表示为：
Leabharlann 传播方向图中：“︱”表示在板面内的分振动 E “●”表示 E 垂直板面的分振动
二个相互垂直的光振动，光强各占一半
tgib n2 n1
12
ib
n2
布儒斯特定律：当自然光以布儒斯特角 ib 入射到二介质界面时，反射光为完全偏振光，振动方向⊥入射面
三. 应用
1. 测量不透明介质的折射率让光线入射到不透明的介质上，改变入射角i 并测反射光线的偏振化程度，当反射光线为完全偏振光时，入射角 ib 即为布儒斯特角，即：
4
2. 偏振化方向：偏振片允许通过的光振动的方向。
偏振片自然光I0

线偏振光I
1 2
偏振化方向
I
I0
※不是只有一个振动方向的光可以通过偏振片，其他方向振动的光在偏振化方向的分量均可以通过偏振片。
偏振片自然光I0

线偏振光I
1 2
偏振化方向
I
I0
※自然光不是只有2个方向的振动，在 0~2p 内有无数个振动方向。
光
的

光电子技术,习题解答

1. 什么是光电子技术？当前光电子技术备受重视的原因是什么？答：光电子技术是研究从红外波、可见光、X射线直至γ射线波段范围内的光波。

电子技术，是研究运用光子和电子的特性，通过一定媒介实现信息与能量转换、传递、处理及应用的科学。

因为光电子技术的飞速发展，使得光电子技术逐渐成为高新科学技术领域内的先导和核心，在科学技术，国防建设，工农业生产、交通、邮电、天文、地质、医疗、卫生等国民经济的各个领域内都获得了愈来愈重要的应用，特别是正逐渐进入人们的家庭，因此光电子技术备受重视。

2. 什么叫光的空间相干性？时间相干性？光的相干性能好差程度分别用什么衡量？它们的意义是什么？答：空间相干性是指在同一时刻垂直于光传播方向上的两个不同空间点上的光波场之间的相干性，空间相干性是用相干面积Ac来衡量，Ac愈大，则光的空间相干性愈好。

时间相干性是指同一空间点上，两个不同时刻的光波场之间的相干性，用相干时间t c=L c／c来衡量，t c愈大，光的时间相干性愈好。

3. 世界上第一台激光器是由谁发明的？它是什么激光器？它主要输出波长为多少？答：1960年5月16日、美国梅曼博士、红宝石激光器、6943Å。

4. 自发辐射与受激辐射的根本差别是什么？为什么说激励光子和受激光子属同一光子态？答：差别在有没有受到外界电磁辐射的作用；因为有相同的频率、相位、波矢和偏振状态。

5. 为什么说三能级系统实现能态集居数分布反转要比四能级系统困难？答：因为三能级系统的上能级为E2，下能级为E1，在E2上停留的时间很短，而四能级系统在E3上呆的时间较长，容易实现粒子数反转。

6. 激光器的基本组成有哪几部分？它们的基本作用是什么？答：组成部分：工作物质、泵浦系统、谐振腔工作物质提供能级系统、泵浦源为泵浦抽运让粒子从下能级到上能级条件、谐振腔起正反馈作用7. 工作物质能实现能态集居数分布反转的条件是什么？为什么？对产生激光来说，是必要条件还是充分条件，为什么？答：工作物质要具有丰富的泵浦吸收带，寿命较长的亚稳态，要求泵浦光足够强；必要条件，因为它还以kkk谐振腔内以提供正反馈。

光通过单轴晶体时的双折射现象

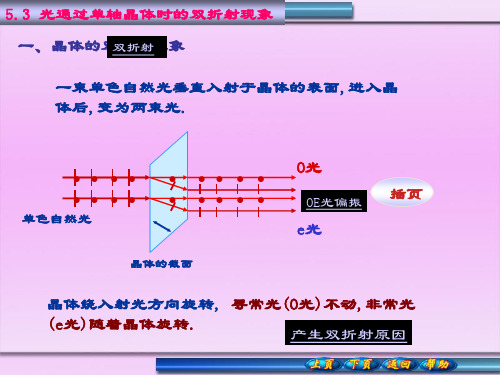
非常光( 非常光 extraordinary light e光): 光 (1) 是振动面平行于自己的主平面的线偏振光是振动面平行于自己的主平面的线偏振光; (2) 一般不符合折射定律在垂直于光轴的方向一般不符合折射定律,在垂直于光轴的方向传播时符合折射定律. 传播时符合折射定律 (3) 沿不同的方向折射率不同传播速度不同沿不同的方向折射率不同, 传播速度不同. 沿光轴的方向折射率和速度与O光相同沿光轴的方向折射率和速度与光相同. 光相同光和e光的主平面相互平行时两光的振动面互相垂直. 当o光和光的主平面相互平行时两光的振动面互相垂直光和光的主平面相互平行时,两光的振动面互相垂直对于e光沿垂直于光轴的方向的折射率称为主折射率,记为记为n 对于光, 沿垂直于光轴的方向的折射率称为主折射率记为 e.
o
e
晶体主截面 O
晶体绕入射光方向旋转时两束光的相对光强不断变化 O’ 入射光振动面
o e
晶体主截面 O
晶体绕入射光方向旋转时两束光的相对光强不断变化 O’ 入射光振动面
o
e
O
晶体主截面
晶体绕入射光方向旋转时两束光的相对光强不断变化 O’ 入射光振动面
o
e
O
晶体主截面
晶体绕入射光方向旋转时两束光的相对光强不断变化 O’ 入射光振动面
方解石晶体实物照片纸面方解石晶体 CaCO3
折射现双折射现象
1、双折射现象用眼睛观看发光点，会看到两个像点，透过方解石晶体，纸面上的字成了的双字
O光和e光
自然光进入各向异性晶体中，光线怎样传播？
两束折射光
▲ 服从折射定律寻常光线
ordinary ray— O光 extra —e光

第八章光在晶体中的传播精品PPT课件

法线入射光
光轴
主截面主截面：光轴和晶体表面光入射点的法线组成的平面。
法线光轴
入射光
eo
主平面：晶体中光（o光或e光）的传播方向与晶体光轴构成的平面。
o光的振动方向垂直于o光的主平面； e光的振动方向平行于e光的主平面。当o光和e光的主平面相互平行时,两光的振动互相垂直.
o光和e光的传播方向
Rasmus Bartholin is remembered especially for his discovery (1669) of the birefringence of a light ray by Iceland crystal (calcite). He published an accurate description of the phenomenon, but since the physical nature of light was poorly understood at the time, he was unable to explain it. It was only after Thomas Young proposed the wave theory of light, c. 1801 that an explanation became possible.
加拿
大树胶
涂黑
格兰—汤普森棱镜
钠光自然光
o e• • •
钠光自然光
o e• •
方解石制成的罗匈棱镜
玻璃和方解石制成的偏振器
第三节：波片和补偿器
将单轴晶体切成的有一定厚度的晶体片，使其光轴平行于表面，叫做波片．当光垂直通过波片时，在波片内分解为 o光e光，因在晶体内垂直于光轴传播，所以o光e光的传播速度不同，这样，传播到波片的后表面o光e光就有了附加的相位差．

物理光学平面光波在晶体界面上的反射和折射

对于各向异性的晶体而言：
①式中的 i 、 r、t 都是对波法线方向而言的,尽管
反射光、折射光的波法线均在入射面内，但它们的光线有可能不在入射面内。
A
B
k i s i n i k r s i n r k t s i n t ( 1 1 0 ) vr vp
A s kB
光在晶体界面上的双反射和双折射
一个半轴长为o,另一个半轴长介于o 和e 之间.
S
B
A
A
R 0
R0 R
e No
1. 惠更斯作图法
将SA 延长与入射光波面相交于R,过 R 作切平面AR,它就是入射光次波面的包迹—入射光波的波阵面。入射光的光线方向和波法线方向均为 AR 方向。
S
B
A
A
R 0
R0 R
e No
1. 惠更斯作图法
n no n n o
光轴
ki ke ko
2) 平面光波在主截面内斜入射
平面光波在主截面内斜入射时,在晶体内将分为 o 光和 e 光, e 光的波法线方向、光线方向一般与o 光不相同，但都在主截面内。
ki
ko ke
se
光轴
2) 平面光波在主截面内斜入射当晶体足够厚时，从晶体下表面射出的是两束振动方向互相垂直的线偏振光，传播方向与入射光相同。
k i s i n i k r s i n r k t s i n t ( 1 1 0 )
或
nisini nrsinr (111) nisini ntsint (112)
(111)式和(112)式就是光在晶体界面上的反射定律和折射定律。
根据图所示的几何关系，由(108)式和(109)式得到
O

晶体光学基础试题及答案

晶体光学基础试题（判断对错/简答）1．除真空以外的任何介质的折射率总是大于1（）2．折射定律表达为折射率为入射角与折射角的正弦之比,所以入射角越大,折射率越大；入射角越小,折射率越小( )3．某介质绝对折射率为光在空气中传播速度与在该介质中速度之比,即N=C O/V（）4．光在某介质中传播速度愈快,折射率愈大( )5．光由光疏介质射入光密介质,永远不会发生全反射()6．光由光密介质射入光疏介质,一定发生全反射()7．均质体有无数个相同的Ｎ或只有一个Ｎ（）8．非均质体有几个不同的Ｎ（）9．自然光射入均质体中，基本仍为自然光，偏光射入仍为偏光，不放生双折射（）10．自然光射入非均质体中一般发生双折射形成两种偏光；偏光射入非均质体中，按入射偏光传播，不发生双折射（）11．光在晶体中传播方向一致，则Ｎ一样（）12．光在晶体中振动方向一致，则Ｎ一样（）光率体基础1. 一轴晶有N e 、N o两个折射率，二轴晶有N g 、N m 、N p三个折射率( )2. 一轴晶N e >N o , 二轴晶N g >N m >N p ( )3. 一轴晶正光性N e >N o；负光性N e <N o ; 二轴晶正光性N g >N m >N p；负光性N g <N m <N p ( )4. 一轴晶光率体切面始终有一个N o，二轴晶光率体切面始终有一个N m（）5. 无论是一轴晶还是二轴晶，具有最大双折率的切面一定平行光轴（）6. 一轴晶有一个光率体圆切面，二轴晶有两个光率体圆切面（）7. 一轴晶有两个主折射率N e 、N o，二轴晶有三个主折射率N g 、N m、N p（）8. 二轴晶光轴面一定是与N g N p面一致（）9. 二轴晶垂直光轴面的任意切面总有一个半径是N m（）10. 一轴晶最大双折率为︱N e–N o︱，二轴晶最大双折率为N g–N m（）11. 二轴晶Bxa一定垂直B xo（）12. 二轴晶Bxa和、B xo构成的切面也一定是与光轴面一致（）13. 二轴晶B xa或B xo不可能是N m（）14. 一轴晶光率体的光轴始终是竖直的（）15. 二轴晶光率体的N g始终是竖直的（）16. 一轴晶N e与Z轴始终一致，二轴晶N g与Z轴始终一致( )17. 二轴晶三个光率体主轴一定与三个结晶轴一致（）18. 一轴晶光轴（N e）始终是竖直的，二轴晶光轴面（OAP）则始终是竖直的（）19. 二轴晶斜方晶系N g 、N m、N p与X、Y、Z轴一致（）20. 二轴晶单斜晶系一定是N m =Y（）单偏光镜下晶体光学性质1. 解理缝一般是暗色细缝（）2. 当解理面与薄片垂直时解理缝最清楚（）3. 某矿物切面见不到解理缝，说明该矿物一定不发育解理（）4. 辉石和长石都发育两组解理，薄片中辉石见到解理的机会少，而长石机会多（）5. 手标本上见到某矿物有颜色，则薄片中一定也有颜色（）6. 均质体矿物在薄片中一定无多色性（）7. 非均质体矿物在薄片中一定有多色性（）8. 薄片中矿物有颜色的切面一定有多色性（）9. 有多色性矿物的没有多色性的切面一般是光率体圆切面（）10. 有多色性的一轴晶只有N e N o面上有多色性，二轴晶只有N g N p面上有多色性（）11. 电气石纵切面平行十字丝纵丝时，所见的颜色是N o（）12. 黑云母解理缝平行十字丝纵丝时，所见的颜色是N p（）13. 普通角闪石（010）面上多色性最明显，可以见到N g和N p的颜色（）14. 普通角闪石（001）面上可以见到两组解理，其锐夹角方向为N m的颜色（）15. 普通角闪石（100）面上只能见到一组解理，也可以见到N m的颜色（）16. 在薄片中某矿物颗粒贝克线在该矿物一侧，则该矿物Ｎ一定＞1.54（）17. 矿物突起越高，Ｎ越大，突起越小，Ｎ越小（）18. 提升物台时，贝克线向折射率大的物质方向移动（）19. 所有非均质体切面都具有闪突起（）20. 所有非均质体椭圆切面都具有闪突起（）正交偏光镜下晶体光学性质（一）１.正交偏光间全消光的矿物颗粒一定是均质体（）２.正交偏光间出现“四明四暗”现象的颗粒一定是非均质体（）３.正交偏光间某矿物所有切面都呈全消光，该矿物一定是均质体（）４.非均质体所有切面都可以见“四明四暗”现象（）５.干涉色与单偏光镜下颜色的形成原理类似（）６.干涉色与光程差是一一对应的，只要干涉色颜色种类一样，则光程差一样（）７.灰色和黄色干涉色一定属于Ⅰ级干涉色（）８.蓝色和绿色干涉色至少是Ⅱ级或以上干涉色（）９.相邻色序对比，紫红对应的光程差一定小于蓝对应的光程差（）１０.同一级别内，紫红对应的光程差也一定小于蓝对应的光程差（）１１.同一薄片中，具有不同干涉色的颗粒，一定是不同种矿物（）１２.同一薄片中，具有相同干涉色的颗粒，一定是同一种矿物（）１３.每一种非均质体矿物，只有一种干涉色（）１４.每一种非均质体矿物，只有一种最高干涉色（）１５.具有最高干涉色的切面一定平行光轴（）１６.平行光轴的切面，一定具有最高干涉色（）１７.单偏光下具有闪突起的矿物颗粒，正交偏光下其干涉色一般比较高（）１８.石英为一轴晶，N o =1.544, N e=1.553，标准薄片厚度下，最高干涉色是Ⅰ级紫红（）１９.方解石为一轴晶，N o=1.658, N e=1.486，最高干涉色达到高级白（）２０.某二轴晶矿物，N g=1.705, N m=1.70, N p=1.693,垂直Bxa切面干涉色是灰色（）正交偏光镜下晶体光学性质（二）１.补色法则中，光率体半径同名平行时，结果干涉色一定比矿片原来的高（）２.补色法则中，光率体半径异名平行时，结果干涉色一定比矿片原来的低（）３.某矿物颗粒干涉色为灰色，加石膏试板后，一个45°位变为蓝，另一个45°位变为黄，干涉色都比原来的高，所以两个45°位都是光率体半径同名平行（）４.某颗粒干涉色为灰色，加石膏试板后，一个45°位变为蓝，那另一个45°位一定变为黄（）５.某颗粒加石膏试板后，一个45°位变为蓝，另一个45°位变为黄，那原来的干涉色一定是灰（）６.某颗粒加石膏试板后，一个45°位变为蓝，另一个45°位变为灰，那原来的干涉色一定是黄（）７.某颗粒干涉色加石膏试板后，两个45°位都变为绿色，说明原来的干涉色一定至少为Ⅱ级（）８.某颗粒干涉色加石膏试板后，只要有一个45°位变为Ⅰ级，说明原来的干涉色一定不超过Ⅱ级（）９.原干涉色为蓝色，加云母试板后，升高位一定变成绿色，降低位一定变成红色（）１０.某矿物颗粒，加云母试板后，一个变成红，另一个变成绿，原来的干涉色一定是蓝色（）１１.原干涉色为黄色，加云母试板后，升高位一定变成红色，降低位一定变成绿色（）１２.某矿物颗粒，加云母试板后，一个变成红，另一个变成绿，原来的干涉色一定是黄色（）１３.一轴晶矿物平行C轴切面为平行消光（）１４.单斜晶系矿物普通角闪石N m =b，其平行（100）的切面是平行消光，平行(010)的切面是斜消光，平行（001）的切面是对称消光（）１５.正光性矿物一定是正延性，负光性矿物一定是负延性（）锥光镜下晶体光学性质（一）１.正交镜下全消光的矿物切面，在锥光镜下也全消光（）２.只有光率体切面为椭圆的矿物颗粒，在锥光镜下才有干涉图（）３.一轴晶垂直光轴切面干涉图就是一个黑十字（）４.正交镜下最高干涉色越高的矿物，其垂直OA切面干涉图干涉色色圈越多（）５.单偏光镜下具有闪突起的矿物，其垂直OA切面干涉图干涉色色圈一般比较多（）６.一轴晶垂直OA切面，波向图中切线方向为N o，放射线方向为N e（）７.一轴晶垂直OA切面，波向图中放射线方向一定为光率体椭圆长半径方向（）８.某一轴晶矿物颗粒在锥光下出现一黑十字，且四个象限均为灰色，现插入石膏试板，发现一、三象限变成蓝色，二、四象限变为黄色，该矿物为负光性（）９.根据上题，把石膏试板换成云母试板，则第一、三象限干涉色变为黄色（）１０.具有多圈干涉色色圈的垂直OA干涉图，从中心向外干涉色逐渐升高，加入石膏试板后，干涉色仍然从中心向外逐渐升高（）１１.具有多圈干涉色色圈的垂直OA干涉图，加入石英楔试板后，发现二、四象限干涉色色圈连续向外移动，该矿物为正光性（）１２.偏心干涉图一般只见黑十字一条横臂或一条竖臂，均无法判断视域外黑十字中心的位置（）１３.当视域内见一条横臂，顺时针转物台，其向上移动，说明黑十字中心在视域右侧（）１４.当视域内见一条竖臂，顺时针转物台，其向左移动，说明黑十字中心在视域下方（）１５.当视域内见一条竖臂，逆时针转物台，其向左移动，继续逆时针转动物台，当该竖臂转到离开视域后，则下一步将会看到一条横臂从上方进入视域（）１６.接上题，当看到一条横臂从上方刚进入视域时，插入石膏试板，若视域的颜色由灰色变成蓝色，其光性符号为正（）１７.具有闪图干涉图的矿物颗粒，去掉锥光系统后，在正交镜下，一般具有比较高的干涉色（）锥光镜下晶体光学性质（二）１.二轴晶垂直Bxa切面干涉图45°位时，两个弯曲黑带顶点连线为光轴方向（）２.二轴晶垂直Bxa切面干涉图的色圈，也是以黑十字交点为中心的同心园色圈（）３.二轴晶垂直Bxa切面干涉图中，两个弯曲黑带顶点连线为N g N p面迹线方向（）４.二轴晶正光性垂直Bxa切面干涉图与负光性垂直Bxo切面干涉图一样（）５.二轴晶垂直Bxa切面干涉图中，两个弯曲黑带顶点凸方连线方向为Bxo投影方向（）６.二轴晶垂直Bxa切面干涉图中，两个弯曲黑带顶点凹方连线方向为Bxa投影方向（）７.二轴晶垂直Bxa切面干涉图中，与两个弯曲黑带顶点连线方向相垂直的方向始终为光轴方向（）８.二轴晶垂直Bxa切面干涉图中，弯曲黑带在Ⅱ、Ⅳ象限时，加试板后，Ⅰ、Ⅲ象限干涉色变化一致，Ⅱ、Ⅳ象限凸方与凹方干涉色变化也一致（）９.垂直Bxa切面干涉图，弯曲黑带在Ⅰ、Ⅲ象限的45°位时，从Ⅱ、Ⅳ象限插入石膏试板，弯曲黑带顶点之间干涉色由灰变蓝，其光性符号是负（）１０.垂直Bxa切面干涉图（色圈多），弯曲黑带在Ⅰ、Ⅲ象限，从Ⅱ、Ⅳ象限插入云母试板，两个弯曲黑带凹方各出现一个对称的小黑团，其光性符号是正（）１１.接上题，若使用石英楔代替云母试板，弯曲黑带顶点之间干涉色圈连续向内移动（）１２.二轴晶垂直OA切面干涉图与一轴晶垂直OA切面干涉图很类似（）１３.二轴晶垂直OA切面干涉图相当于垂直Bxo切面干涉图的一半（）１４.二轴晶垂直OA切面干涉图45°位时，加试板后，弯曲黑带凸方与凹方干涉色变化正好相反（）１５.二轴晶垂直Bxo切面干涉图，也会出现一个粗大黑十字，也叫闪图（）１６.二轴晶垂直Bxo切面干涉图与垂直Bxa切面干涉图类似，只是中心出露轴不同（）１７.二轴晶矿物N g N p面干涉图一定为闪图；反过来，具有闪图特点的切面，一定是N g N p面（）１８.二轴晶闪图干涉图，去掉锥光系统后，在正交偏光间具有该矿物最高干涉色（）１９.二轴晶垂直Bxa切面干涉色一定低于垂直Bxo切面干涉色（）２０.二轴晶垂直Bxa切面与垂直Bxo切面干涉色的相对高低，视光性不同而不同（）填空题1.某矿物为一轴晶，平行c轴方向振动的折射率为1.553，垂直c轴方向振动的折射率为1.544，则该矿物Ne= ，No= ，光性为，最大双折率为，最高干涉色为。

《物理光学》第7章光的偏振与晶体光学基础

vk = vs cos α
z
4、自然光：具有一切可能的振动方向的许多光波的总和。振动方向无规则。自然光可以用相互垂直的两个光矢量表示，这两个光矢量的振幅相同，但位相关系不确定。
没有优势方向
自然光的分解
一束自然光可分解为两束振动方向相互垂直的、一束自然光可分解为两束振动方向相互垂直的、等幅不相干的线偏振光。的、不相干的线偏振光。
寻常光线 (ordinary ray) 和非常光线 (extr- ordinary ray)
o光 : 遵从折射定律
n1 sin i = n2 sin ro sin i ≠ const sin re
自然光 n1 n2 (各向异各向异性媒质) 性媒质
e光 : 一般不遵从折射定律、也不一定在入射面内。
Dx ε xx D = ε y yx Dz ε zx
ε xy ε xz Ex ε yy ε yz E y ε zy ε zz Ez
通过坐标变换，找到主轴方向：x,y,z,则通过坐标变换，找到主轴方向：x,y,z,则：
均匀性及各向异性
2 晶体的介电张量(The dielectric tensor) (The 张量的基础知识：零阶张量(标量): ( ) 如果一个物理量在坐标移动时数值不变，则称为标量(T, (T, m, …) )
一阶张量(矢量)： ( ) 如果一个物理量由三个数表示，而且在坐标移动时如同坐标一样变换，则此物理量称为矢量…
Dx ε x D = 0 y Dz 0
主介电常数双轴晶体：
0
εy
0
0 Ex 0 Ey ε z Ez

晶体的自然双折射

续上
4. 主平面和主截面主平面：晶体中光的传播方向与晶体光轴构成的平面。
o光的主平面
· · · ·
光轴
e光的主平面
o光
光轴
e光
o光的振动方向垂直于o光的主平面； e光的振动方向平行于e光的主平面。
主平面：包含晶体光轴和光线的平面。
主截面：晶体表面的法线与晶体光轴构成的平面。
二. 晶体的主折射率，正晶体、负晶体光矢量振动方向与晶体光轴的夹角不同, 光的传播速度也不同，沿晶体光轴方向o光和e光的传播速度相同。
4 2
2. 二分之一波片
1 ne no d m 2 m 0、 1、 2
A出
光轴
Ae入= Ae出 A入 A0入
使线偏振光振动面转过2 角度三、椭圆与圆偏振光的检偏
A0出
用四分之一波片和偏振片P 可区分出自然光和圆偏振光或部分偏振光和椭圆偏振光。自然光在晶体（波片）内产生的o光和e 光虽然同频率且振动方向相互垂直，但它们之间无固定的位相差，这样的光不能合成椭圆偏振光。
102° A
例如，方解石晶体
光轴 B
光轴是一特殊的方向,凡平行于此方向的直线均为光轴。
•
单轴晶体：只有一个光轴的晶体
双轴晶体：有两个光轴的晶体
方解石
方解石的光轴
通过A或B，并与三个会合钝角的界面成等角的直线方向，就是方解石晶体的光轴方向
（对于严格等棱长的方解
石菱体，即AB连线方向）
与此平行通过晶体的直线都是光轴方向，常用表示
必须与第一步 I 片产生强度极大或极小透振方向重合。
观察现象有消失结论第二步
线偏振光自然光或圆偏振光 a. 令入射光依次通过

在单轴晶体中

线偏振光垂直入射到半波片，透射光仍为线偏振光,假如入射时振动面和主截面之间的夹角为θ, 则透射出来的线偏振光的振动面从原来的方位向转轴方向转过2θ.
⑶全波片: (n o - ne )d k
或：
Δ

2 λ
(
n0

ne
)d

2k
（4）其它任意厚度d,
习惯上称晶片.

2
(a)
有两种类型的双折射晶体
⑴Vo>Ve，(垂轴之间的e光波速为Ve),则称正晶体,以石英代表，在正晶体内，椭球波面内切于球面波面之内。
⑵vo<ve,称负晶休，以冰洲石（方解石）为代表，在负晶体内，椭球波面外切于球面波面之外。
§5.5光在晶体中的传播方向
一.单轴晶体内o光与e光的传播方向：
带来困难， ④不适用对紫外线研究
二.沃拉斯顿棱镜
1.构成（如图）：由两块方解石磨制的直角三棱镜构成，两者光轴方向互相垂直，且光轴都平行于前后通光面。
2.作用：将一束光分解为互相分开的，振动方向互相垂直的平面偏振光。又称棱镜分束镜。
三.波晶片
1.晶片：一块表面平行的单轴晶体，其光轴与晶体表面平行时，o光与e光沿同一方向传播，把这样的晶体叫波晶片。
1)
2
即：振动方向垂直的o光、e光的光程差等于的
奇数倍，位相差等于的奇数倍的晶片， 4
称片。
2
4

⑵ 2 片（半波片）晶片厚度满足

(no
-
ne
)d

(2k

1)
2
或：

2
(no

2.2-光波在电光晶体中的传播.

两偏振分量的相位延迟分别为
n x
n0
1 2
n
3 0
63
E
z
n y
n0
1 2
n
3 0
63
E
z
nz ne
nx 2nxL2L(n012n0363Ez) ny 2nyL2L(n012n0363Ez)
因此，当这两个光波穿过晶体后将产生一个相位差
n y n x 2L 0 36 E n z 3 2 n 0 36 V 3 ( 1 )9
称为电光张量，每个元素的值由具体的晶体决定，它是表征感应极
化强弱的量。下面以常用的KDP晶体为例进行分析。
磷酸二氢钾 KDP（KH2PO4）类晶体属于四方晶系, 42m点群, 是负
单轴晶体, 因此有
nx
这类晶体的电光张量为:
n
y
0
n0,nz
0
ne ,且n0
0
ne,
0
0
0
0
ij
41
0 0
E A 1 x 2 2 E A 2 y 2 2 2E A 1 xA E 2yco ssi2 n
(2)1
这里有了一个与外加电压成正比变化的相位延迟晶体(相当于一个可
调的偏振态变换器)，因此，就可能用电学方法将入射光波的偏振态变换成所需要的偏振态。
E A 1 x 2 2 E A 2 y 2 2 2E A 1 xA E 2yco ssi2 n
0，得到该椭圆的方程为:
(n 1 0 2 6E 3 z)x2 (n 1 0 2 6E 3 z)y2 1 (2 2)8
(1E )x 2 (1E )y 21z 2 1
n 2 0
63z
n 2
63z

光通过双折射晶体

2021/7/1
35
2.洛匈棱镜（Rochon prism）
材料：石英（正晶体）
ne no
制作原理思考
2021/7/1
36
二、波片（ Wave plate, 位相延迟器）它的作用是：
使两个振动方向相互垂直的光产生位相(phase)延迟。
制作：用单轴透明晶体做成的平行平板，光轴与表面平行。
• 自然光入射波片时，出射光仍然是自然光
• 为改变偏振光的偏振态，入射光与波片快轴或慢轴成一定的夹角
2021/7/1
45
三、补偿器(Compensator)
dmin 4no ne
当n0>ne时，e光超前，波片的快轴为e 矢量方向。
2021/7/1
39
性质：
1）线偏光入射时若入射线偏光光矢量方向与快、慢轴方向一致时，出射仍为线偏光；若入射线偏光光矢量方向与快、慢轴都成 45度时，出射光为圆偏光。若入射线偏光光矢量方向与快、慢轴都成其他角度时，出射光为椭圆偏光；
两束折射光中，有一束光遵守折射定律，
称为寻常光（o光）；另外一束一般不遵守折射定律，称为非寻常光（e光）。
说明：1〕o光和e光与晶体密不可分
2〕折射定律的含义
折射定律有两个含义：
A. 折射角的关系，B. 入射光线和折射光线与
2法021线/7/1 同在一个平面。
9
二、晶体特性
方解石晶体结构（Calcite--CaCO3）光轴
称该晶片为二分之一波片。性质：
1）圆（椭圆）偏振光入射时，出射光仍为圆（椭圆）偏振光，只是旋向相反；
2）线偏振光入射时，出射光仍为线偏振光。若
入射的线偏振光与快（慢）轴夹角为，出

光在晶体中的波面

§5.4 光在晶体中的波面
一.单轴晶体中的波面
1.在各向同性介质中，点光源的波阵面是球面，单轴晶体中，o光的波面也是球面。
2.在单轴晶体中，e光的波面是以光轴为转轴的旋转椭球面.即:e光沿各个方向的速度不同，沿光轴方向的速度也为νO；沿垂直于光轴方向的速度与 vo差别最大，以νe表示；沿其它方向的光速介于 νo与νe之间。
3.设晶片的厚度为d,在晶片同o光e光的折射率为
no ne，则通过晶片后两束光的位相差为：
2
(no
ne )d
4.波片:有一定厚度的晶片，或者说有特殊厚度的晶片
⑴
片(四分之一波片）若4 晶片厚度d满足
(no
-ne)d(源自k1)4或：
2
(n0
ne)d
(2k
1)
2
即：振动方向垂直的o光、e光的光程差等于的奇
数倍，位相差等于的奇数倍的晶片，
4
称片。
2
4
⑵ 2片（半波片）晶片厚度满足
(no
-
ne
)d
(2k
1)
2
或：
2
(no
ne )d
(2k
1)
o光、e光程差若等于奇数倍，位相差等于π的奇数倍的晶片，称半波片2。
线偏振光垂直入射到半波片，透射光仍为线偏振光,假如入射时振动面和主截面之间的夹角为θ,则透射出来的线偏振光的振动面从原来的方位向转轴方向转过2θ.
t
BD
C
（C为真空或空气中光速）
❖ ⑶.以A为中心，先以voΔt为半径，（Vo为o光在晶体中的光速）作半圆（实际上是半球面亦即o光的次波面）；再作与它在光轴方向相切的半椭球面，令其另一个半长轴为voΔt，此半椭球面即为e光的次波面。

4.3-4.4晶体光学性质的图形表示

（2）、由先到界面的A点作另一边缘入射线的垂线AB，它便是入射线的波面。求出B到B’的时间（3）、以A为中心，νt为半径（ ν为光在折射介质中的波速）在折射介质中作半圆（实际上是半球面）,这就是另一边缘入射线到达B’点时由A点发出的次波面。（4）、通过B’点作上述半圆的切线（实际上是切面）这就是折射线的波面（包络面）
根据定义，这平面也是两折射线的主平面，这样我们可以判知，两折射光的偏振方向：o光的振动垂直纸面，e光的振动在纸平面内。 e光波法线方向与e 光线方向不一致。对于普遍的一般情况，光轴既不与入射面平行也不与它垂直，这时e光次波面与包络面的切点Ae’和e光本身都不在入射面内，就不能用一张平面图来表示了。
折射率椭球
x
y
z
nz
ny
nx
D
o
因此，折射率椭球的矢径r可以表示为：是D矢量方向的单位矢量。第二、从折射率椭球的原点O出发，作平行于给定波法线方向k0的直线OP，如图所示，再过原点O作一平面与OP垂直，该平面与椭球的截线为一椭圆。椭圆的长轴方向和短轴方向就是对应于波法线方向的两个允许存在的光波的矢量方向，
680
710
光轴
S1
770
130
自然光
由于要使其中一支光发生全反射，利用了方解石和加拿大树胶。加拿大树胶是一种各向同性透明的物质。它对钠黄光的折射率为1.550。介于方解石对寻常光的折射率1.6548和对非常光的主折射率1.5159之间。所以就e光来说，树胶相对于方解石是光密介质；而对o光来说，树胶相对于方解石却是光疏介质。于是在特定的条件下，o光就可能发生全反射，射向棱镜壁，被棱镜壁吸收。
尼科耳棱镜的孔径角约为±140 尼科耳棱镜不适用于高度会聚或发散的光束，价格昂贵，入射光束与出射光束不在一条直线上。对激光：是一种优良的偏振器。 2.格兰棱镜是为改进尼科耳棱镜入射光束与出射光束不在一条直线上，带来使用不便的问题而设计的。特点：端面与底面垂直