二次函数中动点问题_平行四边形(练习)

合集下载

二次函数中动点问题——平行四边形(练习)

2018年04月28日187****6232的初中数学组卷一．解答题（共5小题）1．如图，已知抛物线y=ax2+bx+c经过点A（﹣1，0），点B（3，0）和点C（0，3）．（1）求抛物线的解析式和顶点E的坐标；（2）点C是否在以BE为直径的圆上？请说明理由；（3）点Q是抛物线对称轴上一动点，点R是抛物线上一动点，是否存在点Q、R，使以Q、R、C、B为顶点的四边形是平行四边形？若存在，直接写出点Q、R 的坐标，若不存在，请说明理由．2．如图，已知抛物线y=ax2+bx+c过点A（﹣3，0），B（﹣2，3），C（0，3），其顶点为D．（1）求抛物线的解析式；（2）设点M（1，m），当MB+MD的值最小时，求m的值；（3）若P是抛物线上位于直线AC上方的一个动点，求△APC的面积的最大值；（4）若抛物线的对称轴与直线AC相交于点N，E为直线AC上任意一点，过点E 作EF∥ND交抛物线于点F，以N，D，E，F为顶点的四边形能否为平行四边形？若能，求点E的坐标；若不能，请说明理由．3．如图，抛物线y=x2﹣2x﹣3与x轴交于A、B两点（点A在点B的左侧），直线l与抛物线交于A，C两点，其中点C的横坐标为2．（1）求A，B两点的坐标及直线AC的函数表达式；（2）P是线段AC上的一个动点（P与A，C不重合），过P点作y轴的平行线交抛物线于点E，求△ACE面积的最大值；（3）若直线PE为抛物线的对称轴，抛物线与y轴交于点D，直线AC与y轴交于点Q，点M为直线PE上一动点，则在x轴上是否存在一点N，使四边形DMNQ 的周长最小？若存在，求出这个最小值及点M，N的坐标；若不存在，请说明理由．（4）点H是抛物线上的动点，在x轴上是否存在点F，使A、C、F、H四个点为顶点的四边形是平行四边形？如果存在，请直接写出所有满足条件的F点坐标；如果不存在，请说明理由．4．如图，在平面直角坐标系中，直线y=﹣3x﹣3与x轴交于点A，与y轴交于点C．抛物线y=x2+bx+c经过A，C两点，且与x轴交于另一点B（点B在点A右侧）．（1）求抛物线的解析式及点B坐标；（2）若点M是线段BC上一动点，过点M的直线EF平行y轴交x轴于点F，交抛物线于点E．求ME长的最大值；（3）试探究当ME取最大值时，在x轴下方抛物线上是否存在点P，使以M，F，B，P为顶点的四边形是平行四边形？若存在，请求出点P的坐标；若不存在，试说明理由．5．如图，矩形OABC在平面直角坐标系中，点A在x轴正半轴，点C在y轴正半轴，OA=4，OC=3，抛物线经过O，A两点且顶点在BC边上，与直线AC交于点D．（1）求抛物线的解析式；（2）求点D的坐标；（3）若点M在抛物线上，点N在x轴上，是否存在以A，D，M，N为顶点的四边形是平行四边形？若存在，求出点N的坐标；若不存在，请说明理由．2018年04月28日187****6232的初中数学组卷参考答案与试题解析一．解答题（共5小题）1．如图，已知抛物线y=ax2+bx+c经过点A（﹣1，0），点B（3，0）和点C（0，3）．（1）求抛物线的解析式和顶点E的坐标；（2）点C是否在以BE为直径的圆上？请说明理由；（3）点Q是抛物线对称轴上一动点，点R是抛物线上一动点，是否存在点Q、R，使以Q、R、C、B为顶点的四边形是平行四边形？若存在，直接写出点Q、R 的坐标，若不存在，请说明理由．【分析】（1）将A（﹣1，0）、B（3，0）、C（0，3）三点坐标代入抛物线y=ax2+bx+c 中，列方程组求a、b、c的值即可；（2）根据勾股定理的逆定理可得：∠BCE=90°，可得结论；（3）分两种情况：①以BC为边时，如图1，R在对称轴的右侧时，BC∥RQ，四边形CQRB是平行四边形，根据平移规律先得R的横坐标为4，代入抛物线的解析式可得R（4，﹣5），由平移规律可得Q（1，﹣2）；如图2，R在对称轴的左侧，RC∥BQ，四边形CRQB是平行四边形，同理可得点Q、R的坐标．②以BC为对角线时，如图3，同理根据平移规律可得结论．【解答】解：（1）由题意，得：，解得：，故这个抛物线的解析式为y=﹣x2+2x+3，y=﹣x2+2x+3=﹣（x﹣1）2+4，∴顶点E（1，4）；（2）点C在以BE为直径的圆上，理由是：∵C（0，3），B（3，0），E（1，4），∴BC2=32+32=18，CE2=12+12=2，BE2=（3﹣1）2+42=20，∴BC2+CE2=BE2，∴∠BCE=90°，∴点C在以BE为直径的圆上；（3）存在，分两种情况：①以BC为边时，如图1，R在对称轴的右侧时，BC∥RQ，四边形CQRB是平行四边形，由C到B的平移规律可知：Q的横坐标为1，则R的横坐标为4，当x=4时，y=﹣x2+2x+3=﹣42+2×4+3=﹣16+8+3=﹣5，∴R（4，﹣5），∴Q（1，﹣2）；如图2，R在对称轴的左侧，RC∥BQ，四边形CRQB是平行四边形，由C到B的平移规律可知：Q的横坐标为1，则R的横坐标为﹣2，当x=﹣2时，y=﹣x2+2x+3=﹣4+2×（﹣2）+3=﹣5，∴R（﹣2，﹣5），∴Q（1，﹣8）；②以BC为对角线时，如图3，由C和Q的平移规律可得：R的横坐标为2，当x=2时，y=﹣4+4+3=3，∴R（2，3），根据R到B的平移规律可得：Q（1，0）；综上所述，R（4，﹣5），Q（1，﹣2）或R（﹣2，﹣5），Q（1，﹣8）或R（2，3），Q（1，0）．【点评】本题是二次函数的综合题，考查了待定系数法求解析式，圆周角定理，勾股定理的应用，平行四边形的判定等，分类讨论的思想是（3）的关键．2．如图，已知抛物线y=ax2+bx+c过点A（﹣3，0），B（﹣2，3），C（0，3），其顶点为D．（1）求抛物线的解析式；（2）设点M（1，m），当MB+MD的值最小时，求m的值；（3）若P是抛物线上位于直线AC上方的一个动点，求△APC的面积的最大值；（4）若抛物线的对称轴与直线AC相交于点N，E为直线AC上任意一点，过点E 作EF∥ND交抛物线于点F，以N，D，E，F为顶点的四边形能否为平行四边形？若能，求点E的坐标；若不能，请说明理由．【分析】（1）根据待定系数法，可得答案；（2）利用轴对称求最短路径的知识，找到B点关于直线x=1的对称点B′，连接B'D，B'D与直线x=1的交点即是点M的位置，继而求出m的值．（3）根据平行于y轴的直线上两点间的距离是较大的纵坐标减去较小的纵坐标，可得PE的长，根据三角形的面积，可得二次函数，根据二次函数的性质，可得答案；（4）设出点E的，分情况讨论，①当点E在线段AC上时，点F在点E上方，②当点E在线段AC（或CA）延长线上时，点F在点E下方，根据平行四边形的性质，可得关于x的方程，继而求出点E的坐标．【解答】解：（1）将A，B，C点的坐标代入解析式，得，解得，抛物线的解析式为y=﹣x2﹣2x+3（2）配方，得y=﹣（x+1）2+4，顶点D的坐标为（﹣1，4）作B点关于直线x=1的对称点B′，如图1，则B′（4，3），由（1）得D（﹣1，4），可求出直线DB′的函数关系式为y=﹣x+，当M（1，m）在直线DB′上时，MN+MD的值最小，则m=﹣×1+=．（3）作PE⊥x轴交AC于E点，如图2，AC的解析式为y=x+3，设P（m，﹣m2﹣2m+3），E（m，m+3），PE=﹣m2﹣2m+3﹣（m+3）=﹣m2﹣3mS△APC=PE•|x A|=（﹣m2﹣3m）×3=﹣（m+）2+，当m=﹣时，△APC的面积的最大值是；（4）由（1）、（2）得D（﹣1，4），N（﹣1，2）点E在直线AC上，设E（x，x+3），①当点E在线段AC上时，点F在点E上方，则F（x，﹣x2﹣2x+3），∵EF=DN∴﹣x2﹣2x+3﹣（x+3）=4﹣2=2，解得，x=﹣2或x=﹣1（舍去），则点E的坐标为：（﹣2，1）．②当点E在线段AC（或CA）延长线上时，点F在点E下方，则F（x，﹣x2﹣2x+3），∵EF=DN，∴（x+3）﹣（﹣x2﹣2x+3）=2，解得x=或x=，即点E的坐标为：（，）或（，）综上可得满足条件的点E为E（﹣2，1）或：（，）或（，）．【点评】本题考查了二次函数的综合题，解（1）的关键是待定系数法，解（2）利用轴对称求最短路径；解（3）的关键是利用三角形的面积得出二次函数；解（4）的关键是平行四边形的性质得出关于x的方程，要分类讨论，以防遗漏．3．如图，抛物线y=x2﹣2x﹣3与x轴交于A、B两点（点A在点B的左侧），直线l与抛物线交于A，C两点，其中点C的横坐标为2．（1）求A，B两点的坐标及直线AC的函数表达式；（2）P是线段AC上的一个动点（P与A，C不重合），过P点作y轴的平行线交抛物线于点E，求△ACE面积的最大值；（3）若直线PE为抛物线的对称轴，抛物线与y轴交于点D，直线AC与y轴交于点Q，点M为直线PE上一动点，则在x轴上是否存在一点N，使四边形DMNQ 的周长最小？若存在，求出这个最小值及点M，N的坐标；若不存在，请说明理由．（4）点H是抛物线上的动点，在x轴上是否存在点F，使A、C、F、H四个点为顶点的四边形是平行四边形？如果存在，请直接写出所有满足条件的F点坐标；如果不存在，请说明理由．【分析】（1）令抛物线y=x2﹣2x﹣3=0，求出x的值，即可求A，B两点的坐标，根据两点式求出直线AC的函数表达式；（2）设P点的横坐标为x（﹣1≤x≤2），求出P、E的坐标，用x表示出线段PE 的长，求出PE的最大值，进而求出△ACE的面积最大值；（3）根据D点关于PE的对称点为点C（2，﹣3），点Q（0，﹣1）点关于x轴的对称点为M（0，1），则四边形DMNQ的周长最小，求出直线CM的解析式为y=﹣2x+1，进而求出最小值和点M，N的坐标；（4）结合图形，分两类进行讨论，①CF平行x轴，如图1，此时可以求出F点两个坐标；②CF不平行x轴，如题中的图2，此时可以求出F点的两个坐标．【解答】解：（1）令y=0，解得x1=﹣1或x2=3，∴A（﹣1，0），B（3，0）；将C点的横坐标x=2代入y=x2﹣2x﹣3得y=﹣3，∴C（2，﹣3），∴直线AC的函数解析式是y=﹣x﹣1，（2）设P点的横坐标为x（﹣1≤x≤2），则P、E的坐标分别为：P（x，﹣x﹣1），E（x，x2﹣2x﹣3），∵P点在E点的上方，PE=（﹣x﹣1）﹣（x2﹣2x﹣3）=﹣x2+x+2，∴当x=时，PE的最大值=，△ACE的面积最大值=PE[2﹣（﹣1）]=PE=，（3）D点关于PE的对称点为点C（2，﹣3），点Q（0，﹣1）点关于x轴的对称点为K（0，1），连接CK交直线PE于M点，交x轴于N点，可求直线CK的解析式为y=﹣2x+1，此时四边形DMNQ的周长最小，最小值=|CM|+QD=2+2，求得M（1，﹣1），N（，0）．（4）存在如图1，若AF∥CH，此时的D和H点重合，CD=2，则AF=2，于是可得F1（1，0），F2（﹣3，0），如图2，根据点A和F的坐标中点和点C和点H的坐标中点相同，再根据|HA|=|CF|，求出F4（4﹣，0），F3．综上所述，满足条件的F点坐标为F1（1，0），F2（﹣3，0），F3，F4（4﹣，0）．【点评】本题主要考查二次函数的综合题的知识点，解答本题的关键是熟练掌握对称的知识和分类讨论解决问题的思路，此题难度较大．4．如图，在平面直角坐标系中，直线y=﹣3x﹣3与x轴交于点A，与y轴交于点C．抛物线y=x2+bx+c经过A，C两点，且与x轴交于另一点B（点B在点A右侧）．（1）求抛物线的解析式及点B坐标；（2）若点M是线段BC上一动点，过点M的直线EF平行y轴交x轴于点F，交抛物线于点E．求ME长的最大值；（3）试探究当ME取最大值时，在x轴下方抛物线上是否存在点P，使以M，F，B，P为顶点的四边形是平行四边形？若存在，请求出点P的坐标；若不存在，试说明理由．【分析】（1）先根据直线的解析式求出A、C两点的坐标，然后将A、C的坐标代入抛物线中即可求出二次函数的解析式．进而可根据抛物线的解析式求出B 点的坐标．（2）ME的长实际是直线BC的函数值与抛物线的函数值的差，据此可得出一个关于ME的长和F点横坐标的函数关系式，可根据函数的性质来求出ME的最大值．（3）根据（2）的结果可确定出F，M的坐标，要使以M，F，B，P为顶点的四边形是平行四边形，必须满足的条件是MP∥=BF，那么只需将M点的坐标向左或向右平移BF长个单位即可得出P点的坐标，然后将得出的P点坐标代入抛物线的解析式中，即可判断出是否存在符合条件的P点．【解答】解：（1）当y=0时，﹣3x﹣3=0，x=﹣1∴A（﹣1，0）当x=0时，y=﹣3，∴C（0，﹣3），∴∴，抛物线的解析式是：y=x2﹣2x﹣3．当y=0时，x2﹣2x﹣3=0，解得：x1=﹣1，x2=3∴B（3，0）．（2）由（1）知B（3，0），C（0，﹣3）直线BC的解析式是：y=x﹣3，设M（x，x﹣3）（0≤x≤3），则E（x，x2﹣2x﹣3）∴ME=（x﹣3）﹣（x2﹣2x﹣3）=﹣x2+3x=﹣（x﹣）2+；∴当x=时，ME的最大值为．（3）答：不存在．由（2）知ME取最大值时ME=，E（，﹣），M（，﹣）∴MF=，BF=OB﹣OF=．设在抛物线x轴下方存在点P，使以P、M、F、B为顶点的四边形是平行四边形，则BP∥MF，BF∥PM．∴P1（0，﹣）或P2（3，﹣）当P1（0，﹣）时，由（1）知y=x2﹣2x﹣3=﹣3≠﹣∴P1不在抛物线上．当P2（3，﹣）时，由（1）知y=x2﹣2x﹣3=0≠﹣∴P2不在抛物线上．综上所述：在x轴下方抛物线上不存在点P，使以P、M、F、B为顶点的四边形是平行四边形．【点评】本题着重考查了待定系数法求二次函数解析式、平行四边形的判定和性质等知识点，综合性强，考查学生分类讨论，数形结合的数学思想方法．（2）中弄清线段ME长度的函数意义是解题的关键．5．如图，矩形OABC在平面直角坐标系中，点A在x轴正半轴，点C在y轴正半轴，OA=4，OC=3，抛物线经过O，A两点且顶点在BC边上，与直线AC交于点D．（1）求抛物线的解析式；（2）求点D的坐标；（3）若点M在抛物线上，点N在x轴上，是否存在以A，D，M，N为顶点的四边形是平行四边形？若存在，求出点N的坐标；若不存在，请说明理由．【分析】（1）设抛物线顶点为E，根据题意E（2，3），设抛物线解析式为y=a（x ﹣2）2+3，将A（4，0）坐标代入q求出a即可解决问题；（2）求出直线AC的解析式，利用方程组确定交点坐标即可；（3）分两种情况考虑：①当点M在x轴上方时，如答图1所示；②当点M在x 轴下方时，如答图2所示；分别利用待定系数法即可解决问题；【解答】解：（1）设抛物线顶点为E，根据题意OA=4，OC=3，得：E（2，3），设抛物线解析式为y=a（x﹣2）2+3，将A（4，0）坐标代入得：0=4a+3，即a=﹣，则抛物线解析式为y=﹣（x﹣2）2+3=﹣x2+3x；（2）设直线AC解析式为y=kx+b（k≠0），将A（4，0）与C（0，3）代入得：，解得：，故直线AC解析式为y=﹣x+3，与抛物线解析式联立得：，解得：或，则点D坐标为（1，）；（3）存在，分两种情况考虑：①当点M在x轴上方时，如答图1所示：四边形ADMN为平行四边形，DM∥AN，DM=AN，由对称性得到M（3，），即DM=2，故AN=2，∴N1（2，0），N2（6，0）；②当点M在x轴下方时，如答图2所示：过点D作DQ⊥x轴于点Q，过点M作MP⊥x轴于点P，可得△ADQ≌△NMP，∴MP=DQ=，NP=AQ=3，将y M=﹣代入抛物线解析式得：﹣=﹣x2+3x，解得：x M=2﹣或x M=2+，∴x N=x M﹣3=﹣﹣1或﹣1，∴N3（﹣﹣1，0），N4（﹣1，0）．综上所述，满足条件的点N有四个：N1（2，0），N2（6，0），N3（﹣﹣1，0），N4（﹣1，0）．【点评】此题考查了二次函数综合题、待定系数法确定抛物线解析式，一次函数与二次函数的交点，平行四边形的性质等知识，解题的关键是熟练掌握待定系数法解决问题，学会用分类讨论的思想思考问题，属于中考压轴题．。

中考数学二次函数动点问题-因动点产生的平行四边形问题

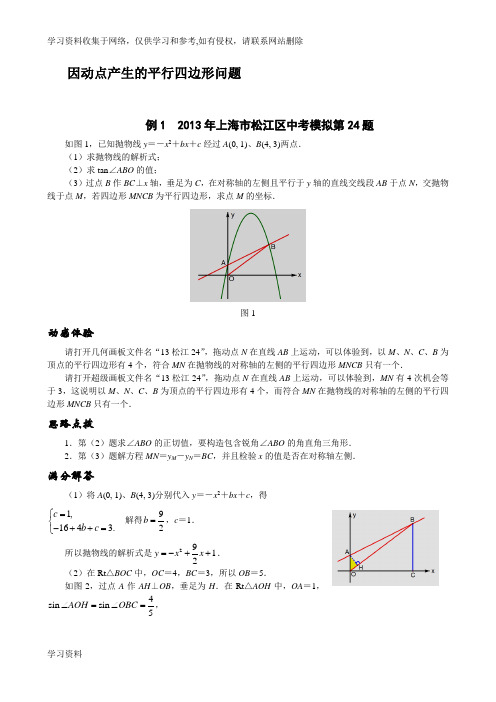
因动点产生的平行四边形问题例1 2013年上海市松江区中考模拟第24题如图1，已知抛物线y ＝－x 2＋bx ＋c 经过A (0, 1)、B (4, 3)两点．（1）求抛物线的解析式；（2）求tan ∠ABO 的值；（3）过点B 作BC ⊥x 轴，垂足为C ，在对称轴的左侧且平行于y 轴的直线交线段AB 于点N ，交抛物线于点M ，若四边形MNCB 为平行四边形，求点M 的坐标．图1动感体验请打开几何画板文件名“13松江24”，拖动点N 在直线AB 上运动，可以体验到，以M 、N 、C 、B 为顶点的平行四边形有4个，符合MN 在抛物线的对称轴的左侧的平行四边形MNCB 只有一个．请打开超级画板文件名“13松江24”，拖动点N 在直线AB 上运动，可以体验到，MN 有4次机会等于3，这说明以M 、N 、C 、B 为顶点的平行四边形有4个，而符合MN 在抛物线的对称轴的左侧的平行四边形MNCB 只有一个．思路点拨1．第（2）题求∠ABO 的正切值，要构造包含锐角∠ABO 的角直角三角形． 2．第（3）题解方程MN ＝y M －y N ＝BC ，并且检验x 的值是否在对称轴左侧．满分解答（1）将A (0, 1)、B (4, 3)分别代入y ＝－x 2＋bx ＋c ，得1,164 3.c b c =⎧⎨-++=⎩ 解得92b =，c ＝1．所以抛物线的解析式是2912y x x =-++．（2）在Rt △BOC 中，OC ＝4，BC ＝3，所以OB ＝5．如图2，过点A 作AH ⊥OB ，垂足为H ．在Rt △AOH 中，OA ＝1，4sin sin 5AOH OBC ∠=∠=，所以4sin 5AH OA AOH =⋅∠=．图2 所以35OH =，225BH OB OH =-=．在Rt △ABH 中，4222tan 5511AH ABO BH ∠==÷=．（3）直线AB 的解析式为112y x =+．设点M 的坐标为29(,1)2x x x -++，点N 的坐标为1(,1)2x x +，那么2291(1)(1)422MN x x x x x =-++-+=-+．当四边形MNCB 是平行四边形时，MN ＝BC ＝3．解方程－x 2＋4x ＝3，得x ＝1或x ＝3．因为x ＝3在对称轴的右侧（如图4），所以符合题意的点M 的坐标为9(1,)2（如图3）．图3 图4考点伸展第（3）题如果改为：点M 是抛物线上的一个点，直线MN 平行于y 轴交直线AB 于N ，如果M 、N 、B 、C 为顶点的四边形是平行四边形，求点M 的坐标．那么求点M 的坐标要考虑两种情况：MN ＝y M －y N 或MN ＝y N －y M ．由y N －y M ＝4x －x 2，解方程x 2－4x ＝3，得27x =±（如图5）．所以符合题意的点M 有4个：9(1,)2，11(3,)2，57(27,)2--，57(27,)2++．图5例2 2012年福州市中考第21题如图1，在Rt△ABC中，∠C＝90°，AC＝6，BC＝8，动点P从点A开始沿边AC向点C以每秒1个单位长度的速度运动，动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动，过点P作PD//BC，交AB于点D，联结PQ．点P、Q分别从点A、C同时出发，当其中一点到达端点时，另一点也随之停止运动，设运动的时间为t秒（t≥0）．（1）直接用含t的代数式分别表示：QB＝_______，PD＝_______；（2）是否存在t的值，使四边形PDBQ为菱形？若存在，求出t的值；若不存在，说明理由，并探究如何改变点Q的速度（匀速运动），使四边形PDBQ在某一时刻为菱形，求点Q的速度；（3）如图2，在整个运动过程中，求出线段PQ的中点M所经过的路径长．图1 图2动感体验请打开几何画板文件名“12福州21”，拖动左图中的点P运动，可以体验到，PQ的中点M的运动路径是一条线段．拖动右图中的点Q运动，可以体验到，当PQ//AB时，四边形PDBQ为菱形．请打开超级画板文件名“12福州21”，拖动点Q向上运动，可以体验到，PQ的中点M的运动路径是一条线段．点击动画按钮的左部，Q的速度变成1.07，可以体验到，当PQ//AB时，四边形PDBQ为菱形．点击动画按钮的中部，Q的速度变成1.思路点拨1．菱形PDBQ必须符合两个条件，点P在∠ABC的平分线上，PQ//AB．先求出点P运动的时间t，再根据PQ//AB，对应线段成比例求CQ的长，从而求出点Q的速度．2．探究点M的路径，可以先取两个极端值画线段，再验证这条线段是不是点M的路径．满分解答（1）QB＝8－2t，PD＝43t．（2）如图3，作∠ABC的平分线交CA于P ，过点P作PQ//AB交BC于Q，那么四边形PDBQ是菱形．过点P作PE⊥AB，垂足为E，那么BE＝BC＝8．在Rt△ABC中，AC＝6，BC＝8，所以AB＝10．图3在Rt△APE中，23cos5AEAAP t===，所以103t=．当PQ//AB时，CQ CPCB CA=，即106386CQ-=．解得329CQ=．所以点Q的运动速度为3210169315÷=．（3）以C为原点建立直角坐标系．如图4，当t＝0时，PQ的中点就是AC的中点E(3，0)．如图5，当t＝4时，PQ的中点就是PB的中点F(1，4)．直线EF的解析式是y＝－2x＋6．如图6，PQ的中点M的坐标可以表示为（62t-，t）．经验证，点M（62t-，t）在直线EF上．所以PQ的中点M的运动路径长就是线段EF的长，EF＝25．图4 图5 图6考点伸展第（3）题求点M的运动路径还有一种通用的方法是设二次函数：当t＝2时，PQ的中点为(2，2)．设点M的运动路径的解析式为y＝ax2＋bx＋c，代入E(3，0)、F(1，4)和(2，2)，得930,4,42 2.a b ca b ca b c++=⎧⎪++=⎨⎪++=⎩解得a＝0，b＝－2，c＝6．所以点M的运动路径的解析式为y＝－2x＋6．例3 2012年烟台市中考第26题如图1，在平面直角坐标系中，已知矩形ABCD的三个顶点B(1, 0)、C(3, 0)、D(3, 4)．以A为顶点的抛物线y＝ax2＋bx＋c过点C．动点P从点A出发，沿线段AB向点B运动，同时动点Q从点C出发，沿线段CD向点D运动．点P、Q的运动速度均为每秒1个单位，运动时间为t秒．过点P作PE⊥AB交AC 于点E．（1）直接写出点A的坐标，并求出抛物线的解析式；（2）过点E作EF⊥AD于F，交抛物线于点G，当t为何值时，△ACG的面积最大？最大值为多少？（3）在动点P、Q运动的过程中，当t为何值时，在矩形ABCD内（包括边界）存在点H，使以C、Q、E、H为顶点的四边形为菱形？请直接写出t的值．图1动感体验请打开几何画板文件名“12烟台26”，拖动点P在AB上运动，可以体验到，当P在AB的中点时，△ACG的面积最大．观察右图，我们构造了和△CEQ中心对称的△FQE和△ECH′，可以体验到，线段EQ 的垂直平分线可以经过点C和F，线段CE的垂直平分线可以经过点Q和H′，因此以C、Q、E、H为顶点的菱形有2个．请打开超级画板文件名“12烟台26”，拖动点P在AB上运动，可以体验到，当P在AB 的中点时，即t=2，△ACG的面积取得最大值1．观察CQ，EQ，EC的值，发现以C、Q、E、H为顶点的菱形有2个．点击动画按钮的左部和中部，可得菱形的两种准确位置。

二次函数动点问题(含答案)

1.如图，已知抛物线1C 与坐标轴的交点依次是(40)A -，，(20)B -，，(08)E ，．（1）求抛物线1C 关于原点对称的抛物线2C 的解析式；（2）设抛物线1C 的顶点为M ，抛物线2C 与x 轴分别交于C D ，两点（点C 在点D 的左侧），顶点为N ，四边形MDNA 的面积为S ．若点A ，点D 同时以每秒1个单位的速度沿水平方向分别向右、向左运动；与此同时，点M ，点N 同时以每秒2个单位的速度沿坚直方向分别向下、向上运动，直到点A 与点D 重合为止．求出四边形MDNA 的面积S 与运动时间t 之间的关系式，并写出自变量t 的取值范围；（3）当t 为何值时，四边形MDNA 的面积S 有最大值，并求出此最大值；（4）在运动过程中，四边形MDNA 能否形成矩形？若能，求出此时t 的值；若不能，请说明理由．[解] （1）点(40)A -，，点(20)B -，，点(08)E ，关于原点的对称点分别为(40)D ，，(20)C ，，(08)F -，．设抛物线2C 的解析式是2(0)y ax bx c a =++≠，则16404208a b c a b c c ++=⎧⎪++=⎨⎪=-⎩，，．解得168a b c =-⎧⎪=⎨⎪=-⎩，，．所以所求抛物线的解析式是268y x x =-+-．（2）由（1）可计算得点(31)(31)M N --，，，．过点N 作NH AD ⊥，垂足为H ．当运动到时刻t 时，282AD OD t ==-，12NH t =+．根据中心对称的性质OA OD OM ON ==，，所以四边形MDNA 是平行四边形．所以2ADN S S =△．所以，四边形MDNA 的面积2(82)(12)4148S t t t t =-+=-++．因为运动至点A 与点D 重合为止，据题意可知04t <≤．所以，所求关系式是24148S t t =-++，t 的取值范围是04t <≤．（3）781444S t ⎛⎫=--+ ⎪⎝⎭，（04t <≤）．所以74t =时，S 有最大值814．提示：也可用顶点坐标公式来求．（4）在运动过程中四边形MDNA 能形成矩形．由（2）知四边形MDNA 是平行四边形，对角线是ADMN ，，所以当AD MN =时四边形MDNA 是矩形．所以OD ON =．所以2222OD ON OH NH ==+．所以22420t t +-=．解之得1222t t =，（舍）．所以在运动过程中四边形MDNA可以形成矩形，此时2t =．[点评]本题以二次函数为背景，结合动态问题、存在性问题、最值问题，是一道较传统的压轴题，能力要求较高。

中考数学专题17 函数动点问题中平行四边形存在性(解析版)

专题17 函数动点问题中平行四边形存在性类型一、平行四边形存在性结论：A C B DA CB Dx x x xy y y y+=+⎧⎨+=+⎩类型二、特殊平行四边形存在性1. 矩形存在性常用解题思路：构造一线三直角（借助相似或三角函数求解）；利用矩形对角线相等（直角三角形斜边的中线等于斜边的一半）借助勾股定理求解等.2. 菱形存在性常用解题思路：利用菱形四条边相等，对角线互相垂直，借助勾股定理等求解.3. 正方形存在性常用解题思路：兼具矩形和菱形二者.【例1】（2018·郑州预测卷）如图，直线y=334x-+与x轴交于点C，与y轴交于点B，抛物线y= 234ax x c++经过B、C两点.（1）求抛物线的解析式；（2）如图，点E是直线BC上方抛物线上的一个动点，当△BEC的面积最大时，求出点E的坐标和最大值；（3）在（2）条件下，过点E作y轴的平行线交直线BC于点M，连接AM，点Q是抛物线对称轴上的动点，在抛物线上是否存在点P，使以点P、Q、A、M为顶点的四边形是平行四边形？若存在，请直接写出点P的坐标；若不存在，请说明理由.【答案】见解析.【解析】解：（1）∵直线y =334x -+与x 轴交于点C ，与y 轴交于点B ，∴B (0,3)，C (4,0)，将B (0,3)，C (4,0)代入y = 234ax x c ++得： 16303a c c ++=⎧⎨=⎩，解得：383a c ⎧=-⎪⎨⎪=⎩， ∴抛物线的解析式为：233384y x x =-++.（2）过点E 作EF ⊥x 轴于F ，交BC 于M ，设E （x ，233384x x -++），则M （x ，334x -+），∴ME =233384x x -++－（334x -+）=23382x x -+∴S △BEC =12×EM ×OC =2EM=2(23382x x -+)=()23234x --+,∴当x =2时，△BEC 的面积取最大值3，此时E (2，3).（3）由题意得：M (2，32)，抛物线对称轴为：x =1，A (－2,0),设P (m ，y )，y =233384m m -++，Q (1，n )①当四边形APQM 为平行四边形时，有：212m -+=+，解得：m =－3，即P (－3，218-)； ②当四边形AMPQ 为平行四边形时，有：－2+m =2+1，即m =5 即P (5, 218-)； ③当四边形AQMP 为平行四边形时，有：2－2=1+m ，得：m =－1，即P (－1，158)；综上所述，抛物线上存在点P ，使以点P 、Q 、A 、M 为顶点的四边形是平行四边形，点P 的坐标为：(－3，218-)，(5, 218-)，(－1，158).【变式1-1】（2018·河师大附中模拟）如图，抛物线y =ax 2+bx +c （a ≠0）与x 轴交于点A (－1，0)、B (3，0)两点，与y 轴交于点C (0，－3).（1）求抛物线的解析式与顶点M 的坐标；（2）求△BCM 的面积与△ABC 面积的比；（3）若P 是x 轴上一个动点，过P 作射线PQ ∥AC 交抛物线于点Q ，随着P 点的运动，在x 轴上是否存在这样的点P ，使以点A 、P 、Q 、C 为顶点的四边形为平行四边形？若存在请直接写出点P 的坐标；若不存在，请说明理由.【答案】见解析.【解析】解：（1）将A (－1，0)，B (3，0)， C (0，－3)代入y =ax 2+bx +c ，得：9303a b c a b c c -+=⎧⎪++=⎨⎪=-⎩，解得：a =1，b =－2，c =－3，即抛物线的解析式为：y=x2－2x－3，顶点M的坐标为：（1，－4）；（2）连接BC，BM，CM，过M作MD⊥x轴于D，如图所示，S△BCM=S梯形ODMC+S△BDM－S△BOC=3，S△ACB=6，∴S△BCM：S△ACB=1：2；（3）存在.①当点Q在x轴上方时，过Q作QF⊥x轴于F，如图所示，∵四边形ACPQ为平行四边形，∴QP∥AC，QP=AC∴△PFQ≌△AOC，∴FQ=OC=3，∴3=x2﹣2x﹣3，解得x或x=1，∴Q，3)或(1，3)；②当点Q在x轴下方时，过Q作QE⊥x轴于E，如图所示，同理，得：△PEQ≌△AOC，∴EQ=OC=3，∴﹣3=x2﹣2x﹣3，解得：x=2或x=0(与C点重合，舍去)，∴Q(2，﹣3)；综上所述，点Q的坐标为：，3)或(1，3)或(2，﹣3).【例2】（2018·郑州三模）如图所示，在平面直角坐标系中，已知抛物线y=ax2+bx－5与x轴交于A(-1,0),B(5,0)两点，与y轴交于点C.（1）求抛物线的解析式；（2）如图2所示，CE∥x轴与抛物线相交于点E，点H是直线CE下方抛物线上的动点，过点H且与y轴平行的直线与BC、CE分别交于点F、G，试探究当点H运动到何处时，四边形CHEF的面积最大，求点H的坐标及最大面积；（3）点M是（1）中所求抛物线对称轴上一动点，点N是反比例函数y=kx图象上一点，若以点B、C、M、N为动点的四边形是矩形，请直接写出满足条件的k的值.【答案】见解析.【解析】解：（1）将A (-1,0),B (5,0)代入y =ax 2+bx －5得：5025550a b a b --=⎧⎨+-=⎩，解得：14a b =⎧⎨=-⎩，即抛物线的解析式为：y =x 2－4x －5.（2）在y =x 2－4x －5中，当x =0时，y =－5，即C (0，－5), ∵CE ∥x 轴，则C 、E 关于直线x =2对称， ∴E (4，－5), CE =4，由B （5,0）, C (0，－5)得直线BC 的解析式为：y =x －5，设H (m ，m 2－4m －5)， ∵FH ⊥CE ， ∴F (m ，m －5)，∴FH = m －5－（m 2－4m －5)= －m 2+5m ， S 四边形CHEF =12·FH ·CE =12（－m 2+5m ）×4 =－2（m －52）2+252，当m =52时，四边形CHEF 的面积取最大值252，此时H (52，354-).（3）设M （2，m ），N (n ，kn)，B (5,0)，C (0，－5)， ①当BC 为矩形对角线时，此时：2+n =5+0，m +kn=0－5，即n =3，设BC 与MN 交于点H ，则H (52，52-)，MH =12BC =2，∴222552222m ⎛⎛⎫⎛⎫-++= ⎪ ⎪ ⎝⎭⎝⎭⎝⎭，解得：m =1或m =－6，当m =1时，k =－18；m =－6时，k =3， ②当BC 为矩形边时，分两种情况讨论：（i ）当点M 在直线BC 下方时，即四边形BCMN 为矩形，则∠BCM=90°，2+5=n+0，m=kn－5，过M作MH⊥y轴于H，则由OB=OC知，∠OCB=45°，∴∠MCH=∠CMH=45°，即CH=MH，∴－5－m=2，解得：m=－7，n=7，k=－14；（ii）当点M在直线BC上方时，即四边形BCNM为矩形，则∠CBM=90°，n+5=2，kn=m－5，设对称轴与x轴交于点H，同理可得：BH=MH，∴3=m，n=－3，k=6；综上所述，k的值为：－18，3，－14或6.【变式2-1】（2019·驻马店二模）如图，抛物线y=-x2+bx+c经过A(-1，0)，B(3，0)两点，且与y轴交于点C，点D是抛物线的顶点，抛物线的对称轴DE交x轴于点E，连接BD．（1）求经过A，B，C三点的抛物线的函数表达式．（2）点P是线段BD上一点，当PE=PC时，求点P的坐标．（3）在（2）的条件下，过点P作PF⊥x轴于点F，G为抛物线上一动点，M为x轴上一动点，N 为直线 PF 上一动点，当以 F ，M ，G ，N 为顶点的四边形是正方形时，请求出点 M 的坐标．【答案】见解析.【解析】解：（1）∵抛物线 y =-x 2+bx +c 经过 A (-1，0)，B (3，0)两点，∴10930b c b c --+=⎧⎨-++=⎩，解得：23b c =⎧⎨=⎩，即抛物线的解析式为：y =-x 2+2x +3.（2）由y =-x 2+2x +3知，C (0，3)，E (1，0)，D (1,4)，可得直线BD 的解析式为：y =-2x +6，设P （m ，-2m +6），由勾股定理得：PE 2=()()22126m m -+-+，PC 2=()22263m m +-+-，由PE =PC ，得：()()22126m m -+-+=()22263m m +-+-，解得：m =2，即P (2，2).（3）∵M 在x 轴上，N 在直线PF 上， ∴∠NFM =90°，由四边形MFNG 是正方形，知MF =MG ，设M (n ，0)，则G (n ，-n 2+2n +3)， MG =|-n 2+2n +3|，MF =|n -2|， ∴|-n 2+2n +3|=|n -2|，解得：n n n n ，故点M 的坐标为：0），0），（12，0），（12-，0）.【变式2-2】（2019·大联考）如图1，抛物线y =ax 2+bx +c 经过点A (-4,0)，B (1,0)，C （0,3），点P 在抛物线上，且在x 轴的上方，点P 的横坐标记为t .（1）求抛物线的解析式；（2）如图2，过点P 作y 轴的平行线交直线AC 于点M ，交x 轴于点N ，若MC 平分∠PMO ，求t 的值.（3）点D 在直线AC 上，点E 在y 轴上，且位于点C 的上方，那么在抛物线上是否存在点P ，使得以点C 、D 、E 、P 为顶点的四边形是菱形？若存在，请直接写出菱形的面积.图1 图2【答案】见解析.【解析】解：（1）∵抛物线y =ax 2+bx +c 经过点A (-4,0)，B (1,0)，C （0,3），∴301640c a b c a b c =⎧⎪++=⎨⎪-+=⎩，解得：39434c b a ⎧⎪=⎪⎪=-⎨⎪⎪=-⎪⎩，即抛物线的解析式为：y =34-x 294-x +3. （2）由A (-4,0)，C (0,3)得直线AC 的解析式为：y =334x +， ∵点P 的横坐标为t ， ∴M (t ,334t +)， ∵PN ∥y 轴， ∴∠PMC =∠MCO ， ∵MC 平分∠PMO ， ∴∠PMC =∠OMC ， ∴∠MCO =∠OMC ，即OM =OC =3，∴OM 2=9，即223394t t ⎛⎫++= ⎪⎝⎭，解得：t =0（舍）或t =7225，∴当MC 平分∠PMO 时，t =7225. （3）设P (t , 34-t 294-t +3)， ①当CE 为菱形的边时，四边形CEPD 为菱形，则PD ∥y 轴，CD =PD ，则D (t ，334t +),∴PD =34-t 294-t +3－（334t +）=34-t 23-t ，由勾股定理得：CD =54t -，∴34-t 23-t =54t -，解得：t =0（舍）或t =73-，即PD =3512，菱形面积为：3512×73=24536； ②当CE 为菱形的对角线时，此时P 与D 点关于y 轴对称，则D (-t , 34-t 294-t +3)，将D 点坐标代入y =334x +，得： 34-t 294-t +3=()334t -+，解得：t =0（舍）或t =－2， PD =4，CE =3，菱形的面积为：12×4×3=6；综上所述，菱形的面积为：24536或6.1.（2019·南阳毕业测试）如图1，抛物线y ＝ax 2+bx +2与x 轴交于A ，B 两点，与y 轴交于点C ，AB ＝4，矩形OBDC 的边CD ＝1，延长DC 交抛物线于点E ．（1）求抛物线的解析式；（2）如果点N 是抛物线对称轴上的一点，抛物线上是否存在点M ，使得以M ，A ，C ，N 为顶点的四边形是平行四边形？若存在，直接写出所有满足条件的点M 的坐标；若不存在，请说明理由．【答案】见解析．【解析】解：（1）∵矩形OBDC 的边CD ＝1， ∴OB ＝1，由AB ＝4，得OA ＝3， ∴A （﹣3，0），B （1，0），∵抛物线y ＝ax 2+bx +2与x 轴交于A ，B 两点， ∴a +b +2=0，9a －3b +2=0，解得：a =23-，b =43-， ∴抛物线解析式为y ＝23-x 243-x +2；（2）以AC 为边或对角线分类讨论： A （﹣3，0），C （0，2），抛物线y ＝23-x 243-x +2的对称轴为x ＝﹣1，设M (m , y M )，N (－1，n )，y M =23-m 243-m +2 ①当四边形ACMN 为平行四边形时，有：312Mm y n -+=-⎧⎨=+⎩，解得：m =2，y M =103-，即M (2，103-)； ②当四边形ACNM 为平行四边形时，有：312Mmy n --=⎧⎨+=⎩，解得：m =－4，y M =103-，即M (－4，103-)； ③当四边形AMCN 为平行四边形时，有：312Mm y n -=-⎧⎨=+⎩，解得：m =－2，y M =2，即M (－2，2)；综上所述，点M 的坐标为（2，103-）或（﹣4，103-）或（﹣2，2）． 2.（2019·开封模拟）如图，直线y ＝﹣x +4与抛物线y ＝﹣12x 2+bx +c 交于A ，B 两点，点A 在y 轴上，点B 在x 轴上．（1）求抛物线的解析式；（2）在x 轴下方的抛物线上存在一点P ，使得∠ABP ＝90°，求出点P 坐标；（3）点E 是抛物线对称轴上一点，点F 是抛物线上一点，是否存在点E 和点F 使得以点E ，F ，B ，O 为顶点的四边形是平行四边形？若存在，求出点F 的坐标；若不存在，请说明理由．【答案】见解析.【解析】解：（1）在y＝﹣x+4中，当x＝0时，y＝4，当y＝0时，x＝4，即点A、B的坐标分别为（0，4）、（4，0），将（0，4）、（4，0），代入二次函数表达式，并解得：b=1，c=4，抛物线的解析式为：y＝﹣12x2+x+4；（2）∵OA＝OB＝4，∴∠ABO＝45°，∵∠ABP＝90°，则∠PBO=45°，若直线PB交y轴于点M，则OM=OB=4，可得直线BP的解析式为：y=x－4，联立：y=x－4，y＝﹣12x2+x+4，得：x=4，y=0(即B点)；x=－4，y=－8，即P(－4，－8).（3）存在；由y＝﹣12x2+x+4知抛物线的对称轴为：x=1，设E(1，m)，F(n，﹣12n2+n+4)，O(0,0)，B(4,0)，①当四边形OBEF是平行四边形时，有：EF=4，∴n-1=-4，即n=-3，F点坐标为（-3，72 -）；②当四边形OBFE是平行四边形时，有：EF=4，n-1=4，即n=5，F点坐标为（5，72 -）；③当四边形OFBE 是平行四边形时，有：410Fn m y =+⎧⎨=+⎩,即n =3，F 点坐标为（3，52）；综上所述：点F 的坐标为（5，72-），（﹣3，72-），（3，52）． 3.（2019·开封二模）如图，抛物线y ＝ax 2+bx +2与直线y ＝﹣x 交第二象限于点E ，与x 轴交于A （﹣3，0），B 两点，与y 轴交于点C ，EC ∥x 轴．（1）求抛物线的解析式；（2）如果点N 是抛物线对称轴上的一个动点，抛物线上存在一动点M ，若以M ，A ，C ，N 为顶点的四边形是平行四边形，请直接写出所有满足条件的点M 的坐标．【答案】见解析.【解析】解：（1）由题意知：A （﹣3，0），C （0，2），EC ∥x 轴 ∴点E 的纵坐标为2， ∵点E 在直线y ＝﹣x 上， ∴点E （﹣2，2），∵将A （﹣3，0）、E （﹣2，2）代入y ＝ax 2+bx +2，得：93204222a b a b -+=⎧⎨-+=⎩，解得：2343a b ⎧=-⎪⎪⎨⎪=-⎪⎩抛物线的解析式为：224233y x x =--+；（2）由224233y x x =--+知，抛物线的对称轴为x =－1，设N (－1，n )，M (m ，224233m m --+)，∵A （﹣3，0），C （0，2），（1）当四边形ACNM 是平行四边形时，有：312Mm n y --=⎧⎨=+⎩，得：m =－4，y M = 103-；即M (－4，103-). （2）当四边形ACMN 是平行四边形时，有：312Mm n y -+=-⎧⎨+=⎩，得：m =2，y M = 103-；即M (2，103-). （3）当四边形ANCM 是平行四边形时，有：312Mmn y -=-+⎧⎨=+⎩，得：m =－2，y M = 2；即M (－2，2).综上所述，M 点的坐标是(－4，103-)，(2，103-)，(－2，2). 4.（2019·名校模考）如图，抛物线y ＝ax 2+bx ﹣1（a ≠0）交x 轴于A ，B （1，0）两点，交y 轴于点C ，一次函数y ＝x +3的图象交坐标轴于A ，D 两点，E 为直线AD 上一点，作EF ⊥x 轴，交抛物线于点F（1）求抛物线的解析式；（2）在平面直角坐标系内存在点G ，使得G ，E ，D ，C 为顶点的四边形为菱形，请直接写出点G 的坐标．【答案】见解析．【解析】解：（1）将y ＝0代入y ＝x +3，得x ＝﹣3．∴A（﹣3，0）．∵抛物线y＝ax2+bx﹣1交x轴于A（﹣3，0），B（1，0）两点，∴109310a ba b+-=⎧⎨--=⎩，解得：1323ab⎧=⎪⎪⎨⎪=⎪⎩抛物线的解析式为y＝13x2+23x﹣1；（2）点G的坐标为（2，1），（﹣，﹣1），（﹣1），（﹣4，3）．①当四边形DCEG是菱形时，CD=CE=EG=4，设E(m，m+3)，则G（m，m+7），由C(0，－1)，E(m，m+3)，得：CE2=m2+(m+4)2=16，解得：m=0（舍）或m=－4，此时G(－4,3)；②当四边形DCGE是菱形时，CG2=16,设E(m，m+3)，则G（m，m－1），即m2+ m2=16，解得：m=m=－此时，G(1)或G(－－1)；③当四边形DGCE是菱形时，设E(m，m+3)，则G（－m，－m－1），此时E在CD的垂直平分线上，即m+3=1，m=－2，此时G(2，1);综上所述，点G的坐标为：(－4,3)、(1)、(－－1)、(2，1).5.（2019·枫杨外国语三模）（2019·枫杨外国语三模）如图，抛物线y＝﹣x2+bx+c与x轴交于A、B两点，与y轴交于点C，点A的坐标为(-1，0)，点C的坐标为(0，3)，点D和点C关于抛物线的对称轴对称，直线AD与y轴交于点E．（1）求抛物线的解析式；（2）点M是抛物线的顶点，点P是y轴上一点，点Q是坐标平面内一点，以A，M，P，Q为顶点的四边形是以AM为边的矩形．若点T和点Q关于AM所在直线对称，求点T的坐标．【答案】见解析.【解析】解：（1）将(-1，0)，(0，3)代入y＝﹣x2+bx+c，得：－1－b+c=0，c=3，解得：b=2，c=3，即抛物线的解析式为：y＝﹣x2+2x+3.（2）由y＝﹣x2+2x+3知，点M(1，4)，分两种情况讨论，①当四边形MAPQ是矩形时，过M作MH⊥x轴于H，则MH=4，AH=2，易证得：∠APO=∠MAH，∴tan∠APO= tan∠MAH，即OA MHOP AH=2，∴OP=12，即P（0，－12），由A(-1，0)、M(1，4)，P（0，－12）得：点Q坐标为（2，72），∵点T和点Q关于AM所在直线对称，即点Q与点T关于点M(1，4)对称，∴T(0，92 )；②当四边形AMPQ是矩形时，同理可得：T(0，12 -)；综上所述，点T的坐标为(0，92)，(0，12-).6.（2019·焦作二模）如图，在平面直角坐标系中，一次函数y=x+b的图象经过点A(-2，0)，与反比例函数kyx=（x>0）的图象交于点B(a，4).（1）求一次函数和反比例函数的表达式；（2）设M是直线AB上一点，过M作MN∥x轴，交反比例函数kyx=（x>0）的图象于点N，若以A，O，M，N为顶点的四边形是平行四边形，求点M的横坐标.【答案】见解析.【解析】解：（1）将A(-2,0)代入y=x+b，得：b=2，即一次函数的解析式为：y=x+2，将B(a，4)代入y=x+2，得：a=2，即B(2，4),将B(2，4)代入kyx=得：x=8，即反比例函数的解析式为：8 yx =.（2）设M(m，m+2)，则N(82m+，m+2)，由题意知，MN∥OA，则需MN=OA=2时，以A，O，M，N为顶点的四边形是平行四边形，∴82mm-+=2，解得：m=2或m=－2（舍）或m=m=－（舍），∴点M的坐标为：（2，+2）.7.（2019·许昌月考）如图1，二次函数y=43x2+bx+c的图象与x轴交于A（3，0），B（﹣1，0）两点，与y轴交于点C．（1）求该二次函数的解析式；（2）设该抛物线的顶点为D，求△ACD的面积（请在图1中探索）；（3）若点P，Q同时从A点出发，都以每秒1个单位长度的速度分别沿AB，AC边运动，其中一点到达端点时，另一点也随之停止运动，当P，Q运动到t秒时，△APQ沿PQ所在的直线翻折，点A恰好落在抛物线上E点处，请直接判定此时四边形APEQ的形状，并求出E点坐标（请在图2中探索）．图1 图2【答案】见解析．【解析】解：（1）∵二次函数y=43x2+bx+c的图象与x轴交于A（3，0），B（﹣1，0），∴493034103b cb c⎧⨯++=⎪⎪⎨⎪⨯-+=⎪⎩，解得：834bc⎧=-⎪⎨⎪=-⎩，即抛物线的解析式为：y=43x2﹣83x﹣4；（2）过点D作DM⊥y轴于点M，y =43x 2﹣83x ﹣4 =43（x ﹣1）2﹣163， ∴点D （1，﹣163）、点C （0，﹣4）， S △ACD =S 梯形AOMD ﹣S △CDM ﹣S △AOC=12×（1+3）×163﹣12×（163﹣4）×1﹣12×3×4 =4；（3）四边形APEQ 为菱形，理由如下：E 点关于PQ 与A 点对称，过点Q 作QF ⊥AP 于F ，由折叠性质知： AP =EP ，AQ =EQ ∵AP =AQ =t ， ∴AP =AQ =QE =EP ， ∴四边形AQEP 为菱形， ∵FQ ∥OC ，∴AF FQ AQOA OC AC ==， ∴345AF FQ t ==∴AF =35t ，FQ =45t ，Q （3﹣35t ，﹣45t ），E （3﹣35t ﹣t ，﹣45t ），∵E 在二次函数y =43x 2﹣83x ﹣4上，∴﹣45t =43（3﹣85t ）2﹣83（3﹣85t ）﹣4，∴t =14564或t =0（舍去）， ∴E （﹣58，﹣2916）．8.（2018·新乡一模）如图，一次函数122y x =-+分别交y 、x 轴于A 、B 两点，抛物线2y x bx c=-++过A ，B 两点.（1）求这个抛物线的解析式；（2）作垂直于x 轴的直线x ＝t ，在第一象限交直线AB 于M ，交这个抛物线于N . 求当t 取何值时，MN 有最大值？最大值是多少？（3）在(2)的情况下，以A ，M 、N 、D 为顶点作平行四边形，直接写出第四个顶点D 的坐标.【答案】见解析【解析】解：（1）在122y x =-+得，当x =0时，y =2；y =0时，x =4，即A （0，2），B （4，0），把A (0，2)，B (4，0)代入2y x bx c =-++，得： 21640c b c =⎧⎨++=⎩-，解得722b c ⎧=⎪⎨⎪=⎩， ∴抛物线解析式为2722y x x =-++. （2）由题意知，1(,2)2M t t -+，27(,2)2N t t t -++，∴MN =2712(2)22t t t -++--+=2(2)4t --+， ∴当t =2时，MN 有最大值4.（3）根据平行四边形的性质，得：D 点坐标为：（0，6），（0，-2）或（4，4）.9.（2019·周口二模）如图，在平面直角坐标系中，抛物线y =ax 2+bx +4与x 轴交于A (-1，0)，B (4，0)两点，与y 轴交于点C ．（1）求这个抛物线的解析式；（2）设E 是该抛物线上位于对称轴右侧的一个动点，过点E 作x 轴的平行线交抛物线于另一点F ，过点E 作EH ⊥x 轴于点H ，再过点F 作FG ⊥x 轴于点G ，得到矩形EFGH ．在点E 的运动过程中，当矩形EFGH 为正方形时，直接写出该正方形的边长．【答案】见解析.【解析】解：（1）∵抛物线y =ax 2+bx +4与x 轴交于A (-1，0)，B (4，0)两点，∴4016440a b a b -+=⎧⎨++=⎩，解得：13a b =-⎧⎨=⎩，即抛物线的解析式为：y =－x 2+3x +4. （2）∵四边形EFGH 是矩形，∴当EF =EH 时，四边形EFGH 是正方形，设E(m, －m2+3m+4)，则F(3－m，－m2+3m+4)，m>32，∴EF=2m－3，EH=|－m2+3m+4|，∴2m－3=|－m2+3m+4|，解得：m或m（舍）或m或m（舍）∴正方形的边长EF2，综上所述，正方形EFGH的边长为：2.10.（2019·郑州一中模拟）如图所示，平面直角坐标系中直线y=x+1交坐标轴于点A、D两点，抛物线y=ax2+bx－3经过A、C两点，点C坐标为（a，5）. 点M为直线AC上一点，过点M作x轴的垂线，垂足为F，交抛物线于点N.（1）求抛物线解析式；（2）是否存在点M，使得以点D、E、M、N为顶点的四边形为平行四边形，如果有，求点M的坐标，如果没有，请说明理由.【解析】解：∵直线y =x +1交坐标轴于点A 、D 两点， ∴A (－1,0)，D (0，1)，∵点C （a ，5）在直线y =x +1上， ∴a =4，即C (4,5)，将A (－1,0)，C (4,5)代入y =ax 2+bx －3得：3016435a b a b --=⎧⎨+-=⎩，解得：12a b =⎧⎨=-⎩， ∴抛物线的解析式为：y =x 2－2x －3. （2）存在，E （0，－3），∴DE =4，由题意知：DE ∥MN ，∴当DE =MN =4时，四边形DENM 是平行四边形，设N (m , m 2－2m －3)，则M (m , m +1)， ∴| m +1-（m 2－2m －3）|=4，解得：m =0（舍）或m =3或m =或m = ，综上所述，点M 的坐标为：（3,4），，）.11.（2019·郑州模拟）如图，已知二次函数23234y ax a x ⎛⎫=--+ ⎪⎝⎭的图象经过点A (4,0),与y 轴交于点B ，在x 轴上有一动点C (m ,0) （0<m <4），过点C 作x 轴的垂线交直线AB 于点E ，交该二次函数图象于点D .（1）求a 的值和直线AB 的解析式；（2）过点D 作DF ⊥AB 于点F ，设△ACE ，△DEF 的面积分别为S 1，S 2，若S 1=4S 2，求m 的值；（3）点H 是该二次函数图象上第一象限内的动点，点G 是线段AB 上的动点，当四边形DEGH 是平行四边形，且平行四边形DEGH 的周长取最大值时，求点G 的坐标.【答案】见解析.【解析】解：（1）将A (4,0)代入23234y ax a x ⎛⎫=--+ ⎪⎝⎭得：a =34-，∴抛物线的解析式为：239344y x x =-++，设直线AB 的解析式为：y =kx +b ， ∴4k +b =0，b =3，即k =34-，b =3， ∴直线AB 的解析式为：y =34-x +3. （2）∵点C 的横坐标为m ，∴D (m , 239344m m -++)，E (m , 34-m +3)，AC =4－m ，DE =239344m m -++－(34-m +3)= 2334m m -+，∵BC ∥y 轴， ∴43AC OA CE OB ==，即443m CE -=， ∴CE =()344m -，AE =()544m -， ∵∠DF A =∠DCA =90°，∠DBF =∠AEC ， ∴△DFE ∽△ACE ， ∵S 1=4S 2， ∴AE =2DE ，即()544m -=2（2334m m -+），解得：m =4（舍）或m =56，即m 的值为56.（3）如图，过点G 作GM ⊥DC 于M ，设G 、H 点横坐标为n ，由DE =2334m m -+，得GH =2334n n -+，2334m m -+=2334n n -+，得：m =n （舍）或n =4－m ，∴MG =4-2m ，由45MG EG =得：EG =()5424m -, ∴C 四边形DEGH =2()25342344m m m ⎡⎤--+⎢⎥⎣⎦=23102m m -++=23161236m ⎛⎫--+ ⎪⎝⎭，∴当m =13时，C 最大，此时n =113，即G (113，14)，E (13，114), 由图象可知当E 、G 互换位置时满足题意，即G (13，114),E (113，14)，综上所述，G 点坐标为：(13，114)，(113，14).13.（2018·郑州模拟）如图，抛物线y ＝﹣x 2+bx +c 与x 轴交于点A 和点B （3，0），与y 轴交于点C （0，3），点D 是抛物线的顶点，过点D 作x 轴的垂线，垂足为E ，连接DB ．（1）求此抛物线的解析式及顶点D 的坐标；（2）点M 是抛物线上的动点，设点M 的横坐标为m ． ①当∠MBA ＝∠BDE 时，求点M 的坐标；②过点M 作MN ∥x 轴，与抛物线交于点N ，P 为x 轴上一点，连接PM ，PN ，将△PMN 沿着MN 翻折，得△QMN ，若四边形MPNQ 恰好为正方形，直接写出m 的值．【答案】见解析.【解析】解：（1）将点B（3，0），C（0，3）代入y＝﹣x2+bx+c，并解得：b=2，c=3，∴抛物线的解析式为y＝﹣x2+2x+3．顶点D（1，4）．（2）①过点M作MG⊥x轴于G，连接BM．则∠MGB＝90°，设M（m，﹣m2+2m+3），∴MG＝|﹣m2+2m+3|，BG＝3﹣m，∵DE⊥x轴，D（1，4），B（3，0），∴∠DEB＝90°，DE＝4，OE＝1，BE＝2，∵∠MBA＝∠BDE，∴tan∠MBA＝tan∠BDE＝12，∴2233m mm-++-＝12解得：m=12-或m=32-或m=3（舍）∴满足条件的点M坐标（12-，74）或（32-，94-）；②∵MN∥x轴，∴点M、N关于抛物线的对称轴对称，∵四边形MPNQ是正方形，∴OP＝1，由∠QPM=∠MPO=45°，得：GM＝GP，即|﹣m2+2m+3|＝|1﹣m|，解得：m或m或m或m即满足条件的m.14.（2017·信阳二模）如图，抛物线y=ax2+bx﹣4与x轴交于A（﹣2，0）、B（8，0）两点，与y轴交于点C，连接BC，以BC为一边，点O为对称中心做菱形BDEC，点P是x轴上的一个动点，设点P的坐标为（m，0），过点P作x轴的垂线l交抛物线于点Q．（1）求抛物线的解析式；（2）当点P在线段OB上运动时，直线l分别交BD、BC于点M、N，试探究m为何值时，四边形CQMD 是平行四边形，此时，请判断四边形CQBM的形状，并说明理由．【答案】见解析.【解析】解：（1）将A（﹣2，0）、B（8，0）代入y=ax2+bx﹣4并解得：a=14，b=32-，即抛物线的解析式为：y=14x232-x－4.（2）由y=14x232-x－4知，C(0，－4),由菱形的性质可知：D（0，4），设直线BD的解析式为：y=kx+n，将点B（8,0）、D（0，4）代入得：k=12-,n=4，即直线BD的解析式为：y=12-x+4,由M（m，12-m+4），Q（m，14m232-m－4）．当MQ=DC时，四边形CQMD为平行四边形．∴12-m+4﹣（14m232-m－4）=8，解得m=4或m=0（舍去）．∴MD∥CQ，MD=CQ，M（4，2），∴M为BD的中点，∴MD=MB．∴CQ=MB，又∵MB∥CQ，∴四边形CQBM为平行四边形．。

专题：二次函数中的动点问题(平行四边形存在性问题)

二次函数中的动点问题（二）平行四边形的存在性问题一.技巧提炼如图1,点人（召,开）、3（忑,儿）、C（X3Os）是坐标平面内不在同一直线上的三点。

平面直角坐标系中是否存在点D,使得以A、B、C、D四点为顶点的四边形为平行四边形，如果存在，请求出点D的坐标。

如图2,过A、B、C分别作BC、AC、AB的平行线，则以不在同一直线上的三点为顶点的平行四边形有三个。

由已知的三点坐标可根据图形平移的坐标性质，直接写出第四个顶点的坐标。

3、平面直角坐标系中直线和直线12:当h时k尸k2；当h丄I2时ki-k2=-14、二次函数中平行四边形的存在性问题：解题思路：（1）先分类（2）再画图（3）后计算二、精讲精练1、已知抛物线y=ax-+bx+c与x轴相交于A、E两点（A、B分别在原点的左右两侧），与y轴正半轴相交于C点，且OA：OB：OC=1：3：3,AABC的面积为6,（如图1）（1）求抛物线的解析式：（2）坐标平面内是否存在点M,使得以点M、A、B、C为顶点四边形是平行四边形？若存在，请求出点M的坐标；若不存在，请说明理由；（3）如图2,在直线BC±方的抛物线上是否存在一动点P,ABCP面枳最大？如果存在，求出最人面积,2、如图，己知抛物线经过A(-2,0),B(・3,3)及原点6顶点为C(1)求抛物线的函数解析式：(2)设点D在抛物线上，点E在抛物线的对称轴上，且以AO为边的四边形AODE是平行四边形，求点D的坐标。

【变式练习】7如图，对称轴为直线x二一的抛物线经过点A(6,0)和B(0,4)・2(1)求抛物线解析式及顶点坐标；(2)设点E(x,y)是抛物线上一动点，且位于第四彖限，四边形0EAF是以0A为对角线的平行四边形, 求平行四边形OEAF的面积S与x之间的函数关系式，并写出自变量x的取值范围；①当平行四边形OEAF的面积为24时，请判断平行四边形0EAF是否为菱形？②是否存在点E,使平行四边形0EAF为正方形？若存在，求出点E的坐标；若不存在，请说明理由.、方法规律1、平行四边形模型探究如图1，点&（內,开）、3（七,儿）、C（X3，”）是坐标平面内不在同一直线上的三点。

二次函数与四边形的动点问题(含问题详解)

72x =B(0,4) A(6,0)E FxyO二次函数与四边形一．二次函数与四边形的形状例1.(浙江义乌市) 如图，抛物线223y x x =--与x 轴交A 、B 两点（A 点在B 点左侧），直线l 与抛物线交于A 、C 两点，其中C 点的横坐标为2．（1）求A 、B 两点的坐标及直线AC 的函数表达式；（2）P 是线段AC 上的一个动点，过P 点作y 轴的平行线交抛物线于E 点，求线段PE 长度的最大值；（3）点G 是抛物线上的动点，在x 轴上是否存在点F ，使A 、C 、F 、G 这样的四个点为顶点的四边形是平行四边形？如果存在，求出所有满足条件的F 点坐标；如果不存在，请说明理由．练习1.(河南省实验区) 23．如图，对称轴为直线72x =的抛物线经过点 A （6，0）和 B （0，4）．（1）求抛物线解析式及顶点坐标；（2）设点E （x ，y ）是抛物线上一动点，且位于第四象限，四边形OEAF是以OA 为对角线的平行四边形．求平行四边形OEAF 的面积S 与x 之间的函数关系式，并写出自变量x 的取值范围；①当平行四边形OEAF 的面积为24时，请判断平行四边形OEAF 是否为菱形？②是否存在点E ，使平行四边形OEAF 为正方形？若存在，求出点E的坐标；若不存在，请说明理由．A练习 2.（四川省德阳市）25.如图，已知与x 轴交于点(10)A ，和(50)B ，的抛物线1l 的顶点为(34)C ，，抛物线2l 与1l 关于x 轴对称，顶点为C '．（1）求抛物线2l 的函数关系式；（2）已知原点O ，定点(04)D ，，2l 上的点P 与1l 上的点P '始终关于x 轴对称，则当点P 运动到何处时，以点D O P P '，，，为顶点的四边形是平行四边形？（3）在2l 上是否存在点M ，使ABM △是以AB 为斜边且一个角为30o的直角三角形？若存，求出点M 的坐标；若不存在，说明理由．练习3.（山西卷）如图，已知抛物线1C 与坐标轴的交点依次是(40)A -，，(20)B -，，(08)E ，．（1）求抛物线1C 关于原点对称的抛物线2C 的解析式；（2）设抛物线1C 的顶点为M ，抛物线2C 与x 轴分别交于C D ，两点（点C 在点D 的左侧），顶点为N ，四边形MDNA 的面积为S ．若点A ，点D 同时以每秒1个单位的速度沿水平方向分别向右、向左运动；与此同时，点M ，点N 同时以每秒2个单位的速度沿坚直方向分别向下、向上运动，直到点A 与点D 重合为止．求出四边形MDNA 的面积S 与运动时间t 之间的关系式，并写出自变量t 的取值范围；（3）当t 为何值时，四边形MDNA 的面积S 有最大值，并求出此最大值；（4）在运动过程中，四边形MDNA 能否形成矩形？若能，求出此时t 的值；若不能，请说明理由．5-4- 3-2-1- 1 2 3 455 4 3 2 1 A EBC '1- O 2l 1lx y二．二次函数与四边形的面积例1.（资阳市）25.如图10，已知抛物线P：y=ax2+bx+c(a≠0) 与x轴交于A、B两点(点A在x 轴的正半轴上)，与y轴交于点C，矩形DEFG的一条边DE在线段AB上，顶点F、G分别在线段BC、AC上，抛物线Px …-3 -2 1 2 …y …-52-4 -520 …(1) 求A、B、C三点的坐标；(2) 若点D的坐标为(m，0)，矩形DEFG的面积为S，求S与m的函数关系，并指出m的取值范围；(3) 当矩形DEFG的面积S取最大值时，连接DF并延长至点M，使FM=k·DF，若点M不在抛物线P上，求k的取值范围.练习1.（辽宁省十二市2007年第26题）．如图，平面直角坐标系中有一直角梯形OMNH，点H的坐标为（－8，0），点N的坐标为（－6，－4）．（1）画出直角梯形OMNH绕点O旋转180°的图形OABC，并写出顶点A，B，C的坐标（点M的对应点为A，点N的对应点为B，点H的对应点为C）；（2）求出过A，B，C三点的抛物线的表达式；（3）截取CE=OF=AG=m，且E，F，G分别在线段CO，OA，AB上，求四边形BEFG的面积S与m之间的函数关系式，并写出自变量m的取值范围；面积S是否存在最小值?若存在，请求出这个最小值；若不存在，请说明理由；（4）在（3）的情况下，四边形BEFG是否存在邻边相等的情况，若存在，请直接写出此时m的值，并指出相等的邻边；若不存在，说明理由．图10练习3.（吉林课改卷）如图，正方形ABCD 的边长为2cm ，在对称中心O 处有一钉子．动点P ，Q 同时从点A 出发，点P 沿A B C →→方向以每秒2cm 的速度运动，到点C 停止，点Q 沿A D →方向以每秒1cm 的速度运动，到点D 停止．P ，Q 两点用一条可伸缩的细橡皮筋联结，设x 秒后橡皮筋扫过的面积为2cm y ．（1）当01x ≤≤时，求y 与x 之间的函数关系式；（2）当橡皮筋刚好触及钉子时，求x 值；（3）当12x ≤≤时，求y 与x 之间的函数关系式，并写出橡皮筋从触及钉子到运动停止时POQ ∠的变化范围；（4）当02x ≤≤时，请在给出的直角坐标系中画出y 与x 之间的函数图象．练习4.（四川资阳卷）如图，已知抛物线l 1：y =x 2-4的图象与x 轴相交于A 、C 两点，B 是抛物线l 1上的动点(B 不与A 、C 重合)，抛物线l 2与l 1关于x 轴对称，以AC 为对角线的平行四边形ABCD 的第四个顶点为D .(1) 求l 2的解析式；(2) 求证：点D 一定在l 2上；(3) □ABCD 能否为矩形？如果能为矩形，求这些矩形公共部分的面积(若只有一个矩形符合条件，则求此矩形的面积)；如果不能为矩形，请说明理由. 注：计算结果不取近似值.B CPO D QA BPCO DQ Ay321 O1 2 x三．二次函数与四边形的动态探究例1.(荆门市)28. 如图1，在平面直角坐标系中，有一张矩形纸片OABC ，已知O (0，0)，A (4，0)，C (0，3)，点P 是OA 边上的动点(与点O 、A 不重合)．现将△PAB 沿PB 翻折，得到△PDB ；再在OC 边上选取适当的点E ，将△POE 沿PE 翻折，得到△PFE ，并使直线PD 、PF 重合．(1)设P (x ，0)，E (0，y )，求y 关于x 的函数关系式，并求y 的最大值；(2)如图2，若翻折后点D 落在BC 边上，求过点P 、B 、E 的抛物线的函数关系式；(3)在(2)的情况下，在该抛物线上是否存在点Q ，使△PEQ 是以PE 为直角边的直角三角形？若不存在，说明理由；若存在，求出点Q 的坐标．例2.（2010年沈阳市第26题）、已知抛物线y ＝ax2＋bx ＋c 与x 轴交于A 、B 两点，与y 轴交于点C ，其中点B 在x 轴的正半轴上，点C 在y 轴的正半轴上，线段OB 、OC 的长（OB <OC ）是方程x 2－10x ＋16＝0的两个根，且抛物线的对称轴是直线x ＝－2．（1）求A 、B 、C 三点的坐标；（2）求此抛物线的表达式；（3）连接AC 、BC ，若点E 是线段AB 上的一个动点（与点A 、点B 不重合），过点E 作EF ∥AC 交BC 于点F ，连接CE ，设AE 的长为m ，△CEF 的面积为S ，求S 与m 之间的函数关系式，并写出自变量m 的取值范围；（4）在（3）的基础上试说明S 是否存在最大值，若存在，请求出S的最大值，并求出此时点E 的坐标，判断此时△BCE 的形状；若不存在，请说明理由．图2OC A Bxy DPE F 图1FE P D y xBA C O例3..(湖南省郴州) 27．如图，矩形ABCD 中，AB ＝3，BC ＝4，将矩形ABCD 沿对角线A 平移，平移后的矩形为EFGH （A 、E 、C 、G 始终在同一条直线上），当点E 与C 重时停止移动．平移中EF 与BC 交于点N ，GH 与BC 的延长线交于点M ，EH 与DC 交于点P ，FG 与DC 的延长线交于点Q ．设S 表示矩形PCMH 的面积，S '表示矩形NFQC 的面积．（1） S 与S '相等吗？请说明理由．（2）设AE ＝x ，写出S 和x 之间的函数关系式，并求出x 取何值时S 有最大值，最大值是多少？（3）如图11，连结BE ，当AE 为何值时，ABE ∆是等腰三角形．练习1.（07年河池市）如图12，四边形OABC 为直角梯形，A （4，0），B （3，4），C （0，4）．点M 从O 出发以每秒2个单位长度的速度向A 运动；点N 从B 同时出发，以每秒1个单位长度的速度向C 运动．其中一个动点到达终点时，另一个动点也随之停止运动．过点N 作NP 垂直x 轴于点P ，连结AC 交NP 于Q ，连结MQ ．（1）点（填M 或N ）能到达终点；（2）求△AQM 的面积S 与运动时间t 的函数关系式，并写出自变量t 的取值范围，当t 为何值时，S 的值最大；（3）是否存在点M ，使得△AQM 为直角三角形？若存在，求出点M 的坐标，若不存在，说明理由．x NM QP H G FE D C B A 图11 Q P N M H GF E D C B A 图10练习2..(江西省) 25．实验与探究（1）在图1，2，3中，给出平行四边形ABCD 的顶点A B D ，，的坐标（如图所示），写出图1，2，3中的顶点C 的坐标，它们分别是(52)，，，；（2）在图4中，给出平行四边形ABCD 的顶点A B D ，，的坐标（如图所示），求出顶点C 的坐标（C 点坐标用含a b c d e f ，，，，，的代数式表示）；归纳与发现（3）通过对图1，2，3，4的观察和顶点C 的坐标的探究，你会发现：无论平行四边形ABCD 处于直角坐标系中哪个位置，当其顶点坐标为()()()()A a b B c d C m n D e f ，，，，，，，（如图4）时，则四个顶点的横坐标a c m e ，，，之间的等量关系为；纵坐标b d n f ，，，之间的等量关系为（不必证明）；运用与推广（4）在同一直角坐标系中有抛物线2(53)y x c x c =---和三个点15192222G c c S c c ⎛⎫⎛⎫-⎪ ⎪⎝⎭⎝⎭，，，，(20)H c ，（其中0c >）．问当c 为何值时，该抛物线上存在点P ，使得以G S H P ，，，为顶点的四边形是平行四边形？并求出所有符合条件的P 点坐标．x图1x图2x图3)x图4答案：一．二次函数与四边形的形状例1.解：（1）令y=0，解得11x =-或23x =∴A （-1，0）B （3，0）；将C 点的横坐标x=2代入223y x x =--得y=-3，∴C （2，-3）∴直线AC 的函数解析式是y=-x-1 （2）设P 点的横坐标为x （-1≤x ≤2）则P 、E 的坐标分别为：P （x ，-x-1）， E （2(,23)x x x --∵P 点在E 点的上方，PE=22(1)(23)2x x x x x -----=-++ ∴当12x =时，PE 的最大值=94（3）存在4个这样的点F，分别是1234(1,0),(3,0),(4(4F F F F - 练习 1.解：（1）由抛物线的对称轴是72x =，可设解析式27(2y a x k =-+．把A 、B 两点坐标代入上式，得227(6)0,27(0) 4.2a k a k ⎧-+=⎪⎪⎨⎪-+=⎪⎩ 解之，得225,.36a k ==- 故抛物线解析式为22725(326y x =--，顶点为725(,).26- （2）∵点(,)E x y 在抛物线上，位于第四象限，且坐标适合22725(326y x =--，∴y<0，即－y>0,－y 表示点E 到OA 的距离．∵OA 是OEAF Y 的对角线， ∴2172264()2522OAE S S OA y y ==⨯⨯⋅=-=--+V ．因为抛物线与x 轴的两个交点是（1，0）的（6，0），所以，自变量x 的取值范围是1＜x ＜6．5-4-3-2-1-12 3D554 32 1 ACEM BC '1-O 2l 1l xy①根据题意，当S = 24时，即274()25242x --+=．化简，得271().24x -=解之，得123, 4.x x == 故所求的点E 有两个，分别为E 1（3，－4），E 2（4，－4）．点E 1（3，－4）满足OE = AE ，所以OEAF Y 是菱形；点E 2（4，－4）不满足OE = AE ，所以OEAF Y 不是菱形． ② 当OA ⊥EF ，且OA = EF 时，OEAF Y 是正方形，此时点E 的坐标只能是（3，－3）．而坐标为（3，－3）的点不在抛物线上，故不存在这样的点E ，使OEAF Y 为正方形．练习2.解：（1）由题意知点C '的坐标为(34)-，．设2l 的函数关系式为2(3)4y a x =--．又Q 点(10)A ，在抛物线2(3)4y a x =--上，2(13)40a ∴--=，解得1a =．∴抛物线2l 的函数关系式为2(3)4y x =--（或265y x x =-+）．（2）P Q 与P '始终关于x 轴对称， PP '∴与y 轴平行．设点P 的横坐标为m ，则其纵坐标为265m m -+，4OD =Q ，22654m m ∴-+=，即2652m m -+=±．当2652m m -+=时，解得36m =±．当2652m m -+=-时，解得32m =±．∴当点P 运动到(362)-，或(362)+，或(322)--，或(322)+-，时， P P OD ' ∥，以点D O P P '，，，为顶点的四边形是平行四边形．（3）满足条件的点M 不存在．理由如下：若存在满足条件的点M 在2l 上，则90AMB ∠=o ，30BAM ∠=o Q （或30ABM ∠=o ），114222BM AB ∴==⨯=．过点M 作ME AB ⊥于点E ，可得30BME BAM ∠=∠=o．112122EB BM ∴==⨯=，3EM =，4OE =．∴点M 的坐标为(43)-，．但是，当4x =时，246451624533y =-⨯+=-+=-≠-．∴不存在这样的点M 构成满足条件的直角三角形．练习3. [解] （1）点(40)A -，，点(20)B -，，点(08)E ，关于原点的5-4-3-2- 1-1 2 3 4554 3 2 1 AEBC '1- O 2l1lxy对称点分别为(40)D ，，(20)C ，，(08)F -，．设抛物线2C 的解析式是2(0)y ax bx c a =++≠，则16404208a b c a b c c ++=⎧⎪++=⎨⎪=-⎩，，．解得168a b c =-⎧⎪=⎨⎪=-⎩，，．所以所求抛物线的解析式是268y x x =-+-．（2）由（1）可计算得点(31)(31)M N --，，，．过点N 作NH AD ⊥，垂足为H ．当运动到时刻t 时，282AD OD t ==-，12NH t =+．根据中心对称的性质OA OD OM ON ==，，所以四边形MDNA 是平行四边形．所以2ADN S S =△．所以，四边形MDNA 的面积2(82)(12)4148S t t t t =-+=-++．因为运动至点A 与点D 重合为止，据题意可知04t <≤．所以，所求关系式是24148S t t =-++，t 的取值范围是04t <≤．（3）781444S t ⎛⎫=--+ ⎪⎝⎭，（04t <≤）．所以74t =时，S 有最大值814．提示：也可用顶点坐标公式来求．（4）在运动过程中四边形MDNA 能形成矩形．由（2）知四边形MDNA 是平行四边形，对角线是AD MN ，，所以当AD MN =时四边形MDNA 是矩形．所以OD ON =．所以2222OD ON OH NH ==+．所以22420t t +-=．解之得1222t t ==，（舍）．所以在运动过程中四边形MDNA可以形成矩形，此时2t =．[点评]本题以二次函数为背景，结合动态问题、存在性问题、最值问题，是一道较传统的压轴题，能力要求较高。

中考数学压轴题二次函数动点问题专题练习

中考数学压轴题二次函数动点问题专题练习二次函数的动点问题已知抛物线经过原点O和x轴上另一点A，它的对称轴x=2与x轴交于点C，直线y=-2x-1经过抛物线上一点B(-2,m)，且与y轴、直线x=2分别交于点D、E。

1) 求m的值及该抛物线对应的函数关系式。

通过点B(-2,m)在直线y=-2x-1上，可以求得m的值以及点B的坐标，进而求得抛物线的解析式。

解析式为y=x^2-x。

2) 求证：①CB=CE；②D是BE的中点。

通过分别求得CB和CE的长度来说明CB=CE。

过点B作BG∥x轴，与y轴交于F、直线x=2交于G，过点E作EH∥x轴，交y轴于H。

由△DFB≌△DHE，证得D是BE的中点。

3) 若P(x,y)是该抛物线上的一个动点，是否存在这样的点P，使得PB=PE？若存在，请求出所有符合条件的点P的坐标；若不存在，请说明理由。

若存在点P使得PB=PE，则点P必在线段BE的中垂线CD上。

动点P又在抛物线上。

通过解直线CD和抛物线对应的函数关系式所联立的方程组，其解即为所求点的坐标。

符合条件的点P应是直线CD与该抛物线的交点。

1.将点D(0,-1)和C(2,0)代入直线方程组，解得直线CD对应的函数关系式为y=x-1.另外，符合条件的点P的坐标为(3+5/22,1/2)或(3-5/22,-1/2)。

2.(1) 直线BC的解析式为y=-2x+5.2) 由三角形面积公式可得△ABC的面积为6.3) 设点M到点B的距离为x，则点N到点C的距离为2x。

由三角形面积公式可得△MNB的面积为(1/2)x(5-x)。

对该函数求导可得其最大值为5/8，此时x=5/4.因此，当点M运动1.25秒时，△MNB的面积最大，最大面积为1.5625.3.(1) 由平行四边形的性质可得FE∥AB，因此∠XXX∠CEG，且XXX。

因此，ΔBEF∽ΔCEG。

2) 当点E在线段BC上运动时，△BEF和△XXX的周长之间的比值为BE/CE，即x/(x+5)。

二次函数与平行四边形有关问题专项训练

二次函数与平行四边形有关问题专项训练1．（2022•攀枝花）如图，二次函数y＝ax2+bx+c的图象与x轴交于原点O，A两点，且二次函数最小值为﹣1，点M（1，m）是其对称轴上一点，y轴上一点B（0，1）．（1）求二次函数的表达式；（）在二次函数图象上是否存在点N，使得以A、B、M、N为顶点的四边形是平行四边形？若存在，直接写出所有符合条件的点N的坐标，若不存在，请说明理由．【解答】解：（1）∵二次函数的最小值为﹣1，点M（1，m）是其对称轴上一点，∴二次函数顶点为（1，﹣1），设二次函数解析式为y＝a（x﹣1）2﹣1，将点O（0，0）代入得，a﹣1＝0，∴a＝1，∴y＝（x﹣1）2﹣1＝x2﹣2x；（2）连接OP，当y＝0时，x2﹣2x＝0，∴x＝0或2，∴A（2，0），∵点P在抛物线y＝x2﹣2x上，∴点P的纵坐标为t2﹣2t，∴S＝S△AOB+S△OAP﹣S△OBP＝+（﹣t2+2t）﹣t＝﹣t2++1；（3）设N（n，n2﹣2n），当AB为对角线时，由中点坐标公式得，2+0＝1+n，∴n＝1，∴N（1，﹣1），当AM为对角线时，由中点坐标公式得，2+1＝n+0，∴n＝3，∴N（3，3），当AN为对角线时，由中点坐标公式得，2+n＝0+1，∴n＝﹣1，∴N（﹣1，3），综上：N（1，﹣1）或（3，3）或（﹣1，3）．2．（2022•内蒙古）如图，抛物线y＝ax2+x+c经过B（3，0），D（﹣2，﹣）两点，与x 轴的另一个交点为A，与y轴相交于点C．（1）求抛物线的解析式和点C的坐标；（2）设点Q在y轴上，点P在抛物线上，要使以点A，B，P，Q为顶点的四边形是平行四边形，求所有满足条件的点P的坐标．（请在图2中探索）【解答】解：（1）将B（3，0），D（﹣2，﹣）代入y＝ax2+x+c，∴，解得，∴y＝﹣x2+x+，令x＝0，则y＝，∴C（0，）；（3）令y＝0，则﹣x2+x+＝0，解得x＝3或x＝﹣1，∴A（﹣1，0），设Q（0，t），P（m，﹣m2+m+），①当AB为平行四边形的对角线时，m＝3﹣1＝2，∴P（2，）；②当AQ为平行四边形的对角线时，3+m＝﹣1，解得m＝﹣4，∴P（﹣4，﹣）；③当AP为平行四边形的对角线时，m﹣1＝3，解得m＝4，∴P（4，﹣）；综上所述：P点坐标为（2，）或（﹣4，﹣）或（4，﹣）．3．（2022•牡丹区三模）如图，直线y＝﹣x+4与x轴交于点C，与y轴交于点B，抛物线y ＝ax2+x+c经过B，C两点．（1）求抛物线的解析式；（2）Q是抛物线对称轴上的动点，在抛物线上是否存在点P，使得以P，Q，B，C为顶点的四边形是平行四边形？若存在，请求出点P的坐标；若不存在，请说明理由．【解答】解：（1）∵直线y＝﹣x+4与x轴交于点C，与y轴交于点B，∴点B，C的坐标分别为B（0，4），C（4，0），把点B（0，4）和点C（4，0）代入抛物线y＝ax2+x+c，得：，解之，得，∴抛物线的解析式为．（32存在．由抛物线可得对称轴是直线x＝1．∵Q是抛物线对称轴上的动点，∴点Q的横坐标为1．①当BC为边时，点B到点C的水平距离是4，∴点Q到点P的水平距离也是4．∴点P的横坐标是5或﹣3，∴点P的坐标为或；②当BC为对角线时，点Q到点C的水平距离是3，∴点B到点P的水平距离也是3，∴点P的坐标为．综上所述，在抛物线上存在点P，使得以P，Q，B，C为顶点的四边形是平行四边形，点P的坐标是或或．4．（2022•东莞市校级一模）如图所示，抛物线y＝x2+bx+c交x轴于A、B两点（点A在点B的左侧），交y轴于点C（0，﹣3），已知AB＝4，对称轴在y轴左侧．（1）求抛物线的表达式；（2）若点N在对称轴上，则抛物线上是否存在点M，使得点A、O、N、M构成平行四边形，若存在，请求出点M的坐标；若不存在，请说明理由；【解答】解：（1）∵抛物线y＝x2+bx+c交y轴于点C（0，﹣3），∴c＝﹣3，∴抛物线的解析式为y＝x2+bx﹣3，设A（x1，0），B（x2，0），由题意得x2﹣x1＝4，∴（x1+x2）2﹣4x1x2＝16，∵x1+x2＝﹣b，x1x2＝﹣3，∴b2+12＝16，∴b＝±2，又∵对称轴在y轴左侧，∴b＝2，∴抛物线的表达式为y＝x2+2x﹣3；（2）存在点M，使得点A、O、N、M构成平行四边形．∵抛物线的解析式为y＝x2+2x﹣3，∴y＝0时，x＝﹣3或x＝1，∴A（﹣3，0），B（1，0），①若OA为边，∴AO∥MN，OA＝MN＝3，∵N在对称轴x＝﹣1上，∴点M的横坐标为2或﹣4，当x＝2时，y＝5，当x＝﹣4时，y＝5，∴M（2，5）或（﹣4，5）；②若OA为对角线时，∵A（﹣3，0），O（0，0），∴OA的中点的坐标为（﹣，0），∵N在直线x＝﹣1上，设M的横坐标为m，∴，∴m＝﹣2，把m＝﹣2代入抛物线解析式得y＝﹣3，∴M（﹣2，﹣3）．综上所述，M的坐标为（2，5）或（﹣4，5）或（﹣2，﹣3）；5．（2022•毕节市）如图，在平面直角坐标系中，抛物线y＝﹣x2+bx+c与x轴交于A，B两点，与y轴交于点C，顶点为D（2，1），抛物线的对称轴交直线BC于点E．（1）求抛物线y＝﹣x2+bx+c的表达式；（2）把上述抛物线沿它的对称轴向下平移，平移的距离为h（h＞0），在平移过程中，该抛物线与直线BC始终有交点，求h的最大值；（3）M是（1）中抛物线上一点，N是直线BC上一点．是否存在以点D，E，M，N为顶点的四边形是平行四边形？若存在，求出点N的坐标；若不存在，请说明理由．【解答】解：（1）∵抛物线y＝﹣x2+bx+c的顶点为D（2，1），∴抛物线的表达式为：y＝﹣（x﹣2）2+1＝﹣x2+4x﹣3．（2）由（1）知，抛物线的表达式为：y＝﹣x2+4x﹣3，令x＝0，则y＝﹣3，∴C（0，﹣3）；令y＝0，则x＝1或x＝3，∴A（1，0），B（3，0）．∴直线BC的解析式为：y＝x﹣3．设平移后的抛物线的解析式为：y＝﹣（x﹣2）2+1﹣h，令﹣（x﹣2）2+1﹣h＝x﹣3，整理得x2﹣3x+h＝0，∵该抛物线与直线BC始终有交点，∴Δ＝9﹣4h≥0，∴h≤．∴h的最大值为．（3）存在，理由如下：由题意可知，抛物线的对称轴为：直线x＝2，∴E（2，﹣1），∴DE＝2，设点M（m，﹣m2+4m﹣3），若以点D，E，M，N为顶点的四边形是平行四边形，则分以下两种情况：①当DE为边时，DE∥MN，则N（m，m﹣3），∴MN＝|﹣m2+4m﹣3﹣（m﹣3）|＝|﹣m2+3m|，∴|﹣m2+3m|＝2，解得m＝1或m＝2（舍）或m＝或m＝．∴N（1，﹣2）或（，）或（，）．②当DE为对角线时，设点N的坐标为t，则N（t，t﹣3），∴，解得m或（舍），∴N（3，0）．综上，点N的坐标为N（1，﹣2）或（，）或（，）或（3，0）．6．（2022•娄底）如图，抛物线y＝x2﹣2x﹣6与x轴相交于点A、B，与y轴相交于点C．（1）请直接写出点A，B，C的坐标；（2）点P（m，n）（0＜m＜6）在抛物线上，当m取何值时，△PBC的面积最大？并求出△PBC面积的最大值．（3）点F是抛物线上的动点，作FE∥AC交x轴于点E，是否存在点F，使得以A、C、E、F为顶点的四边形是平行四边形？若存在，请写出所有符合条件的点F的坐标；若不存在，请说明理由．【解答】解：（1）当x＝0时，y＝﹣6，∴C（0，﹣6），当y＝0时，x2﹣2x﹣6＝0，∴x1＝6，x2＝﹣2，∴A（﹣2，0），B（6，0）；（2）方法一：如图1，连接OP，设点P（m，﹣2m﹣6），∴S△POC＝x P＝＝3m，S△BOP＝|y P|＝+2m+6），∵S△BOC＝＝18，∴S△PBC＝S四边形PBOC﹣S△BOC＝（S△POC+S△POB）﹣S△BOC＝3m+3（﹣+2m+6）﹣18＝﹣（m﹣3）2+，∴当m＝3时，S△PBC最大＝；方法二：如图2，作PQ⊥AB于Q，交BC于点D，∵B（6，0），C（0，﹣6），∴直线BC的解析式为：y＝x﹣6，∴D（m，m﹣6），∴PD＝（m﹣6）﹣（﹣2m﹣6）＝﹣+3m，∴S△PBC＝＝＝﹣（m﹣3）2+，∴当m＝3时，S△PBC最大＝；（3）如图3，当▱ACFE时，AE∥CF，∵抛物线对称轴为直线：x＝＝2，∴F1点的坐标：（4，﹣6），如图4，当▱ACEF时，作FG⊥AE于G，∴FG＝OC＝6，当y＝6时，x2﹣2x﹣6＝6，∴x1＝2+2，x2＝2﹣2，∴F2（2+2，6），F3（2﹣2，6），综上所述：F（4，﹣6）或（2+2，6）或（2﹣2，6）．7．（2022•宜宾）如图，抛物线y＝ax2+bx+c与x轴交于A（3，0）、B（﹣1，0）两点，与y轴交于点C（0，3），其顶点为点D，连结AC．（1）求这条抛物线所对应的二次函数的表达式及顶点D的坐标；（2）在抛物线的对称轴上取一点E，点F为抛物线上一动点，使得以点A、C、E、F为顶点、AC为边的四边形为平行四边形，求点F的坐标；【解答】解：（1）∵抛物线y＝ax2+bx+c经过A（3，0）、B（﹣1，0），C（0，3），∴，解得，∴抛物线的解析式为y＝﹣x2+2x+3，∵y＝﹣（x﹣1）2+4，∴顶点D的坐标为（1，4）；（2）设直线AC的解析式为y＝kx+b，把A（3，0），C（0，3）代入，得，∴，∴直线AC的解析式为y＝﹣x+3，过点F作FG⊥DE于点G，∵以A，C，E，F为顶点的四边形是以AC为边的平行四边形，∴AC＝EF，AC∥EF，∵OA∥FG，∴∠OAC＝∠GFE，∴△OAC≌△GFE（AAS），∴OA＝FG＝3，设F（m，﹣m2+2m+3），则G（1，﹣m2+2m+3），∴FG＝|m﹣1|＝3，∴m＝﹣2或m＝4，当m＝﹣2时，﹣m2+2m+3＝﹣5，∴F1（﹣2，﹣5），当m＝4时，﹣m2+2m+3＝﹣5，∴F2（4，﹣5）综上所述，满足条件点F的坐标为（﹣2，﹣5）或（4，﹣5）；7．（2022•重庆）如图，在平面直角坐标系中，抛物线y＝﹣x2+bx+c与x轴交于点A（4，0），与y轴交于点B（0，3）．（1）求抛物线的函数表达式；（2）点P为直线AB上方抛物线上一动点，过点P作PQ⊥x轴于点Q，交AB于点M，求PM+AM的最大值及此时点P的坐标；（3）在（2）的条件下，点P′与点P关于抛物线y＝﹣x2+bx+c的对称轴对称．将抛物线y＝﹣x2+bx+c向右平移，使新抛物线的对称轴l经过点A．点C在新抛物线上，点D在l上，直接写出所有使得以点A、P′、C、D为顶点的四边形是平行四边形的点D的坐标，并把求其中一个点D的坐标的过程写出来．【解答】解：（1）∵抛物线y＝﹣x2+bx+c与x轴交于点A（4，0），与y轴交于点B （0，3）．∴，∴．∴抛物线的函数表达式为y＝﹣；（2）∵A（4，0），B（0，3），∴OA＝4，OB＝3，由勾股定理得，AB＝5，∵PQ⊥OA，∴PQ∥OB，∴△AQM∽△AOB，∴MQ：AQ：AM＝3：4：5，∴AM＝，，∴PM+，∵B（0，3），A（4，0），∴l AB：y＝﹣，∴设P（m，﹣），M（m，﹣），Q（m，0），∴PM+2MQ＝﹣＝﹣，∵﹣，∴开口向下，0＜m＜4，∴当m＝1时，PM+的最大值为，此时P（1，）；（3）由y＝﹣知，对称轴x＝，∴P'（2，），∵直线l：x＝4，∴抛物线向右平移个单位，∴平移后抛物线解析式为y'＝﹣，设D（4，t），C（c，﹣），①AP'与DC为对角线时，，∴，∴D（4，），②P'D与AC为对角线时，，∴，∴D（4，﹣），③AD与P'C为对角线时，，∴，∴D（4，），综上：D（4，）或（4，﹣）或（4，）．8．（2022•青羊区校级模拟）抛物线y＝ax2+bx+c（a≠0）与x轴交于点A（﹣3，0），B （1，0）两点，与y轴交于点C（0，3），点P是抛物线上的一个动点．（1）求抛物线的函数表达式；（2）如图1，点P在线段AC上方的抛物线上运动（不与A，C重合），过点P作PD⊥AB，垂足为D，PD交AC于点E．作PF⊥AC，垂足为F，求△PEF的面积的最大值；（3）如图2，点Q是抛物线的对称轴l上的一个动点，在抛物线上，是否存在点P，使得以点A，P，C，Q为顶点的四边形是平行四边形？若存在，求出所有符合条件的点P 的坐标；若不存在，说明理由．【解答】解：（1）∵抛物线y＝ax2+bx+c（a≠0）与x轴交于点A（﹣3，0），B（1，0）两点，∴设y＝a（x+3）（x﹣1），把C（0，3）代入，得：3＝a×（0+3）×（0﹣1），解得：a＝﹣1，∴y＝﹣（x+3）（x﹣1）＝﹣x2﹣2x+3，∴该抛物线的函数表达式为y＝﹣x2﹣2x+3；（2）∵A（﹣3，0），C（0，3），∴OA＝OC＝3，∴∠ACO＝45°，∵PD⊥AB，OC⊥AB，∴PD∥OC，∴∠PEF＝∠ACO＝45°，∵PF⊥AC，∴△PEF是等腰直角三角形，如图1，过点F作FH⊥PE于点H，则FH＝PE，∴S△PEF＝×PE×FH＝PE2，当PE最大时，S△PEF最大，设直线AC的解析式为y＝kx+d，则，解得：，∴直线AC的解析式为y＝x+3，设P（t，﹣t2﹣2t+3），则E（t，t+3），∴PE＝﹣t2﹣2t+3﹣（t+3）＝﹣t2﹣3t＝﹣（t+）2+，∵﹣1＜0，∴当t＝﹣时，PE取得最大值，∴S△PEF＝PE2＝×（）2＝，∴△PEF的面积的最大值为；（3）①当AC为平行四边形的边时，则有PQ∥AC，且PQ＝AC，如图2，过点P作对称轴的垂线，垂足为G，设AC交对称轴于点H，则∠AHG＝∠ACO＝∠PQG，在△PQG和△ACO中，，∴△PQG≌△ACO（AAS），∴PG＝AO＝3，∴点P到对称轴的距离为3，又∵y＝﹣（x+1）2+4，∴抛物线对称轴为直线x＝﹣1，设点P（x，y），则|x+1|＝3，解得：x＝2或x＝﹣4，当x＝2时，y＝﹣5，当x＝﹣4时，y＝﹣5，∴点P坐标为（2，﹣5）或（﹣4，﹣5）；②当AC为平行四边形的对角线时，如图3，设AC的中点为M，∵A（﹣3，0），C（0，3），∴M（﹣，），∵点Q在对称轴上，∴点Q的横坐标为﹣1，设点P的横坐标为x，根据中点公式得：x+（﹣1）＝2×（﹣）＝﹣3，∴x＝﹣2，此时y＝3，∴P（﹣2，3）；综上所述，点P的坐标为（2，﹣5）或（﹣4，﹣5）或（﹣2，3）．9．（2022•九龙坡区自主招生）如图1，在平面直角坐标系xOy中，抛物线y＝﹣x2+bx+c 与x轴交于A，B两点，与y轴交于点C，点A，B分别位于原点的左右两侧，且BO＝3AO＝3．已知直线y＝kx+n过B，C两点．（1）求抛物线的表达式；（2）点P是抛物线上的一个动点．①如图1，若点P在第一象限内，连接P A，交直线BC于点D．记△PDC的面积为S1，△ADC的面积为S2，若S1：S2＝1：2，求点P的坐标；②如图2，抛物线的对称轴l与x轴交于点E，过点E作EF⊥BC，垂足为F．点Q是对称轴l上的一个动点，是否存在以点E，F，P，Q为顶点的四边形是平行四边形？若存在，请直接写出点P，Q的坐标；若不存在，请说明理由．【解答】解：（1）∵BO＝3AO＝3．∴AO＝1．∴A（﹣1，0），B（3，0），把A（﹣1，0），B（3，0）代入y＝﹣x2+bx+c得：，解得，抛物线的表达式为y＝﹣x2+2x+3；（2）①∵y＝﹣x2+2x+3，∴点C坐标为（0，3），把B（3，0），C（0，3）代入y＝kx+n得：，解得，∴直线BC的表达式为y＝﹣x+3．过P作PM⊥x轴交BC于M，过A作AN⊥x轴交BC于N，如图1，AN∥PM，∴△PMD∽△AND，∴，∴＝，设P（m，﹣m2+2m+3），则M（m，﹣m+3），∴PM＝﹣m2+2m+3﹣（﹣m+3）＝﹣m2+3m，∵A（﹣1，0），∴N（﹣1，4），∴AN＝4，∴＝，∴m＝1或2，∴点P的坐标为（1，4）或（2，3）；②存在，理由如下：过点F作FG⊥OB于G，如图2中，∵y＝﹣x2+2x+3的对称轴为x＝1，∴OE＝1，∵B（3，0），C（0，3）∴OC＝OB＝3，又∵∠COB＝90°，∴△OCB是等腰直角三角形，∵∠EFB＝90°，BE＝OB﹣OE＝2，∴△EFB是等腰直角三角形，∴FG＝GB＝EG＝1，∴点F的坐标为（2，1），当EF为边时，∵四边形EFPQ为平行四边形，∴QE＝PF，QE∥PF∥y轴，∴点P的横坐标与点F的横坐标同为2，当x＝2时，y＝﹣22+2×2+3＝3，∴点P的坐标为（2，3），∴QE＝PF＝3﹣1＝2，点Q的坐标为（1，2），根据对称性当P（0，3）时，Q（1，4）时，四边形EFQP也是平行四边形．当EF为对角线时，如图3中，∵四边形PEQF为平行四边形，∴QE＝PF，QE∥PF∥y轴，同理求得：点P的坐标为（2，3），∴QE＝PF＝3﹣1＝2，点Q的坐标为（1，﹣2）；综上，点P的坐标为（2，3）时，点Q的坐标为（1，2）或（1，﹣2），P（0，3）时，Q（1，4）．10．（2022•鄂尔多斯）如图，在平面直角坐标系中，抛物线y＝ax2+bx+2经过A（，0），B（3，）两点，与y轴交于点C．（1）求抛物线的解析式；（2）点P在抛物线上，过P作PD⊥x轴，交直线BC于点D，若以P、D、O、C为顶点的四边形是平行四边形，求点P的横坐标；【解答】解：（1）将点A（﹣，0），B（3，）代入到y＝ax2+bx+2中得：，解得：，∴抛物线的解析式为y＝﹣x2+x+2；（2）设点P（m，﹣m2+m+2），∵y＝﹣x2+x+2，∴C（0，2），设直线BC的解析式为y＝kx+c，∴，解得，∴直线BC的解析式为y＝x+2，∴D（m，m+2），∴PD＝|﹣m2+m+2﹣m﹣2|＝|m2﹣3m|，∵PD⊥x轴，OC⊥x轴，∴PD∥CO，∴当PD＝CO时，以P、D、O、C为顶点的四边形是平行四边形，∴|m2﹣3m|＝2，解得m＝1或2或或，∴点P的横坐标为1或2或或；。

二次函数平行四边形存在性问题例题

二次函数平行四边形存在性问题例题例题：已知二次函数f(x) = ax² + bx + c，其中a ≠ 0，现给定两点A(x₁, y₁)和B(x₂, y₂)，求是否存在一个平行四边形ABCD，使得AC和BD都平行于直线y = kx + m。

解题思路：首先，我们需要确定k和m的值，因为平行四边形ABCD中的AC和BD必须平行于直线y = kx + m。

根据平行的性质，我们可以得到AC和BD的斜率都为k。

所以，我们首先需要求得二次函数f(x)的斜率。

二次函数f(x) = ax² + bx + c的斜率可以通过求导得到。

将f(x)对x求导，得到f'(x) = 2ax + b。

所以，二次函数f(x)的斜率k =f'(x)处的斜率 = 2ax + b。

在已知的两点A(x₁, y₁)和B(x₂, y₂)处，可以得到f(x₁) = ax₁² +bx₁ + c = y₁和f(x₂) = ax₂² + bx₂ + c = y₂。

我们可以根据这两个条件，列出方程组，并通过求解方程组来求得平行四边形ABCD的存在性。

方程组如下所示：1. ax₁² + bx₁ + c = y₁2. ax₂² + bx₂ + c = y₂为了方便计算，可以移项，得到以下形式：1'. ax₁² + bx₁ + c - y₁ = 02'. ax₂² + bx₂ + c - y₂ = 0现在我们需要判断是否存在一个平行四边形ABCD，使得AC和BD都平行于直线y = kx + m。

根据平行四边形的性质，可以得知AC的斜率等于k，即AC的斜率为2ax + b，同样，BD的斜率也等于k。

所以我们需要判断是否存在一组x₁、y₁、x₂、y₂的值，使得如下两个方程成立：3. 2ax₁ + b = k4. 2ax₂ + b = k将方程3和方程4化简，得到如下形式：3'. 2ax₁ + b - k = 04'. 2ax₂ + b - k = 0现在我们有了方程2'和方程4'，我们可以组成如下新的方程组：2'. ax₂² + bx₂ + c - y₂ = 04'. 2ax₂ + b - k = 0这是一个二次函数与一次函数的方程组，我们可以通过求解这个方程组来判断是否存在平行四边形ABCD。

二次函数中的平行四边形问题

学习好资料_______________________________________________________________________________________________学习好资料_______________________________________________________________________________________________学习好资料_______________________________________________________________________________________________学习好资料_____________________________________________学习过程一、复习预习（一）利用待定系数法求抛物线解析式的三种常用形式：（1）【一般式】已知抛物线上任意三点时，通常设解析式为，然后解三元方程组求解；__________________________________________________学习好资料_______________________________________________________________________________________________（2）【顶点式】已知抛物线的顶点坐标和抛物线上另一点时，通常设解析式为求解；（3）【交点式】已知抛物线与轴的交点的坐标时，通常设解析式为。

（二）抛物线上两个点A （x 1，y ），B （x 2，y ）之间的关系： (1)如果两点关于对称轴对称，则有对称轴2x 21x x +=；(2)两点之间距离公式：已知两点()()2211y ,x Q ,y ,x P ，则由勾股定理可得：221221)()(y y x x PQ -+-=练一练：已知A （0，5）和B （－2，3），则AB ＝。

二次函数与平行四边形结合专题练习

二次函数与平行四边形结合专题练习1.题目描述：给定抛物线$y=-x^2+bx+c$与$x$轴的交点$A,B$，其中$B$的坐标为$(3,0)$，直线$AD$经过点$A$，与抛物线交于点$D(2,3)$。

求抛物线和直线$AD$的解析式，以及是否存在实数$a$，使得过点$(a,0)$且平行于$AD$的直线$EF$与抛物线交于点$F$，使得四边形$ADEF$为平行四边形，若存在，求出$a$。

2.题目描述：给定抛物线的顶点坐标$M(1,4)$，经过点$N(2,3)$，与$x$轴交于$A,B$，与$y$轴交于点$C$。

求抛物线的解析式，以及证明四边形$CDAN$是平行四边形，其中直线$y=kx+t$经过点$C,M$，与$x$轴交于点$D$。

3.题目描述：给定抛物线经过$A(-1,0),B(5,0),C(x,-\frac{5}{2})$三点。

求抛物线的解析式，以及在抛物线的对称轴上有一点$P$，使得$PA+PC$的值最小，求点$P$的坐标。

另外，给定$x$轴上的一动点$M$，判断是否存在抛物线上的一点$N$，使得四边形$ACMN$为平行四边形，若存在，求点$N$的坐标。

4.题目描述：给定抛物线$y=ax^2+bx+c$经过点$A(-2,0),B(4,0),D(2,4)$，与$y$轴交于点$C$，作直线$BC$，连接$AC,CD$。

求抛物线的函数表达式，以及点$E$满足$\angle ECD=\angle ACO$的坐标，点$M$在$y$轴上且位于点$C$上方，点$N$在直线$BC$上，点$P$为第一象限内抛物线上的一点，若以点$C,M,N,P$为顶点的四边形为菱形，求菱形的边长。

5.题目描述：给定抛物线$y=-x^2+2x+3$与$x$轴的交点$A,B$，与$y$轴的交点为$C$，顶点为$D$。

求点$A,B,C$的坐标以及抛物线的对称轴，连接$BC$，与对称轴交于点$E$，点$P$为线段$BC$上的动点，过点$P$作$PF$平行于$DE$交抛物线于点$F$。

中考二次函数动点问题(含答案)

中考二次函数动点(Dian)问题(含答案)1.如(Ru)图(Tu)①，正(Zheng)方形的(De)顶点的坐标(Biao)分别为，顶(Ding)点在(Zai)第一象限．点从点出发，沿正方形按逆时针方向匀速运动，同时，点从点出发，沿轴正方向以相同速度运动．当点P到达点时，两点同时停止运动，设运动的时间为秒．（1）求正方形ABCD的边长．（2）当点P在边上运动时，的面积（平方单位）与时间t（秒）之间的函数图象为抛物线的一部分（如图②所示），求P Q，两点的运动速度．（3）求（2）中面积S（平方单位）与时间t（秒）的函数关系式及面积S取最大值时点P 的坐标．（4）若点P Q，保持（2）中的速度不变，则点P沿着AB边运动时，的大小随着时间t的增大而增大；沿着边运动时，OPQ∠的大小随着时间t的增大而减小．当点P沿着这两边运动时，使的点P有个．（抛物线的顶点坐标是．[解] （1）作轴于．，．．（2）由图②可知，点P从点A运动到点用了10秒．又．两点的运动速度均为每秒1个单位．（3）方法一：作轴于，则．，即．．．，．即(Ji)．，且(Qie)，当(Dang)时(Shi)，S 有最(Zui)大值．此(Ci)时， ∴点(Dian)P 的坐(Zuo)标为．（8分）方法二：当时，．设所求函数关系式为．抛物线过点，．19195323210b a -=-=⎛⎫⨯- ⎪⎝⎭，且190103≤≤， ∴当193t =时，S 有最大值．此时，∴点P 的坐标为7631155⎛⎫⎪⎝⎭，．（4）．[点(Dian)评(Ping)]本题主要考查函数性质的简单运用和几何知识，是近年来较为流行的试(Shi)题，解题的关键在于结合题目的要求动中取静，相信解决这种问题不会非常难。

． 2. 如(Ru)图(Tu)①，中(Zhong)，，．它的(De)顶点A 的坐(Zuo)标为，顶点B 的坐标为，，点P 从点A 出发，沿的方向匀速运动，同时点Q 从点出发，沿轴正方向以相同速度运动，当点P 到达点C 时，两点同时停止运动，设运动的时间为t 秒．（1）求的度数．（2）当点P 在AB 上运动时，OPQ △的面积S （平方单位）与时间t （秒）之间的函数图象为抛物线的一部分，（如图②），求点P 的运动速度．（3）求（2）中面积S 与时间t 之间的函数关系式及面积S 取最大值时点P 的坐标．（4）如果点P Q ，保持（2）中的速度不变，那么点P 沿AB 边运动时，的大小随着时间t 的增大而增大；沿着BC 边运动时，OPQ ∠的大小随着时间t 的增大而减小，当点P 沿这两边运动时，使的点P 有几个？请说明理由．解: （1）．（2）点P 的运动速度为2个单位/秒．（3）（）．∴当时，S 有最大值为，此时．（4）当点P 沿这两边运动时，90OPQ =∠的点P 有2个． ①当点P 与点A 重合时，，当点P 运动到与点B 重合时，的长是12单位长度，作交y 轴于点，作轴于点，由得：，所以，从而．所以当点P 在AB 边上运动时，90OPQ =∠的点P 有1个． ②同理当点P 在BC 边上运动时，可算得．而构成直角时交y 轴于，，所以，从而90OPQ =∠的点P 也有1个．所以当(Dang)点P 沿这两边运动(Dong)时，90OPQ =∠的(De)点P 有(You)2个(Ge)．3. （本(Ben)题满分(Fen)14分(Fen)）如图，直线与轴交于点，与轴交于点，已知二次函数的图象经过点A 、C 和点.（1）求该二次函数的关系式；（2）设该二次函数的图象的顶点为，求四边形的面积；（3）有两动点、同时从点出发，其中点D 以每秒个单位长度的速度沿折线按O →A →C 的路线运动，点E 以每秒个单位长度的速度沿折线按O →C →A 的路线运动，当D 、E 两点相遇时，它们都停止运动.设D 、E 同时从点O 出发秒时，的面积为S .①请问D 、E 两点在运动过程中，是否存在∥，若存在，请求出此时t 的值；若不存在，请说明理由；②请求出S 关于t 的函数关系式，并写出自变量t 的取值范围；③设是②中函数S 的最大值，那么0S = .解：（1）令，则；令则．∴．∵二次函数的图象过点()04C ，， ∴可设二次函数的关系式为又∵该函数图象过点．∴解之，得，．∴所求二次函数的关系式为（2）∵438342++-=x x y =∴顶(Ding)点M 的坐标(Biao)为过(Guo)点M 作(Zuo)MF轴(Zhou)于F ∴=∴四边(Bian)形AOCM 的面(Mian)积为(Wei)10 （3）①不存在DE ∥OC∵若DE ∥OC ，则点D ，E 应分别在线段OA ，CA 上，此时，在中，．设点E 的坐标为∴，∴ ∵，∴∴∵38=t >2，不满足12t <<．∴不存在DE OC ∥．②根据题意得D ，E 两点相遇的时间为（秒）现分情况讨论如下： ⅰ）当时，；ⅱ）当时，设点E 的坐标为∴，∴∴ⅲ）当2 <<时，设点E 的坐标为，类似ⅱ可得设点D 的坐标为∴，∴∴=③47.关(Guan)于x的(De)二次函数以(Yi)y轴为(Wei)对称轴，且与y 轴(Zhou)的交点在x轴(Zhou)上方．（1）求此抛物线的解析式(Shi)，并在下面的直角坐标系中画出函数的草图；（2）设(She)A是y轴右侧抛物线上的一个动点，过点A作AB垂直于x轴于点B，再过点A作x轴的平行线交抛物线于点，过点D作垂直于x轴于点C，得到矩形ABCD．设矩形ABCD的周长为，点A的横坐标为x，试求l关于x的函数关系式；（3）当点A在y轴右侧的抛物线上运动时，矩形ABCD能否成为正方形．若能，请求出此时正方形的周长；若不能，请说明理由．参考资料：抛物线的顶点坐标是2424b ac ba a⎛⎫-- ⎪⎝⎭，，对称轴是直线．解：（1）据题意得：，．当时，．当时，．又抛物线与y轴的交点在x轴上方，．∴抛物线的解析式为：．函数的草图如图所示．（只要与坐标轴的三个交点的位置及图象大致形状正确即可）（2）解：令，得．不时，，，．当时，，．．关于x 的函数关系是：当02x <<时，；当2x >时，．（3）解法一：当02x <<时，令，得．解(Jie)得（舍(She)），或．将(Jiang)13x =-+代(Dai)入2244l x x =-++，得(De)．当(Dang)2x >时(Shi)，令，得(De)．解得（舍），或．将13x =+代入2244l x x =+-，得．综上，矩形ABCD 能成为正方形，且当时正方形的周长为；当时，正方形的周长为．解法二：当02x <<时，同“解法一”可得13x =-+． ∴正方形的周长．当2x >时，同“解法一”可得13x =+．∴正方形的周长．综上，矩形ABCD 能成为正方形，且当31x =-时正方形的周长为838-；当31x =+时，正方形的周长为838+．解法三：点A 在y 轴右侧的抛物线上，，且点A 的坐标为．令，则．∴，①或②由①解得13x =--（舍），或13x =-+；由②解得13x =-（舍），或13x =+．又，∴当13x =-+838l =；当13x =838l =．综上，矩形ABCD 能成为正方形，且当31x =时正方形的周长为838；当31x =时，正方形的周长为838．5.已知抛物线y ＝ax 2＋bx ＋c 与x 轴交于A 、B 两点，与y 轴交于点C ，其中点B 在x 轴的正半轴上，点C 在y 轴的正半轴上，线段OB 、OC 的长（OB <OC ）是方程x 2－10x ＋16＝0的两个根，且抛物线的对称轴是直线x ＝－2．（1）求A 、B 、C 三点的坐标；（2）求此抛物线的表达式；（3）连接AC 、BC ，若点E 是线段AB 上的一个动点（与点A 、点B 不重合），过点E 作EF ∥AC 交BC 于点F ，连接CE ，设AE 的长为m ，△CEF 的面积为S ，求S 与m 之间的函数关系式，并写出自变量m 的取值范围；（4）在（3）的基础上试说明S 是否存在最大值，若存在，请求出S 的最大值，并求出此时点E 的坐标，判断此时△BCE 的形状；若不存在，请说明理由．解：（1）解方程x 2－10x ＋16＝0得x 1＝2，x 2＝8∵点B 在x 轴的正半轴上，点C 在y 轴的正半轴上，且OB ＜OC ∴点B 的坐标为（2，0），点C 的坐标为（0，8）又∵抛物线y ＝ax 2＋bx ＋c 的对称轴是直线x ＝－2 ∴由抛物线的对称性可得点A 的坐标为（－6，0）（2）∵点(Dian)C （0，8）在(Zai)抛物线y ＝ax 2＋bx ＋c 的(De)图象上 ∴c ＝8，将(Jiang)A （－6，0）、B （2，0）代入(Ru)表达式，得⎩⎨⎧0＝36a －6b ＋80＝4a ＋2b ＋8解(Jie)得⎩⎪⎨⎪⎧a ＝－23b ＝－83∴所求抛物线的表达式(Shi)为y ＝－23x 2－83x ＋8（3）依(Yi)题意，AE ＝m ，则BE ＝8－m ， ∵OA ＝6，OC ＝8，∴AC ＝10 ∵EF ∥AC ∴△BEF ∽△BAC ∴EF AC ＝BE AB 即EF 10＝8－m8 ∴EF ＝40－5m 4过点F 作FG ⊥AB ，垂足为G ，则sin ∠FEG ＝sin ∠CAB ＝45∴FG EF ＝45 ∴FG ＝45·40－5m 4＝8－m ∴S ＝S △BCE －S △BFE ＝12（8－m ）×8－12（8－m ）（8－m ）＝12（8－m ）（8－8＋m ）＝12（8－m ）m ＝－12m 2＋4m 自变量m 的取值范围是0＜m ＜8（4）存在．理由：∵S ＝－12m 2＋4m ＝－12（m －4）2＋8 且－12＜0，∴当m ＝4时，S 有最大值，S 最大值＝8∵m ＝4，∴点E 的坐标为（－2，0） ∴△BCE 为等腰三角形．6.（14分）如图：抛物线经过A （-3，0）、B （0，4）、C （4，0）三点. （1）求抛物线的解析式.（2）已知AD = AB （D 在线段AC 上），有一动点P 从点A 沿线段AC 以每秒1个单位长度的速度移动；同时另一个动点Q 以某一速度从点B 沿线段BC 移动，经过t 秒的移动，线段PQ 被BD 垂直平分，求t 的值；（3）在（2）的情况下，抛物线的对称轴上是否存在一点M ，使MQ+MC 的值最小？若存在，请求出点M 的坐标；若不存在，请说明理由。

九年级数学二次函数动点问题专题练习

∴ 所求的抛物线对应的函数关系式为 y 1 x(x 4) ，即 y 1 x 2 x .
4
4
（2）①直线 y=-2x-1 与 y 轴、直线 x=2 的交点坐标分别为 D(0,-1) E(2,-5).
过点 B 作 BG∥ x 轴，与 y 轴交于 F、直线 x=2 交于 G，则点 G 坐标为(2,3)
二次函数的动点问题
1 如图，已知抛物线经过原点 O 和 x 轴上另一点 A,它的对称轴 x=2 与 x 轴交于点 C，直线 y=-2x-1 经过抛物线上一点 B(-2,m)，且与 y 轴、直线 x=2 分别交于点 D、E.
（1）求 m 的值及该抛物线对应的函数关系式；（2）求证：① CB=CE ；② D 是 BE 的中点；（3）若 P(x，y)是该抛物线上的一个动点，是否存在这样的点 P,使得 PB=PE,若存在，试求出所有符合条件的点 P 的坐标；若不存在，请说明理由
BG⊥直线 x=2，BG=4.在 Rt△ BGC 中，BC= CG 2 BG 2 32 42 5 . ∵ CE=5，∴ CB=CE=5.
②过点 E 作 EH∥ x 轴，交 y 轴于 H，则点 H 的坐标为 H(0,-5).
又点 FD=DH=4，BF=EH=2，∠ BFD=∠ EHD=90°.
∴ △ DFB≌ △ DHE （SAS），∴ BD=DE. 即 D 是 BE 的中点.
(3)由于 PB=PE，∴ 点 P 必在线段 BE 的中垂线 CD 上，又点 P 在抛物线 y 1 x 2 x 上,
4 ∴ 符合条件的点 P 应是直线 CD 与该抛物线的交点.
设直线 CD 对应的函数关系式为 y=kx+b.
其中 C 点的横坐标为 2．（1）求 A、B 两点的坐标及直线 AC 的函数表达式；（2）P 是线段 AC 上的一个动点，过 P 点作 y 轴的平行线交抛物线于 E 点，求线段 PE 长度的最大值；（3）点 G 抛物线上的动点，在 x 轴上是否存在点 F，使 A、C、F、G 这样的四个点为顶点的四边形是

二次函数动点平行四边形问题方法

二次函数动点平行四边形问题方法
解决二次函数中的动点平行四边形问题，可以按照以下步骤进行：
1. 确定二次函数的表达式：首先需要确定二次函数的表达式，可以根据已知的顶点坐标或一般式来求解。

2. 确定动点的坐标：根据平行四边形的性质，动点的坐标可以通过平移来得到。

可以先确定平行四边形的一个顶点坐标，然后通过平移得到其他顶点的坐标。

3. 求解平行四边形的面积：根据平行四边形的性质，可以计算出每个三角形的面积，然后将它们相加得到平行四边形的面积。

4. 求解平行四边形的周长：可以根据平行四边形的性质，通过计算相邻两边之和来得到平行四边形的周长。

例如，如果二次函数的表达式为y=x^2-2x+1，动点A的坐标为(0,1)，B点的坐标为(2,1)，C点的坐标为(1,0)，求平行四边形ABCD的面积和周长。

首先，可以画出函数的图像和三个点的位置，然后根据平行四边形的性质，得到D点的坐标为(3,1)。

然后，可以计算出三角形ABC的面积为1/2，三角形ABD的面积为1/2，所以平行四边形ABCD的面积为1。

最后，可以计算出平行四边形ABCD的周长为4。

通过这种方法，可以解决二次函数中动点平行四边形的问题。

二次函数中平行四边形存在性问题精选全文

可编辑修改精选全文完整版二次函数中平行四边形存在性问题解题原理：对角线互相平分的四边形是平行四边形1. 平行四边形顶点坐标公式平行四边形ABCD的顶点坐标分别为A(x1,y1)、B(x2,y2)、C(x3,y3)、D(x4,y4)，则：x1+x3=x2+x4；y1+y3=y2+y4.证明：如图，连接AC、BD，相交于点E．∵点E为AC的中点，∴E点坐标为(221xx+,231yy+). 又∵点E为BD的中点，∴E点坐标为(242xx+,242yy+).∴x1+x3=x2+x4；y1+y3=y2+y4.即平行四边形对角线两端点的横坐标、纵坐标之和分别相等．2 解题的预备知识如右图，已知不在同一直线上的三点A、B、C，在平面内另找一个点D，使以A、B、C、D为顶点的四边形是平行四边形．答案有三种：以AB为对角线的□ACBD1，以AC为对角线的□ABCD2，以BC为对角线的□ABD3C．3 两类存在性问题解题策略第一步：把四个点的坐标表示出来（如果是动点用字母表示其坐标）第二步：分三种情况讨论对角线（如果四个点中有一组平行例1中PM//OB那么以PM为对角线是不存在的，就可以只讨论以PB、PO为对角线的情况）第三步：利用对角线两端点的横坐标、纵坐标之和分别相等列式。

题型1 有一组对边平行，探究平行四边形存在性问题例1．如图，在平面直角坐标系中，抛物线y=x2+mx+n经过点A（3，0）、B（0，﹣3），点P是直线AB上的动点，过点P作x轴的垂线交抛物线于点M，设点P的横坐标为t．（1）分别求出直线AB和这条抛物线的解析式．（2）是否存在这样的点P，使得以点P、M、B、O为顶点的四边形为平行四边形？若存在，请直接写出点P的横坐标；若不存在，请说明理由．题型2 两个定点、两个动点，（或一个定点、三个动点）探究平行四边形存在性问题例2．如图，抛物线经过A（﹣1，0），B（5，0），C（0，）三点．（1）求抛物线的解析式；（2）点M为x轴上一动点，在抛物线上是否存在一点N，使以A，C，M，N四点构成的四边形为平行四边形？若存在，求点N的坐标；若不存在，请说明理由．习题巩固1．如图，抛物线y=﹣x2+bx+c与y轴交于点A（0，1），过点A的直线与抛物线交于另一点B（3，），过点B作BC⊥x轴，垂足为C．点P是x轴正半轴上的一动点，过点P作PN⊥x轴，交直线AB于点M，交抛物线于点N，设OP的长度为m．（1）求抛物线的解析式；（2）连结CM，BN，当m为何值时，以B、C、M、N为顶点的四边形为平行四边形？2．抛物线：y=x2﹣x﹣与x轴交于A、B（A在B左侧），A（﹣1，0）、B（3，0），顶点为C（1，﹣2）在抛物线上找点P，在y轴上找点E，使以A、B、P、E为顶点的四边形是平行四边形，求点P、E的坐标．2．如图，Rt△OAB如图所示放置在平面直角坐标系中，直角边OA与x轴重合，∠OAB=90°，OA=4，AB=2，把Rt△OAB绕点O逆时针旋转90°，点B旋转到点C的位置，一条抛物线正好经过点O，C，A三点．（1）求该抛物线的解析式；（2）在x轴上方的抛物线上有一动点P，过点P作x轴的平行线交抛物线于点M，分别过点P，点M 作x轴的垂线，交x轴于E，F两点，问：四边形PEFM的周长是否有最大值？如果有，请求出最值，并写出解答过程；如果没有，请说明理由．（3）如果x轴上有一动点H，在抛物线上是否存在点N，使O（原点）、C、H、N四点构成以OC为一边的平行四边形？若存在，求出N点的坐标；若不存在，请说明理由．3．如图，直线y=﹣x+3与x轴交于点C，与y轴交于点B，抛物线y=ax2+x+c经过B、C两点．（1）求抛物线的解析式；（2）如图，点E是直线BC上方抛物线上的一动点，当△BEC面积最大时，请求出点E的坐标和△BEC 面积的最大值？（3）在（2）的结论下，过点E作y轴的平行线交直线BC于点M，连接AM，点Q是抛物线对称轴上的动点，在抛物线上是否存在点P，使得以P、Q、A、M为顶点的四边形是平行四边形？如果存在，请直接写出点P的坐标；如果不存在，请说明理由．4．如图，在矩形OABC中，OA=5，AB=4，点D为边AB上一点，将△BCD沿直线CD折叠，使点B 恰好落在OA边上的点E处，分别以OC，OA所在的直线为x轴，y轴建立平面直角坐标系．（1）求点E坐标及经过O，D，C三点的抛物线的解析式；（2）一动点P从点C出发，沿CB以每秒2 个单位长的速度向点B运动，同时动点Q从E点出发，沿EC以每秒1个单位长的速度向点C运动，当点P到达点B时，两点同时停止运动．设运动时间为t秒，当t为何值时，DP=DQ；（3）若点N在（2）中的抛物线的对称轴上，点M在抛物线上，是否存在这样的点M与点N，使得以M，N，C，E为顶点的四边形是平行四边形？若存在，请求出M点的坐标；若不存在，请说明理由．。

二次函数压轴题：平行四边形

二次函数与平行四边形存在问题【知识要点】1、平行四边形模型探究如图1，点A ()11,x y 、B ()22,x y 、C ()33,x y 是坐标平面内不在同一直线上的三点。

平面直角坐标系中是否存在点D ，使得以A 、B 、C 、D 四点为顶点的四边形为平行四边形，如果存在，请求出点D 的坐标。

ABC xy图1 图2如图2，过A 、B 、C 分别作BC 、AC 、AB 的平行线，则以不在同一直线上的三点为顶点的平行四边形有三个。

由已知的三点坐标可根据图形平移的坐标性质，直接写出第四个顶点的坐标。

一、已知三个定点，再找一个定点构成平行四边形（平面内有三个点满足）例1.已知抛物线b ax ax y ++-=22与x 轴的一个交点为A (-1,0)，与y 轴的正半轴交于点C ． ⑴直接写出抛物线的对称轴，及抛物线与x 轴的另一个交点B 的坐标； ⑵当点C 在以AB 为直径的⊙P 上时，求抛物线的解析式；⑶坐标平面内是否存在点M ,使得以点M 和⑵中抛物线上的三点A 、B 、C 为顶点的四边形是平行四边形？若存在,请求出点M 的坐标；若不存在,请说明理由.练习.已知抛物线22y x x a =-+（0a <）与y 轴相交于点A ，顶点为M .直线12y x a =-分别与x 轴，y 轴相交于B C ，两点，并且与直线AM 相交于点N .(1)填空：试用含a 的代数式分别表示点M 与N 的坐标，则()()M N ，，，；(2)如图，将NAC △沿y 轴翻折，若点N 的对应点N ′恰好落在抛物线上，AN ′与x 轴交于点D ，连结CD ，求a 的值和四边形ADCN 的面积；(3)在抛物线22y x x a =-+（0a <）上是否存在一点P ，使得以P A C N ，，，为顶点的四边形是平行四边形？若存在，求出P 点的坐标；若不存在，试说明理由.二、已知两个定点，再找两个点构成平行四边形①确定两定点连接的线段为一边，则两动点连接的线段应和已知边平行且相等）第（2）题备用图例2．已知，如图抛物线23(0)y ax ax c a =++>与y 轴交于C 点，与x 轴交于A 、B 两点，A 点在B 点左侧。

二次函数中动点问题_平行四边形(练习)