矢量控制系统仿真课程设计
MATLABSIMULINK永磁同步电机矢量控制系统仿真

MATLABSIMULINK永磁同步电机矢量控制系统仿真一、本文概述随着电机控制技术的快速发展,永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)在工业、交通和能源等领域的应用越来越广泛。
矢量控制作为PMSM的一种高效控制策略,能够实现对电机转矩和磁链的精确控制,从而提高电机的动态性能和稳态性能。
然而,在实际应用中,矢量控制系统的设计和调试过程往往复杂且耗时。
因此,利用MATLAB/Simulink进行永磁同步电机矢量控制系统的仿真研究,对于深入理解矢量控制原理、优化控制策略以及提高系统性能具有重要意义。
本文旨在通过MATLAB/Simulink平台,建立永磁同步电机矢量控制系统的仿真模型,并对其进行仿真分析。
本文将对永磁同步电机的基本结构和数学模型进行介绍,为后续仿真模型的建立提供理论基础。
本文将详细阐述矢量控制策略的基本原理和实现方法,包括坐标变换、空间矢量脉宽调制(SVPWM)等关键技术。
在此基础上,本文将利用MATLAB/Simulink中的电机控制库和自定义模块,搭建永磁同步电机矢量控制系统的仿真模型,并对其进行仿真实验。
本文将根据仿真结果,对矢量控制系统的性能进行分析和评价,并提出优化建议。
通过本文的研究,读者可以全面了解永磁同步电机矢量控制系统的基本原理和仿真实现方法,为后续的实际应用提供有益的参考和指导。
本文的研究结果也为永磁同步电机控制技术的发展和应用提供了有益的探索和启示。
二、永磁同步电机数学模型永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)是一种高性能的电机,广泛应用于各种工业领域。
为了有效地对其进行控制,我们需要建立其精确的数学模型。
PMSM的数学模型主要包括电气方程、机械方程和磁链方程。
PMSM的电气方程描述了电机的电压、电流和磁链之间的关系。
在dq旋转坐标系下,电气方程可以表示为:V_d &= R_i I_d + \frac{d\Phi_d}{dt} - \omega_e \Phi_q \ V_q &= R_i I_q + \frac{d\Phi_q}{dt} + \omega_e \Phi_d其中,(V_d) 和 (V_q) 分别是d轴和q轴的电压;(I_d) 和 (I_q) 分别是d轴和q轴的电流;(\Phi_d) 和 (\Phi_q) 分别是d轴和q轴的磁链;(R_i) 是定子电阻;(\omega_e) 是电角速度。
运动控制系统课程设计异步电机矢量控制Matlab仿真实验

目录1 异步电动机矢量控制原理 (2)2 坐标变换 (3)2.1 坐标变换基本思路 (3)2.2 三相——两相坐标系变换(3/2变换) (4)2.3 旋转变换 (5)3 转子磁链计算 (6)4 矢量控制系统设计 (7)4.1 矢量控制系统的电流闭环控制方式思想 (7)4.2 MATLAB系统仿真系统设计 (8)4.3 PI调节器设计 (9)5 仿真结果 (10)5.1 电机定子侧的电流仿真结果 (10)5.2 电机输出转矩仿真结果 (11)心得体会 (13)参考文献 (14)异步电机矢量控制Matlab 仿真实验1 异步电动机矢量控制原理矢量控制系统的基本思路是以产生相同的旋转磁动势为准则,将异步电动机在静止三相坐标系上的定子交流电流通过坐标变换等效成同步旋转坐标系上的直流电流,并分别加以控制,从而实现磁通和转矩的解耦控制,以达到直流电机的控制效果。
所谓矢量控制,就是通过矢量变换和按转子磁链定向,得到等效直流电动机模型,在按转子磁链定向坐标系中,用直流电动机的方法控制电磁转矩与磁链,然后将转子磁链定向坐标系中的控制量经变换得到三相坐标系的对应量,以实施控制。
其中等效的直流电动机模型如图1-1所示,在三相坐标系上的定子交流电流i A 、i B 、i C ,通过3/2变换可以等效成两相静止正交坐标系上的交流i sα和i sβ,再通过与转子磁链同步的旋转变换,可以等效成同步旋转正交坐标系上的直流电流i sm 和i st 。
图1-1 异步电动机矢量变换及等效直流电动机模型在三相坐标系上的定子交流电流,,A B C i i i ,通过3/2变换可以等效成两相静止正交坐标系上的交流s i α和s i β再通过与转子磁链同步的旋转变换,可以等效成同步旋转正交坐标系上的直流电流sm i 和st i 。
m 绕组相当于直流电动机的励磁绕组,sm i 相当于励磁电流,t 绕组相当于电枢绕组,st i 相当于与转矩成正比的电枢电流。
矢量控制变频调速仿真
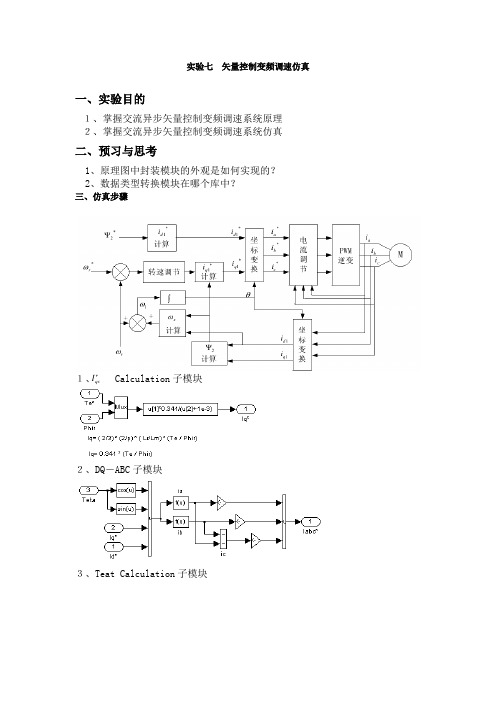
实验七 矢量控制变频调速仿真
一、实验目的
1、掌握交流异步矢量控制变频调速系统原理 2、掌握交流异步矢量控制变频调速系统仿真
二、预习与思考
1、原理图中封装模块的外观是如何实现的?
2、数据类型转换模块在哪个库中?
三、仿真步骤
1、 Calculation 子模块
2、DQ -ABC 子模块
3、Teat Calculation 子模块
*qs
I
4、ABC-DQ子模块
5、 Calculation 子模块
6、Current Regulator 子模块
7、ASR 子模块
异步电机参数:线电压380;额定频率50Hz;;定子内阻0.087Ω;定子漏感0.8mH;转子内阻0.228Ω;转子漏感0.8mH;定、转子漏感34.7;极对数为4。
为逆变器直流电源Vdc 设为780V 。
仿真方法选择为ode23tb 。
仿真时间设为0-3秒。
*ds I
四、仿真原理
五、仿真结果
1、给出转速、电流、转矩的仿真波形
2、给出三相电源和脉冲的波形
(1)定子电流波形
(2)转速波形
(3)转矩波形
(4)三相电源波形
放大之后电压波形
(5)脉冲波形。
异步电动机矢量控制系统的设计与仿真.doc

异步电动机矢量控制系统的设计与仿真.异步电动机矢量控制系统的设计与仿真在矢量控制技术出现之前,现代交流调速系统采用了恒压频比控制策略。
这种控制策略的缺点是,当电机低速旋转或在加减速、负载加减等动态条件下,系统性能显著降低,导致交流调速系统在低速、启动时转矩的动态响应和整个系统的稳定性方面不如DC调速系统,无法满足人们对高精度的要求。
后来,交流异步电动机控制开始从标量控制向矢量控制迈进。
以下是矢量控制理论的简要介绍。
矢量控制发展的基础和核心理论支撑是电机的一些概念,如坐标转换原理、机电能量转换理论等。
这种控制的基本思想和方法是将异步电机模拟成DC电机来控制。
只要建立等效于三相交流绕组组的两相绕组,就可以建立等效于异步电机的DC电机模型,并增加相应的比例积分调节环节,从而可以按照DC 电机的控制策略来控制异步电机。
因此,矢量控制可以实现对电机电磁转矩的动态实时控制,从而优化和提高调速性能。
根据这一思想,我在本项目中成功地进行了MATLAB仿真。
关键词:交流电机;矢量控制调速系统;矢量控制系统的设计与仿真交流调速系统的仿真采用常V/f比控制方法,通常称为标量控制。
采用这种方法的系统在电机低速运行时或在加速、减速、增加负载、减少负载等情况下会出现重大缺陷。
采用矢量控制的交流电机可以达到与恒流电机相同的控制性能,从此交流异步电机控制从标量控制向矢量控制迈进了一大步。
以下是矢量控制理论的简要介绍。
矢量控制发展的基础和核心理论支撑是电机的一些概念,如坐标转换原理、机电能量转换理论等。
这种控制的基本思想和方法是将异步电机模拟成DC电机来控制。
只要建立等效于三相交流绕组组的两相绕组,就可以建立等效于异步电机的DC电机模型,并增加相应的比例积分调节环节,从而可以按照DC电机的控制策略来控制异步电机。
因此,矢量控制可以实现对电机电磁转矩的动态实时控制,从而优化和提高调速性能。
根据这一思想,我在本项目中成功地进行了MATLAB仿真。
异步电动机矢量控制系统的仿真

异步电动机矢量控制系统仿真1.异步电机矢量控制系统的原理及其仿真1.1 异步电动机矢量控制原理异步电机矢量变换控制系统和直接转矩控制系统都是目前已经获得应用的高性能异步电机调速系统,对比直接转矩控制系统,矢量变换系统有可以连续控制,调速范围宽的优点,因此矢量变换控制系统为现代交流调速的重要方向之一。
本文采用的是转子磁场间接定向电流控制型交流异步电机矢量控制系统[1],如图1所示。
图1矢量变换控制系统仿真原理图如果把转子磁链方向按空间旋转坐标系的M轴方向定向,则可得到按转子磁场方式定向下的三相鼠笼式异步电动机的矢量控制方程。
(1)(2)(3)(4)(5)上列各式中,是转子励磁电流参考值;是转差角频率给定值;是定子电流的励磁分量;是定子电流的转矩分量;是定子频率输入角频率;是转子速度;是转子磁场定向角度;是转子时间常数;和分别是电机互感和转子自感。
图4所示控制系统中给定转速与实际电机转速相比较,误差信号送入转速调节器,经转速调节器作用产生给定转矩信号,电机的激磁电流给定信号根据电机实际转速由弱磁控制单元产生,再利用式(1)产生定子电流激磁分量给定信号,定子电流转矩分量给定信号则根据式(2)所示的电机电磁转矩表达式生成。
、和转子时间常数Lr一起产生转差频率信号,与ωr相加生成转子磁场频率给定信号,对积分则得到转子磁场空间角度给定信号。
和经坐标旋转和2/3相变换产生定子三相电流给定信号、和,与定子三相电流实测信号、和相比较,由滞环控制器产生逆变器所需的三相PWM信号。
1.2 异步电机转差型矢量控制系统建模在MATLAB/SIMULINK环境下利用电气系统模块库中的元件搭建交流异步电机转差型矢量控制系统[2],电流控制变频模型如图2所示。
图2 电流控制变频模型图整个仿真图由电气系统模块库中的元件搭建组成,元件的直观连接与实际的主电路相像似,其中主要包括:速度给定环节,PI速度调节器、坐标变换模块、磁场定向模块、滞环电流调节器、IGBT逆变器元件、异步电动机元件以及测量和显示模块。
矢量控制系统仿真课程设计

矢量控制系统的 优点:高精度、 快速响应、宽调 速范围等。
矢量控制系统的 应用领域:电机 驱动、伺服系统、 数控机床等。
磁场定向控制:通过控制电机 的磁场方向,实现转矩和速度 的控制
矢量变换:将三相交流电转换 为直流电,实现电机转矩和速 度的控制
矢量变换控制器:根据电机转 速和电流反馈,计算出电机的
,a click to unlimited possibilities
汇报人:
01
02
03
04
05
06
矢量控制系统的 定义:通过控制 电机定子电流的 幅值和相位,实 现对电机转矩和 转速的精确控制 的一种控制系统。
矢量控制系统的基 本原理:基于磁场 定向控制,通过坐 标变换将三相电流 转换为两相电流, 实现对电机转矩和 转速的解耦控制。
控制量
逆变器:将直流电转换为三 相交流电,驱动电机运行
矢量控制系统的定义和作用 矢量控制系统的基本组成和工作原理 矢量控制系统的特点和应用领域 矢量控制系统的发展趋势和未来展望
提高系统性能和稳定性 降低研发成本和缩短开发周期 优化系统参数和提高控制精度 预测和解决潜在问题
矢量控制系统仿真的概念和原理介 绍
实验结果:通过仿真实验,验证了无刷直流电机矢量控制系统的可行性和有效性,为实际应用提供了理论依据和实践经验。
实践案例介绍:异步 电机矢量控制系统仿 真的原理、实现方法 和应用场景
案例实践过程:详细介 绍异步电机矢量控制系 统仿真的实验步骤、操 作流程和注意事项
案例实践结果:展示异 步电机矢量控制系统仿 真的实验结果,包括性 能指标、控制效果和优 化方案等
确定仿真目标:明确仿真目的 和期望结果
分析需求:对控制系统进行详 细分析,确定所需数据和参数
无速度传感器感应电机矢量控制仿真.

拖动系统课程设计报告书题目:无速度传感器感应电机矢量控制系统设计与仿真专业:姓名:学号:指导教师:课程设计任务书矢量变换控制(Transvector Control),也称磁场定向控制。
它是由德国学者F.Blaschke等人在1971年提出的一种新的优越的感应电机控制方式,是基于dq轴理论而产生的,它的基本思路是把电机的电流分解为d轴电流和q轴电流,其中d轴电流是励磁电流,q轴电流是力矩电流,这样就可以把交流电机的励磁电流和力矩电流分开控制,使得交流电机具有和直流电机相似的控制特性,是为交流电机设计的一种理想的控制理论,大大提高了交流电机的控制特性。
一般将含有矢量变换的交流电动机控制都称为矢量控制,实际上只有建立在等效直流电动机模型上并按转子磁场准确定向的控制,电动机才能获得最优的动态性能。
本文介绍了矢量控制系统的原理及模型的建立,搭建了带转矩内环的转速、磁链闭环矢量控制无速度传感器调速系统的Simulink模型,并用MATLAB最终得到了仿真结果。
关键词:感应电机; 矢量控制; 磁链观测; 速度估算摘要 (iv)目录 (v)1 异步电机及Simulink模型 (1)1.1 异步电动机的稳态等效电路 (1)1.1.1 等效电路中各参数物理意义 (1)1.1.2 感应电机功率流程 (1)1.2 Simulink仿真基础 (2)1.2.1 异步电动机Simulink模型 (2)1.2.2 异步电动机模型参数设置 (3)1.3 电机测试信号分配器模块及参数设置 (4)2 矢量控制 (5)2.1 矢量控制的基本思路 (5)2.2 矢量坐标变换原理 (7)α-坐标系间的变换) (7)2.2.1 定子绕组轴系的相变换(A-B-C和β2.2.2 转子绕组轴系的变换(A-B-C和d-q坐标系间的变换) (8)3 电流正弦PWM技术 (8)4 转子磁链模型的建立 (9)4.1 基于电压电流模型设计转子磁链观测器 (9)4.2 基于转差频率设计的转子磁链观测器 (10)5 转矩计算模块 (11)6 转速推算器的设计 (11)6.1 基于转矩电流误差推算速度的方法 (11)6.2 基于模型参考自适应方法(MARS)的速度估算 (12)ϕ的速度估算方法 (13)6.3 基于空间位置角s7 感应电机矢量控制系统的Simulink仿真 (13)8 结论 (19)参考文献 (19)αβ的感应电机数学模型 (20)附录1 基于0附录2 基于dq0的感应电机数学模型 (21)附录3 基于dq0的转子磁链定向感应电机数学模型 (22)1 异步电机及Simulink 模型 感应电动机是借定子旋转磁场在转子导体中感应电流,从而产生电磁转矩的一种电机。
基于交流电动机的动态模型的间接矢量控制仿真与设计

电力拖动自动控制系统课程设计学院:信息与电气工程学院班级:电气三班学号:姓名:基于交流电动机的动态模型的间接矢量控制仿真与设计一设计目的:应用所学的交、直流调速系统的基本知识与工程设计方法,结合生产实际,确定系统的性能指标与实现方案,进行运动控制系统的初步设计。
应用计算机仿真技术,通过在MATLAB软件上建立运动控制系统的数学模型,对控制系统进行性能仿真研究,掌握系统参数对系统性能的影响。
在原理设计与仿真研究的基础上,应用PROTEL进行控制系统的印制板的设计,为毕业设计的综合运用奠定坚实的基础二设计参数:额定输出功率17KW;定子绕组额定线电压380V;定子绕组额定相电流25A;定子绕组每相电阻0.1欧姆;定子绕组接线形式Y;转子额定转速1430rpm;转子形式:鼠笼式;转子每相折算电阻:1欧姆;转子折算后额定电流50A;额定功率因数:0.75;电机机电时间常数1S;电枢允许过载系数1.5;环境条件:电网额定电压:380/220V; 电网电压波动10%;环境温度:-40~+40摄氏度; 环境相对湿度:10~90%.控制系统性能指标:转差率:3%;调速范围:D=20;电流超调量小于等于5%;空载起动到额定转速时的转速超调量小于等于30%;稳速精度:0.03.三动态模型:(1) 电压方程:ϕP Ri u += (2) 磁链方程:Li =ϕ,i d dLd d L Ri u tiωθ++= (3) 运动方程:tp Ld d n J ω+T=T(4) 转矩方程:i L i n T p θ∂∂=T 21四坐标变换为简化和求解三相异步电机的数学方程,须按图1对电机坐标系的基本方程进行坐标变换,实现电机模型的解耦。
1坐标变换模块图:2W1生成模块:3PI模块变换:4Um,UM 生成模块:图1 永磁容错电机常用坐标系根据坐标变换理论,可得三相静止到两相静止坐标系变换矩阵为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---=2323021211322/3ss C (3-1) 两相静止到两相旋转坐标系变换矩阵:⎥⎦⎤⎢⎣⎡-=θθθθcos sin sin cos C 2/s 2r (3-2) 转子初始磁链在各坐标系分量为:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡023f q d ψψψ (3-3) 可得电机在两相旋转坐标系下的电压方程、磁链方程、转矩方程如下:⎪⎩⎪⎨⎧++=-+=d s q q q qs d d d p Ri U p Ri U ψωψψωψ (3-4) ⎪⎩⎪⎨⎧=+=q q qfd d d iL i L ψψψ23 (3-5) )(d q q d p e i i n T ψψ-= (3-6)五按转子磁链定向实现异步电机矢量控制按转子磁链定向的坐标系称为MT 坐标系,M 轴与转子磁链方向一致。
基于交流电动机动态模型的直接矢量控制系统的仿真与设计

基于交流电动机动态模型的直接矢量控制系统的仿真与设计姓名:班级:电气三班学号:专业:电气工程及其自动化1.引言异步电机的动态数学模型是一个高阶、非线性、强耦合的多变量系统,通过坐标变换,可以使之降阶并化简,但并没有改变其非线性、多变量的本质。
需要高动态性能的异步电机调速系统必须在其动态模型的基础上进行分析和设计,但要完成这一任务并非易事。
经过人们的多年的潜心研究和实践,有几种控制方案已经获得了成功的应用,目前应用最广的就是矢量控制系统。
直接矢量控制就是一种优越的交流电机控制方式,它模拟直流电机的控制方式使得交流电机也能取得与直流电机相媲美的控制效果。
本文研究了交流电动机动态模型的直接矢量控制系统的设计方法。
并用MATLAB 最终得到出仿真结果。
2. 矢量控制系统结构异步电动机经过坐标变换可以等效成直流电动机,那么,模仿直流电动机的控制策略,得到直流电动机的控制量,再经过相应的坐标反变换,就能够控制异步电动机了。
由于进行坐标变换的是电流(代表磁动势)的空间矢量,所以这样通过坐标变换实现的控制系统就称为矢量控制系统(VectorControlSystem),简称VC 系统。
VC 系统的原理结构如图1所示。
图中的给定和反馈信号经过类似于直流调速系统所用的控制器,产生励磁电流的给定信号*m i 和电枢电流的给定信号*t i ,经过反旋转变换1-VR 一得到*αi 和*βi ,再经过2/3变换得到*A i 、*B i 和*C i 。
把这三个电流控制信号和由控制器得到的频率信号1ω加到电流控制的变频器上,所输出的是异步电动机调速所需的三相变频电流。
图1 矢量控制系统原理结构图在设计VC 系统时,如果忽略变频器可能产生的滞后,并认为在控制器后面的反旋转变换器1-VR 与电机内部的旋转变换环节VR 相抵消,2/3变换器与电机内部的3/2变换环节相抵消,则图1中虚线框内的部分可以删去,剩下的就是直流调速系统了。
可以想象,这样的矢量控制交流变压变频调速系统在静、动态性能上完全能够与直流调速系统相媲美。
实验五 矢量控制系统仿真

矢量控制系统仿真
按矢量控制系统结构建立仿真模型,见图1。
其中,异步电动机仿真模型见异步电动机仿真,SVPWM用惯性环节等效代替,若采用实际的SVPWM方法仿真,会产生电流脉动。
转速、转子磁链和两个电流调节器均采用带有积分和输出限幅的PI调节器,两相磁链
rα
ψ和rβ
ψ由电动机模型直接得到,通过直角坐标到极坐标变换(K/P变换)得到转子磁链的幅值和角度,
r
r
jarctg
j
r r r r
j e
β
α
ψ
ψϕ
αβ
ψψψ
=+==
ψ
图2为空载起动和t=3s突加额定负载的定子电流励磁分量
sm
i(上)和转矩分量
st
i(下)仿真结果,图3a是对应的转速ω(上)与转子磁链r
ψ(下)仿真结果,图3b为转速ω
(上)
图1 矢量控制系统仿真模型
与转子磁链r (下)局部放大图。
图2 空载起动和加载的定子电流励磁分量sm i (上)和转矩分量st i (下)仿真结果
ψ(下)仿真结果图3a 空载起动和加载过程ω(上)和r
图3b ω(上)和ψ(下)局部放大。
异步电动机矢量控制系统仿真模型设计本科本科毕业论文

异步电动机矢量控制系统的仿真模型设计中文摘要:矢量控制是在电机统一理论、机电能量转换和坐标变换理论的基础上发展起来的,它的思想就是将异步电动机模拟成直流电动机来控制,通过坐标变换,将定子电流矢量分解为按转子磁场定向的两个直流分量并分别加以控制,从而实现磁通和转矩的解耦控制,达到直流电机的控制效果。
本文针对异步电动机磁链闭环矢量控制进行研究和探索。
通过空间矢量的坐标变换,对系统进行建模,其中包括直流电源、逆变器、电动机、转子磁链电流模型、ASR、ATR、AΨR 等模块。
并对控制系统进行了MATLAB/Simulink仿真分析。
关键词:异步电动机、矢量控制、MATLAB仿真Abstract:Vector control(VC) is based on motor unification principle,energy conversion and vector coordinate transformation theory.By transforming coordinate, The stator current is decomposing two DC parts which orientated as the rotator magnetic field and controlled respectively.So magnetic flux and torque are decoupled. It controls the asynchronous motor as a synchronous way. This paper does some research works of the asynchronous motor flux vector control closed-loop research and exploration. Through the space vector coordinate transformation, and the modeling of system,including DC power supply, inverter, AC motor, rotor flux current model, the ASR, ATR,AΨR and modules. And the control system is MATLAB/Simulink analysis.Key Words:Asynchronous Motor,Vector Control,MATLAB Simulation一、绪论1、交直流调速系统的相关概念及比较交流调速系统是以交流电动机作为控制对象的电力传动自动控制系统。
无速度传感器的矢量控制系统仿真

课程设计任务书学生姓名:专业班级:指导教师:工作单位:武汉理工大学题目: 无速度传感器的矢量控制系统仿真初始条件:电机参数为:额定电压U=380V、频率50=、定子电阻s R=0.252Ω、f Hz额定功率P=2.2KW、定子自感L=0.0016H、转子电阻r R=0.332Ω、额定转速sn=1420rpm、转子自感r L=0.0016H、级对数p n=2、互感m L=0.08H、转动惯量J=0.6Kgm2要求完成的主要任务:(1)设计系统原理图;(2)用MATLAB设计系统仿真模型;(3)能够正常运行得到仿真结果,包括转速、转矩等曲线,并将推算转速与实际转速进行比较参考文献:[1] 洪乃刚.《电力电子和电力拖动控制系统的MATLAB仿真》.北京:机械工业出版社,2005:212-215时间安排:2011年12月5日至2011年12月14日,历时一周半,具体进度安排见下表指导教师签名:年月日系主任(或责任教师)签名:年月日摘要异步电动机具有非线性、强耦合、多变量的性质,要获得高动态调速性能,必须从动态模型出发,分析异步电动机的转矩和磁链控制规律,研究高性能异步电机的调速方案。
矢量控制是目前交流电动机较先进的一种动态模型,它又有基于转差频率控制的、无速度传感器和有速度传感器等多种矢量控制方式。
无速度传感器控制的高性能通用变频器是当前全世界自动化技术和节能应用中受到普遍关心的产品和开发课题。
本文介绍无速度传感器的矢量控制系统的原理和Matlab仿真。
关键词:矢量控制、无速度传感器、Matlab目录1矢量控制概述 (1)2无速度传感器矢量控制系统 (1)3无速度传感器矢量控制方法 (2)4无速度传感器矢量控制系统SIMULINK分析 (3)5仿真结果分析 (8)6学习心得 (9)7参考文献 (1)无速度传感器的矢量控制系统仿真1矢量控制概述空间矢量法是一种应用于交流电机变频调速领域的最重要的闭环控制技术之一,并且常用于交流电机动态建模。
电拖课程课设——异步电动机矢量控制系统建模与仿真

电拖课程课设——异步电动机矢量控制系统建模与仿真(总16页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--目录1 异步电动机矢量控制原理............................ 错误!未定义书签。
2 异步电机的坐标变换................................ 错误!未定义书签。
三相-两相变换.................................. 错误!未定义书签。
静止两相-旋转正交变换.......................... 错误!未定义书签。
3 异步电动机按转子磁链定向的矢量控制系统............ 错误!未定义书签。
按转子磁链定向矢量控制的基本思想............... 错误!未定义书签。
以?-is-?r 为状态变量在mt坐标系中的状态方程.... 错误!未定义书签。
以?-is-?r 为状态变量的mt坐标系上的异步电动机动态结构图错误!未定义书签。
转速闭环后的矢量控制原理框图................... 错误!未定义书签。
转速闭环后的矢量控制系统结构图................. 错误!未定义书签。
4 异步电动机矢量控制系统仿真........................ 错误!未定义书签。
仿真模型的参数计算............................. 错误!未定义书签。
矢量控制系统的仿真模型......................... 错误!未定义书签。
PI调节器设计.................................. 错误!未定义书签。
仿真结果分析................................... 错误!未定义书签。
mt坐标系中的电流曲线...................... 错误!未定义书签。
三相异步电机矢量控制matlab仿真

目录1 设计任务及要求....................................................................................................... 错误!未定义书签。
2 异步电动机数学模型基本原理 ................................................................................ 错误!未定义书签。
异步电机的三相动态数学模型 ............................................................................... 错误!未定义书签。
异步电机的坐标变换 ............................................................................................... 错误!未定义书签。
三相-两相变换...................................................................................................... 错误!未定义书签。
静止两相-旋转正交变换.............................................................................................. 错误!未定义书签。
3 异步电动机按转子磁链定向的矢量控制系统 ....................................................... 错误!未定义书签。
按转子磁链定向矢量控制的基本思想 .................................................................. 错误!未定义书签。
交流电机矢量控制系统仿真设计

调节器输出限幅 上限 下限 75 -75 60 -60 13 -13
ቤተ መጻሕፍቲ ባይዱ流电机矢量控制系统仿真设计
比较方案: 带转矩内环的转速、磁链闭环矢量控制系统
仿真结果如下
三相电流波形
定子磁链轨迹
转子角计算得到的转差频率给定
三相电流波形按比例放大
交流电机矢量控制系统仿真设计
比较方案: 带转矩内环的转速、磁链闭环矢量控制系统
转速响应
经2r/3s变换的三相给定波形
电动机输出转矩
A相电流波形
交流电机矢量控制系统仿真设计
周思纬
明德笃行,自强日新 再见了,敬爱的重庆理工大学
交流电机矢量控制系统仿真设计
方案一:按转差频率控制的异步电动机矢量控制系统的仿真建模
转速调节模块
其中给定环节有定子电流励磁分量im*和转子速度n*。放大器G1、G2和积分 器组成了带限幅的转速调节器 ASR。根据角频率,经过转速调节器得到转矩 * im 电流的给定值
函数运算模块
它是根据定子电流的励磁分量,通过函数f(u)计算得到转差,后经过 和转子频率相加得到定子频率,根据定子频率和矢量转角的关系,对 进行 1 积分,最终得到定子电压矢量转角 。
交流电机矢量控制系统仿真设计
方案一:按转差频率控制的异步电动机矢量控制系统的仿真建模
初稿更改图像如下图:
交流电机矢量控制系统仿真设计
方案一:按转差频率控制的异步电动机矢量控制系统的仿真建模
函数运算器上的示波器组件也现实理想波形:
交流电机矢量控制系统仿真设计
比较方案: 带转矩内环的转速、磁链闭环矢量控制系统 主电路:
交流电机矢量控制系统仿真设计
方案一:按转差频率控制的异步电动机矢量控制系统的仿真建模
毕业论文2矢量控制的异步电动机调速系统仿真设计
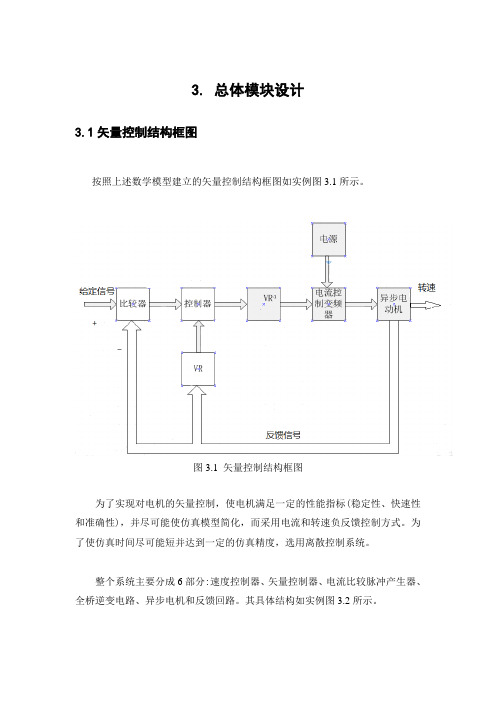
3. 总体模块设计3.1矢量控制结构框图按照上述数学模型建立的矢量控制结构框图如实例图3.1所示。
图3.1矢量控制结构框图为了实现对电机的矢量控制,使电机满足一定的性能指标(稳定性、快速性和准确性),并尽可能使仿真模型简化,而采用电流和转速负反馈控制方式。
为了使仿真时间尽可能短并达到一定的仿真精度,选用离散控制系统。
整个系统主要分成6部分:速度控制器、矢量控制器、电流比较脉冲产生器、全桥逆变电路、异步电机和反馈回路。
其具体结构如实例图3.2所示。
图3.2矢量控制系统结构框图3.2各子系统模块3.2.1求解磁链模块图3.3求解磁链模块3.2.2 求解转子磁链角模块图3.4求解转子磁链角模块该模块是计算θ角,也就是d轴的位置3.2.3 ids*求解模块此模型的作用是根据转子磁通来计算定子电流的励磁分量i d*,模型如下所示图3.5 i ds*求解模块3.2.4 iqs*求解模块此模块的作用是计算定子电流在d、q坐标系下的q分量的给定值i qs*,其内部构造如下所示:图3.6 i qs*求解模块3.2.5 ABC到DQ坐标变换模块ABC-DQ子模块完成从ABC三相定子坐标系到d、q坐标系的变换(3/2变换),在这个模块中,根据定子电流在ABC三相定子坐标系下的分量,经过旋转变换,得出电动机定子电流在d、q坐标系下的转矩分量i qs和励磁分量i ds。
模块的构造如下图:图3.7 ABC到DQ模块3.2.6 DQ到ABC坐标变换模块DQ- ABC子模块是根据定子电流在d、q坐标系下的分量,经过旋转变换得出电动机定子的三相绕组电流的给定值i abc,变换过程如下所示图3.8 DQ到ABC模块3.3 电机参数设置图3.9 异步电动机参数表3.4矢量控制环节模块图3.10 矢量控制环节3.5矢量控制的异步电动机调速系统模块图3.11 矢量控制的异步电动机调速模块交流异步电动机矢量控制系统如上图所示,此系统为转差频率矢量控制方式,按转子磁场定向的异步电机矢量控制框图。
感应电机矢量控制系统的仿真

《运动控制系统》课程设计学院:班级:姓名:学号:日期:成绩:感应电机矢量控制系统的仿真摘要:本文先分析了异步电机的数学模型和坐标变换以及矢量控制基本原理,然后利用Matlab /Simulink软件进行感应电机的矢量控制系统的仿真。
采用模块化的思想分别建立了交流异步电机模块、逆变器模块、矢量控制器模块、坐标变换模块、磁链观测器模块、速度调节模块、电流滞环PWM调节器,再进行功能模块的有机整合,构成了按转子磁场定向的异步电机矢量控制系统仿真模型。
仿真结果表明了该系统转速动态响应快、稳态静差小、抗负载扰动能力强,验证了交流电机矢量控制的可行性和有效性。
关键词:异步电机;坐标变换;矢量控制;Simulink仿真一、异步电机的动态数学模型和坐标变换异步电机的动态数学模型是一个高阶、非线性、强耦合的多变量系统,异步电机的数学模型由下述电压方程、磁链方程、转矩方程和运动方程组成。
电压方程:礠链方程:转矩方程:运动方程:异步电机的数学模型比较复杂,坐标变换的目的就是要简化数学模型。
异步电机数学模型是建立在三相静止的ABC坐标系上的,如果把它变换到两相坐标系上,由于两相坐标轴互相垂直,两相绕组之间没有磁的耦合,仅此一点,就会使数学模型简单了许多。
(1)三相--两相变换(3/2变换)在三相静止绕组A、B、C和两相静止绕组α、β之间的变换,或称三相静止坐标系和两相静止坐标系间的变换,简称3/2 变换。
(2)两相—两相旋转变换(2s/2r变换)从两相静止坐标系到两相旋转坐标系M、T 变换称作两相—两相旋转变换,简称2s/2r 变换,其中s 表示静止,r 表示旋转。
图1、异步电动机的坐标变换结构图二、感应电机矢量控制原理感应电机是指定转子之间靠电磁感应作用,在转子内感应电流以实现机电能量转换的电机。
感应电机是异步电机的一种,异步电机主要是指感应电机。
以上所讲,异步电机的动态数学模型是一个高阶、非线性、强耦合的多变量系统,通过坐标变换,可以使之降阶并化简,但并没有改变其非线性、多变量的本质。
永磁同步电机双闭环矢量控制系统仿真实验指导书

题目1永磁同步电机双闭环矢量控制系统仿真实验目的1. 加深理解永磁同步电机矢量控制系统的工作原理2. 掌握永磁同步电机驱动系统仿真分析方法1. 永磁同步电机双闭环控制系统建模2. 电流控制器设计3. 电流环动态跟随性能仿真实验4. 转速控制器设计5. 转速环抗负载扰动性能仿真实验6. 给出仿真实验结果与理论分析结果的对比及结论三.预习内容注:以下所有找不到的器件均可以通过搜索框搜索Simulink 的启动 在 MATLAB^键入 >>Simulink ,进入 Simulink library , 2014版本的可直接点击MATLAB^面上的Simulink library ,在Simulink 界面 上选择File->New->Model 。
如图1所示:图1 Simuli nk 界面在Simulink —级标题下点击source 将step (阶跃函数)拖入空白文件作为实验要求:一二|一=二二fa-frw|wir-I4MVUMWil^nl转速给定,也可用两个ramp 函数相减,使转速缓慢达到预定转速,如图 2:图2转速给定在Simulink —级标题下点击 Ports & Subsystems 选择Subsystem 放入空 白文件并双击,删除In1和Out1的连线,如图3:图3子函数模块选择 Simulink>Continuous 下的 integrator 、Simulink>discontinuous 下 的 Saturation 、Simulink>math operation 下的 gain 和 Add,连好线后保存并 返回,作为PI 调节器,其中saturation 可设置上下限为100和-100,如图4:EOE1㈢』SRfflECvmvpl> DtocvK 白■tihing ZjBnzFirbJRM □UoTtrt«|iE «I4 *1Q WBMAO Lwtttfi Tjt.«i^rT^ihcp击<4 世更jHirz 詡n*胛―5dnu ^QIFEVt -^ti -Zcrh±d F jTKlicjniBkK>»4C^n-ndrii :.4liE<kk-却 wjn 1 Contwlir Vna^ 3戸tsnr CortnJ &ysJer "ibbhm Wljrfh?rfiTMiKa ;K N II I 士Mrt 11UHLrteddbl Z Edfer VlhECV L 榔 Tge乜虹Hl Bcckl^l PDLCrtVEZ3Enizi ■tuiMrtrtefT!>ooSTm-i一二upFr/fi -derailbCcriQ^tJeT Jfl - 'X J ^^jk>-3iii —印心皿One»3to*MWHIfNFAB4BS^WfW图4 PI 子函数模块设置此PI 调节器输出结果作为lq 的电流给定,同样方法得到一个 PI 调节器, 输出结果作为电压给定,并设置 saturation 上下限为380和-380, Simulink 下 math operation 选择sum 双击并修改第二个“ +”为“-”,如图5:图5转速和电流反馈PI 调节选择Simulink>Ports & Subsystems 下的Subsystem 拖入并双击进入子系 统,并添加2个In1和1个Out1如图6:图6接口模块Simulink>math operation 下选择 Trigonometric Function 、Product 、Subtract 、Add 加入文件,设置好后保存并退出,作为逆 Park 变换,如图7:st&pl. ---------------- ------------------ Im* CJutl ■ -------- —Ini Outl pPIPillr Lith>-flry BrO-^S-e*1 列«.—■ 二 i和応 Edm W l^lp忸口■ CH T *・M 亠LMIWC1k'toW^ ^nidFlnlu*drb A SdEn-^alcrTa-H H M . J F » lilGF } r ■«!P弭―iLCcrrarKir V Ll.«d SteEica £40141*1 Uh I DfSt^rrimbLDQk : dr - El£ JpM-dbMliS- L&fl TkAHH' ■It' Opiaanibar s IM (M >E 磺Mictun LW 匪」■兀济常!IBBff m WflW -------------Si[|ru AIZ.-|Qu££-l HDW N&uipg 5ankH SKMJrr-.es&忙iVil Fu'^fiiW 4 Zd*n. 朗・h ■□■rzr -vta0i4eM4*iCamr —u ncabc: na. Spvfji m "Ik f&ffvUh ■- V'MvH- ^yKtairi CflsfWW &W*H1 T M I WK &&P台戸TboSwK P-plB E-rnh*didKd C«larLs^lcOdufe4 Bio<:l-tM H0L CKteT "OL iris** AcQMiLiUDni T IHMDCFJI . Hi-lfirfm«Ht C-Mtra TtMtENK il (!d«l R^CHI "DntTii E 昭hM^Ek : O0C TitBtoQHW::“-Tfr£ 询山|3口占・口『口 寸• iDFloS^»VI 4HEu u jullu-»>Caii3^M¥«WH■YiiwnSillily* j*iT1OL :1Ei£flM 33- Z-JIH! A&- I HJ *恥enm 忻图7反Park变换再生成一个PI调节器,作为d轴电流调节器,Simulink>source中选择constant 并设置为0,如图8:图8静止坐标系电压生svpwm模块建立过程过于复杂,可参考文献[1][2],只列出总体框图如图9和图10,其中Ts为开关周期,Udc为直流母线电压。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
矢量控制系统仿真课程设计初始条件:根据转差频率矢量控制系统原理图设计对应的simulink 仿真模型,电机参数为:额定功率power=2.2KW,线电压L U =,额定频率50f Hz =;定子电阻0.435s R =Ω,漏感0.002ls H L =;转子电阻,0.816r R =Ω,漏感,0.002lr H L =;互感0.069m H L =,转动惯量0.089.^2J kg m =,极对数2P =,其余参数为0。
要求完成的主要任务:(1)用MATLAB 建立矢量控制系统仿真模型;(2)根据仿真结果分析起动时定子电流励磁分量和转矩分量; (3)根据仿真结果分析起动时转速与转子磁链。
摘 要因为异步电动机的物理模型是一个高阶、非线性、强耦合的多变量系统,需要用一组非线性方程组来描述,所以控制起来极为不便。
异步电机的物理模型之所以复杂,关键在于各个磁通间的耦合。
如果把异步电动机模型解耦成有磁链和转速分别控制的简单模型,就可以模拟直流电动机的控制模型来控制交流电动机。
直接矢量控制就是一种优越的交流电机控制方式,它模拟直流电机的控制方式使得交流电机也能取得与直流电机相媲美的控制效果。
本文研究了矢量控制系统中磁链调节器的设计方法。
并用MATLAB 最终得到了仿真结果。
关键词:矢量控制 非线性 MATLAB 仿真矢量控制系统仿真1设计条件及任务1.1设计条件根据转差频率矢量控制系统原理图设计对应的simulink 仿真模型,电机参数为:额定功率power=2.2KW,线电压2203L V U =,额定频率50f Hz =;定子电阻0.435s R =Ω,漏感0.002ls H L =;转子电阻,0.816r R =Ω,漏感,0.002lr H L =;互感0.069m H L =,转动惯量0.089.^2J kg m =,极对数2P =,其余参数为0。
1.2设计任务(1)用MATLAB 建立矢量控制系统仿真模型;(2)根据仿真结果分析起动时定子电流励磁分量和转矩分量; (3)根据仿真结果分析起动时转速与转子磁链。
2 异步电动机矢量控制原理及基本方程式2.1矢量控制基本原理矢量控制系统的基本思路是以产生相同的旋转磁动势为准则,将异步电动机在静止三相坐标系上的定子交流电流通过坐标变换等效成同步旋转坐标系上的直流电流,并分别加以控制,从而实现磁通和转矩的解耦控制,以达到直流电机的控制效果。
所谓矢量控制,就是通过矢量变换和按转子磁链定向,得到等效直流电动机模型,在按转子磁链定向坐标系中,用直流电动机的方法控制电磁转矩与磁链,然后将转子磁链定向坐标系中的控制量经变换得到三相坐标系的对应量,以实施控制。
其中等效的直流电动机模型如图2-1所示,在三相坐标系上的定子交流电流,,A B C i i i ,通过3/2变换可以等效成两相静止正交坐标系上的交流s i α和s i β再通过与转子磁链同步的旋转变换,可以等效成同步旋转正交坐标系上的直流电流sm i 和st i 。
m 绕组相当于直流电动机的励磁绕组,sm i 相当于励磁电流,t 绕组相当于电枢绕组,st i 相当于与转矩成正比的电枢电流。
其中矢量控制系统原理结构图如图2-2所示。
图2-1 异步电动机矢量变换及等效直流电动机模型图2-2矢量控制系统原理结构图通过转子磁链定向,将定子电流分量分解为励磁分量sm i 和转矩分量st i ,转子磁链r ψ仅由定子电流分量sm i 产生,而电磁转矩e T 正比与转子磁链和定子电流转矩分量的乘积,实现了定子电流的两个分量的解耦。
简化后的等效直流调速系统如图2-3所示。
图2-3简化后的等效直流调速系统2.2按转子磁链定向的基本方程异步电动机在两相同步旋转坐标系上的数学模型包括电压方程、磁链方程和电磁转矩方程。
分别如下:⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+-+-+--+=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡rq rd sq sd r r r s m m s r s r r m m m m s s s m m ss s rq rd sq sd i i i i P L R L P L L L P L R L P L P L L P L R L L P L L P L R u u u u ωωωωωωωω11111 (2-1)⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡rq rd sq sd r mr m m s m s rq rd sq sd i i i i L L L L L L L L 00000000ψψψψ (2-2))(rq sd rd sq m p e i i i i L n T -= (2-3)当两相同步旋转坐标系按转子磁链定向时,应有rd rm r ψψψ== (2-4) 0rq rt ψψ== (2-5)得到dq 坐标系的状态方程2221222121p mp sq r L r m r r sd r sd m s r r m sd r sd sq s r r s rs sq sq m s r r mr sq sd s r s r s n L n dw i T dt JL JL d i dt T T di L R L R L u i w i dt L L T L L L di u L R L R L w i w i dt L L L L L ψψψψσσσψσσσ⎫=-⎪⎪⎪=-+⎪⎪⎬+⎪=-++⎪⎪+⎪=---+⎪⎭(2-6)得到旋转角速度:1msq r rL i T ωωψ=+ (2-7) 得到电磁转矩表达式:r st rmpe i L L n T ψ= (2-8) 得到转子磁链表达式:sm r mr i PT L +=1ψ (2-9)式中: 1ω为同步转速;ω为转子转速; u 为电压;ψ为磁链;i 为电流;R 电阻;L 为电感;p n 为极对数;r T 为转子时间常数且rr rL T R =;σ为电动机漏磁系数且21m s r L L L σ=-;rd P dtψ=为微分因子。
s 表示定子;r 表示转子;d 表示d 轴;q 表示q 轴;m 表示同轴定、转子间的互感。
3 坐标变换3.1坐标变换原理由于异步电动机三相原始动态数学模型相当复杂,分析和求解这组非线性方程十分困难。
在实际应用中必须予以简化,由于直流电动机的主磁通基本上由励磁绕组的励磁电流决定,这是直流电动机的数学模型及其控制系统比较简单的根本原因。
如果能将交流电动机的物理模型等效地变换成类似直流电动机的模式,分析和控制就可以大大简化。
所以,三相绕组可以用相互独立的两相正交对称绕组等效代替,等效的原则是产生的磁动势相等。
其中图3-1和图3-2 分别为三相坐标系和两相坐标系物理模型和静止两相正交坐标系和旋转正交坐标系的物理模型。
图3-1 三相坐标系和两相坐标系物理模型图3-2 静止两相正交坐标系和旋转正交坐标系的物理模型三相绕组A 、B 、C 和两相绕组之间的变换,称作三相坐标系和两相正交坐标系间的变换,简称3/2变换。
图3-3中绘出ABC 和两个坐标系中的磁动势矢量,将两个坐标系原点重合,并使A 轴和α轴重合。
设三相绕组每相有效匝数为3N ,两相绕组每相有效匝数为2N 按磁动势相等的原则,三相合成磁动势与两相合成磁动势相等,故两套绕组在α,β轴上的投影都应相等。
图3-3 三相坐标系和两相正交坐标系中的磁动势矢量因此,2333311cos cos()3322A B C A B C N i N i N i N i N i i i αππ=--=-- (3-1) 23333sinsin()332B C B C N i N i N i N i i βππ=-=- (3-2) 写成矩阵形式,得3211122330A B C i i N i i N i αβ⎡⎤⎡⎤--⎢⎥⎡⎤⎢⎥⎢=⎢⎥⎢⎥⎢⎣⎦⎢⎥⎣⎦⎢⎣ (3-3) 根据变换前后总功率不变,得3223N N =0A B C i i i ++=,最终得到坐标变换式为 30222A B i i i i αβ⎡⎤⎢⎥⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎣⎦⎢⎣(3-4) 相应的逆变换为20362A B ii i i αβ⎡⎤⎢⎥⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎣⎦⎣⎦⎢⎣(3-5) 从静止两相正交坐标系αβ到旋转正交坐标系dq 的变换,称作静止两相-旋转正交变换,简称2s/2r 变换,其中s 表示静止,r 表示旋转,变换的原则同样是产生的磁动势相等。
其静止两相正交坐标系和旋转正交坐标系中的磁动势矢量图如图3-4所示。
图3-4 静止两相正交坐标系和旋转正交坐标系中的磁动势矢量旋转正交变换为2/2cos sin sin cos d s r q i i i C i i i ααββφφφφ⎡⎤⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦⎣⎦ (3-6)静止两相正交坐标系到旋转正交坐标系的变换阵为2/2cos sin sin cos s r C ϕϕϕϕ⎡⎤=⎢⎥-⎣⎦ (3-7) 对(3-6)式进行逆变换可以得到两相静止到两相旋转的变换矩阵为:⎥⎦⎤⎢⎣⎡-==-ϕϕϕϕcos sin sin cos 12222sr rsC C (3-8) 电压和磁链的旋转变换阵与电流旋转变换阵相同。
3.2建立坐标变换模型3.2.1 2r/3s 变换模型根据式子(3-3)和(3-8)可以建立3s/2r 的电路模型结构图如图3-5所示。
图3-5 dqo_to_abc 模块2r/3s 变换为()()()()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++--=13/2cos 3/2sin 13/2cos 3/2sin 1cos sin 32pi pi pi pi C srϕϕϕϕϕϕ (3-9) 3.2.2 3s/2r 变换模型如图3-6为3s/2r 变换模型电路图。
图3-6 abc_to_dq03s/2r 变换为()()()()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+-+-=3/13/13/13/2cos 3/23/2cos 3/2cos 3/23/2sin 3/23/2sin 3/2sin 3/232pi pi pi pi C srϕϕϕϕϕϕ (3-10)4 矢量控制系统设计4.1 矢量控制系统的电流闭环控制方式思想图4-1为电流闭环控制后的系统结构图,转子磁链环节为稳定的惯性环节,对转子可以采用闭环控制,也可以采用开环控制方式;而转速通道存在积分环节,为不稳定结构,必须加转速外环。
常用的电流闭环控制有两种方法:一个是将定子电流两个分量的给定置*smi 和*st i 施行2/3变换,得到三相电流给定值,再经过PWM 控制逆变器输出三相电压,采用电流滞环控制型PWM 变频器,在三相定子坐标系中完成电流闭环控制,如图4-2。
