初三几何探究题
最新九年级数学中考复习:几何探究题--线段问题含答案

(1)猜想线段AE和BG的关系,请直接写出你的结论;
(2)将正方形DEFG绕点D顺时针方向旋转一定角度后(旋转角大于0°,小于或等于360°),如图2,判断(1)中的结论是否仍然成立?如果成立,请予以证明;如果不成立,请说明理由.
问题探究:
(1)如图1,若 、 都是直角,把 绕点A逆时针旋转90°至 ,使AB与AD重合,则 ______度,线段BE、DF和EF之间的数量关系为______;
问题再探:
(2)如图2,若 、 都不是直角,但满足 ,线段BE、DF和EF之间的数量关系是否仍然成立,若成立,请写出证明过程;若不成立,请说明理由.
(1)如图1,求∠BDC的度数(用含α的式子表示).
(2)如图2,当α=60°时,过点D作BD的垂线与直线l交于点E,求证:AE=BD;
(3)如图3,当α=90°时,记直线l与CD的交点为F,连接 .将直线l绕点A旋转,当线段BF的长取得最大值时,直接写出tan∠FBC的值..
17.(1)发现问题:如图1,在等腰直角三角形ABC中,∠ACB=90°,点F为BC上一点,以BF为边作正方形BFED,点E在AB上,若AC=BC=2,BF= ,则 =;
②当点D到直线BC的距离等于2时,DG的长为;
③当以点A、C、D、B为顶点的四边形时矩形时,点P在线段DG上,且∠CPG与∠A互余,连接CP,则直线CP与AB所夹锐角的正切值为.
11.有公共顶点A的正方形ABCD与正方形AEGF按如图1所示放置,点E,F分别在边AB和AD上,DE,M是BF的中点
【观察猜想】
(2)如图2,点D在AC左侧且在点A上方,连接BE交CD于点M,F为BE上一点,连接DF,过点F作FG∥AC交BC延长线于点G,连接GM,EG,AD.若∠EDF+∠EBG=∠DEB,GM=BM.求证:AD=EF.
中考几何探究题目选(四)

纯几何探究(四)如图8-1,已知P 为正方形ABCD 的对角线AC 上一点(不与A 、C 重合),PE ⊥BC 于点E ,PF ⊥CD 于点F .(1) 求证:BP =DP ;(2) 如图8-2,若四边形PECF 绕点C 按逆时针方向旋转,在旋转过程中是否总有BP =DP ?若是,请给予证明;若不是,请用反例加以说明;(3) 试选取正方形ABCD 的两个顶点,分别与四边形PECF 的两个顶点连结,使得到的两条线段在四边形PECF 绕点C 按逆时针方向旋转的过程中长度始终相等,并证明你的结论 .3、(北京课改B 卷)我们给出如下定义:若一个四边形的两条对角线相等,则称这个四边形为等对角线四边形.请解答下列问题:(1)写出你所学过的特殊四边形中是等对角线四边形的两种图形的名称;(2)探究:当等对角线四边形中两条对角线所夹锐角为60时,这对60角所对的两边之和与其中一条对角线的大小关系,并证明你的结论.4、(福建漳州卷)如图,已知矩形33ABCD AB BC ==,,,在BC 上取两点E F ,(E 在F 左边),以EF 为边作等边三角形PEF ,使顶点P 在AD 上,PE PF ,分别交AC 于点G H ,.(1)求PEF △的边长;(2)在不添加辅助线的情况下,当F 与C 不重合时,从图中找出一对相似三角形,并说明理由;(3)若PEF △的边EF 在线段BC 上移动.试猜想:PH 与BE 有何数量关系?并证明你猜想的结论.5、(湖南常德卷)把两块全等的直角三角形ABC 和DEF 叠放在一起,使三角板DEF 的锐角顶点D 与三角板ABC 的斜边中点O 重合,其中90ABC DEF ∠=∠=,45C F ∠=∠=,4AB DE ==,把三角板ABC 固定不动,让三角板DEF 绕点O 旋转,设射线DE 与射线AB 相交于点P ,射线DF 与线段BC 相交于点Q .(1)如图1,当射线DF 经过点B ,即点Q 与点B 重合时,易证APD CDQ △∽△.此时,APCQ =· . (2)将三角板DEF 由图1所示的位置绕点O 沿逆时针方向旋转,设旋转角为α.其中图8-2 图8-1 (第27题) A B C D E FGHP090α<<,问AP CQ ·的值是否改变?说明你的理由.(3)在(2)的条件下,设CQ x =,两块三角板重叠面积为y ,求y 与x 的函数关系式.(图2,图3供解题用)6.(25T)(大连市14分)如图25-1,正方形ABCD 和正方形QMNP ,∠M =∠B ,M 是正方形ABCD 的对称中心,MN 交AB 于F ,QM 交AD 于E . ⑴求证:ME = MF .⑵如图25-2,若将原题中的“正方形”改为“菱形”,其他条件不变,探索线段ME 与线段MF 的关系,并加以证明.⑶如图25-3,若将原题中的“正方形”改为“矩形”,且AB = m BC ,其他条件不变,探索线段ME 与线段MF 的关系,并说明理由.⑷根据前面的探索和图25-4,你能否将本题推广到一般的平行四边形情况?若能,写出推广命题;若不能,请说明理由.图25 - 4图25 - 3图25 - 2图25 -1APQQPQPABCDFM NABCE MNBCD E MNF DPQD AFNME CB8.(2009年江西省)25.如图1,在等腰梯形ABCD 中,AD BC ∥,E 是AB 的中点,过点E 作EF BC ∥交CD 于点F .46AB BC ==,,60B =︒∠. (1)求点E 到BC 的距离; (2)点P 为线段EF 上的一个动点,过P 作PM EF ⊥交BC 于点M ,过M 作MN AB ∥交折线ADC 于点N ,连结PN ,设EP x =.①当点N 在线段AD 上时(如图2),P M N △的形状是否发生改变?若不变,求出PMN△的周长;若改变,请说明理由;②当点N 在线段DC 上时(如图3),是否存在点P ,使PMN △为等腰三角形?若存在,请求出所有满足要求的x 的值;若不存在,请说明理由.B EP A D(O) CQ F M B E P AC Q F D(O) D(O) B (Q ) C F EAP 图1 图2 图37.问题解决如图(1),将正方形纸片ABCD 折叠,使点B 落在CD 边上一点E (不与点C ,D 重合),压平后得到折痕MN .当12CE CD =时,求AMBN的值.类比归纳在图(1)中,若13CE CD =,则AM BN 的值等于 ;若14CE CD =,则AM BN 的值等于 ;若1CE CD n =(n 为整数),则AMBN的值等于 .(用含n 的式子表示) 联系拓广如图(2),将矩形纸片ABCD 折叠,使点B 落在CD 边上一点E (不与点C D ,重合),压平后得到折痕MN ,设()111AB CE m BC m CD n=>=,,则AM BN 的值等于 .(用含m n ,的式子表示)9.若P 为ABC △所在平面上一点,且120APB BPC CPA ∠=∠=∠=°,则点P 叫做ABC △的费马点.(1)若点P 为锐角ABC △的费马点,且60ABC PA PC ∠===°,3,4,则PB 的值为________;方法指导:为了求得AM BN 的值,可先求BN 、AM 的长,不妨设:AB =2图(2)N AB C D EF MA D EBF C图4(备用)AD EBF C图5(备用)A D E BF C图1 图2 A D EBF C PNM 图3 A D EBFCPNM (第25题)(2)如图,在锐角ABC △外侧作等边ACB △′连结BB ′. 求证:BB ′过ABC △的费马点P ,且BB ′=PA PB PC ++.10.(1)如图1,图2,图3,在ABC △中,分别以AB AC ,为边,向ABC △外作正三角形,正四边形,正五边形,BE CD ,相交于点O .①如图1,求证:ABE ADC △≌△;②探究:如图1,BOC ∠= ;如图2,BOC ∠= ;如图3,BOC ∠= .(2)如图4,已知:AB AD ,是以AB 为边向ABC △外所作正n 边形的一组邻边;AC AE ,是以AC 为边向ABC △外所作正n 边形的一组邻边.BE CD ,的延长相交于点O .①猜想:如图4,BOC ∠= (用含n 的式子表示); ②根据图4证明你的猜想.11.在一平直河岸l 同侧有A B ,两个村庄,A B ,到l 的距离分别是3km 和2km ,km AB a =(1)a >.现计划在河岸l 上建一抽水站P ,用输水管向两个村庄供水.方案设计某班数学兴趣小组设计了两种铺设管道方案:图13-1是方案一的示意图,设该方案中管道长度为1d ,且1(km)d P B B A =+(其中BP l ⊥于点P );图13-2是方案二的示意图,设该方案中管道长度为2d ,且2(k m )d P A P B =+(其中点A '与点A 关于l 对称,A B '与l 交于点P ).观察计算(1)在方案一中,1d = km (用含a 的式子表示);(2)在方案二中,组长小宇为了计算2d 的长,作了如图13-3所示的辅助线,请你按小宇同学的思路计算,2d = km (用含a 的式子表示).12.(北京市)25.我们知道:有两条边相等的三角形叫做等腰三角形.类似地,我们定ACBB '第(25)题AB P llAB P A ' C图13-1 图13-2lAB P A 'C图13-3K义:至少有一组对边相等的四边形叫做等对边四边形.(1)请写出一个你学过的特殊四边形中是等对边四边形的图形的名称; (2)如图,在ABC △中,点D E ,分别在AB AC ,上, 设CD BE ,相交于点O ,若60A ∠=°,12DCB EBC A ∠=∠=∠. 请你写出图中一个与A ∠相等的角,并猜想图中哪个四边形 是等对边四边形;(3)在ABC △中,如果A ∠是不等于60°的锐角,点D E ,分别在AB AC ,上,且12DCB EBC A ∠=∠=∠.探究:满足上述条件的图形中是否存在等对边四边形,并证明你的结论.…B O ADEC。
中考数学复习《几何探究型问题》经典题型及测试题(含答案)

中考数学复习《几何探究型问题》经典题型及测试题(含答案)题型解读1.考查类型:①动点探究题;②平移、旋转、折叠探究题;③图形形状变化探究题.2.考查内容:①多与特殊四边形的性质、三角形全等、相似的判定和性质有关;②涉及平移、旋转或折叠的相关性质;③多与二次函数的性质有关.3.备考指导:在做此类题型时,要观察题中已知条件,并结合题设,联系相关的知识解题,对结果猜想题根据前面问题大胆猜想,往往是解题的突破口.类型一动点探究题1.如图,在Rt△ABC中,∠ACB=90°,AC=5 cm,∠BAC=60°,动点M从点B出发,在BA边上以每秒2 cm的速度向点A匀速运动,同时动点N从点C出发,在CB边上以每秒3 cm的速度向点B匀速运动,设运动时间为t秒(0≤t≤5),连接MN.(1)若BM=BN,求t的值;(2)若△MBN与△ABC相似,求t的值;(3)当t为何值时,四边形ACNM的面积最小?并求出最小值.2.如图①,菱形ABCD中,已知∠BAD=120°,∠EGF=60°,∠EGF的顶点G在菱形对角线AC上运动,角的两边分别交边BC、CD于点E、F.(1)如图②,当顶点G运动到与点A重合时,求证:EC+CF=BC;(2)知识探究:①如图③,当顶点G运动到AC中点时,探究线段EC、CF与BC的数量关系;②在顶点G 的运动过程中,若ACCG =t ,请直接写出线段EC 、CF 与BC 的数量关系(不需要写出证明过程);(3)问题解决:如图④,已知菱形边长为8,BG =7,CF =65,当t >2时,求EC 的长度.图①3.已知:如图,在矩形ABCD 中,AB =6 cm ,BC =8 cm .对角线AC ,BD 交于点O ,点P 从点A 出发,沿AD 方向匀速运动,速度为1 cm /s ;同时,点Q 从点D 出发,沿DC 方向匀速运动,速度为1 cm /s ;当一个点停止运动时,另一个点也停止运动.连接PO 并延长,交BC 于点E ,过点Q 作QF∥AC,交BD 于点F.设运动时间为t(s )(0<t<6),解答下列问题: (1)当t 为何值时,△AOP 是等腰三角形?(2)设五边形OECQF 的面积为S(cm 2),试确定S 与t 的函数关系式;(3)在运动过程中,是否存在某一时刻t ,使S 五边形OECQF ∶S △ACD =9∶16?若存在,求出t 的值;若不存在,请说明理由;(4)在运动过程中,是否存在某一时刻t ,使OD 平分∠COP?若存在,求出t 值;若不存在,请说明理由.4.某数学兴趣小组在数学课外活动中,研究三角形和正方形的性质时,做了如下探究:在△ABC 中,∠BAC =90°,AB =AC ,点D 为直线BC 上一动点(点D 不与B ,C 重合),以AD 为边在AD 右侧作正方形ADEF ,连接CF. (1)观察猜想如图①,当点D 在线段BC 上时,①BC 与CF 的位置关系为:____________. ②BC ,CD ,CF 之间的数量关系为:____________(将结论直接写在横线上). (2)数学思考如图②,当点D 在线段CB 的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明. (3)拓展延伸如图③,当点D 在线段BC 的延长线上时,延长BA 交CF 于点G ,连接GE.若已知AB =22,CD =14BC ,请求出GE 的长.类型二 平移、旋转、折叠探究题5.如图①,△ABC 是等腰直角三角形,∠BAC =90°,AB =AC ,四边形ADEF 是正方形,点B 、C 分别在边AD、AF上,此时BD=CF,BD⊥CF成立.(1)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图②,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.(2)当△ABC绕点A逆时针旋转45°时,如图③,延长DB交CF于点H.①求证:BD⊥CF;②当AB=2,AD=32时,求线段DH的长.图①图②图③6.在△ABC中,AB=6,AC=BC=5,将△ABC绕点A按顺时针方向旋转,得到△ADE,旋转角为α(0°<α<180°),点B的对应点为点D,点C的对应点为点E,连接BD,BE.(1)如图,当α=60°时,延长BE交AD于点F.①求证:△ABD是等边三角形;②求证:BF⊥AD,AF=DF;③请直接..写出BE的长;(2)在旋转过程中,过点D作DG垂直于直线AB,垂足为点G,连接CE,当∠DAG=∠ACB,且线段DG与线段AE无公共点时,请直接..写出BE+CE的值.温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.7.已知矩形ABCD中AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.(1)如图①,已知折痕与边BC交于点O,连接AP、OP、OA,若△OCP与△PDA的面积比为1∶ 4,求边CD 的长;(2)如图②,在(1)的条件下擦去AO、OP,连接BP,动点M在线段AP上(点M不与点P、A重合),动点N 在线段AB的延长线上,且BN=PM,连接MN交PB于点F,作ME⊥BP于点E,试问当点M、N在移动过程中,线段EF的长度是否发生变化?若变化,说明变化规律,若不变,求出线段EF的长度.图①图②8.问题情境在综合与实践课上,老师让同学们以“菱形纸片的剪拼”为主题开展数学活动.如图①,将一张菱形纸片ABCD(∠BAD>90°)沿对角线AC剪开,得到△ABC和△ACD.操作发现(1)将图①中的△ACD以A为旋转中心,按逆时针方向旋转角α,使α=∠BAC,得到如图②所示的△AC′D,分别延长BC和DC′交于点E,则四边形ACEC′的形状是________;(2)创新小组将图①中的△ACD以A为旋转中心,按逆时针方向旋转角α,使α=2∠BAC,得到如图③所示的△AC′D,连接DB、C′C,得到四边形BCC′D,发现它是矩形.请你证明这个结论;实践探究(3)缜密小组在创新小组发现结论的基础上,量得图③中BC=13 cm,AC=10 cm,然后提出一个问题:将△AC′D沿着射线DB方向平移a cm,得到△A′C″D′,连接BD′,CC″,使四边形BCC″D′恰好为正方形,求a的值.请你解答此问题;(4)请你参照以上操作,将图①中的△ACD在同一平面内进行一次平移,得到△A′C′D,在图④中画出平移后构造出的新图形,标明字母,说明平移及构图方法,写出你发现的结论,不必证明.9.如图,已知一个直角三角形纸片ACB,其中∠ACB=90°,AC=4,BC=3,E、F分别是AC、AB边上的点,连接EF.(1)如图①,若将纸片ACB的一角沿EF折叠,折叠后点A落在AB边上的点D处,且使S四边形ECBF=3S△EDF,求AE的长;(2)如图②,若将纸片ACB的一角沿EF折叠,折叠后点A落在BC边上的点M处,且使MF∥CA.①试判断四边形AEMF的形状,并证明你的结论;②求EF的长;(3)如图③,若FE 的延长线与BC 的延长线交于点N ,CN =1,CE =47,求AFBF的值.10.如图①,矩形ABCD 中,AB =2,BC =5,BP =1,∠MPN =90°,将∠MPN 绕点P 从PB 处开始按顺时针方向旋转,PM 交边AB(或AD)于点E ,PN 交边AD(或CD)于点F ,当PN 旋转至PC 处时,∠MPN 的旋转随即停止.(1)特殊情形:如图②,发现当PM 过点A 时,PN 也恰好过点D , 此时,△ABP________△PCD(填“≌”或“∽”);(2)类比探究:如图③,在旋转过程中,PEPF 的值是否为定值?若是,请求出该定值;若不是,请说明理由;(3)拓展延伸:设AE =t ,△EPF 的面积为S ,试确定S 关于t 的函数关系式;当S =4.2时,求所对应的t 值.11.如图①,在△ABC中,∠ACB=90°,∠B=30°,AC=1,D为AB的中点,EF为△ACD的中位线,四边形EFGH为△ACD的内接矩形(矩形的四个顶点均在△ACD的边上).(1)计算矩形EFGH的面积;(2)将矩形EFGH沿AB向右平移,F落在BC上时停止移动.在平移过程中,当矩形与△CBD重叠部分的面积为316时,求矩形平移的距离;(3)如图③,将(2)中矩形平移停止时所得的矩形记为矩形E1F1G1H1,将矩形E1F1G1H1绕G1点按顺时针方向旋转,当H1落在CD上时停止转动,旋转后的矩形记为矩形E2F2G1H2,设旋转角为α,求cosα的值.类型三图形形状变化探究题12.如图①,②,③分别以△ABC的AB和AC为边向△ABC外作正三角形(等边三角形)、正四边形(正方形)、正五边形,BE和CD相交于点O.(1)在图①中,求证:△ABE≌△ADC.图①(2)由(1)证得△ABE≌△ADC,由此可推得在图①中∠BOC=120°,请你探索在图②中∠BOC的度数,并说明理由或写出证明过程.图②(3)填空:在上述(1)(2)的基础上可得在图③中∠BOC=________(填写度数).图③图④(4)由此推广到一般情形(如图④),分别以△ABC的AB和AC为边向△ABC外作正n边形,BE和CD仍相交于点O,猜想∠BOC的度数为____________________(用含n的式子表示).13.阅读理解:我们知道,四边形具有不稳定性,容易变形.如图①,一个矩形发生变形后成为一个平行四边形,设这个平行四边形相邻两个内角中较小的一个内角为α,我们把1sinα的值叫做这个平行四边形的变形度.(1)若矩形发生形变后的平行四边形有一个内角是120°,则这个平行四边形的变形度是________;猜想证明:(2)设矩形的面积为S1,其变形后的平行四边形面积为S2,试猜想S1,S2,1sinα之间的数量关系,并说明理由;拓展探究:(3)如图②,在矩形ABCD中,E是AD边上的一点,且AB2=AE·AD,这个矩形发生变形后为平行四边形A1B1C1D1,E1为E的对应点,连接B1E1,B1D1,若矩形ABCD的面积为4m(m>0),平行四边形A1B1C1D1的面积为2m(m>0),试求∠A1E1B1+∠A1D1B1的度数.14.已知AC ,EC 分别为四边形ABCD 和EFCG 的对角线,点E 在△ABC 内,∠CAE +∠CBE=90°. (1)如图①,当四边形ABCD 和EFCG 均为正方形时,连接BF. ①求证:△CAE∽△CBF; ②若BE =1,AE =2,求CE 的长;(2)如图②,当四边形ABCD 和EFCG 均为矩形,且AB BC =EFFC =k 时,若BE =1,AE =2,CE =3,求k 的值;(3)如图③,当四边形ABCD 和EFCG 均为菱形,且∠DAB =∠GEF=45°时,设BE =m ,AE =n ,CE =p ,试探究m ,n ,p 三者之间满足的等量关系(直接写出结果,不必写出解答过程).15.已知点O 是△ABC 内任意一点,连接OA 并延长到E ,使得AE =OA ,以OB ,OC 为邻边作▱OBFC ,连接OF ,与BC 交于点H ,再连接EF.(1)如图①,若△ABC 为等边三角形,求证:①EF⊥BC; ②EF =3BC ;(2)如图②,若△ABC 为等腰直角三角形(BC 为斜边),猜想(1)中的两个结论是否成立?若成立,直接写出结论即可;若不成立,请你直接写出你的猜想结果;(3)如图③,若△ABC 是等腰三角形,且AB =AC =kBC ,请你直接写出EF 与BC 之间的数量关系.类型一 动点探究题1. 解:(1)根据题意BM =2t ,BN =BC -3t ,而BC =5×tan 60°=5 3.∴当BM =BN 时,2t =53-3t ,解得t =103-15. (2)分类讨论:①当∠BMN =∠ACB =90°时,如解图①, △NBM ∽△ABC ,cos B =cos 30°=BM BN ,∴2t 53-3t =32,解得t =157.②当∠BNM =∠ACB =90°时,如解图②, △MBN ∽△ABC ,cos B =cos 30°=BNBM, ∴53-3t 2t =32,解得t =52. 因此当运动时间是157秒或52秒时,△MBN 与△ABC 相似.第1题解图(3)由于△ABC 面积是定值,∴当四边形ACNM 面积最小时,△MBN 面积最大, 而△MBN 的面积是S =12BM ×BN ×sin B=12×2t ×(53-3t)×12=-32t 2+532t , 由于a =-32<0, ∴当t =-5322×(-32)=52时,△MBN 面积最大,最大值是-32×(52)2+532×52=2538, 因此四边形ACNM 面积最小值是12×5×53-2538=7538.2. (1)证明:∵四边形ABCD 是菱形,∠BAD =120°,∴∠BAC =60°,∠B =∠ACF =60°,AB =BC , ∴AB =AC ,∵∠BAE +∠EAC =∠EAC +∠CAF =60°, ∴∠BAE =∠CAF , 在△BAE 和△CAF 中, ⎩⎪⎨⎪⎧∠BAE =∠CAF AB =AC ∠B =∠ACF, ∴△BAE ≌△CAF(ASA ), ∴BE =CF ,∴EC +CF =EC +BE =BC ,即EC +CF =BC ;(2)解:①线段EC ,CF 与BC 的数量关系为: EC +CF =12BC.理由如下:如解图①,过点A 作AE′∥EG ,AF ′∥GF ,分别交BC 、CD 于E′、F′.第2题解图①类比(1)可得:E′C +CF′=BC , ∵G 为AC 中点,AE ′∥EG , ∴CE CE′=CG AC =12, ∴CE =12CE′,同理可得:CF =12CF′,∴CE +CF =12CE′+12CF′=12(CE′+CF′)=12BC ,即CE +CF =12BC ;②CE +CF =1tBC ;【解法提示】类比(1)可得:E′C +CF′=BC , ∵AE ′∥EG ,ACCG =t ,∴CE CE′=CG AC =1t,∴CE =1tCE′,同理可得:CF =1tCF′,∴CE +CF =1t CE′+1t CF′=1t (CE′+CF′)=1t BC ,即CE +CF =1tBC.(3)解:如解图②,连接BD 与AC 交于点H.第2题解图②在Rt △ABH 中,∵AB =8,∠BAC =60°, ∴BH =AB·sin 60°=8×32=43, AH =CH =AB·cos 60°=8×12=4,∴GH =BG 2-BH 2=72-(43)2=1, ∴CG =4-1=3, ∴CG AC =38, ∴t =83(t >2),由(2)②得:CE +CF =1t BC ,∴CE =1t BC -CF =38×8-65=95.∴EC 的长度为95.3. 解:(1)分三种情况: ①若AP =AO ,在矩形ABCD 中,∵AB =6,BC =8, ∴AC =10,第3题解图①∴AO =CO =5,∴AP =5, ∴t =5,②若AP =PO =t , 在矩形ABCD 中, ∵AD ∥BC ,∴∠PAO =∠OCE ,∠APO =∠OEC , 又∵OA =OC ,∴△APO ≌△CEO ,∴PO =OE =t.如解图①,作AG ∥PE 交BC 于点G ,则四边形APEG 是平行四边形, ∴AG =PE =2t ,GE =AP =t. 又∵EC =AP =t ,∴BG =8-2t.在Rt △ABG 中,根据勾股定理知62+(8-2t)2=(2t)2, 解得t =258.第3题解图②③若OP =AO =5,则t =0或t =8,不合题意,舍去. 综上可知,当t =5或t =258时,△AOP 是等腰三角形.(2)如解图②,作OM ⊥BC ,垂足是M ,作ON ⊥CD ,垂足是N. 则OM =12AB =3,ON =12BC =4,∴S △OEC =12·CE·OM =12·t·3=32t ,S △OCD =12·CD·ON =12·6·4=12.∵QF ∥AC ,∴△DFQ ∽△DOC , ∴S △DFQ S △DOC =(DQ DC)2,即S △DFQ 12=(t 6)2,∴S △DFQ =13t 2,∴S 四边形OFQC =12-13t 2,∴S 五边形OECQF =S 四边形OFQC +S △OEC =12-13t 2+32t ,即S =-13t 2+32t +12(0<t <6).(3)存在.理由如下:要使S 五边形OECQF :S △ACD =9∶16,即(-13t 2+32t +12)∶(12×6×8)=9∶16,解得t 1=3,t 2=1.5,两个解都符合题意,∴存在两个t 值,使S 五边形OECQF ∶S △ACD =9∶16,此时t 1=3,t 2=1.5; (4)存在.理由如下:如解图③,作DI ⊥OP ,垂足是I ,DJ ⊥OC ,垂足是J ,第3题解图③作AG ∥PE 交BC 于点G.∵S △OCD =12·OC·DJ =12·5·DJ ,且由(2)知,S △OCD =12,∴DJ =245.∵OD 平分∠POC ,DI ⊥OP ,DJ ⊥OC , ∴DI =DJ =245=4.8.∵AG ∥PE ,∴∠DPI =∠DAG .∵AD ∥BC ,∴∠DAG =∠AGB ,∴∠DPI =∠AGB , ∴Rt △ABG ∽Rt △DIP.由(1)知,在Rt △ABG 中,BG =8-2t , ∴AB DI =BG IP ,∴64.8=8-2t IP, ∴IP =45(8-2t).在Rt △DPI 中,根据勾股定理得 (245)2+[45(8-2t)]2=(8-t)2, 解得t =11239.(t =0不合题意,舍去)4. (1)解:①BC ⊥CF ;②BC =CD +CF. 【解法提示】①∵∠BAC =∠DAF =90°, ∴∠BAD =∠CAF , 又∵AB =AC ,AD =AF , ∴△ABD ≌△ACF , ∴∠ACF =∠ABC =45°, ∵∠ACB =45°,∴∠BCF =90°,即BC ⊥CF ; ②∵△ABD ≌△ACF , ∴BD =CF , ∵BC =CD +BD , ∴BC =CD +CF.(2)解:结论①仍然成立,②不成立. ①证明:∵∠BAC =∠DAF =90°, ∴∠BAD =∠CAF ,又∵AB =AC ,AD =AF , ∴△ABD ≌△ACF ,∴∠ACF =∠ABD =180°-45°=135°, ∵∠ACB =45°, ∴∠BCF =90°,即BC ⊥CF ; ②结论为:BC =CD -CF. 证明:∵△ABD ≌△ACF , ∴BD =CF ,∵BC =CD -BD ,∴BC =CD -CF.(3)解:如解图,过点E 作EM ⊥CF 于M ,作EN ⊥BD 于点N ,过点A 作AH ⊥BD 于点H. ∵AB =AC =22,第4题解图∴BC =4,AH =12BC =2,∵CD =14BC ,∴CD =1,∵∠BAC =∠DAF =90°, ∴∠BAD =∠CAF ,又∵AB =AC ,AD =AF , ∴△ABD ≌△ACF , ∴∠ACF =∠ABC =45°, ∵∠ACB =45°, ∴∠BCF =90°,∴CN =ME ,CM =EN , ∴∠AGC =∠ABC =45°, ∴CG =BC =4,∵∠ADE =90°,∴∠ADH +∠EDN =∠EDN +∠DEN =90°, ∴∠ADH =∠DEN ,又∵∠AHC =∠DNE =90°,AD =DE , ∴△AHD ≌△DNE ,∴DN =AH =2,EN =DH =3, ∴CM =EN =3,ME =CN =3, 则GM =CG -CM =4-3=1, ∴EG =EM 2+GM 2=10.类型二 平移、旋转、折叠探究题5. (1)解:BD =CF 成立.理由如下:∵AC =AB ,∠CAF =∠BAD =θ,AF =AD , ∴△ACF ≌△ABD ,∴CF =BD.(2)①证明:由(1)得,△ACF ≌△ABD , ∴∠HFN =∠ADN , 在△HFN 与△ADN 中,∵∠HFN =∠ADN ,∠HNF =∠AND , ∴∠NHF =∠NAD =90°,第5题解图∴HD ⊥HF ,即BD ⊥CF.②解:如解图,连接DF ,延长AB ,与DF 交于点M , 在△MAD 中,∵∠MAD =∠MDA =45°, ∴∠BMD =90°.在Rt △BMD 与Rt △FHD 中, ∵∠MDB =∠HDF ,∴△BMD ∽△FHD.∵AB =2,AD =32,四边形ADEF 是正方形, ∴MA =MD =322=3,∴MB =MA -AB =3-2=1,BD =MB 2+MD 2=12+32=10, 又∵MD HD =BD FD ,即3HD =106,∴DH =9105.6. (1)①证明:∵△ABC 绕点A 顺时针方向旋转60°得到△ADE , ∴AB =AD ,∠BAD =60°, ∴△ABD 是等边三角形;②证明:由①得△ABD 是等边三角形, ∴AB =BD ,∵△ABC绕点A顺时针方向旋转60°得到△ADE,∴AC=AE,BC=DE,又∵AC=BC,∴EA=ED,∴点B,E在AD的中垂线上,∴BE是AD的中垂线,∵点F在BE的延长线上,∴BF⊥AD,AF=DF;③解:BE的长为33-4;【解法提示】由②知AF=12AD=12AB=3,AE=AC=5,BF⊥AD,由勾股定理得EF=AE2-AF2=4.在等边△ABD中,AB=6,BF⊥AD,∴BF=32AB=33,∴BE=33-4.(2)解:BE+CE的值为13;第6题解图【解法提示】如解图,∵∠DAG=∠ACB,∴∠DAB=2∠CAB.∵∠DAE=∠CAB,∴∠BAE=∠CAB,∴∠BAE=∠CBA,∴AE∥BC,∵AE=AC=BC,∴四边形ACBE是菱形,∴CE 垂直平分AB ,BE =AC =5.设CE 交AB 于M ,则CM ⊥AB ,CM =EM ,AM =BM , ∴在Rt △ACM 中,AC =5,AM =3, 由勾股定理得CM =4, ∴CE =8, ∴CE +BE =13.7. 解:(1)由矩形性质与折叠可知,∠APO =∠B =∠C =∠D =90°, ∴∠CPO +∠DPA =∠DPA +∠DAP =90°, ∴∠DAP =∠CPO , ∴△OCP ∽△PDA , ∴S △OCP S △PDA =(CP DA)2,即14=(CP8)2,∴CP =4,设CD =x ,则DP =x -4,AP =AB =CD =x , ∵AP 2-DP 2=AD 2, ∴x 2-(x -4)2=82, 解得x =10, 故CD =10. (2)第7题解图线段EF 的长度始终不发生变化,为2 5.证明:如解图,过点N 作NG ⊥PB ,与PB 的延长线相交于点G , ∵AB =AP ,∴∠APB =∠ABP =∠GBN , 在△PME 和△BNG 中, ⎩⎪⎨⎪⎧∠MEP =∠NGB =90°∠MPE =∠NBG MP =NB, ∴△PME ≌△BNG(AAS ), ∴ME =NG ,PE =BG , 在△FME 和△FNG 中, ⎩⎪⎨⎪⎧∠MEF =∠NGF ∠MFE =∠NFG ME =NG,∴△FME ≌△FNG(AAS ), ∴EF =GF , ∴EF =12EG ,∵BP =BE +EP =BE +GB =EG , ∴EF =12BP ,∵BP =BC 2+CP 2=82+42=45, ∴EF =12BP =2 5.8. (1)解:菱形.(2)证明:如解图①,作AE ⊥CC′于点E , 由旋转得AC′=AC ,∴∠CAE =∠C′AE =12α=∠BAC ,第8题解图①∵四边形ABCD 是菱形, ∴BA =BC ,BC =DC′, ∴∠BCA =∠BAC , ∴∠CAE =∠BCA , ∴AE ∥BC , 同理AE ∥DC′, ∴BC ∥DC ′,∴四边形BCC′D 是平行四边形, 又∵AE ∥BC ,∠CEA =90°, ∴∠BCC ′=180°-∠CEA =90°,∴四边形BCC′D 是矩形.(3)解:如解图①,过点B 作BF ⊥AC 于点F , ∵BA =BC ,∴CF =AF =12AC =12×10=5.在Rt △BCF 中,BF =BC 2-CF 2=132-52=12. 在△ACE 和△CBF 中,∵∠CAE =∠BCF ,∠CEA =∠BFC =90°, ∴△ACE ∽△CBF , ∴CE BF =AC BC ,即CE 12=1013, 解得CE =12013.∵AC =AC′,AE ⊥CC ′, ∴CC ′=2CE =2×12013=24013.当四边形BCC″D′恰好为正方形时,分两种情况: ①点C″在边CC′上,a =CC′-13=24013-13=7113,②点C″在边C′C 的延长线上,a =CC′+13=24013+13=40913.综上所述,a 的值为7113或40913.第8题解图②(4)解:答案不唯一,例:画出正确图形如解图②所示.平移及构图方法:将△ACD 沿着射线CA 方向平移,平移距离为12AC 的长度,得到△A ′C ′D ,连接A′B ,DC.结论:四边形A′BCD 是平行四边形.9. 解:(1)∵折叠后点A 落在AB 边上的点D 处, ∴EF ⊥AB ,△AEF ≌△DEF , ∴S △AEF =S △DEF .∵S 四边形ECBF =3S △EDF ,∴S 四边形ECBF =3S △AEF .∵S △ACB =S △AEF +S 四边形ECBF ,∴S △ACB =S △AEF +3S △AEF =4S △AEF , ∴S △AEF S △ACB =14. ∵∠EAF =∠BAC ,∠AFE =∠ACB =90°, ∴△AEF ∽△ABC , ∴S △AEF S △ABC =(AE AB )2, ∴(AE AB )2=14. 在Rt △ACB 中,∵∠ACB =90°,AC =4,BC =3, ∴AB =42+32=5, ∴(AE 5)2=14,∴AE =52.(2)第9题解图①①四边形AEMF 是菱形.证明:如解图①,∵折叠后点A 落在BC 边上的点M 处, ∴∠CAB =∠EMF ,AE =ME , 又∵MF ∥CA ,∴∠CEM =∠EMF , ∴∠CAB =∠CEM , ∴EM ∥AF ,∴四边形AEMF 是平行四边形. 又∵AE =ME ,∴四边形AEMF 是菱形.②如解图①,连接AM ,AM 与EF 交于点O ,设AE =x ,则ME =AE =x ,EC =4-x. ∵∠CEM =∠CAB ,∠ECM =∠ACB =90°, ∴△ECM ∽△ACB. ∴EC AC =EMAB , ∵AB =5,AC =4, ∴4-x 4=x5, 解得x =209,∴AE =ME =209,EC =169.在Rt △ECM 中,∵∠ECM =90°,∴CM 2=EM 2-EC 2, 即CM =EM 2-EC 2=(209)2-(169)2=43. ∵四边形AEMF 是菱形,∴OE =OF ,OA =OM ,AM ⊥EF , ∴S 菱形AEMF =4S △AOE =2OE·AO. 在Rt △AOE 和Rt △ACM 中, ∵tan ∠EAO =tan ∠MAC , ∴OE AO =CM AC. ∵CM =43,AC =4,∴AO =3OE ,∴S 菱形AEMF =6OE 2. 又∵S 菱形AEMF =AE·CM ,∴6OE 2=209×43,∴OE =2109,∴EF =4109. (3)如解图②,第9题解图②过点F 作FH ⊥CB 于点H ,在Rt △NCE 和Rt △NHF 中, ∵tan ∠ENC =tan ∠FNH , ∴EC NC =FH NH, ∵NC =1,EC =47,∴FH NH =47, 设FH =x ,则NH =74x ,∴CH =NH -NC =74x -1.∵BC =3,∴BH =BC -CH =3-(74x -1)=4-74x.在Rt △BHF 和Rt △BCA 中,∵tan ∠FBH =tan ∠ABC , ∴HF BH =CA BC , ∴x4-74x =43, 解得x =85,∴HF =85.∵∠B =∠B ,∠BHF =∠BCA =90°, ∴△BHF ∽△BCA , ∴HF CA =BFBA,即HF·BA =CA·BF , ∴85×5=4BF ,∴BF =2,∴AF =AB -BF =3, ∴AF BF =32. 10. 解:(1)△ABP ∽△PCD. 【解法提示】∵∠MPN =90°, ∴∠APB +∠DPC =90°, ∵∠B =90°,∴∠APB +∠BAP =90°, ∴∠DPC =∠BAP , 又∵∠B =∠C =90°, ∴△ABP ∽△PCD.(2)在旋转过程中,PEPF 的值为定值.如解图,过点F 作FG ⊥BC ,垂足为G.第10题解图类比(1)可得:△EBP ∽△PGF , ∴EP PF =PB FG, ∵∠A =∠B =∠FGB =90°, ∴四边形ABGF 是矩形, ∴FG =AB =2, ∵BP =1, ∴PE PF =12, 即在旋转过程中,PE PF 的值为定值12.(3)由(2)知△EBP ∽△PGF , ∴EB PG =BP GF =12, 又∵AE =t , ∴BE =2-t ,∴PG =2(2-t)=4-2t ,∴AF =BG =BP +PG =1+(4-2t)=5-2t ,∴S =S 矩形ABGF -S △AEF -S △BEP -S △PFG=2(5-2t)-12t(5-2t)-12×1×(2-t)-12×2×(4-2t)=t 2-4t +5,即S =t 2-4t +5(0≤t ≤2), 当S =4.2时,4.2=t 2-4t +5,解得:t 1=2-455,t 2=2+455(不合题意,舍去).∴t 的值是2-455.11. 解:(1)如解图①,在△ABC 中, ∵∠ACB =90°,∠B =30°,AC =1, ∴AB =2,又∵D 是AB 的中点,第11题解图①∴AD =1,CD =12AB =1,又∵EF 是△ACD 的中位线,∴EF =DF =12,在△ACD 中,AD =CD ,∠A =60°,∴△ACD 为等边三角形, ∴∠ADC =60°, 在△FGD 中,GF =DF·sin 60°=34, ∴矩形EFGH 的面积S =EF·GF =12×34=38.(2)如解图②,设矩形移动的距离为x ,则0<x ≤12,①当矩形与△CBD 重叠部分为三角形时,则0<x ≤14,重叠部分的面积S =12x·3x =316,第11题解图②∴x =24>14(舍去), ②当矩形与△CBD 重叠部分为直角梯形时,则14<x ≤12,重叠部分的面积S =34x -12×14×34=316, ∴x =38,即矩形移动的距离为38时,矩形与△CBD 重叠部分的面积是316.第11题解图③(3)如解图③,作H 2Q ⊥AB 于Q , 设DQ =m ,则H 2Q =3m , 又DG 1=14,H 2G 1=12,在Rt △H 2QG 1中, (3m)2+(m +14)2=(12)2,解得m 1=-1+1316,m 2=-1-1316<0(舍去),∴cos α=QG 1F 1G 1=-1+1316+1412=3+138.类型三 图形形状变化探究题12. (1)证明:∵△ABD 、△ACE 是等边三角形, ∴AB =AD ,AC =AE ,∠CAE =∠DAB =60°,∴∠CAE +∠BAC =∠DAB +∠BAC ,即∠BAE =∠DAC , 在△ABE 和△ADC 中, ⎩⎪⎨⎪⎧AB =AD ∠BAE =∠DAC AE =AC, ∴△ABE ≌△ADC(SAS ). (2)解:∠BOC =90°.理由如下: 由(1)得△ABE ≌△ADC ,∴∠EBA =∠CDA.∵∠FBA +∠FDA =180°,∴∠FBA -∠EBA +∠FDA +∠CDA =180°, 即∠FBO +∠FDO =180°.在四边形FBOD 中,∠F =90°, ∴∠DOB =360°-∠F -(∠FBO +∠FDO)=90°, ∴∠BOC =90°. (3)解:72°.【解法提示】∠BOC =180°-108°=72°.(4)解:180°-180°·(n -2)n.【解法提示】由(3)可知,∠BOC 度数应为180°减去正多边形内角度数. 13. 解:(1)233.【解法提示】sin 120°=32,故这个平行四边形的变形度是233. (2)1sin α=S 1S 2,理由如下: 如解图,设矩形的长和宽分别为a ,b ,其变形后的平行四边形的高为h ,第13题解图则S 1=ab ,S 2=ah ,sin α=hb ,∴S 1S 2=ab ah =b h , 又∵1sin α=b h ,∴1sin α=S 1S 2. (3)由AB 2=AE·AD ,可得A 1B 21=A 1E 1·A 1D 1,即A 1B 1A 1D 1=A 1E 1A 1B 1. 又∵∠B 1A 1E 1=∠D 1A 1B 1, ∴△B 1A 1E 1∽△D 1A 1B 1, ∴∠A 1B 1E 1=∠A 1D 1B 1, ∵A 1D 1∥B 1C 1,∴∠A 1E 1B 1=∠C 1B 1E 1,∴∠A 1E 1B 1+∠A 1D 1B 1=∠C 1B 1E 1+∠A 1B 1E 1=∠A 1B 1C 1. 由(2)结论1sin α=S 1S 2,可得1sin ∠A 1B 1C 1=4m2m =2,∴sin ∠A 1B 1C 1=12,∴∠A 1B 1C 1=30°,∴∠A 1E 1B 1+∠A 1D 1B 1=30°. 14. (1)①证明:如解图①, ∵∠ACE +∠ECB =45°,∠BCF +∠ECB =45°,第14题解图①∴∠ACE =∠BCF ,又∵四边形ABCD 和EFCG 是正方形, ∴AC BC =CECF=2, ∴△CAE ∽△CBF.②解:∵AE BF =ACBC =2,AE =2,∴BF =AE2=2, 由△CAE ∽△CBF 可得∠CAE =∠CBF , 又∵∠CAE +∠CBE =90°, ∴∠CBF +∠CBE =90°,即∠EBF =90°,第14题解图②由CE 2=2EF 2=2(BE 2+BF 2)=6, 解得CE = 6.(2)解:连接BF ,如解图②,同(1)证△CAE ∽△CBF ,可得∠EBF =90°,AC BC =AE BF, 由AB BC =EFFC=k ,可得BC ∶AB ∶AC =1∶k ∶k 2+1, CF ∶EF ∶EC =1∶k ∶k 2+1,∴CE EF =ACAB =k 2+1k ,AE BF =AC BC=k 2+1, ∴EF =kCE k 2+1,EF 2=k 2CE 2k 2+1,BF =AE k 2+1,BF 2=AE 2k 2+1,∴CE 2=k 2+1k 2×EF 2=k 2+1k2(BE 2+BF 2), ∴32=k 2+1k 2(12+22k 2+1), 解得k =104. (3)解:p 2-n 2=(2+2)m 2.【解法提示】如解图③,连接BF ,同(1)证△CAE ∽△CBF ,可得∠EBF =90°, 过点C 作CH ⊥AB 交AB 延长线于点H , 类比第(2)问得AB 2∶BC 2∶AC 2=1∶1∶(2+2),第14题解图③EF 2∶FC 2∶EC 2=1∶1∶(2+2), ∴p 2=(2+2)EF 2=(2+2)(BE 2+BF 2)=(2+2)(m 2+n 22+2)=(2+2)m 2+n 2,∴p 2-n 2=(2+2)m 2.15. 证明:(1)①连接AH ,如解图①. 第15题解图①∵四边形OBFC 是平行四边形, ∴BH =HC =12BC ,OH =HF ,∵△ABC 是等边三角形, ∴AB =BC ,AH ⊥BC ,在Rt △ABH 中,AH 2=AB 2-BH 2, ∴AH =BC 2-(12BC )2=32BC ,∵OA =AE ,OH =HF ,∴AH 是△OEF 的中位线, ∴AH =12EF ,AH ∥EF ,∴EF ⊥BC.②由①得AH =32BC ,∵AH =12EF∴32BC =12EF ,∴EF =3BC.(2)EF ⊥AB 仍然成立,EF =BC.第15题解图②【解法提示】如解图②,连接AH,∵四边形OBFC是平行四边形,∴BH=HC=12BC,OH=HF,∵△ABC是等腰直角三角形,∴AH⊥BC,在Rt△ABH中,AH2=AB2-BH2=(2BH)2-BH2=BH2,∴AH=BH=12BC,∵OA=AE,OH=HF,∴AH是△OEF的中位线,∴AH=12EF,AH∥EF,∴EF⊥BC,EF=2AH=BC.第15题解图③(3)EF=4k2-1 BC.【解法提示】如解图③,连接AH,∵四边形OBFC是平行四边形,∴BH=HC=12BC,OH=HF,∵△ABC是等腰三角形,AB=kBC,∴AH⊥BC,在Rt△ABH中,AH2=AB2-BH2=(kBC)2-(12=(k2-14)BC2,2BC)∴AH=12-1 BC,24k∵OA=AE,OH=HF,∴AH是△OEF的中位线,∴AH=12EF,AH∥EF,∴EF⊥BC,12-1 BC=12EF,24k∴EF=4k2-1 BC.。
初中数学(几何探究型问题)题库及答案

初中数学(几何探究型问题)题库及答案1.(2019•北京)在△ABC中,D,E分别是△ABC两边的中点,如果DE上的所有点都在△ABC的内部或边上,则称DE为△ABC的中内弧.例如,图1中DE 是△ABC的一条中内弧.(1)如图2,在Rt△ABC中,AB=AC=D,E分别是AB,AC的中点,画出△ABC的最长的中内弧DE,并直接写出此时DE的长;(2)在平面直角坐标系中,已知点A(0,2),B(0,0),C(4t,0)(t>0),在△ABC中,D,E分别是AB,AC的中点.①若t12=,求△ABC的中内弧DE所在圆的圆心P的纵坐标的取值范围;②若在△ABC中存在一条中内弧DE,使得DE所在圆的圆心P在△ABC的内部或边上,直接写出t的取值范围.【解析】(1)如图2,以DE为直径的半圆弧DE,就是△ABC的最长的中内弧DE,连接DE.∵∠A=90°,AB=AC=D,E分别是AB,AC的中点.∴BC sin AC B ===4,DE 12=BC 12=⨯4=2.∴弧12DE =⨯2π=π. (2)如图3,由垂径定理可知,圆心一定在线段DE 的垂直平分线上,连接DE ,作DE 垂直平分线FP ,作EG ⊥AC 交FP 于G .①当t 12=时,C (2,0),∴D (0,1),E (1,1),F (12,1).设P (12,m )由三角形中内弧定义可知,圆心线段DE 上方射线FP 上均可,∴m ≥1.∵OA =OC ,∠AOC =90°. ∴∠ACO =45°. ∵DE ∥OC .∴∠AED =∠ACO =45°.作EG ⊥AC 交直线FP 于G ,FG =EF 12=. 根据三角形中内弧的定义可知,圆心在点G 的下方(含点G )直线FP 上时也符合要求. ∴m 12≤.综上所述,m 12≤或m ≥1. ②如图4,设圆心P 在AC 上.∵P 在DE 中垂线上.∴P 为AE 中点,作PM ⊥OC 于M ,则PM 32=. ∴P (t ,32). ∵DE ∥BC .∴∠ADE =∠AOB =90°.∴AE === ∵PD =PE . ∴∠AED =∠PDE .∵∠AED +∠DAE =∠PDE +∠ADP =90°. ∴∠DAE =∠ADP . ∴AP =PD =PE 12=AE .由三角形中内弧定义知,PD ≤PM .∴12AE 32≤,AE ≤3≤3,解得:t ≤ ∵t >0. ∴0<t≤【名师点睛】此题是一道圆的综合题,考查了圆的性质,弧长计算,直角三角形性质等,给出了“三角形中内弧”新定义,要求学生能够正确理解新概念,并应用新概念解题.2.(2019•天津)在平面直角坐标系中,O为原点,点A(6,0),点B在y轴的正半轴上,∠ABO=30°.矩形CODE的顶点D,E,C分别在OA,AB,OB上,OD=2.(Ⅰ)如图①,求点E的坐标;(Ⅱ)将矩形CODE沿x轴向右平移,得到矩形C′O′D′E′,点C,O,D,E 的对应点分别为C′,O′,D′,E′.设OO′=t,矩形C′O′D′E′与△ABO重叠部分的面积为S.①如图②,当矩形C′O′D′E′与△ABO重叠部分为五边形时,C′E′,E′D′分别与AB相交于点M,F,试用含有t的式子表示S,并直接写出t的取值范围;S t的取值范围(直接写出结果即可).【解析】(Ⅰ)∵点A(6,0).∴OA=6.∵OD=2.∴AD=OA-OD=6-2=4.∵四边形CODE是矩形.∴DE∥OC.∴∠AED=∠ABO=30°.在Rt△AED中,AE=2AD=8,ED===∵OD =2.∴点E 的坐标为(2,.(Ⅱ)①由平移的性质得:O ′D ′=2,E ′D ME ′=OO ′=t ,D ′E ′∥O ′C ′∥OB . ∴∠E ′FM =∠ABO =30°.∴在Rt △MFE ′中,MF =2ME ′=2t ,FE ′===.∴S △MFE ′12=ME ′·FE ′12=⨯t 22=.∵S 矩形C ′O ′D ′E ′=O ′D ′·E ′D =∴S =S 矩形C ′O ′D ′E ′-S △MFE ′.∴S 2=-t 2,其中t 的取值范围是:0<t <2;②当S =O 'A =OA -OO '=6-t .∵∠AO 'F =90°,∠AFO '=∠ABO =30°.∴O 'F ='A =6-t ).∴S 12=(6-t )(6-t )=解得:t =6,或t =6.∴t =6S 时,如图④所示:O 'A =6-t ,D 'A =6-t -2=4-t .∴O 'G =6-t ),D 'F =4-t ).∴S 12=6-t )4-t ) 解得:t 52=.S t 的取值范围为52≤t ≤6.【名师点睛】本题是四边形综合题目,考查了矩形的性质、坐标与图形性质、勾股定理、平移的性质、直角三角形的性质、梯形面积公式等知识;本题综合性强,有一定难度,熟练掌握含30°角的直角三角形的性质时是解题的关键. 3.(2019•陕西)问题提出:(1)如图1,已知△ABC ,试确定一点D ,使得以A ,B ,C ,D 为顶点的四边形为平行四边形,请画出这个平行四边形; 问题探究:(2)如图2,在矩形ABCD 中,AB =4,BC =10,若要在该矩形中作出一个面积最大的△BPC ,且使∠BPC =90°,求满足条件的点P 到点A 的距离; 问题解决:(3)如图3,有一座塔A ,按规定,要以塔A 为对称中心,建一个面积尽可能大的形状为平行四边形的景区BCDE .根据实际情况,要求顶点B 是定点,点B到塔A的距离为50米,∠CBE=120°,那么,是否可以建一个满足要求的面积最大的平行四边形景区BCDE?若可以,求出满足要求的平行四边形BCDE的最大面积;若不可以,请说明理由.(塔A的占地面积忽略不计)【解析】(1)如图记为点D所在的位置.(2)如图.∵AB=4,BC=10,∴取BC的中点O,则OB>AB.∴以点O为圆心,OB长为半径作⊙O,⊙O一定于AD相交于P1,P2两点.连接BP1,P1C,P1O,∵∠BPC=90°,点P不能再矩形外.∴△BPC的顶点P1或P2位置时,△BPC的面积最大.作P1E⊥BC,垂足为E,则OE=3.∴AP1=BE=OB-OE=5-3=2.由对称性得AP2=8.(3)可以,如图所示,连接BD.∵A为BCDE的对称中心,BA=50,∠CBE=120°.∴BD=100,∠BED=60°.作△BDE的外接圆⊙O,则点E在优弧BD上,取BED的中点E′,连接E′B,E′D.则E′B=E′D,且∠BE′D=60°,∴△BE′D为正三角形.连接E′O并延长,经过点A至C′,使E′A=AC′,连接BC′,DC′.∵E′A⊥BD.∴四边形E′D为菱形,且∠C′BE′=120°.作EF⊥BD,垂足为F,连接EO,则EF≤EO+OA-E′O+OA=E′A.∴S△BDE12=·BD·EF12≤·BD·E′A=S△E′BD.∴S平行四边形BCDE≤S平行四边形BC′DE′=2S△E′BD=1002·m2).所以符合要求的BCDE的最大面积为2.【名师点睛】本题属于四边形综合题,考查了平行四边形的判定和性质,圆周角定理,三角形的面积等知识,解题的关键是理解题意,学会添加常用辅助线,属于中考压轴题.4.(2019•海南)如图,在边长为1的正方形ABCD中,E是边CD的中点,点P 是边AD上一点(与点A、D不重合),射线PE与BC的延长线交于点Q.(1)求证:△PDE≌△QCE;(2)过点E作EF∥BC交PB于点F,连结AF,当PB=PQ时.①求证:四边形AFEP是平行四边形;②请判断四边形AFEP是否为菱形,并说明理由.【解析】(1)∵四边形ABCD是正方形.∴∠D=∠ECQ=90°.∵E是CD的中点.∴DE=CE.又∵∠DEP=∠CEQ.∴△PDE≌△QCE.(2)①∵PB=PQ.∴∠PBQ=∠Q.∵AD∥BC.∴∠APB=∠PBQ=∠Q=∠EPD.∵△PDE≌△QCE.∴PE=QE.∵EF∥BQ.∴PF=BF.∴在Rt△P AB中,AF=PF=BF.∴∠APF=∠P AF.∴∠P AF=∠EPD.∴PE∥AF.∵EF∥BQ∥AD.∴四边形AFEP是平行四边形;②四边形AFEP不是菱形,理由如下:设PD=x,则AP=1-x.由(1)可得△PDE≌△QCE.∴CQ=PD=x.∴BQ=BC+CQ=1+x.∵点E、F分别是PQ、PB的中点.∴EF是△PBQ的中位线.∴EF12=BQ12x+=.由①知AP=EF,即1-x12x+ =.解得x1 3 =.∴PD13=,AP23=.在Rt△PDE中,DE1 2 =.∴PE==∴AP≠PE.∴四边形AFEP不是菱形.【名师点睛】本题是四边形的综合问题,解题的关键是掌握正方形的性质、全等三角形的判定与性质、直角三角形的性质、平行四边形与菱形的判定、性质等知识点.5.(2019•江西)在图1,2,3中,已知ABCD,∠ABC=120°,点E为线段BC 上的动点,连接AE,以AE为边向上作菱形AEFG,且∠EAG=120°.(1)如图1,当点E与点B重合时,∠CEF=__________°;(2)如图2,连接AF.①填空:∠F AD__________∠EAB(填“>”“<”“=”);②求证:点F在∠ABC的平分线上.(3)如图3,连接EG,DG,并延长DG交BA的延长线于点H,当四边形AEGH是平行四边形时,求BC的值.AB【解析】(1)∵四边形AEFG是菱形.∴∠AEF=180°-∠EAG=60°.∴∠CEF=∠AEC-∠AEF=60°.故答案为:60°.(2)①∵四边形ABCD是平行四边形.∴∠DAB=180°-∠ABC=60°.∵四边形AEFG是菱形,∠EAG=120°.∴∠F AE=60°.∴∠F AD=∠EAB.故答案为:=.②如图,作FM⊥BC于M,FN⊥BA交BA的延长线于N.则∠FNB=∠FMB=90°.∴∠NFM=60°,又∠AFE=60°.∴∠AFN=∠EFM.∵EF=EA,∠F AE=60°.∴△AEF为等边三角形.∴F A=FE.在△AFN和△EFM中,AFN EFMFNA FME FA FE∠=∠⎧⎪∠=∠⎨⎪=⎩.∴△AFN≌△EFM(AAS)∴FN=FM,又FM⊥BC,FN⊥BA.∴点F在∠ABC的平分线上.(3)如图.∵四边形AEFG是菱形,∠EAG=120°.∴∠AGF=60°.∴∠FGE=∠AGE=30°.∵四边形AEGH为平行四边形.∴GE∥AH.∴∠GAH=∠AGE=30°,∠H=∠FGE=30°.∴∠GAN=90°,又∠AGE=30°.∴GN=2AN.∵∠DAB=60°,∠H=30°.∴∠ADH=30°.∴AD=AH=GE.∵四边形ABCD为平行四边形.∴BC=AD.∴BC=GE.∵四边形ABEH为平行四边形,∠HAE=∠EAB=30°.∴平行四边形ABEN为菱形.∴AB=AN=NE.∴GE=3AB.∴BCAB3.【名师点睛】本题考查的是相似三角形的判定和性质、全等三角形的判定和性质、菱形的性质、平行四边形的性质,掌握全等三角形的判定定理和性质定理、菱形的性质、直角三角形的性质是解题的关键.6.(2019•宁夏)如图,在△ABC中,∠A=90°,AB=3,AC=4,点M,Q分别是边AB,BC上的动点(点M不与A,B重合),且MQ⊥BC,过点M作BC的平行线MN,交AC于点N,连接NQ,设BQ为x.(1)试说明不论x为何值时,总有△QBM∽△ABC;(2)是否存在一点Q,使得四边形BMNQ为平行四边形,试说明理由;(3)当x为何值时,四边形BMNQ的面积最大,并求出最大值.【解析】(1)∵MQ⊥BC.∴∠MQB=90°.∴∠MQB=∠CAB,又∠QBM=∠ABC.∴△QBM∽△ABC.(2)当BQ=MN时,四边形BMNQ为平行四边形.∵MN∥BQ,BQ=MN.∴四边形BMNQ为平行四边形.(3)∵∠A=90°,AB=3,AC=4.∴BC==5.∵△QBM∽△ABC.∴QB QM BMAB AC BC==,即345x QM BM==.解得,QM43=x,BM53=x.∵MN∥BC.∴MN AMBC AB=,即53353xMN-=.解得,MN=525 9 -x.则四边形BMNQ的面积12=⨯(5259-x+x)43⨯x3227=-(x4532-)27532+.∴当x4532=时,四边形BMNQ的面积最大,最大值为7532.【名师点睛】本题考查的是相似三角形的判定和性质、平行四边形的判定、二次函数的性质,掌握相似三角形的判定定理、二次函数的性质是解题的关键.7.(2019•安徽)如图,Rt△ABC中,∠ACB=90°,AC=BC,P为△ABC内部一点,且∠APB=∠BPC=135°.(1)求证:△P AB∽△PBC;(2)求证:P A=2PC;(3)若点P到三角形的边AB,BC,CA的距离分别为h1,h2,h3,求证h12=h2·h3.【解析】(1)∵∠ACB=90°,AB=BC.∴∠ABC=45°=∠PBA+∠PBC.又∠APB=135°.∴∠P AB+∠PBA=45°.∴∠PBC=∠P AB.又∵∠APB=∠BPC=135°.(2)∵△P AB ∽△PBC .∴PA PB ABPB PC BC==. 在Rt △ABC 中,AB =AC .∴ABBC= ∴PB PA ==,. ∴P A =2PC .(3)如图,过点P 作PD ⊥BC ,PE ⊥AC 交BC 、AC 于点D ,E .∴PF =h 1,PD =h 2,PE =h 3. ∵∠CPB +∠APB =135°+135°=270°. ∴∠APC =90°. ∴∠EAP +∠ACP =90°.又∵∠ACB =∠ACP +∠PCD =90°. ∴∠EAP =∠PCD . ∴Rt △AEP ∽Rt △CDP .∴2PE APDP PC==,即322h h =. ∴h 3=2h 2.∴12h ABh BC ==.∴12h .∴2212222322h h h h h h ==⋅=.即:h 12=h 2·h 3.【名师点睛】此题主要考查了相似三角形的判定和性质,等腰直角三角形的性质,判断出∠EAP =∠PCD 是解本题的关键.8.(2019•重庆A 卷)如图,在平行四边形ABCD 中,点E 在边BC 上,连结AE ,EM ⊥AE ,垂足为E ,交CD 于点M ,AF ⊥BC ,垂足为F ,BH ⊥AE ,垂足为H ,交AF 于点N ,点P 是AD 上一点,连接CP .(1)若DP =2AP =4,CP =CD =5,求△ACD 的面积. (2)若AE =BN ,AN =CE ,求证:AD=+2CE .【解析】(1)作CG ⊥AD 于G ,如图1所示:设PG =x ,则DG =4-x .在Rt △PGC 中,GC 2=CP 2-PG 2=17-x 2.在Rt△DGC中,GC2=CD2-GD2=52-(4-x)2=9+8x-x2.∴17-x2=9+8x-x2.解得:x=1,即PG=1.∴GC=4.∵DP=2AP=4.∴AD=6.∴S△ACD12=⨯AD×CG12=⨯6×4=12.(2)连接NE,如图2所示:∵AH⊥AE,AF⊥BC,AE⊥EM.∴∠AEB+∠NBF=∠AEB+∠EAF=∠AEB+∠MEC=90°.∴∠NBF=∠EAF=∠MEC.在△NBF和△EAF中,NBF EAFBFN EFA AE BN∠=∠⎧⎪∠=∠⎨⎪=⎩.∴△NBF≌△EAF.∴BF=AF,NF=EF.∴∠ABC=45°,∠ENF=45°,FC=AF=BF.∴∠ANE=∠BCD=135°,AD=BC=2AF.在△ANE和△ECM中,MEC EAF AN ECANE ECM ∠=∠⎧⎪=⎨⎪∠=∠⎩.∴△ANE≌△ECM.∴CM=NE.又∵NF2=NE2=MC.∴AF2=MC+EC.∴AD=+2EC.【名师点睛】本题考查了平行四边形的性质、全等三角形的判定与性质、勾股定理、三角形面积公式等知识;熟练掌握平行四边形的性质,证明三角形全等是解题的关键.。
2023年九年级数学中考专题:几何探究压轴题

2023年九年级数学中考专题:几何探究压轴题一、解答题1.如图,在ABC 中,4AC =,3BC =,90ACB ∠=︒,D 是边AC 上一动点(不与点A 、C 重合),CE BD ⊥,垂足为E ,交边AB 于点F .(1)当点D 是边AC 中点时,求DE ,EC 的值;(2)设CD x =,AF y =,求y 关于x 的函数关系式,并写出定义域;(3)当EFD △与EFB △相似时,求线段CD 的长.2.【温故知新】黄金分割是一种最能引起美感的分割比例,具有严格的比例性、艺术性、和谐性,蕴藏着丰富的美学价值.我们知道:如图1,点C 把线段AB 分成两部分,如果BC AC AC AB=,那么称点C 为线段AB 的黄金分割点.(1)【问题发现】如图1,点C 为线段AB 的黄金分割点,且AC BC >,若2AB =,请直接写出CB 的值是__________.(2)【问题探究】如图2,在Rt ABC △中,90C ∠=︒,2AC =,1BC =,在BA 上截取BD BC =,再在AC 上截取AE AD =,则AE AC的值为__________. (3)【问题解决】如图3,用边长为6的正方形纸片进行如下操作:对折正方形ABDE 得折痕MN ,连接EN ,将AE 折叠到EN 上,点A 对应点H ,得折痕CE ,试说明:C 是AB 的黄金分割点.3.定义:若连接三角形一个顶点和对边上一点的线段能把该三角形分成一个等腰三角形和一个直角三角形,我们称这条线段为该三角形的智慧线,这个三角形叫做智慧三角形.(1)如图1,在智慧三角形ABC 中,AD BC ⊥,AD 为该三角形的智慧线,1CD =,则BD 长为_____,B ∠的度数为_____.(2)如图2,ABC 为等腰直角三角形,90BAC ∠︒=,2AB =,F 是斜边BC 延长线上一点,连接AF ,以AF为直角边作等腰直角三角形AFE (点A ,F ,E 按顺时针排列),90EAF ∠=︒, CF =AE 交BC 于点D ,连接EC ,EB .当2BDE BCE ∠=∠时,求线段ED 的长;(3)如图3,ABC 中,5AB AC ==,BC =BCD △是智慧三角形,且AC 为智慧线,求BCD △的面积.4.【问题提出】如图1,在等边三角形ABC 内部有一点P ,3PA=,4PB =,5PC =,求APB ∠的度数.(1)【尝试解决】将APC △绕点A 逆时针旋转60︒,得到AP B '△,连接PP ',则APP '为等边三角形. ∵3P P PA '==,4PB =,5P B PC '==,∴222=P P PB P B ''+∴BPP '为三角形∴APB ∠的度数为.(2)【类比探究】如图2,在等边三角形ABC 外部有一点P ,若∠BP A =30°,求证222PA PB PC +=.(3)【联想拓展】如图3,在ABC 中,90BAC ∠︒=,AB AC =.点P 在直线BC 上方且45APB ∠︒=,PC BC ==求PA 的长.5.已知正方形 ABCD 和正方形 CEFG ,连接 AF 交 BC 于点 O ,点 P 是 AF 的中点,过点 P 作 PH DG ⊥ 于 H ,2CD =,1CG =.(1)如图1,点 D ,C ,G 在同一直线上,点 E 在 BC 边上,求 PH 的长;(2)把正方形 CEFG 绕着点C 逆时针旋转 ()0180αα<<.①如图2,当点E 落在AF 上时,求CO 的长;②如图3,当DG =PH 的长.6.在ABC ∆中,点E 为AC 边上一动点,以CE 为边在CE 上方作等边CEN .(1)如图1,EN 与AB 交于点P ,连接PC ,若tan A =,1AE =,5CN =,求PC 的长: (2)如图2.当N 与B 重合时,在BC 上取一点D ,过点D 作DF AC ∥,连接BF ,EF ,过C 作CH EF ⊥交EF 于点H ,若30FBC DFE ︒∠-∠=,求证:CH BF +=;(3)如图3,若BC AB ⊥,且4AB BC ==,过点B 作BQ AC ∥,I 为射线.BQ 上一动点,取AC 中点M ,连接MI ,过点B 作BK MI ⊥交M 于点K ,连接NK ,直接写出NK 的最小值.7.问题情境:如图1,在Rt △ABC 和Rt △BEF 中,∠ACB =∠EFB =90°,AC =3,BC =4,且M ,N 分别为AE ,CF 的中点.(1)猜想证明:如图2,将Rt △BEF 绕点B 按逆时针方向旋转90°,其他条件不变.试判断54AM CN =是否成立?若成立,请写出证明过程;若不成立,请说明理由.(2)解决问题:如图3,将图2中的Rt △BEF 沿BF 所在直线折叠得到Rt BE F ',连接AE ',CF ,并分别取它们的中点P ,H ,连接CP ,FP ,PH .①试判断CP 与FP 之间的数量关系,并说明理由.②若AB =2BE ',BC =2BF ,请直接写出PH 的长.8.【方法尝试】(1)如图1,矩形ABFC 是矩形ADGE 以点A 为旋转中心,按逆时针方向旋转90︒所得的图形,CB ED 、分别是它们的对角线.则CB 与ED 数量关系________,位置关系________.【类比迁移】(2)如图2,在Rt ABC 和Rt ADE △中,90,9,6,3,2BAC DAE AC AB AE AD ∠=∠=︒====.将DAE 绕点A 在平面内逆时针旋转,设旋转角BAE ∠为()0360αα︒<︒,连接,CE BD .请判断线段CE 和BD 的数量关系和位置关系,并说明理由;【拓展延伸】(3)如图3,在Rt ABC 中,90,6ACB AB ∠=︒=,过点A 作AP BC ∥,在射线AP 上取一点D ,连结CD,使得3tan4ACD∠=,请求写出线段BD的最大值.9.如图①,在正方形ABCD中,点N、M分别在边BC、CD上,连接AM、AN、MN.∠MAN=45°,将△AMD 绕点A顺时针旋转90°,点D与点B重合,得到△ABE.易证:△ANM≌△ANE,从而得DM+BN=MN.【实践探究】(1)在图①条件下,若CN=6,CM=8,则正方形ABCD的边长是______.(2)如图②,点M、N分别在边CD、AB上,且BN=DM.点E、F分别在BM、DN上,∠EAF=45°,连接EF,猜想三条线段EF、BE、DF之间满足的数量关系,并说明理由.(3)【拓展应用】如图③,在矩形ABCD中,AB=6,AD=8,点M、N分别在边DC、BC上,连接AM,AN,已知∠MAN=45°,BN=2,求DM的长.10.小圆同学对图形旋转前后的线段之间、角之间的关系进行了拓展探究.(1)猜测探究:在△ABC中,AB=AC,M是平面内任意一点,将线段AM绕点A按顺时针方向旋转与∠BAC 相等的角度,得到线段AN,连接NB.①如图1,若M是线段BC上的任意一点,请直接写出∠NAB与∠MAC的数量关系是,NB与MC的数量关系是;②如图2,点E是AB延长线上点,若M是∠CBE内部射线BD上任意一点,连接MC,(1)中结论是否仍然成立?若成立,请给予证明,若不成立,请说明理由.(2)拓展应用:如图3,在△A 1B 1C 1中,A 1B 1=8,∠A 1B 1C 1=60°,∠B 1A 1C 1=75°,P 是B 1C 1上的任意点,连接A 1P ,将A 1P 绕点A 1按顺时针方向旋转75°,得到线段A 1Q ,连接B 1Q .求线段B 1Q 长度的最小值. 11.如图,在Rt ABC △中,90BAC ∠=︒,AB AC =,D 为AC 边上一点,连接BD ,作AP BD ⊥于点P ,过点C 作CE AC ⊥交AP 延长线于点E .(1)如图1,求证:AD CE =;(2)如图2,以AD ,BD 为邻边作ADBF ,连接EF 交BC 于点G ,连接AG ,①求证:AG EF ⊥;②若点D 为AC 中点,EF 、AB 交于点H ,求BH AB的值. 12.如图1,在ABC 中,90ACB ∠=︒,D 为AC 边上的一点,过点D 作DE AB ⊥,垂足为E ,连接BD ,P 为BD 中点,连接PC ,PE .(1)求证:PC PE =;(2)将图1中ADE 绕着点A 顺时针旋转如图2的位置,其他条件不变,(1)中的结论是否成立?若成立,请证明:若不成立,请说明理由;(3)若10AB =,6AD =,30BAC DAE ∠=∠=︒,在平面内,将Rt ADE △绕点A 旋转一周,当A ,C ,E 三点共线时,请直接写出PCE 的面积.13.如图1,在直角坐标系中,点()2,0A ,点()0,2C ,点D ,点E 分别为OA ,OC 的中点,ODE 绕原点O 顺时针旋转α角(090α︒<<︒)得11OD E ,射线1CD ,1AE 相交于点F .(1)求证:11OCD OAE △≌△;(2)如图2,在ODE 旋转过程中,当点1D 恰好落在线段CE 上时,求AF 的长;(3)如图3,在旋转α角从090α︒≤≤︒逐渐增大ODE 旋转过程中,求点F 的运动路线长.14.已知ABC 为等边三角形,边长为4,点D 、E 分别是BC 、AC 边上一点,连接AD 、BE .AE CD =.(1)如图1,若2AE =,求BE 的长度;(2)如图2,点F 为AD 延长线上一点,连接BF 、CF ,AD 、BE 相交于点G ,连接CG ,已知60,∠=︒=EBF CE CG ,求证:2+=BF GE CF ;(3)如图3,点P 是ABC 内部一动点,顺次连接PA PB PC 、、++的最小值.15.【问题提出】(1)如图1,在ABC 中,90C ∠=︒,BD 平分ABC ∠交AC 于点D ,设CD 的长为m ,点D 到边AB 的距离为n ,则m _______n ;(填“>”“<”或“=”)【问题探究】(2)如图2,在梯形ABCD 中,90A ∠=︒,AD BC ∥,(201AB =,BD 为对角线,且45BDC ∠=︒,求BCD △面积的最小值;【问题解决】(3)某景点有一个形状为菱形ABCD 的草坪,如图3,AB ==60B ∠︒,现欲将该草坪扩建为BEF △,使得点E 、F 分别在BA 、BC 的延长线上,且边EF 经过点D ,为了节省成本,要求扩建后的草坪面积(BEF △的面积)尽可能小,问BEF △的面积是否存在最小值?若存在,求出其最小值;若不存在,请说明理由.16.综合与实践:数学课外小组研究了两个问题,请你帮助解答.问题一:如图1,在矩形ABCD 中,6AB =,8AD =,E ,F 分别为AB ,AD 边的中点,四边形AEGF 为矩形,连接CG .问题二:数学小组对图形的旋转进行了拓展研究,如图4,在平行四边形ABCD 中,=60B ∠︒,6AB =,8AD =,E ,F 分别为AB ,AD 边的中点,四边形AEGF 为平行四边形,连接CG .数学小组发现DF 与CG 仍然存在着特定的数量关系.(1)请直接写出CG 的长是______.如图2,当矩形AEGF 绕点A 旋转(如顺时针旋转)至点G 落在边AB 上时,DF =______,CG =______,DF 与CG 之间的数量关系是______.(2)当矩形AEGF 绕点A 旋转至如图3的位置时,(1)中DF 与CG 之间的数量关系是否还成立?并说明理由.(3)如图5,当平行四边形ABCD 绕点A 旋转(如顺时针旋转),其它条件不变时,数学小组发现DF 与CG 仍然存在着这一特定的数量关系.请你直接写出这个特定的数量关系是______.17.如图,在四边形ABCD 中,AD ∥BC ,∠ABC =90°,AD =CD ,O 是对角线AC 的中点,连接BO 并延长交边AD 或边CD 于点E .(1)如图1,当点E 在AD 上时,连接CE ,求证:四边形ABCE 是矩形.(2)如图2,当点E 在CD 上时,当AC =4,BC =3时,求DAC S △与OBC S的比值.(3)若DE =2,OE =3,直接写出CD 的长.18.已知在正方形ABCD 中,E 是BC 边上一动点,作点B 关于AE 的对称点F ,BF 交AE 于点G ,连结DF .(1)如图1,求DFB ∠的度数;(2)如图2,过点D 作DM BF ⊥交BF 的延长线于点M ,连结,CM CF .若DF CM =,试探究四边形DFCM 的形状,并说明理由;(3)如图3,连结BD ,在AG 上截取=GT GB ,点P ,Q 分别是,AD BD 上的动点.若正方形ABCD 的面积为32,直接写出PTQ 周长的最小值.。
中考几何压轴探究题

中考几何压轴探究题一、在三角形ABC中,D是BC边上的一点,AD是角BAC的角平分线,且BD比DC等于AB比AC,若角BAC等于60度,则角ADC等于多少度?A、90度B、100度C、120度D、150度(答案)C解析:根据题意,可知三角形ABD与三角形ACD在AD上共线,且AD是角BAC的角平分线,所以角BAD等于角CAD等于30度。
又因为BD比DC等于AB比AC,所以三角形ABD与三角形ACD相似。
根据相似三角形的性质,角ADB等于角ACD。
设角ADB为x,则角ACD也为x,角ADC为180度减x。
由于三角形内角和为180度,所以角ADB加角ADC加角DAC等于180度,即x加(180度减x)加30度等于180度,解得角ADC等于120度,故选C。
二、在矩形ABCD中,E是AD的中点,F是AB上的一点,且AF比FB等于1比3,连接EF、CF,若角FEC等于90度,则角DCF等于多少度?A、15度B、30度C、45度D、60度(答案)B解析:设AF为x,则FB为3x,由于E是AD的中点,所以AE等于ED。
在直角三角形FEC 中,由于角FEC等于90度,所以角FEA加角CED等于90度。
又因为三角形FAE与三角形CDE在AE和ED上共线,且AE等于ED,所以三角形FAE与三角形CDE全等,角FAE等于角CDE。
设角FAE为a,则角CDE也为a,角DCF为90度减a。
在直角三角形FBC中,角CFB 等于90度,所以角FCB加角FBC等于90度。
又因为FB比FC等于3比根号10(根据勾股定理计算得出),所以角FBC等于30度,角FCB等于60度。
由于角FCD等于角FCB减角DCF,所以角DCF等于60度减(90度减a),即角DCF等于a减30度。
又因为角CDE等于a,所以角DCF加角CDE等于90度,即2a减30度等于90度,解得a等于60度,所以角DCF等于60度减30度等于30度,故选B。
三、在三角形ABC中,AB等于AC,D是BC上的一点,且BD比DC等于2比1,AD的延长线交三角形ABC的外接圆于点E,则角EDC等于多少度?A、30度B、36度C、45度D、60度(答案)B解析:连接BE,由于AB等于AC,所以角ABC等于角ACB。
中考数学专题复习几何探究练习(三)

中考数学专题复习几何探究练习(三)学校:___________姓名:___________班级:___________考生__________评卷人得分一、解答题1.【感知】如图①,点C是AB中点,CD⊥AB,P是CD上任意一点,由三角形全等的判定方法“SAS”易证△P AC≌△PBC,得到线段垂直平分线的一条性质“线段垂直平分线上的点到线段两端的距离相等”【探究】如图①,在平面直角坐标系中,直线y=-13x+1分别交x轴、y轴于点A和点B,点C是AB中点,CD⊥AB交OA于点D,连结BD,求BD的长【应用】如图①(1)将线段AB绕点A顺时针旋转90°得到线段AB′,请在图①网格中画出线段AB;(2)若存在一点P,使得P A=PB′,且∠APB′≠90°,当点P的横、纵坐标均为整数时,则AP长度的最小值为______.2.如图,在正方形ABCD中,点E是边BC上任意一点(点E不与点B、C重合),连结DE,点C关于DE的对称点为C1,连结AC1并延长交DE的延长线于点M,F是AC1的中点,连结DF.【猜想】如图①,①FDM的大小为度.【探究】如图①,过点A作AM1①DF交MD的延长线于点M1,连结BM.求证:△ABM①①ADM1.【拓展】如图①,连结AC,若正方形ABCD的边长为2,则△ACC1面积的最大值为.3.问题呈现:下图是小明复习全等三角形时遇到的一个问题并引发的思考,请帮助小明完成以下学习任务.请根据小明的思路,结合图①,写出完整的证明过程.结论应用:(1)如图①,在四边形ABCD中,AB AD BC=+,DAB∠的平分线和ABC∠的平分线交于CD边上点P.求证:PC PD=;(2)在(1)的条件下,如图①,若10AB=,1tan2PAB∠=.当PBC有一个内角是45︒时,PAD△的面积是.4.【教材呈现】如图是华师版八年级下册数学教材第117页的部分内容.结合图①,补全证明过程.【应用】如图①,直线EF分别交矩形ABCD的边AD、BC于点E、F,将矩形ABCD 沿EF翻折,使点C的对称点与点A重合,点D的对称点为D′,若AB=3,BC=4,则四边形ABFE的周长为.【拓展】如图①,直线EF分别交▱ABCD的边AD、BC于点E、F,将▱ABCD沿EF翻折,使点C的对称点与点A重合,点D的对称点为D′,若AB=22,BC=4,①C=45°,则EF的长为.5.在等腰直角三角形纸片ABC中,点D是斜边AB的中点,10,AB=点E为BC上一点,将纸片沿DE折叠,点B的对应点为点B'.()1如图①,连接,CD则CD的长为;()2如图①,'B E与AC交于点,//F DB BC'.①求证:四边形'BDB E为菱形;①连接',B C则'B FC的形状为;()3如图①,则CEF∆的周长为;6.【教材呈现】数学课上,赵老师用无刻度的直尺和圆规按照华师版教材八年级上册87页完成角平分线的作法,方法如下:【问题1】赵老师用尺规作角平分线时,用到的三角形全等的判定方法是.【问题2】小明发现只利用直角三角板也可以作①AOB的角平分线,方法如下:步骤:①利用三角板上的刻度,在OA、OB上分别截取OM、ON,使OM=ON.①分别过点M、N作OM、ON的垂线,交于点P.①作射线OP,则OP为①AOB的平分线.(1)请写出小明作法的完整证明过程.(2)当tan①AOB=43时,量得MN=4cm,直接写出MON△的面积.7.教材呈现:如图是华师版九年级上册数学教材第77页的部分内容.定理证明:请根据教材内容,结合图①,写出证明过程.定理应用:在矩形ABCD中,AB=2AD,AC为矩形ABCD的对角线,点E在边AB上,且AE=3BE.(1)如图①,点F在边CB上,连结EF.若13BFCF,则EF与AC的关系为.(2)如图①,将线段AE绕点A旋转一定的角度α(0°<α<360°),得到线段AE',连结CE′,点H为CE'的中点,连结BH.设BH的长度为m,若AB=4,则m的取值范围为.8.在等腰直角三角形纸片ABC中,点D是斜边AB的中点,AB=10,点E为BC上一点,将纸片沿DE折叠,点B的对应点为点B'.(1)如图①,连接CD,则CD的长为;(2)如图①,B'E与AC交于点F,DB'①BC.①求证:四边形BDB'E为菱形;①连接B'C,则①B'FC的形状为;(3)如图①,则①CEF的周长为.9.如图,在ABC中,中线BD,CE相交于点O,F,G分别是OB,OC的中点.(1)求证:四边形DEFG是平行四边形;(2)当四边形DEFG的形状为矩形时,ABC为______三角形;(3)连接OA,当OA BC时,四边形DEFG的形状为______.10.如图1,正方形ABCD的边长为8cm,点F从点B出发,沿射线AB方向以1cm/秒的速度移动,点E从点D出发,向点A以1cm/秒的速度移动(不与点A重合).设点E,F同时出发移动t秒.(1)基础探究:如图1,在点E、F移动过程中,连接CE、CF、EF,判断CE与CF的数量与位置关系,并说明理由.(2)应用拓展:如图2,点G、H分别在边AD、BC上,且217cmGH=,连接EF,当EF与GH交于点P,且45GPE∠=︒,若点P为EF的中点,则CF的长度为________,AP的长度为________.参考答案:1.探究:BD 的长为53;应用:(1)见解析;(2)5.【解析】 【分析】探究:根据直线解析式,求出点A 、B 坐标,得到BO 、AO 的长,设BD 的长为a ,根据勾股定理列方程可求出BD ;应用:(1)根据旋转的性质作图即可;(2)根据题意可知P 点坐标在AB’线段垂直平分线上,如图所示,点P’是垂直平分线上最近的格点,但是此时'’90AP B ∠=︒,不符合题意,根据网格特点可知垂直平分线上下一个格点位置,由网格特点和勾股定理可得符合题意的AP=5. 【详解】 解:探究: 由题意得:当x 0=时,y 1=;当y 0=时,x 3=;()A 3,0∴,()B 0,1. AO 3∴=,BO 1=.设BD 的长为a .①点C 是AB 中点,CD AB ⊥交OA 于点D ,DA DB a ∴==,OD 3a =-.在Rt BOD 中,BOD 90∠=︒,222BD BO DO ∴=+,()22213a a +-=,5a 3∴=,5BD 3=. BD ∴的长为53.应用:(1)如图,线段'AB 即为所求.(2)根据题意可知P点坐标在AB’线段垂直平分线上,如图所示,点P’是垂直平分线上最近的格点,但是此时'’90AP B∠=︒,不符合题意,根据网格特点可知垂直平分线上下一个格点位置,由网格特点和勾股定理可得符合题意的AP=5.【点睛】本题主要考查了线段垂直平分线的性质,熟知线段垂直平分线上的点到线段两端点的距离相等是解题关键.2.(1)45°;(2)证明见解析;(3)22﹣2.【解析】【分析】(1)证明①CDE=①C1DE和①ADF=①C1DF,可得①FDM=12①ADC=45°;(2)先判断出①DAM1=①BAM,由(1)可知:①FDM=45°,进而判断出①AMD=45°,得出AM=AM1,即可得出结论;(3)先作高线C1G,确定①ACC1的面积中底边AC为定值2,根据高的大小确定面积的大小,当C1在BD上时,C1G最大,其①AC1C的面积最大,并求此时的面积.【详解】(1)由对称得:CD=C1D,①CDE=①C1DE,在正方形ABCD中,AD=CD,①ADC=90°,①AD=C1D,①F是AC1的中点,①DF①AC1,①ADF=①C1DF,①①FDM=①FDC1+①EDC1=12①ADC=45°;故答案为:45;(2)①DF①AC1,①①DFM=90°,①①MAM'=90°,在正方形ABCD中,DA=BA,①BAD=90°,①①DAM1=①BAM,由(1)可知:①FDM=45°①①DFM=90°①①AMD=45°,①①M1=45°,①AM=AM1,在:△ABM和△ADM1中,①11BA DABAM DAMAH AM=⎧⎪∠=∠⎨⎪=⎩,①①ABM①①ADM1(SAS);(3)如图,过C1作C1G①AC于G,则1AC CS=12AC•C1G,在Rt△ABC中,AB=BC=2,①AC=2222+=22,即AC为定值,当C1G最大值,△AC1C的面积最大,连接BD交AC于O,当C1在BD上时,C1G最大,此时G与O重合,①CD=C1D=2,OD=12AC=2,①C1G=C1D﹣OD=2﹣2,①1AC CS=12AC•C1G=12×22(2﹣2)=22﹣2,故答案为:22﹣2.此题是四边形综合题,主要考查了正方形的性质、等腰直角三角形的判定和性质、全等三角形的判定和性质等知识,解题的关键是①AMD=45°.3.问题呈现:见解析;结论应用:(1)见解析;(2)403或8 【解析】【分析】问题呈现:由“SAS ”可证△MOP ≌△NOP ,可得PM =PN ;结论应用:(1)在AB 上截取AE =AD ,连接PE ,由“SAS ”可证△ADP ≌△AEP ,△BPC ≌△BPE ,可得PD =PE =PC ;(2)延长AP ,BC 交于点H ,由“ASA ”可证△ADP ≌△HCP ,可得CP =DP ,AD =CH ,S △ADP =S △CPH ,分三种情况讨论,由角平分线的性质和锐角三角函数可求解.【详解】问题呈现:证明:①OC 平分AOB ∠,①AOC BOC ∠=∠.在POM 和PON △中,OP OP POM PON OM ON =⎧⎪∠=∠⎨⎪=⎩.①POM PON △≌△.结论应用:在AB 上截取AE AD =,①AP 平分DAB ∠,①DAP BAP ∠=∠,①AP AP =,①ADP AEP △≌△.①PE PD=.①AB AD BC=+,①BE BC=,①BP平分ABC∠,①ABP CBP ∠=∠.①BP BP=.①PBE PBC△≌△.①PE PC=.①PC PD=.(2)由(1)可证∠D=∠AEP,∠PCB=∠PEB,∵∠AEP+∠PEB=180°,∴∠PCB+∠D=180°,∴AD∥BC,∵AB=10,tan∠P AB=PBPA=12,∴P A=2PB,∵P A2+PB2=AB2,∴PB=25,P A=45,如图③,延长AP,BC交于点H,∵AD∥BC,∴∠DAP=∠H,∴∠H=∠BAP,∴AB=BH=10,又∵PB平分∠ABC,∴BP⊥AP,AP=PH=45,∵∠DAP=∠H,AP=PH,∠DP A=∠CPH,∴△ADP≌△HCP(ASA),∴CP=DP,AD=CH,S△ADP=S△CPH,若∠PBC=45°时,则∠PBC=∠H=45°,∴PB=PH(不合题意舍去),若∠BPC=45°时,则∠HPC=∠BPC=45°,如图④,过点C作CN⊥BP于N,CM⊥PH于M,∴CM=CN,∵S△PBH=12×BP×PH=12×BP×CN+12×PH×CM,∴CM=CN=453,∴S△PCH=12×45×453=403=S△ADP;若∠PCB=45°时,如图⑤,过点P作PF⊥BC于F,∵∠P AB=∠H,∴tan H=tan∠P AB=12,∴12 PFFH,∴FH=2PF,∵PF2+FH2=PH2=80,∴PF=4,FH=8,∵PF⊥BC,∠BCP=45°,∴∠PCB=∠FPC=45°,∴CF=PF=4,∴CH=4,∴S△ADP=S△CPH=12×4×4=8,故答案为:8或403.【点睛】本题是三角形综合题,考查了全等三角形的判定和性质,角平分线的性质,勾股定理,锐角三角函数等知识,添加恰当辅助线构造全等三角形是本题的关键.4.【教材呈现】证明见解析;【应用】434;【拓展】2103;【解析】【分析】教材呈现:由“ASA”可证①AOE①①COF,可得OE=OF,由对角线互相平分的四边形是平行四边形可证四边形AFCE是平行四边形,即可证平行四边形AFCE是菱形;应用:过点F作FH①AD于H,由折叠的性质可得AF=CF,①AFE=①EFC,由勾股定理可求BF的长,EF的长,拓展:过点A作AN①BC,交CB的延长线于N,过点F作FM①AD于M,由等腰直角三角形的性质可求AN=BN=2,由勾股定理可求AE=AF=103,再利用勾股定理可求EF的长.【详解】解:【教材呈现】①四边形ABCD是矩形,①AE①CF,①①EAO=①FCO,①EF垂直平分AC,①AO=CO,①AOE=①COF=90°,①①AOE①①COF(ASA)①OE=OF,又①AO=CO,①四边形AFCE是平行四边形,①EF①AC,①平行四边形AFCE是菱形;【应用】如图,过点F作FH①AD于H,①将矩形ABCD沿EF翻折,使点C的对称点与点A重合,①AF=CF,①AFE=①EFC,①AF2=BF2+AB2,①(4﹣BF)2=BF2+9,①BF=78,①AF=CF=258,①AD①BC,①①AEF=①EFC=①AFE,①AE=AF=258,①①B=①BAD=①AHF=90°,①四边形ABFH是矩形,①AB=FH=3,AH=BF=78,①EH=94,①EF=22EH FH+=81916+=154,①四边形ABFE的周长=AB+BF+AE+EF=3+78+258+154=434,故答案为:434.【拓展】如图,过点A作AN①BC,交CB的延长线于N,过点F作FM①AD于M,①四边形ABCD是平行四边形,①C=45°,①①ABC=135°,①①ABN=45°,①AN①BC,①①ABN=①BAN=45°,①AN=BN=22AB=2,①将▱ABCD沿EF翻折,使点C的对称点与点A重合,①AF=CF,①AFE=①EFC,①AD①BC,①①AEF=①EFC=①AFE,①AE=AF,①AF2=AN2+NF2,①AF2=4+(6﹣AF)2,①AF=103,①AE=AF=103,①AN①MF,AD①BC,①四边形ANFM是平行四边形,①AN①BC,①四边形ANFM是矩形,①AN =MF =2,①AM =22AF MF -=10049-=83, ①ME =AE ﹣AM =23,①EF =22MF ME +=449+=2103, 故答案为:2103. 【点睛】本题是四边形综合题,考查了平行四边形的性质,菱形的性质,折叠的性质,全等三角形的判定和性质,勾股定理等知识,添加恰当辅助线构造直角三角形是本题的关键. 5.(1)5;(2)①见解析;①等腰三角形;(3)52【解析】【分析】(1)利用直角三角形斜边上的中线等于斜边的一半即可求解;(2)①由翻折可知','45DB DB B B =∠=∠=︒,进而证得'//,B E AB 则有∴四边形'BDB E 为平行四边形,由',BD B D =即可得证;①连接CD,易证得','45DB DC DB E DCA =∠=∠=︒进而证得''FB C FCB ∠=∠,则有'FB FC =,即可得出结论;(3)由'FB FC =和'B E BE =得CEF ∆的周长=''CE FC EF CE B F EF CE B E CE BE BC ++=++=+=+=,由等腰直角三角形的性质可求得BC ,即可求得CEF ∆的周长.【详解】解:(1)①①ABC 是等腰直角三角形,D 为斜边AB 的中点,AB=10,①152CD AB ==, 故答案为:5;()2①证明:由翻折可知','45DB DB B B =∠=∠=︒'DB ①BC''45,B EC B ∴∠=∠=︒①'45,B EC B ∠=∠=︒①'EB ①BD∴四边形'BDB E 为平行四边形.又',BD B D =∴四边形'BDB E 为菱形;②如图2,连接CD ,则有CD=BD=AD,由翻折可知','45DB DB DB E B =∠=∠=︒①','45DB DC DB E DCA A =∠=∠=∠=︒,①''DB C DCB ∠=∠①DB E CB F DCA FCB ∠+∠=∠+∠'''①''CB F FCB ∠=∠①'FB FC =,①'B FC 的形状为等腰三角形;故答案为:等腰三角形;(3)如图3,由(2)知'FB FC =,'B E BE =,①CEF ∆的周长=''CE FC EF CE B F EF CE B E CE BE BC ++=++=+=+=,①①ABC 是等腰直角三角形,AB=10,①222100BC AB ==,解得:52BC =,①CEF ∆的周长为52,故答案为:52.【点睛】本题考查等腰直角三角形的性质、直角三角形斜边中线性质、折叠性质、菱形的判定与性质、等腰三角形的判定,解得的关键是认真审题,从图形中分析相关联信息,借助辅助线,利用基本图形的性质进行推理、计算.6.【问题1】SSS ;【问题2】(1)见解析;(2)8.【解析】【分析】问题1:根据SSS证明三角形全等即可.问题2:(1)根据HL证明三角形全等即可解决问题.(2)作MH①OB于H,连接MN.想办法求出ON,MH即可解决问题.【详解】解:问题1:由作图可知:OE=OD,EC=DC,OC=OC,①EOC DOC≌△△(SSS),故答案为SSS.问题2:(1)证明:由作图可知:OM=ON,①①ONP=①OMP=90°,OP=OP,①Rt ONP≌Rt OMP△(HL),①①PON=①POM,即OP平分①AOB.(2)解:作MH①OB于H,连接MN.①tan①AOB=4,3MHOH=①可以假设MH=4k,OH=3k,则OM=ON=5k,①HN=2k,在Rt MNH△中,①222,MN HN MH=+①()()222442,k k=+①255k=(负根已经舍弃),①ON=5k=25,MH=4k=855,①1185258.225MNO S ON MH ==⨯⨯= 【点睛】本题考查的是角平分线的作图与作图原理,三角形全等的判定与性质,锐角三角函数的应用,勾股定理的应用,掌握以上知识是解题的关键.7.定理证明:见解析;定理应用:(1)EF ∥AC ,EF =14AC ;(2)5﹣32≤BH ≤5+32 【解析】【分析】定理证明:延长DE 到F ,使FE =DE ,连接CF ,易证①ADE ①①CFE ,再根据全等三角形的性质,进一步可得出CF ①AB ,从而可证明四边形BCFD 是平行四边形,最后根据平行四边形的性质即可得证;定理应用:(1)取AB ,BC 的中点M ,N ,连接MN .再根据题目中的线段关系,可得出AM =BM ,CN =BN ,ME =EB ,FN =FB ,根据三角形的中位线定理即可得出答案; (2)如图①中,延长CB 到T ,连接AT ,TE ′.根据题意得出BH =12TE ′,再根据矩形的性质可求得AT 的值,结合题意求得AE 的值,最后根据三角形三边关系即可得出答案.【详解】 解:定理证明:如图①中,延长DE 到F ,使FE =DE ,连接CF ,在△ADE 和△CFE 中,AE EC AED CEF DE EF =⎧⎪∠=∠⎨⎪=⎩∴△ADE ≌△CFE (SAS ),∴∠A =∠ECF ,AD =CF ,∴CF ∥AB ,又∵AD =BD ,∴CF=BD,∴四边形BCFD是平行四边形,∴DF∥BC,DF=BC,∴DE∥BC,DE=12BC.定理应用:(1)如图①中,取AB,BC的中点M,N,连接MN.∵AE=3BE,BF:CF=1:3,∴AM=BM,CN=BN,ME=EB,FN=FB,∴MN∥AC,MN=12AC,EF∥MN,EF=12MN,∴EF∥AC,EF=14AC.故答案为:EF∥AC,EF=14AC.(2)如图①中,延长CB到T,连接AT,TE′.∵CH=HE′,CB=BT,∴BH=12TE′,∵四边形ABCD是矩形,∴∠ABC=∠ABT=90°,∵AB=4,BC=AD=BT=2,∴AT=22224225AB BT+=+=,∵AE=3BE,AB=4,∴AE=AE′=3,∴25﹣3≤TE′≤25+3,∴5﹣32≤BH≤5+32.故答案为:5﹣32≤BH≤5+32.【点睛】本题考查了矩形的性质、三角形三边关系、平行四边形的判定及性质、三角形中位线性质、旋转的性质、全等三角形的判定及性质,综合性比较强,添加合适的辅助线,是解题的关键.8.(1)5;(2)①见解析;①等腰三角形;(3)52.【解析】【分析】(1)由直角三角形斜边上的中线性质即可得出答案;(2)①由折叠的性质得B'D=BD,B'E=BE,①B'DE=①BDE,证出B'D=BE,得四边形BDB'E是平行四边形,进而得出结论;①证出CD=B'D,得①DCB'=①DB'C,证出DB'①AC,则①ACB'=90°-①DB'C,证出CD①B'E,则①EB'C=90°-①DCB',得①ACB'=①EB'C,即可得出结论;(3)连接B'C,由等腰直角三角形的性质得BC=22AB=52,①B=45°,CD=12AB=BD,①ACD=12①ACB=45°,证出CF=B'F,进而得出答案.【详解】(1)解:①①ABC是等腰直角三角形,点D是斜边AB的中点,AB=10,①CD=12AB=5,故答案为:5;(2)①证明:由折叠的性质得:B'D=BD,B'E=BE,①B'DE=①BDE,①DB'①BC,①①B'DE=①BED,①①BDE=①BED,①BD=BE,①B'D=BE,①四边形BDB'E是平行四边形,又①B'D=BD,①四边形BDB'E为菱形;①解:①①ABC是等腰直角三角形,点D是斜边AB的中点,AB=BD,①CD=12由折叠的性质得:B'D=BD,①CD=B'D,①①DCB'=①DB'C,①①ACB=90°,①AC①BC,①DB'①BC,①DB'①AC,①①ACB'=90°﹣①DB'C,由①得:四边形BDB'E为菱形,①AB①B'E,①CD①AB,①CD①B'E,①①EB'C=90°﹣①DCB',①①ACB'=①EB'C,①FB'=FC,即①B'FC为等腰三角形;故答案为:等腰三角形;(3)解:连接B'C,如图①所示:①①ABC 是等腰直角三角形,点D 是斜边AB 的中点,AB =10,①BC =22AB =52,①B =45°,CD =12AB =BD ,①ACD =12①ACB =45°, 由折叠的性质得:B 'D =BD ,①B '=①B =45°,①CD =B 'D ,①①DCB '=①DB 'C ,①①FCB '=①FB 'C ,①CF =B 'F ,①①CEF 的周长=EF +CF +CE =EF +B 'F +CE =B 'E +CE =BE +CE =BC =52;故答案为:52.【点睛】 本题是四边形综合题目,考查了菱形的判定与性质、平行四边形的判定与性质、等腰直角三角形的性质、折叠的性质、等腰三角形的判定与性质、直角三角形斜边上的中线性质等知识;本题综合性强,熟练掌握菱形的判定与性质和等腰三角形的判定与性质是解题的关键.9.(1)见解析;(2)等腰;(3)菱形.【解析】【分析】(1)由中线BD ,CE 相交于点O ,可得DE 是ABC 的中位线,可得//DE BC ,12DE BC =,由F 、G 分别是OB ,OC 的中点,可得FG 是OBC 的中位线,可得//FG BC ,12FG BC =,可推出//DE FG ,DE FG =即可; (2)由四边形DEFG 的形状为矩形,可得FD=EG ,OE=OF=OG=OD ,EF①ED ,①EOF=①DOG ,由F 、G 分别是OB ,OC 的中点,可得BO=CO ,,由中线CE ,E 为中点,F 是OB 的中点,可得EF①OA ,可推出OA①ED ,由等腰三角形性质可得OA 平分①EOD ,可证△AOB①①AOC (SAS ),可得AB=AC 即可;(3)连接OA ,由(1)知四边EFGD 为平行四边形,由中位线性质可得AO=2EF ,2BC FG =,由OA BC =,可得EF=FG 即可.【详解】证明:(1)①中线BD ,CE 相交于点O ,①E 、D 分别为AB 、AC 中点,①DE 是ABC 的中位线,①//DE BC ,12DE BC =, 又①F 、G 分别是OB ,OC 的中点,①FG 是OBC 的中位线,①//FG BC ,12FG BC =, ①//DE FG ,DE FG =,①四边形DEFG 是平行四边形;(2)连接OA ,如图①四边形DEFG 的形状为矩形,①FD=EG ,OE=OF=OG=OD ,EF①ED ,①EOF=①DOG , ①F 、G 分别是OB ,OC 的中点,①BO=CO ,①中线CE ,E 为中点,F 是OB 的中点,①EF①OA ,①OA①ED ,①OA 平分①EOD ,①①EOA=①DOA ,①①BOA=①EOF+①EOA=①DOG+①DOA=①COA ,①AO=AO ,①①AOB①①AOC (SAS ),①AB=AC ,①①ABC 为等腰三角形,故答案为:等腰;(3)当OA BC =时,四边形DEFG 的形状为菱形.由(1)知四边EFGD 为平行四边形,①中线CE ,E 为中点,F 是OB 的中点,①EF 为①ABO 的中位线,①AO=2EF ,又①F 、G 分别是OB ,OC 的中点,①FG 是OBC 的中位线,①2BC FG =,①OA BC =,①2EF=2FG ,①EF=FG ,①四边形DEFG 是菱形,故答案为:菱形.【点睛】本题考查平行四边形的判定与性质,等腰三角形的判定,菱形的判定,掌握平行四边形的判定方法与性质,等腰三角形的判定,菱形的判定定理,细心观察图形,利用数形结合从图形中分析线段之间和角之间关系是解题关键.10.(1)CE CF =,CE CF ⊥,理由见解析;(2)217,34;【解析】【分析】 (1)根据正方形的性质和运动的距离可证明()EDC FBC SAS ≌△△,可得CE CF =,再利用角之间的关系可证CE CF ⊥;(2)连接EC ,证明四边形GECH 是平行四边形,即可求出CF ,再利用直角三角形斜边上的中线等于斜边的一半即可求出AP .(1)解:①四边形ABCD为正方形,①CD CB=,90EDC ABC BCD∠=∠=∠=︒,①90FBC EDC∠=∠=︒,①ED FB t==,在EDC△和FBC中,90CD CBFBC EDCED FB=⎧⎪∠=∠=︒⎨⎪=⎩①()EDC FBC SAS≌△△,①CE CF=,ECD BCF=∠∠,①90ECD BCE∠+∠=︒,①90BCF BCE∠+∠=︒,即:90ECF∠=︒,①CE CF=,CE CF⊥,(2)解:连接CE,如图①CE CF=,CE CF⊥,①45CEF∠=︒,①45GPE∠=︒,①CEF GPE∠=∠,①CE GH∥,①GE CH∥,①四边形GECH是平行四边形,①217CE GH==,①CE CF =,①217CF =,①2234EF CF ==,①P 是EF 的中点,AFE △是直角三角形,①1342AP EF ==. 【点睛】本题考查正方形的性质,全等三角形的判定以及性质,平行四边形的判定及性质,直角三角形斜边上的中线等于斜边的一半.(1)的关键是证明()EDC FBC SAS ≌△△,(2)的关键是证明四边形GECH 是平行四边形.。
几何画板探究中考例题

几何画板探究中考例题
几何画板是一个强大的数学软件,可以用来探究和解决各种几何问题,包括中考的几何题目。
以下是一个几何画板探究中考例题的过程:
题目:在Rt△ABC 中,∠C = 90°,AC = 3,BC = 4,点 P 是边 AC、AB
上的动点,则 CP + BP 的最小值为 _______.
首先,在几何画板上绘制出直角三角形 ABC,并标记 AC = 3,BC = 4。
然后,我们注意到当点 P 是 AC、AB 上的动点时,CP + BP 的最小值实际
上是点 B 关于 AC 的对称点 B' 到点 C 的距离。
这是因为当点 P 移动到使得CP + BP 取最小值的点时,△CPB' 会是一个等腰三角形。
接下来,我们需要找到这个最小值。
首先,找到点B 关于AC 的对称点B'。
我们可以使用几何画板的“标记向量”和“平移”工具来完成这一步。
然后,使用线段工具连接点 B' 和 C。
使用“测量”工具测量 B'C 的长度,
这就是 CP + BP 的最小值。
最后,我们注意到 B'C 的长度实际上就是 BC 的长度,因为 B 和 B' 是关于AC 对称的。
所以,CP + BP 的最小值就是 BC 的长度,也就是 4。
通过几何画板的帮助,我们可以直观地理解这个问题,并准确地找到 CP + BP 的最小值。
这不仅帮助我们解决了这个问题,也提高了我们的几何直觉和问题解决能力。
中考几何综合探究练习题

中考几何综合探究练习题中考几何综合探究练习题几何学是数学中的一个重要分支,也是中考数学中的一项重要内容。
几何综合是中考几何学的一项重要考点,需要学生掌握一定的几何知识和解题技巧。
下面我们就来探究一些中考几何综合练习题。
1. 设正方形ABCD的边长为a,E为BC的中点,连接AE并延长到F点,使得EF=EB。
求证:AF⊥BF。
首先,我们可以通过观察正方形的性质来解答这个问题。
正方形的对角线互相垂直,所以我们可以猜测AF⊥BF。
接下来,我们可以通过几何推理来证明这一点。
设正方形ABCD的边长为a,由于E为BC的中点,所以BE=EC=a/2。
又由于EF=EB=a/2,所以EF=EB=EC,即三角形EFC是一个等边三角形。
连接AF和BF,我们需要证明AF⊥BF。
假设AF⊥BF不成立,即AF和BF不垂直。
那么,我们可以通过反证法来证明这个假设的错误。
假设AF和BF不垂直,那么它们一定存在一个交点G。
由于三角形EFC是等边三角形,所以FG=FC=EF=a/2。
又因为三角形AFG和BFG有共边FG,所以它们的另外两边也相等,即AG=BG。
由于正方形ABCD的对角线互相垂直,所以AG和BG也应该互相垂直。
但是,由我们的假设可知,AF和BF不垂直,所以AG和BG也不垂直。
这与我们的假设矛盾,所以假设AF⊥BF不成立。
综上所述,我们可以得出结论:正方形ABCD的边长为a,E为BC的中点,连接AE并延长到F点,使得EF=EB,则AF⊥BF。
2. 在平面直角坐标系中,点A(3,4)、B(6,8)、C(9,6)是一个三角形ABC的三个顶点,点D在平面上,且满足AD=BC。
求证:四边形ABCD是一个平行四边形。
首先,我们可以通过观察三角形ABC和四边形ABCD的点的位置来猜测ABCD是一个平行四边形。
接下来,我们可以通过计算来证明这一点。
点A(3,4)、B(6,8)、C(9,6)是一个三角形ABC的三个顶点,我们可以计算出它们的边长AB、BC和AC的长度。
中考针对性训练几何探究压轴题有答案详解

针对性训练-----几何探究题1.如图1,在正方形ABCD 内有一点P 满足AP=AB ,PB=PC ,连结AC 、PD. (1)求证:△APB ≌△DPC ;(2)求证:∠PAC=21∠BAP ;(3)若将原题中的正方形ABCD 变为等腰梯形ABCD(如图2),AD ∥BC,且BA=AD=DC,形内一点P 仍满足AP=AB ,PB=PC,试问(2)中结论还成立吗若成立请给予证明;若不成立,请说明理由.ABDCP图PCDAB图2.如图1,在中,为锐角,点为射线上一点,联结,以为一边且在的右侧作正方形.(1)如果,,①当点在线段上时(与点不重合),如图2,线段所在直线的位置关系为 __________ ,线段的数量关系为 ;②当点在线段的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;(2)如果,是锐角,点在线段上,当满足什么条件时,(点不重合),并说明理由. (3)若AC=42,BC=3,在(2)的条件下,设正方形ADEF 的边DE 与线段CF 相交于点P ,求线段CP 长的最大值。
3.如图1,在正方形ABCD 中,E 是AB 上一点,F 是AD 延长线上一点,且DF =BE . (1)求证:CE =CF ;图1图2C图3E图2BAEBD图1(2)在图1中,若G 在AD 上,且∠GCE =45°,则GE =BE +GD 成立吗为什么 (3)运用(1)(2)解答中所积累的经验和知识, 完成下题:如图2,在直角梯形ABCD 中,AD ∥BC (BC >AD ),∠B =90°,AB =BC =12,E 是AB 上一点,且∠DCE =45°,BE =4,求DE 的长.4.如图,在Rt △ABC 中,∠A =90º,AB =6,AC =8,D ,E 分别是边AB ,AC 的中点,点P从点D 出发沿DE 方向运动,过点P 作PQ ⊥BC 于Q ,过点Q 作QR ∥BA 交AC 于R ,当点Q 与点C 重合时,点P 停止运动.设BQ =x ,QR =y .(1)求点D 到BC 的距离DH 的长;(2)求y 关于x 的函数关系式(不要求写出自变量的取值范围);(3)是否存在点P ,使△PQR 为等腰三角形若存在,请求出所有满足要求的x 的值;若不存在,请说明理由.5.如图17,点A 是△ABC 和△ADE 的公共顶点,∠BAC +∠DAE =180°,AB =k ·AE ,AC =k ·AD ,点M 是DE 的中点,直线AM 交直线BC 于点N .A B CDER PH QBHABCD E R PH⑴探究∠ANB 与∠BAE 的关系,并加以证明.说明:如果你经过反复探索没解决问题,可以从下面①②中选取一个作为已知条件,再完成你的证明,选取①比选原题少得2分,选取②比选原题少得5分.① 如图18,k =1;②如图19,AB =AC .⑵若△ADE 绕点A 旋转,其他条件不变,则在旋转的过程中⑴的结论是否发生变化如果没有发生变化,请写出一个可以推广的命题;如果有变化,请画出变化后的一个图形,并直接写出变化后∠ANB 与∠BAE 的关系.6.已知,CD 是经过BCA ∠顶点C 的一条直线,CA CB =.E F ,分别是直线CD 上两点,且BEC CFA α∠=∠=∠.(1)若直线CD 经过BCA ∠的内部,且E F ,在射线CD 上,请解决下面两个问题:①如图9-1,若90BCA ∠=o ,90α∠=o,则BE CF ;EFAF -(填“>”,“<”或“=”);②如图9-2,若0180BCA <∠<oo,请添加一个关于α∠与BCA ∠关系的条件 ,使①中的两个结论仍然成立,并证明两个结论成立.(2)如图9-3,若直线CD 经过BCA ∠的外部,BCA α∠=∠,请提出EF BE AF ,,三条线段数量关系的合理猜想(不要求证明).7.在等边ABC ∆的两边AB 、AC 所在直线上分别有两点M 、N ,D 为ABC V 外一点,且︒=∠60MDN ,︒=∠120BDC ,BD=DC. 探究:当M 、N 分别在直线AB 、AC 上移动时,BM 、ABCE FDDABCE F ADFC EB图9-1图9-2图9-3NC 、MN 之间的数量关系及AMN ∆的周长Q 与等边ABC ∆的周长L 的关系.图1 图2 图3(I )如图1,当点M 、N 边AB 、AC 上,且DM=DN 时,BM 、NC 、MN 之间的数量关系是 ; 此时=LQ; (II )如图2,点M 、N 边AB 、AC 上,且当DM ≠DN 时,猜想(I )问的两个结论还成立吗写出你的猜想并加以证明;(III ) 如图3,当M 、N 分别在边AB 、CA 的延长线上时,若AN=x ,则Q= (用x 、L 表示).参考答案1. (1)略(2)略(3)设︒=∠︒=∠y BAP x PAC ,,︒-=∠=∠)60(x DCA CAD 则 ︒=∠y PDCx y x X -+=+6060型得,由得x y 2=即BAP PAC ∠=∠212.(1)①垂直,相等;……………1分B图1②当点D 在BC 的延长线上时①的结论仍成立.………………2分 由正方形ADEF 得 AD =AF ,∠DAF =90º.∵∠BAC =90º,∴∠DAF =∠BAC , ∴∠DAB =∠FAC , 又AB =AC ,∴△DAB ≌△FAC , ∴CF =BD , ∠ACF =∠ABD . ∵∠BAC =90º, AB =AC , ∴∠ABC =45º,∴∠ACF =45º,∴∠BCF =∠ACB +∠ACF =90º. 即 CF ⊥BD .…………5分(2)当∠ACB =45º时,CF ⊥BD (如图). …………6分 理由:过点A 作AG ⊥AC 交CB 或CB 的延长线于点G ,则∠GAC =90º, ∵∠ACB =45°,∠AGC =90°—∠ACB =45°, ∴∠ACB =∠AGC ,∴AC =AG ,∵点D 在线段BC 上,∴点D 在线段GC 上,由(1)①可知CF ⊥BD . …7分 (3)如图:作AQBC 于Q ∵∠ACB=45° AC=42 ∴CQ=AQ=4 ∵∠PCD=∠ADP=90°∴∠ADQ+∠CDP=∠CDP+∠CPD=90° ∴△ADQ ∽△DPC ∴DQ PC =AQCD设CD 为x (0<x <3)则DQ=CQ -CD=4-x 则x PC 4=4x∴PC=41(-x 2+4x)=-41(x -2)2+1≥1 当x=2时,PC 最长,此时PC=13.(1)证明:如图1,在正方形ABCD 中,∵BC =CD ,∠B =∠CDF ,BE =DF , ∴△CBE ≌△CDF . ∴CE =CF .…….3分 (2)GE =BE +GD 成立.理由是:∵△CBE ≌△CDF , ∴∠BCE =∠DCF . ∴∠BCE +∠ECD =∠DCF +∠ECD即∠ECF =∠BCD =90°, 又∠GCE =45°, ∴∠GCF =∠GCE =45°.BA EG∵CE =CF ,∠GCE =∠GCF ,GC =GC , ∴△ECG ≌△FCG . ……..4分∴GE =GF ∴GE =DF +GD =BE +GD .…..5分(3)解:过C 作CG ⊥AD ,交AD 延长线于G . 在直角梯形ABCD 中,∵AD ∥BC ∴∠A =∠B =90°.又∠CGA =90°,AB =BC , ∴四边形ABCG 为正方形. ………6分∴AG =BC =12. 已知∠DCE =45°,根据(1)(2)可知,ED =BE +DG ... 7分设DE =x ,则DG =x -4, ∴AD =AG -DG=12-(x -4)=16-x .在Rt △AED 中, ∵222AE AD DE +=,即()222816+-=x x .解这个方程,得:x =10. ∴DE =10.4.(1),,,. 点为中点,.,. , ,.---------------2分 (2),. ,,,,即关于的函数关系式为:. -------5分 (3)存在,分三种情况: ①当时,过点作于,则. ,,. ,,,. --------8分②当时,, . -------10分 ③当时,则为中垂线上的点,于是点为的中点,. ,,. -----13分综上所述,当为或6或时,为等腰三角形. -----14分5.(1)∠ANB +∠BAE =180º.……1分证明:(法一)如图1,延长AN 到F ,使MF =AM ,连接DF 、EF . ………………2分 ∵点M 是DE 的中点,∴DM =ME , ∴四边形ADFE 是平行四边形,……………3分A BCD ERP H QM2 1 BBM ADNEBC∴AD ∥EF ,AD =EF , ∴∠DAE +∠AEF =180º, ∵∠BAC +∠DAE =180º, ∴∠BAC =∠AEF ,………4分 ∵AB =kAE ,AC =kAD , ∴AD AC AE AB =, ∴EFACAE AB =……6分 ∴△ABC ∽△EAF ∴∠B =∠EAF …………8分 ∵∠ANB +∠B +∠BAF =180º ∴∠ANB +∠EAF +∠BAF =180º 即∠ANB +∠BAE =180º,…………10分(法二)如图2,延长DA 到F ,使AF =AD ,连接EF .………2分 ∵∠BAC +∠DAE =180º,∠DAE +∠EAF =180º,∴∠BAC =∠EAF ,………………3分 ∵AB =kAE ,AC =kAD , ∴AD AC AE AB =, ∴AFACAE AB =,………4分 ∴△ABC ∽△AEF ,………5分∴∠B =∠AEF ,………6分 ∵点M 是DE 的中点,∴DM =ME , 又∵AF =AD , ∴AM 是△DEF 的中位线, ∴AM ∥EF ,……7分 ∴∠NAE =∠AEF ,∴∠B =∠NAE ,……8分 ∵∠ANB +∠B +∠BAN =180º, ∴∠ANB +∠NAE +∠BAN =180º, 即∠ANB +∠BAE =180º.………10分(2)变化.如图3(仅供参考),∠ANB =∠BAE .……12分 选取(ⅰ),如图4.证明:延长AM 到F ,使MF =AM ,连接DF 、EF . ∵点M 是DE 的中点,∴DM =ME∴四边形ADFE 是平行四边形,…………4分 ∴AD ∥FE ,AD =EF , ∴∠DAE +∠AEF =180º, ∵∠BAC +∠DAE =180º, ∴∠BAC =∠DAE , ………6分 ∵AB =kAE ,AC =kAD ,1=k , ∴AB =AE ,AC =AD ,∴AC =EF ,……7分 ∴△ABC ≌△EAF , ∴∠B =∠EAF , …8分 ∵∠ANB +∠B +∠BAF =180º, ∴∠ANB +∠EAF +∠BAF =180º, 即∠ANB +∠BAE =180º.……10分 选取(ⅱ),如图5.M ADNEBCFK H图2A图4图3ABCD EM N证明:∵AB =AC ,∴∠B =21(180º-∠BAC ),…………3分 ∵∠BAC +∠DAE =180º, ∴∠DAE =180º-∠BAC ,∴∠B =21∠DAE , ∵AB =kAE ,AC =kAD ,∴AE =AD , ∵AM 是△ADE 的中线,AB =AC , ∴∠EAM =21∠DAE , ∴∠B =∠EAM ,………4分∵∠ANB +∠B +∠BAM =180º, ∴∠ANB +∠EAM +∠BAM =180º,即∠ANB +∠BAE =180º.…5分6.(1)①=;=; 2分 ②所填的条件是:180BCA α∠+∠=o . 4分证明:在BCE △中,180180CBE BCE BEC α∠+∠=-∠=-∠o o .180BCA α∠=-∠o Q ,CBE BCE BCA ∴∠+∠=∠.又ACF BCE BCA ∠+∠=∠Q ,CBE ACF ∴∠=∠.又BC CA =Q ,BEC CFA ∠=∠, ()BCE CAF AAS ∴△≌△.BE CF ∴=,CE AF =. 又EF CF CE =-Q ,EF BE AF ∴=-. 7分 (2)EF BE AF =+.7.(I )如图1, BM 、NC 、MN 之间的数量关系 BM+NC=MN .此时 32=L Q. (II )猜想:结论仍然成立.证明:如图,延长AC 至E ,使CE=BM ,连接DE .ΘCD BD =,且ο120=∠BDC .∴ο30=∠=∠DCB DBC .又ABC ∆是等边三角形,∴90MBD NCD ∠=∠=o .在MBD ∆与ECD ∆中: A B C D MN图5E⎪⎩⎪⎨⎧=∠=∠=DC BD ECD MBD CE BM∴≅∆MBD ECD ∆(SAS) .∴DM=DE, CDE BDM ∠=∠∴ο60=∠-∠=∠MDN BDC EDN 在MDN ∆与EDN ∆中:⎪⎩⎪⎨⎧=∠=∠=DN DN EDN MDN DE DM ∴≅∆MDN EDN ∆(SAS) ∴MN=NE=NC+BMAMN ∆的周长Q=AM+AN+MN=AB+AC =2AB而等边ABC ∆的周长L=3AB ∴3232==AB AB L Q . (III )如图3,当M 、N 分别在AB 、CA 的延长线上时,若AN=x , 则Q=2x +L 32(用x 、L 表示).8.如图24-1,正方形ABCD 和正方形QMNP , M 是正方形ABCD 的对称中心,MN 交AB 于F ,QM 交AD 于E .(1)猜想:ME 与MF 的数量关系(2)如图24-2,若将原题中的“正方形”改为“菱形”,且∠M =∠B ,其它条件不变,探索线段ME 与线段MF 的数量关系,并加以证明.(3)如图24-3,若将原题中的“正方形”改为“矩形”,且AB:BC=1:2,其它条件不变,探索线段ME 与线段MF 的数量关系,并说明理由.(4)如图24-4,若将原题中的“正方形”改为平行四边形,且∠M =∠B ,AB:BC = m ,其它条件不变,求出ME :MF 的值。
中招考试几何类比探究题集锦一参考答案

中招考试几何类比探究题集锦(附参考答案)参考答案与试题解析一.解答题(共11小题)1.在△ABC中,AB=AC,∠BAC=2∠DAE=2α.(1)如图1,若点D关于直线AE的对称点为F,求证:△ABD≌△ACF;(2)如图2,在(1)的条件下,若α=45°,求证:DE2=BD2+CE2;(3)如图3,若α=45°,点E在BC的延长线上,请直接写出DE2,BD2,CE2三者之间的等量关系.【解答】解:(1)∵点D关于直线AE的对称点为F,∴EF=DE,AF=AD,∠DAE=∠EAF=α∴∠CAE+∠CAF=α∵∠BAC=2∠DAE=2α.∴∠BAD+∠CAE=∠BAC﹣∠DAE=α,∴∠BAD=∠CAF,在△ABD和△ACF中,第1页(共33页)第2页(共33页)∴△ABD ≌△ACF (SAS ),(2)由(1)知,△ABD ≌△ACF (SAS ),∴CF=BD ,∠ACF=∠B ,∵AB=AC ,∠BAC=2α,α=45°,∴△ABC 是等腰直角三角形,∴∠B=∠ACB=45°,∴∠ECF=∠ACB +∠ACF=45°+45°=90°,在Rt △CEF 中,由勾股定理得,EF 2=CF 2+CE 2,∴DE 2=BD 2+CE 2,(3)DE 2=BD 2+CE 2;理由:如图,∵∠BAC=2∠DAE=2α.∴∠DAE=α,∵点D 关于直线AE 的对称点为F ,∴EF=DE ,AF=AD ,∠DAE=∠EAF=α∴∠CAF=∠EAF +∠CAE=α+∠CAE∴∠BAD=∠BAC ﹣∠DAC=2α﹣∠DAC=2α﹣(∠DAE ﹣∠CAE )=2α﹣(α﹣∠CAE)=α+∠CAE∴∠BAD=∠CAF,在△ABD和△ACF中,∴△ABD≌△ACF(SAS),∴CF=BD,∠ACF=∠B,∵AB=AC,∠BAC=2α,α=45°,∴△ABC是等腰直角三角形,∴∠B=∠ACB=45°,∴∠ECF=∠ACB+∠ACF=45°+45°=90°,在Rt△CEF中,由勾股定理得,EF2=CF2+CE2,∴DE2=BD2+CE2,2.(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.猜测DE、BD、CE三条线段之间的数量关系(直接写出结果即可).(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问第(1)题中DE、BD、CE之间的关系是否仍然成立?如成立,请你给出证明;若不成立,请说明理由.(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF 均为等第3页(共33页)边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断线段DF、EF的数量关系,并说明理由.【解答】解:(1)DE=BD+CE.理由如下:如图1,∵BD⊥l,CE⊥l,∴∠BDA=∠AEC=90°又∵∠BAC=90°,∴∠BAD+∠CAE=90°,∠BAD+∠ABD=90°,∴∠CAE=∠ABD在△ABD和△CAE中,,∴△ABD≌△CAE(AAS)∴BD=AE,AD=CE,∵DE=AD+AE,∴DE=CE+BD;(2)如图2,∵∠BDA=∠AEC=∠BAC=α,∴∠DBA+∠BAD=∠BAD+∠CAE=180°﹣α,第4页(共33页)∴∠CAE=∠ABD,在△ADB和△CEA中,,∴△ADB≌△CEA(AAS),∴AE=BD,AD=CE,∴BD+CE=AE+AD=DE;(3)DF=EF.理由如下:由(2)知,△ADB≌△CAE,BD=EA,∠DBA=∠CAE,∵△ABF和△ACF均为等边三角形,∴∠ABF=∠CAF=60°,∴∠DBA+∠ABF=∠CAE+∠CAF,∴∠DBF=∠FAE,∵BF=AF在△DBF和△EAF中,,∴△DBF≌△EAF(SAS),∴DF=EF,∠BFD=∠AFE,第5页(共33页)∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°,∴△DEF为等边三角形.∴DF=EF.3.(1)问题发现如图1,△ABC和△ADE均为等边三角形,点D在边BC上,连接CE.请填空:①∠ACE的度数为60°;②线段AC、CD、CE之间的数量关系为AC=CD+CE.(2)拓展探究如图2,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D在边BC 上,连接CE.请判断∠ACE的度数及线段AC、CD、CE之间的数量关系,并说明理由.(3)解决问题如图3,在四边形ABCD中,∠BAD=∠BCD=90°,AB=AD=2,CD=1,AC与BD交于点E,请直接写出线段AC的长度.第6页(共33页)【解答】解:(1)①∵△ABC和△ADE均为等边三角形,∴AB=AC,AD=AE,∠BAC=∠DAE=∠B=60°,∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE,∴△BAD≌△CAE(SAS),∴∠ACE=∠B=60°,故答案为:60°;②线段AC、CD、CE之间的数量关系为:AC=CD+CE;理由是:由①得:△BAD≌△CAE,∴BD=CE,∵AC=BC=BD+CD,∴AC=CD+CE;故答案为:AC=CD+CE;(2)∠ACE=45°,AC=CD+CE,理由是:如图2,∵△ABC和△ADE均为等腰直角三角形,且∠BAC=∠DAE=90°,∴AB=AC,AD=AE,∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE,第7页(共33页)∴△ABD≌△ACE,∴BD=CE,∠ACE=∠B=45°,∵BC=CD+BD,∴BC=CD+CE,∵在等腰直角三角形ABC中,BC=AC,∴AC=CD+CE;(3)如图3,过A作AC的垂线,交CB的延长线于点F,∵∠BAD=∠BCD=90°,AB=AD=2,CD=1,∴BD=2,BC=,∵∠BAD=∠BCD=90°,∴∠BAD+∠BCD=180°,∴A、B、C、D四点共圆,∴∠ADB=∠ACB=45°,∴△ACF是等腰直角三角形,由(2)得:AC=BC+CD,∴AC===.第8页(共33页)4.【探究发现】如图1,△ABC是等边三角形,∠AEF=60°,EF交等边三角形外角平分线CF所在的直线于点F,当点E是BC的中点时,有AE=EF成立;【数学思考】某数学兴趣小组在探究AE、EF的关系时,运用“从特殊到一般”的数学思想,通过验证得出如下结论:当点E是直线BC上(B,C除外)任意一点时(其它条件不变),结论AE=EF仍然成立.假如你是该兴趣小组中的一员,请你从“点E是线段BC上的任意一点”;“点E是线段BC延长线上的任意一点”;“点E是线段BC反向延长线上的任意一点”三种情况中,任选一种情况,在备用图1中画出图形,并证明AE=EF.【拓展应用】当点E在线段BC的延长线上时,若CE=BC,在备用图2中画出图形,并运用上述结论求出S△ABC :S△AEF的值.【解答】证明:第一种情况:点E是线段BC上的任意一点,可作三种辅助线:方法一:如图1,在AB上截取AG,使AG=EC,连接EG,第9页(共33页)∵△ABC是等边三角形,∴AB=BC,∠B=∠ACB=60°.∵AG=EC,∴BG=BE,∴△BEG是等边三角形,∠BGE=60°,∴∠AGE=120°.∵FC是外角的平分线,∠ECF=120°=∠AGE.∵∠AEC是△ABE的外角,∴∠AEC=∠B+∠GAE=60°+∠GAE.∵∠AEC=∠AEF+∠FEC=60°+∠FEC,∴∠GAE=∠FEC.在△AGE和△ECF中,∴△AGE≌△ECF(ASA),∴AE=EF;方法二:在CA上截取CG=CE,连结GE,证明类似方法一;方法三:延长FC到G,使CG=CE,连结EG,易证△CEG是等边三角形,第10页(共33页)∴CE=EG,∠G=∠ACB=60°,∠CEG=∠AEF=60°,∴∠CEG+∠CEF=∠AEF+∠CEF,即∠GEF=∠AEC,∴△GEF≌△CEA,∴AE=EF.第二种情况:点E是线段BC延长线上的任意一点如图2,可作三种辅助线:①在CF上截取CG=CE,连接GE②延长AC到G,使CG=CE,连结EG;③或延长BA到G,使BG=BE,连结EG.第②种添加辅助线的方法证明如下:证明:延长AC到G,使CG=CE,连结EG,易证△CEG为等边三角形,∴∠G=∠ECF=60°,EG=CE,又∠AEG=∠CEG+∠AEC=60°+∠AEC,∠CEF=∠AEF+∠AEC=60°+∠AEC,第11页(共33页)∴∠AEG=∠CEF,∴△AEG≌△FEC,∴AE=EF.第三种情况:点E是线段BC反向延长线上的任意一点如图3,可作三种辅助线:①延长AB到G,使BG=BE,连结EG;②延长CF到G,使CG=CE,连结EG;③在CE上截取CG=CF,连结GF现就第①种添加辅助线的方法证明如下:证明:延长AB到G,使BG=BE,连结EG,易证△BEG为等边三角形,∴∠G=∠ECF=60°,第12页(共33页)∵∠AEB+∠BAE=∠ABC=60°,∠AEB+∠CEF=∠AEF=60°,∴∠BAE=∠CEF,∵AB=BC,BG=BE,∴AB+BG=BC+BE,即AG=CE,∴△AEG≌△EFC,∴AE=EF.拓展应用:如图4:作CH⊥AE于H点,∴∠AHC=90°.由数学思考得AE=EF,又∵∠AEF=60°,∴△AEF是等边三角形,∴△ABC∽△AEF.第13页(共33页)∵CE=BC=AC,△ABC是等边三角形,∴∠CAH=30°,AH=EH.∴CH=AC,AH=AC,AE=AC,∴.∴==.5.问题情境:在Rt△ABC中,AB=BC,∠B=90°,将一块等腰直角三角板的直角顶点O放在斜边AC上,将三角板绕点O旋转.(1)操作发现:当点O为AC中点时:①如图1,三角板的两直角边分别交AB,BC于E、F两点,连接EF,猜想线段AE、CF与EF之间存在的等量关系:AE2+CF2=EF2(无需证明);②如图2,三角板的两直角边分别交AB,BC延长线于E、F两点,连接EF,判断①中的结论是否成立.若成立,请证明;若不成立,请说明理由;第14页(共33页)(2)类比延伸:当点O不是AC中点时,如图3,三角板的两直角边分别交AB,BC于E、F两点,若=,请直接写出=.【解答】解:(1)①猜想:AE2+CF2=EF2,连接OB,如图1,∵AB=BC,∠ABC=90°,O点为AC的中点,∴OB=AC=OC,∠BOC=90°,∠ABO=∠BCO=45°.∵∠EOF=90°,∴∠EOB+∠BOF=∠FOC+∠BOF.∴∠EOB=∠FOC,在△OEB和△OFC中,,∴△OEB≌△OFC(ASA).∴BE=CF,又∵BA=BC,∴AE=BF.在Rt△EBF中,∵∠EBF=90°,∴BF2+BE2=EF2,∴AE2+CF2=EF2;故答案为:AE2+CF2=EF2;第15页(共33页)②成立.证明:连结OB.如图2,∵AB=BC,∠ABC=90°,O点为AC的中点,∴OB=AC=OC,∠BOC=90°,∠ABO=∠BCO=45°.∵∠EOF=90°,∴∠EOB=∠FOC.在△OEB和△OFC中,,∴△OEB≌△OFC(ASA).∴BE=CF,又∵BA=BC,∴AE=BF.在Rt△EBF中,∵∠EBF=90°,∴BF2+BE2=EF2,∴AE2+CF2=EF2;(2)=,如图3,过点O作OM⊥AB于M,ON⊥BC于N.∵∠B=90°,第16页(共33页)∴∠MON=90°,∵∠EOF=90°,∴∠EOM=∠FON.∵∠EMO=∠FNO=90°,∴△OME∽△ONF,∴=,∵△AOM和△OCN为等腰直角三角形,∴△AOM∽△OCN,∴=,∵=,∴=,故答案为.第17页(共33页)第18页(共33页)6.阅读发现:(1)如图①,在Rt △ABC 和Rt △DBE 中,∠ABC=∠DBE=90°,AB=BC=3,BD=BE=1,连结CD ,AE .易证:△BCD ≌△BAE .(不需要证明) 提出问题:(2)在(1)的条件下,当BD ∥AE 时,延长CD 交AE 于点F ,如图②,求AF 的长.解决问题:(3)如图③,在Rt △ABC 和Rt △DBE 中,∠ABC=∠DBE=90°,∠BAC=∠DEB=30°,连结CD ,AE .当∠BAE=45°时,点E 到AB 的距离EF 的长为2,求线段CD的长为 .【解答】(2)解:如图②中,AB与CF交于点O.由(1)可知:△BCD≌△BAE,∴∠OAF=∠OCB,CD=AE,∵∠AOF=∠COB,∴∠AFO=∠CBO=90°,∴CF⊥AE,∵BD∥AE,∴BD⊥CF,在RT△CDB中,∵∠CDB=90°,BC=3,BD=1,∴CD=AE==2,∵∠BDF=∠DFE=∠DBE=90°,∴四边形EFDB是矩形,∴EF=BD=1,∴AF=AE﹣EF=2﹣1.(3)解:在RT△ABC,RT△EBD中,∵∠ABC=∠DBE=90°,∠BAC=∠DEB=30°,∴AB=BC,BE=BD,∴==,∵∠ABC=∠EBD=90°,∴∠ABE=∠DBC,∴△ABE∽△CBD,∴==,第19页(共33页)第20页(共33页)在RT △AEF 中,∵∠AFE=90°,∠EAF=45°,EF=2,∴AF=EF=2,AE=2,∴=,∴CD=.故答案为.7.如图1,两个完全相同的三角形纸片ABC 和DEC 重合放置,其中∠C=90°,∠B=∠E=30°.(1)操作发现:如图2,固定△ABC,使△DEC绕点C旋转,当点D恰好落在AB边上时,填空:①线段DE与AC的位置关系是DE∥AC;②设△BDC的面积为S1,△AEC的面积为S2,则S1与S2的数量关系是S1=S2.(2)猜想论证当△DEC绕点C旋转到如图3所示的位置时,请猜想(1)中S1与S2的数量关系是否仍然成立?若成立,请证明;若不成立,请说明理由.(3)拓展探究已知∠ABC=60°,BD平分∠ABC,BD=CD,BC=9,DE∥AB交BC于点E(如图4).若在射线BA上存在点F,使S△DCF=S△BDE,请求相应的BF的长.【解答】解:(1)①∵△DEC绕点C旋转点D恰好落在AB边上,∴AC=CD,∵∠BAC=90°﹣∠B=90°﹣30°=60°,第21页(共33页)∴△ACD是等边三角形,∴∠ACD=60°,又∵∠CDE=∠BAC=60°,∴∠ACD=∠CDE,∴DE∥AC;故答案为:DE∥AC;②∵∠B=30°,∠C=90°,∴CD=AC=AB,∴BD=AD=AC,根据等边三角形的性质,△ACD的边AC、AD上的高相等,∴△BDC的面积和△AEC的面积相等(等底等高的三角形的面积相等),即S1=S2=×2×2=2;故答案为:S1=S2;(2)如图,∵△DEC是由△ABC绕点C旋转得到,∴BC=CE,AC=CD,∵∠ACN+∠BCN=90°,∠DCM+∠BCN=180°﹣90°=90°,∴∠ACN=∠DCM,∵在△ACN和△DCM中,,第22页(共33页)∴△ACN≌△DCM(AAS),∴AN=DM,∴△BDC的面积和△AEC的面积相等(等底等高的三角形的面积相等),即S1=S2;(3)如图,过点D作DF1∥BE,易求四边形BEDF1是菱形,所以BE=DF1,且BE、DF1上的高相等,此时S△DCF1=S△BDE;过点D作DF2⊥BD,∵∠ABC=60°,F1D∥BE,∴∠F2F1D=∠ABC=60°,∵BF1=DF1,∠F1BD=∠ABC=30°,∠F2DB=90°,∴∠F1DF2=∠ABC=60°,∴△DF1F2是等边三角形,∴DF1=DF2,∵BD=CD,∠ABC=60°,点D是角平分线上一点,∴∠DBC=∠DCB=×60°=30°,∴∠CDF1=180°﹣∠BCD=180°﹣30°=150°,∠CDF2=360°﹣150°﹣60°=150°,∴∠CDF1=∠CDF2,第23页(共33页)∵在△CDF1和△CDF2中,,∴△CDF1≌△CDF2(SAS),∴点F2也是所求的点,∵∠ABC=60°,点D是角平分线上一点,DE∥AB,∴∠DBC=∠BDE=∠ABD=×60°=30°,又∵BD=4,∴BE=×6÷cos30°=3÷=2,∴BF1=2,BF2=BF1+F1F2=2+2=4,故BF的长为2或4.8.问题解决:如图(1),将正方形纸片ABCD折叠,使点B落在CD边上一点E(不与点C,D 重合),压平后得到折痕MN.当时,求的值.类比归纳:第24页(共33页)在图(1)中,若,则的值等于;若,则的值等于;若(n 为整数),则的值等于.(用含n的式子表示)联系拓广:如图(2),将矩形纸片ABCD折叠,使点B落在CD边上一点E(不与点C,D 重合),压平后得到折痕MN,设,则的值等于.(用含m,n的式子表示)【解答】解:(1)方法一:如图(1﹣1),连接BM,EM,BE.由题设,得四边形ABNM和四边形FENM关于直线MN对称.∴MN垂直平分BE,∴BM=EM,BN=EN.∵四边形ABCD是正方形,∴∠A=∠D=∠C=90°,设AB=BC=CD=DA=2.∵,∴CE=DE=1.第25页(共33页)设BN=x,则NE=x,NC=2﹣x.在Rt△CNE中,NE2=CN2+CE2.∴x2=(2﹣x)2+12,解得x=,即BN=.在Rt△ABM和在Rt△DEM中,AM2+AB2=BM2,DM2+DE2=EM2,∴AM2+AB2=DM2+DE2.设AM=y,则DM=2﹣y,∴y2+22=(2﹣y)2+12,解得y=,即AM=(6分)∴.方法二:同方法一,BN=.如图(1﹣2),过点N做NG∥CD,交AD于点G,连接BE.∵AD∥BC,∴四边形GDCN是平行四边形.∴NG=CD=BC.同理,四边形ABNG也是平行四边形.∴AG=BN=∵MN⊥BE,∴∠EBC+∠BNM=90度.∵NG⊥BC,∴∠MNG+∠BNM=90°,第26页(共33页)∴∠EBC=∠MNG.在△BCE与△NGM中,∴△BCE≌△NGM,EC=MG.∵AM=AG﹣MG,AM=﹣1=.∴.(2)如图1,当四边形ABCD为正方形时,连接BE,=,不妨令CD=CB=n,则CE=1,设BN=x,则EN=x,EN2=NC2+CE2,x2=(n﹣x)2+12,x=;作MH⊥BC于H,则MH=BC,又点B,E关于MN对称,则MN⊥BE,∠EBC+∠BNM=90°;而∠NMH+∠BNM=90°,故∠EBC=∠NMH,则△EBC≌△NMH,∴NH=EC=1,AM=BH=BN﹣NH=﹣1=则:==.故当=,则的值等于;若=,则的值等于;第27页(共33页)(3)若四边形ABCD为矩形,连接BE,=,不妨令CD=n,则CE=1;又==,则BC=mn,同样的方法可求得:BN=,BE⊥MN,易证得:△MHN∽△BCE.故=,=,HN=,故AM=BH=BN﹣HN=,故==.故答案为:;;;.第28页(共33页)第29页(共33页)9.阅读理解:如图1,在直角梯形ABCD 中,AB ∥CD ,∠B=90°,点P 在BC 边上,当∠APD=90°时,易证△ABP ∽△PCD ,从而得到BP•PC=AB•CD ,解答下列问题.(1)模型探究:如图2,在四边形ABCD 中,点P 在BC 边上,当∠B=∠C=∠APD 时,结论BP•PC=AB•CD 仍成立吗?试说明理由;(2)拓展应用:如图3,M 为AB 的中点,AE 与BD 交于点C ,∠DME=∠A=∠B=45°且DM 交AC 于F ,ME 交BC 于G .AB=,AF=3,求FG 的长.【解答】解:(1)∵∠APC=∠APD +∠CPD ,∠APC=∠BAP +∠B (三角形外角定理),∠B=∠APD (已知),∴∠BAP=∠CPD,又∵∠B=∠C,∴△ABP∽△PCD∴=,∴BP•PC=AB•CD;(2)∵∠AFM=∠DME+∠E(三角形外角定理),∠DME=∠A(已知),∴∠AFM=∠A+∠E(等量代换),又∠BMG=∠A+∠E(三角形外角定理),∴∠AFM=∠BMG.∵∠A=∠B,∴△AMF∽△BGM.当∠A=∠B=45°时,∠ACB=180°﹣∠A﹣∠B=90°,即AC⊥BC且AC=BC.∵M为AB的中点,∴AM=BM=,AC=BC=4.又∵△AMF∽△BGM,∴,∴BG===,又∵,CF=4﹣3=1,∴.第30页(共33页)10.基本模型如下图,点B、P、C在同一直线上,若∠B=∠1=∠C=90°,则△ABP∽△PCD成立,(1)模型拓展如图1,点B、P、C在同一直线上,若∠B=∠1=∠C,则△ABP∽△PCD成立吗?为什么?(2)模型应用①如图2,在等腰梯形ABCD中,AD∥BC,AD=1,AB=2,BC=4,在BC上截取BP=AD,作∠APQ=∠B,PQ交CD于点Q,求CQ的长;②如图3,正方形ABCD的边长为1,点P是线段BC上的动点,作∠APQ=90°,PQ交CD于Q,当P在何处时,线段CQ最长?最长是多少?【解答】解:(1)成立,∵∠A=180°﹣(∠B+∠APB),第31页(共33页)∠CPD=180°﹣(∠1+∠APB),∠B=∠1,∴∠A=∠CPD,∵∠B=∠C,∴△ABP∽△PCD;(2)①∵四边形ABCD是等腰梯形,∴∠B=∠C,∵∠B=∠APQ,∴∠B=∠APQ=∠C,由(1)知,△ABP∽△PCD,∴=,∴=,∴CQ=;②设BP=x,CQ=y.∵∠B=∠APQ=90°,∴△ABP∽△PCQ,∴=,即=,∴y=﹣x2+x=﹣(x﹣)2+,第32页(共33页)∴当x=时,y=,最大即当P是BC的中点时,CQ最长,最长为.第33页(共33页)。
2023年九年级中考数学复习:几何探究压轴题(角度问题)(附答案)

2023年九年级中考数学复习:几何探究压轴题(角度问题)1.已知:正方形ABCD ,以A 为旋转中心,旋转AD 至AP ,连接BP DP 、.(1)若将AD 顺时针旋转30︒至AP ,如图1所示,求BPD ∠的度数? (2)若将AD 顺时针旋转α度()090α︒<<︒至AP ,求BPD ∠的度数?(3)若将AD 逆时针旋转α度()0180α︒<<︒至AP ,请分别求出090α︒<<︒、90α=︒、90180α︒<<︒三种情况下的BPD ∠的度数(图2、图3、图4).2.如图1所示,将一个长为6宽为4的长方形ABEF ,裁成一个边长为4的正方形ABCD 和一个长为4、宽为2的长方形CEFD 如图2.现将小长方形CEFD 绕点C 顺时针旋转至CE F D ''',旋转角为a .(1)当点D 恰好落在EF 边上时,求旋转角a 的值;(2)如图3,G 为BC 中点,且0°<a <90°,求证:GD E D ''=;(3)小军是一个爱动手研究数学问题的孩子,他发现在小长方形CEFD 绕点C 顺时针旋转一周的过程中,DCD '与CBD '△存在两次全等,请你帮助小军直接写出当DCD '与CBD '△全等时,旋转角a 的值.3.图1是边长分别为a 和()b a b >的两个等边三角形纸片ABC 和CDE 叠放在一起(C 与C '重合)的图形.(1)操作:固定ABC ,将CDE 绕点C 按顺时针方向旋转20°,连结AD ,BE ,如图2,则ECA ∠=___ ___度,并直接写出线段BE 与AD 的数量关系____ .(2)操作:若将图1中的CDE ,绕点C 按顺时针方向旋转120°,使点B 、C 、D 在同一条直线上,连结AD 、BE ,如图3.①线段BE 与AD 之间是否仍存在(1)中的结论?若是,请证明;若不是,请直接写出BE 与AD 之间的数量关系;②求APB ∠的度数.(3)若将图1中的CDE ,绕点C 按逆时针方向旋转一个角()0360αα<<︒,当α等于多少度时,BCD △的面积最大?请直接写出答案.4.我们定义:如图1,在△ABC 中,把AB 绕点A 顺时针旋转α(0°<α<180°)得到AB ',把AC 绕点A 逆时针旋转β得到AC ′,连接B 'C ',当a +β=180°时,我们称△AB 'C '是△ABC 的“旋补三角形”,△AB 'C 边B 'C '上的中线AD 叫做△ABC 的“旋补中线”.(1)[特例感知]在图2,图3中,△AB 'C ′是△ABC 的“旋补三角形”,AD 是△ABC 的“旋补中线”. ①如图2,当△ABC 为等边三角形,且BC =6时,则AD 长为 . ②如图3,当∠BAC =90°,且BC =7时,则AD 长为 .(2)[猜想论证]在图1中,当△ABC 为任意三角形时,猜想AD 与BC 的数量关系,并给予证明.(如果你没有找到证明思路,可以考虑延长AD 或延长B 'A ,…)(3)[拓展应用]如图4,在四边形ABCD 中,∠BCD =150°,AB =12,CD =6,以CD 为边在四边形ABCD 内部作等边△PCD ,连接AP ,BP .若△P AD 是△PBC 的“旋补三角形”,请直接写出△PBC 的“旋补中线”长及四边形ABCD 的边AD 长.5.如图,已知正方形ABCD ,点E 为AB 上的一点,EF AB ⊥,交BD 于点F .(1)如图1,直按写出DFAE的值____ ___; (2)将△EBF 绕点B 顺时针旋转到如图2所示的位置,连接AE 、DF ,猜想DF 与AE 的数量关系,并证明你的结论;(3)如图3,当BE =BA 时,其他条件不变,△EBF 绕点B 顺时针旋转,设旋转角为(0360)αα︒<<︒,当α为何值时EA =ED ?请在图3或备用图中画出图形并求出α的值.6.如图,已知正方形ABCD ,将AD 绕点A 逆时针方向旋转(090)n n ︒<<到AP 的位置,分别过点C D 、作,CE BP DF BP ⊥⊥,垂足分别为点E 、F .(1)求证:CE EF =;(2)联结CF ,如果13DP CF =,求ABP ∠的正切值;(3)联结AF ,如果AF AB =,求n 的值.7.把两个等腰直角△ABC 和△ADE 按如图1所示的位置摆放,将△ADE 绕点A 按逆时针方向旋转,如图2,连接BD ,EC ,设旋转角α(0°<α<360°).(Ⅰ)当DE ⊥AC 时,旋转角α= 度,AD 与BC 的位置关系是 ,AE 与BC 的位置关系是 ;(Ⅱ)当点D 在线段BE 上时,求∠BEC 的度数; (Ⅲ)当旋转角α= 时,△ABD 的面积最大.8.已知:在Rt ABC 中,90ABC ∠=︒,30BAC ∠=︒,将ABC 绕点A 顺时针旋转一定的角度α得到AED △,点B 、C 的对应点分别是E 、D .(1)如图1,若60α=︒时,连接BE ,求证:AB BE =; (2)如图2,当点E 恰好在AC 上时,求CDE ∠的度数;(3)如图3,点B 、C 的坐标分别是()0,0,()0,2,点Q 是线段AC 上的一个动点,点M 是线段AO 上的一个动点,是否存在这样的点Q 、M 使得CQM 为等腰三角形且AQM 为直角三角形?若存在,请求出满足条件的点M 的坐标;若不存在,请说明理由.9.把边长分别为4和6的矩形ABCO 如图放在平面直角坐标系中,将它绕点C 顺时针旋转a 角,旋转后的矩形记为矩形EDCF .在旋转过程中,(1)如图①,当点E 在射线CB 上时,E 点坐标为;(2)当△CBD 是等边三角形时,旋转角a 的度数是(a 为锐角时); (3)如图②,设EF 与BC 交于点G ,当EG=CG 时,求点G 的坐标;(4)如图③,当旋转角a=90°时,请判断矩形EDCF 的对称中心H 是否在以C 为顶点,且经过点A 的抛物线上.10.如图,ABC 是等边三角形,点D 是BC 边的中点,以D 为顶点作一个120︒的角,角的两边分别交直线AB AC 、于M 、N 两点,以点D 为中心旋转MDN ∠(MDN ∠的度数不变)(1)如图①,若DM AB ⊥,求证:BM CN BD +=;(2)如图②,若DM 与AB 不垂直,且点M 在边AB 上,点N 在边AC 上时,(1)中的结论是否成立?并说明理由;(3)如图③,若DM 与AB 不垂直,且点M 在边AB 上,点N 在边AC 的延长线上时,(1)中的结论是否成立?若不成立,写出BM CN BD 、、之间的数量关系,并说明理由.11.如图1,在Rt ABC △中,90,ACB AC BC ∠==,点D 为AB 边上的一点,将BCD △绕点C 逆时针旋转90得到ACE △,易得BCD ACE ≌,连接BE .(1)求BCE ACD ∠∠+的度数.(2)当5,BC BD ==BE CE 、的长.(3)如图2,在(2)的条件下,取AD 中点F ,连接CF 交BE 于H ,试探究线段BE CF 、的数量关系和位置关系,并说明理由.12.如图①,ABC 和ADE 是有公共顶点的等腰直角三角形,90BAC DAE ∠=∠=︒,点P 为射线,BD CE 的交点.(1)如图②,将ADE 绕点A 旋转,当C 、D 、E 在同一条直线上时,连接BD 、BE ,求证:BD CE =且BD CE ⊥.(2)若8,4AB AD ==,把ADE 绕点A 旋转, ①当90EAC ∠=︒时,求PB 的长;②旋转过程中线段BP 长的最小值是_____ __.13.如图1,ABC 中,90,30,ACB B AD ∠=︒∠=︒是角平分线,点E 、F 分别在边AC 、BC 上,45,CEF CF CD ∠=︒<、将CEF △绕点C 按逆时针方向旋转,使得EF 所在直线交线段AD 于点M ,交线段AB 于点N .(1)当旋转75°时,如图2,直线EF 与AD 的位置关系是____ __,ANM ∠=__ ____°; (2)在旋转一周过程中,试探究:当CE 旋转多少度时,AMN 中有两个角相等.14.菱形ABCD 的对角线AC ,BD 交于点O .(1)如图1,过菱形ABCD 的顶点A 作AE BC ⊥于点E ,交OB 于点H ,若6AB AC ==,求OH 的长; (2)如图2,过菱形ABCD 的顶点A 作AF AD ⊥,且AF AD =,线段AF 交OB 于点H ,交BC 于点E .当D ,C ,F 三点在同一直线上时,求证:2OH OA +=; (3)如图3,菱形ABCD 中,=45ABC ∠︒,点P 为直线AD 上的动点,连接BP ,将线段BP 绕点B 逆时针旋转60°得到线段BQ ,连接AQ ,当线段AQ 的长度最小时,直接写出BAQ ∠的度数.15.(1)阅读理解利用旋转变换解决数学问题是一种常用的方法.如图1,点P 是等边三角形ABC 内一点,P A =1,PB PC =2.求∠BPC 的度数.为利用已知条件,不妨把△BPC 绕点C 顺时针旋转60°得AP C '△,连接PP '.利用这种变换可以求∠BPC 的度数,请写出推理过程; (2)类比迁移如图2,点P 是等腰Rt △ABC 内一点,∠ACB =90°,P A =2,PB PC =1.求∠APC 的度数.16.ABC 为等边三角形,AB =8,AD ⊥BC 于点D ,E 为线段AD 上一点,AE =AE 为边在直线AD 右侧构造等边三角形AEF ,连接CE ,N 为CE 的中点.(1)如图1,EF 与AC 交于点G ,连接NG ,BE ,直接写出NG 与BE 的数量关系;(2)如图2,将AEF △绕点A 逆时针旋转,旋转角为α,M 为线段EF 的中点,连接DN ,MN .当30120α︒<<︒时,猜想∠DNM 的大小是否为定值,如果是定值,请写出∠DNM 的度数并证明,如果不是,请说明理由;(3)连接BN,在AEF△绕点A逆时针旋转过程中,请直接写出线段BN的最大值.17.如图1,在Rt△ABC中,∠ACB=90°,AB=10,BC=6.D、E分别是AB、AC边的中点,连接DE.现将△ADE绕A点逆时针旋转,连接BD,CE并延长交于点F.(1)如图2,点E正好落在AB边上,CF与AD交于点P.①求证:AE•AB=AD•AC;②求BF的长;(2)如图3,若AF恰好平分∠DAE,直接写出CE的长.18.如图①,在ABC中,∠ACB=90°,∠ABC=30°,AC=1,D为ABC内部的一动点(不在边上),连接BD,将线段BD绕点D逆时针旋转60°,使点B到达点F的位置;将线段AB绕点B顺时针旋转60°,使点A到达点E的位置,连接AD,CD,AE,AF,BF,EF.(1)求证:BDA≌BFE;(2)当CD+DF+FE取得最小值时,求证:AD∥BF.(3)如图②,M,N,P分别是DF,AF,AE的中点,连接MP,NP,在点D运动的过程中,请判断∠MPN 的大小是否为定值.若是,求出其度数;若不是,请说明理由.参考答案:1.(1)135︒(2)135︒(3)45︒,45︒,45︒2.(1)30°(3)135°,315°3.(1)40,BE =AD(2)①存在,②60°(3)当α=150°或330°时,BCD △的面积最大4.(1)①3;②3.5(2)AD =12BC ,(3)339=AD5.2(2)2DF AE =,(3)α的值为30°或150°,6.(2)23;(3)307.(Ⅰ)45;垂直;平行;(Ⅱ)90BEC ∠=︒;(Ⅲ)90︒或270︒8.(2)15°;(3)存在,23,03M ⎫⎪⎭或()423,0- 9.(1)E (4,13;(2)60°;(3)13(4,)3G ; (4)点H 不在此抛物线上.10.(2)成立,(3)不成立,BM CN BD -=,11.(1)180BCE ACD ∠+∠=︒(2)BE =CE =(3)2BE CF =;BE CF ⊥,12.(2)①PB =;②413.(1)垂直,60(2)当CE 旋转45°,90°,270°,315°时,△AMN 中有两个角相等14.(3)75︒15.(2)90°16.(1)2BE NG =(2)∠DNM 的大小是定值,为120°(3)17.(1)②18.(3)∠MPN 的值为定值,30°.。
中考数学专题复习_几何探究题
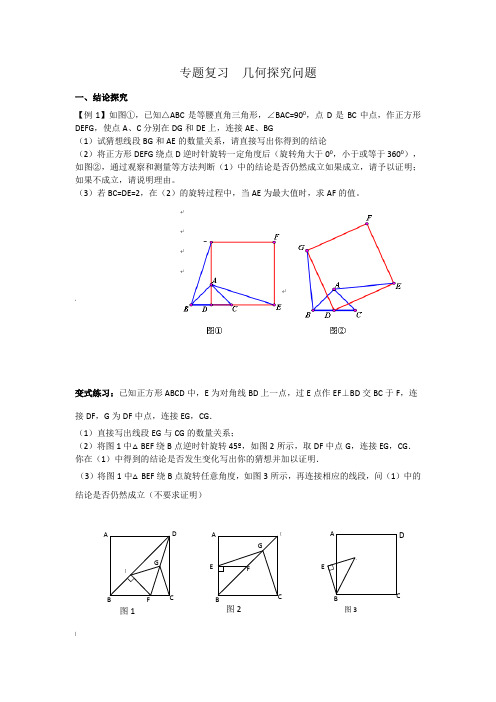
专题复习几何探究问题一、结论探究【例1】如图①,已知△ABC是等腰直角三角形,∠BAC=900,点D是BC中点,作正方形DEFG,使点A、C分别在DG和DE上,连接AE、BG(1)试猜想线段BG和AE的数量关系,请直接写出你得到的结论(2)将正方形DEFG绕点D逆时针旋转一定角度后(旋转角大于00,小于或等于3600),如图②,通过观察和测量等方法判断(1)中的结论是否仍然成立如果成立,请予以证明;如果不成立,请说明理由。
(3)若BC=DE=2,在(2)的旋转过程中,当AE为最大值时,求AF的值。
'变式练习:已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.(1)直接写出线段EG与CG的数量关系;(2)将图1中△BEF绕B点逆时针旋转45º,如图2所示,取DF中点G,连接EG,CG.你在(1)中得到的结论是否发生变化写出你的猜想并加以证明.(3)将图1中△BEF绕B点旋转任意角度,如图3所示,再连接相应的线段,问(1)中的结论是否仍然成立(不要求证明)| A D]G图1FA[EG图2、AE图3DFEC BAB'C'二、条件探究【例2】已知两个全等的直角三角形纸片ABC 、DEF ,如图(1)放置,点B 、D 重合,点F 在BC 上,AB 与EF 交于点G ,∠C=∠EFB=900,∠E=∠ABC=300,AB=DE=4 (1)求证:△EGB 是等腰三角形(2)若纸片DEF 不动,问△ABC 绕点F 旋转最小 度时,四边形ACDE 成为以ED 为底的梯形(如图(2)),求此梯形的高。
,【例3】如图,Rt △AB C 是由Rt △ABC 绕点A 顺时针旋转得到的,连结CC 交斜边于点E ,CC 的延长线交BB 于点F . |(1)证明:△ACE ∽△FBE ;(2)设∠ABC =α,∠CAC =β,试探索α、β满足什么关系时,△ACE 与△FBE 是全等三角形,并说明理由.;E图1A:CD图2三、类比探究 【例4】(1)操作发现:如图,矩形ABCD 中,E 是AD 的中点,将△ABE 沿BE 折叠后得到△GBE ,且点G 在举行ABCD 内部.小明将BG 延长交DC 于点F ,认为GF =DF ,你同意吗说明理由. (2)问题解决:保持(1)中的条件不变,若DC =2DF ,求ABAD的值; /(3)类比探求:保持(1)中条件不变,若DC =nDF ,求ABAD的值.【例5】如果一条直线把一个平面图形的面积分成相等的两部分,我们把这条直线称为这个平面图形的一条面积等分线.如,平行四边形的一条对线所在的直线就是平行四边形的一条面积等分线.(1)三角形的中线、高线、角平分线分别所在的直线一定是三角形的面积等分线的有________;((2)如图1,梯形ABCD 中,AB ∥DC ,如果延长DC 到E ,使CE =AB ,连接AE ,那么有S 梯形ABCD=S △ABE .请你给出这个结论成立的理由,并过点A 作出梯形ABCD 的面积等分线(不写作法,保留作图痕迹);(3)如图,四边形ABCD 中,AB 与CD 不平行,S △ADC >S △ABC ,过点A 能否作出四边形ABCD 的面积等分线若能,请画出面积等分线,并给出证明;若不能,说明理由.AB。
最新九年级中考数学复习:几何探究压轴题(面积问题)

(2)如图2,在等腰三角形ABC中,∠C=120°,点O为AB的中点,点M为AC上一点,将射线OM绕点O顺时针旋转60°交BC于点N,则OM与ON的数量关系是否改变,请说明理由;
9.在△ABC中,CA=CB,∠ACB=a,将△CAD绕点C按逆时针方向旋转角a得到△CBE,点A,D的对应点分别为点B,E.
(1)如图1,若A,D,E三点在同一直线上,则∠CDE=(用含a的代数式表示);
(2)如图2,若A,D,E三点在同一直线上,a=60°,过点C作CF⊥AE于点F,然后探究线段CF,AE,BE之间的数量关系,并证明你的结论;
(3)拓展延伸:把△ADE绕点A在平面内自由旋转,若AD=3,AB=7,请直接写出△PMN面积的最大值.
18.如图1,在等腰三角形ABC中,∠A=120°,AB=AC,点D、E分别在边AB、AC上,AD=AE,连接BE,点M、N、P分别为DE、BE、BC的中点.
(1)观察猜想:图1中,线段NM、NP的数量关系是,∠MNP的大小为;
(2)在三角板旋转的过程中,边 与AB所在直线交于点D,过点D作DE∥ 交 边于点E,连接BE.
①当 时,设AD= ,BE= ,求 与 之间的函数解析式及自变量 的取值范围;
②当 时,求AD的长.
13.在中 中. , ,点E在射线CB上运动.连接AE,将线段AE绕点E顺时针旋转90°得到EF,连接CF.
②如图3,连接AF,若AC=3,CD=1,求S△ADF的取值范围.
2.如图,矩形 中, 为等边三角形.点E,F分别为 边上的动点,且 ,P为 上一动点,连接 ,将线段 绕点B顺时针旋转 至 ,连接 .
中考数学重难点题型:12道几何探究题解析

中考数学重难点题型---12道几何探究题解析考点1 三角形几何探究1.如果三角形的两个内角α与β满足2α+β=90°,那么我们称这样的三角形为“准互余三角形”.(1)若△ABC 是“准互余三角形”,∠C >90°,∠A =60°,则∠B =15°;(2)如图1,在Rt △ABC 中,∠ACB =90°,AC =4,BC =5.若AD 是∠BAC 的平分线,不难证明△ABD 是“准互余三角形”.试问在边BC 上是否存在点E(异于点D),使得△ABE 也是“准互余三角形”?若存在,请求出BE 的长;若不存在,请说明理由.(3)如图2,在四边形ABCD 中,AB =7,CD =12,BD ⊥CD ,∠ABD =2∠BCD ,且△ABC 是“准互余三角形”,求对角线AC 的长.解:(1)∵△ABC 是“准互余三角形”,∠C >90°,∠A =60°,∴2∠B +∠A =90°,解得∠B =15°. (2)如答图1,在Rt △ABC 中,∵∠B +∠BAC =90°,∠BAC =2∠BAD ,∴∠B +2∠BAD =90°, ∴△ABD 是“准互余三角形”. ∵△ABE 也是“准互余三角形”, ∴只有2∠B +∠BAE =90°.∵∠B +∠BAE +∠EAC =90°,∴∠CAE =∠B. ∵∠C =∠C =90°,∴△CAE ∽△CBA ,∴CA 2=CE·CB, ∴CE =165,∴BE =5-165=95.(3)如答图2,将△BCD沿BC翻折得到△BCF,∴CF=CD=12,∠BCF=∠BCD,∠CBF=∠CBD.∵∠ABD=2∠BCD,∠BCD+∠CBD=90°,∴∠ABD+∠DBC+∠CBF=180°,∴点A,B,F共线,∴∠A+∠ACF=90°,∴2∠ACB+∠CAB≠90°,∴只有2∠BAC+∠ACB=90°,∴∠FCB=∠FAC.∵∠F=∠F,∴△FCB∽△FAC,∴CF2=FB·FA,设FB=x,则有x(x+7)=122,∴x=9或x=-16(舍去),∴AF=7+9=16,在Rt△ACF中,AC=AF2+CF2=162+122=20.2.将一副三角尺按图1摆放,等腰直角三角尺的直角边DF恰好垂直平分AB,与AC相交于点G,BC=2 3 cm.(1)求GC的长;(2)如图2,将△DEF绕点D顺时针旋转,使直角边DF经过点C,另一直角边DE与AC相交于点H,分别过H,C作AB的垂线,垂足分别为M,N,通过观察,猜想MD与ND的数量关系,并验证你的猜想.(3)在(2)的条件下,将△DEF沿DB方向平移得到△D′E′F′,当D′E′恰好经过(1)中的点G时,请直接写出DD′的长度.解:(1)在Rt△ABC中,∵BC=23,∠B=60°,∴AC=BC·tan60°=6,AB=2BC=43,在Rt△ADG中,AG=ADcos30°=4,∴CG=AC-AG=6-4=2.(2)结论:DM+DN=2 3.理由:∵HM⊥AB,CN⊥AB,∴∠AMH=∠DMH=∠CNB=∠CND=90°.∵∠A+∠B=90°,∠B+∠BCN=90°,∴∠A=∠BCN,∴△AHM∽△CBN,∴AMCN=HMBN①,同理可证:△DHM∽△CDN,∴DNMH=CNDM②由①②可得AM·BN=DN·DM,∴DMAM=BNDN,∴DM+AMAM=BN+DNDN,∴ADAM=BDDN.∵AD=BD,∴AM=DN,∴DM+DN=AM+DM=AD=2 3.第2题答图(3)如答图,作GK∥DE交AB于K.在△AGK中,AG=GK=4,∠A=∠GKD=30°,作GH⊥AB于H.则AH=AG·cos30°=23,可得AK=2AH=43,此时K与B重合.∴DD′=DB=2 3.考点2四边形几何探究3.我们定义:有一组邻角相等且对角线相等的凸四边形叫做邻对等四边形.概念理解(1)我们所学过的特殊四边形中的邻对等四边形是矩形或正方形; 性质探究(2)如图1,在邻对等四边形ABCD 中,∠ABC =∠DCB ,AC =DB ,AB>CD ,求证:∠BAC 与∠CDB 互补;拓展应用(3)如图2,在四边形ABCD 中,∠BCD =2∠B ,AC =BC =5,AB =6,CD =4.在BC 的延长线上是否存在一点E ,使得四边形ABED 为邻对等四边形?如果存在,求出DE 的长;如果不存在,说明理由.(1)解:矩形或正方形.(2)证明:如答图1,延长CD 至E ,使CE =BA ,连接BE.在△ABC 和△ECB 中,⎩⎨⎧AB =EC ,∠ABC =∠ECB ,BC =CB ,∴△ABC ≌△ECB(SAS), ∴BE =CA ,∠BAC =∠E.∵AC =DB ,∴BD =BE ,∴∠BDE =∠E ,∴∠CDB +∠BDE =∠CDB +∠E =∠BAC +∠CDB =180°,即∠BAC 与∠CDB 互补.(3)解:存在这样一点E ,使得四边形ABED 为邻对等四边形,如答图2,在BC 的延长线上取一点E ,使得CE =CD =4,连接DE ,AE ,BD ,则四边形ABED 为邻对等四边形.理由如下:∵CE =CD ,∴∠CDE =∠CED. ∵∠BCD =2∠ABC ,∴∠ABC =∠DEB ,∴∠ACE =∠BCD.在△ACE 和△BCD 中,⎩⎨⎧AC =BC ,∠ACE =∠BCD ,CE =CD ,∴△ACE ≌△BCD(SAS),∴BD =AE ,四边形ABED 为邻对等四边形. ∵∠CBA =∠CAB =∠CDE =∠CED , ∴△ABC ∽△DEC , ∴AB BC =65=DE CE =DE 4,∴DE =245.4.将矩形ABCD 绕点A 顺时针旋转α(0°<α<360°),得到矩形AEFG.(1)如图,当点E 在BD 上时.求证:FD =CD ;(2)当α为何值时,GC =GB ?画出图形,并说明理由.解:(1)由旋转可得,AE =AB ,∠AEF =∠ABC =∠DAB =90°,EF =BC =AD ,∴∠AEB =∠ABE. ∵∠ABE +∠EDA =90°=∠AEB +∠DEF , ∴∠EDA =∠DEF.∵DE =ED ,∴△AED ≌△FDE(SAS), ∴DF =AE ,∵AE =AB =CD ,∴CD =DF.(2)当GB =GC 时,点G 在BC 的垂直平分线上,分两种情况讨论: ①当点G 在AD 右侧时,如答图1,取BC 的中点H ,连接GH 交AD 于M , ∵GC =GB ,∴GH ⊥BC ,∴四边形ABHM 是矩形, ∴AM =BH =12AD =12AG ,∴GM 垂直平分AD ,∴GD =GA =DA , ∴△ADG 是等边三角形,∴∠DAG =60°, ∴旋转角α=60°;②当点G 在AD 左侧时,如答图2,同理可得△ADG 是等边三角形,∴∠DAG =60°, ∴旋转角α=360°-60°=300°. 综上,α为60°或300°时,GC =GB.5.如图1,边长为4的正方形ABCD 中,点E 在AB 边上(不与点A ,B 重合),点F 在BC 边上(不与点B ,C 重合).第一次操作:将线段EF 绕点F 顺时针旋转,当点E 落在正方形上时,记为点G ; 第二次操作:将线段FG 绕点G 顺时针旋转,当点F 落在正方形上时,记为点H ; 依此操作下去…(1)图2中的△EFD 是经过两次操作后得到的,其形状为等边三角形,求此时线段EF 的长; (2)若经过三次操作可得到四边形EFGH.①请判断四边形EFGH 的形状为正方形,此时AE 与BF 的数量关系是AE =BF ;②以①中的结论为前提,设AE 的长为x ,四边形EFGH 的面积为y ,求y 与x 的函数关系式及面积y 的取值范围.解:(1)如题图2,由旋转性质可知EF =DF =DE ,则△DEF 为等边三角形. 在Rt △ADE 和Rt △CDF 中,⎩⎨⎧AD =CD ,DE =DF ,∴Rt △ADE ≌Rt △CDF(HL).∴AE =CF. 设AE =CF =x ,则BE =BF =4-x ∴△BEF 为等腰直角三角形.∴DE =DF =EF =2(4-x).在Rt △ADE 中,由勾股定理得AE 2+AD 2=DE 2,即x 2+42=[2(4-x)]2, 解得x 1=8-43,x 2=8+43(舍去). ∴EF =2(4-x)=46-4 2.△DEF 的形状为等边三角形,EF 的长为46-4 2.第5题答图(2)①四边形EFGH 的形状为正方形,此时AE =BF.理由如下:依题意画出图形,如答图所示,连接EG ,FH ,作HN ⊥BC 于N ,GM ⊥AB 于M. 由旋转性质可知,EF =FG =GH =HE , ∴四边形EFGH 是菱形, 由△EGM ≌△FHN ,可知EG =FH ,∴四边形EFGH 的形状为正方形,∴∠HEF =90°. ∵∠1+∠2=90°,∠2+∠3=90°,∴∠1=∠3. ∵∠3+∠4=90°,∠2+∠3=90°,∴∠2=∠4.在△AEH 和△BFE 中,⎩⎨⎧∠1=∠3,EH =EF ,∠2=∠4,∴△AEH ≌△BFE(ASA),∴AE =BF.②利用①中结论,易证△AEH ,△BFE ,△CGF ,△DHG 均为全等三角形, ∴BF =CG =DH =AE =x ,AH =BE =CF =DG =4-x.∴y =S 正方形ABCD -4S △AEH =4×4-4×12·x·(4-x)=2x 2-8x +16,∴y =2x 2-8x +16(0<x <4).∵y =2x 2-8x +16=2(x -2)2+8,∴当x =2时,y 取得最小值8;当x =0或4时,y =16.∴y的取值范围为8≤y<16.6.提出问题如图,已知在矩形ABCD中,AB=2,BC=3,点P是线段AD边上的一动点(不与端点A,D重合),连接PC,过点P作PE⊥PC交AB于点E,在点P的运动过程中,图中各角和线段之间是否存在某种关系和规律?特殊求解当点E为AB的中点,且AP>AE时,求证:PE=PC.深入探究当点P在AD上运动时,对应的点E也随之在AB上运动,求整个运动过程中BE的取值范围.解:特殊求解∵PE⊥PC,∴∠APE+∠DPC=90°.∵∠D=90°,∴∠DPC+∠DCP=90°.∴∠APE=∠DCP.∵∠A=∠D=90°,∴△APE∽△DCP,∴APDC=AEDP.设AP=x,则有DP=3-x.而AE=BE=1,∴x(3-x)=2×1,解得x1=2,x2=1.∵AP>AE,∴AP=2,AE=PD=1,∴△APE≌△DCP,∴PE=PC.深入探究设AP=x,AE=y,由AP·DP=AE·DC,可得x(3-x)=2y.∴y=12x(3-x)=-12x2+32x=-12(x-32)2+98.∴在0<x<3范围内,当x =32时,y 最大=98.∵当AE =y 取得最大值时,BE 取得最小值为2-98=78,∴BE 的取值范围为78≤BE<2.7.已知Rt △OAB ,∠OAB =90°,∠ABO =30°,斜边OB =4,将Rt △OAB 绕点O 顺时针旋转60°,如图1,连接BC.(1)填空:∠OBC =60°;(2)如图1,连接AC ,作OP ⊥AC ,垂足为P ,求OP 的长度;(3)如图2,点M ,N 同时从点O 出发,在△OCB 边上运动,M 沿O→C→B 路径匀速运动,N 沿O→B→C 路径匀速运动,当两点相遇时运动停止,已知点M 的运动速度为1.5单位/秒,点N 的运动速度为1单位/秒,设运动时间为x 秒,△OMN 的面积为y ,求当x 为何值时y 取得最大值.最大值为多少?解:(1)由旋转性质可知OB =OC ,∠BOC =60°, ∴△OBC 是等边三角形,∴∠OBC =60°.第7题答图1(2)如答图1中, ∵OB =4,∠ABO =30°, ∴OA =12OB =2,AB =3OA =23,∴S △AOC =12·OA·AB=12×2×23=2 3.∵△BOC 是等边三角形,∴∠OBC =60°,∠ABC =∠ABO +∠OBC =90°, ∴AC =AB 2+BC 2=2r(32+42)=27,∴OP =2S △AOC AC =4327=2217.第7题答图2(3)①当0<x≤83时,M 在OC 上运动,N 在OB 上运动,此时过点N 作NE ⊥OC 且交OC 于点E.如答图2,则NE =ON·sin60°=32x ,∴S △OMN =12·OM·NE=12×1.5x×32x ,∴y =338x 2,∴当x =83时,y 有最大值,最大值为833.第7题答图3②当83<x≤4时,M 在BC 上运动,N 在OB 上运动.如答图3,作MH ⊥OB 于H.则BM =8-1.5x ,MH =BM·sin60°=32(8-1.5x),∴y =12×ON×MH=-338x 2+23x.当x =83时,y 取得最大值,最大值为833.第7题答图4③当4<x≤4.8时,M,N都在BC上运动,作OG⊥BC于G.如答图4,MN=12-2.5x,OG=AB=23,∴y=12·MN·OG=123-532x,当x=4时,y有最大值,最大值为2 3.综上所述,y有最大值,最大值为83 3.8.在菱形ABCD中,∠ABC=60°,点P是射线BD上一动点,以AP为边向右侧作等边△APE,点E 的位置随着点P的位置变化而变化.(1)如图1,当点E在菱形ABCD内部或边上时,连接CE,BP与CE的数量关系是PB=EC,CE与AD 的位置关系是CE⊥AD;(2)当点E在菱形ABCD外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,请说明理由(选择图2,图3中的一种情况予以证明或说理);(3)如图4,当点P在线段BD的延长线上时,连接BE.若AB=23,BE=219,求四边形ADPE的面积.解:(1)结论:PB=EC,CE⊥AD.理由:如答图1中,连接AC.∵四边形ABCD是菱形,∠ABC=60°,∴△ABC,△ACD都是等边三角形,∠ABD=∠CBD=30°.∵△APE是等边三角形,∴AB=AC,AP=AE,∠BAC=∠PAE=60°,∴△BAP≌△CAE,∴BP=CE,∠ABP=∠ACE=30°,延长CE交AD于H,∵∠CAH=60°,∴∠CAH+∠ACH=90°,∴∠AHC=90°,即CE⊥AD.第8题答图2(2)结论仍然成立.理由:如答图2,连接AC交BD于O,设CE交AD于H.∵四边形ABCD是菱形,∠ABC=60°,∴△ABC,△ACD都是等边三角形,∠ABD=∠CBD=30°.∵△APE是等边三角形,∴AB=AC,AP=AE,∠BAC=∠PAE=60°,∴△BAP≌△CAE,∴BP=CE,∠ABP=∠ACE=30°,∵∠CAH=60°,∴∠CAH+∠ACH=90°,∴∠AHC=90°,即CE⊥AD.(3)如答图3,连接AC 交BD 于点O ,连接CE 交AD 于点H , 由(2)可知EC ⊥AD ,CE =BP , 在菱形ABCD 中,AD ∥BC , ∴EC ⊥BC.∵BC =AB =23,BE =219, ∴在Rt △BCE 中,EC =2r(192-2r(3)2)=8,∴BP =CE =8.∵AC 与BD 是菱形的对角线, ∴∠ABD =12∠ABC =30°,AC ⊥BD ,∴BD =2BO =2AB·cos30°=6,∴OA =12AB =3,DP =BP -BD =8-6=2,∴OP =OD +DP =5,在Rt △AOP 中,AP =AO 2+OP 2=27, ∴S 四边形ADPE =S △ADP +S △AEP =12DP·AO+34·AP 2=12×2×3+34×(27)2=8 3.考点3 三角形、四边形混合几何探究9.我们把两条中线互相垂直的三角形称为“中垂三角形”,例如图1,图2,图3中,AF ,BE 是△ABC 的中线,AF ⊥BE ,垂足为P ,像△ABC 这样的三角形均称为“中垂三角形”,设BC =a ,AC =b ,AB =c.特例探索(1)如图1,当∠ABE =45°,c =22时,a =____25____,b =____25____. 如图2,当∠ABE =30°,c =4时,a =____213____,b =____27____. 归纳证明(2)请你观察(1)中的计算结果,猜想a 2,b 2,c 2三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式.拓展应用(3)如图4,在□ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG,AD=25,AB=3,求AF的长.解:(1)∵AF⊥BE,∠ABE=45°,∴AP=BP=22AB=2.∵AF,BE是△ABC的中线,∴EF∥AB,EF=12AB=2,∴∠PFE=∠PEF=45°,∴PE=PF=1.在Rt△FPB和Rt△PEA中,AE=BF=12+22=5,∴AC=BC=25,∴a=b=2 5.如答图1,连接EF.同理可得EF=12×4=2.∵EF∥AB,∴△PEF∽△PBA,∴PFAP=PEPB=EFAB=12.在Rt△ABP中,AB=4,∠ABP=30°,∴AP=2,PB=23,∴PF=1,PE= 3.在Rt△APE和Rt△BPF中,AE=7,BF=13,∴a=213,b=27.(2)猜想:a2+b2=5c2,证明如下:如答图2,连接EF.设∠ABP=α,∴AP=csinα,PB=ccosα,由(1)同理可得PF=12PA=csinα2,PE=12PB=ccosα2, ∴AE 2=AP 2+PE 2=c 2sin 2α+c 2cos 2α4,BF 2=PB 2+PF 2=c 2cos 2α+c 2sin 2α4,∴(b 2)2=c 2sin 2α+c 2cos 2α4,(a 2)2=c 2sin 2α4+c 2cos 2α,∴a 24+b 24=c 2sin 2α4+c 2cos 2α+c 2sin 2α+c 2cos 2α4, ∴a 2+b 2=5c 2.(3)如答图3,连接AC ,EF 交于点H ,AC 与BE 交于点Q ,设BE 与AF 的交点为P. ∵点E ,G 分别是AD ,CD 的中点,∴EG ∥AC. ∵BE ⊥EG ,∴BE ⊥AC.∵四边形ABCD 是平行四边形,∴AD ∥BC ,AD =BC =25,∴∠EAH =∠FCH. ∵E ,F 分别是AD ,BC 的中点, ∴AE =12AD ,BF =12BC ,∴AE =BF =CF =12AD = 5.∵AE ∥BF ,∴四边形ABFE 是平行四边形, ∴EF =AB =3,AP =PF.在△AEH 和△CFH 中,⎩⎨⎧∠EAH =∠FCH ,∠AHE =∠FHC ,AE =CF ,∴△AEH ≌△CFH ,∴EH =FH ,∴EP ,AH 分别是△AFE 的中线,由(2)的结论得AF 2+EF 2=5AE 2,或连接F 与AB 的中点M ,证MF 垂直BP ,构造出“中垂三角形”,由AB =3,BC =12AD =5及(2)中的结论,直接可求AF.10.我们定义:如图1,在△ABC 中,把AB 绕点A 顺时针旋转α(0°<α<180°)得到AB′,把AC 绕点A 逆时针旋转β得到AC′,连接B′C′.当α+β=180°时,我们称△AB′C′是△ABC 的“旋补三角形”,△AB′C′边B′C′上的中线AD 叫做△ABC 的“旋补中线”,点A 叫做“旋补中心”.特例感知(1)在图2,图3中,△AB′C′是△ABC 的“旋补三角形”,AD 是△ABC 的“旋补中线”. ①如图2,当△ABC 为等边三角形时,AD 与BC 的数量关系为AD =12BC ;②如图3,当∠BAC =90°,BC =8时,则AD 长为4. 猜想论证(2)在图1中,当△ABC 为任意三角形时,猜想AD 与BC 的数量关系,并给予证明. 拓展应用(3)如图4,在四边形ABCD ,∠C =90°,∠D =150°,BC =12,CD =23,DA =6.在四边形内部是否存在点P ,使△PDC 是△PAB 的“旋补三角形”?若存在,给予证明,并求△PAB 的“旋补中线”长;若不存在,说明理由.图1 图2 图3 图4解:(1)①∵△ABC 是等边三角形,∴AB =BC =AC =AB′=AC′.∵DB′=DC′, ∴AD ⊥B′C′.∵∠BAC =60°,∠BAC +∠B′AC′=180°, ∴∠B′AC′=120°,∴∠B′=∠C′=30°, ∴AD =12AB′=12BC.②∵∠BAC =90°,∠BAC +∠B′AC′=180°,∴∠B′AC′=∠BAC=90°.∵AB=AB′,AC=AC′,∴△BAC≌△B′AC′,∴BC=B′C′.∵B′D=DC′,∴AD=12B′C′=12BC=4.(2)结论:AD=12 BC.证明如下:如答图1,延长AD到M,使得AD=DM,连接B′M,C′M.∵B′D=DC′,AD=DM,∴四边形AC′MB′是平行四边形,∴AC′=B′M=AC.第10题答图1∵∠BAC+∠B′AC′=180°,∠B′AC′+∠AB′M=180°,∴∠BAC=∠MB′A.∵AB=AB′,∴△BAC≌△AB′M,∴BC=AM,∴AD=12 BC.(3)存在.理由:如答图2,延长AD交BC的延长线于M,作BE⊥AD于E,作线段BC的垂直平分线交BE于P,交BC于F,连接PA,PD,PC,作△PCD的中线PN,第10题答图2连接DF交PC于O.∵∠ADC=150°,∴∠MDC=30°.在Rt△DCM中,CD=23,∠DCM=90°,∠MDC=30°,∴CM=2,DM=4,∠M=60°.在Rt△BEM中,∠BEM=90°,BM=14,∠MBE=30°,∴EM=12BM=7,∴DE=EM-DM=3.∵AD=6,∴AE=DE.∵BE⊥AD,∴PA=PD,PB=PC.在Rt△CDF中,CD=23,CF=6,∴tan∠CDF=3,∴∠CDF=60°=∠CPF,易证△FCP≌△CFD,∴CD=PF.∵CD∥PF.∴四边形CDPF是矩形,∴∠CDP=90°,∴∠ADP=∠ADC-∠CDP=60°,∴△ADP是等边三角形,∴∠ADP=60°.∵∠BPF=∠CPF=60°,∴∠BPC=120°,∴∠APD+∠BPC=180°,∴△PDC是△PAB的“旋补三角形”.在Rt△PDN中,∠PDN=90°,PD=AD=6,DN=3,∴PN=DN2+PD2=r(32+62)=39.考点4 多边形几何探究11.【图形定义】如图,将正n边形绕点A顺时针旋转60°后,发现旋转前后两图形有另一交点O,连接AO,我们称AO为“叠弦”;再将“叠弦”AO所在的直线绕点A逆时针旋转60°后,交旋转前的图形于点P,连接PO,我们称∠OAB为“叠弦角”,△AOP为“叠弦三角形”;【探究证明】(1)请在图1和图2中选择其中一个证明:“叠弦三角形”(△AOP)是等边三角形.(2)如图2,求证:∠OAB=∠OAE′;【归纳猜想】(3)图1、图2中的“叠弦角”的度数分别为15°,24°;(4)图n中,“叠弦三角形”是等边三角形(填“是”或“不是”);(5)图n中,“叠弦角”的度数为60°-180°n.(用含n的式子表示)解:(1)∵四边形ABCD是正方形,由旋转知,AD=AD′,∠D=∠D′=90°,∠DAD′=∠OAP=60°,∴∠DAP=∠D′AO,∴△APD≌△AOD′(ASA),∴AP=AO.∵∠OAP=60°,∴△AOP是等边三角形;第11题答图(2)如答图,作AM⊥DE于M,作AN⊥CB于N.∵五边形ABCDE是正五边形,由旋转知,AE=AE′,∠E=∠E′=108°,∠EAE′=∠OAP=60°,∴∠EAP=∠E′AO.在Rt△AEM和Rt△ABN中,∠AEM=∠ABN=72°,AE=AB,∴Rt△AEM≌Rt△ABN (AAS),∴∠EAM =∠BAN ,AM =AN.在Rt △APM 和Rt △AON 中,AP =AO ,AM =AN , ∴Rt △APM ≌Rt △AON (HL), ∴∠PAM =∠OAN ,∴∠PAE =∠OAB, ∴∠OAE′=∠OAB.(3)由(1)知,△APD ≌△AOD′, ∴∠DAP =∠D′AO.在Rt △AD′O 和Rt △ABO 中,⎩⎨⎧AD′=AB ,AO =AO ,∴Rt △AD′O≌Rt △ABO(HL), ∴∠D′AO=∠BAO.由旋转得,∠DAD′=60°.∵∠DAB =90°, ∴∠D′AB=∠DAB -∠DAD′=30°, ∴∠D′AO=12∠D′AB=15°,∵题图2的多边形是正五边形, ∴∠EAB =5-2×180°5=108°,∴∠E′AB=∠EAB -∠EAE′=108°-60°=48°, ∴同理可得,∠E′AO=12∠E′AB=24°.(4)是(5)同(3)的方法得,∠OAB =[(n -2)×180°÷n-60°]÷2=60°-180°n.考点5 圆形几何探究12.如图,在半径为3 cm 的⊙O 中,A ,B ,C 三点在圆上,∠BAC =75°.点P 从点B 开始以π5cm/s 的速度在劣弧BC 上运动,且运动时间为t s ,∠AOB =90°,∠BOP =n°.(1)求n与t之间的函数关系式,并求t的取值范围;(2)试探究:当点P运动多少秒时,①在BP,PC,CA,AB四条线段中有两条相互平行?②以P,B,A,C四点中的三点为顶点的三角形是等腰三角形?解:(1)∵∠BOP=n°,∴π5t=3πn180,n=12t.当n=150时,150=12t,t=12.5.∴t的取值范围为0≤t≤12.5.(2)①∠BOP=n°,n=12t.如答图1,当BP∥AC时,t=5.理由:∵∠PBA=180°-75°=105°,∠OBA=45°,∴∠OBP=60°.∵OB=OP,∴∠BOP=60°,∴60=12t,t=5.如答图2,当PC∥AB时,t=10.理由:易得∠PBA=∠BAC=75°,∴∠PBO=∠BPO=30°,∴∠BOP=120°,∴120=12t,t=10.综上所述,当点P的运动时间为5 s时,BP∥AC.当点P的运动时间为10 s时,PC∥AB.②在△ABP中,以AB为腰时(如答图3),∠BPA=∠BAP=45°,∠BOP=90°,∴t=7.5. 以AB为底边时(如答图4),∠BPA=45°,∠BAP=67.5°,∠BOP=2×67.5°=135°,∴t=11.25.如答图5,在△APC中,易得∠AOC=120°,∴∠APC=60°,△APC是等边三角形.∴∠AOP=120°,∴∠BOP=30°,t=2.5.如答图6,在△BPC中,∠BPC=105°,只有BP=PC这种情况.此时点P是弧BC的中心,∴∠BOP=75°,t=6.25.综上所述,当点P的运动时间为7.5 s或11.25 s时,△ABP为等腰三角形;当点P的运动时间为2.5 s时,△APC为等边三角形;当点P的运动时间为6.25 s时,△BPC为等腰三角形.。
中考数学压轴题:几何探究题

几何探究题(10道)1.如图①,在锐角△ABC中,∠ABC=45°,高线AD、BE相交于点F.(1)判断BF与AC的数量关系并说明理由.(2)如图②,将△ACD沿线段AD对折,点C落在BD 上的点M,AM与BE相交于点N,当DE∥AM时,①求证:AE=EC;②求∠MAC的度数以及线段NE与AC的数量关系.第1题图解:(1)BF=AC,理由是:∵AD⊥BC,BE⊥AC,∴∠ADB=∠AEF=90°,∵∠ABC=45°,∴△ABD是等腰直角三角形,∴AD =BD ,∵∠AFE =∠BFD ,∴∠DAC =∠EBC ,在△ADC 和△BDF 中,⎪⎩⎪⎨⎧︒=∠=∠=∠=∠90BDF ADC BDAD DBF DAC , ∴△ADC ≌△BDF (ASA ),∴BF =AC ;(2)①由折叠得:MD =DC ,∵DE ∥AM ,∴AE =EC ,②∵AE =EC ,BE ⊥AC ,∴AB =BC ,由(1)得:△ADC ≌△BDF ,∵△ADC ≌△ADM ,∴△BDF ≌△ADM ,∴∠DBF=∠MAD=22.5°,∴∠MAC=2∠MAD=45°,∵∠NEA=90°,∴△AEN是等腰直角三角形,1AC.∴EN=AE=EC,∴EN=22.在长方形ABCD中,点E是AD的中点,将△ABE沿BE折叠后得到对应的△GBE,将BG延长交直线DC于点F.(1)如果点G在长方形ABCD的内部,如图①所示.①求证:GF=DF;1DC,AD=4,求AB的长度.②若DF=2(2)如果点G在长方形ABCD的外部,如图②所示,AD的值. DF=kDC(k>1).请用含k的代数式表示AB第2题图解:(1)①连接EF ,如解图第2题解图根据翻折的性质得,∠EGF =∠A =90°,EG =AE =ED , 在Rt △EGF 和Rt △EDF 中,⎩⎨⎧==EF EF ED EG , ∴Rt △EGF ≌Rt △EDF (HL ),∴GF =DF ;②由①知,GF =DF ,设DF =x ,BC =y ,则GF =x ,AD =y , ∵DC =2DF ,∴CF =x ,DC =AB =BG =2x ,∴BF =BG +GF =3x ;在Rt △BCF 中,BC 2+CF 2=BF 2,即y 2+x 2=(3x )2 ∴y =22x ,∴ABAD =x y 2=2;∵AD=4,(2)由(1)知,GF=DF,设DF=x,BC=y,则GF=x,AD=y,在Rt△BCF中,BC2+CF2=BF2,3.将一副三角尺按图①摆放,等腰直角三角尺的直角边DF 恰好垂直平分AB,与AC相交于点G,BC=23cm.(1)求GC的长;(2)如图②,将△DEF绕点D顺时针旋转,使直角边DF 经过点C,另一直角边DE与AC相交于点H,分别过H、C作AB的垂线,垂足分别为M、N,通过观察,猜想MD与ND的数量关系,并验证你的猜想;(3)在(2)的条件下,将△DEF沿DB方向平移得到△D'E'F',当D'E'恰好经过(1)中的点G时,请直接写出DD'的长度.第3题图解:(1)在Rt△ABC中,∠BAC=30°,BC=23cm,∴AC=23×3=6cm,AB=43cm,又∵AD=BD,GD⊥AB,∴AD=23cm,在Rt△ADG中,∠BAC=30°,∴DG=2cm,AG=4cm,∴GC=AC-AG=6-4=2cm;(2)MD=ND,证明如下:∵D是AB的中点,∠ACB=90°,∠A=30°,∴BC=BD=AD,∵∠B=60°,∴△CDB为等边三角形.1BD,∵CN⊥BD,∴DN=NB=2在△ADH中,∠HDA=180°-60°-90°=30°,∴∠HDA=∠A=30°,1AD,∴MD=ND;∵HM⊥AB,∴AM=MD=2(3)DD'=23cm.【解法提示】如解图,连接GD,GB;∵GD垂直平分AB,∴AG=BG,∴∠GBA=∠A=30°,∠E'D'A=30°,当点D'与点B 重合时,点G在D'E'上,∴DD'=DB=23cm.第3题解图4.(1)如图①,已知等边△ABC,将直角三角板的60°角顶点D任意放在BC边上(点D不与点B、C重合),使两边分别交线段AB、AC于点E、F.①若AB=6,AE=4,BD=2,则CF= ;②求证:△EBD∽△DCF.(2)若将图①中的三角板的顶点D在BC边上移动,保持三角板与边AB、AC的两个交点E、F都存在,连接EF,如图②所示,问:点D是否存在某一位置,使BD的ED平分∠BEF且FD平分∠CFE?若存在,求出BC 值;若不存在,请说明理由.(3)如图③,在等腰△ABC中,AB=AC,点O为BC 边的中点,将三角形透明纸板的一个顶点放在点O处(其中∠MON=∠B),使两条边分别交边AB、AC于点E、F(点E、F均不与△ABC的顶点重合),连接EF.设∠B=α,则△AEF与△ABC的周长之比为(用含α的表达式表示).图①图②图③第4题图解:(1)①4;【解法提示】∵△ABC是等边三角形,∴AB=BC=AC=6,∠B=∠C=60°.∵AE=4,∴BE=2,则BE=BD,∴△BDE是等边三角形,∴∠BED=60°,又∵∠EDF=60°,∴∠CDF=180°-∠EDF-∠B=60°,则∠CDF=∠C=60°,∴△CDF是等边三角形,∴CF=CD=BC-BD=6-2=4.②证明:∵∠EDF=60°,∠B=60°,∴∠CDF+∠BDE=120°,∠BED+∠BDE=120°,∴∠BED=∠CDF.又∠B=∠C=60°,∴△EBD∽△DCF;(2)存在,如解图①,过D作DM⊥BE,DG⊥EF,DN⊥CF,垂足分别是M、G、N,第4题解图①∵ED 平分∠BEF 且FD 平分∠CFE .∴DM =DG =DN .又∠B =∠C =60°,∠BMD =∠CND =90°,∴△BDM ≌△CDN ,∴BD =CD ,即点D 是BC 的中点,∴BC BD =21; (3)如解图②,连接AO ,作OG ⊥BE ,OD ⊥EF ,OH ⊥CF ,垂足分别是G 、D 、H .第4题解图②则∠BGO =∠CHO =90°,∵AB =AC ,O 是BC 的中点,∴∠B =∠C ,OB =OC ,∴△OBG ≌△OCH ,∴OG =OH ,GB =CH ,∠BOG =∠COH =90°-α, 则∠GOH =180°-(∠BOG +∠COH )=2α,∴∠EOF =∠B =α,由(2)题可猜想应用EF =ED +DF =GE +FH (可通过半角旋转证明),则C △AEF =AE +EF +AF =AE +EG +FH +AF =AG +AH =2AG , 设AB =m ,则OB =mcosα,GB =mcos 2α.ααcos cos )(222m m m m OB AB AG OB AB AG C C ABC AEF +-=+=+=∆∆=1-cos α. 5.如图,Rt △ACB 中,∠ACB =90°,AC =BC ,E 点为射线CB 上一动点,连接AE ,作AF ⊥AE 且AF =AE .(1)如图①,过F 点作FD ⊥AC 交AC 于D 点,求证:FD =BC ;(2)如图②,连接BF 交AC 于G 点,若AG =3,CG =1,求证:E 点为BC 中点;(3)当E 点在射线CB 上,连接BF 与直线AC 交于G 点,若BC =4,BE =3,直接写出CGAG 的值.第5题图 (1)证明:∵FD ⊥AC ,∴∠FDA =90°, ∴∠DFA +∠DAF =90°, 同理,∵AF ⊥AE ,∴∠CAE +∠DAF =90°,∴∠DFA =∠CAE ,在△AFD 和△EAC 中,⎪⎩⎪⎨⎧=∠=∠︒=∠=∠AE AF EACAFD ECA ADF 90, ∴△AFD ≌△EAC (AAS ),∴DF =AC ,∵AC =BC ,∴FD =BC ;(2)如解图①,过点F 作FD ⊥AC 于点D ,第5题解图①由(1)得,FD =AC =BC ,AD =CE ,在△FDG 和△BCG 中,⎪⎩⎪⎨⎧=︒=∠=∠∠=∠BC FD BCG FDG BGC FGD 90, ∴△FDG ≌△BCG (AAS ),∴DG =CG =1,∴AD =2,∴CE =2,∵BC =AC =AG +CG =4,∴E 点为BC 中点;(3)311或35.【解法提示】当点E 在CB 的延长线上时,过F 作FD ⊥AG 与AG 的延长线交于点D ,如解图②,第5题解图②BC =AC =4,CE =CB +BE =7,由(1)(2)知:△ADF ≌△ECA ,△GDF ≌△GCB , ∴CG =GD ,AD =CE =7,∴CG =DG =1.5, ∴CG AG =5.15.14+=311, 同理,当点E 在线段BC 上时,CG AG =5.15.14-=35. 6.如图,在Rt △ABC 中,∠BAC =90°,AB =AC ,点D 为AB 延长线上一点,连接CD ,过A 分别作AM ⊥CD ,垂足为M ,交BC 于点N ,作AP ⊥BC ,垂足为P ,交CD 于点Q .(1)求证:AN =CQ ;(2)如图,点E 在BA 的延长线上,且AE =BD ,连接EN 并延长交CD 于点F ,求证:DQ =EN ;(3)在(2)的条件下,当AE =32AB 时,求FNEN 的值.第6题图证明:(1)∵AP ⊥BC ,AM ⊥CD ,∴∠APN =∠CPQ =90°,∴∠PNA +∠NAP =∠NAP +∠CQP =90°,∴∠PNA =∠CQP ,∵AB =AC ,∠BAC =90°,∴AP =PC ,∴△APN ≌△CPQ (ASA ),∴AN =CQ ;(2)如解图①,连接BQ ,第6题解图① 由(1)知:AP 是BC 的垂直平分线, ∴BQ =CQ , ∵AN =CQ ,∴AN =BQ ,∵BQ =CQ ,∴∠QBC =∠QCB =∠NAP ,∵∠PBA =∠PAB =45°,∴∠QBA =∠BAN ,∴∠DBQ =∠NAE ,在△DBQ 和△NAE 中,⎪⎩⎪⎨⎧=∠=∠=AE BD EAN DBQ AN BQ , ∴△DBQ ≌△EAN (SAS ),∴DQ =EN ; (3)∵AE =32AB ,即AB AE =32, ∴设AE =2x ,AB =3x ,则BD =2x ,DC =34x ,如解图②,过E 作EH ⊥AM ,交MA 的延长线于H ,第6题解图②∴∠H =∠AMD =90°,∴EH ∥DC ,∴△AHE ∽△AMD ,∴52322=+==x x x AD AE AM AH , ∵∠MAC =∠CDA ,∠ACN =∠DAQ =45°,∴△DQA ∽△ANC ,∴3535===x x AN DQ AC AD ,由(2)知:CQ=AN,∴设AH=8m,AM=20m,AN=17m,则MN=3m,∵EH∥FM,∴△EHN∽△FMN,7.如图,点P是正方形ABCD外一点,连接PA、PD,作BM⊥PA,垂足为E,使BM=PA,再作CN⊥PD,垂足为F,使CN=PD,连接PM、PN.(1)如图①,当PA=PD时,直接写出线段PM、PN的位置关系和数量关系;(2)在(1)的条件下,若∠APD=40°,则∠ABM= ;(3)如图②,当PA≠PD时,(1)中的结论是否仍然成立,若成立,请给出证明;若不成立,请说明理由.第7题图解:(1)结论:PM=PN,PM⊥PN.理由:如解图①,连接AM,DN.第7题解图①∵四边形ABCD是正方形,∴AB =BC =CD =AD ,∴∠BAD =90°,∵PE ⊥BM ,∴∠AEB =90°,∴∠PAD +∠EAB =90°,∠EAB +∠ABE =90°, ∴∠PAD =∠ABE ,∵PA =PD ,在△PAD 和△ABE 中,⎪⎩⎪⎨⎧=∠=∠=BAAD ABM PAD BMPA , ∴△PAD ≌△MBA (SAS ),∴AM =PD ,∠AMB =∠APD ,∴MA =MB =PA =PD ,同理可证:ND =NC =PA =PD ,∠DNC =∠APD ,∴∠AME =∠DNF ,∵∠AME +∠MAE =90°,∠DNF +∠NDF =90°, ∴∠MAE =∠NDF ,∴∠PAM =∠PDN ,∴△PAM≌△PDN(SAS),∴PM=PN,∠APM=∠DPN=∠AMP=∠DNP,∵∠AME+∠MAE=90°,∠MAE=∠AMP+∠APM=∠APM+∠NPD,∴∠APD+∠APM+∠NPD=90°,∴∠MPN=90°,∴MP⊥PN.(2)70°;【解法提示】∵PA=PD,∠P=40°,∴∠PAD=∠PDA=70°,由(1)可知:∠ABM=∠PAD=70°.(3)结论仍然成立,理由如下:如解图②,连接MA,延长MA交PF于点Q.第7题解图②由(1)可知:∠PAD=∠ABM,在△PAD 和△ABM 中,⎪⎩⎪⎨⎧=∠=∠=BA AD ABM PAD BM PA ∵PA =BM ,AD =BA ,∴△PAD ≌△MBA (SAS ),∴AM =PD ,∠ADP =∠MAB ,∵四边形ABCD 是正方形,∴∠BAD =∠ADC =90°,AB =AD =CD ,∵∠MAB +∠QAD =90°,∴∠QAD +∠ADP =90°,∴∠AQD =90°,∵PF ⊥CN ,∴∠AQD =∠DFC =90°,∴∠ADQ +∠CDF =90°,∠CDF +∠DCF =90°,∴∠ADQ =∠DCF ,在△ADQ 和△DCF 中,⎪⎩⎪⎨⎧=∠=∠∠=∠CD AD DCF ADQ DFC AQD ,∴△AQD ≌△DFC (AAS ),∴AQ =DF ,DQ =CF ,∵PD =CN ,∴PQ =FN ,MQ =PF ,∵∠MQP =∠PFN =90°,∴△MQP ≌△PFN (SAS ),∴PM =PN ,∠MPQ =∠N ,∵∠N +∠FPN =90°,∴∠MPQ +∠FPN =90°,∴∠MPN =90°,∴PM ⊥PN .8、在Rt △ABC 中,∠ACB =90°,∠B =30°,M 为AB 中点,点P 为BC 延长线上一点,CP <BC ,连接PM ,AC =n ,CP =m .(1)如图①,将射线MP 绕点M 逆时针旋转60°交CA 延长线于点D ,且BC =AD +CP.①在图中找出与∠MDC相等的角,并加以证明;m的值;②求n(2)如图②,若将射线MP绕点M顺时针旋转60°交AC延长线于点H,求CH的长(用含有m,n的式子表示)第8题图①第8题图②解:(1)①结论:∠ADM=∠PMA.理由:如解图①,连接CM.∵∠ACB=90°,∠B=30°,∴∠BAC=60°,∵BM=MA,∴CM=MA=BM,∴△AMC是等边三角形,∴∠AMC=∠PMN=60°,∴∠PMC=∠AMD,∵∠BAC=∠AMD+∠ADM=60°,∠AMP+∠PMC=60°∴∠ADM=∠PMA.第8题解图①②如解图①,连接CM、作CK∥AB交PM于点K.∵CK∥AB,由(1)知△AMC是等边三角形,∴∠MAC=∠MCA=∠AMC=60°,MA=MC,∵CK∥AB,∴∠ACK=∠MAC=60°,∠AMK=∠MKC,∴∠DAM=∠MCK=120°,∵∠ADM=∠AMP,∴∠MKC=∠MDA,在△MCK 和△MAD 中,⎪⎩⎪⎨⎧=∠=∠∠=∠MCMA MAD MCK MDAMKC ,∴△MCK ≌△MAD ,∵CK ∥BM ,∴△PKC ∽△PMB ,∴AD =CK ,∵BC =AD +PC ,整理得:m 2+mn -3n 2=0,(3)如解图②,连接CM 、作CK ∥AB 交PM 于点K .第8题解图② ∵∠PMH =∠ACM =60°, ∴∠PMC +∠CMH =∠CMH +∠H ,∴∠CMK =∠H ,∵∠HCM =∠MCK =120°,∴△HCM ∽△MCK ,∴CK CM MC HC =, ∴nm mnn n HC 3+=, ∴HC =mn mn 23+. 9. 已知四边形ABCD 是正方形,△BEF 是等腰直角三角形,∠BEF =90°,BE =EF ,连接DF ,G 为DF 的中点,连接EG,CG,EC.(1)如图①,若点E在CB边的延长线上,直接写出EC的值;EG与GC的位置关系及GC(2)将图①中的△BEF绕点B顺时针旋转至图②所示位置,请问(1)中所得的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;(3)将图①中的△BEF绕点B顺时针旋转α(0°<α<90°),若BE=1,AB=2,当E,F,D三点共线时,求DF的长及tan∠ABF的值.第9题图EC=2,解:(1)EG⊥CG,GC理由如下:如解图①,过G作GH⊥EC于点H,∵∠FEB=∠DCB=90°,∴EF∥GH∥DC,∵G 为DF 中点, ∴H 为EC 中点, ∴EG =GC ,GH =21(EF +DC )=21(EB +BC ), 即GH =EH =HC ,∴∠EGC =90°,即△EGC 是等腰直角三角形, ∴GC EC =2;第9题解图① 第9题解图② (2)解:结论还成立,理由如下:如图②,延长EG 到H ,使EG =GH ,连接CH 、EC ,延长CD 交EH 于点N ,过E 作BC 的垂线交CB 延长线于点R ,交DF 延长线于点Q ,∵在△EFG 和△HDG 中,⎪⎩⎪⎨⎧=∠=∠=HG EG DGH FGE GD GF ,∴△EFG ≌△HDG (SAS ),∴DH =EF =BE ,∠FEG =∠DHG ,∴EF ∥DH ,又易证ER ∥CD ,∴∠1=∠2,∴∠1=∠2=90°-∠3=∠4,∴∠EBC =180°-∠4=180°-∠1=∠HDC ,在△EBC 和△HDC 中,⎪⎩⎪⎨⎧=∠=∠=CD BC HDC EBC DH BE ,∴△EBC ≌△HDC .∴CE =CH ,∠BCE =∠DCH ,∴∠ECH =∠DCH +∠ECD =∠BCE +∠ECD =∠BCD =90°,∴△ECH 是等腰直角三角形, ∵G 为EH 的中点,∴EG ⊥GC ,GCEC =2, 即(1)中的结论仍然成立;(3)解:如解图③,连接BD ,第9题解图③∵在正方形ABCD 中,AB =2,∴BD =2,∴cos ∠DBE =BD BE =21, ∴∠DBE =60°,∴∠ABE =∠DBE -∠ABD =15°,∴∠ABF =45°-15°=30°,∴tan ∠ABF =33,∴DE =3BE =3, ∴DF =DE -EF =3-1.10.在△ABC 和△ADE 中,AB =AC ,∠BAC =120°,∠ADE =90°,∠DAE =60°,F 为BC 中点,连接BE 、DF ,G 、H 分别为BE ,DF 的中点,连接GH .(1)如图①,若D 在△ABC 的边AB 上时,请直接写出线段GH 与HF 的位置关系 ,HFGH = . (2)如图②,将图①中的△ADE 绕A 点逆时针旋转至图②所示位置,其他条件不变,(1)中结论是否改变?请说明理由;(3)如图③,将图①中的△ADE 绕A 点顺时针旋转至图③所示位置,若C 、D 、E 三点共线,且AE =2,AC =5,求线段BE 的长.图① 图② 图③第10题图 解:(1)如解图①,连接DG ,FG .第10题解图①∵AB =AC ,BF =CF ,∴AF ⊥BC ,∴∠BAF =∠CAF =60°,∵ED ⊥AB ,∴∠BFE =∠BDE =90°,∵BG =GE ,∴DG =21BE ,GF =21BE ,∴DG =FG ,∵DH =HF ,∴GH ⊥DF ,∵∠BAE =60°,∴∠ABE +∠AEB =120°,∵DG=BG=GF=GE,∴∠GBD=∠GDB,∠GEF=∠GFE,∴∠BGD+∠EGF=120°,∴∠DGF=60°,∴△DGF是等边三角形,GH=tan60°=3.∴HF(2)结论不变.理由:如解图②,延长ED至S,使DS=DE,连接AS,BS,CE,FG,DG.第10题解图②∵∠ADE=90°,DS=DE,∴AS=AE,∠DAE=∠DAS=60°,∴∠BAC=∠SAE=120°,∴∠SAB=∠EAC,∵AB=AC,∴△ABS≌△ACE.∴BS=CE,∠ABS=∠ACE,∵F,G分别为BC,BE中点,∴DG=FG,∵H为DF中点,∴GH⊥HF,延长SB交CE延长线于T,∵∠ABS+∠ABT=∠ACE+∠ABT=180°,∴∠BAC+∠T=180°,∴∠T=60°,延长FG交BT于P,∴∠T=∠BPF=∠DGF=60°,(3)如解图③,延长ED到H,使得DH=DE,连接AH,BH,作BM⊥EC于M,设BC交AH于点O.第10题解图③∵AD⊥EH,ED=DH,∴AE=AH,∴∠AEH=∠AHE=30°,∴∠EAH=∠BAC=120°,∴∠BAH=∠CAE,∵AB=AC,AH=AE,∴△BAH≌△CAE(SAS),∴∠BHA=∠AEC=30°,BH=CE,∴∠OBA=∠OHC=30°,∵∠AOB =∠COH ,∴△AOB ∽△COH ,∴△AOC ∽△BOH ,∴∠BHO =∠AOC =30°,∴∠BHE =30°+30°=60°,在Rt △ADE 中,∵AE =2,∠AED =30°,在Rt △EBM 中,11)1233()]332(21[22=-++=.。
中考几何探究题目选(三)

纯几何探究(三)1.如图11,已知四边形ABCD 是菱形,G 是线段CD 上的任意一点时,连接BG 交AC 于F ,过F 作FH CD ∥交BC 于H ,可以证明结论FH FG AB BG=成立(考生不必证明). (1)探究:如图12,上述条件中,若G 在CD 的延长线上,其它条件不变时,其结论是否成立?若成立,请给出证明;若不成立,请说明理由;(5分)(2)计算:若菱形ABCD 中660AB ADC ==,∠,G 在直线..CD 上,且16CG =,连接BG 交AC 所在的直线于F ,过F 作FH CD ∥交BC 所在的直线于H ,求BG 与FG 的长.(7分)(3)发现:通过上述过程,你发现G 在直线CD 上时,结论FH FG AB BG=还成立吗?(1分) 2.(07年佛山)在Rt ABC △中,902BAC AB AC ∠===,,点D 在BC 所在的直线上运动,作45ADE ∠=(A D E ,,按逆时针方向). (1)如图1,若点D 在线段BC 上运动,DE 交AC 于E . ①求证:ABD DCE △∽△;②当ADE △是等腰三角形时,求AE 的长.(2)①如图2,若点D 在BC 的延长线上运动,DE 的反向延长线与AC 的延长线相交于点E ',是否存在点D ,使ADE '△是等腰三角形?若存在,写出所有点D 的位置;若不存在,请简要说明理由;②如图3,若点D 在BC 的反向延长线上运动,是否存在点D ,使AD E △是等腰三角形?若存在,写出所有点D 的位置;若不存在,请简要说明理由.3.如图,直线AC ∥BD ,连结AB ,直线AC 、BD 及线段AB 把平面分成①、②、③、④四个图11 A BD FC H G图12A B C D F H G 45 A B D C E 第25题图1 45 45 CD B AE E ' C A B D E第25题图2 第25题图3部分,规定:线上各点不属于任何部分。
《几何综合探究题中考27题》(共55题)2022年中考专练附答案(北京专用)

5年(2016-2020)中考1年模拟数学试题分项详解(北京专用)专题15几何综合探究题中考27题(共45题)一.解答题(共5小题)1.(2020•北京)在△ABC中,∠C=90°,AC>BC,D是AB的中点.E为直线AC上一动点,连接DE.过点D作DF⊥DE,交直线BC于点F,连接EF.(1)如图1,当E是线段AC的中点时,设AE=a,BF=b,求EF的长(用含a,b的式子表示);(2)当点E在线段CA的延长线上时,依题意补全图2,用等式表示线段AE,EF,BF之间的数量关系,并证明.【分析】(1)由三角形的中位线定理得DE∥BC,DE=12BC,进而证明四边形CEDF是矩形得DE=CF,得出CF,再根据勾股定理得结果;(2)过点B作BM∥AC,与ED的延长线交于点M,连接MF,证明△ADE≌△BDM得AE=BM,DE =DM,由垂直平分线的判定定理得EF=MF,进而根据勾股定理得结论.【解答】解:(1)∵D是AB的中点,E是线段AC的中点,∴DE∥BC,DE=12BC,∵∠ACB=90°,∴∠DEC=90°,∵DF⊥DE,∴∠EDF=90°,∴四边形CEDF是矩形,∴DE=CF=12BC,五年中考真题∴CF =BF =b , ∵CE =AE =a ,∴EF =√CF 2+CE 2=√a 2+b 2;(2)AE 2+BF 2=EF 2.证明:过点B 作BM ∥AC ,与ED 的延长线交于点M ,连接MF , 则∠AED =∠BMD ,∠CBM =∠ACB =90°, ∵D 点是AB 的中点, ∴AD =BD ,在△ADE 和△BDM 中, {∠AED =∠BMD ∠ADE =∠BDM AD =BD, ∴△ADE ≌△BDM (AAS ), ∴AE =BM ,DE =DM , ∵DF ⊥DE , ∴EF =MF , ∵BM 2+BF 2=MF 2, ∴AE 2+BF 2=EF 2.2.(2019•北京)已知∠AOB =30°,H 为射线OA 上一定点,OH =√3+1,P 为射线OB 上一点,M 为线段OH 上一动点,连接PM ,满足∠OMP 为钝角,以点P 为中心,将线段PM 顺时针旋转150°,得到线段PN ,连接ON . (1)依题意补全图1;(2)求证:∠OMP=∠OPN;(3)点M关于点H的对称点为Q,连接QP.写出一个OP的值,使得对于任意的点M总有ON=QP,并证明.【分析】(1)根据题意画出图形.(2)由旋转可得∠MPN=150°,故∠OPN=150°﹣∠OPM;由∠AOB=30°和三角形内角和180°可得∠OMP=180°﹣30°﹣∠OPM=150°﹣∠OPM,得证.(3)根据题意画出图形,以ON=QP为已知条件反推OP的长度.由(2)的结论∠OMP=∠OPN联想到其补角相等,又因为旋转有PM=PN,已具备一边一角相等,过点N作NC⊥OB于点C,过点P作PD⊥OA于点D,即可构造出△PDM≌△NCP,进而得PD=NC,DM=CP.此时加上ON=QP,则易证得△OCN≌△QDP,所以OC=QD.利用∠AOB=30°,设PD=NC=a,则OP=2a,OD=√3a.再设DM=CP=x,所以QD=OC=OP+PC=2a+x,MQ=DM+QD=2a+2x.由于点M、Q关于点H对称,即点H为MQ中点,故MH=12MQ=a+x,DH=MH﹣DM=a,所以OH=OD+DH=√3a+a=√3+1,求得a=1,故OP=2.证明过程则把推理过程反过来,以OP=2为条件,利用构造全等证得ON=QP.【解答】解:(1)如图1所示为所求.(2)设∠OPM=α,∵线段PM绕点P顺时针旋转150°得到线段PN∴∠MPN=150°,PM=PN∴∠OPN=∠MPN﹣∠OPM=150°﹣α∵∠AOB =30°∴∠OMP =180°﹣∠AOB ﹣∠OPM =180°﹣30°﹣α=150°﹣α ∴∠OMP =∠OPN(3)OP =2时,总有ON =QP ,证明如下:过点N 作NC ⊥OB 于点C ,过点P 作PD ⊥OA 于点D ,如图2 ∴∠NCP =∠PDM =∠PDQ =90° ∵∠AOB =30°,OP =2 ∴PD =12OP =1∴OD =√OP 2−PD 2=√3 ∵OH =√3+1 ∴DH =OH ﹣OD =1 ∵∠OMP =∠OPN∴180°﹣∠OMP =180°﹣∠OPN 即∠PMD =∠NPC 在△PDM 与△NCP 中 {∠PDM =∠NCP ∠PMD =∠NPC PM =NP∴△PDM ≌△NCP (AAS ) ∴PD =NC ,DM =CP设DM =CP =x ,则OC =OP +PC =2+x ,MH =MD +DH =x +1 ∵点M 关于点H 的对称点为Q ∴HQ =MH =x +1∴DQ =DH +HQ =1+x +1=2+x ∴OC =DQ在△OCN 与△QDP 中 {OC =QD∠OCN =∠QDP =90°NC =PD∴△OCN ≌△QDP (SAS )∴ON=QP3.(2018•北京)如图,在正方形ABCD中,E是边AB上的一动点(不与点A、B重合),连接DE,点A 关于直线DE的对称点为F,连接EF并延长交BC于点G,连接DG,过点E作EH⊥DE交DG的延长线于点H,连接BH.(1)求证:GF=GC;(2)用等式表示线段BH与AE的数量关系,并证明.【分析】(1)如图1,连接DF,根据对称得:△ADE≌△FDE,再由HL证明Rt△DFG≌Rt△DCG,可得结论;(2)证法一:如图2,作辅助线,构建AM=AE,先证明∠EDG=45°,得DE=EH,证明△DME≌△EBH,则EM=BH,根据等腰直角△AEM得:EM=√2AE,得结论;证法二:如图3,作辅助线,构建全等三角形,证明△DAE≌△ENH,得AE=HN,AD=EN,再说明△BNH是等腰直角三角形,可得结论.【解答】证明:(1)如图1,连接DF,∵四边形ABCD是正方形,∴DA=DC,∠A=∠C=90°,∵点A关于直线DE的对称点为F,∴△ADE≌△FDE,∴DA=DF=DC,∠DFE=∠A=90°,∴∠DFG=90°,在Rt△DFG和Rt△DCG中,∵{DF =DC DG =DG, ∴Rt △DFG ≌Rt △DCG (HL ), ∴GF =GC ;(2)BH =√2AE ,理由是:证法一:如图2,在线段AD 上截取AM ,使AM =AE , ∵AD =AB , ∴DM =BE ,由(1)知:∠1=∠2,∠3=∠4, ∵∠ADC =90°,∴∠1+∠2+∠3+∠4=90°, ∴2∠2+2∠3=90°, ∴∠2+∠3=45°, 即∠EDG =45°, ∵EH ⊥DE ,∴∠DEH =90°,△DEH 是等腰直角三角形, ∴∠AED +∠BEH =∠AED +∠1=90°,DE =EH , ∴∠1=∠BEH , 在△DME 和△EBH 中, ∵{DM =BE∠1=∠BEH DE =EH, ∴△DME ≌△EBH (SAS ), ∴EM =BH ,Rt △AEM 中,∠A =90°,AM =AE , ∴EM =√2AE , ∴BH =√2AE ;证法二:如图3,过点H 作HN ⊥AB 于N , ∴∠ENH =90°,由方法一可知:DE =EH ,∠1=∠NEH , 在△DAE 和△ENH 中,∵{∠A=∠ENH ∠1=∠NEH DE=EH,∴△DAE≌△ENH(AAS),∴AE=HN,AD=EN,∵AD=AB,∴AB=EN=AE+BE=BE+BN,∴AE=BN=HN,∴△BNH是等腰直角三角形,∴BH=√2HN=√2AE.4.(2017•北京)在等腰直角△ABC中,∠ACB=90°,P是线段BC上一动点(与点B、C不重合),连接AP,延长BC至点Q,使得CQ=CP,过点Q作QH⊥AP于点H,交AB于点M.(1)若∠P AC=α,求∠AMQ的大小(用含α的式子表示).(2)用等式表示线段MB与PQ之间的数量关系,并证明.【分析】(1)由等腰直角三角形的性质得出∠BAC =∠B =45°,∠P AB =45°﹣α,由直角三角形的性质即可得出结论;(2)连接AQ ,作ME ⊥QB ,由AAS 证明△APC ≌△QME ,得出PC =ME ,△MEB 是等腰直角三角形,由等腰直角三角形的性质即可得出结论. 【解答】解:(1)∠AMQ =45°+α;理由如下: ∵∠P AC =α,△ACB 是等腰直角三角形, ∴∠BAC =∠B =45°,∠P AB =45°﹣α, ∵QH ⊥AP , ∴∠AHM =90°,∴∠AMQ =180°﹣∠AHM ﹣∠P AB =45°+α;(2)PQ =√2MB ;理由如下: 连接AQ ,作ME ⊥QB ,如图所示: ∵AC ⊥QP ,CQ =CP , ∴∠QAC =∠P AC =α, ∴∠QAM =45°+α=∠AMQ , ∴AP =AQ =QM , 在△APC 和△QME 中, {∠MQE =∠PAC ∠ACP =∠QEM AP =QM,∴△APC ≌△QME (AAS ), ∴PC =ME ,∵△MEB 是等腰直角三角形,∴12PQ =√22MB , ∴PQ =√2MB .方法二:也可以延长AC 到D ,使得CD =CQ . 则易证△ADP ≌△QBM .∴BM =PD =√2CD =√2QC =√22PQ , 即PQ =√2MB .5.(2016•北京)在等边△ABC 中,(1)如图1,P ,Q 是BC 边上的两点,AP =AQ ,∠BAP =20°,求∠AQB 的度数;(2)点P ,Q 是BC 边上的两个动点(不与点B ,C 重合),点P 在点Q 的左侧,且AP =AQ ,点Q 关于直线AC 的对称点为M ,连接AM ,PM . ①依题意将图2补全;②小茹通过观察、实验提出猜想:在点P ,Q 运动的过程中,始终有P A =PM ,小茹把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法: 想法1:要证明P A =PM ,只需证△APM 是等边三角形;想法2:在BA 上取一点N ,使得BN =BP ,要证明P A =PM ,只需证△ANP ≌△PCM ;想法3:将线段BP 绕点B 顺时针旋转60°,得到线段BK ,要证P A =PM ,只需证P A =CK ,PM =CK … 请你参考上面的想法,帮助小茹证明P A =PM (一种方法即可).【分析】(1)根据等腰三角形的性质得到∠APQ =∠AQP ,由邻补角的定义得到∠APB =∠AQC ,根据三角形外角的性质即可得到结论;(2)如图2根据等腰三角形的性质得到∠APQ=∠AQP,由邻补角的定义得到∠APB=∠AQC,由点Q 关于直线AC的对称点为M,得到AQ=AM,∠OAC=∠MAC,等量代换得到∠MAC=∠BAP,推出△APM是等边三角形,根据等边三角形的性质即可得到结论.【解答】解:(1)∵AP=AQ,∴∠APQ=∠AQP,∴∠APB=∠AQC,∵△ABC是等边三角形,∴∠B=∠C=60°,∴∠BAP=∠CAQ=20°,∴∠AQB=∠APQ=∠BAP+∠B=80°;(2)如图2,∵AP=AQ,∴∠APQ=∠AQP,∴∠APB=∠AQC,∵△ABC是等边三角形,∴∠B=∠C=60°,∴∠BAP=∠CAQ,(将线段BP绕点B顺时针旋转60°,得到线段BK,要证P A=PM,只需证P A=CK,PM=CK…请你参考上面的想法,帮助小茹证明P A=PM)∵点Q关于直线AC的对称点为M,∴AQ=AM,∠QAC=∠MAC,∴∠MAC=∠BAP,∴∠BAP+∠P AC=∠MAC+∠CAP=60°,∴∠P AM=60°,∵AP=AQ,∴AP=AM,∴△APM是等边三角形,∴AP=PM.证明△ABP≌△ACM≌△BCK一年模拟新题一.解答题(共40小题)1.(2020•丰台区三模)如图,在△ABC中,∠BAC=30°,AB=AC,将线段AC绕点A逆时针旋转α°(0<α<180),得到线段AD,连接BD,交AC于点P.(1)当α=90°时,①依题意补全图形;②求证:PD=2PB;(2)写出一个α的值,使得PD=√3PB成立,并证明.【分析】(1)当α=90°时,①依题意即可补全图形;②根据30度角所对直角边等于斜边一半即可证明PD=2PB;(2)当α的值为60度时,根据等腰三角形的性质即可证明PD=√3PB成立.【解答】解:(1)当α=90°时,①如图即为补全的图形;②证明:∵∠BAC =30°,AB =AC , 根据题意可知:AC =AD , ∴AD =AB , ∴∠ABD =∠ADB , ∵∠CAD =90°, ∴∠DAB =120°,∴∠ABD =∠D =∠BAC =30°, ∴AP =BP ,在Rt △APD 中,∠ADB =30°, ∴PD =2AP , ∴PD =2PB ;(2)当α=60(或120°)时,PD =√3PB 成立, 情况1,如图所示:当α=60°时,过点D 作DF ⊥AC 于点F ,过点B 作BE ⊥AC 于点E ,∴DF ∥BE , ∴△DFP ∽△BEP , ∴DF BE=PD PB,在Rt △ABE 中,∠BAC =30°, ∴AC =AB =2BE ,在Rt △ADF 中,∠CAD =60°, ∴AD =2√33DF , ∵AD =AC =AB , ∴2BE =2√33DE , ∴√3BE =DF , ∴PD =√3PB . 情况2,如图所示:当α=120°时,过点D 作DF ⊥AC 于点F ,过点B 作BE ⊥AC 于点E ,∴DF ∥BE , ∴△DFP ∽△BEP , ∴DF BE=PD PB,在Rt △ABE 中,∠BAC =30°, ∴AC =AB =2BE ,在Rt △ADF 中,∠F AD =60°, ∴AD =2√33DF , ∵AD =AC =AB , ∴2BE =2√33DE ,∴√3BE=DF,∴PD=√3PB.2.(2020•石景山区二模)在△ABC中,AB=AC,D是边BC上的一点(不与点B重合),边BC上点E在点D的右边且∠DAE=12∠BAC,点D关于直线AE的对称点为F,连接CF.(1)如图1,①依题意补全图1;②求证:CF=BD.(2)如图2,∠BAC=90°,用等式表示线段DE,CE,CF之间的数量关系,并证明.【分析】(1)①根据题意补全图形即可;②连接AF,如图1,根据已知条件得到∠3=∠1+∠2.根据轴对称的性质得到AF=AD,∠F AE=∠3=∠1+∠2.根据全等三角形的性质得到结论;(2)连接F A,FE,如图2,根据等腰三角形的性质得到∠1=∠2=45°,求得∠FCE=90°,根据勾股定理即可得到结论.【解答】解:(1)①依题意补全图形,如图1;②证明:连接AF,如图1,∵∠3=12∠BAC,∴∠3=∠1+∠2.∵点F与点D关于直线AE对称,∴AF=AD,∠F AE=∠3=∠1+∠2.∴∠4=∠F AE﹣∠2=(∠1+∠2)﹣∠2=∠1.又∵AC=AB,∴△ACF≌△ABD(SAS),∴CF=BD;(2)线段DE,CE,CF之间的数量关系是DE2=CE2+CF2.证明:连接F A,FE,如图2,∵AB=AC,∠BAC=90°,∴∠1=∠2=45°,由(1)②,可得FE=DE,∠3=∠2=45°,∴∠FCE=90°,在Rt△FCE中,由勾股定理,得FE2=CE2+CF2,∴DE2=CE2+CF2.3.(2020•朝阳区三模)在△ABC中,∠C=90°,AC=BC,点P在线段BA的延长线上,作PD⊥AC,交AC的延长线于点D,点D关于直线AB的对称点为E,连接PE并延长PE到点F,使EF=AC,连接CF.(1)依题意补全图1;(2)求证:AD=CF;(3)若AC=2,点Q在直线AB上,写出一个AQ的值,使得对于任意的点P总有QD=QF,并证明.【分析】(1)依照题意,补全图形即可;(2)通过证明四边形DCFP是矩形,可得PD=CF,由等腰直角三角形的性质可得AD=PD=CF;(3)通过证明△DAQ≌△FCQ,可得QD=QF.【解答】解:(1)补全图形,如图所示:(2)∵∠C=90°,AC=BC,∴∠B=∠CAB=45°,∵PD⊥AC,∴∠PDA=90°,∴∠DP A=90°﹣∠P AD=45°=∠DAP,∴AD=DP,∵点D关于直线AB的对称点为E,∴∠FP A=∠DP A=45°,∴∠DPF=90°,又∵∠PDA=90°=∠ACF,∴四边形DCFP是矩形,∴PD=CF,∴AD=PD=CF;(3)AQ=√2,理由如下:如图2,连接CQ,∵∠C=90°,AC=BC=2,∴AB=2√2,∠B=∠CAB=45°,∵AQ=√2,∴AQ=BQ,又∵∠C=90°,AC=BC=2,∴CQ=AQ=BQ,∠QCA=∠CAQ=45°,∴∠DAQ=∠QCF=135°,又∵AD=CF,∴△DAQ≌△FCQ(SAS),∴FQ=DQ.4.(2020•北京二模)已知菱形ABCD中,∠A=60°,点E为边AD上一个动点(不与点A,D重合),点F在边DC上,且AE=DF,将线段DF绕着点D逆时针旋转120°得线段DG,连接GF,BF,EF.(1)依题意补全图形;(2)求证:△BEF为等边三角形;(3)用等式表示线段BG,GF,CF的数量关系,并证明.【分析】(1)根据题意补全图形即可;(2)易证△ABD为等边三角形,∠BDF=60°,由SAS证得△ABE≌△DBF,得出BE=BF,∠ABE=∠DBF,则∠EBF=∠EBD+∠DBF=∠EBD+∠ABE=60°,即可得出结论;(3)取FG中点H,连接DH,由等腰三角形的性质得出∠DFG=∠DGF=30°,DH⊥GF,由三角函数得出GF=√3DG,易证△BCD为等边三角形,B、D、G三点在同一条直线上,求出BG﹣CF=2DG,即可得出√3(BG﹣CF)=2GF.【解答】(1)解:补全图形,如图1所示:(2)证明:∵四边形ABCD是菱形,∴AB=AD,∵∠A=60°,∴△ABD为等边三角形,∠BDF=60°,∴∠ABD=∠BDC=60°,AB=BD,在△ABE和△DBF中,{AB=BD∠A=∠BDF=60°AE=DF,∴△ABE≌△DBF(SAS),∴BE=BF,∠ABE=∠DBF,∴∠EBF=∠EBD+∠DBF=∠EBD+∠ABE=∠ABD=60°,∴△BEF为等边三角形;(3)解:BG、GF、CF的数量关系为:√3(BG﹣CF)=2GF,理由如下:取FG中点H,连接DH,如图2所示:∵AE=DF=DG,∠FDG=120°,∴∠DFG=∠DGF=30°,DH⊥GF,∴GF=2GH=2DG•cos30°=2DG×√32=√3DG,∵四边形ABCD是菱形,∠A=60°,∴△BCD为等边三角形,∴BD=CD,∠BDC=60°,∵∠FDG=120°,∴∠BDC+∠FDG=180°,即B、D、G三点在同一条直线上,∴BG=BD+DG=CD+DG=CF+DF+DG=CF+2DG,∴BG﹣CF=2DG,∴√3(BG﹣CF)=2√3DG=2GF.5.(2020•朝阳区二模)已知∠AOB=40°,M为射线OB上一定点,OM=1,P为射线OA上一动点(不与点O重合),OP<1,连接PM,以点P为中心,将线段PM顺时针旋转40°,得到线段PN,连接MN.(1)依题意补全图1;(2)求证:∠APN=∠OMP;(3)H为射线OA上一点,连接NH.写出一个OH的值,使得对于任意的点P总有∠OHN为定值,并求出此定值.【分析】(1)根据要求画出图形即可.(2)利用三角形的外角的性质解决问题即可.(3)结论:OH=1时,∠OHN的值为定值.证明△OMP≌△GPN(SAS),推出OP=NG,∠AOB=∠NGP=40°,由OM=OH=PG=1,推出OP=HG,推出GH=GN,推出∠GNH=∠GHN=12(180°﹣40°)=70°可得结论.【解答】(1)解:图形如图所示:(2)证明:如图1中,∵∠MPN=∠AOB=40°,∠APM=∠APN+∠MPN=∠AOB+∠OMP,∴∠APN=∠OMP.(3)解:结论:OH=1时,∠OHN的值为定值.理由:在射线P A设取一点G,使得PG=OM,连接NG.∵PN=PM,∠GPN=∠OMP,∴△OMP≌△GPN(SAS),∴OP=NG,∠AOB=∠NGP=40°,∵OM=OH=PG=1,∴OP=HG,∴GH=GN,∴∠GNH=∠GHN=12(180°﹣40°)=70°,∴∠OHN=180°﹣70°=110°.6.(2020•海淀区二模)如图1,等边三角形ABC中,D为BC边上一点,满足BD<CD,连接AD,以点A 为中心,将射线AD顺时针旋转60°,与△ABC的外角平分线BM交于点E.(1)依题意补全图1;(2)求证:AD=AE;(3)若点B关于直线AD的对称点为F,连接CF.①求证:AE∥CF;②若BE+CF=AB成立,直接写出∠BAD的度数为20°.【分析】(1)由旋转即可补全图形;(2)先判断出∠BAE=∠CAD,再判断出∠ABE=60°=∠C,进而判断出△ABE≌△ACD,即可得出结论;(3)①先判断出AFC=∠ACF,设∠BAD=α,进而表示出∠F AD=α,∠CAF=60°﹣2α,进而得出∠ACF=60°+α再判断出∠CAE=120°﹣α,即可得出结论;②先判断出∠CBG=30°﹣α,进而判断出∠CDF=60°﹣2α,再判断出DF=CF,进而得出∠DCF=∠CDF=60°﹣2α,再判断出∠DCF=α,即可得出结论.【解答】解:(1)补全图形如图1所示;(2)由旋转知,∠DAE=60°,∵△ABC是等边三角形,∴AB=AC,∠ABC=∠C=∠BAC=60°,∴∠DAE=∠BAC,∴∠BAE=∠CAD,∵BE是△ABC的外角的平分线,∴∠ABM=12(180°﹣60°)=60°=∠C,在△ABE和△ACD中,{∠BAE=∠CADAB=AC∠ABE=∠ACD=60°,∴△ABE≌△ACD(SAS),∴AD=AE;(3)①如图2,连接AF,∵点F是点B关于AD的对称点,∴∠BAD=∠F AD,AF=AB,∴AF=AC,∴∠AFC=∠ACF,设∠BAD=α,则∠F AD=α,∴∠CAF=∠BAC﹣∠BAD﹣∠F AD=60°﹣2α,∴∠ACF=12(180°﹣∠CAF)=60°+α,由(2)知,∠BAE=∠CAD=60°﹣α,∴∠CAE=∠BAE+∠BAC=60°﹣α+60°=120°﹣α,∴∠ACF+∠CAE=60°+α+120°﹣α=180°,∴AE∥CF;②如图2,连接BF,设∠BAD=α,∵点F是点B关于AD的对称点,∴AD⊥BF,垂足记作点G,则∠AGB=90°,∴∠ABG=90°﹣α,∵∠ABC=60°,∴∠CBG=30°﹣α,连接DF,则BD=DF,∴∠CDF=2∠CBG=60°﹣2α,由(2)知,△ABE≌△ACD,∴BE=CD,∵BE+CF=AB,∴CD+CF=BC=BD+CD,∴BD=CF,∴DF=CF,∴∠DCF=∠CDF=60°﹣2α,由①知,∠ACF=60°+α,∴∠DCF=∠ACF﹣∠ACB=α,∴60°﹣2α=α,∴α=20°,即∠BAD=20°,故答案为:20.7.(2020•门头沟区二模)如图,在正方形ABCD中,点E,F分别是AB,BC上的两个动点(不与点A,B,C重合),且AE=CF,延长BC到G,使CG=CF,连接EG,DF.(1)依题意将图形补全;(2)小华通过观察、实验、提出猜想:在点E,F运动过程中,始终有EG=√2DF.经过与同学们充分讨论,形成了几种证明的想法:想法一:连接DE,DG,证明△DEG是等腰直角三角形;想法二:过点D作DF的垂线,交BA的延长线于H,可得△DFH是等腰直角三角形,证明HF=EG;…请参考以上想法,帮助小华证明EG=√2DF.(写出一种方法即可)【分析】(1)根据题意画出图形即可;(2)如图,连接DE,DG,根据正方形的性质得到AD=CD,∠A=∠DCF=90°,根据全等三角形的性质得到DE=DF,∠ADE=∠CDF,求得DF=DG,由等腰三角形的性质得到∠CDF=∠CDG,推出△EDG是等腰直角三角形,于是得到结论.【解答】解:(1)依题意补全图形如图所示;(2)如图,连接DE,DG,∵在正方形ABCD中,AD=CD,∠A=∠DCF=90°,∵AE=CF,∴△ADE≌△CDF(SAS),∴DE=DF,∠ADE=∠CDF,∵∠DCF=90°,∴DC⊥FG,∵CF=CG,∴DF=DG,∴∠CDF=∠CDG,∴DE=DG,∠ADE=∠CDG,∵∠ADC=90°,∴∠EDG=90°,∴△EDG是等腰直角三角形,∴EG=√2DG=√2DF.8.(2020•东城区二模)在△ABC 中,AB =AC ,∠BAC =α,点D 是△ABC 外一点,点D 与点C 在直线AB 的异侧,且点D ,A ,C 不共线,连接AD ,BD ,CD .(1)如图1,当α=60°.∠ADB =30°时,画出图形,直接写出AD ,BD ,CD 之间的数量关系; (2)当α=90°,∠ADB =45°时,利用图2,继续探究AD ,BD ,CD 之间的数量关系并证明; (提示:尝试运用图形变换,将要研究的有关线段尽可能转移到一个三角形中)(3)当∠ADB =α2时,进一步探究AD ,BD ,CD 之间的数量关系,并用含α的等式直接表示出它们之间的关系.【分析】(1)先判断出∠BDE =90°,再根据勾股定理得出BD 2+DE 2=BE 2,即BD 2+AD 2=BE 2,再判断出△ABE ≌△ACD (SAS ),得出BE =CD ,即可得出结论;(2)同(1)方法得出DE 2+BD 2=BE 2,进而得出2AD 2+BD 2=BE 2,同(1)的方法判断出BE =CD ,即可得出结论;(3)同(1)的方法得出DE 2+BD 2=BE 2,再判断出DF =2AD •sin α2,即可得出结论.【解答】解:(1)AD 2+BD 2=CD 2,理由:如图1,过AD 为边在AD 上侧作等边三角形ADE ,连接BE , 则AD =DE =AE ,∠DAE =∠ADE =60°, ∵∠ADB =30°,∴∠BDE =∠DBA +∠ADE =90°,在Rt △BDE 中,根据勾股定理得,BD 2+DE 2=BE 2, ∴BD 2+AD 2=BE 2, ∵∠DAE =∠BAC =60°, ∴∠BAE =∠CAD , ∵AB =AC ,∴△ABE ≌△ACD (SAS ),∴BE=CD,∴AD2+BD2=CD2;(2)如图2,过点A作AE⊥AD,且AE=AD,连接BE,DE,∴∠ADE=45°,∵∠BDA=45°,∴∠BDE=90°,根据勾股定理得,DE2+BD2=BE2,∵DE2=2AD2,∴2AD2+BD2=BE2,∵∠DAE=∠BAC=90°,∴∠BAE=∠CAD,∵AB=AC,∴△ABE≌△ACD(SAS),∴BE=CD,∴2AD2+BD2=CD2;(3)如图3,将线段AD绕点A顺时针旋转α得到AE,连接DE,BE,∴∠ADE=12(180°﹣∠DAE)=90°−12α,∵∠ADB=12α,∴∠BDE=90°,根据勾股定理得,DE2+BD2=BE2,∵∠DAE=∠BAC=α,∴∠BAE=∠CAD,∵AB=AC,∴△ABE≌△ACD(SAS),∴BE=CD,∴DE 2+BD 2=CD 2,过点A 作AF ⊥DE 于F ,则DE =2DF , ∴∠DAF =90°﹣∠ADE =12α, 在Rt △ADF 中,sin ∠DAF =DF AD , ∴DF =AD •sin ∠DAF =AD •sin α2,∴DE =2DF =2AD •sin α2,即:(2AD •sin α2)2+BD 2=CD 2.9.(2020•平谷区二模)如图,在△ABM中,∠ABC=90°,延长BM使BC=BA,线段CM绕点C顺时针旋转90°得到线段CD,连结DM,AD.(1)依据题意补全图形;(2)当∠BAM=15°时,∠AMD的度数是60°;(3)小聪通过画图、测量发现,当∠AMB是一定度数时,AM=MD.小聪把这个猜想和同学们进行交流,通过讨论,形成了证明该猜想的几种想法:想法1:通过观察图形可以发现,如果把梯形ABCD补全成为正方形ABCE,就易证△ABM≌△AED,因此易得当∠AMD是特殊值时,问题得证;想法2:要证AM=MD,通过第(2)问,可知只需要证明△AMD是等边三角形,通过构造平行四边形CDAF,易证AD=CF,通过△ABM≌△CBF,易证AM=CF,从而解决问题;想法3:通过BC=BA,∠ABC=90°,连结AC,易证△ACM≌△ACD,易得△AMD是等腰三角形,因此当∠AMD是特殊值时,问题得证.请你参考上面的想法,帮助小聪证明当∠AMD是一定度数时,AM=MD.(一种方法即可)【分析】(1)由题意画出,图形;(2)由旋转的性质可得出△DCM为等腰直角三角形,则∠DMC=45°,∠AMB=75°,可求出答案;(3)根据三种想法证明△AMD为等边三角形即可得出结论.【解答】解:(1)由题意画出图形如图1,(2)如图1,∵∠BAM=15°,∠ABC=90°,∴∠AMB=90°﹣15°=75°,∵线段CM绕点C顺时针旋转90°得到线段CD,∴CM=CD,∠MCD=90°,∴∠CMD=∠MDC=45°,∴∠AMD=180°﹣∠AMB﹣∠DMC=180°﹣75°﹣45°=60°.故答案为:60°.(3)当∠AMB=75°时,AM=DM.想法1证明:如图2,过点A作AE⊥CD交CD的延长线于点E,∵∠AEC=∠C=∠ABC=90°,AB=BC,∴四边形ABCE正方形,∴AB=AE,BC=CE,由(2)可知CM=CD,∴BM=DE,∴△ABM≌△AED(SAS),∴AM=AD,由(2)可知∠AMD=60°,∴△AMD为等边三角形,∴AM=DM.想法2证明:如图3,过点C作CF∥AD交AB于点F,∵AF∥CD,∴四边形AFCD为平行四边形,∴AD=CF,AF=CD,∵AB=AF+BF,BC=BM+CM,AB=BC,∴CD+BF=BM+CM,∵CD=CM,∴BF=BM,又∵AB=BC,∠FBC=∠MBC=90°,∴△ABM≌△CBF(SAS),∴AM=CF,∴AM=AD,又∵∠AMD=60°,∴△AMD为等边三角形,∴AM=DM.想法3证明:如图4,连接AC,∵BC=AB,∠ABC=90°,∴∠ACB=45°,∴∠ACD=45°,又∵CM=CD,AC=AC,∴△ACM≌△ACD(SAS),∴AM=AD,∵∠AMD=60°,∴△AMD为等边三角形,∴AM=DM.10.(2020•西城区二模)在正方形ABCD中,E是CD边上一点(CE>DE),AE,BD交于点F.(1)如图1,过点F作GH⊥AE,分别交边AD,BC于点G,H.求证:∠EAB=∠GHC;(2)AE的垂直平分线分别与AD,AE,BD交于点P,M,N,连接CN.①依题意补全图形;②用等式表示线段AE与CN之间的数量关系,并证明.【分析】(1)由平行线的性质可得出∠AGH=∠GHC.证得∠EAB=∠AGH.则结论得证;(2)①依题意补全图形即可;②连接AN,连接EN并延长,交AB边于点Q.证得NA=NE.得出∠ANE=∠ANQ=90°.则可得出AE=√2CN.【解答】(1)证明:在正方形ABCD中,AD∥BC,∠BAD=90°,∴∠AGH=∠GHC.∵GH⊥AE,∴∠EAB=∠AGH.∴∠EAB=∠GHC.(2)①补全图形,如图所示.②证明:连接AN,连接EN并延长,交AB边于点Q.∵四边形ABCD是正方形,∴点A,点C关于BD对称.∴NA=NC,∠BAN=∠BCN.∵PN垂直平分AE,∴NA=NE.∴NC=NE.∴∠NEC=∠NCE.在正方形ABCD中,BA∥CE,∠BCD=90°,∴∠AQE=∠NEC.∴∠BAN+∠AQE=∠BCN+∠NCE=90°.∴∠ANE=∠ANQ=90°.在Rt△ANE中,∴AE=√2CN.11.(2020•丰台区二模)如图,在Rt△ABC中,∠ABC=90°,将CA绕点C顺时针旋转45°,得到CP,点A关于直线CP的对称点为D,连接AD交直线CP于点E,连接CD.(1)根据题意补全图形;(2)判断△ACD的形状,并证明;(3)连接BE,用等式表示线段AB,BC,BE之间的数量关系,并证明.温馨提示:在解决第(3)问的过程中,如果你遇到困难,可以参考下面几种解法的主要思路.解法1的主要思路:延长BC至点F,使CF=AB,连接EF,可证△ABE≌△CFE,再证△BEF是等腰直角三角形.解法2的主要思路:过点A作AM⊥BE于点M,可证△ABM是等腰直角三角形,再证△ABC∽△AME.解法3的主要思路:过点A作AM⊥BE于点M,过点C作CN⊥BE于点N,设BN=a,EN=b,用含a或b的式子表示AB,BC.…….【分析】(1)根据要求画出图形即可.(2)结论:△ACD是等腰直角三角形.根据等腰直角三角形的定义判断即可.(3)结论:BC+BA=√2BE.延长BC至点F,使CF=AB,连接EF.证明△EAB≌△ECF(SAS),推出BE=EF,∠AEB=∠CEF可得结论.【解答】解:(1)图形如图所示:(2)结论:△ACD是等腰直角三角形.理由:∵A,D关于CP对称,∴AD⊥CP,∠ACP=∠PCD=45°,CA=CD,∴∠ACD=90°,∴△ACD是等腰直角三角形.(3)结论:BC+BA=√2BE.理由:延长BC至点F,使CF=AB,连接EF.∵∠ABC=∠AEC=90°,∴∠BAE+∠BCE=180°,∵∠BCE+∠ECF=180°,∴∠BAE=∠ECF,∵△ACD是等腰直角三角形,CE⊥AD,∴AE=DE,∴CE=AE=ED,∵AB=CF,∴△EAB≌△ECF(SAS),∴BE=EF,∠AEB=∠CEF,∴∠BEF=∠AEC=90°,∴△BEF是等腰直角三角形,∴BF=√2BE,∵BF=BC+CF=BC+BA,∴BC+BA=√2BE.12.(2020•密云区二模)已知:MN是经过点A的一条直线,点C是直线MN左侧的一个动点,且满足60°<∠CAN<120°,连接AC,将线段AC绕点C顺时针旋转60°,得到线段CD,在直线MN上取一点B,使∠DBN=60°.(1)若点C位置如图1所示.①依据题意补全图1;②求证:∠CDB=∠MAC;(2)连接BC,写出一个BC的值,使得对于任意一点C,总有AB+BD=3,并证明.【分析】(1)①根据题意作出图形即可求解;②根据等量关系可证∠CDB=∠MAC;(2)如图2,连接BC,在直线MN上截取AH=BD,连接CH,根据SAS可证△ACH≌△DCB,再根据全等三角形的性质和等边三角形的判定与性质即可求解.【解答】.解:(1)①如图1所示:②证明:∵∠C=60°,∠DBN=60°,∴∠C=∠DBN,∵∠DBN+∠ABD=180°,∴∠C+∠ABD=180°,在四边形ACDB中,∠CDB+∠BAC=180°,∵∠BAC+∠MAC=180°,∴∠CDB=∠MAC;(2)BC=3时,对于任意一点C,总有AB+BD=3.证明:如图2,连接BC,在直线MN上截取AH=BD,连接CH,∵∠MAC=∠CDB,AC=CD,∴△ACH≌△DCB(SAS),∴∠ACH=∠DCB,CH=CB,∵∠DCB+∠ACB=∠ACD=60°,∴∠HCB=∠ACH+∠ACB=60°,∴△HCB是等边三角形,∴BC=BH=BA+BD=3.13.(2020•顺义区二模)已知:在△ABC中,∠ABC=90°,AB=BC,点D为线段BC上一动点(点D不与点B、C重合),点B关于直线AD的对称点为E,作射线DE,过点C作BC的垂线,交射线DE于点F,连接AE.(1)依题意补全图形;(2)AE与DF的位置关系是AE⊥DF;(3)连接AF,小昊通过观察、实验,提出猜想:发现点D在运动变化的过程中,∠DAF的度数始终保持不变,小昊把这个猜想与同学们进行了交流,经过测量,小昊猜想∠DAF=45°,通过讨论,形成了证明该猜想的两种想法:想法1:过点A作AG⊥CF于点G,构造正方形ABCG,然后可证△AFG≌△AFE…想法2:过点B作BG∥AF,交直线FC于点G,构造▱ABGF,然后可证△AFE≌△BGC…请你参考上面的想法,帮助小昊完成证明(一种方法即可).【分析】(1)根据题意正确画图;(2)证明△ABD≌△AED(SSS),可得∠AED=∠B=90°,从而得结论;(3)想法1:如图2,过点A做AG⊥CF于点G,先证明四边形ABCG是正方形,得AG=AB,∠BAG =90°,再证明Rt△AFG≌Rt△AFE(HL),得∠GAF=∠EAF,根据∠BAG=90°及角的和可得结论;想法2:如图3,过点B作BG∥AF,交直线FC于点G,证明四边形ABGF是平行四边形,得AF=BG,∠BGC=∠BAF,再证明Rt△AEF≌Rt△BCG(HL),同理根据∠BCG=90°及等量代换,角的和可得结论.【解答】解:(1)补全图形如图1:(2)AE与DF的位置关系是:AE⊥DF,理由是:∵点B关于直线AD的对称点为E,∴AB=AE,BD=DE,∵AD=AD,∴△ABD≌△AED(SSS),∴∠AED=∠B=90°,∴AE⊥DF;故答案为:AE⊥DF;(3)猜想∠DAF=45°;想法1:证明如下:如图2,过点A做AG⊥CF于点G,依题意可知:∠B=∠BCG=∠CGA=90°,∵AB=BC,∴四边形ABCG是正方形,∴AG=AB,∠BAG=90°,∵点B关于直线AD的对称点为E,∴AB=AE,∠B=∠AED=∠AEF=90°,∠BAD=∠EAD,∴AG=AE,∵AF=AF,∴Rt△AFG≌Rt△AFE(HL),∴∠GAF=∠EAF,∵∠BAG=90°,∴∠BAD+∠EAD+∠EAF+∠GAF=90°,∴∠EAD+∠EAF=45°.即∠DAF=45°.想法2:证明如下:如图3,过点B作BG∥AF,交直线FC于点G,依题意可知:∠ABC =∠BCF =90°, ∴AB ∥FG , ∵AF ∥BG ,∴四边形ABGF 是平行四边形, ∴AF =BG ,∠BGC =∠BAF , ∵点B 关于直线AD 的对称点为E ,∴AB =AE ,∠ABC =∠AED =90°,∠BAD =∠EAD , ∵AB =BC , ∴AE =BC ,∴Rt △AEF ≌Rt △BCG (HL ), ∴∠EAF =∠CBG , ∵∠BCG =90°, ∴∠BGC +∠CBG =90°, ∴∠BAF +∠EAF =90°,∴∠BAD +∠EAD +∠EAF +∠EAF =90°, ∵∠BAD =∠EAD , ∴∠EAD +∠EAF =45°, 即∠DAF =45°. 故答案为:45.14.(2020•武汉模拟)已知,在△ABC 和△EFC 中,∠ABC =∠EFC =90°,点E 在△ABC 内,且∠CAE +∠CBE =90°(1)如图1,当△ABC 和△EFC 均为等腰直角三角形时,连接BF , ①求证:△CAE ∽△CBF ; ②若BE =2,AE =4,求EF 的长;(2)如图2,当△ABC 和△EFC 均为一般直角三角形时,若AB BC=EF FC=k ,BE =1,AE =3,CE =4,求k 的值.【分析】(1)①先判断出∠BCF =∠ACE ,再判断出CE AC=CF BC,即可得出结论;②先判断出∠CBF =∠CAE ,进而判断出∠EBF =90°,再求出BF =2√2,最后用勾股定理求解即可得出结论;(2)先判断出∠BCF =∠ACE ,再判断出CEAC=CF BC,进而判断出△BCF ∽△ACE ,进而表示出BF =√k +1,再表示出EF =√k +1,最后用勾股定理得,BE 2+BF 2=EF 2,建立方程求解即可得出结论.【解答】解:(1)①∵△ABC 和△CEF 都是等腰直角三角形, ∴∠ECF =∠ACB =45°, ∴∠BCF =∠ACE ,∵△ABC 和△CEF 都是等腰直角三角形, ∴CE =√2CF ,AC =√2CB , ∴CE CF =AC CB =√2,∴CE AC=CF BC,∴△BCF ∽△ACE ;②由①知,△BCF ∽△ACE , ∴∠CBF =∠CAE ,AE BF=AC BC=√2,∴BF =√22AE =√22×4=2√2, ∵∠CAE +∠CBE =90°, ∴∠CBF +∠CBE =90°, 即:∠EBF =90°,根据勾股定理得,EF =√BE 2+BF 2=√(2√2)2+22=2√3;(2)如图(2),连接BF ,在Rt △ABC 中,tan ∠ACB =ABBC =k , 同理,tan ∠ECF =k , ∴tan ∠ACB =tan ∠ECF , ∴∠ACB =∠ECF , ∴∠BCF =∠ACE ,在Rt △ABC 中,设BC =m ,则AB =km , 根据勾股定理得,AC =√AB 2+BC 2=m √k 2+1;在Rt △CEF 中,设CF =n ,则EF =nk ,同理,CE =n √k 2+1 ∴CF BC =nm ,CEAC =n√k 2+1m√k 2+1=n m,∴CF BC=CE AC,∵∠BCF =∠ACE , ∴△BCF ∽△ACE , ∴∠CBF =∠CAE , ∵∠CAE +∠CBE =90°, ∴∠CBF +∠CBE =90°, 即:∠EBF =90°, ∵△BCF ∽△ACE , ∴AE BF=AC BC =√k 2+1,∴BF =1√k +1AE =3√k +1,∵CE =4, ∴n √k 2+1=4, ∴n =√k +1, ∴EF =4k√k +1,在Rt △EBF 中,根据勾股定理得,BE 2+BF 2=EF 2,∴12+(3√k 2+1)2=(4k√k 2+1)2,∴k =√63或k =−√63(舍),即:k 的值为√63.15.(2020•丰台区模拟)如图,在正方形ABCD 中,E 是边BC 上的一动点(不与点B 、C 重合),连接DE 、点C 关于直线DE 的对称点为C ′,连接AC ′并延长交直线DE 于点P ,F 是AC ′的中点,连接DF . (1)求∠FDP 的度数;(2)连接BP ,请用等式表示AP 、BP 、DP 三条线段之间的数量关系,并证明; (3)连接AC ,若正方形的边长为√2,请直接写出△ACC ′的面积最大值.【分析】(1)证明∠CDE =∠C 'DE 和∠ADF =∠C 'DF ,可得∠FDP '=12∠ADC =45°;(2)作辅助线,构建全等三角形,证明△BAP ≌△DAP '(SAS ),得BP =DP ',从而得△P AP '是等腰直角三角形,可得结论;(3)先作高线C 'G ,确定△ACC ′的面积中底边AC 为定值2,根据高的大小确定面积的大小,当C '在BD 上时,C 'G 最大,其△ACC ′的面积最大,并求此时的面积. 【解答】解:(1)由对称得:CD =C 'D ,∠CDE =∠C 'DE , 在正方形ABCD 中,AD =CD ,∠ADC =90°, ∴AD =C 'D , ∵F 是AC '的中点,∴DF ⊥AC ',∠ADF =∠C 'DF ,∴∠FDP=∠FDC'+∠EDC'=12∠ADC=45°;(2)结论:BP+DP=√2AP,理由是:如图,作AP'⊥AP交PD的延长线于P',∴∠P AP'=90°,在正方形ABCD中,DA=BA,∠BAD=90°,∴∠DAP'=∠BAP,由(1)可知:∠FDP=45°∵∠DFP=90°∴∠APD=45°,∴∠P'=45°,∴AP=AP',在△BAP和△DAP'中,∵{BA=DA∠BAP=∠DAP′AP=AP′,∴△BAP≌△DAP'(SAS),∴BP=DP',∴DP+BP=PP'=√2AP;(3)如图,过C'作C'G⊥AC于G,则S△AC'C=12AC•C'G,Rt△ABC中,AB=BC=√2,∴AC=√(√2)2+(√2)2=2,即AC为定值,当C'G最大值,△AC'C的面积最大,连接BD,交AC于O,当C'在BD上时,C'G最大,此时G与O重合,∵CD=C'D=√2,OD=12AC=1,∴C'G=√2−1,∴S△AC'C=12AC•C'G=12×2(√2−1)=√2−1.16.(2020•朝阳区模拟)在四边形ABCD中,AB=AD,CB=CD,∠ABC=∠ADC=90°,∠BAD=α,∠BCD=β,点E,F是四边形ABCD内的两个点,满足∠EAF=12α,∠ECF=12β,连接BE,EF,FD.(1)如图1,当α=β时,判断∠ABE和∠ADF之间的数量关系,并证明你的猜想;(2)如图2,当α≠β时,用等式表示线段BE,EF,FD之间的数量关系(直接写出即可).【分析】(1)结论:∠ABE+∠ADF=90°.将△ABE绕点A逆时针旋转90°得到△ADM,将△BCE绕点C顺时针旋转90°得到△CDT,连接FM,TF.证明M,D,T共线,再证明FM=FT.DM=DT即可解决问题.(2)结论:EF2=BE2+DF2.将△ABE绕点A逆时针旋转α度得到△ADM,将△BCE绕点C顺时针旋转β度得到△CDT,连接FM,TF.证明∠FDM=90°,利用勾股定理即可解决问题.【解答】解:(1)结论:∠ABE+∠ADF=90°.理由:∵AB=AD,CB=CD,∠ABC=∠ADC=90°,∠BAD=∠BCD,∴∠BAD=∠BCD=90°,∴四边形ABCD是正方形,∴AB=BC=CD=AD,将△ABE绕点A逆时针旋转90°得到△ADM,将△BCE绕点C顺时针旋转90°得到△CDT,连接FM,TF.∵∠EAF=12×90°=45°,∴∠MAD+∠DAF=∠BAE+∠DAF=45°,∴∠F AM=∠F AE,∵AM=AE,AF=AF,∴△AFM≌△AFE(SAS),∴EF=FM,同法可证:EF=FT,∴FM=FT,∵∠ADM+∠CDT=∠ABE+∠CBE=90°,∴∠MDT=90°+90°=180°,∴M,D,T共线,∵DM=BE,DT=BE,∴DM=DT,∴FD⊥MT,∴∠FDM=90°,∴∠ADM+∠ADF=90°,∵∠ADM=∠ABE,∴∠ABE+∠ADF=90°.(2)结论:EF2=BE2+DF2.理由:∵AD=AB,CD=CB,∴将△ABE绕点A逆时针旋转α度得到△ADM,将△BCE绕点C顺时针旋转β度得到△CDT,连接FM,TF.∵∠EAF=12×∠DAB=12α,∴∠MAD+∠DAF=∠BAE+∠DAF=12α,∴∠F AM=∠F AE,∵AM=AE,AF=AF,∴△AFM≌△AFE(SAS),∴EF=FM,同法可证:EF=FT,∴FM=FT,∵∠ADM+∠CDT=∠ABE+∠CBE=90°,∴∠MDT=90°+90°=180°,∴M,D,T共线,∵DM=BE,DT=BE,∴DM=DT,∴FD⊥MT,∴∠FDM=90°,∴FM2=DM2+DF2,∵FM=EF,DM=BE,∴EF2=BE2+DF2.17.(2020•丰台区模拟)已知C为线段AB中点,∠ACM=α.Q为线段BC上一动点(不与点B重合),点P在射线CM上,连接P A,PQ,记BQ=kCP.(1)若α=60°,k=1,①如图1,当Q为BC中点时,求∠P AC的度数;②直接写出P A、PQ的数量关系;(2)如图2,当α=45°时.探究是否存在常数k,使得②中的结论仍成立?若存在,写出k的值并证明;若不存在,请说明理由.【分析】(1)如图1,作辅助线,构建等边三角形,证明△ADC为等边三角形.根据等边三角形三线合一可得∠P AC=∠P AD=30°;②作辅助线,证明△PCD'≌△PCQ,可得P A=PQ;(2)存在k=√2,如图2,作辅助线,构建全等三角形,证明△P AD≌△PQC(SAS).可得结论.【解答】解:(1)①如图1,在CM上取点D,使得CD=CA,连接AD,∵∠ACM=60°,∴△ADC为等边三角形.∴∠DAC=60°.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
寒假提高班材料六:几何探究题
1、如图1,图2,图3,在ABC △中,分别以AB AC ,为边,向ABC △外作正三角形,正四边形,正五边形,BE CD ,相交于点O .
①如图1,求证:ABE ADC △≌△; ②探究:如图1,BOC ∠= ; 如图2,BOC ∠= ; 如图3,BOC ∠= .
(2)如图4,已知:AB AD ,是以AB 为边向ABC △外所作正n 边形的一组邻边;
AC AE ,是以AC 为边向ABC △外所作正n 边形的一组邻边.BE CD ,的延长相交于点O . ①猜想:如图4,BOC ∠= (用含n 的式子表示);
②根据图4证明你的猜想.
2、请阅读下列材料:
问题:如图1,在菱形ABCD 和菱形BEFG 中,点A B E ,,在同一条直线上,P 是线段()()a a b a b +-的中点,连结
PG PC ,.若60ABC BEF ∠=∠=,探究PG 与PC 的位置关系及
PG
PC
的值. 小聪同学的思路是:延长GP 交DC 于点H ,构造全等三角形,经过推理使问题得到解决. 请你参考小聪同学的思路,探究并解决下列问题:
(1)写出上面问题中线段PG 与PC 的位置关系及PG PC 的值;
(2)将图1中的菱形BEFG 绕点B 顺时针旋转,使菱形BEFG 的对角线BF 恰好与菱形ABCD 的边AB 在同一条直线上,原问题中的其他条件不变(如图2).你在(1)中得
到的两个结论是否发生变化写出你的猜想并加以证明.
(3)若图1中2(090)ABC BEF ∠=∠=<<αα,将菱形BEFG 绕点B 顺时针旋转任意角度,原问题中的其他条件不变,请你直接写出
PG
PC
的值(用含α的式子表示).
3、如图,等腰梯形ABCD 中,AB =4,CD =9,∠C =60°,动点P 从点C 出发沿CD 方向向点D 运动,动点Q 同时以相同速度从点D 出发沿DA 方向向终点A 运动,其
中一个动点到达端点时,另一个动点也随之停止运动. (1)求AD 的长;
(2)设CP =x ,问当x 为何值时△PD Q 的面积达到最大,并求出最大值; (3)探究:在BC 边上是否存在点M 使得四边形PD Q M 是菱形若存在,请找出点
M ,并求出BM 的长;不存在,请说明理由.
4、已知矩形ABCD 和点P ,当点P 在BC 上任一位置(如图(1)所示)时,易证得结论:2222
PA PC PB PD +=+,
D A
B E F
C P
G
图1
D
C G P
A B E F
图2
请你探究:当点P分别在图(2)、图(3)中的位置时,2222
PA PB PC PD
、、和又有怎样的数量关系请你写出对上述两种情况的探究结论,并利用图(2)证明你的结论.
答:对图(2)的探究结论为____________________________________.
对图(3)的探究结论为_____________________________________.
5、如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处.(1)直接写出点E、F的坐标;
(2)设顶点为F的抛物线交y轴正半轴
...于点P,且以点E、F、P为顶点的三角形是等腰三角形,求该抛物线的解析式;
(3)在x轴、y轴上是否分别存在点M、N,使得四边形MNFE的周长最小如果存在,求出周长的最小值;如果不存在,请说明理由.
6、如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连结BG,DE.我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系:
(1)①猜想如图1中线段BG、线段DE的长度关系及所在直线的位置关系;
②将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度α,得到如图2、如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断.
(2)将原题中正方形改为矩形(如图4—6),且AB=a,BC=b,CE=ka,CG=kb (a≠b,k>0),第(1)题①中得到的结论哪些成立,哪些不成立若成立,以图5为例简要说明理由.
(3)在第(2)题图5中,连结DG、BE,且a=3,b=2,k=
1
2
,求22
BE DG
+的值.
7、正方形ABCD中,点O是对角线AC的中点,P是对角线AC上一动点,过点P作PF⊥CD于点F。
如图1,当点P与点O重合时,显然有DF=CF.
⑴如图2,若点P在线段AO上(不与点A、O重合),PE⊥PB且PE交CD于点E。
①求证:DF=EF;
②写出线段PC、PA、CE之间的一个等量关系,并证明你的结论;
⑵若点P 在线段OC 上(不与点O 、C 重合),PE ⊥PB 且PE 交直线CD 于点E 。
请完成图3并判断⑴中的结论①、②是否分别成立若不成立,写出相应的结论(所写结论均不必证明)
8、将一矩形纸片OABC 放在平面直角坐标系中,(00)O ,,(60)A ,,(03)C ,.动点Q 从点O 出发以每秒1个单位
长的速度沿OC 向终点C 运动,运动2
3
秒时,动点P 从点A 出发以相等的速度沿AO 向终点O 运动.当其中一点到达终点时,另一点也停止运动.设点P 的运动时间为t (秒).
(1)用含t 的代数式表示OP OQ ,;
(2)当1t =时,如图1,将OPQ △沿PQ 翻折,点O 恰好落在CB 边
上的
点D 处,求点D 的坐标;
9、(1)探究新知:如图1,已知△ABC 与△ABD 的面积相等, 试判断AB 与CD 的位置关系,并说明理由. (2)结论应用:
① 如图2,点M ,N 在反比例函数x
k
y =
(k >0)的图象上,过点M 作ME ⊥y 轴,过点N 作NF ⊥x 轴,垂足分别为E ,F . 试证明:MN ∥EF .
② 若①中的其他条件不变,只改变点M ,N 的位置如图3所示,请判断 MN 与EF 是否平行.
图1 图2
图
3 图1
图 3。
