关于电阻式触摸屏的线性校准问题
电阻式触摸屏校准算法分析
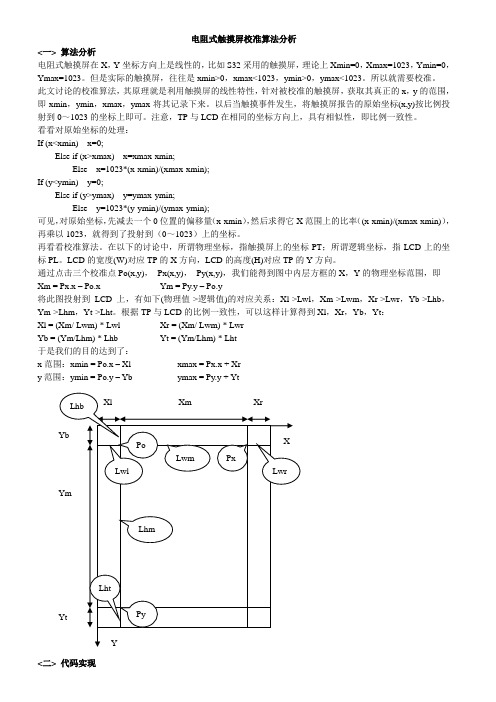
电阻式触摸屏校准算法分析<一> 算法分析电阻式触摸屏在X,Y坐标方向上是线性的,比如S32采用的触摸屏,理论上Xmin=0,Xmax=1023,Ymin=0,Ymax=1023。
但是实际的触摸屏,往往是xmin>0,xmax<1023,ymin>0,ymax<1023。
所以就需要校准。
此文讨论的校准算法,其原理就是利用触摸屏的线性特性,针对被校准的触摸屏,获取其真正的x,y的范围,即xmin,ymin,xmax,ymax将其记录下来。
以后当触摸事件发生,将触摸屏报告的原始坐标(x,y)按比例投射到0~1023的坐标上即可。
注意,TP与LCD在相同的坐标方向上,具有相似性,即比例一致性。
看看对原始坐标的处理:If (x<xmin) x=0;Else if (x>xmax) x=xmax-xmin;Else x=1023*(x-xmin)/(xmax-xmin);If (y<ymin) y=0;Else if (y>ymax) y=ymax-ymin;Else y=1023*(y-ymin)/(ymax-ymin);可见,对原始坐标,先减去一个0位置的偏移量(x-xmin),然后求得它X范围上的比率((x-xmin)/(xmax-xmin)),再乘以1023,就得到了投射到(0~1023)上的坐标。
再看看校准算法。
在以下的讨论中,所谓物理坐标,指触摸屏上的坐标PT;所谓逻辑坐标,指LCD上的坐标PL。
LCD的宽度(W)对应TP的X方向,LCD的高度(H)对应TP的Y方向。
通过点击三个校准点Po(x,y),Px(x,y),Py(x,y),我们能得到图中内层方框的X,Y的物理坐标范围,即Xm = Px.x – Po.x Ym = Py.y – Po.y将此图投射到LCD上,有如下(物理值->逻辑值)的对应关系:Xl->Lwl,Xm->Lwm,Xr->Lwr,Yb->Lhb,Ym->Lhm,Yt->Lht。
电阻触摸屏三点校准法

三点校准法三点校准法较之前面介绍的二点校准法更为精确。
当触摸屏与液晶屏间的角度差很小时,经过推理可以假设触摸屏与液晶显示器各点之间的对应关系为(假设液晶显示器的坐标为(XD, YD),触摸屏的坐标为(X,Y)):XD = AX + BY + CYD =DX + EY + F因为要取三个点进行校准,所以存在六个变量,即要通过六个方程式求出液晶显示器的坐标。
此处要求三个点尽量分散,最好为左上角、中间、右下角三点。
得:XD0 = AX0 + BY0 + CXD1 = AX1 + BY1 + CXD2 = AX2 + BY2 + CYD0 = DX0 + EY0 + FYD1 = DX1 + EY1 + FYD2 = DX2 + EY2 + F可求出 A、B、C、D、E、F的值,一旦这些参数值定下来,便可利用上面的方程组,通过触摸屏上的原始数据计算出它在LCD显示器上的对应点。
推导得出将K作为各方程式的公分母,便可得出未知量:K = (X0-X2)(Y1-Y2)-(X1-X2)(Y0-Y2)A = ((XD0-XD2)(Y1-Y2)-(XD1-XD2)(Y0-Y2))/KB = ((X0-X2)(XD1-XD2)-(XD0-XD2)(X1-X2))/KC = (Y0(X2XD1-X1XD2) + Y1(X0XD2-X2XD0) + Y2(X1XD0-X0XD1))/KD = ((YD0-YD2)(Y1-Y2)-(YD1-YD2)(Y0-Y2))/KE = ((X0-X2)(YD1-YD2)-(YD0-YD2)(X1-X2))/KF = (Y0(X2YD1-X1YD2) + Y1(X0YD2-X2YD0) + Y2(X1YD0-X0YD1))/K。
关于触摸屏校准问题及触摸屏中断过程图解

/*把背景填充为红色*/ Brush_Background(0xF800);
/*画校正用的三个十字坐标*/ //真实点(物理点) drawCross(24,32,0xFF0000); Draw_Text_8_16(28,36, 0x0000,0xFFFF, "1") ; drawCross(216,160,0xFF0000); Draw_Text_8_16(220, 164,0x0000,0xFFFF, "2") ; drawCross(120,288,0xFF0000); Draw_Text_8_16(124,292, 0x0000,0xFFFF, "3") ;
图 6.4 四线电阻屏等效电路图
6.5 等待中断模式等效电路
图 6.6 读取 x 坐标时的等效电路图 XZ=A×XJ+B×YJ+C YZ=D×XJ+E×YJ+F
6.7 读取 Y 坐标时的等效电路
D=[(YD0-YD2)×(YT1-YT2)-(YD1-YD2)×(YT0-YT2)] / K
E=[(XT0-XT2)×(YD1-YD2)-(YD0-YD2)×(XT1-XT2)] / K
F = [YT0×(XT2×YD1 - XT1×YD2) + YT1×(XT0×YD2 - XT2×YD0) + YT2×(XT1×YD0-XT0×YD1)] / K
保存下来的参数即可。
LCD 校准
3点校准:6个未知数K1,A1,B1,K2,A2,B2
校准公式:二元一次方程。
*
*
*
பைடு நூலகம்
XZ1,YZ1 XJ1,YJ1 XZ1=K1XJ1+A1YJ1+B1 YZ1=K2XJ1+A2YJ1+B2
电阻式触摸屏的校准与应用研究

第20卷第12期2007年12月武汉科技学院学报JOURNALOFWUHANUNIVERSITYoFSCIENCEANDENGINEERINGVbl.20No.12Dec.2007电阻式触摸屏的校准与应用研究罗勇刚,夏定纯(武汉科技学院计算机科学学院,湖北武汉430071)摘要:触摸屏作为一种最新的电脑输入设备,是目前最简单、方便、自然的一种人机交互方式。
为了得到可靠的坐标值,在实际应用之前。
往往需要校准。
本文提出了一种校准算法,并用数据证明了其可靠性。
关键词:触摸屏;LCD;屏幕校准中图分类号:TN873文献标识码:A文章编号:1009—5160(2007)--0047--03随着多媒体信息查询及嵌入式技术的发展,触摸屏广泛的应用于国民生产的各个领域用来实现手写输入、。
查询、控制等,触摸屏具有坚固耐用、反应速度快、节省空间、易于交流等许多优点。
触摸屏的种类很多,而且多被装在显示器(CRT)或液晶(LCD)上,本文主要以JX2410为平台,介绍安装在LCD上的电阻技术触摸屏的校准原理、算法及其应用设计。
l电阻式触摸屏的工作原理触摸屏常米代替鼠标或键盘,工作时,我们必须首先用手指或其它物体触摸安装在显示器前端的触摸屏,然后系统根据手指触摸的图标或菜单位置来定位选择信息输入。
电阻触摸屏的屏体部分足一块与显示器表面非常配合的多层复合薄膜,由一层玻璃或有机玻璃作为基层,表面涂有一层透明的导电层(OTI,氧化铟),上面再盖有一层外表面硬化处理、光滑防刮的塑料层,它的内表面也涂有一层OTI,在两层导电层之间有许多细小(小于千分之一英寸)的透明隔离点把它们隔开绝缘。
当手指接触屏幕。
两层OTI导电层出现一个接触点,因其中一面导电层接通Y轴方向的5V均匀电压场,使得侦测层的电压由零变为非零,控制器侦测到这个接通后,进行A/D转换,并将得到的电压值与5V相比,即可得触摸点的Y轴坐标,同理得出x轴的坐标,这就是电阻技术触摸屏的最基本原理。
电阻触摸屏线性不良分析及处理

3触 摸 屏 硬件 的线 性 不 良分 析
触 摸 屏 线 性 扭 曲 , 要 有 两 种 : 种 是 四周 靠 近 电极 位 置 主 一 的扭 曲 ; 一 种是 中 间位 置 的扭 曲 。 另 ( 中间位 置 的 扭 曲一 般都 是 由于 IS划 伤导 致 , 种扭 曲 , 1 ) T 这 线 测 曲线 出现 明显 的折线 , 不是 平稳 的曲线 状 , 图 2 示 , 而 如 所 对
其 中 , 一、 一 分 别 为 x、 向输 出平 均值 与最 佳 直 线 △x △Y Y 间 的最 大 偏 差 ; 一 一X Y 一 ~ 分 别 为 触 摸 屏 X、 向 的量 x … 一 Y Y
2线性度定义
线性 度 定 义 如 下 : 指 触 摸 屏 实 际 接 触 点 与 解 析 点 之 间 的 是 相 似 性 。触 摸 屏 的独 立 线 性 度 定义 为 触 摸屏 的实 际 平 均输 出特 性 曲 线对 最 佳 直 线 的 最 大偏 差 , 传 感 器 满 量 程 输 出 的百 分 比 以
方法 和思 路 。
关键词 : 触摸 屏 ; 线性 度 ; 良分析 ; 理方 法 不 处
中 圈 分 类 号 :P 3 T 36
文 献标 识码 : A
文 章 编 号 :030 0 ( 1)900 — 4 10 - 17 0 1 -07 0 2 0
Al r c : nt i p , n rdu e e l e rpr cil e it e t u h—p n h ss O r i a u f c e t r s ws a a—  ̄d a t I h spa er we it o c t i a i pe of ss i o c h n n r v a el On t e ba i f or n rs ra e f a u e , n er l e
电阻式触摸屏数据校准的一种补偿算法

【 关键词】 触摸屏 ;C 坐标 ; : L D; 补偿 ; 算法
l 引 言 、
P=KX O Y X ' 、+ + T o[. -  ̄ + le X KY Y】 T K
即:
P= KR oO O R iO X , s 0 e cs+ T D【 cs- K s + TK i + KR oOY ] n n
根 据 式 1得 :.
XI AXlBYl C ) l = + + Xm AX2 BY + = + !C
Ym=DX EYo +F
Ym= DXIE + + YIF
Ym= DX +EY2+F
由上 面的 方 程 得 到 :
K (0x (-Y)( - Y— 1 =) 一 _Y- 2 XrX (oY 【 9 - j
【 陈文智. 2 】 嵌入 式 系统 开发原 理与 实践. 北京 : 清华 大学 出版社 ,0 5 20 :
2 0 5
[林晓飞, 3 】 林兵 , 张辉 . 于 AR 嵌 入 式 Ln x应 用 开发 与 实例 教 程 . 基 M iu 清
华 大 学 出版 社 . 0 :2 — 3 2 724 22 0
A:—
( D -k z Y - :- x ( o . ) , Y ) ( m-x : Y - : x % ( o) o Y ) ( )
—
B:—
i , ., ( - ) ( o - o ( -x: f , - ̄ 0 xo x:- x o x O x, x, ) )
—
,、一
f o XJ X,v) I X : Y (  ̄ 一 X :+Y( o 一X: z) : X 0 Xo o ) X: , Xo X ̄ +Y ( o 一 X O o Xt (Y, Y O Y - 2-(o- m) o Y ) (o - o ( , Y ) Y , Y ( - : ) Y )
四线电阻触摸屏校准算法小结

4 -2得yfac = (Y2 -Y1)/(y2 -y1); //得到y轴方向的比例因子
4 + 2得yoff = [(Y2 + Y1)-yfac(y2 + y1)]/2; //得到y轴方向的偏移量
有如下方程组:
X1 = xfac * x1 + xoff; // 1
Y1 = yfac * y1 + yoff; // 2
X2 = xfac * x2 + xoff; // 3
Y2 = yfac * y2 + yoff; // 4
解得:
3 -1得xfac = (X2 -X1)/(x2 -x1); //得到x轴方向的比例因子
OK!所谓的三点触摸校准,四点触摸校准只不过是加了可靠的滤波算法,因为触摸笔和屏
的接触不是很准确的!而像素点是很小的,所以通常都用四点校准,而且经验证这此算法是
必须加的,否则很不准,参见STM32学习笔记相关实验实验例程,已验证通过理论知识:
*触摸屏实际是在普通的lcd上贴了一个触摸膜,没有原生的触摸屏
B=(Xt[0]-Xt[2])*(Xd1-Xd2)-(Xd0-Xd2)*(Xt[1]-Xt[2]);
C=Yt[0]*(Xt[2]*Xd1-Xt[1]*Xd2)+Yt[1]*(Xt[0]*Xd2-Xt[2]*Xd0)+Yt[2]*(Xt[1]*Xd0-Xt[0]*Xd1);
D=(Yd0 -Yd2)*(Yt[1] -Yt[2]) -(Yd1 -Yd2)*(Yt[0] -Yt[2]);
有3个未知数abc,显然需要3个方程
触摸屏材料测试标准之线性测量方法
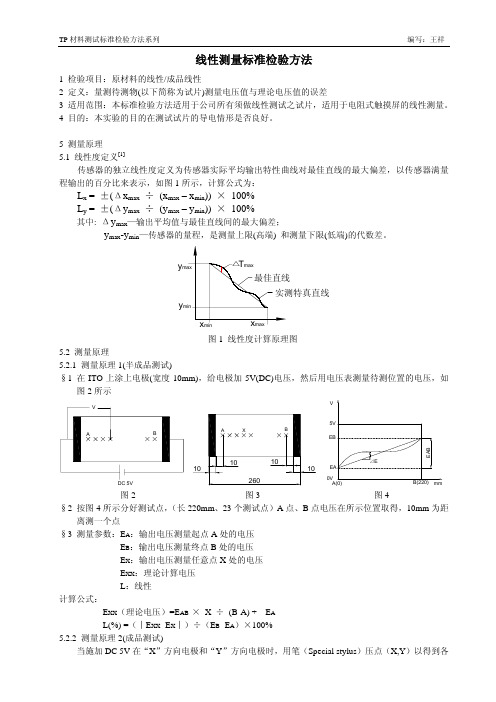
线性测量标准检验方法1 检验项目:原材料的线性/成品线性2 定义:量测待测物(以下简称为试片)测量电压值与理论电压值的误差3 适用范围:本标准检验方法适用于公司所有须做线性测试之试片,适用于电阻式触摸屏的线性测量。
4 目的:本实验的目的在测试试片的导电情形是否良好。
5 测量原理5.1 线性度定义[1]传感器的独立线性度定义为传感器实际平均输出特性曲线对最佳直线的最大偏差,以传感器满量程输出的百分比来表示,如图1所示,计算公式为:L x = ±(Δx max÷ (x max – x min)) × 100%L y = ±(Δy max÷ (y max – y min)) × 100%其中: Δy max—输出平均值与最佳直线间的最大偏差;y max-y min—传感器的量程,是测量上限(高端) 和测量下限(低端)的代数差。
yy图1 线性度计算原理图5.2 测量原理5.2.1 测量原理1(半成品测试)§1 在ITO上涂上电极(宽度10mm),给电极加5V(DC)电压,然后用电压表测量待测位置的电压,如图2所示V0V图2 图3 图4§2 按图4所示分好测试点,(长220mm、23个测试点)A点、B点电压在所示位置取得,10mm为距离测一个点§3 测量参数:E A:输出电压测量起点A处的电压E B:输出电压测量终点B处的电压E X:输出电压测量任意点X处的电压E XX:理论计算电压L:线性计算公式:E XX(理论电压)=E AB × X ÷ (B-A) + E AL(%) =(︱E XX- E X︱)÷(E B- E A)×100%5.2.2 测量原理2(成品测试)当施加DC 5V在“X”方向电极和“Y”方向电极时,用笔(Special stylus)压点(X,Y)以得到各自输出电(E OX , E OY )。
电阻屏四点校准的原理

电阻屏四点校准的原理电阻屏四点校准的原理电阻屏是一种常见的触摸屏技术,广泛应用在智能手机、平板电脑、电子签名板等设备上。
为了确保电阻屏的准确性和稳定性,四点校准成为了必要的步骤。
本文将介绍电阻屏四点校准的原理及其作用。
一、什么是电阻屏四点校准?电阻屏四点校准是一种通过模拟量转换器测量电阻屏上的四个特定点,以确定其电阻分布的过程。
校准的目的是确保电阻屏的触摸响应准确,并消除由于材料特性、温度变化等因素引起的误差。
二、为什么需要电阻屏四点校准?电阻屏是一种基于物理压力感应的触摸屏技术,通过人手或者特制的触笔施加压力来实现操作。
然而,由于材料特性的差异和温度的影响,电阻屏在不同位置的电阻值可能存在差异。
这会导致触摸点定位的偏差,使得用户操作不准确。
因此,四点校准的目的是通过测量和纠正这些差异,使电阻屏的触摸响应更加准确、可靠。
三、电阻屏四点校准的原理1. 准备工作在进行四点校准之前,首先需要提供一组已知准确坐标的参考点。
这些参考点可以通过机器精确标定或者其他测量手段得到。
2. 测量电流四点校准需要在电阻屏上施加小电流。
在校准过程中,首先需要在触摸屏的四个角落施加电流。
3. 测量压力通过测量电流的变化,可以得到一个电压值。
随着压力的施加,电压值也会发生变化。
4. 计算差异校准的关键在于计算不同触摸点之间的电阻差异。
在四点校准中,通过比较四个参考点之间的电阻值,可以确定触摸屏的电阻分布情况。
5. 纠正坐标根据上一步的计算结果,可以计算出每个触摸点的实际坐标。
通过将实际坐标与标定参考点进行比较,可以得到触摸点的偏差。
然后,利用这些偏差可以对触摸点进行纠正,从而提高触摸屏的精度。
四、电阻屏四点校准的优势1. 精确度高通过四点校准,可以准确地测量电阻屏的电阻差异,并计算触摸点的实际坐标。
这种精确度使得用户在操作时能够更加准确地点击、滑动或者缩放屏幕上的内容。
2. 稳定性强由于电阻屏四点校准可以消除由于材料特性和温度变化引起的误差,因此触摸屏的稳定性得到了提高。
电阻式触摸屏线性抖动及飞线问题的分析

电阻式触摸屏线性抖动及飞线问题的分析(苏州瑞阳光电有限公司工程部王祥 215011)关键词:线性抖动飞线MTK平台电阻 PCBLayout 去耦电容延时1 引言在四线电阻式触摸屏的应用中,进行手写操作时,会出现明显的线性抖动和飞线的现象,有发生在X 方向的,也有发生在Y方向的。
本文通过硬件和软件两个方面进行分析线性抖动和飞线的问题,并提出一些解决方案。
2 电阻式触摸屏的工作原理及其系统组成在触摸屏输入控制系统中,触摸屏通常安装在LCD显示器的表面,因此,来自LCM模组的噪声很容易对触摸屏造成干扰。
此外,作为人机输入界面,触摸屏通过人的点击进行信号输入,机械振动也会产生噪声和寄生效应,因使用者和环境的不同产生静电效应和电磁效应等。
这些噪声通常发生在在触摸屏输入控制系统的模拟输入电路中,噪声严重降低了触摸屏输入控制系统的精度和可靠性能。
2.1 系统组成原理触摸屏输入系统由触摸屏、触摸屏控制器和微控制器三部分组成。
图1示出了一个实际的触摸屏输入系统。
图1 触摸屏输入控制系统触摸屏面板与触摸控制器连接部分为模拟I/O接口,触摸控制器与处理器连接部分为数字I/O接口,通过标准的I2C或SPI接口进行连接。
2.2 触摸屏工作原理电阻触摸屏是采用电阻模拟量技术。
它以一层玻璃作为基层,上面涂有一层透明氧化金属(ITO氧化铟)导电层,再盖有一层玻璃或是外表面硬化处理的光滑的塑料层;内表面也涂有一层ITO导电层。
它们之间有许多细小的的透明隔离点把两导电层隔开绝缘,每当有笔或是手指按下时,两导电层就相互接触。
而形成回路,如图2所示。
图2 触摸屏的触摸示意图导电层的两端都涂有一条银胶,称为该工作面的一对电极。
上下两个导电层一个是水平方向,一个是竖直方向,分别用来测量X和Y的坐标位置。
在水平面上的电极称为X+电极和X-电极,在竖直平面的电极称为Y+电极和Y-电极,如图3所示。
工作时,两个电极根据测量需要提供参考电压或是作为测量端对接触点的位置进行测量。
触摸屏的校正

Touch Panel校正因为最近的项目关系,接触到了Touch Panel的校正方法。
虽然以前对Touch在Windows CE的驱动部分还是有一定了解,但是这次发现有了更深的了解:)所以写点东西出来跟大家分享。
1。
前言.....市面上的Touch,以电阻式的比较多,我刚好也是使用的这种。
电阻技术触摸屏分为四线电阻触摸屏、五线电阻触摸屏或更多线电阻触摸屏,但无论哪一类电阻触摸屏都有一个最大共性:电压成线性均匀分布。
正是由于这一特性使得触摸屏的校正和使用非常方便。
电阻式的触摸屏一般会接在板子的ADC上,ADC可以由CPU或者AC97芯片提供。
这样可以将模拟信号转化为数字信号。
读寄存器中的这些数字信号的方法要跟据各个芯片的spec来做,就不做多说了。
当我们从寄存器中读出X和Y的值,这个值一般是不能直接用的,而是要做校正才行。
下面来说说我用的校正方法。
2。
Touch的校正一般的方法有5点法和3点法。
原理都一样。
我使用的是5点法。
2.1物理坐标和逻辑坐标为了方便理解,我们首先引入2个概念,坐标和逻辑坐标。
物理坐标就是触摸屏上点的实际位置,我们通常以液晶上点的个数来度量。
逻辑坐标就是触摸屏上这一点被触摸时A/D转换后的坐标值。
如下图,我们假定液晶最左下角为坐标轴原点A,我们在液晶上再任取一点B(十字线交叉中心),B在X方向距离A 10个点,在Y方向距离A 20个点,那么我们就说液晶上B点所正对的解摸屏上这一点的物理坐标为(10,20)。
如果我们触摸这一点时得到的X向A/D转换值为1 00,Y向 A/D,转换值为200,我们就说这一点的逻辑坐标为(100,200)。
图2-12.2逻辑坐标的计算由于电阻式触摸屏的电压成线性均匀分布,那么A/D转换后的坐标也成线性。
假如我们将液晶最左下角点对应的触摸屏上的点定为物理坐标原点A其物理坐标记为(XA=0,YA=0)其逻辑坐标记为(XLA,YLA)(不一定为0)。
那么触摸屏上任意一点B的逻辑坐标可表达为:XLB=XLA+KXXBYLB=YLA+KYYB 式2-1其中KX、KY分别为触摸屏X方向和Y方向的因子系数,这就像弹簧一样(我们知道弹簧也是线性的),拉力与弹簧伸长正比。
电阻式触摸屏校准算法的优化

B =一[ d y2 2 Yl d m )
G = d 21B Y y 1 )- 2 1 (
3 (o Y3 2 / ) Y2 d 1 ) 一 - ) ]
存 在移 动误 差 ,则假 设 角度 差为 ,缩放 因子 为 颤
和 氏,位 移 因子 为 和 ,可得 到显 示坐 标 : X kR O (+o d xC sO  ̄+ )
触 摸 屏上 任 意取 三 个 点 ( 由于 边 界 点 的线性 度 差 , 所 以要尽 量 避免 ) ,设物 理 坐 标和 显 示坐 标 分别 为
,
Y) , 、 , 和 , ) ) ) 、 ) 乃) 、( , 、
A1 X + B1Y1 C1= l ’1 ‘ +
= — 2 Y- 3 2 ) 1 ) 2Y) — 3 ( 一x 广y) 2
屏和 L D显示图形的点都用矢量来表示 : (, C Q ) Y
为触摸 屏上 的点 ,称 为物理 坐标 ; a Y) L D Q ( d为 C 均, 显示 屏 上 的点 ,称 为 显 示坐 标 。设 物理 坐标 :
控 制设 备 ,简化 了用 户 的操作 _,提供 了更 加友 好 l J
直 接 的人 机 交互 。市场 上较 为常 见的 触摸屏 有 :红
外线 触摸 屏 、电容 式触摸 屏 、 电阻式触 摸屏 和表 面 声 波触摸 屏 。 目前 ,市场 上 应用 比较 多的是 电 阻式 触 摸屏 。 然 而 电阻 式 触摸 屏 在 出 厂时 由于 L D 显 C 示屏 与 触 摸 屏之 间装配 的不对 应 会 引起 机 械误 差 ,
导 电层 ( , _上 形 成 电压 梯度 ,X+作 为 引 出端 Y+ Y ) 测 量 接 触 点 的 电压 ,当 有 外 力使 得 上 下 两层 导 电
STM32f103的电阻触摸屏的五点校正算法

STM32f103的电阻触摸屏的五点校正算法由于电阻式触摸屏就是一种传感器,它利用压力感应进行控制,将矩形区域中触摸点(X,Y)的物理位置转换为代表 X坐标和 Y 坐标的电压。
这里先引入两个概念,物理坐标和逻辑坐标。
物理坐标指触摸屏上点的实际位置,通常以液晶上点的个数来度量。
逻辑坐标指这点被触摸时A/D 转换后的坐标值。
如图1,我们假定液晶最左下角为坐标轴原点A ,在液晶上任取一点B (十字线交叉中心),B 在X 方向距离A 10 个点,在Y 方向距离A20 个点,则这点的物理坐标为(10,20)。
如果我们触摸这一点时得到的X 向A/D 转换值为100,Y 向A/D 转换值为200,则这点的逻辑坐标为(100,200)。
常用的电阻式触摸屏矫正方法有两点校准法和三点校准法。
本文这里介绍的是结合了不同的电阻式触摸屏矫正法的优化算法:五点校正法。
其中主要的原理是使用4点矫正法的比例运算以及三点矫正法的基准点运算。
五点校正法优势在于可以更加精确的计算出X和Y方向的比例缩放系数,同时提供了中心基准点,对于一些线性电阻系数比较差电阻式触摸屏有很好的校正功能。
校正相关的变量主要有:x[5] , y[5] 五点定位的物理坐标xl[5] , yl[5] 五点定位的逻辑坐标KX , KY 横纵方向伸缩系数XLC , YLC 中心基点逻辑坐标XC , YC 中心基点物理坐标(数值采用LCD显示屏的物理长宽分辨率的一半)触摸屏常和点阵式液晶显示(LCD)屏叠加在一起配套使用,构成一个矩形的实际物理平面; 而由用户触摸的触摸点集合经过 A/D 转换器,得到具体显示坐标的集合,这个集合构成了一个逻辑平面。
由于存在误差,这两个平面并不重合,校准的作用就是要将逻辑平面映射到物理平面上,即得到触点在液晶屏上的位置坐标。
校准算法的中心思想也就是要建立这样一个映射函数现有的校准算法大多是基于线性校准, 即首先假定物理平面和逻辑平面之间的误差是线性误差,由旋转和偏移形成。
STM32f103的电阻触摸屏的五点校正算法

STM32f103 的电阻触摸屏的五点校正算法
由于电阻式触摸屏就是一种传感器,它利用压力感应进行控制,将矩形区域中触摸点(X,Y)的物理位置转换为代表X 坐标和Y 坐标的电压。
这里先引入两个概念,物理坐标和逻辑坐标。
物理坐标指触摸屏上点的实际位置,通常以液晶上点的个数来度量。
逻辑坐标指这点被触摸时A/D 转换后的坐标值。
如图1,我们假定液晶最左下角为坐标轴原点A,在液晶上任取一点B(十字线交叉中心),B 在X 方向距离A10 个点,在Y 方向距离A20 个点,则这点的物理坐标为(10,20)。
如果我们触摸这一点时得到的X 向A/D 转换值为100,Y 向A/D 转换值为200,则这点的逻辑坐标为(100,200)。
常用的电阻式触摸屏矫正方法有两点校准法和三点校准法。
本文这里介绍的是结合了不同的电阻式触摸屏矫正法的优化算法:五点校正法。
其中主要的原理是使用4 点矫正法的比例运算以及三点矫正法的基准点运算。
五点校正法优势在于可以更加精确的计算出X 和Y 方向的比例缩放系数,同时提供了中心基准点,对于一些线性电阻系数比较差电阻式触摸屏有很好的校正功能。
校正相关的变量主要有:。
电阻触摸屏的驱动软件安装和校正

1. 连接控制卡与电阻屏2. 通过USB 接口或者RS232接口将控制器连接到主机上。
3. 连接控制器至5VDC 电源。
(USB接口可提供5VDC 电源。
另外,键盘和鼠标接口也可为RS232控制器提供5V电源。
)4. 安装与操作系统匹配的触摸驱动程序。
(windows XP, 2K等等。
)1. 现有的驱动系统驱动可以从网上下载或者CD光盘上获得➢Windows 2000 (家用和个人用版本都可以)➢Windows XP (家用和个人用版本都可以)➢Windows 2003 服务器➢Windows Vista➢Windows 2008 服务器➢Windows CE 5.0 & 6.0➢Linux2. 驱动安装及触摸系统校准指南:A. 请先将电阻式触摸屏、控制器、电脑用正确的电缆线连接。
B. 插入驱动程序CDC. 根据指示完成驱动程序在Windows 2000/XP如下的安装:在双击Setup.exe文件,以启动软件驱动程序的安装。
然后,安装程序将引导用户完成软件安装。
按Next按钮继续安装,然后,一个新的对话框中出现如下,这个对话框提示用户是否安装使用PS/2接口的触摸屏。
因为我们现在的新产品已经不采用PS/2接口,因此请不要选择。
取消选中此复选框,按Next的按钮,继续安装。
然后,新的对话框显示如下,此处,可以选择是否自动运行4点校准。
如果用户需要每次Windows系统启动都自动运行4点校准,请选择“Every system boot up”;如果用户需要安装过后下一次启动后,自动运行一次4点校准,请选择“Next system boot up”;如果用户不需要自动运行4点校准,而是在需要的时候手动运行4点校准,请选择“None”。
最后请按NEXT 的按钮,继续安装。
此时安装程序会弹出一个消息框以提示请用户再次确认USB控制卡与系统的USB连接口连接正确,这样安装程序才能正确安装驱动。
然后,只需按下确定继续弹出一个窗口,用户选择将文件复制到目标路径。
如何校准触摸屏基准参数

如何校准触摸屏基准参数在触摸屏修理工作中,我们发觉电阻式触摸屏在嵌入式系统中用的较多,电阻式触摸屏可分为四线、五线、七线等几种,接下来,我们主要以WinCE触摸屏为例,分析如何校准触摸屏基准参数问题:在我们顺当完成驱动程序安装以及各种功能就都已经预备就绪了,现在就可以实际操作触摸屏幕了。
但一般来说,电阻式触摸屏需要校准,也就是说在驱动启动过程中MDD层要调用相应的DDSI函数来读取注册表中的校正数据校正触摸屏。
抱负状况下,校准程序只要在嵌入式设备初次加电测试过程中运行一次就可以了,参考值会被存储在非易失性存储器中,以免让用户在以后的加电启动期间再做校准。
不过,高质量的触摸屏驱动程序是应当要向用户供应一种进入校准例程的途径,从而在由于温度漂移或其它因素造成校准不精确时进行重新校准。
在抱负状况下,校正触摸屏基准只需两组原始数据,即在屏幕对角读取的最小和最大值。
但在实际应用中,由于很多电阻式触摸屏存在明显的非线性,假如只在最小和最大值之间简洁的插入位置数值会导致驱动程序特别的不精确。
因此,在WinCE中需要猎取多个校准点,常用的校准点数量为5个。
方法如下:1、首先驱动程序在函数DdsiTouchPanelGetDeviceCaps 中设置校准点的个数;2、是系统在TouchDriverCalibrationPointGet中猎取每个校准点的屏幕坐标;3、是在屏幕界面的校准点坐标处显示一个位置符号,用户需要精确地在位置符号按下触摸屏;4、驱动程序通过TouchPanelReadCalibrationPoint函数读取相应的触摸屏坐标值;5、然后再开头下一个校准点,直到循环设定的次数后将采集到的触摸屏坐标值和校准点屏幕坐标送到TouchPanelSetCalibration函数中进行处理,该函数将产生校准基准参数。
校准完成之后,触摸屏便可以开头正常的操作了。
关于电阻式触摸屏的线性校准问题

关于电阻式触摸屏的线性校准问题1 引言阻性触摸屏与LCD 显示器上的各点很难完全准确配合,因此除了采用精确的机械装配技术校准之外,在使用之前还必须进行软件校准。
本文介绍的校准方法首先确定误差源,然后通过三个选定点导出触摸屏的校准矩阵,并用软件方法来实施点与点之间对应关系的校准。
掌握这种技术,对降低嵌入式系统的成本至关重要。
图1所示是一个阻性触摸屏的横截面,其结构十分简单,由上下相对放置的两层结构构成,FILM 和玻璃的内表面涂上薄薄一层导电材料,并用一些透明绝缘隔离点(绝缘点)将导电表面隔开。
当手指或铁笔按压玻璃表面时,上层FILM 产生弯曲接触下层玻璃。
这种结构中层间的距离决定了触摸屏的敏感度。
层间距离越近,敏感度越小,压力就要越大,以使两层结构可靠接触。
玻璃或图1 阻性触摸屏的横截面 图2 触摸屏的等效电路图2所示是触摸屏的等效电路。
通过一个触摸屏控制器(AD 转换器)将电源的正、负极加到一块玻璃的导电层两端,另一块玻璃上的导电层则起到一个电位计游标的作用。
在玻璃上不同的触摸点,导电的情况也不同,数字转换器上便会录得不同的测试电压值,然后控制器将录得的电压值转换成一个二维坐标:X 轴坐标和Y 坐标。
这些控制器每秒钟可进行200次或更多的采样。
采样率通常与背景噪声和控制器质量有关。
智能控制器还具备其它一些功能,如检测到触摸时中断CPU 、在检测到触摸前设定采样率连续进行采样。
没有触摸时,控制器处于待机状态。
由于阻性触摸屏结构简单、操作易懂、所需软硬件有多个厂商可供选择,因此可用于对成本敏感的设计中。
然而,由于触摸屏与它背后的显示器(LCD 或其它)间的对应点很难完全配合,因此几乎所有带阻性触摸屏的设备在出厂前均要经过一定的校准。
否则在触摸屏上点击某一按钮或选择某项功能时,内置的软件便无法对这一点击做出正确响应。
本文介绍的校准方法需要三个目标点/或测试点,然后依次进行触摸测试,以确定该显示屏特有的校准因数。
电阻屏校准方法

电阻屏校准方法引言:电阻屏是现代电子设备中常见的一种输入设备,它通过触摸屏幕上的电阻点来实现对设备的操作。
然而,由于长时间使用、环境变化等原因,电阻屏的灵敏度和准确度可能会下降。
因此,对电阻屏进行校准是非常重要的,本文将介绍一种常用的电阻屏校准方法。
一、校准原理:电阻屏的校准原理是基于电阻值的变化来确定触摸位置的。
当我们触摸屏幕时,电阻屏上的两个电极会接触到一起,形成一个电阻,通过测量这个电阻值的变化,可以确定触摸的位置。
二、校准步骤:1. 打开校准程序:首先,我们需要打开设备的校准程序。
通常情况下,校准程序会在设备的设置菜单中,我们可以根据设备的操作指南找到它。
2. 开始校准:进入校准程序后,会出现一系列的校准点,我们需要按照指示依次点击这些校准点。
在每次点击后,系统会记录下触摸点的坐标,并根据这些数据进行校准计算。
3. 校准完成:完成所有校准点的点击后,系统会自动进行计算,并将校准结果保存起来。
此时,电阻屏的校准就完成了。
三、注意事项:1. 温度影响:电阻屏的灵敏度和准确度受环境温度的影响较大,因此,在校准过程中,应尽量保持设备和手指的温度稳定,避免温度变化对校准结果的影响。
2. 校准周期:电阻屏的灵敏度和准确度会随着时间的推移而降低,因此,建议每隔一段时间对电阻屏进行校准,以保证其正常使用。
3. 校准环境:在进行电阻屏校准时,应选择一个相对稳定、无电磁干扰的环境,以确保校准结果的准确性。
4. 校准方法选择:当出现电阻屏灵敏度下降或触摸位置不准确的情况时,可以尝试使用设备自带的校准程序进行校准。
如果问题依然存在,可以尝试使用专业的校准设备进行进一步的校准。
5. 校准结果验证:完成校准后,建议进行触摸位置的验证,以确保校准结果的准确性。
可以通过在屏幕上绘制直线或进行其他操作来验证触摸位置是否准确。
四、总结:通过本文介绍的电阻屏校准方法,我们可以有效地提高电阻屏的灵敏度和准确度,保证设备的正常使用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
关于电阻式触摸屏的线性校准问题1 引言阻性触摸屏与LCD 显示器上的各点很难完全准确配合,因此除了采用精确的机械装配技术校准之外,在使用之前还必须进行软件校准。
本文介绍的校准方法首先确定误差源,然后通过三个选定点导出触摸屏的校准矩阵,并用软件方法来实施点与点之间对应关系的校准。
掌握这种技术,对降低嵌入式系统的成本至关重要。
图1所示是一个阻性触摸屏的横截面,其结构十分简单,由上下相对放置的两层结构构成,FILM 和玻璃的内表面涂上薄薄一层导电材料,并用一些透明绝缘隔离点(绝缘点)将导电表面隔开。
当手指或铁笔按压玻璃表面时,上层FILM 产生弯曲接触下层玻璃。
这种结构中层间的距离决定了触摸屏的敏感度。
层间距离越近,敏感度越小,压力就要越大,以使两层结构可靠接触。
玻璃或图1 阻性触摸屏的横截面 图2 触摸屏的等效电路图2所示是触摸屏的等效电路。
通过一个触摸屏控制器(AD 转换器)将电源的正、负极加到一块玻璃的导电层两端,另一块玻璃上的导电层则起到一个电位计游标的作用。
在玻璃上不同的触摸点,导电的情况也不同,数字转换器上便会录得不同的测试电压值,然后控制器将录得的电压值转换成一个二维坐标:X 轴坐标和Y 坐标。
这些控制器每秒钟可进行200次或更多的采样。
采样率通常与背景噪声和控制器质量有关。
智能控制器还具备其它一些功能,如检测到触摸时中断CPU 、在检测到触摸前设定采样率连续进行采样。
没有触摸时,控制器处于待机状态。
由于阻性触摸屏结构简单、操作易懂、所需软硬件有多个厂商可供选择,因此可用于对成本敏感的设计中。
然而,由于触摸屏与它背后的显示器(LCD 或其它)间的对应点很难完全配合,因此几乎所有带阻性触摸屏的设备在出厂前均要经过一定的校准。
否则在触摸屏上点击某一按钮或选择某项功能时,内置的软件便无法对这一点击做出正确响应。
本文介绍的校准方法需要三个目标点/或测试点,然后依次进行触摸测试,以确定该显示屏特有的校准因数。
最后通过这些校准因数将触摸屏的对应点与实际显示的对应点完全对应起来。
2 误差的来源有几个误差源会影响触摸屏控制器,使之无法产生正确的对应点X 和Y 坐标。
最主要的误差源是电气噪声、机械误差及放大因子。
此外,操作者的误操作也会有所影响,如手指或铁笔按压时间不够长或压力不够大。
以上所有误差均会产生无用数据,必须对它进行纠正补偿才能使触摸屏正常工作。
在各种电气系统中,由热效应或电磁效应以及系统设计缺陷引起的电气噪声无处不在。
在触摸屏中,由于AD 转换器的前端电路具有高输入阻抗,因此特别容易受到电气噪声的影响。
除了对带有触摸屏控制器的电路小心布局外,我们通常在AD 转换器输入端增加低通滤波器来解决这一问题。
此外也可选择软件方法,舍弃AD 转换中的最小的一、两位,并用算法将一些落在允许误差范围之外的数据点从采样流中去除。
这种软件算法也可消除由使用者产生的误差。
本文所阐述的校准方法可用来解决由于机械误差和放大因素引起的误差。
图3中的圆圈表示触摸屏下的LCD 显示的图形,椭圆则表示当用户顺着LCD 显示的图像画圈时,触摸屏对应点的集合,不过有所夸大。
这个重建的图形显然经过一系列旋转、移位和放大,而且在每个方向变换的参数不一样。
校准的重点则是将触摸屏上显示的这个重建图形经过变换,换算出与LCD显示的图形相一致的对应点集合。
图3 坐标对应关系示意图3 校准的数学基础为了得到一个通用解决方案,我们将每个点描述为一个数学参量。
如图4所示,可将LCD显示器上的每个点当作一个矢量PD,而该点在触摸屏上对应的点则当作矢量P。
此外,我们假设一个参量M,通过这个参量可将P D与P进行换算,即P D = MP (1)这里的M是一个转换矩阵,也是我们要研究的对象。
如果能得到转换矩阵M中相关的数值,那么给定触摸屏上任一点P,我们就可换算出它在LCD显示器上的对应点PD。
现在假设LCD显示器上的任一点都与触摸屏上的某点相对应,但要经过旋转、移位和放大处理。
如果按矢量的长度和角度将每个点用(X,Y)两个坐标来表示,则LCD显示器和触摸屏上的点都可通过以下方程式来表达:P D= [X D , Y D]= [R D cosθD , R D sinθD](2a)P = [X , Y ]= [ R cosθ, R sinθ](2b)如果触摸屏在校准时与显示屏之间存在一个角度差异,为了进行补偿,要进行旋转处理,即θr =θD -θ,θr是角度差。
这样我们便可得到一个中间点:P'= [ R cos〔θ+θr〕, R sin〔θ+θr〕] (3)将每个点的X坐标和Y坐标以不同的因子放大,得到K X和K Y。
考虑放大因子可以得到以下方程式,它更准确地描述了LCD显示器与触摸屏上点与点之间的对应关系:P" = [K X R cos〔θ+θr〕, K Y R sin〔θ+θr〕] (4)最后,我们加上位移因子X T和Y T,得到LCD显示器与触摸屏上点与点之间的对应方程式:P D= [K X R cos〔θ+θr〕+ X T, K Y R sin〔θ+θr〕+ Y T](5)为了将方程式5再次变换以求取方程式中的未知量,假设触摸屏和LCD显示器上点与点之间有一个角度差θr,但这一角度极小,因此sinθr≈θr,而cosθr≈1.0。
根据这一假设我们得出另两个十分有用的近似方程式:cos〔θ+θr〕≈〔cosθ-θr sinθ〕(6a)sin〔θ+θr〕≈〔sinθ+θr cosθ〕(6b)通过以下组合,方程式5可重新表示为:P D= [K X R cosθ-K X Rθr sinθ〕+ X T , K Y R sinθ+θr K Y R cosθ〕+ Y T](7)方程式7的优点在于,它采用触摸屏坐标描述了LCD显示器上的点坐标。
上述方程式也可转换为:P D= [K X X-θr K X Y + X T , θr K Y X + K Y Y + Y T](8)利用我们原先的假设(即实际情况中的放大、旋转和位移因数均为常量),除X和Y之外,上述方程式右边的各项均为常量。
通过采用更方便的方式表达X D和Y D坐标,我们可以得到触摸屏与LCD显示器各点之间的对应关系方程式:X D = AX + BY + C (9b)Y D = DX + EY + F (9b)可见,只有当触摸屏和LCD显示器间的角度差非常小时,才可运用上述公式。
4 校准矩阵一般的校准算法常选取2-5个采样点来收集校准信息。
假设LCD显示器上的对应点可以通过触摸屏上的点转换得到,只需正好3个采样点我们就可得到校准数据。
需要3个采样点的原因在于方程式9a和9b 有三个未知量。
从这3个采样点我们可获得足够的信息来建立并求解这一联立方程组。
采样点的选取也应当考虑到实际情况。
它们必须能得出非冗余的联立方程组,它们不能太靠近触摸屏的边缘(此处呈现非线性),此外它们的间隔必须足够宽,以便尽可能减少放大误差。
图4所示的P0、P1和P2这三个点符合这些条件。
这些点距触摸屏边缘约10%,分布足够散,得出以下非冗余方程式:X D0 = AX0 + BY0 + C (10a)X D1 = AX1 + BY1 + C (10b)X D2 = AX2 + BY2 + C (10c)Y D0 = DX0 + EY0 + F (11a)Y D1 = DX1 + EY1 + F (11b)Y D2 = DX2 + EY2 + F (11c)图4 从而求出A、B、C、D、E和F的值。
一旦这些参数值定下来,便可利用方程式9,通过触摸屏上的原始数据计算出它在LCD显示器上的对应点。
上述联立方程组的未知量已求解出,此处不再推导。
直接跳过中间步骤得出最后结论,将K作为各方程式的公分母,便可得出未知量:K = 〔X0-X2〕〔Y1-Y2〕-〔X1-X2〕〔Y0-Y2〕(12)A = 〔〔X D0-X D2〕〔Y1-Y2〕-〔X D1-X D2〕〔Y0-Y2〕〕/K (13)B = 〔〔X0-X2〕〔X D1-X D2〕-〔X D0-X D2〕〔X1-X2〕〕/K (14)C = 〔Y0〔X2X D1-X1X D2〕+ Y1〔X0X D2-X2X D0〕+ Y2〔X1X D0-X0X D1〕〕/K (15)D = 〔〔Y D0-Y D2〕〔Y1-Y2〕-〔Y D1-Y D2〕〔Y0-Y2〕〕/K (16)E = 〔〔X0-X2〕〔Y D1-Y D2〕-〔Y D0-Y D2〕〔X1-X2〕〕/K (17)F = 〔Y0〔X2Y D1-X1Y D2〕+ Y1〔X0Y D2-X2Y D0〕+ Y2〔X1Y D0-X0Y D1〕〕/K (18)5 软件实现实际的软件实现过程相对简单。
可从/code.htm 上得到程序样本,它包括三个文件:alibrate.c、calibrate.h和sample.c。
第一个文件包含两个函数setCalibrationMatrix()和getDisplayPoint()。
前者实现了方程式13~18,后者则实现了方程式9。
启动文件包含了各种声明,另一个源文件则实现了一个控制台应用程序,这一程序执行校准功能,并示范如何在器件中使用这些函数。
sample.c中的代码假设在调用这些函数前,器件中实现了一个执行程序来采集校准数据。
表1是建议的校准步骤,将这些步骤执行完毕就实现了校准过程,此时设备便可开始从触摸屏系统接收精确的位置信息。
触摸屏控制器中设有中断程序,当程序将数字转换器的输出数据过滤后,它需要调用函数getDisplay-Point()。
通常,getDisplay-Point()函数调用是将触摸屏某点数据存入用户输入队列以前的最后一个步骤。
表1:建议的校准步骤。
=======================================1. 用全组数值调用setCalibrationMatrix()以设置显示屏驱动器,并提供原始存取数据(见sample.c)。
这样就不需要为存取数据构造特殊的函数。
你只需要按照与程序一样的机制获取纵坐标。
2. 在坐标 (XD0,YD0)画出第一个目标。
3. 收集从触摸屏返回的数据,并存储在坐标(X0,Y0)。
4. 在坐标 (XD1,YD1)画出第二个目标。
5. 收集从触摸屏返回的数据,并存储在坐标(X1,Y1)。
6. 在坐标 (XD2,YD2)画出第三个目标。
7. 收集从触摸屏返回的数据,并存储在坐标(X2,Y2)。
8. 采用参考显示数据和其产生的触摸屏数据作为变量,调用setCalibrationMatrix()函数。
=================================6 其它考虑因素执行采样函数是为了保证每次都获得准确结果,因而它的中间值未经过放大。
