导数单元测试题.docx
高中数学选修22:第一章导数及其应用单元测试题.doc

数学选修 2-2 第一章单元测试题一、选择题 ( 本大题共 12 小题,每小题 5 分,共 60 分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.函数f ( x) 的定义域为开区间 ( a,b) ,导函数f′(x) 在( a,b) 内的图像如图所示,则函数 f ( x)在开区间( a,b)内有极小值点()A.1 个B.2 个C.3 个D.4 个1 12.在区间[ 2,2] 上,函数 f ( x)=x2+px+q 与g( x)=2x+x2在1同一点处取得相同的最小值,那么f(x)在[2,2]上的最大值是()C.8D.423.点P在曲线y=x3-x+3上移动,设点P处的切线的倾斜角为α,则α 的取值范围是( )ππ3A.[0 ,2 ] B.[0 ,2 ] ∪[ 4π,π)3 π 3C.[ 4π,π ) D.[ 2,4π]14.已知函数f ( x) =2x4-2x3+3m,x∈R,若f ( x) +9≥0恒成立,则实数 m的取值范围是()3 3A.m≥2 B.m>23 3C.m≤2 D.m<2x2 25.函数f ( x) =cos x-2cos 2的一个单调增区间是 ()f x 0+3 -f x 06.设f ( x) 在x=x0 处可导,且lim Δx=1,Δx→0则 f ′(x0)等于( )A.1 B.0C.3x+97.经过原点且与曲线y=x+5相切的切线方程为()A.x+y=0B.x+25y=0C.x+y= 0 或x+25y=0D.以上皆非8.函数f ( x) =x3+ax2+bx+c,其中a,b,c为实数,当a2-3b<0 时,f ( x) 是()A.增函数B.减函数C.常数D.既不是增函数也不是减函数13 29.若a>2,则方程3x -ax +1=0 在(0,2) 上恰好有 ()A.0 个根B.1 个根C.2 个根D.3 个根1 10.一点沿直线运动,如果由始点起经过t s 后距离为s=4t 4-53t 3+2t 2,那么速度为零的时刻是( )A.1 s 末B.0 sC.4 s 末D.0,1,4 s 末x2,x∈[0,1],2f(x) d x 等于 () 11.设f ( x) =则2-x,x∈ 1,2] ,0D.不存在sin x sin x1 sin x2 12.若函数 f(x) =x,且 0<x1<x2 <1,设 a=x1 ,b=x2 ,则 a,b 的大小关系是 ( )A.a>b B.a<bC.a=b D.a、b的大小不能确定二、填空题 ( 本大题共 4 小题,每小题 5 分,共 20 分.把答案填在题中横线上 )1 3 213.若 f(x) =3x -f ′(1)x +x+5,则 f ′(1) = ________.π π14.已知函数 f(x) 满足 f(x) =f( π-x) ,且当 x∈ -2,2 时,f(x) =x+sin x,设a=f(1) ,b=f(2) ,c=f(3) ,则a、b、c 的大小关系是 ________.15.已知函数f(x) 为一次函数,其图像经过点(2,4) ,且1f(x) d x=3,则函数f(x) 的解析式为________.16.(2010 ·江苏卷) 函数2y=x(x>0)的图像在点 2(a k,a k) 处的切线与x 轴的交点的横坐标为a k+1,其中k∈N*. 若a1=16,则a1+a3+a5的值是________.三、解答题 ( 本大题共 6 小题,共 70 分,解答应出写文字说明、证明过程或演算步骤 )17.(10 分) 如图,直线y=kx分抛物线y=x-x2与x轴所围成图形为面积相等的两部分,求k 的值.18.(12 分) 已知函数 f(x) =x4-4x3+ax2-1 在区间 [0,1] 上单调递增,在区间 [1,2) 上单调递减.(1)求 a 的值;(2)若点 A(x0,f(x0)) 在函数 f(x) 的图像上,求证:点 A关于直线x=1 的对称点 B 也在函数 f(x) 的图像上.19.(12 分) 设 x=- 2 与 x=4 是函数 f(x) =x3+ax2+bx 的两个极值点.(1)求常数 a,b;(2)试判断 x=- 2,x= 4 是函数 f(x) 的极大值还是极小值,并说明理由.20.(12 分) 已知 f(x) =ax3-6ax2+b,x∈[ -1,2] 的最大值为 3,最小值为- 29,求 a,b 的值.21.(12 分)(2010 ·重庆卷 ) 已知函数 f(x) =ax3+x2+ bx( 其中常数a,b∈R) ,g( x) =f ( x) +f′(x) 是奇函数.(1)求 f ( x)的表达式;(2)讨论 g( x)的单调性,并求 g( x)在区间[1,2]上的最大值与最小值.1-x22.(12 分) 已知函数f ( x) =ln( ax+1) +1+x,x≥0,其中a>0.(1)若 f ( x)在 x=1处取得极值,求 a 的值;(2)求 f ( x)的单调区间;(3)若 f ( x)的最小值为1,求 a 的取值范围.参考答案1.答案 A解析设极值点依次为 x1,x2,x3且 a<x1<x2<x3<b,则 f ( x) 在( a,x1) ,( x2,x3) 上递增,在 ( x1,x2) ,( x3,b) 上递减,因此,x1、x3是极大值点,只有x2是极小值点.2.答案 D3.答案 B4.答案 A1解析因为函数 f ( x)=2x4-2x3+3m,所以 f ′(x)=2x3-6x2.令 f ′(x)=0,得 x=0或 x=3,经检验知 x=3是函数的一个最27小值点,所以函数的最小值为 f (3)=3m-2.不等式 f ( x)+9≥0恒成27 3立,即 f ( x)≥-9恒成立,所以3m-2≥-9,解得 m≥2.5.答案 A解析 f ( x)=cos2x-cos x-1,∴f′(x)=-2sin x·cos x+sin x=sin x·(1-2cos x).令 f ′(x)>0,结合选项,选A.6. 答案 D7. 答案 D8. 答案 A9. 答案 B解析 1 3 2设 f ( x ) =3x -ax +1,则2f ′(x )=x -2ax =x ( x -2a ) ,当 x ∈(0,2) 时, f ′(x )<0,f ( x ) 在(0,2) 上为减函数,又 f (0) f (2) =8 111 3-4a +1 = 3 -4a <0,f ( x ) =0 在(0,2) 上恰好有一个根,故选 B.10. 答案 D11. 答案 C解析 数形结合,如图.2f(x) d x = 1x 2d x + 2(2 -x) d x0 11 3 11 22= 3x+ 2x -2x11 1= 3+(4 -2-2+2)5= 6,故选 C .12. 答案Af ′(x) =x cos x -sin x解析 x 2, 令 g(x) =x cos x -sin x ,则g ′(x) =- x sin x +cos x -cos x =- x sin x.∵0<x<1,∴ g ′(x)<0 ,即函数 g(x) 在 (0,1) 上是减函数,得 g(x)<g(0) =0,故 f ′(x)<0 ,函数 f(x) 在(0,1) 上是减函数,得 a>b ,故选A .213. 答案 32 2解析 f ′(x) = x -2f ′(1)x + 1,令 x=1,得 f ′(1) =3.14. 答案 c<a<b解析f(2) = f( π-2) , f(3) = f( π- 3) ,因为 f ′(x) = 1+π ππcos x≥0,故f(x)在-2,2上是增函数,∵2 >π-2>1>π-3>0,∴f( π-2)>f(1)>f( π-3) ,即 c<a<b.2815.答案 f(x) =3x+3解析设函数 f(x) =ax+b(a ≠0) ,因为函数 f(x) 的图像过点(2,4) ,所以有 b=4-2a.∴1 f(x) d x= 1 (ax +4-2a) d x0 01 2 1 1=[ ax +(4 -2a)x] | 0=a+4-2a=1.2 22 8 2 8∴a=3. ∴b=3. ∴f(x) =3x+3.16. 答案21解析2 2∵y′=2x,∴过点( a k,a k)处的切线方程为y-a k=2a k( x1-a k),又该切线与 x 轴的交点为( a k+1,0),所以 a k+1=2a k,即数列{ a k}1是等比数列,首项a1=16,其公比q=2,∴ a3=4,a5=1,∴ a1+a3 +a5=21.17. 解析抛物线 y =x -x 2 与 x 轴两交点的横坐标为x 1=0,x 2=1,所以,抛物线与 x 轴所围图形面积 S = 12) d x =x 2 x 3 11 (x -x 2 -3 0=2-1 13=6.y =x -x 2,又 由此可得抛物线 y =x -x 2 与 y =kx 两交点的横y =kx ,S- 2 x 3 -坐标 x 3= , 4= - ,所以 = 1-k (x - x 2 kx) d x =1 k x - 1k -0 x 1 k 2 02313=6(1 -k) .3又 S = ,所以 (1 -k) 3=1,∴ k =1- 4.622118. 解析 (1) 由函数 f(x) =x4-4x3+ax2-1 在区间 [0,1] 单调递增,在区间 [1,2) 单调递减,∴x =1 时,取得极大值,∴ f ′(1) = 0.又 f ′(x) = 4x3-12x2+2ax ,∴4-12+2a = 0? a = 4.(2) 点 A(x0,f(x0)) 关于直线 x =1 的对称点 B 的坐标为 (2 -x0, f(x0)) ,f(2 -x0) =(2 -x0)4 -4(2 -x0)3 +4(2 -x0)2 -1= (2 -x0)2[(2 -x0) -2]2 -1= x 40-4x30+ ax20- 1=f(x0) ,∴A 关于直线 x =1 的对称点 B 也在函数 f(x) 的图像上.19.解析 f ′(x) =3x2+2ax+b.(1) 由极值点的必要条件可知:12-4a+b=0,f ′( - 2) =f ′(4) = 0,即48+8a+b=0,解得 a=- 3,b=- 24.或f ′(x) = 3x2+2ax+b=3(x +2)(x -4)=3x2-6x-24,也可得 a=- 3,b=- 24.(2) 由 f ′(x) = 3(x +2)(x -4) .当 x<- 2 时, f ′(x) > 0,当- 2<x<4 时, f ′(x) < 0. ∴x=- 2 是极大值点,而当x>4 时, f ′(x) > 0,∴x=4 是极小值点.20.解析 a≠0( 否则 f(x) =b 与题设矛盾 ) ,由f ′(x) = 3ax2-12ax=0 及 x∈[ - 1,2] ,得 x=0. (1) 当 a>0 时,列表:x ( -1,0) 0 (0,2)f ′(x) +0 -f(x) 增极大值 b 减由上表知, f(x) 在[ - 1,0] 上是增函数,f(x) 在[0,2] 上是减函数.则当 x=0 时, f(x) 有最大值,从而b=3.又f( -1) =- 7a+3,f(2) =- 16a+3,∵a>0,∴ f( -1) >f(2) .从而 f(2) =- 16a+3=- 29,得a=2.(2)当 a<0 时,用类似的方法可判断当 x=0 时 f(x) 有最小值.当x=2 时, f(x) 有最大值.从而 f(0) =b=- 29, f(2)=-16a-29=3,得a=- 2.综上, a= 2,b=3 或 a=- 2,b=- 29.21.解析 (1) 由题意得f′(x) = 3ax2+2x+b. 因此g( x) =f ( x) +f′(x)=ax3+(3 a+1) x2+( b+2) x+b.因为函数 g( x)是奇函数,所以g(-x)=- g( x),即对任意实数x,有 a(- x)3+(3 a+1)(-x)2+( b +2)( -x) +b=- [ ax3+(3 a+1) x2+( b+2) x+b] ,从而 3a+1=0,b=0,解得a=-1,b=0,因此f ( x) 的解析式为f ( x) =-x3+x2. 331(2)由(1) 知g( x) =-1x3+2x,所以g′(x) =-x2+2. 3令g′(x)=0,解得x1=-2,x2=2,则当x<-2或x> 2时,g′(x)<0,从而 g( x)在区间(-∞,-2],[ 2,+∞)上是减函数;当- 2<x< 2时,g′(x)>0 ,从而g( x) 在[ - 2, 2] 上是增函数.由前面讨论知, g( x)在区间[1,2] 上的最大值与最小值只能在x=1,2,2 时取得,而g(1)5=3,g( 2) =4 23,g(2)4=3. 因此g( x)在区间 [1,2] 上的最大值为g( 2) =4 2,最小值为3g(2)4=3.22. 分析解答本题,应先正确求出函数 f ( x)的导数f ′(x),再利用导数与函数的单调性、导数与极值、导数与最值等知识求解,并注意在定义域范围内求解.a 2 ax2+a-2解析 (1) f′(x) =ax+1-1+x 2=ax+1 1+x 2,∵f ( x)在 x=1处取得极值,2∴f ′(1)=0,即 a·1+a-2=0,解得 a=1.(2) f′(x) =ax2+a-22,ax+1 1+x∵x≥0, a>0,∴ ax+1>0.①当 a≥2时,在区间[0,+∞)上, f ′(x)>0,∴f( x)的单调增区间为[0,+∞).②当 0<a<2 时,由 f ′(x)>0,解得 x> 2-a a.由 f ′(x)<0,解得 x< 2-a a.∴f ( x)的单调减区间为(0, 2-a 2-a a ) ,单调增区间为 ( a,+∞ ) .(3) 当a≥2时,由 (2) ①知,f ( x) 的最小值为f (0) =1;当 0<a<2,由 (2) ②知,f ( x) 在x=2-aa 处取得最小值,且2-af ( a )< f (0) =1.综上可知,若 f ( x)的最小值为1,则 a 的取值范围是[2,+∞).。
第一章_导数测试卷

导数测试卷第Ⅰ卷(选择题,共50分)一、选择题(本大题共10小题,每小题5分,共50分。
在每一小题给出的四个选项中,只有一项符合题目要求)1、对可导函数,在一点两侧的导数异号是这点为极值点的 ( ) A.充分条件 B.必要条件 C.充要条件 D.既不充分又不必要条件2、设)(x f 是可导函数,且='=∆-∆-→∆)(,2)()2(lim0000x f xx f x x f x 则 ( )A .21B .-1C .0D .-2 3、若曲线4y x =的一条切线l 与直线480x y +-=垂直,则l 的方程为( ) A .430x y --= B .450x y +-= C .430x y -+= D .430x y ++=4、已知3)2(3123++++=x b bx x y 是R 上的单调增函数,则b 的取值范围是 ( )A. 21>-<b b ,或 B. 21≥-≤b b ,或 C. 21<<-b D. 21≤≤-b5、已知函数322+-=x x y 在区间[0,m]上有最大值3,最小值2,则m 的取值范围是 ( )A .),1[+∞B .[0,2]C .]2,(-∞D .[1,2]6、f /(x )是f (x )的导函数,f /(x )的图象如右图所示,则f (x )的图象只可能是( )(A ) (B ) (C ) (D )7、下列说法正确的是 ( ) A. 函数在闭区间上的极大值一定比极小值大; B. 函数在闭区间上的最大值一定是极大值; C. 对于12)(23+++=x px x x f ,若6||<p ,则)(x f 无极值;D.函数)(x f 在区间),(b a 上一定存在最值.8、函数223)(a bx ax x x f +--=在1=x 处有极值10, 则点),(b a 为( )A.)3,3(-B.)11,4(-C. )3,3(-或)11,4(-D.不存在9、函数)(x f 的定义域为开区间),(b a ,导函数)(x f ' 在),(b a 内的图象如图所示,则函数)(x f 在开区间),(b a 内有极小值点( )A .1个B .2个C .3个 D. 4个10、函数)100()2)(1()(-⋅⋅⋅--=x x x x x f 在0=x 处的导数值为( ) A. 0 B. 2100 C. 200 D. 100! 一、 选择题:(5*10=50分)二、填空题(本大题共6小题,每小题5分,共30分。
(完整版)人教版导数测试题含答案
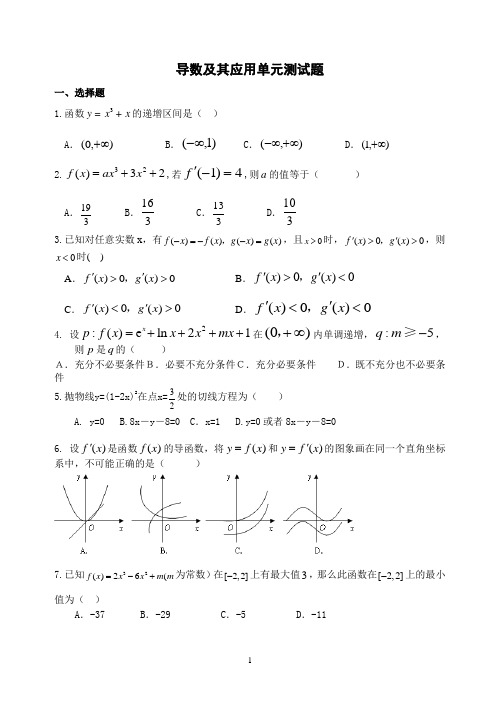
导数及其应用单元测试题一、选择题1.函数3y x x =+的递增区间是( )A .),0(+∞B .)1,(-∞C .),(+∞-∞D .),1(+∞ 2.32()32f x ax x =++,若(1)4f '-=,则a 的值等于( )A .319B .316 C .313D .3103.已知对任意实数x ,有()()()()f x f x g x g x -=--=,,且0x >时,()0()0f x g x ''>>,,则0x <时( )A .()0()0f x g x ''>>,B .()0()0f x g x ''><,C .()0()0f x g x ''<>,D .()0()0f x g x ''<<,4. 设2:()e ln 21xp f x x x mx =++++在(0)+∞,内单调递增,:5q m -≥, 则p 是q 的( )A.充分不必要条件B.必要不充分条件C.充分必要条件 D.既不充分也不必要条件5.抛物线y=(1-2x)2在点x=32处的切线方程为( )A. y=0B.8x -y -8=0 C .x=1 D.y=0或者8x -y -8=06. 设()f x '是函数()f x 的导函数,将()y f x =和()y f x '=的图象画在同一个直角坐标系中,不可能正确的是( )7.已知32()26(f x x x m m =-+为常数)在[2,2]-上有最大值3,那么此函数在[2,2]-上的最小值为( )A .-37B .-29C .-5D .-118.设函数322()3(1)1f x kx k x k =+--+在区间(0,4)上是减函数,则k 的取值范围是()A .13k <B .103k <≤C .103k ≤<D .13k ≤9. 已知二次函数2()f x ax bx c =++的导数为'()f x ,'(0)0f >,对于任意实数x 都有()0f x ≥,则(1)'(0)f f 的最小值为( )A .3B .52C .2D .32二、填空题10.函数ln x e y x=的导数'y =_____________11.若函数343y x bx =-+有三个单调区间,则b 的取值范围是 . 12.已知函数3221()3f x x a x ax b =+++,当1x =-时函数()f x 的极值为712-,则(2)f = .13.函数2cos y x x =+在区间[0,]2π上的最大值是 .三、解答题(共80分) 14.(本题满分12分) 设()33f x x x=+,求函数f(x)的单调区间及其极值;F 图6PED BA15. (本题满分14分) 求证:若x>0,则ln(1+x)>x 1x+;16. (本题满分14分)若函数4)(3+-=bx ax x f ,当2=x 时,函数)(x f 有极值34-, (1)求函数的解析式;(2)若函数k x f =)(有3个解,求实数k 的取值范围.17(本题满分14分)如图6所示,等腰三角形△ABC 的底边AB=CD=3,点E 是线段BD 上异于B 、D 的动点,点F 在BC 边上,且E F ⊥AB ,现沿EF 将△BEF 折起到△PEF 的位置,使P E ⊥AE ,记BE=x ,V (x )表示四棱锥P-ACEF 的体积。
导数单元测试题.doc

导数单元测试题一、选择题(本大题共10小题,每小题5分,共50分) 1.下列求导正确的是( )A .ln ln 1()x x x x-'=B .222()(12)x x xe e x --'=+C .(6cos )6sin x x '=D .2ln )2x x'=2.已知直线1y x =+与曲线ln()y x a =+相切,则a 的值为( )A .1B .2C .-1D .-23.已知3()f x x ax =-在[1,]+∞上是增函数,则a 的最大值是( )A .0B .1C .2D .34.已知函数()f x 在R 上满足2()2(2)88f x f x x x =--+-,则曲线()y f x =在点(1,(1))f 处的切线方程为( )A .21y x =-B .y x =C .32y x =-D .23y x =-+5.已知函数2()23y f x x x ==--+在区间[,2]a 上的最大值为154,则a 等于( ) A .32-B .12C .12-D .1322-或6.已知()f x 的导函数()f x '的图象如图所示,那么()f x 的图象最有可能是( )7.函数32()f x x x x =--的单调减区间是( )A .1(,)3-∞-B .(1,)+∞C .1(,),(1,)3-∞-+∞D .1(,1)3-8.已知32()(6)1f x x ax a x =++++有极大值和极小值,则a 的取值范围为( )A .12a -<<B .36a -<<C .12a a <->或D .36a a <->或9.设a R ∈,若函数3,axy e x x R =+∈有大于零的极值点,则( )A .3a >-B .3a <-C .13a >-D .13a <-10.等比数列{}n a 中,132,4a a ==,函数128()()()()f x x x a x a x a =---…,(0)f '等于( )A .26B .29C .212D .215二、填空题(共20分)11.设()f x 是偶函数,若曲线()y f x =在点(1,(1)f )处的切线的斜率为1,则该曲线在点(1,(1))f --处的切线的斜率为 。
《导数》单元测试题.doc

《导数》单元测试题班级 _______________ 姓名 _______________一、选择题:(每小题5分,共50分)1、函数/(兀)在x = x ()处导数f * (x ())的儿何意义是 A. 在点X = X Q 处的斜率;B. 在点(x (), / (Xo ))处的切线与兀轴所夹的锐角正切值;C. 点(兀°, / (%0 ))与点(0,0)连线的斜率;D. 曲线y = /(无)在点(心,/(◎))处的切线的斜率.A. 函数在闭区间上的极小值一定比极大值小;B. 函数在闭区间上的最人值一定是极人值;C. /(x )在[d,b ]上一定有最大值;D. /U ) = X 3 + /9X 2+2x4-1,若 |〃|<般,则/(兀)无极值.6、对于R 上可导的任意函数/(兀),若满足(x —1) /(x )>0,则必有 A. /(0) 4- /(2) <2/(1); B. /(0) + /(2) <2/(1);2、 3、 曲线y = x 2-3x 上点P 处切线平行与兀轴,则P 点坐标为 3 9 3 9 3 9 A. (— — , — ); B. (—,— — ); C.(——2 4 2 4 2 4函数/(兀)=血3 * * + ]有极值的充要条件是A. a>0 ;B ・ >0; C. QV O ;D.4、设函数/(x )在定义域内可导,y=f (x )的图象如图1所示, 图象可能为则导函数y = f\x )的5.下列说法中正确的是 图1C. f (0) + f (2) >2/(1);D. / (0) + f (2) >2/(1).7、函数y二兀cosx—sinx在下面哪个区间内是增函数yr、冗A. ( —, 一 );B.(龙,2龙);C. ( —, -—);D. ( 2兀,3龙).2 2 2 28、函数/(力的定义域为开区间(a,b ),导函数广⑴在(ab )内的图象如图所示,则函数门、曲线y =X 3+x+\在点(1,3)处的切线方程是 _____________ •12、 曲线)=兀3在点(1,])处的切线与兀轴、直线x = 2所围成的三角形的面积为・ 13、 已知xw/?,奇函数f (x ) = x 3-ax 2-bx-1-c 在[1,H )上单调,则字母a,b,c 应满足的条件是 _______ •14、己知函数/(x ) = mx m -n的导数为 f (x ) = 8x\ 则m n= _____________ 三、解答题:(第1题14分;第2题12分)15>已知函数/(x ) = ax' + bx 2+ ex 在点A :。
(完整版)高二数学导数单元测试题(有答案)

高二数学导数单元测试题(有答案)(一).选择题(1)曲线3231y x x =-+在点(1,-1)处的切线方程为( )A .34y x =-B 。
32y x =-+C 。
43y x =-+D 。
45y x =- a(2) 函数y =a x 2+1的图象与直线y =x 相切,则a = ( )A .18 B .41 C .21D .1 (3) 函数13)(23+-=x x x f 是减函数的区间为( )A .),2(+∞B .)2,(-∞C .)0,(-∞D .(0,2)(4) 函数,93)(23-++=x ax x x f 已知3)(-=x x f 在时取得极值,则a = ( )A .2B .3C .4D .5(5) 在函数x x y 83-=的图象上,其切线的倾斜角小于4π的点中,坐标为整数的点的个数是 ( )A .3B .2C .1D .0(6)函数3()1f x ax x =++有极值的充要条件是 ( )A .0a >B .0a ≥C .0a <D .0a ≤ (7)函数3()34f x x x =- ([]0,1x ∈的最大值是( )A .12B . -1C .0D .1 (8)函数)(x f =x (x -1)(x -2)…(x -100)在x =0处的导数值为( )A 、0B 、1002C 、200D 、100! (9)曲线313y x x =+在点413⎛⎫⎪⎝⎭,处的切线与坐标轴围成的三角形面积为( ) A.19 B.29 C.13 D.23(二).填空题(1).垂直于直线2x+6y +1=0且与曲线y = x 3+3x -5相切的直线方程是 。
(2).设 f ( x ) = x 3-21x 2-2x +5,当]2,1[-∈x 时,f ( x ) < m 恒成立,则实数m 的取值范围为 .(3).函数y = f ( x ) = x 3+ax 2+bx +a 2,在x = 1时,有极值10,则a = ,b = 。
(word完整版)导数的运算练习题

导数的运算练习一、常用的导数公式(1)'C = (C 为常数); (2)()'n x = ; (3)(sin )'x = ; (4)(cos )'x = ; (5)()'x a = ; (6)()'x e = ; (7)_____________; (8)_____________;二、导数的运算法则 1、(1) ; (2);(3)______________________________________; (4)=___________________________________;(C 为常数)2、复合函数的导数设 .三、练习1、已知()2f x x =,则()3f '等于( )A .0B .2xC .6D .9 2、()0f x =的导数是( )A .0B .1C .不存在D .不确定 3、32y x = ) A .23xB .213x C .12- D 33x4、曲线n y x =在2x =处的导数是12,则n 等于( )A .1B .2C .3D .45、若()f x =()1f '等于( )A .0B .13- C .3 D .136、2y x =的斜率等于2的切线方程是( ) A .210x y -+=B .210x y -+=或210x y --=C .210x y --=D .20x y -= 7、在曲线2y x =上的切线的倾斜角为4π的点是( ) A .()0,0 B .()2,4 C .11,416⎛⎫ ⎪⎝⎭ D .11,24⎛⎫⎪⎝⎭8、设()sin y f x =是可导函数,则x y '等于( )A .()sin f x 'B .()sin cos f x x '⋅C .()sin sin f x x '⋅D .()cos cos f x x '⋅ 9、函数()22423y x x=-+的导数是( )A .()2823x x -+B .()2216x -+ C .()()282361x x x -+-D .()()242361x x x -+-10、曲线34y x x =-在点()1,3--处的切线方程是( ) A .74y x =+B .72y x =+C .4y x =-D .2y x =-11、点P 在曲线323y x x =-+上移动,设点P 处切线的倾斜角为α,则角α的取值范围是( )A .0,2π⎡⎤⎢⎥⎣⎦B .30,,24πππ⎡⎤⎡⎫⎪⎢⎥⎢⎣⎦⎣⎭C .3,4ππ⎡⎫⎪⎢⎣⎭ D .3,24ππ⎛⎤ ⎥⎝⎦12、求函数212y x =-在点1x =处的导数。
(完整版)导数测试题(含答案)

B.(0,3)
C.(1,4)
D.(2,+∞)
解析:选 D.f′(x)=(x-3)′ex+(x-3)(ex)′=(x-2)ex,
令 f′(x)>0,解得 x>2,故选 D. 8.“函数 y=f(x)在一点的导数值为 0”是“函数 y=f(x)在这点取极值”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 解析:选 B.对于 f(x)=x3,f′(x)=3x2,f′(0)=0,不能推出 f(x)在 x=0 处取极值,反之 成立.故选 B. 9.函数 f(x)的定义域为开区间(a,b),导函数 f′(x)在(a,b)内的图象如图所示,则函数 f(x)在开区间(a,b)内的极小值点有( )
B.(2,4)
11
11
C.(4,16) 故选 D.
1
D.(2,4)
6.已知函数 f(x)=x,则 f′(-3)=( ) 1
A.4 1
B.9 1
C.-4
D.-9
1
1
解析:选 D.∵f′(x)=-x2,∴f′(-3)=-9. 7.函数 f(x)=(x-3)ex 的单调递增区间是( )
A.(-∞,2)
三、解答题 x
17.求下列函数的导数:(1)y=3x2+xcosx; (2)y=1+x; (3)y=lgx-ex.
18.已知抛物线 y=x2+4 与直线 y=x+10,求: (1)它们的交点; (2)抛物线在交点处的切线方程.
1 19.已知函数 f(x)=3x3-4x+4.(1)求函数的极值; (2)求函数在区间[-3,4]上的最大值和最小值.
解析:令 y′=(x+1)ex=0,得 x=-1. 当 x<-1 时,y′<0;当 x>-1 时,y′>0.
最新导数单元测试
第一章 导数及其应用一、选择题(本题共12小题,每小题5分,共60分) 1.若'0()3f x =-,则000()(3)limh f x h f x h h→+--=( )A .3-B .6-C .9-D .12- 2.函数()323922y x x x x =---<<有( )A .极大值5,极小值27-B .极大值5,极小值11-C .极大值5,无极小值D .极小值27-,无极大值 3.函数xx y 142+=的单调递增区间是( ) A .),0(+∞ B .)1,(-∞ C .),21(+∞ D .),1(+∞ 4.函数xxy ln =的最大值为( ) A .1e - B .e C .2e D .310 5.已知曲线32114732y x x x =++-在点Q 处的切线的倾斜角α满足216sin 17α=,则此切线的方程为( ) 470x y -+=或B.C.470x y --=或D.470x y --=6.抛物线在点M处的切线倾斜角是( )A .30°B .45°C .60°D .90° 7.函数)(x f 的定义域为开区间),(b a ,导函数)(x f '在),(b a 内的图象如图所示,则函数)(x f 在开区间),(b a 内的极小值点有( )A.1个B.2个C.3个D.4个abxy)(x f y ?=O8.已知函数f (x )=12x 3-x 2-72x ,则f (-a 2)与f (-1)的大小关系为( )A .f(-a 2)f(-1) B .f(-a 2)f(-1) C .f(-a 2)f(-1)D .f(-a 2)与f(-1)的大小关系不确定9.已知函数f(x)=x 3+(1-a)x 2-a(a +2)x +b -2(a ≠1)的图象过原点,且在原点处的切线的斜率是-3,则不等式组所确定的平面区域在圆x 2+y 2=4内的面积为( )A.πB. π2C. π3D.2π10.已知函数f(x)=x 3+mx 2+(m +6)x +1既存在极大值又存在极小值,则实数m 的取值范围是( )A .(-1,2)B .(-∞,-3)∪(6,+∞)C .(-3,6)D .(-∞,-1)∪(2,+∞) 二、填空题(本题共4小题,每小题4分,共16分)11.已知直线10x y --=与抛物线2y ax =相切,则______.a = 12.若32()(0)f x ax bx cx d a =+++>在R 上是增函数,则,,a b c 的关系式为 .13.已知sin (ππ)1cos xy x x=∈-+,,,当2y '=时,x = .14.在曲线的切线斜率中斜率最小的切线方程是_________.三、解答题(本题共5小题,共74分) 15.(本小题满分14分)已知c bx ax x f ++=24)( 的图象经过点(0,1),且在1x =处的切线方程是2y x =-.(1)求)(x f y =的解析式;(2)求)(x f y =的单调递增区间.16.(本小题满分14分)已知函数2()ln (0).f x x ax x a =-->(1)若曲线()y f x =在点(1,(1))f 处的切线斜率为-2,求a 的值以及切线方程;(2)若()f x 是单调函数,求a 的取值范围.17.(本小题满分16分)已知函数()ln f x ax x =+()a ∈R . (1)若2a =,求曲线()y f x =在1x =处切线的斜率; (2)求()f x 的单调区间;(3)设2()22g x x x =-+,若对任意1(0,)x ∈+∞,均存在[]20,1x ∈,使得12()()f x g x <,求a 的取值范围.18.已知函数21()2e 2x f x x x a =-+-. (Ⅰ)若1a =,求()f x 在1x =处的切线方程; (Ⅱ)若)(x f 在R 上是增函数,求实数a 的取值范围.19.已知函数,)1()(23bx x b x x f ++-=R b ∈.(Ⅰ)若函数)(x f 在点())1,1(f 处的切线与直线03=-+y x 平行,求b 的值; (Ⅱ)在(Ⅰ)的条件下,求)(x f 在区间]3,0[上的最值.20.设函数22()ln (0)a f x a x a x=+≠. (Ⅰ)已知曲线()y f x =在点(1,(1))f 处的切线l 的斜率为23a -,求实数a 的值; (Ⅱ)讨论函数()f x 的单调性;(Ⅲ)在(Ⅰ)的条件下,求证:对于定义域内的任意一个x ,都有()3f x x ≥-.21.设a ∈R ,函数233)(x ax x f -=.(Ⅰ)若2=x 是函数)(x f y =的极值点,求实数a 的值;(Ⅱ)若函数()()xg x e f x =在]2,0[上是单调减函数,求实数a 的取值范围.第一章 导数及其应用答案一、 选择题 1.D 解析:'0000000()(3)()(3)lim4lim 4()12.4h h f x h f x h f x h f x h f x h h→→+--+--===-2.C 解析:令'23690, 1.yx x x =--==-得 或33时,不满足题意,故舍去.当x 在(-2,2)上变化时,的变化情况如下表: x(-2,-1)-1 (-1,2)+0 - y5由上表可知,函数y 有极大值5,无极小值.3.C 解析:令3'322181180,810,.2x y x x x x x -=-=>->>即得4.A 解析:令'''22(ln )ln 1ln 0, e.x x x x xy x x x -⋅-====得当x 变化时,随x 的变化情况如下表:x(0,e)e(e ,+∞)+ 0-y由上表可知,函数y 在x=e 时取得最大值,最大值.5.C 解析:由得则切线的斜率.因为,当,此时点Q的坐标为(0,)或当时,没有满足题意的点,故舍去.6.B 解析:因为,所以抛物线在点处的切线斜率为1,倾斜角为.7.A 解析:若处取得极小值点,则,在的左侧,在的右侧.据此可知,f(x)在开区间(a,b)内的极小值点有1个.8.A 解析:由题意可得.由=12(3x-7)(x +1)=0,得x=-1或x=73.当时,为增函数;当时,为减函数,当x>时,为增函数.所以f(-1)是函数f(x)在(-∞,0]上的最大值.又因为-a2≤0,故f(-a2)≤ f(-1).9.B 解析:由题意得.解得则不等式组为如图所示,阴影部分的面积即为所求.易知图中两锐角的正切值分别是.设两直线的夹角为,则tan=tan()=12+131-12×13=1,所以=π4,而圆的半径是2,所以不等式组所确定的区域在圆内的面积.10.B 解析:函数f(x)=x3+mx2+(m+6)x+1既存在极大值又存在极小值,所以方程有两个不同的实数根.由得m的取值范围为.二、填空题11.解析:设切点P(x0,y0).因为,所以.由题意知x0-y0-1=0,①y0=ax02,②2ax0=1,③由①②③解得:.12.23b ac ≤ 解析:由题意知'2()320f x ax bx c =++≥恒成立,已知则,即13. 解析:14.3x -y -11=0 解析:因为,令切线的斜率,当k 取最小值时,,此时切线的斜率为3,切点为(-1,-14),切线方程为,即.三、解答题15.解:(1)因为c bx ax x f ++=24)(的图象经过点(0,1),所以1c = ①.'3'()42,(1)421f x ax bx k f a b =+==+= ②.由题意得切点为(1,1)-,则c bx ax x f ++=24)(的图象经过点(1,1)-,得 ③.联立①②③得(2)令得当x 变化时,x- 0 + 0 - 0 +由上表可知,函数的单调递增区间为16.解:(1)由题设,f '(1)=-2a =-2,所以a =1,此时f(1)=0,切线方程为y =-2(x -1),即2x +y -2=0. (2),令=1-8a .当a ≥18时,≤0,f '(x)≤0,f(x)在(0,+∞)单调递减. 当0<a <18时,>0,方程+1=0有两个不相等的正根,不妨设,则当时,f '(x)<0,当时,f '(x)>0,这时f(x)不是单调函数. 综上,a 的取值范围是[18,+). 17.解:(1)由已知1()2(0)f x x x'=+>,(1)213f '=+=. 故曲线()y f x =在1x =处切线的斜率为3.(2)11'()(0)ax f x a x x x+=+=>. ①当0a ≥时,由于0x >,故10ax +>,'()0f x >,所以函数()f x 的单调递增区间为.②当0a <时,由'()0f x =,得1x a=-. 在区间1(0,)a -上,()0f x '>;在区间1(,)a-+∞上,()0f x '<,所以函数()f x 的单调递增区间为,单调递减区间为.(3)由已知,转化为max max ()()f x g x <,max ()2g x =.由(2)知,当0a ≥时,函数()f x 在(0,)+∞上单调递增,值域为R ,故不符合题意.(或者举出反例:存在33(e )e 32f a =+>,故不符合题意.) 当0a <时,函数()f x 在上单调递增,在上单调递减,故()f x 的极大值即为最大值,11()1ln()1ln()f a a a-=-+=----, 所以21ln()a >---,解得31ea <-.18.解:(Ⅰ)由1a =,21()2e 2x f x x x =-+-,3(1)e 2f =-,所以()2e xf x x '=-+-. 又(1)1e f '=-,所以所求切线方程为3(e)(1e)(1)2y x --=--即2(1e)210x y --+=. …5分(Ⅱ)由已知21()2e 2x f x x x a =-+-,得()2e x f x x a '=-+-.因为函数)(x f 在R 上是增函数,所以()0f x '≥恒成立,即不等式 2e 0x x a -+-≥恒成立. ………………9分 整理得2e x x a -+≤.令2(),e x x g x -+=3().e x x g x -'= …………11分 ,(),()x g x g x '的变化情况如下表:由此得3(3)e a g a -≤-=,即的取值范围是(3,e -⎤-∞-⎦. ………………13分19.已知函数,)1()(23bx x b x x f ++-=R b ∈.(Ⅰ)若函数)(x f 在点())1,1(f 处的切线与直线03=-+y x 平行,求b 的值; (Ⅱ)在(Ⅰ)的条件下,求)(x f 在区间]3,0[上的最值.解:(Ⅰ)b x b x x f ++-=')1(23)(2∵函数)(x f 在点())1,1(f 处的切线与直线03=-+y x 平行∴()()11231-=++-='b b f ,解得2=b ………………4分 (Ⅱ)由(Ⅰ)知x x x x f 23)(23+-=,263)(2+-='x x x f ,令0263)(2=+-='x x x f ,解得331,33121+=-=x x . ………………7分 在区间]3,0[上,x ,)(x f ',)(x f 的变化情况如下:所以当=x 3时,6)(max =x f ;当331+=x 时,=min )(x f 932-.20.(本小题满分14分)设函数22()ln (0)a f x a x a x=+≠. (Ⅰ)已知曲线()y f x =在点(1,(1))f 处的切线l 的斜率为23a -,求实数a 的值; (Ⅱ)讨论函数()f x 的单调性;(Ⅲ)在(Ⅰ)的条件下,求证:对于定义域内的任意一个x ,都有()3f x x ≥-. 解:(Ⅰ)()f x 的定义域为{|0}x x >, . ………1分222()a a f x x x'=-. 根据题意,(1)23f a '=-,所以2223a a a -=-,即2210a a -+=,解得1a =. .………4分(Ⅱ)2222(2)()a a a x a f x x x x -'=-=.(1)当0a <时,因为0x >,所以20x a ->,(2)0a x a -<,所以()0f x '<,函数()f x 在(0,)+∞上单调递减. ………6分 (2)当0a >时,若02x a <<,则(2)0a x a -<,()0f x '<,函数()f x 在(0,2)a 上单调递减; 若2x a >,则(2)0a x a ->,()0f x '>,函数()f x 在(2,)a +∞上单调递增. …8分综上所述,当0a <时,函数()f x 在(0,)+∞上单调递减;当0a >时,函数()f x 在(0,2)a 上单调递减,在(2,)a +∞上单调递增. ………9分(Ⅲ)由(Ⅰ)可知2()ln f x x x=+. 设()()(3)g x f x x =--,即2()ln 3g x x x x=++-. 2222122(1)(2)()1(0)x x x x g x x x x x x +--+'=-+==>. ………10分当x 变化时,()g x ',()g x 的变化情况如下表:1x =是()g x 在(0,)+∞上的唯一极值点,且是极小值点,从而也是()g x 的最小值点. 可见()(1)0g x g ==最小值, .………13分 所以()0g x ≥,即()(3)0f x x --≥,所以对于定义域内的每一个x ,都有()3f x x ≥-. ………14分4.设a ∈R ,函数233)(x ax x f -=.(Ⅰ)若2=x 是函数)(x f y =的极值点,求实数a 的值;(Ⅱ)若函数()()x g x e f x =在]2,0[上是单调减函数,求实数a 的取值范围. 解:(Ⅰ)2()363(2)f x ax x x ax '=-=-.因为2x =是函数()y f x =的极值点,所以(2)0f '=,即6(22)0a -=, 所以1a =.经检验,当1a =时,2x =是函数()y f x =的极值点. 即1a =.----------------------------------------------------------------------------------6分(Ⅱ)由题设,'322()(336)x g x e ax x ax x =-+-,又0x e >, 所以,(0,2]x ∀∈,3223360ax x ax x -+-≤, 这等价于,不等式2322363633x x x a x x x x++≤=++对(0,2]x ∈恒成立. 令236()3x h x x x +=+((0,2]x ∈), 则22'22223(46)3[(2)2]()0(3)(3)x x x h x x x x x ++++=-=-<++,---------------------------10分 所以()h x 在区间0,2](上是减函数, 所以()h x 的最小值为6(2)5h =.----------------------------------------------------12分 所以65a ≤.即实数a 的取值范围为6(,]5-∞.-----------------------------------13分。
最新高二导数单元测试题及参考答案+人教版.doc名师优秀教案

高二导数单元测试题一、选择题1、物体运动的方程为3414-=t s ,则当5=t 的瞬时速率为( ) A .5 B. 25 C. 125 D. 6252、已知函数f(x)在x=1处的导数为1,则 xf x f x 2)1()1(lim 0-+→=( ) A .2 B .1 C . 21 D .41 3、函数)1()1(2-+=x x y 在1=x 处的导数等于( )A .1B .2C .3D .44、与直线042=+-y x 的平行的抛物线2x y =的切线方程是( )A .032=+-y xB .032=--y xC .012=+-y xD .012=--y x5、函数13)(3+-=x x x f 在闭区间[-3,0]上的最大值、最小值分别是( )A .1,-1B .1,-17C .3,-17D .9,-19 6、曲线1323+-=x x y 在点(1,-1)处的切线方程为( )A .43-=x yB .23+-=x yC .34+-=x yD .54-=x y 7、函数13)(23+-=x x x f 是减函数的区间为( )A .),2(+∞B .)2,(-∞C .)0,(-∞D .(0,2)8、函数54)(3++=x x x f 的图象在1=x 处的切线与圆5022=+y x 的位置关系是( )A 相切 B. 相交但不过圆心 C. 过圆心 D. 相离9、函数,93)(23-++=x ax x x f 已知3)(-=x x f 在时取得极值,则a =( )A .2B .3C .4D .5 10、设)(x f '是函数)(x f 的导函数,)(x f y '=的图象如右图所示,则)(x f y =的图象最有可能的是( )二、填空题 11、曲线3x y =在点(1,1)处的切线与x 轴、直线2=x 所围成的三角形的面积为 .12、已知 f(x)=(x-1)2+2 ,g(x)=x 2-1, 则f[g(x)]的单调递增区间是13、设y = f (x)是二次函数,方程f (x)=0有两个相等的实根,且f ′(x)=2x +2,则y = f (x)的表达式为 。
(完整版)导数单元测试题(含答案)

导数单元测试题〔实验班用〕一、选择题1.曲线323y x x =-+在点(1,2)处的切线方程为( )A .31y x =-B .35y x =-+C .35y x =+D .2y x = 2.函数21()e x f x x +=⋅,[]1,2-∈x 的最大值为( ).A .14e -B . 0C .2eD . 23e 3.假设函数3()3f x x x a 有3个不同的零点,那么实数a 的取值范围是〔 〕A.(2,2)B.2,2C.(,1)D.(1,)4.假设函数3()63f x x bxb 在(0,1)内有极小值,那么实数b 的取值范围是〔 〕A.1(0,)2B. (,1)C. (0,)D. (0,1)5.假设2a >,那么函数321()13f x x ax 在区间(0,2)上恰好有( )A .0个零点B .3个零点C .2个零点D .1个零点6.曲线x y e =在点2(2)e ,处的切线与坐标轴所围三角形的面积为〔 〕A.294eB.22eC.2eD.22e7.函数()f x 的图象如下图,以下数值排序正确的选项是( ).A .(3)(2)0(2)(3)32f f f f -''<<<-B .(3)(2)0(3)(2)32f f f f -''<<<-C . (3)(2)0(3)(2)32f f f f -''<<<-D .(3)(2)0(2)(3)32f f f f -''<<<-8设(),()f x g x 分别是R 上的奇函数和偶函数, 当0x时,''()()()()0f x g x f x g x ,且(3)0g ,那么不等式()()0f x g x 解集是( )A .(3,0)(3,) B .(3,0)(0,3) C .(,3)(3,) D .(,3)(0,3)9.函数ln ln ()a x f x x+=在1,上为减函数,那么实数a 的取值范围是( )A .a eB .0a eC .a eD .10ea <<10.假设函数)(x f 的导数是)1()(+-='x x x f ,那么函数()(1)g x f x =--的单调减区间是( )A .(1,0)-B .(,1),(0,)-∞-+∞C .(2,1)--D .(,2),(1,)-∞--+∞ 11.二次函数2()f x ax bx c =++的导数为'()f x ,'(0)0f >,对于任意实数x 都有()0f x ≥,那么(1)'(0)f f 的最小值为〔 〕 A .3 B .52 C .2 D .3212.函数2()ln 22a f x x x x =--存在单调递减区间,那么a 的取值范围是〔 〕(A)[1,)-+∞ (B) (1,)-+∞ (C) (,1)-∞- (D) (,1]-∞- 二、填空题13.假设函数2()2ln f x x x =-在其定义域内的一个子区间(1,1)k k -+内不是单调函数,那么实数k 的取值范围是 . 14.点P 在曲线323+-=x x y 上移动,设在点P 处的切线的倾斜角为为α,那么α的取值范围是15.函数3()128f x x x =-+在区间[3,3]-上的最大值与最小值分别为,M m ,那么M m -=_________16.函数()f x 的定义域为[]15,-,局部对应值如下表,()f x 的导函数()y f x '=的图象如下图. 以下关于()f x 的命题: ①函数()f x 的极大值点为0,4; ②函数()f x 在[]02,上是减函数;③如果当[]1x ,t ∈-时,()f x 的最大值是2,那么t 的最大值为4; ④当12a <<时,函数()y f x a =-有4个零点; ⑤函数()y f x a =-的零点个数可能为0,1,2,3,4个. 其中正确命题的序号是 . 三、解答题17.函数)0()(23≠++=a cx bx ax x f ,当1-=x 时()f x 取得极值5,且11)1(-=f .〔1〕求()f x 的单调区间和极小值;〔2〕证明对任意12,x x )3,3(-∈,不等式32|)()(|21<-x f x f 恒成立. 18.函数)1ln(2)(2++=x ax x f ,其中a 为实数. 〔1〕假设()f x 在1=x 处有极值,求a 的值;(2) 假设()f x 在]32[,上是增函数,求a 的取值范围. 19.函数2()ln(1)()f x x ax a x a R =---∈. 〔1〕当1=a 时,求函数)(x f 的最值; 〔2〕求函数)(x f 的单调区间.20.某食品厂进行蘑菇的深加工,每公斤蘑菇的本钱20元,并且每公斤蘑菇的加工费为x -1 0 4 5 ()f x1221t 元〔t 为常数,且25)t ≤≤,设该食品厂每公斤蘑菇的出厂价为x 元〔2540x ≤≤〕,根据市场调查,日销售量q 与e x成反比,当每公斤蘑菇的出厂价为30元时,日销售量为100公斤.〔1〕求该工厂的每日利润y 元与每公斤蘑菇的出厂价x 元的函数关系式;〔2〕假设5=t ,当每公斤蘑菇的出厂价x 为多少元时,该工厂的利润y 最大,求最大值.21.函数1ln ()x f x x+=.〔1〕假设函数在区间1(,)2a a +(0)a >上存在极值,求实数a 的取值范围;〔2〕如果当1≥x 时,不等式()1≥k f x x +恒成立,求实数k 的取值范围.22.设函数2()(1)2ln(1).f x x x =+-+ 〔1〕求函数()f x 的单调区间;〔2〕当11,1xe e时,()f x m 不等式<恒成立,求实数m 的取值范围; 〔3〕假设关于x 的方程2()f x x x a =++在0,2上恰有两个相异实根,求实数a 的取值范围.导数单元测试题答案一、选择题 ACAAD DBDAA CB 二、填空题13.312k14.30,,2415.32 16. ①②⑤三、解答题17.解:〔1〕2()32(0)f x ax bx c a '=++≠,由题意得(1)11(1)5(1)0f f f =-⎧⎪-=⎨⎪'-=⎩ ,即115320a b c a b c a b c ++=-⎧⎪-+-=⎨⎪-+=⎩ ,解得139a b c =⎧⎪=-⎨⎪=-⎩,,.因此x x x x f 93)(23--=,2()3693(1)(3)f x x x x x '=--=+-.当 ),3()1,(+∞--∞∈ x 时,'()0f x >;当)3,1(-∈x 时,'()0f x <. 所以函数()f x 的单调增区间为)1,(--∞和),3(+∞;单调减区间为)3,1(-. 故函数()f x 在3=x 处取得极小值,()(3)27f x f ==-极小值.〔2〕由〔Ⅰ〕知32()39f x x x x =--在)1,3(--上递增,在)3,1(-上递减, 所以max ()(1)5f x f =-=;min ()(3)27f x f =±=-.所以,对任意12,x x )3,3(-∈恒有 12|()()||5(27)|32f x f x -<--=.18.解:〔1〕由得()f x 的定义域为)1(∞+-,. 又2()2,1f x ax x '=++ 因为()f x 在1=x 处有极值,(1)210f a '∴=+=,解之得 1.2a =-〔2〕依题意得()0≥f x '对[23]x ∀∈,恒成立, 即 201≥ax x 2++对[23]x ∀∈,恒成立. 221111()24a x x x ∴>=---++ 对[23]x ∀∈,恒成立.211[23]()24x x ∈∴-++,, [12,6],∈-- 41)21(12++-∴x 11[,],612∈-- 112≥a ∴-.19.解:〔1〕函数2()ln(1)()f x x ax a x a =---∈R 的定义域是(1,)+∞.当1a =时,32()12()2111x x f x x x x -'=--=--, 所以()f x 在3(1,)2为减函数在3(,)2+∞为增函数,所以函数()f x 的最小值为33()ln 224f =+.〔2〕22()2()211a x x a f x x a x x +-'=--=--, ①假设0a ≤时,那么22()221,()21a x x a f x x +-+=-≤>0在(1,)+∞恒成立, 所以()f x 的增区间为(1,)+∞.②假设20,12a a +>>则,故当2(1)2a x +∈,,22()2()01a x x f x x +-'=-≤; 当2[,)2a x +∈+∞时,22()2()01a x x f x x +-=-≥. 所以当0a >时,()f x 的减区间为2(1,)2a +,()f x 的增区间为2(,)2a ++∞.20.解:〔1〕设日销量3030,100,100e e e则x k k q k ==∴=, ………………2分所以日销量30100e e xq =.30100e (20)(2540)e x x t y x --∴=≤≤.………………7分〔2〕当5=t 时,30100e (25)exx y -=. ………………8分30100e (26)e xx y -'∴=. ………………9分026由得y x '≥≤,026由得,y x '≤≥[2526][2640]在,上单调递增,在,上单调递减.y ∴4max 26,100e 当时x y ∴==.………………11分当每公斤蘑菇的出厂价为26元时,该工厂的利润最大,最大值为4100e 元.……12分 21.解:〔Ⅰ〕因为1ln ()x f x x +=, x >0,那么2ln ()x f x x'=-,当01x <<时,()0f x '>;当1x >时,()0f x '<. 所以()f x 在〔0,1〕上单调递增;在(1,)+∞上单调递减, 所以函数()f x 在1x =处取得极大值. 因为函数()f x 在区间1(,)2a a +〔其中0a >〕上存在极值,所以1,11,2a a <⎧⎪⎨+>⎪⎩ 解得112a <<. 〔Ⅱ〕不等式(),1k f x x +≥即为(1)(1ln ),x x k x ++≥记(1)(1ln )(),x x g x x ++=那么min (), 1.k g x x ≤≥所以2[(1)(1ln )](1)(1ln )()x x x x x g x x '++-++'=2ln x xx-=. 令()ln h x x x =-,那么1()1h x x'=-,1x ≥,()0,h x '∴≥[()h x ∴在[1,)+∞上单调递增,min ()(1)10h x h ∴==>,从而()(1)0h x h >≥,所以()0g x '>,故()g x 在[1,)+∞上也单调递增, 所以min ()(1)2g x g ==. 所以2k ≤.22.解:〔2〕函数的定义域为。
第三单元测试卷(导数单元测试卷)

导数单元测试卷时间:120分钟,满分150分一、选择题:本大题共12小题,每小题5分,共60分.每小题给出的选项中,只有一项是符合题目要求的. 1. ★设32()34105f x x x x =-+-,则'(1)f 等于( )A .6 B .8 C .11 D .13 2.★★ 曲线2122y x =+在点51,2⎛⎫- ⎪⎝⎭处的切线的倾斜角为( ) A .34π B .4πC .54π D .4π-3. ★★函数33y x x =-在[]2,3-上( )A .有最大值18,最小值2-B .有最大值2,最小值2-C .没有最大值和最小值D .有最大值18,但是没有最小值4. ★★★如果说某物体作直线运动的时间与距离满足()2()21s t t =-,则其在 1.2t =时的瞬时速度为( ) A .4 B .4- C .4.8 D .0.85.★★ 对于任意x ,有'3()4f x x =,(1)1f =-,则此函数为( )A .4()f x x =B .4()2f x x =-C .4()1f x x =+D .4()2f x x =+6. ★★抛物线y =4x =的点处的切线方程为( )A .4180x y --=B .440x y ++=C .440x y -+=D .4180x y +-= 7. ★★★函数()1sin f x x x =+-()0,2x π∈,则函数( )A .在()0,2π内是增函数B .在()0,2π内是减函数C .在()0,π内是增函数,在(),2ππ内是减函数D .在()0,π内是减函数,在(),2ππ内是增函数 8. ★★★设函数()322()311f x kx k x k =+--+在()0,4上是减函数,则k 的取值范围是( )A .13k <B .103k <≤C .103k ≤<D .13k ≤9. ★★★三次函数当1x =时有极大值4,当3x =时有极小值0,且函数过原点,则此函数是( )A .3269y x x x =++B .3269y x x x =-+C .3269y x x x =--D .3269y x x x =+-10.★★★函数432111432y x x x =++在[]1,1-上的最小值为( )A .0B .2-C .1-D .131211. ★★★点P 在曲线323y x x =-+上移动时,过点P 的切线的倾斜角的取值范围是( )A .[]0,πB .30,,24πππ⎛⎫⎡⎤⎪⎢⎥⎝⎭⎣⎦C .30,,224πππ⎡⎤⎛⎫ ⎪⎢⎥⎣⎦⎝⎭D .30,,24πππ⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦12. ★★★★方程5436151010x x x -++=的实解的集合中( )A .至少有2个元素B .至少有3个元素C .至多有1个元素D .恰好有5个元素 二、填空题:本大题共4小题,第小题5分,共20分13.★★★曲线3y x x =-与直线2y x b =+相切,则实数b = 。
[原创]数学选修1-1《导数及其应用》单元测试卷(含答案).doc
![[原创]数学选修1-1《导数及其应用》单元测试卷(含答案).doc](https://img.taocdn.com/s3/m/76f81788b90d6c85ed3ac6a6.png)
高二数学选修1-1《导数及其应用》单元测试卷班级: 姓名: 座号: 成绩:一、选择题(共7个小题,每小题6分)1、一个物体的运动方程为21s t t =-+,其中s 的单位是米,t 的单位是秒,那么物体在3秒末的瞬时速度是 ( )A .5米/秒B .6米/秒C .7米/秒D .8米/秒2、函数()3f x x x =+的单调递增区间是 ( )A .()0,+∞B .(),1-∞C .(),-∞+∞D .()1,+∞3、已知()3232f x ax x =++且()14f '-=,则实数a 的值等于 ( )A .193B .163C .133D .1034、函数()()22f x x π=的导数是 ( )A .()4f x x π'=B .()24f x x π'=C .()28f x x π'=D .()16f x x π'=5、“函数()00f x '=”是“可导函数()f x 在点0x x =处取到极值”的 条件。
( )A .充分不必要B .必要不充分C .充要D .既不充分也不必要6、已知曲线24x y =的一条切线的斜率为12,则切点的横坐标为 ( ) A .1 B .2 C .3 D .47、设()0sin f x x =,()()10f x f x '=,()()21f x f x '=,,()()1n n f x f x +'=,n ∈N ,则()2005f x = ( )A .sin xB .sin x -C .cos xD .cos x -二、填空题(共3个小题,每小题6分)8、曲线31y x x =++在点()1,3处的切线方程是 .9、已知直线10x y --=与抛物线2y ax =相切,则a = .10、三次函数()3f x ax x =+在(),-∞+∞内是增函数,则a 的取值范围是 .三、解答题(共2个小题,每题20分)11、已知函数()32f x x ax bx c =+++,当1x =-时,取得极大值7;当3x =时,取得极小值.试求a 、b 、c 的值及这个极小值.12、设函数3()3(0)f x x ax b a =-+>.(Ⅰ)若曲线()y f x =在点(2,())f x 处与直线8y =相切,求,a b 的值;(Ⅱ)求函数()f x 的单调区间与极值点.高二数学选修1-1《导数及其应用》单元测试卷参考答案1-5 ACDCB 6-7 AC 8. 410x y --= 9. 1410. 0a > 11、解:()32f x x ax bx c =+++,∴()232f x x ax b '=++由题意知,1-和3是方程2320x ax b ++=的两个实数根 ∴2133133a b ⎧-=-+⎪⎪⎨⎪=-⨯⎪⎩,解得:39a b =-⎧⎨=-⎩()17f -=∴()()()()3211319157f c c -=--⨯--⨯-+=+=∴2c =∴极小值()32333393225f =-⨯-⨯+=-12、(Ⅰ)()'233f x x a =-,∵曲线()y f x =在点(2,())f x 处与直线8y =相切,∴()()()'203404,24.86828f a a b a b f ⎧=-=⎧=⎧⎪⎪⇒⇒⎨⎨⎨=-+==⎪⎩⎪⎩⎩(Ⅱ)∵3()3(0)f x x ax b a =-+>,由()'0f x x =⇒=当(,x ∈-∞时,()'0f x >,函数()f x 单调递增,当(x ∈时,()'0f x <,函数()f x 单调递减,当)x ∈+∞时,()'0f x >,函数()f x 单调递增,∴此时x =()f x 的极大值点,x =()f x 的极小值点.知识改变命运。
导数单元测试题(答案)

导数单元测试题(实验班用)一、选择题1.曲线323y x x =-+在点(1,2)处的切线方程为( )A.31y x =-B.35y x =-+C.35y x =+D.2y x = 2.函数21()e x f x x +=⋅,[]1,2-∈x 的最大值为( ).A.14e -B. 0C.2eD. 23e3.若函数3()3f x x x a =-+有3个不同的零点,则实数a 的取值范围是( )A.(2,2)-B.[]2,2-C.(,1)-?D.(1,)+?4.若函数3()63f x x bx b =-+在(0,1)内有极小值,则实数b 的取值范围是( ) A.1(0,)2B. (,1)-?C. (0,)+?D. (0,1) 5.若2a >,则函数321()13f x x ax =-+在区间(0,2)上恰好有( ) A .0个零点B .3个零点C .2个零点D .1个零点6.曲线xy e =在点2(2)e ,处的切线与坐标轴所围三角形的面积为( )A.294eB.22eC.2eD.22e7.函数()f x 的图象如图所示,下列数值排序正确的是( ).A.(3)(2)0(2)(3)32f f f f -''<<<-B.(3)(2)0(3)(2)32f f f f -''<<<-C. (3)(2)0(3)(2)32f f f f -''<<<-D.(3)(2)0(2)(3)32f f f f -''<<<-8设(),()f x g x 分别是R 上的奇函数和偶函数, 当0x <时,''()()()()0f x g x f x g x +>,且(3)0g -=,则不等式()()0f x g x <解集是( ) A .(3,0)(3,)-?? B .(3,0)(0,3)-? C .(,3)(3,)-??? D .(,3)(0,3)-?? 9.已知函数ln ln ()a x f x x+=在[)1,+?上为减函数,则实数a 的取值范围是( )A .a e ³B .0a e <?C .a e £D .10ea <<10.若函数)(x f 的导数是)1()(+-='x x x f ,则函数()(1)g x f x =--的单调减区间是( )A .(1,0)-B .(,1),(0,)-∞-+∞C .(2,1)--D .(,2),(1,)-∞--+∞11.已知二次函数2()f x ax bx c =++的导数为'()f x ,'(0)0f >,对于任意实数x 都有()0f x ≥,则(1)'(0)f f 的最小值为( ) A .3 B .52 C .2 D .3212.已知函数2()ln 22a f x x x x =--存在单调递减区间,则a 的取值范围是( )(A)[1,)-+∞ (B) (1,)-+∞ (C) (,1)-∞- (D) (,1]-∞- 二、填空题13.若函数2()2ln f x x x =-在其定义域内的一个子区间(1,1)k k -+内不是单调函数,则实数k 的取值范围是 . 14.点P 在曲线323+-=x x y 上移动,设在点P 处的切线的倾斜角为为α,则α的取值范围是15.已知函数3()128f x x x =-+在区间[3,3]-上的最大值与最小值分别为,M m ,则M m -=_________16.已知函数()f x 的定义域为[]15,-,部分对应值如下表,()f x 的导函数()y f x '=的图象如图所示. 下列关于()f x 的命题: ①函数()f x 的极大值点为0,4; ②函数()f x 在[]02,上是减函数;③如果当[]1x ,t ∈-时,()f x 的最大值是2,那么t 的最大值为4;④当12a <<时,函数()y f x a =-有4个零点; ⑤函数()y f x a =-的零点个数可能为0,1,2,3,4个. 其中正确命题的序号是 . 三、解答题17.已知函数)0()(23≠++=a cx bx ax x f ,当1-=x 时()f x 取得极值5,且11)1(-=f .(1)求()f x 的单调区间和极小值;(2)证明对任意12,x x )3,3(-∈,不等式32|)()(|21<-x f x f 恒成立.18.已知函数)1ln(2)(2++=x ax x f ,其中a 为实数. (1)若()f x 在1=x 处有极值,求a 的值;(2) 若()f x 在]32[,上是增函数,求a 的取值范围. 19.已知函数2()ln(1)()f x x ax a x a R =---∈. (1)当1=a 时,求函数)(x f 的最值;(2)求函数)(x f 的单调区间.20.某食品厂进行蘑菇的深加工,每公斤蘑菇的成本20元,并且每公斤蘑菇的加工费为t 元(t 为常数,且25)t ≤≤,设该食品厂每公斤蘑菇的出厂价为x 元(2540x ≤≤),根据市场调查,日销售量q 与e x成反比,当每公斤蘑菇的出厂价为30元时,日销售量为100公斤.(1)求该工厂的每日利润y 元与每公斤蘑菇的出厂价x 元的函数关系式;(2)若5=t ,当每公斤蘑菇的出厂价x 为多少元时,该工厂的利润y 最大,求最大值.21.已知函数1ln ()x f x x+=.(1)若函数在区间1(,)2a a +(0)a >上存在极值,求实数a 的取值范围;(2)如果当1≥x 时,不等式()1≥k f x x +恒成立,求实数k 的取值范围.22.设函数2()(1)2ln(1).f x x x =+-+ (1)求函数()f x 的单调区间;(2)当11,1x e e 轾犏?-犏臌时,()f x m 不等式<恒成立,求实数m 的取值范围; (3)若关于x 的方程2()f x x x a =++在[]0,2上恰有两个相异实根,求实数a 的取值范围.导数单元测试题答案一、选择题 ACAAD DBDAA CB 二、填空题13.312k ? 14.30,,24p p p 轹轹鼢觋È鼢鼢觋腚15.32 16. ①②⑤ 三、解答题17.解:(1)2()32(0)f x ax bx c a '=++≠,由题意得(1)11(1)5(1)0f f f =-⎧⎪-=⎨⎪'-=⎩ ,即115320a b c a b c a b c ++=-⎧⎪-+-=⎨⎪-+=⎩ ,解得139a b c =⎧⎪=-⎨⎪=-⎩,,.因此x x x x f 93)(23--=,2()3693(1)(3)f x x x x x '=--=+-.当 ),3()1,(+∞--∞∈ x 时,'()0f x >;当)3,1(-∈x 时,'()0f x <. 所以函数()f x 的单调增区间为)1,(--∞和),3(+∞;单调减区间为)3,1(-. 故函数()f x 在3=x 处取得极小值,()(3)27f x f ==-极小值.(2)由(Ⅰ)知32()39f x x x x =--在)1,3(--上递增,在)3,1(-上递减, 所以max ()(1)5f x f =-=;min ()(3)27f x f =±=-.所以,对任意12,x x )3,3(-∈恒有 12|()()||5(27)|32f x f x -<--=.18.解:(1)由已知得()f x 的定义域为)1(∞+-,. 又2()2,1f x ax x '=++ 因为()f x 在1=x 处有极值,(1)210f a '∴=+=,解之得 1.2a =-(2)依题意得()0≥f x '对[23]x ∀∈,恒成立,即 201≥ax x 2++对[23]x ∀∈,恒成立.221111()24a x x x ∴>=---++对[23]x ∀∈,恒成立.211[23]()24x x ∈∴-++,, [12,6],∈-- 41)21(12++-∴x 11[,],612∈-- 112≥a ∴-. 19.解:(1)函数2()ln(1)()f x x ax a x a =---∈R 的定义域是(1,)+∞.当1a =时,32()12()2111x x f x x x x -'=--=--, 所以()f x 在3(1,)2为减函数在3(,)2+∞为增函数,所以函数()f x 的最小值为33()ln 224f =+.(2)22()2()211a x x a f x x a x x +-'=--=--, ①若0a ≤时,则22()221,()21a x x a f x x +-+=-≤>0在(1,)+∞恒成立, 所以()f x 的增区间为(1,)+∞.②若20,12a a +>>则,故当2(1)2a x +∈,,22()2()01a x x f x x +-'=-≤; 当2[,)2a x +∈+∞时,22()2()01a x x f x x +-=-≥. 所以当0a >时,()f x 的减区间为2(1,)2a +,()f x 的增区间为2(,)2a ++∞.20.解:(1)设日销量3030,100,100e e e则x k k q k ==∴=, ………………2分所以日销量30100e exq =.30100e (20)(2540)e x x t y x --∴=≤≤.………………7分(2)当5=t 时,30100e (25)e xx y -=.………………8分30100e (26)exx y -'∴=. ………………9分026由得y x '≥≤,026由得,y x '≤≥[2526][2640]在,上单调递增,在,上单调递减.y ∴4max 26,100e 当时x y ∴==.………………11分当每公斤蘑菇的出厂价为26元时,该工厂的利润最大,最大值为4100e 元.……12分 21.解:(Ⅰ)因为1ln ()x f x x +=, x >0,则2ln ()x f x x'=-,当01x <<时,()0f x '>;当1x >时,()0f x '<. 所以()f x 在(0,1)上单调递增;在(1,)+∞上单调递减, 所以函数()f x 在1x =处取得极大值. 因为函数()f x 在区间1(,)2a a +(其中0a >)上存在极值,所以1,11,2a a <⎧⎪⎨+>⎪⎩ 解得112a <<. (Ⅱ)不等式(),1k f x x +≥即为(1)(1ln ),x x k x ++≥记(1)(1ln )(),x x g x x ++=则min (), 1.k g x x ≤≥所以2[(1)(1ln )](1)(1ln )()x x x x x g x x '++-++'=2ln x xx -=. 令()ln h x x x =-,则1()1h x x'=-,1x ≥,()0,h x '∴≥[()h x ∴在[1,)+∞上单调递增,min ()(1)10h x h ∴==>,从而()(1)0h x h >≥,所以()0g x '>,故()g x 在[1,)+∞上也单调递增, 所以min ()(1)2g x g ==. 所以2k ≤.22.解:(2)函数的定义域为(1,).-+∞。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
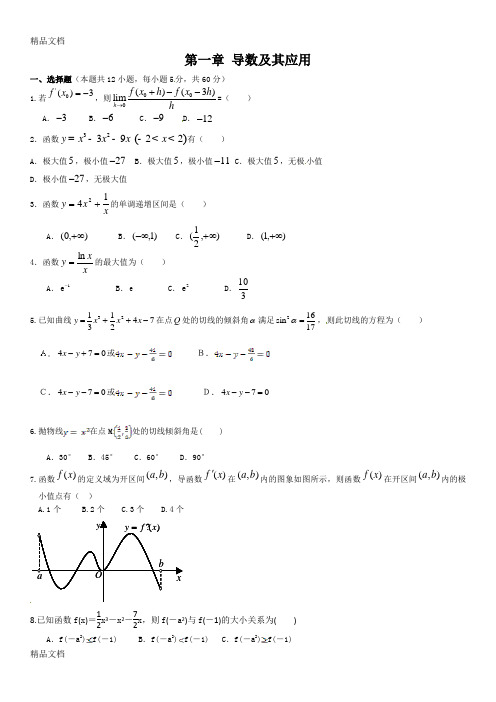
一、选择题1.曲线y x33x2在点(1,2)处的切线方程为 ( )A. y 3x 1B.y3x 5C.y 3x 5D.y 2x2.函数f (x) x2e x 1 ,x2,1 的最大值为( ).A. 4e1B. 0C.e2D.3e23. 若函数f ( x) =x3 -3x +a 有3 个不同的零点,则实数 a 的取值范围是()A. (- 2, 2)B.[- 2,2 ]C.(-? , 1)D.(1,+ ? )4. 若函数f ( x) =x3 -6bx + 3b 在 (0,1) 内有极小值,则实数 b 的取值范围是()A. (0,1) B.(- ?,1) C.(0, + ?) D.(0,1) 215. 若a 2,则函数 f ( x) =x3 -ax 2 + 1在区间 (0, 2) 上恰好有()3A.0个零点B.3个零点C.2个零点D. 1个零点6.曲线y e x在点 (2, e2 ) 处的切线与坐标轴所围三角形的面积为()A.9e2B.2e2C. e2D. e2 427.函数f (x)的图象如图所示,下列数值排序正确的是().A. 0f(2) f (3)f (3) f (2)32B.0f(3)f (3) f (2)f(2) 32C.0 f (3) f (2)f (3) f (2)32D.0f (3) f (2)f(2)f(3) 328 设 f (x), g (x) 分别是R上的奇函数和偶函数,当 x < 0时 , f'( x)g ( x) +f ( x) g ' (x) > 0, 且g(- 3) = 0,则不等式 f ( x) g(x) < 0解集是()A .(- 3,0) ? (3,?)B. (- 3,0) ? (0,3)C.(- ? ,3) ? (3,?)D. (- ? ,3) ? (0,3)9.已知函数f ( x)ln a ln x在 [1,+ ?)上为减函数,则实数 a 的取值范围是()xA.a 3 e B. 0 < a ? e C.a£e D.0 a1e10.若函数f ( x)的导数是f ( x)x( x1) ,则函数 g(x) f (x1)的单调减区间是( )A .( 1,0)B. (,1), (0,)C. (2,1) D. (,2),(1,) 11.已知二次函数 f ( x)ax2bx c 的导数为 f'( x) , f '(0)0 ,对于任意实数x 都有 f (x) 0,则f (1)的最小值为()f '(0)A.3B.5C. 2D.3 2212.已知函数f ( x)ln x a x22x 存在单调递减区间,则 a 的取值范围是()2(A) [ 1,) (B)(1,)(C)(,1)(D)(,1]二、填空题13. 若函数f ( x)2x2ln x 在其定义域内的一个子区间( k1,k1)内不是单调函数,则实数 k 的取值范围是.14.点 P 在曲线y x3x2上移动,设在点 P 处的切线的倾斜角为为,则的取3值范围是15.已知函数 f ( x) x312 x 8 在区间 [ 3,3] 上的最大值与最小值分别为M ,m ,则M m_________16.已知函数的定义域为,部分对应值如下表,的导函数的图象如图所示.下列关于的命题:①函数的极大值点为,;- 1045②函数在上是减函数;1221③如果当时,的最大值是2,那么的最大值为 4;④当时,函数有个零点;⑤函数的零点个数可能为0,1, 2, 3, 4 个.其中正确命题的序号是.三、解答题17 .已知函数f (x)ax3bx 2cx(a0) ,当x 1 时 f ( x)取得极值5,且f (1)11.( 1)求f (x)的单调区间和极小值;( 2)证明对任意x1, x2(3,3) ,不等式 | f (x1 ) f ( x2 ) |32 恒成立.18.已知函数f ( x)ax2 2 ln( x1) ,其中a为实数.( 1)若f (x)在x 1处有极值,求 a 的值;(2) 若f (x)在[ 2,3]上是增函数,求 a 的取值范围.19.已知函数f ( x)x2ax a ln( x 1) (a R) .(1)当a 1时,求函数 f ( x)的最值;(2)求函数f ( x)的单调区间.20.某食品厂进行蘑菇的深加工,每公斤蘑菇的成本20 元,并且每公斤蘑菇的加工费为t 元( t 为常数,且2≤t≤5),设该食品厂每公斤蘑菇的出厂价为x 元(25≤x ≤ 40 ),根据市场调查,日销售量q 与e x成反比,当每公斤蘑菇的出厂价为30 元时,日销售量为100 公斤.( 1)求该工厂的每日利润y 元与每公斤蘑菇的出厂价x 元的函数关系式;( 2)若t5 ,当每公斤蘑菇的出厂价x 为多少元时,该工厂的利润y 最大,求最大值.21.已知函数 f ( x)1ln x.x( 1)若函数在区间1上存在极值,求实数 a 的取值范围;(a, a2) (a 0)( 2)如果当 x ≥ 1时,不等式 f ( x) ≥k 恒成立,求实数 k 的取值范围.x122.设函数 f (x)(1 x) 2 2ln(1 x).( 1)求函数 f ( x) 的单调区间;轾( 2)当1-时 , 不等式 f ( x)m 恒成立,求实数 m 的取值范围;x? 犏1,e 1犏臌e( 3)若关于 x 的方程 f (x) x 2x a 在 [0,2 ]上恰有两个相异实根,求实数a 的取值范围.导数单元测试题答案一、选择题ACAAD DBDAA CB3轹 p 鼢 轹1? k0,332二、填空题 13. 14.鼢p, p15.16.①②⑤觋è2 觋2 鼢4腚三、解答题17. 解:( 1) f ( x)3ax 2 2bx c(a0),f (1) 11a b c 11a 1, 由题意得f ( 1) 5,即a b c5 ,解得b 3,f ( 1) 03a 2b c 0c9.因此 f (x)x 33x 2 9x ,f ( x)3x 2 6x9 3(x 1)( x 3) .当 x ( , 1)(3, ) 时, f '( x) 0 ;当 x( 1,3) 时, f '( x) 0 .所以函数 f (x) 的单调增区间为 ( ,1) 和 (3, ) ;单调减区间为 ( 1,3) .故函数 f ( x) 在 x 3 处取得极小值, f (x)极小值f (3) 27.( 2)由(Ⅰ)知f ( x) x 33x 2 9x 在 ( 3, 1)上递增,在 ( 1,3) 上递减,所以 f (x)max f ( 1) 5; f ( x) min f (3) 27 .所以,对任意 x 1, x 2 ( 3,3) 恒有 | f (x 1) f ( x 2 ) | | 5 ( 27) |32 .18.解:( 1)由已知得 f ( x) 的定义域为 ( 1, ) .又 f ( x)2ax2 , 因为 f ( x) 在 x 1处有极值,x 1f (1)2a 10,解之得 a1 .2( 2)依题意得 f ( x) ≥ 0 对 x[2,3] 恒成立,即ax2 ≥ 0对 x [2,3] 恒成立.x 1a11对x [2,3] 恒成立.x 2x1( x 212)4Q x [2,3],( x 1)21 [12, 6],241[11],a ≥1 .( x 1) 26 ,121212 419.解:( 1)函数 f (x)x 2 ax a ln( x 1) (aR ) 的定 域是 (1,) .1 ,f ( x) 2x 12x( x 3)当 a1x2 ,x 11所以 f (x) 在 (1,3) 减函数在 (3 ,) 增函数,22所以函数 f ( x) 的最小 f ( 3)3 ln 2 .24( 2)f ( x)2xa a2x( x a 2 2), x1 x 1①若 a ≤ 0 ,a2≤ 1, f (x)2x( x a 2)x2 >0 在 (1, ) 恒成立,21所以 f ( x) 的增区 (1,) .a2a 22x(x a2)②若 a0, 则 1,故当 x) , f ( x)2≤ 0 ;2(1,2x1[ a 2, ) , f ( x) 2x( x a 2)当 xx 2 ≥ 0 .2 1 所以当 a0 时, f ( x) 的减区间为 (1,a 2 ) , f ( x) 的增区间为 ( a 2, ) .2220.解:( 1) 日 量 qk x , 则 k30 100, k 100e 30, ⋯⋯⋯⋯⋯⋯ 2 分e e 所以日 量 q100e 30 .e xy100e 30(x 20t )(25 ≤ x ≤ 40) .⋯⋯⋯⋯⋯⋯ 7 分e x( 2)当 t 5, y100e 30 (x 25) .⋯⋯⋯⋯⋯⋯ 8 分e xy100e 30 (26 x)⋯⋯⋯⋯⋯⋯ 9 分e x.由 y ≥ 0得 x ≤ 26 , 由 y ≤ 0得 x ≥ 26,y 在[25,26]上单调递增,在 [26,40]上单调递减 .当 x 26时 , y max 100e 4 .⋯⋯⋯⋯⋯⋯ 11 分当每公斤蘑菇的出厂价26 元 , 工厂的利 最大,最大100e 4 元.⋯⋯ 12 分21.解:(Ⅰ)因f ( x) 1 ln x , x>0 , f(x)ln x ,xx 2当 0 x 1 , f ( x) 0 ;当 x 1 , f ( x)0 .所以 f ( x) 在( 0, 1)上 增;在 (1, ) 上 减,所以函数 f (x) 在 x 1 取得极大 .因 函数 f (x) 在区( a, a 1 (其中 a 0)上存在极 ,2)a1, 解得1a1.所以1 1, a22(Ⅱ)不等式f (x) ≥x k , 即 ( x1)(1 ln x) ≥ k,1xg (x)(x 1)(1 ln x) , k ≤ g ( x)min , x ≥ 1.x所以 g (x)[( x 1)(1 ln x)] x ( x1)(1 ln x)x ln x .x 2x 2令 h(x) xln x , h ( x)1 1,xQ x ≥ 1 ,h ( x) ≥ 0, [ h( x) 在 1,) 上 增,h( x) min h(1) 1 0 ,从而 h( x) ≥ h(1)0 ,所以 g ( x) 0 ,故 g( x) 在 1,) 上也 增,所以 g( x)min g(1) 2 .所以 k ≤ 2 .22.解:( 2)函数的定义域为( 1,).。
