人教版初三数学竞赛及答案
初中数学竞赛一、 填空题(1~5题每小题6分，6~10题每小题8分，共70分）1. 在2002当中嵌入一个数码组成五位数2002，若这五位数能被7整除，则嵌入的数码“”是________________。
【解析】 2或9 设“”中数字为a ，那么五位数2002的数值为210000100220002100a a ⨯+⨯+=+⨯，因为2002除以7的余数为3，所以，要使得五位数2002能被7整除，那么100a ⨯除以7的余数必须为4，而0，100，200，300，，900中，被7除余数为4的只有200和900，即2a =或者9，所以，嵌入的数码“”是2或92. 若实数a 满足32a a a <<，则不等式1x a ax +>-解为_____________。
【解析】 11ax a-<+ 已知32a a a <<，即232(1)0(1)0a a a a a a a a ⎧-=-<⎪⎨-=-<⎪⎩ （1） 如果0a >，上不等式组等价于201010a a a ⎧>⎪-<⎨⎪-<⎩即，0111a a a >⎧⎪>⎨⎪-<<⎩，这是一个矛盾不等式组，所以这种情况应舍去。
（2） 如果0a <，上不等式组等价于201010a a a ⎧<⎪->⎨⎪->⎩，即0111a a a a <⎧⎪<⎨⎪<->⎩或者，解得1a <-，此时，不等式1x a ax +>-等价于(1)1a x a +>-，因为1a <-，即10a +<，那么(1)1a x a +>-等价于11a x a -<+，所以，原不等式的解为11ax a-<+。
3. 如图，一张矩形纸片沿BC 折叠，顶点A 落在点'A 处，第二次过'A 再折叠，使折痕DE BC 若2AB =.3AC =,则梯形BDEC 的面积为______________。
【解析】 9EC A'DB A由纸片的折叠方式知，'A BC ABC ∆≅∆，所以，过A 点到BC 的高等于过'A 点到BC 的高，即ABC ∆中BC 上的高与ADE ∆中DE 上的高的比例为1:2=，又因为DE BC 所以ABCADE ∆∆，由相似三角形的性质得ABC ∆的面积：ADE ∆的面积21124⎛⎫== ⎪⎝⎭，从而，梯形BDEC 的面积为ABC ∆的面积的3倍，已知2AB =，3AC =，所以，ABC ∆的面积为12332⨯⨯=从而梯形BDEC 的面积为339⨯=。
4. 已知关于正整数n 的二次式2(y n an n =+为实常数），若当且仅当5n =，y 最小值，则实数a 的取值范围是_________________.【解析】 119a -<<-5. 如图，在平面直角坐标系中有一个正方形ABCD ,它的4个顶点10,0A （）、(0,10)B 、(10,0)C -、(010)D -，，则该正方形内及边界上共有_____________【解析】 221已知(10,0)A 、(0,10)B ，所以，直线AB 的方程为10y x =-+在ABO ∆内，当一个点的横坐标为1时，如果这个点在直线AB 上，那么这个点的纵坐标为1109-+=，所以，只要横坐标为1，纵坐标大于等于0小于等于9的点都在ABO ∆的内部或者AB 边或者AO 边上，共10个点，显然这些点均符合题意。
同理，当一个点的横坐标为2 时，如果这个点在直线AB 上，那么这个点的纵坐标为2108-+=，所以，只要横坐标为2，纵坐标大于等于0小于等于8的点都在ABO ∆的内部或者AB 边或者AO 边上，共9个点，显然这些点均符合题意。
当一个点的横坐标为9时，如果这个点在直线AB 上，那么这个点的纵坐标为9101-+=，所以，只要横坐标为9，纵坐标大于等于0小于等于1的点都在ABO ∆的内部或者AB 边或者AO 边上，共2个点，显然这些点均符合题意。
当一个点的横坐标为10时，只有（10，0）点符合题意，所以，在ABO ∆内共有1098111555++++=⨯=个点符合题意，由正方形的对称性知，BOC ∆、DOC ∆、AOD ∆中各有55个点符合题意，显然，（0，0）点也符合题意。
综上，符合题意的点共有5541221⨯+=个。
6. 如图，P 为ABC ∆形内一点，点D 、E 、F 分别在BC 、CA 、AB 上，过A 、B 、C 分别作PD 、PE 、PF 的平行线，交对边或对边的延长线于点X 、Y 、Z 若14PD PA =，13PE BY =，则PFCZ=________________。
ZY ECF PDBXA【解析】5127. 若ABC ∆，且中线AD 、BE 的长分别为1和2，则中线CF 的长为____________________。
【解析】8. 计算：222222221299110050002200500010050009999005000k k k +++++=-+-+-+-+___________ 【解析】 999. 若正数x 、y 、z 满足()4xyz x y z ++=，则()()x y y z ++的最小可能值为______________。
【解析】 4因为x 、y 、0z >，则()()()x y y z xy yy xz yz x y z y yz ++=+++=+++， 令()x y z y a ++=，yz b =，则()()()x yy z xy yy xzyz x y z yyz a b ++=+++=+++=+，又因为22a b+≥===，所以a b +的最小值为4，即()()x y y z ++的最小值为4。
10. 若关于x13c =恰有两个不同的实数解，则实数a 的取值范围______。
【解析】 0a ≥或316a =-y =2y =，那么原方程等价于2110(1)23y y a +--=y =，所以，211023y y a +--=必有一个实数解，未完二、(16分)已知p 为质数，使二次方程222510x px p p -+--=的两根都是整数，求出p 的所以可能值。
【解析】 因为已知整系数二次方程有整数根，所以2244(51)4(51)p p p p ∆=---=+为完全平方，从而，51p +为完全平方，，令251p n +=，注意到2p ≥，故4n ≥，且n 为整数，于是5(1)(1)p n n =+-则1n +、1n -中至少有一个是5的倍数，即51n k =± (k 为正整数)，因此，25125101p k k +=±+，(52)p k k =±，由p 为质数，521k ±>，知1k =，3p =或7；当3p =时，已知方程变成2670x x --=，解得11x =-，27x =；当7p =时，已知方程变成214130x x -+=，解得11x =，213x =，所以3p =或7。
三、(16分)已知XYZ ∆是直角边长为l 的等腰直角三角形90Z ∠=（），它的3个顶点分别在等腰(90)Rt ABC C ∆∠=的三边上，求ABC ∆直角边长的最大可能值。
【解析】 (1)如图BX顶点Z 在斜边AB 上，取XY 的中点M ，选CM 、ZM 、CZ 并作边AB 上的高CN ，则12CZ CM MZ XY ≤+=CZ ≤，所以CN ≤，2CA =≤(2)如图顶点Z 在直角边(CA 或)CB 上，由对称性，不妨设Z 在CA 上，设CX x =，CZ y =，并过Y 作YH CA ⊥于H ，易证ZYH XZC ∆≅∆，得HZ CX x ==,HY CZ y ==，又显然AHY ∆为等腰三角形，则AH y =，设AC b =，则2y x b +=，则2x b y =-，在CXZ ∆中，由勾股定理有222(2)1y b y +-=，即225410y by b -+-=，因为y 为实数，则2221620(1)2040b b b ∆=--=-≥，b ≤，当b =时，5y =，5x =综合(1)、(2)知，b 四、(18分)平面上有7个点，他们之间可以连一些线段，使7点中的任意3点必存在2点有线段相连，问至少要连多少条线段？证明你的结论。
【解析】（1） 若7个点中，有一点孤立（即它不与其他点连线），则剩下6点每2点必须连线，此时至少要连15条。
（2） 若7个点中，有一点只与另一点连线，则剩下5点每2点必须连线，此时至少要连11条。
（3） 若每点至少引出3条线段，则至少要连732⨯条线段，由于线段数为整数，故此时至少要连11条。
（4） 若每点至少引出2条线段，且确有一点（记为A ）只引出2条线段AB 、AC ，则不与A 相连的4点每2点必须相连，要连4362⨯=条，由B 引出的线段至少有2条，即除BA 外还至少xB X有一条，因此，此时至少要连6219++=条，图中所给出的是连++=条线的情况。
6219综合（1）~（4）,至少要连9条线段，才能满足要求。
数学初三奥赛试题及答案
数学初三奥赛试题及答案一、选择题（每题3分，共30分）1. 下列哪个数是无理数？A. 0.1010010001…（每两个1之间0的个数逐次增加）B. √2C. 0.33333…D. 1/7答案：B2. 如果一个等腰三角形的底边长为6，腰长为5，那么它的面积是多少？A. 12B. 15C. 18D. 20答案：B3. 一个数列的前四项为1, 4, 9, 16，这个数列的通项公式是什么？A. \(n^2\)B. \(2n\)C. \(2^n\)D. \(n(n+1)\)答案：A4. 一个圆的直径为10，那么它的面积是多少？A. 25πB. 50πC. 100πD. 200π答案：B5. 计算下列表达式的值：\((2x + 3)(2x - 3)\)A. \(4x^2 - 9\)B. \(4x^2 + 9\)C. \(9 - 4x^2\)D. \(-4x^2 + 9\)答案：A6. 一个数的相反数是-5，那么这个数是：A. 5B. -5C. 0D. 10答案：A7. 一个数的绝对值是5，那么这个数可以是：A. 5B. -5C. 5或-5D. 以上都不是答案：C8. 一个长方体的长、宽、高分别为2, 3, 4，那么它的体积是多少？A. 24B. 26C. 28D. 30答案：A9. 下列哪个选项是方程\(x^2 - 5x + 6 = 0\)的解？A. 2B. 3C. 1和2D. 2和3答案：C10. 一个等差数列的前三项为2, 5, 8，那么它的第五项是多少？A. 11B. 12C. 15D. 18答案：A二、填空题（每题4分，共20分）1. 一个数的平方等于它的相反数，这个数是______。
答案：0或12. 如果一个数的立方等于它本身，那么这个数可以是______。
答案：-1, 0, 13. 一个等比数列的前三项为2, 6, 18，那么它的公比是______。
答案：34. 一个圆的周长为44π，那么它的半径是______。
人教版 初三数学 竞赛专题：平行线分线段成比例(包含答案)
人教版 初三数学 竞赛专题：平行线分线段成比例（含答案）【例1】如图，在梯形ABCD 中，AD ∥BC ，AD ＝a ，BC ＝b ，E ，F 分别是AD ，BC 的中点，且AF 交BE 于P ，CE 交DF 于Q ，则PQ 的长为＿＿＿＿．【例2】如图，在△ABC 中，D ，E 是BC 的三等分点，M 是AC 的中点，BM 交AD ，AE 于G ，H ，则BG ︰GH ：HM 等于（ ）A ．3︰2︰1B ．4︰2︰1C ．5︰4︰3D ．5︰3︰2【例3】如图，□ABCD 中，P 为对角线BD 上一点，过点P 作一直线分别交BA ，BC 的延长线于Q ，R ，交CD ，AD 于S ，T ． 求证：PQ •PT ＝P R •PS ．【例4】梯形ABCD 中，AD //BC ，AB ＝DC ．（1）如图1，如果P ，E ，F 分别是BC ，AC ，BD 的中点，求证：AB ＝PE ＋PF ；（2）如图2，如果P 是BC 上的任意一点（中点除外），PE ∥AB ，PF ∥DC ，那么AB ＝PE ＋PF 这个结论还成立吗？如果成立，请证明；如果不成立，说明理由．QARBCD SPABCDEGH MQA BCDEFP【例5】如图，已知AB ∥CD ，AD ∥CE ，F ，G 分别是AC 和FD 的中点，过G 的直线依次交AB ，AD ，CD ，CE 于点M ，N ，P ，Q ．求证：MN ＋PQ ＝2PN ．【例6】已知：△ABC 是任意三角形．（1）如图1，点M ，P ，N 分别是边AB ，BC ，CA 的中点，求证：∠MPN ＝∠A ； （2）如图2，点M ，N 分别在边AB ，AC 上，且AM AB ＝13，AN AC ＝13，点P 1，P 2是 边BC 的三等分点，你认为∠MP 1N ＋∠MP 2N ＝∠A 是否正确？请说明你的理由；ABCM NP图1ABC MN1P 2P 图2AMNBC1P 2P 2009P g g g 图3QA BCDEFGM NPA B CD E FP图2A BCD E F P图1能力训练A 级1．设K ＝a b c c +-＝a b c b -+＝a b ca-++，则K ＝＿＿＿＿． 2．如图，AD ∥EF ∥BC ，AD ＝15，BC ＝21，2AE ＝EB ，则EF ＝＿＿＿＿．3．如图，在△ABC 中，AM 与BN 相交于D ，BM ＝3MC ，AD ＝DM ，则BD ︰DN ＝＿＿＿＿． 4．如图，ABCD 是正方形，E ，F 是AB ，BC 的中点，连结EC 交DB ，交DF 于G ，H ，则EG ︰GH ︰HC ＝＿＿＿＿．5．如图，在正△ABC 的边BC ，CA 上分别有点E ，F ，且满足BE ＝CF ＝a ，EC ＝F A ＝b （a ＞b ），当BF 平分AE 时，则ab的值为（ ） ABCD6．如图，△ABC 中，AD 是BC 边上的中线，F 是AD 上的一点，且AF ︰FD ＝1︰5，连结CF 并延长交AB 于E ，则AE ︰EB 等于（ ）A ．1︰10B ．1︰9C ．1︰8D ．1︰77．如图，PQ ∥AB ，PQ ＝6，BP ＝4，AB ＝8，则PC 等于（ ） A ．4B ．8C ．12D ．168．如图，EF ∥BC ，FD ∥AB ，BD ＝35BC ，则BE ︰EA 等于（ ）A ．3︰5B ．2︰5C ．2︰3D ．3︰29．（1）阅读下列材料，补全证明过程．已知，如图，矩形ABCD 中，AC ，BD 相交于点O ，OE ⊥BC 于E ，连结DE 交OC 于点F ，作FGABCDE F第6题QABCP第7题AB CDEF 第8题A BCD E F 第2题ABCD M N第3题ABCDEFGH第4题A BCEFG第5题⊥BC 于G ．求证：点G 是线段BC 的一个三等分点．（2）请你依照上面的画法，在原图上画出BC 的一个四等分点．（要求：保留画图痕迹，不写画法及证明过程）10．如图，已知在□ABCD 中，E 为AB 边的中点，AF ＝12FD ，FE 与AC 相交于G ． 求证：AG ＝15AC ．11．如图，梯形ABCD 中，AD ∥BC ，EF 经过梯形对角线的交点O ，且EF ∥AD ． （1）求证：OE ＝OF ； （2）求OE AD ＋OEBC的值； （3）求证：1AD ＋1BC ＝2EF．12．如图，四边形ABCD 是梯形，点E 是上底边AD 上的一点，CE 的延长线与BC 的延长线交于点F ，过点E 作BA 的平行线交CD 的延长线于点M ，MB 与AD 交于点N ．求证：∠AFN ＝∠DME ．ABCDE FGO第9题ABCDEG第10题ABCD EFO第11题B 级1．如图，工地上竖立着两根电线杆AB ，CD ，它们相距15cm ，分别自两杆上高出地面4m ，6m 的A ，C 处，向两侧地面上的E ，D 和B ，F 点处，用钢丝绳拉紧，以固定电线杆，那么钢丝绳AD 与BC 的交点P 离地面的高度为＿＿＿＿m ．2．如图，□ABCD 的对角线交于O 点，过O 任作一直线与CD ，BC 的延长线分别交于F ，E 点．设BC ＝a ，CD ＝b ，CF ＝c ，则CE ＝＿＿＿＿．3．如图，D ，F 分别是△ABC 边AB ，AC 上的点，且AD ︰DB ＝CF ︰F A ＝2︰3，连结DF 交BC 边的延长线于点E ，那么EF ︰FD ＝＿＿＿＿．4．如图，设AF ＝10，FB ＝12，BD ＝14，DC ＝6，CE ＝9，EA ＝7，且KL ∥DF ，LM ∥FE ，MN ∥ED ，则EF ︰FD ＝＿＿＿＿．5．如图，AB ∥EF ∥CD ，已知AB ＝20，CD ＝80，那么EF 的值是（ ） A ．10B ．12C ．16D ．186．如图，CE ，CF 分别平分∠ACB ，∠ACD ，AE ∥CF ，AF ∥CE ，直线EF 分别交AB ，AC 于A BCDE F第5题ABCD EF L KM N第4题AB DEFM第6题ABCDEF O第2题ABCD EF 第3题QABCD EF 第1题ABCDEF M NP点M ，N ．若BC ＝a ，AC ＝b ，AB ＝c ，且c ＞a ＞b ，则EM 的长为（ ）A ．2c a- B ．2a b- C ．2c b- D ．2a b c+- 7．如图，在□ABCD 的边AD 延长线上取一点F ，BF 分别交AC 与CD 于E ，G ．若EF ＝32，GF ＝24，则BE 等于（ ）A ．4B ．8C ．10D ．12E ．168．如图，在梯形ABCD 中，AB ∥CD ，AB ＝3CD ，E 是对角线AC 的中点，直线BE 交AD 于点F ，则AF ︰FD 的值是（ ）A ．2B ．53C ．32D ．19．如图，P 是梯形ABCD 的中位线MN 所在直线上的任意一点，直线AP ，BP 分别交直线CD 于E ，F ．求证：MN NP ＝1()2AE BFEP FP+．10．如图，在四边形ABCD 中，AC 与BD 相交于O ，直线l 平行于BD 且与AB ，DC ，BC ，AD 及AC 的延长线分别交于点M ，N ，R ，S 和P ．求证：PM ·PN ＝P R ·PS ．ABCDEF第11题SA R BC DMN OPl第10题ABCD EFG第7题ABCDE F第8题ABCD E F MNP第9题11．如图，AB⊥BC，CD⊥BC，B，D是垂足，AD和BC交于E，EF⊥BD于F．我们可以证明：11AB CD+＝1EF成立（不要求证出）．以下请回答：若将图中垂直改为AB∥CD∥EF，那么，（1）11AB CD+＝1EF还成立吗？如果成立，请给出证明；如果不成立，请说明理由．（2）请找出S△ABD，S△BED和S△BDC的关系式，并给出证明．12．在Rt△ABC中，∠BAC＝90°，AD平分∠BAC，过D点的直线PQ交边AC于点P，交边AB的延长线于点Q．（1）如图1，当PQ⊥AC时，求证：11AQ AP+＝AD；（2）如图2，当PQ不与AD垂直时，（1）的结论还成立吗？证明你的结论；（3）如图3，若∠BAC＝60°，其它条件不变，且11AQ AP+＝nAD，则n＝＿＿＿＿（直接写出结果）参考答案AQB CDP图1AQB CDP图2AQB CDP图3例1aba b+ 提示：由AP DQ a PF QF b ==,推得PQ ∥AD 。
(完整word版)九年级数学竞赛及答案
同顺序的取法的种数有（）B . 6 种C . 10 种D . 12 种、填空题(本大题共 6个小题，每小题 5分，共30 分)2014年吉安县桐坪中学数学竞赛九年级试题（刘书文）（本卷满分120分，考试时间120分钟） 、选择题（本大题共 6个小题，每小题 5分，共30分） 1.从长度是2cm ，2cm ， 4cm , 4cm 的四条线段中任意选三条线段，这 三条线段能够组成等腰三角形的概率是（ ） B. C. D. 1 （第2题图）2.如图，M 是厶ABC 的边BC 的中点，AN 平分/ BAC , AN 丄BN 于 N ,且 AB=10, BC=15, MN=3，则△ ABC 的周长为（ ） A . 38 B . 39 C . 40 D. 41 23.已知 xy =1，且有 5x 22011x 9 =0 , 9y 22011y • 5 =0 ,则-的值等于( y 5 9 2011A .—B .C .D . 9 5 54.已知直角三角形的一直角边长是 4,以这个直角三角形的三边 为直径作三个半圆（如图所示），已知两个月牙形（带斜线的阴 影图形）的面积之和是10，那么以下四个整数中，最接近图 中两个弓形（带点的阴影图形）面积之和的是（ ）)A . 6B. 7C . 8D . 95. 如图，Rt A ABC 中，AB 丄AC , AB=3, AC=4 , P 是 BC 边上一点， 作 PE 丄 AB 于 E , PD 丄 AC 于 D ，设 BP = x ,贝U PD+PE =（）x x 7 12x 12x 2 A. -3 B. 4C. -D.5525256. 计算机中的堆栈是一些连续的存储单元，在每个堆栈中数据的存入、取 出按照“先进后出”的原则，如图，堆栈（1）中的2个连续存储单元已依次存入数据b , a ，取出数据的顺序是 a , b ;堆栈（2）的3个 连续存储单元已依次存入数据 e , d , c ，取出数据的顺序是 c , d ,ne ，现在要从这两个堆栈中取出5个数据（每次取出 1个数据），则不7•若x2— 2x —1 —4=0，则满足该方程的所有根之和为&如图，等边三角形ABC中，D，E分别为AB, BC边上的两个动点，且总使AD=BE ,FGAE与CD交于点F , AG丄CD于点G ,贝UAF4 2. 22a -3xa +2 2 mt[9.已知a2 -a -^0，且一- ，贝V x=_________ •a3+2xa2—a 310•元旦期间，甲、乙两人到特价商店购买商品，已知两人购买商品的件数相同，且每件商品的单价只有8元和9元两种.若两人购买商品一共花费了172元，则其中单价为9元的商品有 ______________ 件.11 •如图，已知电线杆AB直立于地面上，它的影子恰好照在土坡的坡面CD和地面BC上，如果CD 与地面成45°，/ A=60o, CD=4m, BC= (4. 6 - 2、2) m，则电线杆AB 的长为 ________________ m.三、解答题(本大题共4个小题，共60分)13. (本题满分10分) 已知平行四边形ABCD的两边AB, AD的长是关于x的pm 1方程：X2—mx+ —=0的两个实数根，2 4(1) 当m为何值的，四边形ABCD是菱形？求出这时菱形的边长；(2) 当AB=2时，平行四边形ABCD的周长是多少?14 (本题满分10分)•如图所示，不透明圆锥 DEC 放在水平面上，在A 处灯光照射下形成影子，设BP 过圆锥底面的圆心，已知圆锥的高为(1) 求/ B 的度数；15.(本题满分20分)如图，将 OA = 6, AB = 4的矩形OABC 放置在平面直角坐标系中， 动点M , N以每秒1个单位的速度分别从点 A , C 同时出发，其中点M 沿AO 向终点O 运动，点N 沿CB 向终点B 运动，当两个动点运动了 t 秒时，过点 N 作NP 丄BC ,交OB 于点P ,连接MP .点 B 的坐标为 _____________ ;用含 t 的式子表示点 P 的坐标为 _________________ ; 记厶OMP 的面积为S,求S 与t 的函数关系式(0 < t < 6);并求t 为何值时，S 有 最大值？ 试探究：当S 有最大值时，在y 轴上是否存在点 T ,使直线MT 把厶ONC 分割成 三角形和四边形两部分，且三角形的面积是△ ONC 面积的1 ?若存在，求出点 T2 ..3 m ，底面半径为 2 m , BE=4 m. (1) (2) (3)的坐标；若不存在，请说明理由16.(本题满分20分)(1)请在图①中作出两条直线，使它们将圆面四等分；(2)如图21②，M是正方形ABCD内一定点，请在图21②中作出两条直线(要求其中一M),使它们将正方形ABCD的面积四等分，并说明理由.条直线必须过点(3)如图③，在四边形ABCD中，AB// CD , AB+CD=BC,点P是AD的中点，如果AB=a, CD=b,且b>a,那么在边BC上是否存在一点Q,使PQ所在直线将四边形ABCD的面积分成相等的两部分？若存在，求出BQ的长；若不存在，说明理由.2013年九年级试卷 参考答案5 分，共 30 分）1 —6 C D B A DAC— 16 1 7. 2 - 6 ； 8. A :； B : ； 9. 4 ； 10. 12； 11. 62 ；5211（亍-1） （-；,-1）. 2 2 三、解答题：（每题20分，共60分） 13.解：（1）v 四边形 ABCD 为菱形, ••• AB=AD.m 1又T △ =m 2— 4 （ ~ — 4 ） =m 2— 2m+1=（m — 1）2. .••当（m — 1）2=0，即卩m=1时，四边形 ABCD 是菱形.1 1 1 _2 _________________ ____________________=0 得 X — X+ =0 ,• X 1=X 2=.44 21•菱形ABCD 的边长为-.m 1m 1（1） 把 x=2 代入 x 2 — mx+ —=0 得 4— 2m+— =0,2 4 2455 m 1 5解得 m=.把 m= 代入 x 2 — mx+ ~ —： =0 得 x 2— ? x+1=0,、选择题（每小题 、填空题（每小题 5分，共30分）：12.m 把 m=1 代入 x 2— mx+ —2•••四边形ABCD 为平行四边形V•平行四边形ABCD 的周长为2 点拨：把平行四边形的边长与一元二次方程的根相联系，那么平行四边形的性质和一元二 次方程根的性质都要掌握•首先平行四边形变为菱形，各边相等，那么一元二次方程就有两 个相等的实数根•对于（2）就是已知一元二次方程的一根再求另一根 22.解：（1）圆锥的高DO=2 3 m.在 Rt △ DOB 中，OB=BE+EO=4+2=6（m ）. 二 BD 2=BO 2+DO 2=62+（2 .3）2=48. ••• BD=4 3 m,则 BD=2DO.•••/ B=30° .(2)过A 作AF 丄BP 于F.•••/ ACP= / B+Z BAC=2 / B , •••/ B=Z BAC=30° .• AC=BC=BE+EC=8(m).在 Rt △ ACF 中，Z CAF=90°—Z ACP=90° - 2Z B=30• CF= AC=4(m).• AF=.AC 2-CF 2 = .82-42 =4 3 (m). 故光源A 距水平面的高度为 4 3 m.点拨：投影问题在本题中转化为在直角三角形中求角度和边长的问题，通过作高，构造直 角三角形，应用直角三角形中边、角之间的关系去求值.214. ............................................................................................................................................... 解：(1) (6, 4); ( t,_t ).(其中写对 B 点得 1 分) .......................................31 2(2) - SA OMP = X OM X — t ,2 31 211S = X( 6 -1 )X — t = t 2+2t = (t ~3)2 3 (0 < t <6 ).解得 1 1X 1=2,X 2=22 3 3 3•••当t =3时，S有最大值. ............................ 8分(3)存在.由(2)得：当S有最大值时，点M、N的坐标分别为：M ( 3, 0), N ( 3, 4), 则直线ON的函数关系式为:设点T的坐标为（0, b）,则直线MT的函数关系式为:3b4 b 4b 4 b4 !x解方程组 y 得x 龙3jy = _b x b yI 3 I. •直线ON 与MT 的交点R 的坐标为(3b 4b ). 4 +b'4 +b• .1 . 1 -S A OCN = X 4 X 3 = 6,.. S A ORT = OCN = 2 . • 2 3一、 当点T 在点O 、C 之间时，分割出的三角形是△ OR 1T 1, 二、 如图，作 R 1D 1丄y 轴，D 1为垂足， 则 S A O R 1T1= 1?RD 1?OT = 1 ? 3b ?b = 2. 2 2 4+b• 3b 2 -4b -16=0, b = 2 2 13 .• b 1 = 2 2 13 , b ? = 2-2 13(不合题意，舍去) 3 3 3 此时点T 1的坐标为(0, 2 213) ........ .................... 3 ② 当点T 在OC 的延长线上时，分割出的三角形是△ R 2NE , 3b —12 •••点E 的纵坐标为4，•由①得点E 的横坐标为 --- b 作R 2D 2丄CN 交CN 于点D 2,贝U1 13b -12 4b 96S^ R 2NE = ?EN?D 2= ?(3 ) ? (4 ): 2 2 b 4 +b b(4 +b) ••• b 2 4b -48=0, b=彳 16 448 = 2 13 _2. 10分15分2 --b r 2.13 -2 , b 2 = -2*3-2 (不合题意，舍去). •此时点T 2的坐标为(0, 2,13-2 ). 2*2用),T 2 (0, 2/13-2 )符合条件.…20分 3综上所述，在y 轴上存在点「(0 15 (1)如答图3①.答图3(3) 如答图3②理由如下： •••点O 是正方形 ABCD 的对角线的交点，•••点O 是正方形 ABCD 的对称中心，• AP=CQ ,EB=DF ，在△ AOP 和厶 EOB 中，•••/ AOP=90° -Z AOE ,/ BOE=90° -Z AOE ,•••/AOP= Z BOE ,v OA=OB ,Z OAP=Z EBO=45°, •••△ AOP ◎△ BOE ,• AP=BE=DF=CQ , 设O到正方形ABCD 一边的距离为d ,1 1 12 (AP+AE ) d=2 ( BE+BQ ) d=㊁(CQ+CF )边形BEOQ= S 四边形CQOF =S 四边形DPOF ,•直线EF 、OM 将正方形ABCD 面积四等分;答图4（3）存在，当BQ = CD=b 时，PQ 将四边形ABCD 的面积二等分.理由如下：如答图 4,延长BA 至点E ,使AE=b ，延长CD 至点F ,使DF =a ，连接EF. • BE // CF , BE=CF , •四边形BCFE 为平行四边形， ■/ BC=BE=a+b ,•平行四边形 BCFE 为菱形•连接BF 交AD 于点M , 则厶 MAB ◎△ MDF , • AM = DM.即点P 、M 重合••••点P 是菱形EBCF 对角线的交点， 在 BC 上截取 BQ=CD = b ，贝U CQ=AB=a.设点P 到菱形EBCF 一边的距离为d.连接CP ,即 S 四边形ABQP =S 四边形PQCD .•当BQ=b 时，直线PQ 将四边形ABCD 的面积分成相等的两部分d=2(PD + DF ) d ,• S 四边形 AEOP =S 四--& ABP +S ^QBP = 2(AB+BQ)d= (CQ+CD)d=S ^CQP +S ^oDP ,。
人教版 九年级数学上册 竞赛专题：圆与圆的位置关系(含答案)
人教版 九年级数学上册 竞赛专题：圆与圆的位置关系（含答案）【例1】 如图，大圆⊙O 的直径a AB =cm ，分别以OA ，OB 为直径作⊙O 1和⊙O 2，并在⊙O 与⊙O 1和⊙O 2的空隙间作两个等圆⊙O 3和⊙O 4，这些圆互相内切或外切，则四边形3241O O O O 的面积为________cm 2.【例2】 如图，圆心为A ，B ，C 的三个圆彼此相切，且均与直线l 相切.若⊙A ，⊙B ， ⊙C 的半径分别为a ，b ，c （b a c <<<0），则a ，b ，c 一定满足的关系式为（ ） A.c a b +=2 B.c a b +=2C.b ac 111+= D.ba c 111+=【例3】 如图，已知两圆内切于点P ，大圆的弦AB 切小圆于点C ，PC 的延长线交大圆于点D .求证： （1）∠APD =∠BPD ；（2）CB AC PC PB PA ∙+=∙2.B【例4】 如图⊙O 1和⊙O 2相交于点A 及B 处，⊙O 1的圆心落在⊙O 2的圆周上，⊙O 1的弦AC 与⊙O 2交于点D .求证：O 1D ⊥BC .【例5】 如图，在直角梯形ABCD 中，AD ∥BC ，AB ⊥BC ，AD =1,AB =2，DC =22，点P 在边BC 上运动（与B ，C 不重合）.设PC =x ，四边形ABPD 的面积为y . （1）求y 关于x 的函数关系式，并写出自变量x 的取值范围； （2）若以D 为圆心，21为半径作⊙D ，以P 为圆心，以PC 的长为半径作⊙P ，当x 为何值时，⊙D 与⊙P 相切？并求出这两圆相切时四边形ABPD 的面积.【例6】 如图，ABCD 是边长为a 的正方形，以D 为圆心，DA 为半径的圆弧与以BC 为直径的半圆交于另一点P ，延长AP 交BC 于点N ，求NCBN的值. PBCDADCPBA【能力与训练】1.如图，⊙A ，⊙B 的圆心A ，B 在直线l 上，两圆的半径都为1cm .开始时圆心距AB ＝4cm ，现⊙A ，⊙B 同时沿直线l 以每秒2cm 的速度相向移动，则当两圆相切时，⊙A 运动的时间为_______秒.2.如图，O 2是⊙O 1上任意一点，⊙O 1和⊙O 2相交于A ，B 两点，E 为优弧AB 上的一点，EO 2及延长线交⊙O 2于C ，D ，交AB 于F ，且CF ＝1，EC ＝2，那么⊙O 2的半径为_______.（第1题图）（第2题图）（第3题图）3.如图，半圆O的直径AB ＝4,与半圆O 内切的动圆O 1与AB 切于点M .设⊙O 1的半径为y ，AM 的长为x ，则y 与x 的函数关系是_________________.（要求写出自变量x 的取值范围）4.已知直径分别为151+和315-的两个圆，它们的圆心距为115-，这两圆的公切线的条数是__________.5.如图，⊙O 1和⊙O 2相交于点A ，B ，且⊙O 2的圆心O 2在圆⊙O 1的圆上，P 是⊙O 2上一点.已知∠A O 1B ＝60°，那么∠APB 的度数是（ ） A.60° B.65° C.70° D.75°6.如图，两圆相交于A 、B 两点，过点B 的直线与两圆分别交于C ，D 两点.若⊙O 1半径为5，⊙O 2的半径为2，则AC ：AD 为（ ）A.52:3B.3:52C.1:52D.2:5 （第5题图） （第6题图） （第7题图）N PB A CD E7.如图，⊙O 1和⊙O 2外切于点T ，它们的半径之比为3:2，AB 是它们的外公切线，A ，B 是切点，AB ＝64，那么⊙O 1和⊙O 2的圆心距是（ ）A.65B.10C.610D.1339208.已知两圆的半径分别为R 和r （r R >），圆心距为d .若关于x 的方程0)(222=-+-d R rx x 有两相等的实数根，那么这两圆的位置关系是（ ）A.外切B.内切C.外离D.外切或内切9.如图，⊙O 1与⊙O 2相交于A ，B 两点，点O 1在⊙O 2上，点C 为⊙O 1中优弧AB ⌒上任意一点，直线CB 交⊙O 2于D ，连接O 1D .（1）证明：DO 1⊥AC ；（2）若点C 在劣弧AB ⌒上，（1）中的结论是否仍成立？请在图中画出图形，并证明你的结论.图1 图210.如图，已知⊙O 1与⊙O 2外切于点P ，AB 过点P 且分别交⊙O 1和⊙O 2于点A ，B ，BH 切⊙O 2于点B ，交⊙O 1于点C ，H .（1）求证：△BCP ∽△HAP ；（2）若AP :PB ＝3：2，且C 为HB 的中点，求HA :BC .11.如图，已知⊙B ，⊙C 的半径不等，且外切于点A ，不过点A 的一条公切线切⊙B 于点D ，切⊙C 于点E ，直线AF ⊥DE ，且与BC 的垂直平分线交于点F .求证：BC ＝2AF .12.如图，AB 为半圆的直径，C 是半圆弧上一点.正方形DEFG 的一边DG 在直径AB 上，另一边DE 过△ABC 得内切圆圆心O ，且点E 在半圆弧上.（1）若正方形的顶点F 也在半圆弧上，求半圆的半径与正方形边长的比；（2）若正方形DEFG 的面积为100，且△ABC 的内切圆半径4 r ，求半圆的直径AB .1.相交两圆的半径分别为5cm 和4cm ，公共弦长为6cm ，这两圆的圆心距为_______.2.如图，⊙O 过M 点，⊙M 交⊙O 于A ，延长⊙O 的直径AB 交⊙M 于C .若AB ＝8，BC ＝1，则AM ＝_______.D AP（第2题图） （第3题图） （第4题图）3.已知圆环内直径为a cm ，外直径为b cm ，将50个这样的圆环一个接着一个环套环地连成一条锁链，那么这条锁链拉直后的长度为___________cm .4.如图，已知PQ ＝10，以PQ 为直径的圆与一个以20为半径的圆相切于点P .正方形ABCD 的顶点A ，B 在大圆上，小圆在正方形的外部且与CD 切于点Q .若AB ＝n m +，其中m ，n 为整数，则=+n m ___________.5.如图，正方形ABCD 的对角线AC ，BD 交于点M ，且分正方形为4个三角形，⊙O 1，⊙O 2，⊙O 3，⊙O 4，分别为△AMB ，△BMC ，△CMD ，△DMA 的内切圆.已知AB ＝1.则⊙O 1，⊙O 2，⊙O 3，⊙O 4所夹的中心（阴影）部分的面积为（ ）A.(4)(316π--B. (34π-C.(4)(34π-- D. 416π-（第5题图） （第6题图） （第7题图）6.如图，⊙O 1与⊙O 2内切于点E ，⊙O 1的弦AB 过⊙O 2的圆心O 2，交⊙O 2于点C ，D .若AC ：CD :BD ＝2:4:3，则⊙O 2与⊙O 1的半径之比为（ ）A.2:3B.2:5C.1:3D.1:47.如图，⊙O 1与⊙O 2外切于点A ，两圆的一条外公切线与⊙O 1相切于点B ，若AB 与两圆的另一条外公切线平行，则⊙O 1与⊙O 2的半径之比为（ ）A.2:5B.1:2C.1:3D.2:38.如图，已知⊙O 1与⊙O 2相交于A ，B 两点，过点A 作⊙O 1的切线，交⊙O 2于点C ，过点B 作两圆的割线分别交⊙O 1，⊙O 2于点D ，E ，DE 与AC 相交于点P . （1）求证：PA PE PC PD ∙=∙（2）当AD 与⊙O 2相切且P A ＝6，PC ＝2，PD ＝12时，求AD 的长.DA9.如图，已知⊙O 1和⊙O 2外切于A ，BC 是⊙O 1和⊙O 2的公切线，切点为B ，C .连接BA 并延长交⊙O 1于D ，过D 点作CB 的平行线交⊙O 2于E ，F . （1）求证：CD 是⊙O 1的直径；（2）试判断线段BC ，BE ，BF 的大小关系，并证明你的结论.10.如图，两个同心圆的圆心是O ，大圆的半径为13，小圆的半径为5，AD 是大圆的直径，大圆的弦AB ，BE 分别与小圆相切于点C ，F ，AD ，BE 相交于点G ，连接BD . （1）求BD 的长；（2）求2ABE D ∠+∠的度数；（3）求BGAG的值.11.如图，点H 为△ABC 的垂心，以AB 为直径的⊙O 1与△BCH 的外接圆⊙O 2相交于点D ，延长AD 交CH 于点P .求证：P 为CH 的中点.12.如图，已知AB 为半圆O 的直径，点P 为直径AB 上的任意一点，以点A 为圆心，AP 为半径作⊙A ，⊙A 与半圆O 相交于点C ，以点B 为圆心，BP 为半径作⊙B ，⊙B 与半圆O 相交于点D ，且线段CD 的中点为M .求证：MP 分别与⊙A ，⊙B 相切.参考答案例121a 6提示：连接14QP CP ==必过点O ，则34O O ⊥AB ，设⊙3O ，⊙4O 的半径为xcm ，在Rt △31O O O 中，有222a a a x =x 424⎛⎫⎛⎫⎛⎫+-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，解得x= a 6.例2 D 提示：连接AB ，1AA ，1BB ，作2AB ⊥1BB ，则22222ABAB BB =+，即()()2222a b =b a AB ++-，得22211=A B 4ab AB =，同理，211A 4ac C =，2114bc C B =，由111111=A B AC C B +，故.例3 提示：⑴过P 点作两圆的公切线. ⑵即证PA PB PC PD ∙=∙. 例4 12B OC B A C ∠=∠，1112BO D BAC BO C ∠=∠=∠，则1O D 为1BO C ∠的平分线，又11O B O C =，故1O D BC ⊥.例5 ⑴过D 作DQ ⊥BC 于Q ，则BQ=AD=1，AB=DQ=2，CQ=，故B()1y=13x 2=4x2+-⨯-（0<x<3）.⑵分两种情况讨论：①当⊙P 与⊙D 外切时，如图1，QC=2，PC=x ，QP= 2x -，PD=x+12，DQ=2，在Rt △DQP 中，由()22212x 2=x+2⎛⎫-+ ⎪⎝⎭得，31x=20，3149y=4=2020-.②当⊙P 与⊙D 内切时，如图2，PC=x ，QC=2，PQ=x-2，PD=x-12，DQ=2，在Rt △DPQ 中，由()2221x 22=x-2⎛⎫-+ ⎪⎝⎭得，31x=12，3117y=4=1212-. 例6 就图1给出解答：连接CP 并延长交AB 于点Q ，连接BP ，得∠BPC90°，又22QAQP CQ QB =∙=，得AQ=QB=12AB ，在Rt △CQP 中，2214BQ QP CQ QP BC CP CQ CP ∙===∙.过Q 作QM ∥BC 交AN 于M ，则MQ=12BN .由△MQP ∽△NCP ，得14MQ QP CN CP ==，故BN NC＝2142MQ MQ = .A 级1．12或32 2.2 3．y ＝214x -＋x (0＜x ＜4) 4. 3条 5．D 6．D 7．B 8．D 9．提示：(1)连结AB ，A 1O ，并延长交⊙1O 于E ，连结CE ． (2)结论仍然成立． 10．(1)略 (2)提示：设AP ＝3t ，由BC ·BH ＝BP ·BA ，BH ＝2BC ，BC t .易证△HAP ∽△BAH ，得HA ＝t ，故HABC=11．连结BD ，CE ，作BM ⊥CE 于M ，作HN ⊥CE 于N ，则BM ∥HN ．∵H 是BC 的中点，故N 是CM 的中点，∴CN ＝12CM ＝12（CE －EM ）＝12(CE －BD )，而AH ＝BH －AB ＝12BC －AB ＝12 (AB ＋AC ) –AB ＝12(AC －AB )，因此CN ＝AH ．由CE ⊥DE ，AF ⊥DE ，得CE //AF ，故∠NCH ＝∠HAF ，又∠CNH ＝∠AHF ＝90°，得△CNH ≌△AHF ，从而BC ＝2CH ＝2AF .12. (l :2 提示：由题意，设正方形边长为l ，则22212Rl l ⎛⎫=+ ⎪⎝⎭，得R :l :2．由2ED ＝AD ×DB ，DE ＝10，得AD ×DB ＝l 00．设AC 与内切圆交点S ，CB 与内切圆交点H ，设AD ＝r ，DB ＝100x．AB ＝x ＋100x， AS ＝AD ＝x ，BH ＝BD ＝100x．又△ABC 为直角三角形。
人教版九年级数学竞赛专题：平面几何的定值问题(含答案)
（第 3 题图）
（第 4 题图）
4.如图，正△ABO 的高等于⊙O 的半径，⊙O 在 AB 上滚动，切点为 T，⊙O 交 AO，BO 于 M，N，则 弧 MTN（ ）
A.在 0°到 30°变化
B.在 30°到 60°变化
C.保持 30°不变
D.保持 60°不变
5.如图，AB 是⊙O 的直径，且 AB=10，弦 MN 的长为 8.若 MN 的两端在圆上滑动时，始终与 AB 相交， 记点 A，B 到 MN 的距离分别为 h1，h2，则∣h1-h2∣等于（ ）
A
C
(P) O
D
B
①
D
A
C P O
B D ①
D
C
PB O
D ①
O
C A
P
①
B
O
C
P
A (B)
①
O
(D)C
A(B)
P ①
（2）已知⊙O 的半径为一定值 r，若点 P 是不在⊙O 上的一个定点，请你过点 P 任作一直线交⊙O 于 不重合的两点 E，F. PE·PF 的值是否为定值？为什么？由此你发现了什么结论？请你把这一结论用文 字叙述出来.
（第 7 题图）
（第 8 题图）
8.如图，设 H 是等腰三角形 ABC 两条高的交点，在底边 BC 保持不变的情况下让顶点 A 至底边 BC 的 距离变小，这时乘积 S△ABC·S△HBC 的值变小、变大，还是不变？证明你的结论.
9.如图，在平面直角坐标系 xOy 中，抛物线 y 1 x 2 4 x 10 与 x 轴的交点为点 A，与 y 轴的交点 18 9
人教版九年级数学竞赛专题：平面几何的定值问题（含答案）
【例 1】 如图，已知 P 为正方形 ABCD 的外接圆的劣弧A⌒D上任意一点.求证： PA PC 为定值. PB
初三数学竞赛试卷答案
一、选择题1. 下列各数中，绝对值最小的是（）A. -3B. -2C. 0D. 1答案：C解析：绝对值表示一个数与0的距离，因此绝对值最小的数是0。
2. 若a > b，则下列不等式中正确的是（）A. a + 2 > b + 2B. a - 2 > b - 2C. a + 2 < b + 2D. a - 2 < b - 2答案：A解析：根据不等式的性质，两边同时加上或减去同一个数，不等号的方向不变。
3. 已知一元二次方程x^2 - 5x + 6 = 0，则其判别式Δ等于（）A. 1B. 4C. 9D. 16答案：B解析：一元二次方程的判别式Δ = b^2 - 4ac，代入a = 1, b = -5, c = 6，得Δ = (-5)^2 - 4×1×6 = 25 - 24 = 1。
4. 在直角坐标系中，点P(2, 3)关于y轴的对称点坐标是（）A. (2, -3)B. (-2, 3)C. (2, 3)D. (-2, -3)答案：B解析：关于y轴对称的点，其横坐标互为相反数，纵坐标相同。
5. 下列函数中，是奇函数的是（）A. y = x^2B. y = 2xC. y = x^3D. y = x^4答案：C解析：奇函数满足f(-x) = -f(x)，代入选项中只有y = x^3满足条件。
二、填空题6. 若a + b = 5，ab = 6，则a^2 + b^2的值为______。
答案：37解析：利用平方差公式，a^2 + b^2 = (a + b)^2 - 2ab = 5^2 - 2×6 = 25 - 12 = 13。
7. 在等腰三角形ABC中，底边BC = 8，腰AB = AC = 10，则顶角A的度数为______。
答案：60°解析：在等腰三角形中，底边上的高将底边平分，因此顶角A的度数为60°。
8. 若等比数列的前三项分别为2，4，8，则该数列的公比q为______。
人教版 初三数学竞赛专题：平面几何的定值问题(包含答案)
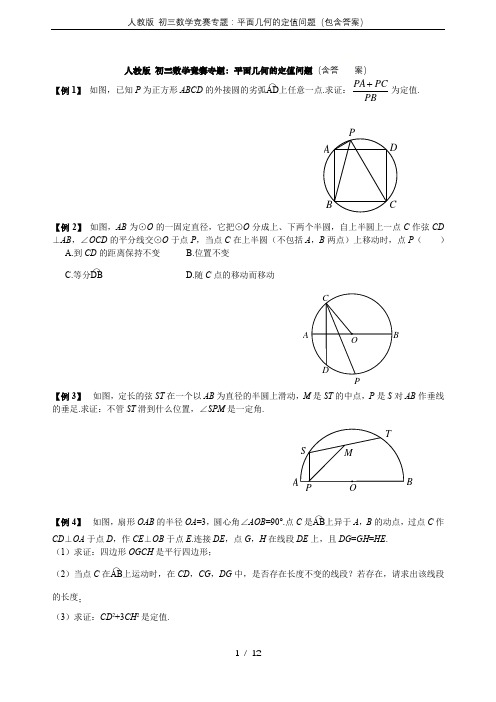
人教版 初三数学竞赛专题：平面几何的定值问题（含答案）【例1】 如图，已知P 为正方形ABCD 的外接圆的劣弧AD⌒上任意一点.求证：PA PC PB为定值.【例2】 如图，AB 为⊙O 的一固定直径，它把⊙O 分成上、下两个半圆，自上半圆上一点C 作弦CD ⊥AB ，∠OCD 的平分线交⊙O 于点P ，当点C 在上半圆（不包括A ，B 两点）上移动时，点P （ ） A.到CD 的距离保持不变 B.位置不变C.等分DB⌒ D.随C 点的移动而移动【例3】 如图，定长的弦ST 在一个以AB 为直径的半圆上滑动，M 是ST 的中点，P 是S 对AB 作垂线的垂足.求证：不管ST 滑到什么位置，∠SPM 是一定角.【例4】 如图，扇形OAB 的半径OA =3，圆心角∠AOB =90°.点C 是AB⌒上异于A ，B 的动点，过点C 作CD ⊥OA 于点D ，作CE ⊥OB 于点E .连接DE ，点G ，H 在线段DE 上，且DG =GH =HE .（1）求证：四边形OGCH 是平行四边形；（2）当点C 在AB ⌒上运动时，在CD ，CG ，DG 中，是否存在长度不变的线段？若存在，请求出该线段的长度；（3）求证：CD 2+3CH 2是定值.P AB CDAPB【例5】 如图1，在平面直角坐标系xOy 中，点M 在x 轴的正半轴上，⊙M 交x 轴于A ，B 两点，交y 轴于C ，D 两点，且C 为弧AE 的中点，AE 交y 轴于G 点.若点A 的坐标为（-2，0），AE =8. （1）求点C 的坐标；（2）连接MG ，BC ，求证：MG ∥BC ；（3）如图2，过点D 作⊙M 的切线，交x 轴于点P .动点F 在⊙M 的圆周上运动时，PFOF的比值是否发生变化？若不变，求出比值；若变化，说明变化规律.（图1）（图2）【例6】 如图，已知等边△ABC 内接于半径为1的圆O ，P 是⊙O 上的任意一点.求证：P A 2+PB 2+PC 2为定值.【能力训练】1.如图，点A ，B 是双曲线xy 3上的两点，分别经过A ，B 两点向x 轴，y 轴作垂线段.若S 阴影=1，则BOACE HG D A=+21S S _______.（第1题图） （第3题图） （第4题图）2.从等边三角形内一点向三边作垂线段，已知这三条垂线段的长分别为1，3，5，则这个等边三角形的面积是__________.3.如图，OA ，OB 是⊙O 任意两条半径，过B 作BE ⊥OA 于E ，又作OP ⊥AB 于P ，则定值OP 2+EP 2为_________.4.如图，在菱形ABCD 中，∠ABC =120°，F 是DC 的中点，AF 的延长线交BC 的延长线于点E ，则直线BF 与直线DE 所夹的锐角的度数为（ ）A.30°B.40°C.50°D.60°5.如图，在⊙O 中，P 是直径AB 上一动点，在AB 同侧作A A '⊥AB ，AB B B ⊥'，且A A '=AP ，B B '=BP .连接B A ''，当点P 从点A 移动到点B 时，B A ''的中点的位置（ ） A ．在平分AB 的某直线上移动 B.在垂直AB 的某直线上移动 C.在弧AMB 上移动 D.保持固定不移动（第5题图） （第6题图） 6.如图，A ，B 是函数xky =图象上的两点，点C ，D ，E ，F 分别在坐标轴上，且分别与点A ，B ，O 构成正方形和长方形.若正方形OCAD 的面积为6，则长方形OEBF 的面积是（ ） A.3 B.6 C.9 D.127.（1）经过⊙O 内或⊙O 外一点P 作两条直线交⊙O 于A ，B 和C ，D 四点，得到如图①~⑥所表示的六种不同情况.在六种不同情况下，P A ，PB ，PC ，PD 四条线段之间在数量上满足的关系式可以用同一个式子表示出来.请你首先写出这个式子，然后只就如图②所示的圆内两条弦相交的一般情况给出它的证明.A ABCDEFAB'（2）已知⊙O 的半径为一定值r ，若点P 是不在⊙O 上的一个定点，请你过点P 任作一直线交⊙O 于不重合的两点E ，F . PE ·PF 的值是否为定值？为什么？由此你发现了什么结论？请你把这一结论用文字叙述出来.8.在平面直角坐标系中，边长为2的正方形OABC 的两顶点A ，C 分别在y 轴，x 轴的正半轴上，点O 在原点，现将正方形OABC 绕O 点顺时针旋转，当A 点第一次落在直线x y =上时停止旋转.旋转过程中，AB 边交直线x y =于点M ，BC 边交x 轴于点N .（1）求OA 在旋转过程中所扫过的面积；（2）旋转过程中，当MN 与AC 平行时，求正方形OABC 旋转度数；（3）设△MBN 的周长为P ，在正方形OABC 旋转的过程中，P 值是否有变化？请证明你的结论.⑥⑤④③②①P(B )A PB9.如图，AB 是半圆的直径，AC ⊥AB ，AC =AB .在半圆上任取一点D ，作DE ⊥CD ，交直线AB 于点E ，BF ⊥AB ，交线段AD 的延长线于点F .（1）设弧AD 是x °的弧，若要点E 在线段BA 的延长线上，则x 的取值范围是_______.（2）不论点D 取在半圆的什么位置，图中除AB ＝AC 外，还有两条线段一定相等.指出这两条相等的线段，并予证明.（第9题图） （第10题图）（第11题图）10.如图，内接于⊙O 的四边形ABCD 的对角线AC 与BD 垂直相交于点K ，设⊙O 的半径为R .求证： （1）2222DK CK BK AK +++是定值； （2）2222DA CD BC AB +++是定值.11.如图，设P 是正方形ABCD 外接圆劣弧弧AB 上的一点，求证：DPCP BPAP ++的值为定值.1.等腰△ABC 的底边BC 为定长2，H 为△ABC 的垂心.当顶点A 在保持△ABC 为等腰三角形的情况下 改变位置时，面积S △ABC ·S △HBC 的值保持不变，则S △ABC ·S △HBC =________.2.已知A ，B ，C ，D ，E 是反比例函数xy 16=（x ＞0）图象上五个整数点（横、纵坐标均为整数），分别过这些点向横轴或纵轴作垂线段，以垂线段所在的正方形边长为半径作四分之一圆周的两条弧，组成如图所示的五个橄榄形（阴影部分），则这五个橄榄形的面积总和是__________（用含π的代数式表示）.P D CB A A折叠，使点A ，B 落在六边形ABCDEF 的内部，记∠C ＋∠D ＋ ）A. ∠1＋∠2＝900°－2α B. ∠1＋∠2＝1080°－2α C. ∠1＋∠2＝720°－α D. ∠1＋∠2＝360°－21α（第3题图） （第4题图）4.如图，正△ABO 的高等于⊙O 的半径，⊙O 在AB 上滚动，切点为T ，⊙O 交AO ，BO 于M ，N ，则弧MTN （ ）A.在0°到30°变化B.在30°到60°变化C.保持30°不变D.保持60°不变5.如图，AB 是⊙O 的直径，且AB =10，弦MN 的长为8.若MN 的两端在圆上滑动时，始终与AB 相交，记点A ，B 到MN 的距离分别为h 1，h 2，则∣h 1-h 2∣等于（ ）A.5B.6C.7D.8（第5题图） 12GF EDCHBAB6.如图，已知△ABC 为直角三角形，∠ACB =90°，AC =BC ，点A ，C 在x 轴上，点B 坐标为（3，m ）（m ＞0），线段AB 与y 轴相交于点D ，以P （1，0）为顶点的抛物线过点B ，D . （1）求点A 的坐标（用m 表示） （2）求抛物线的解析式；（3）设点Q 为抛物线上点P 至点B 之间的一动点，连接PQ 并延长交BC 于点E ，连接BQ 并延长交AC 于点F .试证明：FC （AC +EC ）为定值.7.如图，已知等边△ABC 内接于圆，在劣弧AB 上取异于A ，B 的点M .设直线AC 与BM 相交于K ，直线CB 与AM 相交于点N .证明线段AK 和BN 的乘积与M 点的选择无关.（第7题图） （第8题图）8.如图，设H 是等腰三角形ABC 两条高的交点，在底边BC 保持不变的情况下让顶点A 至底边BC 的距离变小，这时乘积S △ABC ·S △HBC 的值变小、变大，还是不变？证明你的结论.9.如图，在平面直角坐标系xOy 中，抛物线10941812--=x x y 与x 轴的交点为点A ，与y 轴的交点为点B .过点B 作x 轴的平行线BC ，交抛物线于点C ，连接AC .现有两动点P ，Q 分别从O ，C 两点同时出发，点P 以每秒4个单位的速度沿OA 向终点A 移动，点Q 以每秒1个单位的速度沿CB 向点B 移动.点P 停止运动时，点Q 也同时停止运动.线段OC ，PQ 相交于点D ，过点D 作DE ∥OA ，交CA 于E ，射线QE 交x 轴于点F .设动点P ，Q 移动的时间为t （单位：秒）. （1）求A ，B ，C 三点的坐标和抛物线的顶点坐标；（2）当t 为何值时，四边形PQCA 为平行四边形？请写出计算过程； （3）当290<<t 时，△PQF 的面积是否总是定值？若是，求出此值；若不是，请说明理由； （4）当t 为何值时，△PQF 为等腰三角形，请写出解答过程.NKMB AC HCBA（第9题图） （第10题图） 10.已知抛物线C 1：12121+-=x x y ，点F （1,1）. （1）求抛物线C 1的顶点坐标；（2）若抛物线C 1与y 轴的交点为A ，连接AF ，并延长交抛物线C 1于点B ，求证：211=+BFAF . （3）抛物线C 1上任意一点P （x P ，y P ）（0＜x P ＜1），连接PF ，并延长交抛物线C 1于点 Q （x Q ，y Q ），试判断211=+QFPF 是否成立？请说明理由.11.已知A ，B 是平面上的两个顶点，C 是位于AB 一侧的一个动点，分别以AC ，BC 为边在△ABC 外作正方形ACDE 和正方形BCFG .求证：不论C 在直线AB 同一侧的任何位置，EG 的中点P 的位置不变. 参考答案例 1 延长PC 至E ，使CE ＝AP ，连结BE ，则△BCE ≌△BAP ，及△PBE 为等腰直角三角形，故PA PC CE PC PEPB PB PB++=== 例2 B 提示：连结AC ，BC ，可以证明P 为APB 的中点． 例3 ∵SP ⊥OP ，OM ⊥ST ，∴S ，M ，O ，P 四点共圆，于是∠SPM ＝∠SOM ＝12∠SOT 为定角． 例4 (1)连结OC 交DE 于M ，则OM ＝CM ， EM ＝DM ，而DG ＝ HE ，则HM ＝GM 故四边形OGCH 是平行四边形． (2)DG 不变．DE ＝OC ＝OA ＝3 .DG ＝13DE ＝13×3＝1． (3)设CD ＝x ，延长OG 交CD 于N ，则CN ＝DN ＝12 x ，229CE x =- ， 2214DN x = .∴22394ON x =-，而ON ＝32CH ，∴22143CH x =-．故CD 2＋3CH 2＝x 2＋3(4－13x 2)＝x 2＋12－x 2为定值． 例5 ⑴C (0，4) ⑵先求得AM ＝CM ＝5，连接MC 交AE 于N ，由△AO G ∽△ANM ，得OG AO MN AN =，O G ＝32，38OG OM OC OB ==，又∠BOC ＝∠G OM ，∴△G OM ∽△COB ，∠G MO ＝∠CBO ，得M G ∥BC ．⑶连结DM ，则DM ⊥PD ，DO ⊥PM ，DO 2＝OM •OP ，OP ＝163．动点F 在⊙M 的圆周上运动时，从特殊位置探求OFPF的值．当F 与点A 重合时，2316523OF AO PF AP ===-；当点F 与点B 重合时，8316583OF OB PF PB ===+；当点F 不与点A ，B 重合时，连接OF 、PF 、MF ，∴DM 2＝MO •MP ，∴FM 2＝MO •MP ，即FM MPOM FM=，又∠OMP ＝∠FMP ，∴△MFO ∽△MPF ，35OF MO PF MF ==，故OF PF 的比值不变，比值为35． 例6 ∠BPC ＝120°，在△BPC 中，由余弦定理得BC 2＝PB 2＋PC 2－2PB •PC ＝BC 2，又由上托勒密定理得BC •P A ＋PC •AB ，而AB ＝BC ＝AC ，∴P A ＝PB ＋PC ，从而P A 2＋ PB 2＋ PC 2＝ (PB ＋PC )2＋ PB 2＋ PC 2＝2 (PB 2＋PC 2＋PB •PC )＝2BC 2＝2×()23＝6．故P A 2＋PB 2＋PC 2为定值．A 级 1．4提示：∵S 1＋S 阴＝ S 2＋S 阴＝xy ＝3，∴S 1＋S 2＝2xy －2S 阴＝6－2＝4．2．273 提示：1＋3＋5＝9是等边三角形的高． 3．r 2提示：先考查OB 与OA 垂直的情形．4．D 提示：延长BF 交DE 于点M ，连接BD ，则△BCD 为等边三角形，BF 平分∠CBD ．∵F 为CD 中点，且AD ∥CE ，∴△ADF 与△ECF 关于点F 中心对称．∴CE ＝AD ＝CD ，∴∠CEM=30°，∠DMF=60°，5．D 提示：A′B′的中点均在⊙O 的上半圆的中点处． 6．B 提示：S 正方形OCAD ＝OD •OC ＝A A x y k =＝6，∴S OEBF ＝OE •OF ＝x B •y B k =＝6． 7．⑴略⑵当点P在⊙O 内时，过P 作直径CD ，则PE •PF ＝PD •PC ＝r 2－OP 2为定值；当点P 在⊙O 外时，PE •PF 为定值22OP r -．结论：过不在圆上的一个定点任作一条直线与圆相交，则这点到直线与圆相交点的两条线段长的积为定值． 8．⑴2π⑵22.5° ⑶P 值无变化．理由如下：如图，延长BA 交y 轴于E 点，可证明△OAE ≌△OCN ，得OE ＝ON ，AE ＝CN ，又∠MOE ＝∠MON ＝45°，OM ＝ON ，∴△OME ≌△OMN ，得MN ＝ME ＝AM ＋AE ＝AM ＋CN ．∴P ＝MN ＋BN ＋BM ＝AM ＋CM ＋CN ＋BN ＋BM ＝AB ＋AC ＝4．9．⑴0＜x ＜90 ⑵BE ＝BF 提示：连接BD ，可证明△BDF ∽△ADB ，△BDE ∽△ADC ． 10．⑴作OP ⊥BD 于P ，OQ ⊥AC 于Q ，连接AO ，则AO 2＝()()221122BK DK CK AK ⎡⎤⎡⎤-++⎢⎥⎢⎥⎣⎦⎣⎦，又AK •CK ＝BK •DK ，得AK 2＋BK 2＋CK 2＋DK 2＝4R 2为定值． ⑵作直径DE ，连接AE ，BE ，CE ，AB 2＋CD 2＝4R 2，AD 2＋BC 2＝4R 2，故AB 2＋BC 2＋CD 2＋DA 2＝8K 2为定值． 11．设正方形的边长为a ，根据托勒密定理，对于四边形APBC 和四边形APBD ，有CP •a ＝AP •a ＋BP •2a ，DP •a ＝BP •a ＋AP •2a ，两式相加并整理得(CP ＋DP )a ＝(AP ＋BP )(a ＋2a )，从而21AP BPCP DP+=-+为定值．B 级1．1 提示：不妨设∠A 为锐角，AD ，BE ，CF 为△ABC 的三条高，H 为垂心，由AB ＝AC 知∠HBD ＝∠HCD ＝∠HAE ，∠HDC ＝∠CDA ＝90°，故R t △CHD ∽R t △ACD ．∴AD DC DC HD =，即AD •HD ＝DC 2＝14BC 2＝1．∴S △ABC •S △HBC ＝2111224BC AD BC HD BC ⎛⎫⎛⎫⋅⋅⋅= ⎪ ⎪⎝⎭⎝⎭＝1．当∠A ≥90°时，结论成立．2．13π－26 提示：∵A ，B ，C ，DE 是反比例函数y ＝16x(x ＞0)图象上五个整数点，由图象可知，这些点的横坐标分别为1，2，4，8，16．∴五个正方形的边长分别为1，3，4，2，1．∴这五人橄榄形的面积总和是2221111112211122222444424242πππ⎡⎤⎛⎫⎛⎫⎛⎫⨯-⨯⨯+⨯-⨯⨯+⨯-⨯⨯ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦＝5π－10＋8π－16＝13π－26． 3．B 提示：如图，设F A 的延长线与CB 的延长线交于点P ，G A ′的延长线与HB ′的延长线交于点P ′．由对称性可知∠1＝2∠APP ′，∠2＝2∠BPP ′．∴∠1＋∠2＝2∠APB ．∵∠APB ＝540°－α，∴∠1＋∠2＝1080°－2α． 4．D 5．B 提示：如图，设AB 与MN 交于点C ，过点O 作OD ⊥MN 于D ，连接FO 并延长交EB 于G ．由垂径定理，得OD ＝2254-＝3．由△AFO ≌△B G O ，得AF ＝B G ，即h 1＝B G ．由AF ⊥MN ，BE ⊥MN ，得△FOD ∽△F G E ．∴12OD FO GE FG ==．∴E G ＝2OD ＝6，∴12h h AF BE -=-＝E G ＝6． 6．⑴A (3－m ，0) ⑵y ＝x 2－2x ＋1 ⑶过点Q 作QM ⊥AC 于M ，过点Q 作QN ⊥BC 于N ，设Q 点的坐标为(x ，x 2－2x ＋1)，则QM ＝CN ＝(x －1)2，MC ＝QN＝3－x ．∵QM ∥CE ，∴PQM ∽△PEC ．∴QM PMEC PC=，即()2112x x EC--=，得EC ＝2(x －1)．∵QN ∥CF ，∴△BQN ∽△BFC ．∴QN BN FC BC =，即()24134x x FC ---=，得FC ＝41x +．又AC ＝4，∴FC (AC ＋EC )＝()44211x x +-⎡⎤⎣⎦+＝8为定值． 7．提示：易证△ABK ∽△BNA ，故AK •BN ＝AB 2为定值，即AK 与BN 的乘积与M 点的选择无关． 8．提示：S △ABC •S △HBC ＝116BC 4，由于BC 是不变的，所以当点A 至BC 的距离变小时，乘积S △ABC •S △HBC 保持不变． 9．⑴A (18，0)，B (0，－10)，顶点坐标为(4，－989)⑵若四边形PQCA 为平行四边形，由于QC ∥P A ，故只要QC ＝P A 185． ⑶即可，而P A ＝18－4t ，CQ ＝t ，故18－4t ＝t ，得t ＝设点P 运动t s ，则OP ＝4t ，CQ ＝t ，0＜t ＜4.5．说明P在线段OA 上，且不与点O ，A 重合．由于QC ∥OP 知△QDC ∽△PDO ，故144QD QC t DP OP t ===．同理QC ∥AF ，故14QC CE AF EA ==，即14t AF =，∴AF ＝4t ＝OP ．∴PF ＝P A ＋AF ＝P A ＋OP ＝18．又点Q 到直线PF 的距离d ＝10，∴S △PQF ＝12•PF •d ＝12×18×10＝90．于是S △PQF 的面积总为定值90． ⑷由前面知道，P (4t ，0)，F (18＋4t ，0)，Q (8－t ，－10)，0≤t ≤4.5．构造直角三角形后易得PQ 2＝(4t －8＋t )2＋102＝，FQ 2＝(18＋4t －8＋t )2＋102＝(5t ＋10)2＋100．①若FP ＝FQ ，即182＝(5t ＋10)2＋100，故25(t ＋2)2＝224，(t ＋2)2＝24425．∵2≤t ＋2≤6.5，∴t ＋2＝244414255=．∴t ＝ 4145－2． ②若QP ＝QF ，即(5t －8)2＋100＝(5t ＋10)2＋100，即(5t －8)2＝(5t ＋10)2，无0≤t ≤4.5的t 满足． ③若PQ ＝PF ，即(5t －8)2＋100＝182，∴(5t －8)2＝224．由于224≈15，又0≤5t ≤22.5，∴－8≤5t －8≤14.5，14.52＝22984124⎛⎫= ⎪⎝⎭＜224．故没有t (0≤t ≤4.5)满足此方程．综上所述，当t ＝4145－2时，△PQ R 为等腰三角形． 10．⑴C 1的顶点坐标为(1，12). ⑵略 ⑶作PM ⊥AB 于M ，作QN ⊥AB 交AB 延长线于N ，∴PM ＝1－y P ，FM ＝1－x P ．在R t △PMF 中，PF 2＝(1－y P )2＋(1－x P )2＝1－2y P ＋y P 2＋1－2x P ＋x P 2，又∵点P 在抛物线上，∴y P ＝12x P 2－x P ＋1，∴PF 2＝1－x P 2＋2x P －2＋y P 2＋1－2x P ＋x P 2＝y P 2，∴PF ＝y P ，同理，QF ＝y Q ，易证△PMF ∽△QNF ，则PM QN PF QF =，∴11Q P y y PF QF --=，即11PF QF PF QF --=，∴11PF QF+＝2． 11．先从特殊情况出发．当△ABC 是等腰直角三角形时，点P 与点C 重合，此时点P 的位置在AB 的中垂线上，且到AB的距离为12AB ，如图①所示．下面就一般情况来证明上面的结论(结论②所示)．过C ，E ，G 分别作直线AB 的垂线CH ，EM ，G N ，垂足分别是H ，M ，N ．容易证明△AEM ≌△ACH ，△B G N ≌△BCH ．从而有AM ＝CH ＝BN ，EM ＝AH ，G N ＝BH ．这样，线段AB 的中点O 也是线段MN 的中点，连接OP ，则OP 是梯形EMN G 的中位线，从而OP ⊥AB ，OP ＝12(EM ＋G N )＝ 12(AH ＋BH )＝12AB ．∴无论点C 在AB 同一侧的位置如何，E G 中点P 的位置不变．。
九年级数学竞赛题(含答案)
初三数学竞赛题（含答案）（全卷满分120分考试时间90分）姓名_________班级________指导教师_________ 得分_________一 .单项选择题（每题6分，共30分）1.22016－22017＝( )A.-22016B.-2C. 22016D.22.若关于x 的多项式x 2-6x+m 2是一个完全平方式，则m=( ) A. 3 B. ±3 C. 9 D. ±93.圆锥的侧面展开是圆心角为90°的扇形，则圆锥的母线与底面半径之比为（） A . 6:1 （B ）. 4:1 （C ）.3:1 （D ）.2:14.如图，在矩形ABCD 中，AB=10，BC=5，点E 、F 分别在AB 、CD 上，将矩形ABCD 沿EF 折叠，使点A 、D 分别落在矩形AB CD 外部的点A 1、D 1处，则阴影部分图形的周长为（） A.15 B.20 C.25 D.305.如图，矩形ABCD 中，AB AD 2=，E 是AD 边上一点，AD nDE 1=（n 为大于2的整数），连接BE ，作BE 的垂直平分线分别交AD 、BC 于点F ，G ，FG 与BE 的交点为O ，连接BF和EG .记四边形BFEG 的面积为1S ，矩形ABCD 的面积为2S ，当301721=S S 时，n = （ ）A.3B. 4C.6D.8第4题图第5题图二 .填空题（每题6分，共30分）6.已知2cos 2β+3sin β-3=0,则锐角β＝________. 7.化简：324324--+＝________8.（1+2+3+…+99）（2+3+4+…+100）－（1+2+3+…+100）（2+3+4+…99）＝________. 9.已知关于x 的分式方程111=--++x kx k x 的解为负数，则k 的取值范围是_______. 10.如图，点A 1，A 2依次在的图象上，点B 1，B 2依次在x 轴的正半轴上，若ΔA 1OB 1 ,ΔA 2B 1B 2均 为等边三角形，则点B 2的坐标为 ． 三．解答题（每题20分，共60分）11.为了迎接“十•一”小长假的购物高峰．某运动品牌专卖店准备购进甲、乙两种运动鞋．其中甲、乙两种运动鞋的进价和售价如下表：已知：用3000元购进甲种运动鞋的数量与用2400元购进乙种运动鞋的数量相同．（1）求m 的值；（2）要使购进的甲、乙两种运动鞋共200双的总利润（利润=售价﹣进价）不少于21700元，且不超过22300元，问该专卖店有几种进货方案？（3）在（2）的条件下，专卖店准备对甲种运动鞋进行优惠促销活动，决定对甲种运动鞋每双优惠a （50＜a ＜70）元出售，乙种运动鞋价格不变．那么该专卖店要获得最大利润应如何进货？BCAD12. 如图，抛物线y=x2－2x+c的顶点A在直线l：y=x－5上．（1）求抛物线顶点A的坐标；（2）设抛物线与y轴交于点B，与x轴交于点C．D（C点在D点的左侧），试判断△ABD的形状；（3）在直线l上是否存在一点P，使以点P、A．B．D为顶点的四边形是平行四边形？若存在，求点P的坐标；若不存在，请说明理由．13.如图，在△ABC中，已知AB=AC=5，BC=6，且△ABC≌△DEF，将△DEF与△ABC重合在一起，△ABC不动，△ABC不动，△DEF运动，并满足：点E在边BC上沿B到C的方向运动，且DE、始终经过点A，EF与AC交于M点．（1）求证：△ABE∽△ECM；（2）探究：在△DEF运动过程中，重叠部分能否构成等腰三角形？若能，求出BE的长；若不能，请说明理由；（3）当线段AM最短时，求重叠部分的面积．数学竞赛答案1.A2.B3.D4. D5. C6.3007.28.1009. k＞1/2, 且k≠1 10.(26,0)11. 解：（1）依题意得，=，整理得，3000（m﹣20）=2400m，解得m=100，经检验，m=100是原分式方程的解，所以，m=100；（2）设购进甲种运动鞋x双，则乙种运动鞋（200﹣x）双，根据题意得，，解不等式①得，x≥95，解不等式②得，x≤105，所以，不等式组的解集是95≤x≤105，∵x是正整数，105﹣95+1=11，∴共有11种方案；（3）设总利润为W，则W=（140﹣a）x+80（200﹣x）=（60﹣a）x+16000（95≤x≤105），①当50＜a＜60时，60﹣a＞0，W随x的增大而增大，所以，当x=105时，W有最大值，即此时应购进甲种运动鞋105双，购进乙种运动鞋95双；②当a=60时，60﹣a=0，W=16000，（2）中所有方案获利都一样；③当60＜a＜70时，60﹣a＜0，W随x的增大而减小，所以，当x=95时，W有最大值，12. 解：（1）∵顶点A的横坐标为x==1，且顶点A在y=x－5上，∴当x=1时，y=1－5=－4，∴A（1，－4）．（2）△ABD是直角三角形．将A（1，－4）代入y=x2－2x+c，可得，1－2+c=－4，∴c=－3，∴y=x2－2x－3，∴B（0，－3）当y=0时，x2－2x－3=0，x1=－1，x2=3∴C（－1，0），D（3，0），BD2=OB2+OD2=18，AB2=（4－3）2+12=2，AD2=（3－1）2+42=20，BD2+AB2=AD2，∴∠ABD=90°，即△ABD是直角三角形．（3）存在．由题意知：直线y=x－5交y轴于点A（0，－5），交x轴于点F（5，0）∴OE=OF=5，又∵OB=OD=3∴△OEF与△OBD都是等腰直角三角形∴BD∥l，即PA∥BD则构成平行四边形只能是PADB或PABD，如图，过点P作y轴的垂线，过点A作x轴的垂线并交于点C设P（x1，x1－5），则G（1，x1－5）则PC=|1－x1|，AG=|5－x1－4|=|1－x1|PA=BD=3由勾股定理得：（1－x1）2+（1－x1）2=18，x12－2x1－8=0，x1=－2，4∴P（－2，－7），P（4，－1）存在点P（－2，－7）或P（4，－1）使以点A．B．D．P为顶点的四边形是平行四边形．第12题图第13题图S△AEM =．13.（1）证明：∵AB=AC，∴∠B=∠C，∵△ABC≌△DEF，∴∠AEF=∠B，又∵∠AEF+∠CEM=∠AEC=∠B+∠BAE，∴∠CEM=∠BAE，∴△ABE∽△ECM；（2）解：∵∠AEF=∠B=∠C，且∠AME＞∠C，∴∠AME＞∠AEF，∴AE≠AM；当AE=EM时，则△ABE≌△ECM，∴CE=AB=5，∴BE=BC－EC=6－5=1，当AM=EM时，则∠MAE=∠MEA，∴∠MAE+∠BAE=∠MEA+∠CEM，即∠CAB=∠CEA，又∵∠C=∠C，∴△CAE∽△CBA，∴，∴CE =，∴BE=6－=；（3）解：设BE=x，又∵△ABE∽△ECM，∴，即：，∴CM=－+x=－（x－3）2+，∴AM=－5－CM ═（x－3）2+，∴当x=3时，AM 最短为，又∵当BE=x =3=BC时，∴点E为BC的中点，∴AE⊥BC，∴AE ==4，此时，EF⊥AC，∴EM ==，。
人教版初中数学《第29章图论初步》竞赛专题复习(含答案)
人教版初中数学《第29章图论初步》竞赛专题复习(含答案)第29章图论初步29.1.1某某大型晚会有2022个人参加，已知他们每个人至少认识其中的一个人．证明：必有一个人至少认识其中的二个人．解析2022这个数目较大，我们先考虑：某小型晚会有5人参加，已知他们每个人至少认识其中的一个人．证明：必有一个人至少认识其中的二个人．用5个点v1、v2、v3、v4、v5表示5个人，如果两个人彼此认识（本章中的“认识”都是指相互认识），就在表示这两个人的顶点之间连一条边．对顶点功来说，由于v1所表示的人至少认识其他4个人的一个，不妨设v1与v2认识，即v1和v2相邻，同样，设v3与v4相邻，如图所示．对于顶点v5来说，无论它与v1、v2、v3、v4哪个相邻，都会出现一个顶点引出两条边的情况．于是问题得以解决．v1v5v2v3v4用同样的方法可以证明，对2022个人来说，命题成立．其实，把2022换成任意一个大于l的奇数，命题也成立．29.1.2某在一间房子里有n（n>3）个人，至少有一个人没有和房子里每个人握手，房子里可能与每个人都握手的人数的最大值是多少？解析用n个顶点表示n个人，若某两个人握过手，就在他们相应的顶点之间连一条边，这样就得到了一个图G．因为不是任何两个人都握过手，所以G的边数最多是完全图Kn（即n个点每两点之间恰连一条边）的边数减1，去掉的那条边的两个端点v和v所表示的两个人未握过手．所以房子里可能与每个人都握手的人数的最大值是n2．29.1.3某某某九名数学家在一次国际数学会议上相遇，发现他们中的任意三个人中，至少有两个人可以用同一种语言对话．如果每个数学家至多可说三种语言，证明至少有三个数学家可以用同一种语言对话．解析用9个点v1，v2，…，v9表示这九名数学家，如果某两个数学家能用某种语言对话，就在他们相应的顶点之间连一条边并涂以相应的颜色．我们要证明的是：存在三个顶点vi、vj、vk，使得边（vi，vj）和（vi，vk）是同色的．这样的，vi、vj、vk这三名数学家就能用同一种语言对话．下面就顶点v1，分两种情形：（1）v1与v2，…，v9均相邻，由于每个数学家至多能说三种语言，所以每一个顶点引出的边的颜色至多是三种．根据抽屉原理知，从v1发出的8条边中至少有2条是同色的，不妨设为（v1，、（v1，．于v2）v3）是v1、v2、v3所表示的三名数学家能用同一种语言对话．见图（a）．v2v3v1v9(a)v1v2(b)v3v4v5v6v1514637v4v51110129v8v22v3(c)v68v7（2）v1与v2，v3，…，v9中的至少一点不相邻，不妨设功与功不相邻．由于任意三个数学家中，至少有两个人可以用同一种语言对话，所以，v3，v4，…，v9中的每一个不是和研相邻就是和功相邻，根据抽屉原理可知，其中至少有4个点与v1或v2相邻．不妨设v3、v4、v5、v6与v1相邻，如图（b），再对v1引出的这4条边用抽屉原理可得，至少有2条边是同色的，设为（v1，v3）、（v1，v4）．于是v1、v3、v4所表示的三名数学家能用同一种语言对话．评注若本题中的九改成八，则命题不成立．反例如图（c）所示．图中每条边旁的数字表示不同的语种．29.1.4某某证明任何一群人中，至少有两个人，它们的朋友数目相同．解析设任意给定的一群人有n个．用顶点表示这n个人．当且仅当顶点u、v表示的两个人是朋友时令u、v相邻，得到n个顶点的简单图G．对G中任意某，由于它可以和其他n1个顶点相邻，所以顶点某的度d（某）满足0≤d某≤n1，即图G的顶点度只能是n个非负数0，1，…，n1中的一个．如果图G的顶点的度都不相同，则图G具有0度顶点u和n1度顶点v．n1度顶点和G中其他顶点都相邻，特别地和顶点u相邻．但0度顶点u和G中任何顶点都不相邻，矛盾．这就证明了G中必定有两个顶点，它们的度相同．也就是说，这群人必有两个人，他们的朋友一样多．29.1.5某某某有一个参观团，其中任意四个成员中总有一名成员原先见过其他三名成员．证明：在任意四名成员中，总有一名成员原先见过所有成员．解析用图论语言表示即：图G的任意四点中至少有一个顶点和其他三个顶点相邻．证明图G任意四个顶点中至少一个顶点和G中其他所有顶点都相邻．用反证法．如果命题不成立，则G中有四个点某、y、z、w，它们和图G中的其他所有顶点不都相邻．于是存在四个顶点某、y、z、w（不一定不同）它们依次与某、y、z、w都不相邻．如图．所以某不是y、z、w中的一个，且y与某是两个不同的顶点．如果y与某不同，则某、y、某、y中没有一个顶点和其他三个顶点都相邻，和已知矛盾．所以y和某重合．同理可证，z和某重合．于是某和y、z、w都不相邻，和已知矛盾．这就证明了图G中任意四个顶点中至少有一个顶点和G的其他所有顶点都相邻．某'某ww'yy'zz'29.1.6某某是否存在这样的多面体，它有奇数个面，每个面有奇数条棱？解析不存在这样的多面体．事实上，如果这样的多面体存在，那么用顶点表示这个多面体的面，并且仅当vi、vj所代表的两个面有公共棱时，在图G相应的两顶点之间连一条边，依题意dv是奇数，于是奇数个奇数和也是奇数．而这一个图中的顶点的和为偶数矛盾．评注关于图G的顶点和边数之间的关系，有如下定理：图G中边数的两倍等于顶点度数之和．即若G中n个顶点为v1，v2，…，vn，边数为e，则dv1dv2dvn2e．29.1.7某n名选手进行对抗赛，每名选手至多赛一场，每场两名选手参加，已赛完n1场．证明：至少有一名选手赛过三次．解析把选手看成顶点．当且仅当vi、vj所代表的两名选手比赛过时，令vi、vj相邻，得到含n个顶点的简单图．由于总共赛过n1场，所以，图G的边数是n1．于是dv1dv2dvn2n1．如果图G中所有顶点的度都不超过2，则由上式得到2n1dv1dv2dvn≤2n，这不可能．因此图G中至少有一个顶点某，它的度至少是3．于是，顶点某所表示的选手至少赛过三次．29.1.8某某一航空线路共连结50个城市，现要求从一个城市到另一城市至多需换乘两次飞机，问航空线路最少要多少条（任两城市之间的航空线路数为0或1）？解析不妨将50个城市看成50个点，它们之间连的线构成一连通图．图论告诉我们，如果每一点的度（即出发的线条数）至少为2，则由于边数为点度之和的一半，其数值不小于50；若有一个点的度为1（显然连通图不存在度为0的孤立点），则可通过删去该点证明。
人教版 九年级数学 竞赛专题：代数最值问题(含答案)
人教版 九年级数学 竞赛专题：代数最值问题（含答案）【例1】当x 变化时，分式12156322++++x x x x 的最小值是 ．【例2】已知1≤y ，且12=+y x ，则223162y x x ++的最小值为（ ）A.719 B. 3 C. 727 D. 13 【例3】()21322+-=x x f ，在b x a ≤≤的范围内最小值2a ，最大值2b ，求实数对(a ，b ).【例4】（1）已知211-+-=x x y 的最大值为a ，最小值b ，求22b a +的值． （2）求使()168422+-++x x 取得最小值的实数x 的值．（3）求使2016414129492222+-+++-++y y y xy x x 取得最小值时x ，y 的值．【例5】如图，城市A 处位于一条铁路线上，而附近的一小镇B 需从A 市购进大量生活、生产用品，如果铁路运费是公路运费的一半，问：该如何从B 修筑一条公路到铁路边，使从A 到B 的运费最低？【例6】（1）设r x ，1+r x ，…，k x （r k >），为k －r ＋1个互不相同的正整数，且x r ＋x r ＋1＋…＋x k ＝2019，求k 的最大可能值．（2）a ，b ，c 为正整数，且432c b a =+，求c 的最小值．（能力训练A 级1．已知三个非负数a ，b ，c ，满足3a ＋2b ＋c ＝5和2a ＋b －3c ＝1，若m ＝3a ＋b －7c ，则m 的最小值为___________，最大值为 ．2．多项式p ＝2x 2－4xy ＋5y 2－12y ＋13的最小值为 ．3．已知x ，y ，z 为实数，且x ＋2y －z ＝6，x －y ＋2z ＝3，那么x 2＋y 2＋z 2的最小值为 ． 4．若实数a ，b ，c ，满足a 2＋b 2＋c 2＝9，则代数式(a －b )2＋(b －c )2＋(c －a )2的最大值为 ( ) 5．已知两点A (3，2)与B (1，－1)，点P 在y 轴上且使P A ＋PB 最短，则P 的坐标是（ ）A.(0，21-) B.(0，0) C.(0，611) D.(0，41-)6．正实数x ，y 满足1=xy ，那么44411y x +的最小值为（ ） A.21 B. 85 C. 1 D. 45E.27．某公司试销一种成本单价为500元/件的新产品，规定试销时的销售单价不低于成本单价，又不高于800元/件，经试销调查，发现销售量y (件)与销售单价x (元/件)可近似看作一次函数b kx y +=的关系（如图所示）.（1）根据图象，求一次函数b kx y +=的解析式；（2）设公司获得的毛利润（毛利润=销售总价-成本总价）为S 元． ①试用销售单价x 表示毛利润；②试问：销售单价定为多少时，该公司可获得最大毛利润？最大毛利润是多少？此时的销量是多少？8．方程()()06122=-+-+m x m x 有一根不大于1-，另一根不小于1，（1）求m 的取值范围；（2）求方程两根平方和的最大值与最小值．9．已知实数a ，b 满足122=++b ab a ，求22b ab a +-的最大值与最小值．10.已知a ，b ，c 是正整数，且二次函数c bx ax y ++=2的图象与x 轴有两个不同的交点A ，B ，若点A ，B 到原点的距离都小于1，求a ＋b ＋c 的最小值．11．某单位花50万元买回一台高科技设备，根据对这种型号设备的跟踪调查显示：该设备投入使用后，若将养护和维修的费用均摊到每一天，则有结论：第x 天应付的养护与维修费为()⎥⎦⎤⎢⎣⎡+-500141x 元．（1）如果将设备从开始投入使用到报废所需的养护与维修费及购买设备费用的总和均摊到每一天，叫作每天的平均损耗，请你将每天的平均损耗y （元）表示为使用天数x （天）的函数．（2）按照此行业的技术和安全管理要求，当此设备的平均损耗达到最小值时，就应当报废，问：该设备投入使用多少天应当报废？B 级1．a ，b 是正数，并且抛物线b ax x y 22++=和a bx x y ++=22都与x 轴有公共点，则22b a +的最小值是 ．2．设x ，y ，z 都是实数，且满足x ＋y ＋z ＝1，xyz ＝2，则z y x ++的最小值为 ． 3．如图，B 船在A 船的西偏北45°处，两船相距210km ，若A 船向西航行，B 船同时向南航行，且B 船的速度为A 船速度的2倍，那么A 、B 两船的最近距离为 km ．4．若a ，b ，c ，d 是乘积为1的四个正数，则代数式a 2＋b 2＋c 2＋d 2＋ab ＋bc ＋ac ＋ad ＋bd ＋cd 的最小值为（ ）A. 0B. 4C. 8D. 105．已知x ，y ，z 为三个非负实数，且满足3x ＋2y ＋z ＝5，x ＋y －z ＝2. 若s ＝2x ＋y －z ，则s 的最大值与最小值的和为（ ）A. 5B.423 C. 427 D. 4356．如果抛物线()112----=k x k x y 与x 轴的交点为A ，B ，顶点为C ，那么△ABC 的面积的最小值为（ ）A.1B.2C.3D.47．某商店将进货价每个10元的商品按每个18元售出时，每天可卖出60个，商店经理到市场上做了一番调查后发现，若将这种商品的售价（在每个18元的基础上）每提高1元，则日销售量就减少5个；若将这种商品的售价（在每个18元的基础上）每降低1元，则日销量就增加10个，为获得每日最大利润，此商品售价应定为每个多少元？8．有甲、乙两种商品，经营销售这两种商品所能获得的利润依次是p （万元）和q （万元），它们与投入资金x （万元）的关系有经验公式：x q x p 53,51==.今有3万元资金投入经营甲、乙两种商品，为获得最大利润，对甲、乙两种商品的资金投入分别应为多少？能获得多大的利润？9．已知为x ，y ，z 为实数，且5=++z y x ，3=++zx yz xy ，试求z 的最大值与最小值．10．已知三个整数a ，b ，c 之和为13，且bca b =，求a 的最大值和最小值，并求出此时相应的b 与c 值．11．设x 1，x 2，…，x n 是整数，并且满足： ① －1≤x i ≤2，i ＝1，2，…，n ② x 1＋x 2＋…＋x n ＝19 ③ x 12＋x 22＋…＋x n 2＝99求x 13＋x 23＋…＋x n 3的最大值和最小值．12．已知x 1，x 2，…，x 40都是正整数，且x 1＋x 2＋…＋x 40＝58，若x 12＋x 22＋…＋x 402的最大值为A ，最小值为B ，求A ＋B 的值．参考答案例1. 4 提示：原式=112-62-+）（x . 例2. B 提示：由-1≤y ≤1有0≤x ≤1，则z =2x 2+16x +3y 2=14x 2+4x +3是开口向上，对称轴为71-=x 的抛物线.例3. 分三种情况讨论：①0≤a <b ，则f (x )在a ≤x ≤b 上单调递减，∴f (a )=2b ，f (b )=2a ，即⎪⎪⎩⎪⎪⎨⎧+-=+-=213222132222b a a b 解得⎩⎨⎧==31b a ②a <b ≤0，则f (x )在a ≤x ≤b 上单调递增，∴f (a )=2a ，f (b )=2b ，即⎪⎪⎩⎪⎪⎨⎧+-=+-=213222132222b b a a 此时满足条件的（a ，b ）不存在. ③a <0<b ，此时f (x )在x =0处取得最大值，即2b =f (0)=213,b =413,而f (x )在x =a 或x =b 处取最小值2a .∵a <0，则2a <0，又∵f (b )=f (413)=021341321-2>+⨯）（，∴f (a )=2a ，即2a =2132-2+a ，则⎪⎩⎪⎨⎧=--=413172b a 综上，（a ，b ）=(1，3)或（17-2-，413） 例4. （1）121≤≤x ，y 2 = 21+216143-2+-）（x .当x =43时，y 2取得最大值1，a =1； 当21=x 或x =1时，y 2取得最小值21，b =22.故a 2+b 2=23.(2) 如图，AB =8，设AC =x ，则BC =8- x ，AD =2，CD =42+x ，BE =4，CE =16)-8(2+x BF =AD =2.10)24(816)8(4222222=++=+=≥+=+-++EF DF DE CE CD x x当且仅当D ，C ，E 三点共线时，原式取最小值.此时△EBC ∽△DAC ，有224===DA EB CA BC ,从而x =AC =3831=AB .故原式取最小值时，x =38. (3)如图， 原式=[]2222222)24()13()32()01(032--0y x y x -+-+-+-+-+）（）（=AB +BC +CD ≥AD ，其中A （-2,0），B （0，3x ）,C (1,2y ),D (3,4),并且当点B ，C 在线段AD 上时，原式取得最小值，此时5423=x ，5432=y .例5. 由S =ay m y n a 2)(22+--，得an -S +2ay =a 22n y -，两边平方，经整理得0)()(4322222=+-+-+m a S an y S an a y a .因为关于y 的一元二次方程有实数解，所以[][]0)(34)(422222≥+-⨯--m a S an a S an a ，可化为2223-m a an S ≥）（.∵S >an ，∴am an S 3-≥，即am an S 3+≥，故S 最小=am an 3+.例6（1）设x 1≥1，x 2≥2，x k ≥k ，于是1+2+…+k ≤x 1+x 2+…+x k = 2019，即120192k(k )+≤ k (k +1)≤4006，∵62×63=3906<4006<4032=63×64，∴k ≤62. 当x 1=1，x 2=2，…x 61=61，x 62=112时，原等式成立，故k 的最大可能值为62.（2） 若取⎩⎨⎧=+=-222ba cb ac ，则2)1(2+=b b c 由小到大考虑b ，使2)1(+b b 为完全平方数.当b =8时，c 2=36，则c =6，从而a =28.下表说明c 没有比6更小的正整数解.显然，表中c 4-x 3的值均不是完全平方数，故cA 级1．57- 111- 2．1 3．14 提示：y =5－x ,z =4－x ，原式=3(x －3)2+14． 4．A 提示：原式=27－(a +b +c )2． 5．D 6．C 7．(1)y =－x +1000(500≤x ≤800) (2)①S =(x －500)(－x +1000)=－x 2+1500x －500000(500≤x ≤800);②S －(x －750)2+62500,即销售单价定为750时，公司可获最大毛利润62500元，此时销量为250件． 8．（1）－4≤m ≤2 （2）设方程两根为x 1，x 2，则x 12+x 22=4(m －34)2+1034，由此得x 12+x 22最小值为1034，最大值为101． 9．设a 2－ab +b 2=k ，又a 2+ab +b 2=1②，由①②得ab =12(1－k )，于是有（a +b )2=12(3－k )≥0，∴k ≤3，从而a +b =．故a ，b 是方程t 2t +12k -=0的两实根，由Δ≥0，得133k ≤≤． 10．设A （x 1,0)，B （x 2，0)，其中 x 1，x 2是方程ax 2+bx +c =0的两根，则有x 1+x 2=b a -<0，x 1x 2=ca>0，得x 1<0，x 2<0，由Δ=b 2－4ac >0，得b >|OA |=|x 1|<1，|OB |=|x 2|<1，∴－1<x 1<0，－1<x 2<0，于是ca=x 1x 2<1，c <a ．由于a 是正整数，已知抛物线开口向上，且当x =－1时，对应的二次函数值大于0，即a －b +c >0，a +c >b ．又a ，b ，c 是正整数，有a +c ≥b+1，从而a +c ，则211,12>≥，于是a >4，即a ≥5，故b≥b ≥5．因此，取a =5，b =5，c =1，y =5x 2+5x +1满足条件，故a +b +c 的最小值为11． 11．（1）该设备投入使用x 天，每天平均损耗为y =11111[500000(0500)(1500)(2500)(500)]4444x x -+⨯++⨯++⨯++++=11(1)[500000500x ]42x x x -++⨯=500000749988x x ++． (2)y =500000749988x x ++7749999988≥=．当且仅当5000008xx =，即x =2000时，等号成立．故这台设备投入使用2000天后应当报废．B 级 1．20 提示：a 2－8b ≥0，4b 2－4a ≥0，从而a 4≥64b 2≥64a ，a ≥4，b 2≥4． 2．4 提示：构造方程． 3． 提示：设经过t 小时后，A ，B 船分别航行到A 1，B 1，设AA 1=x ，则BB 1=2x ，B 1A 1=4．D 提示：a 2+b 2≥2ab ，c 2+d 2≥2cd ，∴a 2+b 2+c 2+d 2≥2(ab +cd )≥．∴ab +cd ≥2，同理bc +ad ≥2，ac +bd ≥2． 5．A 提示：x =s －2≥0,y =5－43s ≥0，z =1－13s ≥0，解得2≤s ≤3，故s 的最大值与最小值的和为5． 6．A 提示：|AB ，C (2125,24k k k -++-），ABC S =k 2+2k +5=(k +1)2+4≥4． 7．设此商品每个售价为x 元，每日利润为S 元．当x ≥18时，有S =[60－5（x －18)](x －10)=－5(x －20)2+500，即当商品提价为20元时，每日利润为500元；当x ≤18时，S =[60+10（18－x )](x －10)=－10(x －17)2+490，即当商品降价为17元时，每日利润最大，最大利润为490元，综上，此商品售价应定为每个20元． 8．设对甲、乙两种商品的资金投入分别为x ，(3－x )万元，设获取利润为s ，则s 15x =s －15x 两边平方，经整理得x 2+(9－10s )x +25s 2－27=0，∵关于x 的一元二次方程有实数解，∴（9－10s )2－4×（25s 2－27)≥0，解得1891.05180s ≤=，进而得x =0.75（万元），3－x =2.25(万元）．即甲商品投入0.75万元，乙商品投入2.25万元，获得利润1.05万元为最大． 9．y =5－x －z ，代入xy ＋yx ＋zx =3，得x 2＋(z －5)x ＋(z 2－5z ＋3)=0．∵x 为实数，∴Δ=(z －5)2－4(z 2－5z ＋3)≥0，解得－1≤z ≤133,故z 的最大值为133，最小值为－1． 10．设b c x a b==，则b =ax ，c =ax 2，于是，a ＋b ＋c =13，化为a (x 2＋x ＋1)=13．∵a ≠0，∴x 2＋x ＋1－13a =0 ①．又a ，b ，c 为整数，则方程①的解必为有理数，即Δ=52a－3>0，得到1≤a ≤523，为有理数，故1≤a ≤16．当a =1时，方程①化为x 2＋x －12=0，解得x 1=－4，x 2=3． 故a min =1，b =－4，c =16 或a min =1，b =3，c =9．当a =16时，方程①化为x 2＋x ＋316=0．解得x 1=－34，x 2=－14．故a min =16，b =－12，c =9；或a min =16，b =－4，c =1． 11．设x 1，x 2，…，x n 中有r 个－1，s 个1，t 个2，则219499r s t r s t -++=⎧⎨++=⎩，得3t ＋s =59，0≤t ≤19．∴x 13＋x 23＋…＋x n 3=－r ＋s ＋8t =6t ＋19．∴19≤x 13＋x 23＋…＋x n 3≤6×19＋19=133．∴在t =0，s =59，r =40时，x 13＋x 23＋…＋x n 3取得最小值19；在t =19，s =2，r =21时，x 13＋x 23＋…＋x n 3取得最大值133． 12．∵把58写成40个正整数的和的写法只有有限种，∴x 12＋x 22＋…＋x 402的最大值和最小值存在．不妨设x 1≤x 2≤…≤x 40．若x 1>1，则x 1＋x 2=(x 1－1)＋(x 2＋1)，且(x 1－1)2＋(x 2＋1)2=x 12＋x 22＋2(x 2－x 1)＋2>x 12＋x 22．于是，当x 1>1时，可以把x 1逐步调整到1，此时，x 12＋x 22＋…＋x 402的值将增大．同理可以把x 2，x 3，…，x 39逐步调整到1，此时x 12＋x 22＋…＋x 402的值将增大．从而，当x 1，x 2，…，x 39均为1，x 40=19时，x 12＋x 22＋…＋x 402取得最大值，即A =22239111+++个＋192=400．若存在两个数x i ，x j ，使得x j －x i ≥2（1≤i ＜j ≤40），则（x i ＋1)2＋(x j －1)2=x i 2＋x j 2－2(x i －x j －1)<x i 2＋x j 2．这表明，在 x 1，x 2，…，x 40中，若有两个数的差大于1，则把较小的数加1，较大的数减1此时，x 12＋x 22＋…＋x 402的值将减小，因此，当x 12＋x 22＋…＋x 402 取得最小值时，x 1，x 2，…，x 40中任意两个数的差都不大于1． 故 当x 1=x 2=…=x 22=1，x 23=x 24=…=x 40=2时，x 12＋x 22＋…＋x 402取得最小值，即222111+++22个222222+++⋯+=94从而，A+B=494.。