西安工业大学2018线性代数考试试题

合集下载

2018考研数学线性代数真题及考点解析

承载梦想启航为来只为一次考上研2018考研数学线性代数真题及考点解析2018年考研数学，线代代数部分，从总体上来说还是比较稳定的，没有太大的波动。

从历年真题也能够看的出来，有些题目改编自以往的真题，好多年前题目重新回炉，编制新题。

接下来我们从两点来分析考研数学，线代部分。

同学们说我没有见过这个考题，命题人可能把数学一的考题修一修，修成数学二的题，也可能把数学二的题修一修，修成数学三的题。

今年的卷子都有一个大题，二次型，平方+平方+平方等于0，我们都知道，平方+平方+平方等于0，意味着每一个小括弧都等于0，这样就构成了三个子方程罗列在一起就是一道方程组的题，这种考法在很久以前数学一考过。

现在摇身一变，变成了一二三方程组的考题。

线性代数的的题以真题为主，反复的练和反复的琢磨，要把数学一二三的真题混搭一起练，这是给19考生的一点建议。

考点上还是围绕代数的主干知识点。

线性代数在考卷中，只有5到题目，两个选择一个填空两个解答，5道题34分考一本书，自然这5到题，命题人考代数的核心主干的知识作为5道题的考查对象。

比如今年来来回回都是把重点放在了书的后半部分，二次型和方程组等等这些知识点上，这是代数理论性、使用性和综合性都是最高的一部分了。

我们一开始学线代代数从行列式到方程组，这属于代数的基础。

到后面向量和方程组到核心理论的部分，最后两章特征值和二次型是综合应用的环节。

历年的代数题比较偏重于最后的几章考查，这是我说目前代数的考研形式，考题的难度和考题的特征。

大学线性代数试题及答案

大学线性代数试题及答案一、选择题（每题5分，共20分）1. 设矩阵A是一个n阶方阵，若A的行列式|A|=0，则矩阵AA. 可逆B. 不可逆C. 一定是对角矩阵D. 一定是单位矩阵答案：B2. 向量组α1, α2, ..., αn线性无关的充分必要条件是A. 它们的坐标成比例B. 它们的坐标不成比例C. 它们的线性组合系数不全为零D. 它们的线性组合系数全为零答案：B3. 设A是m×n矩阵，B是n×m矩阵，则AB一定是A. m阶方阵B. n阶方阵C. m阶方阵或n阶方阵D. 零矩阵答案：A4. 若矩阵A满足A^2=A，则称矩阵A为幂等矩阵，那么幂等矩阵A. 一定是对角矩阵B. 一定是单位矩阵C. 一定是对称矩阵D. 以上都不对答案：D二、填空题（每题5分，共20分）1. 设A是3阶方阵，且|A|=2，则|2A|=______。

答案：42. 若向量α=(1, 2, 3)，β=(4, 5, 6)，则向量α与β的点积为______。

答案：223. 设矩阵A的特征值为λ1, λ2, ..., λn，则矩阵A^T的特征值为______。

答案：λ1, λ2, ..., λn4. 设A是3阶方阵，且A^(-1)存在，则A^(-1)A=______。

答案：E三、简答题（每题10分，共30分）1. 简述线性方程组有唯一解的条件。

答案：线性方程组有唯一解的条件是系数矩阵的行列式不为零。

2. 解释什么是特征值和特征向量，并给出求特征值和特征向量的方法。

答案：特征值是方阵A的标量λ，使得存在非零向量x，满足Ax=λx。

特征向量是与特征值对应的非零向量x。

求特征值和特征向量的方法是先求矩阵的特征多项式，然后解方程求得特征值，再将特征值代入方程组求得特征向量。

3. 说明什么是矩阵的秩，并简述求矩阵秩的方法。

答案：矩阵的秩是指矩阵中线性无关行（列）的最大数目。

求矩阵秩的方法通常是通过初等行变换将矩阵化为阶梯形矩阵，然后计算非零行的数量。

西安工业大学高数期末考试题附标准答案试题

高等数学(H)期末参考答案、填空题(每小题 3分，共36 分)u = ln ..x 2• y 2• z 2，则它在点 M °(1, -1,1)处地方向导数地最大值为f (x, y) =2x 2 ax xy 22y 在点(1, -1)处取得极值，则常数 a =「5.7.设平面曲线L 为下半圆周y 二 - .1 - x28.设匕为曲面z = . x 2 y 2在0岂z 乞1地部分，贝U I I xdS 二0 .10.设y 1, y 2, y 是微分方程 9 p(x)y ' q(x)y 二f (x)地三个不同地解，且 y —社=常 y 2 -y 3数，则微分方程地通解为C’y , -y 2) • C 2(y 2 - y 3) * % .2 21 2，贝U [ (x + y ) ds = (1 -ds = ? 4 兀=三5.空线 y 2 二 2x, z 2 = 1「x 在点 (>,J 处地切线方程为1 x --2 1=_y -1 .2 z ―— 2 1 一 2i 22 2x _x 26.改变积分次序：I dx ,f (x, y)dy -1 1 • 1 _y°dy 亠口？ f(x,y)dx .L 1 1.lim 1 —X f1 xy-V二 lim i 1 — xy丿劣xy 丿 Jlim 1 丄阚Ixy 丿Hr 12.函数z二z(x, y)由方程e^ sin 》=0确定，则 —=xcyF yF1 y-cos- x x xz xeco 显X ~2 xz x e3.设函数4.设函数 9.设 f (x) n -xe1,--•：：： x ■ 0 ,则其以2兀为周期地傅里叶级数在处收敛于 0 岂 x ：二'11.函数f(x) =1 展开为x 地幕级数地形式为 a 」yx n(-2, 2).2—x n^2n41112.微分方程y y = xe x地通解为Cx - xe xx-------二、计算下列各题(每小题6分，共18分)1•设z 二f(y,e xy)，y =(x)，其中f,「均为一阶可微函数，求 x解:虫=f 「yx 2 yf 2 e xy( y xy)dxx二2f 2 e xy( (x) X : (x))x2.求曲面z =4(x 2y 2)与平面z = 2所围立体地体积. 2解：所围立体在xoy 面地投影域D ： x2• y 2_ 4，所围立体地体积V = M[4_；(x 2+y 2)] _2Rxdy = 2JJdxdy —1 2二.22d ： r rdr =8 二-4 二-4 ■:解：设曲面在第一卦限地切点地坐标为M (x, y, z)，令F (x, y,z) = x 22y 23z 2「66，则切平面地法向量n = (F x , F y , F Z )M 二(2x, 4y, 6z),已知平面x y ^1地法向量n 1 =(1, 1, 1)依题意n//ni ，即空=41 =央令t1 1 1代入曲面方程中解地 x =6, y =3, z=2，即切点坐标为 M (6, 3, 2). 三、计算下列各题(每小题6分，共18分)1.设门是由锥面.x 2 y 2与半球面z= J -x 2 -y 2围成地空间区域,dz dx(x 2 y 2)dxdyD3.在曲面x 2 2y 23z-66上第一卦限部分求一点，使该点地切平面与已知平面2x s(x)_ (1 _x)2 _1 xx2(5 (1))，1s(2)二x+ x 2_ I X(2n-1)于 . n 1 2 _(1 - X) 1 x=2边界地外侧，求曲面积分[jxdydz- ydzdx • zdxdy .Q(x, y,z)=y ， R(x, y,z) = z ，由高斯公式有cP cQcR ■i I xdydz ydzdx zdxdy 二 ()dv ¥ ¥r rr L\、x _y_z= 3 ! i idv = 3 o dr °4d [；r 2sin ： drQ=3 2 二(1 2) [=(2-、2)二 2 3 13 572.写出级数--飞 N •…地通项，判别该级数地敛散性.若级数收敛时，试求其和2 2 2 2limUnl^im 1,n = u n n=2 2n —12由比值审敛法知该级数收敛.令解：已知 P(x, y,z) = x , 解：该数项级数地通项为 U n 二2n -1 2n;级数为正项级数，由于s(x) oOoo八(2n -1) x n= 2x'二 nxn -1oOn=2x®(x)-s 2(x) x (—1,1)，x :: Xo3(t)dt 二 I 。

2013年西安工业大学线性代数考试试题及答案评分标准(A卷)

2012级线性代数考试试题（A 卷）2012－2013学年第2学期5小题，每小题4分，总计20分）1、设n 阶方阵,,A B C 满足关系式ABC E =，其中E 为n 阶单位矩阵，则必有（）. (A) ACB E =； (B) CBA E =；（C ）BAC E =；（D ）BCA E =.2、设A 、B 均是3阶矩阵，且2, 2A B ==-，则112A B *-=（）（A ）2-；（B ）1-；（C ）21-；（D ）41-. 3、设向量组321,,ααα线性无关，向量1β能由321,,ααα线性表出，向量2β不能由321,,ααα线性表出，则必有（）（A ）121,,βαα线性相关；（B ）121,,βαα线性无关；（C ）221,,βαα线性相关；（D ）221,,βαα线性无关. 4、设线性方程组(Ⅰ) b Ax =,其导出组(Ⅱ) 0=Ax ,则必有( ).（A ）(Ⅰ)有无穷多解,则(Ⅱ)仅有零解；（B ）(Ⅰ)仅有唯一解,则(Ⅱ)仅有零解；（C ）若(Ⅱ)有非零解,则(Ⅰ)有无穷多解；（D ）若(Ⅱ)仅有零解,则(Ⅰ)有唯一解.5、设1111111111111111A ⎛⎫ ⎪⎪= ⎪⎪⎝⎭，4000000000000000B ⎛⎫⎪⎪= ⎪⎪⎝⎭，则A 与B （）.(A) 合同且相似； (B) 合同但不相似；(C) 不合同但相似； (D) 不合同且不相似. 5小题，每小题4分，总计20分）1. 已知414243123452221127, 312451112243150D A A A ==++=则，=+4544A A ;2. 已知A 21401134⎛⎫= ⎪-⎝⎭，131012131402B ⎛⎫ ⎪- ⎪= ⎪- ⎪-⎝⎭，则()TAB =___________; 3. 设01000010********A ⎛⎫ ⎪⎪= ⎪⎪⎝⎭，则3A 的秩为______; 4. 设三阶方阵A 的特征值分别为1, 2, 3-，则2A A E +-= ____; 5. 已知2221231231223(,,)22f x x x x x x x x tx x =++++为正定的，则参数t 的取值范围是 .三、（12分）设423110,123A ⎛⎫ ⎪= ⎪ ⎪-⎝⎭且2,AX A X =+ 求X ．四、（10分）求向量组()T3,0,1,21-=α，()T4,2,3,12-=α，()T 1,2,0,33-=α，()T 6,4,2,24-=α的秩及一个极大无关组，并将其余的向量（如果有的话）.用此极大无关组线性表出.五、（12分）求非齐次线性方程组⎪⎩⎪⎨⎧=++++=++++=++++2275532155432722543215432154321x x x x x x x x x x x x x x x 的通解.六、（14分）设211121112A ⎛⎫ ⎪= ⎪ ⎪⎝⎭，判断A 能否对角化，若能，求可逆阵P ，使1P AP -为对角阵，并求20A .12分，其中（1）题5分，（2）题7分)（1）设B A ,是n 阶方阵，且B 可逆，满足O B AB A =++22，证明：A 和AB +都是可逆矩阵； (5分)（2）设向量组,,αβγ线性无关,证明: 向量组,,αββγγα+++也线性无关. (7分)2012~2013学年第2学期期末考试《线性代数》试卷（A ）标准答案和评分标准一、选择题（5二、填空题（5×4分）1. 9, 18-;2. 6207586⎛⎫ ⎪-- ⎪ ⎪-⎝⎭; 3. 1 ; 4. 11 ; 5. 22<<-t三、解：由2AX A X =+，得(2)A E X A -=…………………………………1分由于2232110,210,121A E A E ⎛⎫ ⎪-=--=-≠ ⎪ ⎪-⎝⎭所以2A E -可逆；于是1(2)X A E A -=-………………………………………………………4分()132231001210012110010110010121001223100~r r A E E ↔-⎛⎫⎛⎫⎪ ⎪-=-- ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭因为211123132(1)226121001121001101021~011011~011011~011011065102065102001164r r r r r r r r r+⨯-++-----⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭13233(1)100143~010*********r r r r r ++⨯---⎛⎫ ⎪-- ⎪⎪-⎝⎭，1143(2)153164A E ---⎛⎫ ⎪-=-- ⎪ ⎪-⎝⎭…………………8分 1143423386(2)1531102961641232129X A E A -----⎛⎫⎛⎫⎛⎫⎪⎪ ⎪=-=--=-- ⎪⎪ ⎪ ⎪⎪ ⎪---⎝⎭⎝⎭⎝⎭故 ………12分四、解：以每个向量作为列构造一个矩阵，对该矩阵施以初等行变换.设()432,,,αααα=A 2132130202243416-⎡⎤⎢⎥--⎢⎥=⎢⎥⎢⎥-⎣⎦……………………..…………2分 1302011200110000⎡⎤⎢⎥⎢⎥−−−→⎢⎥⎢⎥⎣⎦行变换－－⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡−−→−0000110010101001行变换…………………………4分故()3=A r ……………………………………………………………………6分321,ααα，为向量组4321,αα,α,α的一个极大无关组…………………………………8分3214αααα++=……………………………………………………………10分五、解：将该方程组表示为：Ax b =，其中112121234523557A ⎛⎫ ⎪= ⎪ ⎪⎝⎭，12345x x x x x x ⎛⎫⎪⎪ ⎪= ⎪ ⎪⎪⎝⎭，71522b ⎛⎫ ⎪= ⎪ ⎪⎝⎭()3132112127112127123451512345152355722000000r r r r A A b --⎛⎫⎛⎫⎪ ⎪==−−−→ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭2112112127101211011338011338000000000000r r r r -----⎛⎫⎛⎫⎪ ⎪−−−→−−−→ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭………………………4分得同解方程组⎩⎨⎧=+++-=--+8331254325431x x x x x x x x移项得 ⎩⎨⎧+---=-++-=8331254325431x x x x x x x x …………………………………………6分取3450x x x ===，得线性方程组的一个特解：0(18000)T η=-……………………………………………………8分在对应的齐次线性方程组134********x x x x x x x x =-++⎧⎨=---⎩中，取345100x x x ⎛⎫⎛⎫ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭，010⎛⎫ ⎪ ⎪ ⎪⎝⎭及001⎛⎫⎪⎪ ⎪⎝⎭得基础解系为：111100ξ-⎛⎫ ⎪- ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭，223010ξ⎛⎫ ⎪- ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭，313001ξ⎛⎫ ⎪- ⎪⎪= ⎪ ⎪ ⎪⎝⎭………………………10分于是所求的通解为：1231234512111338100001000010x x x x k k k x x --⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪--- ⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪ ⎪==+++ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭，（123,,k k k ∈ℜ）. ………………………………………………………………………………………12分六、解：令()()2211121410112A E λλλλλλ--=-=---=-得的特征值为14λ=，231λλ==………………………………..…….3分1 对应14λ=，解方程组()40A E x -=由2111014121011112000r A E --⎛⎫⎛⎫⎪ ⎪-=-−−→- ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭得基础解系 1111p ⎛⎫⎪= ⎪ ⎪⎝⎭， ………………….………………………………5分2 对应132==λλ，解方程组()0=-X E A由111111111000111000r A E ⎛⎫⎛⎫ ⎪ ⎪-=−−→ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭得基础解系 2110p -⎛⎫ ⎪= ⎪ ⎪⎝⎭，3101p -⎛⎫⎪= ⎪ ⎪⎝⎭， ……………………………………7分因此，三阶矩阵A 有三个线性无关的特征向量，所以它可相似对角化…………..8分.令()123111,,110101P p p p --⎛⎫ ⎪== ⎪ ⎪⎝⎭，则1411P AP -⎛⎫ ⎪= ⎪ ⎪⎝⎭于是1411A P P -⎛⎫⎪= ⎪ ⎪⎝⎭， 20201411A P P -⎛⎫⎪= ⎪ ⎪⎝⎭……………………………10分计算得 111111213112P -⎛⎫⎪=-- ⎪ ⎪--⎝⎭………………………………………………12分所以2020202020120202020202044241411141424131414142A P P -⎛⎫⎛⎫+--⎪ ⎪==-+-⎪ ⎪ ⎪ ⎪--+⎝⎭⎝⎭…………….……14分七、(1) 证明: 由O B AB A =++22,得2)(B B A A -=+, ………………1分两边取行列式,由方阵行列式性质及B 可逆,有()012≠-=+B B A A n, ………………………………………3分从而 0,0≠+≠B A A 且.故 B A A +和都是可逆矩阵 …………………………………… 5分（2）证明：方法一（定义法）设 123()()()0k k k αββγγα+++++=，……………………………1分必有 131232()()()0k k k k k k αβγ+++++= （*） …………… 2分已知,,αβγ线性无关，所以（*）式的系数全为零，即⎪⎩⎪⎨⎧=+=+=+.0,0,0232131k k k k k k ……………4分其系数行列式02110011101≠=， ……………5分所以上述关于321,,k k k 的方程组只有零解，即0321===k k k ， ………6分故向量组,,αββγγα+++也线性无关 …………………………………7分方法二（利用矩阵的秩）因为()()101,,,,110011αββγγααβγ⎛⎫ ⎪+++= ⎪ ⎪⎝⎭…………2分由于10111020011=≠，故101110011⎛⎫⎪⎪ ⎪⎝⎭可逆，………………………………4分所以()(),,,,3R R αββγγααβγ+++==，…………………………6分故,,αββγγα+++线性无关………………………………………7分编辑：张永锋2013/6/9。

线性代数大学试题及答案

线性代数大学试题及答案一、选择题（每题5分，共20分）1. 设矩阵A为3阶方阵，且|A|=2，则矩阵A的伴随矩阵|adj(A)|的值为（）。

A. 4B. 8C. 2D. 1答案：B2. 若向量a=(1, 2, 3)，向量b=(2, 3, 4)，则向量a和向量b的点积为（）。

A. 11B. 12C. 13D. 14答案：C3. 设矩阵A和矩阵B为同阶方阵，且AB=I，则矩阵A和矩阵B互为（）。

A. 伴随矩阵B. 逆矩阵C. 转置矩阵D. 正交矩阵答案：B4. 设矩阵A为3阶方阵，且A的特征多项式为f(λ)=λ(λ-1)(λ-2)，则矩阵A的特征值为（）。

A. 0, 1, 2B. 0, 1, 3C. 1, 2, 3D. 2, 3, 4答案：A二、填空题（每题5分，共20分）1. 设矩阵A=\[\begin{bmatrix}1 & 2 \\ 3 & 4\end{bmatrix}\]，则矩阵A的行列式|A|=______。

答案：-22. 设向量a=(1, 2)，向量b=(3, 4)，则向量a和向量b的叉积为向量c=(______, ______)。

答案：-2, 63. 设矩阵A=\[\begin{bmatrix}1 & 2 \\ 3 & 4\end{bmatrix}\]，矩阵B=\[\begin{bmatrix}2 & 1 \\ 4 & 3\end{bmatrix}\]，则矩阵A和矩阵B的乘积AB=______。

答案：\[\begin{bmatrix}10 & 11 \\ 22 & 25\end{bmatrix}\]4. 设矩阵A的特征值为λ1=2，λ2=3，则矩阵A的特征多项式为f(λ)=______(λ-2)(λ-3)。

答案：(λ-2)(λ-3)三、解答题（每题10分，共60分）1. 已知矩阵A=\[\begin{bmatrix}1 & 2 \\ 0 & 3\end{bmatrix}\]，求矩阵A的逆矩阵。

2018-2019学年线性代数试题及答案.ppt

1 1 2 23, 2 1 2 3, 3 1 2 ,
线性无关。
3、设4阶方阵A满足条件 3E 2A 0, AAT 2E, A 0 求A的伴随矩阵 A 的一个特征值。
五、解矩阵方程（满分7分）
2 设矩阵 A 3
2 6
1 3
三、计算行列式（每小题5分，共10 分）
410 5 1、 D 3 1 1 2
2 0 6 4 2 5 3 2
218
1 a1 1
2、Dn 1 1
1 1 a2
1 1
1 1 1 a3 1
其中 ai 0 (i 1,2, , n)
1
1

1

n1 n (1 i1 ai ) i1 ai
一、填空题（每小题2分，共14分）
1、设A是3阶矩阵，且 A ，1A 是A的伴随矩阵，则：
2
(3A)1 2A
16 27
2、设四元非齐次线性方程组 Ax b 的系数矩阵A的秩为3，且
1 (1,2,3,4)T ,2 (2,3,4,5)T 是该方程组的两个解，则
方程组 Ax b 的通解为: (1,2,3,4)T k(1,1,1,1)T , k R
则 A B 32
2 0 0
2 0 0
6、已知矩阵 A 0 0 1 与 B 0 y 0 相似，
0 1 x
0 0 1
则x 0
y 1
7、已知实二次型
f (x1, x2 , x3 ) a(x12 x22 x32 ) 4x1x2 4x1x3 4x2 x3
0
可知

3 2
是A的一个特征值。

西安交大西工大考研备考期末复习线性代数测试题及答案

1 1 1 1. 2 1 0 ,
1 1 0
1 1 1 1
2.
1 1
1 1
1 1
1 1
1 1 1 1
四、证明题(每小题8分，共16分)
1. A, B为两个n阶方阵,且 ABA B1,证明:
秩E AB 秩E AB n.
2. 设A为m n实矩阵,证明: 秩AT A 秩A.
线性无关?
3. 求实数a和b, 使向量组1 1,1,0,0,2 0,1,1,0 3 0,0,1,1与向量组1 1, a, b,1, 2 2,1,1,2, 3 0,1,2,1等价.
三、证明题 (每小题8分，共24分)．
1.设A为m n矩阵, B为n m矩阵,且m n,试证明
det(AB) 0.
1 1 2 31 3 1 1 2 2 1. D5 2 3 1 1 0 1 2 3 01 2 2 1 1 0
x y y y z x y y 2. Dn z z x y
z z zx
三、解答题(9分)．
问 , 取何值,齐次方程组
x1 x2 x1 x2
x3 x3
0 0
x1 2x2 x3 0
五、(每小题5分，共20分)求下列矩阵．
1 2
3
1n , 2
2 12 1,
3
2;
3
lim
12 0
1 13
1 n 1;
n 0 0 1 5
4
A
1 0
0 1
1 n 0 .
0 0 1
六、(6分)设A
4 1
2 1
3 0,
AB
A
2B,
求
B．
1 2 3
七、(每小题3分,共6分)设n阶矩阵 A 的伴随矩阵为 A ，证明：

线性代数期末试卷及解析(4套全)2018科大

线性代数期末试卷一一、填空题（本题共6小题，每小题4分，满分24分，把答案填在题中横线上）（5）设矩阵210120001⎛⎫ ⎪= ⎪ ⎪⎝⎭A ，矩阵B 满足*2=+ABA BA E ，其中*A 为A 的伴随矩阵，E 是单位矩阵，则||=B __________.解：||=B 19.显然||3=A ，在等式*2=+ABA BA E 两端右乘A 得36=+AB B A (36)-=A E B A 上式取行列式03030||3003=-B故 1||9=B . 方法二：因||3=A ，则*31||||9-==A A将**2=+ABA BA E 移项得 *(2)-=A E BA E 两端取行列式得1||91⋅⋅=B ，故1||9=B .二、选择题（本题8小题，每小题4分，满分32分. 在每小题给出的四个选项中，只有一个是符合题目要求的，把所选项前的字母填在题后的括号内.）（11）设A 是3阶方阵，将A 的第1列与第2列交换得B ，再把B 的第2列加到第3列得C ，则满足=AQ C 的可逆矩阵Q 为（A ）010100.101⎛⎫ ⎪ ⎪ ⎪⎝⎭ （B ）010101001⎛⎫ ⎪ ⎪ ⎪⎝⎭. （C ）010100011⎛⎫ ⎪ ⎪ ⎪⎝⎭. （D ）011100001⎛⎫ ⎪⎪ ⎪⎝⎭.解：（D ）正确. 由题意12=AE B ，其中12010100001⎛⎫⎪= ⎪ ⎪⎝⎭E 为第一种类型初等矩阵，23(1)=BE C ，其中23100(1)011001⎛⎫ ⎪= ⎪ ⎪⎝⎭E 为第三种类型初等矩阵.于是有 1223(1)==AE E C AQ则 1223010100011(1)100011100001001001⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪=== ⎪⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭Q E E与所给答案比较，选（D ）.（12）设,A B 为满足=AB 0的任意两个非零矩阵，则必有（A ）A 的列向量组线性相关，B 的行向量组线性相关. （B ）A 的列向量组线性相关，B 的列向量组线性相关. （C ）A 的行向量组线性相关，B 的行向量组线性相关. （D ）A 的行向量组线性相关，B 的列向量组线性相关. 解：（A ）正确.设A 为m n ⨯矩阵，B 为n p ⨯矩阵，因为 =AB 0故 ()()r r n +≤A B ，其中(),()r r A B 分别表示矩阵,A B 的秩.又因为,A B 皆是非零矩阵，故()0,()0r r >>A B ，所以()r n <A ，()r n <B .因此A 的列秩数，B 的行秩数小于n ，这说明A 的列向量组线性相关，B 的行向量组线性相关，故选（A ）.取101000⎛⎫= ⎪⎝⎭A ，100110⎛⎫⎪= ⎪⎪-⎝⎭B ，则0000⎛⎫= ⎪⎝⎭AB ，由B 的列向量组线性无关知（B ）、（D ）错误.取101010-⎛⎫= ⎪⎝⎭A ，100110⎛⎫⎪= ⎪ ⎪-⎝⎭B ，则0000⎛⎫= ⎪⎝⎭AB ，由A 的行向量组线性无关知（C ）错误.三、解答题（本题共9小题，满分94分. 解答应写出文字说明、证明过程或演算步骤.）（20）（本题满分9分）设有齐次线性方程组121212(1)0,2(2)20,(2)()0,n nn a x x x x a x x n nx nx n a x ++++=⎧⎪++++=⎪≥⎨⎪⎪++++=⎩L L L L L试问a 取何值时，该方程组有非零解，并求出其通解.解法1 对方程组的系数矩阵A 作初等行变换，有11111111222220000aa a a a n n n n a na a ++⎛⎫⎛⎫ ⎪ ⎪+- ⎪ ⎪=→= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪+-⎝⎭⎝⎭A B L L L L L L L L L L. 当0a =时，()1r n =<A ，故方程组有非零解，其同解方程组为120n x x x +++=L ，由此得基础解系为T T T121(1,1,0,,0),(1,0,1,,0),,(1,0,0,,1)n -=-=-=-ηηηL L L L ，于是方程组的通解为1111n n x k k --=++ηηL ，其中11,,n k k -L 为任意常数. 当0a ≠时，对矩阵B 作初等行变换，有(1)1111000221002100.001001n n a a n n +⎛⎫++⎛⎫ ⎪⎪⎪-⎪-→→⎪ ⎪⎪ ⎪ ⎪ ⎪-⎪⎝⎭-⎝⎭B L L L L L L L L LL可知(1)2n n a +=-时，()1r n n =-<A ，故方程组也有非零解，其同解方程组为 1213120,30,0,n x x x x nx x -+=⎧⎪-+=⎪⎨⎪⎪-+=⎩M由此得基础解系为T(1,2,,)n =ηL ，于是方程组的通解为x k =η，其中k 为任意常数. 解法2 方程组的系数行列式为111112222(1)||.2n aa n n a a nnn n a-+++⎛⎫==+ ⎪⎝⎭+A L L L LL当||0=A ，即0a =或(1)2n n a +=-时，方程组有非零解.当0a =时，对系数矩阵A 作初等行变换，有1111111122220000,0000n n n n ⎛⎫⎛⎫ ⎪ ⎪⎪ ⎪=→ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭A L L L L L L L L L L 故方程组的同解方程组为120,n x x x +++=L 由此得基础解系为T T T121(1,1,0,,0),(1,0,1,,0),,(1,0,0,,1)n -=-=-=-ηηηL L L L ，于是方程组的通解为1111n n x k k --=++ηηL ，其中11,,n k k -L 为任意常数.当(1)2n n a +=-时，对系数矩阵A 作初等行变换，有 11111111222220000aa a a an n n n a na a ++⎛⎫⎛⎫⎪⎪+-⎪ ⎪=→ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪+-⎝⎭⎝⎭A L L LLL L L L L L . 1111000021002100.00101a n n +⎛⎫⎛⎫⎪⎪--⎪ ⎪→→ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭L L LL L L L L L L 故方程组的同解方程组为1213120,30,0,n x x x x nx x -+=⎧⎪-+=⎪⎨⎪⎪-+=⎩M由此得基础解系为T(1,2,,)n =ηL ，于是方程组的通解为x k =η，其中k 为任意常数. （21）（本题满分9分）设矩阵12314315a -⎛⎫⎪=-- ⎪ ⎪⎝⎭A 的特征方程有一个二重根，求a 的值，并讨论A 是否可相似对角化.解：A 的特征多项式为1232201431431515a aλλλλλλλ-----=-------11010(2)143(2)13315115aa λλλλλλ-=--=---------2(2)(8183)a λλλ=--++.若2λ=是特征方程的二重根，则有22161830a -++=，解得2a =-.当2a =-时，A 的特征值为2,2,6，矩阵1232123123-⎛⎫⎪-=- ⎪ ⎪--⎝⎭E A 的秩为1，故2λ=对应的线性无关的特征向量有两个，从而A 可相似对角化.若2λ=不是特征方程的二重根，则28183a λλ-++为完全平方，从而18316a +=，解得23 a=-.当23a=-时，A的特征值为2,4,4，矩阵32341032113⎛⎫⎪-⎪-= ⎪⎪--⎪⎝⎭E A的秩为2，故4λ=对应的线性我关的特征向量只有一个，从而A不可相似对角化.线性代数期末试卷二一、填空题（本题共6小题，每小题4分，满分24分. 把答案填在题中的横线上.）（6）同数学（一）一、（5）.二、选择题（本题共8小题，每小题4分，满分32分. 在每小题给出的四个选项中，只有一个是符合题目要求的，把所选项目前的字母填在题后的括号内.）（13）同数学（一）二、（11）. （14）同数学（一）二、（12）.三、解答题（本题共9小题，满分94分. 解答应写出文字说明、证明过程或演算步骤.）（22）（本题满分9分）设有齐次线性方程组1234123412341234(1)0,2(2)220,33(3)30,444(4)0,a x x x x x a x x x x x a x x x x x a x ++++=⎧⎪++++=⎪⎨++++=⎪⎪++++=⎩试问a 取何值时，该方程组有非零解，并求出其通解.解法1 对方程组的系数矩阵A 作初等行变换，有111111112222200.33333004444400aa a a a a a a a a a ++⎛⎫⎛⎫ ⎪ ⎪+- ⎪ ⎪=→= ⎪ ⎪+- ⎪ ⎪ ⎪ ⎪+-⎝⎭⎝⎭A B 当0a =时，()14r =<A ，故方程组有非零解，其同解方程组为 12340x x x x +++=.由此得基础解系为T T T123(1,1,0,0),(1,0,1,0),(1,0,0,1)=-=-=-ηηη，于是所求方程组的通解为112233k k k =++x ηηη，其中123,,k k k 为任意常数. 当0a ≠时，11111000021002100,3010301040014001a a ++⎛⎫⎛⎫ ⎪ ⎪--⎪ ⎪→→ ⎪ ⎪-- ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭B 可知10a =-时，()34r =<A ，故方程组也有非零解，其同解方程组为12131420,30,40,x x x x x x -+=⎧⎪-+=⎨⎪-+=⎩由此得基础解系为 T(1,2,3,4)=η，于是所求方程组的通解为 k =x η，其中k 为任意常数. 解法2 方程组的系数行列式311112222||(10)33334444aa a a a a++==+++A .当||0=A ，即0a =或10a =-时，方程组有零解. 当0a =时，对系数矩阵A 作初等行变换，有11111111222200003333000044450000⎛⎫⎛⎫⎪⎪⎪ ⎪=→ ⎪ ⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭A ，故方程组的同解方程组为12340.x x x x +++= 其基础解系为T T T123(1,1,0,0),(1,0,1,0),(1,0,0,1)=-=-=-ηηη，于是所求方程组的通解为112233k k k =++x ηηη，其中123,,k k k 为任意常数. 当10a =-时，对A 作初等行变换，有911191112822201000337330010*******0010--⎛⎫⎛⎫⎪ ⎪--⎪ ⎪=→⎪ ⎪-- ⎪ ⎪⎪ ⎪--⎝⎭⎝⎭A91110000210021003010301040014001-⎛⎫⎛⎫⎪⎪--⎪ ⎪→→⎪ ⎪-- ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭，故方程组的同解方程组为2131412,3,4,x x x x x x =⎧⎪=⎨⎪=⎩其基础解系为T(1,2,3,4)=η，于是所求方程组的通解为x k =η，其中k 为任意常数. （23）（本题满分9分）同数学（一）三、（21）.线性代数期末试卷三一、填空题（本题共6小题，每小题4分，满分24分. 把答案填在题中横线上）（4）二次型222123122331(,,)()()()f x x x x x x x x x =++-++的秩为_________.解：秩为 2 .222123122331(,,)()()()f x x x x x x x x x =++-++ 222123121323222222x x x x x x x x x =++++-于是二次型f 的表示矩阵为211121112⎛⎫ ⎪=- ⎪ ⎪-⎝⎭A易求得()2r =A ，故二次型f 的秩为2.二、选择题（本题8小题，每小题4分，满分32分. 在每小题给出的四个选项中，只有一个是符合题目要求的，把所选项前的字母填在题后的括号内.）（12）设n 阶矩阵A 与B 等价，则必有（A ）当||(0)a a =≠A 时，||a =B . （B ）当||(0)a a =≠A 时，||a =-B . （C ）当||0≠A 时，||0=B . （D ）当||0=A 时，||0=B . 解：（D ）正确.因为n 阶矩阵A 与B 等价，故存在n 阶可逆矩阵,P Q 使 =PAP B故 ||||||||=B P A Q当||0=A 时，自然有||0=B ，故（D ）正确.当||0≠A 时，由||,||P Q 皆不为零，故||0≠B ，所以（C ）错误.当||0a =≠A 时，||||||a =B P Q ，仅由A 与B 等价，无法推出||||1=±P Q ，故（A ）、（B ）不正确.当,A B 相似时，（A ）才正确.（13）设n 阶矩阵A 的伴随矩阵*≠A 0，若1234,,,ξξξξ是非齐次线性方程组=Ax b 的互不相等的解，则对应的齐次线性方程组=Ax 0的基础解系.（A ）不存在. （B ）仅含一个非零解向量. （C ）含有两个线性无关的解向量. （D ）含有三个线性无关的解向量. 解：（B ）正确.因*=A 0，故*A 中至少有一个非零元素. 由于*A 中元素恰为A 的1n -阶代数余子式所组成，故A 至少有一个1n -阶子式非零，这表明()1r n ≥-A .现断言()r n ≠A ，否则A 可逆，则线性方程组=Ax b 有惟一解，这与12,ξξ是非齐次线性方程组=Ax b 不同的解矛盾.由此必有()1r n =-A ，所以齐次线性方程组=Ax 0的解空间维数为(1)1n n --=，即=Ax 0的基础解仅含一个非零解向量. 可见（B ）正确，（A ）错误.尽管从1234,,,ξξξξ是非齐次线性方程组=Ax b 的互不相等的解，可以得出=Ax 0有三个不同的非零解，如121314,,,---ξξξξξξ但是它们是成比例的线性相关解，也就是说=Ax 0不会有两个，更不会有三个线性无关的解向量，即（C ）、（D ）不正确.三、解答题（本题共9小题，满分94分. 解答应写出文字说明、证明过程或演算步骤.）（20）（本题分13分）设T T T 123(1,2,0),(1,2,3),(1,2,2)a a b a b ==+-=---+ααα，T(1,3,3)=-β. 试讨论当,a b为何值时，（I ）β不能由123,,ααα线性表示；（II ）β可由123,,ααα惟一地线性表示，并求出表示式；（III ）β可由123,,ααα线性表示，但表示式不惟一，并求出表示式. 解：设有数123,,k k k ，使得112233k k k ++=αααβ. （*）记123(,,)=A ααα. 对矩阵()Aβ施以初等行变换，有1111()22230323a b a a b -⎛⎫ ⎪=+-- ⎪ ⎪-+-⎝⎭A β111101000a b a b -⎛⎫ ⎪→- ⎪ ⎪-⎝⎭.（I ）当0,a b =为任意常数时，有1111()0010001b -⎛⎫ ⎪=- ⎪ ⎪-⎝⎭A β.可知()()r r ≠A A β. 故方程组（*）无解，β不能由123,,ααα线性表示.（II ）当0a ≠，且a b ≠时()()3r r ==A A β，故方程组（*）有惟一解 123111,,0,k k k a a=-== 则β可由123,,ααα惟一地线性表示，其表示式为1211(1)a a=-+βαα.（III ）当0a b =≠时，对()A β施以初等行变换，有110011()011.0000a a ⎛⎫- ⎪ ⎪⎪=- ⎪ ⎪ ⎪ ⎪⎝⎭A β. 可知()()2r r ==A A β，故方程组（*）有无穷多解，其全部解为123111,(),k k c k c a a=-=+=，其中c 为任意常数.β可由123,,ααα线性表示，但表示式不惟一，其表示式为12311(1)()c c a a=-+++βααα. （21）（本题满分13分）111b b bb b b ⎛⎫ ⎪⎪= ⎪ ⎪ ⎪⎝⎭A L L M M M L. （I ）求A 的特征值和特征向量；（II ）求可逆矩阵P ，使得1-P AP 为对角矩阵. 解：（I ）1º当0b ≠时，11||1b b b b bbλλλλ-------=---E A L LM M ML1[1(1)][(1)]n n b b λλ-=-----.故A 的特征值为121(1),1n n b b λλλ=+-===-L .对于11(1)/n b λ=+-，设A 的属于特征值1λ的一个特征向量为1ξ，则1111[1(1)]1b b b b n b b b ⎛⎫⎪ ⎪=+- ⎪ ⎪ ⎪⎝⎭ξξL L M M M L ，解得T1(1,1,,1)=ξL ，所以全部特征向量为T1(1,1,,1)k k =ξL （k 为任意非零常数）.对于21n b λλ===-L ，解齐次线性方程组[(1)]0b --=E A x ，由111000(1)000b b b b b b b b b b ---⎛⎫⎛⎫⎪ ⎪---⎪ ⎪--=→ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪---⎝⎭⎝⎭E A L L LL M M M M M M L L，解得基础解系T2(1,1,0,,0)=-ξL ，T3(1,0,1,,0)=-ξL ，… …T(1,0,0,,1)n =-ξL .故全部特征向量为2233n n k k k +++ξξξL （2,,n k k L 是不全为零的常数）. 2º当0b =时，特征值11n λλ===L ，任意非零列向量均为特征向量. （II ）1º当0b ≠时，A 有n 个线性无关的特征向量，令12(,,,)n =P ξξξL ，则 1diag{1(1),1,,1}.n b b b -=+---P AP L 2º当0b =时，=A E ，对任意可逆矩阵P ，均有 1-=P AP E .注：T1(1,1,,1)=ξL 也可由求解齐次线性方程组1()λ-=E A x 0得出.线性代数期末试卷四一、填空题（本题共6小题，每小4分，满分24分. 把答案填在题中横线上.）（4）设1010100,001--⎛⎫ ⎪== ⎪ ⎪-⎝⎭A B P AP ，其中P 为三阶可逆矩阵，则200422-=B A _________. 解：300030001⎛⎫ ⎪ ⎪ ⎪-⎝⎭. 由010100001-⎛⎫ ⎪= ⎪ ⎪-⎝⎭A 得2100010001-⎛⎫ ⎪=- ⎪ ⎪⎝⎭A ，故4=A E ，其中E 是3阶单位阵，所以2004=A E .由1-=B P AP 得200412004-==B P A P E于是 20042210020030022010020030001002001-⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪-=-=--= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭BA E A . （5）设33()ij a ⨯=A 是实正交矩阵，且T 111,(1,0,0)a b ==，则线性方程组=Ax b 的解是__________.解：T (1,0,0).在方程=Ax b 两端左乘TAT T =A Ax A b 则 2131T 122232121323331311100a a a a a a a a a a ⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪=== ⎪⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭x A b将 12131a a ⎛⎫ ⎪= ⎪ ⎪⎝⎭x 代回=Ax b 有2131122232121323331311100a a a a a a a a a a ⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪= ⎪⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭由此得22121311a a ++=因A 为实矩阵，故12130a a ==，因此=Ax b 的解为100⎛⎫ ⎪= ⎪ ⎪⎝⎭x .二、选择题（本题共8小题，每小题4分，满分32分. 在每小题给出的四个选项中，只有一个是符合题目要求的，把所选项前的字母填在题后的括号内.）（12）同数学（三）二、（12）.三、解答题（本题共9小题，满分94分. 解答应写出文字说明、证明过程或演算步骤.）（20）（本题满分13分）设线性方程组1234123412340,220,3(2)(4)41,x x x x x x x x x x x x λμλμ+++=⎧⎪+++=⎨⎪+++++=⎩已知T(1,1,1,1)--是该方程组的一个解. 试求（I ）方程组的全部解，并用对应的齐次线性方程组的基础解系表示全部解；（II ）该方程组满足23x x =的全部解.解：将T (1,11,1)--代入方程组，得λμ=. 对方程组的增广矩阵施以初等变换，得 1102112032441λλλλ⎛⎫ ⎪= ⎪ ⎪++⎝⎭A 102101311.002(21)2121λλλλλλ---⎛⎫ ⎪→ ⎪ ⎪---⎝⎭（I ）当12λ≠时，有 1001011010.221100122⎛⎫ ⎪ ⎪ ⎪→-- ⎪ ⎪ ⎪ ⎪⎝⎭A 因()()34r r ==<A A ，故方程组有无穷多解，全部解为T T 11(0,,,0)(2,1,1,2)22k =-+--ξ，其中k 为任意常数.当12λ=时，有 11101220131100000⎛⎫-- ⎪ ⎪→ ⎪ ⎪ ⎪⎝⎭A .因()()24r r ==<A A ，故方程组有无穷多解，全部解为T T T 121(,1,0,0)(1,3,1,0)(1,2,0,2)2k k =-+-+--ξ，其中12,k k 为任意常数.（II ）当12λ≠时，由于23x x =，即 1122k k -+=-. 解得12k =，方程组的解为T T T 111(0,,,0)(2,1,1,2)(1,0,0,1)222=-+--=-ξ. 当12λ=时，由于23x x =，即 121132k k k --=. 解得121142k k =-，故全部解为 T T 2111311(,,,0)(,,,2)444222k =-+---ξ，其中2k 为任意常数.[注]：在题（II ）中，12λ=时，解得21122k k =-时，全部解也可以表示为 T T 1(1,0,0,1)(3,1,1,4)k =-+-ξ，其中1k 为任意常数.（21）（本题满分13分）设三阶实对称矩阵A 的秩为122,6λλ==是A 的二重特征值. 若T T T 123(1,1,0),(2,1,1),(1,2,3)===--ααα都是A 的属于特征值6的特征向量. （I ）求A 的另一特征值和对应的特征向量；（II ）求矩阵A .解：（I ）因为126λλ==是A 的二重特征值，故A 的属于特征值6的线性无关的特征向量有2个. 由题设可得123,,ααα的一个极大无关组为12,αα，故12,αα为A 的属于特征值6的线性无关的特征向量.由()2r =A 可知，||0=A ，所以A 的另一特征值30λ=. 设30λ=所对应的特征向量为T 123(,,)x x x =α，则有T T120,0==αααα，即 121230,20.x x x x x +=⎧⎨++=⎩ 解得此方程组的基础解系为T (1,1,1)=-α，即A 的属于特征值30λ=的特征向量为T (1,1,1)c c =-α，（c 为不为零的任意常数）.（II ）令矩阵123(,,)=P ααα，则1600060000-⎛⎫ ⎪= ⎪ ⎪⎝⎭P AP ，所以 1600060000-⎛⎫ ⎪= ⎪ ⎪⎝⎭A P P .又1011112333111333-⎛⎫ ⎪- ⎪ ⎪=- ⎪ ⎪ ⎪- ⎪⎝⎭P ，故422242.224⎛⎫ ⎪=- ⎪ ⎪-⎝⎭A。

西安工业大学高数期末考试题附标准答案试题

2018-2019-1-线代A卷+答案

将解向量分别单位化可得
1
2, 5
1, 5
0
T
,
Байду номын сангаас
2
0,
0,
1T
,
3
1, 5
2 5
,
0
T
......3 分
2
5
令
P
1,2
,3
1 5
0
0 0 1
1
5 2 5 0
,则
P 1 AP
PT
AP
2 0 0
0 3 0
0
0
...1
分
7
16（10 分）解：对T 作初等行变换化为行最简形得
1 1 3 6
故 A 12 11 1 ......2 分
2
r12r2
0
1
00
3
4
2分
0 0 1 1 2 3
2 0 1
所以
A1
0
3
4
....1
分
1 2 3
3
13（10
分）解：由于 T
1 3
,
1 2
,1 12
3 ......3
分
且 An T n T T n1 3n1T ......3 分
3
1 3/ 2 3
而
T
2
0 0
1 0 3 0
1 0 0 ...3 分 3
r2
-
1 3
r3 +2r2
1 0
2 1
31 4/3 4/3
0 0
1/ 3
0
2
分
r33
r2
4 3
r3
r13r3

2018年线代期末试卷

10、设 n 阶矩阵 A 满足 A2 A 2I ，则下列矩阵中哪个可能不可逆（ B ）
(A) A 2I
(B) A I
(C) A I
(D) A
二、计算题（本题共 4 小题，满分 32 分）
5123 11、（8 分）计算行列式 D 3 5 1 2 的值。
2351 1235
11 1 2 3 11 1 2
4、设 A 为 n 阶可逆方阵，A* 为 A 的伴随矩阵，若 A 的一个特征值为，则 A* 必有一个特征值 A / 。
5、二次型 f (x1, x2 , x3 ) 5x12 x22 cx32 4x1x2 2x1x3 2x2 x3 为正定的，则 c 的取值
范围是 c＞2
。
6、已知 4 阶方阵 A 的第三列元素依次为 1，3，-2，2，它们的余子式的值分别为 3，-2，1，1，则 A =（ A ）
c1c 2
r 2r1
3
c1
4
1
1
答案： D 11 5 1 2 0 4 1 1 112 3 2 （5 分）
11 c1c3
c1c 4
3
5
1 0 r3r1 r 4r1
2
3
2
11 2
11 2 3 5 0 1 1 2
11 39 429 （8 分）
1 0 2 0
12、（8
分）已知矩阵
A
1 11
1 2 1
a5 k1a1 k2a2 k3a3 k4a4 ，则 a5 k1(l2a2 l3a3 l4a4 ) k2a2 k3a3 k4a4 ，这说明
a5 能由 a2 , a3, a4 线性表示，矛盾。所以 a5 不能由 a2 , a3, a4 线性表示。（6 分）

西安工程大学线性代数2018-2019学年第二学期试题A卷答案及评分标准

西安工业大学20182019→学年第二学期线性代数期末考试试卷（A ）参考答案及评分标准一、选择题（每题2分，共20分）1、D2、D3、B4、C5、C6、B7、C8、A9、C 10、C 二、填空题(每题4分，共20分)11、9-，18； 12、222061⎛⎫ ⎪- ⎪ ⎪⎝⎭； 13、12-，17-； 14、0 15、4k >三、解：15331533201101055311201610114131021911D ------==----……………………………..3分11103200112033515----=112320011103351)5(-----=13320011103351)5(------=……………………………………………………..7分()153311111(5)51120023211002--⎛⎫=-=-⨯⨯⨯-⨯-- ⎪⎝⎭-55-=………………..12分注：其它合理的做法请阅卷教师酌情给分.四，解：由2XA B E -=可得2XA B E =+ ……………………………………………2分因为10A =≠，所以A 可逆，且1010100001A -⎛⎫ ⎪=- ⎪ ⎪⎝⎭…………………………5分1202210002B E -⎛⎫⎪+= ⎪ ⎪⎝⎭……………………………………………………………7分()12X B E A -=+……………………………………………………………..9分210120002⎛⎫ ⎪=- ⎪ ⎪⎝⎭………………………………………………………………12分五、证一：定义法设存在一组数12,,,r k k k 使得11220r r k k k βββ+++=………………………..2分即()()11212120r r k k k αααααα+++++++=整理得()()1212320r r r r k k k k k k k ααα+++++++++=…………………6分由于向量组12,,,r ααα线性无关，故1223000r rr k k k k k k k +++=⎧⎪+++=⎪⎨⎪⎪=⎩……………………….9分解之得120r k k k ====，故向量组12,,,βββr 线性无关…………………….12分证二：由题意可得()()1212111011,,,,,,001βββααα⎛⎫⎪ ⎪= ⎪⎪⎝⎭r r ……………………5分令111011001⎛⎫⎪ ⎪= ⎪⎪⎝⎭K ，由于10K =≠，所以K 可逆……………………………8分再由题设可得向量组12,,,r ααα与向量组12,,,βββr 等价，又因为向量组12,,,r ααα线性无关，故向量组12,,,βββr 线性无关…………………………12分六、解：3132112127112127123451512345152355722000000r r r r A --⎛⎫⎛⎫⎪ ⎪=−−−→ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭2112112127101211011338011338000000000000r r r r -----⎛⎫⎛⎫⎪ ⎪−−−→−−−→ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭……………….4分得同解方程组⎩⎨⎧=+++-=--+8331254325431x x x x x x x x ，移项得⎩⎨⎧+---=-++-=8331254325431x x x x x x x x取3450x x x ===，得线性方程组的一个特解0(18000)T η=-…………………….…………………………8分在对应的齐次线性方程组134********x x x x x x x x =-++⎧⎨=---⎩中，取345100x x x ⎛⎫⎛⎫ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭，010⎛⎫ ⎪ ⎪ ⎪⎝⎭及001⎛⎫⎪⎪ ⎪⎝⎭得基础解系为：111100ξ-⎛⎫ ⎪- ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭，223010ξ⎛⎫ ⎪- ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭，313001ξ⎛⎫ ⎪- ⎪⎪= ⎪ ⎪ ⎪⎝⎭……………………………10分于是所求的通解为1122330ξξξη=+++x k k k （123,,k k k ∈ℜ）……………..12分七、解：由()229125A a =-=⨯⨯得2a =…………………………………………4分⑴ 当11λ=，解方程组()0A E x -=由100100022011022000A E ⎛⎫⎛⎫⎪ ⎪-=→ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭，得基础解系为()10,1,1Tξ=-……………………………………………6分⑵ 当22λ=，解方程组()20A E x -=由0000102012001021000A E ⎛⎫⎛⎫ ⎪ ⎪-=→ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭，得基础解系为()21,0,0Tξ=……………………………………………8分⑶ 当35λ=，解方程组()50A E x -=由3001005022011022000A E -⎛⎫⎛⎫ ⎪ ⎪-=-→- ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭，得基础解系为()30,1,1Tξ=……………………………………………10分令()0123010,,11101P ξξξ⎛⎫ ⎪==- ⎪ ⎪⎝⎭，则0110020005P AP -⎛⎫⎪= ⎪ ⎪⎝⎭……………12分。

西工大线性代数1试题(15-11)

⎜⎛ a 1 1 ⎟⎞⎜⎛ x1 ⎟⎞ ⎜⎛0⎟⎞
6．设方程组 ⎜ 1 a 1 ⎟⎜ x2 ⎟ = ⎜0⎟ 的基础解系所含向量个数为 1，则 a 的值为(
)．
⎜⎝ 1 1 a ⎟⎠⎜⎝ x3 ⎟⎠ ⎜⎝0⎟⎠
⎜⎛1 0 1⎟⎞
⎜⎛
⎟⎞
7．已知 A, B 均为 3 阶矩阵，满足 AB + E = A2 + B ，如 A = ⎜ 0 2 0⎟ ，则 B = ⎜
4．设 A = (α1,α2,α3) 为正交矩阵，其中α1,α2,α3 为列向量，则 3α1Tα1 − 2α2Tα3 = ( )． 5 ．设 α1,α2 ,α3 均为 3 维列向量，矩阵 A = (α1,α1 − α2,2α3 − α2 ) ， B = (α1,α2,α3) ，如 det A = 2 ，则 det B = ( )．
⎟．
⎜⎝1 0 1⎟⎠
⎜⎝
⎟⎠
8. 若 f = 2x12 + x22 + 2x32 + 2tx1x2 + 2x2x3 为正定二次型，则 t 满足的范围是(
)．
9. 设 3 阶矩阵 A 与 B 相似，如1,−2 是 A 的特征值，B 的对角元之和为 3，则 B 的特征值
为(
)．
二、(10 分) 计算 n 阶行列式
1 2 2L 2 2
2 2 2L 2 2
2 Dn = M
2 M
3 M
L
2 M
2 M
2 2 2 L n −1 2
2 2 2L 2 n
三、(10
分)
设 α1
=
⎜⎛ ⎜
1 2
⎟⎞ ⎟
，α2
=
⎜⎛ 3⎟⎞ ⎜0⎟

西安交大西工大考研备考期末复习线性代数第二部分矩阵带答案

第二章矩阵基础练习一．填空1设A 为3阶方阵，且3A =，则2A -=-______________答案：-2；2当λ=_______________时，矩阵11312050λ-⎛⎫ ⎪- ⎪ ⎪⎝⎭为奇异矩阵.答案：-33对于方阵A B 、，若AXB C =，则X ＝____________________答案：11A CB --4已知AB B A -=，其中120210002B -⎛⎫ ⎪= ⎪ ⎪⎝⎭，则A ＝_____________.答案：11021102002⎛⎫ ⎪ ⎪ ⎪-⎪ ⎪ ⎪ ⎪⎝⎭5设A 为方阵,满足022=--E A A ,则=-1A ___________________答案：)(211E A A -=-6设B A ,都是5阶矩阵,且2,31=-=-B A ,则=A B答案：332-7设A 为3阶方阵,*A为伴随矩阵,81=A ,则*1831A A -⎪⎭⎫ ⎝⎛-=___________ 答案：答案：58设B A ,都是n 阶方阵,且3,2==B A 则=00BA .答案：61⋅-n )(9设⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=1101201112111111A ，则.4A = 答案：8110设,101014321121⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-t y x x 则=2x 答案：-1二．计算题1设矩阵A B ，满足关系式2()AB A B =+，其中301 110014A ⎛⎫⎪= ⎪ ⎪⎝⎭，求矩阵B .答案：1044864806--⎛⎫ ⎪-- ⎪ ⎪-⎝⎭2设01000000200000010000000000021000053A n n ⎛⎫⎪⎪⎪⎪=- ⎪ ⎪⎪⎪ ⎪⎝⎭，求1A - 答案：10000010*******0021000010000310052n n ⎛⎫ ⎪ ⎪ ⎪⎪ ⎪⎪ ⎪ ⎪ ⎪⎪- ⎪- ⎪ ⎪-⎝⎭ 3已知11111111 11111111A ---⎛⎫⎪---⎪= ⎪--- ⎪---⎝⎭，求n A （n 为正整数）. 答案：当2n k =时，22nkA E =；当21n k =+时，22nkA A =．4设已知⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-----=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=461351341,121011322,58269212163C B A ,求.))((432A A A A BC BC A +-+-+答案：解：E A E BC ==2,原式A E A E A A A A E E A +=+=+-+-+=5432))((⎪⎪⎪⎭⎫ ⎝⎛----=482610212162 5设⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=3200430000100001A , 求.16A 答案：解：令 ⎪⎪⎭⎫⎝⎛--==⎪⎪⎭⎫ ⎝⎛=3243,1001C E B EC E B ==1616⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=100001000010000100016161616C B C B A6已知⎥⎦⎤⎢⎣⎡-=3102A ,且,BA AB =试求二阶方阵B . 答案：令⎪⎪⎭⎫ ⎝⎛=d b c a B 使⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-31023102d b c a d b c a 即⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎭⎫⎝⎛--d d b c c a c d a b c a32323322 即⎩⎨⎧-==ba d c 0得⎪⎪⎭⎫ ⎝⎛-=b a b aB 0,其中b a ,是任意实数.7设,,100010001,00000089E A A A D c b a B c b a A ++++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=求DB .答案：))((89E A E A A A DB -++++=E A -=10⎪⎪⎪⎭⎫ ⎝⎛---=100010001101010c b a DB8设⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=0011002221003100A ,试用矩阵分块法求1-A . 答案：⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎪⎭⎫⎝⎛--=00001100222100310021A A A ⎪⎪⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛-=-51515352,2131111A A⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛-=-21412141,1122122A A ⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡--=⎪⎪⎭⎫ ⎝⎛=---0051510053522141002141000011121A A A 9设⎪⎪⎪⎭⎫ ⎝⎛---=111011001A ,求.)4()2(21E A E A -+-答案：⎪⎪⎪⎭⎫⎝⎛--=⎪⎪⎪⎭⎫ ⎝⎛=+--110011001111011001)2(11E A⎪⎪⎪⎭⎫ ⎝⎛------=-⎪⎪⎪⎭⎫ ⎝⎛---=-321032003402101200142E E A⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫ ⎝⎛------⎪⎪⎪⎭⎫ ⎝⎛--=-+-311031003321032003110011001)4()2(21E A E A或)2)(2()2()4()2(121E A E A E A E A E A -++=-+--)2)(2()2()4()2(121E A E A E A E A E A -++=-+-- 10设,02=++A AB A 其中⎪⎪⎪⎭⎫ ⎝⎛=a c b b a c c b a A ，（c b a ,,是互不相等的正实数）求方阵B .答案：{}0)()()()(21222≠-+-+-++=a c c b b a c b a A故由0) =++E B A A 知0=++E B A⎪⎪⎪⎭⎫ ⎝⎛------------=--=a c b b a c c b aA EB 111三．证明题1设AB ，为n 阶矩阵，且A 为对称阵，证明TB AB 也是对称矩阵.答案：提示：用对称矩阵的定义验证；2设A 为n 阶非零矩阵，*A 为A 的伴随矩阵，且*T A A =，证明 0A ≠.答案：提示：211nj j a A ==∑3设D C B A ,,,是n 阶矩阵，且0≠A 及.CA AC =证明：.CB AD DC B A -=答案：证明：由⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫⎝⎛---B CA D B A D C B A E CAE1100 得BCA D B A DCB A E CA E 1100---=-即.1CB AD B CA D A DCB A -=-⋅=-自测题一、填空题1设对于三阶矩阵A 有32,2=+=E A A ,则=+A A 242___________.答案：482设矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=121120131020013987654321x x x x x x x x x A ,则=A _____________________.答案：.120120120113⎪⎪⎪⎭⎫ ⎝⎛-=A3 已知方阵A 满足02=++cE bA aA (c b a ,,为常数0≠c ),则=-1A；答案：)(11bE aA cA +-=-4 设矩阵33)(⨯=j i a A ，j i A 是||A 中元素j i a 的代数余子式，j i j i A a =，13121132a a a ==，已知011>a ，则=11a 。

西安工业大学高数09-10第一学期（1）期末考题及答案分析

西安⼯业⼤学⾼数09-10第⼀学期（1）期末考题及答案分析⾼等数学（A ）期末考试试题⼀、单项选择题（每⼩题3分，共15分）1.当0→x 时，下列变量极限不存在的是（）. （A ）x arctan ；（B ）xx 1sin；（C ）xx +-11ln；（D ）x e 1.2.0)(,0)(00<''='x f x f 是函数)(x f y =在0x x =处取得极⼤值的⼀个（）（A ）充分必要条件；（B ）充分条件，⾮必要条件；（C ）必要条件，⾮充分条件；（D ）既⾮充分条件，⼜⾮必要条件.3.下列等式成⽴的是（）（A ）)()(x f dx x f d =?；（B ）dx x f dx x f d )()(=?；（C ）)()(x f dx x f ='? （D ）dx x f dx x f ?=')()(. 4.设)(x f 在],[b a 上⾮负，在),(b a 内,0)(,0)(>''>'x f x f 记[])()(21b f a f ab I +-=，dxx f I b a=)(2，)()(3a f a b I -=，则（）（A ）321I I I <<；（B ）132I I I <<；（C ）123I I I <<；（D ）213I I I <<. 5.关于函数dte t xf t)1()(的极值，正确的是（）（A ）极⼩值为f -=1)1(；（B ）极⼩值为 e f -=2)1(；（C ）极⼤值为 e f -=1)1(；（D ）极⼤值为 e f -=2)1(. ⼆、填空题（每⼩题3分，共15分） 1.设0→x 时，)cos(1ax -与12 -xe是等价⽆穷⼩，则=a .2.设函数)(x f 可导，)(cos 2x f y =，则=dy .3.设曲线的⽅程是)1ln(2x y +=，则曲线的拐点是 .4.不定积分=+?dx x x 1 .5.设曲线)(x f y =上任⼀点),(y x M 处的切线，恒垂直于此点与原点的连线，则y满⾜的微分⽅程是 .三、完成下列各题（每⼩题6分，共36分） 1. 求极限??--→x e xx 111lim 0. 2. 设 ,212=-=tt ey e x 求 22dx yd . 3.设函数)(x y 是由1)1(022=+-?dt t y x y所确定，求dy .4.设xx sin 是)(x f 的⼀个原函数，求dx x f x ?')(.5设?∞+-∞→=+121lim dx xex xaxx ，求a .6.求⼀阶微分⽅程yedxdy x -=-+1)1(的通解.四、（7分）设())1(1ln )(21>++=?x xx dt tt f x ，求dxx f ?)(.五、（7分）已知)(x f 在点6=x 的邻域内为可导函数,且,0)(lim 6=→x f x ,2009)(lim 6='→x f x 求极限 .)6()(lim3666x dtdu u f t x t x -→六、（8分）在抛物线)30(2≤≤=x x y 上求⼀点P ,过P 点作抛物线的切线，使此切线与抛物线及直线3,0==x y 所围成的图形⾯积最⼩.七、（7分）设 ,0<+≥+=x ex x x f x 求?-2)1(dx x f .⼋、（5分）已知函数)(x f 在),2[∞+上可导，0)(>x f ，且满⾜不等式)(])([x f x xf -≤'.试证在),2[∞+上2)(xA x f ≤，其中A 为与x ⽆关的常数.⾼等数学（A ）期末考试试题参考答案及评分标准（2010年1⽉5⽇）⼀、单项选择题（每⼩题3分，共15分） 1.D 2.B 3.B 4.C 5.B ⼆、填空题（每⼩题3分，共15分）.12±2. xdx sin )x (cosf 22'- 3 . )ln ,(21±4. C )x ()x (++-+2325132152 5.yx dxdy -=三、完成下列各题（每⼩题6分，共36分）.1. 解：)e (x )e (x lim x e lim xxx x x 1111100---=??? ?--→→……………………………………………..1分 21x x +-=→………………………………………………..2分xel i mxx 210-=→………………………………………………….....2分2120-=-=→xx limx ………………………………………………….1分2. 解：ttt eee dxdy 1222==………………………………………………………………………3分tttteeee dxy d 322222121-…………………………………...…………………….3分3. 解：两端同时对x 求导得…………………………………………………………………..1分 0122 2=+-+dxdy )y (dxdy xxy ………………………………………………….3分2212x y xy dxdy -+=……………………………………………………………..….1分即dx xy xydy 2212-+=………………………………………..………………………1分4. 解：由题意知2xxsin x cos x )xx sin ()x (f -='=……………………………………2分则)x (df x dx )x (f x ??=' ………………………………………………………. …….…1分 dx )x (f )x (xf ?-=…………………………………………………………….…… 2分C xx sin x cos C xx sin x………………………….1分5解：因为 aaxx axx ex lim x lim 2222121=+=??+∞→∞→………………………………2分[][]+∞-+∞→+∞-+∞-+∞-+∞--+-=+-=-=?111xxxee)ex (lim dx exexdedx xeeeelim e)e (lim xx xx 2111=+-+-=-+∞→+∞→……………..…………………..3分所以 )(l n a eea122122-= =………………………………...………....1分6.解：由题意得y+11,也即dx x dy eeyy 111+=+……………………….2分两端同时积分得C ln )x ln()e ln(dx x dy eeyyy++=+?+=+?11111………3分所以原微分⽅程的通解为 )x (C ey11+=+ 或 []11-+=)x (C ln y ………….....1分四、（7分）解：对()211xx ln dt t)t (f x ++=?两端同时求导得……………………..1分222x (xx x)x (f +=+=++++ =……...2分C x)x(d xdx xx dx )x (f ++=++= +=∴2222111121 1…………...3分五、（7分）解：2 6603666636)x (du)u (f x lim)x x t x --=-→→…………………………2分)x ()x (xf du )u (f limxx --=?→6666………………………………………………2分660-'---=→)x (f x )x (f )x (f limx …………………………………………2分2009= …………………………………………………………………...…1分六、（8分）在抛物线)x (x y 302≤≤=上求⼀点P ,过P 点作抛物线的切线，使此切线与抛物线及直线30==x ,y 所围成的图形⾯积最⼩.解：设切点P 的坐标为)x ()y ,x (30000≤≤，则切线斜率为002x )x (y ='，切线⽅程为 )x x (x y y 0002-=-，即2002x x x y -=，…………………………….1分令0=y ，得切线与x 轴交点的横坐标为20x ，令3=x ，得切线与直线3=x 交点的纵坐标为2006x x -，要使此切线与抛物线及直线30==x ,y 所围成的图形⾯积最⼩，既是切线与直线30==x ,y 所围成的图形⾯积最⼤…………………………………………….2分设该⾯积为S ,则)x x )(x ()x (S 2000062321--=………………..……………….2分[]0000020026641262321641x )x ()x ()x )(x ()x x ()x (S ---=--=')x )(x (002643--=………………………..……………………………..2分令00=')x (S ，得惟⼀驻点20=x ，依题意，该驻点就是使)x (S 0取得最⼤值的点，所以所求的点P 的坐标为),()y ,x (4200=…………………………………………...…….1分七、（7分）解：?---======-11111201dx )x (f dt )t (f dx )x (f x t ……………………..2分[]1001100111111111)x ln(de)ee(dx xdx exxxx+++-=+++=--….3分[][][])e (ln )x ln()eln(x x12111001+=+++-=-………….........………2分⼋、（5分）已知函数)x (f 在),[∞+2上可导，0>)x (f ，且满⾜不等式)x (f ])x (xf [-≤'.试证在),[∞+2上2xA )x (f ≤，其中A 为与x ⽆关的常数.证：由于)x (f 在),[∞+2上可导，0>)x (f ，则x)x (f )x (f )x (f )x (f x )x (f )x (f ])x (xf [2-≤'?-≤'+?-≤'…..2分于是当2>x 时有dt t dt )t (f )t (f x x ?-≤'222……………………………….1分即[][]222222442222x)(f )x (f x(f )x (f x ln )(f )x (f ln t ln )t (f ln x x ≤≤≤?-≤-令)(f A 24=，代⼊即证………………………………………………………………2分。

西安工业大学2018线性代数考试试题

西安工业大学试题纸注意：所有题目都在试卷上作答，第三题至第七题要有计算或证明过程一、单项选择题（每题4分，共24分）1.行列式=---=efcfbfde cd bdaeac abD （） ()A abcdef 4 ()B abcdef 4- ()C abcdef ()D def abc 22-2.设矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=333231232221131211a a a a a a a a a A ，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+++=133312321131131211232221a a a a a a a a a a a a B ， ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1000010101P ， ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1010100012P ，则有（） ()A B P AP =21 ()B B P AP =12 ()C B A P P =21 ()D B A P P =123．设4321,,,αααα是4个同维向量，如果向量组321,,ααα线性相关，那么（）()A 321,,ααα中必有零向量； ()B 向量组21,αα必定线性相关；()C 向量组21,αα必定线性无关； ()D 向量组4321,,,αααα必定线性相关 4.设矩阵()nm ija A ⨯=，O AX =仅有零解的充分必要条件是（）()A A 的列向量组线性相关 ()B A 的行向量组线性相关.()C A 的列向量组线性无关 ()D A 的行向量组线性无关 5.设矩阵A 的特征多项式2)4)(1(++=-λλλA E ，则A ＝（）()A －4 ()B －16 ()C 4 ()D 166．实二次型32312322212232x x x x x x x f +-++=是（）二次型.()A 正定 ()B 负定 ()C 不定 ()D 半正定二、填空题（每题4分，共20分）1. 设432163021-1118751=D ，4j A 为4j a 的代数余子式（1,2,3,4j =），则 =-++44434241A A A A .2.设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=543022001A 为可逆矩阵，*A 是A 的伴随矩阵，则()=-*1A3.已知矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=x A 10100002与⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=10000002y B 相似，则=y 4.设A 是n 阶方阵，E 是n 阶单位阵，且有0=-E A A 4-22，则()=+-1E A5.设向量()Tx 4,8,11-=和()Tk x 5,,42-=分别是实对称矩阵A 的属于特征值1λ和2λ的特征向量（21λλ≠），则=k三.已知⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=100110111A ，且E AX A =-2，其中E 为3阶单位阵，求矩阵X 。

2018线性代数试卷A(1)

5.设是非齐次线性方程组的个解则是方程组的解的充分必要条件是
三、解答题(本题满分50分,共5小题每小题10分)
1.已知，求 .
2.设，且，求
3.求下列向量组的秩及其一个极大线性无关组，并将其余向量用该极大线性无关组线性表示：
4.已知求矩阵
5.设四元非齐次线性方程组的系数矩阵的秩为已知是它的两个不同的解向量求该方程组的通解
3.以下结论错误的是
(A) (B) (C) (D)
4.矩阵的逆矩阵为
(A) (B) (C) (D)
5.矩阵的秩等于
(A) (B) (C) (D)
二、填空题(本题满分25分,共5小题,每小题5分)
1.一个向量线性相关的充要条件是
2.设为阶矩阵且则齐线性方程组的基础解系含个向量
3.计算
4.已ቤተ መጻሕፍቲ ባይዱ方程组无解则
江西师范大学
考试卷
年级专业(学科)2018—2019学年第1学期
课程号：255538课程名称：线性代数A卷
考试形式：开卷闭卷其他要求：
一、选择题(本题满分25分,共5小题,每小题5分)
1.行列式
(A) (B) (C) (D)
2.设均为阶方阵且则
(A) (B) (C) (D)

工大线性代数期末试卷及参考答案(A)

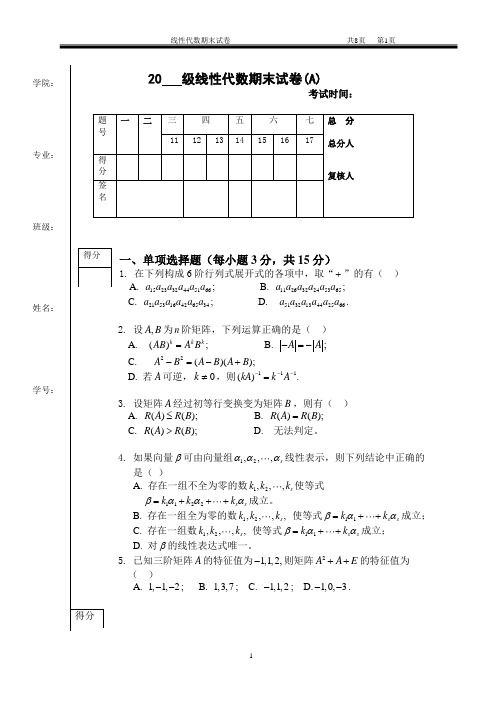
学院：专业：班级：姓名：学号：,,s α线性表示，则下列结论中正确的 2,,s k k 使等式s s k α+成立。

存在一组全为零的数12,,,,s k k k 使等式11s s k α+成立； 2,,,s k k 使等式1s s k k βαα=+成立；的线性表达式唯一。

的特征值为1,1,2,-则矩阵2A E ++的特征值为1,3,7; C. 1,1,2-; 1,0,3-.二、填空题（每小题3分，共15分）6．设(,1,2)ij A i j = 为行列式2131D =中元素ij a 的代数余子式，则11122122A A A A =7．设4阶方阵520021000012011A ⎛⎫⎪ ⎪= ⎪- ⎪⎝⎭，则1A -=8．设线性方程组1231231232202020x x x x x x x x x λ-+=⎧⎪-+=⎨⎪+-=⎩有非零解，则λ=9．已知向量组123(3,2,0,1),(3,0,,0),(1,2,4,1)ααλα===--的秩为2，则λ=10．设n 阶方阵A 的特征值为12,,,n λλλ，则kA （k 为常数）的特征值为三、计算n 阶行列式（本题14分）11. 211112111112n D =四、证明题（每小题8分，共16分）12．已知对于n 阶方阵A ，存在自然数k ，使得0k A =，试证明矩阵E A -可逆，并写出其逆矩阵的表达式。

13. 设向量组12:,,,L A ααα和向量组12:,,,,S B βββ的秩分别为p 和q ，试证明：若A 可由B 线性表示，则p q ≤。

五、解矩阵方程（14分）14．设412221311A -⎛⎫ ⎪= ⎪ ⎪-⎝⎭，132231B -⎛⎫ ⎪= ⎪ ⎪-⎝⎭，求X 使AX B =.六、解答题（每小题10分，共20分）15. 设11,11A ⎛⎫= ⎪-⎝⎭121101B ⎛⎫= ⎪--⎝⎭，求AB .16. 设()12340,4,2,(1,1,0),(2,4,3),(1,1,1)αααα===-=-，求该向量组的秩和一个最大无关组，并将其余向量表示成最大无关组的线性组合。

西安交大西工大考研备考期末复习线性代数前三章自测带答案

线性代数前三章自测题1．=-===ij ij n a D a a D 则若,a n )1(-2. 在五阶行列式中3524415312a a a a a 的符号为= —3. =+++=443424144,A A A A c db a ac bd a d b c d cb a D 则设四阶行列式0 4．在函数()321112x xx x x x x f 中---=的系数是=-25. 四阶行列式a b c d b ad c c da b d cb a ------=()22222d c b a +++ 6. ().21121121i i i i n n i i i i n n n n ---次对换后变为排列可经排列 7． =⎪⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=*-*A A A A n A 1541det ,31det ,,1则为其伴随矩阵阶方阵为设()31n - 8. ==⎪⎪⎪⎭⎫ ⎝⎛=≠t O AB t B O A 则且阶方阵设,,35342531,3 49. ==-13,A E A 则已知2A 10. =+=*-A A A A 32,1,1且为三阶矩阵设12511．=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---13112522100110012⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----3161343102125210010002121 12. n n ⎪⎪⎪⎭⎫ ⎝⎛∞→51001101121lim =⎪⎪⎪⎭⎫ ⎝⎛00000000013．线性方程组⎪⎪⎪⎩⎪⎪⎪⎨⎧=-=-=-=-=-515454343232121a x x a x x a x x a x x a x x 有解的充要条件是054321=++++a a a a a14．()()==*A R A R A 则且秩阶方阵为设,3,4115．矩阵⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=0011102210111000A 的秩是=2 16. 齐次线性方程组⎪⎩⎪⎨⎧=+=++=++0302032321321x kx x x x x kx x 只有零解，则k 应满足的条件是53≠k ． 17． ,2,321011324B A AB A +=⎪⎪⎪⎭⎫ ⎝⎛-= 求B 。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

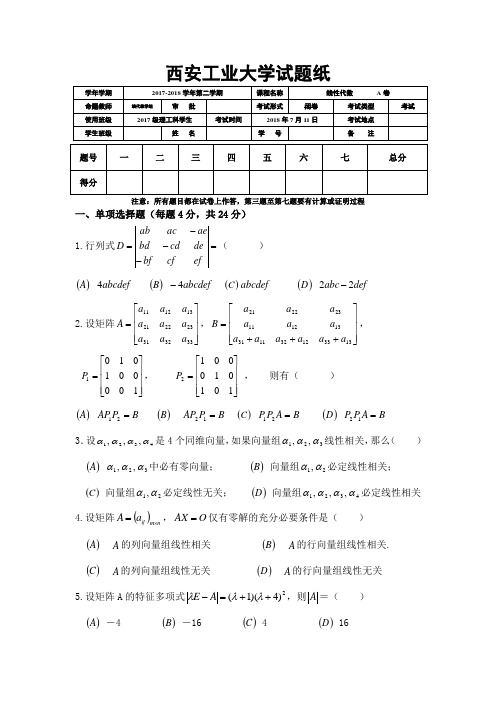
西安工业大学试题纸
注意：所有题目都在试卷上作答，第三题至第七题要有计算或证明过程
一、单项选择题（每题4分，共24分）
1.行列式=---=ef
cf
bf
de cd bd
ae
ac ab
D （） ()A abcdef 4 ()B abcdef 4- ()C abcdef ()D def abc 22-
2.设矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=3332
31
2322
21
131211
a a a a a a a a a A ，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+++=133312
3211
311312
1123
2221
a a a a a a a a a a a a B ， ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1000010101P ， ⎥⎥
⎥⎦
⎤
⎢⎢⎢⎣⎡=1010100012P ，则有（） ()A B P AP =21 ()B B P AP =12 ()C B A P P =21 ()D B A P P =12
3．设4321,,,αααα是4个同维向量，如果向量组321,,ααα线性相关，那么（）
()A 321,,ααα中必有零向量； ()B 向量组21,αα必定线性相关；
()C 向量组21,αα必定线性无关； ()D 向量组4321,,,αααα必定线性相关 4.设矩阵()
n
m ij
a A ⨯=，O AX =仅有零解的充分必要条件是（）
()A A 的列向量组线性相关 ()B A 的行向量组线性相关.
()C A 的列向量组线性无关 ()D A 的行向量组线性无关 5.设矩阵A 的特征多项式2)4)(1(++=-λλλA E ，则A ＝（）
()A －4 ()B －16 ()C 4 ()D 16
6．实二次型32312
322212232x x x x x x x f +-++=是（）二次型.
()A 正定 ()B 负定 ()C 不定 ()D 半正定
二、填空题（每题4分，共20分）
1. 设4
32163021
-111
8751
=
D ，4j A 为4j a 的代数余子式（1,2,3,4j =），则 =-++44434241A A A A .
2.设⎥⎥⎥⎦
⎤
⎢⎢⎢⎣⎡=543022001A 为可逆矩阵，*A 是A 的伴随矩阵，则()
=-*
1
A
3.已知矩阵⎥⎥
⎥⎦
⎤⎢⎢⎢⎣⎡=x A 10100002与⎥⎥⎥⎦⎤
⎢⎢⎢⎣⎡-=10000002y B 相似，则=y 4.设A 是n 阶方阵，E 是n 阶单位阵，且有0=-E A A 4-22，则()=+-1
E A
5.设向量()T
x 4,8,11-=和()T
k x 5,,42-=分别是实对称矩阵A 的属于特征值1
λ和2λ的特征向量（21λλ≠），则=k
三.已知⎥⎥
⎥⎦
⎤
⎢⎢⎢⎣⎡--=100110111A ，且E AX A =-2
，其中E 为3阶单位阵，求矩阵X 。

（10分）
四、设矩阵⎥⎥⎥⎦
⎤⎢⎢⎢⎣⎡--=μλ3651231121A ，已知()2=A R ，求λ与μ的值.（10分）
五，求向量组()T
,2,4,21=α，()T
0,1,12=α，()T 1,3,23=α，()T
2,5,34=α的一个极
大线性无关组，并将其余向量表示成该极大无关组的线性组合. （10分）
六. 问常数λ取何值时,方程组⎪⎩⎪
⎨⎧+=+++=++=+3
246224321
32131λλλx x x x x x x x 有解,并求出其解的一般形式.
（12分）
七. 设矩阵⎥⎥⎥⎦
⎤
⎢⎢⎢⎣⎡-=202020201A ，求一个正交矩阵P ，使得Λ=-AP P 1
为对角矩阵.（14分）。

西安工业大学2018线性代数考试试题

2018考研数学线性代数真题及考点解析

大学线性代数试题及答案

西安工业大学高数期末考试题附标准答案试题

2013年西安工业大学线性代数考试试题及答案评分标准(A卷)

线性代数大学试题及答案

2018-2019学年线性代数试题及答案.ppt

西安交大西工大 考研备考期末复习 线性代数测试题及答案

线性代数期末试卷及解析(4套全)2018科大

西安工业大学高数期末考试题附标准答案试题

2018-2019-1-线代A卷+答案

2018年线代期末试卷

西安工程大学线性代数2018-2019学年第二学期试题A卷答案及评分标准

西工大线性代数1试题(15-11)

西安交大西工大 考研备考期末复习 线性代数第二部分 矩阵带答案

西安工业大学高数09-10第一学期（1）期末考题及答案分析

西安工业大学2018线性代数考试试题

2018线性代数试卷A(1)

工大线性代数期末试卷及参考答案(A)

西安交大西工大 考研备考期末复习 线性代数前三章自测带答案

西安交大西工大考研备考期末复习线性代数测试题及答案

西安交大西工大考研备考期末复习线性代数第二部分矩阵带答案

西安交大西工大考研备考期末复习线性代数前三章自测带答案