图形拼接.matlab代码
2013年数学建模B题碎纸片的拼接复原

年
9 月 15 日
赛区评阅编号(由赛区组委会评阅前进行编号) :
1
2013 高教社杯全国大学生数学建模竞赛
编 号 专 用 页
赛区评阅编号(由赛区组委会评阅前进行编号) :
赛区评阅记录(可供赛区评阅时使用) : 评 阅 人 评 分 备 注
全国统一编号(由赛区组委会送交全国前编号) :
全国评阅编号(由全国组委会评阅前进行编号) :
2
三.模型假设
1. 所有碎纸片的拼接都可以忽略边缘效应,即可无缝地融合在一起; 2. 对于仅纵切的两块待拼接的碎纸片,可用像素点灰度值矩阵的相似度大于 0.6 作为 判别标准; 3. 对既纵切又横切的碎纸片,拼接后原图形四周的像素点是 255; 4. 人工干预可以准确的选择出不确定的待拼接图形; 5. 对于既纵切又横切的两块待拼接的碎片,先进行行拼接,再进行列拼接; 6. 假设给定待拼接碎纸片边缘平滑。
二.问题分析
第一问中, 对于中、 英文的纵切单面文件, 可以选择矩阵相关性匹配算法, 在 MATLAB 中导入图形后,将图形中的变量转换为矩阵的形式,采用矩阵相似度比较法,提取待拼 接图形中第一列和最后一列像素点灰度值, 用 corr2 函数进行相似度比较, 然后根据相 关系数的大小来判断待拼接图形文字区域的相似程度,相关系数(0 表示毫不相关,-1 和 1 表示完全相关,靠近-1 或 1 表示相似程度较大) 。 由此得到待拼接图形的相应位置,从而实现文字的拼接。 第二问中,中、英文的纵横切单面文件拼接复原的处理问题,在上一问的基础上将 问题简化为 19 次行方向的碎片拼接,对一拼接的行再进行列方向上的拼接。依然使用 矩阵相关性算法,在 MATLAB 中导入图形后,将各个图形的变量转换为的相应的矩阵形 式,矩阵相似度比较,提取待拼接图形四周边缘像素点灰度值,用 corr2 函数进行相似 度比较, 然后根据相关系数的大小来判断带拼接图形文字区域的相似程度。 由于图形数 量多, 相关系数不能唯一确定一张拼接图形, 此时要进行人工干预, 筛选出合适的图形, 再对剩余的待拼接图进行矩阵相似度比较,得到行方向的图形。最后根据 MATLAB 软件 编写的程序和人工干预拼接处整张图形。 第三问中,对于中、英文的纵横切双面文件的拼接复原,在第二问的基础上需要比 较正反两面, 在比较的过程中其中一张有可能出现正反两面与另一张图像在算法中计算 出来的相关系数几乎差不多,此时可能要进行人工干预,选出那张是正面还是反面。
MATLAB绘图函数代码及图形

')
case 2,result = M1-M2; case 3,result = M1*M2; case 4,result = M1/M2; end disp('The result is :'); disp(result); end %End function 第三题 矩阵的操作 function y=f3 while(1) disp('--------------------------------------'); disp('1 - 转置'); disp('2 - 求秩'); disp('3 - 求逆'); disp('4 - 行列式'); disp('0 -Exit'); ch = input('Choose an item to continue:'); if( ch == 0) return; end M = input('Enter the Matrix:'); switch(ch) case 1,result = M'; case 2,result = rank(M); case 3,result = inv(M); case 4,result = det(M); end disp('The transform result is :'); disp(result); end %End function end end end 第四题 向量的判定 function y=f4(vec_1,vec_2,dem_1) vec_1=input(' 第一个向量:') vec_2=input(' 第二个向量:') Sel_2=input(' 选择: 1 -判断两向量是否共线 2 -判断三向量是否共面') if Sel_2==1 A=[vec_1;vec_2] if rank(A)==1 disp(' 两向量共线!') else disp(' 两向量不共线!') end else if Sel_2==2
在Matlab中进行图像融合与图像叠加的方法与技巧

在Matlab中进行图像融合与图像叠加的方法与技巧引言:随着数字图像处理和计算机视觉领域的发展,图像融合和图像叠加变得越来越重要。
图像融合是指将多幅图像合成为一幅具有更清晰、更丰富信息的图像,而图像叠加则是在保留所叠加图像的原始信息的同时,使图像更加丰富和易于理解。
Matlab作为一种强大的科学计算工具,提供了丰富的图像处理函数和工具箱,可以很方便地进行图像融合与图像叠加。
一、图像融合的方法与技巧1. 融合算法图像融合的基本方法有加权平均法、空间域融合法、频域融合法、小波融合法等。
加权平均法是最简单的方法,通过计算图像像素的平均值来融合。
空间域融合法是通过对直接融合的图像进行空间域操作来提取融合结果。
频域融合法则是通过将图像转换到频域,然后进行频域操作来实现融合。
小波融合法是基于小波变换的方法,利用小波分析的多尺度分解能力对图像进行分析和融合。
根据具体需求和图像的特点,选择合适的融合算法是非常重要的。
2. 图像预处理在进行图像融合之前,通常需要进行图像预处理,以提高融合结果的质量。
常用的图像预处理方法包括灰度拉伸、直方图均衡化、滤波等。
灰度拉伸是通过对图像的像素值进行线性变换,将图像像素值的范围拉伸到合适的范围内,从而增加图像的对比度。
直方图均衡化则是将图像的像素值在灰度直方图上均匀分布,以增强图像的细节。
滤波是通过对图像进行滤波操作,如低通滤波、高通滤波等,以去除图像中的噪声和不需要的细节。
3. 图像融合的策略图像融合的策略可以根据具体需求来选择。
常见的策略包括全局融合和局部融合。
全局融合是将所有图像的信息进行融合,得到整体的融合结果。
而局部融合则是将不同图像的不同区域进行融合,以保留更多的细节和纹理。
根据具体应用和需求,选择合适的融合策略可以使融合结果更加符合实际需求。
4. 参数设置与调整在进行图像融合过程中,不同的算法和方法有各自的参数,根据不同的图像和具体应用,需要适时地进行参数的设置和调整。
图像处理matlab及图像融合图像镶嵌图像拼接

图像处理matlab及图像融合图像镶嵌图像拼接在实际的对图像处理过程中,由于我们读出的图像是unit8型,⽽在MATLAB的矩阵运算中要求所有的运算变量为double型(双精度型)。
因此读出的图像数据不能直接进⾏相加求平均,因此必须使⽤⼀个函数将图像数据转换成双精度型数据。
MATLAB中提供了这样的函数:im2double函数,其语法格式为:I2 = im2double(I1)其中I1是输⼊的图像数据,它可能是unit8或unit16型数据,通过函数的变化输出I2为⼀个double型数据,这样两图像数据就可以⽅便的进⾏相加等代数运算.要把double的图像(范围是0到1)再次转化为256灰度值的,可以这样Igrey= uint8(I2*255)图像类型转换函数:dither() 通过颜⾊抖动,把真彩图像转换成索引图像或灰度图象转换成⼆值图像gray2ind() 将灰度图像(或⼆值图像)转换成索引图像grayslice() 通过设定的阈值将灰度图象转换成索引图像im2bw() 通过设定亮度阈值将灰度、真彩、索引图象转换成⼆值图像ind2gray() 将索引图象转换成灰度图象ind2rgb() 将索引图象转换成真彩⾊图像mat2gray() 将⼀个数据矩阵转换成⼀幅灰度图象rgb2gray() 将真彩转换成灰度图象rgb2ind() 将真彩转换成索引图象图像类型与类型间的转换1。
索引图像:包括⼀个数据矩阵X和⼀个⾊图阵MAP。
矩阵元素值指向MAP中的特定颜⾊向量。
2。
灰度图像:数据矩阵I,I中的数据代表了颜⾊灰度值。
矩阵中的元素可以是double类型、8位或16位⽆符号的整数类型。
3。
RGB图像:即真彩图像。
矩阵中每个元素为⼀个数组,数组的元素定义了像素的红、绿、蓝颜⾊值。
RGB数组可以是double类型、8位或16位⽆符号的整数类型。
4。
⼆值图像:⼀个数据阵列,每个象素只能取0或1。
矩阵的基本运算⾏列式求值:det(A)矩阵加减:+、-矩阵相乘:*矩阵左除:A/B %相当于inv(A)*B矩阵右除:A\B %相当于A*inv(B)矩阵的幂:^矩阵转置:'矩阵求共轭(实部相同,虚部相反):conj(X)矩阵求逆:inv(X)级数的求和与收敛symsum(fun,var,a,b):其中fun是通项表达式,var为求和变量,a为求和起点,b为求和终点例如:I为1/[n*(2n+1)]从1到正⽆穷的和,求Isyms n;f1=1/(n*(2*n+1));I=symsum(f1,n,1,inf)计算结果为:I =2-2*log(2)空间曲⾯mesh()函数语法:mesh(Z):mesh(X,Y,Z,C):其中C是⽤来定义相应点颜⾊等属性的数组例:求x^2+y^2=z的空间曲⾯x=-4:4;y=x;[X,Y]=meshgrid(x,y);%⽣成x,y坐标Z=X.^2+Y.^2;mesh(X,Y,Z)曲⾯图[x,y]=meshgrid(xa,ya) 当xa,ya分别为m维和n维⾏向量,得到x和y均为n⾏m列矩阵。
图像拼接算法及实现(二).

图像拼接算法及实现(二)3.3.2 特征点匹配法比值匹配法利用图像特征较少,而且在图像发生小角度旋转的时候容易发生误匹配。
基于特征点的匹配法可以很好的解决这类问题。
特征点主要指图像中的明显点,如房屋角点、圆点等。
用于点特征提取得算子称为有利算子或兴趣算子。
自七十年代以来出现一系列各不相同、各有特色的兴趣算子,较知名的有Moravec算子、Hannah算子与Foistner等。
本文采用Moravec算子进行特征点提取:Moravec算子的基本思想是,以像素点的四个主要方向上最小灰度方差表示该像素点与邻近像素点的灰度变化情况,即像素点的兴趣值,然后在图像的局部选择具有最大的兴趣值得点(灰度变化明显得点)作为特征点,具体算法如下:(1)计算各像素点的兴趣值IV (interest value),例如计算像素点(c,r)的兴趣值,先在以像素点((cr)为中心的n n的影像窗口中(如图3.3.2所示的5 5的窗口),计算四个主要方向相邻像元灰度差的平方和。
图3.3.2 Moravec 算子特征点提取示意图VVVV其中k=INT(n/2)。
取其中最小者为像元((c,r)的兴趣值:IV(c,r)=V=min{ V , V , V }(2)根据给定的阂值,选择兴趣值大于该阐值的点作为特征点的候选点。
设V 为事先设定好的闭值,如果V > V,则V为特征点的候选点。
阑值得选择应以候选点中包括需要的特征点,而又不含过多的非特征点。
(3)在候选点中选取局部极大值点作为需要的特征点。
在一定大小的窗口内(可不同于兴趣值计算窗口),去掉所有不是最大兴趣值的候选点,只留下兴趣值最大者,该像素即为一个特征点。
在有了以上的特征点提取的基础上,基于特征点匹配算法主要步骤如下:(1)在参考图像T的重叠部分中选取4个区域,每个区域利用Moravec算子找出特征点。
(2)选取以特征点为中心的区域,本文大小选择7X7的区域,在搜索图S中寻找最相似的匹配。
matlab字符串拼接函数

matlab字符串拼接函数Matlab是一种功能强大的编程语言和数值计算环境,提供了丰富的字符串处理函数,其中包括字符串拼接函数。
本文将深入探讨Matlab中的字符串拼接函数,并介绍其使用方法和一些实际应用场景。
在Matlab中,字符串拼接函数主要有两种,分别是strcat和strjoin。
首先我们来介绍strcat函数。
strcat函数用于将两个或多个字符串进行拼接,并返回拼接后的结果。
它的基本语法如下:```matlabresult = strcat(str1, str2, str3, ...)```其中,str1、str2、str3等参数表示要拼接的字符串,可以是字符数组或字符向量。
这些参数可以有多个,用逗号隔开。
拼接后的结果存储在result变量中。
在使用strcat函数时,需要注意的是,参数中的字符串必须是同一类型,即要么都是字符数组,要么都是字符向量。
如果参数中有一个或多个是空字符串或空字符向量,则函数会自动忽略它们。
下面是一个示例:```matlabstr1 = 'Hello, ';str2 = 'world!';result = strcat(str1, str2);disp(result);```运行上述代码,输出结果为"Hello, world!"。
可以看到,strcat 函数将str1和str2拼接在一起,并输出结果。
除了strcat函数,Matlab还提供了strjoin函数来进行字符串的拼接。
strjoin函数的语法如下:```matlabresult = strjoin(str_array, delimiter)```其中,str_array参数表示要拼接的字符串数组,delimiter参数表示拼接时的分隔符。
函数会将str_array中的字符串按照delimiter指定的分隔符进行拼接,并返回拼接后的结果。
下面是一个使用strjoin函数的示例:```matlabstr_array = {'apple', 'banana', 'orange'};delimiter = '-';result = strjoin(str_array, delimiter);disp(result);```运行上述代码,输出结果为"apple-banana-orange"。
matlab数组合并命令

matlab数组合并命令Matlab是一种用于数值计算和数据可视化的强大软件工具,它提供了许多方便的数组操作命令,其中包括数组合并命令。
在本文中,我们将探讨一些常用的数组合并命令,并介绍它们的用法和应用场景。
我们来介绍一下最简单的数组合并命令——"[]"。
在Matlab中,方括号可以用来创建数组,并且可以通过逗号将多个数组合并到一起。
例如,我们可以使用以下命令将两个数组合并成一个新的数组:```matlaba = [1, 2, 3];b = [4, 5, 6];c = [a, b];```在上述代码中,我们首先创建了两个数组a和b,然后使用方括号将它们合并成一个新的数组c。
这样,数组c中就包含了数组a和b 中的所有元素。
在这个例子中,数组c的结果将是[1, 2, 3, 4, 5, 6]。
除了使用方括号,Matlab还提供了一些特殊的数组合并命令,如"cat"和"vertcat"。
这些命令可以用于将多个数组沿着指定的维度进行合并。
例如,我们可以使用"cat"命令将两个行向量合并成一个矩阵:```matlaba = [1, 2, 3];b = [4, 5, 6];c = cat(1, a, b);```在上述代码中,我们使用了"cat"命令将数组a和b沿着垂直方向(即第一个维度)合并成一个新的矩阵c。
这样,矩阵c的结果将是一个2行3列的矩阵,其中第一行是数组a的元素,第二行是数组b的元素。
类似地,"vertcat"命令也可以用于将多个数组沿着垂直方向进行合并。
它的用法与"cat"命令相似,只是不需要指定维度参数。
例如,我们可以使用以下命令将两个行向量合并成一个矩阵:```matlaba = [1, 2, 3];b = [4, 5, 6];c = vertcat(a, b);```在上述代码中,我们使用了"vertcat"命令将数组a和b沿着垂直方向合并成一个新的矩阵c。
MatLab图形绘制功能口令及代码
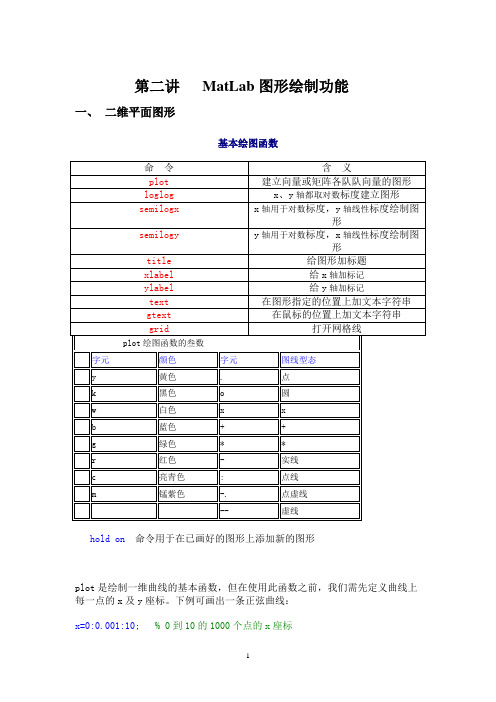
第二讲MatLab图形绘制功能一、二维平面图形基本绘图函数hold on 命令用于在已画好的图形上添加新的图形plot是绘制一维曲线的基本函数,但在使用此函数之前,我们需先定义曲线上每一点的x及y座标。
下例可画出一条正弦曲线:x=0:0.001:10; % 0到10的1000个点的x座标y=sin(x); % 对应的y座标plot(x,y); % 绘图Y=sin(10*x);plot(x,y,'r:',x,Y,'b') % 同时画两个函数若要改变颜色,在座标对後面加上相关字串即可:x=0:0.01:10;plot(x,sin(x),'r')若要同时改变颜色及图线型态(Line style),也是在坐标对後面加上相关字串即可:plot(x,sin(x),'r*')用axis([xmin,xmax,ymin,ymax])函数来调整图轴的范围axis([0,6,-1.5,1])MATLAB也可对图形加上各种注解与处理:xlabel('x轴'); % x轴注解ylabel('y轴'); % y轴注解title('余弦函数'); % 图形标题legend('y = cos(x)'); % 图形注解gtext('y = cos(x)'); % 图形注解 ,用鼠标定位注解位置grid on; % 显示格线fplot的指令可以用来自动的画一个已定义的函数分布图,而无须产生绘图所须要的一组数据做为变数。
其语法为fplot('fun',[xmin xmax ymin ymax]),其中fun 为一已定义的函数名称,例如sin, cos等等;而xmin, xmax, ymin, ymax则是设定绘图横轴及纵轴的下限及上限。
以下的例子是将一函数 f(x)=sin(x)/x 在-20<x<20,-0.4<y<1.2之间画出:>> fplot('sin(x)./x',[-20 20 -0.4 1.2])【例】画椭圆1232222=+y xa = [0:pi/50:2*pi]';%角度 π20- X = cos(a)*3; %参数方程 Y = sin(a)*2;plot(X,Y);xlabel('x'), ylabel('y'); title('椭圆')图形窗口的分割一般用命令subplot: subplot(2,2,1);subplot(2,3,4);MATLAB还有其他各种二维绘图函数,以适合不同的应用,详见下表。
