钢结构基本原理课后习题答案完全版
(完整版)钢结构基本原理课后习题与答案完全版
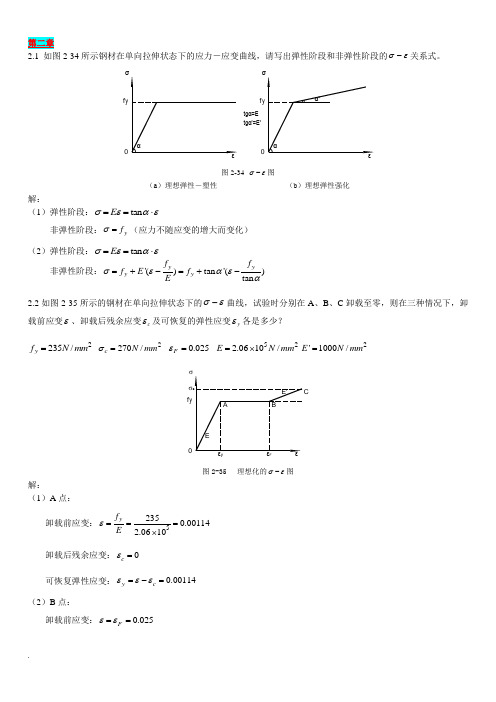
2.1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
tgα'=E'f y 0f y 0tgα=E 图2-34 σε-图(a )理想弹性-塑性(b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化) (2)弹性阶段:tan E σεαε==⋅ 非弹性阶段:'()tan '()tan y y y y f f f E f Eσεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少?2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =f yσ图2-35 理想化的σε-图解:(1)A 点:卸载前应变:52350.001142.0610y f Eε===⨯卸载后残余应变:0c ε=可恢复弹性应变:0.00114y c εεε=-=(2)B 点:卸载前应变:0.025F εε==卸载后残余应变:0.02386y c f Eεε=-=可恢复弹性应变:0.00114y c εεε=-=(3)C 点: 卸载前应变:0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变:0.05869cc Eσεε=-=可恢复弹性应变:0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
同济大学钢结构基本原理课后习题答案完全版

第二章如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
图2-34 σε-图(a )理想弹性-塑性 (b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化)(2)弹性阶段:tan E σεαε==⋅非弹性阶段:'()tan '()tan yyy y f f f E f E σεαεα=+-=+-如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少? 2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =图2-35 理想化的σε-图解:(1)A 点:卸载前应变:52350.001142.0610yf E ε===⨯卸载后残余应变:0c ε= 可恢复弹性应变:0.00114y c εεε=-=(2)B 点:卸载前应变:0.025F εε== 卸载后残余应变:0.02386y c f E εε=-= 可恢复弹性应变:0.00114y c εεε=-=(3)C 点:卸载前应变:0.0250.0350.06'c y F f E σεε-=-=+= 卸载后残余应变:0.05869c c E σεε=-= 可恢复弹性应变:0.00131y c εεε=-=试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
同济大学钢结构基本原理_沈祖炎_课后习题答案完全版
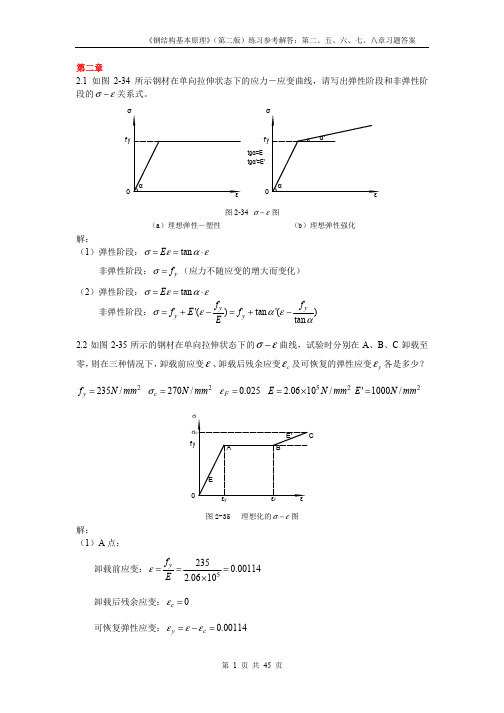
第二章 2.1 如图 2-34 所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶 段的 σ − ε 关系式。
σ σ
fy
fy tgα=E tgα'=E'
α'
0
α ε
0
α ε
图 2-34 σ − ε 图 (a)理想弹性-塑性 (b)理想弹性强化
σ 2 = −80 N / mm2 ,B 点的正应力 σ1 = −20 N / mm2 , σ 2 = −120 N / mm2 ,求梁 A 点与 B 点
的应力比和应力幅是多少? 解: (1)A 点: 应力比:ρ = (2)B 点: 应力比:ρ =
σ2 80 =− = −0.667 σ1 120
应力幅:△σ = σ max − σ min = 120 + 80 = 200 N / mm 2
第 95 页-4.4:
解:截面参数
A = 300 × 12 × 2 + 8 × 376 = 10208 mm 2
I xn =
1 1 × 300 × 400 3 − × (300 − 8) × 376 3 = 3.065 × 10 8 mm 4 12 12
第 5 页 共 45 页
《钢结构基本原理》 (第二版)练习参考解答:第二、五 × 502622.2 − = − = 0 ⇒ M = 502622.2 N ⋅ m ⇒ q = = 62827.8 N m 17280 5790208 A W 82
故: 当 q ≤ 62827.8 N m (0.628kN/cm)时,不考虑稳定问题 当 q > 62827 .8 N m 时,应考虑稳定问题
同济大学钢结构基本原理课后习题答案完全

第二章如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
图2-34 σε-图(a )理想弹性-塑性 (b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化)(2)弹性阶段:tan E σεαε==⋅非弹性阶段:'()tan '()tan yyy y f f f E f E σεαεα=+-=+-如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少? 2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =图2-35 理想化的σε-图解:(1)A 点:卸载前应变:52350.001142.0610yf E ε===⨯卸载后残余应变:0c ε= 可恢复弹性应变:0.00114y c εεε=-=(2)B 点:卸载前应变:0.025F εε== 卸载后残余应变:0.02386y c f E εε=-= 可恢复弹性应变:0.00114y c εεε=-=(3)C 点:卸载前应变:0.0250.0350.06'c y F f E σεε-=-=+= 卸载后残余应变:0.05869c c E σεε=-= 可恢复弹性应变:0.00131y c εεε=-=试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
同济大学钢结构基本原理(沈祖炎)课后习题答案

同济大学钢结构基本原理(沈祖炎)课后习题答案完全版第二章2.1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
tgα'=E'f 0f 0tgα=E 图2-34 σε-图(a )理想弹性-塑性(b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化) (2)弹性阶段:tan E σεαε==⋅ 非弹性阶段:'()tan '()tan y y y y f f f E f Eσεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少?2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =f 0σF图2-35 理想化的σε-图解:(1)A 点:卸载前应变:2350.001142.0610y f Eε===⨯卸载后残余应变:0c ε=可恢复弹性应变:0.00114y c εεε=-=卸载前应变:0.025F εε== 卸载后残余应变:0.02386y c f Eεε=-=可恢复弹性应变:0.00114y c εεε=-=(3)C 点: 卸载前应变:0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变:0.05869cc Eσεε=-=可恢复弹性应变:0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
钢结构基本原理课后习题与答案完全版电子教案

钢结构基本原理课后习题与答案完全版2.1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
tgα'=E'f y 0f y 0tgα=E图2-34 σε-图(a )理想弹性-塑性 (b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化)(2)弹性阶段:tan E σεαε==⋅非弹性阶段:'()tan '()tan yyy y f f f E f E σεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少?2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =f y 0σF图2-35 理想化的σε-图解:(1)A 点:卸载前应变:52350.001142.0610y f E ε===⨯卸载后残余应变:0c ε= 可恢复弹性应变:0.00114y c εεε=-=(2)B 点:卸载前应变:0.025F εε== 卸载后残余应变:0.02386y c f E εε=-= 可恢复弹性应变:0.00114y c εεε=-=(3)C 点:卸载前应变:0.0250.0350.06'c y F f E σεε-=-=+= 卸载后残余应变:0.05869c c E σεε=-=可恢复弹性应变:0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
同济大学钢结构基本原理(沈祖炎)课后习题答案完全版

同济大学钢结构基本原理(沈祖炎)课后习题答案完全版1. 引言同济大学钢结构基本原理是一门介绍钢结构基本知识和原理的课程。
在学习过程中,课后习题是检验学生掌握程度的重要方式。
本文是同济大学钢结构基本原理(沈祖炎)课后习题的完全版答案。
2. 第一章2.1 选择题1.D2.A3.B4.C5.A2.2 填空题1.拱2.跨度3.支点4.平行5.水平2.3 解答题1.我们可以通过使用方法一和方法二来计算桁架的支反作用力。
方法一使用刚度法,方法二使用Joints法。
具体步骤如下:方法一:–计算桁架的节点刚度矩阵。
–将所有节点刚度矩阵相加得到整个桁架的刚度矩阵。
–构造一个受力平衡的方程组,解得桁架的支反作用力。
方法二:–构造一个支座方程组,解得支座反力。
–通过节点内力平衡,计算出节点的内力。
2.钢结构的主要优点有:–高强度:钢材具有较高的强度和抗拉性能,使得钢结构能够承受较大的荷载。
–轻质:相对于混凝土结构来说,钢结构的自重较轻,可以减少建筑物的结构材料的使用量,降低建筑成本。
–施工速度快:由于钢结构可以在工厂中预制,因此施工速度较快,可以缩短工期,减少施工成本。
–可拆装性好:钢结构可以拆装,便于改建和迁移。
3.塔式起重机是利用强大的垂直支撑能力用高耸的塔架将货物一拉再拉的起重设备。
它是用来适应高空起重和物料搬移的一种机械。
结构上,塔式起重机主要由塔式结构、起升机构、回转机构和顶部配重组成。
其中,塔式结构是起重机的主要承重部分,承担起重机自重和起升机构的荷载。
塔式结构通常使用钢材制作,因为钢材具有较高的强度和抗拉性能,能够承受大的荷载。
此外,塔式起重机的钢结构也具有较好的可拆装性,便于施工和维护。
3. 第二章3.1 选择题1.B2.D3.A4.C5.B3.2 填空题1.核算按简化梁简化支承条件方式2.弹性模量3.建筑结构4.弹性变形5.线弹性3.3 解答题1.三个节点的坐标分别为A(0, 0),B(0, 4),C(4, 0)。
同济大学钢结构基本原理(沈祖炎)课后习题答案完全版-(1)

第二章2.1如图2-34所示钢材在单向拉伸状态下的应力一应变曲线,请写出弹性阶段和非弹性阶段的关系式。
解:(1)弹性阶段: E tan非弹性阶段:f y (应力不随应变的增大而变化)(2)弹性阶段: Etan非弹性阶段:f y E'(f y tan '( -^)yE ytan(b )理想弹性强化2.2如图2-35所示的钢材在单向拉伸状态下的曲线,试验时分别在 A 、B 、C 卸载至零,则在三种情况下,卸载前应变、卸载后残余应变及可恢复的弹性应变 y 各是多少?2f y 235N/mm 22c 270N / mm25 2 2F 0.025 E 2.06 105N/mm 2E' 1000N/mm 2解:图C图2-35理想化的 图(1 ) A 点:卸载前应变:f y235E 5 1 r2.06 105卸载后残余应变:c0可恢复弹性应变:y c0.00114 (2) B 点:卸载前应变:F0.025卸载后残余应变:c 也E0.02386可恢复弹性应变:y c0.00114(3) C 点:卸载前应变:F c f y0.025 0.035 0.06E'卸载后残余应变:ccE0.05869可恢复弹性应变:y c0.001312.3试述钢材在单轴反复应力作用下,钢材的曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材曲线与反复应力大小和作用时间关系:当构件反复力| | f y时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材曲线基本无变化;当丨丨f y时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
钢材曲线会相对更高而更短。
另外,载一定作用力下,作用时间越快,钢材强度会提高、而变形能力减弱,钢材曲线也会更高而更短。
同济大学钢结构基本原理(沈祖炎)课后习题答案完全版

第二章2.1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
tgα'=E'f 0f 0tgα=E 图2-34 σε-图(a )理想弹性-塑性(b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化) (2)弹性阶段:tan E σεαε==⋅ 非弹性阶段:'()tan '()tan y y y y f f f E f Eσεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少?2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =f 0σF图2-35 理想化的σε-图解:(1)A 点:卸载前应变:2350.001142.0610y f Eε===⨯卸载后残余应变:0c ε=可恢复弹性应变:0.00114y c εεε=-=卸载前应变:0.025F εε== 卸载后残余应变:0.02386y c f Eεε=-=可恢复弹性应变:0.00114y c εεε=-=(3)C 点: 卸载前应变:0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变:0.05869cc Eσεε=-=可恢复弹性应变:0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
同济大学钢结构基本原理_沈祖炎_课后习题答案完全版

Ak = 34 J )的特殊镇静钢(低合金钢)
( 3 ) Q390E :屈服强度 f y = 390 N / mm 2 、质量等级 E (要求提供 -400C 时纵向冲击功
Ak = 27 J )的特殊镇静钢(低合金钢)
( 4 ) Q235D :屈服强度 f y = 235 N / mm 2 、质量等级 D (要求提供 -200C 时纵向冲击功
按式(4-20)
Mx Mx N 1500 × 10 3 + ≤ fd ⇒ + ≤ 215 ⇒ M x ≤ 779386.1N ⋅ m An γW xn 17280 1.05 × 5790208 q= 8 M x 8 × 779386.1 ≤ = 97423.3 N m (0.974kN/cm) l2 82
解: (1)弹性阶段: σ = Eε = tan α ⋅ ε 非弹性阶段: σ = f y (应力不随应变的增大而变化) (2)弹性阶段: σ = Eε = tan α ⋅ ε 非弹性阶段: σ = f y + E '(ε −
fy E
) = f y + tan α '(ε −
fy tan α
)
2.2 如图 2-35 所示的钢材在单向拉伸状态下的 σ − ε 曲线,试验时分别在 A、B、C 卸载至 零, 则在三种情况下, 卸载前应变 ε 、 卸载后残余应变 ε c 及可恢复的弹性应变 ε y 各是多少?
按式(4-17)
N p = Af y = 17280 × 245 = 4233600N (4233.6kN)
N 1500 × 10 3 = = 0.35 > 0.13 Np 4233600
第 4 页 共 45 页
《钢结构基本原理》 (第二版)练习参考解答:第二、五、六、七、八章习题答案
同济钢结构基本原理课后习题答案完全版

y
fy 235
166.7
,查表得 0.257 )
Ncrd Af d 0.257 26.11102 310 208.0kN
5.3 图 5-25 所示为一轴心受压构件 ,两端铰接 ,截面形式为十字形.设在弹塑性范围内 E / G 值 保持常数,问在什么条件下,扭转屈曲临界力低于弯曲屈曲临界力,钢材为 Q235. 5.4 截面由钢板组成的轴心受压构件 ,其局部稳定计算公式是按什么准则进行推导得出的. 5.5 两端铰接的轴心受压柱,高 10m,截面为三块钢板焊接而成,翼缘为剪切边 ,材料为 Q235,强 度设计值
1 1 I x 2 ( 500 203 20 500 2602 ) 8 5003 1.436 109 mm4 12 12 1 1 I y 2 20 5003 500 83 4.167 108 mm4 12 12
A 2 500 20 500 8 24000mm2
fy E
0.02386
可恢复弹性应变: y c 0.00114 (3) C 点: 卸载前应变: F
c f y
E'
0.025 0.035 0.06
卸载后残余应变: c
c
E
0.05869
可恢复弹性应变: y c 0.00131 2.3 试述钢材在单轴反复应力作用下,钢材的 曲线、钢材疲劳强度与反复应力大小和 作用时间之间的关系。 答:钢材 曲线与反复应力大小和作用时间关系:当构件反复力 f y 时,即材料处于 弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材 曲线基本无变 化;当 f y 时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连 续进行,钢材 曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、 极限强度提高,而塑性韧性降低(时效现象) 。钢材 曲线会相对更高而更短。另外, 载一定作用力下,作用时间越快,钢材强度会提高、而变形能力减弱,钢材 曲线也会 更高而更短。 钢材疲劳强度与反复力大小和作用时间关系: 反复应力大小对钢材疲劳强度的影响以应力比 或应力幅(焊接结构)来量度。一般来说,应力比或应力幅越大,疲劳强度越低;而作用时 间越长(指次数多) ,疲劳强度也越低。 2.4 试述导致钢材发生脆性破坏的各种原因。 答: ( 1)钢材的化学成分,如碳、硫、磷等有害元素成分过多; ( 2)钢材生成过程中造成的 缺陷,如夹层、偏析等; (3)钢材在加工、使用过程中的各种影响,如时效、冷作硬化以及 焊接应力等影响; ( 4)钢材工作温度影响,可能会引起蓝脆或冷脆; ( 5)不合理的结构细部 设计影响,如应力集中等; ( 6)结构或构件受力性质,如双向或三向同号应力场; (7)结构 或构件所受荷载性质,如受反复动力荷载作用。 2.5 解释下列名词: (1)延性破坏 延性破坏,也叫塑性破坏,破坏前有明显变形,并有较长持续时间,应力超过屈服点 fy、并达到抗拉极限强度 fu 的破坏。 (2)损伤累积破坏 指随时间增长, 由荷载与温度变化, 化学和环境作用以及灾害因素等使结构或构件产生 损伤并不断积累而导致的破坏。
同济大学钢结构基本原理(沈祖炎)课后习题答案完全版

第二章2.1如图2-34所示钢材在单向拉伸状态下的应力一应变曲线,请写出弹性阶段和非弹性阶 段的 关系式。
解:(1)弹性阶段:E tan非弹性阶段:f y (应力不随应变的增大而变化)(2)弹性阶段:E tanf yf y 非弹性阶段:f y E'( 丄)f y tan '( 匚)Etan卸载后残余应变: c 0可恢复弹性应变:(2) B 点:(b )理想弹性强化2.2如图2-35所示的钢材在单向拉伸状态下的曲线,试验时分别在 A 、B 、C 卸载至零,则在三种情况下,卸载前应变、卸载后残余应变 c 及可恢复的弹性应变y 各是多少?2f y 235N/mm 22c270 N / mm 2F 0.025 E 2.06 105N/mm 2 E' 1000N/mm 2解:(1)A 点:卸载前应f yE235 2.06 1050.001140.00114图图2-35 理想化的 图卸载前应变:F0.025卸载后残余应变:c0.02386E可恢复弹性应变:y c0.00114(3) C点:c fy卸载前应变:F0.025 0.035 0.06 E'卸载后残余应变:c c0.05869 E可恢复弹性应变:y c0.001312.3试述钢材在单轴反复应力作用下,钢材的曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材曲线与反复应力大小和作用时间关系:当构件反复力| | fy时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材曲线基本无变化;当I I fy时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
钢材曲线会相对更高而更短。
另外,载一定作用力下,作用时间越快,钢材强度会提高、而变形能力减弱,钢材曲线也会更高而更短。
钢结构基本原理课后习题答案

钢结构基本原理课后习题答案【篇一:钢结构基本原理(沈祖炎)课后习题答案完全版】2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的???关系式。
00图2-34 ???图(a)理想弹性-塑性(b)理想弹性强化解:(1)弹性阶段:??e??tan???非弹性阶段:??fy(应力不随应变的增大而变化)(2)弹性阶段:??e??tan???非弹性阶段:??fy?e(??fye)?fy?tan?(??fytan?)2.2如图2-35所示的钢材在单向拉伸状态下的???曲线,试验时分别在a、b、c卸载至零,则在三种情况下,卸载前应变?、卸载后残余应变?c及可恢复的弹性应变?y各是多少?fy?235n/mm2 ?c?270n/mm2 ?f?0.025e?2.06?105n/mm2e?1000n/mm20f图2-35 理想化的???图解:(1)a点:卸载前应变:??fye?235卸载后残余应变:?c?0 可恢复弹性应变:?y????c?0.00114卸载前应变:???f?0.025 卸载后残余应变:?c???fye?0.02386 可恢复弹性应变:?y????c?0.00114(3)c点:卸载前应变:???f??c?fye?0.025?0.035?0.06 ?卸载后残余应变:?c???c?0.05869 e可恢复弹性应变:?y????c?0.001312.3试述钢材在单轴反复应力作用下,钢材的?作用时间之间的关系。
??曲线、钢材疲劳强度与反复应力大小和答:钢材???曲线与反复应力大小和作用时间关系:当构件反复力??fy时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材???曲线基本无变化;当??fy时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材???曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
同济大学沈祖炎钢结构基本原理课后习题全套答案
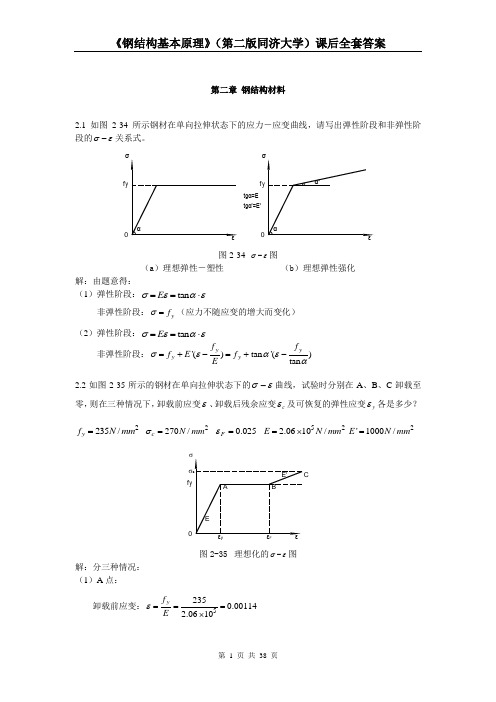
第二章 钢结构材料2.1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
tgα'=E'f 0f 0tgα=E 图2-34 σε-图(a )理想弹性-塑性 (b )理想弹性强化解:由题意得:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化) (2)弹性阶段:tan E σεαε==⋅ 非弹性阶段:'()tan '()tan y y y y f f f E f Eσεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少?2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =f 0σF图2-35 理想化的σε-图解:分三种情况: (1)A 点:卸载前应变:52350.001142.0610y f Eε===⨯卸载后残余应变:0c ε=可恢复弹性应变:0.00114y c εεε=-=(2)B 点: 卸载前应变:0.025F εε== 卸载后残余应变:0.02386y c f Eεε=-=可恢复弹性应变:0.00114y c εεε=-=(3)C 点: 卸载前应变:0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变:0.05869cc Eσεε=-=可恢复弹性应变:0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
钢结构基本原理(沈祖炎)课后习题答案完全版.docx

《钢结构基本原理》(第二版)练习参考解答:第二、五、六、七、八章习题答案第二章2.1如图2-34所示钢材在单向拉伸状态下的应力一应变曲线,请写出弹性阶段和非弹性阶 段的二-:关系式。
图2-34 二 _ ;图(a )理想弹性—塑性(b )理想弹性强化解:(1) 弹性阶段: ;:=E ;=ta n 、£;非弹性阶段: 二=f y (应力不随应变的增大而变化)(2) 弹性阶段:E ;=ta n _:「:非弹性阶段:二一 f y ∙ E'(;f y) _ f y tan :•'(;- J y)Etan 二2.2如图2-35所示的钢材在单向拉伸状态下的;「-;曲线,试验时分别在 A 、B 、C 卸载至 零,则在三种情况下,卸载前应变;、卸载后残余应变J C 及可恢复的弹性应变;y 各是多少?f y =235N∕mm 2 二 c =270N∕mm 2 ;F =0∙025 E =2.06 105 N ∕mm 2 E' =IOOON ∕mm 2卸载后残余应变:;c =0 可恢复弹性应变:0.00114(2) B 点:解: (1) A 点:卸载前应f y E 2352.06 IO 5= 0.00114 Cr图2-35 理想化的;「-;图卸载前应变:;=τ -0.025、、f y卸载后残余应变: C 0.02386E可恢复弹性应变:;y - ;- ;C =0.00114(3) C 点:■ c _ f y卸载前应变:;=;F - y=0.025 ■ 0.035 =0.06F E'■ C卸载后残余应变: C - =0.05869E可恢复弹性应变:■:y - ;- ;- =0.001312.3试述钢材在单轴反复应力作用下,钢材的二-;曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材;「-;曲线与反复应力大小和作用时间关系:当构件反复力二_ f y时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材匚-:曲线基本无变化;当|「| fy时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材二-;曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
钢筋结构基本原理课后习题与答案完全版

2.1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
tgα'=E'f y0f y 0tgα=E图2-34 σε-图(a )理想弹性-塑性 (b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化)(2)弹性阶段:tan E σεαε==⋅非弹性阶段:'()tan '()tan yyy y f f f E f E σεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少?2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =图2-35 理想化的σε-图解:(1)A 点:卸载前应变:52350.001142.0610yf E ε===⨯卸载后残余应变:0c ε= 可恢复弹性应变:0.00114y c εεε=-=(2)B 点:卸载前应变:0.025F εε== 卸载后残余应变:0.02386y c f E εε=-= 可恢复弹性应变:0.00114y c εεε=-=(3)C 点:卸载前应变:0.0250.0350.06'c y F f E σεε-=-=+= 卸载后残余应变:0.05869cc E σεε=-=可恢复弹性应变:0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
tgα'=E'f y0f y 0tgα=E图2-34 σε-图(a )理想弹性-塑性 (b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化)(2)弹性阶段:tan E σεαε==⋅非弹性阶段:'()tan '()tan y y y y f f f E f E σεαεα=+-=+-'如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =f y 0σF图2-35 理想化的σε-图解:(1)A 点:卸载前应变:52350.001142.0610yf E ε===⨯卸载后残余应变:0c ε=可恢复弹性应变:0.00114y c εεε=-= }(2)B 点:卸载前应变:0.025F εε==卸载后残余应变:0.02386y c f E εε=-= 可恢复弹性应变:0.00114y c εεε=-=(3)C 点:卸载前应变:0.0250.0350.06'c y F f E σεε-=-=+= 卸载后残余应变:0.05869c c E σεε=-= 可恢复弹性应变:0.00131y c εεε=-=试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
`答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
钢材σε-曲线会相对更高而更短。
另外,载一定作用力下,作用时间越快,钢材强度会提高、而变形能力减弱,钢材σε-曲线也会更高而更短。
钢材疲劳强度与反复力大小和作用时间关系:反复应力大小对钢材疲劳强度的影响以应力比或应力幅(焊接结构)来量度。
一般来说,应力比或应力幅越大,疲劳强度越低;而作用时间越长(指次数多),疲劳强度也越低。
试述导致钢材发生脆性破坏的各种原因。
答:(1)钢材的化学成分,如碳、硫、磷等有害元素成分过多;(2)钢材生成过程中造成的缺陷,如夹层、偏析等;(3)钢材在加工、使用过程中的各种影响,如时效、冷作硬化以及焊接应力等影响;(4)钢材工作温度影响,可能会引起蓝脆或冷脆;(5)不合理的结构细部设计影响,如应力集中等;(6)结构或构件受力性质,如双向或三向同号应力场;(7)结构或构件所受荷载性质,如受反复动力荷载作用。
解释下列名词:(1)延性破坏延性破坏,也叫塑性破坏,破坏前有明显变形,并有较长持续时间,应力超过屈服点fy 、并达到抗拉极限强度fu 的破坏。
(2)损伤累积破坏\指随时间增长,由荷载与温度变化,化学和环境作用以及灾害因素等使结构或构件产生损伤并不断积累而导致的破坏。
(3)脆性破坏脆性破坏,也叫脆性断裂,指破坏前无明显变形、无预兆,而平均应力较小(一般小于屈服点fy )的破坏。
(4)疲劳破坏指钢材在连续反复荷载作用下,应力水平低于极限强度,甚至低于屈服点的突然破坏。
(5)应力腐蚀破坏应力腐蚀破坏,也叫延迟断裂,在腐蚀性介质中,裂纹尖端应力低于正常脆性断裂应力临界值的情况下所造成的破坏。
(6)疲劳寿命指结构或构件中在一定恢复荷载作用下所能承受的应力循环次数。
一两跨连续梁,在外荷载作用下,截面上A 点正应力为21120/N mm σ=,2280/N mm σ=-,B 点的正应力2120/N mm σ=-,22120/N mm σ=-,求梁A 点与B 点的应力比和应力幅是多少¥解:(1)A 点:应力比:21800.667120σρσ==-=- 应力幅:2max min 12080200/N mm σσσ=-=+= (2)B 点:应力比:12200.167120σρσ=== 应力幅:2max min 20120100/N mm σσσ=-=-+= 指出下列符号意义: (1)Q235AF (2)Q345D (3)Q390E(4)Q235D 答:(1)Q235AF :屈服强度2235/y f N mm =、质量等级A (无冲击功要求)的沸腾钢(碳素结构钢)(2)Q345D :屈服强度2345/y f N mm =、质量等级D (要求提供-200C 时纵向冲击功34k A J =)的特殊镇静钢(低合金钢)?(3)Q390E :屈服强度2390/y f N mm =、质量等级E (要求提供-400C 时纵向冲击功27k A J =)的特殊镇静钢(低合金钢)(4)Q235D :屈服强度2235/y f N mm =、质量等级D (要求提供-200C 时纵向冲击功27k A J =)的特殊镇静钢(碳素结构钢)根据钢材下选择原则,请选择下列结构中的钢材牌号:(1)在北方严寒地区建造厂房露天仓库使用非焊接吊车梁,承受起重量Q>500KN 的中级工作制吊车,应选用何种规格钢材品种(2)一厂房采用焊接钢结构,室内温度为-100C ,问选用何种钢材答:(1)要求钢材具有良好的低温冲击韧性性能、能在低温条件下承受动力荷载作用,可选Q235D 、Q345D 等;(2)要求满足低温可焊性条件,可选用Q235BZ 等。
钢材有哪几项主要机械指标各项指标可用来衡量钢材哪些方面的性能答:主要机械性能指标:屈服强度y f 、极限强度u f 以及伸长率5δ或10δ,其中,屈服强度y f 、极限强度u f 是强度指标,而伸长率5δ或10δ是塑性指标。
【影响钢材发生冷脆的化学元素是哪些使钢材发生热脆的化学元素是哪些答:影响钢材发生冷脆的化学元素主要有氮和磷,而使钢材发生热脆的化学元素主要是氧和硫。
第四章第五章影响轴心受压稳定极限承载力的初始缺陷有哪些在钢结构设计中应如何考虑某车间工作平台柱高,轴心受压,两端铰接.材料用I16,Q235钢,钢材的强度设计值2215/d f N mm =.求轴心受压稳定系数ϕ及其稳定临界荷载.如改用Q345钢2310/d f N mm =,则各为多少—解答:查P335附表3-6,知I16截面特性,26.57, 1.89,26.11x y i cm i cm A cm === 柱子两端较接, 1.0x y μμ== 故柱子长细比为 1.0260039.665.7x x x l i μλ⨯===,2600 1.0137.618.9y y y l i μλ⨯===因为x y λλ<,故对于Q235钢相对长细比为5137.6235 1.482.0610yf E λλππ===⨯钢柱轧制, /0.8b h ≤.对y 轴查P106表5-4(a)知为不b 类截面。
故由式5-34b 得()223212ϕααλλλ⎡=++⎢⎣()2210.9650.300 1.48 1.482 1.48⎡=+⨯+-⎢⎣⨯ 0.354= !(或计算137.6λ=,再由附表4-4查得0.354ϕ=)故得到稳定临界荷载为20.35426.1110215198.7crd d N Af kNϕ==⨯⨯⨯= 当改用Q365钢时,同理可求得 1.792λ=。
由式5-34b 计算得0.257ϕ= (或由166.7λ=,查表得0.257ϕ=) 故稳定临界荷载为20.25726.1110310208.0crd d N Af kNϕ==⨯⨯⨯= 图5-25所示为一轴心受压构件,两端铰接,截面形式为十字形.设在弹塑性范围内/E G 值保持常数,问在什么条件下,扭转屈曲临界力低于弯曲屈曲临界力,钢材为Q235.截面由钢板组成的轴心受压构件,其局部稳定计算公式是按什么准则进行推导得出的.|两端铰接的轴心受压柱,高10m,截面为三块钢板焊接而成,翼缘为剪切边,材料为Q235,强度设计值2205/d f N mm =,承受轴心压力设计值3000kN (包括自重).如采用图5-26所示的两种截面,计算两种情况下柱是否安全.图5-26 题解答:截面特性计算:对a)截面:32394112(5002020500260)8500 1.436101212x I mm =⨯⨯⨯+⨯⨯+⨯⨯=⨯ 3384112205005008 4.167101212y I mm =⨯⨯⨯+⨯⨯=⨯2250020500824000A mm =⨯⨯+⨯=244.6x i mm ==131.8y i mm==\对b)截面:32384112(4002540025212.5)104009.575101212x I mm =⨯⨯⨯+⨯⨯+⨯⨯=⨯33841122540040010 2.667101212y I mm=⨯⨯⨯+⨯⨯=⨯24002524001024000A mm =⨯⨯+⨯=199.7x i mm ==105.4y i mm==整体稳定系数的计算:钢柱两端铰接,计算长度10000ox oy l l mm ==对a)截面: 1000040.88244.6ox x x l i λ=== 1000075.87131.8ox y y l i λ===对b)截面: 1000050.08199.7kxx x l i λ=== 1000094.88105.4ox y y l i λ===根据题意,查P106表5-4(a),知钢柱对x 轴为b 类截面,对y 轴为c 类截面. @对a)截面:对x 轴:40.880.440x λπ===()223212x x x x ϕααλλλ⎡=++-⎢⎣()2210.9650.30.440.4420.44⎡=⨯+⨯+⎢⨯⎣ 0.895=(或计算40.88λ=,再由附表4-4查得0.896x ϕ)对y 轴:25.870.816y λπ===()223212y y y y ϕααλλλ⎡=++⎢⎣()2210.9060.5950.8160.81620.816⎡=⨯+⨯+⎢⨯⎣ * 0.604=(或计算75.87λ=,再由附表4-5查得0.604y ϕ)故取该柱的整体稳定系数为0.604ϕ=对b)截面,同理可求得0.852x ϕ=,0.489y ϕ=,故取该柱截面整体稳定系数为0.489ϕ= 整体稳定验算:对a)截面0.604240002052971.68 3000 crd d N Af kN kN ϕ==⨯⨯=<不满足。
