matlab--算法大全--第04章__动态规划
动态规划求解方法的Matlab实现及应用

方法, 在工程技术、 科学管理、 工农业生产及军事等 领域都有广泛的应用。在理论上, 动态规划是求解 这类问题全局最优解的一种有效方法, 特别是对于 实际中的某些非线性规划问题可能是最优解的唯 一方法。然而, 动态规划仅仅是解决多阶段决策问 题的一种方法, 或者说是考查问题的一种途径, 而 不是一种具体的算法。就目前而言, 动态规划没有 统一的标准模型, 其解法也没有标准算法, 在实际 应用中, 需要具体问题具体分析。动态规划模型的 求解问题是影响动态规划理论和方法应用的关键 所在, 而子问题的求解和大量结果的存储、 调用更 是一个难点所在。然而, 随着计算机技术的快速发 展, 特别是内存容量和计算速度的增加, 使求解较
&
动态规划的基本模型
实际中, 要构造一个标准的动态规划模型, 通
常需要采用以下几个步骤: 把 !划分阶段 按照问题的时间或空间特征, 问题分为若干个阶段。这些阶段必须是有序的或 者是可排序的 (即无后向性) , 否则, 应用无效。 " 选择状态 将问题发展到各个阶段时所处
收稿日期: !""# $ "% $ &% 作者简介: 于
+
++,
求解方法的实践与应用
[,] 最佳组队问题
在文献 [,] 中的第 + 个问题: “确定最佳组队问 题, 即要求给出 ,- 名队员组成 . 个队的组队方案, 使整体竞赛水平最高, 并给出每个队的竞赛水平” 。 文献 [,] 建立了最佳组队的动态规划模型, 其 模型的基本方程以逆序形式给出, 即
阶段的
) 允许决策集合为 %( , 指标函数为 &( " #" % & ) " #" % & , 。当求解时, 由边界条件从 " ! & 开始, 由前向 $" )
基于Matlab的动态规划算法的实现及应用

基于Matlab的动态规划算法的实现及应用动态规划(Dynamic Programming)是一种用来求解多阶段最优化问题的方法,在许多领域中都得到了广泛的应用。
本文将介绍如何使用Matlab实现动态规划算法,并通过一个具体的应用案例来说明其使用方法和效果。
动态规划算法的基本思想是将一个问题分解成多个阶段,每个阶段的最优解可以通过前一阶段的最优解来计算得到。
具体实现时,需要定义一个状态转移方程来描述问题的阶段之间的关系,以及一个递推公式来计算每个阶段的最优解。
在Matlab中,可以使用矩阵来表示问题的状态和状态转移方程,使用循环结构来进行递推计算。
下面以求解最长递增子序列(Longest Increasing Subsequence)为例来说明动态规划算法在Matlab中的实现和应用。
最长递增子序列是一个经典的动态规划问题,给定一个序列,找出一个最长的子序列,使得子序列中的元素是递增的。
可以使用动态规划算法来求解该问题。
定义一个状态数组dp,其中dp(i)表示以第i个元素结尾的最长递增子序列的长度。
初始化dp数组为1,表示每个元素自身就是一个递增子序列。
然后,使用一个循环结构遍历序列的每个元素,计算以当前元素结尾的最长递增子序列的长度。
具体实现时,需要比较当前元素与之前的元素的关系,如果当前元素大于之前的元素,则可以将当前元素加入到之前的最长递增子序列中,并更新dp(i)为dp(j)+1,其中j为小于i的所有元素的位置。
遍历dp数组,找出其中的最大值,即为整个序列的最长递增子序列的长度。
下面是Matlab代码的实现:```matlabfunction LIS = LongestIncreasingSubsequence(nums)N = length(nums);dp = ones(1, N);for i = 1:Nfor j = 1:i-1if nums(i) > nums(j)dp(i) = max(dp(i), dp(j)+1);endendendLIS = max(dp);end```以上代码定义了一个函数LongestIncreasingSubsequence,输入参数为一个序列nums,输出结果为最长递增子序列的长度LIS。
基于Matlab的动态规划算法的实现及应用

基于Matlab的动态规划算法的实现及应用动态规划是一种解决多阶段决策过程的优化技术。
它的主要思想是将问题分成几个阶段,在每个阶段用一个状态来描述问题,然后找到在每个阶段中符合条件的最优状态值,以便决定在一个阶段结束的时候采取什么决策。
在Matlab中,可以非常方便地实现动态规划算法。
这里简要介绍一下基于Matlab的动态规划算法的实现及应用。
首先,我们需要定义状态转移方程。
状态转移方程是动态规划算法的核心,决定了如何从一个状态转移到另一个状态。
例如,我们要用动态规划算法求解一个背包问题,物品的重量为w1,w2,w3,w4,w5,物品的价值为v1,v2,v3,v4,v5,背包的容量为W。
那么状态转移方程可以定义如下:dp(i,j) = max(dp(i-1,j), dp(i-1,j-w(i))+v(i))其中dp(i,j)表示前i个物品放入容量为j的背包中所能得到的最大价值。
i表示物品的数量,j表示背包的容量。
w(i)表示第i个物品的重量,v(i)表示第i个物品的价值。
上式中的max表示在当前状态下,应该选择哪个状态值。
然后我们需要初始化第一个状态dp(1,j),当只考虑第1个物品时,dp(1, j)的值与w(1)和v(1)有关。
当物品数量为0时,dp(i, j)的值为0。
接下来,我们可以使用循环以及状态转移方程来计算出dp(i,j)的值,最终得到最优的解。
在Matlab中,可以利用循环完成状态转移方程的计算,例如:dp(1,:) = (w(1) <= j).*v(1);在上述代码中,利用循环计算每个状态的最大价值。
第一行是初始化第一个状态,即当只有一个物品的时候,dp(1, j)的值为v(1)或0。
第二行是循环计算后续状态的最大价值,根据状态转移方程进行计算。
在实际应用中,动态规划算法可以用于诸如最优路径规划、时间序列分析、机器学习等领域。
例如,在机器学习中,动态规划算法可以用于序列模型的预测和分类问题。
基于Matlab的动态规划程序实现

动态规划方法的Matlab 实现与应用动态规划(Dynamic Programming)是求解决策过程最优化的有效数学方法,它是根据“最优决策的任何截断仍是最优的”这最优性原理,通过将多阶段决策过程转化为一系列单段决策问题,然后从最后一段状态开始逆向递推到初始状态为止的一套最优化求解方法。
1.动态规划基本组成(1) 阶段 整个问题的解决可分为若干个阶段依次进行,描述阶段的变量称为阶段变量,记为k(2) 状态 状态表示每个阶段开始所处的自然状况或客观条件,它描述了研究问题过程的状况。
各阶段状态通常用状态变量描述,用k x 表示第k 阶段状态变量,n 个阶段决策过程有n+ 1个状态。
(3) 决策 从一确定的状态作出各种选择从而演变到下一阶段某一状态,这种选择手段称为决策。
描述决策的变量称为决策变量,决策变量限制的取值范围称为允许决策集合。
用()k k u x 表示第k 阶段处于状态k x 时的决策变量,它是k x 的函数。
用()k k D x Dk(xk)表示k x 的允许决策的集合。
(4) 策略 每个阶段的决策按顺序组成的集合称为策略。
由第k 阶段的状态k x 开始到终止状态的后部子过程的策略记为{}11(),(),,()k k k k n n u x u x u x ++ 。
可供选择的策略的范围称为允许策略集合,允许策略集合中达到最优效果的策略称为最优策略。
从初始状态*11()x x =出发,过程按照最优策略和状态转移方程演变所经历的状态序列{}****121,,,,n n x x x x + 称为最优轨线。
(5) 状态转移方程 如果第k 个阶段状态变量为k x ,作出的决策为k u ,那么第k+ 1阶段的状态变量1k x +也被完全确定。
用状态转移方程表示这种演变规律,记为1(,)k k k x T x u +=。
(6) 指标函数 指标函数是系统执行某一策略所产生结果的数量表示,是衡量策略优劣的数量指标,它定义在全过程和所有后部子过程上,用()k k f x 表示。
基于Matlab的动态规划算法的实现及应用

基于Matlab的动态规划算法的实现及应用动态规划是一种常用的优化算法,可以在给定的约束条件下,求解具有最优解的问题。
它通过将原问题拆分成若干子问题,并保存子问题的解,从而避免重复计算,减少运算量,提高算法的效率。
在Matlab中,可以通过使用递归或迭代的方式来实现动态规划算法。
下面将介绍一种基于Matlab的动态规划算法的实现及应用。
我们需要确定问题的状态,即在求解过程中需要保存的信息。
然后,定义状态转移方程,即问题的解与其子问题的解之间的关系。
确定边界条件,即问题的基本解。
以求解斐波那契数列为例,斐波那契数列的定义如下:F(0) = 0F(1) = 1F(n) = F(n-1) + F(n-2) (n>=2)我们可以使用动态规划算法来求解斐波那契数列。
定义一个数组dp,用来保存每个子问题的解。
然后,通过迭代的方式,计算从小到大的每个子问题的解,直到得到问题的最优解。
在Matlab中,可以使用以下代码实现动态规划算法求解斐波那契数列:```matlabfunction [result] = Fibonacci(n)% 初始化数组dpdp = zeros(1, n+1);% 定义边界条件dp(1) = 0;dp(2) = 1;% 迭代计算每个子问题的解for i = 3:n+1dp(i) = dp(i-1) + dp(i-2);end% 返回问题的最优解result = dp(n+1);end```运行以上代码,输入一个整数n,即可求解斐波那契数列的第n项。
除了求解斐波那契数列,动态规划算法还可以应用于其他许多领域,如路径规划、背包问题等。
在路径规划中,我们可以使用动态规划算法来求解最短路径或最优路径;在背包问题中,我们可以使用动态规划算法来求解能够装入背包的最大价值。
动态规划算法是一种强大的优化算法,在Matlab中的实现也相对简单。
通过定义问题的状态、状态转移方程和边界条件,我们可以使用动态规划算法来求解各种不同类型的问题。
基于Matlab的动态规划算法的实现及应用

基于Matlab的动态规划算法的实现及应用动态规划算法是解决许多计算问题的有效方法,它可以用于组合优化、资源分配和时间序列分析等方面。
Matlab是一种高级计算软件,提供了许多内置函数,使得动态规划算法的实现变得简单。
一、动态规划算法的基本思想动态规划算法是一种优化技术,可以用于解决一些复杂的计算问题。
它的基本思想是把一个大问题分解成一系列子问题,通过解决子问题得到整体的最优解。
在动态规划算法中,通常使用递推式来描述问题的最优解。
在Matlab中,动态规划算法的实现通常包括以下几个步骤:1.定义状态变量:根据问题的特性,定义一组状态变量,用于描述问题的状态。
2.制定状态转移方程:根据问题的条件和规则,制定一组状态转移方程,用于计算问题的最优解。
3.构建转移矩阵:将状态转移方程转化为矩阵形式,便于计算和优化。
4.初始化状态变量:将初始状态赋值给状态变量,用于递推计算。
5.递推计算:根据状态转移矩阵和当前状态,计算下一时刻状态的值,直到达到目标状态。
6.输出最优解:输出最终状态对应的最优解。
三、应用实例1.背包问题背包问题是一种组合优化问题,目标是在给定的一组限制条件下,尽可能地装满容量限制的背包。
动态规划算法可以有效解决背包问题。
function [optx,optf]=knapsack(w,v,c)%w:物品的重量; v:物品的价值; c:背包容量%optx:最优解; optf:最优解对应的函数值n=length(w); %物品数量f=zeros(n+1,c+1); %状态变量fx=zeros(1,n); %物品的选择变量xfor i=1:nfor j=1:cif j<w(i) %背包容量不足的情况f(i+1,j)=f(i,j);else %背包容量足够的情况f(i+1,j)=max(f(i,j),f(i,j-w(i))+v(i));endendendoptf=f(n+1,c); %最优解j=c; %从后往前寻找物品for i=n:-1:1if f(i+1,j)>f(i,j)x(i)=1;j=j-w(i);endendoptx=x; %最优解2.最长公共子序列问题最长公共子序列问题是一种字符串匹配问题,目标是在两个字符串中找到最长的公共连续子序列。
《动态规划MATLab》课件

寻找最优子结构
将问题拆分为多个子问题,并定义子问 题之间的关系。
初始条件与边界条件定义
确定初始条件和边界条件,为求解过程 提供基础。
动态规划常见问题
1 背包问题
在给定容量和价值的情况 下,选择合适的物品放入 背包,使得背包中物品的 总价值最大化。
2 最长公共子序列
3 最长上升子序列
在给定两个序列的情况下, 找到它们之间最长的公共 子序列。
《动态规划MATLab》 PPT课件
这个《动态规划MATLab》PPT课件将帮您深入了解动态规划算法及其在 MATLab中的应用。通过丰富的示例和清晰的代码演示,您将掌握动态规划求 解问题的步骤和常见方法。
什么是动态规划
定义
动态规划是一种用于解决最优化问题的算法思想,通过将问题拆分为多个子问题并保存已计 算的中间结果,以减少重复计算的次数。
在给定序列的情况下,找 到其中最长的上升子序列。
MATLab介绍
基本语法
MATLab具有简洁而灵活的 语法,易于学习和使用。
数组与矩阵操作
MATLab提供了丰富的数组 和矩阵操作函数,方便快捷 地处理数据。
函数与脚本文件
MATLab支持函数和脚本文 件的编写与调用,使程序逻 辑更加结构化。
使用MATLab进行动态规划问题求解
1
用MATLab实现背包问题
通过MATLab编写代码,解决背包问题,得出最优解。
2
用MATLab实现最长公共子序列
利用MATLab函数,找到两个序列之间的最长公共子序列。
3
用MATLab实现最长上升子序列
使用MATLab算法,求解给定序列的最长上升子序列。
总结
动态规划思想及其应用
基于Matlab的动态规划算法的实现及应用

基于Matlab的动态规划算法的实现及应用动态规划算法是一种解决多阶段决策问题的优化方法,它可以在每个阶段选择最优决策,并且在各个阶段间保持最优子结构,从而达到整体最优的目的。
在实际应用中,动态规划算法被广泛用于求解优化问题、路径规划、资源分配等方面。
本文将介绍基于Matlab 的动态规划算法的实现及应用,并深入探讨其在实际问题中的应用。
一、动态规划算法的基本原理动态规划算法的基本原理是通过将问题分解为子问题,并计算每个子问题的最优解,然后存储下来以供后续使用。
最终得到整体最优解。
动态规划算法通常包括以下几个步骤:1. 确定状态和状态转移方程:首先需要确定问题的状态,然后建立状态之间的转移关系,也就是状态转移方程。
状态转移方程描述了问题的子问题之间的关系,是动态规划算法的核心。
2. 初始化:初始化动态规划数组,将初始状态下的值填入数组中。
3. 状态转移:利用状态转移方程计算出各个阶段的最优解,并将其存储在动态规划数组中。
4. 求解最优解:根据动态规划数组中存储的各个阶段的最优解,可以得到整体最优解。
Matlab是一种强大的计算软件,具有丰富的数值计算函数和可视化工具,非常适合实现动态规划算法。
下面以一个简单的背包问题为例,介绍如何在Matlab中实现动态规划算法。
假设有n件物品,每件物品的重量为w[i],价值为v[i]。
现在有一个容量为C的背包,问如何选择物品放入背包,使得背包中物品的总价值最大。
我们需要确定问题的状态和状态转移方程。
在这个问题中,我们可以定义状态dp[i][j]表示在前i件物品中选择若干个放入容量为j的背包中所能获得的最大价值。
状态转移方程可以表示为:dp[i][j] = max(dp[i-1][j], dp[i-1][j-w[i]] + v[i])然后,我们可以利用Matlab实现这个动态规划算法,代码如下:```matlabfunction max_value = knapsack(w, v, C)n = length(w);dp = zeros(n+1, C+1);for i = 1:nfor j = 1:Cif j >= w(i)dp(i+1,j+1) = max(dp(i,j+1), dp(i,j-w(i)+1)+v(i));elsedp(i+1,j+1) = dp(i,j+1);endendendmax_value = dp(n+1,C+1);end```三、动态规划算法在实际问题中的应用动态规划算法在实际问题中有着广泛的应用,下面以路径规划问题为例,介绍动态规划算法的应用。
动态规划选址,背包matlab

%选址问题cleara=[150 170 210 260 310;150 165 220 170 320;150 180 230 265 310;150 190 215 240 300]%第一年到第五年的选址费用b=[0 5 10 9;5 0 7 6;10 7 0 8;9 6 8 0]%从地址i转到地址j的转移费用f=zeros(4,6);%存储指标函数的值v=zeros(4,1);%存储决策变量的值ff=zeros(5,1);%存储指标函数的值c=zeros(5,1);%存储最终所选地址for s=5:-1:1%用逆推法求解for k=1:4v=a(:,s)+b(:,k);f(k,s)=min(v+f(:,s+1));endff(s,1)=min(f(:,s));c(s,1)=min(find(f(:,s)==ff(s,1)));%找到一列中最小元素所在的行,如果有两行相等则取较小行endff,c% 背包问题A=10; %背包的重量极限n=3; %物品的种数a=[3 4 5]; %第i件物品的单件重量c=[4 5 6]; %第i件物品的单件价值%%%%%%%%%%%%%%%%%%%s=0:1:A;x{1}=floor(s./a(1));f{1}=c(1).*x{1};for i=1:A+1xvalue{1}{i}=x{1}(i); %xvalue为最优路径endfor i=2:nfor j=0:10tmax=floor(s(j+1)/a(i))+1;ff{j+1}=ones(1,tmax);for t=1:tmaxff{j+1}(t)=(t-1)*c(i)+f{i-1}(s(j+1)-(t-1)*a(i)+1); %临时取值:(t-1)*c(i)+f(i)xval{j+1}{t}=[xvalue{i-1}{s(j+1)-(t-1)*a(i)+1},t-1]; %每种ff取值的x 的路径endfff=ones(1,tmax);fff=ff{j+1};[f{i}(j+1),k]=max(fff);xvalue{i}{j+1}=xval{j+1}(k); %通过k值确定最优路径endend[fmax,h]=max(f{n}); %最优解finalx=xvalue{n}{h}; %最优路径finalxfmax。
基于Matlab的动态规划算法的实现及应用

基于Matlab的动态规划算法的实现及应用动态规划算法是一种解决多阶段决策过程的优化问题的方法,它可以用于求解最优化问题、路径规划、序列匹配等多种应用场景。
在计算机科学领域,动态规划算法被广泛应用于图像处理、机器学习、自然语言处理等诸多领域中。
本文介绍了基于Matlab的动态规划算法的实现及其应用。
一、动态规划算法概述动态规划算法是一种通过将原问题分解成子问题来求解最终问题的优化方法。
它的核心思想是利用子问题的最优解来推导出原问题的最优解。
动态规划算法通常用于解决有重叠子问题和最优子结构性质的问题,这些问题的解可以通过递归地求解子问题而得到。
动态规划算法的一般步骤如下:1. 定义子问题:将原问题分解成若干子问题,确定子问题的状态和状态转移方程。
2. 利用子问题的最优解来递推原问题的最优解,并存储中间结果。
动态规划算法具有较强的通用性和灵活性,可以适用于多种不同类型的问题,如背包问题、最短路径问题、序列匹配问题等。
尤其在处理具有多阶段决策过程的问题时,动态规划算法能够有效地求解最优解。
二、Matlab中的动态规划算法实现Matlab是一种功能强大的科学计算软件,它提供了丰富的数值计算和数据可视化功能,也支持通过编程语言实现各种算法。
在Matlab中,可以通过编写脚本或函数来实现动态规划算法。
下面以一个经典的动态规划问题——斐波那契数列为例,介绍如何在Matlab中实现动态规划算法。
斐波那契数列是一个经典的递归算法问题,其定义如下:F(0) = 0F(1) = 1F(n) = F(n-1) + F(n-2),其中n>1我们可以用递归的方式来求解斐波那契数列:```matlabfunction result = fibonacci(n)if n == 0result = 0;elseif n == 1result = 1;elseresult = fibonacci(n-1) + fibonacci(n-2);endend```递归方法存在重复计算的问题,效率较低。
matlab求动态规划最优解

matlab求动态规划最优解求解步骤:(1)将过程划分为恰当的阶段。
(2)选择状态变量Xk,使它既能描述过程的状态,又满足无后效性,同时确定允许状态集合Xk。
(3)选择决策变量Uk,确定允许决策集合Uk(Xk)。
(4)写出状态转移方程。
(5)确定阶段指标Vk(xk,Wx)及指标函数Vkn的形式。
(6)写出基本方程即最优值函数满足的递归方程,以及端点条件。
例题:最短路线问题阶段按过程的演变划分,状态由各段的初始位置确定,决策为从各个状态出发的走向,即有Xk+1=Uk(Xk),阶段指标为相邻两段状态间的距离dk(Xk,Uk(Xk)),指标函数为阶段指标之和,最优值函数fk(Xk)是由出发Xk到终点的最短距离(或最小费用),基本方程为:fk(Xk)=min[dk(Xk,Uk(Xk))+fk+1(Xk+1)],k=n,n-1...,2,1,fn+1(Xn+1)=0利用这个模型可以算出例1的最短路线为AB1C2D1E2F2G,相应的最短距离为18。
动态规划的最优性原理:无论过去的状态跟决策如何,对前面的决策所形成的状态而言,后续决策必须构成最优策略。
对于动态规划而言,重要的并不是所谓的模板,比较重要的是在动态规划中,推导的思维方式。
在个人看来动态规划实际就是编程解决大量数据的决策问题的一种重要编程理念和编程思路。
在动态规划的思路即是反向确立后三次状态改变的两次决策量的最优决策,确定了该最优决策之后每次反向推导一步,穷举倒数第三次的不同决策所带来的状态变化量,与之前所得到的的最优决策量进行加成处理(可能加和也可能相减或相乘相除,具体视情况而定),将所得后三次决策的总决策量对比选取最优值,作为后四步的最优状态变化值。
先前重复推导,最终得到该问题的最优策略。
动态规划讲义 含matlab算法

例 3 图 货郎担问题Fra bibliotek例 4 图 旅行路线图
【分析】这两个问题看起来很非常相似,但本质上是完全不同的。为了方便讨论,可 以将每个顶点标记号码。由于必然经过最右边的顶点 7,所以一条路(P1-P2)可以看做两条 路(P1-7)与(P2-7)的结合。因此,这个题目的状态可以用两条道路结合的形式表示。可以 把这些状态中,两条路中起始顶点相同的状态归于一个阶段,设为阶段[P1,P2]。
S2: K=2,有: F2(B1)=min{d2(B1,C1)+F3(C1),d2(B1,C2)+f3(C2),d2(B1,C3)+F3(C3)}=min {9,12,14}=9
F2(m)=min{d2(B2,c2)+f3(C2),d2(B2,C4)+F3(C4)}=min{16,10}=10
S4:k=1,有: F1(A)=min{d1(A,B1)+F2(B1),d1(A,B2)+F2(B2)}=min{13,13}=13
在现实生活中,有一类活动的过程,由于它的特殊性,可将过程分成若干个互相联系 的阶段,在它的每一阶段都需要作出决策,从而使整个过程达到最好的活动效果。因此各个 阶段决策的选取不能任意确定,它依赖于当前面临的状态,又影响以后的发展。当各个阶段 决策确定后,就组成一个决策序列,因而也就确定了整个过程的一条活动路线。这种把一个 问题看做是一个前后关联具有链状结构的多阶段过程就称为多阶段决策过程,这种问题称为 多阶段决策最优化问题。
最优化原理与无后效性
上面已经介绍了动态规划模型的基本组成,现在需要解决的问题是:什么样的“多阶段 决策问题”才可以采用动态规划的方法求解?
一般来说,能够采用动态规划方法求解的问题必须满足.最优化原理和.无后效性原则。
最新matlab 动态规划讲义

m a t l a b动态规划讲义第四章动态规划§1 引言1.1 动态规划的发展及研究内容动态规划(dynamic programming)是运筹学的一个分支,是求解多阶段决策问题的最优化方法。
20世纪50年代初R. E. Bellman等人在研究多阶段决策过程(multistep decision process)的优化问题时,提出了著名的最优性原理(principle of optimality),把多阶段过程转化为一系列单阶段问题,逐个求解,创立了解决这类过程优化问题的新方法—动态规划。
1957年出版了他的名著《Dynamic Programming》,这是该领域的第一本著作。
动态规划问世以来,在经济管理、生产调度、工程技术和最优控制等方面得到了广泛的应用。
例如最短路线、库存管理、资源分配、设备更新、排序、装载等问题,用动态规划方法比用其它方法求解更为方便。
虽然动态规划主要用于求解以时间划分阶段的动态过程的优化问题,但是一些与时间无关的静态规划(如线性规划、非线性规划),只要人为地引进时间因素,把它视为多阶段决策过程,也可以用动态规划方法方便地求解。
仅供学习与交流,如有侵权请联系网站删除谢谢51应指出,动态规划是求解某类问题的一种方法,是考察问题的一种途径,而不是一种特殊算法(如线性规划是一种算法)。
因而,它不象线性规划那样有一个标准的数学表达式和明确定义的一组规则,而必须对具体问题进行具体分析处理。
因此,在学习时,除了要对基本概念和方法正确理解外,应以丰富的想象力去建立模型,用创造性的技巧去求解。
例1 最短路线问题下面是一个线路网,连线上的数字表示两点之间的距离(或费用)。
试寻求一条由A到G距离最短(或费用最省)的路线。
例2 生产计划问题工厂生产某种产品,每单位(千件)的成本为1(千元),每次开工的固定成本为3(千元),工厂每季度的最大生产能力为6(千件)。
经调查,市场对该产品的需求量第一、二、三、四季度分别为2,3,2,4(千件)。
Matlab中的动态规划方法与示例分析

Matlab中的动态规划方法与示例分析引言动态规划是一种解决多阶段决策问题的优化方法,它通过将问题分解为若干阶段,在每个阶段中做出最优决策,从而得到整体最优解。
Matlab作为一种强大的计算工具,提供了丰富的函数和工具箱来支持动态规划的求解。
本文将通过介绍动态规划的基本原理和算法,结合几个实际示例,展示在Matlab中如何应用动态规划方法解决实际问题。
一、动态规划的基本原理动态规划的基本原理是通过自底向上的递推关系,将一个大问题分解为若干个子问题,并将每个子问题的最优解存储起来,以便在解决更大的问题时进行查找和利用。
具体地,动态规划有三个关键要素:最优子结构、边界条件和状态转移方程。
最优子结构是指一个问题的最优解可以由其子问题的最优解组成。
它是动态规划的关键特点,也是将问题分解为子问题并递归求解的基础。
边界条件是指问题的边界情况和初始状态,可以是递归求解的终止条件。
状态转移方程是指描述子问题之间关系的方程,它将子问题的最优解与大问题的最优解联系起来。
在求解过程中,通过将问题划分为子问题并依次求解,最终得到整体最优解。
二、动态规划的算法实现在Matlab中,可以通过定义递归函数或使用循环结构来实现动态规划算法。
递归函数的实现方式简单直观,但由于递归调用的开销较大,可能导致算法的效率较低。
循环结构的实现方式相对复杂,但可以通过数组或矩阵来存储子问题的最优解,以减少重复计算,提高算法的效率。
在实际应用中,动态规划可以通过以下步骤来实现:1. 确定问题的最优子结构、边界条件和状态转移方程。
2. 定义数组或矩阵来存储子问题的最优解。
3. 利用循环结构或递归函数,按照自底向上的顺序计算和存储子问题的最优解。
4. 根据存储的子问题最优解,计算并返回大问题的最优解。
三、动态规划实例分析1. 背包问题背包问题是动态规划中经典的例子,它的目标是在限制总重量的情况下,选择一些物品放入背包,使得背包中物品的总价值最大化。
动态规划方法的matlab实现及其应用

动态规划方法的matlab实现及其应用(龙京鹏,张华庆,罗明良,刘水林) (南昌航空大学,数学与信息科学学院,江西,南昌)摘要:本文运用matlab语言实现了动态规划的逆序算法,根据状态变量的维数,编写了指标函数最小值的逆序算法递归计算程序。
两个实例的应用检验了该程序的有效性,同时也表明了该算法程序对众多类典型的动态规划应用问题尤其是确定离散型的应用问题的通用性,提供了求解各种动态规划问题的有效工具。
关键词:动态规划基本方程的逆序算法 MATLAB实现MATLAB Achieve For Dynamic Programming and Its Application(JingpengLong,HuaqingZhang,MingliangLuo,ShuilinLiu)(School of Mathematics and Information Science,Nanchang HangkongUniversity,Nanchang,China)Abstract:This article achieves the reverse algorithm of dynamic programming by using the matlab language,and prepares the recursive calculation program of reverse algorithm which thetargetfunctionvalueisthesmallest.Theapplicationoftwoexamplesshowthattheprogram is effective,and this algorithm program is general to many typical application of dynamic programming,especially the application of deterministic discrete.This algorithm program provides a effective tool to the solution of a variety of dynamic programming problems. Key words:dynamic programming;reverse algorithm;Matlab achievement动态规划是一类解决多阶段决策问题的数学方法, 在工程技术、科学管理、工农业生产及军事等领域都有广泛的应用。
基于MATLAB的动态规划常用算法的实现

第7卷 第4期2008年12月 太原师范学院学报(自然科学版)JOU R N AL O F T AI YU AN N O RM A L U N IV ERSIT Y (Nat ur al Science Edition) V o l.7N o.4 D ec.2008基于M AT LA B 的动态规划常用算法的实现孙 宝 王希云(太原科技大学数学系,山西太原030024) 〔摘要〕 运用M ATLAB 编程实现了动态规划的逆序、顺序、双向混合算法,并分别应用于求解几类典型问题,验证了该方法的有效性,同时表明该程序对求解动态规划多类典型问题是通用的,丰富了M AT LAB 优化工具箱,具有一定的应用价值.〔关键词〕 动态规划;逆序算法;顺序算法;混合双向算法;M ATLAB〔文章编号〕 1672-2027(2008)04-0026-05 〔中图分类号〕 O 221.3 〔文献标识码〕 A0 引言动态规划(Dy nam ic Prog ramming )是求解决策过程最优化的有效数学方法[1].它是根据“最优决策的任何截断仍是最优的”这一原理,通过将多阶段决策过程转化为一系列单阶段问题,逐个求解的优化求解方法.目前常用的方法有逆序、顺序以及双向混合算法.M ATLAB 是决策系统的优化计算和设计的有力工具,但该工具箱中尚无动态规划计算的程序文档.本文通过求解几类动态规划典型问题将三种常用算法用M atlab 实现,体现了程序的通用性,拓展了M ATLAB 语言的相关程序,克服了该程序使用的局限性,提供了求解相关动态规划问题的有效工具,丰富了M ATLAB 优化工具箱.1 动态规划的基本模型实际中,要构造一个标准的动态规划模型,通常需要采用以下几个步骤[2]:1)划分阶段:按照问题的时间或空间特征,把问题分为若干个阶段.这些阶段必须是有序的或者是可排序的(即无后向性),否则,应用无效.2)选择状态:将问题发展到各个阶段时所处的各种客观情况用不同的状态表示,称为状态.状态的选择要满足无后效性和可知性,即状态不仅依赖于状态的转移规律,还依赖于允许决策集合和指标函数结构.3)确定决策变量与状态转移方程:当过程处于某一阶段的某个状态时,可以做出不同的决策,描述决策的变量称为决策变量.在决策过程中,由一个状态到另一个状态的演变过程称为状态转移.4)写出动态规划的基本方程:动态规划的基本方程一般根据实际问题可分为两种形式,逆序形式和顺序形式.动态规划基本方程的逆序形式为:f k (x k )=opt u k ∈D k (x k ){v k (x k ,u k )+f k +1(x k +1)},k =n ,n -1,…,2,1边界条件:f n +1(x n +1)=0或f n (x n )=v n (x n ,u n )其中第k 阶段的状态为x k ,其决策变量u k 表示状态处于x k +1的决策,状态转移方程为x k +1=T k (x k ,u k ),k 阶段的允许决策集合记为D k (x k ),v k (x k ,u k )为指标函数.当求解时,由边界条件从k =n 开始,由后向前逆推,逐阶段求出最优决策和过程的最优值,直到最后求出f 1(x 1)即得到问题的最优解.类似地,动态规划基本方程的顺序形式为:收稿日期:2008-08-14 作者简介:孙 宝(1981-),男,山西太谷人,太原科技大学数学系在读研究生,助教,主要从事最优化理论及其应用研究.f k (x k +1)=opt u k ∈D k (x k +1){v k (x k +1,u k )+f k -1(x k )},k =1,2,…,n -1,n边界条件:f 0(x 1)=0 不同于以上单向递推算法的双向混合算法的基本方程为:ff k (x k +1)=max /min[V k (x k +1,u k )+f f k -1(x k )],k =1,2,…f b j (y j )=m ax /m in[V j (y j ,u j )+f b j +1(y j +1)],j =n ,n -1,…始端条件:ff 0(x 1)=0;x k =T k (x k +1,u k )终端条件:f b n +1(y n +1)=0;y j +1=T J (y j ,j ).2 几类典型问题的实现本段将针对几类动态规划典型问题利用三种常用算法及M atlab 程序实现其结果.下面以资源分配问题为例来具体说明求解过程.2.1 建立动态规划模型1)把问题的演变过程划分为恰当的阶段.将A ,B ,C ,D 四个要害划分为4个阶段k = 4.2)选择状态变量,使之既能描述过程的演变又满足无后效性.令状态量x k 为第k 个要害处应派往的巡逻队数.图1 逆序算法程序Fig .1 T he backw ard algo rithm pr ocedur e3)选择决策变量u k 及相应的允许决策集合D k (x k )={u k 2≤u k ≤4}(k =1,2,3,4). 4)写出状态转移方程状态转移方程:x k +1=x k -u k .5)写出指标函数指标函数为:V k ,4=∑4i =k p k (u k )用p k (u k )表示k 阶段派出的巡逻队数为u k .6)写出基本方程先考虑给D 部位派巡逻队,k =4基本方程为:f 4(x 4)=m in {p 4(x 4)+f 5(x 5)},f 5(x 5)=02.2 算法主程序框图(逆序算法为例,见图1)在这里仅以动态规划逆序算法进行讨论,顺序算法类似.对于各个阶段的子问题的求解方法基本都是相同的,在当前阶段的所有子问题求得最优决策以后,通过状态转移方程可以确定出下一阶段的状态和允许状态集合,从而可以在决策集合上来寻求这个新阶段的最优决策.从第n个阶段出发,直到第一个阶段为止,即可得到全过程的最优决策.2.3 逆序、顺序、双向混合算法的实现结果[3]2.3.1 基于M ATLAB 的动态规划逆序算法的实现复杂系统可靠性问题描述:某电子设备由5种元件1,2,3,4,5组成,其可靠性分别为0.9,0.8,0.5,0.7,0.6.为保证电子设备系统的可靠性,同种元件可并联多个.现允许设备使用元件的总数为15个,问如何设计使设备可靠性最大的元件安排方案.27 第4期 孙 宝等:基于M A T LA B 的动态规划常用算法的实现28太原师范学院学报(自然科学版) 第7卷 表1 复杂系统可靠性问题T able1 T he pro blem o f co mplex system r eliability基于M A T LA B的动态规划逆序算法对复杂系统可靠性问题的实现目标函数functio n y=O bjF un(v,f)状态转移方程functio n y=T ransF un(k,x,u)决策函数functio n u=DeciseF un(k,x)指标函数functio n v=SubO bjF un(k,x,u)5种元件分别并联的个数2,2,4,3,4系统总可靠性最优结果0.8447 资源分配问题描述:某警卫部门共有12支巡逻队,负责4个要害部位A,B,C,D的警卫巡逻。
动态规划MATLAB求解
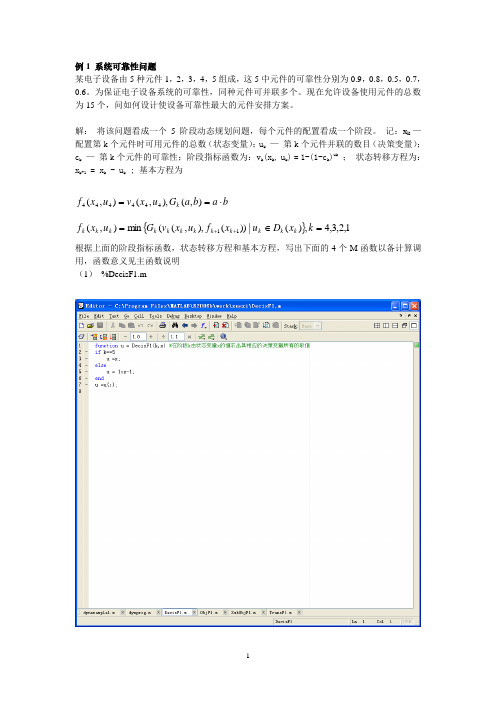
例1 系统可靠性问题某电子设备由5种元件1,2,3,4,5组成,这5中元件的可靠性分别为0.9,0.8,0.5,0.7,0.6。
为保证电子设备系统的可靠性,同种元件可并联多个。
现在允许设备使用元件的总数为15个,问如何设计使设备可靠性最大的元件安排方案。
解: 将该问题看成一个5阶段动态规划问题,每个元件的配置看成一个阶段。
记:x k —配置第k 个元件时可用元件的总数(状态变量);u k — 第k 个元件并联的数目(决策变量);c k — 第k 个元件的可靠性;阶段指标函数为:v k (x k , u k ) = 1-(1-c k )uk; 状态转移方程为: x k+1 = x k - u k ; 基本方程为b a b a G u x v u x f k ⋅==),(),,(),(444444{}1,2,3,4,)(|))(),,((m in ),(11=∈=++k x D u x f u x v G u x f k k k k k k k k k k k k根据上面的阶段指标函数,状态转移方程和基本方程,写出下面的4个M 函数以备计算调用,函数意义见主函数说明 (1) %DecisF1.m(2) SubObjF1.m(3) TransF1.m(4) ObjF1.m(5) 调用主程序计算dynexample1.m(6) 主程序dynprog.m(7) MATLAB主窗口运行程序。
其结果表明1,2,3,4,5 号元件分别并联2,2,4,3和4个,系统可靠性最大为0.8447例2 资源分配问题某工业部门根据国家计划的安排,拟将某种高效率的设备5台,分配给所属的甲、乙、丙三个工厂,各工厂若获得这种设备之后,可以为国家提供的盈利如下表,问这五台如何分配给各工厂才能使国家得到的盈利最大?设备台数工厂甲乙丙0 0 0 01 3 5 42 7 10 63 9 11 114 12 11 125 13 11 12解:将问题安工厂分为三个阶段,甲、乙、丙3个工厂分别编号为1,2,3。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
推至 k = 1,故这种解法称为逆序解法。当然,对某些动态规划问题,也可采用顺序解
法。这时,状态转移方程和递归方程分别为:
xk = Tkr (xk+1, uk ), k = 1,L, n
,
⎪⎧ f0 (x1)= 0或1
⎨ ⎪⎩
f
k
(
xk
+1
)
=
opt {vk (xk+1, uk ) ⊗
uk
∈U
r k
数由 v j ( j = 1,2,L, n) 组成,常见的形式有:
阶段指标之和,即
n
∑ Vk,n (xk , uk , xk+1,L, xn+1 ) = v j (x j , u j ) , j=k
阶段指标之积,即
n
∏ Vk,n (xk , uk , xk+1,L, xn+1 ) = v j (x j , u j ) , j=k
G ,或定义为1 ,即 x7 = 1 。
根据过程演变的具体情况,状态变量可以是离散的或连续的。为了计算的方便有时 将连续变量离散化;为了分析的方便有时又将离散变量视为连续的。
状态变量简称为状态。 2.1.3 决策 当一个阶段的状态确定后,可以作出各种选择从而演变到下一阶段的某个状态,这 种选择手段称为决策(decision),在最优控制问题中也称为控制(control)。 描述决策的变量称决策变量(decision variable),变量允许取值的范围称允许决策
决策变量简称决策。 2.1.4 策略
决策组成的序列称为策略(policy)。由初始状态 x1 开始的全过程的策略记作 p1n ( x1 ) ,即
p1n ( x1 ) = {u1( x1 ),u2 ( x2 ),L,un ( xn )} . 由第 k 阶段的状态 xk 开始到终止状态的后部子过程的策略记作 pkn ( xk ) ,即
数应具有可分离性,即Vk,n 可表为 xk , uk ,Vk+1, n 的函数,记为
Vk,n (xk , uk , xk+1 ,L, xn+1 ) = ϕk (xk , uk ,Vk+1,n (xk +1 , uk+1 ,L, xn+1 ))
并且函数ϕk 对于变量Vk+1, n 是严格单调的。
过程在第 j 阶段的阶段指标取决于状态 x j 和决策 u j ,用 v j ( x j , u j ) 表示。指标函
集合(set of admissible decisions)。用 uk ( xk ) 表示第 k 阶段处于状态 xk 时的决策变量,
它是 xk 的函数,用Uk ( xk ) 表示 xk 的允许决策集合。在例 1 中 u2 (B1 ) 可取 C1,C2 或 C3 ,
可记作 u2 (1) = 1,2,3 ,而U2 (1) = {1,2,3} 。
+1
(
xk
+1
)
f k−1 (xk )}, k
= 1,L, n
例 3 用 lingo 求解例 1 最短路线问题。
model:
Title Dynamic Programming;
sets:
vertex/A,B1,B2,C1,C2,C3,C4,D1,D2,D3,E1,E2,E3,F1,F2,G/:L;
road(vertex,vertex)/A B1,A B2,B1 C1,B1 C2,B1 c3,B2 C2,B2 C3,B2 C4,
动态规划问世以来,在经济管理、生产调度、工程技术和最优控制等方面得到了广 泛的应用。例如最短路线、库存管理、资源分配、设备更新、排序、装载等问题,用动 态规划方法比用其它方法求解更为方便。
虽然动态规划主要用于求解以时间划分阶段的动态过程的优化问题,但是一些与时 间无关的静态规划(如线性规划、非线性规划),只要人为地引进时间因素,把它视为 多阶段决策过程,也可以用动态规划方法方便地求解。
C1 D1,C1 D2,C2 D1,C2 D2,C3 D2,C3 D3,C4 D2,C4 D3,
D1 E1,D1 E2,D2 E2,D2 E3,D3 E2,D3 E3,
E1 F1,E1 F2,E2 F1,E2 F2,E3 F1,E3 F2,F1 G,F2 G/:D;
endsets
data:
D=5 3 1 3 6 8 7 6
§2 基本概念、基本方程和计算方法 2.1 动态规划的基本概念和基本方程 一个多阶段决策过程最优化问题的动态规划模型通常包含以下要素。 2.1.1 阶段 阶段(step)是对整个过程的自然划分。通常根据时间顺序或空间顺序特征来划分阶
段,以便按阶段的次序解优化问题。阶段变量一般用 k = 1,2,L, n 表示。在例 1 中由 A 出发为 k = 1,由 Bi (i = 1,2) 出发为 k = 2 ,依此下去从 Fi (i = 1,2) 出发为 k = 6 ,共 n = 6 个阶段。在例 2 中按照第一、二、三、四季度分为 k = 1,2,3,4 ,共四个阶段。
阶段指标之极大(或极小),即
Vk ,n
(xk
,uk
,
xk+1 ,L,
xn+1 )
=
max(min)v
k≤ j≤n
j
(x
j
,u
j
)
.
这些形式下第 k 到第 j 阶段子过程的指标函数为Vk, j (xk , uk ,L, x j+1 ) 。
根据状态转移方程指标函数 Vk,n 还可以表示为状态 xk 和策略 pkn 的函数,即
pkn ( xk ) = {uk ( xk ),L,un ( xn )} , k = 1,2,L, n − 1. 类似地,由第 k 到第 j 阶段的子过程的策略记作
-57-
pkj ( xk ) = {uk ( xk ),L,u j ( x j )}.
可供选择的策略有一定的范围,称为允许策略集合(set of admissible policies),用
2.1.2 状态 状态(state)表示每个阶段开始时过程所处的自然状况。它应能描述过程的特征并 且无后效性,即当某阶段的状态变量给定时,这个阶段以后过程的演变与该阶段以前各 阶段的状态无关。通常还要求状态是直接或间接可以观测的。 描述状态的变量称状态变量(state variable)。变量允许取值的范围称允许状态集合
先建立起动态规划的数学模型:
(i)将过程划分成恰当的阶段。
(ii)正确选择状态变量 xk ,使它既能描述过程的状态,又满足无后效性,同时确
定允许状态集合 X k 。
(iii)选择决策变量 uk ,确定允许决策集合Uk ( xk ) 。
(iv)写出状态转移方程。
(v)确定阶段指标 vk ( xk ,uk ) 及指标函数Vkn 的形式(阶段指标之和,阶段指标之
(1)
在例 1 中状态转移方程为 xk +1 = uk ( xk ) 。
2.1.6. 指标函数和最优值函数 指标函数(objective function)是衡量过程优劣的数量指标,它是定义在全过程和所有
后部子过程上的数量函数,用Vk,n (xk , uk , xk+1,L, xn+1 ) 表示, k = 1,2,L, n 。指标函
=
n,L,1
(2)
在上述方程中,当 ⊗ 为加法时取 fn+1(xn+1) = 0 ;当 ⊗ 为乘法时,取 fn+1(xn+1) = 1。动
态规划递归方程是动态规划的最优性原理的基础,即:最优策略的子策略,构成最优子
策略。用状态转移方程(1)和递归方程(2)求解动态规划的过程,是由 k = n + 1 逆
2.1.7 最优策略和最优轨线
使指标函数 Vk,n 达到最优值的策略是从 k 开始的后部子过程的最优策略,记作
pk*n = {uk* ,L, un*}。 p1*n 是全过程的最优策略,简称最优策略(optimal policy)。从初始
状 态 x1(= x1* ) 出 发 , 过 程 按 照 p1*n 和 状 态 转 移 方 程 演 变 所 经 历 的 状 态 序 列
应指出,动态规划是求解某类问题的一种方法,是考察问题的一种途径,而不是 一种特殊算法(如线性规划是一种算法)。因而,它不象线性规划那样有一个标准的数 学表达式和明确定义的一组规则,而必须对具体问题进行具体分析处理。因此,在学习 时,除了要对基本概念和方法正确理解外,应以丰富的想象力去建立模型,用创造性的 技巧去求解。
{x1*
,
x2*
,L,
x* n +1
}
称最优轨线(optimal
trajectory)。
-58-
2.1.8 递归方程 如下方程称为递归方程
⎪⎧ fn+1( xn+1 ) = 0或1
⎨ ⎪⎩
fk (xk )
=
opt {vk ( xk , uk ) ⊗
uk ∈U k ( xk )
f k +1 ( xk +1 )}, k
(set of admissible states)。用 xk 表示第 k 阶段的状态变量,它可以是一个数或一个向量。
用 X k 表示第 k 阶段的允许状态集合。在例 1 中 x2 可取 B1, B2 ,或将 Bi 定义为
i(i = 1,2) ,则 x2 = 1 或 2 ,而 X 2 = {1,2} 。 n 个阶段的决策过程有 n + 1 个状态变量,xn+1 表示 xn 演变的结果。在例 1 中 x7 取
例 1 最短路线问题
图 1 是一个线路网,连线上的数字表示两点之间的距离(或费用)。试寻求一条由 A 到 G 距离最短(或费用最省)的路线。
