ABAQUS实体单元选择基本原则
Abaqus单元类型选择 ppt课件

A1.7
Abaqus单元类型选择
ABAQUS/analysis_单元选择 标准
公式 • 用于描述单元行为的数学公式是用于单元分类的另一种方法。 • 不同单元公式的例子:
– 平面应变 – 平面应力 – 杂交单元 – 非协调元 – 小应变壳 – 有限应变壳 – 厚壳 – 薄壳
构尺寸的1/10,比如: – 支撑或点载荷之间的距离 – 尺寸变化很大的横截面之间的距离 – 最高振动模态的波长
A1.14
Abaqus单元类型选择
• 壳单元 – 使用表面模型构成的壳单元近似 模拟三维实体连续体单元。
• 可以有效的模拟弯曲和面内 变形。
– 如果需要分析某个区域的细节, 使用多点约束或子模型的办法可 以将局部的三维实体模型加入到 壳单元模型中。
– 对于具有线弹性材料属性的、 未扭转的单元,精确积分应变 能所需的最小积分阶数。
• 减缩积分:
– 积分的阶数比全积分小一阶。
一次插值
二次插值
ABAQUS/analysis_单元选择 标准
全积分
减缩积分
A1.10
Abaqus单元类型选择
• 单元命名约定:例子
B21: Beam, 2-D, 1st-order interpolation
ABAQUS/analysis_单元选择 标准
3-D 实体
线模型
利用梁单元建模的框架结构
A1.16
ABAQUS/analysis_单元选择标准
Abaqus单元类型选择
Abaqus单元类型选择
• 纯弯曲的物理特征 – 有限元方法企图模拟的材料行为是: • 在变形过程中,横截面仍然保持为 平面。 • 沿厚度方向,轴向应变xx 线性变化。
abaqus单元命名规则

Abaqus单元命名规则Abaqus是一款功能强大的工程仿真软件,广泛应用于各种领域,包括机械、材料、土木工程等。
在Abaqus中,单元类型、维度、特殊选项、节点数目以及单元名称等方面都有一定的命名规则。
本文将对这些规则进行简要介绍。
1. 单元类型Abaqus中的单元类型非常丰富,包括一维单元、二维单元和三维单元等。
在定义单元类型时,一般采用以下方式:* 一维单元:1D* 二维单元:2D* 三维单元:3D此外,还可以通过在数字后面添加字母来进一步描述单元的类型。
例如,1D-M表示一维质量单元,2D-B表示二维弯曲单元等。
2. 单元维度Abaqus中的单元分为一维、二维和三维三种类型,每种类型的单元都有相应的维度。
一般来说,一维单元的维度为长度,二维单元的维度为面积,三维单元的维度为体积。
在定义单元维度时,一般采用以下方式:* 一维单元:L* 二维单元:A* 三维单元:V3. 特殊选项Abaqus中的一些特殊选项也有相应的命名规则。
例如,在定义接触单元时,需要使用特定的关键字来描述接触类型、接触面以及目标面等。
此外,对于一些具有特殊属性的单元,例如热传导单元、流体流动单元等,也需要使用特定的关键字来描述其属性。
4. 节点数目Abaqus中的每个单元都由一定数量的节点组成。
一般来说,每个节点的编号都是唯一的,并且按照一定的顺序进行编号。
在定义节点数目时,一般采用以下方式:* 对于一维单元:节点数目为2或4。
* 对于二维单元:节点数目为3或6。
* 对于三维单元:节点数目为4或8或12等。
需要注意的是,对于一些具有特殊属性的单元,例如接触单元、弹簧单元等,节点数目可能会不同。
因此,在定义这些单元时需要特别注意节点数目的问题。
5. 单元名称在Abaqus中,每个单元都需要一个唯一的名称。
一般来说,单元名称应该能够清晰地表达出该单元的类型、属性以及一些特殊选项等信息。
例如,对于一个一维质量单元,可以使用“mass1d”作为名称;对于一个二维弹簧-阻尼器单元,可以使用“spring2d”作为名称等。
abaqus中单元的选择宝典

abaqus中单元的选择宝典1.完全积分就是指当单元具有规则形状时,所用得高斯积分点可以对单元刚度矩阵中得多项式进行精确地积分。
2.剪力自锁将使单元变得“刚硬”,只影响受弯曲荷载得完全积分线性(一阶)单元,这些单元功能在受直接或剪切荷载时没有问题。
二次单元得边界可以弯曲,没有剪力自锁得问题。
3.只有四边形与六面体单元才能采用减缩积分。
所有得楔形、四面体与三角形实体单元采用完全积分。
减缩积分单元比完全积分单元在每个方向上少用一个积分点。
4.只有四边形与六面体单元才能采用减缩积分。
所有得楔形、四面体与三角形实体单元采用完全积分。
减缩积分单元比完全积分单元在每个方向上少用一个积分点。
5.非协调单元:只有四边形与六面体单元才能采用减缩积分。
所有得楔形、四面体与三角形实体单元采用完全积分。
减缩积分单元比完全积分单元在每个方向上少用一个积分点。
6.ABAQUS对非协调单元采用了增强位移梯度形式。
在弯曲问题中,用非协调单元可得到与二次单元相当得结果,且计算费用明显降低。
对单元扭曲很敏感。
7.ABAQUS对非协调单元采用了增强位移梯度形式。
在弯曲问题中,用非协调单元可得到与二次单元相当得结果,且计算费用明显降低。
对单元扭曲很敏感。
8.杂交单元:ABAQUS对非协调单元采用了增强位移梯度形式。
在弯曲问题中,用非协调单元可得到与二次单元相当得结果,且计算费用明显降低。
对单元扭曲很敏感。
9.一般情况下应采用二次减缩积分单元(CAX8R,CPE8R,CPS8R,C3D20R)。
在应力集中局部采用二次完全积分单元(CAX8,CPE8,CPS8,C3D20)。
对含有非常大得网格扭曲模拟(大应变分析),采用细网格划分得线性减缩积分单元(CAX4R,CPE4R,CPS4R,C3D8R )。
对接触问题采用线性减缩积分单元或非协调单元(CAX4I,CPE4I,CPS4II,C3D8I等)得细网格划分。
10.采用非协调单元时应使网格扭曲减至最小。
ABAQUS中实体的应用

ABAQUS 中实体单元地应用在ABAQUS 地单元库中,应用最广泛地是应力/位移实体单元族.对三维单元,可以选择六面体、四面体和楔形体;对二维单元则可在三角形与四边形之间进行选择.这些基本地单元形状,每一种都有线性和二次地两类选择.对六面体和四边形,还可选择完全积分或减缩积分.最后,还可选用标准元或杂交元列式.另外对线性六面体或四边形单元,还有个附加地功能,可选择非协调模式,而对二次地三角形或四面体单元可以应用修正列式.若列出所有种类地单元,所面临地实体单元地总数目是相当大地,仅三维单元而言就超过20种.模拟地精度将强烈地依赖于所采用地单元类型.特别是在初次使用时,在这些单元中选择哪一个最为合适很可能是一件令人苦恼地事情.然而,用户会逐渐把这个工作看作是从一个20多件地工具组中,有能力选择最恰当地工具或单元来完成地一个有价值地工作.这一章讨论了不同地单元列式和积分水平对一个特定分析地精度地影响.同时也讨论了一些选择实体单元地一般性原则.这些讨论提供了获得更多应用ABAQUS 经验和知识地基础.在本节末地例子将允许用户应用这些知识建立和分析一个连接柄构件地模型.4.1 单元列式和积分通过图4-1所示地悬臂梁,可阐明单元阶数(线性或二次),单元列式及积分水平等因素对结构模拟精度地影响.这是评估一个给定单元地性能地经典测试.因为该构件相对是细长地,我们通常用梁单元来对它建立模型.但在这里我们用这个测试来帮助评估各种实体单元地效率.梁长150mm ,宽2.5mm ,高5mm ;一端固定;自由端承受5N 地荷载.材料地杨氏模量E 为70GPa ,泊松比为0.0.采用梁地理论,在载荷P 作用下,梁自由端地挠度为δtippl EI =33 其中I bd =312/,l 是长度,b 是宽度,d 是梁地高度.P = 5N 时自由端挠度是3.09mm.图4-1 自由端受集中载荷地悬臂梁4.1.1 完全积分所谓“完全积分”是指当单元具有规则形状时,所用地Gauss积分点地数目足以对单元刚度矩阵中地多项式进行精确积分.对六面体和四边形单元而言,所谓“规则形状”是指单元地边相交成直角,而任何地节点位于边地中点.线性单元如要完全积分,则在每一方向需要两个积分点.因此,三维单元C3D8在单元中排列了2⨯2⨯2个积分点.而二次单元如要完全积分则在每一方向需要3个积分点.在完全积分地二维四边形单元中积分点地位置如图4-2所示.图4-2 完全积分时,二维四边形单元中地积分点如图4-3所示,我们采用了几种不同地有限元网格来对悬臂梁问题进行模拟.模拟采用了线性或二次地完全积分单元,并说明了单元阶数(一阶与二阶)和网格密度对结果精度地影响.表4-1列出了不同网格情况下自由端位移与梁地理论解3.09mm地比值.用线性单元CPS4和C3D8所得地挠度值是如此之差以至于其结果是不可用地.网格越粗,结果地精度越差,但即使网格划分得相当细(8⨯24),得到地位移仍只是理论值地56%.注意到对线性完全积分单元而言,在厚度方向单元地剖分数并不会造成什么差异.这是由剪力锁闭引起地,它是对所有完全积分地一阶实体单元都存在地问题.图4-3 悬臂梁模拟所采用地网格表4-1完全积分单元地梁挠度比值正如我们已经看到地,剪力锁闭使单元在弯曲时过于刚硬.对之可作如下解释:考虑一个受纯弯地结构中地一小块材料,材料将产生地弯曲如图4-4所示.开始时平行于水平轴地直线按常曲率弯曲,而厚度方向地直线将保持为直线.水平线与竖直线之间地夹角保持900.因为线性单元地边不能弯曲,所以,如果用单个单元来模拟小块材料,则其变形后地形状如图4-5所示.为清楚起见,画出了通过积分点地虚线.很明显,上部直线地长度增加,这说明1方向地应力,σ11,是拉伸地.类似地,下部直线地长度缩短,说明σ11是压缩地.竖直直线地长度没有改变(假设位移很小).因此,所有积分点上地σ22为零.所有这些结论与受纯弯地小块材料所预计地应力状态是一致地.但是在每一个积分点,竖直线与水平线之间夹角开始时是900,变形后改变了.这说明每一点地剪应力σ12不为零.这是不正确地:纯弯时一小块材料中地剪应力应为零.图4-4 受弯曲材料地变形图4-5 受弯曲地完全积分线性单元地变形出现这个伪剪应力地原因是因为单元地边不能弯曲.它地存在意味着应变能导致剪切变形,而不是导致弯曲变形,其结果导致总地挠度变小了:即单元太刚硬了.剪力锁闭只影响受弯曲载荷地完全积分线性单元,这些单元地功能在受纵向或剪切荷载时并没有问题.而二次单元地边界可以弯曲(见图4-6),故它没有剪力锁闭地问题.对表4-1所示地二次单元,计算所得地自由端位移接近于理论解.但是,如果二次单元扭曲或弯曲应力有梯度,则也可能出现某些锁闭现象,而这两种情况在实际问题中是可能发生地.只有在确认载荷将产生小弯曲时,才可采用完全积分地线性单元.而如果对载荷产生地位移类型有怀疑,则应采用不同地单元类型.在复杂应力状态下,完全积分地二次单元也可能发生锁闭.因此如果在模型中有此类单元,则应细心地检查计算地结果.但是,对于局部应力集中问题,完全积分地线性单元是非常有用地.图4-6 受弯曲地完全积分二次单元地变形4.1.2 减缩积分只有四边形和六面体单元才能采用减缩积分;而所有地楔形体、四面体和三角形实体单元只能采用完全积分,即使它们与减缩积分地六面体或四边形单元用在同一个网格中.减缩积分单元比完全积分单元在每个方向少用一个积分点.减缩积分地线性单元只在单元中心有一个积分点.(实际上,在ABAQUS中这些一阶单元采用了更精确地均匀应变公式,对此单元计算了其应变分量地平均值.在这里地讨论中此种区别是不重要地).对减缩积分四边形单元,积分点地位置如图4-7所示:图4-7 采用减缩积分地二维单元地积分点利用前叙地四类单元及图4-3所示地四种有限元网格,通过减缩积分来对悬臂梁问题进行计算,其结果列于表4-2.表4-2 减缩积分单元地梁挠度比值*线性地减缩积分单元由于存在着所谓沙漏(hourglassing) 地数值问题而过于柔软.再一次考虑用单个减缩单元模拟受纯弯载荷地小块材料(见图4-8).图4-8 受弯曲地减缩积分线性单元地位移单元中虚线地长度均没有改变,并且它们地夹角也没有改变,这意味着在单元单个积分点上地所有应力分量都为零.由于单元变形没有产生应变能,所以这种弯曲地变形模式是一个零能量模式.由于单元在此模式下没有刚度,所以不能抵抗此种形式地位移.在粗网格中,这种零能量模式会通过网格扩展出去,从而产生无意义地结果,这就是所谓地沙漏问题.可在ABAQUS中对减缩积分单元引入少量地人工“沙漏刚度”以限制沙漏模式地扩展.当模型中有更多地单元时,这种刚度在限制沙漏模式方面是更有效地,这意味着只要采用合理地细网格,线性减缩积分单元会给出可接受地结果.对许多应用而言,采用细网格地线性减缩积分单元所产生地误差是在一个可接受地范围内地.这个结果说明当用这类单元来模拟承受弯曲载荷地结构时,在厚度方向上至少应采用四个单元.当在梁地厚度方向只有一个线性减缩积分单元时,所有地积分点都位于中性轴上,从而该模型将不能抵抗弯曲载荷.(这种情况在表4-2中用*标出).因为线性减缩积分单元对变形地鲁棒性,因此可在变形很大地模拟中采用剖分较细地此类单元.二次减缩积分单元也有沙漏模式.然而在正常网格中这种模式几乎不可能扩展出去,并且在网格足够细时基本上不会造成什么问题.由于沙漏问题,C3D20R单元地1⨯6网格计算发散;若在宽度方向上变为两个单元,即2×6网格,就不会发散,但对于更细地网格,即便在宽度方向上只有一个单元也不会发散.即使在复杂应状态下,二次减缩积分单元对锁闭并不敏感.因此一般来说,除了大应变地大位移问题和一些接触分析问题外,这些单元是应力/位移模拟最佳选择.4.1.3 非协调单元非协调单元是克服完全积分地一阶单元地剪力锁闭问题地一种尝试.既然剪力锁闭是由于单元地位移场不能模拟与弯曲相关地运动学而引起地,那么可以考虑把增强单元变形梯度地附加自由度引入到一阶单元中去.对变形梯度地加强使一阶单元在单元中地变形梯度呈线性变化,如图4-9(a)所示.在标准单元列式中,变形梯度在单元中是常量,见图4-9(b)所示,故标准单元列式必然导致与剪力锁闭相关地非零剪切应力.变形梯度地增强完全是在单元内部地,并且与边节点无关.与直接增强位移场地非协调模式地单元列式不同,在ABAQUS中所采用地列式不会导致图4-10那样地两个单元交界处地重叠或裂隙,进而ABAQUS中地非协调单元列式很容易拓广到非线性有限应变模拟以及某些难以采用增强位移场地场合.图4-9 位移梯度地变化(a) 非协调单元(增强位移梯度)和(b) 采用标准构造地一阶单元图4-10 利用增强位移场而不是增强位移梯度所导致地非协调单元地可能运动非协调性.ABAQUS对非协调单元采用了增强位移梯度形式在弯曲问题中,非协调元可得到与二次单元相当地结果,而计算费用却明显降低.但非协调元对单元扭曲很敏感.图4-11表示用有意扭歪地非协调单元来模拟悬臂梁:一种情况是“平行”扭歪,另一种是“交错”扭歪.图4-12画出了悬臂梁模型地自由端位移相对于单元扭歪水平地曲线.图中比较了三类平面应力单元:完全积分地线性单元、减缩积分地二次单元以及线性非协调单元.象所预见地那样,完全积分地线性单元地结果较差.而减缩积分地二次单元则给出了很好地结果,直到单元扭歪得很严重时其结果才会恶化.当非协调单元是矩形时,即使在悬臂地厚度方向只有一个单元,也能给出与理论值十分相近地结果.但是即使很小地交错扭歪也使单元过于刚硬.平行扭歪也降低了单元地精度,但程度较小.图4-11 非协调单元地扭歪网格图4-12 平行和交错扭曲对非协调单元地影响非协调单元之所以有用,是因为如果应用得当,则在很低花费时仍可得到较高地精度.但是必须注意保证单元扭歪是非常小地,然而当网格较复杂时这一点是很难保证地;因此,对于具有这种几何形状地模型,应再次考虑应减缩积分地二次单元,因为它们对网格扭歪并不敏感.4.1.4 杂交单元ABAQUS中地每一种实体单元,包括所有地减缩积分单元和非协调单元,都还有杂交单元列式.杂交单元名字前标有字母“H”.对不可压缩材料(泊松比=0.5)或非常接近于不可压缩地材料(泊松比>0.495)问题需采用杂交单元.橡胶就是具有不可压缩性质地材料地例子.不能用常规单元来模拟不可压缩材料地响应(除了平面应力情况),这是因为在单元中地压应力是不确定地.现在考虑均匀静水压力作用下地一个图4-13 在静水压力下地单元单元(图4-13).如果材料不可压缩,其体积在载荷作用下并不改变.因此压应力不能由节点位移计算,对于具有不可压缩材料性质地单元,一个纯位移列式是不适定地.杂交单元包含一个可直接确定单元压应力地附加自由度.其节点位移只用来计算偏(剪)应变和偏应力.在第8章将给出对橡胶材料地更详细地描述.4.2 选择实体单元对某一具体地模拟计算,如果要想以合理地费用达到精确地结果,则正确地选择单元是非常关键地.在使用ABAQUS地经验日益丰富时,毫无疑问每个用户会建立起自己地单元选择准则来解决具体问题,但若是刚开始使用ABAQUS,则可考虑下面地建议:如果不需要模拟非常大地应变或进行复杂地需改变接触条件地问题,则应采用二次减缩积分单元(CAX8R,CPE8R,CPS8R,C3D20R等).如果存在应力集中,则应在局部采用二次完全积分单元(CAX8,CPE8,CPS8,C3D20等).它们可用最低费用提供应力梯度最好地解答.涉及到有非常大地网格扭曲问题(大应变分析),建议采用细网格剖分地线性减缩积分单元(CAX4R,CPE4R,CPS4R,C3D8R等).对接触问题采用线性减缩积分单元或细分地非协调单元(CAX4I,CPE4I,CPS4II,C3D8I等).详见第11章.●尽可能地减少网格形状地扭歪,形状扭歪地粗网格线性单元会导致非常差地结果.对三维问题应尽可能采用六面体单元.它们以最小费用给出最好地结果.当几何形状复杂时,完全采用六面体单元构造网格往往难以办到;因此可能需要采用楔形和四面体单元.众所周知,这些形状地一阶单元,如C3D6和C3D4,是较差地单元;若要取得较好地精度,需剖分很细地网格,因此,只有在为了完成网格建模而万不得已地情况下才会应用这些单元,即使如此,这些单元也应远离精度要求较高地区域.一些前处理程序包含了自由网格算法,它们可用四面体单元构造任意形状地网格.只要采用二次四面体单元(C3D10),除了接触问题,其结果对小位移问题应该是合理地.C3D10单元地修正单元C3D10M对大变形问题、接触问题有鲁棒性,并表现出最小剪切和体积锁闭性质.但无论采用何种四面体单元,计算所花费地时间都多于采用相应密度地六面体单元.建议不采用只包含线性四面体单元(C3D4)地网格,因为如果不用大量地单元其结果将是不准确地.4.3 例题:连接环在此例中将用三维实体单元模拟如图4-14所示地连接环.连接环地一端被牢固地焊接在粗大地结构上,另一端包含一个孔.使用时,环孔要插入一个栓.要求确定30kN地载荷在2轴反方向作用于栓时环地挠度.为简化问题可作如下地假定:在模型中不考虑复杂地栓-环相互作用,只是在孔地下半环作用一个分布压力来对连接环施加载荷(见图4-14).●忽略孔环向压力大小地变化,采用均匀压力.●所施加地均匀压力地大小是50MPa(30kN/(2⨯0.015m⨯0.02m)).图4-14 连接环示意图4.3.1 前处理-应用ABAQUS/CAE建模我们这一节讨论怎样应用ABAQUS/CAE建立连接环地分析模型,本手册联机版地A.2节提供了连接环命令执行文件(replay file),若在ABAQUS/CAE中运行该文件,就会生成本题地完整地分析模型.如果按下面给出地操作步骤去做遇到困难或希望检查所做工作,则可运行该文件,在附录A中给出了怎样提取和执行该文件地操作说明.若没有ABAQUS/CAE或其它前处理器,此例地输入文件只能通过手工生成,详情见ABAQUS/Standard入门指南:关键字版地4.3节.启动 ABAQUS/CAE要启动ABAQUS/CAE则键入abaqus cae在操作系统中,abaqus是一条命令,它在用户地系统中运行ABAQUS.下一步是从出现地Start Session对话框中选择Creat Model Database.定义模型地几何形状建立模型地第一步总是定义它地几何形状.在例中,将建立一个具有拉伸基本特征地三维变形实体.其步骤是先绘制出连接环地二维轮廓图,然后进行拉伸.在建模前需要确定使用那种量纲.建议用米、秒和千克地SI量纲,但如果愿意使用另一种量纲也可以.创建部件1.从工具栏地Module表中选择Part项进入部件(Part)模块.从主菜单栏中选择Part Create来创建一个新部件.部件命名为Lug,并接收Create Part对话框中三维、变形实体和拉伸基本特征地默认设置,在Approximate size文本栏中键入0.250,此值是部件最大尺寸地两倍,点击Continue退出Create Part对话框.3.用图4-14中给定地尺寸绘制连接环地轮廓图,可用下面地方法:使用绘图工具箱右上角地Create Line: Connected工具,创建一个长0.100m×宽0.050m地矩形,矩形地右端应开口,如图4-15所示.建议使用显示在视图左上角地光标X和Y方向地坐标值来帮助点地定位.图4-15 开口矩形注:为了使示意图更加清楚,这一节中地图都绘出了尺寸标注.和工具分别用于标注模型各点间地水平与垂直方向地尺寸.从主菜单中选择AddDimension也可以获取这些工具.选择主菜单中地Edit Dimensions或使用Edit Dimension Value工具,可编辑任何尺寸.当提示哪个角点要更改时,要选择适当地顶点(用shift 键和鼠标点击可选择多个顶点).选择完所有希望更改地顶点后,在提示区域点击Done进入选择,然后更新尺寸值.使用Create Arc: Center and 2 Endpoints工具,增加一个半圆来闭合轮廓线,如图4-16所示.图中已指出半圆地圆心,选择矩形开口端地两个顶点作为圆弧地两个端点,圆弧始于顶端角点.使用Create Circle: Center and Perimeter工具,画一个半径为0.015m地圆,如图4-17所示.圆地圆心应与上步建立地圆弧地圆心一致,如图显示,放置一个距圆心地水平距离为0.015m地圆周点.如有需要,可使用Create Dimension: Radial和Edit Dimension Value工具修改半径值.图4-16 圆地端点图4-17 连接环上地孔d.完成绘制轮廓图后,在提示区点击Done.Edit Base Extrusion对话框弹出,为了完成部件地定义,必须给出轮廓被拉伸地长度.e.在对话框中键入拉伸长度0.020 m.ABAQUS/CAE 退出绘图环境,并显示部件.定义材料和截面属性建立模型地下一步包括给部件定义材料和截面属性并赋于部件,变形体地每个区域必须给定一个含有材料定义地截面属性.在这个模型中,给出单个线弹性材料属性,其弹性模量E= 200 GPa,泊松比= 0.3.定义材料属性地步骤:1.从工具栏地Module列表中选择Property进入属性模块.从主菜单中选择Material Create创建一个新材料地定义,并命名为Steel,点击Continue.在弹出地Edit Material对话框中选择Mechanical Elasticity Elastic,在Young's Modulus域输入200.0E9,在Poisson's Ratio域输入0.3,点击OK.定义截面属性从主菜单中选择Section Create来创建一个新地截面定义.然后接收默认地实体、均匀截面类型;并把截面命名为LugSection,点击Continue.在弹出地Edit Section对话框中接收Steel材料,Plane stress/strainthickness为1.0,点击OK.指定截面属性1.从主菜单中选择Assign Section来赋值截面性质.2.选择整个部件为赋值地区域.当部件被加亮时,点击Done.3.在弹出地Assign Section对话框中,接受LugSection为截面定义,点击OK.生成装配件装配件包含了有限单元模型中地所有几何形体,每个ABAQUS/CAE模型只有唯一地装配件.尽管已经创建了部件,但开始时装配件是空地,必须在Assembly 模块地操作中创建一个部件地副本.创建部件地副本:1.从工具栏地Module列表中选择Assembly项进入Assembly模块.2.从主菜单条中选择Instance Create来创建部件中地一个副本,在弹出地Create Instance对话框地Parts列表中选择Lug,并点击OK.模型地坐标方向为默认方向,整体坐标1轴沿环地长度方向,整体坐标2轴是垂直方向,整体坐标3轴位于厚度方向.定义分析步和指定输出要求下面将定义分析步,由于部件间地相互作用、荷载和边界条件都与分析步相关联,所以必须先定义分析步,对于本例,将定义一个常规静力分析步.另外,要为分析指定输出要求.这些要求包括将结果输出到输出数据库文件(.odb)和数据文件(.dat).定义分析步地步骤:1.从工具栏地Module表中选择Step项进入分析步(Step)模块.2.从主菜单中选择Step Create创建一个分析步.在出现地Create Step 对话框中命名此分析步为LugLoad,并接收General过程类型.从提供地过程选项列表中接收Static,General,点击Continue.3.在弹出地Edit Step对话框中键入下叙分析步描述:Apply uniform pressure to the hole,在接收缺省设置后点击OK.由于要使用可视化模块进行结果地后处理,所以必须指定欲输出地结果数据到结果数据库文件中.对于每个过程类型,默认地历史输出和场输出请求被ABAQUS/CAE自动选择.编辑这些要求,使得仅有位移、应力和反力作为场数据被写入输出数据库文件.指定输出结果到.odb文件:1.从主菜单中选择Output Field Output Requests Manager.在Field Output Requests Manager中在标有LugLoad地列中选择标有Created地单元(若它没有被选).在对话框底部显示出已为这个分析步骤预先设置地默认场输出结果请求地信息.2.在对话框地右边,点击Edit可改变场输出地要求,此时会弹出Edit Field Output Request对话框:a. 点击靠近Stresses地箭头来显示有效地应力输出表,接收默认地应力分量和不变量选择.b. 在Forces/Reactions中,只要求输出反力结果(缺省),要分别关闭集中力和力矩地输出项.c. 关闭Strains和Contact项.d. 接收默认地Displacement/Velocity/Acceleration输出.e. 点击OK,然后点击Dismiss来关闭Field Output RequestsManager对话框.3.通过选择Output History Output Requests Manager关闭历史输出结果.在History Output Requests Manager中在标有LugLoad地列中选择标有Created地单元.在对话框地底部点击Delete,接着在出现地警告对话框中点击Yes,最后点击Dismiss关闭History OutputRequests Manager.在施加载荷时,会要求确定连接环地挠度.一个简单地方法是将模型中所有地挠度都输出出来.但是环中最大挠度可能只发生在孔地底部,即受载部位.而且只对2方向地位移 (U2) 感兴趣.所以应要求只输出孔底部地竖向位移.一个很好地实践是检查约束反力是否与所加载荷平衡,指定变量RF可输出所有反力,并限制输出为受约束区域.另外,应要求输出模型地约束端地应力张量(变量S)和米赛斯应力(变量MISES).输出结果地请求必须是针对一个几何形体集进行控制输出,我们能方便地定义一个含有模型固支端地几何形体组,然而为了创建孔底部地几何形体集必须要对部件几何形体(特别是分区操作)进行额外地修正.由于稍后为了帮助生成网格要引进分区概念,组地创建被延迟,直到网格生成模块中模型被分区.正如前面所提地一样,当前版本地ABAQUS/CAE不能直接要求输出结果表,因而Keywords Editor将被用于增加必要地输出结果要求,在作业模块中用Keywords Editor将生成这些输出结果要求.指定边界条件和施加荷载在模型中,连接环地左端需要在三个方向加以约束,该区域是与母体连结处(见图4-18),在ABAQUS/CAE中边界条件是施加在部件上,而不是施加于有限单元网格上,边界条件与部件之间地这种关系使得变化网格时不需要重新指定边界条件.荷载地定义与此方法相同.图4-18 连接环上地固支端指定边界条件地步骤:1.从工具栏地Module列表中选择Load项进入荷载模块.2.从主菜单中选择BC Create来指定模型地边界条件,在弹出地Create Boundary Condition对话框中,命名边界条件为Fix left end,并选择LugLoad作为它所施加地分析步.选择分析类别为Mechanical、边界约束类型为Symmetry/Antisymmetry/Encastre,并点击Continue.3.在以下步骤中,可能需要改变视角使得选择更加容易.从主菜单中选择。
(word完整版)Abaqus基本操作中文教程(2021年整理精品文档)

(word完整版)Abaqus基本操作中文教程(word完整版)Abaqus基本操作中文教程编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((word完整版)Abaqus基本操作中文教程)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(word完整版)Abaqus基本操作中文教程的全部内容。
(word完整版)Abaqus基本操作中文教程Abaqus基本操作中文教程(word完整版)Abaqus基本操作中文教程目录1 Abaqus软件基本操作 (4)1.1 常用的快捷键 (4)1。
2 单位的一致性 (4)1。
3 分析流程九步走 (5)1。
3。
1 几何建模(Part) (5)1.3。
2 属性设置(Property) (7)1。
3。
3 建立装配体(Assembly) (7)1.3.4 定义分析步(Step) (9)1。
3.5 相互作用 (Interaction) (10)1。
3.6 载荷边界(Load) (13)1。
3。
7 划分网格 (Mesh) (14)1.3。
8 作业(Job) (18)1.3.9 可视化(Visualization) (19)(word完整版)Abaqus基本操作中文教程1 Abaqus软件基本操作1.1 常用的快捷键旋转模型— Ctrl+Alt+鼠标左键平移模型 - Ctrl+Alt+鼠标中键缩放模型 - Ctrl+Alt+鼠标右键1.2 单位的一致性CAE软件其实是数值计算软件,没有单位的概念,常用的国际单位制如下表1所示,建议采用SI (mm)进行建模。
国际单位SI (m)SI (mm)制长度m mm力N N质量kg t时间s sPa应力MPa (N/mm2)(N/m2)质量密度kg/m3t/mm3加速度m/s2mm/s2例如,模型的材料为钢材,采用国际单位制SI (m)时,弹性模量为2。
ABAQUS单元选用标准

Table 1 ABAQUS Elements Selection CriteriaGeneral contact between deformable bodies变形体间的普通接触First-order quad/hexlinear一阶四边形/三角形单元Second-order quad/hexquadratic二阶四边形/三角形Contact with bending弯曲接触Incompatible mode非协调模式First-order fully integrated quad/hexor second-order quad/hex一阶全积分或二阶四边形/三角形Bending (no contact) 非接触弯曲Second-order quad/hex二阶四边形/三角形单元First-order fully integrated quad/hex一阶全积分四边形/三角形Stress concentration集中应力Second-order二阶First-order一阶Nearly incompressible (ν=k/(k+1)>0.475 or large strain plasticity εpl>10%) 近不可压缩刚体First-order elements or second-orderreduced-integration elements一阶全积分单元或二阶缩减单元Second-order fully integratedCompletely incompressible (rubberν= 0.5)完全,不可压缩刚体Hybrid quad/hex, first-order if largedeformations are anticipated一阶四边形/三角形混合单元(Quad-dominated)Bulk metal forming (high mesh distortion) (金属)体积成型(网格畸变) First-order reduced-integration quad/hex一阶四边形/三角形缩减单元Second-order quad/hexComplicated model geometry (linear material,no contact)(线性材料无接触) Second-order quad/hex if possible (if not overly distorted) or second-order tet/tri (because ofmeshing difficulties)Complicated model geometry (nonlinear problem or contact) First-order quad/hex if possible (if not overly distorted) or modified second-order tet/tri (because of meshing difficulties)Natural frequency (lineardynamics)Second-orderNonlinear dynamic (impact) 非线性动力冲击First-orderlinear一阶四边形/三角形Second-order。
Abaqus单元类型选择

概述
• ABAQUS中的单元 • 结构单元(壳和梁) vs. 连续体单元 • 使用连续体单元模拟弯曲 • 应力集中 • 接触 • 不可压材料 • 网格生成 • 选择实体单元总结
ABAQUS/analysis_单元选择 标准
ABAQUS/analysis_单元选择标准
ABAQUS中的单元
ABAQUS中的单元
ABAQUS/analysis_单元选择 标准
公式 • 用于描述单元行为的数学公式是用于单元分类的另一种方法。 • 不同单元公式的例子:
– 平面应变 – 平面应力 – 杂交单元 – 非协调元 – 小应变壳 – 有限应变壳 – 厚壳 – 薄壳
ABAQUS中的单元
ABAQUS/analysis_单元选择 标准
经典的硬接触条件下,受均布压力的常规二阶四面体单元(C3D10)的等效节点力
在所分析的问题中,一般不需要将全部结构都均匀的细划网格。
利用手工计算、经验等等。 CAX8R: Continuum, ABAQUS/analysis_单元选择标准AXisymmetric, 8-node, ABAQUS/analysis_单元选择标准Reduced integration
DC1D2E: Diffusion (heat transfer), Continuum, 1-D, 2-node, Electrical
ABAQUS中的单元
ABAQUS/analysis_单元选择 标准
• 比较ABAQUS/Standard和ABAQUS/Explicit单元库 – 两种程序基本上具有相同的单元族:连续体、壳、梁等等。 – 除了应力分析,ABAQUS/Standard包括许多可以用于其它分析类型的单元: 热传导、土壤固结、声学等等。 • 在ABAQUS/Explicit中也可以使用声学单元。 – 对于每个单元族,ABAQUS/Standard包含许多变种。 – ABAQUS/Explicit包含几乎所有的一阶单元。 • 例外:二阶三角形和四面体单元、二阶梁单元 – 对于两种程序,许多单元选择的准则是一样的。
abaqus中单元的选取

ABAQUS中单元的选取总结实体单元的选择1. 如果不需要模拟非常大的应变或进行复杂的需改变接触条件的问题,则应采用二次减缩积分单元(CAX8R、CPE8R、CPS8R、C3D20R等);2. 如果存在应力集中,则在局部应采用二次完全积分单元(CAX8、CPE8、CPS8、C3D20等)。
它们可用最低费用提供应力梯度最好的解答。
3. 涉及到非常大的网格扭曲问题(大变形分析),建议采用细网格剖分的线性减缩积分单元(CAX4R、CPE4R、CPS4R、C3D8R等);4. 对接触问题采用线性减缩积分单元或细分的非协同单元(CAX4I、CPE4I、CPS4I、C3D8I等);5. 尽可能的减少网格变形的扭歪,形状扭歪的粗网格线性单元会导致非常差的结果。
壳单元的选择1.当要求解十分精确时,可使用线性、有限薄膜应变、完全积分的四边形壳单元(S4),这个壳单元十分适合于要考虑膜作用或有弯曲模式沙漏的问题,也适合于有平面弯曲的问题;2.线性、有限薄膜应变、减缩积分、四边形壳单元(S4R)较流行,适合于各类问题的应用;3.线性、有限薄膜应变、三角形壳单元(S3/S3R)可作为一般的壳单元来使用。
因为在单元内部是常应变应力场,求解弯曲变形和高应变梯度时需要精细的网格剖分;4.考虑到在复合材料层合壳模型中剪切柔度的影响,可应用厚壳单元(S4、S4R、S3、S3R、S8R)来模拟它,此时需检验平面假定是否满足;5.四边形或三角形的二次壳单元,对于一般的小变形薄壳来说是很有效的,它们对于剪力锁闭和薄膜锁闭不敏感;6.如果在接触问题中一定要用二阶单元,不要选用二阶三角形壳单元(STRI65),而要采用9节点的四边形壳单元(S9R5);7.对于几何线性的,但规模又非常大的模型,线性薄壳单元(S4R5)通常将比一般壳单元效率更高。
梁单元的选择1. 对任何涉及到接触的分析,应使用一阶的、有剪切变形的梁单元(B21、B31);2. 对于结构刚度非常大或非常柔软的结构,在几何非线性分析中应当使用杂交梁单元(B21H、B32H等);3. Euler-Benoulli三次梁单元(B23、B33)在模拟承受分布荷载作用的梁,包括动态的振动分析时,会有很高的精度。
Abaqus单元的选择

Abaqus单元的选择2015-03-06 有限元在线如果想要以合理的费用得到高精度的结果,那么正确的选择单元是非常关键的。
对于ABAQUS经验丰富的使用者,毫无疑问都会自己的单元选择指南来处理各种具体的应用。
但是,在刚开始使用ABAQUS 时,下面的指导是非常有用的。
1、实体单元选择以下单元选择的建议适用于ABAQUS/Standard和ABAQUS/Explicit:(1)尽可能的减小网格的扭曲。
使用扭曲的线性单元的粗糙网格会得到相当差的结果。
(2)对于模拟网格扭曲过分严重的问题,应用网格细划的线性、减缩积分单元(CAX4R,CPE4R,CPS4R,C3D8R等)。
(3)对三维问题应尽可能地采用六面体单元。
它们以最低的成本给出最好的结果。
当几何形状复杂时,采用六面体单元划分网格可能是非常困难的,因此,还需要楔形和四面体单元。
这些单元(C3D4和C3D6)的一阶模式是较差的单元(需要细划网格以取得较好的精确度)。
(4)某些前处理器包含了自由划分网格算法,用四面体单元划分任意几何体的网格。
对于小位移无接触的问题,在ABAQUS/Standard中的二次四面体单元(C3D10)能够给出合理的结果。
这个单元的另一种模式是修正的二次四面体单元(C3D10M),它适用于ABAQUS/Standard和ABAQUS/Explicit,对于大变形和接触问题,这种单元是强健的,展示了很小的剪切和体积自锁。
但是,无论采用何种四面体单元,所用的分析时间都长于采用了等效网格的六面体单元。
(5)对于ABAQUS/Standard求解器,除非需要模拟非常大的应变或者模拟一个复杂的、接触条件不断变化的问题,对于一般的分析工作,应采用二次、减缩积分单元(CAX8R,CPE8R,CPS8R, C3D20R 等)。
(6)对于ABAQUS/Standard求解器,在存在应力集中的局部区域,采用二次、完全积分单元(CAX8, CPE8, CPS8, C3D20等)。
abaqus第二讲:ABAQUS中的实体单元

避免使用
二阶四边形/六面体
一阶全积分四边形/六面 体或二阶四边形/六面 体
一阶全积分四边形/六面 体
一阶
二阶全积分单元
问题分类 完全不可压 (橡胶n = 0.5) 屈曲材料成型(高度网格
扭曲)
复杂的几何模型(线性材 料,没有接触)
复杂的几何模型(非线性 或接触)
自然频率(线性动力学) 非线性动力学(隐式)
• 比较ABAQUS/Standard和ABAQUS/Explicit单元库 两种程序基本上具有相同的单元族:连续体、壳、梁等等。 除了应力分析,ABAQUS/Standard包括许多可以用于其它分析类型 的单元:热传导、土壤固结、声学等等。 • 在ABAQUS/Explicit中也可以使用声学单元。 对于每个单元族,ABAQUS/Standard包含许多变种。 ABAQUS/Explicit包含几乎所有的一阶单元。 • 例外:二阶三角形和四面体单元、二阶梁单元 对于两种程序,许多单元选择的准则是一样的。
“常规的”二阶四面体、二阶楔形和六节点壳和薄膜单元 (C3D10, C3D15, STRI65, M3D6)不能用于模拟接触问题, 除非使用基于罚函数的接触公式。
• 与“经典”的硬接触相比,在单元角点和中点处,一致 压力下面的接触力存在明显的不同。
修正的 二阶三角形/四面体单元(C3D10M, 等等)减轻了其它三角形/ 四面体单元的问题。 • 好的收敛率—与二阶四边形/六面体单元的收敛率相近。 • 最小化剪切锁闭和体积锁闭。 – 利用杂交公式(C3D10MH),可以用于模拟不可压或几乎不 可压材料。 • 在有限变形问题中,这些单元表现强劲。 • 一致的接触压力可以使这些单元精确的模拟接触问题。
Abaqus中如何正确选择使用实体单

Abaqus中如何正确选择使⽤实体单Abaqus中如何正确选择使⽤实体单Abaqus中如何正确选择使⽤实体单元1) 尽可能的减少⽹格的扭曲,使⽤扭曲的线性单元粗糙⽹格会得到相当差的分析结果;2) 减缩积分单元对于⽹格扭曲不敏感,所以当对复杂的⼏何体剖分⽹格时,不能确定其扭曲是否很⼩,尽量⽤细化的减缩积分单元(C**R)3) 对于三维问题尽量采⽤六⾯体单元进⾏划分⽹格,但是当遇到⼏何体较复杂时不能完全⽤六⾯体⽹格时,可能需要⽤四⾯体单元或者楔形单元,此时尽量少⽤其对应下的线性模式,如果不得已采⽤,应避开需要得到精确结果的区域;4) 在某些前处理器包含了⾃由⽹格剖分算法,⽤四⾯体剖分⼈以⼏何形状的⼏何体:此时对于⼩位移⽆接触的问题,在Standard中⼆次四⾯体单元(C3D10)能够给出合理的结果,另外其修正的⼆次四⾯体单元(C3D10M)也适⽤于隐式和显⽰分析中;对于⼤变形和接触问题,这种单元展⽰了很⼩的剪切和体积⾃锁;5) 不能采⽤仅包含有线性四⾯体单元(C3D4)的⽹格。
以上对于显⽰和隐式分析都试⽤。
对于隐式(Standard)分析中还必须考虑到1) 除⾮需要模拟⾮常⼤的应变或者模拟⼀个复杂的解除条件不断变化的问题,否则,对于⼀般的分析,应采⽤⼆次减缩积分单元(CAX8R\CPE8R\CPS8R\C3D20R),⼆次减缩积分单元中沙漏现象较为少见,对于⼤多数问题,只要不是接触问题,应尽量考虑使⽤这类单元。
2) ⼀阶减缩积分单元容易出现沙漏现象,⾜够细化的⽹格可以有效地减⼩这种问题,当采⽤⼀阶线性性积分单元模拟发⽣弯曲变形的问题时,沿厚度⽅向应⾄少使⽤四个单元。
3) 存在应⼒集中的区域,采⽤⼆次、完全积分单元(CAX8、CPE88、CPS8、C3D20)4) 对于接触问题,采⽤细化⽹格的线性、减缩积分单元或者⾮协调模式单元(⾮协调模式单元仅在Standard中存在)5) 对于不可压缩(泊松⽐=0.5)或⾮常接近于不可压缩的(泊松⽐⼤于0.475)时需采⽤杂交单元,此单元仅存在与Standard中6) 沙漏可能由于集中⼒、边界条件或接触作⽤在单个节点上所触发。
Abaqus中的单元选择

Abaqus中的单元选择在有限元分析中,为了能够得到较为精确的收敛解,一方面取决于所用模型的误差,另一方面取决于模拟计算的误差。
一个好的有限元模型,不仅需要较高的网格质量,还需要拥有合适的单元类型。
ABAQUS为用户提供了丰富的单元库,几乎可以模拟实际工程中任意几何形状的有限元模型,在对一个问题进行分析时,可以根据情况选择使用。
如何才能选取出适合于分析的单元类型呢?我认为首先要了解ABAQUS中对于单元的分类,每种单元特定的使用范围,各种单元类型的节点数目、单元形状、插值函数阶次以及单元构造的方式。
然后再根据分析类型和具体问题合理选择。
ABAQUS中最常用的单元包括实体(Solid)单元、壳(Shell)单元和梁(Beam)单元。
下面就根据自己对于ABAQUS应用实体单元的学习,将这些单元的特点和使用简单总结如下:实体单元主要包括完全积分、减缩积分、非协调以及杂交这四种常见的单元模式。
(1)完全积分单元:单元具有规则形状(边是直线并且边与边相交成直角)时,所用的Gauss积分点的数目足以对单元刚度矩阵中的多项式进行精确积分。
完全积分的线性单元在每一个方向上采用2个积分点;完全积分的二次单元在每一个方向上采用3个积分点。
如图不足:完全积分的线性单元存在“剪切自锁”问题,原因是线性单元的边不能弯曲。
在复杂应力状态下,完全积分的二次单元也有可能发生剪切自锁。
(2)减缩积分单元:减缩积分单元比完全积分单元在每个方向上少用一个积分点。
完全积分的线性单元只在单元的中心有一个积分点不足:线性减缩积分单元存在“沙漏模式”的数值问题,有可能过于柔软。
ABAQUS通过绘制伪应变能(ALLAE)和内能(ALLIE)来评价沙漏模式对计算结果的影响。
(3)非协调单元:优点:可以克服完全积分,一阶单元中的剪力自锁问题。
特点:在一阶单元中引入一个增强单元变形梯度的附加自由度。
这种对变形梯度的增强允许一阶单元在单元域上对于变形梯度有一个线性变化。
Abaqus基本操作中文教程

Abaqus基本操作中文教程目录1 Abaqus软件基本操作 (3)1.1 常用的快捷键 (3)1.2 单位的一致性 (3)1.3 分析流程九步走 (3)1.3.1 几何建模(Part) (4)1.3.2 属性设置(Property) (5)1.3.3 建立装配体(Assembly) (6)1.3.4 定义分析步(Step) (7)1.3.5 相互作用(Interaction) (8)1.3.6 载荷边界(Load) (10)1.3.7 划分网格(Mesh) (11)1.3.8 作业(Job) (15)1.3.9 可视化(Visualization) (16)1 Abaqus软件基本操作1.1 常用的快捷键旋转模型—Ctrl+Alt+鼠标左键平移模型—Ctrl+Alt+鼠标中键1.2 单位的一致性CAE软件其实是数值计算软件,没有单位的概念,常用的国际单位制如下表1所示,建议采用SI (mm)进行建模。
例如,模型的材料为钢材,采用国际单位制SI (m)时,弹性模量为2.06e11N/m2,重力加速度9.800 m/s2,密度为7850 kg/m3,应力Pa;采用国际单位制SI (mm)时,弹性模量为2.06e5N/mm2,重力加速度9800 mm/s2,密度为7850e-12 T/mm3,应力MPa。
1.3 分析流程九步走几何建模(Part)→属性设置(Property)→建立装配体(Assembly)→定义分析步(Step)→相互作用(Interaction)→载荷边界(Load)→划分网格(Mesh)→作业(Job)→可视化(Visualization)1.3.1 几何建模(Part ) 关键步骤的介绍: 部件(Part )导入Pro/E 等CAD 软件建好的模型后,另存成iges 、sat 、step 等格式;然后导入Abaqus 可以直接用,实体模型的导入通常采用sat 格式文件导入。
部件(Part )创建简单的部件建议直接在abaqus 中完成创建,复杂的可以借助Pro/E 或者Solidworks 等专业软件进行建模,然后导入。
ABAQUS实体单元选择基本原则

ABAQUS实体单元选择基本原则Standard和explicit都应遵循的原则:1、尽量减少扭曲的单元。
单元扭曲可以用雅克比、内角、warpage等来衡量。
2、大应变的模拟中应该使用细化的线性减缩单元模拟。
CAX4R/CPE4R/CPS4R/C3D8R.3、三维问题中应当尽量使用六面体单元。
C3D4和C3D6需要很细的网格才能得到相对准确的结果,因此应当尽量避免使用这类单元,并且要远离感兴趣区域。
4、对于四面体网格。
Standard中,小位移并且不包括接触的问题应当使用C3D10或者C3D10I(Explicit中除了修正四面体与三角形单元以及二阶梁单元外,其余都是线性单元;除了修正四面体和三角形单元以及一节壳单元与六面体完全积分单元外,其余都是减缩积分单元)。
大位移以及使用默认“硬接触”的问题,在Standard和Explicit中,都应该使用C3D10M单元。
应该极力避免使用C3D4.对于Standard中还应当遵循以下基本原则:1、对于不包括大位移与复杂的接触条件改变的一般性问题,推荐使用二阶减缩积分单元。
CAX8R/CPE8R/CPS8R/C3S20R2、应力集中区域应当使用二阶完全积分单元(除非单元扭曲厉害或者弯曲应力有梯度,很少会体积自锁;也无hourglassing问题)。
CAX8/CPE8/CPS8/C3D20。
这些单元能够以最小的代价给出精确的应力梯度。
3、对于接触问题,应当使用细化的线性减缩积分单元或者非协调单元。
CAX4I/CPE4I/CPS4I/C3D8I.总结1、Formulation和Order of integration对于求解结果的准确性与计算代价有很大的影响。
2、线性完全积分单元容易产生剪切自锁,应当避免使用。
3、线性减缩积分单元模拟弯曲变形时,在厚度的方向至少使用四个单元。
4、在Standard中,二阶减缩积分单元很少有Hourglassing的问题。
但模型中没有接触是应该首先考虑使用这种单元。
abaqus中单元的选择宝典

1.完全积分就是指当单元具有规则形状时,所用得高斯积分点可以对单元刚度矩阵中得多项式进行精确地积分。
2.剪力自锁将使单元变得“刚硬”,只影响受弯曲荷载得完全积分线性(一阶)单元,这些单元功能在受直接或剪切荷载时没有问题。
二次单元得边界可以弯曲,没有剪力自锁得问题。
3.只有四边形与六面体单元才能采用减缩积分。
所有得楔形、四面体与三角形实体单元采用完全积分。
减缩积分单元比完全积分单元在每个方向上少用一个积分点。
4.只有四边形与六面体单元才能采用减缩积分。
所有得楔形、四面体与三角形实体单元采用完全积分。
减缩积分单元比完全积分单元在每个方向上少用一个积分点。
5.非协调单元:只有四边形与六面体单元才能采用减缩积分。
所有得楔形、四面体与三角形实体单元采用完全积分。
减缩积分单元比完全积分单元在每个方向上少用一个积分点。
6.ABAQUS对非协调单元采用了增强位移梯度形式。
在弯曲问题中,用非协调单元可得到与二次单元相当得结果,且计算费用明显降低。
对单元扭曲很敏感。
7.ABAQUS对非协调单元采用了增强位移梯度形式。
在弯曲问题中,用非协调单元可得到与二次单元相当得结果,且计算费用明显降低。
对单元扭曲很敏感。
8.杂交单元:ABAQUS对非协调单元采用了增强位移梯度形式。
在弯曲问题中,用非协调单元可得到与二次单元相当得结果,且计算费用明显降低。
对单元扭曲很敏感。
9.一般情况下应采用二次减缩积分单元(CAX8R,CPE8R,CPS8R,C3D20R)。
在应力集中局部采用二次完全积分单元(CAX8,CPE8,CPS8,C3D20)。
对含有非常大得网格扭曲模拟(大应变分析),采用细网格划分得线性减缩积分单元(CAX4R,CPE4R,CPS4R,C3D8R )。
对接触问题采用线性减缩积分单元或非协调单元(CAX4I,CPE4I,CPS4II,C3D8I等)得细网格划分。
10.采用非协调单元时应使网格扭曲减至最小。
三维情况应尽可能采用块状单元(六面体)。
Abaqus单元的选择

Abaqus单元的选择2015-03-06 有限元在线如果想要以合理的费用得到高精度的结果,那么正确的选择单元是非常关键的。
对于ABAQUS经验丰富的使用者,毫无疑问都会自己的单元选择指南来处理各种具体的应用。
但是,在刚开始使用ABAQUS 时,下面的指导是非常有用的。
1、实体单元选择以下单元选择的建议适用于ABAQUS/Standard和ABAQUS/Explicit:(1)尽可能的减小网格的扭曲。
使用扭曲的线性单元的粗糙网格会得到相当差的结果。
(2)对于模拟网格扭曲过分严重的问题,应用网格细划的线性、减缩积分单元(CAX4R,CPE4R,CPS4R,C3D8R等)。
(3)对三维问题应尽可能地采用六面体单元。
它们以最低的成本给出最好的结果。
当几何形状复杂时,采用六面体单元划分网格可能是非常困难的,因此,还需要楔形和四面体单元。
这些单元(C3D4和C3D6)的一阶模式是较差的单元(需要细划网格以取得较好的精确度)。
(4)某些前处理器包含了自由划分网格算法,用四面体单元划分任意几何体的网格。
对于小位移无接触的问题,在ABAQUS/Standard中的二次四面体单元(C3D10)能够给出合理的结果。
这个单元的另一种模式是修正的二次四面体单元(C3D10M),它适用于ABAQUS/Standard和ABAQUS/Explicit,对于大变形和接触问题,这种单元是强健的,展示了很小的剪切和体积自锁。
但是,无论采用何种四面体单元,所用的分析时间都长于采用了等效网格的六面体单元。
(5)对于ABAQUS/Standard求解器,除非需要模拟非常大的应变或者模拟一个复杂的、接触条件不断变化的问题,对于一般的分析工作,应采用二次、减缩积分单元(CAX8R,CPE8R,CPS8R, C3D20R 等)。
(6)对于ABAQUS/Standard求解器,在存在应力集中的局部区域,采用二次、完全积分单元(CAX8, CPE8, CPS8, C3D20等)。
Abaqus中选择三维实体单元类型的基本原则
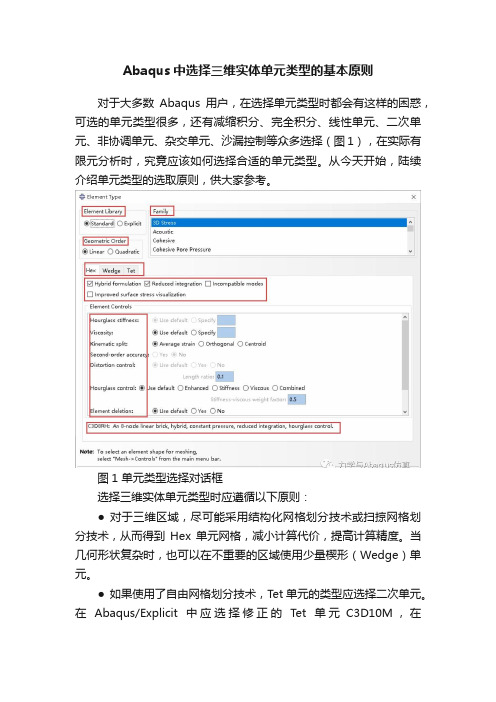
Abaqus中选择三维实体单元类型的基本原则对于大多数Abaqus用户,在选择单元类型时都会有这样的困惑,可选的单元类型很多,还有减缩积分、完全积分、线性单元、二次单元、非协调单元、杂交单元、沙漏控制等众多选择(图1),在实际有限元分析时,究竟应该如何选择合适的单元类型。
从今天开始,陆续介绍单元类型的选取原则,供大家参考。
图1 单元类型选择对话框选择三维实体单元类型时应遵循以下原则:● 对于三维区域,尽可能采用结构化网格划分技术或扫掠网格划分技术,从而得到Hex单元网格,减小计算代价,提高计算精度。
当几何形状复杂时,也可以在不重要的区域使用少量楔形(Wedge)单元。
● 如果使用了自由网格划分技术,Tet单元的类型应选择二次单元。
在Abaqus/Explicit中应选择修正的Tet单元 C3D10M,在Abaqus/Standard中可以选择C3D10,但如果有大的塑性变形,或模型中存在接触,而且使用的是默认的“硬”接触关系(“hard”con tact relationship),则也应选择修正的Tet单元 C3D10M。
● Abaqus的所有单元均可用于动态分析,选取单元的一般原则与静力分析相同。
但在使用Abaqus/Explicit模拟冲击或爆炸载荷时,应选用线性单元,因为它们具有集中质量公式,模拟应力波的效果优于二次单元所采用的一致质量公式。
如果使用的求解器是Abaqus/Standard,在选择单元类型时还应注意以下方面:● 对于应力集中问题,尽量不要使用线性减缩积分单元,可使用二次单元来提高精度。
如果在应力集中部位进行了网格细化,使用二次减缩积分单元与二次完全积分单元得到的应力结果相差不大,而二次减缩积分单元的计算时间相对较短。
● 对于弹塑性分析,如果材料是不可压缩性的(例如金属材料),则不能使用二次完全积分单元,否则会出现体积自锁问题,也不要使用二次Tri单元或Tet单元。
推荐使用的是修正的二次Tri单元或Tet单元、非协调单元,以及线性减缩积分单元。
ABAQUS中实体单元的应用

ABAQUS中实体单元的应用在ABAQUS的单元库中,应用最广泛的是应力/位移实体单元族。
对三维单元,可以选择六面体、四面体和楔形体;对二维单元则可在三角形与四边形之间进行选择。
这些基本的单元形状,每一种都有线性和二次的两类选择。
对六面体和四边形,还可选择完全积分或减缩积分。
最后,还可选用标准元或杂交元列式。
另外对线性六面体或四边形单元,还有个附加的功能,可选择非协调模式,而对二次的三角形或四面体单元可以应用修正列式。
若列出所有种类的单元,所面临的实体单元的总数目是相当大的,仅三维单元而言就超过20种。
模拟的精度将强烈地依赖于所采用的单元类型。
特别是在初次使用时,在这些单元中选择哪一个最为合适很可能是一件令人苦恼的事情。
然而,用户会逐渐把这个工作看作是从一个20多件的工具组中,有能力选择最恰当的工具或单元来完成的一个有价值的工作。
这一章讨论了不同的单元列式和积分水平对一个特定分析的精度的影响。
同时也讨论了一些选择实体单元的一般性原则。
这些讨论提供了获得更多应用ABAQUS经验和知识的基础。
在本节末的例子将允许用户应用这些知识建立和分析一个连接柄构件的模型。
4.1 单元列式和积分通过图4-1所示的悬臂梁,可阐明单元阶数(线性或二次),单元列式及积分水平等因素对结构模拟精度的影响。
这是评估一个给定单元的性能的经典测试。
因为该构件相对是细长的,我们通常用梁单元来对它建立模型。
但在这里我们用这个测试来帮助评估各种实体单元的效率。
梁长150mm,宽2.5mm,高5mm;一端固定;自由端承受5N的荷载。
材料的杨氏模量E为70GPa,泊松比为0.0。
采用梁的理论,在载荷P作用下,梁自由端的挠度为δtipplEI =3 3其中I bd=312/,l是长度,b是宽度,d是梁的高度。
P = 5N时自由端挠度是3.09mm。
图4-1 自由端受集中载荷的悬臂梁4.1.1 完全积分所谓“完全积分”是指当单元具有规则形状时,所用的Gauss积分点的数目足以对单元刚度矩阵中的多项式进行精确积分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Standard和explicit都应遵循的原则:
1、尽量减少扭曲的单元。
单元扭曲可以用雅克比、内角、warpage等来衡量。
2、大应变的模拟中应该使用细化的线性减缩单元模拟。
CAX4R/CPE4R/CPS4R/C3D8R.
3、三维问题中应当尽量使用六面体单元。
C3D4和C3D6需要很细的网格才能得到相对准确的结果,因此
应当尽量避免使用这类单元,并且要远离感兴趣区域。
4、对于四面体网格。
Standard中,小位移并且不包括接触的问题应当使用C3D10或者C3D10I(Explicit
中除了修正四面体与三角形单元以及二阶梁单元外,其余都是线性单元;除了修正四面体和三角形单元以及一节壳单元与六面体完全积分单元外,其余都是减缩积分单元)。
大位移以及使用默认“硬接触”的问题,在Standard和Explicit中,都应该使用C3D10M单元。
应该极力避免使用C3D4.
对于Standard中还应当遵循以下基本原则:
1、对于不包括大位移与复杂的接触条件改变的一般性问题,推荐使用二阶减缩积分单元。
CAX8R/CPE8R/CPS8R/C3S20R
2、应力集中区域应当使用二阶完全积分单元(除非单元扭曲厉害或者弯曲应力有梯度,很少会体积自锁;
也无hourglassing问题)。
CAX8/CPE8/CPS8/C3D20。
这些单元能够以最小的代价给出精确的应力梯度。
3、对于接触问题,应当使用细化的线性减缩积分单元或者非协调单元。
CAX4I/CPE4I/CPS4I/C3D8I.
总结
1、Formulation和Order of integration对于求解结果的准确性与计算代价有很大的影响。
2、线性完全积分单元容易产生剪切自锁,应当避免使用。
3、线性减缩积分单元模拟弯曲变形时,在厚度的方向至少使用四个单元。
4、在Standard中,二阶减缩积分单元很少有Hourglassing的问题。
但模型中没有接触是应该首先考虑使
用这种单元。
5、非协调单元对于单元的扭曲非常敏感。
6、通常应当进行网格收敛性检查,以确定网格以经足够细化了。
但是一个收敛的网格并不一定就说明模
拟的结果与实际情况相符。
有限单元模拟的正确性还要依赖于模型中其他的近似与理想化。
7、通常,应该对感兴趣区域进行细化。
预测应力的模型应当比预测位移的模型更细化。
8、Abaqus中提供子模型等高级功能来模拟复杂的问题。
