用布莱克曼窗设计数字带通滤波器
基于matlab窗函数的FIR带通滤波器设计
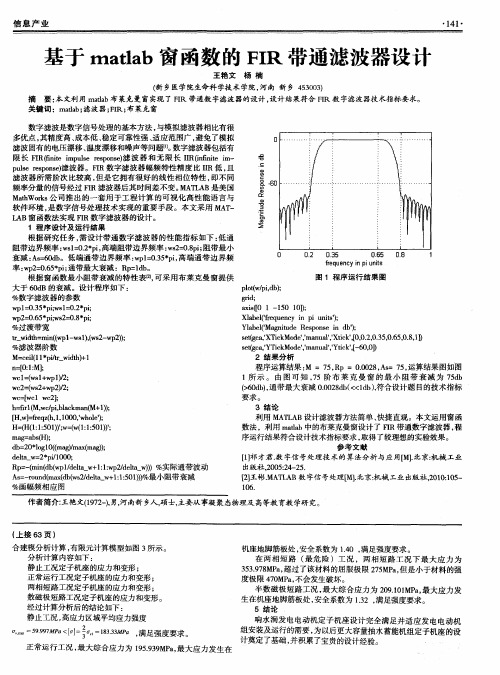
X l a b e l ( ’ f r e q u e n c y i n p i u n i t s ’ ) ; Y l a b d( 。 Ma g n i t u d e R e s p o n s e i n d b ’ ) ; s e t ( g c a , ’ X T i c k Mo d e ' , ' ma n u a l ' , ' X t i c k ’ , [ 0 , 0 . 2 , 0 . 3 5 , 0 . 6 5 , 0 . 8 , 1 1 ) s e t ( g c a , ’ Y T i e k Mo d e ’ , ’ ma J 1 u a l ’ , ’ Y t i c k ’ , [ - 6 0 , o ] ) 2 结 果 分 析
程序运算结果 : M =7 5 , R p= O . 0 0 2 8 , A s =7 5 , 运算结果 图如图 1 所 示。由图可知 , 7 5阶 布 莱 克 曼 窗 的最 小 阻带 衰 减 为 7 5 d b ( > 6 0 d b ) , 通带最大衰减 O . O 0 2 8 d b ( < < l d b ) , 符合设计题 目的技 术指标
口
:
:
限长 F I R( i f n i t e i m p u l s e r e s p o n s e ) 滤波 器 和 无 限 长 l i B( i n f i n i t e i m — p u l s e r e s p o n s e ) 滤波器 。F I R数字 滤波器幅频特性精 度 比 I I R低 , 且 滤波器所 需阶次 比较 高 , 但是 它拥有很好 的线性相位 特性 , 即不 同 昱 . 印 频率分量的信号经过 F I R滤波器后 其时间差 不变 。 MA T L A B是美 国 Ma t h Wo r k s 公司推 出 的一 套用 于工程计算 的可 视化高 性能语 言 与 软 件环境 , 是 数字信号处理技术 实现的重要手段 。本 文采用 M A T _ L A B窗 函数法实现 F I R数字滤波器的设计 。 至 1程序设计及运行结果 I 根 据研究任务 , 需设计 带通数字滤 波器 的性 能指标如 下 : 低通 阻带边界频 率 : w s l = 0 . 2 * p i , 高端阻带边界频率 : w s 2 = 0 . 8 p i ; 阻带最小 口 衰减: A s = 6 0 d b 。低端通带边 界频率 : w p l = 0 . 3 5 " p i , 高端 通带边界 频 率: w p 2 = 0 . 6 5 " p i ; 通带最大衰减 :R p = l a b 。 根 据窗 函数最小 阻带衰减 的特性 表[ 2 1 , 可采用布莱 克曼 窗提供 大于6 0 d B的衰减 。设 计程序如下 : p l o t ( w / p i , d b ) ; d ; %数字滤波器的参数
数字信号处理第三次实验FIR

FIR数字滤波器的设计一、实验目的(1)掌握用窗函数法、频率采样法及优化设计法设计FIR数字滤波器的原理及方法,熟悉相应的MATLAB编程。
(2)熟悉线性相位FIR滤波器的幅频特性和相频特性。
(3)了解各种不同窗函数对滤波器性能的影响。
二、实验内容1.窗函数归一化的幅度谱clear;N=45;W1=boxcar(N);W2=hamming(N);W3=blackman(N);[h1,p1]=freqz(W1,1);subplot(3,1,1);plot(p1/pi,20*log(abs(h1)));title('矩形窗');xlabel('归一化频率/\pi');ylabel('幅度/dB');[h2,p2]=freqz(W2,1);subplot(3,1,2);plot(p2/pi,20*log(abs(h2)));title('汉明窗');xlabel('归一化频率/\pi');ylabel('幅度/dB');[h3,p3]=freqz(W3,1);subplot(3,1,3);plot(p3/pi,20*log10(abs(h3)));title('布莱克曼窗');xlabel('归一化频率/\pi');ylabel('幅度/dB');00.10.20.30.40.50.60.70.80.91-100100矩形窗归一化频率/π幅度/d B0.10.20.30.40.50.60.70.80.91-200200汉明窗归一化频率/π幅度/d B00.10.20.30.40.50.60.70.80.91-200200布莱克曼窗归一化频率/π幅度/d B分析:特点:矩形窗:具有最窄的主瓣宽度,最大的旁瓣峰值; 汉明窗:主瓣稍宽,但有较小的旁瓣; 布莱克曼窗:主瓣宽度最宽,旁瓣最小。
基于Blackman窗的数字带通滤波器设计

wp 2=0 . 6 5 p i ; ws 2=0 . 8 p i ;
As = 60 ,
t r
_
w i d t h=m i n ( ( w p 1 - w s 1 ) , ( w s 2 - w p 2 ) ) N =c e i l ( 1 1 * p i / t r _ w i d t h ) + 1%: N = 7 5
・
1 1 2 ・
科 技 论 坛
基于 B l a c k ma n 窗的数字带通滤波器设计
王艳 文 干 勉
( 新 乡医学院生物医学工程学院, 河南 新乡 4 5 3 0 0 3 )
摘 要: 本 文利 用 B l a e k ma n 窗 实现 了 F I R 带通 数 字 滤波 器的 设 计 , 设计结果符合 F I R 数 字 滤 波 器技 术 指 标要 求 。 关键词 : Ma t l a b , 滤波器 ; F I R; B l a c k ma n 窗
U
U
U 贽 Biblioteka " b U H I
f r eq ue ncy t n a un舡
图 1 滤 波器 时域 中实 际的 脉 冲 响应 曲线 和 频 域 中 幅度 响应 曲线
2 结果分 析
设 计程 序如 下 :
ws l = 0. 2 pi ;wpl = 0. 35 pi ;
n = f 0 : l : N l
程序运算结果 : N=7 5( 滤波器的阶数) , R p=0 . 0 0 2 8( 实际的通 带波动 ) , A s=7 5( 实际的阻带衰减 ) 。 从上面结果可以看到,利用 B l a c k m a n窗昕 十的 7 5阶带通滤波 器滤波器 , 通带内的最大波动为 0 . 0 0 2 8 ( < 1 d B ) , 阻带内最小衰减 7 5 d B ( > 6 0 d B ) , 满足指标要求 。图 1 是此滤波器时域中实际的脉冲响应曲线
实验7 窗函数法设计FIR数字滤波器

实验7窗函数法设计FIR数字滤波器一、实验目的掌握窗函数法设计F1R数字滤波器的原理和具体方法二、实验设备与环境计算机、Mat1ab软件环境三、实验基础理论1>基本原理窗函数设计法的基本思想为,首先选择一个适当的理想的滤波器Hd(,3),然后用窗函数截取它的单位脉冲响应%(九),得到线性相位和因果的FIR滤波器,这种方法的重点是选择一个合适的窗函数和理想滤波器,使设计的滤波器的单位脉冲响应逼近理想滤波器的单位脉冲响应。
2、设计步骤(1)给定理想滤波器的频率响应Hd("3),在通带上具有单位增益和线性相位,在阻带上具有零响应。
一个带宽为g(3c<Tr)的低通滤波器由下式给定h(e j^=(eW∣ω∣≤ωc虱)一1Oωc<∣ω∣<π其中α为采样延迟,其作用是为了得到因果的系统。
(2)确定这个滤波器的单位脉冲响应为了得到一个h(n)长度为N的因果的线性相位FIR滤波器,我们令N-Ia=-2-(3)用窗函数截取hd(τι)得到所设计FIR数字滤波器h(n)h(n)=h d(n)w(n)3、窗函数的选择常用的窗函数有矩形窗、汉宁窗、海明窗、布莱克曼窗、凯瑟窗等。
Mat1ab提供了一些函数用于产生窗函数,如下表所示:在设计过程中我们需要根据给定的滤波器技术指标,选择滤波器长度N 和窗函数3(n)°表7.2列出了常用的窗函数的一些特性,可供设计时参考。
其中幻是修正的零阶贝塞尔函数,参数B 控制最小阻带衰减,这种窗函数对于相同的N 可以提供不同的过渡带宽。
由于贝塞尔函数比较更杂,这种窗函数的设计方程很难推导,然而幸运的是,有一些经验设计方程可以直接使用。
已知给定的指标叫Msc,Rp 和4,滤波器长度N 和凯瑟窗参数B 可以按如下凯瑟窗设计方程给出过渡带宽:∆ω=ωst -ωp入一7.95 2.285∆ω_(0.1102(4-8.7) ,P=iθ.5842(4-21)04+0.07886(4-21), 四、实验内容1、设计一个数字低通FIR 滤波器,其技术指标如下ωp =0.2τr,RP=0.25dBωst =0.3τr,A s =50dB分别采用矩形窗、汉宁窗、海明窗、布莱克曼窗、凯瑟窗设计该滤波器。
基于matlab布拉克曼窗的数字滤波器设计

科技视界Science&Technology VisionScience&Technology Vision科技视界(上接第55页)4试验结果为了验证开环功率补偿的效果,我们对AV1487B信号源进行如下试验:1)使用AV2434功率计对AV1487B信号源进行闭环功率补偿,以保证ALC闭环状态下的功率准确;2)设置信号源功率为0dBm,使用功率计以100MHz为步进对信号源进行用户功率平坦度,通过该校准获得了闭环下信号源的功率平坦度数据;3)对信号源进行开环功率补偿操作,存储补偿数据;4)将信号源ALC环路打到开环状态,使用功率计进行用户功率平坦度补偿,得到开环状态下的功率平坦度数据;5)对比两份数据的差异。
经过对比开/闭环状态下的功率平坦度数据,开环功率与闭环功率在功率为0dBm时的最大差值小于0.4dB,开环功率准确度达到了±0.6dB。
5结论开环功率补偿技术作为一种新型的信号源稳幅技术,目前已经应用于AV1487、AV1461、AV1464等型号的信号源,通过了大量用户实际使用的检验,有效解决了窄脉冲调制下信号源的功率漂移和功率突变问题,开环输出功率准确稳定,取得了良好的效果。
[1]现代通信测量仪器[M].中国电子科技集团公司第四十一研究所.[2]赵习智.微波信号源功率控制技术[J].科技信息,2008,18:447-448.[责任编辑:王迎迎]数字滤波是数字信号处理的基本方法,与模拟滤波器相比有很多优点,其精度高、成本低、稳定可靠性强、适应范围广,避免了模拟滤波固有的电压漂移、温度漂移和噪声等问题[1]。
数字滤波器包括有限长FIR(finite impulse response)滤波器和无限长IIR(infinite impulseresponse)滤波器。
FIR数字滤波器幅频特性精度比IIR低,且滤波器所需阶次比较高,但是它拥有很好的线性相位特性,即不同频率分量的信号经过FIR滤波器后其时间差不变。
基于MATLAB的布莱克曼窗FIR数字低通滤波器设计程序

wst=0.5*pi;wp=0.3*pi;deltaw=wst-wp;%过渡带宽△w的计算N0=ceil(11*pi/deltaw);%按布莱克曼窗计算所需的滤波器长度N0N=N0+mod(N0+1,2);%为了实现第一类偶对称滤波器,应确保其长度N为奇数n=[0:1:N-1];wc=(wst+wp)/2;%截止频率取为两边缘频率的平均值hd=ideallp(wc,N);%求理想脉冲响应wdbla=(blackman(N))';%求窗函数h=hd.*wdbla;%设计的脉冲响应应为理想脉冲响应与窗函数乘积[db,mag,pha,grd,w]=myfreqz(h,[1]);%对设计结果进行检验dw=2*pi/2000;%频率分辨率Rp=-(min(db(1:wp/dw+1)))%检验通带波动As=-round(max(db(wst/dw+1:501)))%检验最小阻带衰减figure(1)subplot(2,2,1);stem(n,wdbla);title('布莱克曼窗')%绘制布莱克曼窗函数axis([0 N-1 0 1.1]);ylabel('w(n)');text(N+1,0,'n')subplot(2,2,2);stem(n,h);title('实际脉冲响应')%绘制实际脉冲响应axis([0 N-1 -0.4 0.5]);xlabel('n');ylabel('h(n)')subplot(2,2,3);plot(w/pi,db);%绘制幅度响应title('幅度响应(单位:dB)');grid;xlabel('频率(单位: pi)');ylabel('分贝数')axis([0 1 -150 10]);set(gca,'XTickMode','manual','XTick',[0,0.2,0.35,0.65,0.8,1])set(gca,'YTickMode','manual','YTick',[-60,0])n=0:6000;k=n/2000;f1=2*pi*350;f2=2*pi*600;x=sin(f1*k)+sin(f2*k);y=filter(h,[1],x);x1=sin(f1*k);x2=sin(f2*k);figure(2)subplot(2,2,1);plot(x1);title('x1的图形');grid;axis([0 100*pi -5 5]);ylabel('x1');subplot(2,2,2);plot(x2);title('x2的图形');grid;axis([0 100*pi -5 5]);ylabel('x2)');subplot(2,2,3);plot(x);title('x的图形');grid;axis([0 100*pi -5 5]);ylabel('x');subplot(2,2,4);plot(y);title('y的图形'); grid;axis([0 100*pi -5 5]);ylabel('y');。
武汉理工大学 基于矩形窗、三角窗、海明窗、汉宁窗、布拉克曼窗的FIR数字滤波器设计

1.基于矩形窗的FIR数字低通滤波器设计参数如下:主程序:% 基于矩形窗的FIR数字低通滤波器设计wp=2*pi*1.75/15;ws=2*pi*3.25/15w=(wp+ws)/2;N=ceil(4*pi/(ws-wp));n=0:1:(N-1);alpha=(N-1)/2;m=n-alpha+eps;hd=sin(w*m)./(pi*m); %得到理想低通滤波器 B=boxcar(N);string=['Boxcar,N=',num2str(N)];h=hd.*(B)'; %得到FIR数字滤波器[H,w]=freqz(h,[1],1024); %求其频率响应db=20*log10(abs(H)+eps); %得到幅值pha=angle(H); %得到相位figure(1);subplot(2,2,1);stem(n,h,'r');axis([0,N-1,-0.1,0.35]);xlabel('n');ylabel('h(n)');title('实际低通滤波器的h(n)');text((0.3*N),0.275,string);subplot(2,2,2);plot(w/pi,db,'r');axis([0,1,-100,5]);xlabel('w/pi');ylabel('dB');title('衰减特性(dB)');grid;subplot(2,2,3);plot(w,pha);hold on;plot(0:4,zeros(5),'k');title('相频特性');xlabel('频率(rad)');ylabel('相位(rad)');axis([0,3.2,-4,4]);subplot(2,2,4);plot(w,abs(H));title('频率特性');xlabel('频率W(rad)');ylabel('幅值');axis([0,3.15,0,1.5]);text(0.9,1.3,string);2.基于矩形窗的带通滤波器的设计参数如下:子程序:function hd=ideal_bs(Wcl,Wch,N)alpha=(N-1)/2;n=0:1:N-1;m=n-alpha+eps;hd=[sin(Wch*m)-sin(Wcl*m)]./(pi*m);function hd=ideal_bs(Wcl,Wch,N)alpha=(N-1)/2;n=0:1:N-1;m=n-alpha+eps;hd=[sin(Wch*m)-sin(Wcl*m)]./(pi*m);主程序:clear all;Wph=2*pi*4.75/15;Wpl=2*pi*2.5/15;Wsl=2*pi/15;Wsh=2*pi*6.25/15;tr_width=min((Wpl-Wsl),(Wsh-Wph)); %过渡带宽度N=ceil(4*pi/tr_width); %滤波器长度n=0:1:N-1;Wcl=(Wsl+Wpl)/2; %理想滤波器的截止频率Wch=(Wsh+Wph)/2;hd=ideal_bs(Wcl,Wch,N); %理想滤波器的单位冲击响应w_ham=(boxcar(N))';string=['矩形窗','N=',num2str(N)];h=hd.*w_ham; %截取取得实际的单位脉冲响应[db,mag,pha,w]=freqz_m2(h,[1]); %计算实际滤波器的幅度响应subplot(3,2,1);stem(n,hd);title('理想脉冲响应hd(n)')axis([-1,N,-0.5,0.8]);xlabel('n');ylabel('hd(n)');subplot(3,2,2);stem(n,w_ham);axis([-1,N,0,1.1]);xlabel('n');ylabel('w(n)');text(1.5,1.3,string);subplot(3,2,3);stem(n,h);title('实际脉冲响应h(n)');axis([0,N,-1.4,1.4]);xlabel('n');ylabel('h(n)');subplot(3,2,4);plot(w,pha);title('相频特性');axis([0,3.15,-4,4]);xlabel('频率(rad)');ylabel('相位(?)');subplot(3,2,5);plot(w/pi,db);title('幅度特性(dB)');axis([0,1,-80,10]);xlabel('频率(pi)');ylabel('分贝数');subplot(3,2,6);plot(w,mag);title('频率特性')axis([0,3.15,0,1.5]);xlabel('频率(rad)');ylabel('幅值');fs=15000;t=(0:100)/fs;x=sin(2*pi*t*750)+sin(2*pi*t*5000)+sin(2*pi*t*6100); q=filter(h,1,x);[a,f1]=freqz(x);f1=f1/pi*fs/2;[b,f2]=freqz(q);f2=f2/pi*fs/2;figure(2);subplot(2,1,1);plot(f1,abs(a));title('输入波形频谱图');xlabel('频率');ylabel('幅度')subplot(2,1,2);plot(f2,abs(b));title('输出波形频谱图');xlabel('频率');ylabel('幅度')3.基于矩形窗的FIR数字带阻滤波器设计参数:主程序:clear all;Wph=2*pi*6.25/15;Wpl=2*pi/15;Wsl=2*pi*2.5/15;Wsh=2*pi*4.75/15;tr_width=min((Wsl-Wpl),(Wph-Wsh));%过渡带宽度N=ceil(4*pi/tr_width);%滤波器长度n=0:1:N-1;Wcl=(Wsl+Wpl)/2;%理想滤波器的截止频率Wch=(Wsh+Wph)/2;hd=ideal_bs(Wcl,Wch,N);%理想滤波器的单位冲击响应w_ham=(boxcar(N))';string=['矩形窗','N=',num2str(N)];h=hd.*w_ham;%截取取得实际的单位脉冲响应[db,mag,pha,w]=freqz_m2(h,[1]);%计算实际滤波器的幅度响应delta_w=2*pi/1000;subplot(3,2,1);stem(n,hd);title('理想脉冲响应hd(n)')axis([-1,N,-0.5,0.8]);xlabel('n');ylabel('hd(n)');subplot(3,2,2);stem(n,w_ham);axis([-1,N,0,1.1]);xlabel('n');ylabel('w(n)');text(1.5,1.3,string);subplot(3,2,3);stem(n,h);title('实际脉冲响应h(n)');axis([0,N,-1.4,1.4]);xlabel('n');ylabel('h(n)');subplot(3,2,4);plot(w,pha);title('相频特性');axis([0,3.15,-4,4]);xlabel('频率(rad)');ylabel('相位(Φ)'); subplot(3,2,5);plot(w/pi,db);title('幅度特性(dB)');axis([0,1,-80,10]);xlabel('频率(pi)');ylabel('分贝数'); subplot(3,2,6);plot(w,mag);title('频率特性')axis([0,3,0,2]);xlabel('频率(rad)');ylabel('幅值');fs=15000;t=(0:100)/fs;x=sin(2*pi*t*750)+sin(2*pi*t*3000)+sin(2*pi*t*6100);q=filter(h,1,x);[a,f1]=freqz(x);f1=f1/pi*fs/2;[b,f2]=freqz(q);f2=f2/pi*fs/2;figure(2);subplot(2,1,1);plot(f1,abs(a));title('输入波形频谱图');xlabel('频率');ylabel('幅度')subplot(2,1,2);plot(f2,abs(b));title('输出波形频谱图');xlabel('频率');ylabel('幅度');调用程序1:function hd=ideal_bs(Wcl,Wch,m);alpha=(m-1)/2;n=[0:1:(m-1)];m=n-alpha+eps;hd=[sin(m*pi)+sin(Wcl*m)-sin(Wch*m)]./(pi*m)调用程序2:function[db,mag,pha,w]=freqz_m2(b,a)[H,w]=freqz(b,a,1000,'whole');H=(H(1:1:501))'; w=(w(1:1:501))';mag=abs(H);db=20*log10((mag+eps)/max(mag));pha=angle(H);4.基于三角窗的FIR数字高通滤波器设计参数:子程序:function hd=ideal_hp1(Wc,N)alpha=(N-1)/2;n=0:1:N-1;m=n-alpha+eps;%hd=[sin(pi*m)-sin(Wc*m)]/(pi*m);hd=[sin(pi*m)-sin(Wc*m)]./(pi*m);function[db,mag,pha,w]=freqz_m2(b,a)[H,w]=freqz(b,a,1000,'whole');H=(H(1:1:501))';w=(w(1:1:501))';mag=abs(H);db=20*log10((mag+eps)/max(mag));pha=angle(H);主程序:clear all; Ws=6.5/15*piWp=3.5/15*pitr_width=Ws-Wp;%过渡带宽度N=ceil(8*pi/tr_width);%滤波器长度n=0:1:N-1;Wc=(Ws+Wp)/2;%理想滤波器的截止频率hd=ideal_hp1(Wc,N);%理想滤波器的单位冲击响应w_ham=(triang(N))'; string=['三角窗','N=',num2str(N)];h=hd.*w_ham;%截取得到的实际的单位脉冲响应[db,mag,pha,w]=freqz_m2(h,[1]);%计算实际滤波器的幅度响应delta_w=2*pi/1000;Ap=-(min(db(Ws/delta_w+1:1:501)));%实际通带波纹As=-round(max(db(1:1:Wp/delta_w+1)));%实际阻带波纹subplot(3,2,1);stem(n,hd);title('理想脉冲响应hd(n)');axis([0,N-1,-0.5,0.5]);xlabel('n');ylabel('hd(n)'); subplot(3,2,2);stem(n,w_ham);axis([0,N-1,0,1.1]);xlabel('n');ylabel('w(n)');text(1.5,1.3,string);subplot(3,2,3);stem(n,h);title('实际脉冲响应hd(n)');axis([0,N,-1.4,1.4]);xlabel('n');ylabel('hd(n)');subplot(3,2,4);plot(w,pha);title('想频特性');axis([0,3.15,-4,4]);xlabel('频率(pi)');ylabel('相位(o)'); subplot(3,2,5);plot(w/pi,db);title('幅度特性(dB)');axis([0,1,-100,10]);xlabel('频率(pi)');ylabel('(分贝数)'); subplot(3,2,6);plot(w,mag);title('频率特性');axis([0,2.95,0,1.5]);xlabel('频率(rad)');ylabel('幅值');fs=12000;t=(0:100)/fs;x=sin(2*pi*t*750)+sin(2*pi*t*1500)+sin(2*pi*t*3000);q=filter(h,1,x);[a,f1]=freqz(x);f1=f1/pi*fs/2;[b,f2]=freqz(q);f2=f2/pi*fs/2;figure(2);subplot(2,1,1);plot(f1,abs(a));title('输入波形频谱图');xlabel('频率');ylabel('幅度')subplot(2,1,2);plot(f2,abs(b));title('输出波形频谱图');xlabel('频率');ylabel('幅度')检验程序:用含多种频率成份离散时间信号作输入信号,得到通过滤波器后与输出信号的对比结果fs=20000;t=(0:100)/fs;x=sin(2*pi*t*1500)+sin(2*pi*t*4000)+sin(2*pi*t*8000);%输入信号 q=filter(h,1,x);%滤波处理,得到输出信号[a,f1]=freqz(x);f1=f1/pi*fs/2;[b,f2]=freqz(q);f2=f2/pi*fs/2;figure(2);subplot(2,1,1);plot(f1,abs(a));title('输入波形频谱图');xlabel('频率');ylabel('幅度');subplot(2,1,2);plot(f2,abs(b));title('输出波形频谱图');xlabel('频率');ylabel('幅度')图形示例:低通部分检验图形:低通部分。
用窗函数法设计FIR数字低通滤波器要点

河北科技大学课程设计报告学生姓名: 学号:专业班级:课程名称:学年学期指导教师:20年月课程设计成绩评定表目录1. 窗函数设计低通滤波器1.1设计目的 (1)1.2设计原理推导与计算 (1)1.3设计内容与要求 (2)1.4设计源程序与运行结果 (3)1.5思考题……………………………………………………………………101.6心得体会 (14)参考文献……………………………………………………………………… 151.窗函数设计低通滤波器1.1设计目的1. 熟悉设计线性相位数字滤波器的一般步骤。
2. 掌握用窗函数法设计FIR 数字滤波器的原理和方法。
3. 熟悉各种窗函数的作用以及各种窗函数对滤波器特性的影响。
4. 学会根据指标要求选择合适的窗函数。
1.2设计原理推导与计算如果所希望的滤波器的理想的频率响应函数为()ωj d e H ,则其对应的单位脉冲响应为()()ωπωωππd e e H n h j j d d ⎰-=21 (4.1)窗函数设计法的基本原理是设计设计低通FIR 数字滤波器时,一般以理想低通滤波特性为逼近函数()ωj e H ,即()⎪⎩⎪⎨⎧≤<≤=-πωωωωωαωc c j jd ,,e e H 0,其中21-=N α()()()[]()a n a n d e e d e eH n h c j j j j d d cc--===⎰⎰---πωωπωπωαωωωαωππωsin 2121用有限长单位脉冲响应序列()n h 逼近()n h d 。
由于()n h d 往往是无限长序列,而且是非因果的,所以用窗函数()n ω将()n h d 截断,并进行加权处理,得到:()()()n n h n h d ω=(4.2)()n h 就作为实际设计的FI R数字滤波器的单位脉冲响应序列,其频率响应函数()ωj e H 为()()nj N n j en h eH ωω∑-==1ﻩ ﻩ(4.3)式中,N 为所选窗函数()n ω的长度。
使用布莱克曼窗设计的FIR滤波器正文

使用布莱克曼窗设计的FIR滤波器正文布莱克曼窗(Blackman window)是一种常用于信号处理中的窗函数。
在设计FIR滤波器时,窗函数用于减小信号在滤波器频率响应两侧的泄漏效应,并使滤波器的频率响应能够更好地接近于所需的频率响应。
FIR滤波器是一种数字滤波器,由有限个数量的线性时不变系统相连接而成,因此其频率响应是离散的。
FIR滤波器的设计中,通过选择合适的滤波器特性和频率响应来实现信号的滤波。
而窗函数则作为FIR滤波器设计的一部分,用于对滤波器的频率响应进行调整。
布莱克曼窗是一种常用的窗函数,具有良好的频谱特性。
它的形式为:w(n) = 0.42 - 0.5cos(2πn/(N-1)) + 0.08cos(4πn/(N-1))其中,n为窗函数中的采样点的索引,N为窗函数的长度。
在FIR滤波器的设计中,首先确定所需的频率响应,然后根据频率响应的形状选择一个合适的窗函数。
布莱克曼窗通常用于需要较小的波纹和较宽的主瓣宽度的滤波器设计中。
通过使用布莱克曼窗,可以减小滤波器的过渡带宽度,并且主瓣的振幅变化相对较小。
在具体应用中,FIR滤波器的设计通常是一个迭代的过程。
首先,根据所需的频率响应确定滤波器的理想幅度响应。
然后,使用窗函数对理想幅度响应进行加权,得到实际的频率响应。
最后,通过对频率响应进行快速傅里叶变换(FFT)等处理得到滤波器的系数。
而布莱克曼窗作为一种窗函数,可以通过计算窗函数的数学表达式并应用到滤波器设计的实际过程中。
总结起来,布莱克曼窗是一种常用的窗函数,广泛应用于FIR滤波器的设计中。
通过使用布莱克曼窗,可以调整滤波器的频率响应,减小滤波器频率响应两侧的泄漏效应,并使滤波器的频率响应能够更好地接近所需的频率响应。
在具体的应用中,布莱克曼窗可以通过计算其数学表达式并应用到滤波器设计的过程中来实现。
matlab用布莱克曼窗设计fir滤波器代码

matlab用布莱克曼窗设计fir滤波器代码如何使用Matlab设计带有布莱克曼窗的FIR滤波器。
布莱克曼窗是一种用于设计数字滤波器的常见窗函数之一。
它具有非常好的频域特性,可以用于实现各种滤波器,比如低通、高通、带通、带阻等。
在本文中,我们将详细介绍如何使用Matlab来设计带有布莱克曼窗的FIR 滤波器。
步骤1:确定设计规格在设计FIR滤波器之前,我们首先需要确定滤波器的一些规格,如滤波器的类型(低通、高通等)、截止频率、阶数等。
这些规格将决定最终滤波器的性能。
假设我们要设计一个低通滤波器,截止频率为0.2,阶数为50。
步骤2:计算滤波器系数使用Matlab的fir1函数可以计算出FIR滤波器的系数。
该函数的使用语法如下:h = fir1(N, Wn, window)其中,N表示滤波器的阶数,Wn表示归一化的截止频率,window表示所采用的窗函数。
对于布莱克曼窗,我们可以使用matlab中的blackman函数来生成窗函数:window = blackman(N+1)在这里,我们需要注意一个细节:由于Matlab的fir1函数使用的是双边频率表示法,而我们通常使用的是单边频率表示法。
因此,我们需要将截止频率进行一些处理,将其从正常范围[0, 0.5]映射到[-0.5, 0.5]上。
Wn = 2 * 0.2完成上述计算后,我们可以编写Matlab代码如下:N = 50;Wn = 2 * 0.2;window = blackman(N+1);h = fir1(N, Wn, window);步骤3:绘制滤波器的频率响应为了验证我们设计的滤波器效果,我们可以绘制其频率响应。
使用freqz 函数可以绘制滤波器的幅频特性:freqz(h,1)上述代码将绘制出滤波器的振幅响应和相位响应。
步骤4:应用滤波器完成滤波器的设计后,我们可以将其应用于信号上。
假设我们有一个需要滤波的信号x,我们可以使用filter函数实现滤波效果:y = filter(h, 1, x)其中,x表示输入信号,y表示输出信号。
巴特沃斯低通滤波器和基于凯塞窗的FIR滤波器设计以及布莱克曼窗(三阶升余弦窗)的FIR滤波器

数字信号处理作业设计报告姓名:李文娟学号:2009124042专业:计算机应用学院:信息工程学院2009 年1月8 号数字信号处理作业设计报告一、目的1.增进对MATLAB的认识,加深对数字信号处理理论方面的理解。
2.掌握数字信号处理中IIR和FIR滤波器的设计。
3.了解和掌握用MATLAB实现IIR和FIR滤波器的设计方法、过程,为以后的设计打下良好基础。
二、数字信号处理课程设计1.IIR(无限脉冲响应)模拟滤波器设计(1)设计题目:巴特沃斯型模拟低通滤波器设计(2)设计要求:(通带最大衰减Rp=1,阻带最小衰减Rs=40,通带边界频率Wp=1000hz,阻带边界频率Ws=5000hz,滤波器类型:巴特沃斯低通滤波器)(3)设计原理:①根据要求选择滤波器参数②通过公式计算过渡比:PS KΩ=Ω偏离参数:1K=滤波器的阶数:1lglgK NK =3dB 截止频率:Butterworth 模拟低通滤波器221()1a Nc H j Ω=⎛⎫Ω+ ⎪Ω⎝⎭幅度平方函数:其中,N 为滤波器的阶数,c Ω为通带截止频率。
(4)Matlab 源程序:wp=2*pi*1000; ws=2*pi*5000; Rp=1; As=40;[N,wc]=buttord(wp,ws,Rp,As,'s') %巴特沃斯模拟低通滤波器阶数和3db 截止频率 [B,A]=butter(N,wc,'s') %计算巴特沃斯模拟低通滤波器系统函数中分子和分母的系数向量 freqs(B,A); % 绘出系统的幅频特性和相频特性曲线(5)结果和仿真波形: 结果:N = 4 wc =9.9347e+003 B =1.0e+015 *0 0 0 0 9.7414 A =1.0e+015 *0.0000 0.0000 0.0000 0.0026 9.7414仿真波形:2.IIR (无限脉冲响应)数字滤波器设计 (1)设计题目:巴特沃斯型数字低通滤波器(2)设计要求:(通带最大衰减rp=3db ,阻带最小衰减rs=20db ,通带边界频率fp=100hz ,阻带边界频率fs=300hz ,采样频率Fs=1khz )(3)设计原理:IIR 数字滤波器的系统函数为1z -的有理分式:1011()1Nk k N k k b zH z a z -=-==+∑∑设计IIR 滤波器的系统函数,就是要确定()H z 的阶数N 及分子分母多项式的系数ka 和kb ,使其()()j j z e H e H z ωω==满足指定的频率特性。
matlab窗函数法设计带通滤波器

matlab窗函数法设计带通滤波器在MATLAB中,可以使用窗函数法设计数字滤波器。
窗函数方法是一种基于时域设计技术,通过在滤波器的脉冲响应上乘以一个窗函数,从而改变其频率特性。
这种方法不需要进行频域变换,因此在计算上具有一定的简便性。
下面将详细介绍如何使用MATLAB实现带通滤波器的设计。
带通滤波器的目标是在给定的频率范围内传递信号,并在其他频率上进行衰减。
通常,设计带通滤波器的步骤如下:1. 确定滤波器的通带频率范围和截止频率。
通带是需要通过的频率范围,而截止频率是指在此频率以上或以下信号进行衰减。
2. 根据通带和截止频率选择合适的滤波器类型。
常见的滤波器类型包括Butterworth滤波器、Chebyshev滤波器和椭圆滤波器等。
3. 根据滤波器类型和要求的频率响应,确定滤波器的阶数。
滤波器的阶数决定了滤波器的频率选择性能。
4. 选择一个合适的窗函数。
窗函数定义了滤波器的脉冲响应。
5. 使用MATLAB中的filter函数将得到的窗口脉冲响应应用于要进行滤波的信号。
下面假设我们要设计一个带通滤波器,通带频率范围为f1和f2,截止频率为f3和f4,并且设定了滤波器的阶数为N。
首先,我们需要选择合适的滤波器类型。
在MATLAB中,可以使用butter函数来设计Butterworth滤波器。
此函数的语法如下:[b, a] = butter(N, [f1, f2]/(Fs/2), 'bandpass')其中,N是滤波器的阶数,[f1, f2]是通带频率范围,Fs是采样频率。
然后,选择一个合适的窗函数,常用的窗函数包括矩形窗、汉宁窗、布莱克曼窗等。
可以使用MATLAB中的窗函数函数hamming生成汉宁窗。
例如,可以使用以下代码生成一个长度为N+1的汉宁窗:w = hamming(N+1)接下来,我们需要通过将窗函数应用于滤波器的点数响应来计算滤波器的系数。
可以使用MATLAB中的filter函数将窗口响应与滤波器的截止频率进行卷积。
数字信号处理课程设计---使用布莱克曼窗设计的FIR滤波器

语音信号滤波去噪——使用布莱克曼窗设计的FIR滤波器摘要本课程设计主要是用麦克风采集一段语音信号,绘制其波形并观察其频谱。
然后在该语言信号中加一个噪音,利用布莱克曼窗设计一个FIR滤波器,对该语音信号进行虑噪处理,然后比拟滤波前后的波形与频谱。
在本课程设计中,是用MATLAB的集成环境完成一系列的设计。
首先对加噪的语音信号进行虑波去噪处理,再比拟滤波前后的频率响应曲线,假设一样那么满足所设计指标,否那么不满足。
也可以调用函数sound听滤波前后其语音信号是否带有噪声。
假设无噪声也说明该滤波器的设置也是成功的。
关键词语音信号;MATLAB;FIR滤波器;滤波去噪;1 引言人们在语音通信的过程中将不可防止的会受到来自周围环境的干扰,例如传输媒介引入的噪声,通信设备内部的电噪声,乃至其他讲话者的话音等。
正因为有这些干扰噪声的存在,接受者接受到的语音已不是原始的纯洁语音信号,而是受噪声干扰污染的带噪声语音信号。
而本课程设计就是利用MATLAB集成环境用布莱克曼窗的方法设计一个FIR滤波器,对语音信号进行滤波去噪处理,并将虑噪前后的频谱图进行比照。
1.1 课程设计目的数字信号处理课程设计是数字信号处理课程的重要实践性环节,是学生在校期间一次较全面的工程师能力训练,在实现学生总体培养目标中占有重要地位。
综合运用本课程的理论知识进行频谱分析以及滤波器设计,通过理论推导得出相应结论,并利用MATLAB 作为编程工具进行计算机实现,从而复习稳固了课堂所学的理论知识,提高了对所学知识的综合应用能力,并从实践上初步实现了对数字信号的处理。
本课程设计能使学生对通信工程领域各种技术的DSP实现的设计有较熟练的掌握。
且通过自身的实践,对DSP的设计程序、内容和方法有更深入的掌握,提高实际运用的能力。
并可综合运用这些知识解决一定的实际问题,使学生在所学知识的综合运用能力上以及分析问题、解决问题能力上得到一定的提高。
〔1〕、录制一段个人自己的语音信号,并对录制的信号进行采样,画出采样后语音信号的时域波形和频谱图。
用布莱克曼窗设计数字带通滤波器

福建农林大学金山学院信息工程系课程设计报告课程名称:数字信号处理课程设计题目:用布莱克曼窗设计数字带通滤波器姓名:系:信息与机电工程专业:电子信息工程年级:学号:指导教师:职称:年月日课程设计结果评定目录1课程设计的目的 (1)2课程设计的要求 (1)3课程设计报告内容 (1)3.1数字滤波器简介 (1)3.2 FIR滤波器的设计原理 (2)3.3窗函数法设计原理 (4)3.4用窗函数法设计FIR滤波器的步骤 (5)3.5设计题目及程序的代码 (6)3.6设计并用matlab仿真后的结果 (9)4总结 (10)用布莱克曼窗设计数字带通滤波器1.课程设计的目的通过自己设计并建立数字信号处理系统,掌握数字信号处理系统的的基本原理,加深对数字信号处理的认识,提高实际应用、动手能力。
学会使用MATLAB 仿真工具,使得计算机模拟实现对数字信号处理系统的仿真;掌握FIR滤波器的参数选择及设计方法;提高Matlab下的程序设计能力及综合应用能力;理解用窗函数设计数字滤波器的基本思想。
2.课程设计的要求1.巩固和加深对数字信号处理课程的基本知识的理解和掌握;2.提高综合运用所学的理论知识和方法独立分析和解决问题的能力;3.学会使用MATLAB,掌握MATLAB的程序设计方法;4.综合运用数字信号处理的基本理论,基本概念,基本方法进行频谱分析和IIR滤波器以及FIR滤波器的设计;5.了解和掌握用MATLAB实现IIR和FIR滤波器的设计方法、过程;6.设计的题目要求达到一定工作量,并具有一定的深度和难度;7.能独立编写出课程设计说明书,准确分析设计结果。
3.课程设计报告内容3.1 数字滤波器简介数字滤波器(Digital Filter)是由数字乘法器、加法器和延时单元组成的一种装置。
其功能是对输入离散信号的数字代码进行运算处理,以达到改变信号频谱的目的。
由于电子计算机技术和大规模集成电路的发展,数字滤波器已可用计算机软件实现,也可用大规模集成数字硬件实时实现。
FIR带通滤波器设计

1.2利用窗函数法设计FIR滤波器
1.2.1窗函数法设计FIR滤波器的基本思想
窗函数法的基本思想是要选取某一种合适的理想频率选择性滤波器,这种滤波器总是有一个非因果,无限长的脉冲响应,然后将它的脉冲响应截断(或加窗)以得到一个线性相位和因果的FIR滤波器,因为必须设计一个因果可实现的FIR滤波器[1]。
(5)布莱克曼窗
布莱克曼窗的幅度函数主要由五部分组成,他们的位移都不同,其幅度也是不同的W (w)使旁瓣再进一步抵消。旁瓣峰值幅度进一步增加,其幅度谱主瓣宽度是矩形窗的3倍。设计程序时用backman函数调用。
(6)凯塞窗
以上几种窗函数是各以一定主瓣加宽为代价,来换取某种程度的旁瓣抑制,窗函数的主瓣宽度和旁瓣峰值衰耗是矛盾的,一项指标的提高总是以另一项指标的下降为代价,窗口选择实际上是对两项指标作权衡。而两项指标是跳变的,于是有人提出可调整窗,适当修改参数,可在这两项指标间作连续的选择。常用的可调整窗是凯塞(Kaiser)窗。而凯窗则是全面地反映主瓣与旁瓣衰减之间的交换关系,可以在它们两者之间自由地选择它们的比重。
频带为F的连续信号 f(t)可用一系列离散的采样值f(t1),f(t1±Δt),f(t1±2Δt),...来表示,只要这些采样点的时间间隔Δt≤1/2F,便可根据各采样值完全恢复原来的信号f(t)。这是时域采样定理的一种表述方式。时域采样定理的另一种表述方式是:当时间信号函数f(t)的最高频率分量为fm时,f(t)的值可由一系列采样间隔小于或等于1/2fm的采样值来确定,即采样点的重复频率f≥2fm。
基于Blackman窗的FIR数字带通滤波器设计

课程设计课程设计名称:基于Blackman窗的FIR数字带通滤波器设计专业班级:学生姓名:学号:指导教师:课程设计时间: 2010.6.21-2010.6.25数字信号处理专业课程设计任务书说明:本表由指导教师填写,由教研室主任审核后下达给选题学生,装订在设计(论文)首页1 需求分析数字滤波器可以理解为是一个计算程序或算法,将代表输入信号的数字时间序列转化为代表输出信号的数字时间序列,并在转化过程中,使信号按预定的形式变化。
数字滤波器有多种分类,根据数字滤波器冲激响应的时域特征,可将数字滤波器分为两种,即无限长冲激响应(iir )滤波器和有限长冲激响应(fir )滤波器。
iir 数字滤波器具有无限宽的冲激响应,与模拟滤波器相匹配。
所以iir 滤波器的设计可以采取在模拟滤波器设计的基础上进一步变换的方法。
fir 数字滤波器的单位脉冲响应是有限长序列。
它的设计问题实质上是确定能满足所要求的转移序列或脉冲响应的常数问题,设计方法主要有窗函数法、频率采样法和等波纹最佳逼近法等。
因此设计FIR 滤波器的方法之一可以从时域出发,截取有限长的一段冲击响应作为H(z)的系数,冲击响应长度N 就是系统函数H(z)的阶数。
只要N 足够长,截取的方法合理,总能满足频域的要求。
一般这种时域设计、频域检验的方法要反复几个回合才能成功。
要设计一个线性相位的FIR 数字滤波器,首先要求理想频率响应)(jwd e H 。
)(jwd e H 是w 的周期函数,周期为π2,可以展开成傅氏级数:)(jwd e H =∑∞-∞=-n jwn de n h)(其中)(n h d 是与理想频响对应的理想单位抽样响应序列。
但不能用来作为设计FIR DF 用的h(n),因为)(n h d 一般都是无限长、非因果的,物理上无法实现。
为了设计出频响类似于理想频响的滤波器,可以考虑用h(n)来近似)(n h d 。
窗函数的基本思想:先选取一个理想滤波器(它的单位抽样响应是非因果、无限长的),再截取(或加窗)它的单位抽样响应得到线性相位因果FIR 滤波器。
吹管音乐滤波去噪用布拉克曼窗设计的FIR滤波器

《吹管音乐信号滤波去噪--使用布拉克曼窗设计的FIR滤波器》第1页共17页吹管音乐滤波去噪—用布拉克曼窗设计的FIR滤波器学生姓名:指导老师:胡双红摘要本课程设计的主要内容是利用布拉克曼窗设计一个FIR滤波器。
以MATLAB软件为平台,对一段加噪音乐信号进行滤波去噪处理并根据滤波前后的波形和频谱分析滤波性能。
首先从网上下载一段音乐信号,加入一单频噪声,然后设计滤波器进行滤波去噪处理,最后比较滤波前后的波形和频谱并进行分析。
通过分析结果,滤波后的音乐信号与原始信号基本一致,即设计的FIR滤波器能够去除信号中所加单频噪声,达到了设计目的。
关键词课程设计;滤波去噪;FIR滤波器;布拉克曼窗;MATLAB1 引言本课程设计主要是加噪音乐信号的滤波去噪处理。
从网站上下载一段吹管乐器演奏乐曲,绘制波形并观察其频谱特点,加入一个单频噪声,用布拉克曼窗设计一个满足指标的FIR滤波器,对该音乐信号进行滤波去噪处理,比较滤波前后波形和频谱并进行分析,根据结果和学过的理论得出合理结论。
1.1 课程设计目的《数字信号处理》课程设计目的在于让学生综合数字信号处理和MATLAB并实现一个较为完整的小型滤波系统。
这一点与验证性的基本实验有本质性的区别。
开设课程设计环节的主要目的是通过系统设计、软件仿真、程序安排与调试、写报告等步骤,使学生初步掌握工程设计的具体步骤和方法,提高分析问题和解决问题的能力,提高实际应用水平。
我们这次的课程设计就要运用MATLAB软件的帮助才能实现,最重要的是有利于态度的培养,在课程设计中,我们可能经常犯很多小错误,可能要通过反复修改、调试才能成功,但这种现象会随着学习的深入而慢慢改观。
这当中就有一个严谨治学、一丝不苟的科学精神的培养,还有一个不怕失败、百折不饶品格的锻炼。
1.2课程设计的要求(1)滤波器指标必须符合工程设计。
(2)设计完后应检查其频率响应曲线是否满足指标。
(3)处理结果和分析结论应该一致,而且应符合理论。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
福建农林大学金山学院信息工程系课程设计报告课程名称:数字信号处理课程设计题目:用布莱克曼窗设计数字带通滤波器姓名:系:信息与机电工程专业:电子信息工程年级:学号:指导教师:职称:年月日课程设计结果评定目录1课程设计的目的 (1)2课程设计的要求 (1)3课程设计报告内容 (1)3.1数字滤波器简介 (1)3.2 FIR滤波器的设计原理 (2)3.3窗函数法设计原理 (4)3.4用窗函数法设计FIR滤波器的步骤 (5)3.5设计题目及程序的代码 (6)3.6设计并用matlab仿真后的结果 (9)4总结 (10)用布莱克曼窗设计数字带通滤波器1.课程设计的目的通过自己设计并建立数字信号处理系统,掌握数字信号处理系统的的基本原理,加深对数字信号处理的认识,提高实际应用、动手能力。
学会使用MATLAB 仿真工具,使得计算机模拟实现对数字信号处理系统的仿真;掌握FIR滤波器的参数选择及设计方法;提高Matlab下的程序设计能力及综合应用能力;理解用窗函数设计数字滤波器的基本思想。
2.课程设计的要求1.巩固和加深对数字信号处理课程的基本知识的理解和掌握;2.提高综合运用所学的理论知识和方法独立分析和解决问题的能力;3.学会使用MATLAB,掌握MATLAB的程序设计方法;4.综合运用数字信号处理的基本理论,基本概念,基本方法进行频谱分析和IIR滤波器以及FIR滤波器的设计;5.了解和掌握用MATLAB实现IIR和FIR滤波器的设计方法、过程;6.设计的题目要求达到一定工作量,并具有一定的深度和难度;7.能独立编写出课程设计说明书,准确分析设计结果。
3.课程设计报告内容3.1 数字滤波器简介数字滤波器(Digital Filter)是由数字乘法器、加法器和延时单元组成的一种装置。
其功能是对输入离散信号的数字代码进行运算处理,以达到改变信号频谱的目的。
由于电子计算机技术和大规模集成电路的发展,数字滤波器已可用计算机软件实现,也可用大规模集成数字硬件实时实现。
数字滤波器广泛用于数字信号处理中,如电视、VCD、音响等。
数字滤波器是一个离散时间系统(按预定的算法,将输入离散时间信号转换为所要求的输出离散时间信号的特定功能装置)。
应用数字滤波器处理模拟信号时,首先须对输入模拟信号进行限带、抽样和模数转换。
数字滤波器输入信号的抽样率应大于被处理信号带宽的两倍,其频率响应具有以抽样频率为间隔的周期重复特性,且以折叠频率即1/2抽样频率点呈镜像对称。
为得到模拟信号,数字滤波器处理的输出数字信号须经数模转换、平滑。
数字滤波器具有高精度、高可靠性、可程控改变特性或复用、便于集成等优点。
数字滤波器在语言信号处理、图像信号处理、医学生物信号处理以及其他应用领域都得到了广泛应用。
数字滤波器有低通、高通、带通、带阻等类型。
它可以是时不变的或时变的、因果的或非因果的、线性的或非线性的。
应用最广的是线性、时不变数字滤波器。
3.2 FIR 滤波器的设计原理滤波器的单位脉冲响应h(n)长度为N ,那么 H(z)是z-1 的N-1次多项式(FIR 滤波器的阶数是N-1)该系统在z 平面上有N-1个零点,在z=0处有一个N-1重极点。
系统永远稳定。
1. 线性相位FIRDF设FIRDF 的单位脉冲响应h (n )长度为N ,则其频率响应函数为H (e j ω)=Hg (ω)ej θ(ω) 式中, Hg (ω)称为幅度特性函数,是ω的实函数(可以取负值),与| H (e jω) |不同;θ(ω)称为相位特性函数。
2. 线性相位条件对FIRDF 时域约束10()()N nn H z h n z --==∑()()N j j n n H e h n e ωω--==∑103.线性相位FIR滤波器幅度特性H g(ω)的特点h(n)对称性h(n)长度N幅度函数Hg(ω)相位特性θ(ω)可以设计的滤波器类型第一类线性相位偶对称奇数ω=0, π, 2π三点偶对称四种滤波器都可设计第一类线性相位偶对称偶数关于ω=π奇对称,关于ω=0, 2π偶对称不能实现高通和带阻滤波特性。
第二类线性相位奇对称奇数ω=0, π, 2π三点奇对称只能设计带通滤波器第二类线性相位奇对称偶数关于ω=π偶对称,关于ω=0, 2π奇对称可设计高通、带通滤波器,不能设计低通和带阻12Nω--12Nω--12Nω--1/22Nπω---1/22Nπω---线性相位FIR 数字滤波器的零点分布特点3.3 窗函数法设计原理一个理想数字滤波器的频率响应为Hd(ej ω),对应的时域序列为滤波器的单位脉冲响应hd(n),是无限长非因果的。
设计FIR-DF 就是要设计一个数字系统,去逼近理想数字滤波器的频率响应为Hd(ej ω)。
窗函数法就是对无限长的hd(n)加窗(用窗函数与之相乘,从而使之变成有限长的)下面主要介绍课程设计中用到的布莱克曼窗。
其频谱函数为:线性相位FIR 数字滤波器的零点分布)(1π4cos 08.01π2cos 5.042.0)(Bl n R N n N n n N ⎥⎦⎤⎢⎣⎡-+--=ω⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+-=⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛--)()()(1π4j R 1π4j R 1π2j R 1π2j R j R j Bl e e 04.0 e )e (25.0)e (42.0)e (N N N N W W W W W W ωωωωωω3.4 用窗函数法设计FIR 滤波器的步骤(1) 选择窗函数类型和长度,写出窗函数w (n )表达式。
根据阻带最小衰减选择窗函数w (n )的类型,再根据过渡带宽度确定所选窗函数的长度N。
(2) 构造希望逼近的频率响应函数H d(ej ω)。
布莱克曼窗的四种波形其幅度函数为这样其幅度函数由五部分组成。
它们都是移位不同,且幅度也不同的Wrg(w)函数,使旁瓣再进一步抵消。
旁瓣峰值幅度进一步增加,其幅度谱主瓣宽度是矩形窗的3倍。
布莱克曼窗的四种波形如下图所示。
参数为:α n=-57 dB;ΔB =12π/N ;α s=-74 dB 。
⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-++⎪⎭⎫ ⎝⎛--+⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-++⎪⎭⎫ ⎝⎛--+=1π41π404.0 1π21π225.0)(42.0)(Rg Rg Rg Rg Rg Blg N W N W N W N W W W ωωωωωωj j (1)/2d dg (e )()eN H H ωωω--=c dg c 1 ||()0 ||πH ωωωωω≤⎧=⎨<≤⎩(3) 计算:或者可以直接写出低通单位脉冲响应(4) 加窗得到设计结果:h(n)=h d(n)w(n)3.5 设计题目及程序的代码用窗函数法设计数字带通滤波器:下阻带边缘:Ws1=0.2pi,As=60dB下通带边缘:Wp1=0.35pi,Rp=1dB 上通带边缘:Wp2=0.65pi,Rp=1dB上阻带边缘:Ws2=0.8pi,As=60dB根据窗函数最小阻带衰减的特性。
以及关参照窗函数的基本参数表,选择布莱克曼窗可达到75dB最小阻带衰减,其过渡带为11pi/N。
以下为用布莱克曼窗设计数字带通滤波器的程序代码:clear all;wp1=0.35*pi;wp2=0.65*pi;ws1=0.2*pi;ws2=0.8*pi;As=60;tr_width=min((wp1-ws1),(ws2-wp2)); %过渡带宽度M=ceil(11*pi/tr_width)+1 %滤波器长度M=75n=[0:1:M-1];wc1=(ws1+wp1)/2; %理想带通滤波器的下截止频率wc2=(ws2+wp2)/2; %理想带通滤波器的上截止频率hd=ideal_lp(wc2,M)-ideal_lp(wc1,M);w_bla=(blackman(M))'; %布莱克曼窗h=hd.*w_bla; %截取得到实际的单位脉冲响应[db,mag,pha,grd,w]=freqz_m(h,[1]); %计算实际滤波器的幅度响应delta_w=2*pi/1000;ωπππωω⎰-=deeHnh n jjdd)(21)(sin(())()()cdnh nnωαπα-=-Rp=-min(db(wp1/delta_w+1:1:wp2/delta_w)) %实际通带纹波As=-round(max(db(ws2/delta_w+1:1:501))) %实际通带纹波As=75%plotssubplot(2,2,1);stem(n,hd);title('ideal impulse response') %理想单位脉冲响应hd(n) axis([0 M-1 -0.4 0.5]);xlabel('n');ylabel('hd(n)')subplot(2,2,2);stem(n,w_bla);title('blackman window') %布莱克曼窗w(n)axis([0 M-1 0 1.1]);xlabel('n');ylabel('w(n)')subplot(2,2,3);stem(n,h);title('actual impulse response') %实际单位脉冲响应hd(n) axis([0 M-1 -0.4 0.5]);xlabel('n');ylabel('h(n)')subplot(2,2,4);plot(w/pi,db);axis([0 1 -150 10]);title('magnitude response in db'); %幅度响应(dB)grid;xlabel('frequence in pi units');ylabel('decibles')在设计过程中调用的子程序:function hd=ideal_lp(wc,M);%计算理想低通滤波器的脉冲响应%------------------------------------%[hd]=ideal_lp(wc,M)%hd=理想脉冲响应0到M-1%wc=截止频率% M=理想滤波器的长度%alpha=(M-1)/2;n=[0:1:(M-1)];m=n-alpha+eps; %加上一个很小的值eps避免除以0的错误情况出现hd=sin(wc*m)./(pi*m);以及function [db,mag,pha,grd,w]=freqz_m(b,a);%Modified version of freqz subroutine%-------------------------------------%[db,mag,pha,grd,w]=freqz_m(b,a);% db=Relative magnitude in dB computed over 0 to pi radians% mag=absolute magnitude computed over 0 to pi radians% pha=Phase response in radians over 0 to pi radians% grd=Group delay over 0 to pi radians% w=501 frequency samples between 0 to pi radians% b=numerator polynomial of H(z) (for FIR: b=h)% a=denominator polynomial of H(z) (for FIR: a=[1])%[H,w]=freqz(b,a,1000,'whole');H=(H(1:1:501))';w=(w(1:1:501))';mag=abs(H);db=20*log10((mag+eps)/max(mag)); pha=angle(H);grd=grpdelay(b,a,w);3.6 设计并用matlab仿真后的结果4.总结设计带通滤波器是首先要计算出过渡带。
