信号与系统习题集(郑君里)
郑君里《信号与系统》(第3版)(上册)(课后习题 绪 论)【圣才出品】

圣才电子书
(1) ut ut T sin 4π t ;
T
(2) ut 2ut T ut 2T sin 4π t 。
T
解:(1)信号 sin 4π t 的周期为 T ,截取信号 sin 4π t 在区间[0,T]上的波形如
T
2
T
图 1-5(a)所示。
(2)信号 sin 4π t 的周期为 T ,截取信号 sin 4π t 在区间[0,T]上的波形,在区
2
1-3 分别求下列各周期信号的周期 T:
(1) cos10t cos30t;
(2) e j10t ;
(3) 5sin8t2 ;
(4)
1n
ut
nT
ut
nT
T
n为正整数。
|
解:(1)分量 cos(10t) 的周期T1
2 10
5
,分量 cos(30t) 的周期T2
,两者的 15
最小公倍数是 ,所以此信号的周期T 。
eatu(t) 台eatu(t t0 ) eatu(t t0 ) ea(tt0 )u(t t0 )
eatu(t) ea(tt0 )u(t t0 )
(2)表达式(1-17)为
t
(f )d
1
=
a
(1 eat ), (0
t
t0 )
1 a
(1
e at
)
1 a
1
e a (tt0 )
以上各式中 n 为正整数。
解:(1) eat sin(t) 时间、幅值均连续取值,故为连续时间信号(模拟信号);
(2) enT 时间离散、幅值连续,故为离散时间信号(抽样信号);
(3) cos(n ) 时间、幅值均离散,故为离散时间信号(数字信号);
信号与系统-郑君里试题

《信号与系统》A 卷一、选择题(每题2 分,共10 分)1、连续线性时不变系统的单位冲激响应h t为系统的 ()A. 零输入响应B.零状态响应C.自由响应D.强迫响应2、如图所示的周期信号f t的傅立叶级数中所含的频率分量是()A .余弦项的偶次谐波,含直流分量B .余弦项的奇次谐波,无直流分量C .正弦项的奇次谐波,无直流分量D .正弦项的偶次谐波,含直流分量f(t)1t-3 -2 -112 33、瞬态响应分量应是 ( ) 。
A. 零输入响应的全部B.零状态响应的全部C. 全部的零输入响应和部分的零状态响应D.全部的零输入响应和全部的零状态响应4、如果两个信号分别通过系统函数为 H s 的系统后,得到相同的响应,那么这两个信号 ()A .一定相同B .一定不同C .只能为零D .可以不同5、已知系统微分方程为drt 2r te t ,若 r 01, e tsin 2t u t ,解得全响应为dtr t5e 2t2sin 2t, t0 。
全响应中2sin 2t为( )44 242A .零输入响应分量B .自由响应分量C .零状态响应分量D .稳态响应分量二、填空题(每题 3 分,共 30 分)1、t f t dt________________。
2、某一 LTI离 散 系 统 , 其 输 入 x n 和 输 出 y n 满足如下线性常系数差分方程,y( n)1y(n 1) x( n)1x( n 1) ,则系统函数 H z 是 ________________。
233、 t t 0 f t dt________________。
4、已知 f tF ( ) ,则 f 2t 的傅里叶变换为 ________________。
5、已知信号 f t 的傅立叶变换为 F ,则信号 f at t 0 的傅立叶变换为 ________________。
6、已知信号 f t 的拉普拉斯变换为 F s ,则信号 f t 的拉普拉斯变换为 ________________。
《信号与系统》(郑君里)课后习题答案
(t )
2
非线性:设 r1 ( t ) = e1
( t ) 、 r2 ( t ) = e2 2 ( t ) ,
2 2 2 2
则⎡ ⎣ c1e1 ( t ) + c2 e2 ( t ) ⎤ ⎦ = c1 e1 ( t ) + c2 e2
2
( t ) + 2c1c2e1 ( t ) e2 ( t ) ≠ c1r1 ( t ) + c2 r2 ( t )
5
即 输 入 x1 ( t ) , x2 ( t ) 得 到 的 输 出 分 别 为 y1 ( t ) , y2 ( t ) , T ⎡ ⎣ x1 ( t ) ⎤ ⎦ = y1 ( t ) ,
T⎡ 。 ⎣ x2 ( t ) ⎤ ⎦ = y2 ( t ) ,则 T ⎡ ⎣ c1 x1 ( t ) + c2 x2 ( t ) ⎤ ⎦ = c1 y1 ( t ) + c2 y2 ( t ) ( c1 , c2 为常数)
解题过程:
(a-1)
(a-2)
(a-3)
4
(a-4)
(b) f ( t ) 为偶函数,故只有偶分量,为其本身
(c-1)
(c-2)
(c-3)
(c-4)
(d-1)
(d-2)
(d-3)
(d-4)
1-20 分析过程:本题为判断系统性质:线性、时不变性、因果性 (1)线性(Linearity) :基本含义为叠加性和均匀性
f (t )
1 1
f ( 3t )
→
→
-2
-1
0
1
-2/3
f ( 3t − 2 )
→
1/3
f ( −3t − 2 )
信号与系统习题集(郑君里)

信号与系统习题答案(注:教材---郑君里编)习题一1-7 绘出下列各信号的波形:图a:[][]11()(2)(2)()(2)()(2)22f t t u t u t t u t u t =++-----[](1)(2)(2)2tu t u t =-+--图b:)2(2)1()()();2(4)]2()1([2)]1()([)(-+-+=-+---+--=t u t u t u t f t u t u t u t u t u t f图c :[])()()sin()(T t u t u t T E t f --=π1-12 绘出下列各时间函数的波形图,注意它们的区别: (1))]1()([--t u t u t ; (2))1(-t tu ; (3))1()]1()([-+--t u t u t u t ;)1(-tf(t)求f(-t),讨论图7(b)(c)(a)⇒ ⇒方法二:(1))()()(00t f dt t t t f -=-⎰∞∞-δ ;(2)⎰∞∞-=-)()()(00t f dt t t t f δ ;(3)1)2()2()(000==--⎰∞∞-tu dt t t u t t δ;(4)⎰∞∞-=-=--0)()2()(000t u dt t t u t t δ;(5)⎰∞∞---=++2)2()(2e dt t t e t δ;(6)2166sin6)6()sin (+=+=-+⎰∞∞-ππππδdt t t t ;(7)⎰∞∞----=--01)]()([0t j t j e dt t t t e ωωδδ ;1-15 电容C 1与C 2串联,以阶跃电压源v(t)=Eu(t)串联接入,试分别写出回路中的电流i(t)、每个电容两端电压vc 1(t)、vc 2(t)的表示式。
电路如图:2121c c c c +*=⇒电路电流)()(2121t E c c dt Ct i c δ+==)()(1)()()(1)(2112221211t u c c Ec dt t i c t v t u c c Ec dt t i c t v c c ⎰⎰+==+==1-20 判断下列系统是否为线性的、时不变的、因果的?(1)dt t de t r )()(=;(2))()()(t u t e t r = ;V C1(t) V C2(t)(3) )()](sin[)(t u t e t r = ; (4) )1()(t e t r -= ; (5) )2()(t e t r = ;(6))()(2t e t r = ;(7)⎰∞-=td e t r ττ)()( ;(8) ⎰∞-=td e t r 5)()(ττ 。
《信号与系统引论》(第二版)郑君里 课后题答案 客观题(附答案)

《信号与系统》复习参考练习题一、单项选择题:14、已知连续时间信号,)2(100)2(50sin )(--=t t t f 则信号t t f 410cos ·)(所占有的频带宽度为() A .400rad /s B 。
200 rad /s C 。
100 rad /s D 。
50 rad /sf如下图(a)所示,其反转右移的信号f1(t) 是()15、已知信号)(tf如下图所示,其表达式是()16、已知信号)(1tA、ε(t)+2ε(t-2)-ε(t-3)B、ε(t-1)+ε(t-2)-2ε(t-3)C、ε(t)+ε(t-2)-ε(t-3)D、ε(t-1)+ε(t-2)-ε(t-3)17、如图所示:f(t)为原始信号,f1(t)为变换信号,则f1(t)的表达式是()A、f(-t+1)B、f(t+1)C、f(-2t+1)D、f(-t/2+1)18、若系统的冲激响应为h(t),输入信号为f(t),系统的零状态响应是()19。
信号)2(4sin 3)2(4cos 2)(++-=t t t f ππ与冲激函数)2(-t δ之积为( )A 、2B 、2)2(-t δC 、3)2(-t δD 、5)2(-t δ,则该系统是()>-系统的系统函数.已知2]Re[,651)(LTI 202s s s s s H +++= A 、因果不稳定系统 B 、非因果稳定系统C 、因果稳定系统D 、非因果不稳定系统21、线性时不变系统的冲激响应曲线如图所示,该系统微分方程的特征根是( )A 、常数B 、 实数C 、复数D 、实数+复数22、线性时不变系统零状态响应曲线如图所示,则系统的输入应当是( )A 、阶跃信号B 、正弦信号C 、冲激信号D 、斜升信号23. 积分⎰∞∞-dt t t f )()(δ的结果为( )A )0(fB )(t f C.)()(t t f δ D.)()0(t f δ24. 卷积)()()(t t f t δδ**的结果为( )A.)(t δB.)2(t δC. )(t fD.)2(t f25. 零输入响应是( )A.全部自由响应B.部分自由响应C.部分零状态响应D.全响应与强迫响应之差 2A 、1-eB 、3eC 、3-eD 、127.信号〔ε(t)-ε(t -2)〕的拉氏变换的收敛域为 ( )A.Re[s]>0B.Re[s]>2C.全S 平面D.不存在28.已知连续系统二阶微分方程的零输入响应)(t y zi 的形式为t t Be Ae 2--+,则其2个特征根为() A 。
信号与系统习题答案(注教材---郑君里编)

《信号与系统》课程习题与解答第三章习题(教材上册第三章p160-p172)3-1~3-3,3-5,3-9,3-12,3-13,3-15~3-17,3-19,3-22,3-24,3-25,3-29,3-32第三章习题解答3-2 周期矩形信号如题图3-2所示。
若:求直流分量大小以及基波、二次和三次谐波的有效值。
解:直流分量 ⎰⎰--=⨯==2222301105)(1ττv Edt dt t f T a TTf(t)为偶函数,∴0=nb)(2cos )(222T n Sa T E tdt n t f T a n πττωττ⎰-== )(21T n Sa T E a F n n πςτ==基波 =1a )1.0s i n (20)(2πππττ=T Sa T E有效值 39.11.0sin 22021≈=ππa二次谐波有效值 32.122≈a三次谐波有效值 21.123≈a3-3 若周期矩形信号)(1t f 和 )(2t f 波形如题图3-2所示,)(1t f 的参数为s μτ5.0=,s T μ1=,E=1V ;)(2t f 的参数为s μτ5.1=,s T μ3=,E=3V ,分别求:(1))(1t f 的谱线间隔和带宽(第一零点位置),频率单位以kHz 表示; (2))(2t f 的谱线间隔和带宽; (3) )(1t f 和 )(2t f 的基波幅度之比; (4) )(1t f 基波与)(2t f 三次谐波幅度之比。
解:(1))(1t f s μτ5.0= s T μ1= E=1V 谱线间隔:khZ T 10001==∆带宽:KHzB f 20001==τ(2) )(2t f s μτ5.1= s T μ3= E=3V间隔:khZ T 310001==∆谱线带宽:KHzB f 320001==τ(3) )(1t f 基波幅度:ππτ2)2cos(4201==⎰dt t T E T a )(2t f 基波幅度:ππτ6)2cos(4201==⎰dt t T E T a幅度比:1:3(4) )(2t f 三次谐波幅度:ππτ2)23cos(4203-=⨯=⎰dt t T E T a 幅度比:1:13-5 求题图3-5所示半波余弦信号的傅立叶级数。
郑君里信号与系统习题答案

第三章 傅里叶变换一.周期信号的傅里叶级数二.傅里叶变换例题•例题1:傅里叶级数——频谱图 •例题2:傅里叶变换的性质 •例题3:傅里叶变换的定义 •例题4:傅里叶变换的性质 •例题5:傅里叶变换的性质 •例题6:傅里叶变换的性质•例题7:傅里叶变换的性质、频响特性 •例题8:傅里叶变换的性质 •例题9:抽样定理–例题10:周期信号的傅里叶变换例3-1 周期信号 1. 画出单边幅度谱和相位谱;()⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛++=328cos 265sin cos 3ππt t t t f 形式频谱:离散性、谐波性、收敛性 周期矩形脉冲信号的频谱特点定义及傅里叶变换存在的条件 典型非周期信号的频谱冲激函数和阶跃信号的傅里叶变换 性质→应用:调制和解调→频分复用 周期信号的傅里叶变换:由一些冲激函数组成 抽样信号的傅里叶变换→抽样定理→应用:时分复用2. 画出双边幅度谱和相位谱。
单边幅度谱和相位谱双边幅度谱和相位谱例3-2 分析:f (t )不满足绝对可积条件,故无法用定义求 其傅里叶变换,只能利用已知典型信号的傅里叶 变换和性质求解。
下面用三种方法求解此题。
方法一:利用傅里叶变换的微分性质 方法二:利用傅里叶变换的积分性质 方法三:线性性质方法一:利用傅里叶变换的微分性质要注意直流,设f A(t )为交流分量,f D(t )为直流分量,则 其中()⎪⎭⎫⎝⎛+-+⎪⎭⎫ ⎝⎛-++=ππππ328cos 2265cos cos 3t t t t f ⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛-+=38cos 2315cos cos 3ππt t t()。
的傅里叶变换求信号 )(ωF t f ()()()t f t f t f D A +=()()()ωωωD A F F F +=()()()[]2321=∞+∞-=f f t f D ()()ωπδω3=D F ()()t f t f A'='()⎪⎭⎫ ⎝⎛-='211t G t f A ()ωωωωj Ae F j -⎪⎭⎫ ⎝⎛=∴2Sa方法二:利用傅里叶变换的积分性质方法三:利用线性性质进行分解此信号也可以利用线性性质进行分解,例如例3-3已知信号f (t )波形如下,其频谱密度为F (j ω),不必求出F (j ω)的表达式,试计算下列值:()ωωωωj e F j A -⎪⎭⎫⎝⎛=∴2Sa ()()()()ωπδωωωωωω32Sa +⎪⎭⎫ ⎝⎛=+=∴-j e F F F j DA ())(11t f t f +=的积分为)()(21t f t f ()ωωωj e F -⎪⎭⎫ ⎝⎛=2Sa 2()()()ωωωπωωωπωωωj e e j F j j --⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛⎥⎦⎤⎢⎣⎡+=∴2Sa 2Sa 11 ()[]()()ωωωπδωωωj e F F F j -⎪⎭⎫ ⎝⎛+=+=∴2Sa 311()[])1(2)1()()1()(-+--++-=t u t u t u t t u t f ()ωωπδj 1-()2121ωωωωωj e e j j j j ---+-()ωωωπδj e j -+22()()()ωπδωωω312+-=∴-j e F j ()()01=ωωF ()()⎰∞∞-ωωd 2F -t tj d ω(()⎰∞-====∴5.1d 00t t f F F ωω令t =0,则 则例3-4按反褶-尺度-时移次序求解已知方法二:按反褶-时移-尺度次序求解已知方法三利用傅里叶变换的性质其它方法自己练习。
信号与系统作业答案郑君里版

《信号与系统》习题与答案第一章1.1 画出信号[])()(sin )(00t t a t t a t f --=的波形。
1.2 已知信号[])2()1()1()(--++=t u t u t t f ,画出)32(+-t f 的波形。
1.3已知信号[])2()1()1()(--++=t u t u t t f ,试求它的直流分量。
答案:01.4 已知信号[])2()1()1()(--++=t u t u t t f ,试求它的奇分量和偶分量。
答案:偶分量:[][][])2()1()1(5.0)1()1()1()2()1(5.0---++--+++-+-t u t u t t u t u t u t u t奇分量:[][][])2()1()1(5.0)1()1()1()2()1(5.0---++--+++-+-t u t u t t u t u t t u t u t1.5 信号⎩⎨⎧=20)(tt f≥<t t 是否是奇异信号。
答案:二阶以上导数不连续,是奇异信号。
1.6 已知)(t f 是有界信号,且当∞→t 时0)(→t f ,试问)(t f 是否是能量有限信号。
答案:不一定。
1.7 对一连续三角信号进行抽样,每周期抽样8点,求抽样所得离散三角序列的离散角频率。
答案:4/πθ=1.8 以s 5.0=s T 的抽样间隔对下列两个三角信号抽样,写出抽样所得离散序列的表达式,画出它们的波形。
比较和说明两波形的差别,为什么? (1) t t f 4cos)(1π= (2)t t f 415cos)(2π= 答案:两个离散序列是相同的。
1.9 判断下列信号是否是周期信号。
如果是周期信号,试确定其周期。
(1) t C t B t A t f 9cos 7cos 4sin )(++= 答案:是周期函数,周期π2=T 。
(2) n j d n f 8e)(π-= 答案:是周期信号,周期16=N1.10 求下列表达式的函数值(1) ⎰∞∞--dt t t t f )()(0δ; 答案:)(0t f - (2) ⎰∞∞--dt t t t f )()(0δ; 答案:)(0t f(3) ⎰∞∞---dt t t u t t )2()(00δ; 答案:当00>t 时为1;当00<t 时为0 (4) ⎰∞∞---dt t t u t t )2()(00δ; 答案:当00<t 时为1;当00>t 时为0 (5) ⎰∞∞--++dt t t e t )2()(δ; 答案:2e 2- (6) ⎰∞∞--+dt t t t )6()sin (πδ; 答案:2/16/+π(7)[]⎰∞∞----dt t t t e t j )()2(0δδω; 答案:0e 2/1t j ω--1.11 判断下列系统是否线性、时不变和因果(1) tt e t r d )(d )(=; 答案:线性,时不变,因果 (2) )()()(t u t e t r =; 答案:线性,时变,因果(3) [])()(sin )(t u t e t r =; 答案:非线性,时变,因果 (4) )1()(t e t r -=; 答案:线性,时变,非因果 (5) )2()(t e t r =; 答案:线性,时变,非因果 (6) )()(2t e r r =; 答案:非线性,时不变,因果1.12 试证明:)()0(')(')0()(')(t f t f t t f δδδ-=。
郑君里《信号与系统》(第3版)课后习题(离散傅里叶变换以及其他离散正交变换)【圣才出品】

图 9-6
图形如图 9-7 所示。
图 9-7
9-13 证 明 频 移 定 理 : 若
。
证明:令
,则
,则
由于
及
都是以 N 为周期的函数,所以
。
10 / 33
圣才电子书 十万种考研考证电子书、题库视频学习平台
9-14 已知有限长序列
,试利用频移定理求:
解:(1)
(2)
9-15 利用教材例 9-3 的结果,分别求该例中的
圣才电子书 十万种考研考证电子书、题库视频学习平台
第 9 章 离散傅里叶变换以及其他离散正交变换
9-1 图 9-1 所示周期序列 xP(n),周期 N=4,求
。
解:周期 N=4,则根据定义有
图 9-1
9-2 若 周 期 序 列 xP(n) 为 实 数 序 列 , 则 。试证明此特性。
x(n)=xP(n)RN(n),求 x(n)的离散傅里叶变换
。
解:根据 DFT 定义,有
由题 9-1 知,
则
故
。
9-7 任意假设一个实周期序列 xP(n),其周期为 N。若 x(n)=xP(n)RN(n),绘出
序列。
解:设 xP(n)如图 9-3(a)所示,由定义有
,即
序列
为 xP(n)序列以 n=0 为轴反转所得,如图 9-3(b)所示。
4 / 33
圣才电子书 十万种考研考证电子书、题库视频学习平台
图 9-3 9-8 若已知有限长序列 x(n)如下式
求 建议写作矩阵形式。
解:根据定义
,再由所得结果求 ,可写出矩阵形式
,验证你的计算是正确的,
因为 故
,所以
信号与系统作业答案郑君里版

信号与系统作业答案郑君里版1.1 1.2 1.3画出信号f(t)sin a(t t0) 的波形。
a(t t0)已知信号f(t) (t 1) u(t 1) u(t 2) ,画出f( 2t 3)的波形。
已知信号f(t) (t 1) u(t 1) u(t 2) ,试求它的直流分量。
答案:01.4 已知信号f(t) (t 1) u(t 1) u(t 2) ,试求它的奇分量和偶分量。
答案:偶分量:0.5(1 t) u(t 2) u(t 1) u(t 1) u(t 1) 0.5(t 1) u(t 1) u(t 2)奇分量:0.5(t 1) u(t 2) u(t 1) t u(t 1) u(t 1) 0.5(t 1) u(t 1) u(t 2)1.5 信号f(t)2 tt 0是否是奇异信号。
t 0答案:二阶以上导数不连续,是奇异信号。
1.6 已知f(t)是有界信号,且当t 时f(t) 0,试问f(t)是否是能量有限信号。
答案:不一定。
1.7 对一连续三角信号进行抽样,每周期抽样8点,求抽样所得离散三角序列的离散角频率。
答案:/41.8 以Ts 0.5s的抽样间隔对下列两个三角信号抽样,写出抽样所得离散序列的表达式,画出它们的波形。
比较和说明两波形的差别,为什么?(1)f1(t) cos4t (2)f2(t) cos15t 4答案:两个离散序列是相同的。
1.9 判断下列信号是否是周期信号。
如果是周期信号,试确定其周期。
(1)f(t) Asin4t Bcos7t Ccos9t 答案:是周期函数,周期T 2 。
(2)fd(n) ejn8答案:是周期信号,周期N 161.10 求下列表达式的函数值(1)(2)(3)(4)(5)(6)(7)f(t t0) (t)dt;答案:f( t0)f(t0 t) (t)dt;答案:f(t0)(t t0)u(t t02)dt;答案:当t0 0时为1;当t0 0时为0 (t t0)u(t 2t0)dt;答案:当t0 0时为1;当t0 0时为0(e t t) (t 2)dt;答案:e2 2 (t sint) (t 6)dt;答案:/6 1/2e j t (2t) (t t0) dt;答案:1/2 e j t01.11 判断下列系统是否线性、时不变和因果de(t);答案:线性,时不变,因果dt(2)r(t) e(t)u(t);答案:线性,时变,因果(1)r(t)(3)r(t) sin e(t) u(t);答案:非线性,时变,因果(4)r(t) e(1 t);答案:线性,时变,非因果(5)r(t) e(2t);答案:线性,时变,非因果(6)r(r) e2(t);答案:非线性,时不变,因果1.12 试证明:f(t) '(t) f(0) '(t) f'(0) (t)。
信号与系统-郑君里 试题

《信号与系统》 A 卷一、选择题(每题2分,共10分)1、连续线性时不变系统的单位冲激响应()t h 为系统的( ) A. 零输入响应 B. 零状态响应 C. 自由响应 D. 强迫响应2、如图所示的周期信号()t f 的傅立叶级数中所含的频率分量是( ) A .余弦项的偶次谐波,含直流分量B .余弦项的奇次谐波,无直流分量C .正弦项的奇次谐波,无直流分量D .正弦项的偶次谐波,含直流分量3A. 零输入响应的全部 B. 零状态响应的全部C. 全部的零输入响应和部分的零状态响应D. 全部的零输入响应和全部的零状态响应 4、如果两个信号分别通过系统函数为()s H 的系统后,得到相同的响应,那么这两个信号( ) A .一定相同 B .一定不同 C .只能为零 D .可以不同 5、已知系统微分方程为()()()t e t r dtt dr =+2,若()10=+r ,()()()t u t t e ⋅=2sin ,解得全响应为()⎪⎭⎫ ⎝⎛-+=-22sin 42452πt e t r t ,0≥t 。
全响应中⎪⎭⎫ ⎝⎛-22sin 42πt 为( ) A .零输入响应分量B .自由响应分量C .零状态响应分量D .稳态响应分量二、填空题(每题3分,共30分) 1、()()=⎰∞∞-dt t f t δ________________。
2、某一LTI 离散系统,其输入()n x 和输出()n y 满足如下线性常系数差分方程,)1n (x 31)n (x )1n (y 21)n (y -+=--,则系统函数()z H 是________________。
3、()()=-'⎰∞∞-dt t f t t 0δ________________。
4、已知()t f )(ωF ↔,则()t f 2-的傅里叶变换为________________。
5、已知信号()t f 的傅立叶变换为()ωF ,则信号()0t at f -的傅立叶变换为________________。
信号与系统(郑君里)课后答案 第一章习题解答

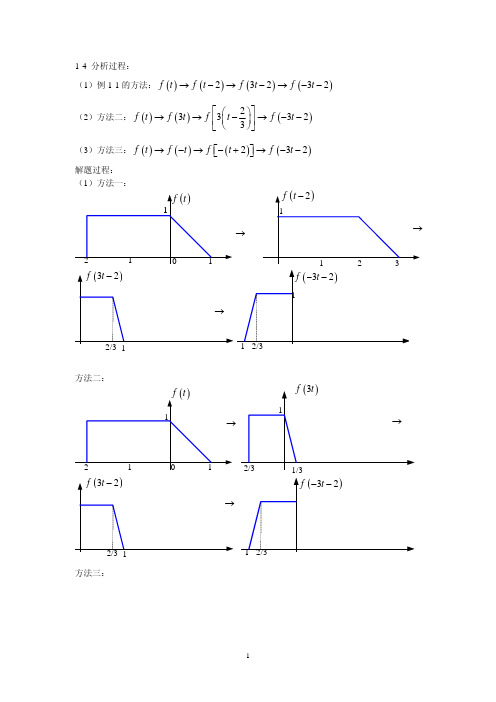
1-4 分析过程:(1)例1-1的方法:()()()()23232f t f t f t f t →−→−→−− (2)方法二:()()()233323f t f t f t f t ⎡⎤⎛⎞→→−→−−⎜⎟⎢⎥⎝⎠⎣⎦(3)方法三:()()()()232f t f t f t f t →−→−+→−−⎡⎤⎣⎦ 解题过程:(1)方法一:方法二:(1)()−f at 左移0t :()()()000−+=−−≠−⎡⎤⎣⎦f a t t f at at f t at (2)()f at 右移0t :()()()000−=−≠−⎡⎤⎣⎦f a t t f at at f t at (3)()f at 左移0t a :()()000⎡⎤⎛⎞+=+≠−⎜⎟⎢⎥⎝⎠⎣⎦t f a t f at t f t at a (4)()f at 右移0t a :()()000⎡⎤⎛⎞−−=−+=−⎜⎟⎢⎥⎝⎠⎣⎦t f a t f at t f t at a 故(4)运算可以得到正确结果。
注:1-4、1-5题考察信号时域运算:1-4题说明采用不同的运算次序可以得到一致的结果;1-5题提醒所有的运算是针对自变量t 进行的。
如果先进行尺度变换或者反转变换,再进行移位变换,一定要注意移位量和移位的方向。
1-9 解题过程: (1)()()()2tf t eu t −=− (2)()()()232tt f t ee u t −−=+(3)()()()255ttf t e eu t −−=− (4)()()()()cos 1012tf t et u t u t π−=−−−⎡⎤⎣⎦1-12 解题过程:((((注:1-9、1-12题中的时域信号均为实因果信号,即()()()=f t f t u t 1-18 分析过程:任何信号均可分解为奇分量与偶分量之和的形式,即()()()()1e o f t f t f t =+其中,()e f t 为偶分量,()o f t 为奇分量,二者性质如下:()()()()()()23e e o o f t f t f t f t =−=−−()()13∼式联立得()()()12e f t f t f t =+−⎡⎤⎣⎦ ()()()12o f t f t f t =−−⎡⎤⎣⎦ 解题过程:(a-1) (a-2)(a-3)(a-4)f t为偶函数,故只有偶分量,为其本身(b) ()(c-1)(c-2)(c-3)(c-4)(d-1)(d-2)(d-3)(d-4)1-20 分析过程:本题为判断系统性质:线性、时不变性、因果性(1)线性(Linearity):基本含义为叠加性和均匀性即输入()1x t ,()2x t 得到的输出分别为()1y t ,()2y t ,()()11T x t y t =⎡⎤⎣⎦,()()22T x t y t =⎡⎤⎣⎦,则()()()()11221122T c x t c x t c y t c y t +=+⎡⎤⎣⎦(1c ,2c 为常数)。
信号与系统习题课(郑君里)

d2 d d g (t ) g (t ) g (t ) u (t ) u (t ) (t ) u (t ) dt 2 dt dt
起始状态: 其解的形式为: 对
g (0 ) g (0 ) 0
g (t ) Ae
1 3 ( j )t 2 2
Ae
1 3 ( j )t 2 2
5t
C1 e1 ( )d C2 e2 ( )d
5
5t
C1r1 (t ) C2 r2 (t )
由于
e(t t0 ) e( t0 )d
5t
线性的
t0 a
5t t 0
e(a)da
5 ( t t 0 )
(t ) et u(t )
第二章
习题 2-4
连续时间系统的时域分析
2 2 2 0 (1)系统的特征方程: 特征根为:1 1 j, 2 1 j t 零输入响应的形式: rzi (t ) e ( A1 cost A2 sin t ) 将 r (0 ) 1, r(0 ) 2 代入上式,求出常数:
q(t ) a1q(t ) a0q(t ) e(t )
将代入原微分方程,得
q (t ) 和 r (t )
满足:
r (t ) b0q(t ) b1q(t )
将和用方框图实现,得到如下系统仿真框图
b1
e (t )
q(t )
q(t )
r (t )
a1
而
C1r1 (t ) C2 r2 (t ) C1 sin[e1 (t )]u(t ) C2 sin[e2 (t )]u(t )
信号与系统作业任务答案解析郑君里版

《信号与系统》习题与答案第一章1.1 画出信号[])()(sin )(00t t a t t a t f --=的波形。
1.2 已知信号[])2()1()1()(--++=t u t u t t f ,画出)32(+-t f 的波形。
1.3已知信号[])2()1()1()(--++=t u t u t t f ,试求它的直流分量。
答案:01.4 已知信号[])2()1()1()(--++=t u t u t t f ,试求它的奇分量和偶分量。
答案:偶分量:[][][])2()1()1(5.0)1()1()1()2()1(5.0---++--+++-+-t u t u t t u t u t u t u t奇分量:[][][])2()1()1(5.0)1()1()1()2()1(5.0---++--+++-+-t u t u t t u t u t t u t u t1.5 信号⎩⎨⎧=20)(t t f 0≥<t t 是否是奇异信号。
答案:二阶以上导数不连续,是奇异信号。
1.6 已知)(t f 是有界信号,且当∞→t 时0)(→t f ,试问)(t f 是否是能量有限信号。
答案:不一定。
1.7 对一连续三角信号进行抽样,每周期抽样8点,求抽样所得离散三角序列的离散角频率。
答案:4/πθ=1.8 以s 5.0=s T 的抽样间隔对下列两个三角信号抽样,写出抽样所得离散序列的表达式,画出它们的波形。
比较和说明两波形的差别,为什么? (1) t t f 4cos)(1π= (2)t t f 415cos)(2π= 答案:两个离散序列是相同的。
1.9 判断下列信号是否是周期信号。
如果是周期信号,试确定其周期。
(1) t C t B t A t f 9cos 7cos 4sin )(++= 答案:是周期函数,周期π2=T 。
(2) n j d n f 8e)(π-= 答案:是周期信号,周期16=N1.10 求下列表达式的函数值(1) ⎰∞∞--dt t t t f )()(0δ; 答案:)(0t f - (2) ⎰∞∞--dt t t t f )()(0δ; 答案:)(0t f(3) ⎰∞∞---dt t t u t t )2()(00δ; 答案:当00>t 时为1;当00<t 时为0 (4) ⎰∞∞---dt t t u t t )2()(00δ; 答案:当00<t 时为1;当00>t 时为0 (5)⎰∞∞--++dt t t e t )2()(δ; 答案:2e 2-(6) ⎰∞∞--+dt t t t )6()sin (πδ; 答案:2/16/+π(7)[]⎰∞∞----dt t t t e t j )()2(0δδω; 答案:0e 2/1t j ω--1.11 判断下列系统是否线性、时不变和因果(1) tt e t r d )(d )(=; 答案:线性,时不变,因果 (2) )()()(t u t e t r =; 答案:线性,时变,因果 (3) [])()(sin )(t u t e t r =; 答案:非线性,时变,因果 (4) )1()(t e t r -=; 答案:线性,时变,非因果 (5) )2()(t e t r =; 答案:线性,时变,非因果 (6) )()(2t e r r =; 答案:非线性,时不变,因果1.12 试证明:)()0(')(')0()(')(t f t f t t f δδδ-=。
郑君里信号与系统习题答案

郑君⾥信号与系统习题答案第三章傅⾥叶变换⼀.周期信号的傅⾥叶级数⼆.傅⾥叶变换例题例题1:傅⾥叶级数——频谱图 ?例题2:傅⾥叶变换的性质 ?例题3:傅⾥叶变换的定义 ?例题4:傅⾥叶变换的性质 ?例题5:傅⾥叶变换的性质 ?例题6:傅⾥叶变换的性质例题7:傅⾥叶变换的性质、频响特性 ?例题8:傅⾥叶变换的性质 ?例题9:抽样定理–例题10:周期信号的傅⾥叶变换例3-1 周期信号 1. 画出单边幅度谱和相位谱;()?--??? ??++=328cos 265sin cos 3ππt t t t f 形式频谱:离散性、谐波性、收敛性周期矩形脉冲信号的频谱特点定义及傅⾥叶变换存在的条件典型⾮周期信号的频谱冲激函数和阶跃信号的傅⾥叶变换性质→应⽤:调制和解调→频分复⽤周期信号的傅⾥叶变换:由⼀些冲激函数组成抽样信号的傅⾥叶变换→抽样定理→应⽤:时分复⽤2. 画出双边幅度谱和相位谱。
单边幅度谱和相位谱双边幅度谱和相位谱例3-2 分析:f (t )不满⾜绝对可积条件,故⽆法⽤定义求其傅⾥叶变换,只能利⽤已知典型信号的傅⾥叶变换和性质求解。
下⾯⽤三种⽅法求解此题。
⽅法⼀:利⽤傅⾥叶变换的微分性质⽅法⼆:利⽤傅⾥叶变换的积分性质⽅法三:线性性质⽅法⼀:利⽤傅⾥叶变换的微分性质要注意直流,设f A(t )为交流分量,f D(t )为直流分量,则其中()?+-+? -++=ππππ328cos 2265cos cos 3t t t t f ?++??? ??-+=38cos 2315cos cos 3ππt t t()。
的傅⾥叶变换求信号 )(ωF t f ()()()t f t f t f D A +=()()()ωωωD A F F F +=()()()[]2321=∞+∞-=f f t f D ()()ωπδω3=D F ()()t f t f A'='()??? ??-='211t G t f A ()ωωωωj Ae F j -??=∴2Sa⽅法⼆:利⽤傅⾥叶变换的积分性质⽅法三:利⽤线性性质进⾏分解此信号也可以利⽤线性性质进⾏分解,例如例3-3已知信号f (t )波形如下,其频谱密度为F (j ω),不必求出F (j ω)的表达式,试计算下列值:()ωωωωj e F j A -??=∴2Sa ()()()()ωπδωωωωωω32Sa +??? ??=+=∴-j e F F F j DA ())(11t f t f +=的积分为)()(21t f t f ()ωωωj e F -??? ??=2Sa 2()()()ωωωπωωωπωωωj e e j F j j --??? ??+=??? ???+=∴2Sa 2Sa 11 ()[]()()ωωωπδωωωj e F F F j -??? ??+=+=∴2Sa 311()[])1(2)1()()1()(-+--++-=t u t u t u t t u t f ()ωωπδj 1-()2121ωωωωωj e e j j j j ---+-()ωωωπδj e j -+22()()()ωπδωωω312+-=∴-j e F j ()()01=ωωF ()()?∞∞-ωωd 2F -t tj d ω(()?∞-====∴5.1d 00t t f F F ωω令t =0,则则例3-4按反褶-尺度-时移次序求解已知⽅法⼆:按反褶-时移-尺度次序求解已知⽅法三利⽤傅⾥叶变换的性质其它⽅法⾃⼰练习。
北京邮电郑君里《信号与系统》课后答案

第一章1.8 系统的数学模型如下,试判断其线性、时不变性和因果性。
其中X (0-)为系统的初始状态。
(2)()()2f t y t e = (5)()()cos2y t f t t = (8)()()2y t f t = 解:(2)()()2f t y t e = ① 线性: 设 ()()()()1122,f t y t f t y t →→,则 ()()()()122212,f tf t y t e y t e==那么 ()()()()()()()112211222221122a f t a f t a f t a f t a f t a f t y t ee e +⎡⎤⎣⎦+→==,显然,()()()1122y t a y t a y t ≠+,所以是非线性的。
② 时不变性设()()11,f t y t →则 ()()()()10122110,f t t f t y t e y t t e-=-=设()()102,f t t y t -→则()()()102210f t t y t e y t t -==-,所以是时不变的。
③ 因果性因为对任意时刻 t 1,()()121f t y t e =,即输出由当前时刻的输入决定,所以系统是因果的。
(5)()()cos2y t f t t = ① 线性: 设 ()()()()1122,f t y t f t y t →→,则 ()()()()1122cos2,cos2y t f t t y t f t t ==那么()()()()()()()112211221122cos 2cos 2cos 2a f t a f t y t a f t a f t t a f t t a f t t +→=+=+⎡⎤⎣⎦, 显然()()()1122y t a y t a y t =+,所以系统是线性的。
② 时不变性设()()11,f t y t →则 ()()()()()1110100cos2,cos2y t f t t y t t f t t t t =-=--设()()102,f t t y t -→则()()()21010cos2y t f t t t y t t =-≠-,所以是时变的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
信号与系统习题答案(注:教材---郑君里编)习题一1-7 绘出下列各信号的波形:图a:[][]11()(2)(2)()(2)()(2)22f t t u t u t t u t u t =++-----[](1)(2)(2)2tu t u t =-+--图b:)2(2)1()()();2(4)]2()1([2)]1()([)(-+-+=-+---+--=t u t u t u t f t u t u t u t u t u t f图c :[])()()sin()(T t u t u t T E t f --=π1-12 绘出下列各时间函数的波形图,注意它们的区别: (1))]1()([--t u t u t ; (2))1(-t tu ; (3))1()]1()([-+--t u t u t u t ;)1(-tf(t)求f(-t),讨论图7(b)(c)(a)⇒ ⇒方法二:(1))()()(00t f dt t t t f -=-⎰∞∞-δ ;(2)⎰∞∞-=-)()()(00t f dt t t t f δ ;(3)1)2()2()(000==--⎰∞∞-tu dt t t u t t δ;(4)⎰∞∞-=-=--0)()2()(000t u dt t t u t t δ;(5)⎰∞∞---=++2)2()(2e dt t t e t δ;(6)2166sin6)6()sin (+=+=-+⎰∞∞-ππππδdt t t t ;(7)⎰∞∞----=--01)]()([0t j t j e dt t t t e ωωδδ ;1-15 电容C 1与C 2串联,以阶跃电压源v(t)=Eu(t)串联接入,试分别写出回路中的电流i(t)、每个电容两端电压vc 1(t)、vc 2(t)的表示式。
电路如图:2121c c c c +*=⇒电路电流)()(2121t E c c dt Ct i c δ+==)()(1)()()(1)(2112221211t u c c Ec dt t i c t v t u c c Ec dt t i c t v c c ⎰⎰+==+==1-20 判断下列系统是否为线性的、时不变的、因果的?(1)dt t de t r )()(=;(2))()()(t u t e t r = ;V C1(t) V C2(t)(3) )()](sin[)(t u t e t r = ; (4) )1()(t e t r -= ; (5) )2()(t e t r = ;(6))()(2t e t r = ;(7)⎰∞-=td e t r ττ)()( ;(8) ⎰∞-=td e t r 5)()(ττ 。
解:线性系统满足齐次性和叠加性;时不变系统的参数不随时间而变化,即:在同样起始状态下,系统响应与激励施加于系统的时刻无关;因果系统在t 0时刻的响应只与t=t 0与t<t 0时刻的输入有关。
(1) 激励 响应e(t) dt t de t r )()(=ae(t)⇒===)()()]([)(1t ar dt t de a dt t ae d t r 线性系统e(t-t 0) ⇒-=-=)()()(002t t r dt t t de t r 时不变系统)(0t e)()()(0003t r dt t de t r ==⇒系统的响应仅与t<t 0时刻有关,所以系统为因果系统(2) 激励 响应e(t))()()(t u t e t r =ae(t) ⇒==)()()()(1t ar t u t ae t r 系统为线性系统e(t-t 0))()()()()()(00002t t u t t e t t r t u t t e t r --=-≠-=⇒系统为时变系统e(t 0) )()()(0003t u t e t r =⇒系统为因果系统(3) 激励 响应 e(t) )()](sin[)(t u t e t r =ae(t))()](sin[)()()](sin[)(1t u t e a t ar t u t ae t r =≠=⇒系统为非线性系统e(t-t 0))()](sin[)()()](sin[)(00002t t u t t e t t r t u t t e t r --=-≠-=⇒系统为时变系统e(t 0))()()](sin[)()](sin[)(000003t r t u t e t u t e t r ===⇒系统为因果系统⇒(4) 激励 响应e(t) r(t)=e(1-t)ae(t) ⇒=-=)()1()(1t ar t ae t r 系统为线性系统)(0t t e -)1()](1[)()1()(00002t t e t t e t t r t t e t r +-=--=-≠--=⇒系统为时变系统)(0t e)1()(003t e t r -= 当t =0时,)1()1(0e t e =-,即系统响应中有0t t >时刻的响应,⇒系统为非因果系统(5) 激励 响应 )(t e )2()(t e t r =)(t ae ⇒==)()2()(1t ar t ae t r 系统为线性系统)(0t t e - ⇒-=-≠-=)()](2[)2()(0002t t r t t e t t e t r 系统为时变系统)(0t e ⇒≠=)()2()(0003t r t e t r 系统响应中只有0t t ≥时刻的响应,⇒系统为非因果系统(6) 激励 响应 )(t e )()(2t e t r =)(t ae ⇒=≠=)()()()(2221t ar t ae t e a t r 系统为非线性系统)(0t t e - ⇒-=-=)()()(0022t t r t t e t r 系统为时不变系统)(0t e ⇒=)()(0203t e t r 系统响应仅于0t t =时刻的激励有关⇒系统为因果系统(7) 激励 响应)(t eττd e t r t)()(⎰∞-=)(t ae⇒===⎰⎰∞-∞-)()()()(1t ar d e a d ae t r t t ττττ系统为线性系统)(0t t e -00t-t 200-0()() e(u)duu ()()tt t r t e t d t u e d r t t ττττττ-∞∞--∞=--===-⎰⎰⎰令令⇒系统为时不变系统)(0t e ⇒=⎰∞-ττ0)()(03t d e t r 系统响应仅于0t t =时刻的激励有关⇒系统为因果系统(8) 激励 响应e(t)⎰∞-=td e t r 5)()(ττae(t)⎰⎰∞-∞-⇒==t t d e a d ae t r 551)()()(ττττ系统为线性系统)(0t t e -⎰⎰⎰⎰-∞-∞∞∞-=≠==-=)(5t -5t -0t -5t -050200)()t -r(t )d e(e(u)du t - )()(t t td e u u d t e t r ττττττττ令令⇒系统为时变系统)(0t eΘ)()(0503⎰∞-=t d e t r ττ系统响应于0t t ≥时刻的激励有关系统为非因果系统信号与系统习题答案(注:教材---郑君里编)习题二2-1 对下图所示电路图分别列写求电压的微分方程表示。
图(a):微分方程:11222012()2()1()()()2()()()()2()()()c cc di t i t u t e t dtdi t i t u t dtdi t u t dt du t i t i t dt ⎧+*+=⎪⎪⎪+=⎪⇒⎨⎪=⎪⎪⎪=-⎩图(b ):微分方程:⎪⎪⎪⎩⎪⎪⎪⎨⎧-==+++=+++⎰⎰2021'2'21'2'11)(01)(1Ri t v Ri Mi Li dt i Ct e Ri Mi Li dt i C)()(1)(2)()2()(2)()(33020022203304422t e dtd MR t v C t v dt d C R t v dt d C L R t v dt d RL t v dt d M L =+++++-⇒ 图(c)微分方程:dt i C i L t v ⎰==211'101)(⎪⎪⎪⎩⎪⎪⎪⎨⎧===⇒⎰dt t v L i t v L i dtdt v L i dt d)(1)(1)(10110'1122011∵ )(122111213t i dt d L C i i i i +=+=)(0(1]1[][101011022110331t e dt dR t v RL v dt d RR L C v dt d R C R C v dt d CC μ=+++++⇒图(d)微分方程:⎪⎩⎪⎨⎧+-=++=⎰)()()()()(1)()(11111t e t Ri t v t v dt t i C t Ri t e μRC v dt d 1)1(1+-⇒μ)(11t e V CR = ∵)()(10t v t v μ=)()(1)1(0'0t e R vt v R Cv v =+-⇒2-4 已知系统相应的其次方程及其对应的0+状态条件,求系统的零输入响应。
(1)2)0(,1)0( 0)(2)(2)('22===++++r r t r t r dt d t r dt d 给定:;特征方程:0222=++αα特征根: +-=11αj --=12αj零输入响应:t t e A e A t r 2121)(αα+=代入初始条件,⇒2A 121=-=A)sin 3(cos 2)(21t t e e e t r t t t -=+-=-αα(2) 2)0(,1)0( 0)()(2)('22===++++r r t r t r dt d t r dt d 给定: ;特征方程: 0122=++αα特征根: 121-==αα零输入响应:te A t A t r -+=)()(21代入初始条件,⇒1A 321==Ate t t r -+=)13()((3) 1)(0,0)0()0( 0)()(2)("'2233====+++++r r r t r dt d t r dt d t r dt d 给定:特征方程: 0223=++ααα特征根: 121-==αα 0=α零输入响应:321)()(A e A t A t r t++=- 代入初始条件,⇒1A 1A 321=-==At e t t r -+-=)1(1)(2-5 给定系统微分方程、起始状态以及激励信号分别为以下三种情况:(1) )()(,0_)0(),()(2)(t u t e r t e t r t r dt d===+(2) )()(,0_)0(),(3)(2)(t u t e r t e dt dt r t r dt d ===+(3))()(,1_)0(,1_)0(),()(4)(3)(2'22t u t e r r t e dt dt r t r dt d t r dt d ====++试判断在起始点是否发生跳变,据此对(1)(2)分别写出其r(0+)值,对(3)写出r(0+)和r’(0+)值。
