surfer 的插值方介绍
Surfer8.0绘图软件三维地形图软件的使用

Surfer8.0绘图软件的使用3.1 软件运行环境及特点Golden Software Surfer 8.0 (以下简称Surfer)是一款画三维图(等值线,image map,3d surface)的软件,是美国Golden Software公司的系列绘图软件之一。
该软件简单易学,可以在几分钟内学会主要内容,且其自带的英文帮助文件(help菜单)是相当完美且容易阅读的,对如何使用Surfer,解释的很详细,只要学过英语的人都可以很快上手。
Surfer的主要功能是绘制等值线图(contour map),是具有插值功能的绘图软件,因此,即使你的数据是不等间距的,依然可以用它作图。
此外它还可以绘制张贴图、分类张贴图、矢量图、影像图、线框图、3d surface map,等形式的图形,其功能是比较强大的。
Surfer的安装比较简单(目前,只有Windows操作系统下的版本,最为常用的是8.0版本),只要按其提示缺省安装即可。
其安装软件的大小不到30M,一般的计算机硬件基本能够顺利使用该软件。
安装好Surfer以后,其环境界面如图3-1所示。
命令菜单绘图命令目标管理窗口工作区状态栏图3-1 Surfer8.0软件界面·22·3.2 软件界面及命令菜单Surfer软件的界面非常友好,继承了Windows操作系统软件的特点。
从图3-1中可以看到,其最上方为命令菜单,在命令菜单的下方是命令菜单中的快捷工具栏(共两行),左侧的空白区域为目标管理窗口,用来更加方便的管理绘制的各个图形要素,右侧的空白区域为工作区,用来绘制图形,最右侧的一个竖条工具栏是绘图命令的快捷方式。
下面详细介绍各个命令菜单的主要内容。
3.2.1文件菜单(F)“文件菜单”如图3-2所示,主要是对文件进行操作,如文件的建立、加载、打印设置等。
图3-2 文件菜单新建—用来新建一个工作窗口,点击后即出现图3-1界面。
打开—打开一个已经存在的Surfer可以识别的文件。
Surfer使用教程

第3章Surfer8.0绘图软件的使用3.1 软件运行环境及特点Golden Software Surfer 8.0 (以下简称Surfer)是一款画三维图(等值线,image map,3d surface)的软件,是美国Golden Software公司的系列绘图软件之一。
该软件简单易学,可以在几分钟内学会主要内容,且其自带的英文帮助文件(help菜单)是相当完美且容易阅读的,对如何使用Surfer,解释的很详细,只要学过英语的人都可以很快上手。
Surfer的主要功能是绘制等值线图(contour map),是具有插值功能的绘图软件,因此,即使你的数据是不等间距的,依然可以用它作图。
此外它还可以绘制张贴图、分类张贴图、矢量图、影像图、线框图、3d surface map,等形式的图形,其功能是比较强大的。
Surfer的安装比较简单(目前,只有Windows操作系统下的版本,最为常用的是8.0版本),只要按其提示缺省安装即可。
其安装软件的大小不到30M,一般的计算机硬件基本能够顺利使用该软件。
安装好Surfer以后,其环境界面如图3-1所示。
命令菜单绘图命令目标管理窗口工作区状态栏图3-1 Surfer8.0软件界面3.2 软件界面及命令菜单Surfer软件的界面非常友好,继承了Windows操作系统软件的特点。
从图3-1中可以看到,其最上方为命令菜单,在命令菜单的下方是命令菜单中的快捷工具栏(共两行),左侧的空白区域为目标管理窗口,用来更加方便的管理绘制的各个图形要素,右侧的空白区域为工作区,用来绘制图形,最右侧的一个竖条工具栏是绘图命令的快捷方式。
下面详细介绍各个命令菜单的主要内容。
3.2.1文件菜单(F)“文件菜单”如图3-2所示,主要是对文件进行操作,如文件的建立、加载、打印设置等。
图3-2 文件菜单新建—用来新建一个工作窗口,点击后即出现图3-1界面。
打开—打开一个已经存在的Surfer可以识别的文件。
Surfer软件插值方法

Surfer软件插值方法1、距离倒数乘方法距离倒数乘方格网化方法是一个加权平均插值法,可以进行确切的或者圆滑的方式插值。
方次参数控制着权系数如何随着离开一个格网结点距离的增加而下降。
对于一个较大的方次,较近的数据点被给定一个较高的权重份额,对于一个较小的方次,权重比较均匀地分配给各数据点。
计算一个格网结点时给予一个特定数据点的权值与指定方次的从结点到观测点的该结点被赋予距离倒数成比例。
当计算一个格网结点时,配给的权重是一个分数,所有权重的总和等于1.0。
当一个观测点与一个格网结点重合时,该观测点被给予一个实际为1.0 的权重,所有其它观测点被给予一个几乎为0.0 的权重。
换言之,该结点被赋给与观测点一致的值。
这就是一个准确插值。
距离倒数法的特征之一是要在格网区域内产生围绕观测点位置的"牛眼"。
用距离倒数格网化时可以指定一个圆滑参数。
大于零的圆滑参数保证,对于一个特定的结点,没有哪个观测点被赋予全部的权值,即使观测点与该结点重合也是如此。
圆滑参数通过修匀已被插值的格网来降低"牛眼"影响。
2、克里金法克里金法是一种在许多领域都很有用的地质统计格网化方法。
克里金法试图那样表示隐含在你的数据中的趋势,例如,高点会是沿一个脊连接,而不是被牛眼形等值线所孤立。
克里金法中包含了几个因子:变化图模型,漂移类型和矿块效应。
3、最小曲率法最小曲率法广泛用于地球科学。
用最小曲率法生成的插值面类似于一个通过各个数据值的,具有最小弯曲量的长条形薄弹性片。
最小曲率法,试图在尽可能严格地尊重数据的同时,生成尽可能圆滑的曲面。
使用最小曲率法时要涉及到两个参数:最大残差参数和最大循环次数参数来控制最小曲率的收敛标准。
4、多元回归法多元回归被用来确定你的数据的大规模的趋势和图案。
你可以用几个选项来确定你需要的趋势面类型。
多元回归实际上不是插值器,因为它并不试图预测未知的Z 值。
它实际上是一个趋势面分析作图程序。
Surfer插值方法介绍 中英混合版

一篇英文文章,用百度翻译翻译的还有一篇中文文章供参考满满的诚意,求赏金ABSTRACTSURFER is a contouring and 3D surface mapping program, which quickly and easily transforms random surveying data, using interpolation, into continuous curved face contours. In particular, the new version, SURFER 8.0, provides over twelve interpolation methods, each having specific functions and related parameters. In this study, the 5 meter DTM was used as test data to compare the various interpolation results; the accuracy of these results was then discussed and evaluated.摘要冲浪是一个轮廓和三维表面的绘制程序,并迅速和容易地变换随机测量数据,使用插值,成连续的曲面轮廓。
特别是,新版本,上网8,提供超过十二的插值方法,每一个具有特定功能和相关参数。
在这项研究中,5米DTM作为测试数据,比较不同的插值结果;讨论和评价,然后这些结果的准确性。
1. INTRODUCTIONHow to adequately use exist numerous wide-distributed height points has been an important topic in the field of spatial information. Normally, contouring is the way to accurately describe the terrain relief by means of Scenography, Shading, Hachure and Layer Tinting in a way which is best fit to the habit of human vision.Presently, discretely collected height points have to be interpolated to form curved faces, the selection of spatial interpolation methods decide the quality, accuracy and follow-up analysis applications. Interpolation methods are used here to calculated the unknown heights of interested points by referring to the elevation information of neighboring points. There are a great many commercial interpolation software, however, most of them are tiny and designed to solve specific problems with limited versatility. The SURFER is a software developed by US GOLDEN company, and the newest version 8.0 contains up to 12 interpolation methods to been free chosen for various needs. Users are suggested to first have the basic understanding of every interpolation methods before he or she can effectively select parameters in every interpolation methods. In the following paper, we will introduce every interpolation method in SURFER.1。
surfer插值
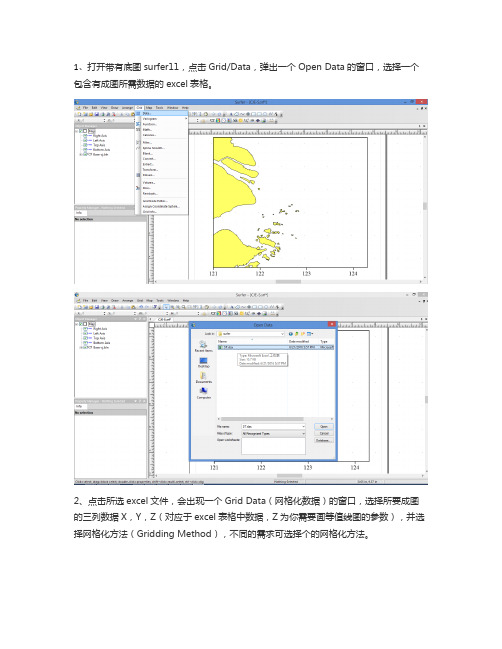
1、打开带有底图surfer11,点击Grid/Data,弹出一个Open Data的窗口,选择一个包含有成图所需数据的excel表格。
2、点击所选excel文件,会出现一个Grid Data(网格化数据)的窗口,选择所要成图的三列数据X,Y,Z(对应于excel表格中数据,Z为你需要画等值线图的参数),并选择网格化方法(Gridding Method),不同的需求可选择个的网格化方法。
3、选择存路径等,最后点击OK,就会输出一个grd文件并关闭Gridding Report, 得到插值的网格化grd.文件。
4、选择菜单栏Map/New/Contour Map,或者右击左边菜单栏里的Map/Add/Contour Layer,
5、找到上面的grd文件所在位置,点击打开,就得到所要的平面等值线图(未上色)。
如果等值线不够平滑,可以点击Contours...,在左下属性管理(Property Manager)选择General/Smoothing,进行None,Low,Medium,High四种不同程度地平滑
6、然后就是为等值线图上色;点击Contours...,在左下属性管理(Property Manager)选择Levels/Filled Contours/Fill Colors,勾选Fill Contours和Color Scale。
Surfer插值方法介绍 中英混合版

一篇英文文章,用百度翻译翻译的还有一篇中文文章供参考满满的诚意,求赏金ABSTRACTSURFER is a contouring and 3D surface mapping program, which quickly and easily transforms random surveying data, using interpolation, into continuous curved face contours. In particular, the new version, SURFER 8.0, provides over twelve interpolation methods, each having specific functions and related parameters. In this study, the 5 meter DTM was used as test data to compare the various interpolation results; the accuracy of these results was then discussed and evaluated.摘要冲浪是一个轮廓和三维表面的绘制程序,并迅速和容易地变换随机测量数据,使用插值,成连续的曲面轮廓。
特别是,新版本,上网8,提供超过十二的插值方法,每一个具有特定功能和相关参数。
在这项研究中,5米DTM作为测试数据,比较不同的插值结果;讨论和评价,然后这些结果的准确性。
1. INTRODUCTIONHow to adequately use exist numerous wide-distributed height points has been an important topic in the field of spatial information. Normally, contouring is the way to accurately describe the terrain relief by means of Scenography, Shading, Hachure and Layer Tinting in a way which is best fit to the habit of human vision.Presently, discretely collected height points have to be interpolated to form curved faces, the selection of spatial interpolation methods decide the quality, accuracy and follow-up analysis applications. Interpolation methods are used here to calculated the unknown heights of interested points by referring to the elevation information of neighboring points. There are a great many commercial interpolation software, however, most of them are tiny and designed to solve specific problems with limited versatility. The SURFER is a software developed by US GOLDEN company, and the newest version 8.0 contains up to 12 interpolation methods to been free chosen for various needs. Users are suggested to first have the basic understanding of every interpolation methods before he or she can effectively select parameters in every interpolation methods. In the following paper, we will introduce every interpolation method in SURFER.1。
3D Surfer用户使用手册

3D Surfer用户使用手册1.原始数据读入 (1)1.1数据文件格式: (1)1.2打开数据文件 (1)1.3数据读入 (2)2.三维数据插值 (2)2.1成像列选择 (2)2.2三维插值 (3)2.3数据的三维网格化 (3)3.三维数据体成像 (4)4.三维数据等值面成像 (4)5.色标制作 (4)6.三维图形切割 (5)7.切片制作 (6)7.1切片的方向 (6)7.2增加切片 (6)7.3删除切片 (6)7.4旋转切片 (7)(1)参数旋转 (7)(2)鼠标旋转 (7)7.5结束切片制作 (7)8.三维标注 (7)8.1标注文件 (7)8.2 打开标注文件 (7)8.3 删除标注 (8)9.图形输入/输出 (8)9.1图形输入 (8)9.2图形输出 (8)10.显示设置 (8)10.1常规设置 (8)10.2 坐标及刻度设置 (9)10.3 地层分层显示 (12)10.4 图层透明显示 (12)11.数据处理 (13)12.叠加地形 (15)13.导入图形 (15)13.1导入Surfer GRID切片 (15)13.2导入Surfer GRID曲面 (16)13.3 添加3D 图元 (16)13.4 载入测井数据 (16)13.5 图元管理 (17)(1)删除图元 (18)(2)调整图元色标 (18)(3)叠加颜色剖面 (18)(4)图元位置调整 (18)(5)图元缩放 (18)(6)图元旋转 (19)(7)图元透明处理 (19)(8)表面贴图 (19)简介三维数据成像软件3D Surfer主要用于地质、工程、科学计算等三维数据体的三维可视化成像显示。
它支持两种成像方式:体成像和等值面成像。
利用3D Surfer可以将数据在三维空间进行三维可视化显示,并且具有图形旋转、图形放缩、三维虚拟漫游、分层显示、图形切割、制作切片交互等功能。
3D Surfer 2.0 支持Surfer切片图、高程模型图、曲折剖面、透明图层、叠加地形、贴图等功能。
Surfer+80等值线绘制中的十二种插值方法

! $ /012 ! 67&89: " AB # YZ G &:>?[\ %* h ++ " K! * n :@ F U[\V ! " = a #&# ? @ A B 8 I 8 : N : M P J A G < >D I 7 @ !" ! TU ! RS ! YZ G µ:&8 ’ ?^" Q! ± & t &«Ù @ © ¡ 80 v 3 !D ¯R: @ [\º» % " = < # &# $ * ? @ A B 8 8 B V B G J D : K JD I J H H !I
$ 6 4 / # $ 0 ( # U P :+ J M T : MO 7 T L F A M :@ A K :; : M B I A G3 1 c * )O 7 T L F A M :I 7 @ A G OAL F 7d E 0@ Q EB ! P B I PI A G; : M J G B GF B G K 7 F O 7 : M A L B G G N B M 7 G ? L P M : : ? K B @ : G O B 7 G A 8 M A P B IK M A F B G 7 T L F A M : F Q H: H Q HO @ : G L D ( LI A G; :J O : KT 7 MK M A F B G O 7 8 B G :@ A > cO L : M : 7 M A @! O P A K 7 FH : 7 @ 7 M P 7 8 7 B I A 8 HB Q! H Q H ! @ A : I L 7 M M A PA G KO 77 GD U P :+ J M T : M a 9 $ B O L P :P B P : O L : K B L B 7 GA LQ M : O : G L D ( LQ M 7 N B K : O " # Q N H H H ! ! ! B G I 8 J K B G M B B G B G N : M O :K B O L A G I :L 7AQ 7 F : M 7 8 G 7 @ B A 8 S B G K O7 T B G L : M 7 8 A L B 7 G@ : L P 7 K O He H H Q E Q ! M : M : O O B 7 G F P B I PI A G T J 8 T B 8 8 B G L : M 7 8 A L B 7 GM : J B M : @ : G L 7 T K B T T : M : G L A 8 B I A L B 7 GK B M : I L B 7 GD U P B O H Q X Q Q A M L B I 8 : B G L M 7 K J I : O " #S B G K O7 T B G L : M 7 8 A L B 7 G@ : L P 7 K O B G+ J M T : M a 9 $! A G KJ O B G L P : A L L M B ; J L :K A ? Q H L A7 T. F P B I PB O T M 7 @\ 7 7 GO J M T A I : L 7@ A S :AO B @ 8 :A G A 8 O B O D Q E $ ( ( 7 + % $ & / O J M T : M B O 7 8 B G : M B K K B G H H .8 â Û N {¯ - x i { z 5 × $ Z f à ; %
surfer插值方法

一、GIS中使用的一些插值方法(SURFER中也会用到如下的一些插值方法)Inverse Distance to a Power(反距离加权插值法)Kriging(克里金插值法)Minimum Curvature(最小曲率)Modified Shepard's Method(改进谢别德法)Natural Neighbor(自然邻点插值法)Nearest Neighbor(最近邻点插值法)Polynomial Regression(多元回归法)Radial Basis Function(径向基函数法)Triangulation with Linear Interpolation(线性插值三角网法)Moving Average(移动平均法)Local Polynomial(局部多项式法)1、距离倒数乘方法距离倒数乘方格网化方法是一个加权平均插值法,可以进行确切的或者圆滑的方式插值。
方次参数控制着权系数如何随着离开一个格网结点距离的增加而下降。
对于一个较大的方次,较近的数据点被给定一个较高的权重份额,对于一个较小的方次,权重比较均匀地分配给各数据点。
计算一个格网结点时给予一个特定数据点的权值与指定方次的从结点到观测点的该结点被赋予距离倒数成比例。
当计算一个格网结点时,配给的权重是一个分数,所有权重的总和等于1.0。
当一个观测点与一个格网结点重合时,该观测点被给予一个实际为1.0 的权重,所有其它观测点被给予一个几乎为0.0 的权重。
换言之,该结点被赋给与观测点一致的值。
这就是一个准确插值。
距离倒数法的特征之一是要在格网区域内产生围绕观测点位置的"牛眼"。
用距离倒数格网化时可以指定一个圆滑参数。
大于零的圆滑参数保证,对于一个特定的结点,没有哪个观测点被赋予全部的权值,即使观测点与该结点重合也是如此。
圆滑参数通过修匀已被插值的格网来降低"牛眼"影响。
2、克里金法克里金法是一种在许多领域都很有用的地质统计格网化方法。
Surfer8_0等值线绘制中的十二种插值方法

第1期
陈欢欢等 : Surfer 8 1 0 等值 线绘制中的十二种插值方法
53
简单、 对系统要求低等优点得到广大用户的青睐, 成为普及度最高的绘 图软件之一。其最高版本 Surfer8 1 0 提供了十二种插值方法 , 用户可以根据 不同的需要选择不同方法来进行插值 , 来对其进 行分析, 以达到自己想要的效果。要科学地选择 插值方法和灵活地进行参数设置, 必须要熟悉各 种插值方法的 基本理论知识 , 下面 将介绍 Surf2 er8 1 0 中的十二种插值方法及其应用实例。
2 1 3 最小曲率法( Minimum Curvature) 最小曲率法广泛应用于地球科学, 是构造出具 有最小曲率的曲面, 使其穿过空间场的每一点, 并尽 可能使曲面变得光滑 。使用最小曲率法时要涉及 到两个参数: 最大偏差参数 ( Maximum Residuals) 和 最大循环次数( Maximum It eration paramet er) 参数来 控制最小曲率的收敛标准, 而且最小曲率法要求至 少有四个点。最小曲率法试图在尽可能严格地尊重 数据的同时, 生成尽可能圆滑的曲面。最小曲率法 主要考虑曲面的光滑性, 因此插值的成果容易失真, 往往超出了最大值和最小值的范畴, 由此绘出的等 值线与实际相差较大。实际应用中此法只能作为平 滑估值, 绘出的降水量等值线主要用于定性研究降 水的空间分布及走向。 2 1 4 改进谢别德法( Modified Shepard's Method) 使用反距离加权插值法, 当增加、 删除或改变一 个点时, 需要重新计算权函数 w i ( x, y) , 为了克服反 距离加权插值法的这一缺陷, 改进谢别德法同样使 用距离倒数加权的最小二乘方的方法, 主要有以下 两个方面的改进
18 Surfer8_0等值线绘制中的十二种插值方法

第 1 期 陈欢欢等 : Surfer 81 0 等值线绘制中的十二种插值方法
53
简单 、对系统要求低等优点得到广大用户的青睐 , 成为普及度最高的绘图软件之一 。其最高版本 Surfer81 0 提供了十二种插值方法 ,用户可以根据 不同的需要选择不同方法来进行插值 ,来对其进 行分析 ,以达到自己想要的效果 。要科学地选择 插值方法和灵活地进行参数设置 ,必须要熟悉各 种插值方法的基本理论知识 ,下面将介绍 Surf2 er81 0 中的十二种插值方法及其应用实例 。
其中 , di ( x , y) = ( x - xi) 2 + ( y - yi) 2 ,表示由离散 点( xi , yi) 至 P( x , y) 点的距离。这种方法的优点是 可以通过权重调整空间插值等值线的结构。
212 克里金插值法( Kriging)
克里金插值法 ,又称克立格法是法国 G ·马特
1 引 言
在地质工作中 ,总是可以得到大量研究对象 的各方面特性或特征数据 ,在对其进行分析时 ,往
往借助于其等值线来对其进行一些必要的分析 。 要将大量数据进行处理并以等值线的形式呈现 , 这就需要一套能方便绘制等值线的绘图工具 。在 众多的商业化绘图软件中 ,美国 GOLD EN 软件 公司的 Surfer 软件 ,以其方便 、直观 、快捷 、安装
权插值求 P 点属性值。其插值原理是待插值点邻域
内已知散乱点属性值的加权平均 ,权的大小与待插
点的邻域内散乱点之间的距离有关 ,是距离 k (0 ≤k
≤2) ( k 一般取 2) 次方的倒数。即 :
i ( x , y) ]k
n
1 i =1 [ di ( x , y) ]k
隆教授以南非矿山地质工程师 D ·G ·克立格的名
surfer插值方法介绍

1、距离倒数乘方法距离倒数乘方格网化方法是一个加权平均插值法,可以进行确切的或者圆滑的方式插值。
方次参数控制着权系数如何随着离开一个格网结点距离的增加而下降。
对于一个较大的方次,较近的数据点被给定一个较高的权重份额,对于一个较小的方次,权重比较均匀地分配给各数据点。
计算一个格网结点时给予一个特定数据点的权值与指定方次的从结点到观测点的该结点被赋予距离倒数成比例。
当计算一个格网结点时,配给的权重是一个分数,所有权重的总和等于1.0。
当一个观测点与一个格网结点重合时,该观测点被给予一个实际为 1.0 的权重,所有其它观测点被给予一个几乎为 0.0 的权重。
换言之,该结点被赋给与观测点一致的值。
这就是一个准确插值。
距离倒数法的特征之一是要在格网区域内产生围绕观测点位置的"牛眼"。
用距离倒数格网化时可以指定一个圆滑参数。
大于零的圆滑参数保证,对于一个特定的结点,没有哪个观测点被赋予全部的权值,即使观测点与该结点重合也是如此。
圆滑参数通过修匀已被插值的格网来降低"牛眼"影响。
2、克里金法克里金法是一种在许多领域都很有用的地质统计格网化方法。
克里金法试图那样表示隐含在你的数据中的趋势,例如,高点会是沿一个脊连接,而不是被牛眼形等值线所孤立。
克里金法中包含了几个因子:变化图模型,漂移类型和矿块效应。
3、最小曲率法最小曲率法广泛用于地球科学。
用最小曲率法生成的插值面类似于一个通过各个数据值的,具有最小弯曲量的长条形薄弹性片。
最小曲率法,试图在尽可能严格地尊重数据的同时,生成尽可能圆滑的曲面。
使用最小曲率法时要涉及到两个参数:最大残差参数和最大循环次数参数来控制最小曲率的收敛标准。
4、多元回归法多元回归被用来确定你的数据的大规模的趋势和图案。
你可以用几个选项来确定你需要的趋势面类型。
多元回归实际上不是插值器,因为它并不试图预测未知的 Z 值。
它实际上是一个趋势面分析作图程序。
克里格空间插值法

1.7 区域变量
设x为样点在1,2或3维空间的位置,x点的随机变量Z值为:
其中m(x)是描述Z结构项的一个确定性数,c’(x)是描述随机 区域变异但空间相关的残余项,即区域变量,ξ "是残余的空间不相 关的高斯噪音项(服从标准正态分布,即平均值为0,方差为 α 2)。 如果没有趋势,那么m(x)等于样区数据的平均值,而且任何两点x 和x+h(h为间隔距离)之间的平均值或期望值的差为0。 使用Z(x),Z(x+h)表示随机变量Z在位置x,x+h的观测值, 区域化变量理论假设任意两点Z的差值的方差仅取决于位置间的距离h。
二 克里格插值
计算理论方差函数是确定插值权重的基本 过程,是预测未知位置属性值的克里格方 法(Kriging)的基础。D.G.Krige是南 非采矿工程学家,在1951年提出了矿产品 位和储量估值方法。法国地统计学家 Matheron(1971)命名了这种方法,并在 此基础上提出了区域化变量理论,使传统 的地学方法与统计方法相结合,形成了完 整的方法体系。
1.9 理论变异函数模型
4.高斯模型(Gaussian model)
变程为
。
1.9 理论变异函数模型
图是球状模型、指数模型和高斯模型的 比较,可以看出,球状模型的变程最小, 指数的模型变程最大,高斯模型的变程介 于二者之间。球状模型和指数模型过原点 存在切线,高斯模型则没有。
1.9 理论变异函数模型
1.2.2局部插值方法
只使用邻近的数据点来估计未知点的值, 包括几个步骤: a.定义一个邻域或搜索范围; b.搜索落在此邻域范围的数据点; c.选择表达这有限个点的空间变化的数学 函数; d.为落在规则格网单元上的数据点赋值。 重复这个步骤直到格网上的所有点赋值完 毕。
(surf、grapher制图作业)-赵晓亮-作业二

作业二给定数据文件(作业数据二.dat),对surfer软件的各种网格化插值方法进行比较,并提交一份实验报告。
1:方法的原理背景介绍2: 十二种插值方法在等值线图上的反映:3:十二种插值方法的差别及比较说明1》首先说明十二种插值方法的原理背景1.克里金法克里金法是一种在许多领域都很有用的地质统计格网化方法。
克里金法试图那样表示隐含在你的数据中的趋势,例如,高点会是沿一个脊连接,而不是被牛眼形等值线所孤立。
克里金法中包含了几个因子:变化图模型,漂移类型和矿块效应。
2.反距离加权方法反距离加权方法是一个加权平均插值法,可以进行确切的或者圆滑的方式插值。
方次参数控制着权系数如何随着离开一个格网结点距离的增加而下降。
对于一个较大的方次,较近的数据点被给定一个较高的权重份额,对于一个较小的方次,权重比较均匀地分配给各数据点。
计算一个格网结点时给予一个特定数据点的权值与指定方次的从结点到观测点的该结点被赋予距离倒数成比例。
当计算一个格网结点时,配给的权重是一个分数,所有权重的总和等于1.0。
当一个观测点与一个格网结点重合时,该观测点被给予一个实际为 1.0 的权重,所有其它观测点被给予一个几乎为0.0 的权重。
换言之,该结点被赋给与观测点一致的值。
这就是一个准确插值。
距离倒数法的特征之一是要在格网区域内产生围绕观测点位置的"牛眼"。
用距离倒数格网化时可以指定一个圆滑参数。
大于零的圆滑参数保证,对于一个特定的结点,没有哪个观测点被赋予全部的权值,即使观测点与该结点重合也是如此。
圆滑参数通过修匀已被插值的格网来降低"牛眼"影响。
3. 最小曲率法最小曲率法广泛用于地球科学。
用最小曲率法生成的插值面类似于一个通过各个数据值的,具有最小弯曲量的长条形薄弹性片。
最小曲率法,试图在尽可能严格地尊重数据的同时,生成尽可能圆滑的曲面。
使用最小曲率法时要涉及到两个参数:最大残差参数和最大循环次数参数来控制最小曲率的收敛标准。
Surfer8.0十二种空间插值方法

2. 等值线绘制基本原理和十二种空间插值方法介绍2.1 等值线绘制基本原理等值线绘制的基本原理是,根据空间上若干离散点的属性数据(如地面高程数据、水文观测站测得的降水量和蒸发量数据、气象站测得的气压、风力、风向值等),通过内插法生成一系列光滑曲线,即等值线(同一条等值线上任意一点的属性值相等)。
需要指出的是,有的软件又将上述空间数据内插的过程称为格网化,其实二者略有不同。
所谓格网化是指采用一定的格网化方法(即数学模型)对不规则分布的原始数据点进行插值,生成在原始数据分布范围内规则间距的数据点分布[2]。
格网化最终形成的是空间上离散的格网,而不是连续的线。
无论是绘制等值线或是格网化,构建或选用合适的数学模型均是其核心关键[3]。
2.2 S urfer 8.0十二种空间插值方法介绍2.2.1反距离加权插值法(Inverse Distance to a Power)反距离加权插值法,又称谢别德法(Shepard)[4],其插值原理是将待插值点邻域内已知散乱点属性值进行加权平均,权的大小与待插点的邻域内散乱点之间的距离有关,是距离k次方的倒数(0≤k≤2,k一般取值为2)。
反距离加权插值法综合了泰森多边形的邻近点法和多元回归法等渐变方法的长处,它假设A点的属性值是在局部邻域内中所有数据点的距离加权平均值,可以进行确切的或者圆滑的方式插值。
当计算一个格网结点时,给予一个特定数据点的权值,该权值与指定方次的结点到观测点的距离倒数成比例,给每个格网结点配给的权重是一个分数,所有权重的总和等于1.0。
当一个观测点与一个格网结点重合时,该观测点被给予一个实际为1.0的权重,所有其它观测点被给予一个几乎为0.0的权重[5][6],并且其必须指定一个大于0的平滑系数,平滑系数通过修匀已被插值的格网来降低某些“凸显”数据展现。
反距离加权插值法是一种精确性插值法,插值生成的表面的最大值和最小值只会出现在已知样本点的位置。
Surfer中网格化方法的选取方法

7.8
9
1013.8
15
16.2
-4.8
0.6
1.8
3
4.2
5.4
6.6
7.8
9
10.2
11.4
12.6
13.8
15
16.2 -0.8 -1.6 -2.4 -3.2 -4
105 90 75 60 45
C— 反 距 离 加 权 D— 最 小 曲 率
-0.8 -1.6 -2.4 -3.2 -4 -4.8 0.6 1.8 3 4.2 5.4 6.6 7.8 9 10.2 11.4 12.6 13.8 15 16.2
最小曲率法(Minimum curvature)
采用迭代的方法逐次求取网格节点数据,其插值面类似一个薄的、 线性—弹性形变板,该“板”经过所有的数据点,且每个数据点具 有最小曲率。 由于最小曲率法采用全区的数据进行网格化,因而比较适合于数据 分布不均匀的情况。在尽可能体现原数据的同时,最小曲率法产生 尽可能的光滑曲面,绘制的图件比较美观。 使用最小曲率法需要用最大偏差参数和最大循环次数参数来控制最 小曲率的收敛标准,且要求至少有4个点。 该方法速度快,适合于大量(1000个以上)数据的网格化,由于其 主要考虑曲面的光滑性,不能达到精确的插值结果,容易超出最大 值和最小值的范畴。
采用最小曲率法网格生成的图1D,与图2B克里格插值方法的效果基 本相同,有2个低阻异常区域,由一些渐变的异常点组成,有利于异常区 的圈定和解释。 采用径向基函数法网格生成的图1E,整个断面呈矩形,网格化的结 果是扩大了实测数据边界,没有数据的区域插值产生,可分辨出局部高阻 异常,因此有利于局部异常区的圈定和解释。但图形左侧和右侧等值线杂 乱,表示插值效果不好。 采用最近邻点法网格生成的图1F,整个断面呈矩形,网格化的 结果是扩大了实测数据边界,没有数据的区域插值产生,呈现2个 孤立的低阻异常区域,异常区等值线稀疏,边界呈矩形。
等值线绘图软件Surfer的数学模型介绍

等值线绘图软件Surfer介绍用微机绘制等值线,最关键一点的是对原始数据进行格网化插值。
格网化是指采用的格网化方法(即数学模型)对不规则分布的原始数据点进行插值,生成在原始数据分布范围内规则间距的数据点分布。
因此,数学模型是绘制等值线的核心。
Surfer采用了七种数学模型,每种数学模型都有其相关的参数设置。
通过对数学模型的选择和进行灵活的参数设置,可以绘制各种类型的等值线图。
下面把这七种数学模型作一简单介绍:1、距离倒数乘方法距离倒数乘方格网化方法是一个加权平均插值法,可以进行确切的或者圆滑的方式插值。
方次参数控制着权系数如何随着离开一个格网结点距离的增加而下降。
对于一个较大的方次,较近的数据点被给定一个较高的权重份额,对于一个较小的方次,权重比较均匀地分配给各数据点。
计算一个格网结点时给予一个特定数据点的权值与指定方次的从结点到观测点的该结点被赋予距离倒数成比例。
当计算一个格网结点时,配给的权重是一个分数,所有权重的总和等于1.0。
当一个观测点与一个格网结点重合时,该观测点被给予一个实际为1.0 的权重,所有其它观测点被给予一个几乎为 0.0 的权重。
换言之,该结点被赋给与观测点一致的值。
这就是一个准确插值。
距离倒数法的特征之一是要在格网区域内产生围绕观测点位置的"牛眼"。
用距离倒数格网化时可以指定一个圆滑参数。
大于零的圆滑参数保证,对于一个特定的结点,没有哪个观测点被赋予全部的权值,即使观测点与该结点重合也是如此。
圆滑参数通过修匀已被插值的格网来降低"牛眼"影响。
2、克里金法克里金法是一种在许多领域都很有用的地质统计格网化方法。
克里金法试图那样表示隐含在你的数据中的趋势,例如,高点会是沿一个脊连接,而不是被牛眼形等值线所孤立。
克里金法中包含了几个因子:变化图模型,漂移类型和矿块效应。
3、最小曲率法最小曲率法广泛用于地球科学。
用最小曲率法生成的插值面类似于一个通过各个数据值的,具有最小弯曲量的长条形薄弹性片。
surfer插值法介绍

在科学计算领域中,空间插值是一类常用的重要算法,很多相关软件都内置该算法,其中GodenSoftware 公司的Surfer软件具有很强的代表性,内置有比较全面的空间插值算法,主要包括:Inverse Distance to a Power(反距离加权插值法)Kriging(克里金插值法)Minimum Curvature(最小曲率)Modified Shepard's Method(改进谢别德法)Natural Neighbor(自然邻点插值法)Nearest Neighbor(最近邻点插值法)Polynomial Regression(多元回归法)Radial Basis Function(径向基函数法)Triangulation with Linear Interpolation(线性插值三角网法)Moving Average(移动平均法)Local Polynomial(局部多项式法)下面简单说明不同算法的特点。
1、距离倒数乘方法距离倒数乘方格网化方法是一个加权平均插值法,可以进行确切的或者圆滑的方式插值。
方次参数控制着权系数如何随着离开一个格网结点距离的增加而下降。
对于一个较大的方次,较近的数据点被给定一个较高的权重份额,对于一个较小的方次,权重比较均匀地分配给各数据点。
计算一个格网结点时给予一个特定数据点的权值与指定方次的从结点到观测点的该结点被赋予距离倒数成比例。
当计算一个格网结点时,配给的权重是一个分数,所有权重的总和等于1.0。
当一个观测点与一个格网结点重合时,该观测点被给予一个实际为1.0 的权重,所有其它观测点被给予一个几乎为0.0 的权重。
换言之,该结点被赋给与观测点一致的值。
这就是一个准确插值。
距离倒数法的特征之一是要在格网区域内产生围绕观测点位置的"牛眼"。
用距离倒数格网化时可以指定一个圆滑参数。
大于零的圆滑参数保证,对于一个特定的结点,没有哪个观测点被赋予全部的权值,即使观测点与该结点重合也是如此。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
多项式作趋势面能较好地反映连续变化的分布趋势,这在地质科学中常用到。一般说多项式次数越高,则
趋势面与实测数据偏差越小,但是,并不能说它就与实际情况最符合,这还要在实践中检验.次数较高的趋
势面只在采样点附近效果较好,在外推和内插的效果方面不好,因而在实际应用的效果并不理想。在实际
下两个方面的改进 ~ :
(1)通过修改反距离加权插值法的权函数wl(at",y)一1/[d 扛,y)3 ,使其只能在局部范围内起作用,
以改变反距离加权插值法的全局插值性质,即它利用了局部最小二乘方法来消除或减少所生成等值线的
“鸭蛋”外观
(2)同时用节点函数Q(一y)来代替离散点(。。 )的属性值≈,Q( , )是一个插值于( , )点的
反距离加权插值法是GIS软件根据点数生成规则格网数据文件的最常见的方法,计算值易受数据点
集群的影响,计算结果常出现一种孤立点数据明显高于周围数据点的“鸭蛋”分布模式,可在插值过程中通
过动态修改搜索准则进行一定程度的改进。使用反距离加权插值法对数据进行格网化时,可以指定一个圆
滑参数 圆滑参数要求大于零。对于一个特定的结点.没有哪个观测点被赋予全部的权值,即使观测点与
该结点重合也是如此。圆滑参数通过修匀已被插值的格网来降低“鸭蛋”影响。
1.2 克里金插值法
克里金(Kriging)插值法又称空间自协方差最佳插值法,它是以法国D.G.Krige的名字命名的一种最
优内插法。克里金法广泛地应用于地下水模拟、土壤制图等领域,是一种很有用的地质统计格网化方法 它
加权插值求P点属性值。距离加权插值法综合了泰森多边形的邻近点法和多元回归法的渐变方法的长
处,它假设P点的属性值是在局部邻域内中所有数据点的距离加权平均值,可以进行确切的或者圆滑的
方式插值。周围点与P点因分布位置的差异,对P( )影响不同,我们把这种影响称为权函数m , ),方
次参数控制着权系数如何随着离开一个格网结点距离的增加而下降 对于一个较大的方次,较近的数据点
有时需要排除网格文件中的无值数据的区域,在搜索椭圆(Search Ellipse)设置一个值,对无数据区域
赋予该阿格文件里的空白值。设置的搜索半径的大小要小于该阿格文件数据值之间的距离,所有的无数据
同格节点都被赋予空白值。在使用最近邻点插值同格化法,将一个规则间隔的 z数据转换为一个网格
文件时,可设置阿格问隔和XYZ数据的数据点之间的间距相等。
最近邻点插值阿格化法没有选项,它是均质且无变化的,对均匀间隔的数据进行插值很有用.同时,它
对填充无值数据的区域很有效
1.7 多元回归法
多元回归(Polynomial Regression)是用来确定数据的大规模的趋势和图案 多元回归实际上不是插值
器,因为它并不预测未知的z值,它只是根据空间的采样数据,拟台一个数学曲面,用该数学曲面来反映
最近邻点插值法(Nearest Neighbor)又称泰森多边形方法,泰森多边形(Thiesen,又叫Dirichlet或
Voronoi多边形)分析法是荷兰气象学家A.H_Thiessen提出的一种分析方法。最初用于从离散分布气象
站的降雨量数据中计算平均降雨量,现在GIS和地理分析中经常采用泰森多边形进行快速的赋值_2]。实际
空间分布的变化情况,它实际上是一个趋势面分析作图程序。趋势面分析是对地质特征的空同分布进行研究和分析的一种方法,它是用某种形式的函数所代表的
曲面来逼近该地质特征的空间分布。这个函数从总体上反映了采样数据的区域性变化趋势,称为趋势面部
分;采样数据的实测值与这个函数对应值之差,称为偏差部分,它反映了,局部性的变化。这就是说,把采样
二次多项式.即有Q( 。 )一≈( 1。2,? ,n)。而且Q . )在点 , )附近与函数属性值z(x, )具
有局部近似的性质。因此,如果认为距离( , )较远的点对Q( , )影响不大,则可以认为在(z , )点
附近, 。 )就可以近似地表示函数属性值 , )了。改进谢别德法可以是一个准确或圆滑插值器。
基函数的形式往往是髓 , )=^(4),这里的盔表示由点(z, )到第i个数据点的距离。径向基函数插值
法是多个数据插值方法的组合。根据生成一个圆滑曲面适应数据的能力.许多人认为其中的复二次函数是
最好的方法 一。所有径向基函数插值法都是准确的插值器,它们都能尽量适应你的数据。若要生成一个更
圆滑的曲面.对所有这些方法都可以引入一个圆滑系数。
数据的实测值分解成两部分,趋势面部分和偏差部分,趋势面部分用一个函数表示,它反映采样数据的总
体变化,可以认为是由大范囝的系统性因素引起的;偏差部分反映了,局部性的变化特点,可以认为由局部
因素和随机因素引起的一 一。
使用多元回归法进行趋势面分析要考虑两个方面的问题 一是趋势面函数(数学表达式)的确定;二是
合,即加权线性平均,无偏是指理论上估计值的平均值等于实际样本值的平均值,即估计的平均误差为0,
最优是指估计的误差方差最小一
1.3 最小曲率法
最小曲率法(Minimum Curvature)广泛应用于地球科学 用最小曲率法生成的插值面类似于一个通过
各个数据值、具有最小弯曲量的长条形薄薄的弹性片。最小曲率法试图在尽可能严格地尊重数据的同时,
进行加权平均来估计块段品位的方法。但它仍是一种光滑的内插方法 在数据点多时,其内插的结果可信
度较高 :。
克里金法类型分常规克里金插值(常规克里金模型/克里金点模型)和块克里金插值。常规克里金插值
其内插值与原始样本的容量有关,当样本数量较少的情况下,采用简单的常规克里金模型内插的结果图会
出现明显的凹凸现象;块克里金插值是通过修改克里金方程以估计子块B内的平均值来克服克里金点模
首先考虑的是空间属性在空间位置上的变异分布.确定对一个待插点值有影响的距离范围,然后用此范围
内的采样点来估计待插点的属性值。该方法在数学上可对所研究的对象提供一种最佳线性无偏估计(某点
处的确定值)的方法。它是考虑了信息样品的形状、大小及与待估计块段相互间的空间位置等几何特征以
及品位的空间结构之后,为达到线性、无偏和最小估计方差的估计,而对每一个样品赋与一定的系数,最后
上,最近邻点插值的一个隐含的假设条件是任一阿格点p(x,y)的属性值都使用距它最近的位置点的属性
值,用每一个网格节点的最邻点值作为待的节点值 。当数据已经是均匀问隔分布,要先将数据转换为
SURFER的网格文件,可以应用最近邻点插值法;或者在一个文件中,数据紧密完整,只有少数点没有取
值,可用最近邻点插值法来填充无值的数据点。
型的缺点,对估算给定面积实验小区的平均值或对给定格网大小的规则格网进行插值比较适用。块克里金
插值估算的方差结果常小于常规克里金插值,所以,生成的平滑插值表面不会发生常规克里金模型的凹凸
现象。按照空间场是否存在漂移(drift)可将克里金插值分为普通克里金和泛克里金,其中普通克里金
(Ordinary Kriging简称OK法)常称作局部最优线性无偏估计.所谓线性是指估计值是样本值ห้องสมุดไป่ตู้线性组
生成尽可能圆滑的曲面[s。最小曲率法不是一个精确的插值法.也就是说在插值的过程中不可能总是完全
尊重数据。
使用最小曲率法时要涉及到两个参数:最大偏差参数(Maximum Residuals)和最大循环次数(
Maximum Iteration parameter)参数来控制最小曲率的收敛标准,而且最小曲率法要求至少有四个点
引言
在地学的研究工作中,不可避免地要应用某种手段获取能够反映研究对象各方面特性或特征的数据,
例如磁力、重力、化学勘探数据、钻探获得的岩面标高、海底或陆地的地形标高和地理要素指标等等。为了
方便深人研究.要将数据处理并以等值线图的形式呈现。目前,绘制等值线的软件不少,但是,它们往往是
为满足各自的需要而以小程序的形式开发出来,采用单一的插值方法,功能比较简单,适用性不广。这里介
在用改进谢别德法作为格网化方法时要涉及到圆措参数的设置 圆滑参数是使改进谢别德法能够象
一个圆滑插值器那样工作,增加圆滑参数的值可增强圆滑的效果。
1.5 自然邻点插值法
自然邻点插值法(Natural Ndghbor)是Surfer7、0才有的网格化新方法。自然邻点插值法广泛应用于
一些研究领域中。其基本原理是对于一组泰森(Thiessen)多边形,当在数据集中加入一个新的数据点(目
应用中,对起伏变化比较缓和的简单采样数据配合次数较低的趋势面,就可以反映出区域背景;而变化复
杂且起伏较多的采样数据要配合次数较低高的趋势面 l 。
使用多元回归法时要涉及到曲面定义和指定xY的最高次数设置,在曲面定义中选择所需的多项式
类型,可选用的曲面类型:简单平面(Simple planar surface)、双线性鞍(Bi—linear saddle)、二次曲面
1_4 改进谢别德法
改进谢别德法(ModifiedQuadratic Shepard)是由Franke及Nielson提出,它仍是一个与距离成反比的
加权方法。在使用反距离加权插值法时,当增加、删除或改变一个点时,需要重新计算权函数m(z, ),为
了克服反距离加权插值法的这一缺陷,改进谢别德法同样使用距离倒数加权的最小二乘方的方法,但有以
绍的SURFER是美国COLDEN软件公司的产品,用于绘制等值线图及相应的三维图形,是科技工作者
特别是地学研究人员必备的软件,应用极广。sURFER 目前的最高版本为7.O3,它提供的内插方法多达
