数字图像加密算法之图像融合技术加密
一种基于Arnold变换的数字图像加密算法

第35卷第3期2009年5月 光学技术OPTICAL TECHN IQU E Vol.35No.3May 2009文章编号:100221582(2009)0320384204一种基于Arnold 变换的数字图像加密算法Ξ任洪娥,尚振伟,张健(东北林业大学信息与计算机工程学院,哈尔滨 150040)摘 要:提出了一种基于Arnold 变换的均匀数字图像加密算法。
将传统的Arnold 变换进行改进,加入两个参数a ,b ,并利用Logistic 映射产生参数序列。
将数字图像分块,对每个图像块分别进行参数不同的Arnold 变换,由此实现对图像的位置置乱。
另外将Arnold 变换推广至多维,用于图像的灰度置乱,从而构造一个位置置乱和灰度置乱相结合的图像加密算法。
实验仿真结果表明该算法能够取得很好的加密效果,且具有密钥空间大,密钥敏感性强,以及能够抵御统计和已知明文攻击等优点。
基本满足图像加密的有效性和安全性要求。
关键词:Arnold 变换;Logistic 映射;数字图像加密中图分类号:TP301.6 文献标识码:AAn algorithm of digital image encryption based on Arnold transformationRE N H ong 2e ,SH ANG Zhen 2wei ,ZH ANG Jian(College of Information and Computer Engineering ,Northeast Forestry University ,Harbin 150040,China )Abstract :A digital image encryption algorithm is presented based on Arnold transformation.The traditional Arnold trans 2formation is improved by adding two parameters a and b ,furthermore the Logistic map is used to generate the parameter se 2quences.The digital image is blocked and the Arnold transformation with different parameters is carried out on each image block of the digital image ,thus image location scrambling is achieved.In addition the Arnold transformation is extended to multi 2di 2mensional then used on the image gray scrambling ,so as to construct an algorithm combine both the position scrambling and the gray scrambling.The results of simulation show that this algorithm can achieve good image encryption effect.And it has a large key space ,key sensitivity and many other advantages such as withstand statistical and known expressly attack.It basically meets the effectiveness and security requirements of image encryption.K ey w ords :Arnold transformation ;logistic map ;digital image encryption0 引 言图像作为人类认识和表达世界的基本方法,应用极为广泛,从古老的壁画、象形文字到今天的数字化视频,图像一直伴随着人类历史的发展。
数字复合图像加密传输技术研究

数字复合图像加密传输技术研究第一章绪论数字复合图像加密传输技术是一种将传输的信息经过加密处理后再进行传输的技术,旨在保护信息的安全性。
该技术已经广泛应用于金融、军事、安全等领域,成为网络时代信息传输和保护的重要手段。
本文将就数字复合图像加密传输技术进行探讨和研究。
第二章相关技术的研究数字图像处理技术可分为两类,即基于空间域的技术和基于频率域的技术。
前者通过对图像像素点的分析来实现图像的增强、滤波、锐化等功能;后者则通过对图像进行傅里叶变换来实现对图像的处理。
同时,数字图像加密也是一种重要技术。
目前,常见的数字图像加密方法包括基于混沌的图像加密技术、基于分形的图像加密技术、基于小波变换的图像加密技术等。
第三章数字复合图像加密传输技术的研究数字复合图像包括利用多种图像融合技术将两张及以上数字图像进行复合,生成一个新的图像。
数字复合图像集合中的每一幅图像都被看作是新形成的复合图像的一个部分。
数字复合图像加密传输技术的实现基于该原理,即将数字复合图像进行加密后传输,以保证传输安全。
基于此原理,数字复合图像加密传输技术主要有以下几种实现方式:(1)基于小波变换的数字复合图像加密传输技术小波变换作为一种不可逆的数字信号处理技术,已经应用于数字图像处理领域中,其具有多分辨率分析、逼近精度高等特点。
基于小波变换的数字复合图像加密传输技术实现两张及以上图片的复合,并通过对小波系数进行变换,进行加密处理后再进行传输。
(2)基于混沌系统的数字复合图像加密传输技术混沌系统是一种非线性动力学系统,其中包含的混沌现象具有很强的不可预测性和随机性。
基于混沌系统的数字复合图像加密传输技术的原理是将原始信号与混沌信号进行复合加密,传输前先进行去噪处理,提高混沌系统的加密性能与稳定性。
(3)基于分形编码的数字复合图像加密传输技术分形编码是一种将图像信息分解成若干个小块,并通过对小块进行自相似变换来实现信息的编码和压缩。
基于分形编码的数字复合图像加密传输技术的原理是将两幅以上分形编码图像进行复合加密,传输前先进行去噪处理,提高分形编码的加密性能与稳定性。
基于Hill密码的数字图像加密算法

摘要:低阶的加密矩阵具有易于计算的特点,应用于加密将使算法效率提高。
混沌序列具有容易生成、对初始条件敏感等特点,可用于生成大量的低相关度的低阶矩阵。
提出了一种以古典的Hill密码为理论基础的图像加密算法,通过Logistic映射生成相应低阶加密矩阵,并利用其进行数字图像加密,得到了较好的结果。
关键词:Hill密码;Logistic;映射;图像加密1 引言随着互联网技术与多媒体技术的快速发展, 人们之间的多矩阵中序列可取任意一种排列。
排列方式作为密钥的一部分。
为论述简易,下文中序列取默认排列方式。
媒体通信逐渐成为信息交流的重要手段。
人们通过网络交流的Eij 是一个取值于[0,255] 的整数,其取值视加密者的需要各种信息往往与自身利益相关。
因此,信息的保密与安全显得日益重要。
图像在人们用于交互的多媒体信息占有较大比重。
传统的加密技术将其作为普通数据流进行加密,而不考虑图像数据的特点,因此有一定的局限性[1]。
Hill 密码是一类替代密码,其优点有可隐藏明文字母频率,表示简洁,易于计算机实现,可使用可逆矩阵加密解密等。
可将之应用于图像加密。
Hill 密码的关键在于加密矩阵。
如果加密矩阵不可逆,密文将无法还原成明文。
Bibhudendra 等人提出应用构造自逆矩阵[2]对信息进行加密以克服这一弱点。
其自逆矩阵的构造采用伪随机数并且元素之间具有很强相关性,因此易于破解。
文献[1]就此提出使用混沌序列来构造加密矩阵,但是其构造方法较为复杂。
文中应用低阶方阵构成的序列来对图像进行加密,其计算简易,可轻松解决加密矩阵的可逆性控制问题;又应用混沌映射产生序列中方阵的元素,使方阵之间的相关性较低,从而使密文难于破解。
2 图像的矩阵模型对于任一大小为m×n的图像I,I中的每个像素P ij(i= 0,1,2,…m;j=0,1,2,…n)的颜色都由三原色红、绿、蓝(R、G、B)组成。
像素的任意原色在计算机中表示为一个整数x,取值范围为x∈[0,255]。
LSB数字图像加密技术

LSB数字图像加密技术实验一:LSB 信息隐藏实验【实验目的】:一、熟悉MATLAB 基本操作二、完成LSB 实验【实验内容】:(请将你实验完成的项目涂“■”)实验完成形式:■ 用MA TLAB 函数实现LSB 信息隐藏和提取■ 用MA TLAB 命令行方式实现LSB 信息隐藏和提取□ 其它:(请注明)实验选择载体:■ 256×256灰度图像■ 256×256RGB 图像■ 任意大小的RGB 图像实验效果和分析:■ 分析了LSB 算法的抗攻击能力■ 能随机选择嵌入位(考虑安全性因素)■ 嵌入位均匀分布于载体□ 信息提取的检错/纠错□ 其它:(请注明)【实验工具及平台】:■ Windows+Matlab ■ 其它:(请注明) WinHex【实验涉及到的相关算法】:1、RGB 图像的每个像素有三个颜色分量(r,g,b )构成,且r,g,b 三个颜色分量都是取值(0,1)内的,为了便于计算机的“位”概念相联系,进行LSB 操作,我们想(0,1)与(0,255)进行对应。
10255doubleuint8图一在uint8中修改单位1,实际上就是相应修改像素值1/256=0.0039。
嵌入过程:for (i=1;i<=像素序列个数;i++)综合评分:i i s c →For(i=1;i<=秘密消息长度;i++)//将选取的像素点的最不重要位依次替换成秘密信息 i i j j i s c m →?图二提取过程:For(i=1;i<=秘密消息长度;i++) {i i j ? //序选取()i i j m LSB c ← }图三本实验中LSB 认为是图片中每个像素的最低位bit 值【实验分析】:1、顺序隐藏,256*256灰度图,LSB=1原始图像隐藏信息的图像LSB空域信息隐秘LSB空域信息隐秘位置隐秘消息的像素未隐秘消息的像素隐藏的信息:左图是原始图像与隐写图像的区别,可以看到左边的白色部分是两幅图的不一样之处,也就是隐秘消息的地方,因为是顺序隐秘,所以很容易检测出。
数字图像加密算法的研究与实现

数字图像加密算法的研究与实现摘要数字图像加密是进行数字图像信息保密的一种手段。
随着信息技术的飞速发展,数字图像在各个领域中有着极为广泛的运用,那么数字图像中所包含的信息安全性应受到重视。
数字图像本身具有数据量较大的特点,用传统的的加密方法往往无法达到加密的要求,许多学者对数字图像的信息安全性进行了多次研究并提出了许多强而有效的算法。
本文研究并实现了一种基于混沌序列置乱的数字图像加密算法,通过密钥产生混沌序列,将该混沌序列进行逻辑排序,并以此排列方法对数字图像进行加密。
该算法隐私性较强,在数字图像的加密和解密过程中均需要密钥的参与,因此不知道密钥的用户无法恢复数字图像,具有良好的保密性。
关键词:数字图像混沌加密数据隐藏AbstractDigital image encryption algorithm is a method about keeping the information of digital image secret.With the quick development of informational technology,the digital image has been utilized in many areas,so the security of message that digital images carry should be paid attention.Particularly ,digital images have the characteristic of a large amount of data,it can not meet demands about encryption that encrypting data in traditional way,which leads to a lot of scholars have spent much time and energy on researching the security about digital image information and illustrated many effective algorithm.This article discuss and illustrate a kind of digital image encryption algorithm based on chaotic array disruption,producing chaotic array according to the key,then logically arranging existed chaotic array,finally encrypt digital image with same logic.It shows better privacy.This process requires keys participating in both encryption and deciphering,so anyone does not know the key who can not rebuild the original image.Key words:digital image chaotic encryption hiding data目录摘要 (I)Abstract (II)绪论 (1)1数字图像加密的基础理论 (4)1.1密码学的介绍 (4)1.2 图像加密技术 (4)1.3数字图像的置乱 (5)1.4混沌加密简介 (5)1.5混沌加密安全性分析 (6)2开发工具简介 (8)3基于混沌的数字图像加密算法 (11)3.1数字图像混沌加密算法总体设计 (11)3.2 数字图像混沌加密算法 (11)3.3数字图像混沌解密算法 (13)4实验仿真与结果 (14)4.1编程实现相关函数及其方法 (14)4.2仿真结果 (14)4.2.1非彩色图像实验仿真 (14)4.2.2彩色图像实验仿真 (16)结论 (18)附录1混沌加密与混沌解密算法代码 (19)绪论计算机和网络的飞速发展为多媒体数字产品的使用、传播提供了极其便利的途径,然而由于数字产品具有极易被复制和修改的特性,使得数字作品的信息安全问题和版权保护成为迫切需要解决的难题。
数字图像加密技术研究与应用

数字图像加密技术研究与应用随着信息和通信技术的不断发展,人们对信息的保密性要求越来越高。
特别是在互联网高度发达的时代,数字图像成为了人们交流、存储和传递信息的重要手段。
在这样的背景下,数字图像加密技术的研究和应用已成为了热门话题。
数字图像加密技术作为一种保护数字图像安全性的手段,通过将数字图像进行加密处理,从而达到信息的保密目的。
根据操作方法的不同,数字图像加密技术可以分为对称和非对称两种加密方式。
对称加密方式是指加密和解密使用同一密钥的方式。
其中,常见的加密算法有DES、AES和IDEA等。
具体操作过程是,通过密钥将明文图像加密后得到密文图像,接着再通过同一密钥进行解密操作,得到原始的明文图像。
对称加密方式速度较快,但是密钥的传递和保护是一个重要的问题。
因为只要密钥暴露,那么加密就会失去保密效果。
非对称加密方式则是指加密和解密使用不同密钥的方式。
其中,常见的加密算法有RSA和DSA等。
具体操作过程是,将一对密钥产生后将其分为私钥和公钥两部分。
私钥只有所有者才能拥有,而公钥则可以分发给任何需要发送信息的人。
通过公钥进行加密操作,得到密文图像,接着使用私钥进行解密操作,得到原始的明文图像。
非对称加密方式安全性较高,但是处理时间较对称加密方式长。
除了对称和非对称加密方式外,数字图像加密技术还有基于混沌和分形等数学理论的加密方式。
这些加密方式一般被称为“新型加密技术”,通过利用非线性的动态特征进行图像加密,提高了加密系统的安全性,同时也在加密系统中应用了数学领域中的前沿技术,具有较强的科技含量。
数字图像加密技术的研究是为了解决数字图像安全问题,并促进数字图像的更加广泛和更多样的应用。
这些应用包括但不限于在线交易、电子商务、视频会议、多媒体信息系统等。
同时,数字图像加密技术还可以用于政府、军队、企业等领域中,保护机密信息的安全性。
然而,在数字图像加密技术的研究和应用过程中,还存在一些问题亟待解决。
比如密钥管理、加密算法的可靠性和鲁棒性、加密速度等问题。
数字图像加密技术

程 clear RGB=imread('lenna.jpg');
序 s=size(RGB); 一 r=randsample(s(1),s(1));
RGBS=RGB(r,:,:); t=1;j=1;f=1:r; while t<=length(r)
f(j)=find(r==t); t=t+1; j=j+1; end f; RGBE=RGBS(f,:,:); subplot(1,2,1);imshow(RGBS);title('加密后','fontsize',20); subplot(1,2,2);imshow(RGBE);title('解密后','fontsize',20);是随着信息安全与保密被重视而发展起来的。
良好的数字图像加密算法一方面可以达到使非法使用者无法破译图像内
容的目的。 Digital image encryption, decryption technology is with the
development of information security and confidentiality are considered. Good digital image encryption algorithm based on the one hand, can achieve the purpose of making illegal users unable to decipher image content.
基于Matlab的数字图像加密 解密技术研究
Contents
1
概述
2
随机打乱各层的行或列
3
像素点随机打乱
数字图像加密算法研究与实现.doc

海南大学毕业论文(设计)题目:数字图像加密算法研究与实现学号:姓名:年级:二零一零级学院:信息科学技术学院系别:通信工程系专业:通信工程指导教师:完成日期:2014 年5月 1 日摘要近十年来,随着信息网络技术的飞速发展,多媒体技术在各领域的应用可谓是日新月异。
数字图像无疑已经成为互联网的主要交互对象之一。
数字图像在军事系统、政府机构、医疗系统、国防系统和金融系统等重要机构中得到了广泛应用,这也意味着图像在传输的过程中存在着巨大的安全隐患。
若在传输的时候被第三方恶意的拦截、随意篡改、非法拷贝、任意传播,后果将会很严重。
所以数字图像的安全传输问题,受到了大众的普遍重视。
因此信息安全已成为人们关心的焦点,也是当今的研究热点和难点。
为了实现数字图像保密,实际操作中一般先将二维图像转换成一维数据,再采用传统加密算法进行加密。
与普通的文本信息不同,图像和视频具有时间性、空间性、视觉可感知性,还可进行有损压缩,这些特性使得为图像设计更加高效、安全的加密算法成为可能。
本文重点介绍了基于混沌理论的图像加密算法,对比并研究了几个典型的混沌系统:Logistic映射、Hemon映射、Lorenz系统以及猫映射。
最后,在matlab7.8环境下,对灰度图像进行了基于Logistic映射的加密解密,并得出正确的结果。
关键词:Logistic映射;图像加密;混沌系统;位置置乱AbstractIn the past ten years, with the rapid development of information network technology, the application of multimedia technology in all fields is change rapidly. Digital image has become one of the main object of the internet. Interactive image has been widely used in the important organization of military system, government agencies, medical systems defense systems and financial systems, this also means that the image has many security hidden troubles in the interactive process. If the transmission was malicious third party interception, tamper with, illegal copy, spread, the consequences will be very serious. So the digital image security problems of interaction, has attracted much attention from the public. Therefore, information security has become the focus of people's concern is also the hot spot and difficulty. In order to realize the digital image encryption, the actual operation of the video general first two-dimensional image into one-dimensional data then adopts the traditional encryption. Unlike ordinary text, images and with temporal, spatial, visual perceptibility, also can be loss compression, these features make the image encryption algorithm to design more efficient, safe possible. Image encryption algorithm has gained abundant research achievements, people have designed many image encryption algorithmThis paper introduces image encryption algorithm based on chaotic theory, and studied several typical chaotic systems: Logistic mapping; Lorenz system and cat map. In the matlab7.8 environment, Logistic mapping of the encryption and decryption based on a gray image of arbitrary input, and can get the correct resultsKeywords:Logistic map; image encryption; chaotic system; position scrambling目录1 绪论 (1)1.1 研究背景 (1)1.2 研究方法 (1)1.3 研究内容 (2)2 数字图像加密理论概述 (3)2.1数字图像的基本知识 (4)2.2 数字图加密算法的性能要求 (4)2.3 数字图像加密算法的分类 (5)2.3.1基于矩阵变换像素置换的图像加密技术 (5)2.3.2基于秘密分割与秘密共享的图像加密技术 (6)2.3.3基于现代密码体制的图像加密技术 (6)2.3.4基于混沌理论的图像加密算法 (7)3 基于混沌理论的图像加密算法 (8)3.1 混沌的基本理论 (8)3.1.1 Li-Yorke的混沌定义 (8)3.1.2 Devaney 的混沌定义 (9)3.1.3 Melnikov 的混沌定义 (10)3.2混沌的特征 (10)3.3常见的混沌系统的研究方法 (11)3.4几种典型的混沌系统 (12)3.5.1 Logistic映射 (12)3.5.2 Henon映射 (15)3.5.3 Lorenz系统 (155)3.5.4猫映射 (12)4 基于Logistic映射的图像加密/解密研究与实现 (17)4.1基于Logistic映射的像素值加密及解密方案 (17)4.2基于Logistic映射的像素位置加密及解密 (19)4.2.1具体加密方案 (20)4.2.2解密方案 (20)4.3实验结果以及仿真分析 (21)4.3.1基于像素点置乱图像加密/解密的实验结果及分析 (21)4.3.2基于像素位置置乱图像加密/解密的实验结果及分析 .. (23)4.3.3结合像素点与位置的双重置乱分析 (25)5 总结 (28)致谢 (28)参考文献 (29)1 绪论1.1 研究背景近十年来,随着信息网络技术的飞速发展,多媒体技术在各领域的应用可谓是日新月异。
图像加密技术

1引言随着宽带网和多媒体技术的发展,图像数据的获取、传输、处理遍及数字时代的各个角落。
安全问题也日益严重。
很多图像数据需要进行保密传输和存储,例如军用卫星拍摄的图片、新型武器图纸、金融机构建筑图等,还有些图像信息根据法律必须要在网络上加密传输,例如在远程医疗系统中,患者的病历和医学影像等[1]。
由于这些图像数据的特殊性,图像加密技术将它们处理为杂乱无章的类似噪音的图像,使未授权者无法浏览或修改这些信息。
近十年来,用光信息处理技术来进行数据加密和保障数据安全引起了相当的关注。
Pefregier和Javidi最早发表了这个领域的研究论文[2]。
由于光学信息处理系统的高度并行性和超快处理速度[3],光学安全(optical security)技术对信息安全技术的发展具有重要的理论意义和应用前景。
光学加密技术提供了一个更加复杂的环境,并且和数字电子系统相比,他对于攻击更有抵抗力。
另外,由于傅里叶光学信息处理系统具有读写复振幅的能力,而该复振幅信息由于其相位部分在普通光源下是无法看到的,故不能用仅对光强敏感的探测器,如CCD摄像机、显微镜等,进行读和写。
因此利用光学信息处理对光学图像进行安全加密是一种行之有效的方法。
1995 年, Philippe Refregier 等[4]提出了双随机相位编码方法,这种方法具有较好的安全性和鲁棒性。
从此光学加密技术进入快速发展时期。
研究人员随后提出了基于分数傅里叶变换的加密方法、基于菲涅耳变换的加密方法、基于联合变换相关器的加密系统、利用离轴数字全息的加密系统和利用相移干涉技术的加密系统等大量新的或改进的加密系统,使得光学加密领域的研究异彩纷呈。
虽然目前光学加密技术的发展方兴未艾,但其前景不可估量。
总的来说,与电子手段相比,现有的光学加密系统还存在一些缺点:可实施性、灵活性与稳定性都有待提高。
以下将从基于傅里叶变换的双相位编码图像的加密原理入手,将其推广到分数阶傅里叶域,并介绍几种方法,以及基于分数阶傅里叶变换的其他图像加密方法。
数字图像加密技术综述

数字图像加密技术综述作者:何纪辉王倩赵瑛来源:《计算机时代》2022年第10期摘要:综述了一些传统图像加密体制以及目前研究应用较多的图像加密技术。
简述了两大密钥体制的发展情况,分析了基于矩阵变换和像素置乱的图像加密技术。
介绍了混沌理论在图像加密中的应用,同时包括与混沌系统并用的其他加密技术,如基于DNA编码的混沌图像加密、基于压缩感知的混沌图像加密,以及基于光学成像的混沌图像加密。
阐述了各加密技术的特点及其应用情况,分析其优缺点。
对未来的发展趋势做出假设。
关键词:密码学; 图像加密; 矩阵变换; 混沌加密中图分类号:TP309 文獻标识码:A 文章编号:1006-8228(2022)10-12-05Overview of digital image encryption technologyHe Jihui, Wang Qian, Zhao Ying(School of Information Engineering, Inner Mongolia University of Science and Technology, Baotou, Inner Mongolia 014010, China)Abstract: In this paper, some traditional image encryption systems and image encryption techniques that are currently researched and applied are reviewed. The development of the two key systems is briefly described, and the image encryption technology based on matrix transformation and pixel scrambling is analyzed. The application of chaos theory in image encryption is introduced,and other encryption techniques used with chaotic systems are also included, such as chaotic imageencryption based on DNA coding, chaotic image encryption based on compressed sensing, and chaotic image encryption based on optical imaging. The characteristics and application of each encryption technology are expounded, and its advantages and disadvantages are analyzed. Assumptions are made about the future development trend.Key words: cryptography; image encryption; matrix transformation; chaotic encryption0 引言在图像信息加密的过程中,信息加密的速度、空间的占用率、密文的复杂程度、抗噪能力以及抗攻击性都是反映图像加密算法优劣性的重要指标。
图像加密技术综述

图像加密技术综述随着数字图像技术的快速发展,图像数据的应用越来越广泛,但同时也带来了越来越多的安全问题。
为了保护图像数据的安全性,图像加密技术应运而生。
本文将概述图像加密技术的历史、定义、分类,并深入探讨图像加密技术的研究意义、具体实现方法以及未来发展趋势。
一、图像加密技术概述图像加密技术是一种通过特定的加密算法将图像数据转换为不可读或不可用的形式,以保护图像数据的安全性和机密性的技术。
根据加密原理的不同,图像加密技术可以分为可逆加密和不可逆加密两类。
其中,可逆加密是指通过加密算法将图像数据转换为可逆的加密图像,解密时可以通过相应的解密算法将加密图像恢复成原始图像;不可逆加密是指通过加密算法将图像数据转换为不可逆的形式,解密时无法恢复原始图像。
二、图像加密技术详解1.密码技术密码技术是图像加密技术的核心,包括密码的建立和破解方法两个方面。
其中,密码的建立是指通过特定的算法和密钥生成加密图像的过程;破解方法则是指通过一定的技术手段和工具尝试破解加密图像的过程。
在密码技术中,密钥的管理和安全分发是关键问题,需要采取有效的措施来确保密钥的安全性和机密性。
2.图像处理技术图像处理技术是实现图像加密的必要手段,包括图像的预处理、加密处理、解密处理等。
在预处理阶段,需要对输入的原始图像进行一些必要的处理,如调整图像大小、改变图像格式等,以便于进行后续的加密处理;加密处理则是将预处理后的图像通过特定的加密算法转换为加密图像;解密处理则是将加密图像通过相应的解密算法恢复成原始图像。
3.安全威胁分析在图像加密技术中,安全威胁是不可避免的。
这些威胁可能来自于恶意攻击者、病毒、黑客等。
为了应对这些威胁,需要深入分析可能存在的安全漏洞和攻击手段,并采取有效的措施来提高加密算法的安全性和鲁棒性。
例如,可以采用一些复杂度较高的加密算法来增加破解难度;或者采用多层次加密的方法来增加破解成本和时间。
4.未来发展方向随着技术的不断发展和进步,图像加密技术也在不断发展和演变。
数字图像加密技术的研究

数字图像加密技术的研究近年来,随着数字图像在各个领域的广泛应用,保护图像的安全性和隐私性变得尤为重要。
数字图像加密技术应运而生,成为保护图像隐私的重要手段。
本文将探讨数字图像加密技术的研究现状以及其在保护图像安全性方面的应用。
数字图像加密技术是一种基于密码学原理的技术,通过对图像进行加密转换,使得除了授权者之外的任何人无法理解图像的内容。
在图像加密过程中,首要考虑的是加密算法的安全性和效率。
常见的数字图像加密算法有DES(数据加密标准)、RSA (一种非对称加密算法)以及AES(高级加密标准)等。
这些算法通过对图像像素值的置乱、置换和替换等操作,实现对图像的加密保护。
同时,为了提高加密效率,研究者们还提出了很多优化算法,如基于混沌系统的加密算法和基于人工智能的加密算法等。
数字图像加密技术的研究不仅仅局限于加密算法的设计,也涉及到加密密钥的生成和管理、加密图像传输和解密等方面。
密钥的生成和管理是加密技术的核心问题之一。
目前,常用的密钥生成方法有基于密码学的方法、基于混沌系统的方法和基于生物特征的方法等。
这些方法都旨在生成强大的密钥,保证加密的安全性。
而加密图像的传输和解密则需要保证图像在传输过程中不被篡改,同时能够被授权者正确解密。
为了实现这一目标,研究者们提出了很多解决方案,如基于公钥密码学的数字签名、数字水印技术以及多重加密技术等。
数字图像加密技术的研究不仅在保护个人隐私方面具有重要意义,还在军事、医学、金融等领域有广泛的应用。
例如,在军事领域,加密技术可以用于保护机密图像的传输和存储,防止敌方获取敏感信息。
在医学领域,加密技术可以用于保护医学影像的隐私,防止未经授权的人员获取患者的隐私信息。
在金融领域,加密技术可以用于保护金融交易的安全性,防止黑客攻击和信息泄露。
综上所述,数字图像加密技术的研究对于保护图像的安全性和隐私性具有重要意义。
当前,这一领域的研究主要集中在加密算法的设计和密钥的生成管理等方面。
基于超混沌系统的融合数字图像加密研究
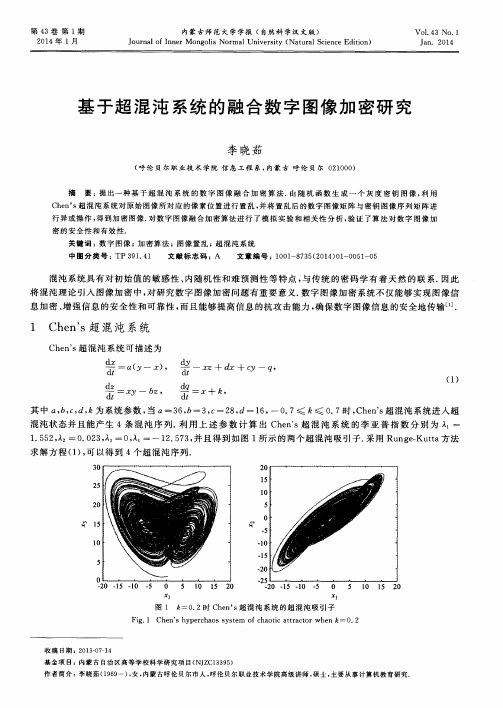
( 2 ) 的索引值 ; l y与 相 同.
( 3 )
其中 [ ・ , ・ ] 一s o r t ( ・ ) 是排序索引函数 , / 是对 X升序排列后得到 的新序列 , l x是 步骤 5 : 将z z, z 组 合成 一个 二维 矩 阵 , 利 用 以下 公 式置乱 矩 阵 Oe :
Vo 1 . 43 No .1
J a n .2 0 1 4
基 于超 混 沌 系统 的 融合 数 字 图像 加 密 研 究
李 晓 茹
( 呼 伦 贝 尔职 业 技 术 学 院 信 息 工程 系 , 内 蒙 古 呼伦 贝 尔 0 2 1 0 0 0 )
摘
要 :提 出 一 种 基 于 超 混 沌 系 统 的 数 字 图像 融 合 加 密 算 法. 由 随机 函数 生 成一个 灰 度 密钥 图像 , 利 用
步骤 3 :根 据 系 统 ( 1 ) , 在 初 始 值 , , z , q 及系统 参 数 a , b , f , d , k的条件下 产 生 的两条 混沌分 别 为 X
步骤 4 : 对 混沌 序列 x, y进 行排 序. 排 序公 式 为 :
,
_ 厂 ] 一s o r t ( x) , E l y, f y] 一s o r t ( y) ,
第 4 3卷 第 1 期
2 0 1 4年 1月
内蒙 古 师 范 大学 学报 ( 自然 科 学 汉 文 版 )
J o u r n a l o f I n n e r Mo n g o l i a No r ma l Un i v e r s i t y( Na t u r a l S c i e n c e Ed i t i o n )
密的安全性和有效性.
数字图像加密技术

reshape:该函数可将矩阵重新排列,调用方式为reshape(A,m,n,q)即将
矩阵A重置为m*n*q的矩阵。
find:可找出矩阵中某一元素的位置
2
准备知识
A(b):可将矩阵A中的元素按照向量b的顺序重新排列
原理:
用imread函数将图像读入矩阵RGB中, RGB是一个m行n
列3层的矩阵。
用randsample产生一个与图像矩阵RGB的行数m相等的
整数随机数列并返回到r中。这样就可以将原图像矩阵的行随 机打乱,将打乱后的矩阵返回至RGBS中。 用find函数找出向量r内从1到m的元素的位置并返回到向
量f。至此就可以将打乱的图像还原。
程 序 一
clear RGB=imread('lenna.jpg'); s=size(RGB); r=randsample(s(1),s(1)); RGBS=RGB(r,:,:); t=1;j=1;f=1:r; while t<=length(r) f(j)=find(r==t); t=t+1; j=j+1; end f; RGBE=RGBS(f,:,:); subplot(1,2,1);imshow(RGBS);title('加密后','fontsize',20); subplot(1,2,2);imshow(RGBE);title('解密后','fontsize',20);
程 序 五
clear RGB=imread('lenna.jpg'); s=size(RGB); r=rand(s(1),s(2),s(3))*50; RGBD=im2double(RGB); RGBS=RGBD.*r; RGBE=RGBS./r; subplot(1,2,1);imshow(RGBS);title('加密后','fontsize',20); subplot(1,2,2);imshow(RGBE);title('解密后','fontsize',20);
数字图像加密技术研究与应用

数字图像加密技术研究与应用一、前言在数字化时代,人们对于信息安全的需求和重视程度越来越高。
图像是信息传递的重要形式之一,因此数字图像的加密技术显得尤为重要。
本文将从理论研究和实际应用方面,介绍数字图像加密技术的研究现状和发展趋势。
二、数字图像加密技术的概述1. 加密技术的定义与分类数字图像加密技术是对传输和存储的数字图像数据进行加密和解密的技术,以保证数据传输和存储的安全。
常见的加密技术包括对称加密和非对称加密。
2. 对称加密技术对称加密技术指加密和解密使用的密钥相同的技术。
这种加密方式的优势是加密和解密速度快,但是相应的安全性较低。
常见的对称加密算法包括DES、AES等。
3. 非对称加密技术非对称加密技术指加密和解密使用不同密钥的技术。
这种加密方式的优势是安全性高,但是加密和解密速度慢。
常见的非对称加密算法包括RSA、DSA等。
4. 数字图像加密技术的应用领域数字图像加密技术在军事、政务、金融、医疗等领域有着广泛应用。
特别是在网络传输中,数字图像加密技术不仅可以保证图像传输的隐私和安全,也可以保证传输的完整性和可靠性。
三、数字图像加密技术的研究现状1. 数字图像加密技术的研究方向数字图像加密技术的研究主要集中在以下方面:(1)加密算法的研究,如对称加密算法、非对称加密算法等。
(2)水印技术的研究,如数字水印、鲁棒水印等。
(3)图像压缩与加密技术的结合研究,如JPEG加密等。
(4)量子加密技术的研究,如基于量子密钥分发协议的图像加密技术等。
2. 数字图像加密技术的难点数字图像加密技术的研究还存在一些难点,如抗攻击能力差、速度慢、不稳定性等问题。
另外,数字图像加密技术还需要考虑图像的保真性,即对于图像加密处理后,图像保持原有的特征和内容。
四、数字图像加密技术的应用案例1. 图像加密技术在传统媒体中的应用在传统媒体上,数字图像加密技术可以用于图片、视频的保密传输和存储。
例如,对于政府机关、客户数据等敏感信息的传输和存储,数字图像加密技术有着广泛应用。
数字图像加密技术

数字图像加密技术1、引言随着电脑网络的开放、共享性以及互联程度的日益扩大,Internet 得到了飞速的发展和应用,网络的重要性及其对社会的影响也越来越大。
与此同时,网络的安全保密问题也已成为日益严重的现实问题。
近年来,无论官方还是民间机构,都对信息的安全存储、保密传输、真伪验证等问题高度重视。
2、数字图像加密技术的背景知识一幅二维平面图像可用一个二元函数I= f (x, y) 来表示,(x, y) 表示二维空间坐标系中一个坐标点的位置, 则f (x, y) 代表图像在这一点的灰度值, 与图像在这一点的亮度相对应。
并且图像的亮度值是有限的, 因而函数I= f (x, y) 也是有界的。
在图像数字化之后, I= f (x, y) 则相应于一个矩阵, 矩阵元素所在的行与列就是图像显示在电脑屏幕上诸像素点的坐标, 元素的数值就是该像素的灰度(通常有256 等级, 用整数0 至255 表示)。
常见的加密算法,如DES 、AES 、RSA 等都是针对文本、数据加密而提出的。
对于在数字图像方面的加密来说,常见的也是采用这些文本加密技术的思想。
但是,文本和图像也存在很多区别,主要是:〔1〕图像信息量非常大.(2) 相邻像素具有相关性. 由于图像的可视性,一定区域内色彩是相似的,因此相邻像素间有很强的相关性. 文本加密技术并没有考虑这种相关性,而是依次加密每个像素.(3) 加密图像在解密时常允许一定失真. 这种图像失真只要控制在人的视觉内是完全可以接受的.显然在加密和解密时,需要考虑图像的这种特点. 文本加密技术没有考虑失真度的问题.(4) 需要预处理. 数字图像一般以二维数组的数据格式存储,而文本加密技术都要求先将待加密的数据转换为二进制的数据流,如果图像很大的话,需要一定的图像预处理时间,降低了加密效率.3、数字图像加密方法1〕基于Arnold 变换的图像加密算法(1)基于二维Arnold 变换的图像加密算法Arnold 变换是Arnold 在研究环面上的自同态时提出的一种变换,俗称猫脸变换。
(完整word版)数字图像加密与实现

数字图像加密与实现摘要:随着Internet技术与多媒体技术的飞速发展,数字化信息可以以不同的形式在网络上方便、快捷地传输。
多媒体通信逐渐成为人们之间信息交流的重要手段。
多媒体信息安全技术的研究主要有两种方法:多媒体信息加密和多媒体信息隐藏技术。
信息加密与信息隐藏从不同的角度保证信息的安全,如果我们将信息加密与信息隐藏有机地相结合,可进一步提高信息的安全性.关键词:计算机;数字图像;加密;实现在分析数字图像的结构和特点,对数字图像进行加密和解密,即:利用一定的算法对一副图像进行加密以达到不暴露原始图像的目的,然后进行解密以达到恢复原始图像的目的。
一、数字图像加密技术1、数字图像加密的原理与通用模型数字图像加密就是在发送端采用一定的算法作用于一幅图像明文,使其变成不可识别的密文,达到图像保密的目的。
在接收端采用相应的算法解密,恢复出原文。
其通用算法模型如图1-1所示:2、数字图像加密的典型算法目前国内外对数字图像加密的研究主要采用以下几种方法:(1)基于矩阵变换像素置换的图像加密技术1)Arnold变换,俗称猫脸变换.设像素的坐标x,y∈S={0,1,2,…,N—1},则Arnold变换为:公式(2—4)Arnold变换可以看做是裁剪和拼接的过程。
通过这一过程将离散化的数字图像矩阵S中的点重新排列.由于离散数字图像是有限点集,这种反复变换的结果,在开始阶段S中像素点的位置变化会出现相当程度的混乱,但由于动力系统固有的特性,在迭代进行到一定步数时会恢复到原来的位置.2)按幻方做图像像素置乱变换。
这种变换实质上是矩阵的初等变换,并且由于幻方矩阵是一有限维矩阵,经过n次置换,又会回到原来的位置,因而也可以用(1)所述的方法加以破译,固其加密效果也是不好的。
但若能把初等矩阵变换转化为某种非线性变换则有可能增强置乱效果,再结合其它的现代密码学的一些成熟的加密算法如DES,RSA等则可以增加算法的保密性[6]。
一种基于MD5值的数字图像加密新算法

被篡改 。
算法 , 它既解决 了图像传输过程 中的恶意篡改和传输差错问题 ,
同时利用 图像位 加密技术 , 图像 本身的 MD 值 作为加密 的周 将 5 期 序列 , 采用独特 的加密方法 对图像进行合理有序 的加密 , 从而 达 到图像安 全传 输 的 目的。此算 法 易实 现 、 运算 量小 、 用 多 应 样、 效果好 , 在实 现验证 图像完整性 功能 的同时 , 解决 了图像安
ec ne和 R A D t Sc ryIc的 R n dL Rvs 开发 出来 , S a eu t n a i o a . iet l 经 MD 、 3和 MD 2 MD 4发展 而来。它的作用是让大容量信息在用数 字签名软件签署私人 密匙前被” 压缩 ” 成一种 保密的格式 ( 就是
( 8}( on 一1 el t )+1 8¥CU t ) ) ; l : On) ] )
En d
c u t o n + 1 o n =c u t : En d En d
4 )根据加密效果 和应用需要决定是否进行第二次加密 , 如 果需要 , 则计算第一次加密之后 的图片的 MD 5值 , 重复 步骤 2 ) 和 3 并且可根 据需要 , ) 进行第三 、 四次加 密。如果不需要 , 第 结
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数字图像加密算法之图像融合技术加密
随着宽带网的发展,图像数据开始在网上流行,基于有些图像数据的敏感性,因而图像数据的保护越来越受到关注。
图像融合技术是利用图像灰度值进行插值融合的新技术,利用该技术可实现对灰度图像的融合。
我们在图像融合技术的基础上,结合混沌序列的伪随机特性,给出了一种基于混沌序列的图像文件加密技术,同时,结合给出的图像文件加密效果的评价标准,通过实验验证了该方法是一种高效、稳定的图像文件加密技术。
二、图像融合技术
基于图形( Graphics)的融合技术主要是应用线性插值技术进行不同图形之间的融合过渡。
对于图像(Image)的融合可以将图形的融合技术应用于图像的处理上,但由于图像的复杂程度远大于图形,所以应用这些技术时,算法效率很低,而且,一般只能得到近似计算。
从构成图像的像素角度考虑,基于图像的像素灰度值,可以在两幅同等大小的图像之间进行线性插值,实现对两幅图像的快速融合,具体方法是:对两幅同样大小的图像进行插值融合,记原图像为F,目标图像为D,插值结果图像为E,两幅图像上对应像素(i,j)的灰度值分别记为F(i,j)和O(i,j),其中F(i,j)为原图像在(i,j)处的像素灰度值,O(i,j)为目标图像在(i,j)处的像素灰度值。
插值的方程为:
根据以上公式计算出的E(i,j)即为插值结果图像在(i,j)处的灰度值,当v的值从0变化到l 时,相应的结果图像从原图像F变化到目标图像O。
图1即是根据以上方法进行融合的结果,经过实验比较发现,当v的值等于1时,得到的结果图像即为目标图像。
二、图像文件加密技术
在利用混沌序列进行图像文件加密的算法中,基于加密算法安全性的要求,一般多采用类似于密码学中的Feistel型结构,通过循环迭代的加密,逐步增加加密图像的混乱程度,从而实现对图像的加密。
通过图1图像融合的图例可以发现,在图像融合的中间过程,结果图像具有一定程度的混乱。
根据这一结果,结合混沌序列良好的伪随机性,可以将这种方法应用于图像文件加密,具体方法是:取两幅同样大小的图像,其中需要加密的图像称为原图像Image,另一幅图像称为密铜图像Kinrage,根据图像大小生成的混沌序列记为:{ai,j},i=1,2,…,M,j=1,2,…,N,其中M×N是图像的大小.对混沌序列进行归一化处理,利用混沌序列对两幅图像进行融合,融合过程为:
则得到具有一定混乱度的倒像Enimage,根据加密的需要进行迭代加密,则得到最终的加密图像文件。
结合传统的图像融合算法,给出直接应用图像融合技术的数宁图像加密算法如下:
图像加密算法1:基于图像融合的图像加密算法
Step1:输入密钥图像Kinrage和原图像Image,同时给出混沌序列的初始值ao。
Step2:根据图像生成相应的混沌序列,对混沌序列的值进行归一化处理,使其满足:
Step3:利用混沌序列{ai}对两幅图像进行融合加密,得到Enimage。
Step4:定义Enimage为新的原图像,Image为新的密钥剧像,返回Step2。
直到迭代加密过程完成。
以上图像加密算法中,每一次循环加密可采用不同的混沌序列,也可采用相唰的混沌序列,密钥定义为密钥图像和混沌序列的初始值。
利用图像加密算法1加密图像文件的图例如下图2,其中混沌序列为Logistic映射:0。
通过图2可以看出,利用图像加密算法1加密的效果很不理想,分析原因,主要有以下几点:一、在图像文件加密过程中所应用的混沌序列进行了归一化,这与图像融合技术保持一致,但在加密过程中,这造成Enimage(i,j)必然介于Image(i,j)与Kimage(i,j)的灰度值之间,不管迭代多少次,这样的限制条件都无法改变。
二、利用密钥图像作为整个加密系统的部分密钥,这样就造成密钥所占空间过大1,传输的成本相应增加,从而影响到算法的实际使用。
基于以上分析,我们给出改进的基于图像融合技术的数字图像加密算法。
在改进的图像加密算法中,设需加密图像为Image,大小为M×N,根据图像生成混沌序列
记为:
{ai,j},i=1,2,…,M,j=1,2,…,N,对该混沌序列进行简单的离散化如下:
A(i,j)= round(ai,j×256)
如果将矩阵A看成是图像的灰度矩阵,则可由混沌序列生成一幅灰度图像Kimage,作为即将加密的密钥图像,现在,根据加密需要生成融合过程的混沌序列{bi,j},i=1,2,…,M,j=1,2,…,N,进行计算:
在以上融合计算中,在插值系数bi,j前乘2的原因有以下两点:
一、可以使结果图像的灰度值范围不受限制条件的约束;
二、在计算机中,乘2的计算效率很高,保证不影响算法的效率。
图像加密算法2:改进的基于图像融合的图像加密算法
Stcp1:输入原图像Image,同时给出混沌序列的初始值ao和b0。
Step2:根据ao生成混沌序列{ai,j},i=1,2,…,M,j=1,2,…,N,离散化后得到密钥图像kimage的灰度矩阵。
Step3:生成相应的混沌序列{bi,j},i=1,2,…,M,j=1,2,…,N。
Step4:利用混沌序列{bi,j}对Image和Kimage进行融合加密,得到加密图像Enimage;Step5:定义Enimage为新的原图像,Image为新的密钥图像,返回Step2。
直到迭代加
密过程完成。
图像文件解密过程为图像文件加密的逆过程,根据捅值公式(3)分析可知,在得到相同的混沌序列的前提下,相应的解密过程为:
其中,当bi,j时,则Image(i, j)=Kimoge(i,j)。
可以发现,公式(3)和公式(4)除了插值的系数不同外,在形式上是一样的,说明解密过程也是一种插值过程,所以根据公式(4),参考算法2,可以得到相应的解密算法。
三、图像加密算法性能分析
基于融合技术的图像加密算法,安全性依赖于所用混沌序列的安全性,从公式(3)可知,当Kimage(i,j)和bi,j都不可知。
通过Eniurage(i, j)直接解出Image(i,j)是不可能的,而当图像较大时,相应生成的密钥图像灰度矩阵也会很大,采用穷举法进行破解也是困难的,其时间复杂度为O(M×N×256)。
同时,由于图像文件加密过程是在像素灰度值之例进行插值计算,所以除了要生成密钥图像灰度矩阼以外,其余的混沌序列不需要进行相应的离散化处理,这样,可以保证图像加密算法具有较高的效率。
四、图像加密算法图例
图3是采用真实图像作为密钥图像的加密效果图。
图4是采用混沌序列生成图像作为密钥图像的加密效果图,通过图4可以看出,加密效果随着迭代次数的增加是稳定的。
具体的加密
结果为:。
