第四章执行测试S
北师大版七年级数学下册第四章同步测试题及答案
∴∠BAC=180°﹣∠ABC﹣∠ACB=60°.
∵AE平分∠BAC,
∴∠BAE= ∠BAC=30°.
(2)∵∠CAE=∠BAE=30°,∠ACB=80°,
∴∠AEB=∠CAE+∠ACB=110°,
∵AD是BC边上的高,
∴∠ADE=90°,
∴∠DAE=∠AEB﹣∠ADE=20°.
13.解:(1)∵a+b=4,a2+b2=8,
∴(a+b)2=a2+2ab+b2=8+2ab=16,
∴ab=4,
(a﹣b)2=(a+b)2﹣4ab=16﹣16=0;
(2)∵a、b、c是△ABC的三边,
∴a+b>c,b+c>a,a+c>b,
∴|a+b﹣c|﹣|c﹣a+b|﹣|b﹣c﹣a|+|b﹣a﹣c|
(第10题图)
三.解答题(共8小题)
11.(1)下列图中具有稳定性是(填序号)
(2)对不具稳定性的图形,请适当地添加线段,使之具有稳定性.
(3)图5所示的多边形共条对角线.
(第11题图)
12.小辉用7根木条钉成一个七边形的木架,他为了使该木架稳固,想在其中加上四根木条,请你在图1、2、3中画出你的三种想法,并说明加上木条后使该木架稳固所用的数学道理.
(第12题图)
13.如图1,直线AM⊥AN,AB平分∠MAN,过点B作BC⊥BA交AN于点C;动点E、D同时从A点出发,其中动点E以2m/s的速度沿射线AN方向运动,动点D以1m/s的速度运动;已知AC=6cm,设动点D,E的运动时间为t.
(1)当点D在射线AM上运动时满足S△ADB:S△BEC=2:1,试求点D,E的运动时间t的值;
北师大版八年级数学上册第四章达标测试卷附答案

北师大版八年级数学上册第四章达标测试卷一、选择题(每题3分,共30分)1.下列表示y是x的函数的是()2.下列函数中,是一次函数的是()A.y=-8x B.y=1 xC.y=(m+1)x+1 D.y=8x2+13.一次函数y=2x+4的图象与y轴的交点坐标是()A.(0,-4) B.(0,4) C.(2,0) D.(-2,0) 4.若直线y=kx+b经过第二、三、四象限,则()A.k>0,b>0 B.k>0,b<0 C.k<0,b>0 D.k<0,b<0 5.一次函数y=-3x+1的图象过点(x1,y1),(x1+1,y2),(x1+2,y3),则() A.y1<y2<y3B.y3<y2<y1C.y2<y1<y3D.y3<y1<y26.对于函数y=-3x+1,下列结论正确的是()A.它的图象必经过点(-1,3)B.它的图象经过第一、二、三象限C.当x>1时,y<0D.y的值随x值的增大而增大7.如图,直线y=kx+b经过点A,B,则k的值为()A.3 B.32 C.23D.-32(第7题)(第8题)8.如图,它是小明从学校到家行进的路程s(单位:m)与时间t(单位:min)的函数图象.观察图象,从中得到如下信息,其中不正确...的是() A.学校离小明家1 000 mB.小明用了20 min到家C.小明前10 min走了路程的一半D.小明后10 min比前10 min走得快9.函数y=ax+b的图象如图所示,则函数y=bx+a的大致图象正确的是()10.一列快车从甲地开往乙地,一列慢车从乙地开往甲地,两车同时出发,两车离乙地的距离s(km)与行驶时间t(h)的函数关系如图所示,则下列结论中错误..的是()A.甲、乙两地的路程是400 kmB.慢车行驶速度为60 km/hC.相遇时快车行驶了150 kmD.快车出发后4 h到达乙地二、填空题(每题3分,共30分)11.已知y=(k-4)x|k|-3是正比例函数,则k=________.12.已知直线y=kx+b,若k+b=-5,kb=6,那么该直线不经过第________象限.13.若点(m,n)在函数y=2x+1的图象上,则2m-n=________.14.已知点(-3,2),(a,a+1)在函数y=kx-1的图象上,则k=________,a =________.15.直线y=2x+b与x轴的交点坐标是(2,0),则关于x的方程2x+b=0的解是__________.16.一次函数的图象与直线y=-x+1平行,且过点(8,2),那么此一次函数的表达式为______________.17.某公园的门票实行的收费标准是:每天进园前20人(含20人)每人20元,超过20人时,超过部分每人加收10元,则应收门票费用y(元)与游览人数x(x>20)之间的函数表达式为__________________________________.18.某天,某巡逻艇凌晨1:00出发巡逻,预计准点到达指定区域,匀速行驶一段时间后,因出现故障耽搁了一段时间,故障排除后,该艇加快速度仍匀速前进,结果恰好准点到达.如图是该巡逻艇行驶的路程y(单位:n mile)与所用时间t(单位:h)的函数图象,则该巡逻艇原计划准点到达的时刻是__________.(第18题)(第20题)19.直线y=k1x+b1(k1>0)与y=k2x+b2(k2<0)相交于点(-2,0),且两直线与y 轴围成的三角形面积为4,那么b1-b2=________.20.已知A地在B地正南方3 km处,甲、乙两人同时分别从A,B两地向正北方向匀速直行,他们与A地的距离s(单位:km)与所行时间t(单位:h)之间的函数关系的图象如图中的OC和FD所示.当他们行走3 h后,他们之间的距离为________km.三、解答题(21,22题每题8分,23,24题每题10分,其余每题12分,共60分)21.已知一次函数y=kx+b的图象经过M(0,2),N(1,3)两点.(1)求k,b的值;(2)若一次函数y=kx+b的图象与x轴的交点为A(a,0),求a的值.22.如图,正比例函数y=2x的图象与一次函数y=-3x+k的图象交于点P(1,m),求:(1)k的值;(2)两条直线与x轴围成的三角形的面积.23.已知一次函数y=kx+b的图象经过点A(0,2)和点B(-a,3),且点B在正比例函数y=-3x的图象上.(1)求a的值;(2)求一次函数的表达式,并画出它的图象;(3)若P(m,y1),Q(m-1,y2)是这个一次函数图象上的两点,试比较y1与y2的大小.24.某销售公司推销一种产品,设x(件)是推销产品的数量,y(元)是付给推销员的月报酬.公司付给推销员的月报酬的两种方案如图所示,推销员可以任选一种与公司签订合同,看图解答下列问题:(1)求每种方案y关于x的函数表达式;(2)当选择方案一所得报酬高于选择方案二所得报酬时,求x的取值范围.25.如图,直线y=kx+6与x轴、y轴分别交于点E,F,点E的坐标为(-8,0),点A的坐标为(-6,0),点P(x,y)是第二象限内的直线上的一个动点.(1)求k的值;(2)在点P的运动过程中,写出△OP A的面积S与x的函数表达式,并写出自变量x的取值范围;(3)探究:当P运动到什么位置(求点P的坐标)时,△OP A的面积为27 8?26.周末,小明骑自行车从家里出发到野外郊游.他从家出发0.5 h后到达甲地,游玩一段时间后按原速前往乙地.小明离家1 h 20 min后,妈妈驾车沿相同路线前往乙地.如图是他们离家的路程y(单位:km)与小明离家时间x(单位:h)的函数图象.已知妈妈驾车的速度是小明骑车速度的3倍.(1)求小明骑车的速度和在甲地游玩的时间.(2)小明从家出发多少小时后被妈妈追上?此时离家多远?(3)若妈妈比小明早10 min到达乙地,求从家到乙地的路程.答案一、1.D 2.A 3.B 4.D 5.B 6.C7.B8.C9.B10.C二、11.-412.一13.-114.-1;-115.x=216.y=-x+1017.y=30x-200(x>20)18.7:0019.420.1.5三、21.解:(1)将M,N的坐标代入一次函数表达式,得b=2,k+b=3,解得k=1.故k,b的值分别是1和2.(2)将k=1,b=2代入y=kx+b,得y=x+2.因为点A(a,0)在y=x+2的图象上,所以0=a+2.所以a=-2.22.解:(1)因为正比例函数y=2x的图象与一次函数y=-3x+k的图象交于点P(1,m),所以把点P(1,m)的坐标代入,得m=2,m=-3+k,解得k=5.(2)由(1)可得点P的坐标为(1,2),故所求三角形的高为2.由(1)可得一次函数的表达式为y=-3x+5.令y=0,则0=-3x+5,得x=5 3.所以一次函数的图象与x轴交点的横坐标为5 3.所以所求三角形的面积为12×53×2=53.23.解:(1)因为点B(-a,3)在正比例函数y=-3x的图象上,所以3=-3×(-a),则a=1.(2)由(1)得点B的坐标为(-1,3).将点A(0,2)和点B(-1,3)的坐标代入y=kx+b,得b=2,-k+b=3,解得k=-1.所以一次函数的表达式为y =-x +2.画图象略. (3)因为-1<0,所以y 随x 的增大而减小. 又因为m >m -1, 所以y 1<y 2.24.解:(1)设方案一的表达式为y =kx ,把(40,1 600)代入表达式,可得k =40,故表达式为y =40x ;设方案二的表达式为y =ax +b ,把(40,1 400)和(0,600)代入表达式,可得a =20,b =600,故表达式为y =20x +600.(2)根据两直线相交可得方程40x =20x +600,解得x =30.结合图象可得,当x >30时,选择方案一所得报酬高于选择方案二所得报酬. 25.解:(1)因为点E (-8,0)在直线y =kx +6上,所以-8k +6=0.所以k =34.(2)由(1)得y =34x +6,所以S =12×6×⎝ ⎛⎭⎪⎫34x +6. 所以S =94x +18(-8<x <0).(3)由S =94x +18=278得x =-132,则y =34×⎝ ⎛⎭⎪⎫-132+6=98, 所以P ⎝ ⎛⎭⎪⎫-132,98.故当P 运动到点⎝ ⎛⎭⎪⎫-132,98处时,△OP A 的面积为278.26.解:(1)观察图象,可知小明骑车的速度为100.5=20(km/h),在甲地游玩的时间是1-0.5=0.5(h).(2)妈妈驾车的速度为20×3=60(km/h).如图,设直线BC 对应的函数表达式为y =20x +b 1,把点B (1,10)的坐标代入,得20×1+b 1=10,则b 1=-10.所以直线BC 对应的函数表达式为y =20x -10.设直线DE 对应的函数表达式为y =60x +b 2,把点D ⎝ ⎛⎭⎪⎫43,0的坐标代入,得60×43+b 2=0,则b 2=-80. 所以直线DE 对应的函数表达式为y =60x -80.当小明被妈妈追上时,两人走过的路程相等,则20x -10=60x -80, 解得x =1.75,20×(1.75-1)+10=25(km).所以小明从家出发1.75 h 后被妈妈追上,此时离家25 km. (3)设从妈妈追上小明的地点到乙地的路程为z km. 根据题意,得z 20-z 60=1060,解得z =5. 所以从家到乙地的路程为5+25=30(km).。
数据结构第四章考试题库(含答案)

第四章串一、选择题1.下面关于串的的叙述中,哪一个是不正确的?()【北方交通大学 2001 一、5(2分)】A.串是字符的有限序列 B.空串是由空格构成的串C.模式匹配是串的一种重要运算 D.串既可以采用顺序存储,也可以采用链式存储2 若串S1=‘ABCDEFG’, S2=‘9898’ ,S3=‘###’,S4=‘’,执行concat(replace(S1,substr(S1,length(S2),length(S3)),S3),substr(S4,i ndex(S2,‘8’),length(S2))) 其结果为()【北方交通大学 1999 一、5 (25/7分)】A.ABC###G0123 B.ABCD###2345 C.ABC###G2345 D.ABC###2345E.ABC###G1234 F.ABCD###1234 G.ABC###012343.设有两个串p和q,其中q是p的子串,求q在p中首次出现的位置的算法称为()A.求子串 B.联接 C.匹配 D.求串长【北京邮电大学 2000 二、4(20/8分)】【西安电子科技大学 1996 一、1 (2分)】4.已知串S=‘aaab’,其Next数组值为()。
【西安电子科技大学 1996 一、7 (2分)】A.0123 B.1123 C.1231 D.12115.串‘ababaaababaa’的next数组为()。
【中山大学 1999 一、7】A.9 B.2 C.6 D.456.字符串‘ababaabab’的nextval 为()A.(0,1,0,1,04,1,0,1) B.(0,1,0,1,0,2,1,0,1)C.(0,1,0,1,0,0,0,1,1) D.(0,1,0,1,0,1,0,1,1 )【北京邮电大学 1999 一、1(2分)】7.模式串t=‘abcaabbcabcaabdab’,该模式串的next数组的值为(),nextval数组的值为()。
人教版八年级物理上册《第四章光现象》单元测试卷含答案

人教版八年级物理上册《第四章光现象》单元测试卷含答案1.下列成语所描述的光现象成因与“小孔成像”的成因相同的是()A. 海市蜃楼B. 一叶障目C. 杯弓蛇影D. 镜花水月2. 对于①小孔成像;②平面镜成像;③放大镜成像;④电影银幕上的像;⑤汽车后视镜中的像,其中()A. 属于虚像的是②③④B. 由于折射而形成的像是①③C. 属于实像的是①②③D. 由于反射而形成的像是②⑤3. 在太阳光的照耀下,人们看到玫瑰花呈鲜艳的红色,这是因为玫瑰花()A. 吸收了太阳光中的红光B. 发出了太阳光中的红光C. 反射了太阳光中的红光D. 透过了太阳光中的红光4.能自行发光的物体叫做光源,下列物体属于光源的是A.太阳B.地球C.月亮D.房屋5.下列不是光沿直线传播的例子的是A.看不到不透明体后的物体B.日食和月食C.太阳落到地平线下还能看见D.人的身影早晚长,中午短6.关于光的反射,下列说法正确的是()A.当入射光线与反射面的夹角为30°时,反射角也为30°B.入射光线靠近法线时,反射光线也靠近法线C.入射角增大5°时,反射光线与入射光线的夹角也增大5°D.镜面反射遵守光的反射定律,漫反射不一定遵守光的反射定律7.如图所示,向右匀速行驶的动车桌面上有杯水,一束光斜射到水面上,保持人射光方向不变.动车减速时( )A.入射角不变,折射角不变B.入射角变小,折射角变小C.入射角变大,折射角变大D.入射角变大,折射角变小8.喷水鱼因特殊的捕食方式而得名,能喷出一股水柱,准确击落空中的昆虫作为食物,下列各图中能正确表示喷水鱼看到的昆虫像的光路图是()A. B. C. D.9.电焊工人在焊接时,要戴上防护眼罩,这主要是为了 ( )A.防止火星飞溅到眼睛上,把眼睛烫伤 B.防止紫外线对人眼的伤害C.防止红外线对人眼的伤害 D.为了使眼睛看到焊接点10.下列关于平面镜成像的说法,正确的是( )A. 平面镜成像是光的折射现象B. 平面镜所成的像是实像C. 平面镜所成的像是虚像D. 人越靠近平面镜,人在平面镜中的像就越大11.池中水的深度是2m,月球到地球的距离为3.8×105km,月球在池中的像到水面的距离是,水中的月是像(填实或虚)。
高一数学(必修一)《第四章-指数函数与对数函数》练习题及答案解析-人教版

高一数学(必修一)《第四章 指数函数与对数函数》练习题及答案解析-人教版班级:___________姓名:___________考号:___________一、单选题1.某超市宣传在“双十一”期间对顾客购物实行一定的优惠,超市规定:①如一次性购物不超过200元不予以折扣;②如一次性购物超过200元但不超过500元的,按标价给予九折优惠;③如一次性购物超过500元的,其中500元给予9折优惠,超过500元的部分给予八五折优惠.某人两次去该超市购物分别付款176元和441元,如果他只去一次购买同样的商品,则应付款( )A .608元B .591.1元C .582.6元D .456.8元2.德国天文学家,数学家开普勒(J. Kepier ,1571—1630)发现了八大行星的运动规律:它们公转时间的平方与离太阳平均距离的立方成正比.已知天王星离太阳平均距离是土星离太阳平均距离的2倍,土星的公转时间约为10753d .则天王星的公转时间约为( )A .4329dB .30323dC .60150dD .90670d3.函数()f x = )A .()1,0-B .(),1-∞-和()0,1C .()0,1D .(),1-∞-和()0,∞+4.将进货价为每个80元的商品按90元一个出售时,能卖出400个,每涨价1元,销售量就减少20个,为了使商家利润有所增加,则售价a (元/个)的取值范围应是( )A .90100a <<B .90110a <<C .100110a <<D .80100a <<5.某市工业生产总值2018年和2019年连续两年持续增加,其中2018年的年增长率为p ,2019年的年增长率为q ,则该市这两年工业生产总值的年平均增长率为( )A .2p q +;B .()()1112p q ++-;C ;D 1.6.某污水处理厂为使处理后的污水达到排放标准,需要加入某种药剂,加入该药剂后,药剂的浓度C (单位:3mg/m )随时间t (单位:h )的变化关系可近似的用函数()()()210010419t C t t t t +=>++刻画.由此可以判断,若使被处理的污水中该药剂的浓度达到最大值,需经过( )A .3hB .4hC .5hD .6h7.某同学参加研究性学习活动,得到如下实验数据:以下函数中最符合变量y 与x 的对应关系的是( )A .129y x =+B .245y x x =-+C .112410x y =⨯- D .3log 1y x =+ 8.某种植物生命力旺盛,生长蔓延的速度越来越快,经研究,该一定量的植物在一定环境中经过1个月,其覆盖面积为6平方米,经过3个月,其覆盖面积为13.5平方米,该植物覆盖面积y (单位:平方米)与经过时间x (x ∈N )(单位:月)的关系有三种函数模型x y pa =(0p >,1a >)、log a y m x =(0m >,1a >)和y nx α=(0n >,01α<<)可供选择,则下列说法正确的是( )A .应选x y pa =(0p >,1a >)B .应选log a y m x =(0m >,1a >)C .应选y nx α=(0n >,01α<<)D .三种函数模型都可以9.已知函数()21,1,8, 1.x x f x x x ⎧-≤=⎨>⎩若()8f x =,则x =( ) A .3-或1 B .3- C .1 D .310.函数e 1()sin 2e 1x x f x x +=⋅-的部分图象大致为( ) A . B .C .D .二、填空题11.2021年8月30日第九届未来信息通信技术国际研讨会在北京开幕.研讨会聚焦于5G 的持续创新和演进、信息通信的未来技术前瞻与发展、信息通信技术与其他前沿科技的融合创新.香农公式2log 1S C W N ⎛⎫=+ ⎪⎝⎭是被广泛公认的通信理论基础和研究依据,它表示在受噪声干扰的信道中,最大信息传递速率C 取决于信道带宽W 、信道内信号的平均功率S ,信道内部的高斯噪声功率N 的大小,其中S N 叫作信噪比.若不改变信道带宽W ,而将信噪比S N从11提升至499,则最大信息传递速率C 大约会提升到原来的______倍(结果保留1位小数).(参考数据:2log 3 1.58≈和2log 5 2.32≈)12.已测得(,)x y 的两组值为(1,2)和(2,5),现有两个拟合模型,甲21y x =+,乙31y x =-.若又测得(,)x y 的一组对应值为(3,10.2),则选用________作为拟合模型较好.13.半径为1的半圆中,作如图所示的等腰梯形ABCD ,设梯形的上底2BC x =,则梯形ABCD 的最长周长为_________.三、解答题14.如图,某中学准备在校园里利用院墙的一段,再砌三面墙,围成一个矩形花园ABCD ,已知院墙MN 长为25米,篱笆长50米(篱笆全部用完),设篱笆的一面AB 的长为x 米.(1)当AB 的长为多少米时,矩形花园的面积为300平方米?(2)若围成的矩形ABCD 的面积为 S 平方米,当 x 为何值时, S 有最大值,最大值是多少?15.以贯彻“节能减排,绿色生态”为目的,某单位在国家科研部门的支持下,进行技术攻关,采用了新工艺,把二氧化碳转化为一种可利用的化工产品.已知该单位每月的处理量最少为400吨,最多为600吨,月处理成本y (百元)与月处理量x (吨)之间的函数关系可近似地表示为212800200y x x =-+. (1)该单位每月处理量为多少吨时,才能使每吨的平均处理成本最低?(提示:平均处理成本为y x) (2)该单位每月处理成本y 的最小值和最大值分别是多少百元? 16.如图,以棱长为1的正方体的三条棱所在直线为坐标轴,建立空间直角坐标系O xyz -,点P 在线段AB 上,点Q 在线段DC 上.(1)当2PB AP =,且点P 关于y 轴的对称点为M 时,求PM ;(2)当点P 是面对角线AB 的中点,点Q 在面对角线DC 上运动时,探究PQ 的最小值.17.经销商经销某种农产品,在一个销售季度内,每售出1 t 该产品获利润500元,未售出的产品,每1 t 亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了130 t 该农产品.以X (单位: t ,100150)X )表示下一个销售季度内的市场需求量,T (单位:元)表示下一个销售季度内经销该农产品的利润.(1)将T 表示为X 的函数;(2)根据直方图估计利润T 不少于57000元的概率;(3)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,并以需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若需求量[100X ∈,110),则取105X =,且105X =的概率等于需求量落入[100,110)的频率),求T 的分布列.18.为发展空间互联网,抢占6G 技术制高点,某企业计划加大对空间卫星网络研发的投入.据了解,该企业研发部原有100人,年人均投入()0a a >万元,现把研发部人员分成两类:技术人员和研发人员,其中技术人员有x 名(*x ∈N 且4575x ≤≤),调整后研发人员的年人均投入增加4x %,技术人员的年人均投入调整为275x a m ⎛⎫- ⎪⎝⎭万元. (1)要使调整后研发人员的年总投入不低于调整前的100人的年总投入,则调整后的技术人员最多有多少人?(2)是否存在实数m 同时满足两个条件:①技术人员的年人均投入始终不减少;②调整后研发人员的年总投入始终不低于调整后技术人员的年总投入?若存在,求出m 的值;若不存在,请说明理由.19.某公司今年年初用81万元收购了一个项目,若该公司从第1年到第x (N x +∈且1x >)年花在该项目的其他费用(不包括收购费用)为()20x x +万元,该项目每年运行的总收入为50万元.(1)试问该项目运行到第几年开始盈利?(2)该项目运行若干年后,公司提出了两种方案:①当盈利总额最大时,以56万元的价格卖出;②当年平均盈利最大时,以92万元的价格卖出.假如要在这两种方案中选择一种,你会选择哪一种?请说明理由.20.某工厂产生的废气必须经过过滤后排放,规定排放时污染物的残留含量不得超过原污染物总量的0.5%.已知在过滤过程中的污染物的残留数量P (单位:毫克/升)与过滤时间t (单位:小时)之间的函数关系为0ekt P P -=⋅(k 为常数,0P 为原污染物总量).若前4个小时废气中的污染物被过滤掉了80%,那么要能够按规定排放废气,还需要过滤n 小时,求正整数n 的最小值.21.某科技企业生产一种电子设备的年固定成本为600万元,除此之外每台机器的额外生产成本与产量满足一定的关系式.设年产量为x (0200x <,N x ∈)台,若年产量不足70台,则每台设备的额外成本为11402y x =+万元;若年产量大于等于70台不超过200台,则每台设备的额外成本为2264002080101y x x =+-万元.每台设备售价为100万元,通过市场分析,该企业生产的电子设备能全部售完.(1)写出年利润W (万元)关于年产量x (台)的关系式;(2)当年产量为多少台时,年利润最大,最大值为多少?22.为进一步奏响“绿水青山就是金山银山”的主旋律,某旅游风景区以“绿水青山”为主题,特别制作了旅游纪念章,决定近期投放市场,根据市场调研情况,预计每枚该纪念章的市场价y (单位:元)与上市时间x (单位:天)的数据如下表:(1)根据上表数据,从下列函数中选取一个恰当的函数描述每枚该纪念章的市场价y 与上市时间x 的变化关系并说明理由:①(0)y ax b a =+≠,②()20y ax bx c a =++≠,③()log 0,0,1b y a x a b b =≠>≠,④(0)a y b a x=+≠; (2)利用你选取的函数,求该纪念章市场价最低时的上市天数及最低市场价;(3)利用你选取的函数,若存在()10,x ∈+∞,使得不等式()010f x k x -≤-成立,求实数k 的取值范围.四、多选题23.函数()()22x x af x a R =+∈的图象可能为( )A .B .C .D .五、双空题24.某种病毒经30分钟可繁殖为原来的2倍,且已知病毒的繁殖规律为y=e kt (其中k 为常数;t 表示时间,单位:小时;y 表示病毒个数),则k=____,经过5小时,1个病毒能繁殖为____个.25.已知长为4,宽为3的矩形,若长增加x ,宽减少2x ,则面积最大,此时x =__________,面积S =__________.参考答案与解析1.【答案】B【分析】根据题意求出付款441元时的实际标价,再求出一次性购买实际标价金额商品应付款即可.【详解】由题意得购物付款441元,实际标价为10441=4909元 如果一次购买标价176+490=666元的商品应付款5000.9+1660.85=591.1元.故选:B.2.【答案】B【分析】设天王星和土星的公转时间为分别为T 和T ',距离太阳的平均距离为r 和r ',根据2323T r T r =''2r r '= 结合已知条件即可求解.【详解】设天王星的公转时间为T ,距离太阳的平均距离为r土星的公转时间为T ',距离太阳的平均距离为r '由题意知2r r '= 10753T d '= 所以323238T r r T r r ⎛⎫=== ⎪'''⎝⎭所以1075310753 2.82830409.484T d '==≈⨯=故选:B.3.【答案】B【分析】分别讨论0x ≥和0x <,利用二次函数的性质即可求单调递减区间.【详解】当0x ≥时()f x 210x -+≥解得11x -≤≤,又21y x =-+为开口向下的抛物线,对称轴为0x =,此时在区间()0,1单调递减当0x <时()f x == ()21y x =+为开口向上的抛物线,对称轴为1x =-,此时在(),1-∞-单调递减综上所述:函数()f x =(),1-∞-和()0,1.故选:B.4.【答案】A【分析】首先设每个涨价x 元,涨价后的利润与原利润之差为y 元,结合条件列式,根据0y >,求x 的取值范围,即可得到a 的取值范围.【详解】设每个涨价x 元,涨价后的利润与原利润之差为y 元则290,(10)(40020)1040020200a x y x x x x =+=+⋅--⨯=-+.要使商家利润有所增加,则必须使0y >,即2100x x -<,得010,9090100x x <<∴<+<,所以a 的取值为90100a <<.故选:A5.【答案】D【分析】设出平均增长率,并根据题意列出方程,进行求解【详解】设该市2018、2019这两年工业生产总值的年平均增长率为x ,则由题意得:()()()2111x p q +=++解得11x =,21x =因为20x <不合题意,舍去 故选D .6.【答案】A【分析】利用基本不等式求最值可得.【详解】依题意,0t >,所以11t +>所以()()()()()()221001100110010010164191012116121t t C t t t t t t t ++===≤==++++++++++ 当且仅当1611t t +=+,即t =3时等号成立,故由此可判断,若使被处理的污水中该药剂的浓度达到最大值,需经过3h .故选:A .7.【答案】D 【分析】结合表格所给数据以及函数的增长快慢确定正确选项.【详解】根据表格所给数据可知,函数的增长速度越来越慢A 选项,函数129y x =+增长速度不变,不符合题意. BC 选项,当3x ≥时,函数245y x x =-+、112410x y =⨯-增长越来越快,不符合题意. D 选项,当3x ≥时,函数3log 1y x =+的增长速度越来越慢,符合题意.故选:D8.【答案】A【解析】根据指数函数和幂函数的增长速度结合题意即可得结果.【详解】该植物生长蔓延的速度越来越快,而x y pa =(0p >,1a >)的增长速度越来越快 log a y m x =(0m >,1a >)和y nx α=(0n >,01α<<)的增长速度越来越慢故应选择x y pa =(0p >,1a >).故选:A.9.【答案】B【分析】根据分段函数的解析式,分段求解即可.【详解】根据题意得x ≤1x2−1=8或188x x >⎧⎨=⎩ 解得3,x =-故选:B10.【答案】B【分析】结合图象,先判断奇偶性,然后根据x 趋近0时判断排除得选项.【详解】解:()e 1sin 2e 1x x f x x +=⋅-的定义域为()(),00,∞-+∞()()()e 1e 1sin 2sin 2e 1e 1x x x xf x x x f x --++-=⋅-=⋅=⎡⎤⎣⎦-- ()f x ∴是偶函数,排除A ,C . 又0x >且无限接近0时,101x x e e +>-且sin 20x >,∴此时()0f x >,排除D故选:B .11.【答案】2.5【分析】设提升前最大信息传递速率为1C ,提升后最大信息传递速率为2C ,根据题意求出21C C ,再利用指数、对数的运算性质化简计算即可【详解】设提升前最大信息传递速率为1C ,提升后最大信息传递速率为2C ,则由题意可知()122log 111log 12C W W =+= ()222log 1499log 500C W W =+= 所以()()232322222222122222log 25log 500log 2log 523log 523 2.328.96 2.5log 12log 2log 32log 32 1.58 3.58log 23C W C W ⨯+++⨯====≈=≈+++⨯所以最大信息传递速率C 会提升到原来的2.5倍.故答案为:2.512.【答案】甲【分析】将3x =分别代入甲乙两个拟合模型计算,即可判断.【详解】对于甲:3x =时23110y =+=,对于乙:3x =时8y =因此用甲作为拟合模型较好.故答案为:甲13.【答案】5【分析】计算得出AB CD ==ABCD 的周长为y,可得出22y x =++()0,1t,可得出224y t =-++,利用二次函数的相关知识可求得y 的最大值.【详解】过点B 、C 分别作BE AD ⊥、CF AD ⊥垂足分别为E 、F则//BE CF ,//BC EF 且90BEF ∠=,所以,四边形BCFE 为矩形所以2EF BC x ==AB CD =,BAE CDF ∠=∠和90AEB DFC ∠=∠= 所以,Rt ABE Rt DCF ≅所以12AD EF AE DF x -===-,则OF OD DF x =-= CF =AB CD ∴===设梯形ABCD 的周长为y ,则2222y x x =++=++其中01x <<令()0,1t =,则21x t =-所以()2222212425y t t t ⎛=+-+=-++=-+ ⎝⎭所以,当t =y 取最大值,即max 5y =. 故答案为:5.【点睛】思路点睛:解函数应用题的一般程序:第一步:审题——弄清题意,分清条件和结论,理顺数量关系;第二步:建模——将文字语言转化成数学语言,用数学知识建立相应的数学模型;第三步:求模——求解数学模型,得到数学结论;第四步:还原——将用数学方法得到的结论还原为实际问题的意义;第五步:反思回顾——对于数学模型得到的数学结果,必须验证这个数学解对实际问题的合理性.14.【答案】(1)15米;(2)当 x 为12.5米时, S 有最大值,最大值是312.5平方米.【分析】(1)设篱笆的一面AB 的长为 x 米,则(502)m BC x =-,根据“矩形花园的面积为300平方米”列一元二次方程,求解即可;(2)根据题意,可得(502)S x x =-,根据二次函数最值的求法求解即可.(1)设篱笆的一面AB 的长为 x 米,则(502)m BC x =-由题意得(502)300x x -=解得1215,10x x ==50225x -≤12.5x ∴≥15x ∴=所以,AB 的长为15米时,矩形花园的面积为300平方米;(2)由题意得()()22502250212.5312.5,12.525S x x x x x x =-=-+=--+≤<12.5x ∴=时, S 取得最大值,此时312.5S =所以,当 x 为12.5米时, S 有最大值,最大值是312.5平方米.15.【答案】(1)400吨 (2)最小值800百元,最大值1400百元【分析】(1)求出平均处理成本的函数解析式,利用基本不等式求出最值;(2)利用二次函数单调性求解最值.(1)由题意可知,二氧化碳的每吨平均处理成本为18002200y x x x =+-,显然[]400,600x ∈由基本不等式得:1800222200y x x x =+-≥= 当且仅当1800200x x =,即400x =时,等号成立 故每月处理量为400吨时,才能使每吨的平均处理成本最低;(2)212800200y x x =-+ 对称轴220012200x -=-=⨯ 函数212800200y x x =-+在[400,600]单调递增 当400x =时,则2min 14002400800800200y =⨯-⨯+= 当600x =时,则2max 160026008001400200y =⨯-⨯+= 答:该单位每月处理成本y 的最小值800百元,最大值1400百元.16.【答案】【分析】(1)根据空间直角坐标系写出各顶点的坐标,再由2PB AP =求得121,,33OP ⎛⎫= ⎪⎝⎭,得到P 与M 的坐标,再利用两点距离公式求解即可;(2)由中点坐标公式求得111,,22P ⎛⎫ ⎪⎝⎭,再根据题意设点(,1,)Q a a ,最后利用两点间的距离公式与一元二次函数配方法求PQ 的最小值.(1)所以()22211222131133333PM ⎛⎫⎛⎫=++-++= ⎪ ⎪⎝⎭⎝⎭. (2)因为点P 是面对角线AB 的中点,所以111,,22P ⎛⎫ ⎪⎝⎭,而点Q 在面对角线DC 上运动,故设点(,1,)Q a a[0,1]a ∈则(PQ a ===[0,1]a ∈所以当34a =时,PQ 取得最小值33,1,44Q ⎛⎫ ⎪⎝⎭. 17.【答案】(1)80039000,[100,130)65000,[130,150]X X T X -∈⎧=⎨∈⎩(2)0.7(3)59400 【分析】(1)由题意先分段写出,当[100x ∈,130)和[130x ∈,150)时的利润值,利用分段函数写出即可;(2)由(1)知,利润T 不少于57000元,当且仅当120150x ,再由直方图知需求量[120X ∈,150]的频率为0.7,由此估计得出结论;(3)先求出利润与X 的关系,再利用直方图中的频率计算利润分布列,最后利用公式求其数学期望.(1)解:由题意得,当[100X ∈,130)时500300(130)80039000T X X X =--=-当[130X ∈,150]时50013065000T =⨯=80039000,[100,130)65000,[130,150]X X T X -∈⎧∴=⎨∈⎩(2)解:由(1)知,利润T 不少于57000元,当且仅当120150X .由直方图知需求量[120X ∈,150]的频率为0.7所以下一个销售季度的利润T 不少于57000元的概率的估计值为0.7;(3)解:由题意及(1)可得:所以T 的分布列为:18.【答案】(1)最多有75人 (2)存在 7m =【分析】(1)根据题目要求列出方程求解即可得到结果(2)根据题目要求①先求解出m 关于x 的取值范围,再根据x 的取值范围求得m 的取值范围,之后根据题目要求②列出不等式利用基本不等式求解出m 的取值范围,综上取交集即可 (1)依题意可得调整后研发人员有()100x -人,年人均投入为()14%x a +万元则()()10014%100x x a a -+≥,解得075x ≤≤.又4575x ≤≤,*x ∈N 所以调整后的奇数人员最多有75人.(2)假设存在实数m 满足条件.由条件①,得225x a m a ⎛⎫-≥ ⎪⎝⎭,得2125x m ≥+. 又4575x ≤≤,*x ∈N 所以当75x =时,2125x +取得最大值7,所以7m ≥. 由条件②,得()()210014%25x x x a a m x ⎛⎫-+≥- ⎪⎝⎭,不等式两边同除以ax 得1002112525x x m x ⎛⎫⎛⎫-+≥- ⎪⎪⎝⎭⎝⎭,整理得100325x m x ≤++因为10033725x x ++≥=,当且仅当10025x x =,即50x =时等号成立,所以7m ≤. 综上,得7m =.故存在实数m 为7满足条件.19.【答案】(1)第4年 (2)选择方案②,理由见解析【分析】(1)设项目运行到第x 年的盈利为y 万元,可求得y 关于x 的函数关系式,解不等式0y >可得x 的取值范围,即可得出结论;(2)计算出两种方案获利,结合两种方案的用时可得出结论.(1)解:设项目运行到第x 年的盈利为y 万元则()25020813081=-+-=-+-y x x x x x由0y >,得230810x x -+<,解得327x <<所以该项目运行到第4年开始盈利.(2)解:方案①()22308115144=-+-=--+y x x x当15x =时,y 有最大值144.即项目运行到第15年,盈利最大,且此时公司的总盈利为14456200+=万元方案②818130303012y x x x x x ⎛⎫=-+-=-+≤- ⎪⎝⎭ 当且仅当81x x=,即9x =时,等号成立. 即项目运行到第9年,年平均盈利最大,且此时公司的总盈利为12992200⨯+=万元.综上,两种方案获利相等,但方案②时间更短,所以选择方案②.20.【答案】10【分析】由题可得()400180%e k P P --=,求得ln 54k =,再由000.5%e kt P P -≥可求解. 【详解】由题意,前4个小时消除了80%的污染物因为0e kt P P -=⋅,所以()400180%ek P P --= 所以40.2e k -=,即4ln0.2ln5k -==-,所以ln 54k =则由000.5%e kt P P -≥,得ln 5ln 0.0054t ≥- 所以4ln 20013.2ln 5t ≥≈ 故正整数n 的最小值为14410-=.21.【答案】(1)2**160600,070,N 264001480,70200,N x x x x W x x x x ⎧-+-<<∈⎪⎪=⎨⎛⎫⎪-+∈ ⎪⎪⎝⎭⎩;(2)当年产量为80台时,年利润最大,最大值为1320万元.【分析】(1)根据题意,分段表示出函数模型,即可求解;(2)根据题意,结合一元二次函数以及均值不等式,即可求解.(1)当070x <<,*N x ∈时 211100406006060022W x x x x x ⎛⎫=-+-=-+- ⎪⎝⎭; 当70200x ≤≤,*N x ∈时26400208064001001016001480W x x x x x x ⎛⎫⎛⎫=-+--=-+ ⎪ ⎪⎝⎭⎝⎭. ∴.2**160600,070,N 264001480,70200,N x x x x W x x x x ⎧-+-<<∈⎪⎪=⎨⎛⎫⎪-+∈ ⎪⎪⎝⎭⎩; (2)①当070x <<,*N x ∈时 221160600(60)120022W x x x =-+-=--+ ∴当60x =时,y 取得最大值,最大值为1200万元.②当70200x ≤≤,*N x ∈时6400148014801320W x x ⎛⎫=-+≤- ⎪⎝⎭ 当且仅当6400x x =,即80x =时,y 取得最大值1320∵13201200>∴当年产量为80台时,年利润最大,最大值为1320万元.22.【答案】(1)选择()20y ax bx c a =++≠,理由见解析(2)当该纪念章上市10天时,市场价最低,最低市场价为每枚70元(3)k ≥【分析】(1)由表格数据分析变量x 与变量y 的关系,由此选择对应的函数关系;(2)由已知数据求出函数解析式,再结合函数性质求其最值;(3)不等式可化为()17010210x k x -+≤-,由条件可得()min 17010210x k x ⎡⎤-+≤⎢⎥-⎣⎦,利用函数的单调性求()17010210y x x =-+-的最小值,由此可得k 的取值范围. (1)由题表知,随着时间x 的增大,y 的值随x 的增大,先减小后增大,而所给的函数(0)y ax b a =+≠ ()log 0,0,1b y a x a b b =≠>≠和(0)a y b a x =+≠在(0,)+∞上显然都是单调函数,不满足题意,故选择()20y ax bx c a =++≠.(2)得42102,36678,40020120,a b c a b c a b c ++=⎧⎪++=⎨⎪++=⎩∴当10x =时,y 有最小值,且min 70y =.故当该纪念章上市10天时,市场价最低,最低市场价为每枚70元.(3)令()()()1701010210f x g x x x x ==-+--(10,)x ∞∈+因为存在()10,x ∈+∞,使得不等式()0g x k -≤成立则()min k g x ≥.又()()17010210g x x x =-+-在(10,10+上单调递减,在()10++∞上单调递增 ∴当10x =+()g x取得最小值,且最小值为(10g +=∴k ≥23.【答案】ABD【解析】根据函数解析式的形式,以及图象的特征,合理给a 赋值,判断选项.【详解】当0a =时()2x f x =,图象A 满足; 满足;图象C 过点()0,1,此时0a =,故C 不成立.故选:ABD【点睛】思路点睛:函数图象的辨识可从以下方面入手:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置.(2)从函数的单调性,判断图象的变化趋势;(3)从函数的奇偶性,判断图象的对称性;(4)从函数的特征点,排除不合要求的图象.24.【答案】2ln2 1024【详解】当t=0.5时,y=2,∴2=12e k ,∴k=2ln 2,∴y=e 2t ln 2 当t=5时,y=e 10ln 2=210=1 024.25.【答案】1 1212【详解】S =(4+x) 32x ⎛⎫- ⎪⎝⎭=-22x +x +12=-12 (x 2-2x)+12=-12 (x -1)2+252. 当x =1时,S max =252,故填1和252.。
七年级数学第四章测试题

七年级数学第四章测试题一. 填空题1.在关系式S=45t中,自变量是, 因变量是, 当t=1.5时,S= 。
2.已知等腰三角形的底为3,腰长为x,则周长y可以表示为。
3.如图,表示的是小明在6点---8点时他的速度与时间的图像,则在6点----8点的路程是千米.4.如图,假设圆柱的高是5cm,当圆柱的底面半径由小到大变化时,(1)圆柱的体积如何变化? ,在这个变化过程中,自变量是,因变量是.(2)如果圆柱底面半径为r(cm),那么圆柱的体积V(cm3)可以表示为.(3)当r由1cm变化到10cm时,V由cm3变化到cm3.5.如图所示,圆锥的底面半径是2 厘米,当圆锥的高由小到大变化时,圆锥的体积也随之而发生了变化.(1)在这个变化过程中,自变量是______________,因变量是_________ ;(2)如果圆锥的高为h (厘米),那么圆锥的体积V(厘米3)与h 的关系式是_____________;(3)当高由1 厘米变化到10厘米时,圆锥的体积由________厘米3变化到_______ 厘米3.6.如图所示,长方形的长为12,宽为x .(1)若设长方形的面积S,则面积S与宽x之间的关系是.(2)若用C表示长方形的周长,则周长C与宽x之间的关系是.二.选择题7.正常人的体温一般在37℃左右,但一天中的不同时刻不尽相同.下图反映了一天24小时内小明体温的变化情况,下列说法错误的是【】A.清晨5时体温最低B.下午5时体温最高C.这一天中小明体温T(单位:℃)的范围是36.5≤T≤37.5D.从5时至24时,小明体温一直是升高的。
8.一天,小军和爸爸去登山,已知山脚到山顶的路程为300米,小军先走了一段路程,爸爸才开始出发,图中两条线段分别表示小军和爸爸离开山脚登山的路程s(米)与登山所用的时间t(分钟)的关系(从爸爸开始登山时计时)。
根据图像,下列说法错误的是【】A.爸爸开始登山时,小军已走了50米B.爸爸走了5分钟,小军仍在爸爸的前面C.小军比爸爸晚到山顶D.爸爸前10分钟登山的速度比小军慢,10分钟之后登山的速度比小军快9. 如图表示某加工厂今年前5个月每月生产某种产品的产量c(件)与时间t(月)之间的关系,则对这种产品来说,该厂【】A.1月至3月每月产量逐月增加,4、5两月产量逐月减小B.1月至3月每月产量逐月增加,4、5两月产量与3月持平C.1月至3月每月产量逐月增加,4、5两月产量均停止生产D. 1月至3月每月产量不变,4、5两月均停止生产10.小强和小敏练短跑,小敏在小强前面12米。
《海盗派测试分析》读书笔记

《海盗派测试分析》第一章了解测试任务KYM –Know Your Mission了解测试的用户以及用户的需求为什么要做KYM大多数情况下,测试人员接到任务以后,会一头扎进项目中去,开始冥思苦想如何更好的完成任务,但是,比HOW更重要的是先想清楚WHY的问题,了解清楚任务本身一级任务的背景,明确最终要达到的目的,然后再开始考虑HOW的问题,并且在执行任务的过程中,不断地深入理解WHY,不断地迭代和优化WHY,使得最终我们输出的WHAT和任务目标始终是对齐的,我把这种做法叫Konw Your MissionKYM会启发我们问出各种各样的问题,提醒我在关注具体的测试细节之前先要收集必要的信息,了解测试任务的背景。
无论是开发人员还是测试人员或者是需求分析人员,最好在项目早期尽早地使用KYM,更好地了解用户,提前发现风险怎么做KYM问问题的能力对于测试人员来说是非常重要的,KYM的本质就是通过不断的问问问题,收集信息,了解上下文,对测试最终要达成的目标有个更加清晰的认识,这个目标将会不断的指引着测试人员的一切活动,无论是测试分析,测试设计还是测试执行、测试管理等活动,都围绕测试的目标进行,KYM就像航海中的灯塔一样,时刻帮助测试人员辨别方向用‘CIDTESTD引导词法’做KYM,集中做一次KYM的时间为15分钟~2小时,把握主干,忽略细节KYM主要是4个大的方面的收集信息:了解用户、了解项目、了解产品、了解测试任务本身怎么避免做很差的KYM将KYM形式化:用CIDTESTED制作KYM思维导图模板,并强制大家必须使用重结果而不重过程:规定每个测试人员都要输出一张KYM思维导图来,并进行互相评比,KYM过于关注需求的细节第二章测试覆盖大纲TCO–Test Coverage Outline TCO可以帮助达成3个目的:信息提炼、信息重组、心中有数。
内容重组包含两层意思:对信息源中提取的信息进行重新组织,以及对于信息源中没有的信息的添加。
第四章图形的相似单元测试北师大版2024—2025学年秋季九年级上册

第四章图形的相似单元测试北师大版2024—2025学年秋季九年级上册考生注意:本试卷共三道大题,23道小题,满分120分,时量120分钟注意事项:1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分。
笞卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第I卷时,选出每小题答案后,把答案填写在答题卡上对应题目的位置,填空题填写在答题卡相应的位置写在本试卷上无效。
3.回答第II卷时,将答案写在第II卷答题卡上。
4.考试结束后,将本试卷和答题卡一并交回。
第I卷一、选择题(每题只有一个正确选项,每小题3分,满分36分)1.在比例尺是1:8000的地图上,中山路的长度约为25cm,该路段实际长度约为()A.3200m B.3000m C.2400m D.2000m2.如图,用放大镜将贺兰山旅游图标放大,这两个图形之间属于以下哪种图形变换()A.相似B.平移C.轴对称D.旋转3.已知=,则下列式子中正确的是()A.a:b=c2:d2B.a:d=c:bC.a:b=(a+c):(b+d)D.a:b=(a﹣d):(b﹣d)4.下列说法中,不正确的是()A.等边三角形都相似B.等腰直角三角形都相似C.矩形都相似D.正八边形都相似5.以下四组线段中,成比例的是()A.3,4,6,8B.2,3,4,5C.1,2,3,4D.5,6,7,8 6.如果两个相似三角形的相似比是1:2,那么它们的周长比是()A.2:1B.1:4C.1:D.1:27.如图,每个小正方形边长均为1,则下列图中的三角形(阴影部分)与图中△ABC相似的是()A.B.C.D.8.如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为,点A,B,E在x轴上.若正方形ABCD的边长为2,则点F坐标为()A.(8,6)B.(9,6)C.D.(10,6)9.如图,在▱ABCD中,E是AB边的中点,则S△AEG:S平行四边形ABCD的值为()A.B.C.D.10.如图,在矩形ABCD中,E、F分别在BC、CD上运动(不与端点重合),连接BF、AE,交于点P,且满足.连接CP,若AB=4,BC=6,则CP的最小值为()A.2﹣3B.2﹣2C.5D.3二.填空题(6小题,每题3分,共18分)11.若,则=.12.如图,已知AC∥EF∥BD,如果AE:EB=2:3,CD=6,那么DF的长等于.13.如图,在▱ABCD中,AD=16,∠ABC的平分线交AD于点F,交CD的延长线于点E,若S△EDF:S四边形FBCD=9:55,则AB=.14.若,则k=.15.如图,△ABC∽△CBD,AB=9,BD=25,则BC=.16.如图,矩形ABCD中,AB=3,BC=10,点P是AD上的一个动点,若以A,P,B为顶点的三角形与△PDC相似,则AP=.第II卷第四章图形的相似单元测试北师大版2024—2025学年秋季九年级上册姓名:____________ 学号:____________准考证号:___________一、选择题12345678910题号答案二、填空题11、_______ 12、______13、_______ 14、______15、_______ 16、______三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)17.已知,求的值.18.如图,AB∥CD∥EF,BF=20.(1)若AC=3,CE=5,求DF的长;(2)若AC:CE=2:3,求DF的长.19.在△ABC中,∠BAC=90°,AB=AC,点D是BC边上一点,过点D作∠ADE=45°,DE交AC于点E,求证:△ABD∽△DCE.20.如图,在△ABC中,AD是角平分线,点E在边AC上,且AD2=AE•AB,连接DE.(1)求证:△ABD∽△ADE;(2)若CD=3,CE=2,求AE的长.21.如图,△ABC中,D、E两点分别在BC、AD上,且AD为∠BAC的角平分线,若∠ABE=∠C,=.(1)求证:△AEB∽△ADC.(2)求△BDE与△ABC的面积比.22.如图,在正方形ABCD中,点E在边AD上,过点D作DK⊥BE于K,且DK=.(1)若AE=ED,求正方形ABCD的周长;(2)若∠EDK=22.5°,求正方形ABCD的面积.23.如图,AB=4,CD=6,F在BD上,BC、AD相交于点E,且AB∥CD∥EF.(1)若AE=3,求ED的长.(2)求EF的长.24.如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.(1)求证:AC2=AB•AD;(2)求证:CE∥AD;(3)若AD=8,AB=12.求的值.25.问题1:如图①,在△ABC中,AB=4,D是AB上一点(不与A,B重合),DE∥BC,交AC于点E,连接CD.设△ABC的面积为S,△DEC的面积为S′.(1)当AD=3时,=;(2)设AD=m,请你用含字母m的代数式表示.问题2:如图②,在四边形ABCD中,AB=4,AD∥BC,AD=BC,E是AB上一点(不与A,B重合),EF∥BC,交CD于点F,连接CE.设AE=n,四边形ABCD的面积为S,△EFC的面积为S′.请你利用问题1的解法或结论,用含字母n的代数式表示.。
第四章测量的信度

一般来说, 重测的时间间隔越短, 那么各种施测情境 的变化就越小, 重测信度系数就会越大。
重测信度系数较大时, 说明该测量工具前、后两次 的测量结果比较一致。结果具有较好的跨时间上的 稳定性。
定义2: 信度是被试团体真分数与实得分数相关系数的平 方
定义3: 信度是一个测验X(A卷)与它的任意一个平行测验 (B卷)的相关系数
由于真分数的方差无法统计,可转化为: rxx=(S2x-S2E)/S2x =1- S2E/S2x 该定义有两点需要注意: 第一、信度指的是一组测验分数或一列测量的特性,
X―1.96SE<T≤X+1.96SE
• 例:在一个智力测验中,某个被试的IQ为100,这是否反 映了他的真实水平? 如果再测一次,他的分数将改变多 少?
• 已知该智力测验的标准差为15,信度系数为.84,则其IQ
的测量标准误和可能范围为: 勇于开始,才能找到成
•
功的路
注意几点: (1)SE对真分数做的是区间估计,不可能由此得到一
课后作业
1.某智力测验的信度r=0.75,某次施测得到标准差为 3.00,则该测验的测量标准误是多少,若某被试得分 为100,试估计其真分数1- =.95的置信区间
2. 某测验的信度为0.75。要使该测验的信度达到 0.90,须增加多少题目(原测验长度的多少倍) ?
3.一个包含10个题目的测验,信度为0.50,若增至 50个题目,其信度将是多少?
•
真分数的估计区间为:
X-1.个人测验的真分数的大小 。
自动控制理论》四章随堂测试
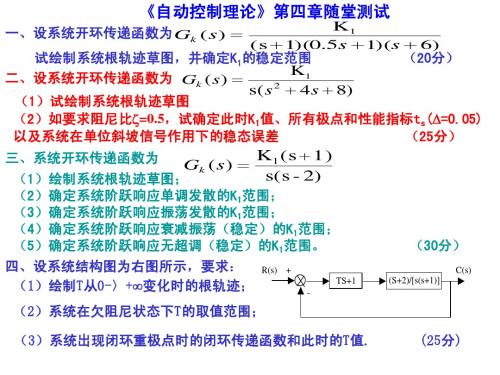
Gk ( s ) =
k1 k1 = s( s 2 + 4 s + 8) s( s + 2 − 2 j )( s + 2 + 2 j )
系统开环极点为: 系统开环极点为:
p1 = 0, p2 = −2 + 2 j, p3 = −2− 2 j
无开环零点, 无开环零点,三条根轨迹趋向无穷远 实轴上的根轨迹:( :(-∞ 实轴上的根轨迹:( ∞,0] 渐近线倾角: 渐近线倾角:φ = ± 180 ( 2 q + 1 ) ( q = 0 ,1 , 2 ) = ± 60 ° ,180 °
根轨迹与虚轴的交点:用劳斯判据法可求得 稳定范围: 根轨迹与虚轴的交点:用劳斯判据法可求得k1稳定范围 0 < k1 < 32 与虚轴交点坐标: 与虚轴交点坐标: 2 2 j 绘制根轨迹图如下 ± 绘制根轨迹图如下:
3j
(2) 过坐标原点作 β|=60°等阻尼线 与根轨迹相 过坐标原点作|β °等阻尼线,与根轨迹相 交点坐标为: 交, 交点坐标为 s1= -1±1.73j Kg=8 ±
实轴上的根轨迹: 实轴上的根轨迹: (-∞,-6],[-2,-1] 渐近线倾角: 渐近线倾角: φ = ± 180 ( 2 q + 1) ( q = 0 ,1, 2 ) = ± 60 °,180 °
n−m
渐近线与实轴的交点坐标: 渐近线与实轴的交点坐标:
∑
3
n
σa =
i =1
pi −
∑
m
j =1
zj =
n−m
= − 1.25
( 2 k + 1) × 1 8 0 ° ϕa = = 4 5 ° ,1 3 5 ° , 2 2 5 ° , 3 1 5 ° n−m
2024-2025学年八年级物理上册 第四章 单元测试卷(沪科版)

2024-2025学年八年级物理上册第四章单元测试卷(沪科版)一、选择题(每题3分,共30分)1.放在凸透镜主光轴上焦点F与透镜之间的光源S发出的光,通过凸透镜后的光路如图所示,则下列说法正确的是()(第1题)A.凸透镜可以对光起发散作用B.焦点F是凸透镜起会聚作用和发散作用的分界点C.凸透镜对光的作用的光路是不可逆的D.通过凸透镜后的光发散程度比原来小,因此凸透镜的作用是对光起会聚作用2.如图所示,MN为透镜L的主光轴,AB为一条从左边射向透镜后折射的光线,由此可以判定()(第2题)A.若L是凸透镜,B点一定是L的焦点B.若B点是L的焦点,则L一定不是凸透镜C.若B点是L的焦点,AB的入射光线一定平行于主光轴D.若AB的入射光线是从无穷远处主光轴上一点发出的,则L一定不是凹透镜3.[2024·长治模拟]摄影师在东方明珠塔下,利用水晶球作为道具拍摄。
在水晶球中可以看到“东方明珠塔”倒立、缩小的像。
则下列说法正确的是()A.水晶球相当于一个凸透镜B.水晶球相当于一个凹透镜C.水晶球中所成的像是虚像D.水晶球远离东方明珠塔时,其中的像变大4.[2024·扬州江都区月考]如图所示,A、B、C、D在凸透镜的主光轴上,F为焦点,若保持凸透镜和光屏的位置不变,则物体放在哪个位置时,可能在光屏上观察到物体成倒立、放大的实像()(第4题)A.A点B.B点C.C点D.D点5.[2024·溧阳模拟]小明同学的奶奶年龄大了,总看不清手机屏幕,需要把手机拿得远远的才能勉强看清,细心的小明在网上帮奶奶购买了一个手机屏幕放大器,将手机放在支架处,透过透明的屏幕放大器即可看到手机屏幕放大的像,如图所示为其观看效果。
下列分析不正确的是()(第5题)A.屏幕放大器相当于一个凸透镜B.透过屏幕放大器看到的像是实像C.手机放在屏幕放大器的1倍焦距以内D.小明奶奶戴远视眼镜即可看清近处物体6.[2024·淄博一模]小李利用纸筒M、N,焦距为10cm的凸透镜和半透明薄膜,制成一个模型照相机,如图所示。
化学选修4第四章测试题

第四章练习题1.废电池造成污染的问题日益受到关注。
集中处理废电池的首要目的是A .回收石墨电极B .回收电池外壳的金属材料C .防止电池中渗泄的电解液腐蚀其他物品D .防止电池中汞、镉和铅等重金属离子对土壤和水源的污染2.下列事实中,与电化学腐蚀无关的是A .用铜质铆钉铆接铁板,铁板易被腐蚀B .为了保护海轮的船壳,常在船壳上附加锌块C .在空气中,银器表面会生成一层黑色的物质D .埋在潮湿土壤里的铁管比埋在干燥土壤里的铁管更容易被腐蚀3.关于电解,下列叙述正确的是A .电解MgCl 2 饱和溶液,可制得金属镁B .电解NaCl 溶液一段时间后,向阴极附近的溶液中滴入酚酞溶液,溶液呈无色C .若在铁表面镀锌,铁作阳极D .用电解法精炼铜时,粗铜作阳极4.废电池造成污染的问题日益受到关注。
集中处理废电池的首要目的是A .回收石墨电极B .利用电池外壳的金属材料C .防止电池中渗泄的电解液腐蚀其他物品D .防止电池中汞、镉和铅等重金属离子对土壤和水源的污染 5.原电池的反应原理是A .储存电能B .氧化还原反应C .化合价升降D .化学能转化为热能6.保护地下钢管不受腐蚀,可使它连接A .铜板B .石墨C .直流电源负极D .直流电源正极 7.镍镉可充电电池在现代生活中有广泛应用,它的充、放电反应按下式进行:Cd+2NiOOH+2H 2O Cd(OH)2+2Ni(OH)2由此可知,该电池放电时的负极是 ( )A .CdB .NiOOHC .Cd(OH)2D .Ni(OH)2充电 放电8.关于电解NaCl 溶液,下列叙述正确的是 ( )A .电解时在阳极得到氯气,在阴极得到金属钠B .若向阳极附近的溶液中滴入KI 溶液,溶液呈棕色C .若向阴极附近的溶液中滴入酚酞溶液,溶液呈无色D .电解一段时间后,将电解液全部转移到烧杯中,充分搅拌后溶液呈中性9.废电池造成污染的问题日益受到关注,集中处理废电池的首要目的是A .回收石墨电极B .利用电池外壳的金属材料C .防止电池中渗泄的电解液腐蚀其他物品D .防止电池中汞、镉和铅等重金属离子对土壤和水源的污染 10.下列说法不正确的是A .电化学腐蚀过程伴随有电流产生,化学腐蚀过程却没有B .根据氧化还原反应Zn(s)+Fe 2+(aq)=Zn 2+(aq)+Fe(s)设计一个原电池时,负极是Zn ,正极可以是碳棒,电解质溶液是FeCl 2C .氢氧燃料电池中,负极室通入的气体是氧气D .盐桥是具有导电作用的装置,其作用是将两个半电池连接起来11.铅蓄电池的电池反应为:Pb(s) + PbO 2(s) + 2H 2SO 4(aq) 2PbSO 4 (s)+ 2H 2O(l)。
小升初语文总复习精练课件-第章 句子-第四章复习检测|语文S版(共16张PPT)

大家,我
没有……完成……
6.有喜有忧,有笑有泪,有花有草,有香有色。
省略号:( ) ” 表示说话断断续续 1.送去,怕这和氏璧是有去无回了;
十四、读句子,用加点词语造句。
3.“空山新雨后,天气晚来秋。
八、扩写下列句子。(6分)
1.操场上摆着鲜花。 __学校的操场上整齐地摆着五颜六色的鲜花。 2.大熊猫吃着竹叶。
凶狠的大灰狼吃掉了一只小兔。
引六号、: 请(写出表3下示.列引破用“折号) 空的不同山用法新。 雨后,天气晚来秋。明月松间照,清泉石上
流。”哦,这首诗我懂得。引号:( 表示引用 2.这种境界,既使人惊叹,又叫人舒服;
七、请指出下面的标点在句子中的作用。
)
. …… …… 任务。 4 “我……对不起 3.我敢保证,这次校运动会我们可能得冠军。
六、请写出下列破折号的不同用法。(6分)
1.“哗——哗——”我循声望去,原来是一位清洁工在扫地。
( 表示声音延长 )
2.我远远望见一条明如玻璃的带子 ( ( 3 )你看,路两旁,渠边上,沟底里,到处缀满了黄绿色的无核葡萄。
除了脚印,什么也别留下。
——河。
十二、按要求改写下列句子,但不能改变句意。
明 ) 2.这种境界,既使人惊叹,又叫人舒服;
A.大地把沉睡着的春风吹醒了。 B.从这个小故事中,说明了一个大问题。
C.我幼稚的心灵中充满了和大人不同。
D.客家民居被誉为“世界民居奇葩”。
四、请给下列语句加上标点符号。(3分)
1.送去,怕这和氏璧是有去无回了;不送去,又怕秦国派 兵来打。
2.你看过《红楼梦》这本书吗? 3.礼拜天,姐姐买来了鸡、鸭、鱼等肉食品。
人教版高一物理必修第一册第四章运动和力的关系章节测试

2020-2021学年高一物理人教版(2019)必修第一册章节测试第四章运动和力的关系1.下列说法中正确的是( )A.亚里士多德发现了力是改变物体运动状态的原因,而不是维持物体运动的原因B.伽利略在对亚里士多德关于物体下落论断的怀疑下,做了著名的斜面实验,并应用实验观察和逻辑推理,得出轻重物体自由下落一样快的结论C.伽利略在亚里士多德、笛卡尔等科学家关于力与运动关系研究的基础上,运用理想实验和归谬法得出了惯性定律D.牛顿第一定律是通过多次实验总结出来的一条实验定律2.如图所示,小明乘坐电梯上楼,他站在静止的电梯厢中,按动上楼按钮后电梯由静止开始竖直向上先做匀加速运动,经3.0 s电梯达到最大速度6.0 m/s。
若小明的质量为50 kg,210m/sg ,对于这个加速运动的过程,下列说法中正确的是( )A.小明对电梯厢底板的压力大小为500 N,小明处于超重状态B.小明对电梯厢底板的压力大小为600 N,小明处于超重状态C.小明对电梯厢底板的压力大小为400 N,小明处于失重状态D.小明对电梯厢底板的压力大小为500 N,小明处于失重状态3.如图所示,轻质弹簧的上端固定在电梯的天花板上,弹簧下端悬挂一个小铁球,在电梯竖直运行时,乘客发现弹簧的伸长量比电梯静止时的伸长量小,这一现象表明此过程中( )A.电梯一定是在下降B.电梯一定是在上升C.乘客一定处在超重状态D.乘客一定处在失重状态4.在水平的路面上有一辆匀速行驶的小车,车上固定一盛满水的碗,现突然发现碗中的水洒出,水洒出的情况如图示,则关于小车在此种情况下的运动,下列叙述正确的是()A.小车匀速向左运动B.小车可能突然向左加速C.小车可能突然向左减速D.小车可能突然向右加速5.如图所示,一长木板放在斜面上,材料相同的两个小滑块P Q、放置在长木板上,且滑块P的质量大于滑块Q的质量,长木板在外力作用下向上运动,滑块、始终、和长木板相对静止。
现使长木板突然停下来并保持不动,滑块P QP Q在长木板上,则滑块P Q、之间的距离将( )A.保持不变B.一直增大C.一直减小D.条件不足,无法判断6.有一堆砂子在水平面上堆成圆锥形,稳定时底角为α,如图所示。
北师大版初中九年级数学上册第四章素养基础测试卷课件

(3)△OAB的内部一点M的坐标为(a,b),直接写出点M在△OA2B2中的对应点M2的
坐标为
.
解析 (1)如图,点P为所作,P点坐标为(-5,-1).
(2)如图,△OA2B2为所作. (3)点M在△OA2B2中的对应点M2的坐标为(2a,2b).
18. (新独家原创,★☆☆)(8分)如图,在正方形ABCD中,E是CD边上任意一点,连接 AE,过E作EF⊥AE交BC于F,若AD=5,DE=2,求CF的长.
4
到图②的位置,则图②中 BD的值为
5
CE
. 对应目标编号M9104005
第15题图
答案 4 5
解析 在题图①中,∵∠ABC=90°,AB=8,BC=6,∴AC= AB2 BC2 = 82 62 =10. ∵DE∥BC,∴△ADE∽△ABC,
∴ AD = AE .在题图②中,∵将△ADE绕A点顺时针旋转到题图②的位置,∴∠DAB=
.
答案 5 2
解析 ∵四边形ABCD是平行四边形,∴AD∥BC,OA=OC, 又∵BE∥AC,∴四边形AEBC是平行四边形, ∴AC=BE,∴BE=2OA,∵BE∥AC,
∴△OAF∽△EBF,∴ OF = AF = OA = 1 ,∴ S AEF = EF =2, S OBF = BF =2,
EF BF BE 2 S AOF OF S AOF AF
璃管的内径DE正对“30”刻度线,已知AB的长为5 mm,DE∥AB,则玻璃管内径
DE的长度为
(
)
B
A. 2.5 mm
B. 3 mm
C. 3.5 mm
D. 4 mm
解析 B 根据题意得CD=30,AC=50,∵DE∥AB,∴△CDE∽△CAB,∴ CD=
北师大版九年级上册数学第四章测试题(附答案)
北师大版九年级上册数学第四章测试题(附答案)一、单选题(共12题;共24分)1.如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交DB于点F,则△DEF的面积与△BAF的面积之比为()A. 1:3B. 3:4C. 1:9D. 9:162.如图,在正方形网格上有两个相似三角形△ABC和△DEF,则∠BAC的度数为()A. 105°B. 115°C. 125°D. 135°3.在△ABC中,DE∥BC,交AB于D,交AC于E,且AD∶DB=1∶2,则下列结论正确的是( )A. DE:BC=1:2B. DE:BC=1:3C. △ADE的周长:△ABC的周长=1:2D. S△ADE:S△ABC=1:34.已知a:b=3:2,则a:(a﹣b)=()A. 1:3B. 3:1C. 3:5D. 5:35.下列各组中的四条线段成比例的是().A. 1cm,2cm,20cm,40cmB. 1cm,2cm,3cm,4cmC. 4cm,2cm,1cm,3cmD. 5cm,10cm,15cm,20cm6.如图是小明设计用手电来测量某古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD =12米,那么该古城墙的高度是( )A. 6米B. 8米C. 18米D. 24米7.“相似的图形”是()A. 形状相同的图形B. 大小不相同的图形C. 能够重合的图形D. 大小相同的图形8.同一时刻,身高1.6米的小强在阳光下的影长为0.8米,一棵大树的影长为4.8米,则这棵树的高度为()A. 2.4米B. 9.6米C. 2米D. 1.6米9.如图,在平面直角坐标系中有一个四边形ABCD,现将四边形ABCD各顶点的横坐标和纵坐标都乘2,得到四边形A1B1C1D1,则四边形A1B1C1D1的面积与四边形ABCD的面积之比为()A. 2:1B. 3:1C. 4:1D. 5:110.如图,在△ABC中,点D,E分别在AB,AC上,且,则: ( )A. 1:2B. 1:4C. 1:8D. 1:911.如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD= .其中正确的结论有()A. 4个B. 3个C. 2个D. 1个12.在平面直角坐标系中,已知点E(﹣4,2),F(﹣2,﹣2),以原点O为位似中心,相似比为,把△EFO 缩小,则点E的对应点E′的坐标是()A. (﹣2,1)B. (﹣8,4)C. (﹣8,4)或(8,﹣4)D. (﹣2,1)或(2,﹣1)二、填空题(共6题;共12分)13.如图在△ABC中,点D、E分别在AB、AC上,且DE∥BC,已知AD=2,DB=4,AC=4.5,则EC=________.14.如图,在正方形ABCD中,AB=4,E是BC边的中点,F是CD边上的一点,且DF=1。
人教版七年级上册数学第四章测试题(含答案)
人教版七年级上册数学第四章测试题(含答案)(考试时间:120分钟满分:120分)分数:____________第Ⅰ卷(选择题共30分)一、选择题(每小题3分,共30分)1.下列图形中,∠1和∠2互为余角的是(D)A BC D2.如图,某同学的家在A处,书店在B处,星期日他到书店去买书,想尽快赶到书店,则他选择最近的一条路线是(B)A.A→C→D→BB.A→C→F→BC.A→C→E→F→BD.A→C→M→B3.如图,下列图形中,是四棱柱的侧面展开图的为(A)A B C D4.如图所示,将左边的图形折成一个立方体后为右边的四个立方体中的(B)A BC D5.下列判断中错误的有(D)①延长射线OA;②直线比射线长,射线比线段长;③如果线段P A=PB,那么点P是线段AB的中点;④连接两点间的线段,叫做两点间的距离.A.0个B.2个C.3个D.4个6.如图,下列说法中不正确的是(D)A.OC的方向是南偏东30°B.OA的方向是北偏东45°C.OB的方向是西偏北30°D.∠AOB的度数是75°7.以长方形3 cm长的边所在直线为轴旋转一周形成圆柱体甲,以长方形2 cm长的边所在直线为轴旋转一周形成圆柱体乙,记两个圆柱的体积为V甲,V乙,侧面积为S甲,S乙,则下列式子中正确的是(A)A.V甲<V乙,S甲=S乙B.V甲>V乙,S甲>S乙C.V甲=V乙,S甲=S乙D.V甲>V乙,S甲<S乙8.★点P,Q在线段AB中点的同一侧,点P将AB分为2∶3的两段,点Q将AB分为3∶4的两段,若PQ=2 cm,则AB的长为(C)A.80 cm B.75 cm C.70 cm D.60 cm9.★如图,∠AOB=∠COD,若∠AOD=110°,∠BOC=70°,则以下结论中正确的有①∠AOC=∠BOD=90°;②∠AOB=20°;③∠AOB=∠AOD-∠AOC;④∠AOB=2 11∠BOD.(C)A.1个B.2个C.3个D.4个10.射线OA上有B,C两点,若OB=8,BC=2,线段OB,BC的中点分别为D,E,则线段DE的长为(D)A.5 B.3 C.1 D.5或3第Ⅱ卷(非选择题共90分)二、填空题(每小题3分,共24分)11.一个角的补角是36°35′,这个角是143°25′.12.C ,D 是直线AB 上两点,D 是AC 的中点,且BC =13AC ,DC =3 cm ,则AB = 4或8 cm.13.如图,O 为直线AB 上一点,已知∠1=40°,OD 平分∠BOC ,则∠AOD = 110° .第13题图 第14题图14.如图,点A ,O ,B 在同一条直线上,射线OD 平分∠BOC ,射线OE 在∠AOC 的内部,且∠DOE =90°,写出图中所有互为余角的角: ∠1与∠3,∠1与∠4,∠2与∠3,∠2与∠4 .15.如图,一个正三棱柱的底面边长为3 cm ,侧棱长为5 cm ,则此三棱柱共有 3 个侧面,侧面展开图的面积为 45 cm 2.16.★有两根木条,一根长60 cm ,另一根长100 cm ,将它们的一端重合,放在同一条直线上,则两根木条的中点间的距离是 80cm 或20cm .17.★如图①所示的纸片是∠AOB 的一部分,OC 平分∠AOB ,如图②,把∠AOB 沿OC 对折成∠COB (OA 与OB 重合),从O 点引一条射线OE ,使∠BOE =12∠EOC ,再沿OE 把角剪开,若剪开后得到的3个角中最大的一个角为80°,则∠AOB = 120 °.18.★如图,下列几何体是由棱长均为1的小立方体按一定规律在地面上摆成的,若将露出的表面都涂上颜色(底面不涂色),则第n 个几何体中只有两个面涂色的小立方体共有 (8n -4) 个.选择、填空题答题卡一、选择题(每小题3分,共30分) 题号12345678 9 10 得分 答案 D B A B D D A CCD二、填空题(每小题3分,共24分)得分:________11. 143°25′ 12. 4或8 13. 110°14. ∠1与∠3,∠1与∠4,∠2与∠3,∠2与∠4 15. 3 45 16. 80cm 或20cm 17. 120 18. (8n -4)三、解答题(共66分)19.(8分)计算:(1)48°39′+67°31′-21°17′;解:原式=116°10′-21°17′=94°53′.(2)23°53′×3-107°43′÷5.解:原式=71°39′-21°32′36″=50°6′24″.20.(9分)如图,已知A,B,O三点.根据下列要求画图:(1)连接线段AB;(2)画射线OA、射线OB;(3)在线段AB上取一点C,在射线OA上取一点D(点C,D不与点A重合),画直线CD,使直线CD与射线OB交于点E.题图答图解:如图.21.(8分)如图,已知∠AOE是平角,∠DOE=20°,OB平分∠AOC,且∠COD∶∠BOC =2∶3,求∠BOC的度数.解:设∠COD=2x°,则∠BOC=3x°.∵OB平分∠AOC,∴∠AOB=3x°.∴2x+3x+3x+20=180.解得x=20.∴∠BOC=3×20°=60°.22.(10分)李老师到市场买菜,发现如果把10千克的菜放到托盘秤上,指标盘上的指针转了180度.第二天李老师就给同学们出了两个问题.(1)如果把0.6千克的菜放到托盘秤上,指针转过多少度角?(2)如果指针转了7°12′,这些菜有多少千克?解:(1)由题意得(180÷10) ×0.6=10.8(度).即指针转过10.8度角.(2)(10÷180)×7°12′=0.4(千克).故这些菜有0.4千克.23.(10分)画图并计算:如图,已知线段AB =2 cm ,延长线段AB 至点C ,使得BC =12AB ,再反向延长AC 至点D ,使得AD =AC .(1)准确地画出图形,并标出相应的字母;(2)线段DC 的中点是哪个点?线段AB 的长是线段DC 长的几分之几? (3)求出线段BD 的长度.解:(1)画图如图所示..(2)线段DC 的中点是点A ,线段AB 的长是线段DC 长的13.(3)∵BC =12AB =12×2=1(cm).∴AC =AB +BC =2+1=3(cm).∵AD =AC =3 cm ,∴BD =DA +AB =3+2=5(cm).24.(9分)已知m ,n 满足算式(m -6)2+||n -2=0.(1)求m ,n 的值;(2)已知线段AB =m ,在直线AB 上取一点P ,恰好使AP =nPB ,点Q 为PB 的中点,求线段AQ 的长.解:(1)m =6,n =2.(2)线段AB =6,AP =2PB ,①当点P 在线段AB 上时,如图①, ∵P A +PB =AB ,而AB =6,AP =2PB , ∴2PB +PB =6, ∴PB =2,AP =4.∵点Q 是BP 的中点,∴PQ =12PB =1,∴AQ =AP +PQ =4+1=5;②当点P 在线段AB 的延长线上时,如图②, ∵P A =PB +AB ,AB =6,AP =2PB , ∴6+PB =2PB ,PB =6, ∵点Q 为BP 的中点, ∴BQ =12PB =3,∴AQ =AB +BQ =6+3=9, ∴线段AQ 的长为5或9.25.(12分)如图①,点O 为直线AB 上一点,将直角三角板OMN 的直角顶点放在点O 处,射线OC 平分∠MOB .① ②(1)若∠AOM =30°,求∠CON 的度数;(2)若∠AOM =α,直接写出∠CON 的度数(用含α的代数式表示);(3)将图①中的直角三角板OMN 绕顶点O 顺时针旋转至图②的位置,一边OM 在射线OB 的上方,另一边ON 在直线AB 的下方.①探究∠AOM 和∠CON 的度数之间的关系,写出你的结论,并说明理由; ②当∠AOC =3∠BON 时,求∠AOM 的度数. 解:(1)∵∠AOM =30°,∴∠BOM =180°-∠AOM =150°. ∵∠MON =90°,OC 平分∠BOM , ∴∠CON =∠MON -12∠BOM =15°.(2)∵∠AOM =α,∴∠BOM =180°-∠AOM =180°-α. ∵∠MON =90°,OC 平分∠BOM , ∴∠CON =∠MON -12∠BOM =12α.故∠CON =12α.(3)设∠AOM =β,则∠BOM =180°-β, ①∠AOM =2∠CON ,理由:∵OC 平分∠BOM ,∴∠MOC =12∠BOM =12(180°-β)=90°-12β.∵∠MON =90°,∴∠CON =∠MON -∠MOC =12β,∴∠AOM =2∠CON ;②由①知∠BON =∠MON -∠BOM =β-90°, ∠AOC =∠AOM +∠MOC =90°+12β,∵∠AOC =3∠BON ,∴90°+12β=3(β-90°),解得β=144°,∴∠AOM =144°.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
PPT文档演模板
第四章执行测试S
驱动模块和桩模块都是额外的开销, 虽然在单元测试中必须编写,但并不需要 作为最终的产品提供给用户。
PPT文档演模板
第四章执行测试S
单元测试的通过标准
• 正确地实现规定的功能 • 错误处理正确 • 边界条件处理正确 • 达到预定的代码覆盖率(语句覆盖、判定
覆盖、条件组合覆盖、路径覆盖等)。 一般要求语句覆盖率达到100%。
通常,在测试以后紧接着要进行调试。
实际上,测试工作和调试工作是交叉进行的
。
PPT文档演模板
第四章执行测试S
进行测 试
找出缺 陷
缺陷分 配
进行调 试
PPT文档演模板
第四章执行测试S
注意:
• 即使通过单元测试后没有出现问题的模块, 集成在一起也有可能出现问题。即使一个 软件成功运行了许多年,仍然会不断出现 bug,干扰软件的使用
构建一个驱动模块(main()函数 的驱动模块),里面至少能够调用 fun1()并输出调用结果。
int fun1(int x,int y) {return x+y; }
PPT文档演模板
第四章执行测试S
如何测试main模块?
#include <stdio.h> void main(void) {int a=1,b=2,c; c=fun1(a,b); printf(“%d”,c); }
PPT文档演模板
void main(void) { int a[5]; int i=0; printf(“please input 5 datas\n”); for(i=0;i<5;i++) { scanf(“%d”,&a[i]); iszero(a[i]); }
第四章执行测试S
• 静态测试,参照c语言编码规范,检查程序中是否存在不符 合规范的地方,发现没有注释
第四章执行测试S
•4.3 执行单元测试
• 什么是单元测试(unit testing)?
指对软件中的最小可测试单元进行检查和验证。单
元,一般应根据实际情况判定其具体含义,如,C中,单元 指1个函数,java中,单元指1个类,图形化软件中也可以 是1个窗口、1个菜单等,单元就是认为规定的最小被测试 的模块。
第四章执行测试S
PPT文档演模板
2020/11/28
第四章执行测试S
第四章 执行测试
• 4.1 测试执行概述 • 4.2 执行系统测试 • 4.3 执行单元测试 • 4.4 执行集成测试
PPT文档演模板
第四章执行测试S
•被 块
测
模
•单元 •测试
•…
•被 块
测
模
•单元 •测试
•…
•被测模块 •单元 •测试
PPT文档演模板
第四章执行测试S
单元测试代码的一般结构
• 驱动模块一般结构: Int DriverModule( ) {…. 调用被测试的模块; 处理运行结果; ….}
桩模块一般结构:
Int StubModule(.…)
{….
Return 返回值;
….}
单元测试代码应该与单元代码保持一致,每当单元代 码发生变化,需确认单元测试代码是否需要更新;单元 测试代码通常不完全等同于所模拟的真实模块,一般只 模拟一个或一些运行情况,返回一个执行所需要的值。
PPT文档演模板
第四章执行测试S
• 在单元测试的过程中,会综合运用静态测试技术和动态 测试技术。
• 在进行单元测试的过程中,一般会使用白盒测试,但也 会结合使用黑盒测试。
• 单元测试是针对程序模块进行正确性检验的测试工作。 在编码的过程中作单元测试,其花费是最小的,
• 在代码编写完成后的单元测试工作主要分为两个步骤:
• 局部数据结构:测试其内部的数据能否保持完 整性,包括内部数据的内容、形式及相互关系 不发生错误。
• 独立的路径:在单元测试中,最主要的测试是 针对路径的测试。
• 边界条件:软件常常在边界地区发生问题。
• 错误处理:测试出错处理的要点是模块在工作 中发生了错误,其中的出错处理设施是否有效。
PPT文档演模板
• 少于30代码行的函数一般不需要做单元测试,只要代码 走查即可。
PPT文档演模板
第四章执行测试S
测试与调试
调试:利用测试结果和测试过程中提供的信息 进行全面分析,找出bug的根源和出错原因, 修正已发现的bug的过程。
调试与测试的区别:
测试的目的:寻找和发现缺陷。测试可由非开发人 员完成。
调试的目的:找出缺陷的原因,并修正缺陷。调试 必须由开发人员完成。
假设main()和fun1()分别由两个 程序员开发且进度不同,进行测试 时:
✓若没有fun1()函数,如何测试 main()?
构建一个桩模块(fun1()的桩模 块),至少能够被main()调用并有一 个返回值。
//桩模块 int fun1(int x,int y) {return 2*x+y; }
PPT文档演模板
第四章执行测试S
•4.3.2 动态跟踪
• 测试—排错—调试
• 单元测试时,应该对模块进行如下检查:
• 对模块内所有独立的执行路径至少测试一次; • 对所有的逻辑判定,取“真“与”假“的情况至少各
执行一次; • 在循环的边界和运行界限内执行循环体; • 测试内部数据的有效性等等。
PPT文档演模板
第四章执行测试S
•4.3.3 单元测试的重点
• 单元测试针对每个程序的模块,主要测试5个方面 的问题:
——模块接口、局部数据结构、边界条件、独立
的路径和错误处理。•模块接口
•出错处理
•局部数据结构
•边界条件
PPT文档演模板
•模块
•独立的路径
第四章执行测试S
• 单元测试的重点:
• 模块接口:检查参数个数、数据类型、顺序是 否正确,确定返回值的类型及有效性;
PPT文档演模板
软件测试过程
•设 计 信 息 •集成 •测试
•集成 •测试
•软 件 需 求
•系统 •测试
•*
•用户信 息其它元 素
•验收 •交 付 用 •测试 户
•*
•软件测试的过程流程
第四章执行测试S
4.1 测试执行概述
• 测试执行过程
•建立测试环境
•执行测试用例
•记录测试结果
•报告测试结果
• 管理有软件错误
PPT文档演模板
第四章执行测试S
案例 单元测试例子
#include <stdio.h> void iszero(int m) { if(m!=0) printf(“%d”,m); else printf(“%d”,1); }
程序功能:若输入的数组元素不 等于0,则输出元素值;若输入的数组 元素值为0,则输出1。
• 不同公司、不同的项目会有不同的复查项检查清单, 例如下面的一些典型复查项:
• 函数入口处的形式参数的合法性 • 有没有显然的数组越界操作 • 代码的注释量是否符合公司规范 • 是否设置了适当的出错处理
• ……
• 静态测试也可采用一些辅助工具软件进行,例如PC-
Lint一款C/C++语言代码静态测试工具。
•执行测试的过程,也是不断发现缺陷的过程。在发现和 记录了软件缺陷后,还需要对缺陷进行管理,包括对缺 陷的分类、报告、重现、跟踪和统计分析。
PPT文档演模板
第四章执行测试S
例子
#include <stdio.h> void iszero(int m) { if(m!=0) printf(“%d”,m); else printf(“%d”,1); }
int fun1(int x,int y) {return x+y; }
PPT文档演模板
假设main()和fun1()分别由两个 程序员开发且进度不同,进行测试 时: ✓若没有main()函数,如何测试 fun1()?
✓若没有fun1()函数,如何测试 main()?
第四章执行测试S
如何测试fun1模块?口标准:通常在编码完成后进行,在前 期应准备,如写单元测试计划、编测试用例、单元测 试代码等。一般由白盒测试工程师、开发人员完成。
单元测试的依据: 项目的详细设计文档和源程序(包括代码和注释)。
如何进行单元测试?
一般先静态地检查代码是否符合规范,然后动态地运 行代码并检查运行结果。
• 某个单元中可以接受的误差,可能经过多 次集成后被扩大到无法接受的程度,这是 集成测试要重点关注的。(单元缺陷的累 积扩散效应)
PPT文档演模板
• 人工静态检查
• 动态执行跟踪
PPT文档演模板
第四章执行测试S
•4.3.1 静态检查
• 合格的代码应该具备以下性质:
• 正确性:指代码逻辑必须正确,能够实现预期的 功能
• 清晰性:指代码必须简明、易懂,注释准确没有 歧义
• 规范性:指代码必须符合企业所定义的共同规范 包括命名规则,代码风格等等
• 一致性:指代码必须在命名上风格上都保持统一 • 高效性:指代码不但要满足以上性质,而且需要
#include <stdio.h> //驱动模块 void main(void) {int a=1,b=2,c; c=fun1(a,2*b); printf(“%d”,c); }
假设main()和fun1()分别由两个 程序员开发且进度不同,进行测试 时:
✓若没有main()函数,如何测试 fun1()?
测试方式: 主要用白盒测试。
PPT文档演模板
第四章执行测试S
如何进行单元测试?
单元测试的一般步骤:
