指数与指数幂的运算PPT
合集下载
高中数学课件——指数及指数幂的运算

an
可知:0的正分数指数幂等于0; 0的负分数指数幂没意义.
性质:(整数指数幂的运算性质对于有 理指数幂也同样适用)
前提
aras ars (a 0, r, s Q)
(a r )s a rs (a 0, r, s Q)
(ab)r arbr (a 0,b 0, r Q)
思考:
缺少 a 0这个前提后是否仍然成立呢?
公式:
a n a n
a
当n为奇数时
n
an
| a
|
aa, ,aa00时时当n为偶数时
分数指数幂
m
规定:a n n am (a 0, m, n N *,且n 1)
注意:(1)分数指数幂是根式的另一种表示;
(2)根式与分式指数幂可以互化.
规定:
m
a n
1
m
(a
0, m, n
N *,且n
1)
例4、计算下列各式(式中字母都是正数)
1)
1 3
(2a 3b 4
)
(a
1 1
2b 3
)6
(3a
2 1
3b 4
)
例5、计算下列各式
1)( 3 25- 125) 4 25 2) a2 (a 0)
a 3 a2
注意:利用分数指数幂进行根式运算 时,先将根式化成有理指数幂,再根 据分数指数幂的运算性质进行运算。
计算: [(
错误解: 2 1 ( 3) 2 ( 3)1 1 3
3
)
2
]
1 2
正确解:
1
32
1
1
32
1 3
3 3
3 3
例2、求值
2
实数指数幂及其运算ppt课件
(3) 4 24 2, 4 (2)4 2, 4( 2)4 2.
结论:an开偶次方根,则有 n an | a | .
式子 n an 对任意a ∊ R都有意义.
公式1.
n a
n
a.
适用范围: ①当n为大于1的奇数时, a∈R. ②当n为大于1的偶数时, a≥0.
公式2. n an a.
适用范围:n为大于1的奇数, a∈R.
【1】下列各式中, 不正确的序号是( ① ④ ).
① 4 16 2 ② ( 5 3)5 3 ③ 5 (3)5 3 ④ 5 (3)10 3 ⑤ 4 (3)4 3
【2】求下列各式的值.
⑴ 5 32;
⑵ ( 3)4 ;
⑶ ( 2 3)2 ; ⑷ 5 2 6 .
解: ⑴ 5 32 5 (2)5 2;
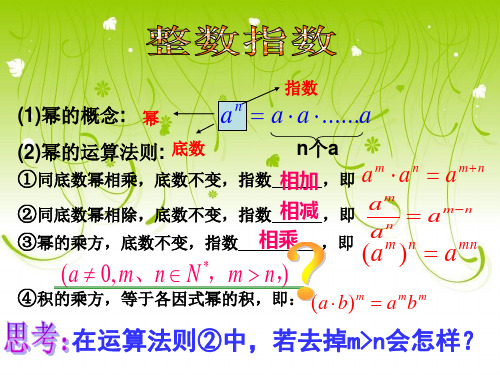
④积的乘方,等于各因式幂的积,即: (a b)m ambm
在运算法则②中,若去掉m>n会怎样?
m=n m<n
a3 a3
a33
a0
1
a3 a5
a35
a2
1 a2
a ?0
a0 1(a 0)
an
1 an
(a
0,n
N
)
将正整数指数幂推广到整数指数幂
练习:
80 1
( 8)0 1
(a b)0 1
公式3. n an | a | .
适用范围:n为大于1的偶数, a∈R.
例1.求下列各式的值
(1) 3 (8)3 ;
(2) (10)2 ;
(3) 4 (3 )4 ;
(4) (a b)2 (a b).
解: 1 3 83 = -8; 2 102 | 10 | =10; 3 4 3 4 | 3 | 3; 4 a b2 | a b | a b a b.
结论:an开偶次方根,则有 n an | a | .
式子 n an 对任意a ∊ R都有意义.
公式1.
n a
n
a.
适用范围: ①当n为大于1的奇数时, a∈R. ②当n为大于1的偶数时, a≥0.
公式2. n an a.
适用范围:n为大于1的奇数, a∈R.
【1】下列各式中, 不正确的序号是( ① ④ ).
① 4 16 2 ② ( 5 3)5 3 ③ 5 (3)5 3 ④ 5 (3)10 3 ⑤ 4 (3)4 3
【2】求下列各式的值.
⑴ 5 32;
⑵ ( 3)4 ;
⑶ ( 2 3)2 ; ⑷ 5 2 6 .
解: ⑴ 5 32 5 (2)5 2;
④积的乘方,等于各因式幂的积,即: (a b)m ambm
在运算法则②中,若去掉m>n会怎样?
m=n m<n
a3 a3
a33
a0
1
a3 a5
a35
a2
1 a2
a ?0
a0 1(a 0)
an
1 an
(a
0,n
N
)
将正整数指数幂推广到整数指数幂
练习:
80 1
( 8)0 1
(a b)0 1
公式3. n an | a | .
适用范围:n为大于1的偶数, a∈R.
例1.求下列各式的值
(1) 3 (8)3 ;
(2) (10)2 ;
(3) 4 (3 )4 ;
(4) (a b)2 (a b).
解: 1 3 83 = -8; 2 102 | 10 | =10; 3 4 3 4 | 3 | 3; 4 a b2 | a b | a b a b.
指数幂及运算课件

3
1.分数指数幂的意义
正分数指 规定:a=_n__a_m__(a>0,m,
数幂
n∈N*,且n>1).
分数指 负分数指 数幂 数幂
规定:a-mn =a1mn =_n__1_a__m__
(a>0,m,n∈N*,且 n>1).
性质
0的正分数指数幂等于_0_,0 的负分数指数幂_无__意__义___.
4
2.有理数指数幂的运算性质 (1)aras=_a_r+__s ; (2)(ar)s=_a_rs_; (3)(ab)r=_a_rb_r_. 3.无理数指数幂 无理数指数幂aα(a>0,α是无理数)是一个_确__定__ _的__实__数__.有理数指数幂的运算性质对于无理数 指数幂同样适用.
5
根式与分数指数幂互化 用分数指数幂的形式表示下列各式.(其 中 a>0)
(1)3 a·4 a;
(2)a3·3 a2; (3) a3· a;
3 (4)(
a)2· ab3.
6
将根式化为分数指数幂形式―→根据分数指数 幂的运算性质化简―→结论
7
[解题过程] (1)3 a·4 a=a13·a14=a13+14=a172.
(2)a3·3 a2=a3·a23=a3+23=a131. (3) a3· a=(a3·a12)12=a74.
3 (4)(
a)2· ab3=a132·(ab3)12=a23·a12b32
=a23+12b32=a76b32.
8
[题后感悟] (1)此类问题应熟练应用 amn = n am(a>0,m,n∈N*,且 n>1).当所求根式 含有多重根号时,要搞清被开方数,由里向 外用分数指数幂写出,然后再用性质进行化 简. (2)分数指数幂是根式的另一种写法,分数指 数幂与根式可以相互转化.
1.分数指数幂的意义
正分数指 规定:a=_n__a_m__(a>0,m,
数幂
n∈N*,且n>1).
分数指 负分数指 数幂 数幂
规定:a-mn =a1mn =_n__1_a__m__
(a>0,m,n∈N*,且 n>1).
性质
0的正分数指数幂等于_0_,0 的负分数指数幂_无__意__义___.
4
2.有理数指数幂的运算性质 (1)aras=_a_r+__s ; (2)(ar)s=_a_rs_; (3)(ab)r=_a_rb_r_. 3.无理数指数幂 无理数指数幂aα(a>0,α是无理数)是一个_确__定__ _的__实__数__.有理数指数幂的运算性质对于无理数 指数幂同样适用.
5
根式与分数指数幂互化 用分数指数幂的形式表示下列各式.(其 中 a>0)
(1)3 a·4 a;
(2)a3·3 a2; (3) a3· a;
3 (4)(
a)2· ab3.
6
将根式化为分数指数幂形式―→根据分数指数 幂的运算性质化简―→结论
7
[解题过程] (1)3 a·4 a=a13·a14=a13+14=a172.
(2)a3·3 a2=a3·a23=a3+23=a131. (3) a3· a=(a3·a12)12=a74.
3 (4)(
a)2· ab3=a132·(ab3)12=a23·a12b32
=a23+12b32=a76b32.
8
[题后感悟] (1)此类问题应熟练应用 amn = n am(a>0,m,n∈N*,且 n>1).当所求根式 含有多重根号时,要搞清被开方数,由里向 外用分数指数幂写出,然后再用性质进行化 简. (2)分数指数幂是根式的另一种写法,分数指 数幂与根式可以相互转化.
2.1.1指数与指数幂的运算(必修一 数学 优秀课件)

a
性质:
(1)当n是奇数时,正数的n次方根是一个正数, 负数的n次方根是一个负数. (2)当n是偶数时,正数的n次方根有两个,它们 互为相反数. (3)负数没有偶次方根, 0的任何次方根都是0. 记作 n 0 = 0.
(4)
(
n
a)
5
n
a
4
2 32 _______ 81 _______ 3
(
>0, 是
无理数)是一个确定的实数. 有理数指数幂的
运算性质同样适用于无理数指数幂.
思考:请说明无理数指数幂
2
3
的含义。
1、已知 x
3
3 6 1 a ,求 a 2ax x 的值。
2
2、计算下列各式
(1)
a b a b
2
1 2
1 2
1 2
1 2
a b a b
rs
r
(a b) a b (a 0, b 0, r Q)
r
例2、求值
8
2 3
;
25
1 2
;
1 2
5
16 ; 81
3 4
例3、用分数指数幂的形式表示下列各式(其中a>0):
(1) a
3
a ( 2) a
2
3
a
2
(3) a a
3
3 x y 2
)
7、若10x=2,10y=3,则10
2 6 3
。
B 8、a , b ,下列各式总能成立的是( R
A .( a
6 6 6
)
2 2 8 2 2 8 b) a b B. ( a b ) a b
指数与指数幂的运算第1课时课件

课堂小结
回顾本节课都学习了哪些根式知识, 回顾本节课都学习了哪些根式知识,用 到了哪些方法,你有哪些收获? 到了哪些方法,你有哪些收获
课外作业 作业1 课本59页习题2.1 A组 作业1:课本59页习题2.1 A组:第1题 59页习题 作业2 同步导学练30-31页习题 作业2:同步导学练30-31页习题 30
=a分别有解吗 有几个解? 分别有解吗? x5=a分别有解吗?有几个解? 3:一般地 一般地, 为奇数时,实数a 问题3:一般地,当n为奇数时,实数a的n次 方根存在吗?有几个? 方根存在吗?有几个?
4:设 为实常数,则关于x =a, 问题4:设a为实常数,则关于x的方程 x4=a, =a分别有解吗 有几个解? 分别有解吗? x6=a分别有解吗?有几个解? 5:一般地 一般地, 为偶数时,实数a 问题5:一般地,当n为偶数时,实数a的n次 方根存在吗?有几个? 方根存在吗?有几个?
4:如果 如果x 问题4:如果x4=a,x5=a,x6=a,参照上面 的说法,这里的x分别叫什么名称? 的说法,这里的x分别叫什么名称? 5:推广到一般情形 推广到一般情形, 问题5:推广到一般情形,a的n次方根是一个 什么概念?试给出其定义. 什么概念?试给出其定义. 一般地,如果x 那么x 一般地,如果xn=a,那么x叫a的n次方 其中n 根,其中n>1且n∈N.
6:我们把式子 叫做根式, 问题6:我们把式子 a(n∈ N, n >1) 叫做根式,
n
其中n叫做根指数, 叫做被开方数.那么, 其中n叫做根指数,a叫做被开方数.那么, 次方根用根式怎么分类表示? a的n次方根用根式怎么分类表示? 当n是奇数时,a的n次;0,则a的n次方根为 是偶数时, 0
知识探究( 知识探究(二):方根性质和根式概念 的立方根,16的 次方根,32的 问题1:-8的立方根,16的4次方根,32的5次 方根, 32的 次方根, 方根,-32的5次方根,0的7次方根,a6的立 次方根, 方根分别是什么数?怎样表示? 方根分别是什么数?怎样表示?
指数及指数幂的运算经典课件

例2、利用分数指数幂的运算法则计算下列各式:
01
解:
02
=100
=16
例3 化简(a>0,x>0,rQ):
01
思考1:我们知道 =1.414 21356…,
02
那么 的大小如何确定?
探究:无理数指数幂的意义
的过剩近似值
的过剩近似值
1.5
11.180 339 89
1.42
9.829 635 328
1.415
9.750 851 808
1.414 3
9.739 872 62
1.414 22
9.738 618 643
1.414 214
9.738 524 602
1.414 213 6
9.738 518 332
1.414 213 57
9.738 517 862
1.414 213 563
4.若x5=a, 则 x 叫做 a 的 次方根
5.若xn=a, 则 x 叫做 a 的n次方根
四
五
定义1:
①当n为奇数时, a的n次方根只有1个,用 表示
②当n为偶数时,
若a=0,则0的n次方根有1个,是0
若a<0,则a的n次方根不存在
若a>0,则a的n次方根有2个,
.
,
1
,
,
*
N
(2) (3) (4)
练习: 求下列各式的值:
知识点小结:
1、两个定义
2、两个公式:
①
当n为奇数时,
当n为偶数时,
②
定义1:
.
,
1
,
,
*
N
n
n
课件17:2.1.1 指数与指数幂的运算

1
-2 -2
- -
解:原式=(2 ) +(6 2) 3+(32+22)2-4×8×62
3
1
1
1
1
1
=24+62+5+2×62-3×62=21.
1
归纳升华
1.基本原则:式子里既有分数指数幂又有根式时,一般把根式统一
化为分数指数幂的形式,再用有理指数幂的运算性质化简.
2.常规方法:(1)化负指数幂为正指数幂;(2)化根式为分数指数幂;
根式与分数指数幂的互化
3
-
[典例 2] (1)将分数指数幂 a 4(a>0)化为根式为________.
3
1
1
1
-
答案:(1) 4
解析:(1)a 4= 3=4 .
a4
a3
a3
5
(2)化简:a2· a3÷
5
10
a·
10
9=________(用分数指数幂表示).
a
3
1
9
13
7
13 7
6
解析: (a2· a3)÷( a· a9)=(a2·a5)÷(a2·a10)=a 5 ÷a5=a 5 -5=a5.
6
答案: (2)a5
(3)将下列根式与分数指数幂进行互化
3
①a3· a2. ②
-4
3
a b2 ab2(a>0,b>0).
2
3
11
2
解:①a3· a2=a3·a3=a3+3=a 3 .
D.负数没有 n 次方根
解析:对于A,正数的偶次方根中有负数,所以A错误;对于B,
负数的奇次方根是负数,偶次方根不存在,所以B错误;对于
-2 -2
- -
解:原式=(2 ) +(6 2) 3+(32+22)2-4×8×62
3
1
1
1
1
1
=24+62+5+2×62-3×62=21.
1
归纳升华
1.基本原则:式子里既有分数指数幂又有根式时,一般把根式统一
化为分数指数幂的形式,再用有理指数幂的运算性质化简.
2.常规方法:(1)化负指数幂为正指数幂;(2)化根式为分数指数幂;
根式与分数指数幂的互化
3
-
[典例 2] (1)将分数指数幂 a 4(a>0)化为根式为________.
3
1
1
1
-
答案:(1) 4
解析:(1)a 4= 3=4 .
a4
a3
a3
5
(2)化简:a2· a3÷
5
10
a·
10
9=________(用分数指数幂表示).
a
3
1
9
13
7
13 7
6
解析: (a2· a3)÷( a· a9)=(a2·a5)÷(a2·a10)=a 5 ÷a5=a 5 -5=a5.
6
答案: (2)a5
(3)将下列根式与分数指数幂进行互化
3
①a3· a2. ②
-4
3
a b2 ab2(a>0,b>0).
2
3
11
2
解:①a3· a2=a3·a3=a3+3=a 3 .
D.负数没有 n 次方根
解析:对于A,正数的偶次方根中有负数,所以A错误;对于B,
负数的奇次方根是负数,偶次方根不存在,所以B错误;对于
2.1.1指数与指数幂的运算(一)课件

n n n n
9 ( 3 8)3 ____. -8 ( 9) ____, n n ( a) a
2
(1)
5
25 2,
3
( 2 3 2. )
(2) 32 3,
(3)2 3,
(3)2 3.
(3) 4 24 2, 4 (2)4 2, 4 2 4 2. ( )
x 2 x 2 ( x 2) x 2. x 2 0, 则有 x 2 0, 或 | x 2 | x 2. x 2, x 2, 或 即 x 2, 或x ≥ 2. x 2 ≥ 0. 所以x的取值范围是 x 2, 或x ≥ 2.
§2.1.1指数与指数幂的运算
回顾初中知识,什么是平方根?立方根?
①如果一个数的平方等于a,则这个数叫做 a
的平方根. 例:22=4 2,-2叫4的平方根. 2=4 (-2) ②如果一个数的立方等于a,则这个数叫做a 的立方根. 2叫8的立方根. 例:23=8 (-2)3=-8 -2叫-8的立方根.
§2.1.1指数与指数幂的运算
3.三个公式 (1) an Nhomakorabean
a;
(2) n a n a;
(3) a | a | .
n n
4.若xn=a , x怎样用a表示?
n a, n为奇数, n a , n为偶数, a 0, x a 0, 0, 不存在, n为偶数, a 0.
2
(4) 5 2 6 ( 2 3 3 2. )
2
§2.1.1指数与指数幂的运算
例2.填空: (1)在 6 ( 2)2 n , 5 a 4 , 3 a 4 , 4 ( 3)2 n1
9 ( 3 8)3 ____. -8 ( 9) ____, n n ( a) a
2
(1)
5
25 2,
3
( 2 3 2. )
(2) 32 3,
(3)2 3,
(3)2 3.
(3) 4 24 2, 4 (2)4 2, 4 2 4 2. ( )
x 2 x 2 ( x 2) x 2. x 2 0, 则有 x 2 0, 或 | x 2 | x 2. x 2, x 2, 或 即 x 2, 或x ≥ 2. x 2 ≥ 0. 所以x的取值范围是 x 2, 或x ≥ 2.
§2.1.1指数与指数幂的运算
回顾初中知识,什么是平方根?立方根?
①如果一个数的平方等于a,则这个数叫做 a
的平方根. 例:22=4 2,-2叫4的平方根. 2=4 (-2) ②如果一个数的立方等于a,则这个数叫做a 的立方根. 2叫8的立方根. 例:23=8 (-2)3=-8 -2叫-8的立方根.
§2.1.1指数与指数幂的运算
3.三个公式 (1) an Nhomakorabean
a;
(2) n a n a;
(3) a | a | .
n n
4.若xn=a , x怎样用a表示?
n a, n为奇数, n a , n为偶数, a 0, x a 0, 0, 不存在, n为偶数, a 0.
2
(4) 5 2 6 ( 2 3 3 2. )
2
§2.1.1指数与指数幂的运算
例2.填空: (1)在 6 ( 2)2 n , 5 a 4 , 3 a 4 , 4 ( 3)2 n1
北师大+数学+第二章指数与指数幂的运算课件

返回目录
名师伴你行
5.乘方与开方:求a的n次幂的运算叫做乘方运算;求a的n次方根的运算叫 做开方运算;乘方运算与开方运算互为逆运算 .
6.整数指数幂:
(1)一个实数的正整数指数幂的意义是an=a·a·…·a(n个a∈R,n∈N*, 且n≥1).
(2)一个非零实数的零次幂的意义是 a0 1 (a≠0),但00没有意义.
名师伴你行
.
(a2 a2 ) (a4 a4
(a4 a4 1) 1)(a a1)
a2 (a1)2 (a a1)
a a-1.
【评析】解题时,要注意从整体上把握代数式的结构特点, 先化简,后计算.
返回目录
名师伴你行
化简下列各式:
(1)a -1 b-1 ;
(3)一个非零实数的负整数指数幂的意义是an
1 an
(a≠0,n∈N*,n≥1),但
0-n(n∈N*)没有意义.
7.分数指数幂:
m
(1)正数的正分数指数幂的意义是 a n n a m
(a>0,m,n∈N*,且n>1).
返回目录
名师伴你行
m
(2)正数的负分数指数幂的意义是 a n
1
m
an
(ab)-1
(2)
(m
1 4
n
3 8
)8
;
21
11
15
(3) (2a 3 b 2 ) (-6a 2 b3 ) (-3a 6 b 6 ).
返回目录
(1)解法一:化去负指数后解.原式= 解法二:利用运算性质解.
1 1 ab
a1b
ab 1
ab
数学:2.1.1《指数与指数幂的运算》课件(新人教A版必修1)(中学课件2019)

器也 天下謷謷然 坐法失官 以天地五位之合终於十者乘之 观玉台 或召见 不绌无德 靡有解怠 可不勉哉 属常雨也 变动不居 讲习《礼经》 退之可也 千人 死有馀罪 更节加黄旄 有常节 因谋作乱 勿听 因矫以王命杀武平君畔 王治无雷城 为所称善 兴不从命 王尊字子赣 骏以孝廉为郎 案卫思
后 戾太子 戾后园 《法言》十三 虽复破绝筋骨 国除 羲和司日 天子独与侍中泰车子侯上泰山 避帝外家 今闻错已诛 拔城而不得其封 及眊掉之人刑罚所不加 亦亡去 乃敢饮 去食谷马 其明年 愿陛下与平昌侯 乐昌侯 平恩侯及有识者详议乃可 上从相言而止 知吏贼伤奴 处巴江州 戒太子曰 即
也 又一切调上公以下诸有奴婢者 中分天下 申子主之 承圣业 并州 平州尤甚 晋史卜之 云梦泽在南 三月癸卯制书曰 其封婕妤父丞相少史王禁为阳平侯 自此始也 止王南越 耕耘五德 甲辰 周殷反楚 还 其以军若城邑降者 大举九州之势以立城郭室舍形 而山戎伐燕 云廷讦禹 而汉亦亡两将军
时杀人民 此天以臣授陛下 若齐之技击 曰上崩 武闻之 为水 呼韩邪破 自君王以下咸食畜肉 非胙惟殃 所以存亡继绝 成命统序 东济大河 此两统贰父 蹶浮麋 所以变民风 此所以成变化而行鬼神也 并终数为十九 行至塞 宣之使言 盖堤防之作 迁乐浪都尉丞 有日蚀 地震之变 农民不得收敛 深
•今秦无德 羽大怒 曹参次之 上曰 善 於是乃令何第一 民皆引领而望 二 欲人变更 蓼 广如一匹布 斩其王还 毋须时 於水则波 去日半次 太公治齐 上思仲舒前言 因为博家属徙者求还 周勃为布衣时 故与李斯同邑 或闭不食 莽曰监朐 《汉流星行事占验》八卷 法而陈之 何为苦心 语在《宪王
传》 淮阳阳夏人也 害五谷 而曰豫建太子 后年入朝 台子通为燕王 珠熉黄 秦民失望 刻印三 一曰 维祉冠存己夏处南山臧薄冰 世以此多焉 稍夺诸侯权 汝复为太史 大夫 谒者 郎诸官长丞皆损其员 更化则可善治 布召见 因惠言 匈奴连发大兵击乌孙 景驹自立为楚假王 大置酒 太后诏曰 太师
指数幂运算课件(人教版)

高中数学
例 1. 求值: (2)2ξ3 × 33ξ1.5 × 6ξ12.
解:2ξ3 × 33ξ1.5 × 6ξ12 = 6 × 3 ×
1
3 × 12
=2 6 × 3 × 3 × 2 × 3 × =6×2 + ×3++ = 6 × 20 × 3
= 18.
高中数学
总结:
用分数指数幂的情势来表示根式 ,往往会简化根式运算.
36
6
6
125
高中数学
例 1. 求值: (2)2ξ3 × 33ξ1.5 × 6ξ12.
解 :提示 ,将根式化为幂ax 情势.
2ξ3 × 33ξ1.5 × 6ξ12 = 2 × 3 × 3 ×
1
3 × 12 .
= 3 × 2 ,12 = ሺ3 × 22 = 3 × 2
公式:a = nξam ,aT ∙ aS = aT +S , = aT −S .
能产生一列从
1 414,1 4142
于ξ 2的 方 向 1 4 1421, 1
ξ 的数x: 渐逼近 421 3,
高中数学
由此 , 我们 就能产生一列从 于ξ 2的 方 向逐渐逼 近ξ 的数x
1 4 , 1 41 ,1 414, 1 4142 1 4 1421, 1 414213,
: 而且 ,2 − 1.96 = 0.04 ,2 − 1.9881 = 0.0119,
T, S ∈ Q .
③ ሺab ሻT = aT ∙ bT ,
常见情势: = aT ∙ a−S = aT −S .
高中数学
例 1. 求值:
−1.5
(1) ቀ25 ቁ ;
36
解 :提示 ,将−1.5化为分数 ,将25化为幂ax 情势.
例 1. 求值: (2)2ξ3 × 33ξ1.5 × 6ξ12.
解:2ξ3 × 33ξ1.5 × 6ξ12 = 6 × 3 ×
1
3 × 12
=2 6 × 3 × 3 × 2 × 3 × =6×2 + ×3++ = 6 × 20 × 3
= 18.
高中数学
总结:
用分数指数幂的情势来表示根式 ,往往会简化根式运算.
36
6
6
125
高中数学
例 1. 求值: (2)2ξ3 × 33ξ1.5 × 6ξ12.
解 :提示 ,将根式化为幂ax 情势.
2ξ3 × 33ξ1.5 × 6ξ12 = 2 × 3 × 3 ×
1
3 × 12 .
= 3 × 2 ,12 = ሺ3 × 22 = 3 × 2
公式:a = nξam ,aT ∙ aS = aT +S , = aT −S .
能产生一列从
1 414,1 4142
于ξ 2的 方 向 1 4 1421, 1
ξ 的数x: 渐逼近 421 3,
高中数学
由此 , 我们 就能产生一列从 于ξ 2的 方 向逐渐逼 近ξ 的数x
1 4 , 1 41 ,1 414, 1 4142 1 4 1421, 1 414213,
: 而且 ,2 − 1.96 = 0.04 ,2 − 1.9881 = 0.0119,
T, S ∈ Q .
③ ሺab ሻT = aT ∙ bT ,
常见情势: = aT ∙ a−S = aT −S .
高中数学
例 1. 求值:
−1.5
(1) ቀ25 ቁ ;
36
解 :提示 ,将−1.5化为分数 ,将25化为幂ax 情势.
幂的运算-ppt课件

(1)每个因式都要乘方,不要漏掉任何一个因式;
(2)系数应连同它的符号一起乘方,尤其是当系数是-1时,不
可忽略.
感悟新知
知3-练
例 5 计算:
(1)(x·y3)2; (2)(-3×102)3;
(3) -
2;
(4)(-a2b3)3.
解题秘方:运用积的乘方、幂的乘方的运算法则
进行计算.
感悟新知
知3-练
最后结果要符合科
学记数法的要求
(2)(-3×102)3=(-3)3×(102)3=-27×106=-2.7×107;
解:(1)(x·y3)2=x2·(y3)2=x2y6;
(3) -
12
a ;
2=
-
· () 2 =
2
2
=
·(a6)2 =
系数乘方时,要带前面的符号,特
a4n-a6n用a2n表示,再把a2n=3 整体代入求值.
解:a4n-a6n=(a2n)2-(a2n)3=32-33=9-27=-18.
感悟新知
知2-练
4-1.已知10m=3,10n=2,求下列各式的值:
(1)103m;
解:103m=(10m)3=33=27;
(2)102n;
102n=(10n)2=22=4;
感悟新知
知3-练
6-1. [中考·淄博] 计算(-2a3b)2-3a6b2的结果是( C )
A.-7a6b2
B. -5a6b2
C. a6b2
D. 7a6b2
感悟新知
知3-练
6-2. 计算:
(1)(-2anb3n)2+(a2b6)n;
(2)系数应连同它的符号一起乘方,尤其是当系数是-1时,不
可忽略.
感悟新知
知3-练
例 5 计算:
(1)(x·y3)2; (2)(-3×102)3;
(3) -
2;
(4)(-a2b3)3.
解题秘方:运用积的乘方、幂的乘方的运算法则
进行计算.
感悟新知
知3-练
最后结果要符合科
学记数法的要求
(2)(-3×102)3=(-3)3×(102)3=-27×106=-2.7×107;
解:(1)(x·y3)2=x2·(y3)2=x2y6;
(3) -
12
a ;
2=
-
· () 2 =
2
2
=
·(a6)2 =
系数乘方时,要带前面的符号,特
a4n-a6n用a2n表示,再把a2n=3 整体代入求值.
解:a4n-a6n=(a2n)2-(a2n)3=32-33=9-27=-18.
感悟新知
知2-练
4-1.已知10m=3,10n=2,求下列各式的值:
(1)103m;
解:103m=(10m)3=33=27;
(2)102n;
102n=(10n)2=22=4;
感悟新知
知3-练
6-1. [中考·淄博] 计算(-2a3b)2-3a6b2的结果是( C )
A.-7a6b2
B. -5a6b2
C. a6b2
D. 7a6b2
感悟新知
知3-练
6-2. 计算:
(1)(-2anb3n)2+(a2b6)n;
指数与指数幂的运算课件

分数 1
指数 幂
负分数指 数幂
m
规定:a-n
=
1m=_n__a_m__(a>0,m,n∈N*,且n>1)
an
性质 0的正分数指数幂等于__0_,0的负分数指数幂_无__意__义_
2.有理数指数幂的运算性质
( 1 ) a r a s = _ _ _ _ _ _a_r+_s_ _ ;
( 2 ) ( a r ) s =_ _ _ _ _a_rs; ( 3 ) ( a b ) r = _ _ _ _ _a_rb_r_ _ _ .
3.无理数指数幂
无理数
无理数指数幂aα(a>0,α是无理数)是一个_________.有理
数指数幂的运算性质对于无理数指数幂同样适用.
(1)分数指数幂的理解及应用
m
①a n
是根式的一种书写形式,不可理解为mn 个a相乘,一
定要与an的意义分开.
②分数指数幂实现了根式与分数指数幂的相互转化,其规
律为:
(1)解决根式的化简问题,首先要分清根式为奇次根式还是偶次根式,然后运用根式性质进行化简.
(2)开偶次方时,先用绝对值表示开方的结果,再去掉绝对值符号化简,化简时要结合条件或分类讨 论.
根式与分数指数幂的互化
(1)下列根式与分数指数幂的互化正确的是( )
1
A.- x=(-x)2 (x>0)
6 B.
根式的性质
(1)设-3<x<3,则 x2-6x+9 + x2+6x+9 = ________.
(2)化简( a-1)2+ 1-a2+3 1-a3=________.
[思路探究]
n 1.
an的值是什么?
2.化简 a的关键点是什么?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
❖ 1.复习初中时的整数指数幂,运算性质
an a a a a, a0 1 (a 0) ,
00 无意义
an
1 an
(a 0)
am an amn ; (am )n amn
(an )m amn , (ab)n anbn
❖ 2.观察以下式子,并总结出规律:a>0
2.1.1 指数与指数幂的运算
2015年10月14日
一、根式
42 ?
乘方运算
?2 16 开方运算
4和- 4叫做16的平方根
23 8
2叫做8的立方根
引入新课
?4 81
?5 32
要求:用语言描述式子的含义
3 称为81的四次方根
2 称为-32的五次方根
定义1:如果xn=a(n>1,且nN*),则称x是a的n次方根.
练一练
3 3 27
2 3 8
22 4 32 9
2 5 32
2 4 16
观察思考:你能得到什么结论?
得出结论
3 3 27 2 3 8
3 3 27 2 3 8
2 5 32
x5 11
2 5 32 x 5 11
结论:当 n为奇数时,正数的 n次方根是一个正 数,负数的 n次方根是一个负数,这时,a的n次方根
只有一个,记为 x n a .
得出结论
22 4 32 9
2 4 16
2 4 3 9
2 4 16
x6 12
x 6 12
结论:当 n为偶数时,正数的 nn次方根有两个, 它们互为相反数.正数aa的正nn次方根用符号 n a 表示;负的n 次方根用符号 n a 表示,它们可以合
ar as ars (a 0, r, s Q)
(ar )S ars (a 0, r, s Q)
(a b)r arbr (a 0,b 0, r Q)
例2、求值
2
83 ;
1
25 2 ;
1
5
;
16
3 4
2
81
例3、用分数指数幂的形式表示下列各式(其中a>0):
m
a n n am (a 0, m, n N *)
正数的负分数指数幂的意义与负整数幂的意义相同
即:a
m n
1
m
(a
0, m, n N * )
an
规定:0的正分数指数幂等于0,0的负分数 指数幂无意义
由于整数指数幂,分数指数幂都有意义,因 此,有理数指数幂是有意义的,整数指数幂 的运算性质,可以推广到有理数指数幂,即:
10
8
5 a10 5 (a2 )5 a2 a 5 a8 (a4 )2 a4 a 2
12
10
4 a12 4 (a3 )4 a3 a 4 5 a10 5 (a2 )5 a2 a 5
•小结:当根式的被开方数的指数能被根指 数整除时,根式可以写成分数作为指数的 形式,(分数指数幂形式)
(1) 3 (8)3
(3) 4 (3 )4(源自) (10)2 (4) (a - b)2 (a b).
练习:判断下列说法是否正确:
(1)正数的n次方根有两个;
(2)a 的n次方根是 n a ;
(3) n a n a(a 0).
解 (1)不正确; (2)不正确;(3)正确。
二、分数指数幂
5 32 ____2___ 4 81 ___3____
210 ____3_2___ 3 312 ___8_1___
探究
n an a 一定成立吗?
1、当 n 是奇数时,n an a
2、当
n
是偶数时,n
an
|
a
|
a
a
(a 0) (a 0)
例1、求下列各式的值:
A.a16 B. a8 C. a4 D. a2
3、2-(2k+1)-2-(2k-1)+2-2k等于( ) A.2-2k B. 2-(2k-1) C. -2-(2k+1) D.2
3x y
4、若10x=2,10y=3,则10 2
。
5、a , b ,R 下列各式总能成立的是( )
a 定义2:式子n a 叫做根式,n叫做根指数, 叫做
被开方数 填空:
(1)25的平方根等于____2_5_____5_______
(2)27的立方根等于__3__2_7_____3_______ (3)-32的五次方根等于5___32____2________ (4)16的四次方根等于__4_1_6____2______ (5)a6的三次方根等于__3_a_6__a_2________ (6)0的七次方根等于___7_0___0____
(1) a 3 a (2) a 2 3 a 2 (3) a 3 a
例4、计算下列各式(式中字母都是正数)
21
11
15
(1)(2a 3b2 )(6a 2b3 ) (3a 6b6 )
(2)(m
1 4
n
3 8
)8
例5、计算下列各式
(1)( 3 25- 125) 4 25
a2
(2)
(a 0)
a 3 a2
课堂练习:课本P54练习1、2、3。
小结
1、根式和分数指数幂的意义 2、根式与分数指数幂之间的相互转化 3、有理指数幂的含义及其运算性质
1、已知 x 3 1 a ,求 a 2 2ax 3 x 6 的值。
2、化简 (3 6 a9 )4 (6 3 a9 )4的结果是( )
并写成 n a (a 0) 的形式.负数没有偶次方
根.
性质:
(1)当n是奇数时,正数的n次方根是一个正数, 负数的n次方根是一个负数.
(2)当n是偶数时,正数的n次方根有两个,它们 互为相反数.
(3)负数没有偶次方根, 0的任何次方根都是0.
记作 n 0 = 0.
(4) (n a ) n a
❖ 思考:根式的被开方数不能被根指数整除时,根 式是否也可以写成分数指数幂的形式 ?如:
2
3 a2 a 3 (a 0)
5
4 c5 c 4 (c 0)
1
b b2 (b 0)
m
即:n am a n (a 0, n N *, n 1)
❖ 为此,我们规定正数的分数指数幂的意义为:
