三年级下册数学思维拓展训练简单的周期问题
三年级下册数学试题-思维训练:周期问题(练习含答案)全国通用

春夏周期问题:……第一步:确定周期(起点、终点)观察画图1周期问题:1 , 4 、 第二步:总数÷周期=组数…余数如果没有余数,表示周期的最后一个。
常见类型1.2.表格中的周期 3.巧填数表 4.星期问题 5.连乘积末位再接2盏蓝灯,然后又是4盏红灯、2盏蓝灯、 这样排下去。
问⑴第100盏灯是 颜色。
⑵前150盏彩灯中有 盏蓝灯。
2 2003 1 分,1个5分的顺序排列起来。
⑴最后1枚是 分硬币 ⑵这200枚硬币一共价值 钱。
,2 2 3 ( “ ” A 4 ) , 出发沿逆时针方向绕五边形走,到乙点拐第一个弯,拐第101个弯在 点。
戊甲 丁乙丙2【例1】儿童节的夜景真漂亮,街上的彩灯按照4盏红灯、 再接2盏蓝灯,然后又是4盏红灯、2盏蓝灯、这 样排下去。
问⑴第100盏灯是_______颜色。
⑵前150盏彩灯中有_______盏蓝灯。
【例2】小莉把平时积存下来的200枚硬币按3个1分,2个2分,1个5分的顺序排列起来。
⑴最后1枚是_______分硬币 ⑵这200枚硬币一共价值________钱 【例3】如图所示,从甲点出发沿逆时针方向绕五边形走,到乙点拐第一个弯,拐第101个弯在____点。
4 ,,2005 ,你数到哪个手指上?5 9286 ,,码都是它前面两个数码积的个位数,那么前100……11 108个数码的和是( )。
7 2 96 31456 2012 2 2 2 ……2,【例7】甲、乙、丙、丁四个停车场分别停放着10、7、5、4辆车。
从停放汽车最多的车场中往另外三个车场各开去一辆汽车,称为一次调整。
那么经过1998次这样的调整后,甲场中停放着多少辆汽车?3 【例4】伸出你的右手,从大拇指开始数,数到2005时,你数到哪个手指上?【例5】有一串数9286…,从第三个数字起,每一个数码都是它前面两个数码积的个位数,那么前100个数码的和是( )。
【例6】2012个2连乘2×2×……×2,乘积的末位数是几?【例8】下个月有一个快乐的六一儿童节,而且下个月有5个星期六,4个星期日,开心的同学们,你们知道下个月的19号是星期几吗?4测试题1.在下面的一串数8、7、4、9、0、3、2、5、0、7、2、9……中,从第四个数起,每个数都是它前面三个数之和的个位数字。
三年级数学思维训练导引(奥数)第07讲 周期问题
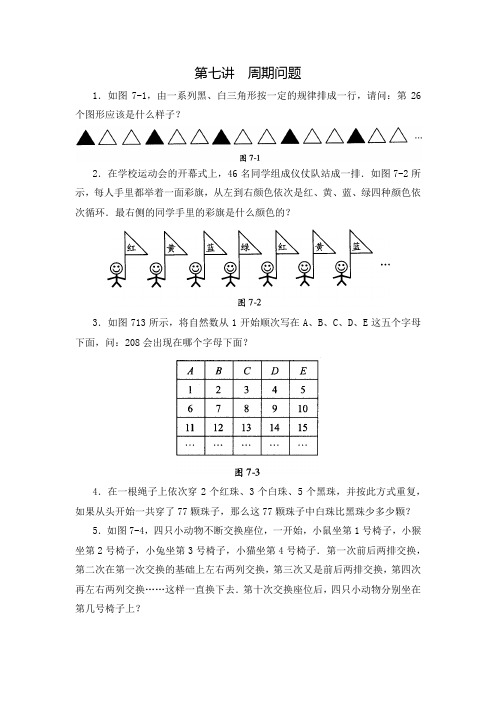
第七讲周期问题1.如图7-1,由一系列黑、白三角形按一定的规律排成一行,请问:第26个图形应该是什么样子?2.在学校运动会的开幕式上,46名同学组成仪仗队站成一排.如图7-2所示,每人手里都举着一面彩旗,从左到右颜色依次是红、黄、蓝、绿四种颜色依次循环.最右侧的同学手里的彩旗是什么颜色的?3.如图713所示,将自然数从1开始顺次写在A、B、C、D、E这五个字母下面,问:208会出现在哪个字母下面?4.在一根绳子上依次穿2个红珠、3个白珠、5个黑珠,并按此方式重复,如果从头开始一共穿了77颗珠子,那么这77颗珠子中白珠比黑珠少多少颗?5.如图7-4,四只小动物不断交换座位,一开始,小鼠坐第1号椅子,小猴坐第2号椅子,小兔坐第3号椅子,小猫坐第4号椅子.第一次前后两排交换,第二次在第一次交换的基础上左右两列交换,第三次又是前后两排交换,第四次再左右两列交换……这样一直换下去.第十次交换座位后,四只小动物分别坐在第几号椅子上?6.将一些自然数排成一列,其中任意相邻的五个数之和都等于15.已知第一个数等于1,第二个数等于2,第三个数等于3,第四个数等于4.问:(1)请写出这个数列的前十项;(2)第一百个数等于多少?7. lOO位同学从左到右排成一行,然后按如下规律从左向右报数:先让第一位同学报1,然后从第二位同学开始,每位同学都把前一位同学所报的数乘以7,再报出乘积的个位来.请问:第100个同学报的是几?8.(1)如图7-5所示,甲、乙两只蚂蚁,分别沿正方形ABCD和AEFG按照顺时针的方向爬行.甲2分钟能爬完正方形的一条边,乙1分钟能爬完正方形的一条边,现在两只蚂蚁在A点同时出发,那么50分钟后甲、乙分别在什么位置?(2)如图7-5所示,如果蚂蚁甲从C点出发,沿着C→D→A→E→F→G→A→B→C 的路线爬行,1分钟能爬完正方形的一条边;蚂蚁乙从F点出发,沿着F→G→A→B→C→D→A→E→F的路线爬行,2分钟能爬完正方形的一条边,它们同时出发,90分钟后甲、乙分别在什么位置?9.一只蜗牛从深30米的井底向上爬,第一天向上爬了6米;第二天休息,于是向下滑了4米;第三天再向上爬6米;第四天又向下滑4米……按这样的规律进行下去,蜗牛第几天才能爬到井口?10.(1)今天是星期六,再过60天是星期几?(2) 2008年6月1日是星期日,2008年8月1日是星期几?(3) 2008年2月8日是星期五,2009年2月8日是星期几?1.图7-6是一行按规律排列的图形.请问:第88个图形应该是什么?2.观察图7-7中黑、白两色三角形的变化规律.请问:前200个图形中有多少个白色三角形?3.如图7-8所示,表格中每行的文字都是循环出现的:第一行是“黎曼假设”4个汉字不断重复,第二行是“庞加莱猜想”5个汉字不断重复,第三行则是“哥德巴赫猜想”6个汉字不断重复.第200列从上到下依次是哪3个汉字?4.阿奇和其他5个小朋友围成一圈,圆圈中央摆放着55个乒乓球.从阿奇开始,小朋友们沿逆时针方向依次拿球,每人每次拿3个,直到把乒乓球全部拿完为止(最后剩下的球不足3个就全拿).阿奇总共拿到了几个球?5.如图7-9,电子跳蚤每跳一步,可从一个圆圈跳到相邻的圆圈.现在,一只红跳蚤从标有数“1”的圆圈按顺时针方向跳了100步,落在一个圆圈里.一只黑跳蚤也从标有数“l”的圆圈起跳,但它是沿着逆时针方向跳了200步,落在另一个圆圈里,这两个圆圈里的数的乘积是多少?6.(1)工厂的仓库里有80吨货物,这些货物都由同一辆卡车负责运输.第一天卡车往仓库里运进50吨,第二天运出了60吨,第三天又运进50吨,第四天再运出60吨……如此不停地运下去.第几天的时候,仓库里的货物恰好被运完?(2)工厂的仓库里有80吨货物,同样是由一辆卡车负责货物的运输.第一天,卡车从仓库里运出60吨,第二天再运进50吨,第三天又运出60吨,第四天再运进50吨……如此不停地运下去.第几天的时候,仓库里的货物恰好被运完?7.如图7-10所示,16幅图按规律排成一排.其中前三幅图已经画出,请按规律画出第16幅图的样子.8.甲、乙、丙、丁兄弟四人各收藏了一些宝石.每天早上他们都要聚在一起,重新分配宝石,分配的规则就是:拥有宝石最多的人分给其他三人每人l 颗.如果第1天早上分配完之后,甲、乙、丙、丁四人分别有10、7、5、4颗宝石,那么第100天早上分完宝石后,四个人手中分别有几颗宝石?9.500名士兵排成一排,第一次从左到右1至3循环报数,第二次从左到右1至4循环报数.请问:既报过1又报过4的士兵有多少名?10.如图7-11,伸出左手,然后从大拇指起开始数数.当数到200的时候,正好数到哪根手指?11.今天是2008年3月16日星期日,阿奇研究日历时,发现再过1天是2008年3月17日星期一,再过2天则是2008年3月18日星期二……请问:(1)再过多少天才是2008年儿童节呢?(2) 2008年的儿童节是星期几?12.哥哥比妹妹大5岁,而且两人生日相同.如果哥哥是1982年6月17日星期四出生的,那么妹妹是在星期几出生的?妹妹出生后第一次在星期二过生日的时候是哪一年?1.观察图7-12中图形的规律,第200个图形应该是下面A、B、C、D四个图形中的哪一个?2.如图7-13所示,7个小朋友围成一圈,沿顺时针方向依次编号为1—7.然后,按如下方法给他们发糖:先给l号小朋友1块糖;然后沿顺时针方向隔过一个人后,给3号小朋友1块糖;再沿顺时针方向隔过两个人后,给6号小朋友l 块糖;接着又沿顺时针方向隔过一个人后,给1号小朋友1块糖……如此反复地间隔一个人、两个人,直到1997块糖全部分完,那么最先发到糖的那位小朋友一共得到了多少块糖?3.如图7-14所示,用红、黄、蓝3种颜色的彩笔,按规律给表格染色,第20行和第30列交叉处的方格所染的颜色是什么?4.(1)某月有31天,有4个星期二和4个星期五,那么这个月的20日是星期几?(2)某月的星期二比星期一多,那么这个月的25日是星期几?5.500名士兵排成一排,第一次从左到右1-5循环报数,第二次从右到左1—4循环报数.请问:既报1又报5的士兵有多少名?6.有六十多人站成一行,从左到右由1开始按l、2、3、4依次循环报数,然后从右到左由1开始按1、2、3依次循环报数,最后发现刚好有12个人既报了1又报了2.请问:这一行最少有多少人?最多有多少人?7.实验室里有两只不同的怪钟,每只钟只有一个指针,而且都是每分钟跳一次,第一只钟一圈有12个格,格线上依次标着0—11,指针一次跳过2个格(例如从4跳到6).第二只钟一圈有7个格,格线上依次标着0至6,指针一次跳过3个格.开始时两个指针都指向0,如果把这看作两个指针第1次指向同一个标数,那么当两个指针第30次指向同一个标数时,它们的指针指着哪个数字?8.如图7-15,在A、B两地之间有7个车站,一辆列车不停地往返于A、B 两地之间.它从A出发,每天行驶到下一站,到达B地后的下一天又回到7号站,如此反复.已知列车第4次驶入4号站时是星期六,那么它第20次驶入5号站时是星期几?。
小学三年级数学周期应用题

小学三年级数学周期应用题一、引言在小学数学教学中,周期应用题是培养学生分析问题、解决问题的能力的重要手段之一。
通过周期应用题的练习,学生可以将数学知识应用于实际生活中的场景,提高他们的问题解决能力和数学思维能力。
本文将给出一些小学三年级数学周期应用题的示例,并提供详细的解题思路。
二、题目一:小明买水果小明去市场买了一袋苹果,第一天买了3个,第二天买了4个,之后每天都多买一个。
问,小明一共买了多少个苹果?解题思路:我们可以使用等差数列的概念来解答这个问题。
假设小明一共买了n天,那么第一天他买了3个苹果,第二天他买了4个苹果,以此类推,第n天他买了3+(n-1)个苹果。
根据等差数列的求和公式,可以得到:n/2*(3+(3+(n-1)))。
计算得出,小明一共买了10个苹果。
三、题目二:多少袋糖果班里有24个学生,老师给每个学生发了3颗糖果,还剩下多少颗糖果没有发完?解题思路:我们可以使用除法来解决这个问题。
将总共的糖果数24除以每个学生分到的糖果数3,所得的商即为发到学生手中的袋数。
然后将这个商再乘以每个学生分到的糖果数3,所得的积即为已经分发给学生的糖果数。
将总共的糖果数24减去已经分发给学生的糖果数,所得的差即为剩下的糖果数。
计算得出,剩下的糖果数为12颗。
四、题目三:小红的花朵小红家的花园里有10朵花,每朵花每天都会开放一朵新花,连续开放7天后,小红家的花园中一共有多少朵花?解题思路:我们可以使用累加的思想来解答这个问题。
首先,第一天小红家的花园中有10朵花。
第二天,花园中新增了1朵花,所以第二天一共有11朵花。
以此类推,第三天有12朵花,第四天有13朵花,一直到第七天有16朵花。
所以,连续开放7天后,小红家的花园中一共有16朵花。
五、题目四:小明的零花钱小明每天都能得到2块钱的零花钱,他存了5天后,一共存了多少钱?解题思路:我们可以使用乘法来解决这个问题。
小明每天得到2块钱的零花钱,所以他存的钱数应该是2的倍数。
三年级思维训练。第9讲 周期问题

三年级思维训练。
第9讲周期问题三年级思练训练第9讲:周期问题在日常生活中,有一些按照一定规律不断重复的现象,如十二生肖、一年有春夏秋冬四个季节、一个星期有七天等等。
这些常见的周期问题,我们称为简单周期问题。
解决这类问题,我们需要利用余数的知识。
解题步骤如下:仔细审题,找出重复出现的规律,然后利用除法算式求出余数,最后根据余数求出正确的结果。
例题1:有一列数5、6、2、4、5、6、2、4……(1)求第129个数;(2)求这129个数的和。
题一:1、有一列数1、4、2、8、5、7、1、4、2、8、5、7……(1)求第58个数;(2)求这58个数的和。
2、XXX把积存下来的游戏币按先四个1元、再三个2元、最后两个5元的顺序排列。
求(1)第111个游戏币的面值;(2)这111个游戏币的面值之和。
3、河岸上种了100棵桃树,第一棵是蟠桃树,后面两棵是水蜜桃树,后面三棵是大青桃树,接下来总是按一棵蟠桃树,两棵水蜜桃树,三棵大青桃树这样的规律种下去。
求第100棵是哪种桃树?三种桃树各有多少棵?例题2:我国农历用鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪这12种动物按顺序轮流代表每年。
如果公元1年是鸡年,那么公元2001年是什么年?题二:1、如果公元3年是猪年,那么公元2000年是什么年?2、如果公元6年是虎年,那么21世纪的第一个虎年是哪一年?3、公元2001年是蛇年,公元2年是什么年?例题3:表格中每一列的两个符号组成1组,如第一组“A 万”第2组“B事”……第20组是什么?题三:1、表格中每一列两个符号为一组,如第一组为“a1”第二组为“b2”……第25组是什么?2、有同样大小的红珠、白珠、黑珠共120颗,按先3颗红珠后2颗白珠再1颗黑珠排列。
求(1)白珠的数量;(2)第68颗珠子的颜色。
三年级数学思维训练:周期问题(三年级)竞赛测试.doc

三年级数学思维训练:周期问题(三年级)竞赛测试姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题(每空xx 分,共xx分)【题文】如图,由一系列黑、白三角形按一定的规律排成一行.请问:第26个图形应该是什么样子?【答案】第26个图形是【解析】试题分析:黑、白三角形按的规律排列.即3个图形一个周期.用26÷3=8(周)…2(个).即循环排列8次后的第二个图形.是解:26÷3=8(周)…2(个).即循环排列8次后的第二个图形.是答:第26个图形是点评:本题考查规律型问题中的图形变化问题,.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.【题文】在学校运动会的开幕上,46名同学组成仪仗队站成一排.如图,每人手里都举着一面采旗,从左到右颜色依次是红、黄、蓝、绿四种颜色依次循环.最右侧的同学手里的彩旗是什么颜色的?【答案】黄色的.【解析】试题分析:彩旗的颜色是按红、黄、蓝、绿四种颜色依次循环.它的循环周期是4人.用46÷4=11(周)…2(人),余数是2人.即从左到右第46个同学手里的彩旗与第二个同学手里的彩旗的颜色相同.据此解答.解:46÷4=11(周)…2(人),余数是2人.即从左到右第46个同学手里的彩旗与第二个同学手里的彩旗的颜色相同,是黄色.答:最右侧的同学手里的彩旗是黄色的.点评:本题考查规律型问题中的图形变化问题,.对于找规律的题目首先应找出哪些部分发生了变化,是评卷人得分按照什么规律变化的.【题文】如图,将自然数从1开始顺次写在A、B、C、D、E这五个字母下面,问:208会出现在哪个字母下面?A B C D E1 2 3 4 56 7 8 9 1011 12 13 14 15……………【答案】字母C.【解析】试题分析:通过表中前3组数的排列顺序,我们发现,数的排列是以5为周期循环的.一个数除以5,若没有余数,则写在E的下面,余1写在A的下面;余2,写在2的下面;余3写在3的下面;余4写在4的下面.用208÷5=41…3,所以208会出现在3的下面.解:208÷5=41 (3)所以208会出现在3的下面,就是字母C的下面.答:208会出现在字母C的下面.点评:本题考查规律型问题中的图形变化问题,.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.【题文】在一根绳子上依次穿2个红珠、3个白珠、5个黑珠,并按此方式重复,如果从头开始一共穿了77颗珠子,那么这77颗珠子中白珠比黑珠少多少颗?【答案】13个.【解析】试题分析:周期为2+3+5=10(个),然后看77里面有几个周期:77÷10=7(组)…7(个),后7个珠为2个红珠,3个白珠,2个黑珠,所以白珠共3×7+3=24(个),黑珠共5×7+2=37(个),由此即可求出白珠比黑珠少的个数.解:2+3+5=10(个)77÷10=7(组)…7(个)后7个珠为2个红珠,3个白珠,2个黑珠所以白珠共3×7+3=24(个)黑珠共5×7+2=37(个)白珠比黑珠少37﹣24=13(个);答:白珠比黑珠少13个.点评:明确一周期是10个,然后求出77里面有几个周期,是解答此题的关键.【题文】如图,四只小动物不断交换座位,一开始,小鼠坐第1号椅子,小猴坐第2号椅子,小兔坐第3号椅子,小猫坐第4号椅子.第一次前后两排交换,第二次在第一次交换的基础上左右两列交换,第三次又是前后两排交换,第四次再左右两更交换…这样一直换下去.第十次交换座位后,四只小动物分别坐在第几号椅子上?【答案】第十次交换座位后,猫坐在1号椅子上,兔坐在2号椅子上,猴坐在3号椅子上,鼠坐在4号椅子上.【解析】试题分析:根据题意,四只小动物交换座位4次后回到原来的座位.即每个小动物的座次是以4为周期循环的.交换10次,即循环2周后座次与第二次的座次相同.解:10÷4=2(周)…2(次).所以交换10次座位后与第二次的座次相同.座次如下:答:第十次交换座位后,猫坐在1号椅子上,兔坐在2号椅子上,猴坐在3号椅子上,鼠坐在4号椅子上.点评:本题考查规律型问题中的图形变化问题,.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.【题文】将一些自然数排成一列,其中任意相邻的五个数之和都等于15.已知第一个数等于1,第二个数等于2,第三个数等于3,第四个数等于4.问:(1)请写出这个数列的前十项;(2)第一百个数等于多少?【答案】(1)这个数列的前十项是:1、2、3、4、5、1、2、3、4、5;(2)5.【解析】试题分析:(1)因为1+2+3+4+5=15,所以第五个数等于5,根据任意相邻的五个数之和都等于15,可以写出这个数列的前十项是:1、2、3、4、5、1、2、3、4、5;(2)由这个数列的前十项,归纳出这个数列是按1、2、3、4、5周期性排列的;即5个数为一个周期,由此即可求出第一百个数等于多少.解:(1)因为1+2+3+4+5=15,所以第五个数等于5;根据任意相邻的五个数之和都等于15,所以这个数列的前十项是:1、2、3、4、5、1、2、3、4、5;答:这个数列的前十项是:1、2、3、4、5、1、2、3、4、5.(2)这个数列是按1、2、3、4、5周期性排列的,即5个数为一个周期;100÷5=20(个),即第一百个数正好排完20个周期,故第一百个数是5.答:第一百个数等于5.点评:解答本题的关键是根据这个数列的前十项,归纳出这个数列是按1、2、3、4、5周期性排列的.【题文】100位同学从左到右排成一行,然后按如下规律从左向右报数:先让第一位同学报1,然后从第二位同学开始,每位同学都把前一位同学所报的数乘以7,再报出乘积的个位来.请问:第100个同学报的是几?【答案】3.【解析】试题分析:先求出前几个同学的报数:1、7、9、3、1、7、9、3、1…,从这些数中归纳出这个数列是按1、7、9、3周期性排列的;即4个数为一个周期,由此即可求出第一百个数等于多少.解:前几个同学的报数为:1、7、9、3、1、7、9、3、1…,归纳出这个数列是按1、7、9、3周期性排列的;即4个数为一个周期;100÷4=25(个),即第一百个数正好排完25个周期,故第一百个数是3;答:第100个同学报的是3.点评:此题主要考查了数的规律,关键是归纳出这个数列是按1、7、9、3周期性排列的.【题文】(1)如图,甲、乙两只蚂蚁,分别沿正方形ABCD和AEFG按照顺时针的方向爬行.甲2分钟能爬完正方形的一条边,乙1分钟能爬完正方形的一条边,现在两只蚂蚁在A点同时出发,那么50分钟后甲、乙分别在什么位置?(2)如图,如果蚂蚁甲从C点出发,沿着C→D→A→E→F→G→A→B→C的路线爬行,1分钟能爬完正方形的一条边;蚂蚁乙从F点出发,沿着F→G→A→B→C→D→A→E→F的路线爬行,2分钟能爬完正方形的一条边.它们同时出发,90分钟后甲、乙分别在什么位置?【答案】(1)甲在B点位置,乙在F点位置.(2)甲回到了A点,乙在D点位置.【解析】试题分析:(1)甲2分钟能爬完正方形的一条边,那么爬完一圈需要8分钟;乙1分钟能爬完正方形的一条边,那么爬完一圈需要4分钟,50里有几个8分钟,甲就爬了几圈,50里有几个4分钟,乙就爬了几圈,正好除尽又回到原点,如果有余数,看余数的时间内爬到哪儿就可以;(2)甲爬完一圈需要4分钟,乙爬完一圈需要16分钟,看90分钟能爬几圈,最后和第1问一样分析即可.解:(1)甲爬完一圈用的时间:2×4=8分钟乙爬完一圈用的时间:1×4=4分钟50÷8=6圈…2分钟50÷4=12圈…2分钟答:甲在B点位置,乙在F点位置.(2)甲1分钟能爬完正方形的一条边,一圈是八条边,90÷8=11圈…2分钟乙2分钟能爬完正方形的一条边,一圈是八条边,90÷(8×2)=5圈…10分钟答:甲回到了A点,乙在D点位置.点评:本题考查周期性问题,先根据题意找出一个周期是多少才是关键.【题文】一只蜗牛从深30米的井底向上爬,第一天向上爬了6米;第二天休息,于是向下滑了4米;第三天再向上爬6米;第四天又向下滑4米…按这样的规律进行下去,蜗牛第几天才能爬到井口?【答案】第25天【解析】试题分析:一只蜗牛从30米深的井底向上爬,它白天爬上来6米,第二天休息,于是向下滑了4米,当它爬到(30﹣6)米处时,再爬1天,就能爬到井口,所以只要求出它爬山(30﹣6)米,需要多少天,再加上1天即可,据此解答.解:(30﹣6)÷(6﹣4)+1=24÷2+1=12+1=13(天)12×2+1=25(天)答:这只蜗牛第25天才能爬出井口.点评:本题的关键是它爬到(30﹣6)米处时,它再用一天的时间就能爬出井口.【题文】(1)今天是星期六,再过60天是星期几?(2)2008年6月1日是星期日,2008年8月1日是星期几?(3)2008年2月8日是星期五,2009年2月8日是星期几?【答案】(1)星期三;(2)星期五;(3)星期日.【解析】试题分析:(1)求出60天里面有几个7天,还余几天,根据余数判断即可;(2)求出2008年6月1日到8月1日一共有多少天,然后用天数除以7,根据余数情况判断即可;(3)因为2008年是闰年,所以2008年有366天,用366除以7,根据余数情况判断即可.解:(1)60÷7=8(周)…4(天);今天是星期六,那么4天后是星期三;(2)30+31=61(天)61÷7=8(周)…5(天);因为2008年6月1日是星期日,所以2008年8月1日是星期五;(3)因为2008年是闰年,所以2008年有366天,366÷7=52(周)…2(天);因为2008年2月8日是星期五,所以2009年2月8日是星期日.点评:解答此类问题的关键是:首先求出经过的天数,然后再除以7,求出经过了几周,还余几天,根据余数情况判断即可.【题文】如图是一行按规律排列的图形,请问:第88个图形应该是什么?【答案】第88个图形是圆.【解析】试题分析:5个图形一个周期.用88÷5=17(周)…3(个).即循环排列17次后的第三个图形是圆.解:88÷5=17(周)…3(个).即循环排列17次后的第三个图形圆.答:第88个图形是圆.点评:本题考查规律型问题中的图形变化问题,.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.【题文】观察图中黑、白两色三角形的变化规律,请问:前200个图形中有多少个白色三角形?【答案】133个.【解析】试题分析:黑、白三角形按的规律排列.即3个图形一个周期.用200÷3=66(周)…2(个).即循环排列66次后的第二个图形,是.因为每一循环由2个白色三角形,因此,200个图形中共有白色三角形66×2+1.解:3个图形一个周期.200÷3=66(周)…2(个).即循环排列66次后的第二个图形,是白色三角形.因此200个图形中共有白色三角形66×2+1=133(个).答:前200个图形中有133个白色三角形.点评:本题考查规律型问题中的图形变化问题.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.【题文】表格中每行的文字都是循环出现的:第一行是“黎曼假设”4个汉字不断重复,第二行是“庞加莱猜想”5个汉字不断重复,第三行则是“哥德巴赫猜想”6个汉字不断重复.第200列从上到下依次是哪3个汉字?黎曼假设黎曼假设黎…庞加莱猜想庞加莱猜…哥德巴赫猜想哥德巴…【答案】设,想,德【解析】试题分析:根据题干可知,汉字排列是:“黎曼假设”4个汉字不断重复,每4个汉字为一个循环周期,由此用汉字总数除以4计算出200个汉字是第几个周期的第几个即可;第二行和第三行都这样求得即可.解:因为“黎曼假设”4个汉字不断重复,200÷4=50(组)所以第200列的第一个汉字是:设;第二行是“庞加莱猜想”5个汉字不断重复,200÷5=40(组)所以200列的第二个汉字是:想;第三行则是“哥德巴赫猜想”6个汉字不断重复,200÷6=33(组)…2(个)所以200列的第三个汉字是:德答:第200列从上到下依次是:设,想,德哲3个汉字.点评:根据题干得出每一行汉字排列的周期规律是解决本题的关键.【题文】阿奇和其他5个小朋友围成一圈,圆圈中央摆放着55个乒乓球.从阿奇开始,小朋友们沿逆时针方向依次拿球,每人每次拿3个,直到把乒乓球全部拿完为止(最后剩下的球不足3个就全拿).阿奇总共拿了几个球?【答案】10个【解析】试题分析:阿奇和其他5个小朋友围成一圈,那么一共有6个小朋友,每人每次拿3个,一个周期拿18个,55个乒乓球拿了几个周期,55÷18=3…1,据此解答即可.解:(5+1)×3=18(个)55÷18=3(个周期)…1(个)3×3+1=10(个)答:阿奇总共拿了10个球.点评:根据题干得出小朋友们拿乒乓球排列的周期规律是解决本题的关键.【题文】如l…;若余数为6,圆圈所标的数字是7.确定顺时针方向,然后再求100被7整除后余数是多少来决定是哪个数;确定逆时针方向,然后再求200被7整除后余数是多少来决定是哪个数.解:根据题意可知是1,2,3,4,…,7即7个数是一个循环.①100÷7=14…2,按顺时针方向跳,故该圆圈所标的数字是3.②200÷7=28…4;按逆时针方向跳,故该圆圈所标的数字是4.3×5=15.答:这两个圆圈里数字的乘积是15.点评:主要考查了学生通过特例分析从而归纳总结出一般结论的能力.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.通过分析找到各部分的变化规律后直接利用规律求解.【题文】(1)工厂的仓库里有80吨货物,这些货物都由同一辆卡车负责运输.第一天卡车往仓库里运进50吨,第二天运出了60吨,第三天又运进50吨,第四天再运出60吨…如此不停地运下去.第几天的时候,仓库里的货物恰好被运完?(2)工厂的仓库里有80吨货物,同样是由一辆卡车负责货物的运输.第一天,卡车从仓库里运出60吨,第二天再运进50吨,第三天又运出60吨,第四天再运进50吨…如此不停地运下去.第几天的时候,仓库里的货物恰好被运完?【答案】(1)第16天(2)第5天【解析】试题分析:(1)第一天卡车往仓库里运进50吨,第二天运出了60吨,则两天合起来看作一个周期,相当于一个周期运出:60﹣50=10(吨),以后每两天运出10吨,则用80÷10×2即为仓库里的80吨货物恰好被运完的天数;(2)第一天卡车从仓库里运出60吨,第二天再运进50吨,则两天合起来看作一个周期,相当于一个周期运出:60﹣50=10(吨),则两个周期后剩余:80﹣10﹣10=60(吨),即两个周期后第一天正好运出60吨,故运完共用:2×2+1=5(天);解:(1)80÷10×2=16(天)答:第16天的时候,仓库里的货物恰好被运完.(2)两天合起来看作一个周期,相当于一个周期运出:60﹣50=10(吨);则两个周期后剩余:80﹣10﹣10=60(吨),即两个周期后第一天正好运出60吨,故运完共用:2×2+1=5(天);答:第5天的时候,仓库里的货物恰好被运完.点评:解答(1)、(2)两题计算方法不同,因为问题(1)一个周期后的第一天是运进,而问题(2)一个周期后的第一天是运出.【题文】如图,16幅图按规律排成一排,其中前三幅图已经画出,请按规律画出第16幅图的样子.【答案】【解析】试题分析:通过观察可知,这些图形每四个为一周期,第五个和第一个的图形是一样的,16÷4=4个,也就是说第16幅图和第四幅图是一样的,据此解答即可.解:这些图形每四个为一周期,第五个和第一个的图形是一样的,16÷4=4个,也就是说第16幅图和第四幅图是一样的:这四个脸谱是按顺时针排列的,根据第一、二、三幅图,可知第四幅图如图:点评:抓住题干,得出这组图形排列的周期特点是解决此类问题的关键.【题文】甲、乙、丙、丁兄弟四人各收藏一些宝石.每天早上他们都要聚在一起,重新分配宝石,分配的规则是:拥有宝石最多的人分给其他三人每人1颗.如果第1天早上分配完之后,甲、乙、丙、丁四人分别有10、7、5、4颗宝石,那么第100天早上分完宝石后,四个人手中分别有几颗宝石?【答案】四个人手中分别有5、6、8、7颗宝石.【解析】试题分析:先列出前几天每人人宝石的数量,找到规律:第一天:10、7、5、4;第二天:7、8、6、5;第三天:8、5、7、6;第四天:5、6、8、7;第五天:6、7、5、8;第六天:7、8、6、5;…,除去第一天的,后面每四天为一个周期.(100﹣1)÷4=24(组)…3(天),余3就是第3个,因为除去了第一天,所以周期从第二天开始,因此第100天的数量和第四天的数量一样多.据此解答.解:第一天:10、7、5、4;第二天:7、8、6、5;第三天:8、5、7、6;第四天:5、6、8、7;第五天:6、7、5、8;第六天:7、8、6、5;…,因此每四天为一个周期.(100﹣1)÷4=24(组)…3(天),余3就是第3个,因为除去了第一天,所以周期从第二天开始,因此第100天的数量和第四天的数量一样多.所以第100天早上分完宝石后,四个人手中分别有:5、6、8、7颗宝石.答:第100天早上分完宝石后,四个人手中分别有5、6、8、7颗宝石.点评:解决周期问题关键在于找出周期,根据周期推出结果.【题文】500名士兵排成一排,第一次从左到右1至3循环报数,第二次从左到右1至4循环报数.请问:既报过1又报过4的士兵有多少名?【答案】41名【解析】试题分析:若将这500名士兵从左到右依次编号,则第一次报数时,编号能被3整除的士兵报1;第二次报数时,编号能被4整除的士兵报4,所以既报1又报4的士兵的编号既能被3整除又能被4整除,即能被12整除,在1至500这500个自然数中能被12整除的数共有41个,所以既报1又报5的士兵共有41名.解:1又报4的士兵都是3×4=12的倍数,500÷12=41(人)…8(人)答:既报1又报4的士兵有41名点评:解答此题时应通过分析得出:既报1又报4的士兵的编号既能被12整除,进而分析解答得出.【题文】如图,伸出左手,估后从大拇指起开始数,当数到200的时候,正好数到哪根手指?【答案】食指上.【解析】试题分析:从大拇指到小指再到食指的过程堪称一个循环,一个循环就是8,接下来又从大拇指开始另一次循环,由此用200÷8,看求出的得数,如果是整数,答案就是此循环数中的最后一个数,如果有余数,看余数在循环数中第几个数对应的手指即可.解:200÷8=25能够整除,故数到25个周期结束的时候恰好到了200,所以数到200正好到了食指上.答:当数到200的时候,正好数到食指上.点评:解答此题的关键是根据数字与拇指的关系,得出8个数是一个循环,由此即可求出答案.【题文】今天是2008年3月16日星期日,阿奇研究日历时,发现再过1天是2008年3月17日星期一,再过2天则是2008年3月18日星期二…请问:(1)再过多少天才是2008年儿童节呢?(2l答:2008年的儿童节是星期日.点评:本题考查日期的推算:注意先算出经过的天数,注意大月小月,根据一周是7天算出儿童节是周几即可.【题文】哥哥比妹妹大5岁,而且两人生日相同.如果哥哥是1982年6月17日星期四出生的,那么妹妹是在星期几出生的?妹妹出生后第一次在星期二过生日的时候是哪一年?【答案】星期三;1997年.【解析】试题分析:妹妹的出生年份用哥哥的年份加上5即可,推天数时,注意1984年是闰年;平年是52周余1天,闰年52周余2天,据此推出解答即可.解:1982+5=1987妹妹是1987年6月17日出生,1983年,1985年,1986年,1987年都是平年,都有365天,而1984年是闰年全年366天,365+366+365+365+365=365×5+1=1826(天)1826÷7=260(周)…6(天)4+6﹣7=3答:妹妹是在星期三出生的.因为平年是:365÷7=52(周)…1(天)闰年是366÷7=52(周)…2(天)而1988年是闰年,过生日时是周五,1989年是平年,过生日时是周六1990年是平年,过生日时是周日,1991年是平年,过生日时是周一,1992年是闰年,过生日时是周三,1993年是平年,过生日时是周四,1994年是平年,过生日时是周五,1995年是平年,过生日时是周六,1996年是闰年,过生日时是周一,1997年是平年,过生日时是周二,答:妹妹出生后第一次在星期二过生日的时候是1997年.点评:本题考查日期的推算:注意平年和闰年,平年365天,闰年366天.【题文】观察图中图形的规律,第200个图形应该是下面A、B、C、D四个图中的哪一个?【答案】A【解析】试题分析:先看颜色是:一白两黑,3个一个周期,200÷3=60(个)…2(个),所以第200个是黑色的;再看形状,黑色的五角星是:AA AC AC CA CA…有可能对称性,200÷10=20,据此解答即可.解:根据观察及其分析:一白两黑,3个一个周期,200÷3=60(个)…2(个),所以第200个是黑色的;200÷10=20故答案为:A.点评:本题考查图形的变化规律,正确分析图形的形状及其颜色的变化规律是解答本题的关键.【题文】如图,7个小朋友围成一圈,沿顺时针方向依次编号为1﹣7.然后,按如下方法给他们发糖:先给1号小朋友1块糖;然后沿顺时针方向隔过一个人后,给3号小朋友1块糖;再沿顺时针方向隔过两个人后,给6号小朋友1块糖;接着又沿顺时针方向隔过一个人后,给1号小朋友1块糖…如此反复地间隔一个人、两个人,直到1997块糖全部分完,那么最先发到糖的那位小朋友一共得到了多少块糖?【答案】286块.【解析】试题分析:通过演练操作,找出一周期,确定一周期中的数以及各个小朋友一周期能分到的糖:发现周期中的数是(1,3,6,1,4,6,2,4,7,2,5,7,3,5),所以一周期中1号小朋友被分到了2次,故有42块糖,然后由1997÷14=142(次)…9,得出进行了142次周期以及第15周期中轮到了7号小朋友,据此解答即可.解:周期中的数是(1,3,6,1,4,6,2,4,7,2,5,7,3,5),所以一周期中1号小朋友被分到了2次,故有42块糖,1997÷14=142(次)…9(块),得出进行了142次周期以及第15周期中轮到了7号小朋友,所以1号小朋友拿到:142×2+2=286(块)答:最先发到糖的那位小朋友一共得到了286块糖.点评:本题考查周期性的问题,正确找出一个周期的数字是关键.【题文】如图,用红、黄、蓝3种颜色的彩笔,按规律给表格染色.第20行和第30列交叉处的方格所染的颜色是什么?【答案】红色.【解析】试题分析:因为第1列、第2列、第3列、第4列的第1个方格的颜色分别是红、黄、蓝、红…,30÷3=10,所以第30列的第1个方格应染蓝色;又因为第30列的第1个、第2个、第3个、第4个方格的颜色分别是蓝、红、黄、蓝,20÷3=6…2,所以第30列的第20个方格的颜色是红色,即第20行和第30列交叉处的方格所染的颜色是红色,据此解答即可.解:因为第1列、第2列、第3列、第4列的第1个方格的颜色分别是红、黄、蓝、红…,30÷3=10,所以第30列的第一个方格应染蓝色;又因为第30列的第1个、第2个、第3个、第4个方格的颜色分别是蓝、红、黄、蓝,20÷3=6…2,所以第30列的第20个方格的颜色是红色,即第20行和第30列交叉处的方格所染的颜色是红色.答:第20行和第30列交叉处的方格所染的颜色是红色.点评:此题主要考查了通过操作实验探索规律的问题的应用,解答此题的关键是首先判断出第30列的第1个方格应涂蓝色.【题文】(1)某月有31天,有4个星期二和4个星期五,那么这个月的20日是星期几?(2)某月的星期二比星期一多,那么这个月的25日是星期几?【答案】星期四;星期五.【解析】试题分析:(1)因为是31天,31÷7=4(周)…3(天),有4个星期二和4个星期五,所以余下的三天是星期一、星期六,星期日,各为各5个.即星期六为这月的1号.22号为星期六,20日就是星期四.(2)由于这月有4个星期多1、2或3天,星期二的天数比星期一的天数多,则这月1日是星期二,依此推算这个月的25日是星期几.解:(1)31÷7=4(周)…3(天),要有4个星期二和4个星期五,所以余下的三天是星期一、星期六,星期日,各为各5个.即星期六为这月的1号,三周后的22号为星期六,则20号是星期四;答:那么这个月的20日是星期四.(2)要使这个月的星期二比星期一多,则此月的1号是星期二,(25﹣1)÷7=3(周)…3(天)2+3=5余数是3,即25号是星期五;答:那么这个月的25日是星期五.点评:解决这类问题先求出经过的天数,再求经过的天数里有几周还余几天,再根据余数推算.【题文】500名士兵排成一排,第一次从左到右1﹣5循环报数,第二次从右到左1﹣4循环报数.请问:既报1又报5的士兵有多少名?【答案】25名.【解析】试题分析:若将这500名士兵从左到右依次编号,则第一次报数时,编号能被5整除的士兵报1;第二次报数时,编号能被4整除的士兵报4,所以既报1又报4的士兵的编号既能被5整除又能被4整除,即能被20整除,在1至500这500个自然数中能被20整除的数共有25个,所以既报1又报5的士兵共有25名.解:1又报5的士兵都是4×5=20的倍数,500÷20=25(人);答:既报1又报5的士兵有25名.点评:解答此题时应通过分析得出:既报1又报5的士兵的编号既能被5整除,进而分析解答得出.【题文】有六十多人站成一行,从左到右由1开始按1、2、3、4依次循环报数,然后从右到左由1开始按1、2、3依次循环报数,最后发现刚好有12个人既报了1又报了2.请问:这一行最少有多少人?最多有多少人?【答案】最多69人;最少有62人.【解析】试题分析:因从左到右由1开始按1、2、3、4;1、2、3、4;…报数.然后从右到左由1开始按1、2、3;1、2、3;…报数,所以既报了1又报了2的人应是3和4的最小公倍数,即3×4=12.5组12人就有60人,错开一个位置,才能即报1有报2,所以最少62人;在5组的前4个后有4,错开一个位置,最多有69个人;如下图所示:。
小学数学思维训练《周期问题》PPT

月12日是星期几?
3月:31-17+1=15(天) 周期:三、四、五、六、日、一、二
4月:30天 5月:12天 共: 15+30+12=57(天)
57÷7=8(组)……1(天) 星期三
知识总结
一、周期:重复出现 周期长度:1个周期内的个数
二、总数÷每组数=组数……余数
三、求第几个数 看余数 余几则数几 无余看末尾
第45个数: 1
“1” 每组出现 2 次
10×2+2 =22(次)
挑战 3
有一个数列:5、0、3、2、3、7、2、3、7、2、3、7……, 在这个数列中,前 27 个数的和是多少?
27-3=24(个) 24÷3=8(组) 每组和:2+3+7=12 8×12 +(5+0+3)=104
挑战 4
2021 年 3 月 17 日是星期三,从这一天起,请问:2021 年 5
周期问题
思考
东东看到有一串符号以: 列(1)你知道第15个符号应该是什么? (2)第65个呢? (1)
15÷3=5(5个:
……的规律排
挑战 1
有一个数列 3、7、4、5、3、7、4、5、3、7、4、5…在这个数列中, 第 36 个数是多少?
36÷4=9(组) 余几则数几 无余看末尾 第36个数: 5
四、求出现几次 1、先看1组次数 1组次数×组数 2、再看余数、非周期
五、求和 1、先看1组和 1组和×组数 2、再加余数、非周期
挑战 2
有一个数列:2、8、2、1、1、6、2、1、1、6、2、1、1、 6……,在这个数列中,第 45 个数是多少?前 45 个数中,数 字“1”出现了多少次? 数字“2”出现了多少次?
45-2=43(个)
“2” 每组出现 1 次
三年级周期问题练习题

三年级周期问题练习题一、选择题1. 下列哪个选项不是周期问题?A. 一周有七天B. 一年四季C. 一天有24小时D. 一年有365天2. 一个周期性事件,如果每5天发生一次,那么从今天开始,第30天是第几次发生?A. 第5次B. 第6次C. 第7次3. 一个钟表的秒针,每60秒转一圈,那么转5圈需要多少秒?A. 300秒B. 500秒C. 600秒4. 一年有4个季节,如果从春天开始数,那么第9个季节是什么?A. 春天B. 夏天C. 秋天二、填空题5. 如果一周有7天,今天是星期三,那么5天后是星期______。
6. 一个班级有40名学生,每4名学生一组,可以分成______组。
7. 一个周期性事件每7天发生一次,如果今天是第1次发生,那么第28天是第______次发生。
8. 一年四季,如果从春天开始数,那么第12个月是______。
三、判断题9. 如果一个周期性事件每10天发生一次,那么第100天是第11次发生。
()10. 一年有12个月,每个月都有30天。
()11. 一个钟表的时针,每12小时转一圈,那么转3圈需要36小时。
()12. 一周有7天,如果今天是星期日,那么明天是星期一。
()四、计算题13. 一个班级有45名学生,每5名学生一组,可以分成多少组?剩余几名学生?14. 一个钟表的分针,每60分钟转一圈,那么转4圈需要多少分钟?15. 如果一个周期性事件每8天发生一次,那么从今天开始,第48天是第几次发生?16. 一年有365天,如果今天是1月1日,那么第100天是哪一天?五、应用题17. 小明的爸爸每周都会带他去一次公园,如果今天是1月1日,小明的爸爸带他去公园,那么2月1日小明的爸爸还会带他去公园吗?18. 一个班级有48名学生,每6名学生一组,可以分成多少组?剩余几名学生?19. 一个钟表的秒针每60秒转一圈,如果现在是下午3点整,那么秒针转了3圈后是几点几分?20. 一个班级有36名学生,每9名学生一组,可以分成多少组?剩余几名学生?六、拓展题21. 如果一个周期性事件每3天发生一次,那么从今天开始,第27天是第几次发生?22. 一年有12个月,如果每个月的第一天都是星期日,那么这个月的最后一天也是星期日吗?23. 一个班级有52名学生,每7名学生一组,可以分成多少组?剩余几名学生?24. 如果一个钟表的时针每12小时转一圈,现在是上午9点,那么时针转了2圈后是几点?通过这些练习题,三年级的学生可以加深对周期问题的理解,并提高解决相关问题的能力。
(完整版)三年级奥数周期问题练习题

(完整版)三年级奥数周期问题练习题【例 1】⼩兔和⼩松⿏做游戏,他们把⿊、⽩两⾊⼩球按下⾯的规律排列:●●○●●○●●○…你知道它们所排列的这些⼩球中,第90个是什么球?第100个⼜是什么球呢?【巩固】美美有⿊珠、⽩珠共102个,她想把它们做成⼀个链⼦挂在⾃⼰的床头上,她是按下⾯的顺序排列的:○●○○○●○○○●○○○……那么你知道这串珠⼦中,最后⼀个珠⼦应是什么颜⾊吗?美美怕这种颜⾊的珠⼦数量不够,你能帮她算出这种颜⾊在这串珠⼦中共有多少个吗?【例 2】⼩倩有⼀串彩⾊珠⼦,按红、黄、蓝、绿、⽩五种颜⾊排列.⑴第73颗是什么颜⾊的?⑵第10颗黄珠⼦是从头起第⼏颗?⑶第8颗红珠⼦与第11颗红珠⼦之间(不包括这两颗红珠⼦)共有⼏颗珠⼦?【巩固】奥运会就要到了,京京特意做了⼀些“北京欢迎你”的条幅,这些条幅连起来就成了:“北京欢迎你北京欢迎你北京欢迎你……”依次排列,第28个字是什么字?【巩固】节⽇的校园内挂起了⼀盏盏⼩电灯,⼩明看出每两个⽩灯之间有红、黄、绿各⼀盏彩灯.也就是说,从第⼀盏⽩灯起,每⼀盏⽩灯后⾯都紧接着有3盏彩灯.那么第73盏灯是什么颜⾊的灯?【例 3】节⽇的夜景真漂亮,街上的彩灯按照5盏红灯、再接4盏蓝灯、再接1盏黄灯,然后⼜是5盏红灯、4盏蓝灯、1盏黄灯、……这样排下去.问:⑴第150盏灯是什么颜⾊?⑵前200盏彩灯中有多少盏蓝灯?【巩固】在⼀根绳⼦上依次穿2个红珠、2个⽩珠、5个⿊珠,并按此⽅式反复,如果从头开始数,直到第50颗,那么其中⽩珠有多少颗?【巩固】⼩莉把平时积存下来的200枚硬币按3个1分,2个2分,1个5分的顺序排列起来.⑴最后1枚是⼏分硬币⑵这200枚硬币⼀共价值多少钱?【巩固】桌⼦上摆了很多硬币,按⼀个⼀⾓,两个五⾓,三个⼀元的次序排列,⼀共19枚硬币.问:最后⼀个是多少钱的?第⼗四个是多少钱的?【巩固】有249朵花,按5朵红花,9朵黄花,13朵绿花的顺序轮流排列,最后⼀朵是什么颜⾊的花?这249朵花中,什么花最多,什么花最少?最少的花⽐最多的花少⼏朵?【例 4】如图所⽰,每列上、下两个字(字母)组成⼀组,例如,第⼀组是“我,A”,第⼆组是“们,B⑴写出第62组是什么?⑵如果“爱,C”代表1991年,那么“科,D”代表1992年……问2008年对应怎样的组?【巩固】在图所⽰的表中,将每列上、下两个字组成⼀组,例如第⼀组为(新奥),第⼆组为(北林),【例 5】如右图,是⼀⽚刚刚收割过的稻⽥,每个⼩正⽅形的边长是1⽶,A 、B 、C 三点周围的阴影部分是圆形的⽔洼。
三年级数学下册思维扩展

三年级下册(暑假修正版)校名:长清区实验小学班级:__________姓名:__________目录(1)位置与方向 (1)(2)除法 (3)(3)乘法 (9)(4)年月日 (11)(5)周长 (16)(6)面积 (18)(7)数学广角 (21)解题策略:利用口诀、利用方向盘、东南西北按照顺时针排序、画图法、解题方法:画图解题引领:一只蚂蚁从A点出发,先向西爬行了100厘米,再向北爬行了45厘米,然后向东爬行了60厘米,最后向南爬行了45厘米到达B点。
A、B两地相距多少厘米?先确定一个A点,再根据题目的叙述通过画图的方式,将这只蚂蚁爬行的方向表示出来,即可解决此类题目。
如图:(上北下南,左西右东)100-60=40(厘米)答:A、B两地相距40厘米。
小练兵:(画图解决以下问题、上北下南左西右东)⒈一只蚂蚁从A点先向北爬行了30厘米,再向南爬行了36厘米到达B点。
A、B两地相距多少厘米?2. 小华从公园出发,先向北走了30米,再向东走了36米,然后向北走了30米,最后向西走了36米到达超市。
公园和超市两地相距多少米。
3. 小明向东走4步,然后向西走3步,再向东走2步,再向西走1步。
现在小明向什么方向走几步就能回原地?4. 张华和王林从同一个地方出发,张华向北走150米,王林向南走180米,两人相距多少米?5. 张丽先向东走5步,左转向前走4步,再左转向前走5步,现在张丽面向什么方向?如果想尽快回到原地,那么可以怎样走?6、一只蚂蚁从A点出发,先向西爬行了3厘米,再向北爬行6厘米,然后向东爬9厘米,最后向南爬12厘米,如果这只蚂蚁要回到A点,但是只能直角拐弯,那么它至少要爬多少厘米7. 小蓝去上学,她的前面是东,向左转过了90度的弯道后,她的左、右面分别变为什么方向?8. 小娟向东走5步,然后向西走4步,再向东走3步,再向西走2步,再向东走1步。
现在小娟在出发点的什么方向几步远的地方?除法解题策略:找规律、进一法、去尾法一、周期问题周期问题的含义:在日常生活中,有许多现象都是按照一定的规律、依次不断重复出现的,我们把这种现象叫作周期现象,而重复出现一次的个数叫作周期。
三年级周期问题练习题

三年级周期问题练习题周期问题是数学中的一个重要知识点,也是三年级数学学习的一部分。
通过解决周期问题,学生可以提高他们的逻辑思维能力和数学运算能力。
本文将为三年级的学生提供一些周期问题的练习题,帮助他们巩固和应用所学知识。
一、简单的周期问题1. 有一辆车每隔5分钟经过一次红绿灯,现在已经经过了4次红绿灯,请问过了多少分钟?2. 小明每隔3天去一次游泳馆,现在已经去了8次,请问他一共去了多少天?3. 水龙头每隔2秒可以滴一滴水,如果水龙头已经滴了100滴水,请问一共经过了多少秒?二、复杂的周期问题1. 张三每5天倒一次垃圾桶,李四每7天倒一次垃圾桶,如果他们同时从今天开始倒垃圾桶,请问多少天后他们会同时倒垃圾桶?2. 小明每隔3个小时喝一次水,小红每隔4个小时喝一次水,如果他们同时从现在开始喝水,请问多少小时后他们会同时喝水?三、运用周期问题解决实际问题1. 公交车每隔20分钟经过一次车站,小明每隔5分钟就能到达车站。
如果小明刚好错过了公交车,请问他需要等多久才能赶上下一趟车?2. 小明每隔2天吃一次饭,小红每隔3天吃一次饭。
如果小明和小红都在今天开始吃饭,请问多少天后他们会同时吃饭?四、拓展问题1. 目前为止,小明每年都过生日,如果小明今年5岁,请问他过了多少次生日?2. 一只青蛙每隔6分钟跳一次,它每次跳跃的距离是3米。
如果过了15分钟,这只青蛙一共跳了多远?通过解决上述的周期问题,希望能够帮助三年级的学生巩固和应用所学的知识。
在解决这些问题的过程中,同学们可以灵活运用数学运算,如加法、减法和乘法。
同时,这些问题的解决过程也需要培养学生的逻辑思维和分析能力。
周期问题不仅仅存在于数学中,实际生活中也存在着各种各样的周期。
通过解决这些练习题,同学们可以将抽象的概念与实际生活相结合,更好地理解和应用所学知识。
希望同学们通过这些练习题的训练,能够对周期问题有更深入的理解,并能够在实际生活中灵活运用。
只有通过不断的练习和实践,才能够真正掌握和应用所学的知识。
【三年级】巧算周期问题

【三年级】巧算周期问题周期问题是数学中一个常见的话题,对孩子们的数学思维发展和数学能力的提升都有很大的帮助。
学习周期问题,能够增强孩子们的数学逻辑思考能力,让孩子们更深刻地理解数学知识。
下面是一个有趣的巧算周期问题,我们一起来看看吧。
小明发现,每隔15天,同一天的星期几会重复出现。
比如说,6月1日是星期一,那么在6月15日,7月1日,7月15日,8月1日……都是星期一。
同样,在6月2日是星期二,那么在6月16日,7月2日,7月16日,8月2日……都是星期二。
小明很聪明,他想知道,从今天开始算起,第一个出现两次的是哪个星期几?读完问题,我们可以先观察它提供的信息:每隔15天,同一天的星期几会重复出现。
我们可以通过这个信息推理出,每隔7天后,星期几会变化一次。
也就是说,如果我们已经知道今天是星期几,那么向后推7天,星期几就会变化一次。
那么,如果我们跳跃一天一天地推算,是否可以找到第一个出现两次的星期几呢?尝试一下!假设今天是星期一,那么再过7天就是星期一。
再过7天是星期一,再过7天是星期一,再过7天是星期一,再过7天是星期一……15天后又回到了今天的星期一。
过了100天后,星期一出现了14次,但是还没有出现两次。
过了200天后,星期一出现了28次。
我们已经知道,15天后会回到今天的星期一,那么在第30天的时候,应该也是星期一。
理解了这个规律之后,我们就可以通过巧算的方式找到第一个出现两次的星期几了。
思路我们先随便选一个某天开始算,每隔一天去判断它是星期几,然后记录下来。
当星期几出现了两次的时候,就找到了答案。
我们可以先定义两个变量:count:表示已经找到几个星期几了。
last:表示上一次出现的那个星期几的编号。
那么,下一步该怎么做呢?我们可以先用一个循环不停地处理每一天的数据,每循环一次,就将日期往后推一天。
在循环中,我们需要完成两个任务:判断当前这一天是星期几。
当我们发现当前这一天是和上一次出现的那个星期几一样的时候,就可以记录下来。
【小学三年级数学】周期问题练习题(详解版)

(组)
(颗),所以红珠与白珠的和比黑珠多 颗.
2 广场上的彩旗按照 红、 蓝、 橙的顺序排列,请问第 面彩旗是
色.
答案 橙 解析
(面),
(组)
(面),第 面是橙色的.
3 奥运会时,京京特意做了一些“北京欢迎你”的条幅,条幅连起来成了:“北京欢迎你北京欢迎你北
京欢迎你……”依次排列,前 个字中“北”出现
次.
答案
解析
(组)…… (个),
故答案为: .
(次).
4 周期数列:计算下列数列的第 项分别是多少?
、、、、、、、、
.
、、、、、、、、、、、、、
.
、、、、、、、、、、、、、
.
答案 1. 2. 3.
解析 根据数列的周期性找规律 、、、、、、、、 . 、、、、、、、、、、、、、 . 、、、、、、、、、、、、、 .
9 小朋友们玩游戏,如图,有 把椅子摆成一个圆圈,依次编上从 到 的号码.现在小林从第 号
椅子顺时针走 个,再逆时针走 个,又顺时针走 个,再逆时针走 个,又顺时针走 个,这
时他到了第
号椅子.
答案 解析
小林从第 号椅子顺时针走 个,再逆时针走 个,又顺时针走 个,再逆时针走 个,又顺
时针走 个,实际小林顺时针走了
周期问题练习题
1 在一根绳子上从头开始依次穿 颗红珠、 颗白珠、 颗黑珠、 颗红珠、 颗白珠、 颗黑珠、 ,并按此方式重复,如果一共穿了 颗珠子,那么这 颗珠子中红珠与白珠的和比黑珠多 颗.
答案
解析 根据题意,依次穿 颗红珠、 颗白珠、 颗黑珠、 颗红珠、 颗白珠、 颗黑珠;可知 个珠
子为一个周期,每一周期中红珠与白珠的和与黑珠相同;
7
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
27-5=22(天) 22÷7=3(周)……1(天)
一 二 三 四 五 六 日 一 二 三 四 五 六 日 ……
答:2006年2月27日是星期一。
340÷5=68
E
(组)
340÷4=85(组) 华
答:第340组是“E, 华”。
周期是5
周期是 4
周期是7
26÷7=3(组)……5
3×(7+4+2+5+6+1+0)+7+4+2+5+6 =3×25+24 =75+24 =99
9、简单的周期问题(二)
在日常生活中,有许多现象 都是按照一定的规律、依次不断 重复出现的,我们把这种现象叫 做周期现象,而重复出现的一节 的个数叫做周期 。
周期问题解题策略 :
1、确定周期,找到总量 2、总量÷周期=组数……余数
3、看余数:余几就是周期里的第几个 没有余数:周期里的最后一个
周期是6 53÷6=8(组)……5(个) 答:第53个图形是黑色的三角形。
1、看组数
2、看余数
答:前26个数字之和是99.
个位分别为:2、4、8、6、2、4、8、6、2、4、8、6、…… 200÷4=50(组)
答:积的个位是6.
红 黄 黄 红 黄 黄 红 黄 黄 红 黄 黄 红…… 73÷3=24(组)……1(朵) 24×2=48(朵)
答:有48朵黄花。
解决周期问题求和的关键是发现规律, 找到周期,求出组数和余数。常用的方 法:
