光的干涉现象
光的干涉现象

光的干涉现象光的干涉现象是光学中一种重要的现象,它揭示了光波的波动性质以及光的性质与行为。
干涉现象包括两种类型:两条光波的叠加干涉和单条光波的多普勒干涉。
这篇文章将详细介绍光的干涉现象和其应用。
1. 叠加干涉1.1 双缝干涉双缝干涉是光的干涉现象中最经典的例子之一。
在双缝干涉实验中,光通过两个并排的狭缝,形成多个光束。
这些光束相互干涉,产生明暗条纹,常称为干涉条纹。
干涉条纹的出现可以解释为光的波动性质导致的波峰和波谷的叠加。
1.2 条纹间距干涉条纹的间距可以由下式计算得到:d·sinθ = mλ其中,d表示双缝之间的距离,θ为入射光的角度,m为干涉条纹的级次,λ为入射光波长。
1.3 干涉的明暗条件当条纹间距d·sinθ等于整数倍的光波长时,干涉条纹呈现明亮的状态,这是因为波峰和波峰叠加导致光强增强。
当条纹间距d·sinθ等于半整数倍的光波长时,干涉条纹呈现暗淡状态,这是因为波峰和波谷叠加导致光强减弱。
2. 多普勒干涉2.1 多普勒效应多普勒效应是指当光源或观察者相对于彼此运动时,引起光频率的改变现象。
当光源相对于观察者靠近时,光频率增加,光波变蓝偏;当光源相对于观察者远离时,光频率减少,光波变红偏。
2.2 多普勒干涉的应用多普勒干涉可以应用于光学测速仪器中。
通过测量观察者接收到的多普勒效应下的光频率,可以计算出物体相对于观察者的速度和方向。
3. 干涉的应用3.1 干涉仪干涉仪是一种利用光的干涉现象进行测量和研究的仪器。
常见的干涉仪包括迈克尔逊干涉仪和扫描干涉仪。
干涉仪可以用于测量长度、折射率、表面粗糙度等物理参数的精密测量。
3.2 干涉光谱仪干涉光谱仪利用光的干涉现象对光谱进行解析和测量。
典型的干涉光谱仪是菲涅尔干涉光谱仪,它可以测量出样品的折射率、薄膜的厚度、光学材料的色散性质等。
3.3 全息术全息术是一种记录和重现光的干涉图样的技术。
通过记录光的相位和幅度信息,全息术可以制作出具有立体感的光学图像。
光学中的干涉现象

光学中的干涉现象光的干涉现象是光学中一个重要而又神奇的现象,它揭示了光波的波动性质以及光的波动性与粒子性之间的关系。
在本文中,我们将深入探讨干涉现象的基本原理、应用以及一些相关实验。
一、干涉现象的基本原理干涉现象是指当两个或多个光波相遇时,由于波的叠加而产生明暗相间的干涉条纹。
这是由于光波是一种波动性质所导致的。
光波的干涉可以分为两种类型:光的同相干干涉和光的非相干干涉。
同相干干涉是指两个光源发出的光波相干,即波长相同、频率相同,相位差恒定,这种干涉现象是由单一光源或者光源经过分波器产生的;非相干干涉是指两个或多个不同相位、不同频率的光波相遇产生干涉。
干涉现象的产生需要满足以下两个条件:一是干涉波源的强度满足叠加定律,二是干涉波源的相位差满足特定的条件。
二、光的干涉现象的应用干涉现象在光学中有多种应用,下面我们就来介绍其中一些典型的应用。
1. 双缝干涉双缝干涉是最基本的光的干涉实验之一。
通过在屏幕上放置两个细缝,以平行光垂直照射这两个缝隙,可以观察到明暗相间的干涉条纹。
双缝干涉实验证明了光的波动性,同时也证实了光波的干涉原理。
该实验在光学研究、衍射光栅的制造以及光学仪器的设计中有重要应用。
2. 薄膜干涉薄膜干涉是基于光在介质界面上发生反射和折射的现象。
当光波入射到介质表面上时,一部分光会反射回来,另一部分光会继续传播并发生折射。
当光波经过介质表面后再次反射回来时,两路光波之间的相位差会导致干涉效应。
这一现象被广泛应用于光学薄膜涂层、光学器件设计以及反光镜、透镜等光学元件的制造。
3. 多光束干涉多光束干涉是指有多个光波源同时向同一点辐射光线,产生明暗相间的干涉纹。
这一干涉现象可以应用于激光干涉仪、光学干涉仪、光纤传感器等领域。
在这些应用中,多光束干涉既可以用于测量,也可以用于干扰。
三、光的干涉实验除了上述应用之外,还有一些其他的光的干涉实验也为我们揭示了光波的性质而做出了重要的贡献。
1. 麦克斯韦环实验麦克斯韦环实验是基于在凸透镜和平凸镜之间放置一层液体作为薄层介质,通过观察干涉圆环的形成来研究光波的传播与干涉特性。
光的干涉现象

光的干涉现象光的干涉现象是光学中重要而又有趣的现象之一。
它揭示了光的波动性质,并深化了人们对光的理解。
本文将通过对光的干涉现象的介绍和实例分析,探讨其原理、应用以及对科学研究和技术发展的影响。
一、光的干涉现象简介光的干涉现象指的是两束或多束光波相互叠加产生的干涉条纹现象。
当两束光波的相位差满足某一特定条件时,它们在空间中会相互干涉。
干涉的结果是光的强弱发生变化,形成了明暗相间的条纹。
在光的干涉现象中,存在两种类型的干涉:同态干涉和非同态干涉。
同态干涉是指两束来自同一光源的光波相互叠加产生的干涉现象,如杨氏双缝干涉和牛顿环等。
非同态干涉是指两束或多束不同光源的光波相互叠加产生的干涉现象,如薄膜干涉和透明薄板干涉等。
二、光的干涉现象原理光的干涉现象可以用波的叠加原理解释。
当两束光波相遇并叠加时,它们的电场强度相互叠加,形成一个新的电场强度分布。
而光的亮暗程度与电场强度的平方成正比,因此,新的电场强度分布也决定了光的亮暗程度。
在同态干涉中,双缝干涉是最典型的实例。
当一束光通过一个有两个细缝的屏幕时,射到屏幕后,光波会分成两束继续传播。
这两束光波在屏幕后再次相遇并叠加,产生干涉现象。
干涉的结果是在屏幕上形成一系列明暗相间的条纹,称为干涉条纹。
三、光的干涉现象应用光的干涉现象在科学研究和技术应用中具有重要意义。
以下是一些常见的应用。
1. 干涉测量:利用光的干涉现象,可以进行高精度的测量。
例如,通过测量干涉条纹的间距和光波的波长,可以计算出被测物体的长度或形状。
2. 光学薄膜:通过在透明介质表面上涂敷一层薄膜,可以利用薄膜的干涉现象来改变光的反射和透射性质。
这在光学元件的设计和制造中有广泛的应用。
3. 涡旋光:涡旋光是一种具有自旋角动量的光。
通过制造特殊形状的相位板,可以实现光的幅度和相位的分离,产生具有涡旋光性质的光束。
涡旋光在光学通信和光学显微镜等领域有重要应用。
4. 光学干涉仪器:干涉仪器是利用光的干涉现象设计和制造的仪器。
光的干涉与衍射的现象与公式

光的干涉与衍射的现象与公式在物理学中,光的干涉与衍射是两种常见的光现象,它们具有不同的特点和应用。
本文将探讨光的干涉与衍射的基本概念、现象以及相关的公式。
一、光的干涉现象与公式光的干涉是指两束或多束光波相遇时产生的相互作用。
干涉可以分为干涉条纹的产生和干涉的条件两个方面。
1. 干涉条纹的产生当两条相干光波相遇时,它们会相互干涉形成一系列的亮暗条纹,称为干涉条纹。
这是因为两束光波以相同的频率、相同的相位或相干长度相遇,其光强的叠加会出现干涉现象。
2. 干涉的条件光的干涉需要满足以下几个条件:a. 光源必须是相干光源,即光波的频率和相位相同。
b. 光波的干涉路径差应小于波长的一半。
关于干涉现象的描述和分析,我们可以使用以下公式:1. 干涉条纹的宽度公式干涉条纹的宽度可以通过以下公式计算:Δx = λL/d其中,Δx表示干涉条纹的宽度,λ为入射光波的波长,L为光源到屏幕的距离,d为狭缝或介质的厚度。
2. 杨氏双缝干涉公式杨氏双缝干涉公式描述了双缝干涉条纹的位置和间距:y = mλD/d其中,y表示干涉条纹的位置,m为干涉级数,λ为光的波长,D为两缝到屏幕的距离,d为两缝的间距。
3. 薄膜干涉公式薄膜干涉是指光线穿过薄膜发生的干涉现象,可以用以下公式描述:2nt = (m + 1/2)λ其中,n为薄膜的折射率,t为薄膜的厚度,m为暗纹的干涉级数,λ为入射光的波长。
二、光的衍射现象与公式光的衍射是当光波通过一个小孔或物体的边缘时,会发生弯曲和弥散的现象。
衍射的大小与光的波长和衍射物体的尺寸相关。
1. 衍射公式光的衍射可以使用弗能尔衍射公式来进行描述:a sinθ = mλ其中,a为衍射孔的尺寸,θ为衍射角,m为衍射级数,λ为入射光的波长。
2. 单缝衍射公式单缝衍射是一种常见的衍射现象,可以通过以下公式来计算条纹的位置和间距:y = mλL/a其中,y表示条纹的位置,m为衍射级数,λ为入射光的波长,L为光源到屏幕的距离,a为衍射孔的宽度。
什么是光的干涉

什么是光的干涉光的干涉是一种光学现象,指的是两个或多个光波相互作用而产生的干涉效应。
当两束光波相遇时,它们会相互干涉并形成干涉图样,这是由于光的波动性质所致。
光的干涉现象在自然界和科学研究中有着广泛的应用。
1. 光的波动性质光既具有粒子性也具有波动性,光的波动性是光的干涉现象的基础。
光波的传播速度是有限的,它会沿着直线传播,并在传播过程中产生交迭、叠加和干涉。
2. 干涉的条件光的干涉需要满足两个基本条件:一是光源必须是相干光源,即光源发出的光波具有相同的频率、相位和振幅;二是光波必须在空间中交迭或叠加。
3. 干涉的类型光的干涉可以分为两类:一是光的干涉分为建设性干涉和破坏性干涉,二是光的干涉又可以分为薄膜干涉、杨氏双缝干涉、杨氏双缝干涉、菲涅尔双棱镜干涉等多种类型。
4. 建设性干涉和破坏性干涉当两束光波相遇且波峰与波峰相重叠(或波谷与波谷相重叠)时,它们会产生建设性干涉,此时干涉图样中会出现明亮的干涉条纹,光强增强;相反,当波峰与波谷相重叠时,它们会产生破坏性干涉,此时干涉图样中会出现暗淡的干涉条纹,光强减弱或消失。
5. 薄膜干涉薄膜干涉是指光在由两个介质分界面分离的薄膜上反射和透射产生的干涉现象。
当光波从一个介质射入到另一个介质时,会发生反射和透射。
光的反射和透射在介质的界面上发生相位差,不同相位差会导致干涉效应。
薄膜干涉常用于衬底上的光学薄膜和光学元件的设计。
6. 杨氏双缝干涉杨氏双缝干涉是一种经典的干涉实验,由英国科学家杨恩斯提出。
它通过将光通过两个狭缝,让光波以波前偏斜的方式形成干涉条纹。
杨氏双缝干涉实验证明了光的波动性和光的干涉现象,为光的本质提供了重要的证据。
7. 菲涅尔双棱镜干涉菲涅尔双棱镜干涉是将平行光通过两个类似楔形棱镜所形成的干涉图样。
这种干涉实验是由法国科学家菲涅尔提出的,可以用来测量光的波长和探测光的相位差。
菲涅尔双棱镜干涉被广泛应用于光学检测、波长测量和多种光学仪器的设计中。
光的干涉现象

光的干涉现象光的干涉现象是一种光波的现象,它涉及到光的波动性和波动性的特性。
光的干涉是由于光波的相位差引起的,当两个或多个光波相遇时,它们会相互干涉并产生干涉条纹。
这个现象是一个重要的实验现象,对于理解光的性质和波动理论有着重要的意义。
1. 波动理论的基础在讨论光的干涉现象之前,我们首先需要了解一些关于波动理论的基础。
光波是一种电磁波,它的传播速度是光速。
光的波长决定了它的颜色,而频率则决定了光的亮度。
波动理论可以解释光的反射、折射和衍射等现象,而光的干涉则是波动理论的一个重要的应用。
2. 干涉的分类光的干涉可以分为两类:一类是同源干涉,也称为相干干涉;另一类是非同源干涉,也称为相干干涉。
同源干涉是指来自同一光源的两束或多束光波相互干涉;非同源干涉是指来自不同光源的光波相互干涉。
在实际应用中,我们经常遇到的是同源干涉。
3. 干涉条件光的干涉需要满足一定的条件。
首先,干涉波源必须是相干的,也就是说它们的相位和频率必须是相同的。
其次,干涉波源之间必须存在一定的相位差。
当光波相遇时,如果它们的相位差为整数倍波长,它们就会相长干涉,形成亮条纹;如果相位差为半整数倍波长,它们就会相消干涉,形成暗条纹。
4. 干涉现象的实验为了观察和研究光的干涉现象,人们进行了许多实验。
其中最经典的实验是杨氏双缝干涉实验。
在这个实验中,一个狭缝板上有两个非常接近的小缝,通过它们射出的光线会在屏幕上形成干涉条纹。
这个实验可以直观地展示光的干涉现象,并且被广泛应用于教学和科学研究中。
5. 干涉在实际应用中的意义光的干涉现象在科学研究和工程应用中有着广泛的应用价值。
在光学领域,干涉现象被用于测量光的波长和频率,以及研究光的性质和波动理论。
在工程应用中,干涉现象被用于制造光栅、干涉仪等光学仪器,以及进行光学显微镜和激光干涉测量等精密测量。
6. 光的干涉的应用举例光的干涉现象在许多实际应用中发挥着重要的作用。
例如,在光学显微镜中,干涉现象可以提高显微镜的分辨率和测量精度;在激光干涉测量中,干涉现象可以实现纳米级尺度的测量精度;在光学通信中,干涉现象可以实现光纤的调制和解调等功能。
光的干涉介绍光的干涉现象和干涉条纹

光的干涉介绍光的干涉现象和干涉条纹光的干涉是指当两束或多束光波相遇时,由于光的波动性质导致的干涉现象。
在光的干涉过程中会产生特殊的条纹形状,称为干涉条纹。
一、光的干涉现象光的干涉现象发生在两束或多束光波相遇的地方。
在这种相遇中,光波的振幅叠加会导致干涉条纹的出现。
干涉条纹是一系列明暗相间的条纹,形成于光波的相位差引起的干涉效应。
光的干涉主要有两种类型:干涉的构造系、干涉的逆构造系。
1. 干涉的构造系干涉的构造系是指由具有一定宽度及形状的光源发出的光线通过一组反射、折射、透射等干涉器件后形成的干涉现象。
常见的构造系干涉有杨氏双缝干涉、杨氏双晶片干涉等。
杨氏双缝干涉是光线通过两个狭缝时发生的干涉现象。
当两束光波穿过两个缝隙后再次相遇时,会形成一系列明暗相间的干涉条纹。
这是因为两束光波会相互干涉,产生相位差,使得某些区域光波增强,某些区域光波减弱。
2. 干涉的逆构造系干涉的逆构造系是指光通过一个或多个薄膜、介质或颗粒等非均匀物体后形成的干涉现象。
逆构造系干涉不需要特殊设备,可以在日常生活中观察到。
常见的逆构造系干涉有牛顿环、薄膜干涉等。
牛顿环是一种通过光在凸透镜和平板玻璃之间的干涉现象。
当光波通过凸透镜后投射到平板玻璃上时,由于光线进入和离开平板玻璃时会发生折射,导致相位差的变化。
这种相位差的变化会在平板玻璃和凸透镜之间形成一系列明暗相间的环形条纹。
二、干涉条纹的特点和应用干涉条纹的特点有以下几点:1. 明暗相间: 干涉条纹由一系列明暗相间的区域组成,暗条纹对应波峰和波谷的相消干涉,明条纹对应波峰和波峰或波谷和波谷的相长干涉。
2. 呈现交替: 干涉条纹的交替现象是由于相位差的变化引起的。
相位差的增加或减少会导致暗条纹和明条纹的位置变化。
3. 间隔均匀: 干涉条纹的间隔大小与光的波长、光的入射角以及干涉器件的性质有关。
根据干涉条纹的特性,可以通过测量干涉条纹的间隔来推断光的波长。
干涉条纹的应用广泛,特别是在光学领域。
光的干涉现象

光的干涉现象光的干涉现象是光学中的一种重要现象,它是指两束或多束光波相互叠加时所产生的干涉效应。
这种现象能够揭示光的波动性质,为我们深入研究光学提供了重要的实验依据。
本文将从光的干涉原理、干涉模式以及干涉在实际应用中的重要性等方面进行探讨。
一、光的干涉原理光的干涉现象是基于光的波动性质而产生的。
根据互相干涉的光波传播规律,我们可以将干涉现象分为两类:构造干涉和疏进建立。
1. 构造干涉构造干涉是指两束相干光波叠加后形成明暗交替的干涉条纹的现象。
这种干涉是由于光波在空间中的干涉途程有差异而产生的。
当两个光波的光程差为整数倍波长时,它们相互加强,形成明亮的条纹;而当光程差为半整数倍波长时,它们相互抵消,形成暗纹。
著名的双缝干涉实验就是一个典型的构造干涉现象。
2. 疏进建立疏进建立是指当两束光波相交时,它们在交叉区域内相互干涉而产生的干涉现象。
在这种干涉中,光的传播路径并不造成干涉途程差异,而主要取决于光波在交叉区域内的相位差。
当光波的相位差为奇数倍π时,交叉区域会出现暗纹;而相位差为偶数倍π时,会出现明纹。
著名的杨氏双缝干涉实验正是一种疏迷新建的干涉现象。
二、干涉模式光的干涉现象可分为几种常见的模式,每种模式都有自己独特的特点和应用。
1. Young's 双缝干涉由托马斯·杨提出的Young's 双缝干涉是一种经典的构造干涉模式。
它利用了两个相隔较远的狭缝,使光波通过后产生干涉,从而形成明暗条纹。
这种干涉模式常用于电子显微镜和各类干涉仪器。
2. Michelson 干涉仪Michelson 干涉仪是一种基于疏进建立干涉的仪器,常用于精确测量光的波长、折射率、长度等参数。
它利用半透镜和半反射镜构成干涉仪的臂,通过调节一臂的光程,观察干涉条纹的变化,从而获得精确的测量结果。
3. 薄膜干涉薄膜干涉是一种在厚度为波长级别的薄膜上发生的干涉现象。
这种干涉模式广泛应用于光学涂层、薄膜制备和表面形貌测量等领域。
光的干涉现象及其应用解析

光的干涉现象及其应用解析光的干涉现象是指当光通过不同的光程到达某一点时,由于相位的差异而产生的干涉效应。
干涉现象是光波性质的重要体现,不仅能揭示光的波动性质,还能应用于科学研究、技术革新以及各种测量中。
本文将对光的干涉现象及其应用进行解析。
一、光的干涉现象的基本原理光的干涉现象的基本原理可以概括为两束相干光的叠加。
当两束相干光以一定的角度汇聚或相交时,会在交叉区域产生明暗相间的干涉条纹。
这是由于光的相位差引起光强的叠加干涉所形成的。
二、光的干涉现象的分类及特点1. 单色光干涉:指由单一波长的光线所引起的干涉现象。
其特点是形成的干涉条纹清晰明确,颜色纯净。
2. 白光干涉:指由多种波长的光线所引起的干涉现象。
其特点是形成的干涉条纹带有彩色,颜色会随观察角度的变化而改变。
3. 平行光干涉:指两束光线平行地入射在平面上的干涉现象。
常见的平行光干涉装置有杨氏双缝干涉仪和劳埃德镜。
4. 斜光干涉:指两束光线斜着入射在平面上的干涉现象。
常见的斜光干涉装置有米氏干涉仪等。
三、光的干涉现象的应用1. 干涉仪:光的干涉现象在干涉仪中得到了广泛应用。
例如,杨氏双缝干涉仪可以通过干涉条纹的形成来测量光的波长,进而实现对光的性质的研究;劳埃德镜则可以用于测量物体的形状、厚度等。
2. 薄膜干涉:基于光的干涉现象,利用薄膜对光的反射和透射进行调控,可以实现光的增透、减透等功能。
这在光学镀膜、光学仪器制造等领域有着广泛的应用。
3. 光谱分析:通过光的干涉现象,可以将光分解成不同的波长,从而实现对光谱的分析。
利用光的干涉现象结合像差补偿技术,还可以实现高分辨率、高灵敏度的光谱测量。
4. 空间干涉:光的干涉可以应用于干涉测量领域,如干涉测量技术、干涉计量技术等,用于精密测量目标的位移、形状等参数。
四、光的干涉现象的研究进展随着科学技术的不断发展,对光的干涉现象的研究也在不断深入。
目前,已经提出了许多新的干涉技术,如数字全息术、斑图测量技术等。
光的干涉现象

光的干涉现象光是一种电磁波,当两束或多束光波相遇时,会发生干涉现象。
干涉现象是一种光的波动性质的表现,它揭示了光的波粒二象性的重要特征,同时在实践中也具有广泛的应用。
本文将就光的干涉现象展开探讨。
1. 干涉现象的基本原理干涉现象的产生是由于光波是波动性质的体现。
当两束光波相遇时,它们的电磁波幅度会叠加。
如果波峰与波峰相遇,波谷与波谷相遇,则会形成加强的干涉条纹,称为构造性干涉;相反,如果波峰与波谷相遇,则会形成减弱或者彼此抵消的干涉条纹,称为破坏性干涉。
这种干涉现象的形成和叠加原理密切相关。
2. 杨氏双缝干涉实验杨氏双缝干涉实验是阐明光的干涉现象的重要实验之一。
实验设备由一个狭缝和两个狭缝组成。
当通过这两个缝中间垂直照射光源时,会在屏幕上形成一系列明暗相间的干涉条纹,这是由于两束光线的干涉造成的。
这个实验充分证明了光的波动性质和叠加原理,并且可以通过观察干涉条纹的位置和间距来测量光的波长。
3. 光的干涉现象的应用光的干涉现象不仅仅是一种物理现象,它在实际应用中也具有广泛的价值。
a. 干涉测量技术:光的干涉现象可以用于测量非常小的长度尺度,比如测量薄膜厚度、测量微小物体的位移等。
利用干涉技术,可以提高测量精度,用于制造业、科学研究等领域。
b. 光的多波束干涉:除了双缝干涉实验,光的干涉还可以通过多个光源产生干涉现象。
这种多波束干涉被广泛应用于光学仪器的设计和构造,比如光栅、干涉仪、调制器等。
c. 光的波导干涉:光的干涉现象在光波导器件中得到广泛应用。
通过构造光波导的材料和结构,可以实现光的传输、控制和调制,并且能够利用干涉效应实现光的分光和合束,以及光的激光功率调制。
4. 光的干涉现象的未来发展随着科技的不断进步和发展,光的干涉现象在更广泛的领域将会得到应用和发展。
特别是在光通信、光计算和光存储等领域,光的干涉现象将会发挥重要的作用。
例如,基于光的干涉原理设计的光计算和光存储器件可以大大提高计算和存储的速度和容量。
光学光的干涉现象及干涉条纹解释

光学光的干涉现象及干涉条纹解释光的干涉现象是指当两束或多束光波相交时,由光波的叠加而产生明暗相间的条纹现象。
这是光的波动性质所导致的,根据不同的光源和干涉方式,干涉现象可以具有不同的特点和应用。
1. 干涉现象的基本原理干涉现象基于光的波动性质,可以通过光的传播速度和光的相位差来解释。
当两束光波相交时,如果它们的相位差为整数倍的波长,那么它们的振幅将叠加,光强增强,形成明条纹;相位差为奇数个半波长时,振幅将相互抵消,光强减弱,形成暗条纹。
2. 干涉实验中的光源干涉实验中光源的选择对于产生干涉现象起着重要的作用。
常用的光源有自然光、单色光和相干光。
自然光由多个不同波长的光波组成,因此产生多种干涉条纹;单色光只包含某一特定波长的光波,能够产生清晰且稳定的干涉条纹;而相干光是一种光波在多次反射和折射后形成的,具有高度的一致性和稳定性,可用于精密干涉测量。
3. 干涉实验中的干涉方式干涉实验中常见的干涉方式有双缝干涉、薄膜干涉和牛顿环干涉。
双缝干涉是利用两个狭缝间的光波干涉产生的明暗条纹。
薄膜干涉是通过光在不同折射率的介质中传播时产生的干涉现象,例如油膜和气泡表面的干涉条纹。
牛顿环干涉利用透明介质和光的反射干涉形成的干涉圆环。
4. 干涉条纹解释干涉条纹的解释可以通过光程差和相位差来理解。
光程差是指两束光波在到达观察点之前所走的光路长度之差,而相位差则是光波振动状态的差异。
当光程差为整数倍波长时,相位差为0,光波振动状态一致,明条纹出现;当光程差为半波长时,相位差为π,光波振动状态相反,暗条纹出现。
5. 干涉现象的应用干涉现象在科学研究和技术应用中具有广泛的应用。
例如,干涉测量可以用于测量薄膜厚度、折射率和表面形貌;干涉显示可以用于制造三维显示和光学元件;干涉光谱学可以用于分析物质的光学性质和结构等。
总结起来,光学光的干涉现象是光的波动性质所引起的现象,通过光的波长、相位差和光程差的关系解释了干涉条纹的出现。
光的干涉现象

光的干涉现象光的干涉现象是一个引人入胜的领域,它揭示了光的波动性和颜色的奥秘。
干涉是光在交叠时发生的现象,当光波遇到一个障碍物或通过两个紧密相邻的光源时,光波会交织在一起形成干涉条纹。
通过研究光的干涉现象,我们能够更深入地了解光的本质及其在现实生活中的应用。
一. 干涉现象的起源及基本原理光的干涉现象最早可以追溯到17世纪,以英国科学家牛顿和意大利科学家海森堡为代表的研究者通过实验观测到了光的干涉条纹。
这些实验的结果证明了光是波动的,进一步建立了光波的干涉理论。
光的干涉现象可以用波动理论来解释。
当两个光波相交时,它们的振幅相互叠加形成一个新的波动。
如果两个光波的振幅处于同相位(即波峰和波峰相重叠或波谷和波谷相重叠),则干涉增强,形成明亮的干涉条纹。
相反,如果两个光波的振幅处于反相位(即波峰和波谷相重叠),则干涉消弱,形成暗淡的条纹。
这样,通过观察条纹的明暗变化,我们可以推断光波之间的相位关系。
二. 光的干涉应用由于光的干涉现象的特殊性质,它在科学和工程领域中有着广泛的应用。
1. 干涉测量技术光的干涉测量技术是一种高精度的测量方法,可以用于测量各种物理量,如长度、厚度和折射率等。
通过观察干涉条纹的形态和变化,我们可以确定被测量物体的性质和形态,这对于制造和检测精密仪器非常重要。
2. 光的干涉在干涉仪中的应用干涉仪是一种基于光的干涉现象构建的仪器,被广泛应用于科学实验和工程测量中。
例如,迈克耳逊干涉仪和薄膜干涉仪是两种常见的干涉仪器。
迈克耳逊干涉仪通过分束器将光分为两束,然后再通过一系列反射镜和波片,最后重新交汇形成干涉条纹。
薄膜干涉仪则利用薄膜表面的反射和透射特性来产生干涉现象,用于测量薄膜的厚度和折射率。
3. 光的干涉在光谱学中的应用光谱学是研究光的波长和频率分布的科学。
通过利用光的干涉现象,我们可以分析物质的光谱特征,从而揭示物质的组成和结构。
例如,通过观察杨氏干涉仪中的干涉条纹,我们可以测量光的波长,进而得到样品中不同元素的成分及其浓度。
光的干涉现象知识点

光的干涉现象知识点光的干涉现象是光学中的一种重要现象,它揭示了光波的特性和波动性质。
本文将深入探讨光的干涉现象的相关知识点,从双缝干涉到薄膜干涉,让我们一起来了解其中的奥秘。
1. 光的波动性在解释光的干涉现象之前,我们需要了解光的波动性质。
光是电磁波,具有波粒二象性,既可被视为波,又可被视为由光子组成的粒子。
2. 干涉现象的概念干涉是指两个或多个波的叠加所产生的相加或相消效应。
当光波遇到具有一定条件的传播介质或物体时,会产生干涉现象。
3. 双缝干涉双缝干涉是最为经典的干涉实验。
通过在光路上设置两个相距较近的狭缝,使不同波源发出的光束相遇并叠加。
在干涉屏上观察到交替明暗的条纹,称为干涉条纹。
4. 单缝衍射除了双缝干涉外,单缝衍射也是一种常见的光学现象。
当单一光源经过一个狭缝照射到屏幕上时,光波会在缝口边缘发生衍射,形成一系列衍射条纹。
5. 干涉的条件实现光的干涉需要满足一定的条件,包括相干光源、宽度适当的缝隙以及相对稳定的干涉装置。
6. 马吕斯干涉仪马吕斯干涉仪是一种常用的干涉装置,由两个凸透镜和一对半透半反镜组成。
通过调节透镜的位置和倾斜角度,可以实现干涉级数的调节。
7. 薄膜干涉薄膜干涉是指光波在两个介质界面之间传播时发生的干涉现象。
光波在由两种折射率不同的介质界面形成的薄膜中,反射和透射多次发生干涉,产生彩色的干涉条纹。
8. 薄膜干涉的应用薄膜干涉现象在实际应用中具有重要的意义。
例如,薄膜干涉被广泛应用于涂层技术、光学仪器中的反射镜和透镜、彩色薄膜的制备等。
9. 多光束干涉除了双缝干涉和薄膜干涉,还存在着多光束干涉现象。
多光束干涉是指多个光源产生的光波在一定条件下相互干涉的现象。
10. 光的相干性干涉现象的实现需要光源的相干性,即光波之间具有确定的相位关系。
相干性是衡量光波相位关系的一个重要参数。
总结:光的干涉现象是光学中的重要内容,通过对光波的叠加效应和波动性质的研究,揭示了光的特性和行为规律。
光的干涉
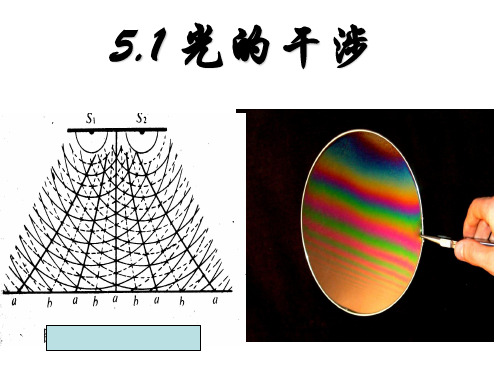
3、关于光在竖直肥皂液薄膜上产生的干涉现象,下列说 法中正确的是( A、 )C A.干涉条纹的产生是由于光在薄膜前后两表面发生反射, 形成的两列光波叠加的结果 B.若出现明暗相间的条纹相互平行,说明肥皂膜的厚度是 均匀的
C.用绿色光照射薄膜产生的干涉条纹间距比黄光照射间距
小 D.薄膜上的干涉条纹基本上是竖直的
3 2
五、薄膜干涉 肥皂泡看起来常常是彩 色的,雨后公路积水上 面漂浮的油膜,看起来 也是彩色的。这些现象 是怎样形成的呢?
观察肥皂薄膜上干涉条纹
1.薄膜干涉的成因
如图所示,竖直放置的肥皂薄膜由于
受到重力的作用,下面厚、上面薄.因 此,在薄膜上不同的地方,从膜的前、 后表面反射的两列光波叠加,在某些位 置,这两列波叠加后互相加强,出现亮 条纹;在另一些地方,叠加后互相削弱, 出现暗条纹.故在单色光照射下,就出
暗条纹形成的原因
双缝 屏幕
取P点上方的点Q1,与两个狭缝S1、 S2路程差δ= Q1 S2- Q1 S1=λ/2 当其中一条光传来的是波峰,另 一条传来的就是波谷,其中一条 光传来的是波谷,另一条传来的 一定是波峰,Q1点总是波峰与波 谷相遇,振幅最小,Q1点总是振 动减弱的地方,故出现暗纹。
S1 S2
3λ/2
δ= 3λ/2
以此类推
当光程差δ= 半波长的奇数倍时出现暗纹
双缝
屏幕
Q3 第三暗纹 Q2 第二暗纹
δ=5λ/2
δ=3λ/2 δ=λ/2 δ=λ/2
S1 S2
Q 1 第一暗纹
Q1 / 第一暗纹 Q2 / 第二暗纹 Q3 / 第三暗纹
δ=3λ/2 δ=5λ/2
总结规律
(1)空间的某点距离光源S1 和S2的路程差为0、1 λ、2 λ、3 λ、等波长的整数倍 (半波长的偶数倍)时,该点 为振动加强点。 (2)空间的某点距离光 源S1和S2的路程差为λ /2、3 λ/2、5λ/2、等 半波长的奇数倍时,该点 为振动减弱点。
光的干涉现象

光的干涉现象光的干涉现象是光学中一种非常重要的现象,它揭示了光波的波动性质和干涉效应。
干涉现象是指两个或多个光波相互叠加时产生的干涉条纹的现象。
这一现象在科学研究和实际应用中都有着广泛的应用,例如在光学仪器的设计和生物医学领域的成像技术中。
干涉现象最早由英国物理学家托马斯·杨在1801年发现。
他利用一对狭缝让光通过,并观察到了明暗相间的干涉条纹。
这一实验为光的波动性提供了有力的证据,并为后来的干涉理论奠定了基础。
光的干涉现象可以分为两种类型:构造干涉和破坏干涉。
构造干涉是指两束或多束光波叠加时,相位差固定的情况下产生的干涉现象。
这种干涉现象可以通过杨氏实验来观察到。
杨氏实验中,一束光经过一个狭缝后,会形成一组平行的光线,这组光线再经过另一个狭缝后,就会发生干涉现象。
当两束光的相位差为整数倍波长时,它们会相长干涉,形成明条纹;当相位差为半整数倍波长时,它们会相消干涉,形成暗条纹。
这些明暗相间的条纹是构造干涉的结果。
破坏干涉是指两束或多束光波叠加时,相位差不固定的情况下产生的干涉现象。
这种干涉现象可以通过杨氏实验的改进版——扩展光源干涉实验来观察到。
在扩展光源干涉实验中,使用一个狭缝代替原来的点光源,让光通过后形成一个扩展的光源。
当这个扩展的光源经过一块玻璃板或薄膜时,会发生干涉现象。
这是因为玻璃板或薄膜会引起光的相位差,从而产生干涉条纹。
这些干涉条纹的形状和颜色取决于玻璃板或薄膜的性质和厚度。
光的干涉现象不仅在实验室中可以观察到,在自然界中也有很多干涉现象的例子。
例如,彩虹就是太阳光经过水滴后发生的干涉现象。
当太阳光进入水滴后,会发生折射、反射和散射,然后再次折射出来。
这个过程中,光的相位差会发生变化,从而产生彩虹的干涉条纹。
光的干涉现象在现代科学和技术中有着广泛的应用。
例如,在光学仪器的设计中,干涉现象可以用来测量物体的形状和厚度。
利用干涉仪的原理,可以制造出高精度的测量仪器,如激光干涉仪和干涉显微镜。
光的干涉现象

光的干涉现象光的干涉现象是光学中一种重要的现象,它揭示了光波的特性以及光的行为。
干涉实验的结果不仅令人叹为观止,还对解释光的本质提供了有力的证据。
本文将介绍光的干涉现象、干涉的主要类型以及干涉实验的原理和应用。
一、干涉是指两束(或多束)光波在相遇时产生的干涉现象。
这种相遇可以是两束光波来自同一光源,也可以是来自不同的光源。
干涉现象的基础是光的波动性质以及光的相位差。
当两束波波峰或波谷同时到达某一点时,它们相互增强,叫做构成性干涉;而当波峰和波谷同时到达某一点时,它们相互抵消,使得光强变弱或者完全消失,叫做破坏性干涉。
二、干涉的主要类型在光的干涉现象中,主要有两种类型的干涉,即相干光的干涉和非相干光的干涉。
相干光的干涉是指光源发出的两束相干光经过分束器或反射产生的相干干涉。
相干光的干涉常见的实验有杨氏双缝干涉实验、自发光照明干涉等。
非相干光的干涉是指来自不同光源的两束或多束光波相遇产生的干涉。
这种干涉实验中的光源通常不是单色光源,而是如白光等连续光源。
干涉实验的结果将呈现出一系列的颜色条纹,以及光的分光能力。
三、干涉实验的原理和应用干涉实验的原理可以通过光的波动性质来解释。
光的波动模型认为光是一种电磁波,具有波长、频率和振幅等特性。
当光波经过不同的光程差后相遇时,会出现干涉现象。
干涉实验在科学研究和技术应用中具有广泛的应用。
首先,干涉实验是检验光的波动理论的有效手段之一。
通过观察和分析干涉条纹,我们可以验证光波理论的正确性,并进一步深入研究光的本质。
其次,干涉实验也被广泛应用于光学仪器和设备的设计和制造中。
比如在干涉仪、激光干涉仪和光学测量等领域,干涉实验的原理和技术都得到了充分的利用。
干涉实验的结果可以帮助我们测量物体的形状、薄膜的厚度等参数,并且在光学通信、光学信息存储和光学计算等领域也发挥着重要的作用。
总结:光的干涉现象是光学中的重要现象,揭示了光波的特性和行为。
干涉实验的结果在理论研究和技术应用上都具有重要的意义。
物理光学的干涉现象

物理光学的干涉现象干涉现象是物理光学中一个重要的现象,它揭示了光波的波动性质,并为我们理解光的传播和性质提供了深入的见解。
本文将介绍干涉现象的基本概念、原理和应用。
一. 干涉现象的基本概念干涉是指两个或多个光波相互叠加而产生的现象。
当两个光波相遇时,它们的振幅和相位会相互影响,进而改变光波的强度和方向。
干涉现象的关键在于光的波动性,只有当光波以波动的形式传播时,才能发生干涉现象。
二. 干涉现象的原理干涉现象的原理可以用两个光波的叠加原理来解释。
当两个光波相遇时,它们的电场强度会相加并形成新的光波,其振幅和相位取决于原始光波的振幅和相位。
根据叠加原理,当两个光波的相位一致时,它们的振幅叠加会增强光强,称为构成干涉的两个光波为相干光波;当两个光波的相位相差半个波长时,它们的振幅叠加会减弱光强,称为相消干涉。
三. 干涉现象的分类干涉现象可以根据光波的来源和干涉的性质来进行分类。
根据光波的来源,干涉可以分为自行干涉和外行干涉。
自行干涉是指来自同一光源的两束光波相互干涉,例如杨氏干涉的实验;外行干涉是指来自不同光源的光波相互干涉,例如望远镜的干涉。
根据干涉的性质,干涉可以分为等厚干涉和非等厚干涉。
等厚干涉是指光波通过具有等厚度的介质产生的干涉现象,例如牛顿环;非等厚干涉是指光波通过具有不同厚度的介质产生的干涉现象,例如楞次干涉。
四. 干涉现象的应用干涉现象在许多实际应用中发挥着重要作用。
以下列举了几个常见的应用:1. 干涉仪:干涉仪是一种利用干涉现象测量光的波长、厚度和折射率等物理量的仪器。
它可以利用干涉现象来实现高精度的测量和检测。
2. Michelle干涉光谱仪:Michelle干涉光谱仪是一种基于干涉现象测量光谱的仪器。
它通过光的干涉来分析光的频谱成分,广泛应用于光谱学和光学研究领域。
3. 光学薄膜:光学薄膜是一种利用干涉现象精确控制光的传播和反射的薄膜。
它在光学器件和光学成像等领域具有重要的应用价值。
《光的干涉》课件

特定的干涉条纹。
实验步骤
1. 制备不同厚度的薄膜样品。
2. 将光源对准薄膜,使光波入射到薄 膜表面。
3. 观察薄膜表面的干涉条纹,分析干 涉现象与薄膜厚度的关系。
迈克尔逊干涉仪
实验目的:利用迈克尔逊干涉仪观察不同波长的光的干 涉现象。 实验步骤
2. 将不同波长的光源依次对准迈克尔逊干涉仪。
实验原理:迈克尔逊干涉仪通过分束器将一束光分为两 束,分别经过反射镜后回到分束器,形成干涉。
1. 调整迈克尔逊干涉仪,确保光路正确。
3. 观察不同波长光的干涉条纹,分析干涉现象与波长 的关系。
04
光的干涉的应用
光学干涉测量技术
干涉仪的基本原理
干涉仪利用光的干涉现象来测量长度、角度、折射率等物理量。干涉仪的精度极高,可以达到纳米级 别。
光的波动性是指光以波的形式传播, 具有振幅、频率和相位等波动特征。
光的干涉是光波动性的具体表现之一 ,当两束或多束相干光波相遇时,它 们会相互叠加产生加强或减弱的现象 。
波的叠加原理
波的叠加原理是物理学中的基本原理之一,当两列波相遇时,它们会相互叠加, 形成新的波形。
在光的干涉中,当两束相干光波相遇时,它们的光程差决定了干涉加强或减弱的 位置。
多功能性
光学干涉技术将向多功能化发展,实现同时进行 多种参数的测量和多维度的信息获取。
光学干涉技术的挑战与机遇
挑战
光学干涉技术面临着测量精度、 稳定性、实时性等方面的挑战, 需要不断改进和完善技术方法。
机遇
随着科技的不断进步和应用需求 的增加,光学干涉技术在科学研 究、工业生产、医疗等领域的应 用前景将更加广阔。
光的干涉现象及双缝干涉的原理

光的干涉现象及双缝干涉的原理光的干涉现象是光学中一种重要的现象,它揭示了光波的波动性质。
而双缝干涉是一种经典的干涉实验,通过它可以更加深入地理解光的干涉现象的原理。
一、光的干涉现象光的干涉现象是指两个或多个光波相互叠加时形成明暗条纹的现象。
这种现象可以用波动光学的理论来解释,即光是以波动的形式传播的。
当两个波峰或两个波谷相遇时,它们会叠加并形成更强的光强,称为增强干涉;而当一个波峰与一个波谷相遇时,则会相互抵消,产生光强减弱的区域,称为消减干涉。
光的干涉现象可以用于测量物体的薄膜厚度、波长等,并且在干涉仪等实验中起到重要的作用。
其中,双缝干涉是一种经典的干涉实验。
二、双缝干涉的原理双缝干涉实验是通过让光通过两个狭缝而形成干涉条纹的实验。
它的原理可以用光的波动性质来解释。
当平行光通过两个狭缝时,每个狭缝都可以看作是一个次级波源。
这两个波源发出的波动通过相干光的叠加形成了一系列明暗相间的干涉条纹。
在双缝干涉实验中,条纹的形成受到光的波长、狭缝间距以及观察屏幕距离等因素的影响。
光的波长越短,干涉条纹间距越小;狭缝间距越大,干涉条纹间距越大;观察屏幕距离越远,干涉条纹越模糊。
此外,双缝干涉实验还可以得出光的波动性质与光的传播速度之间的关系,即相干光的波长与频率满足传播速度等于光速的关系。
三、实际应用光的干涉现象及双缝干涉的原理不仅在科学研究中有重要应用,也在实际生活中有着许多应用。
例如,干涉测微计是一种利用双缝干涉原理进行精密测量的仪器。
它利用干涉条纹的变化来测量物体的长度、厚度等。
此外,光的干涉现象还在光学显微镜、干涉仪等光学仪器中广泛应用,用于观察和测量微小结构和物体的性质。
在光学材料的研究中,干涉现象也被广泛应用。
例如,通过改变薄膜的厚度或者材料的折射率,可以实现光的干涉现象在材料的表面上的控制,从而制备出具有特殊光学性质的材料,用于光电子器件、光学传感器等领域。
总结:光的干涉现象及双缝干涉的原理是光学中的重要内容。
光的干涉现象的解释与计算

光的干涉现象的解释与计算光的干涉现象是指当两束或多束光波经过叠加时产生的干涉现象。
这种现象是由光的波动性质所引起的,它揭示了光波的波动性和波动现象的一些重要特性。
本文将解释光的干涉现象的原理,并介绍了几种常见的干涉计算方法。
一、光的干涉原理光的干涉是基于波的相干性原理,即两束或多束光波的相位关系会影响它们的叠加结果。
当两束光波的相位差为整数倍的波长时,它们达到叠加增强的状态,称为相长干涉;而当相位差为半整数倍的波长时,它们达到叠加减弱的状态,称为相消干涉。
干涉现象的发生需要满足一定的条件,例如光源的相干性和光的干涉程度等。
二、干涉计算方法(一)双缝干涉计算:双缝干涉是最经典的光的干涉实验之一,它的计算方法可以通过以下公式进行表达:I = I1 + I2 + 2√(I1×I2)×cos(δ)其中,I代表干涉图案的强度,I1和I2分别表示通过两个独立缝隙的光线的强度,δ是相位差。
通过这个公式,我们可以计算出不同干涉条件下的干涉图案的强度分布情况。
(二)杨氏双缝干涉计算:杨氏双缝干涉是一种经典的干涉实验,它使用的是一束单色光通过两个狭缝形成的干涉条纹。
在这种情况下,干涉计算方法可以用以下公式表示:y = λL/d其中,y代表干涉条纹的间距,λ是光的波长,L是光的传播距离,d是两个缝隙之间的距离。
通过这个公式,我们可以计算出干涉条纹之间的间距。
(三)薄膜干涉计算:薄膜干涉是一种基于薄膜的光学现象,在这种情况下,干涉计算方法可以用以下公式表示:2nt = (m + 1/2)λ其中,nt是薄膜的等效厚度,m是干涉条纹的次序,λ是光的波长。
通过这个公式,我们可以计算出薄膜干涉的条纹间距和薄膜厚度之间的关系。
(四)光栅干涉计算:光栅是一种具有周期性结构的光学元件,它可以产生多束光波的干涉现象。
光栅干涉的计算方法可以用以下公式表示:dsinθ = mλ其中,d是光栅的周期,θ是入射角度,m是干涉条纹的次序,λ是光的波长。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
光的干涉现象.txt 只有两列光波的频率相同,位相差[1]恒定,振动方向一致的相干光源,才能产生光的干涉。
由两个普通独立光源发出的光,不可能具有相同的频率,更不可能存在固定的相差,因此,
不能产生干涉现象。
[编辑本段]说明
①在交迭区域内各处的强度如果不完全相同而形成一定的强弱分布,显示出固定的图象
叫做干涉图样。
也即对空间某处而言,干涉迭加后的总发光强度不一定等于分光束的发光强
度的迭加,而可能大于、等于或小于分光束的发光强度,这是由波的叠加原理决定的(即波
峰和波峰相加为两倍的波峰)。
②通常的独立光源是不相干的。
这是因为光的辐射一般是由原子的外层电子激发后自动
回到正常状态而产生的。
由于辐射原子的能量损失,加上和周围原子的相互作用,个别原子
的辐射过程是杂乱无章而且常常中断,持续对同甚短,即使在极度稀薄的气体发光情况下,
和周围原子的相互作用已减至最弱,而单个原子辐射的持续时间也不超过10^-8秒。
当某个
原子辐射中断后,受到激发又会重新辐射,但却具有新韵初相位。
这就是说,原子辐射的光
波并不是一列连续不断、振幅和频率都不随时间变化的简谐波,即不是理想的单色光,而是
如图所示,在一段短暂时间内(如τ=10-8s)保持振幅和频率近似不变,在空间表现为一段有
限长度的简谐波列。
此外,不同原子辐射的光波波列的初相位之间也是没有一定规则的。
这
些断续、或长或短、初相位不规则的波列的总体,构成了宏观的光波。
由于原子辐射的这种
复杂性,在不同瞬时迭加所得的干涉图样相互替换得这样快和这样地不规则,以致使通常的
探测仪器无法探测这短暂的干涉现象。
尽管不同原子所发的光或同一原子在不同时刻所发的光是不相干的,但实际的光干涉对
光源的要求并不那么苛刻,其光源的线度远较原子的线度甚至光的波长都大得多,而且相干
光也不是同一时刻发出的。
这是因为实际的干涉现象是大量原子发光的宏观统计平均结果,
从微观上来说,光子只能自己和自己干涉,不同的光子是不相干的;但是,宏观的干涉现象
却是大量光子各自干涉结果的统计平均效应。
③由于六十年代激光的问世,已使光源的相干性大大提高,同时快速光电探测仪器的出
现,探测仪器的时间响应常数缩短,以至可以观察到两个独立光源的干涉现象。
另,在现在
的高中课本中,已经有光的干涉实验,用激光或者同一灯泡通过双缝进行实验).
1963年玛格亚和曼德用时间常数为10^-8~10^-9秒的变像管拍摄了两个独立的红宝石
激光器发出的激光的干涉条纹。
可目视分辨的干涉条纹有23条。
④相干光的获得。
对于普通的光源,保证相位差恒定成为实现干涉的关键。
为了解决发
光机制中初相位的无规则迅速变化和干涉条纹的形成要求相位差恒定的矛盾,可把同一原子
所发出的光波分解成两列或几列,使各分光束经过不同的光程,然后相遇。
这样,尽管原始
光源的初相位频繁变化,分光束之间仍然可能有恒定的相位差,因此也可能产生干涉现象。
通常采用的方法有两种:
a.分波阵面法。
将点光源的波阵面分割为两部分,使之分别通过两个光具组,经反射、
折射或衍射后交迭起来,在一定区域形成干涉。
由于波阵面上任一部分都可看作新光源,而
且同一波阵面的各个部分有相同的位相,所以这些被分离出来的部分波阵面可作为初相位相
同的光源,不论点光源的位相改变得如何快,这些光源的初相位差却是恒定的。
杨氏双缝、
菲涅耳双面镜和洛埃镜等都是这类分波阵面干涉装置。
b.分振幅法。
当一束光投射到两种透明媒质的分界面上,光能一部分反射,另一部分折
射。
这方法叫做分振幅法。
最简单的分振幅干涉装置是薄膜,它是利用透明薄膜的上下表面
对入射光的依次反射,由这些反射光波在空间相遇而形成的干涉现象。
由于薄膜的上下表面
的反射光来自同一入射光的两部分,只是经历不同的路径而有恒定的相位差,因此它们是相
干光。
另一种重要的分振幅干涉装置,是迈克耳孙干涉仪。
⑤光的干涉现象是光的波动性的最直接、最有力的实验证据。
光的干涉现象是牛顿微粒模型根本无法解释的,只有用波动说才能圆满地加以解释。
由牛顿微粒模型可知,两束光的微粒数应等于每束光的微粒之和,而光的干涉现象要说明的却是微粒数有所改变,干涉相长处微粒数分布多;干涉相消处,粒子数比单独一束光的还要少,甚至为零。
这些问题都是微粒模型难以说明的。
再从另一角度来看光的干涉现象,它也是对光的微粒模型的有力的否定。
因为光总是以3×10^8m/s的速度在真空中传播,不能用人为的方法来使光速作任何改变(除非在不同介质中,光速才有不同。
但对于给定的一种介质,光速也是一定的)。
干涉相消之点根本无光通过。
那么按照牛顿微粒模型,微粒应该总是以3×10^8m/s的速度作直线运动,在干涉相消处,这些光微粒到那里去了呢?如果说两束微粒流在这些点相遇时,由于碰撞而停止了,那么停止了的(即速度不再是3×lO^8m/s,而是变为零)光微粒究竟是什么东西呢?如果说是移到干涉相长之处去了,那么又是什么力量使它恰恰移到那里去的呢?所有这些问题都是牛顿微粒模型根本无法回答的。
然而波动说却能令人信服地解释它,并可由波在空间按一定的位相关系迭加来定量地导出干涉相长和相消的位置以及干涉图样的光强分布的函数解析式。
因此干涉现象是波的相干迭加的必然结果,它无可置疑地肯定了光的波动性,我们还可进一步把它推广到其他现象中去,凡有强弱按一定分布的干涉图样出现的现象,都可作为该现象具有波动本性的最可靠最有力的实验证据。
多情只有春庭月,犹为离人照落花。
昔我往矣,杨柳依依;今我来思,雨雪霏霏。
