最小二乘法线性拟合y
三种常用的拟合直线方法

三种常用的拟合直线方法
在数学和统计学中,拟合直线是一种常用的数据分析方法,可以用来描述两个变量之间的关系。
下面介绍三种常用的拟合直线方法: 1. 最小二乘法:最小二乘法是一种常用的拟合直线方法,它通过将数据点到直线的距离的平方和最小化来确定直线的位置。
该方法适用于线性回归问题,即适用于自变量和因变量之间呈线性关系的情况。
2. 线性规划法:线性规划法是一种将数据点拟合到直线上的方法,它通过寻找一条直线,使得所有数据点到该直线的距离之和最小化。
与最小二乘法不同的是,线性规划法可以适用于非线性回归问题。
3. 非线性规划法:非线性规划法是一种将数据点拟合到曲线上的方法,它通过寻找一条曲线,使得所有数据点到该曲线的距离之和最小化。
该方法适用于非线性回归问题,如指数、对数等曲线拟合。
无论选择哪种方法,拟合直线都是一种重要的数据分析方法,可以帮助我们更好地理解数据之间的关系,从而为决策提供更加准确的依据。
- 1 -。
最小二乘法拟合原理

最新资料推荐最小二乘法拟合原理最小二乘法拟合原理最小二乘拟合在物理实验中经常要观测两个有函数关系的物理量。
根据两个量的许多组观测数据来确定它们的函数曲线,这就是实验数据处理中的曲线拟合问题。
这类问题通常有两种情况:一种是两个观测量x与y之间的函数形式已知,但一些参数未知,需要确定未知参数的最佳估计值;另一种是x与y之间的函数形式还不知道,需要找出它们之间的经验公式。
后一种情况常假设x与y之间的关系是一个待定的多项式,多项式系数就是待定的未知参数,从而可采用类似于前一种情况的处理方法。
一、最小二乘法原理在两个观测量中,往往总有一个量精度比另一个高得多,为简单起见把精度较高的观测量看作没有误差,并把这个观测量选作x,而把所有的误差只认为是y的误差。
设x和y的函数关系由理论公式y = f (x; cl , c2 , cm) (0-0-1 ) 给出,其中cl , c2 , cm是m个要通过实验确定的参数。
对于每组观测数据(xi , yi ) i = 1, 2 , , N。
都对应于xy平面上一个点。
若不存在测量误差,则这些数据点都准确落在理论曲线上。
只要选取m组测量值代入式(0-0-1 ),便得到方程组yi1 / 12=f (x; cl , c2 , cm)(0-0-2 )式中i = 1,2 , , m.求m个方程的联立解即得m个参数的数值。
显然Nm时,参数不能确定。
在Nm的情况下,式(0-0-2)成为矛盾方程组,不能直接用解方程的方法求得m个参数值,只能用曲线拟合的方法来处理。
设测量中不存在着糸统误差,或者说已经修正,则y 的观测值yi围绕着期望值f (x ;cl ,c2 , cm)摆动,其分-布为正态分布,则yi的概率密度为p yi 1 yi f xi;c1, c2, ............................... , cm exp 2 2 i2 i2 ,式中i是分布的标准误差为简便起见,下面用C代表(cl,c2,cm)。
最小二乘法知识

最小二乘法知识最小二乘法是一种最优化方法,经常用于拟合数据和解决回归问题。
它的目标是通过调整模型参数,使得模型的预测值与观测值之间的差异最小。
最小二乘法的核心思想是最小化误差的平方和。
对于给定的数据集,假设有一个线性模型y = β₀ + β₁x₁ + β₂x₂ + ... +βₙxₙ,其中β₀, β₁, β₂, ... , βₙ 是需要求解的未知参数,x₁, x₂, ... , xₙ 是自变量,y 是因变量。
那么对于每个样本点 (xᵢ, yᵢ),可以计算其预测值ŷᵢ = β₀ + β₁x₁ + β₂x₂ + ... + βₙxₙ,然后计算预测值与实际值之间的差异 eᵢ = yᵢ - ŷᵢ。
最小二乘法的目标是使得误差的平方和最小化,即最小化目标函数 E = ∑(yᵢ - ŷᵢ)²。
对于简单的线性回归问题,即只有一个自变量的情况下,最小二乘法可以通过解析方法求解参数的闭合解。
我们可以通过求偏导数,令目标函数对参数的偏导数等于零,求解出参数的最优解。
然而,对于复杂的非线性回归问题,解析方法通常不可行。
在实际应用中,最小二乘法通常使用迭代方法进行求解。
一种常用的迭代方法是梯度下降法。
梯度下降法通过反复进行参数更新的方式逐步降低目标函数的值,直到收敛到最优解。
具体而言,梯度下降法首先随机初始化参数的值,然后计算目标函数对于每个参数的偏导数,根据偏导数的方向更新参数的值。
迭代更新的过程可以通过下式表示:βₙ = βₙ - α(∂E/∂βₙ)其中,α 是学习率参数,控制每次更新参数的步长。
学习率需要适当选择,过小会导致收敛过慢,过大会导致震荡甚至不收敛。
最小二乘法除了可以用于线性回归问题,还可以用于其他类型的回归问题,比如多项式回归。
在多项式回归中,我们可以通过增加高次项来拟合非线性关系。
同样地,最小二乘法可以通过调整多项式的系数来使得拟合曲线与实际数据更加接近。
除了回归问题,最小二乘法还可以应用于其他领域,比如数据压缩、信号处理和统计建模等。
最小二乘法的拟合

一、最小二乘法与最小一乘法1.什么时候用最小二乘法在研究两个变量之间的关系时,可以用回归分析的方法进行分析。
当确定了描述两个变量之间的回归模型后,就可以使用最小二乘法估计模型中的参数,进而建立经验方程.例如,在现实世界中,这样的情形大量存在着:两个变量X和Y(比如身高和体重)彼此有一些依赖关系,由X 可以部分地决定Y的值,但这种关系又是不确定的.人们常常借助统计学中的回归模型来寻找两个变量之间的关系,而模型的建立当然是依据观测数据.首先通过试验或调查获得x和Y的一组对应关系(x1,Y1),(x2,Y2),…,(x n,Y n),然后回答下列5个问题:1. 这两个变量是否有关系?(画出散点图,作直观判断)2. 这些关系是否可以近似用函数模型来描述?(利用散点图、已积累的函数曲线形状的知识和试验数据,选择适当的回归模型,如一元线性模型y=b0+b1x,二次函数模型y=b0+b1x+b2x2等)3. 建立回归模型.4. 对模型中的参数进行估计,最小二乘法是这些参数的一种常用估计方法.5. 讨论模型的拟合效果.在上述第3步中,设所建立的回归模型的一般形式是,其中Y称为响应变量,x称为解释变量或协变量;是一个由参数决定的回归函数;是一个不可观测的随机误差.为了通过试验数据来估计参数的值,可以采用许多统计方法,而最小二乘法是目前最常用、最基本的.由的估计值决定的方程称为经验回归方程或经验方程.教科书中涉及的回归模型是最简单的一元线性模型Y=b0+b1x+,此时模型的拟合效果可以通过Pearson相关系数来描述。
事实上,在线性回归模型中可以证明相关指数等于相关系数的平方.2.什么是最小二乘法思想简单地说,最小二乘的思想就是要使得观测点和估计点的距离的平方和达到最小.这里的“二乘”指的是用平方来度量观测点与估计点的远近(在古汉语中“平方”称为“二乘”),“最小”指的是参数的估计值要保证各个观测点与估计点的距离的平方和达到最小.例如,对于回归模型,若,…,为收集到的观测数据,则应该用来估计,这里是的估计值。
最小二乘法 线性与非线性拟合

最小二乘法线性与非线性拟合最小二乘法实现数据拟合最小二乘法原理函数插值是差值函数p(x)与被插函数f(x)在节点处函数值相同,即p( )=f( ) (i=0,1,2,3……,n),而曲线拟合函数不要求严格地通过所有数据点( ),也就是说拟合函数在处的偏差=不都严格地等于零。
但是,为了使近似曲线能尽量反应所给数据点的变化趋势,要求| |按某种度量标准最小。
即=为最小。
这种要求误差平方和最小的拟合称为曲线拟合的最小二乘法。
(一)线性最小二乘拟合根据线性最小二乘拟合理论,我们得知关于系数矩阵A的解法为A=R\Y。
例题假设测出了一组,由下面的表格给出,且已知函数原型为y(x)=c1+c2*e^(-3*x)+c3*cos(-2*x)*exp(-4*x)+c4*x^2试用已知数据求出待定系数的值。
在Matlab中输入以下程序x=[0,0.2,0.4,0.7,0.9,0.92,0.99,1.2,1.4,1.48,1.5]';y=[2.88;2.2576;1.9683;1.9258;2.0862;2.109;2.1979;2.5409;2.9627;3.155;3.2052];A=[ones(size(x)) exp(-3*x),cos(-2*x).*exp(-4*x) x.^2];c=A\y;c'运行结果为ans =1.22002.3397 -0.6797 0.8700下面画出由拟合得到的曲线及已知的数据散点图x1=[0:0.01:1.5]';A1=[ones(size(x1)) exp(-3*x1),cos(-2*x1).*exp(-4*x1) x1.^2];y1=A1*c;plot(x1,y1,x,y,'o')事实上,上面给出的数据就是由已知曲线y(x)= 0.8700-0.6797*e^(-3*x)+ 2.3397*cos(-2*x)*exp(-4*x)+ 1.2200*x^2产生的,由上图可见拟合效果较好。
最小二乘法的线性拟合

8
4.3 数表与线图的公式化处理
前面介绍的数表与线图的程序化处理方法,这种方法虽然 解决了数表和线图在CAD作业中的存储和检索问题,但还存 在下述一些缺点:
1)占用大量计算机内存。数表和线图的程序化处理,要将 数表中的全部数据编进计算程序中,实现数据的自动检索。 当数表很庞大时,所占内存很大。一般情况下,一个设计计 算程序常常需要使用多个数表,则所占内存更加庞大,严重 时甚至会影响程序的正常运行。
4
4.2.2 直线图的公式化处理
1、直角坐标直线图的公式化处理
(a)直齿轮
(b)斜齿轮
5
2、对数坐标直线图的公式化处理
对数坐标中的直线方程可写为:
注意:一般程序语言中,只有lnx (自然对数)无十进制对数 lgx ,所以编程时,要进行换底运算。
lg x ln x ln10
6
3、区域图的公式化处理
2)效率低,占机时间长。通常设计所使用到的仅是数表中 的一小部分数据,有时甚至只是其中的一、二个。但数表程 序化处理对数表中的每个数据,无论在当时的计算程序中
是否被用到,都必须顺序地将全部数据读入内存。
检索时,一般又得顺序地从头检索至所需的那个
9
数据为止。
4.3.1 曲线拟合
数表程序化处理一般只适用于数表较小(数据 量较小)、计算程序使用数表个数不多的情况。对 于比较大型的计算程序,常常需使用很多的数表, 数据量很大,在这种情况下数表的处理就要采用其 它的方法。其中一种方法就是本节所要介绍的曲线 拟合。
常用的处理方法有三种:
1
(1)线图所表示的各参数之间本来就有计算公 式,只是由于计算公式复杂.为了便于手工计算 将公式绘成线图,以供设计时查用。对于这类线 图处理的方法为:找到线图原有公式,将公式编 写成程序。这是最精确的程序化处理方法,但难 以找到。
最小二乘法求出直线拟合公式

最小二乘法求出直线拟合公式最小二乘法是一种常用的线性回归方法,用于求出最佳的拟合直线公式。
其基本思想是通过最小化观测数据与拟合直线之间的误差来确定最佳的直线参数。
假设我们有一组观测数据(xi, yi),其中xi表示自变量的取值,yi表示因变量的取值。
我们的目标是找到一条直线y = mx + c,使得观测数据点到这条直线之间的误差最小。
首先,我们定义观测数据点到拟合直线的误差为:ei = yi - (mx + c)。
我们的目标是最小化所有观测数据点的误差之和:min Σ(ei^2) = min Σ(yi - (mx + c))^2为了求解上述最小化问题,我们需要对误差函数关于参数m和c进行求导,并令导数等于零。
这样可以得到参数的最优解。
对于参数m的求解,我们有以下等式:d/dm Σ(ei^2) = d/dm Σ(yi - (mx + c))^2 = 0通过对上述等式进行求导和化简,我们得到以下方程:m * Σ(xi^2) + c * Σ(xi) = Σ(xi * yi)类似地,对于参数c的求解,我们有以下等式:d/dc Σ(ei^2) = d/dc Σ(yi - (mx + c))^2 = 0通过对上述等式进行求导和化简,我们得到以下方程:m * Σ(xi) + c * n = Σ(yi)其中,n表示观测数据点的数量。
最终,我们可以通过解上述方程组,求得最佳的直线参数m和c,从而得到直线的拟合公式。
拓展:最小二乘法不仅可以应用在线性回归问题中,还可以拓展到非线性回归问题。
例如,如果观测数据点遵循多项式分布,则可以使用多项式回归来拟合数据。
此时,最小二乘法的基本原理是相同的,只是拟合的模型变为多项式函数。
此外,最小二乘法还可以应用于其他问题,例如数据平滑、参数估计等。
它是一种常用的统计学方法,可以在各种实际问题中得到广泛的应用。
最小二乘法线性拟合

4.最小二乘法线性拟合(非常好)我们知道,用作图法求出直线的斜率a 和截据b ,可以确定这条直线所对应的经验公式,但用作图法拟合直线时,由于作图连线有较大的随意性,尤其在测量数据比较分散时,对同一组测量数据,不同的人去处理,所得结果有差异,因此是一种粗略的数据处理方法,求出的a 和b 误差较大。
用最小二乘法拟合直线处理数据时,任何人去处理同一组数据,只要处理过程没有错误,得到的斜率a 和截据b 是唯一的。
最小二乘法就是将一组符合Y=a+bX 关系的测量数据,用计算的方法求出最佳的a 和b 。
显然,关键是如何求出最佳的a 和b 。
(1) 求回归直线设直线方程的表达式为:bx a y += (2-6-1)要根据测量数据求出最佳的a 和b 。
对满足线性关系的一组等精度测量数据(x i ,y i ),假定自变量x i 的误差可以忽略,则在同一x i 下,测量点y i 和直线上的点a+bx i 的偏差d i 如下:111bx a y d --=222bx a y d --=n n n bx a y d --=显然最好测量点都在直线上(即d 1=d 2=……=d n =0),求出的a 和b 是最理想的,但测量点不可能都在直线上,这样只有考虑d 1、d 2、……、d n 为最小,也就是考虑d 1+d 2+……+d n 为最小,但因d 1、d 2、……、d n 有正有负,加起来可能相互抵消,因此不可取;而|d 1|+|d 2|+……+ |d n |又不好解方程,因而不可行。
现在采取一种等效方法:当d 12+d 22+……+d n2对a 和b 为最小时,d 1、d 2、……、d n 也为最小。
取(d 12+d 22+……+d n 2)为最小值,求a 和b 的方法叫最小二乘法。
令 ∑==ni idD 12=2112][i i ni ni ib a y dD --==∑∑== (2-6-2)D 对a 和b 分别求一阶偏导数为:][211∑∑==---=∂∂ni i n i i x b na y a D][21211∑∑∑===---=∂∂n i i n i i n i i i x b x a y x b D再求二阶偏导数为:n a D 222=∂∂; ∑==∂∂ni i x b D 12222 显然: 0222≥=∂∂n a D ; 021222≥=∂∂∑=n i i x b D 满足最小值条件,令一阶偏导数为零:011=--∑∑==ni i ni ix b na y(2-6-3)01211=--∑∑∑===ni i ni i ni ii x b x a yx (2-6-4)引入平均值: ∑==ni i x n x 11; ∑==n i i y n y 11;∑==n i i x n x 1221; ∑==ni i i y x n xy 11则: 0=--x b a y02=--x b x a xy (2-6-5) 解得: x b y a -= (2-6-6)22xx y x xy b --=(2-6-7)将a 、b 值带入线性方程bx a y +=,即得到回归直线方程。
最小二乘法公式

最小二乘法公式是一个数学的公式,在数学上称为曲线拟合,此处所讲最小二乘法,专指线性回归方程!最小二乘法公式为b=y(平均)-a*x(平均)。
拓展资料:
曲线拟合俗称拉曲线,是一种把现有数据透过数学方法来代入一条数式的表示方式。
科学和工程问题可以通过诸如采样、实验等方法获得若干离散的数据,根据这些数据,我们往往希望得到一个连续的函数(也就是曲线)或者更加密集的离散方程与已知数据相吻合,这过程就叫做拟合。
历史
1801年,意大利天文学家朱赛普·皮亚齐发现了第一颗小行星谷神星。
经过40天的跟踪观测后,由于谷神星运行至太阳背后,使得皮亚齐失去了谷神星的位置。
随后全世界的科学家利用皮亚齐的观测数据开始寻找谷神星,但是根据大多数人计算的结果来寻找谷神星都没有结果。
时年24岁的高斯也计算了谷神星的轨道。
奥地利天文学家海因里希·奥尔伯斯根据高斯计算出来的轨道重新发现了谷神星。
高斯使用的最小二乘法的方法发表于1809年他的著作《天体运动论》中。
法国科学家勒让德于1806年独立发明“最小二乘法”,但因不为世人所知而默默无闻。
勒让德曾与高斯为谁最早创立最小二乘法原理发生争执。
1829年,高斯提供了最小二乘法的优化效果强于其他方法的证明,因此被称为高斯-马尔可夫定理。
第5章-1 曲线拟合(线性最小二乘法)讲解
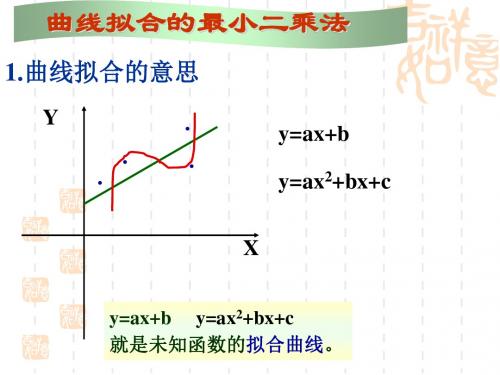
求所需系数,得到方程: 29.139a+17.9b=29.7076 17.9a+11b=18.25
通过全选主元高斯消去求得:
a=0.912605
b=0.174034
所以线性拟合曲线函数为: y=0.912605x+0.174034
练习2
根据下列数据求拟合曲线函数: y=ax2+b
x 19 25 31 38 44 y 19.0 32.3 49.0 73.3 97.8
∑xi4 a + ∑xi2 b = ∑xi 2yi
∑xi2 a + n b = ∑yi
7277699a+5327b=369321.5 5327a+5b=271.4
曲线拟合的最小二乘法
1.曲线拟合的意思
Y
.
.
.
.
y=ax+b y=ax2+bx+c
X
y=ax+b y=ax2+bx+c 就是未知函数的拟合曲线。
2最小二乘法原理
观测值与拟合曲线值误差的平方和为最小。
yi y0 y1 y2 y3 y4…… 观测值 y^i y^0 y^1 y^2 y^3 y^4…… 拟合曲线值
拟合曲线为: y=(-11x2-117x+56)/84
x
yHale Waihona Puke 1.61 1.641.63 1.66
1.6 1.63
1.67 1.7
1.64 1.67
1.63 1.66
1.61 1.64
1.66 1.69
1.59 1.62
最小二乘法求拟合直线公式

最小二乘法求拟合直线公式
直线拟合求最佳经验公式的一种数据处理方法是最小二乘法(又称作
一元线性回归),它可克服用作图法求直线公式时图线的绘制引入的误差,结果更精确,在科学实验中得到了广泛的应用。
1.最小二乘法的理论基础:
若两物理量x、y满足线性关系,并由实验等精度地测得一组实验数据,且假定实验误差主要出现在上,设拟合直线公式为,当所测各值与拟
合直线上各估计值之间偏差的平方和最小,即时,所得拟合公式即为最佳
经验公式。
2.用最小二乘法求最佳经验公式:
设由实验数据求得最佳经验公式为y=a+bx,根据最小二乘法原理有:即:
化为:
其解为:
将得出的、代入即可得最佳经验公式。
的不确定度与很多因素有关,如实验数据的多少、实验数据之间的关
系与直线关系的符合程度(即以下介绍的相关系数)、实验数据的分散度
等等,在此不作介绍。
excel表格最小二乘法拟合

excel表格最小二乘法拟合一、最小二乘法拟合原理1. 基本概念- 在Excel表格中进行最小二乘法拟合,首先要理解最小二乘法的基本原理。
最小二乘法是一种数学优化技术,它通过最小化误差的平方和寻找数据的最佳函数匹配。
- 对于一组给定的数据点(x_i,y_i)(i = 1,2,·s,n),假设我们要拟合的函数为y = f(x),那么误差e_i=y_i - f(x_i)。
最小二乘法的目标就是使∑_{i = 1}^ne_{i}^2最小。
2. 线性拟合(以一元线性为例)- 对于一元线性函数y = ax + b,我们要根据给定的数据点(x_i,y_i)确定a和b 的值。
- 根据最小二乘法原理,a和b的计算公式为:- a=frac{n∑_{i = 1}^nx_iy_i-∑_{i = 1}^nx_i∑_{i = 1}^ny_i}{n∑_{i =1}^nx_{i}^2-(∑_{i = 1}^nx_i)^2}- b=frac{∑_{i = 1}^ny_i - a∑_{i = 1}^nx_i}{n}二、Excel中的操作步骤(以线性拟合为例)1. 准备数据- 在Excel中输入要拟合的数据,将自变量x的值放在一列(例如A列),因变量y的值放在另一列(例如B列)。
2. 绘制散点图- 选中数据(包括x和y的值),点击“插入”选项卡,选择“散点图”。
这一步可以直观地观察数据的分布情况。
3. 添加趋势线(进行拟合)- 在散点图上右键单击其中一个数据点,选择“添加趋势线”。
- 在弹出的“设置趋势线格式”对话框中:- 选择“线性”类型(如果是进行线性拟合)。
- 勾选“显示公式”和“显示R平方值”。
“显示公式”会给出拟合得到的线性方程y = ax + b的具体表达式,“显示R平方值”可以用来评估拟合的好坏,R^2的值越接近1,说明拟合效果越好。
三、实例演示假设我们有以下一组数据:x y1 23 44 55 61. 数据输入- 在Excel的A1 - A5单元格分别输入1、2、3、4、5,在B1 - B5单元格分别输入2、3、4、5、6。
用最小二乘法拟合直线

用最小二乘法拟合直线
最小二乘法是一种常用的拟合直线的方法。
它通过最小化实际数据点与拟合直线之间的垂直距离的平方和,来确定最佳拟合直线的参数。
具体步骤如下:
1. 给定一组实际数据点,包括各自的横坐标和纵坐标。
2. 假设拟合直线的方程为y = ax + b,其中a为斜率,b为截距。
3. 迭代计算,求解出a和b的值,使得所有数据点到拟合直线的垂直距离的平方和最小化。
4. 最后得到的拟合直线即为最佳拟合直线,它尽可能地接近实际数据点,使得误差最小化。
最小二乘法拟合直线在数据处理和分析中广泛使用,能够找到数据的整体趋势,并且能够通过拟合直线来预测未知数据点的值。
它在统计学、经济学和工程等领域具有重要的应用价值。
用Matlab进行最小二乘法线性拟合(求传感器非线性误差、灵敏度)
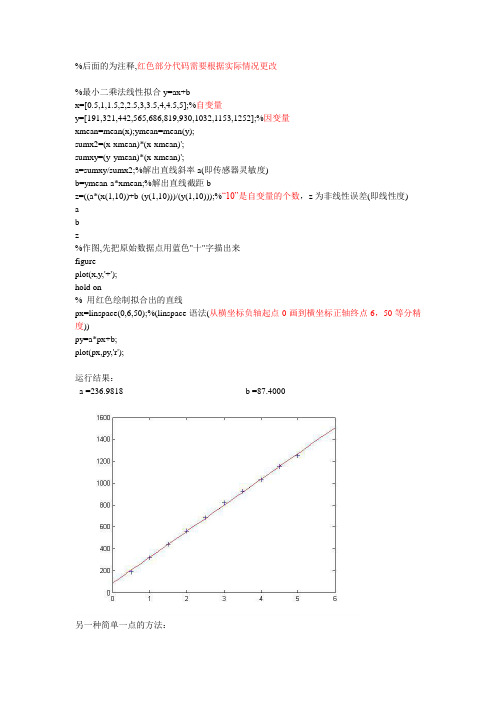
%后面的为注释,红色部分代码需要根据实际情况更改%最小二乘法线性拟合y=ax+bx=[0.5,1,1.5,2,2.5,3,3.5,4,4.5,5];%自变量y=[191,321,442,565,686,819,930,1032,1153,1252];%因变量xmean=mean(x);ymean=mean(y);sumx2=(x-xmean)*(x-xmean)';sumxy=(y-ymean)*(x-xmean)';a=sumxy/sumx2;%解出直线斜率a(即传感器灵敏度)b=ymean-a*xmean;%解出直线截距bz=((a*(x(1,10))+b-(y(1,10)))/(y(1,10)));%“10”是自变量的个数,z为非线性误差(即线性度)abz%作图,先把原始数据点用蓝色"十"字描出来figureplot(x,y,'+');hold on% 用红色绘制拟合出的直线px=linspace(0,6,50);%(linspace语法(从横坐标负轴起点0画到横坐标正轴终点6,50等分精度))py=a*px+b;plot(px,py,'r');运行结果:a =236.9818b =87.4000另一种简单一点的方法:%最小二乘法线性拟合y=ax+bx=[0.5,1,1.5,2,2.5,3,3.5,4,4.5,5];%自变量y=[191,321,442,565,686,819,930,1032,1153,1252];%因变量p=polyfit(x,y,1);p运行结果:p =236.9818 87.4000。
最小二乘法拟合原理

最小二乘法拟合原理最小二乘法(Least Squares Method)是一种常用的线性回归分析方法,用于拟合数据点到一个理论模型的直线或曲线的原理。
它的目标是通过最小化实际数据点与拟合曲线之间的垂直距离(也称为残差)的平方和来找到最佳的拟合曲线。
假设我们有一个包含n个数据点的数据集,其中每个数据点的坐标可以表示为(xi,yi)。
我们希望找到一个模型y=f(x,θ),其中x是自变量,θ是模型的参数,使得对于每个数据点,模型预测的y值与实际的观测值之间的差异最小化。
yi = yi_true + ei以线性回归为例,模型可以表示为y=θ0+θ1x,其中θ0和θ1是要估计的参数。
我们的目标是找到最佳的θ0和θ1,使得所有数据点的残差平方和最小。
残差可以定义为:ei = yi - (θ0 + θ1xi)为了最小化残差平方和,我们需要对残差平方和进行求导,并令导数等于零。
这样一来,我们就能得到使得残差平方和最小的参数估计值。
对于线性回归而言,最小二乘法的公式可以写为:θ1 = (sum(xi - x_mean)(yi - y_mean))/(sum(xi - x_mean)^2)θ0 = y_mea n - θ1x_mean其中,x_mean和y_mean分别是自变量和因变量的均值。
需要注意的是,最小二乘法只是一种估计参数的方法,它没有办法告诉我们模型是否真实有效。
为了评估拟合效果,我们还需要使用一些指标,如决定系数(coefficient of determination),来评估拟合曲线与数据之间的拟合程度。
总结起来,最小二乘法是一种通过最小化实际数据点与拟合曲线之间的垂直距离的平方和来找到最佳的拟合曲线的方法。
它的原理建立在数据具有随机误差,且服从独立同分布的正态分布的假设上。
通过最小二乘法,我们可以估计出模型的参数,以及评估拟合程度,从而对数据进行分析、预测与优化。
excel 最小二乘法拟合

excel 最小二乘法拟合
最小二乘法是一种用于拟合数据的数学方法。
它通过找到最小化
实际观测值与拟合函数之间的残差平方和的参数值,来确定一个最佳
的拟合函数。
首先,我们需要有一组实际观测值,这些观测值通常以 (x, y)
的形式给出。
我们要找到一个函数 y=f(x),将这些观测值拟合得最好。
在最小二乘法中,我们假设拟合函数是一个线性函数,即 f(x)
= a*x + b。
然后,我们通过最小化残差平方和来确定 a 和 b 的值。
求解最小二乘法拟合的过程包括以下几个步骤:
1. 计算观测值的平均值:x̄和ȳ,其中x̄为 x 的平均值,ȳ为 y 的平均值。
2. 计算 x 和 y 的偏差项:Δx = x - x̄和Δy = y - ȳ。
3. 计算拟合函数的参数 a 和 b:
a = (∑(Δx*Δy)) / (∑(Δx^2))
b = ȳ - a*x̄
4. 根据得到的参数 a 和 b,得到拟合函数 y=f(x)。
通过这些步骤,我们可以使用最小二乘法拟合数据并得到一个近
似的拟合函数。
拟合函数可以帮助我们预测或估计其他未知观测值的
结果。
需要注意的是,最小二乘法拟合在某些情况下可能不适用,例如
数据存在严重偏离线性关系或存在异常值的情况。
此外,拟合结果的
准确性也取决于观测值的数量和质量。
总的来说,最小二乘法是一种广泛应用于数据拟合的方法,它可
以通过找到最小化残差平方和的参数值,提供一个最佳的拟合函数。
线性回归最小二乘法公式

线性回归最小二乘法公式一、线性回归的概念线性回归是回归分析的一种,用于描述在影响因素和结果之间存在着线性关系的研究领域。
在波士顿房屋数据中,我们可以用线性回归来研究一个房屋的价格(Dependent Variable)是如何被不同的房屋特征(Independent Variable),如房屋大小,房间数量,地段位置等影响的。
二、最小二乘法原理最小二乘法(Least Square Method,LSM)是一种进行数据拟合的最常用的优化方法。
它的核心思想是通过求取数据的总平方偏差最小的解来拟合数据,这里的平方偏差反映的是拟合数据和原始数据之间的差异,拟合数据和原始数据越相似,总偏差越小,就可以认为这种拟合越好。
最小二乘法的核心就是求得使总平方偏差最小的参数向量$\beta$,即解下式:$$ \min|Y-X\beta|^2$$其中$Y$是未知变量矩阵,$X$是已知变量矩阵,$\beta$是拟合参数。
根据最小二乘法的原理,下面继续推广为多元线性回归模型:$$ \min|Y-X\beta|^2$$等价于:$$\min\sum_{i=1}^n(y_i-\beta_0-\sum_{j=1}^px_{ij}\beta_j)^2 $$其中$y_i$是未知变量,$\beta_0$是常量,$x_{ij}$是已知变量,$\beta_j$是拟合参数。
最小二乘法的推广,从成本函数中分离出了不同的参数,也扩展到了多元线性回归中。
多元线性回归模型为:$$Y = \beta_0+\sum_{j=1}^px_{ij}\beta_j $$为求得上述通式中参数$\beta$的值,我们可以得到最小二乘法的解:$$\beta=(X^T X)^{-1} X^T Y$$从上述式中我们可以看出,最小二乘法为我们提供了一种数据拟合的优化方法,以达到模型最佳的预测效果。
最小二乘法公式推导过程

最小二乘法公式推导过程最小二乘法是一种最常用的数据拟合方法,主要用于回归分析和曲线拟合等数据处理领域中。
其核心思想是通过最小化残差平方和,找到一条最佳拟合直线(或曲线),使预测结果与实际观测值间的误差最小化。
最小二乘法的具体应用可以分为两个步骤。
第一步是建立模型,根据实际数据的分布情况建立数学模型。
常见的模型有线性回归模型、多项式回归模型、指数回归模型等等。
第二步则是通过最小化残差平方和来求解使模型拟合结果最优的参数。
下面我们就来具体了解一下最小二乘法的公式推导过程。
首先,我们先给出一个简单的线性回归模型:y = ax + b,其中x 为自变量,y为因变量,a和b是待求解的参数。
假设我们有n个数据点,其中第i个数据点的实际观测值为yi,预测值为a xi + b,那么第i个数据点的残差 ei=yi-a xi -b。
我们的目标是通过最小化所有数据点残差平方和来找到最佳拟合直线(或曲线)的参数。
即最小化S=∑(ei)²,其中i=1,2,…,n。
下面是最小二乘法的公式推导过程:(1)将S展开:S=(e1)²+(e2)²+...+(en)²=(y1-a x1-b)²+(y2-a x2-b)²+...+(yn-a xn-b)²=(y1²-2a x1 y1-2b y1+a² x1²+2a b x1+b²)+(y2²-2a x2 y2-2b y2+a² x2²+2a b x2+b²)+...+(yn²-2a xn yn-2b yn+a² xn²+2a bxn+b²)=(y1²+y2²+...+yn²)+(a² x1²+a² x2²+...+a² xn²)+(n b²)-2a(x1 y1+x2 y2+...+xn yn)-2b(y1+y2+...+yn)a+2(n a b x1+...+n a b xn)(2)将S对a、b分别求偏导:∂S/∂a=2(a x1²+a x2²+...+a xn²)-2(x1 y1+x2 y2+...+xn yn)-2(n a b x1+...+n a b xn)∂S/∂b=2(n b)-2(y1+y2+...+yn)+2(a x1+...+a xn)(3)令∂S/∂a=0,∂S/∂b=0,我们可以得到两个方程:a=(n∑xy-∑x∑y)/(n∑x²-(∑x)²)b=(∑y-a∑x)/n其中,∑表示sigma符号,∑xy为x和y的乘积之和,∑x²为x 的平方和,∑y²为y的平方和,∑x和∑y分别为x和y的和,n为数据点的数量。
最小二乘法求出直线拟合公式

最小二乘法求出直线拟合公式
最小二乘法是通过找到最小化观测数据与拟合直线之间的误差平方和
而确定直线的拟合公式。
以下是求出直线拟合公式的步骤:
1. 收集一组观测数据,包括自变量和因变量的取值。
自变量是用来解
释变化的变量,因变量是要预测或估计的变量。
2. 假设直线的表达式为 y = mx + b,其中 m 是斜率,b 是截距。
3. 对每个观测数据点 (x_i, y_i),计算其对应的预测值 y' = mx_i
+ b。
4. 计算每个观测数据点的误差 e_i = y_i - y',即观测值与预测值
之间的差异。
5. 计算误差的平方和S = Σ(e_i^2),即所有观测数据点误差的平方
的总和。
6. 使用最小二乘法的思想,目标是找到斜率 m 和截距 b 的值,使得
误差平方和 S 最小化。
7. 最小二乘法的公式根据矩阵运算求得,可以通过以下公式计算出斜
率和截距的估计值:
m = (Σ(x_i - x_mean)(y_i - y_mean)) / (Σ(x_i - x_mean)^2) b = y_mean - m * x_mean
其中,x_mean和y_mean分别为自变量和因变量的平均值。
8. 得出斜率和截距的估计值后,就可以得到直线的拟合公式 y = mx + b。
通过最小二乘法求得的直线拟合公式可以用于预测因变量值,或者对数据进行拟合和估计。
最小二乘法线性详细说明

利用最小二乘法计算出b, a得出回归方程即两个变 量之间的关系式。
计算 s ,并利用肖维涅准则判断有无粗差。
如果有粗差,剔除后重复①,②,③步骤计算。
如无粗差,计算b , a ,给出最后的回归方程。
26
〔例题〕
用伏安法测电阻,测量数据如表。问能否拟 合成线性关系曲线?若可以,试判断有无粗
只有相关系数 R≥ R时0 ,才能用线性回归方程
y=a+bx来描述数据的的分布规律。否则毫无 意义。
24
回归方程的精密度
根据统计理论还可以求出a和b的标准偏差分别 为:
b s
sx x
a b
xi2 n
xi2
s
nsxx
25
回归分析法的运算步骤
首先计算R,判断是否能拟合成线性曲线。 R≥ R0
b2 s11 s2 y s12 s1y
s s s 11 22
2 12
a y b1x1 b2 x 2
32
公式中:
s11
x2 1i
(
x1i)2 n
s22
x2 2i
(
x2i)2 n
s12
b=0,a= y , 从而得到y= y 的错误结论。这说明数据点
的分布不是线性,不能拟合为线性关系曲线。
