第七章作业答案
第七章 作业管理与接口习题及答案
第七章作业管理与接口习题及答案一、填空题1．作业是由① 、② 和③ 组成的。
【答案】①程序、②数据、③作业说明书【解析】从用户的角度看，作业是在一次应用业务处理过程中，从输入开始到输出结束，用户要求计算机所作的有关该次业务处理的全部工作。
从系统的角度看，作业是一个比程序更广泛的概念，它由程序、数据和作业说明书组成。
系统通过作业说明书控制文件形式的程序和数据，使之执行和操作。
2．批处理系统中，是以① 为单位把程序和数据调入② 以便执行。
【答案】①作业，②内存【解析】从系统的角度看，作业是批处理系统抢占内存的单位，而分时系统不存在作业的概念。
3．处理机调度算法中:“相应比高者优先”其相应比是采用公式：相应比＝确定的。
【答案】响应比=（等待时间+计算时间）/计算时间【解析】本算法的思想是对“计算时间”短的小作业优先处理；对“等待时间”长的作业，即使该作业“计算时间”不是很短，也可得到较高的响应比，获得运行的机会。
二、单项选择题1．在一个以批处理为主的系统中，为了保证系统的吞吐率，总是要力争缩短用户作业的。
（A）周转时间（B）运行时间（C）提交时间（D）完成时间【答案】（A）【解析】周转时间是衡量批处理系统的重要指标。
2．作业在系统中存在与否的唯一标志是。
（A）源程序（B）作业说明书（C）作业控制块（D）目的程序【答案】（C）【解析】系统是根据作业控制块 JCB来感知作业的存在的。
3．作业调度从处于① 状态的队列中选取适当的作业投入运行。
从作业提交给系统到作业完成的时间间隔叫做② 。
③ 是指作业从进入后备队列到被调度程序选中时的时间间隔。
（A）运行（B）提交（C）后备（D）完成（E）停止（F）周转时间（G）响应时间（H）运行时间（I）等待时间（J）触发时间【答案】①（C），②（F），③（I）4．在批处理系统中，周转时间是。
（A）作业运行时间（B）作业等待时间和运行时间之和（C）作业的相对等待时间（D）作业被调度进入内存到运行完毕的时间【答案】（B）【解析】周转时间是作业提交给系统到作业完成的时间间隔，因此其周转时间是作业等待时间和运行时间之和。
生物药物分析第七章作业答案
单选题1、下列不属于水溶性的维生素的是1/46A.维生素EB.维生素B12C.泛酸D.维生素C正确答案：A试题解析：水溶性维生素包括维生素B族和C族，维生素E属于脂溶性2、维生素是一类？2/46A.高分子有机化合物B.低分子有机化合物C.无机化合物D.微生物化合物正确答案：B试题解析：维生素是一类维持人体正常生理代谢功能所必需的低分子有机化合物3、下列维生素中参与转氨基作用的是3/46A.磷酸吡哆醛B.泛酸C.TPPD.烟酰胺正确答案：A试题解析：磷酸吡哆醛和磷酸吡哆酸是维生素Ｂ６在生物体内存在的主要形式，它们是氨基转移酶的辅酶，它们之间相互转变起着传递氨基的作用4、维生素E的多种异构体中哪个活性最高4/46A.α－生育酚B.β－生育酚C.γ－生育酚D.δ－生育酚正确答案：A试题解析：维生素Ｅ又名生育酚，包括８种化合物，即α－生育酚、β－生育酚、γ－生育酚、δ－生育酚和α－生育酚、β－生育酚、γ－生育酚、δ－三烯生育酚，α生育酚是自然界中分布最广泛、含量最丰富、活性最高的维生素Ｅ形式。
5、下列不是维生素E鉴别方法的是5/46A.硝酸反应B.三氯化铁反应C.三氯化锑反应D.紫外光谱法正确答案：C试题解析：三氯化锑反应用于鉴别维生素A6、在维生素E的三氯化铁鉴别反应中，与联吡啶生成红色配离子的是6/46A.NO3-B.Cl-C.Fe3+D.Fe2+正确答案：D试题解析：维生素Ｅ在碱性条件下，水解生成游离的生育酚，生育酚经乙醚提取后，可被FeCl3氧化成生育醌；同时被还原为Fe2+ ,Fe2+与联吡啶生成红色的配位离子。
7、维生素E的0.01%无水乙醇液，有最大吸收的波长处在7/46A.284nmB.254nmC.332nmD.620nm正确答案：A8、关于维生素C，不正确的是8/46A.不溶于水B.不溶于乙醚C.含有不饱和键D.无臭味酸正确答案：A试题解析：维生素C属于水溶性9、下列药物的碱性溶液，加入铁氰化钾后，再加正丁醇，显蓝色荧光的是9/46A.维生素AB.维生素CC.维生素B1D.维生素E正确答案：C试题解析：维生素B1鉴别-硫色素荧光反应10、能发生硫色素特征反应的药物是10/46A.维生素AB.维生素CC.维生素B1D.维生素E正确答案：C试题解析：硫色素反应是维生素B1的专属性鉴别反应11、2，6-二氯靛酚反应利用什么性质进行鉴定维生素C11/46A.糖的性质B.酸性C.还原性D.荧光反应正确答案：C试题解析：2，6-二氯靛酚为氧化剂，维生素C具有还原性12、测定维生素C注射液的含量时，在操作过程中要加入丙酮，这是为了12/46A.保持维生素C的稳定B.增加维生素C的溶解度C.加快反应速度D.消除抗氧剂的干扰正确答案：D试题解析：注射剂中常含有作为抗氧剂的亚硫酸氢钠，在滴定前应加入丙酮（或甲醛）使之与亚硫酸氢钠反应生成加成物而掩蔽起来，以消除干扰13、维生素C碘量法测定要排除亚硫酸的影响则在滴定前加入13/46A.丙酮B.酒石酸C.草酸D.丙醇正确答案：A试题解析：注射剂中常含有作为抗氧剂的亚硫酸氢钠，在滴定前应加入丙酮（或甲醛）使之与亚硫酸氢钠反应生成加成物而掩蔽起来，以消除干扰14、维生素C可在三氯醋酸或盐酸存在下，经水解、脱羧、失水等反应，转变成糠醛，再与吡咯在50℃反应生成什么颜色14/46A.蓝色B.无色C.红色D.黄色正确答案：A试题解析：维生素C利用糖的性质鉴别15、维生素C的含量测定主要基于其什么性质15/46A.糖的性质B.酸性C.还原性D.荧光反应正确答案：C试题解析：维生素C的含量测定基于其具有强的还原性，可被不同氧化剂定量氧化而进行。
第七章-统计指数作业试题及答案
第七章统计指数一、判断题1.分析复杂现象总体的数量变动，只能采用综合指数的方法。
（）2.在特定的权数条件下，综合指数与平均指数有变形关系。
（）3.算术平均数指数是通过数量指标个体指数，以基期的价值量指标为权数，进行加权平均得到的。
（）4.在简单现象总量指标的因素分析中，相对量分析一定要用同度量因素，绝对量分析可以不用同度量因素。
（）5.设p表示单位成本，q表示产量，则∑p1q1－∑p0q1表示由于产品单位成本的变动对总产量的影响。
（）6.设p表示价格，q表示销售量，则∑p0q1－∑p0q0表示由于商品价格的变动对商品总销售额的影响。
（）7.从指数化指标的性质来看，单位成本指数是数量指标指数。
（）8.如果各种商品价格平均上涨5%，销售量平均下降5%，则销售额指数不变。
（）1、×2、√3、√4、×5、×6、×7、×8、×。
二、单项选择题三、1.广义上的指数是指（）。
四、 A.价格变动的相对数 B.物量变动的相对数五、 C.社会经济现象数量变动的相对数 D.简单现象总体数量变动的相对数六、2.编制总指数的两种形式是（）。
七、 A.数量指标指数和质量指标指数 B.综合指数和平均数指数八、 C.算术平均数指数和调和平均数指数 D.定基指数和环比指数九、3.综合指数是（）。
十、 A.用非全面资料编制的指数 B.平均数指数的变形应用十一、 C.总指数的基本形式 D.编制总指数的唯一方法十二、 4.当数量指标的加权算术平均数指数采用特定权数时，计算结果与综合指数相同，其特定权数是（）。
十三、 A.q1p1 B.q0p1 C.q1p0 D.q0p0十四、 5.当质量指标的加权调和平均数指数采用特定权数时，计算结果与综合指数相同，其特定权数是（）。
十五、 A.q1p1 B.q0p1 C.q1p0 D.q0p0十六、 6.在由三个指数所组成的指数体系中，两个因素指数的同度量因素通常（）。
清华大学土力学课后答案-第七章课后习题
csoil csoil cos H cr sin cos tan soil (cos sin cos 2 tan soil )
20 , csoil 15kPa , soil 20 , 16kN / m3 , H cr .
刀客李广信土力学第七章习题作业
解：Fs
[ 'cos wi sin( )] tan 'sin wi cos( ) Fs 0.745
20 , 32 , ' 10kN / m3 , w 10kN / m3 , 0
(2)土柱与基岩上表面之间crock 10kPa , rock 15 H cr crock 7.37 m (cos sin cos 2 tan rock )
解：w
mw e 0.70 0.264， ms Gs 2.65
Gs (1 w)* w 2.65*1.264*10 19.70kN/m3 1 e 1 0.7 取1m宽土柱研究 W' 'V (19.70 10) *1* 4 38.8kN
[(3273.04
3062.78 ) sin 21.80 300.53] tan18 115 Fs 3062.78 (3273.04 ) cos 21.80 Fs
当 Fs 1, Fs 1.22说明安全系数 1. 解方程得到 : Fs 1.016
7 5 在天然重度为 =18kN/m3 , 25 , c 8kPa的土层中开挖基坑，基坑深度 H 10m,问极限角 多大？若以1: 0.5的坡度开挖，极限开挖深度多大？ 解答： (1) N c 8 0.0444 H 18*10
第7章部分作业答案
第七章 部分作业答案7.4.8 已知Y100L1-4型异步电动机的某些额定技术数据如下：2.2 kW 380V Y 接法 1420r/min 82.0cos =φ %81=η 试计算:（1）相电流和线电流的额定值及额定负载时的转矩;（2）额定转差率及额定负载时的转子电流频率。
设电源频率为50Hz 。
解：（1）A U P I I l N l P 5%8182.038032200cos 3=⨯⨯⨯===φηm N n P T N N N •=⨯=⨯=8.1414202.295509550 （2）%33.5%100150014201500%100=⨯-=⨯-=O N O N n n n S Hz f S f N 67.250%33.512=⨯==7.4.9 有台三相异步电动机，其额定转速为1470r/min ，电源频率为50Hz 。
在（a ）起动瞬间（b ）转子转速为同步转速32时（c ）转差率为0.02时三种情况下，试求：（1）定子旋转磁场对定子的转速；（2）定子旋转磁场对转子的转速；（3）转子旋转磁场对转子的转速；（4）转子旋转磁场对定子的转速；（5）转子旋转磁场对定子旋转磁场的转速。
解：（1）定子旋转磁场对定子的转速：在（a ）（b ）（c ）三种情况下均为1500 r/min 。
（2）定子旋转磁场对转子的转速：（a ）起动瞬间：1500 r/min ；（b ）转子转速为同步转速32时：500 r/min ； （c ）转差率为0.02时：30 r/min 。
（3）转子旋转磁场对转子的转速：（a ）起动瞬间：1500 r/min ；（b ）转子转速为同步转速32时：500 r/min ； （c ）转差率为0.02时：30 r/min 。
（4）转子旋转磁场对定子的转速：在（a ）（b ）（c ）三种情况下均为1500 r/min 。
（5）转子旋转磁场对定子旋转磁场的转速：在（a ）（b ）（c ）三种情况下均为0。
液压作业第7章作业答案
第7章作业答案一、选择题1．在采用节流阀的进油口节流调速回路中，当负载一定，节流阀开口减小，液压泵工作压力（ C )A．最大B．减， C．不变2．在采用节流阀的回油路节流调速回路中，当不考虑系统的泄漏损失和溢流阀的调压偏差，但负载增大是，试分析: 1)活塞的运动速度（ b ) 2）液压泵输出功率（ c ） 3）液压泵输入功率( c )；a．最大 b．减小 c．基本不变 d．可能最大也可能减小3．某铣床要在切削力变化范围较大的场合下顺铣和逆铣工作,在选择该铣床的调速回路时，你认为选择下列调速回路中的（ B ）种比较合适。
A．采用节流陶进油路节流调速回路B．采用节流阀回油路节流调速回路c．采用调速阀进油路节流调速回路D．采用调速阀回油路节流调速回路4．在动作顺序要改变的液压系统中宜用（ A ),A．用行程开关和电磁阀控制的顺序动作回路…、”B．用行程换向阀控制韵顺序动作回路‘C．用压力继电控制的顺序动作回路D．用行程孔控制的顺序动作回路5．为了使工作机构在任意位置可靠地停留,且在停留时其工作机构在受力的情况下不发生位移，通常采用( D ）。
A、卸荷回路B、调压回路C、平衡回路D、锁紧回路。
二．判断题正确的在括号内填Y 错的在括号内填 N20．系统要求有良好的低速稳定性，可采用容积节流调速回路 ( Y )2l、在旁路节流回路中，若发现溢流阀在系统工作时不溢流，说明溢流阀有故障。
（ N ）三读懂下列油路图,指出图中有哪一种或几种基本回路。
并简要说明工作原理.四、综合分析题1、读下列油路图，填写电磁铁动作顺序表第一题第二题注:所有电磁铁吸合为“+”，断开为“-”，吸合断开均可,也为“-”第一题1YA 2YA 3YA 4YA 5YA 快进中速进给慢速进给快退（2）当油缸运动到端点,负载无穷大，试分析在下列情况下，将A B C点3、如图所示：（2）系统的动作顺序为:A缸快速运动到位加紧——B缸快进——B缸1工进-—B缸2工进-—B缸快退-—A缸快速退回-—油泵卸荷。
自动控制原理作业第七章参考答案
7.1 求下列矩阵的若尔当型及其变换矩阵（1）010001341⎡⎤⎢⎥⎢⎥⎢⎥---⎣⎦解：矩阵的特征值为：1230.78,0.11 1.95,0.11 1.95i i λλλ=-=-+=--，因此可化为对角线规范型：0.780.11 1.950.11 1.95ii -⎡⎤⎢⎥-+⎢⎥⎢⎥--⎣⎦变换矩阵为：1232221231111110.780.11 1.950.11 1.950.61-3.8 - 0.42i -3.8 + 0.42i P i i λλλλλλ⎡⎤⎡⎤⎢⎥⎢⎥==--+--⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦（2）540430461⎡⎤⎢⎥--⎢⎥⎢⎥-⎣⎦解：矩阵的特征值为：1231λλλ===，()2rank I A -=，表明1λ=的几何重数为3-()rank I A -=1，即该特征值对应一个若尔当块。
所以该矩阵的若尔当型为：11111⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦，变换矩阵0410404040P ⎡⎤⎢⎥=-⎢⎥⎢⎥--⎣⎦（3）421043521⎡⎤⎢⎥⎢⎥⎢⎥-⎣⎦解：矩阵的特征值为：1232, 2.21, 6.79λλλ=-==，因此可化为对角线规范型：2 2.21 6.79-⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦，变换矩阵为00.40.610.410.370.780.810.350.46P ⎡⎤⎢⎥=-⎢⎥⎢⎥--⎣⎦（4）010001340⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦解：矩阵的特征值为：1232.3,1, 1.3λλλ==-=-，因此可化为对角线规范型：2.31 1.3⎡⎤⎢⎥-⎢⎥⎢⎥-⎣⎦，变换矩阵为30.1 2.130.25 2.7530.583.58P -⎡⎤⎢⎥=-⎢⎥⎢⎥-⎣⎦7.2已知系统状态方程，求状态变换阵P ，使系统变为对角线型（假设系统的特征值为123,,λλλ）（1）012010001x x a a a ⎡⎤⎢⎥=⎢⎥⎢⎥---⎣⎦解：123222123111P λλλλλλ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦（2）123100100a x a x a -⎡⎤⎢⎥=-⎢⎥⎢⎥-⎣⎦解：系统的特征方程为：32123det()00I A a a a λλλλ-=⇒+++= 设变换矩阵123[,,],i i i i P v v v v Av v λ==满足 设123[,,]Ti i i i v v v v =，则有：11212132313(1)(2)(3)i i i i i i i i i i i a v v v a v v v a v v λλλ-+=⎧⎪-+=⎨⎪-=⎩ 由（1）得211()(4)i i i v a v λ=+由（2）（4）得23121()(5)i i i i v a a v λλ=++ 代入（3）得321123()0i v a a a λλλ+++=所以1i v 是任意常数，取为1，则21i i v a λ=+，2312i i i v a a λλ=++所以112131222111221223132111P a a a a a a a a a λλλλλλλλλ⎡⎤⎢⎥=+++⎢⎥⎢⎥++++++⎣⎦7.3证明：对于具有互相不同特征值12,,,n λλλ 的矩阵1211000010000010000n n a a A a a --⎡⎤⎢⎥-⎢⎥⎢⎥=⎢⎥-⎢⎥⎢⎥-⎣⎦能将其变换为对角矩阵形式的变换矩阵为：11122111212121211111111n n n n n n n n n n n a a P a a a a a a a a λλλλλλλλλλ------⎡⎤⎢⎥++⎢⎥⎢⎥=++++⎢⎥⎢⎥⎢⎥++++++⎣⎦证明：系统的特征方程为：111det()00nn n n I A a a a λλλλ---=⇒++++=设变换矩阵12[,,,],n i i i i P v v v v Av v λ== 满足 设12[,,,]Ti i i in v v v v = ，则有：21111212213231211211111111()()()(1)0(2)i i i i i i i i i i i i i i i n n n i in i in in i i n i n i i in i in n i v a v a v v v a v v v v a a v a v v v v a a v a v v v a v λλλλλλλλλλ-----=+⎧-+=⎧⎪⎪-+==++⎪⎪⎪⎪⇒⎨⎨⎪⎪-+==+++⎪⎪-=⎪⎪+=⎩⎩将（1）代入（2）得11110n n i i n i n i a a a v λλλ--++++= 对比系统特征方程可知11i v =满足。
数字逻辑第七章作业答案
H’·L’·R’
1
IDLE
R R·H’ 1 H’
R1
H
R2
L2
H’(L’+R’) 1
L3 1 H+LR L L·H’·R’ IDLE 1 R3 1 H’(L’+R’) R R·H’·L’ H+LR
H’(L’+R’) 1 L1 H+LR 1 H+L·R H H+LR R1 1H’(L’+R’) LR3
R
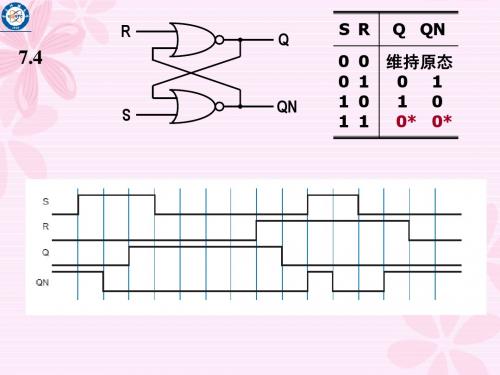
7.4
S
Q
S R 0 0 1 1 0 1 0 1
Q QN 维持原态 0 1 1 0 0* 0*
QN
R
Q
7.5
S QN
7.6 利用带有使能端的T触发器和组合逻辑构造D触发 器
D触发器：Q* = D （转移方程） T触发器的特征方程：Q*= EN·Q’ + EN’·Q=ENQ 所以，激励方程：EN = DQ
W’Y’
X’YZ
X’Z’
对A状态，不满足完备性，少了(X+YZ)’ 对B状态，不满足互斥性，多了W’Y’ 对C状态，满足二义性 对D状态，不满足互斥性，多了XY，并且不满足完备性， 少了(X+Y’)’
L2
7.24修改状态图
L3
H’ 1
H’ 1
H
L1
1 L L·H’·R’ H 1 H+L·R H H
H’·L’·R’
R2
Transition list
Q2Q1Q0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 S 转移表达式 S* Q2*Q1*Q0* 0 0 1 1 0 0 0 0 0 0 1 0 0 1 1 0 1 0 H’·L’·R’ IDLE L1 IDLE L·H’·R’ R·H’·L’ R1 H+L·R LR3 H’·(L’+R’) L2 L1 H+LR LR3
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
0
0
4
0.035
0.1 0.00825 4.033
0.03
1 0.01225 4.049
ε
0.025
10 0.019 4.076
0.02
100 0.0275 4.11
0.015
1000 0.03475 4.139
0.01
10000 0.04625 4.185
0.005
0
0
2000
4000
6000
8000
蠕变现象会影响受力材料的长期尺寸稳定性，应力松弛会使弹性材料的受力能 力随时间变差。而内耗现象则会使高速行驶的汽车轮胎发热而爆胎，但也可利用 内耗来制成吸音防震材料。
2.：画图 1）现有 A 聚苯乙烯与顺丁橡胶的共混物（20:80 重量比）；B 乳液聚合的丁苯橡胶（无规
共聚物，20:80 重量比）, C SBS（苯乙烯与丁二烯三嵌段共聚物，其中 B:S 为 80:20），和
t（分） 0.1
1
10
100
1000
1049
4.076
4.11
4.139
4.185
试作其蠕变曲线，如果 Boltzmann 原理有效，在 100 分钟时负荷加倍，问 10000 分时蠕变 伸长是多少？
答：计算 ε，做蠕变曲线 ε-t 曲线
0.05
0.045
t
ε
l
0.04
黏＝ 弹
弹 黏
d d弹 d黏
dt dt dt
由于， 弹 E弹
黏＝
d 黏 dt
则有
d 1 d dt E dt
上式便是Maxwell模型的运动方程式，即应力－应变方程。 2) τ=η/E=1012/1010=100(s) 3) 对于应力松弛，从 1）的运动方程，在 ε=0，初始应力为 σ0 的条件下积分得到：
D 高抗冲聚苯乙烯（HIPS）（顺丁橡胶粒子增韧聚苯乙烯，S:B 为 80:20）在同一张图中 画出三个样品的储能模量、力学损耗因子与温度的动态力学曲线。
1） E’
B
D
A,C
tgδ
2）在同一张图-1中10画-出55 A 聚氯乙烯、B10聚0 氯乙烯+20%DEP 和聚氯乙烯T+℃40%DEP 的动态
第 7 章 聚合物的粘弹性 1.举例说明聚合物的动态粘弹性和静态粘弹性的四个典型现象，为什么聚合物具有这些现
象?这些现象在材料应用时有哪些利弊?
在一定温度和压力的外界条件下，聚合物的静态粘弹性表现为蠕变和应力松弛， 动态粘弹性表现为滞后和力学损耗。 蠕变：在一定温度和恒定应力作用下，聚合物应变随时间增加而逐渐增大的现象。 如软质 PVC 丝钩着一定质量的砝码，就会慢慢地伸长；解下砝码后，丝会慢慢地 回缩。这就是软质 PVC 丝的蠕变和回复现象。坐久了的沙发；晾晒着的毛衣都是 蠕变的实例。 应力松弛：在一定温度和恒定应变条件下，试样内部的应力随时间增加而逐渐衰 减的现象。如拉伸一块未交联的橡胶至一定长度，并保持长度不变，随时间增加， 橡胶的回弹力逐渐减小到零。例如松紧带；密封件在受外力时，密封效果逐渐变 差（密封的重要问题） 滞后：在一定温度和交变应力作用下，聚合物应变会落后于应力的现象 内耗：交变应力作用下，由于滞后，则每一循环变化中就会产生能量损耗，以热能 形式散发，以热耗散的能量与最大储能模量之比 ψ=2πtg δ 来表征。 如高速行驶的汽车轮胎会发热。原因：聚合物是具有一定柔性的长链分子的聚集 体，在外力作用下，聚合物的链段会发生运动而改变构象，但由于链段运动的摩 擦力很大，而使形变具有时间依赖性。
0.04625 0.04600 0.09225
∴ 10000分钟时蠕变伸长为4×（1+0.09225）=4.369英寸
5. 将一块橡胶试片—端夹紧，另一端加上负荷，使之自由振动。已知振动周期为 0.60s， 振幅每一周期减少 5％、试计算：
(1) 橡胶试片在该频率(或振幅)下的对数减量(△)和损耗角正切(tgδ)；
10000
12000
根据Bolzmann叠加原理，总应变 t 0 t 1 t 100
t
ε(10000)=0.04625
因两次加的负荷一样，故可从蠕变曲线中查出 9900 分时，l=4.184 英寸 ε(9900)=0.04600
t 0 t 0 t 100
0 10000 0 9900
答: 原理：利用时－温等效转换原理；
方法：在短期内和不同温度下测其力学性能
数据处理：利用WLF方程求出移动因子 logT 并画出叠合曲线，则从叠合曲线上，便
可查找十年后任一时刻得力学性能。
4. 聚乙烯试样长 4 寸，宽 0.5 寸，厚 0.125 寸，加负荷 62.5 磅进行蠕变试验，得到数据如 下：
(t) 0et / =σ0×e-50/100=0.6065σ0
(2) 假定△＝0.02，问多少周期后试样的振动振幅将减少到起始值的—半？
（1（ （2（
Δ=ln（1/1-0.05）=0.0512 tgδ=Δ/π=0.0163 当 Δ=0.02 时，ln（A1/A2）=ln（A2/A3）.......=ln（An-1/An）
则 ln（A1/A2）+ln（A2/A3）.......+ln（An-1/An）= ln（A1/A n） 即 ln（2/1）=（n-1）Δ n=35.7 约 36 个周期后降到原振幅的一半。
6. 某聚合物的粘弹性行为可以用模量为 1010Pa 的弹簧与粘度为 1012Pa·s 的粘壶组合而
成的 maxwell 模型描述。推导此聚合物的运动方程（画出力学模型示意图）和松弛时间。
若将长、宽、厚为 10、1、0.25cm 样条拉长到 11cm，计算 50s 后维持此长度需要多大力？
答：
1)弹簧与黏壶串联模型即为下图的Maxwell模型。当一外力作用在模型上时，弹簧与黏壶所 受的应力相同，总形变为两者的加和，即
力学损耗与温度的关系曲线。
C
2）
tgδ
C
B
-50 0 50 100
T℃
3.什么是时温等效原理?该原理在预测聚合物材料的长期使用性能方面和在聚合物加工过程 中各有哪些指导意义？今有一种在 25℃恒温下使用的非晶态聚合物（Tg=-20℃） 现需要 评价这一材料在连续使用十年后的蠕变性能. 试设计一种实验, 可以在短期内(例如一个月 内)得到所需要的数据. 说明这种实验的原理、方法以及实验数据的大致处理步骤。