两种电源等效变换
第三章第五节两种电源模型的等效变换

五、电源等效变换及化简原则
1.注意点(3)
注意:
(1)IS与US的方向一致。
(2)等效变换对外电路等效,对电源内部不等效。
(3)恒压源和恒流源之间不能等效。
I
电流源
IIS
对外等效
IS
3.结论
四、举例
教学(学习)
反思
学习过程
备注
(教师复备栏及学生笔记)
课前复习:
戴维宁定理的内容。
新授:
一、电压源
1.电压源:为电路提供一定电压的电源。
2.恒压源:电源内阻为零,电源提供恒定不变的电压。
3.恒压源的特点
(1)它的电压恒定不变。
(2)通过它的电流可以是任意的,且决定于与它连接的外电路负载的大小。
4.符号
二、电流源
1.电流源:为电路提供一定电流的电源。
2.两个并联的电压源不能直接合并成一个电压源,但两个并联的电流源可以直接合并成一个电流源。
3.两个串联的电流源不能直接合并成一个电流源,但两个串联的电压源可以直接合并成一个电压源。
4.与恒压源并联的电流源或电阻均可去除;与恒流源串联的电压源或电阻均可去除。
练习:
习题(《电工基础》第2版周绍敏主编)
1.是否题(9)、(10)。
2.恒流源:电源内阻为无穷大,电源将提供恒定不变的电流。
3.恒流源的特点
(1)它提供的电流恒定不变,不随外电路而改变。
(2)电源端电压是任意的,且决定于外电路。
4.符号
三、电压源与电流源的等效变换
电源模型等效互换

《电工技术》知识点:电源模型等效互换由图(a ):由图(b ):IRLR 0+–UsU +–(a) 电压源模型等效变换条件:U S = I S R 0R LR 0U R 0U I SI +–(b) 电流源模型或电源的等效变换(外特性相同)U = U S -IR 0I =I S -U /R 0U = I S R 0–IR 0SS R U I②理想电压源与理想电流源之间无等效关系。
①电压源和电流源的等效关系只对外电路而言,对电源内部则是不等效的。
例:当R L = 时,电压源的内阻R 0中不损耗功率,而电流源的内阻R 0中则损耗功率。
③任何一个电压源U S 和某个电阻R 串联的电路,都可化为一个电流为I S 和这个电阻并联的电路。
注意事项电源的等效变换④等效变换时,两电源的参考方向要一一对应。
R 0+–U S a b I S R 0ab R 0–+U S a bI S R 0a b 注意事项电源的等效变换例:试用电压源与电流源等效变换的方法计算2 电阻中的电流。
6V 3 +–+–12V 2A6 112I(a)电源的等效变换解:6V 3 +–+–12V 2A 6 112I(a)2A3 122V +–I2A61(b)等效变换条件:U S = I S R 0或SS R U I电源的等效变换解:2A3 122V +–I2A61(b)等效变换条件:U S = I S R 0或SS R U I电源的等效变换4A22 22V +–I(c)由图(b)可得(c)A1A 22228I –8V +–22V +2 I(d)2由图(c)可得(d)4A22 22V +–I(c)解:电源的等效变换电源的等效变换。
项目12两种电源模型的等效变换和戴维南定理验证

03
掌握电源模型等效变换的方法和步骤。
实验目的和步骤
01 实验步骤
02
1. 搭建电压源电路,测量并记录相关电压和电流数据
。
03
2. 将电压源电路转换为等效的电流源电路。
实验目的和步骤
3. 搭建电流源电路,测量并记录相关 电压和电流数据。
4. 对比两种电源模型下的实验数据, 验证等效变换的正确性。
其中,电压源的电压等于该网络的开路电压,电阻等于该网络内部所有独 立源置零(电压源短路、电流源开路)后的等效电阻。
定理条件和适用范围
定理条件
线性含源一端口网络。
适用范围
适用于任何线性含源一端口网络,无论其内部结构和参数如何。
定理意义和应用价值
定理意义
简化了电路分析和计算过程,提供了一种求解复杂电路的有效方法。
在项目过程中,团队成员积极协作,充分发挥各自的专业优势,共同解决了实验过程中 遇到的技术难题,提高了团队整体的研究能力和水平。
存在问题与不足
在实验过程中,由于设备精度和 实验条件的限制,部分实验数据 的测量存在一定的误差,对实验 结果的准确性产生了一定影响。
对于某些特殊电路结构,戴维南 定理的适用性有待进一步研究和 探讨。目前的研究主要集中在简 单电பைடு நூலகம்和常规电路的分析上,对 于复杂电路和特殊电路的处理方 法还有待完善。
实验目的和步骤
1
3. 根据戴维南定理,计算等效电源的参数;
2
4. 将实验电路中的电源替换为等效电源,再次测 量并记录实验数据;
3
5. 分析实验数据,验证戴维南定理的正确性。
实验数据和结果分析
电源电压:10V
电源内阻:2Ω
实验数据和结果分析
两种电源的等效变换PPT课件

图 1-10 电压源
电压源的模型:如图中虚线框内部分。即用一个电阻和 理想电压源的串联组合来表示。
2020/10/13
4
② 电流源 为电路提供一定电流 的电源。
理想电流源(恒流源):电源内阻为 无穷大,并能提供一个恒定不变 的电流。
恒流源的两个特点:电流恒定不 变;电压可任意。
感谢阅读!为了方便学习和使用,本文档的内容可以在下载后随意修改,调整和打印。欢迎下载!
汇报人:XXXX 日期:20XX年XX月XX日
14
2、什么是恒流源?电流 源的模型结构?
3、两种电源模型的等效 变换的条件是什么?
2020/10/13
2
动画
IS
E r0
E rS
E r0 r0 rS
IS rS
2020/10/13
3
讨论问题1
1、电压源和电流源的概念与模型
① 电压源: 为电路提供一定 电压的电源。
理想电压源(恒压源):电源内阻 为零,并能提供一个恒定不 变的电压。
第5节 两种电源模型的等效变换
阅读内容
动画
讨论
练习
小结
作业
内容与要求: 1、建立电压源、电流源的概
念。 2、了解两种电源的等效变换。 本节的重点:
两种电源的概念。 本节的难点: 两种电源的等效变换
2020/10/13
1
阅读内容
• 请阅读教材第46~49页
• 思考问题:
1、什么是恒压源?电压 源的模型结构?
2020/10/13
9
作业
• 教材第52页习题:15、16
2020/10/13
10
两种电源模型的等效变换

电压源模型的等效变换
等效变换是指将一个电源模型转换为 另一个电源模型,使得两个模型在相 同的电路中产生相同的作用。
对于电压源模型,可以通过串并联电 阻的方式进行等效变换,使得电压源 在电路中的行为与另一个电源模型一 致。
电流源模型的等效变换
对于电流源模型,同样可以通过串并联电阻的方式进行等效 变换,使得电流源在电路中的行为与另一个电源模型一致。
造成损坏。
两种电源模型的优缺点比较
电压源模型优点
能够提供稳定的输出电 压,适用于需要恒压供
电的场合。
电压源模型缺点
在负载变化时,输出电 压可能会受到影响。
电流源模型优点
能够提供稳定的输出电 流,适用于需要恒流供
电的场合。
电流源模型缺点
在负载变化时,输出电 流可能会受到影响。
04
电源模型的选择与使用
注意电源模型在不同工作条件下 的适用性。
在使用多个电源模型时,应保持 模型一致性,避免出现矛盾和误
差。
电源模型的改进与优化建议
根据实际应用反馈对电源模型进行持 续改进和优化。
加强与行业内其他研究者的交流与合 作,共同推动电源模型的发展和创新。
引入先进的建模方法和算法,提高电 源模型的精度和适用性。
改进等效变换方法
目前的等效变换方法可能无法处理某些复杂的电路问题。 未来研究可以尝试改进等效变换方法,使其能够更好地适 应各种电路分析需求。
探索混合电源模型
在实际应用中,有些电源既不是完全线性的,也不是完全 非线性的。未来研究可以探索如何建立混合电源模型,以 及如何对其进行等效变换。
THANKS
感谢观看
而变化。这种模型考虑了电源内阻的影响,能更准确地描述实际电源的
电工基础两种电源模型的等效变换
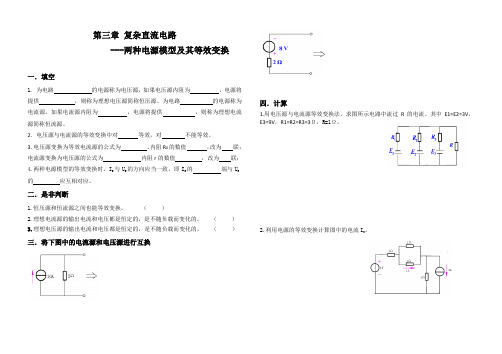
第三章复杂直流电路
---两种电源模型及其等效变换
一.填空
1.为电路的电源称为电压源,如果电压源内阻为,电源将提供,则称为理想电压源简称恒压源。
为电路的电源称为电流源,如果电流源内阻为,电源将提供,则称为理想电流源简称恒流源。
2.电压源与电流源的等效变换中对等效,对不能等效。
3.电压源变换为等效电流源的公式为,内阻R0的数值,改为联;电流源变换为电压源的公式为内阻r的数值,改为联;
4.两种电源模型的等效变换时,I
S 与U
S
的方向应当一致,即I
S
的端与U
S
的应互相对应。
二.是非判断
1.恒压源和恒流源之间也能等效变换。
()
2.理想电流源的输出电流和电压都是恒定的,是不随负载而变化的。
()
3.理想电压源的输出电流和电压都是恒定的,是不随负载而变化的。
()三.将下图中的电流源和电压源进行互换
四.计算
1.用电压源与电流源等效变换法,求图所示电路中流过R的电流。
其中E1=E2=3V,E3=9V,R1=R2=R3=3Ω,R=1Ω。
2.利用电源的等效变换计算图中的电流I
3。
3.试用电压源与电流源等效变换的方法计算图中2Ω电阻中的电流I。
两种电源模型的等效变换

本章小结
一、基夫尔霍定律 二、支路电流法 三、叠加定理 四、戴维宁定理 五、两种实际电源模型的等效变换
第21页/共27页
一、基夫尔霍定律
1.电流定律
电流定律的第一种表述:在任何时刻,电路中流入任一节 点中的电流之和,恒等于从该节点流出的电流之和,即
I流入= I流出 。
电流定律的第二种表述:在任何时刻,电路中任一节点上的 各支路电流代数和恒等于零,即
US1
US2
图 3-19 例题 3-7
第17页/共27页
解: (1)先将两个电压源等效变换成两个电流源,如图 3-20 所示:两个电流源的电流分别为:IS1 US1 /R1 4 A, IS2 US1 /R2 1 A
图 3-20 例题 3 - 7 的两个电压源等效成两个电流源
第18页/共27页
IS= IS1 + IS2
a
a
IS1
IS2
b
IS b
第13页/共27页
3、两个电流源并联,可以用一个 等效的电流源替代,替代的条件是
IS= IS1 + IS2 RS= RS1 // RS2
第14页/共27页
【例 1】如图 3-18 所示的电路,已知电源电动势US = 6 V, 内阻 R0 = 0.2 ,当接上 R = 5.8 负载时,分别用电压源模型和 电流源模型计算负载消耗的功率和内阻消耗的功率。
对于具有 b 条支路、n 个节点的电路,可列出 (n 1) 个独 立的电流方程和 b (n 1) 个独立的电压方程。
第24页/共27页
三、叠加定理
当线性电路中有几个电源共同作用时,各支路的电流(或电 压)等于各个电源分别单独作用时在该支路产生的电流(或电压) 的代数和(叠加) 。
3.3电源等效变换

3.3 两种电源模型的等效变换导学案电子专业考纲:理解电压源和电流源的概念,并掌握它们之间的等效变换。
一、电压源1、定义:为电路提供一定电压的电源。
如图(a )(a) (b)理想电压源:为电路提供恒定不变电压的电源。
如图(b)(教师帮助学生分析电压源和理想电压源为电路提供电压和电流的特点)二、电流源通常所说的电流源一般是指理想电流源,其基本特性是所发出的电流固定不变(I s )或是一定的时间函数i s (t ),但电流源的两端电压却与外电路有关。
实际电流源是含有一定内阻r S 的电流源。
三、两种实际电源模型之间的等效变换实际电源可用一个理想电压源E 和一个电阻r 0串联的电路模型表示,其输出电压U 与输出电流I 之间关系为U = E - r 0I实际电源也可用一个理想电流源I S 和一个电阻r S 并联的电路模型表示,其输出电压U 与输出电流I 之间关系为U = r S I S - r S I对外电路来说,实际电压源和实际电流源是相互等效的,等效变换条件是r 0 = r S , E = r S I S 或 I S = E /r 0四、电源之间的等效变换注意事项:① 。
② 。
③ 。
④ 。
⑤ 。
【课前练习】一、判断题1、对外电路来说,一个有源二端网络可以用一个电压源来等效替代。
( )2、如果网络具有两个引出端与外电路相连不管其内部结构如何这样的网络就叫做二端网络。
( )3、理想电压源只是从电路中抽象出来的一种理想元件,实际上并不存在。
( )二、选择题1、如图1所示电路中,电流I值为 ( )A.2A B.-2 A C.4A D.-4A2、如图2所示电路中,电阻R2减小时,电流I将( )A.增大 B.减小 C.不变 D.不能确定3、如图3所示电路中的电压U为()A.2.5V;B.5V;C.7.5V;D.10V图1 图2 图3三、填空题1、如图4所示电路中,电流I= A,电阻消耗功率为,电流源的功率为,电压源的功率为。
电源的电路模型及其等效变换知识

串联
uS= uSk ( 注意参考方向)
2. 电流源的串、并联
并联 电压相同的电压源 才能并联,且每个 电源中流过的电流 不确定。
并联: 可等效成一个理想电流源 i S( 注意参考方向).
n
is isk 1
串联: 电流相同的理想电流源才能串联,并且每个电
流源的端电压不能确定。
3. 电压源与其它元件的并联 u=us (对所有的电流i) 整个并联组合可等效为一个电压为us的电压源。
一.网孔电流 假想的沿网孔边界流动的电流。没有物
理意义,它的引入是为了简化计算。
i1 R1
+ uS1
–
a
i2
im1
R2 +
im2
uS2
–
b
i3
网孔电流分别为im1, im2
支路电流可由网孔电流表出,
R3
等于流经该支路的网孔电流的
代数和。
i1= im1 i2= im1- im2 i3= im2
二. 网孔电流法:以网孔电流为未知变量列写电路方 程分析电路的方法。利用KVL和VAR。
a
例
I1
I2
R1
R2
US1
US2
I3 b=3 , n=2 , l=3
R3
变量:I1 , I2 , I3
KCL KVL
a:
-
I1-
b I2+ I3= 0
一个独立方程
b: I1+I2- I3= 0
I1R1- I2R2=US1- US2
I2R2+ I3R3= US2 二个独立方程
I1R1+ I3R3= US1
4. 电流源与其它元件的串联 i=is (对所有的电压u) 整个串联组合可等效为一个电流为is的电流源。
电源的两种模型及其等效变换.

● 电流源
实际电流源的外特性——输出电压和电流均随RL而定。
理想电流源的外特性——其输出电流恒定不变,输出电压随
RL而定。
即: U= IS RL
电源的等效变换
● 电压源与电流源等效互换
I
I
+
+
+
US
-
U
RL
IS
I0 RS U
RL
R0 –
-
等效变换的条件
R0 = RS
IS = US / R0 或 US =IS RS
电源的2种模型及等效变换
电源的等效变换
电压源 电流源
电源的等效变换
电压源 电流源
电源的等效变换
● 电源的等效变换
电源是任何电路中都不可缺少的重要组成部分,实际电源 有电池、发电机、信号源等。
电压源和电流源是从实际电源抽象得到的电路模型。
电源的等效变换
● 电压源
电压源—为电路提供一定电压的电源。 输出电压: U= RLE / (R0+RL ) 输出电流由外电路RL 而定
I +
IS
I0 RS U
RL
-
实际电流源模型
● 电流源
电源的等效变换
理想电流源—如果电源内阻为无穷大,电源将对外电路提供 一个恒定不变的电流,叫做理想电流源,简称恒流源。
输出电流恒定, 即: I=IS
输出电压取决于外电路负载电阻的大小,即: U= IS RL
I
+
IS
U
RL
-
理想电流源模型
电源的等效变换
I
+
+
E -
U
RL
R0 –
2第五节 两种电源模型的等效变换

一、理想电源模型的连接
1.电压源的连接
(1)串联
n个电压源串联,可用一个等效电压源来替代,等效电压源的电压等于各串联电压源电压的代数和。即
(2)并联
n个电压源,只有在各电压源电压值相等,极性一致的情况下才允许并联,否则违背VL。其等效电路为其中的任一电压源。
2.电流源的连接
2.注意:
(1)转换前后US与Is的方向,Is应该从电压源的正极流出。
(2)进行电路计算时,恒压源串电阻和恒电流源并电阻两者之间均可等效变换,RS不一定是电源内阻。
(3)恒压源和恒流源不能等效互换。
(4)恒压源和恒流源并联,恒流源不起作用,对外电路提供的电压不变。 恒压源和恒流源串联,恒压源不起作用,对外电路提供的电流不变。
(1)串联
n个电流源,只有在各电流源电流值相等且方向一致的情况下才允许串联,否则违背KCL。其等效电路为其中的任一电流源。
(2)并联
n个电流源并联电路可等效为一个电流源,等效电流源的电流为各并联电流源电流的代数和,即:
二、实际电压源与电流源的转换
1.特性:电压源可以等效转换为一个理想的电流源IS和一个电阻RS的并联,电流源可以等效转换为一个理想电压源US和一个电阻RS的串联。即转换公式:US=RSIS
(5)与恒压源并联的电阻不影响恒压源的电压,电阻可除去,不影响其它电路的计算结果;与恒流源串联的电阻不影响恒流源的电流,电阻可除去,不影响其它电路的计算结果;但在计算功率时电阻的功率必须考虑。
(6)等效转换只适用于外电路,对内电路不等效。
例2-3:如图
下图电流源的转换
例2-4:如图
下图电压源的转换
例2-5:如图电压源、电流源的转换
《电工基础》课件——1.8电源等效变换

电源的等效转换
例题
如图3A所示,已知 US1=12V,R1=3Ω,US2=36V,R2=6Ω,R3=8Ω,求R3中的电流I3
依据电路图我们可以看到两 个电压源模型处于并联状态, 且电压、内电阻不相等,无 法进行等效合并,因此需要 把电压源模型转化成电流源 模型。
电源的等效转换
例题
US1转换后
2Ω
等效电路如图3-c所示
电源的等效转换
例题
此时电路变为R0与R3并联的分流电路, 流经R3的电流为
I3
R0 R0 R3
IS
2
2 8
(2)A
0.4A
电源的等效转换
① 电压控制电压源变换为电流源 等效条件 iS=μu1/Rs, GS=1/RS ② 电流控制电压源变换为电流源 等效条件为 iS=γi1/Rs GS=1/RS
R=R1+R2+R3 U=U1+U2+U3 I=U/R=U/(R1+R2+R3)
电源的等效转换
实际电压源和实际电流源存在一定的等效关系, 此等效是指实际电压源和实际电流源端口的的电 压、电流在转换过程中保持不变。
电源的等效转换
独立电压源的伏安特性为端电压U=US-UR=US-RsI 得到方程1 独立电流源的伏安特性为I=Is-Ir=Is-UGs 得到方程2 改变独立电流源伏安特性的样式,求得U=(Is-Ir)/Gs 得到方程3 当满足外部等效
电源的等效转换
③电压控制电流源变换为电压源 等效条件为 US=δU1/Gs RS=1/GS ④电流控制电流源变换为电压源 等效条件为 iS=γi1/Rs GS=1/RS
电源的等效转换 讨论答疑
叠加定理是否仅适 用于直流电路而不 适用于交流电路的 分析和计算?
实际电源的两种模型及其等效变换

2 b
- 3V + 4
e
U 3
4
1.2V
ab
(4 2 4)
a
+
4 Uab -
2 b
思考:如图,求ab间的最简等效电路
12
12
12 + 10V 2A
a 5
b
12 + 10V2A
a 5
b
a
2A
5
b
9、有关受控源
受控电压源、电阻的串联组合和受控电流源、电导 的并联组合也可以用上述方法进行变换。 此时应把受控电源当作独立电源处理,但应注意在 变换过程中保存控制量所在支路,而不要把它消掉。
电流源模型端口短路时, 并联电导Gs中无电流。
i º
i
iS IiS Gs
iS Gs IiS
º
(3) 理想电压源与理想电流源不能相互转换。
4. 多个电压源模型串联
+ us1 - - us2 +
+ usn -
+ us -
R1
R2
Rn
R
us usi
R Ri
5. 多个电流源模型并联 一个节点
is1 G1
例8.
a+ i
uR
i
b-
(a)
ai
+
R
u
-Leabharlann iRb-+
(b)
对(a), 端口VCR为:u=R(i-i)=(1- )Ri 对(b), 端口VCR为:u=Ri-iR=(1- )Ri 对(a) 、(b), 其端口VCR相同, 故(a) 、(b)对外电路等效 注:受控源和独立源一样可以进行两种模型的等效变换。
§1-9 电源的等效变换

u
B
⇒
3A
5Ω
u
B
⇒
5Ω
+ 15V 15 -
u
- B
X
几点说明
(1) 两种电源模型对于原电路可以等效替代,对外 两种电源模型对于原电路可以等效替代, 负载提供相同的功率,但电源内部不等效。 负载提供相同的功率,但电源内部不等效。 在上例的AB端口接上一负载电阻 在上例的 端口接上一负载电阻 RL = 4Ω A 通过运算可知: 通过运算可知: + 电 R = 4Ω u 对于原电路, 对于原电路,电压源模型和电 − 源 的吸收功率均为: 流模型计算 RL 的吸收功率均为: B 2 2 100 15 5 PL = W ×4 = 3 ×4 = 9 5+ 4 4+5 电压源 电流源
X
所示电路,求电流i和受控电压源发出的 功率。
1Ω Ω
i
3Ω Ω
6V
+ u −
2Ω Ω
0.5u
解答
2 u= 6 = 4V 1+ 2
4 6 = 3i + 0.5u = 3i + 0.5 × 4 = 3i + 2 ⇒ i = A 3
• 受控源发出的功率 P = −0.5ui = − 8 W
3
工程应用——散热风扇的速度控制 散热风扇的速度控制 工程应用
3 Ω 7
1 V 7
(c)
i
+
u
-
(d)
X
等效电路的另一个例子
例:试解释如下电路的等效原理。
例题4 求图( 所示单口网络的等效电阻。 例题 求图(a)所示单口网络的等效电阻。
先将电路等效变换为如图 解: 所示,由图可得: (b)所示,由图可得:
简述电压源与电流源的等效变换方法

电压源与电流源是电路中常见的两种基本元件,它们分别以恒定的电压和恒定的电流来驱动电路。
在电路分析和设计中,经常需要将电压源转换为等效的电流源,或将电流源转换为等效的电压源,以便更方便地进行电路分析和计算。
下面将分别介绍电压源与电流源的等效变换方法。
一、将电压源转换为等效的电流源1. 理论基础电压源的等效电流源转换是基于欧姆定律进行的。
根据欧姆定律,电流等于电压除以电阻,即I=V/R。
我们可以将电压源转换为等效的电流源,通过在电压源的正负端并联一个等效电阻,使得该电阻上的电流等于电压源的电压除以电阻值。
2. 转换公式电压源转换为等效电流源的公式为:I=V/R,其中I为等效电流源的输出电流,V为电压源的电压,R为等效电流源的电阻。
3. 举例说明假设有一个5V的电压源,需要将其转换为等效的电流源。
如果我们希望等效电流源的输出电流为1A,那么根据公式I=V/R,可得等效电阻R=V/I=5Ω。
我们可以在电压源的正负端并联一个5Ω的电阻,即可将电压源转换为等效的电流源。
二、将电流源转换为等效的电压源1. 理论基础电流源的等效电压源转换同样是基于欧姆定律进行的。
根据欧姆定律,电压等于电流乘以电阻,即V=IR。
我们可以将电流源转换为等效的电压源,通过在电流源的两端串联一个等效电压源,使得该电压等于电流源的电流乘以电阻值。
2. 转换公式电流源转换为等效电压源的公式为:V=IR,其中V为等效电压源的输出电压,I为电流源的电流,R为等效电压源的电阻。
3. 举例说明假设有一个2A的电流源,需要将其转换为等效的电压源。
如果我们希望等效电压源的输出电压为10V,那么根据公式V=IR,可得等效电阻R=V/I=5Ω。
我们可以在电流源的两端串联一个10V的电压源,并在其正负端串联一个5Ω的电阻,即可将电流源转换为等效的电压源。
电压源与电流源的等效变换方法可以在电路分析和设计中起到重要的作用。
通过合理应用这些方法,可以使得电路分析更加简便和直观,为电路设计提供重要的参考依据。
电工技术:实际电压源与实际电流源的等效变换

学习要点
(1)两种实际电源模型等效变换的方法及其在电路分析中的应用 (2)受控源等效变换的方法及其在电路分析中的应用
一、实际电源模型的等效变换
I
实际电源
I RS
+ _
U IS US RS RS
I
R
U
US
I S=US /RS
US=RSI S
R
U
实际电压源模型
U I =US /RS I =0 U =0
R=0 R→∞
IR =S II SS U= =0 IU =0
实际电流源模型
一、实际电源模型的等效变换
注意: (1)理想电压源内阻为0,理想电流源内阻为∞,它们之间不能进行等效 变换;
(2)等效变换只是对外电路等效,而电源的内部是不等效的,以负载开路
为例,电压源模型的内阻消耗功率为0,而电流源模型的内阻消耗功率为
IS2RS;
(3)电路中需要分析计算的支路不能变换,否则变换后的结果就不是原来
所要计算的值。
一、实际电源模型的等效变换
例:电路如图中所示,利 解:
2A 2Ω + 6A 6V 2Ω 2Ω
用电源的等效变换计算 I
的大小。
2A 2Ω + 6A 6V 2Ω 2Ω
I
7Ω
I
7Ω 3A 2Ω 6A
2A 2Ω 2Ω
的大小。
2A 2Ω + 6A 6V 2Ω 2Ω
I
7Ω
I
7Ω
2Ω + 4V + 9V 1Ω
I
7Ω
一、实际电源模型的等效变换
例:电路如图中所示,利 解:
用电源的等效变换计算 I
(完整版)第五节两种电源的等效变换习题

第五节 两种电源的等效变换
1、为电路 的电源称为电压源,如果电压源内阻为__________;电源将提供_______________,则称为理想电压源,简称恒压源;为电路 的电源称为电流源,如果电流源内阻为____ _____ ,电源将提供________________则称为理想电流源,简称恒流源。
2、将下图中的电流源和电压源进行互换
4、将下图中的有源二端网络等效变换为一个电压源
二、判断
( )1、理想的电压源和理想的电流源可以等效变换。
( )2、一个有源二端网络可以用一个等效电压源来代替。
三、选择题
1、如图9所示,两个电源的功率是 。
A 、PE=4W (消耗) , PI=4W (产生)
B 、PE=4W (产生) , PI=4W (消耗)
C 、PE=4W (消耗) , PI=8W (产生)
D 、PE=4W (产生) , PI=8W (消耗) 2、如图10,正确的答案是
A 、恒流源Is1消耗的功率为30W
B 、恒流源Is1输出的功率为30W
C 、恒流源Is2消耗的功率为5W
D 、恒流源Is2输出的功率为5W
3A
2A +
_
5A +
_
2+
_。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例2:将图(a)中的电流源转化为等效电压 源,并画出其等效电路。
解:
V S I S R S 10 m A 1 . 0 =10 V
内阻相等。 所以等效电路如图(b)
例3:用电源模型等效变换的方法 求图(a)电路的电流I1和I2。 解:将原电路变换为图(c)电路,由此 可得:
5 I 1 I 2 I 2 1 3 1 1A 2 2 A 10 5
(4)只要一个电动势为E的理想电压源和某个 电阻R串联的电路,都可以化为一个电流为 IS 的理想电流源和这个电阻并联的电路。
例1:将图1中的电压源转化为等效电流源, 并画出等效电路。
图1 解:
IS VS RS 100 V 47 2 . 13 A
图2
内阻相等。 所以图2所示即为等效电路。
电压源与电流源的等效变换
南阳市宛西中专
恒压源与恒流源特性比较
且两种电源模型的内阻相等。
等效变换的注意事项: (1) “等效”是指“对外”等效(等效互 换前后对外伏--安特性一致),对内不等 效。
(RO不消耗
能量)
对内不等效
(RO消耗能量)
(2)恒压源和恒流源不能等效互换。
(3)电源等效互换时,恒压源 E 与电源内阻 R0的串联,恒流源 IS 与电源内阻 R0 的并 联,且转换前后 E 与 Is 的方向保持不变。
ห้องสมุดไป่ตู้I2
5 10 5
3 1A
I 1 I 2 2 1 2 1A
