编译原理第4章作业答案

合集下载

编译原理-第4章语法分析--习题答案

第4章语法分析习题答案1．判断（1）由于递归下降分析法比较简单，因此它要求文法不必是LL(1)文法。

(× )LL(1)文法。

(× )（3）任何LL(1)文法都是无二义性的。

(√)（4）存在一种算法，能判定任何上下文无关文法是否是LL(1) 文法。

(√)(× )（6）每一个SLR(1)文法都是LR(1)文法。

(√)（7）任何一个LR(1)文法，反之亦然。

(× )（8）由于LALR是在LR(1)基础上的改进方法，所以LALR(× )（9）所有LR分析器的总控程序都是一样的，只是分析表各有不同。

(√)（10）算符优先分析法很难完全避免将错误的句子得到正确的归约。

(√)2．文法G[E]：E→E+T|TT→T*F|FF→(E)|i试给出句型(E+F)*i的短语、简单短语、句柄和最左素短语。

答案：画出语法树，得到：短语: (E+F)*i ，(E+F) ，E+F ，F ，i简单短语: F ，i句柄: F最左素短语: E+F3．文法G[S]：S→SdT | TT→T<G | GG→(S) | a试给出句型(SdG)<a的短语、简单短语、句柄和最左素短语。

答案：画出语法树，得到：短语：(SdG)<a 、（SdG）、SdG 、G 、a简单(直接)短语：G 、a句柄：G最左素短语：SdG4．对文法G[S]提取公共左因子进行改写，判断改写后的文法是否为LL(1)文法。

S→if E then S else SS→if E then SS→otherE→b答案：提取公共左因子；文法改写为：S→if E then S S'|otherS'→else S|E→bLL(1)文法判定：① 文法无左递归② First(S)={if,other}, First(S')={else, }First(E)={b}Follow(S)= Follow(S')={else,#}Follow(E)={then}First(if E then S S')∩First(other)=First(else S)∩First( )=③First(S')∩Follow(S')={else}不为空集故此文法不是LL(1)文法。

编译原理第4章答案

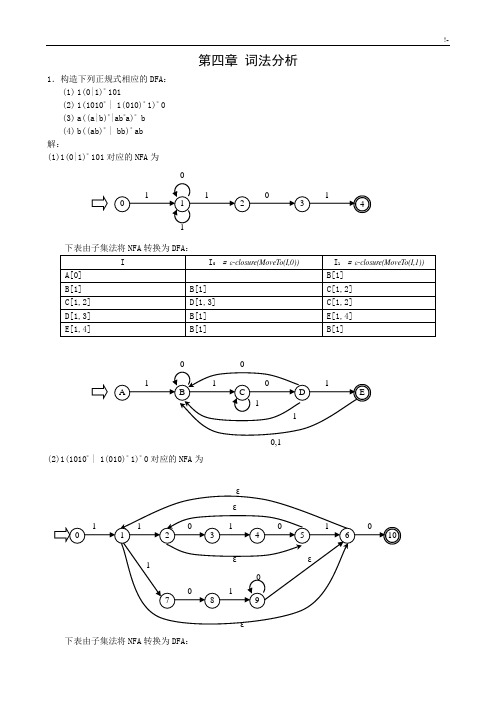
第四章词法分析1．构造下列正规式相应的DFA：(1)1(0|1) * 101(2)1(1010* | 1(010) * 1)* 0(3)a((a|b) * |ab * a)* b(4)b((ab)* | bb) * ab解：(1)1(0|1) * 101 对应的 NFA为1101012341下表由子集法将NFA 转换为 DFA：I I0=ε-closure(MoveTo(I,0))I1=ε-closure(MoveTo(I,1))A[0]B[1]B[1]B[1]C[1,2]C[1,2]D[1,3]C[1,2]D[1,3]B[1]E[1,4]E[1,4]B[1]B[1]001101A B C D E110,1(2)1(1010 * | 1(010) * 1)* 0 对应的 NFA 为εε1101010 01234561εε101978ε下表由子集法将NFA 转换为 DFA：I I=ε-closure(MoveTo(I,0))I1= ε-closure(MoveTo(I,1))A[0]B[1,6]B[1,6]C[10]D[2,5,7]C[10]D[2,5,7]E[3,8]B[1,6]E[3,8]F[1,4,6,9] F[1,4,6,9]G[1,2,5,6,9,10]D[2,5,7]G[1,2,5,6,9,10]H[1,3,6,9,10]I[1,2,5,6,7] H[1,3,6,9,10]J[1,6,9,10]K[2,4,5,7] I[1,2,5,6,7]L[3,8,10]I[1,2,5,6,7] J[1,6,9,10]J[1,6,9,10]D[2,5,7]K[2,4,5,7]M[2,3,5,8]B[1,6]L[3,8,10]F[1,4,6,9] M[2,3,5,8]N[3]F[1,4,6,9] N[3]O[4]O[4]P[2,5]P[2,5]N[3]B[1,6]1L111111010B I KA D E F M00110 00C11G H J101NP O(3)a((a|b) * |ab * a)* b(略 )(4)b((ab) * | bb) * ab(略 )2．已知 NFA=（ {x,y,z},{0,1},M,{x},{z} ）其中：M(x,0)={z},M(y,0)={x,y},M(z,0)={x,z},M(x,1)={x}, M(y,1)=φ ,M(z,1)={y},构造相应的 DFA。

编译基础学习知识原理第4章规范标准答案

第四章词法分析1．构造下列正规式相应的DFA ：(1) 1(0|1)*101(2) 1(1010* | 1(010)* 1)*(3) a((a|b)*|ab *a)*b(4) b((ab)* | bb)*ab 解：(1)1(0|1)*101对应的NFA 为下表由子集法将NFA 转换为DFA ：(2)1(1010* | 1(010)* 1)*0对应的NFA 为下表由子集法将NFA 转换为DFA ：(3)a((a|b)*|ab*a)* b (略)(4)b((ab)* | bb)* ab (略)2．已知NFA=（{x,y,z},{0,1},M,{x},{z}）其中：M(x,0)={z},M(y,0)={x,y},M(z,0)={x,z},M(x,1)={x}, M(y,1)=φ,M(z,1)={y},构造相应的DFA。

解：根据题意有NFA图如下0，1 下表由子集法将NFA转换为DFA：下面将该DFA最小化：(1)首先将它的状态集分成两个子集：P1={A,D,E},P2={B,C,F}(2)区分P2:由于F(F,1)=F(C,1)=E,F(F,0)=F并且F(C,0)=C,所以F，C等价。

由于F(B,0)=F(C,0)=C,F(B,1)=D,F(C,1)=E,而D，E不等价（见下步），从而B与C，F可以区分。

有P21={C,F},P22={B}。

(3)区分P1:由于A，E输入0到终态，而D输入0不到终态，所以D与A，E可以区分，有P11={A,E},P12={D}。

(4)由于F(A,0)=B,F(E,0)=F,而B，F不等价，所以A，E可以区分。

(5)综上所述，DFA可以区分为P={{A}，{B}，{D}，{E}，{C，F}}。

所以最小化的DFA如下：3.将图4.16确定化：图4.16解：下表由子集法将NFA转换为DFA：14.把图4.17的(a)和(b)分别确定化和最小化：(a) (b)解： (a):可得图（a1），由于F(A,b)=F(B,b)=C,并且F(A,a)=F(B,a)=B,所以A,B 等价，可将DFA 最小化，即：删除B ，将原来引向B 的引线引向与其等价的状态A ，有图(a2)。

编译原理第4章习题答案

S-> S’ S’->(S)SS’| First( (S)SS’) = { （ } Follow(S)=Follow(S’)= { (, ),$ }
预测分析表
非终结符 S （ S->S’ ） S->S’ $ S->S’
S’
S’->(S)SS’
S’->
S’->
S’->
冲突
仔细分析后，发现该文法 S->S(S)S| 是二义性文法。二义性文法不可能是LL(1)文法。例如：( ) ( )
S->aS’ S’->aS’AS’|Ɛ A->+|*
First(S) = First(aS’)={a} First(S’)= First(aS’AS’) ∪ First(Ɛ)= {a} ∪{Ɛ}= {a, Ɛ} First(A) = { +,*}
Follow(S) ={$} 因为 S->aS’，所以把Follow(S)加入到Follow(S’)中。因为 S’->aS’AS’的第一个S’ ，所以把First(AS’)={+,*}加入到Follow(S’)中。因为 S’->aS’AS’的第二个S’ ，所以Follow(S)加入到Follow(S’)中。所以，Follow(S’)= {$, +,*} 对 S’->aS’AS’的A ，当A后面的S’推导出非空时，把First(S’)-{Ɛ}={a}加入到Follow(A)中。对 S’->aS’AS’的A ，当A后面的S’推导出空时，把Follow(S’)={$,+,*}加入到Follow(A)中。所以，Follow(A)= {a, +,*,$} 对于S’->aS’AS’|Ɛ，因为First(aS’AS’) ∩Follow(S’)={a} ∩{$,+,*}=空集,所以没有冲突。对于A->+|*，因为First(+) ∩First(*)={+} ∩{*}=空集,所以没有冲突。所以该文法是LL(1)文法。

编译原理第四章参考答案

编译原理第四章参考答案1.1考虑下⾯⽂法G1S->a|^|(T)T->T,S|S消去G1的左递归。

然后对每个⾮终结符，写出不带回溯的递归⼦程序。

答:：(1)消除左递归:S->a|^|(T)T-> ST’T’->,S T’|ε(2)first(S)={ a , ^ , ( } first(T)= { a , ^ , ( } first(T’)={ , ε}First(a)={a},First(^)={^},First( (T) )={ ( }S的所有候选的⾸符集不相交First(,ST’)={,} ,First(ε)={ε},T’的所有候选的⾸符集不相交Follow(T’)=Follow(T)={ )}first(T’)∩Follow(T’)={}所以改造后的⽂法为LL(1)⽂法。

不带回溯的递归⼦程序如下：S( ){if (lookahead=’a’) advance;Else if(lookahead=’^’) advance;Else if(lookahead=’(’){advance;T();if(lookahead=’)’) advance;else error();}Else error();}T( ){S( );T’( ):}T’->,S T’|εT’( ){if (lookahead=’,’){advance;T’();}Else if(lookahead=Follow(T’)) advance;Else error;}有⽂法G(S):S→S+aF|aF|+aFF→*aF|*a(1)改写⽂法为等价⽂法G[S’]，消除⽂法的左递归和回溯(2)构造G[S’]相应的FIRST和FOLLOW集合；(3)构造G[S’]的预测分析表，以此说明它是否为LL(1)⽂法。

(4)如果是LL(1)⽂法，请给出句⼦a*a+a*a*a的预测分析过程该⽂法为LL(1)⽂法，因为它的预测分析表中⽆冲突项。

编译原理龙书第四章答案

编译原理龙书第四章答案编译原理是计算机科学中的一门基础课程，是用于教授计算机程序的设计、构建和优化的学科，常常被用于编写编译器和解释器。

在编译原理课程中，龙书（Compilers: Principles, Techniques, and Tools）是一本经典的教材，其中第四章主要讲述了词法分析器的设计和实现。

以下是第四章的答案，按照列表划分：1. 什么是词法分析器？词法分析器（Lexical Analyzer）是编译器的组成部分之一，它用于将程序中的字符序列转换为一系列单词或词法单元（Lexeme），以便后续的语法分析和语义分析使用。

2. 词法分析器的工作流程是什么？词法分析器的工作流程如下：（1）读入字符序列。

（2）将字符序列划分为一个个词法单元，或者检查字符序列是否合法。

（3）生成一个词法单元序列，并将其传递给语法分析器。

3. 词法单元的定义是什么？词法单元是编程语言中的一个基本单元，它是对代码中的一个单一概念进行编码的基本方式。

例如，在C语言中，词法单元包括关键字（如int，if，while等）、标识符（Identifier，即自定义变量名）、运算符和特殊符号等。

4. 有哪些方法可以实现词法分析器？可以使用正则表达式、自动机等方法实现词法分析器。

其中，正则表达式可以表示字符串的集合，因此可以将其用于识别单词类别；自动机是根据输入字符序列转换状态的一种计算模型，因此可以用于实现有限自动机（Deterministic Finite Automaton）和非确定有限自动机（Nondeterministic Finite Automaton）等。

5. DFA和NFA分别是什么？DFA和NFA都是有限自动机的一种，但在转换动作上有所不同。

DFA 是确定的有限自动机，即在状态转换时只有唯一的一个选择；而NFA 是非确定的有限自动机，即在状态转换时可以有多个选择。

6. DFA和NFA之间有什么关系？DFA和NFA虽然在转换动作上不同，但它们可以互相转化。

编译原理第4章答案

第四章词法分析1．构造下列正规式相应的DFA ：(1) 1(0|1)*101(2) 1(1010*| 1(010)*1)*0 (3) a((a|b)*|ab *a)*b (4) b((ab)*| bb)*ab 解：(1)1(0|1)*101对应的NFA 为下表由子集法将NFA 转换为DFA ：(2)1(1010*| 1(010)*1)*0对应的NFA 为 10,1下表由子集法将NFA转换为DFA：(3)a((a|b)*|ab *a)*b (略) (4)b((ab)*| bb)*ab (略)2．已知NFA=（{x,y,z},{0,1},M,{x},{z}）其中：M(x,0)={z},M(y,0)={x,y},M(z,0)={x,z},M(x,1)={x}, M(y,1)=φ,M(z,1)={y},构造相应的DFA 。

解：根据题意有NFA 图如下下表由子集法将NFA 转换为DFA ：0，1下面将该DFA最小化：(1)首先将它的状态集分成两个子集：P1={A,D,E},P2={B,C,F}(2)区分P2:由于F(F,1)=F(C,1)=E,F(F,0)=F并且F(C,0)=C,所以F，C等价。

由于F(B,0)=F(C,0)=C,F(B,1)=D,F(C,1)=E,而D，E不等价（见下步），从而B与C，F可以区分。

有P21={C,F},P22={B}。

(3)区分P1:由于A，E输入0到终态，而D输入0不到终态，所以D与A，E可以区分，有P11={A,E},P12={D}。

(4)由于F(A,0)=B,F(E,0)=F,而B，F不等价，所以A，E可以区分。

(5)综上所述，DFA可以区分为P={{A}，{B}，{D}，{E}，{C，F}}。

所以最小化的DFA如下：3.将图确定化：1101111解：下表由子集法将NFA 转换为DFA ：4.把图的(a)和(b)分别确定化和最小化：(a) (b)解： (a):下表由子集法将NFA 转换为DFA ：0，1a可得图（a1），由于F(A,b)=F(B,b)=C,并且F(A,a)=F(B,a)=B,所以A,B 等价，可将DFA 最小化，即：删除B ，将原来引向B 的引线引向与其等价的状态A ，有图(a2)。

编译原理第四章作业答案

非终结符
FIRSTVT
LASTVT
E
+ * ↑( i
+ * ↑) i
T
* ↑( i
* ↑) i
F
↑( i
↑)i
P
（i
)i
2).关系 1.由#E#，知 # = # ；由（E）知（ = ） 2.求 < 关系考察对象：文法中终结符号在前，非终结符号在后的相邻符号对由#E # < FIRSTVT(E) 由+T + < FIRSTVT(T) 由*F * < FIRSTVT(F) 由↑F ↑< FIRSTVT(F) 由(E ( < FIRSTVT(E)
T→F
F→-P
F→P
P→(E)
P→i
(1) 构造 G 的算符优先矩阵；
(2) 指出 G 不是算符优先文法，即指出具有多重定义的优先矩阵元素；
(3)将 G 改写为算符优先文法。
解：
（1）求每个非终结符号的 FIRSTVT 集和 LASTVT 集
S→E
E→E-T|T
T→T*F|F
F→-P|P
P→(E)|i
Z 11 Z 12 Z 13
(S
A
B ) = (φ (S ) + () [S ] + [])Z 21
Z 22
Z
23
Z 31 Z 32 Z 33
Z 11 Z 12 Z 13 ε φ φ A B φ Z 11 Z 12 Z 13
Z 21
Z 22
Z
23
=
φ
ε
φ
+
ε
φ
φ
Z
21
Z 22

编译原理第4章习题解答

第4章习题解答：1，2，3，4 解答略！5. 解答：(1)× (2)√ (3)× (4)√ (5)√ (6)√(7)×(8)×6. 解答：(1)A：④ B：③ C：③ D：④ E：②(2)A：④ B：④ C：③ D：③ E：②7.解答：(1) 消除给定文法中的左递归，并提取公因子：bexpr→bterm {or bterm }bterm→bfactor {and bfactor}bfactor→not bfactor | (bexpr) | true |false(2) 用类C语言写出其递归分析程序:void bexpr();{bterm();WHILE(lookahead =='or') { match ('or');bterm();}}void bterm();{bfactor();WHILE(lookahead =='and'){ match ('and');bfactor();}} void bfactor();{if (llokahead=='not') then {match ('not');bfactor();}else if(lookahead=='(') then {match (‘(');bexpr();match(')');}else if(lookahead =='true')then match ('true) else if (lookahead=='false')then match ('false');else error;}8. 解答：消除所给文法的左递归，得G'：S →(L)|aL → SL'L'→ ,SL' |实现预测分析器的不含递归调用的一种有效方法是使用一张分析表和一个栈进行联合控制，下面构造预测分析表：根据文法G'有：First(S) = { ( , a ) Follow(S) = { ) , , , #}First(L) = { ( , a ) Follow(L) = { ) }First(L') = { ,} Follow(L') = { ) }按以上结果，构造预测分析表M如下：文法G'是LL(1)的，因为它的LL(1)分析表不含多重定义入口。

编译原理(第三版)第4章课后练习及参考答案中石大版第4章课后练习及参考答案

第4章练习P72作业布置：P723，7，9，11提示1：判断两个正规式是否相等，应判断两个正规式所产生的正规集是否一样。

完成此项任务需要经过四个阶段：第一，画出正规式的NFA；第二，由NFA变换到DFA；第三，将DFA最小化；第四，画出最小化DFA的有限自动机。

如果要判断的正规式的最小化DFA的有限自动机是一样的，则正规式等价；反之，则不等价。

提示2：构造正规表达式的最小化的DFA方法是：首先，按规则将正规表达式用NFA表示；其次，使用ε-closure(Move())将NFA转变为DFA；最后使用子集法将DFA最小化。

对于这类题目要多做练习，熟能生巧。

解：由于从S 出发任何输入串都不能到达状态E 和F ，所以，状态E ，F 为多余的状态，不予考虑。

这样，可以写出文法G[S]对应的NFA M ：NFA M={k, Σ, f, S, Z}K={S, A, B, Q, D, Z} S={S} Z={Z} F(S, a)=A f(S, b)=Q F(A, a)=A f(A, b)=B f(A,b)=ZF(B, b)=D f(B, a)=QF(Q, a)=Q f(Q, b)=D f(Q,b)=Z F(D, b)=B f(D, a)=A NFA M 的状态转换图为：下表由子集法将NFA 转换为DFA ：a由上表可知：(1)因为C、D是DFA的终态，其他是非终态，可将状态集分成两个子集：P1={S, A, B, E, F}，P2={C, D}。

(2)因为{A, B}b={C, D}为终态，{S, E, F}b={B, E, F}为非终态，所以P1可划分为：P11={S, E, F}，P12={A, B}。

编译原理教程课后习题答案——第四章

第四章语义分析和中间代码生成4.1 完成下列选择题：(1) 四元式之间的联系是通过实现的。

a. 指示器b. 临时变量c. 符号表d. 程序变量(2) 间接三元式表示法的优点为。

a. 采用间接码表，便于优化处理b. 节省存储空间，不便于表的修改c. 便于优化处理，节省存储空间d. 节省存储空间，不便于优化处理(3) 表达式(┐A∨B)∧(C∨D)的逆波兰表示为。

a. ┐AB∨∧CD∨b. A┐B∨CD∨∧c. AB∨┐CD∨∧d. A┐B∨∧CD∨(4) 有一语法制导翻译如下所示：S→bAb {print″1″}A→(B {print″2″}A→a {print″3″}B→Aa) {print″4″}若输入序列为b(((aa)a)a)b，且采用自下而上的分析方法，则输出序列为。

a. 32224441 b. 34242421c. 12424243d. 34442212【解答】(1) b (2) a (3) b (4) b4.2 何谓“语法制导翻译”？试给出用语法制导翻译生成中间代码的要点，并用一简例予以说明。

【解答】语法制导翻译(SDTS)直观上说就是为每个产生式配上一个翻译子程序(称语义动作或语义子程序)，并且在语法分析的同时执行这些子程序。

也即在语法分析过程中，当一个产生式获得匹配(对于自上而下分析)或用于归约(对于自下而上分析)时，此产生式相应的语义子程序进入工作，完成既定的翻译任务。

用语法制导翻译(SDTS)生成中间代码的要点如下：(1) 按语法成分的实际处理顺序生成，即按语义要求生成中间代码。

(2) 注意地址返填问题。

(3) 不要遗漏必要的处理，如无条件跳转等。

例如下面的程序段：if (i>0) a=i+e-b*d; else a=0;在生成中间代码时，条件“i>0”为假的转移地址无法确定，而要等到处理“else”时方可确定，这时就存在一个地址返填问题。

此外，按语义要求，当处理完(i>0)后的语句(即“i>0”为真时执行的语句)时，则应转出当前的if语句，也即此时应加入一条无条件跳转指令，并且这个转移地址也需要待处理完else之后的语句后方可获得，就是说同样存在着地址返填问题。

编译原理第四章典型习题答案

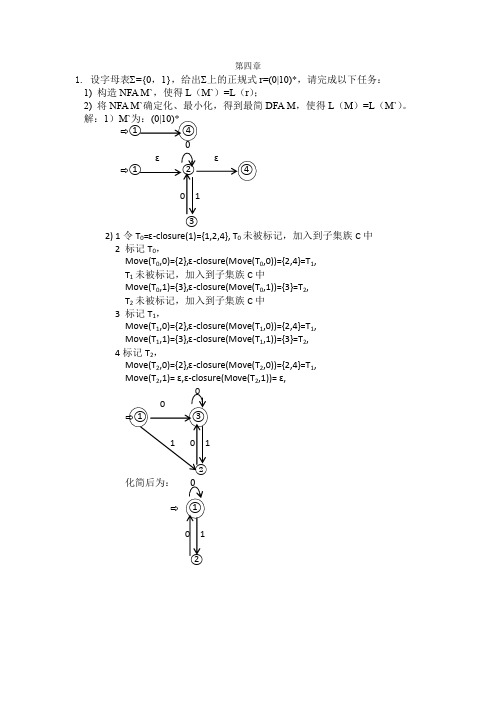
第四章1.设字母表∑={0，1}，给出∑上的正规式r=(0|10)*，请完成以下任务：1) 构造NFA M`，使得L（M`）=L（r）；2) 将NFA M`确定化、最小化，得到最简DFA M，使得L（M）=L（M`）。

解：1）M`③2) 1令T0=-closure(1)={1,2,4}, T0未被标记，加入到子集族C中2 标记T0，Move(T0,0)={2},-closure(Move(T0,0))={2,4}=T1,T1未被标记，加入到子集族C中Move(T0,1)={3},-closure(Move(T0,1))={3}=T2,T2未被标记，加入到子集族C中3 标记T1，Move(T1,0)={2},-closure(Move(T1,0))={2,4}=T1,Move(T1,1)={3},-closure(Move(T1,1))={3}=T2,4标记T2，Move(T2,0)={2},-closure(Move(T2,0))={2,4}=T1,Move(T2,1)=,-closure(Move(T2,1))=,化简后为：2.已知正规文法G1(S为开始符号)G1: S→0A|1BA→1S|1B→0S|01）该文法产生语言是什么？请用正规式表示；2）构造最简的确定有限自动机DFA，并画出状态转换图。

解：1)S=0A|1BS=(0(1S|1))|(1(0S|0))S=(01(S|))|(10(S|))S=(01|10)(S|)S=(01|10)(01|10)*2)NFA为：②③④ɛɛ①ɛ 1 0 ɛ⑤⑥⑦ɛNFA转化为DFA：1令T0=-closure(1)={1,2,5}, T0未被标记，加入到子集族C中2 标记T0，Move(T0,0)={3},-closure(Move(T0,0))={3}=T1,T1未被标记，加入到子集族C中Move(T0,1)={6},-closure(Move(T0,1))={6}=T2,T2未被标记，加入到子集族C中3 标记T1，Move(T1,0)=,-closure(Move(T1,0))=,Move(T1,1)={4},-closure(Move(T1,1))={4,8,9,10,13,17}=T3,T3未被标记，加入到子集族C中4标记T2，Move(T2,0)={7},-closure(Move(T2,0))={ 4,8,9,10,13,17}=T4,T4未被标记，加入到子集族C中Move(T2,1)=,-closure(Move(T2,1))=,5标记T3，Move(T3,0)={11},-closure(Move(T3,0))={11}=T5,T5未被标记，加入到子集族C中Move(T3,1)={14},-closure(Move(T3,1))={14}=T6,T6未被标记，加入到子集族C中6标记T4，Move(T4,0)={11},-closure(Move(T4,0))={11}=T5,Move(T4,1)={14},-closure(Move(T4,1))={14}=T6,7标记T5，Move(T5,0)=,-closure(Move(T5,0))=,Move(T5,1)={12},-closure(Move(T5,1))={9,10,12,13,16,17}=T7,T7未被标记，加入到子集族C中8标记T6，Move(T6,0)={15},-closure(Move(T6,0))={ 9,10,13,15,16,17}=T8,T8未被标记，加入到子集族C中Move(T6,1)=,-closure(Move(T6,1))=,9标记T7，Move(T7,0)={11},-closure(Move(T7,0))={11}=T5,Move(T7,1)={14},-closure(Move(T7,1))={14}=T6,10标记T8，Move(T8,0)={11},-closure(Move(T8,0))={11}=T5,Move(T8,1)={14},-closure(Move(T8,1))={14}=T6,则DFA为：②①1化简后为：②①13.将R=a(a|d)*转换成相应的正规文法。

编译原理第4章习题及答案(词法分析)

4.7消除下列εFA的ε边：
解：
4.8构造以下3型文法相应的最简自动机(“最简自动机”应该是“最简确定自动机”)：
G:S → aS|bA|a
A → aS|bA|bB
B →bB | b
解：
a
b
Ia
Ib
-S
SZ
A
-S
SZ
A
A
S
AB
+SZ
SZ
A
B
BZ
A
S
AB
+Z
AB
S
ABZ
+ABZ
S
ABZ
4.9构造以下自动机相应的3型文法G：
（3）由正规式(1|…|9)(0|1|2|…|9)*构造的DFA3为：
（4）依题意构造的DFA4为：
（5）确定有限自动机与3型文法等价。而“a和b的个数相等的所有ab串”属上下文有关，需要1型文法描述，故确定有限自动机不能描述。
4.4构造下列正规式相应的NFA，然后转换为DFA：
（1）(a|b)*a(a|b|ε)
习题第4章词法分析
4.1编写以下字符串集的正规式（若没有正规式则说明原因）：
（1）以a开头和结尾的所有小写字母串；
（2）以a开头或/和结尾的所有小写字母串；
（3）不以0开头的所有数字串；
（4）每个5均在每个1之前的所有数字串；
（5）a和b的个数相等的所有ab串。
4.2简述由下列正规式生成的语言：
（1）(a|b)*a(a|b|ε)
4.5构造自动机A1和A2，使得
L(A1)={ε,an,ban|n≥1}
L(A2)={ε,(ab)n|n≥1}
4.6将下列NFA确定化：
4.7消除下列εDA的ε边：

编译原理第4章习题解答

第四章习题解答4.1词法分析的主要任务是对源程序进行扫描，从中识别出单词，它是编译过程的第一步，也是编译过程中不可缺少的部分。

4.2单词符号一般分为五类：关键字、标识符、常数、运算符和界限符。

分别用整数1、2、3、4、5表示。

对于这种非一符一个类别码的编码形式，一个单词符号除了给出它的单词类别码之外，还要给出它的自身值。

标识符的自身值被表示成按字节划分的内部码。

常数的自身值是其二进制值。

由于语言中的关键字、运算符和界限符的数量都是确定的，因此，对这些单词符号可采用一符一个单词类别码。

如果采取一符一个单词类别码，那么这些单词符号的自身值就不必给出了。

4.3设计词法分析程序有如下几种方法：①由正规文法设计词法分析程序——程序设计语言的单词一般都可以用正规文法描述，从正规文法可构造一个FA。

再对FA确定化和状态个数最少化，最后得到一个化简了的DFA。

这个DFA正是词法分析程序的设计框图，这样，由DFA编制词法分析程序就容易了。

②由正规表达式设计词法分析程序——正规表达式也是描述单词的一种方便工具。

由正规表达式转换成NDFA，然后再对它确定化和状态个数最少化，可得一个DFA。

再由DFA编制词法分析程序。

4.4符号表在编译程序中具有十分重要的意义，它是编译程序中不可缺少的部分。

在编译程序中，符号表用来存放在程序中出现的各种标识符及其语义属性。

一个标识符包含了它全部的语义属性和特征。

标识符的全部属性不可能在编译程序的某一个阶段获得，而需要在它的各个阶段中去获得。

在编译程序的各个阶段，不仅要用获取的标识符信息去更新符号表中的内容，添加新的标识符及其属性，而且需要去查找符号表，引用符号表中的信息。

因为，符号表是编译程序进行各种语义检查（即语义分析）的依据，是进行地址分配的依据。

标识符处理的基本思想是，当遇到定义性标识符时，先去查符号表（标识符表）。

如果此标识符已在符号表中登记过，那么表明该标识符被多次声明，将作为一个错误，因为一个标识符只能被声明一次；如果标识符在符号表中未登记过，那么将构造此标识符的机内符，并在符号表中进行登记。

编译原理英文版第四章答案

Chapter 4 Answers - Compiler Principles Exercise 1Question:Consider the following context-free grammar (CFG):S → a | BB → a1.Is the language generated by this CFG ambiguous? Justify your answer.2.If the CFG is ambiguous, provide a string that can be generated in twodifferent ways.Answer:1.The language generated by this CFG is not ambiguous. In order toprove this, we need to show that for every valid string in the language, there isa unique deriv ation tree. Let’s analyze the grammar to determine thisuniqueness:•The production rule S → a is a direct derivation from the start symbol S, resulting in the terminal symbol a. Since this is the only possible derivation from S, it is unambiguous.•The production rule S → B has B as its right-hand side. The production rule B → a is the only production rule for B, so B will eventually derive theterminal a. Therefore, the derivation from S to the single terminal a is unique.Hence, we can conclude that the language generated by this CFG is not ambiguous because there is a unique derivation for every valid string.2.Since the language is not ambiguous, we cannot provide a string thatcan be generated in two different ways, as every valid string has only onederivation.Exercise 2Question:Consider the following context-free grammar (CFG):E → E + E | E * E | id1.Starting with the non-terminal symbol E, apply the productions of thegrammar to generate the string id + id * id.2.Draw a parse tree for the string id + id * id using the abovegrammar.Answer:1.To generate the string id + id * id, we can apply the productions ofthe grammar as follows:E (Starting with E)E + E (Using E → E + E)E + E * E (Using E → E * E)id + id * id (Using E → id)2.The parse tree for the string id + id * id is as follows:E_____|_____| | |E + E| |E E| |id __|__| |E *| |E id|idExercise 3Question:Provide a context-free grammar (CFG) for the language of palindromes over the alphabet {a, b}.Answer:We can define a context-free grammar (CFG) to generate palindromes over the alphabet {a, b} as follows:S → ε | a | b | aSa | bSbExplanation: - The production rule S → ε generates an empty string (epsilon). - The production rules S → a and S → b generate single characters a and b respectively. - The production rules S → aSa and S → bSb generate palindromes. Here, the recursive non-terminal S is enclosed between the same terminal symbols a or b.This CFG covers all possible palindromes over the alphabet {a, b}, including empty strings, single characters, and palindromic strings of various lengths.Exercise 4Question:Consider the following context-free grammar (CFG):S → AaBA → ε | aAB → ε | bB1.What is the language generated by this CFG?2.Determine if the CFG is ambiguous. If so, provide a string that can begenerated in two different ways.Answer:1.The language generated by this CFG consists of strings with a prefix ofa and a suffix of b. The generated language can be represented as:L = {anbm | n ≥ 0, m ≥ 0}Where an represents zero or more a and bn represents zero or more b.2.The CFG is ambiguous. Here is an example of a string that can begenerated in two different ways: aab.Possible derivations:•Derivation 1:S (Start with S)AaB (Using S → AaB)aaABb (Using A → aA)aaBb (Using A → ε)aab (Using B → bB)•Derivation 2:S (Start with S)AaB (Using S → AaB)AaaBBb (Using A → aA)aaBBb (Using A → ε)aaBb (Using B → ε)aab (Using B → bB)Thus, the string aab can be derived in two different ways, making the grammar ambiguous.Exercise 5Question:Consider the following context-free grammar (CFG):E → E + D | DD → D * F | FF → idStarting with the non-terminal symbol E, apply the productions of the grammar to generate the string id + id * id.Answer:To generate the string id + id * id, we can apply the productions of the grammar as follows:E (Starting with E)E + D (Using E → E + D)D + D (UsingE → D)D + D * F (Using D → D * F)F + D * F (Using D → F)id + D * F (Using F → id)id + D * id (Using F → id)id + D * id * F (Using D → F)id + id * F (Using F → id)id + id * id (Using F → id)Hence, the string id + id * id can be generated by applying the productions of the given grammar starting with the non-terminal symbol E.。

编译原理第四章答案

“编译技术”第四章作业4-1 已知文法G[C]：C→iEtS|iEtSeSE→ a|bS→ a+b|a*b(1)提取左公共因子；(2)计算修改后文法的每个非终结符的FIRST集和FOLLOW集；(3)给出递归下降分析程序。

(3)递归下降分析程序void match(token t){if(lookahead=='t')lookahead = nexttoken;else error;}void C(){if(lookahead=='i'){match('i');E();if(lookahead=='t'){match('t');S();Cprime();}else error;}else error;}void Cprime(){if(lookahead=='e'){match('e');S();}}void E(){if(lookahead=='a')match('a');else if(lookahead=='b')match('b');else error;}void S(){if(lookahead=='a'){match('a');Sprime();}}void Sprime(){if (lookahead=='+'){match('+');if(lookahed=='b'){match('b');}else error();}else if(lookahead=='*'){match('*');if(lookahead=='b'){match('b');}else error();}}4-2 已知文法G[Z]：Z→Az|bA→ Za|a(1)删除左递归；(2)计算修改后文法的每个非终结符的FIRST集和FOLLOW集；(3)给出递归下降分析程序。

编译原理第四章习题解答

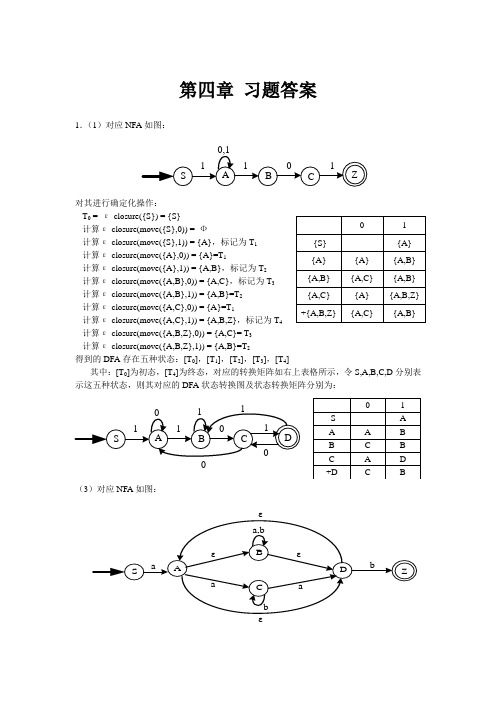
第四章习题答案1．（1）对应NFA 如图：对其进行确定化操作：T 0 = ε-closure({S}) = {S}计算ε-closure(move({S},0)) = Ф计算ε-closure(move({S},1)) = {A}，标记为T 1 计算ε-closure(move({A},0)) = {A}=T 1计算ε-closure(move({A},1)) = {A,B}，标记为T 2计算ε-closure(move({A,B},0)) = {A,C}，标记为T 3计算ε-closure(move({A,B},1)) = {A,B}=T 2 计算ε-closure(move({A,C},0)) = {A}=T 1计算ε-closure(move({A,C},1)) = {A,B,Z}，标记为T 4 计算ε-closure(move({A,B,Z},0)) = {A,C}= T 3 计算ε-closure(move({A,B,Z},1)) = {A,B}=T 2得到的DFA 存在五种状态：[T 0]，[T 1]，[T 2]，[T 3]，[T 4]其中：[T 0]为初态，[T 4]为终态，对应的转换矩阵如右上表格所示，令S,A,B,C,D 分别表示这五种状态，则其对应的DFA 状态转换图及状态转换矩阵分别为：（3）对应NFA 如图：εT 0 = ε-closure({S}) = {S}计算ε-closure(move({S},a)) = {A,B,D}，标记为T 1 计算ε-closure(move({S},b)) = Ф计算ε-closure(move({A,B,D},a)) = {A,B,C,D}，标记为计算ε-closure(move({A,B,D},b)) = {A,B,D,Z}，标记为T 3 计算ε-closure(move({A,B,C,D},a)) = {A,B,C,D}= T 2计算ε-closure(move({A,B,C,D},b)) = {A,B,C,D,Z}，标记为T 4 计算ε-closure(move({A,B,D,Z},a)) = {A,B,C,D}= T 2 计算ε-closure(move({A,B,D,Z},b)) = {A,B,D,Z}= T 3 计算ε-closure(move({A,B,C,D,Z},a)) = {A,B,C,D}= T 2 计算ε-closure(move({A,B,C,D,Z},b)) = {A,B,C,D,Z}= T 4 得到的DFA 存在五种状态：[T 0]，[T 1]，[T 2]，[T 3]，[T 4]其中：[T 0]为初态，[T 3],[T 4]为终态，对应的转换矩阵如左下表格所示，令S,A,B,C,D 分别2．根据题意，可以得其NFA 状态转换图如下图所示：T 0 = ε-closure({x}) = {x} 计算ε-closure(move({x},0)) = {z}，标记为T 1 计算ε-closure(move({x},1)) = {x}=T 0 计算ε-closure(move({z},0)) = {x, z}，标记为T 2 计算ε-closure(move({z},1)) = {y}，标记为T 3 计算ε-closure(move({x, z},0)) = {x, z}= T 2 计算ε-closure(move({x, z},1)) = {x, y}，标记为T 4 计算ε-closure(move({y},0)) = {x, y}= T 4 计算ε-closure(move({y},1)) = Ф计算ε-closure(move({x, y},0)) = {x, y, z}，标记为T 5 计算ε-closure(move({x, y},1)) = {x}= T 0计算ε-closure(move({x, y, z},0)) = {x, y, z}= T 5 计算ε-closure(move({x, y, z},1)) = {x, y}= T 4得到的DFA 存在六种状态：[T 0]，[T 1]，[T 2]，[T 3]，[T 4]，[T 5]其中：[T 0]为初态，[T 1],[T 2],[T 5]为终态，对应的转换矩阵如右上表格所示，令A,B,C,D,E,F 分别表示这六种状态，则其对应的DFA 状态转换图及状态转换矩阵分别为：3．状态转换图如图所示：对其进行确定化操作：T 0 = ε-closure({S}) = {S}计算ε-closure(move({S},0)) = {V ,Q}，标记为T 1 计算ε-closure(move({S},1)) = {Q,U}，标记为T 2 计算ε-closure(move({V ,Q},0)) = {V,Z}，标记为T 3 计算ε-closure(move({V ,Q},1)) = {Q,U}= T 2计算ε-closure(move({Q,U},0)) = {V}，标记为T 4计算ε-closure(move({Q,U},1)) = {Q,U,Z}，标记为T 5 计算ε-closure(move({V,Z},0)) = {Z}= T 3 计算ε-closure(move({V,Z},1)) = {Z}= T 3计算ε-closure(move({V},0)) = {Z}=T 4 计算ε-closure(move({V},1)) = Ф计算ε-closure(move({Q,U,Z},0)) = {V ,Z}，标记为T 6 计算ε-closure(move({Q,U,Z},1)) = {Q,U,Z}= T 5 计算ε-closure(move({Z},0)) = {Z}= T 6 计算ε-closure(move({Z},1)) = {Z}= T 3得到的DFA 存在七种状态：[T 0]，[T 1]，[T 2]，[T 3]，[T 4]，[T 5]，[T 5] 其中：[T 0]为初态，[T 3],[T 5],[T 6]为终态，对应的转换矩阵如右上表格所示，令A,B,C,D,E,F,G 分别表示这七种状态，则其对应的DFA 状态转换图及状态转换矩阵分别为：4．（a ）对其进行确定化操作： T 0 = ε-closure({0}) = {0}计算ε-closure(move({0},a)) = {0,1}，标记为T 1计算ε-closure(move({0},b)) = {1}，标记为T 2计算ε-closure(move({0,1},a)) = {0,1}=T 1计算ε-closure(move({0,1},b)) = {1}= T 2计算ε-closure(move({1},a)) = {0}=T 0 计算ε-closure(move({1},b)) =Ф得到的DFA 存在三种状态：[T 0]，[T1]，[T 2]其中，[T 0]为初态，[T 0],[T 1]为终态，对应的转换矩阵如右上表格所示，令A,B,C 分别表示这三种状态，则其对应的DFA 状态转换图及状态转换矩阵如下：对其进行最小化操作：该DFA 无多余状态，进行初始划分，得终态组{A,B}，非终态组{C}对终态组{A,B}进行审查，输入符号a 后，状态A,B 均转换成状态B ；输入符号b 后，状态A,B 均转换成状态C ，由此可知，状态A,B 等价，不能再分。

编译原理龙书第四章答案

编译原理龙书第四章答案
1.什么是有效性检查？
答：有效性检查是语法分析中的一项重要检查，是指检查语言结构中
的各部分是否有效，即结构是否符合语言的语法规则。

2.什么是语法分析？
答：语法分析是指将文法定义的模式应用到给定的输入字符串中来识
别出输入字符串的结构特征，以确定给定的输入是否符合语法定义。

3.扩展BNF与简化后的BNF有什么区别？
答：扩展BNF使用更多的符号，可以更准确地表示文法的定义；而简
化后的BNF则把文法的定义层次降低，使用更少的符号，实现文法简化。

4.语法分析生成器的工作原理是什么？
答：语法分析生成器使用上下文无关文法定义的语句，根据文法定义
生成语法分析程序，它包括词法分析器和语法分析器。

当词法分析器处理
输入的字符串时，语法分析器就自动检查输入字符串是否满足文法定义。

5.什么是四元式？
答：四元式是源程序翻译成中间代码的基本单位，它用四元组的形式：(操作码，运算数1，运算数2，结果)来表示一条指令，便于后续的代码
优化和目标代码生成。

6.什么是类型检查？
答：类型检查是指在语义分析中，用来检查程序中表达式和变量的类
型是否合理。

编译原理第4章作业答案

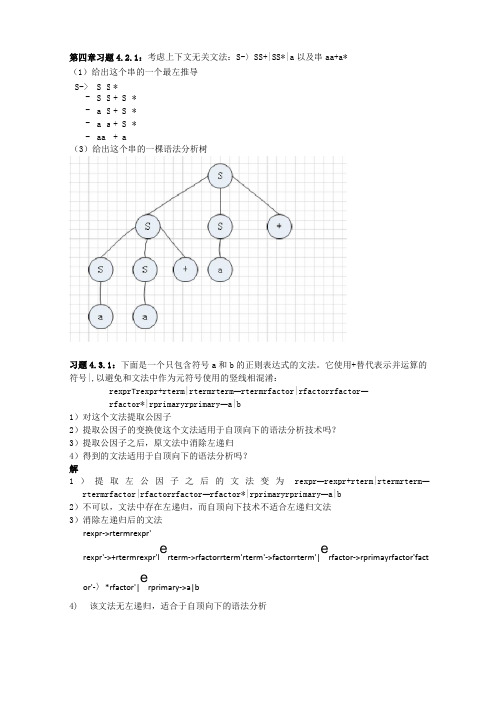
第四章习题4.2.1：考虑上下文无关文法：S-〉SS+|SS*|a 以及串aa+a* （1）给出这个串的一个最左推导 S-> S S *-> S S + S * -> a S + S * -> a a + S * -aa +a（3）给出这个串的一棵语法分析树习题4.3.1：下面是一个只包含符号a 和b 的正则表达式的文法。

它使用+替代表示并运算的符号|,以避免和文法中作为元符号使用的竖线相混淆：rexpr T rexpr+rterm|rtermrterm —rtermrfactor|rfactorrfactor —rfactor*|rprimaryrprimary —a|b1）对这个文法提取公因子2）提取公因子的变换使这个文法适用于自顶向下的语法分析技术吗？ 3）提取公因子之后，原文法中消除左递归4）得到的文法适用于自顶向下的语法分析吗？解1）提取左公因子之后的文法变为rexpr —rexpr+rterm|rtermrterm —rtermrfactor|rfactorrfactor —rfactor*|rprimaryrprimary —a|b 2）不可以，文法中存在左递归，而自顶向下技术不适合左递归文法 3）消除左递归后的文法rexpr->rtermrexpr'rexpr'->+rtermrexpr'l e rterm->rfactorrterm'rterm'->factorrterm'|erfactor->rprimayrfactor'fact or'-〉*rfactor'|erprimary->a|b4) 该文法无左递归，适合于自顶向下的语法分析习题4.4.1：为下面的每一个文法设计一个预测分析器，并给出预测分析表。

可能要先对文法进行提取左公因子或消除左递归 (3)S-〉S(S)S|*(5)S->(L)|aL->L,S|S 解 (3)①消除该文法的左递归后得到文法S-〉S'S'-〉(S)SS'|*②计算FIRST 和FOLLOW 集合FIRST(S)={(,*}FOLLOW(S)={),$} FIRST(S')={(,*}FOLLOW(S')={),$}③构建预测分析表①消除该文法的左递归得到文法S-〉(L)|a L->SL' L'-〉,SL'|£②计算FIRST 与FOLLOW 集合FIRST(S)={(,a}FOLLOW(S)={),,,$}FIRST(L)={(,a}FOLLOW(L)={)} FIRST(L')={,,£}FOLLOW(L')={)}习题4.4.4计算练习4.2.2的文法的FIRST 和FOLLOW 集合3)S T S(S)S|5) S T (L)|a,L T L,S|S 解：3)FIRST(S)={£,(}FOLLOW(S)={(,),$} 5) FIRST(S)={(,a}FOLLOW(S)={),,,$}FIRST （L ）={（,a}FOLLOW （L ）={）,,}习题4.6.2为练习4.2.1中的增广文法构造SLR 项集，计算这些项集的GOTO 函数，给出这个文法的语法分析表。

编译原理第4章作业答案

编译原理-第4章 语法分析--习题答案

编译原理第4章答案

编译基础学习知识原理第4章规范标准答案

编译原理第4章习题答案

编译原理第四章参考答案

编译原理龙书第四章答案

编译原理第4章答案

编译原理第四章作业答案

编译原理第4章习题解答

编译原理(第三版)第4章课后练习及参考答案中石大版第4章课后练习及参考答案

编译原理教程课后习题答案——第四章

编译原理第四章典型习题答案

编译原理第4章习题及答案(词法分析)

编译原理 第4章习题解答

编译原理英文版第四章答案

编译原理第四章答案

编译原理第四章 习题解答

编译原理龙书第四章答案

编译原理第4章作业答案

编译原理-第4章语法分析--习题答案

编译原理第4章习题解答

编译原理第四章习题解答