2014年深圳市中考数学模拟试题(4)及答案
2014年深圳市中考数学试题及答案

2014年深圳市中考数学试卷一、选择题(每小题3分,共36分.每小题给出4个选项,其中只有一个是正确..的) 1、9的相反数是( )A 、-9B 、9C 、9±D 、91± 2、下列图形中是轴对称图形但不是中心对称图形的是( )3“快的打车”一夜之间红遍大江南北,据统计,2014年“快的打车”账户流水总金额达到47.3亿元,47.3亿用科学计数法表示为( ) A 、81073.4⨯ B 、91073.4⨯ C 、101073.4⨯ D 、111073.4⨯ 4、由几个大小相同的正方形组成的几何图形如图所示,则它的俯视图是( )5、在-2,1,2,1,4,6中正确的是( )A 、平均数3B 、众数是-2C 、中位数是1D 、极差为8 6、已知函数b ax y +=经过(1,3),(0,-2)求b a +=( )A 、-1B 、-3C 、3D 、7 7、下列方程没有实数根的是( )A 、1042=+x x B 、03832=-+x x C 、0322=+-x x D 、12)3)(2(=--x x 8、如图、△ABC 和△DEF 中,AB=DE 、∠B=∠DEF , 添加下列哪一个条件无法证明△ABC ≌△DEF ( ) A 、AC ∥DF B 、∠A=∠D C 、AC=DF D 、∠ACB=∠F9、袋子里有4个球,标有2,3,4,5,先抽取一个并记住,放回,然后再抽取一个,抽取的两个数字之和大于6的概率是( ) A 、21 B 、127 C 、85 D 、4310、小明去爬山,在山脚看山顶角度为30°,小明在坡比为5:12的山坡上走了1300米,此时小明看山顶的角度为60°,求此山的高度( ) A 、5250600- B 、2503600- EFDCBADC B A 125600A BC D11、二次函数c bx ax y ++=2的图像如图所示,下列正确的个数为①bc >0; ②c a 32-< 0; ③b a +2>0;④02=++c bx ax 有两个解121,,x x x >0,2x < 0;⑤c b a ++>0; ⑥当x >1时, y 随x 增大而减小。
2014年广东省深圳市龙岗区中考模拟考试数学试题及答案

2014年深圳市龙岗区中考模拟考试数学试题第一部分 选择题(本题共12小题,每小题3分,共36分.每小题给出4个选项,其中只有一个是正确的) 1.2014的相反数是( ) A .2014B .2014-C .20141D .20141-2.“辽宁号”航母的满载排水量为67500吨,数据67500用科学记数法表示为( ) A .210675⨯B .21075.6⨯C .41075.6⨯D .51075.6⨯3.下列图形中,既是..轴对称图形又是..中心对称图形的是( )A B C D4.下图是由八个完全相同的小正方体组成的几何体,其主视图是( )正面 A B C D 5.下列计算中,正确..的是( ) A .9132=- B .()332-=-C .326m m m =÷D .()222b a b a -=-6.已知⊙O 1与⊙O 2的半径R 、r 分别是方程01272=+-x x 的两根,且圆心距1=d ,那么⊙O 1与⊙O 2的位置关系是( ) A .外离B .外切C .相交D .内切7.已知一个多边形的每一个内角都等于135°,则这个多边形是( )A .正六边形B .正八边形C .正十边形D .正十二边形D8.下列命题中,错误..的是( ) A .平行四边形的对角线互相平分B .对角线相等的四边形是矩形C .一组对边平行,一组对角相等的四边形是平行四边形D .顺次连接等腰梯形各边中点所得的四边形为菱形9.某中学九(1)班学生为希望工程捐款,该班50名学生的捐款情况统计如图1所示,则他们捐款金额的众数和中位数分别是( ) A .16,15 B .15,16 C .20,10D .10,20图1 图210.如图2,在边长为9的等边△ABC 中,BD =3,∠ADE =60°,则AE 的长为( ) A .6B .7C .7.5D .811.如图3,菱形OABC 的顶点A 在x 轴的正半轴上,顶点C 的坐标为(3,4).反比例函数xky =(x >0)的图象经过顶点B ,则k 的值为( ) A .32 B .24C .20D .12图3 图412.如图4,在Rt ABC △中,︒=∠90C ,6=AC ,8=BC ,⊙O 为ABC △的内切圆,点D 是斜边AB 的中点,则ODA ∠tan 的值为( ) A .2 B C .34D .2第二部分 非选择题填空题(本题共4小题,每小题3分,共12分) 13.分式方程312-=x x 的解为______________. 14.如图5,已知圆锥的底面半径OA =3cm ,高SO =4cm ,则该圆锥的侧面积为 ______________cm 2.15.如图6,交警为提醒广大司机前方道路塌陷在路口设立了警示牌.已知立杆AD 的高度是3m ,从侧面B 点测得警示牌顶端C 点和底端D 点的仰角分别是60°和45°.那么警示牌CD 的高度为______________ m .16.如图7,在平面直角坐标系中,Rt △OAB 的顶点A 在x 轴的正半轴上。
2014年广东省深圳市中考数学试卷及答案解析

2014年广东省深圳市中考数学试卷参考答案与试题解析一、选择题(共12小题,每小题3分,满分36分) 1.(3分)9的相反数是( ) A .﹣9B .9C .±9D .19【解答】解:9的相反数是﹣9, 故选:A .2.(3分)下列图形中是轴对称图形但不是中心对称图形的是( )A .B .C .D .【解答】解:A 、此图形不是中心对称图形,也不是轴对称图形,故A 选项错误; B 、此图形不是中心对称图形,是轴对称图形,故B 选项正确; C 、此图形是中心对称图形,也是轴对称图形,故C 选项错误; D 、此图形是中心对称图形,不是轴对称图形,故D 选项错误. 故选:B .3.(3分)支付宝与“快的打车”联合推出优惠,“快的打车”一夜之间红遍大江南北.据统计,2014年“快的打车”账户流水总金额达到47.3亿元,47.3亿用科学记数法表示为( ) A .4.73×108B .4.73×109C .4.73×1010D .4.73×1011【解答】解:47.3亿=47 3000 0000=4.73×109, 故选:B .4.(3分)由几个大小相同的正方形组成的几何图形如图,则它的俯视图是( )A .B .C .D .【解答】解:从上面看第一层右边一个,第二层三个正方形, 故选:A .5.(3分)在﹣2,1,2,1,4,6中正确的是( ) A .平均数3B .众数是﹣2C .中位数是1D .极差为8【解答】解:A 、这组数据的平均数为:(﹣2+1+2+1+4+6)÷6=12÷6=2,故A 选项错误;B 、在这一组数据中1是出现次数最多的,故众数是1,故B 选项错误;C 、将这组数据从小到大的顺序排列为:﹣2,1,1,2,4,6,处于中间位置的两个数是1,2,那么由中位数的定义可知,这组数据的中位数是:(1+2)÷2=1.5,故C 选项错误;D 、极差6﹣(﹣2)=8,故D 选项正确. 故选:D .6.(3分)已知函数y =ax +b 经过(1,3),(0,﹣2),则a ﹣b =( ) A .﹣1B .﹣3C .3D .7【解答】解:∵函数y =ax +b 经过(1,3),(0,﹣2), ∴{a +b =3b =−2, 解得{a =5b =−2,∴a ﹣b =5+2=7. 故选:D .7.(3分)下列方程没有实数根的是( ) A .x 2+4x =10 B .3x 2+8x ﹣3=0C .x 2﹣2x +3=0D .(x ﹣2)(x ﹣3)=12【解答】解:A 、方程变形为:x 2+4x ﹣10=0,Δ=42﹣4×1×(﹣10)=56>0,所以方程有两个不相等的实数根,故A 选项不符合题意;B 、Δ=82﹣4×3×(﹣3)=100>0,所以方程有两个不相等的实数根,故B 选项不符合题意;C 、Δ=(﹣2)2﹣4×1×3=﹣8<0,所以方程没有实数根,故C 选项符合题意;D 、方程变形为:x 2﹣5x ﹣6=0,Δ=52﹣4×1×(﹣6)=49>0,所以方程有两个不相等的实数根,故D 选项不符合题意. 故选:C .8.(3分)如图,△ABC 和△DEF 中,AB =DE 、∠B =∠DEF ,添加下列哪一个条件无法证明△ABC ≌△DEF ( )A .AC ∥DFB .∠A =∠DC .AC =DFD .∠ACB =∠F【解答】解:∵AB =DE ,∠B =∠DEF ,∴添加AC ∥DF ,得出∠ACB =∠F ,即可证明△ABC ≌△DEF ,故A 、D 都正确; 当添加∠A =∠D 时,根据ASA ,也可证明△ABC ≌△DEF ,故B 正确; 但添加AC =DF 时,没有SSA 定理,不能证明△ABC ≌△DEF ,故C 不正确; 故选:C .9.(3分)袋子里有4个球,标有2,3,4,5,先抽取一个并记住,放回,然后再抽取一个,所抽取的两个球数字之和大于6的概率是( ) A .12B .712C .58D .34【解答】解:画树状图得:∵共有16种等可能的结果,抽取的两个球数字之和大于6的有10种情况, ∴抽取的两个球数字之和大于6的概率是:1016=58.故选:C .10.(3分)小明去爬山,在山脚看山顶角度为30°,小明在坡比为5:12的山坡上走1300米,此时小明看山顶的角度为60°,则山的高度是( )A.(600﹣250√3)米B.(600√3−250)米C.(350+350√3)米D.500√3米【解答】解:∵BE:AE=5:12,√52+122=13,∴BE:AE:AB=5:12:13,∵AB=1300米,∴AE=1200米,BE=500米,设EC=x米,∵∠DBF=60°,∴DF=√3x米.又∵∠DAC=30°,∴AC=√3CD.即:1200+x=√3(500+√3x),解得x=600﹣250√3.∴DF=√3x=(600√3−750)米,∴CD=DF+CF=600√3−250(米).答:山高CD为(600√3−250)米.故选:B.11.(3分)二次函数y=ax2+bx+c图象如图,下列正确的个数为()①bc>0;②2a﹣3c<0;③2a+b>0;④ax2+bx+c=0有两个解x1,x2,当x1>x2时,x1>0,x2<0;⑤a+b+c>0;⑥当x>1时,y随x增大而减小.A.2B.3C.4D.5【解答】解:①∵抛物线开口向上,∴a>0,∵对称轴在y轴右侧,∴a,b异号即b<0,∵抛物线与y轴的交点在负半轴,∴c<0,∴bc>0,故①正确;②∵a>0,c<0,∴2a﹣3c>0,故②错误;③∵对称轴x=−b2a<1,a>0,∴﹣b<2a,∴2a+b>0,故③正确;④由图形可知二次函数y=ax2+bx+c与x轴的两个交点分别在原点的左右两侧,即方程ax2+bx+c=0有两个解x1,x2,当x1>x2时,x1>0,x2<0,故④正确;⑤由图形可知x=1时,y=a+b+c<0,故⑤错误;⑥∵a>0,对称轴x=1,∴当x>1时,y随x增大而增大,故⑥错误.综上所述,正确的结论是①③④,共3个. 故选:B .12.(3分)如图,已知四边形ABCD 为等腰梯形,AD ∥BC ,AB =CD ,AD =√2,E 为CD 中点,连接AE ,且AE =2√3,∠DAE =30°,作AE ⊥AF 交BC 于F ,则BF =( )A .1B .3−√3C .√5−1D .4﹣2√2【解答】解:如图,延长AE 交BC 的延长线于G , ∵E 为CD 中点, ∴CE =DE , ∵AD ∥BC ,∴∠DAE =∠G =30°, 在△ADE 和△GCE 中, {∠DAE =∠G∠AED =∠GEC CE =DE, ∴△ADE ≌△GCE (AAS ), ∴CG =AD =√2,AE =EG =2√3, ∴AG =AE +EG =2√3+2√3=4√3, ∵AE ⊥AF ,∴AF =AG tan30°=4√3×√33=4, GF =AG ÷cos30°=4√3÷√32=8,过点A 作AM ⊥BC 于M ,过点D 作DN ⊥BC 于N , 则MN =AD =√2,∵四边形ABCD 为等腰梯形, ∴BM =CN ,∵MG =AG •cos30°=4√3×√32=6,∴CN =MG ﹣MN ﹣CG =6−√2−√2=6﹣2√2,∵AF ⊥AE ,AM ⊥BC , ∴∠F AM =∠G =30°, ∴FM =AF •sin30°=4×12=2,∴BF =BM ﹣MF =6﹣2√2−2=4﹣2√2. 故选:D .二、填空题(共4小题,每小题3分,满分12分) 13.(3分)因式分解:2x 2﹣8= 2(x +2)(x ﹣2) . 【解答】解:2x 2﹣8=2(x +2)(x ﹣2).14.(3分)在Rt △ABC 中,∠C =90°,AD 平分∠CAB ,AC =6,BC =8,CD = 3 .【解答】解:如图,过点D 作DE ⊥AB 于E , ∵∠C =90°,AC =6,BC =8, ∴AB =√AC 2+BC 2=√62+82=10, ∵AD 平分∠CAB , ∴CD =DE ,∴S △ABC =12AC •CD +12AB •DE =12AC •BC , 即12×6•CD +12×10•CD =12×6×8,解得CD =3. 故答案为:3.15.(3分)如图,双曲线y =kx 经过Rt △BOC 斜边上的点A ,且满足AO AB=23,与BC 交于点D ,S △BOD =21,求k = 8 .【解答】解:过A 作AE ⊥x 轴于点E . ∵S △OAE =S △OCD , ∴S 四边形AECB =S △BOD =21, ∵AE ∥BC , ∴△OAE ∽△OBC , ∴S △OAE S △OBC=S △OAES △OAE +S 四边形AECB=(AOOB)2=425,∴S △OAE =4, 则k =8. 故答案是:8.16.(3分)如图,下列图形是将正三角形按一定规律排列,则第5个图形中所有正三角形的个数有 485 .【解答】解:第一个图形正三角形的个数为5, 第二个图形正三角形的个数为5×3+2=2×32﹣1=17, 第三个图形正三角形的个数为17×3+2=2×33﹣1=53, 第四个图形正三角形的个数为53×3+2=2×34﹣1=161, 第五个图形正三角形的个数为161×3+2=2×35﹣1=485. 如果是第n 个图,则有2×3n ﹣1个 故答案为:485. 三、解答题17.计算:√12−2tan60°+(√2014−1)0﹣(13)﹣1.【解答】解:原式=2√3−2√3+1﹣3=﹣2. 18.先化简,再求值:(3x x−2−x x+2)÷xx 2−4,在﹣2,0,1,2四个数中选一个合适的代入求值.【解答】解:原式=3x(x+2)−x(x−2)(x+2)(x−2)•(x+2)(x−2)x =3(x +2)﹣(x ﹣2)=3x +6﹣x +2=2x +8,当x =1时,原式=2+8=10. 19.关于体育选考项目统计图项目 频数 频率 A 80 b B c 0.3 C 20 0.1 D 40 0.2 合计a1(1)求出表中a ,b ,c 的值,并将条形统计图补充完整. 表中a = 200 ,b = 0.4 ,c = 60 .(2)如果有3万人参加体育选考,会有多少人选择篮球?【解答】解:(1)a=20÷0.1=200,c=200×0.3=60,b=80÷200=0.4,故答案为:200,0.4,60,补全条形统计图如下:(2)30000×0.4=12000(人).答:3万人参加体育选考,会有12000人选择篮球.20.已知BD垂直平分AC,∠BCD=∠ADF,AF⊥AC,(1)证明四边形ABDF是平行四边形;(2)若AF=DF=5,AD=6,求AC的长.【解答】(1)证明:∵BD垂直平分AC,∴AB=BC,AD=DC,在△ADB 与△CDB 中,{AB =BC AD =DC DB =DB,∴△ADB ≌△CDB (SSS )∴∠BCD =∠BAD ,∵∠BCD =∠ADF ,∴∠BAD =∠ADF ,∴AB ∥FD ,∵BD ⊥AC ,AF ⊥AC ,∴AF ∥BD ,∴四边形ABDF 是平行四边形,(2)解:∵四边形ABDF 是平行四边形,AF =DF =5,∴▱ABDF 是菱形,∴AB =BD =5,∵AD =6,设BE =x ,则DE =5﹣x ,∴AB 2﹣BE 2=AD 2﹣DE 2,即52﹣x 2=62﹣(5﹣x )2解得:x =75,∴AE =√AB 2−BE 2=245, ∴AC =2AE =485.21.某“爱心义卖”活动中,购进甲、乙两种文具,甲每个进货价高于乙进货价10元,90元买乙的数量与150元买甲的数量相同.(1)求甲、乙进货价;(2)甲、乙共100件,将进价提高20%进行销售,进货价少于2080元,销售额要大于2460元,求有几种方案?【解答】解:(1)设乙进货价x 元,则甲进货价为(x +10)元,由题意得90x =150x+10解得x =15,经检验x =15是原方程的根,则x +10=25,答:甲进货价为25元,乙进货价15元.(2)设进甲种文具m 件,则乙种文具(100﹣m )件,由题意得{25m +15(100−m)<208025m(1+20%)+15(100−m)(1+20%)>2460解得55<m <58所以m =56,57则100﹣m =44,43.有两种方案:进甲种文具56件,则乙种文具44件;或进甲种文具57件,则乙种文具43件.22.如图,在平面直角坐标系中,⊙M 过原点O ,与x 轴交于A (4,0),与y 轴交于B (0,3),点C 为劣弧AO 的中点,连接AC 并延长到D ,使DC =4CA ,连接BD .(1)求⊙M 的半径;(2)证明:BD 为⊙M 的切线;(3)在直线MC 上找一点P ,使|DP ﹣AP |最大.【解答】(1)解:∵M 过原点O ,与x 轴交于A (4,0),与y 轴交于B (0,3), ∴AB 是⊙O 的直径,由题意可得出:OA 2+OB 2=AB 2,AO =4,BO =3,∴AB =5,∴圆的半径为52;(2)证明:由题意可得出:M (2,32) 又∵C 为劣弧AO 的中点,由垂径定理且 MC =52,故 C (2,﹣1)过 D 作 DH ⊥x 轴于 H ,设 MC 与 x 轴交于 K ,则△ACK ∽△ADH ,又∵DC =4AC ,故 DH =5KC =5,HA =5KA =10,∴D (﹣6,﹣5)设直线AB 表达式为:y =kx +b ,{4k +b =0b =3, 解得:{k =−34b =3故直线AB 表达式为:y =−34x +3,同理可得:根据B ,D 两点求出BD 的表达式为y =43x +3,∵k AB ×k BD =﹣1,∴BD ⊥AB ,BD 为⊙M 的切线;(3)解:取点A 关于直线MC 的对称点O ,连接DO 并延长交直线MC 于P ,此P 点为所求,且线段DO 的长为|DP ﹣AP |的最大值;设直线DO 表达式为 y =kx ,∴﹣5=﹣6k ,解得:k =56,∴直线DO 表达式为 y =56x又∵在直线DO 上的点P 的横坐标为2,y =53,∴P (2,53), 此时|DP ﹣AP |=DO =√62+52=√61.23.如图,直线AB 的解析式为y =2x +4,交x 轴于点A ,交y 轴于点B ,以A 为顶点的抛物线交直线AB 于点D ,交y 轴负半轴于点C (0,﹣4).(1)求抛物线的解析式;(2)将抛物线顶点沿着直线AB 平移,此时顶点记为E ,与y 轴的交点记为F ,①求当△BEF 与△BAO 相似时,E 点坐标;②记平移后抛物线与AB 另一个交点为G ,则S △EFG 与S △ACD 是否存在8倍的关系?若有请直接写出F 点的坐标.【解答】解:(1)直线AB 的解析式为y =2x +4,令x =0,得y =4;令y =0,得x =﹣2.∴A (﹣2,0)、B (0,4).∵抛物线的顶点为点A (﹣2,0),∴设抛物线的解析式为:y =a (x +2)2,点C (0,﹣4)在抛物线上,代入上式得:﹣4=4a ,解得a =﹣1,∴抛物线的解析式为y =﹣(x +2)2.(2)平移过程中,设点E 的坐标为(m ,2m +4),则平移后抛物线的解析式为:y =﹣(x ﹣m )2+2m +4,∴F (0,﹣m 2+2m +4).①∵点E 为顶点,∴∠BFE <90°,∴若△BEF 与△BAO 相似,只能是点E 作为直角顶点,∴△BAO ∽△BFE ,∴OA EF =OB BE ,即2EF =4BE ,可得:BE =2EF .如答图2﹣1,过点E 作EH ⊥y 轴于点H ,则点H 坐标为:H (0,2m +4).∵B (0,4),H (0,2m +4),F (0,﹣m 2+2m +4),∴BH=|2m|,FH=|﹣m2|.在Rt△BEF中,由射影定理得:BE2=BH•BF,EF2=FH•BF,又∵BE=2EF,∴BH=4FH,即:4|﹣m2|=|2m|.若﹣4m2=2m,解得m=−12或m=0(与点B重合,舍去);若﹣4m2=﹣2m,解得m=12或m=0(与点B重合,舍去),此时点E位于第一象限,∠BEF为锐角,故此情形不成立.∴m=−1 2,∴E(−12,3).②假设存在.联立抛物线:y=﹣(x+2)2与直线AB:y=2x+4,可求得:D(﹣4,﹣4),∴S△ACD=12×4×4=8.∵S△EFG与S△ACD存在8倍的关系,∴S△EFG=64或S△EFG=1.联立平移抛物线:y=﹣(x﹣m)2+2m+4与直线AB:y=2x+4,可求得:G(m﹣2,2m).∴点E与点G横坐标相差2,即:|x G|﹣|x E|=2.当顶点E在y轴左侧时,如答图2﹣2,S△EFG=S△BFG﹣S△BEF=12BF•|x G|−12BF|x E|=12BF•(|x G|﹣|x E|)=BF.∵B(0,4),F(0,﹣m2+2m+4),∴BF=|﹣m2+2m|.∴|﹣m2+2m|=64或|﹣m2+2m|=1,∴﹣m2+2m可取值为:64、﹣64、1、﹣1.当取值为64时,一元二次方程﹣m2+2m=64无解,故﹣m2+2m≠64.∴﹣m2+2m可取值为:﹣64、1、﹣1.∵F(0,﹣m2+2m+4),∴F坐标为:(0,﹣60)、(0,3)、(0,5).同理,当顶点E在y轴右侧时,点F为(0,5);综上所述,S△EFG与S△ACD存在8倍的关系,点F坐标为(0,﹣60)、(0,3)、(0,5).。
深圳中学2014年中考数学一模试卷(含答案)

深圳中学2014年中考第一次模拟考试数学考生须知:1.本试卷共5页。
全卷满分150分。
考试时间为120分钟。
试题包含选择题和非选择题。
考生答题全部答在答题卡上,答在本试卷上无效。
2.请将自己的姓名、考试证号用0.5毫米黑色墨水签字笔填写在答题卡上。
3.答选择题必须用2B铅笔将答题卡上对应的答案标号涂黑。
如需改动,请用橡皮擦干净后,再选涂其它答案。
答非选择题必须用0.5毫米黑色墨水签字笔写在答题卡的指定位置,在其它位置答题一律无效。
一、选择题(共10小题,每小题3分,共30分.).C D.C D..C D.5.(3分)如图,已知Rt△ABC中,∠C=90°,BC=3,AC=4,则sinA的值为().C D.7.(3分)如图,图1是一个底面为正方形的直棱柱;现将图1切割成图2的几何体,则图2的俯视图是().C D.210.(3分)如图,将边长为a的正六边形A1A2A3A4A5A6在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为().C D.二、填空题(共6小题,每小题3分,共18分,请将答案填在答题卡上).11.(3分)因式分解:a2+2a=_________.12.(3分)某市在市中心建了一个文化广场,建成后总面积达163500平方米,成为该市“文化立市”和文化产业大发展的新标志,把163500平方米用科学记数法可表示为_________平方米.13.(3分)如图,等腰梯形ABCD中,AB∥DC,BE∥AD,梯形ABCD的周长为26,DE=4,则△BEC的周长为_________.14.(3分)已知⊙O1与⊙O2的半径分别是方程x2﹣4x+3=0的两根,且圆心距O1O2=t+2,若这两个圆相切,则t=_________.15.(3分)双曲线y1、y2在第一象限的图象如图,,过y1上的任意一点A,作x轴的平行线交y2于B,交y轴于C,若S△AOB=1,则y2的解析式是_________.16.(3分)若a1=1﹣,a2=1﹣,a3=1﹣,…;则a2014的值为_________.(用含m的代数式表示)三、解答题(本大题共9题,满分102分.解答应写出文字说明、证明过程或演算步骤).17.(9分)解不等式组,并把解集在数轴上表示出来.18.(9分)如图,已知:在△ABC中,AB=AC,∠BAF=∠CAE,求证:BE=CF.19.(10分)化简求值:,其中x=2.20.(10分)“初中生骑电动车上学”的现象越来越受到社会的关注,某校利用“五一”假期,随机抽查了本校若干名学生和部分家长对“初中生骑电动车上学”现象的看法,统计整理制作了如下的统计图,请回答下列问题:(1)这次抽查的家长总人数为_________;(2)请补全条形统计图和扇形统计图;(3)从这次接受调查的学生中,随机抽查一个学生恰好抽到持“无所谓”态度的概率是_________.21.(12分)某市为争创全国文明卫生城,2008年市政府对市区绿化工程投入的资金是2000万元,2010年投入的资金是2420万元,且从2008年到2010年,两年间每年投入资金的年平均增长率相同.(1)求该市对市区绿化工程投入资金的年平均增长率;(2)若投入资金的年平均增长率不变,那么该市在2012年需投入多少万元?22.(12分)马航事件牵动了全国甚至全世界人们的心,当得知MH370客机最后失踪地点是在印度洋南部某海域C处,“雪龙”号科考船立即从B处出发以60km/h的速度前往搜救.已知出发时在B 测得搜救指挥基地A的方位角为北偏东80°,测得失踪地点C的方位角为南偏东25°.航行10小时后到达C处,在C处测得A的方位角为北偏东20°.求C到A的距离.23.(12分)如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.(1)求证:CD为⊙O的切线;(2)求证:∠C=2∠DBE;(3)若EA=AO=2,求图中阴影部分的面积.(结果保留π)24.(14分)如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于F,连接DF.(1)证明:∠BAC=∠DAC,∠AFD=∠CFE.(2)若AB∥CD,试证明四边形ABCD是菱形;(3)在(2)的条件下,试确定E点的位置,使得∠EFD=∠BCD,并说明理由.25.(14分)如图,已知抛物线的方程C1:y=﹣(x+2)(x﹣m)(m>0)与x轴相交于点B、C,与y轴相交于点E,且点B在点C的左侧.(1)若抛物线C1过点M(2,2),求实数m的值;(2)在(1)的条件下,求△BCE的面积;(3)在(1)条件下,在抛物线的对称轴上找一点H,使BH+EH最小,并求出点H的坐标;(4)在第四象限内,抛物线C1上是否存在点F,使得以点B、C、F为顶点的三角形与△BCE相似?若存在,求m 的值;若不存在,请说明理由.深圳中学2014年中考第一次模拟试卷数学答案一、选择题(共10小题,每小题3分,共30分.).C D.C D..C D.5.(3分)如图,已知Rt△ABC中,∠C=90°,BC=3,AC=4,则sinA的值为().C D.sinA==7.(3分)如图,图1是一个底面为正方形的直棱柱;现将图1切割成图2的几何体,则图2的俯视图是().C D.210.(3分)如图,将边长为a的正六边形A1A2A3A4A5A6在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为().C D.a,C=C=aa a+++l=二、填空题(共6小题,每小题3分,共18分,请将答案填在答题卡上).11.(3分)因式分解:a2+2a=a(a+2).12.(3分)某市在市中心建了一个文化广场,建成后总面积达163500平方米,成为该市“文化立市”和文化产业大发展的新标志,把163500平方米用科学记数法可表示为 1.635×105平方米.13.(3分)如图,等腰梯形ABCD中,AB∥DC,BE∥AD,梯形ABCD的周长为26,DE=4,则△BEC的周长为18.14.(3分)已知⊙O1与⊙O2的半径分别是方程x2﹣4x+3=0的两根,且圆心距O1O2=t+2,若这两个圆相切,则t=2或0.15.(3分)双曲线y1、y2在第一象限的图象如图,,过y1上的任意一点A,作x轴的平行线交y2于B,交y轴于C,若S△AOB=1,则y2的解析式是y2=.解:∵=..16.(3分)若a1=1﹣,a2=1﹣,a3=1﹣,…;则a2014的值为1﹣.(用含m的代数式表示)﹣=1=,=1=m=﹣.三、解答题(本大题共9题,满分102分.解答应写出文字说明、证明过程或演算步骤).17.(9分)解不等式组,并把解集在数轴上表示出来.18.(9分)如图,已知:在△ABC中,AB=AC,∠BAF=∠CAE,求证:BE=CF.19.(10分)化简求值:,其中x=2.20.(10分)“初中生骑电动车上学”的现象越来越受到社会的关注,某校利用“五一”假期,随机抽查了本校若干名学生和部分家长对“初中生骑电动车上学”现象的看法,统计整理制作了如下的统计图,请回答下列问题:(1)这次抽查的家长总人数为100;(2)请补全条形统计图和扇形统计图;(3)从这次接受调查的学生中,随机抽查一个学生恰好抽到持“无所谓”态度的概率是.扇形统计图:赞成:,反对:×=.21.(12分)某市为争创全国文明卫生城,2008年市政府对市区绿化工程投入的资金是2000万元,2010年投入的资金是2420万元,且从2008年到2010年,两年间每年投入资金的年平均增长率相同.(1)求该市对市区绿化工程投入资金的年平均增长率;(2)若投入资金的年平均增长率不变,那么该市在2012年需投入多少万元?22.(12分)马航事件牵动了全国甚至全世界人们的心,当得知MH370客机最后失踪地点是在印度洋南部某海域C处,“雪龙”号科考船立即从B处出发以60km/h的速度前往搜救.已知出发时在B 测得搜救指挥基地A的方位角为北偏东80°,测得失踪地点C的方位角为南偏东25°.航行10小时后到达C处,在C处测得A的方位角为北偏东20°.求C到A的距离.×=300×=100kmCA=300+100=1003)+23.(12分)如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.(1)求证:CD为⊙O的切线;(2)求证:∠C=2∠DBE;(3)若EA=AO=2,求图中阴影部分的面积.(结果保留π)BD=2BF=2××﹣24.(14分)如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于F,连接DF.(1)证明:∠BAC=∠DAC,∠AFD=∠CFE.(2)若AB∥CD,试证明四边形ABCD是菱形;(3)在(2)的条件下,试确定E点的位置,使得∠EFD=∠BCD,并说明理由.25.(14分)如图,已知抛物线的方程C1:y=﹣(x+2)(x﹣m)(m>0)与x轴相交于点B、C,与y轴相交于点E,且点B在点C的左侧.(1)若抛物线C1过点M(2,2),求实数m的值;(2)在(1)的条件下,求△BCE的面积;(3)在(1)条件下,在抛物线的对称轴上找一点H,使BH+EH最小,并求出点H的坐标;(4)在第四象限内,抛物线C1上是否存在点F,使得以点B、C、F为顶点的三角形与△BCE相似?若存在,求m 的值;若不存在,请说明理由.((=,∴)﹣=2(•±+2∴∴((EC=。
2014年广东省深圳市中考数学试卷及答案

2014年广东省深圳市中考数学试卷及答案一、选择题1、9的相反数()1A:-9 B:9 C:±9 D:9答案:A解析:考点:相反数,有理数的概念中考常规必考,多第一题。
2、下列图形中是轴对称图形但不是中心对称图形的是()答案:B解析:考点:轴对称和中心对称。
中考常规必考。
3、支付宝与”快的打车”联合推出优惠,”快的打车”一夜之间红遍大江南北,据统计,2014年”快的打车”账户流水总金额达到47.3亿元,47.3亿元用科学计数法表示为()A:4.73×108B: 4.73×109 C:4.73×1010 D:4.73×1011答案:B解析:考点:科学计数法。
中考常规必考。
4、由几个大小相同的正方形组成的几何图形如图所示,则它的俯视图为()A B C D答案:A解析:考点:三视图A:平均数3 B:众数是-2 C:中位数是1 D:极差为8答案:D解析:考点:数据的代表。
极差:最大值-最小值。
6-(-2)=8。
平均数:(-2+1+2+1+4+6)÷6=2。
众数:1。
中位数:先由小到大排列:-2,1,1,2,4,6,中间两位为1和2,则中位数计算为:(1+2)÷2=1.5.6,已知函数y=ax+b经过(1,3)(0,-2),求a-b=()A:-1 B:-3 C:3 D:7答案:D解析:考点:待定系数法求函数解析式。
代入(1,3),(0,-2)到函数解析式y=ax+b得,a+b=3,b=-2,则a=5,b=-2,a-b=77、.下列方程中没有实数根的是()A、x2+4x=10B、3x2+8x-3=0C、x2-2x+3=0D、(x-2)(x-3)=12答案:C考点:判根公式的考察:△=b2-4ac。
C项中△<0,无实数根。
8、如图,△ABC和△DEF中,AB=DE, ∠B=∠DEF,添加下列哪一个条件无法证明△ABC≌△DEF()A、AB∥DEB、∠A=∠DC、AC=DFD、∠ACB=∠F答案:C考点:三角形全等的条件:SSS、SAS、AAS、ASA、HL。
2014深圳中考数学试题及答案解析

深圳市2014年中考数学真题及答案一、选择题1.9的相反数是()A.-9B.9C.±9D.91 【答案】A【考点】有理数的相反数2.下列图形中是轴对称图形但不是中心对称图形的是A. B. C. D.【答案】B 【考点】轴对称与中心对称3.支付宝与快的打车联合推出优惠,快的打车一夜之间红遍大江南北,据统计,2014年快的打车账户流水总金额达到47.3亿元,47.3亿用科学计数法表示为( )A.4.73×810B.47.3×810C.4.73 ×910D.4.73 ×1110【答案】C【考点】科学计数法4.由几个大小相同的正方形组成的几何图形如图所示,则它的俯视图为( )A. B. C. D.【答案】A【考点】三视图5.在-2,1,2,1,4,6中正确的是( )A. 平均数3B.众数是-2C.中位数是1D.极差为8【答案】D【考点】数据的代表6.已知函数y=ax+b 经过(1,3)(0,-2),则a-b 的值为( )A.-1B.-3C.3D.7【答案】D【考点】一次函数的解析式【解析】函数经过(1,3)(0,-2),所以⎩⎨⎧=-+=b ba 23,得⎩⎨⎧-==25b a ,所以a-b=77.下列方程没有实数根的是( ) A.2x +4X=10 B.32x +8X-3=0C.2x -2X+3=0D.(X-2)(X-3)=12【答案】C【考点】一元二次方程的判别式8.如图,△ABC 和△DEF 中,AB=DE ,∠B=∠DEF ,添加下列哪一个条件无法证明△ABC ≌△DEF ( )A. ∠A =∠DB. AC=DfC. AC ∥DFD.∠ACB=∠F【答案】B【考点】全等三角形的判定9.袋子里有4个球,标有2,3,4,5,先抽取一个并记住,放回,然后再抽取一个,抽取的两个球数字之和大于6的概率是( )A.21B. 127 C.85 D.43 【答案】C【考点】概率之树状图或列表法【解析】10.小明去爬山,在山脚看山顶角度为30°,小明在坡比为5:12的山坡上走1300米,此时小明看山顶的角度为60°,求山高( )A. 600-2505B.6003-250C.350+3503D.5003【答案】B【考点】三角函数应用【解析】依题意:ED :DB :EB=5:12:13∵BE=1300∴DB=1200,ED=500设EF=X∵∠ABC=30°,∠AEF=60°∴BC=3AC ,AF=3EF∴1200+X=3(3X+500)∴X=600-2503∴AC=3+500=6003-250 11.二次函数y=a 2x +bx+c 图像如图所示,下列正确的个数为( )①bc >0;②2a+b >0;③a+b+c >0;④2a-3c <0;⑤a 2x +bx+c=0有一个正根和一个负根;⑥当x >1时,y 随x 增大而减小A. 2B.3C.4D.5【答案】B【考点】二次函数图像与系数的关系。
1405032014深圳中考数学模拟试卷附答案

2014年深圳市数学全真模拟试卷第一部分 (选择题,共36分)一、选择题:本部分共12小题,每小题3分,共36分.每小题给出4个选项,其中只有一个是正确的. 1.12-的倒数为( ) A .2B .2-C .12D .12-2.今年第七届深圳文博会圆满落幕,成交额再创新高.总成交额达1245.4亿元,这个数据用科学记数法表示为(保留三个有效数字)( ) A .1.25×103元 B .1.24×103元 C .1.25×1011元D .1.24×1011元3.下列运算正确的是( ) A .()323626xy x y -=-B .()222x y x y +=+ C .22()()x y x y x y -+--=-D .235()a a =4.下列不等式组的解集,在数轴上表示为如图1所示的是( )A .1020x x ->⎧⎨+≤⎩B .1020x x -≤⎧⎨+<⎩C .1020x x +≥⎧⎨-<⎩D .1020x x +>⎧⎨-≤⎩5.下列图形中既是中心对称图形,又是轴对称图形的是( )A B C D6.下列四个命题中,假.命题的是( ) A .四条边都相等的四边形是菱形 B .有三个角是直角的四边形是矩形C .对角线互相垂直平分且相等的四边形是正方形D .一组对边平行,另一组对边相等的四边形是等腰梯形7.如图2,由6个大小相同的正方体搭成的几何体,则关于它的视图说法正确的是( ) A .主视图的面积最大 B .左视图的面积最大 C .俯视图的面积最大D .三个视图的面积一样大-1 0 1 2图1图2ADEPBC图6图3OAB图4Oyx8.如图3,将半径为2cm 的圆形纸片折叠后,圆弧恰好经过圆心O ,则折痕AB 的长为( ) A .2cm B .3cm C .23cm D .25cm9.下列说法中正确的是( )A .“打开电视,正在播放《新闻联播》”是必然事件B .某次抽奖活动中奖的概率为1100,说明每买100张奖券,一定有一次中奖 C .数据1,1,2,2,3的众数是3D .想了解深圳市居民人均年收入水平,宜采用抽样调查 10.如图4为反比例函数3k y x-=的图象,当x >0时,y 随x 的增大而增大,则k 的取值范围是( ) A .k <3 B .k ≤3 C .k >3D .k ≥311.小亮早晨从家骑车到学校,先上坡后下坡,行程情况如图5所示.若返回时上坡、下坡的速度仍保持不变,那么小明从学校骑车回家用的时间是( ) A .48分钟B .37.2分钟C .30分钟D .33分钟12.如图6,正方形ABCD 的面积为12,△ABE 是等边三角形,点E 在正方形ABCD 内,在对角线AC 上有一点P ,使PD +PE 的和最小,则这个最小值为( ) A .23B .26C .3D .6第二部分 (非选择题,共64分)二、填空题(本题共4小题,每小题3分,共12分). 13.因式分解:24ab a -=___________________________.14.如图7,在ΔABC 中,∠C =90°,∠ABC 的平分线BD 交AC 于点D ,若BD =10厘米,BC =8厘米,则点D 到直线AB 的距离是__________厘米.15.如图8,边长为1的小正方形构成的网格中,⊙O 的圆心O 在格点上,半径为1,则∠AED 的正切值等路程/百米 时间/分钟30 9636 018 图5O yx(A )A 1C1 1 2BA 2A 3B 3 B 2 B 1 图9图7D ACB图8OA BCDE于_________.16.如图9,已知点(00)A ,,(30)B ,,(01)C ,,在△ABC 内依次作等边三角形,使一边在x 轴上,另一个顶点在BC 边上,作出的等边三角形分别是第1个△AA 1B ,第2个△B 1A 2B 2,第3个△B 2A 3B 3,…,则第n 个等边三角形的边长等于_________.三、解答题(本题共7小题,其中第17小题6分,第18小题6分,第19小题7分,第20小题7分,第21小题8分,第22小题9分,第23小题9分,共52分.)17.(本题6分)计算:()()12011012tan 601sin 45cos30123-⎛⎫︒-+-+︒-︒-- ⎪⎝⎭18.(本题6分)解不等式组53(1)13722x x x x >+⎧⎪⎨≤-⎪⎩19.(本题7分)某校为了举办“庆祝建党90周年”的活动,小明调查了本校所有学生,将调查的结果制作扇形统计图和条形统计图(如图10所示),根据图中给出的信息,回答下列问题(1)该学校学生有_________人.(2分)(2)学校赞成举办运动会比赛的学生所占圆心角为_________度.(3分) (3)学校赞成举办演讲比赛的学生有_________人.(2分)活动形式A B C人数160图10A :文化演出B :运动会C :演讲比赛C AB40% 35%20.(本题7分)如图11,在△ABC 中,BC >AC ,点D 在BC 上,且DC =AC ,∠ACB 的平分线CF 交AD于F ,点E 是AB 的中点,连结EF . (1)求证:EF ∥BC ;(4分)(2)若四边形BDFE 的面积为6,求△ABD 的面积.(3分)21.(本题8分)2011年深圳大运会某工程,在工程招标时,接到甲、乙两个工程队的投标书.施工一天,需付甲工程队工程款12万元,乙工程队工程款5万元.工程领导小组根据甲、乙两队的投标书测算,有如下方案:(1)甲队单独完成这项工程刚好如期完成; (2)乙队单独完成这项工程要比规定日期多用6天;(3)若甲、乙两队合做3天,余下的工程由乙队单独做也正好如期完成.试问:①这项工程的工期是多少天(5分)②在不耽误工期的前提下,你觉得哪一种施工方案最节省工程款?请说明理由.(3分)F ABCDE图1122.(本题9分)抛物线对称轴为直线x =4,且过点O (0,0),()2,10B --,A 是抛物线与x 轴另一个交点. (1)求二次函数的解析式;(3分)(2)如图12,点C 从O 点出发,沿x 轴以每秒钟一个单位的速度运动,矩形CDEF 内接于抛物线,C 、D 在x 轴上,E 、F 在抛物线上,运动时间t (0<t <4)为何值时,内接矩形CDEF 的周长最长?并求周长的最大值;(3分)(3)在(2)中内接矩形CDEF 的周长取得最大的条件下,x 轴上是否存在点P 使△PEF 为直角三角形(P 为直角顶点),若存在,请求P 点坐标;若不存在,说明理由. (3分)23.(本题9分)如图13,在直角坐标系中,点A ,B ,C 的坐标分别为(1-,0),(3,0),(0,3),D (1,m )在直线BC 上,⊙A 是以A 为圆心,AD 为半径的圆. (1)求m 的值;(2分)(2)求证:⊙A 与BC 相切;(2分)(3)在x 负半轴上是否存在点M ,使MC 与⊙A 相切,若存在,求点M 的坐标;若不存在,说明理由;(2分)(4)线段AD 与y 轴交于点E ,过点E 的任意一直线交⊙A 于P 、Q 两点,问是否存在一个常数K ,始终满足PE •QE =K ,如果存在,请求出K 的值;若不存在,请说明理由.(3分)y A OBCDEF QPx图13 OACDFE图1258 64 2 y x参 考 答 案一、选择题(每题3分,共36分)1.B 2.C 3.C 4.D 5.C 6.D 7.C 8.C 9.D 10.A 11.B 12.A 二、填空题(每题3分,共12分)13.(2)(2)a b b +- 14.6 15.12 16.32n 三、解答题17.解:原式=23311233--+-=- 18.解:解不等式(1)得32x >解不等式(2)得72x ≤ 不等式组的解集为3722x <≤ 19.解:(1)400 (2)126 (3)10020.(1)证明:∵AC =CD ,CF 是ACD ∠的平分线,∴F 是AD 的中点,又∵E 是AB 的中点,EF //BD ,(2)∵EF //BD ,∴AEF ABD ∠=∠,AFE ADB ∠=∠,∴AEF ∆∽ABD ∆∴214AEF ABD S AE S AB ∆∆⎛⎫== ⎪⎝⎭,68114ABD S ∆==- 21.(1)设这项工程的工期需要x 天,根据题意得:316xx x +=+,解得:x =6 经检验x =6是方程的解,答:完成这项工程的需要6天 (2)方案一:6×12=72万元,方案二不符合题意,方案三:3×12+6×5=66万元,∵66<72,选择方案三22.(1)2142y x x =-+(2)设(,0)C t ,四边形CDEF 的周长为l则22212()2(482)416(2)202l CD FC t t t t t t =+=-++-=-++=--+ 当点C 的坐标为(2,0)时,,四边形CDEF 的周长有最大值20 (3)由(2)得:(2,0),(6,0),(2,6),(6,6)C D F E设(,0)P m ,由222PE PF EF +=得:222226(2)(6)64m m +-+-+=化简得:28480m m -+=,240b ac ∆=-<,∴方程无解,∴点P 不存在 23.(1)设BC 的直线方程为y kx b =+,将B 、C 点代入可得1,3k b =-=,则BC 直线方程为3y x =-+,将D (1,m )点代入得m =2.(2)由222AD BD AB +=得:AD BC ⊥,∴⊙A 与BC 相切(3)存在(21,0)M -,理由如下:假设点M ,连接CM 与圆切于点N ,连AN ,则AN CM ⊥则ANM ∆∽COM ∆,AN MNOC OM=,设(,0)M t ,则()218223t t---=-解得:21t =-或t =3(舍去)(4)存在k =6,理由如下:当PQ 与y 轴重合时,(71)(71)6k =-+=当PQ 与y 轴不重合时,设y 轴与圆交于点R 与F ,连接PF 与QR ,∵,QER PEF RQE EFP ∠=∠∠=∠,∴ERQ ∆∽EPF ∆,∴ER EQPE EF=, 则=k(71)(71)6PE QE ER EF ∙=∙=-+=。
2014年深圳市中考数学全真模拟试卷含答案 (精选4套)

5、考试结束,请将本试卷和答题卡一并交回.
第一部分选择题
(4)、存在点N,做一条与BC平行的直线,平移,
当它与抛物线有一个交点时,此时以BC为底的三角形
高度最大。抛物线与该直线的交点,就是所求的N点。
易求BC的K值为 ,所以设动直线为:
,与抛物线联立:
(1分)
所以 (1分)
过N做y轴的平行线,交BC于一点,求此点坐标
BC: ,令x=4,解得y=2,∴三角形BCN面积的最大值= (1分)
A.0B.2C.-2D.0或2
7.用配方法解方程 ,配方后的方程是( )
A. B. C. D.
8.若一次函数 的函数值 随 的增大而减小,且图象与 轴的负半轴相交,那么对 和 的符号判断正确的是()
A. B. C. D.
9.如图,将△ 绕着点 顺时针旋转50°后得到△ .若∠ =40°.
∠ =110°,则∠ 的度数是()
21、(1)证明:正方形ABCD中,∠BAD=90°,AD=AB,
∵AF⊥AE,∴∠FAB+∠BAE=90°
∵∠DAE+∠BAE=90°,∴∠FAB=∠DAE -----2分
∵∠FBA=∠D=90°,∴△ABF≌△ADE
∴AE=AF -------------4分
(2)解:在Rt△ABF中,∠FBA=90°,AF=7,BF=DE=2
在Rt△BCF中,设BC=x米,则BF=2x,CF=
在Rt△BCE中,∠BEC=60°,CE=
深圳市2014年中考第一轮模拟考试(一模)数学试题

第二部分
非选择题
填空题(本题共 4 小题,每小题 3 分,共 12 分) 13.分解因式: 4 x2 9 =__________. 4 3 0 的解为 14.方程 . x x2 15.如图,三个小正方形的边长都为 1 ,则图中阴影部分面积的 和是 (结果保留 ) . 16.如图,一段抛物线: y x x 4 0 x 4 ,记为 C1 , 它与 x 轴交于点 O , A1 ; 将 C1 绕点 A1 旋转 180° 得 C2 ,交 x 轴于点 A2 ; 将 C2 绕点 A2 旋转 180° 得 C3 ,交 x 轴于点 A3 ; …… 如此进行下去,直至得 C10 .若 P 37, m 在第 10 段抛物线 C10 上,则 m =_________. 第 16 题图 第 15 题图
解答题(本题共 7 小题,其中第 17 题 5 分,第 18 题 6 分,第 19 题 7 分,第 20 题 8 分,第 21 题 8 分,第 22 题 9 分,第 23 题 9 分,共 52 分) 17. (5 分)计算: (1)3 | 3 2 | 2sin 60 4 .
2 5x2 2 x 3 6 . 18. (6 分)先化简,再求值: ,其中 x 2 x 4 x2 x2 3
19. (7 分)某学校为了解学生课外阅读的情况,对学生“平均每天课外阅读的时间”进行了随机抽样调查,下图 是根据调查结果绘制的两幅不完整的统计图.请你根据统计图提供的信息,解答以下问题:
第 22 题图
第 17 题图 (1)平均每天课外阅读的时间为“ 0.5 ~1 小时”部分的扇形图的圆心角为______度; (2)本次一共调查了_________名学生; (3)将条形图补充完整; (4)若该校有 1680 名学生,请估计该校有多少名学生平均每天课外阅读的时间在 0.5 小时以下. 20. (8 分)如图,已知矩形 ABCD 中, AB 4cm , AD 10cm ,点 P 在边 BC 上移动,点 E 、 F 、 G 、 H 分 别是 AB 、 AP 、 DP 、 DC 的中点. ⑴求证: EF GH 5cm ; EF ⑵求当 APD 90 时, 的值. GH
2014深圳中考数学试卷答案

2014深圳中考数学试卷(word 版)答案一、选择题1、A2、B3、B4、A5、D6、D7、C8、C9、C 10、B11、B12、D二、填空题 13、)2)(2(2+-x x 14、315、8C16、485三、解答题17、-218、19、21、【解析】(1)设乙每件x 元,则甲每件(x+10)元1015090+=x x 解得:x=15,经检验x=15是原方程的解,所以,甲每件25元,乙每件15元. (2)设甲y 件,则乙(100-y )件)100%)(201(15%)201(25y y -+++⨯>2460)100(1525y y -+<2080 解得:55<y <58∵y 为整数 ∴y=56或57,∴有两种方案:①甲56件,乙44件,②甲57件,乙43件。
22、(1)解:∵A (4,0),B(0,3);故AO=4,BO=3,由勾股定理的AB=5,∴⊙M 的半径为2.5;(2)如图,连接BC ,直线MC 交OA 于E ∵C 是弧OA 中点,∴由圆的对称性知:MC 垂直平分OA , ∴AE=2,在Rt △AEM 中由勾股定理得ME=23,∴CE=1, ∵AB 是直径,∴∠ACB=900,∵弧OC=弧AC ,∴∠ABC=∠CAE ,∴Rt △ABC ∽Rt △CAE ,∴21==AE CE BC AC ,BC=2AC ; ∵CD=4AC, ∴21==BC AC DC BC , 又∵∠ACB=∠BCD=900, ∴△ABC ∽△BDC , ∴∠BAC=∠DBC ,∴∠DBA=∠DBC+∠ABC=∠BAC+∠ABC=900, ∴BD 为 ⊙M 的切线;【解法2】分别求出:CE=1,AE=2,AC=5,BC=25,CD=45,BD=10,AD=55,AB=5; ∵BD 2+AB 2=AD 2,∴∠DBA=900,∴BD 为 ⊙M 的切线;(3)如图,取A 关于MC 的对称点O ,连DO 并延长交MC 于P ,P 为所求,此时线段DO 的长为|DP-AP|最大值;求出D (-6,-5),由D 、O 得直线DO 为:x y 65=,因为P 的横坐标为2,所以P (2,35),此时|DP-AP|=DO=61;23、(1)设抛物线解析式为:2)2(+=x a y ,将C (0,-4)代入解得:1-=a ,∴解析式为2)2(+-=x y ;(2)【解法1】设E (m ,2m+4),经分析只能是△BEF ∽△BOA ,EF ⊥BE ,m <0; 如图,作EH ⊥y 轴于H ,由y=2x+4得A (-2,0)、B (0,4)故AO=2,BO=4,∵∠ABO=∠FBE=∠EBH (公共角),∠EFB=∠EFH (公共角),∠AOB=∠FEB=∠EHB=∠FHE=900; ∴△AOB ∽△FEB ∽△EHB ∽△FHE ; ∴21===BO AO BH EH EH FH ,∴EH=-m ,HF=-21m, BH=-2m,BF=-25m ; ∴F(0, 25m+4), 设平移后的抛物线顶点式为:42)(2++--=m m x y ,将F(0,25m+4)代入解得,m 1=0(舍),m 2=21-; ∴E (21-,3)。
2014年深圳市龙岗区中考模拟考试数学试题参考答案
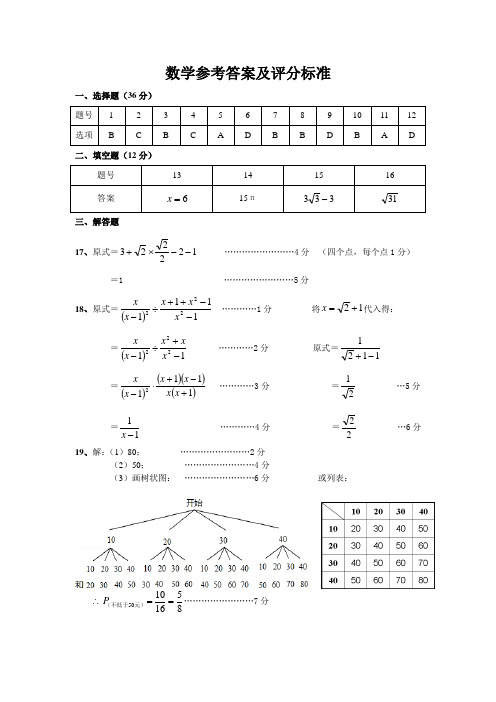
数学参考答案及评分标准一、选择题(36分)二、填空题(12分)三、解答题 17、原式=122223--⨯+……………………4分 (四个点,每个点1分) =1 ……………………5分18、原式=()1111222--++÷-x x x x x…………1分 将12+=x 代入得: =()11222-+÷-x xx x x…………2分 原式=1121-+ =()()()()11112+-+⋅-x x x x x x…………3分 =21 …5分=11-x …………4分 =22 …6分 19、解:(1)80; ……………………2分(2)50; ……………………4分(3)画树状图: ……………………6分 或列表:∴85161050==元)(不低于P ……………………7分20、(1)证明:∵正方形ABCD∴BC=DC ,∠B=∠FDC=90° ………………2分 又∵BE=DF∴△CBE ≌△CDF (SAS ) ∴CE=CF ………………3分(2)解:由(1)得:△CBE ≌△CDF∴∠BCE=∠DCF ………………4分 ∴∠BCE+∠ECD=∠DCF+∠ECD 即∠ECF=∠BCD=90° 又∵∠GCE=45°∴∠GCF=∠GCE=45° ………………5分 ∵CE=CF ,∠GCE=∠GCF ,GC=GC∴△ECG ≌△FCG (SAS ) ………………7分 ∴GE=GF=DG+DF= DG+BE=3+5=8 ………………8分21、(1)连接OE ∵OD=OE∴∠1=∠2 ………………1分 ∵BD=BF∴∠1=∠F ………………2分∴∠2=∠F∴OE ∥BF ………………3分 又∵BF ⊥AC ∴OE ⊥AC∴AC 与⊙O 相切 ………………4分 (2)由(1)得:OE ∥BF∴△AOE ∽△ABC ………………5分∴AB AOBC OE = ………………6分 即12126rr -=∴4=r ………………7分 ∴S⊙O =π2r =π24⨯=16π ………………8分22、(1)设每台空调、电风扇的进货价分别为y x ,元,由题可得:⎩⎨⎧=+=+22500301017400208y x y x ………………2分 解得:⎩⎨⎧==1501800y x ………………3分所以每台空调进货价为1800元,每台电风扇进货价为150元(2))60)(1508.0250()18008.02500(a a w --⨯+-⨯= ………………5分 3000150+=a ………………6分(3)由题可得:⎩⎨⎧≥+≤-+6000300015045300)60(1501800a a a ………………7分解得:2220≤≤a∴222120或或=a ………………8分 ∴有三种方案:①空调20电风扇40②空调21电风扇39 (未列出三种方案不扣分) ③空调22电风扇38方案③,当22=a 时,w 最大,最大值为6300元 ………………9分23、解:(1)D (1-,1)、A ’(3,1) ………1分(只得其中一个也给1分) 设抛物线的解析式为c bx ax y ++=2将D (1-,1)、A (0,4)、A ’(3,1)代入得:⎪⎩⎪⎨⎧=++==+-13941c b a c c b a ………2分解得:⎪⎩⎪⎨⎧==-=421c b a ∴422++-=x x y ………3分或:5)1(2+--=x y ………3分 (2)根据旋转:∠CED ’ =90°∴△CED ’∽△CAB ………4分∴2''⎪⎭⎫⎝⎛=∆∆CB CD S S CAB CED即2'10123⎪⎪⎭⎫⎝⎛=∆CED S ………5分 ∴203'=∆CED S ………6分 或:易得:13+=x y BC 与231''+-=x y D A ………4分 (只得其中一个也给1分)由⎪⎩⎪⎨⎧+-=+=23113y x y 得E (103,1019) ………5分 ∴20321031'=⨯=∆CED S ………6分 (3)易得:4'+-=x y AA设P (t ,422++-t t ),则Q (t ,4+-t ) ………7分∴PQ =()()4422+--++-t t t =t t 32+-∴()827232323322'+⎪⎭⎫ ⎝⎛--=⋅+-=∆t t t S APA∴△AP A ’的最大面积为827………8分 此时,P (23,419) ………9分。
深圳市2014年中考数学模拟试题四及答案

深圳市2014年中考数学模拟试题四及答案时间:90分钟一、(本部分共12小题,每小题3分,共36分) 1.若一个数的相反数是2,则这个数是( ) A .2B .2-C .21 D .21-2.图1中几何体的俯视图是( )3.《爸爸去哪儿》是2013年很受欢迎的电视节目,电影《爸爸去哪儿》更是成为马年春节 电影市场的宠儿,票房收入约699000000元,近似数699000000用科学计数法表示为( ) A .7109.69⨯ B .81099.6⨯ C .91099.6⨯ D .910699.0⨯ 4.下列计算正确的是( )A 532)(a a =B .236a a a =÷C .32a a a =⋅D .222)(b a b a -=-5.用直尺和圆规作一个角的平分线的示意图如图2所示,则能说明∠AOC=∠BOC 的依据是( ) A .(AAS) B .(SAS) C .(ASA) D .(SSS)6.有五张卡片(形状、大小、质地都相同),正面分别画有下列图形:①线段;②正三角形;③平行四边形; ④等腰梯形;⑤圆.将卡片背面朝上洗匀,从中随机抽取一张,正面图形一定满足既是轴对称图形,又是 中心对称图形的概率是( ) A .51 B .52 C .53 D .547.我市某小区开展了“节约用水为环保作贡献”的活动,为了解居民用水情况,在小区随机抽查了10户则关于这10户家庭的月用水量,下列说法错误的是( )A .方差是4B .极差是2C .平均数是9D .众数是98.如图3,直线l ∥m ,将含有45°角的三角形板ABC 的直角顶点C 放在直线m 上,若∠1 =25°,则∠2的度数为( )A .15°B .20°C .25°D.45° 9.不等式组⎩⎨⎧≥->-024213x x 的解集在数轴上表示为( )A B C D 图1 图3图2A B C D 10.为庆祝“六一”儿童节,某幼儿园举行用火柴棒摆“金鱼”比赛.如图所示:按照上面的规律,摆第n 个“金鱼”需用火柴棒的根数为( ) A .26n + B .86n + C .44n + D .8n11.如图4所示的边长为1正方形网格中,网格线的交点称为格点.已知A 、B 是两格点,如果C 也 是图中的格点,且使得△ABC 为等腰三角形,则BC 的长不可能是( ) A .2 B .2 C .5 D .1012.在锐角三角形ABC 中,BD ⊥AC 于D ,CE ⊥AB 于E ,且ABC AD E S S ∆∆=21,则=∠A ( ) A .︒75 B .︒60 C .︒45 D .︒30二、填空题(本题共4小题,每小题3分,共12分) 13.二元一次方程组⎩⎨⎧=-=+112312y x y x 的解是___________.14.已知x 为整数,且918232322-++--+x x x x 为正整数,则整数=x ___________. 15.如图5,点A 在双曲线xky =上,且OA =4,过A 作AC ⊥x 轴,垂足为C , OA 的垂直平分线交OC 于B ,△ABC 的周长为72,则=k ___________.16.如图6,A MON ,20︒=∠为射线OM 上一点,OA=4,D 为射线ON 上一点,8=OD ,C 为射线AM 上任意一点,B 是线段OD 上任意一点,那么折线ABCD 的长CD BC AB ++的最小值是___________. 三、解答题:(本题共7小题,共52分) 17.(本题5分)计算:02)23(45sin 2)21(16-+︒--+-图5图6图418.(本题6分)在景新中学2014年“爱心压岁钱”捐款活动中,小亮对甲,乙两班捐款情 况进行统计,得到如下三条信息:信息一:甲班共捐款400元,乙班共捐款360元;信息二:乙班平均每人捐款钱数比甲班平均每人捐款钱数少20%;信息三:甲班比乙班少5人;请你根据以上三条信息,列方程求出甲班平均每人捐款多少元?19.(本题7分)某校组织了由八年级800名学生参加的校园安全知识竞赛,安老师为了了解同学们对校园安全知识的掌握情况,从中随机抽取了部分同学的成绩作为样本,把成绩按优秀、良好、及格、不及格4个级别进行统计,并绘制成了如图的条形统计图和扇形统计图(部分信息未给出), 请根据以上提供的信息,解答下列问题:(1)(2分)被抽取的部分学生有_________人;(2)(3分)请补全条形统计图,在扇形统计图中表示及格的扇形的圆心角是_________度; (3)(2分)请估计八年级的800名学生中达到良好和优秀的有_________人.20.(本题7分)如图8,在△ABC 中,D 、E 分别是AB 、AC 的中点,BE=2DE ,延长DE 到点F ,使得 EF=BE ,连接CF .图7(1)图7(2)(1)(3分)求证:四边形BCFE 是菱形;(2)(4分)若CE=4,∠BCF=120°,求菱形BCFE 的面积.21.(本题8分)如图9,为了求河的宽度,在河对岸岸边任意取一点A ,再在河这边沿河边取两点B 、C ,使得∠ABC =︒60,BC 长 为30米,量得∠ACB =︒45. 求河的宽度(即求△ABC 中BC 边上的高AD 的长)(精确到0.1米,参考数据:73.13,41.12=≈).22.(本题9分)如图10(1),在平面直角坐标系中, ⊙1O 与x 轴相切于点A (3,0),与y 轴相交于B 、C 两点,且BC=8,连接AB 、1O B .(1)(3分)AB 的长=___________; (2)(3分)求证:∠AB 1O =∠ABO ;(3)(3分)如图10(2),过A 、B 两点作⊙2O 与y 轴的负半轴交于点M ,与1O B 的延长线交于点N ,连接AM 、 MN ,当⊙2O 的大小变化时,∠AB 1O 与∠AMN 始终相等, 问BM -BN 的值是否变化,为什么? 如果不变,请求出 BM -BN 的值.23.(本题10分)如图11所示,对称轴是1-=x 的抛物线与x 轴交于A 、B(1,0)两点,与y 轴交于点C (3,0),作直线AC ,点P 是线段AB 上不与点A 、B 重合的一个动点,过点P 作y 轴的平行线,交直线AC 于点D ,交抛物线于点E ,连结CE 、OD. (1)(3分)求抛物线的函数表达式;图10(2) x图10(1)(2)(3分)当P在A、O之间时,求线段DE长度s的最大值;(3)(4分)连接AE、BC,作BC的垂直平分线MN分别交抛物线的对称轴、x轴于F、N,连接BF、OF,若∠EAC=∠OFB,求点P的坐标.图11(1)图11(2)参考答案及评分意见第一部分 选择题(本部分共12小题,每小题3分,共36分.每小题给出4个选项,其中只有一个是正确的) 9 10 11 12 第二部分 非选择题三、解答题:(本题共7小题,其中第17题5分,第18题6分,第19、20题各7分,第21题8分,第22题9分,第23题10分,共52分) 17.解:原式=122244+⨯-+ …………………………4分 =19-=8 …………………………5分 18.解:设甲班平均每人捐款x 元,根据题意,得.5400%)201(360=--xx …………………………2分解这个方程,得.10=x …………………………4分 经检验,10=x 是所列方程的根. …………………………5分 所以,甲班平均每人捐款10元. …………………………6分 19.解:(1)100; …………………………2分 (2)如图所示(2分): 108; …………………5分 (3)480. …………………………7分20.(1)证明:∵D 、E 分别是AB 、AC 的中点,∴DE ∥BC 且2DE=BC , 又∵BE=2DE ,EF=BE , ∴EF=BC ,EF ∥BC ,∴四边形BCFE 是平行四边形, …………………………2分 又∵BE=FE ,∴四边形BCFE 是菱形; …………………………3分 (2)解:∵∠BCF=120°, ∴∠EBC=60°,∴△EBC 是等边三角形, …………………………4分 ∴菱形的边长为4,高为2, …………………………6分 ∴菱形的面积为4×2=8. …………………………7分21.解:设AD=x , 在中ADC Rt ∆,=∠CAD ∠ACB =45°x AD CD ==∴ ……………………2分在中ABD Rt ∆, ︒=∠60ABC ,︒=∠∴30BADx BD =︒30tan ,x BD 33=∴, ………………………4分 BC CD BD =+ ,即3033=+x x (或由ABC ACD ABD S S S ∆∆∆=+得到) ………5分 解得31545-=x 1.19≈ …………………………7分 河的宽度为1.19米. …………………………8分或解:设AD=x 在中ADC Rt ∆,=∠CAD ∠ACB =45°x AD CD ==∴ ……………………2分∵BC=30,∴BD=x -30,在中ABD Rt ∆, ︒=∠60ABC ,︒=∠∴30BAD , ∴AB=x 260-, ……………………4分由勾股定理,得222AB BD AD =+,222)260()30(x x x -=-+ ……………5分解得31545-=x 1.19≈ ………………………7分 河的宽度为1.19米. ………………………8分22.(13分(2)证明:连接1O A ,则有1O A ⊥AO ,1O A =1O B , …………………………4分∴1O A ∥OB ,∠1O BA=∠1O AB , …………………………5分 ∴ ∠1O AB =∠OBA ,∴ ∠AB 1O =∠ABO ; …………………………6分(3)BM -BN 的值不变.理由为:在MB 上取一点G ,使MG=BN ,连接AN 、∵∠AB 1O =∠ABO ,∠AB 1O =∠AMN ,∴∠ABO=∠AMN , 又∵∠ABO=∠ANM , ∴∠AMN=∠ANM ,7分 8分∵AO ⊥BG , ∴BG=2BO=2,∴BM -BN=BM -MG=BG=2其值不变. …………………………9分23.解:(1)由A 、B )0,1(关于1-=x 对称,得)0,3(-A , …………………………1分 设抛物线为)3)(1(+-=x x a y ,(或设一般式) 将点C )3,0(代入,得3)1(3⨯-⨯=a ,解得,1-=a∴抛物线的函数表达式;32)3)(1(2+--+--=x x x x y 或 …………3分 (2)由B 、C 两点的坐标可求得直线BC 的表达式:3+=x y , …………4分x图10(1)∴,325,5OC GN BN ==-==(G 为对称轴与x 轴的交点) ………7分 可得△FNG ≌△BCO ,GF=OB=1=OG,∴ ︒=∠45FOG , ∴∠OFB=FBG ∠-︒45 ∵ ∠EAC=∠OFB,∴∠EAC=FBG ∠-︒45 …………8分当点P 在A 、O 之间时,∵ FBG EAC EAC ADP AEP ∠=∠-︒=∠-∠=∠45 9分当点P 在B O 、之间时,∵ FBG EAC EAC DAP EAP ∠=∠-︒=∠-∠=∠45 10分(用相似三角形解酌情给分)。
2014年中考数学模拟考试及参考答案(1-4)

参考答案(一)一、选择题: 1.C 2.A 3.D 4.C 5.C二、填空题:6.2x ≥- 7.7.94×106 8.39.4- 10.6 11.3π 12. 3 13.9,37三、解答题: 14.4 15.x 1=31+-,x 2=31-- 16.化简为:2—x .当22-=x 时,原式=2. 17.P (小菲两次都能摸到白球)=164=4118.(1)小山的高为25米;(2)铁架高约43.3米. 19.(1)80 ,40%;(2)补全条形图(略);(3)380.20.解:(1)∵∠ABC =90°, ∴OB ⊥BC ..∵OB 是⊙O 的半径, ∴CB 为⊙O 的切线..又∵CD 切⊙O 于点D , ∴BC =CD ;.(2)由△ADE ∽△ABD ..∴AD AB =AE AD ..∴21BE +=12,∴BE =3,.∴所求⊙O 的直径长为3. 21.(1)2(21010)(5040)101102100y x x x x =-+-=-++(015x <≤且x 为整数) (2)当2200y =时,21011021002200x x -++=,解得:12110x x ==,.当1x =时,5051x +=,当10x =时,5060x +=.所以,当售价定为每件51或60元时,每个月的利润为2200元. ∴当售价不低于51元且不高于60元且为整数时,每个月的利润不低于2200元(或当售价分别为51,52,53,54,55,56,57,58,59,60元时,每个月的利润不低于2200元).22.①∵∠EAB+∠BAP=90°,∠PAD+∠BAP=90°,∴∠EAB=PAD ,又∵AE=AP ,AB=AD ,∴△APD ≌△AEB ;②∵△APD ≌△AEB ,∴∠APD=∠AEB ,又∵∠AEB=∠AEP+∠BEP ,∠APD=∠AEP+∠PAE , ∴∠BEP=∠PAE=90°,∴EB ⊥ED ;③∵EF=BF= ,AE=1,∴在Rt △ABF 中,AB 2=(AE+EF )2+BF 2=4+ ,∴S 正方形ABCD =4+ (下图)23.(1)解:设所求的抛物线解析式()20y ax bx c a =++≠∵点A B C 、、均在此抛物线上.∴42016404a b c a b c c -+=⎧⎪++=⎨⎪=-⎩ ∴1214a b c ⎧=⎪⎪=-⎨⎪=-⎪⎩∴所求的抛物线解析式为2142y x x =--, ∴顶点D 的坐标为912⎛⎫- ⎪⎝⎭, (2)EBC △的形状为等腰三角形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
深圳市2014年初中毕业生学业考试数学模拟试卷说明:1.试题卷共4页,答题卡共4页。
考试时间90分钟,满分100分。
2.请在答题卡上填涂学校.班级.姓名.考生号,不得在其它地方作任何标记。
3.本卷选择题1—12,每小题选出答案后,用2B 铅笔将答题卷选择题答题区内对应题目的答案标号涂黑;非选择题的答案(含作辅助线)必须用规定的笔,写在答题卷指定的答题区内,写在本卷或其他地方无效。
第一部分 选择题一、选择题(本题共有12小题,每小题3分,共36分,每小题有四个选项,其中只有一个是正确的) 1.9的算术平方根是( ) A .3 B .–3 C .±3 D .6 2.下列所给图形中,)3.环境监测中PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.如果1微米=0.000001米,那么数据0.0000025用科学记数法可以表示为( ) A .6105.2⨯ B .5105.2-⨯ C .6105.2-⨯ D .7105.2-⨯4.一组数据3,x ,4,5,8的平均数为5,则这组数据的众数、中位数分别是( ) A .4,5 B .5,5 C .5,6 D .5,85.某商场在“庆五一”促销中推出“1元换2.5倍”活动,小红妈妈买一件标价为600元的衣服,她实际需要付款( ) A .240元 B .280元 C .480元 D .540元 6.下列运算正确的是( )A .532532a a a =+B .236a a a =÷C .623)(a a =-D .222)(y x y x +=+ 7.下列命题中错误..的是( ) A .等腰三角形的两个底角相等 B .对角线互相垂直的四边形是菱形 C .矩形的对角线相等 D .圆的切线垂直于过切点的直径8.已知两圆的半径是4和5,圆心距x 满足不等式组⎪⎩⎪⎨⎧+<-+>+23245252x x x x ,则两圆的 位置关系是( ) A .相交 B . 外切 C .内切 D . 外离9.如图1,在平面直角坐标系中,点P 在第一象限,⊙P与x 轴相切于点Q ,与y 轴交于M (0,2)、N (0,8)两 点,则点P 的坐标是( ) A .(5,3) B .(3,5) C .(5,4) D .(4,5)10.已知甲车行驶35千米与乙车行驶4515千米,设甲车的速度为x 千米/小时,依据题意列方程正确的是( )A .154535-=x x B .x x 451535=+ C .xx 451535=- D .154535+=x xA .B .C .D .D图511.已知:如图2,∠MON=45º,OA 1=1,作正方形A 1B 1C 1A 2,面积记作S 1;再作第二个正方形A 2B 2C 2A 3,面积记作S 2; 继续作第三个正方形A 3B 3C 3A 4,面积记作S 3;点A 1、A 2、 A 3、A 4……在射线ON 上,点B 1、B 2、B 3、B 4……在射线 OM 上,……依此类推,则第6个正方形的面积S 6是(A .256B .900C .1024D .409612.在课题学习后,同学们为教室窗户设计一个遮阳蓬,小明同学绘制的设计图如图3所示,其中,AB 表示窗户,且AB=2.82米,△BCD 表示直角 遮阳蓬,已知当地一年中在午时的太 阳光与水平线CD 的最小夹角α为18°,最大夹角β为66°,根据以上数据,计算出遮阳蓬中CD 的长是( ) (结果精确到0.1)(参考数据:sin18°≈0.31,tan18°≈0.32sin66°≈0.91,tan66°≈2.2)A .1.2 米B .1.5米C .1.9米D .2.5米第二部分 非选择题二、填空题(本题共有4小题,每小题3分,共12分) 13.分解因式:x xy xy +-22= . 14.一个不透明的口袋中,装有黑球5个,红球6个,白球7个,这些球除颜色不同外,没有 任何区别,现从中任意摸出一个球,恰好是 红球的概率= .15.如图4, 点A 在双曲线xy 2=上,点B 在双曲线xky =上,且AB ∥x 轴,点C 、D在x 轴上,若四边形ABCD 为矩形, 且 它的面积为3,则k= .16.如图5,在矩形ABCD 中,AB=3,BC=9, 把矩形ABCD 沿对角线BD 折叠,使点C 与点F 重合,BF 交AD 于点M ,过点C作CE ⊥BF 于点E ,交AD 于点G ,则MG 的长=N12345三、解答题(本题共7小题,其中第17题5分,第18题6分,第19题8分,第20题8分,第21题8分,第22题8分,第23题9分,共52分)17.(5分)计算:32145sin 82-+⎪⎭⎫⎝⎛-︒⨯-18.(6分)化简,求值: 44912122++-÷⎪⎭⎫⎝⎛++x x x x ,其中x=419.(8分)已知:如图6,在平行四边形ABCD 中,连接对角线BD ,作AE ⊥BD 于E ,CF ⊥BD 于F, (1)求证:△AED ≌△CFB (4分)(2)若∠ABC=75°,∠ADB=30°,AE=3,求平行四边形ABCD 的周长?(4分)B图620.(8分)为了贯彻“减负增效”精神,掌握九年级600名学生每天的自主学习情况,某校学生会随机抽查了九年级的部分学生,并调查他们每天自主学习的时间.根据调查结果,制作了两幅不完整的统计图(图7-1,图7-2),请根据统计图中的信息回答下列问题: (1)本次调查的学生人数是 人;(2分)(2)图7-2中α是_____度,并将图7-1条形统计图补充完整;(2分) (3)请估算该校九年级学生自主学习时间不少于1.5小时有 人;(2分)(4)老师想从学习效果较好的4位同学(分别记为A 、B 、C 、D ,其中A 为小亮)随机选择两位进行学习经验交流,用列表法或树状图的方法求出选中小亮A 的概率.(2分)21.(8分)植树节前夕,某林 场组织20辆汽车装运芒果 树、木棉树和垂叶榕三种树木共100按计划20辆车都要装运,每辆汽车只能装运同一种树木,且必须装满.根据表格提供的信息,解答下列问题.(1)设装运芒果树的车辆数为x ,装运木棉树的车辆数为y ,求y 与x 之间的函数关系式;(2分) (2)如果安排装运芒果树的车辆数不少于5辆,装运木棉树的车辆数不少于6辆,那么车辆的安排有几种方案?并写出每种安排方案?(3分)(3)若要求总运费最少,应采用(2)中哪种安排方案?并求出最少总运费?(3分)22.(8分)如图8-1,在正方形ABCD 和正方形BEFG 中,点A ,B ,E 在同一条直线上,连接DF ,且P 是线段DF 的中点,连接PG ,PC .图7-2图7-1(1)如图8-1中,PG 与PC 的位置关系是 ,数量关系是 ;(2分)(2) 如图8-2将条件“正方形ABCD 和正方形BEFG ”改为“矩形ABCD 和矩形BEFG ”其它条件不变,求证:PG=PC ;(3分)(3)如图8-3,若将条件“正方形ABCD 和正方形BEFG ”改为“菱形ABCD 和菱形BEFG ”,点A ,B ,E 在同一条直线上,连接DF ,P 是线段DF 的中点,连接PG 、PC ,且∠ABC=∠BEF=60°,求PCPG 的值.(3分)23.(9分)已知:如图9-1,抛物线经过点O 、A 、B 三点,四边形OABC 是直角梯形,其中点A 在x 轴上,点C 在y 轴上,BC ∥OA ,A (12,0)、B (4,8).图8-3图8-2图8-1(1)求抛物线所对应的函数关系式;(3分)(2)若D为OA的中点,动点P自A点出发沿A→B→C→O的路线移动,速度为每秒1个单位,移动时间记为t秒.几秒钟后线段PD将梯形OABC的面积分成1﹕3两部分?并求出此时P点的坐标;(3分)(3)如图9-2,作△OBC的外接圆O′,点Q是抛物线上点A、B之间的动点,连接OQ交⊙O′于点M,交AB于点N.当∠BOQ=45°时,求线段MN的长.(3分)深圳市2014年初中毕业生学业考试数学模拟试卷参考答案及评分标准一、选择题(每小题3分,共36分): ADCBA CBADD CB二、填空题(每小题3分,共12分):13.()21-y x 14.3115. 5 16.411 三、解答题: 17.原式 = 342222+-⨯ ………………… 4分(每个知识点得1分)= 2–4+3 =1 ………………………… 5分18.解::原式 = ()()()33222212+-+⨯⎪⎭⎫ ⎝⎛++++x x x x x x ……………………… 2分= ()()()332232-++⨯++x x x x x …………………………………… 3分=32-+x x …………………………………………… 4分当x=4代入32-+x x =3424-+ =6……………………… 6分19.(1)证明:∵ 平行四边形ABCD∴AD=BC,AD∥BC ………………1分 ∴∠ADE=∠CBF ……………2分 又∵AE⊥BD 于E ,CF⊥BD 于F∴∠AED=∠CFB=90º …………… 3分∴△AED≌△CFB (AAS) ………………4分 (2)解:在Rt△AED 中∵∠ADE=30º AE=3∴AD=2AE=2×3=6 …………1分 ∵∠ABC =75º ∠ADB=∠CBD=30º∴∠ABE=45º …………2分在Rt△ABE 中 ∵sin45º=ABAE∴2345sin == AEAB …………3分 ∴平行四边形ABCD 的周长l=2(AB+AD)=()26122362+=+ ……4分(其他证明方法参考给分)20.(1)40; ……………………2分图7-1人数(2)54,补充图形如图7-1; …………共2分 (注:填空1分,图形1分)(3)330; …………………… 2分 (4)解:列表如下P(A)=21126= ………2分 (注:列表法或树状图正确得1分,求概率得1分,没有列表法或树状图直接求概率不得分) 21.解(1)设装运芒果树的车辆数为x ,装运木棉树的车辆数为y ,装运垂叶榕的车辆数为(20-x-y ). 由题意得:()10020456=--++y x y x ……………………………1分 ∴202+-=x y ……………………2分(2)∵()x x x y x =+---=--2022020∴故装运垂叶榕也为 x 辆.根据题意得:⎩⎨⎧≥+-≥62025x x ……………………1分解得75≤≤x ∵ x 为整数, ∴x 取5,6,7 ……2分 故车辆有3种安排方案,方案如下:方案一: 装运芒果树5辆车, 装运木棉树10辆车, 装运垂叶榕5辆车; 方案二: 装运芒果树6辆车, 装运木棉树8辆车, 装运垂叶榕6辆车;方案三: 装运芒果树7辆车, 装运木棉树6辆车, 装运垂叶榕7辆车.………3分 (3)解法一:设总运费为W 元,则W=180416051206⨯+⨯+⨯x y x=16000160+-x ……………………1分 ∵W 是 x 是的一次函数,160-=k <0,∴W 随x 的增大而减少.∴当x=7时, W 最小 =-160×7+16000=14880 元 …………2分 答:应采用(2)中方案三,当x=7时, W 最少费用为14880 元.………3分解法二:方案一的总运费W1=6×5×120+5×10×160+4×5×180=15200(元) 方案二的总运费W2=6×6×120+5×8×160+4×6×180=15040(元)方案三的总运费W3=6×7×120+5×6×160+4×7×180=14880 (元)……………2分 ∴应采用(2)中方案三,当x=7时, W 最少费用为14880 元。
