金属晶体堆积模型复习及计算
合集下载
常见晶体模型及晶胞计算
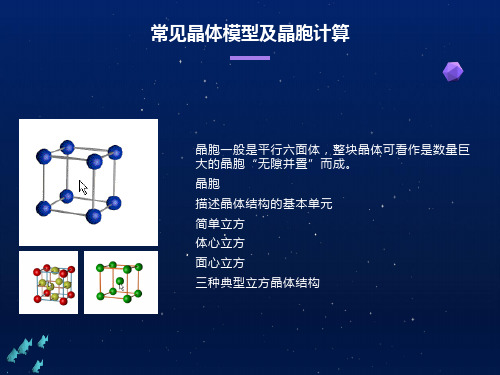
确定配位数
晶胞中微粒个数的计算,求化学式
小结:高考常见题型
1、(2013·江苏,21A(1)) 元素X 位于第四周期,其基态原子的内层轨道全部排满电子,且最外层电子数为2。元素Y基态原子的3p 轨道上有4个电子。
X与Y所形成化合物晶体的晶胞如右图所示。 ①在1个晶胞中,X离子的数目为 。 ②该化合物的化学式为 。
Mg、Zn、Ti 每个晶胞含 个原子 六方最密堆积的配位数 =12 2
④面心立方最密堆积(铜型)
Cu、Ag、Au 面心立方堆积的配位数 =12 每个晶胞含 个原子 4
面心立方最密堆积的空间占有率
=74%
金属晶体的四种堆积模型对比
堆积模型
采纳这种堆积的典型代表
(3)若NaCl晶体的密度为ρg/cm3,则 NaCl晶体中Na+与Na+间的最短距离是多少?
a/2
a/2
=
练习
CsCl的晶体结构
(1)每个Cs+( Cl-)周围等距且紧邻的Cl- (Cs+)有 个, Cs+( Cl-)的配位数为 。
8
8×1/8=1
6
——晶胞为体心立方体
8
(2)每个Cs+ ( Cl-)周围 等距且紧邻的Cs+ ( Cl-)有 个。
1
3
6
4
2
A
5
密置层
配位数为4
配位数为6
返
A
B
A
B
A
返
第三层的另一种排列方式,是将球对准第一层的 2,4,6 位,不同于 AB 两层的位置,这是 C 层。
1
2
3
4
5
6
1
2
3
晶胞中微粒个数的计算,求化学式
小结:高考常见题型
1、(2013·江苏,21A(1)) 元素X 位于第四周期,其基态原子的内层轨道全部排满电子,且最外层电子数为2。元素Y基态原子的3p 轨道上有4个电子。
X与Y所形成化合物晶体的晶胞如右图所示。 ①在1个晶胞中,X离子的数目为 。 ②该化合物的化学式为 。
Mg、Zn、Ti 每个晶胞含 个原子 六方最密堆积的配位数 =12 2
④面心立方最密堆积(铜型)
Cu、Ag、Au 面心立方堆积的配位数 =12 每个晶胞含 个原子 4
面心立方最密堆积的空间占有率
=74%
金属晶体的四种堆积模型对比
堆积模型
采纳这种堆积的典型代表
(3)若NaCl晶体的密度为ρg/cm3,则 NaCl晶体中Na+与Na+间的最短距离是多少?
a/2
a/2
=
练习
CsCl的晶体结构
(1)每个Cs+( Cl-)周围等距且紧邻的Cl- (Cs+)有 个, Cs+( Cl-)的配位数为 。
8
8×1/8=1
6
——晶胞为体心立方体
8
(2)每个Cs+ ( Cl-)周围 等距且紧邻的Cs+ ( Cl-)有 个。
1
3
6
4
2
A
5
密置层
配位数为4
配位数为6
返
A
B
A
B
A
返
第三层的另一种排列方式,是将球对准第一层的 2,4,6 位,不同于 AB 两层的位置,这是 C 层。
1
2
3
4
5
6
1
2
3
人教版高中化学选修三课件:第三章 专题课 晶体堆积模型及晶胞相关计算ppt

例5 右图为NaCl晶胞结构,已知FexO晶体晶胞结构为 NaCl型,由于晶体缺陷,x值小于1。测知FexO晶体的
密度为ρ=5.71g/cm3,晶胞边长为4.28×10-10m。
探究1:已知铜晶胞是面心立方晶胞,其晶胞特征如右图所示。 若已知该晶体的密度为a g/cm3,NA代表阿伏加德罗常数,相对原子质量为64 , 请回答:
[来源:学科网]
①晶胞中铜原子的配位数为________ ,一个晶胞中原子的数目为________; ②该晶体的边长为_______________,铜原子半径为________(用字母表示)。 列式并计算Cu空间利用率________________
D.YBa2Cu4O7
题型4、 晶体密度、粒子间距离的计算
例4右图为NaCl晶胞结构示意图。 (1)用X射线衍射法测得晶胞的边长为a cm,求该温度下NaCl晶体的密度。
ρ=m/V=
(2)晶体的密度为ρg/cm3,则晶体中Na +与Na+之间的最短距离是多少?
[练习3]. 已知 NaCl 的摩尔质量为 M g·mol-1, 食盐晶体的密度为ρg·cm-3,若下图中Na+与最邻 近的Cl- 的核间距离为 a cm,那么阿伏加德罗常 数的值可表示为 D
【巩固练习】 1.Al2O3在一定条件下可制得AlN,其晶体结构如图2所示,该 晶体中Al的配位数是_________ .
2.六方氮化硼在高温高压下,可以转化为立方氮化硼,其结构与金刚石相似, 硬度与金刚石相当,晶胞边长为361.5pm,立方氮化硼晶胞中含有______个 氮原子、_______个硼原子,立方氮化硼的密度是____________g·cm-3(只 要求列算式,不必计算出数值,阿伏加德罗常数为NA)
高考化学二轮复习:关于几种常见晶体结构与计算

原子晶体熔化时,要破坏共价键,所以原
子晶体的熔沸点都很高
109º28´
共价键
宜城市第一中学化学教研组
宜城市第一中学
金刚石晶胞中含碳原子数:
8× +6× +4= 8
金刚石晶胞的棱边a与碳原子半径r 的关系:
金刚石的空间利用率
金刚石
P0=
= 34.0%
宜城市第一中学化学教研组
宜城市第一中学
练习2:2016. 37.[化学——选修3:物质结构与性质](15分)
•
7.“画竹”是本文的线索,本文记述 文与可 画竹的 情形, 以充满 感情的 笔触回 忆两人 的交往 ,以及 文与可 死后自 己的悲 慨,又 从文与 可的创 作经验 中总结 出艺术 创作的 规律, 熔叙事 、抒情 、议论 于一炉 。
•
8.总之,说明文中使用生动活泼的语 言,不 仅能增 强文章 内容表 达上的 形象性 、可感 性和文 学色彩 ,使读 者获得 不同程 度的美 感体验 ,受到 美的陶 冶,还 有助于 加深读 者对说 明内容 的理解 ,增知 益智。
•
5.在乡土社会里,地缘关系也是如此 。每一 家以自 己的地 位做中 心,周 围划出 一个圈 子,个 圈子是 “街坊 ”。可 是这不 是一个 固定的 团体, 而是一 个范围 。范围 的大小 也要依 着中心 的势力 厚薄而 定。
•
6.在这种富于伸缩性的网络里,随时 随地是 有一个 “己” 作中心 的。这 并不是 个人主 义,而 是自我 主义。 在个人 主义下 ,一方 面是平 等观念 ,指在 同一团 体中各 分子的 地位相 等,个 人不能 侵犯大 家的权 利;一 方面是 宪法观 念,指 团体不 能抹煞 个人, 只能在 个人们 所愿意 交出的 一分权 利上控 制个人 。
子晶体的熔沸点都很高
109º28´
共价键
宜城市第一中学化学教研组
宜城市第一中学
金刚石晶胞中含碳原子数:
8× +6× +4= 8
金刚石晶胞的棱边a与碳原子半径r 的关系:
金刚石的空间利用率
金刚石
P0=
= 34.0%
宜城市第一中学化学教研组
宜城市第一中学
练习2:2016. 37.[化学——选修3:物质结构与性质](15分)
•
7.“画竹”是本文的线索,本文记述 文与可 画竹的 情形, 以充满 感情的 笔触回 忆两人 的交往 ,以及 文与可 死后自 己的悲 慨,又 从文与 可的创 作经验 中总结 出艺术 创作的 规律, 熔叙事 、抒情 、议论 于一炉 。
•
8.总之,说明文中使用生动活泼的语 言,不 仅能增 强文章 内容表 达上的 形象性 、可感 性和文 学色彩 ,使读 者获得 不同程 度的美 感体验 ,受到 美的陶 冶,还 有助于 加深读 者对说 明内容 的理解 ,增知 益智。
•
5.在乡土社会里,地缘关系也是如此 。每一 家以自 己的地 位做中 心,周 围划出 一个圈 子,个 圈子是 “街坊 ”。可 是这不 是一个 固定的 团体, 而是一 个范围 。范围 的大小 也要依 着中心 的势力 厚薄而 定。
•
6.在这种富于伸缩性的网络里,随时 随地是 有一个 “己” 作中心 的。这 并不是 个人主 义,而 是自我 主义。 在个人 主义下 ,一方 面是平 等观念 ,指在 同一团 体中各 分子的 地位相 等,个 人不能 侵犯大 家的权 利;一 方面是 宪法观 念,指 团体不 能抹煞 个人, 只能在 个人们 所愿意 交出的 一分权 利上控 制个人 。
常见晶体模型及晶胞计算
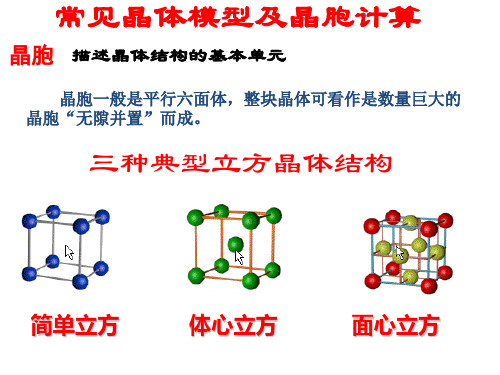
(二) 确定配位数
(三) 晶体的密度及微粒间距离 的计算
练习
1、(2013·江苏,21A(1)) 元素X 位于第四周期,其基态原子的内层轨道全部 排满电子,且最外层电子数为2。元素Y基态原子的 3p 轨道上有4个电子。
X与Y所形成化合物晶体的晶胞 如右图所示。
①在1个晶胞中,X离子的数目 为4 。
=
58.5 / NA×4 a3
(3)若NaCl晶体的密度为ρg/cm3,则 NaCl晶体中Na+与 Na+间的最短距离是多少?
CsCl的晶体结构——晶胞为体心立方体
(1)每个Cs+( Cl-)周围等距 且紧邻的Cl- (Cs+)有 8 个, Cs+( Cl-)的配位数为 8 。 (2)每个Cs+ ( Cl-)周围 等距且紧邻的Cs+ ( Cl-)有 6 个。 (3)每个晶胞中含 1 个Cs+、含8×1/8=1个Cl-,故每 个晶胞中含有 1 个“CsCl”结构单元; N(Cs+) ︰ N( Cl-) = 1︰1 ,化学为 CsCl 。
(4)能否 把“NaCl”称为分子式?
练习
-的距离为 a cm,该晶体密度为
(1)设NaCl晶胞的边长为acm,则
示晶为胞中Na+和Cl-的最近距离(( 即小)立
方体的边长)为 a/2 cm,则晶胞中 同种离子的最近距离为 a/2 cm。
(2)晶胞的边长为acm,求NaCl晶 体的密度。
ρ
=
M / NA×晶胞所含粒子数 晶胞的体积
思考:NaCl、CsCl同属AB型离子晶体, NaCl晶体中 Na+的配位数与CsCl晶体中Cs+的配位数是否相等?
CaF2的晶体结构
(三) 晶体的密度及微粒间距离 的计算
练习
1、(2013·江苏,21A(1)) 元素X 位于第四周期,其基态原子的内层轨道全部 排满电子,且最外层电子数为2。元素Y基态原子的 3p 轨道上有4个电子。
X与Y所形成化合物晶体的晶胞 如右图所示。
①在1个晶胞中,X离子的数目 为4 。
=
58.5 / NA×4 a3
(3)若NaCl晶体的密度为ρg/cm3,则 NaCl晶体中Na+与 Na+间的最短距离是多少?
CsCl的晶体结构——晶胞为体心立方体
(1)每个Cs+( Cl-)周围等距 且紧邻的Cl- (Cs+)有 8 个, Cs+( Cl-)的配位数为 8 。 (2)每个Cs+ ( Cl-)周围 等距且紧邻的Cs+ ( Cl-)有 6 个。 (3)每个晶胞中含 1 个Cs+、含8×1/8=1个Cl-,故每 个晶胞中含有 1 个“CsCl”结构单元; N(Cs+) ︰ N( Cl-) = 1︰1 ,化学为 CsCl 。
(4)能否 把“NaCl”称为分子式?
练习
-的距离为 a cm,该晶体密度为
(1)设NaCl晶胞的边长为acm,则
示晶为胞中Na+和Cl-的最近距离(( 即小)立
方体的边长)为 a/2 cm,则晶胞中 同种离子的最近距离为 a/2 cm。
(2)晶胞的边长为acm,求NaCl晶 体的密度。
ρ
=
M / NA×晶胞所含粒子数 晶胞的体积
思考:NaCl、CsCl同属AB型离子晶体, NaCl晶体中 Na+的配位数与CsCl晶体中Cs+的配位数是否相等?
CaF2的晶体结构
金属堆积

,
1
2
两 个 密 置 层 密 置 堆 积
三 个 密 置 层 密 置 堆 积
六方堆积
面心立方 堆积
3.六方堆积(镁型)镁、锌、钛等属于六方堆积
第一种: 将第三层球对准第一层的球 A
1 6 5 4
2
3
B
A B
于是每两层形成一个 周期,即 AB AB 堆积方 式,形成六方堆积。
A
上图是此种六方 堆积的前视图
阅读课文P76《资料卡片》,并填写下表
堆积模型 简单立方 钾型( bcp ) 镁型(hcp) 铜型(ccp) 典型代表 空间利 用率 配位数 晶胞
金属晶体的四中堆积模型对比
能力训练
1.下列有关金属元素特征的叙述中正确的是
A.金属元素的原子只有还原性,离子只有氧 化性 B.金属元素在化合物中一定显正价
A
C B A
1 6
2 3
5
4
C B
配位数 12 ( 同层 6, 上下层各 3 )
A 此种立方紧密堆积的前视图
铜型(面心立方最密堆积)
1 ABC铜型面心立方晶胞的抽取
C
B
B
A C B A
A C
B
晶胞内原子数:4
配位数:12 空间利用率: 74% 典型金属:Cu Ag Au
三、金属晶体的四种堆积模型对比
第二节 金属晶体的原子 堆积模型
金属晶体的原子堆积模型
(1)几个概念 配位数:在晶体中与每个微粒紧密相邻的 微粒个数 空间利用率:晶体的空间被微粒占满的体积 百分数,用它来表示紧密堆积的程度
空间利用率= 球体积 晶胞体积 100%
一、 二维平面堆积方式
非密置层
行列对齐,四球一空 非最紧密排列 配位数:4
金属晶体堆积模型复习及计算

1个晶胞所含微粒数为:8×1/8 + 1 = 2
请计算:空间利用率?
以体心立方晶胞为例,计算晶胞中原子的 空间占有率。
小结:(2)钾型 (体心立方堆积)
配位数:8
(3)面心立方:在立方体顶点的微粒为8 个晶胞共有,在面心的为2个晶胞共有。
微粒数为: 8×1/8 + 6×1/2 = 4
请计算:空间利用率?
B
此种立方紧密堆积的前视图A
7 1 9
6
5
8 2
3 4
10
11
12
这种堆积晶胞空间利用率高(74%),属于 最密置层堆集,配位数为 ,许多金属(如 Mg、Zn、Ti等)采取这种堆积方式。
回顾镁型的晶胞
1200
平行六面体
找铜型的晶胞
C B A
回顾:配位数 每个小球周围距离最近的小球数
=19.36g/cm3 1nm=10-9m=10-7cm
复习1pm=10-12m
练2:
现有甲、乙、丙、丁四种晶胞,可推知甲
晶晶体体体的中化的与学化的式学粒 为式子—为E—个F——D或—数—C——F比2——E—为;或——丁—C—1—晶—2:D1——体——;的—;丙化乙晶学 式为—X—Y——2Z——。
BA
甲
DC
乙
F
E
丙
Z X
Y
丁
练3: 甲
乙
丙
上图甲、乙、丙分别为体心堆积、面心立方堆积、 六方堆积的结构单元,则甲、乙、丙三种结构单
元中,金属原子个数比为——1—:—2:—3————。
乙晶胞中所含金属原子数为8×1/8+6×1/2=4 晶胞中所含金属原子数为12×1/6+2×1/2+3=6
请计算:空间利用率?
以体心立方晶胞为例,计算晶胞中原子的 空间占有率。
小结:(2)钾型 (体心立方堆积)
配位数:8
(3)面心立方:在立方体顶点的微粒为8 个晶胞共有,在面心的为2个晶胞共有。
微粒数为: 8×1/8 + 6×1/2 = 4
请计算:空间利用率?
B
此种立方紧密堆积的前视图A
7 1 9
6
5
8 2
3 4
10
11
12
这种堆积晶胞空间利用率高(74%),属于 最密置层堆集,配位数为 ,许多金属(如 Mg、Zn、Ti等)采取这种堆积方式。
回顾镁型的晶胞
1200
平行六面体
找铜型的晶胞
C B A
回顾:配位数 每个小球周围距离最近的小球数
=19.36g/cm3 1nm=10-9m=10-7cm
复习1pm=10-12m
练2:
现有甲、乙、丙、丁四种晶胞,可推知甲
晶晶体体体的中化的与学化的式学粒 为式子—为E—个F——D或—数—C——F比2——E—为;或——丁—C—1—晶—2:D1——体——;的—;丙化乙晶学 式为—X—Y——2Z——。
BA
甲
DC
乙
F
E
丙
Z X
Y
丁
练3: 甲
乙
丙
上图甲、乙、丙分别为体心堆积、面心立方堆积、 六方堆积的结构单元,则甲、乙、丙三种结构单
元中,金属原子个数比为——1—:—2:—3————。
乙晶胞中所含金属原子数为8×1/8+6×1/2=4 晶胞中所含金属原子数为12×1/6+2×1/2+3=6
2020高考热点---金属晶体四类晶胞空间利用率的计算

2、面方堆积的配位数 12
3、每个晶胞含 4个原子
4、晶胞边长为a
5、空间利用率=
六方立方晶体
六方最密堆积(镁型) 1、金属---Mg、Zn、Ti 2、六方最密堆积的配位数 12
3、每个晶胞含 2 个原子
4、晶胞边长为a a=2r 5、晶胞高为h h=
V球
2
4
3
r3
(晶胞中有2个球)
6、空间利用率=
V球 V晶胞 100% 74.05%
2、简单立方堆积的配位数 6
3、每个晶胞含 1个原子
4、晶胞边长为a a=2r
5、空间利用率=
体心立方晶体
1、体心立方堆积(钾型) K、Na、Fe 2、体心立方堆积的配位数 8
3、每个晶胞含 2 个原子
4、晶胞边长
5、空间利用率=
面心立方晶体
面心立方堆积
球半径为r
1、金属——铜型 Cu、Ag、Au
金属晶体的四种堆积模型对比
堆积模型
采纳这种堆 积的典型代
表
空间利 用率
配位数
简单立方 Po(钋) 52%
6
体心立方 (钾型)
K、Na、Fe
68%
2
面心立方最
密(铜型) Cu, Ag, Au 74%
12
晶胞
简单立方晶体
简单立方堆积
球半径为r
1、唯一金属——钋
3、每个晶胞含 4个原子
4、晶胞边长为a
5、空间利用率=
六方立方晶体
六方最密堆积(镁型) 1、金属---Mg、Zn、Ti 2、六方最密堆积的配位数 12
3、每个晶胞含 2 个原子
4、晶胞边长为a a=2r 5、晶胞高为h h=
V球
2
4
3
r3
(晶胞中有2个球)
6、空间利用率=
V球 V晶胞 100% 74.05%
2、简单立方堆积的配位数 6
3、每个晶胞含 1个原子
4、晶胞边长为a a=2r
5、空间利用率=
体心立方晶体
1、体心立方堆积(钾型) K、Na、Fe 2、体心立方堆积的配位数 8
3、每个晶胞含 2 个原子
4、晶胞边长
5、空间利用率=
面心立方晶体
面心立方堆积
球半径为r
1、金属——铜型 Cu、Ag、Au
金属晶体的四种堆积模型对比
堆积模型
采纳这种堆 积的典型代
表
空间利 用率
配位数
简单立方 Po(钋) 52%
6
体心立方 (钾型)
K、Na、Fe
68%
2
面心立方最
密(铜型) Cu, Ag, Au 74%
12
晶胞
简单立方晶体
简单立方堆积
球半径为r
1、唯一金属——钋
金属晶体堆积模型及计算公式

----体心立方堆积:
5 8 1
6 7 2
4
3
这种堆积晶胞是一个体心立方,每个晶胞含 2 个原子,属于非密置层堆积,配位数 为 8 ,许多金属(如Na、K、Fe等)采取这种 堆积方式。
空间利用率的计算
(2)体心立方:在立方体顶 点的微粒为8个晶胞共享,处 于体心的金属原子全部属于 该晶胞。 微粒数为:8×1/8 + 1 = 2
1200
平行六面体
每个晶胞含 2 个原子
铜型(面心立方紧密堆积)
7 6 5 1 8 9 4 2 3
12
10 11
这种堆积晶胞属于最密置层堆集,配位数 为 12 ,许多金属(如Cu、Ag、Au等)采取这 种堆积方式。
(3)面心立方:在立方体顶点的微粒为8 个晶胞共有,在面心的为2个晶胞共有。 微粒数为: 8×1/8 + 6×1/2 = 4 空间利用率: 4×4лr3/3 (2×1.414r)3
分子间以范德 通过金属键形成的 华力相结合而 晶体 成的晶体
作用力
构成微粒 物 理 性 质 实例 熔沸点
共价键
原子 很高
范德华力
分子 很低
金属键
金属阳离子和自由 电子 差别较大
硬度
导电性
很大
无(硅为半导体) 金刚石、二氧化硅、 晶体硅、碳化硅
很小
无 Ar、S等
差别较大
导体 Au、Fe、Cu、钢 铁等
= 74.05%
堆积方式及性质小结
堆积方式 晶胞类型 空间利 配位数 用率 简单立 方堆积 简单立方 52% 68% 74% 74% 6 8 12 实例
Po Na、K、Fe
体心立方 体心立方 堆积 六方最 密堆积 六方
金属晶体堆积模型复习及计算

质量为183.9,半径为0.137nm。
a
求⑴晶胞的边长;⑵计算金属钨的密度。
晶胞中每个顶角金各有属一钨个的钨晶原子胞,与这已个钨原子为8个晶胞 共原用子,,每 那个 么钨 ,原 这经子 个有 晶学胞1过/中8的属含于哪钨该原种晶子晶胞为,型2 体个心,有一个金属 则ρ=2×183.9/6.02×类10似23×?(0.316×10-7)3
堆积方式及性质小结
堆积方式 晶胞类型 空间利 配位数 用率
实例
简单立 方堆积
简单立方
52%
6
Po
体心立方 密堆积
体心立方
68%
8
Na、K、Fe
六方最 密堆积
六方
74% 12 Cu、Ag、Au
面心立方 面心立方 最密堆积
74%
12
精品课件
Mg、Zn、Ti
精品课件
体 心 立 方 堆 积
配位数:8
精品课件
(1)图中正方形边长 a, (2)铜的原子半径 R
晶胞中每个顶角各有1个铜原子,这个铜原子为8个晶胞 共用,每个铜原子有1/8属于该晶胞,面心有6个金属 原子,有1/6属于该晶胞,1个晶胞中含铜原子4 个,
则ρ= 4×63.54/6.02×1023×(R×10-7)3 =8.936g/cm3
R=
nm
面心(铜型)堆积方式的空间利用率计算
a a
面心
精品课件
课外练习
1、已知金属铜为面心立方晶体,如图所示,
铜的相对原子质量为63.54,密度为
8.936g/cm3,试求
(1)图中正方形边长 a, (2)铜的原子半径 R
r
R
精品课件
R o
a
R
金属晶体的堆积模型

二、 金属晶体的原子堆积模 型
精品课件
金属晶体原子平面排列方式有几种?
探究
2 1A3
4
2
1
3
A
6
4
5
配位数为4 非密置层
精品课件
配位数为6 密置层
非密置层层层堆积情况1: 相邻层原子在同一直线上的堆积
金属晶体的堆积方式──简单立方堆积
精品课件
简单立方堆积
配位数:6 晶胞含金属原子数 1
例: (Po) 精品课件
精品课件
2).立方面心结构 立方面心结构的配位数=12(即每个圆球有12个最
近的邻居,同一层有六个,上一层三个,下一层三 个)。立方密堆积中可以取出一个立方面心的单位 来,每个单位中有四个圆球,球心的位置是000;0 1/2 1/2;1/2 0 1/2;1/2 1/2 0。
等径圆球的最紧密堆积方式,在维持每个球的周围 的情况等同的条件下,就只有上述两种,它们的空 间利用率最高(74.05%)。
精品课件
立方体边长=a';
立方体对角线=
a';
四面体边长=
a';
精品课件
精品课件
设圆半径为R,晶胞棱长为a,晶胞面对角
线长
则
晶胞体
积
立方面心晶胞中含4个圆球,每个球体积
为:
立方最密堆积虽晶胞大小不同,每个晶胞中 含球数不同。但计算得到空间占有率相同。
精品课件
而体心立方堆积(bcp)则空间占有率低一些。 体对角线长为 晶胞体积 体心立方晶胞含2个球
精品课件
2、某些金属晶体(Cu、Ag、Au)的原子按面心 立方的形式紧密堆积,即在晶体结构中可以 划出一块正立方体的结构单元,金属原子处 于正立方体的八个顶点和六个侧面上,试计 算这类金属晶体中原子的空间利用率。
精品课件
金属晶体原子平面排列方式有几种?
探究
2 1A3
4
2
1
3
A
6
4
5
配位数为4 非密置层
精品课件
配位数为6 密置层
非密置层层层堆积情况1: 相邻层原子在同一直线上的堆积
金属晶体的堆积方式──简单立方堆积
精品课件
简单立方堆积
配位数:6 晶胞含金属原子数 1
例: (Po) 精品课件
精品课件
2).立方面心结构 立方面心结构的配位数=12(即每个圆球有12个最
近的邻居,同一层有六个,上一层三个,下一层三 个)。立方密堆积中可以取出一个立方面心的单位 来,每个单位中有四个圆球,球心的位置是000;0 1/2 1/2;1/2 0 1/2;1/2 1/2 0。
等径圆球的最紧密堆积方式,在维持每个球的周围 的情况等同的条件下,就只有上述两种,它们的空 间利用率最高(74.05%)。
精品课件
立方体边长=a';
立方体对角线=
a';
四面体边长=
a';
精品课件
精品课件
设圆半径为R,晶胞棱长为a,晶胞面对角
线长
则
晶胞体
积
立方面心晶胞中含4个圆球,每个球体积
为:
立方最密堆积虽晶胞大小不同,每个晶胞中 含球数不同。但计算得到空间占有率相同。
精品课件
而体心立方堆积(bcp)则空间占有率低一些。 体对角线长为 晶胞体积 体心立方晶胞含2个球
精品课件
2、某些金属晶体(Cu、Ag、Au)的原子按面心 立方的形式紧密堆积,即在晶体结构中可以 划出一块正立方体的结构单元,金属原子处 于正立方体的八个顶点和六个侧面上,试计 算这类金属晶体中原子的空间利用率。
高中化学常见晶体模型及晶胞计算

小结:高考常见题型 (一) 晶胞中微粒个数的计算, 求化学式
(二) 确定配位数
(三) 晶体的密度及微粒间距离 的计算
练习
-的距离为 a cm,该晶体密度为
(1)设NaCl晶胞的边长为acm,则
示晶为胞中Na+和Cl-的最近距离(( 即小)立
方体的边长)为 a/2 cm,则晶胞中 同种离子的最近距离为 a/2 cm。
思考:NaCl、CsCl同属AB型离子晶体, NaCl晶体中 Na+的配位数与CsCl晶体中Cs+的配位数是否相等?
CaF2的晶体结构
(1)每个Ca2+周围等距且 紧邻的F-有 8 个, Ca2+配 位数为 8 。
(2)每个F-周围等距且紧 邻的Ca2+有 4 个, F-配位 数为 4 。
FCa2+
金属晶体的四种堆积模型对比
堆积模型
采纳这种堆积 的典型代表
空间利用率
配位数
简单立方
Po(钋)
52%
6
体心立方 (钾型)
K、Na、Fe
68%
8
六方最密 (镁型)
Mg、Zn、Ti
74%
12
面心立方最密 (铜型)
Cu, Ag, Au
74%
12
晶胞
原子晶体
金刚石
该晶胞实际分摊到的碳原子数为 (4 + 6 ×1/2 + 8 ×1/8) = 8个。
(3)每个晶胞中含 4 个Ca2+、含 8 个F-, Ca2+和 F-的个数比是 1︰2 。
3、金属晶体:
①简单立方堆积 唯一金属——钋 简单立方堆积的配位数 =6
每个晶胞含 1 个原子
球半径为r 正方体边长为a r=a/2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
V球 V晶胞 100% 74.05%
练习:甲
乙
丙
上图甲、乙、丙分别为体心堆积、面心立方堆积、 六方堆积的结构单元,则甲、乙、丙三种结构单
元中,金属原子个数比为——1—:—2:—3————。
乙晶胞中所含金属原子数为8×1/8+6×1/2=4 丙晶胞中所含金属原子数为12×1/6+2×1/2+3=6
1个晶胞所含微粒数为:8×1/8 + 1 = 2
请计算:空间利用率?
(3)面心立方:在立方体顶点的微粒为8 个晶胞共有,在面心的为2个晶胞共有。
微粒数为: 8×1/8 + 6×1/2 = 4
请计算:空间利用率?
计算面心立方晶胞中 原子的空间占有率:
2 2
2
面 心
a
a
(4)六方密堆积(镁型)的空间利用率计算 解:
( IA,VB,VIB)
(3)镁型和铜型
金属晶体的两种最密堆积方式──镁型和铜型
镁型
铜型
镁型
12
6
3
54
铜型
12
6
3
54
12
6
3
54
12
6
3
54
12
6
3
54
12
6
3
54
配位都是数 12 ( 同层 6, 上下层各 3 )
镁型
铜型
A
A
C
B
B
A
A
B
C
A
B
此种立方紧密堆积的前视图A
7 1 9
6
5
8 2
1.晶体中原子空间利用率的计算 (1)计算晶胞中的微粒数 (2)计算晶胞的体积
(一)简单立方:在立方体顶点的 微粒为8个晶胞共享,
微粒数为:8×1/8 = 1
4πr3/3 空间利用率:(2r)3
=
52.36%
(2)体心立方:在立方体顶 点的微粒为8个晶胞共享,处 于体心的金属原子全部属于 该晶胞。
3 4
10
11
12
这种堆积晶胞空间利用率高(74%),属于 最密置层堆集,配位数为 ,许多金属(如 Mg、Zn、Ti等)采取这种堆积方式。
回顾镁型的晶胞
1200
平行六面体
找铜型的晶胞
C B A
回顾:配位数 每个小球周围距离最近的小球数
简单立方堆积:
6
体心立方堆积:
8
六方紧密堆积:
12
பைடு நூலகம்
第三节 金属晶体
金属晶体的四种堆积模型及简单计算
(1)简单立方堆积:
非最紧密堆积,空间利用率低(52%)
配位数是 6 个。
只有金属钋(Po)采取这种堆积方式
5
6
8
7
1
2
4
3
(2)钾型(体心立方堆积) 非密置层堆积
每个晶胞含 2 个原子,空间利用率不高(68%), 配位数为 8 ,
许多金属(如Na、K、Fe等)采取这种堆积方式。
面心立方紧密堆积: 12
金属晶体中有关计算
空间利用率的计算
1、空间利用率:指构成晶体的原子、离子或 分子在整个晶体空间中所占有的体积百分比。
空间利用率 =
球体积 100%
晶胞体积
空间利用率的计算
2、空间利用率的计算步骤: (1)计算晶胞中的微粒数 (2)计算晶胞的体积
3、复习:
金属晶体中有关计算
四点间的夹角均为60°
先求S
在镁型堆积中取出六方晶胞,平行六面体的底是
平行四边形,各边长a=2r,则平行四边形的面积:
S a a sin 60 3 a2 2
平行六面体的高: 再求h
h 2边长为a的四面体高
2 6 a 2 6 a
3
3
V球
2
4
3
r3
(晶胞中有2个球)
