完整及不完整缓和曲线
非完整缓和曲线起始点曲率半径问题

非完整缓和曲线起始点曲率半径问题
一、是否为非完整缓和曲线?
用A^2=R*Ls公式来验证
A为已知缓和曲线参数;
R为缓和曲线所接圆曲线的半径;
Ls为已知该段缓和曲线的长度;
当等式成立即为完整缓和曲线,否则即为非完整缓和曲线;
二、非完整缓和曲线起始点曲率半径计算(起点与终点计算方法相同):
1、计算第一线元终点对应的完整缓和曲线长度:
L=A^2/R
2、计算对应的第一线元完整缓和曲线舍弃段的长度L1:
L1=L-L S
3、计算得出第一线元缓和曲线(非完整)起点曲率半径R1:
R1=A^2/L1
A为已知缓和曲线参数;
R为已知缓和曲线所接圆曲线的半径;
Ls为已知该段缓和曲线的长度;
L为计算该段完整缓和曲线的长度;
L1该段完整缓和曲线舍弃段的长度;
R1第一线元缓和曲线起点(非完整)曲率半径。
匝道等不完整缓和曲线计算解释和说明

匝道等不完整缓和曲线坐标计算随着全站仪在道路工程施工测量中的普及,传统的中线放样方法逐渐被淘汰。
目前道路工程中线放样时,只要能计算出中线上任意一点的坐标,用全站仪或者GPS RTK的坐标放样功能就可很方便、快捷地完成实地放样。
道路线形是由直线、圆曲线、缓和曲线三种线形组合而成的,而直线与圆曲线组合的线形(见图一)中桩坐标计算比较简单,在此不作阐述。
下面就缓和曲线与其它两种线形组合的线形中桩坐标计算予以分析。
缓和曲线与其它两种线形组合构成的线形主要有缓和曲线的完整形(即基本形)(见图二)和非完整形(即卵形)(见图三)二种。
一、基本形曲线中桩坐标计算:1、对于第一缓和曲线及圆曲线段(ZH~YH)(如图四),建立以ZH为坐标原点,切线方向为X′轴,半径方向为Y′轴的曲线坐标系(X′O′Y′)。
先计算曲线各点在曲线坐标系下的坐标。
⑴对于第一缓和曲线段(ZH~HY)内任一点i(此时L=Ki-KZH)若圆曲线半径R≥100m时,则X i ′=L-L5/(40R2Ls12) 公式①Y i ′=L3/(6RLs1) 公式②若圆曲线半径R<100m时,则X′=L-L5÷[40(RLS )2]+L9÷[3456(RLS)4]–L13÷[599040(RLS)6]+L17÷[175472640(RLS )8]- L21÷[7.80337152×1010(RLS)10](公式③)Y′=L3÷[6(RLS )] - L7÷[336(RLS)3]+L11÷[42240(RLS)5] - L15÷[9676800(RLS )7]+L19÷[3530096640(RLS)9] - L23÷[1.8802409472×1012(RLS)11](公式④)⑵对于圆曲线段(HY~YH)上任一点iX i ′=q+Rsin¢iY i ′=R(1-cos¢i)+pL=Ki-KZH¢i=(L- Ls1)*180/(Rπ)+β内移值P=Ls12/(24R)切线增值q= Ls1/2- Ls13/(240R2)综合⑴、⑵,根据不同坐标系的相互转换,可得ZH~YH上任一点i的中桩测量坐标为:X i =XZH+cosA×Xi′-sinA×f×Yi′(公式⑤)Y i = YZH+sinA×Xi′+cosA×f×Yi′(公式⑥)式中f为线路的转向系数,右转时f=1,左转时f=-1 。
路线缓和曲线计算

第3期(总第165期)2004年6月山西交通科技SHANXI SCIENCE &TEC HNOLOGY OF COMMUNICATIONS No.3Jun.收稿日期:2004 03 04;修回日期:2004 04 02作者简介:武文兵(1964- ),男,山西清徐人,所长,工程师,1990年西安公路学院函授本科毕业,同济大学在读工程硕士研究生。
路线缓和曲线计算武文兵(山西省交通规划勘察设计院,山西 太原 030012)摘要:就缓和曲线精确计算公式,以及完整、不完整缓和曲线上任意点的大地坐标给出了计算方法,并举例进行计算。
关键词:计算;完整回旋线;不完整回旋线;大地坐标中图分类号:U412.34 文献标识码:A 文章编号:1006 3528(2004)03 0005 031 精确计算公式1.1 计算公式我国 公路路线设计规范(JTJ 011-94) 7.4.1条规定采用回旋线作为缓和曲线。
公路设计手册!路线 列出的回旋线参数方程如下式:x =l -l 540R 2L 2s +l 93456R 4L 4s-∀,(1)y =l 36R L s -l 7336R 3L 3s+∀,(2)式中:x ,y ###回旋线上任一点的局部坐标;l###回旋线上任一点至起点的弧长;R ###回旋线终点处的曲率半径;L s###回旋线全长。
在使用过程中我们发现,其计算精度往往不能满足勘察设计和施工放线的要求,为此我们推导出了下面的精确公式:x =l -l 540R 2L 2s +l 93456R 4L 4s -l 13599040R 6L 6s+l 17175472640R 8L 8s -l 217.80337152∃1010R 10L 10s+l254.904976384∃1013R 12L 12s-∀,(3)y =l 36RL s -l 7336R 3L 3s +l 1142240R 5L 5s -l 159676800R 7L 7s+l 193530096640R 9L 9s-l 231.880240947∃1012R 11L 11s+l 271.377317369∃1015R 13L 13s-∀。
关于公路测量中圆曲线、缓和曲线(完整缓和曲线和非完整缓和曲线)的计算示例

关于公路测量圆曲线、缓和曲线(完整缓和曲线和非完整缓和曲线)的计算示例新浪微博:爱疯记录仪例:某道路桥梁中,A匝道线路。
已知交点桩号及坐标:SP,K9+000(2957714.490,485768.924);JD1,K9+154.745(2957811.298,485889.647);EP,K9+408.993(2957786.391,486158.713)。
SP—JD1方位角:51°16′25″;转角:右44°00′54.06″;JD1—EP方位角:95°17′20″。
由图纸上“A匝道直线、曲线及转角表”得知:K9+000—K9+116.282处于第一段圆曲线上,半径为385.75m;K9+116.282—K9+151.282处于第一段缓和曲线上,K9+151.282的半径为300m,缓和曲线要素A1=217.335,Ls1=35m;K9+151.282—K9+216.134处于第二段圆曲线上,半径为300m;K9+216.134—K9+251.134处于第二段缓和曲线上,K9+251.134的半径为1979.5,缓和曲线要素A2=111.245,Ls2=35m;K9+251.134—K9+408.933处于第三段圆曲线上,半径为1979.5m。
求:K9+130、K9+200、K9+230、K9+300的中桩坐标,切线方位角,左5米边桩的坐标,右10米边桩的坐标。
解:首先,我们知道要求一个未知点的坐标,必须知道起算点坐标,起算点至未知点的方位角,起算点至未知点的直线距离,然后利用坐标正算的计算公式,就可以直接求出未知点的坐标。
那么,关于圆曲线和缓和曲线(包括完整缓和曲线和非完整缓和曲线)的计算,我们需要知道如何求出起算点至圆曲线或缓和曲线上某点的方位角和直线距离。
下面,先列出关于圆曲线和缓和曲线中角度和距离计算的相关公式。
附:A匝道直线、曲线及转角表。
】下载地址:/view/f0677e38cdbff121dd36a32d7375a417866fc18f1 / 102 / 10y 轴。
完整及不完整缓和曲线

转载自测量空间!本帖最后由 wenyajun 于 2010-9-30 16:30 编辑关于不同类型缓和曲线的起点、终点曲率半径判断方法目前在匝道或线路施工坐标计算中经常遇到缓和曲线,实际中相信有很多测友选择用积木法或叫线元法正反算程序进行线路坐标计算,这就牵涉到线元的起点终点曲率半径判断的问题,一般的直线元,圆曲线元的起点终点半径判断,比较容易,可能令大家感觉麻烦的就是缓和曲线起点终点半径判断问题,缓和曲线有时候判断算对了,有时候却坐标算不对,究其原因,其实问题出于该缓和曲线是否是完整缓和曲线引起的。
关于这点,相关的课本教材上没有明确的讲述,网上对此问题的解释也是散见于不同的论文著作中,对于测量新手来说,线元法程序是非常适用上手的,但却往往因为遇到不完整缓和曲线的起点或终点的半径判断计算不出来导致坐标计算错误,的确是件令人恼火的事情,在此我就把自己的判断经验做一论述,给用线元法程序的测友们一同分享,当然高手们请一笑而过,也可留下你的经验与大家一起分享交流学习。
第一:先说说完整缓和曲线和不完整缓和曲线以及不对称缓和曲线与对称缓和曲线的概念问题,以免混为一谈.1.当对于单独一段缓和曲线从其完整与否来讲是分为完整与不完整两类;当对于一个单交点内的两段缓和曲线(即常说的第一缓和曲线和第二缓和曲线而言)又有对称缓和曲线与不对称缓和曲线之分。
由此看来,完整与对称与否是针对缓和曲线两个方面来看待区分的。
2.缓和曲线我们的测量教材上讲述的其实就是完整缓和曲线,也可以知道缓和曲线上:各个点的半径是不同的,起点到终点的半径值过度是从正无穷大到所接圆曲线半径之过度如从ZH向HY方向;或者是从所接圆曲线半径值向正无穷大过度的,如从YH向HZ方向。
那么由此可以不难判断出来,完整缓和曲线就是符合上述特征的,那么不完整的缓和曲线就是不符合上述特征的,但是线路上的平曲线设计时候一般缓和曲线不单独存在的,整体上缓和曲线前或后一般都是要连接一个圆曲线的,那么不完整缓和曲线其实就是在完整缓和曲线上截取的一段,一般就是去掉了半径无穷大的那端而是从某个点开始的半径值向所接圆曲线半径值过度的。
平曲线参数的案例讲解

平曲线参数的案例讲解前段时间有个同事在输入线路平曲线参数时遇到了困难,让我帮他解决一下,我相信有很多测量人员都遇到过这个问题,由于知识储备不足,在输入一些比较复杂的平曲线参数时真的是“一时难倒英雄汉”。
岁末闲暇下来,我便萌生了写篇文章的想法,想与我的测量同行们交流一下。
我结合了自己所参与过的项目的线路,给大家列举了三个案例,主要讲一下平曲线参数的起点问题及不完整缓和曲线。
我想和大家交流一下,在输入这些平曲线参数时自己的思路,其中也会提及到一些大家可能还未掌握的关于平曲线参数的知识点。
案例(一):校正起点桩号如上表所示,这是文莱高速第5标段的主线的直曲表,我在测量软件里用交点法输入了平曲线参数,但当我计算逐桩坐标时,发现与逐桩坐标表上的坐标并不一致,我便意识到肯定是平曲线参数输入有误,我检查了一遍测量软件上输入的平曲线参数,发现软件自动计算的交点桩号与图纸所给的交点桩号并不一致,我便意识到有可能起点桩号输入有误,我又看了一遍直曲表终于发现了问题所在。
我是以交点JD19作为线路起点输入的平曲线参数,但是图纸所给的直曲表是从整条文莱高速线路中截取的一段,对应着第5标段的线路。
我们都知道直曲表上的交点并不在线路上,而起点是一定在线路上的,所以交点JD19并不能作为线路的起点。
如果把交点JD19作为线路的起点,那么起始段的线路也就发生了改变,如上图所示,从图一中正确的线路变为了图二中错误的线路。
而第5标段线路的起点桩号是K45+900,从直曲表中可以看出,起点是位于交点JD20的第二缓和曲线上,如果以交点JD19作为起点的话,发生改变的JD19-YZ直线段是在第5标段线路以外的,因此仍然可以以交点JD19作为第5标段线路的起点,第5标段的线路也就变成了图二所示的线路,只不过需要校正一下起点桩号。
为什么要校正作为起点的交点JD19的桩号呢,这就要弄清楚交点桩号是如何定义的。
其实交点桩号并不是交点对应主线上的桩号,而是由公式交点桩号=ZH/ZY点桩号+第一切线长T1得到的,如上图三所示。
不完全缓和曲线计算

切线长为 TJDΟO1 = 551868 , TJDΟO2 = 331426 外矢距为 E = 111091 ,曲线 O1 Q = 511994 则主点坐标 O1 (9 4641915 ,4 7711882) ,
意点切线与起点切线夹角 βP (这里称之为不完全缓
和曲线转角) 。如图 1 所示 。
ls1
+
l
=
A2 R
βO1
=
ls21 2A2
βO2
=
ls22 2A2
βO P
=
( ls1 + l) 2 2A2
βP =βOP - βO1
=
( ls1 + l) 2 2A2
-
ls21 2A2
βP
=
l R1
+
l2 2A2
P 在路线测量坐标系中的坐标为 XP = 9 4551162 YP = 4 7501869
上面都是通过电算程序计算所得 。
本文所讨论的内容对于互通立交匝道的设计和施
工放样有很大参考作用 。
通过计算得
图5
β= 63°48′47″4 R2 = 40 , ls = 81 ls1 = 9 , ls2 = 90
+
3
l10 840 R1
A8
-
l11 42 240A10
+
……
如以 R2 小半径建立切线支距坐标系( l 为 P 点到 O2 的曲线长) ,则
β=
l R2
平曲线认识

第三讲公路平面坐标计算1、平曲线认识道路是一个三维空间的工程结构物,它的中线是一个空间曲线,叫路线,其在水平面的投影就是平面线形。
道路平面线形由于受到沿线地形、地质、水文、气候等自然条件和人为条件的制约而改变方向。
在路线平面方向的转折处为满足行车要求,需要用适当的曲线把前、后直线连接起来,这种曲线称为平曲线。
平曲线包括圆曲线和缓和曲线。
①圆曲线要素主点桩号计算:ZY点里程=JD点里程-TQZ点里程=ZY点里程+L/2 YZ点里程=ZY点里程+LJD里程=QZ里程+D/2(校核)②缓和曲线要素切线长: 外距:曲线长:()s s 18022180l aR l a R L h +=+-=πβπ切线加长:q =/2-3/(240R2)圆曲线相对切线内移量:p = 2/(24R)切曲差 Dh = 2T -Lh上式中:α 为线路转向角;β0为缓和曲线角; 其中q 、p 、β0缓和曲线参数。
ZH 桩号 = JD 桩号-T HY 桩号 = ZH 桩号+QZ 桩号 = HY 桩号+L/2YH 桩号 = QZ 桩号+L/2 = HY 桩号+L = ZH 桩号++LHZ 桩号 = YH 桩号+= ZH 桩号+LhJD 桩号 = ZY 桩号-Th +Dh (检核)m)2)((q tgp R T ++=α)(m 2sec)(R p R E -+=αLs Ls Ls Ls Ls Ls注意:上面计算需要大家掌握主点桩号计算,五大主点:ZH、HY、QZ、YH、HZ,还会遇到一些特殊点例如起点QD、终点ZD、公切点GQ。
可以判断下图即可。
重点知识必须掌握(线元法基础):直线:曲率为0,起终点半径无穷大。
圆曲线:具有一定曲率半径的圆弧,半径为固定值。
缓和曲线:在直线与圆曲线之间或两个不同半径的圆曲线之间设置的曲率连续变化的曲线(指从直线上半径无穷大到圆曲线的定值之间曲率半径逐渐变化的过渡段),我国公路缓和曲线的形式采用回旋线。
(曲率为半径的倒数)A1,A2——缓和曲线参数R——圆曲线半径Ls1,Ls2——缓和曲线长度一段完整缓和曲线满足公式:A²=R x Ls1,A²=R x Ls2入缓和曲线:从ZH点到HY点,A固定不变,随着Ls1的增大,半径从∞减小到R出缓和曲线:从YH点到HZ点,A固定不变,随着Ls2的减小,半径从R增大到∞如果A²≠R x Ls,那么这段缓和曲线是不完整的,叫做不完整缓和曲线。
非完整缓和曲线计算实例
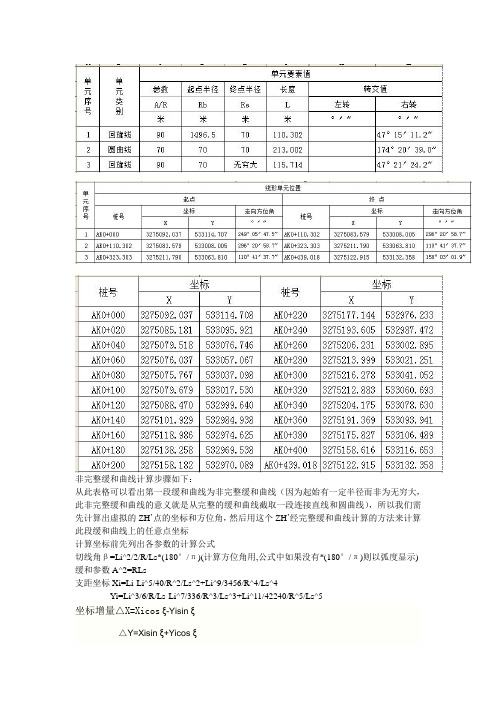
非完整缓和曲线计算步骤如下:从此表格可以看出第一段缓和曲线为非完整缓和曲线(因为起始有一定半径而非为无穷大,此非完整缓和曲线的意义就是从完整的缓和曲线截取一段连接直线和圆曲线),所以我们需先计算出虚拟的ZH’点的坐标和方位角,然后用这个ZH’经完整缓和曲线计算的方法来计算此段缓和曲线上的任意点坐标计算坐标前先列出各参数的计算公式切线角β=Li^2/2/R/Ls*(180°/π)(计算方位角用,公式中如果没有*(180°/π)则以弧度显示) 缓和参数A^2=RLs支距坐标Xi=Li-Li^5/40/R^2/Ls^2+Li^9/3456/R^4/Ls^4Yi=Li^3/6/R/Ls-Li^7/336/R^3/Ls^3+Li^11/42240/R^5/Ls^5坐标增量△X=Xicosξ-Yisin ξ△Y=Xisin ξ+Yicos ξ在第一缓和曲线时,ξ为ZH到JD的方位角,曲线左转时Yi为负号带入,右转时以正号代入在第二缓和曲线时,ξ为HZ到JD的方位角,曲线左转时Yi为正号带入,右转时以负号代入备注:Li:所求点弧长(此点至ZH‘的里程距离)R:曲线半径(以接圆曲线的半径为准)Ls:缓和曲线长(此为非完整缓和曲线,以计算出的完整缓和曲线长为准,而不是截取的缓和曲线长)开始计算:1. 先计算出虚拟的ZH’点桩号,因为根据缓和参数公式A^2=RLs,表格中已知缓和参数为90,半径为70所以求得缓和曲线长Ls=A^2/R=90^2/70=115.714,而根据表格知道实际缓和曲线长为110.302,则在起点里程AK0+000之前还有115.714-110.302=5.412M,所以此段缓和曲线的起点里程应为AK -5.4122. 计算切线角根据公式β=Li^2/2/R/Ls*(180°/π)=5.412^2/2/70/115.714*(180°/π)=0°6′12.93″3. 计算虚拟起点ZH‘方位角α,因为此线路为右转,从起点计算曲线任意点方位角时应为加,现在倒过来计算方位角所以为减,由已知条件得知AK0+000方位角为249°5′47.5″,所以虚拟ZH‘的方位角ξ为249°5′47.5″-0°6′12.93″=248°59′34.57″4. 计算虚拟起点ZH‘坐标,Xi=Li-Li^5/40/R^2/Ls^2+Li^9/3456/R^4/Ls^4=5.412-5.412^5/40/70^2/115.714^2+5.412^9/3456/70^4/115.714^4=5.412Yi=Li^3/6/R/Ls-Li^7/336/R^3/Ls^3+Li^11/42240/R^5/Ls^5=5.412^3/6/70 /115.714-5.412^11/42240/70^5/115.714^5=0.0033线路右转,在第一缓和曲线上,则Yi以正号代入△X=Xicosξ-Yisin ξ=5.412*cos(248°59′34.57″)-0.0033*sin(248°59′34.57″)=-1.937△Y=Xisin ξ+Yicosξ=5.412*sin(248°59′34.57″)+0.0033*cos(248°59′34.57″)=-5.0535虚拟起点ZH‘的坐标为(由于虚拟点在线元起点的前面(如果是在第二缓和曲线时虚拟点再线元终点的后面,则还是正常计算,为加上坐标增量)所以计算时应倒过来计算,所以为减去坐标增量)XZH‘=XZH-△X=3275092.037-(-1.937)=3275093.974YZH‘=YZH-△Y=533114.707-(-5.0535)=533119.7615. 现在可以开始由于虚拟点ZH‘来计算此段缓和曲线上的任意点,这里先计算缓和曲线终点HY点的坐标(HY点里程为ZH‘+115.714=AK0+110.302)Xi=Li-Li^5/40/R^2/Ls^2+Li^9/3456/R^4/Ls^4=115.714-115.714^5/40/70^ 2/115.714^2+115.714^9/3456/70^4/115.714^4=108.059Yi=Li^3/6/R/Ls-Li^7/336/R^3/Ls^3+Li^11/42240/R^5/Ls^5=115.714^3/6/ 70/115.714-115.714^7/336/70^3/115.714^3+115.714^11/42240/70^5/115.714 ^5=30.359线路右转,在第一缓和曲线上,则Yi以正号代入△X=Xicosξ-Yisin ξ=108.059*cos(248°59′34.57″)-30.359*sin(248°59′34.57″)=-10.396△Y=Xisin ξ+Yicosξ=108.059*sin(248°59′34.57″)+30.359*cos(248°59′34.57″)=-111.760XHY=XZH‘+△X=3275093.974+(-10.396)=3275083.578YHY=YZH‘+△Y=533119.761 +(-111.760)=533008.001切线角β= Li^2/2/R/Ls*(180°/π)=115.714^2/2/70/115.714*(180°/π)=47°21′23.76″所以HY点方位角为虚拟点ZH’加上(因为线路右转)47°21′23.76″=248°59′34.57″+47°21′23.76″=296°20′58.33″6.接着计算曲线上任意点坐标,方法同上,比如计算AK0+020的坐标(这里的AK0+020实际为AK0+025.412)曲线长Li为25.412,半径R为70,计算如下:Xi=Li-Li^5/40/R^2/Ls^2+Li^9/3456/R^4/Ls^4=25.412-25.412^5/40/70^2/ 115.714^2+25.412^9/3456/70^4/115.714^4=25.408Yi=Li^3/6/R/Ls-Li^7/336/R^3/Ls^3+Li^11/42240/R^5/Ls^5=25.412^3/6/7 0/115.714-25.412^7/336/70^3/115.714^3+25.412^11/42240/70^5/115.714^5= 0.3376线路右转,在第一缓和曲线上,则Yi以正号代入△X=Xicosξ-Yisin ξ=25.408*cos(248°59′34.57″)-0.3376*sin(248°59′34.57″)=-8.7932△Y=Xisin ξ+Yicosξ=25.408*sin(248°59′34.57″)+0.3376*cos(248°59′34.57″)=-23.840X=XZH‘+△X=3275093.974+(-8.7932)=3275085.181Y=YZH‘+△Y=533119.761 +(-23.840)=533095.921切线角β= Li^2/2/R/Ls*(180°/π)=25.412^2/2/70/115.714*(180°/π)=2°17′2.22″所以HY点方位角为虚拟点ZH’加上(因为线路右转)2°17′2.22″=248°59′34.57″+2°17′2.22″=251°16′36.79″。
匝道坐标计算实例(非常实用)

0
备注 弧度制 1.050259
R2*Ls1 =A12 8100
备注
值(左转“+”,右转“-”)
位角(左转“-”,右转“+”) 利用公式反算
坐标增量 △X 16.19957485 △Y 0.08747836
ZH
任一点 与ZH完整 点弧长 L0 16.2
16.19981 1.066459 1.061059
0.005399988
0.0162
-1
ZH完整点切线方位角β ZH完整-M0直线方位角β X完整 Y完整
切线方位角=M0点切线方位角±转角值(左转“+”,右转“-”)
第一段完整曲线要素 ZH完整坐标 X 3435389.441 Y 500174.9586 ZH完整桩号 K0+702.747
弦长C= 偏角= √△X2+△Y2 arctg(△Y/△X)
(切线)方位 角β 1 1.066458665
转角值= 2 L0 /2*R2*Ls1
参数g (左偏-1, 右偏+1)
直线
(适用正推)直线方位角=偏角±切线方位角(左转“-”,右转“+”) X0=X完整+C*COS(ZH完整-M0直线方位角) Y0=Y完整+C*SIN(ZH完整-M0直线方位角)
3435389.441 500174.9586
缓和曲线 完整性 不完整
备注 A12=Ls1*R2
整
不是直线方位角)
说明:①现以第一段曲线上任一点坐标和方位角反推ZH完整点坐标,切线方位角(不是直线方位角) ②不用改变坐标系 第一段缓和曲线上任一点曲线元素 任一点坐标M0 X0 Y0 3435397.346 500189.099 任一点M0桩号 K0+718.947 度 60 (切线)方位角β 0 分 秒 10 31.4
不完整缓和曲线计算式的推导

不完整缓和曲线计算式的推导作者:郑飞舟张卫华来源:《科技资讯》2011年第19期摘要:在现有完整缓和曲线公式的基础上,通过三角函数和坐标平移推算出不完整缓和曲线的计算方程式。
关键词:不完整缓和曲线极坐标放样中图分类号:TP3 文献标识码:A 文章编号:1672-3791(2011)07(a)-0204-01目前我国路桥建设发展越来越快,在路桥设计当中经常使用不完整缓和曲线。
在施工测量中的较多使用全站仪极坐标测量放样,需要对不完整缓和曲线上任意点位进行准确的计算。
完整缓和曲线的计算已经得到广泛的应用,本文将在完整缓和曲线计算公式的基础上推导出不完整缓和曲线的计算方程式。
1 完整缓和曲线公式在《工程测量学》中对缓和曲线的定义为:缓和曲线是设置在直线和圆曲线之间的一种线性。
其缓和曲线方程应用公式为:(1)式中,为曲线长,为缓和曲线长度,为圆曲线半径。
根据曲线上某一点的长度即可计算该点在以直缓点为原点,以直线前进方向为X轴方向所组成坐标系的平面坐标。
2 不完整缓和曲线计算式在实际应用当中还会碰到一种缓和曲线,是设置在大圆曲线与小圆曲线之间的缓和曲线,称为不完整缓和曲线。
当遇到不完整缓和曲线时,不能采用缓和曲线方程应用公式计算,但可以根据缓和曲线方程应用公式推导出不完整缓和曲线方程式。
2.1 不完整缓和曲线计算式推导如图1,缓和曲线要素中大圆曲线半径为,小圆曲线半径为,缓和曲线长度为。
将此缓和曲线小圆向大圆方向延长至半径无穷大时,这个点可以看作是直缓点,直缓点到大圆曲线与缓和曲线的交点长度为。
根据缓和曲线的特点:曲线上任一点的曲率半径与该点至起点的曲线长成反比,即可得: 根据此式可推出缓和曲线长度(如图1):建立一个以ZH1为原点,以ZH1至JD为X轴方向的直角坐标系。
坐标系中,为以ZH1为直缓点的缓和曲线长度,ZH点坐标计算方程式为:式中两圆间缓和曲线上任一点坐标计算方程式为:式中,为以ZH点为起点的缓和曲线长度。
道路平曲线概念讲解
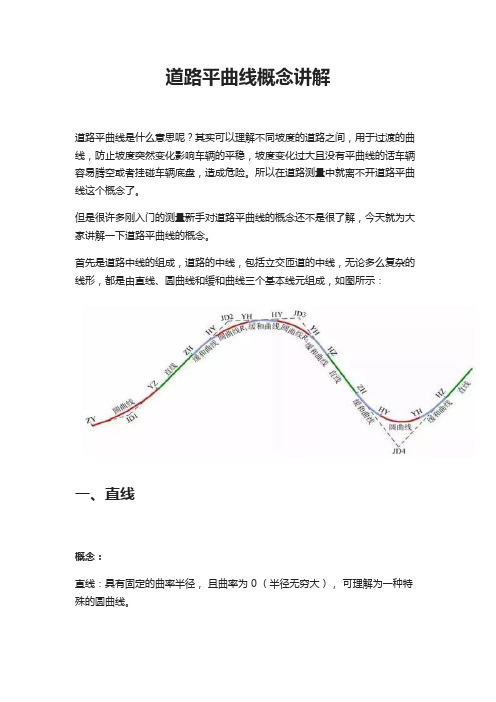
道路平曲线概念讲解道路平曲线是什么意思呢?其实可以理解不同坡度的道路之间,用于过渡的曲线,防止坡度突然变化影响车辆的平稳,坡度变化过大且没有平曲线的话车辆容易腾空或者挂碰车辆底盘,造成危险。
所以在道路测量中就离不开道路平曲线这个概念了。
但是很许多刚入门的测量新手对道路平曲线的概念还不是很了解,今天就为大家讲解一下道路平曲线的概念。
首先是道路中线的组成,道路的中线,包括立交匝道的中线,无论多么复杂的线形,都是由直线、圆曲线和缓和曲线三个基本线元组成,如图所示:一、直线概念:直线:具有固定的曲率半径,且曲率为 0 (半径无穷大),可理解为一种特殊的圆曲线。
特点:1)两点之间以直线为最短。
2)笔直的道路给人以短捷、直达的良好印象。
3)汽车在直线上行驶受力简单,方向明确,驾驶操作简易。
4)测设施工方便。
二、缓和曲线概念:缓和曲线 :为了使路线的平面线形更加符合汽车的行驶轨迹、离心力逐渐变化,确保行车的安全和舒适,需要在直线和圆曲线之间或半径相差较大的两个同向圆曲线之间设置一段曲率连续变化的曲线,此曲线称为缓和曲线。
目前我国公路设计中,以回旋线作为缓和曲线。
缓和曲线类型:1.完整缓和曲线 :判断标准: A²=R x Ls2、非完整缓和曲线:判断标准: A²≠R x LsA= 缓和曲线参数缓和曲线三、圆曲线概念:圆曲线:即圆的一部分(圆弧),具有固定的曲率半径。
特点1、曲线上任一点曲率半径R为常数2、大半径的圆曲线线形美观、顺适、行车舒适,是公路上常采用的线形。
四、道路中常见的线形组合在道路及立交匝道设计中,实际采用的线形往往是直线、圆曲线、缓和曲线中的一种或几种组合而成。
主要有以下几种:(1)基本型曲线是按“直线-回旋曲线-圆曲线-回旋曲线-直线”的顺序组合起来的线型。
基本型中,又可以根据其中两个回旋曲线参数相等与否而分为对称式和不对称式两种。
(2)S 型曲线把两个反向圆曲线用回旋曲线连接起来的线型,GQ处R=∞。
缓和曲线

在此引入一个“虚拟延伸”的观点,让这段这不完整的缓和曲线延伸成一段完整的缓和
曲线至 HZ′(桩号 K40+440.720,注意这点不在设计线路上)
知β=(90×33.5302)/(190×π×63.530)= 2°40′5.89″
B?
484443.327 EXE
Y=484448.4151
EXE
I=222.6015582
在圆曲线段,你正反算都可以,所要注意是起始方位角的不同,半径正负号的变化。
以上讨论了基本曲线的六种情况的中桩坐标计算,应该说上面两套程序都可以解决了,
如果对于不对称的缓和曲线所组成的基本曲线以上程序完全适用。
以上都是讨论的完整的缓和曲线,如果对于一段不完整的缓和曲线(在卵形曲线中经常
-39703.767 EXE
R?
以上同理
35 EXE
M?
30 EXE
N?
191°52′45″-180 EXE
I=15.81260512 注意这是反向方位角
EXE
A?
3103847.328 EXE
T?
36.497 EXE
X=3103823.3
EXE
B?
484443.327 EXE
Y=484438.5534.
L5 I=N+( L-K-M/2)×180/R/ π◢
L6 GOTO 0 R——曲线半径 L——待求点桩号 K——ZH 点桩号 M——缓和曲线长
姚永庆
N——起始方位角
T——切线长
I——待求点切线方位角
第 L3,L4 行太长太复杂,仔细看一下它有好多相同的计算语段,只要多用几个存储键
就行了。
操作
显示
说明
不完整缓和曲线的切线

不完整缓和曲线的切线在生活中,我们经常会遇到不完整缓和曲线。
那么,什么是不完整缓和曲线呢?简单来说,就是一条曲线只在某个区间内缓慢地变化,而在另外的区间中则变化迅速。
在数学上,“不完整缓和曲线”的定义是指一种函数,其导数在区间内缓慢变化,而在另外的区间中则变化较快。
对于不完整缓和曲线,我们需要注意的是它们的切线。
切线是一种在曲线上某一点处与该点切线相切的直线。
在不完整缓和曲线中,由于其导数在某些区间内缓慢变化,因此切线可能会有一些特殊的性质。
接下来,我们来详细了解一下。
首先,在不完整缓和曲线上,由于导数的变化缓慢,切线会有一个平稳的过渡,这也就意味着,切线的旋转会非常缓慢,而不像一般的曲线那样旋转非常迅速。
因此,我们可以根据切线的旋转特性,来进行更加稳定的预测和计算。
其次,在不完整缓和曲线上,切线的斜率变化也会比较缓慢。
这意味着,当我们使用切线进行预测时,我们可以更加精确地预测曲线的走势,而不是直接猜测。
此外,由于切线的斜率变化较缓慢,因此我们可以更加稳健地进行风险控制,以免在交易中发生意外的亏损。
最后,我们需要指出的是,在不完整缓和曲线上,切线的旋转和斜率的变化都比较缓慢。
这也就意味着,我们需要花费更多的时间来进行分析和计算。
只有在深入分析了不完整缓和曲线的各种特点以后,我们才能够更加准确地使用切线进行预测和计算。
综上所述,当我们遇到不完整缓和曲线时,我们需要注意其切线的变化特点。
通过了解切线的旋转和斜率的变化,我们可以更加准确地进行预测和计算,以便在交易中获得更高的收益率。
因此,我们要认真研究不完整缓和曲线的各种特点,并结合自己的实际情况,来进行合理而稳健的交易。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
转载自测量空间!
本帖最后由 wenyajun 于 2010-9-30 16:30 编辑
关于不同类型缓和曲线的起点、终点曲率半径判断方法
目前在匝道或线路施工坐标计算中经常遇到缓和曲线,实际中相信有很多测友选择用积木法或叫线元法正反算程序进行线路坐标计算,这就牵涉到线元的起点终点曲率半径判断的问题,一般的直线元,圆曲线元的起点终点半径判断,比较容易,可能令大家感觉麻烦的就是缓和曲线起点终点半径判断问题,缓和曲线有时候判断算对了,有时候却坐标算不对,究其原因,其实问题出于该缓和曲线是否是完整缓和曲线引起的。
关于这点,相关的课本教材上没有明确的讲述,网上对此问题的解释也是散见于不同的论文著作中,对于测量新手来说,线元法程序是非常适用上手的,但却往往因为遇到不完整缓和曲线的起点或终点的半径判断计算不出来导致坐标计算错误,的确是件令人恼火的事情,在此我就把自己的判断经验做一论述,给用线元法程序的测友们一同分享,当然高手们请一笑而过,也可留下你的经验与大家一起分享交流学习。
第一:先说说完整缓和曲线和不完整缓和曲线以及不对称缓和曲线与对称缓和曲线的
概念问题,以免混为一谈.
1.当对于单独一段缓和曲线从其完整与否来讲是分为完整与不完整两类;当对于一个单交点内的两段缓和曲线(即常说的第一缓和曲线和第二缓和曲线而言)又有对称缓和曲线与不对称缓和曲线之分。
由此看来,完整与对称与否是针对缓和曲线两个方面来看待区
分的。
2.缓和曲线我们的测量教材上讲述的其实就是完整缓和曲线,也可以知道缓和曲线上:各个点的半径是不同的,起点到终点的半径值过度是从正无穷大到所接圆曲线半径之过度如从ZH向HY方向;或者是从所接圆曲线半径值向正无穷大过度的,如从YH向HZ方向。
那么由此可以不难判断出来,完整缓和曲线就是符合上述特征的,那么不完整的缓和曲线就是不符合上述特征的,但是线路上的平曲线设计时候一般缓和曲线不单独存在的,整体上缓和曲线前或后一般都是要连接一个圆曲线的,那么不完整缓和曲线其实就是在完整缓和曲线上截取的一段,一般就是去掉了半径无穷大的那端而是从某个点开始的半径值向所接圆曲线半径值过度的。
3.对称与不对称缓和曲线是相对于一个单交点内的两段缓和曲线(即常说的第一缓和曲线和第二缓和曲线而言),当两个缓和曲线长度相等时候则称之为对称缓和曲线,自然此时的切线长、缓和曲线参数A值都是相等的,反之不相等就称为不对称缓和曲线,自然切线长、缓和曲线是不相等的。
第二:由此可以看出对于缓和曲线而言,对称与否很容易分辨判断无需赘述,完整与否不
易区分,也是这里重点要说的问题.
1.完整与不完整缓和曲线的区别判断方法:综上所述,完整缓和曲线与不完整缓和曲线的判断其实就在于验证完整缓和曲线参数方程A^2=R*Ls这个等式成立与否就可。
(A为已
知的缓和曲线参数,R为缓和曲线所接圆曲线的半径,Ls为该段缓和曲线的长度)理论上,当该式子成立时候,那就是完整缓和曲线无疑,当不成立时候那就可判断为不完整缓和曲线了。
实际工作操作时候验证方法如下:先把R*Ls的乘积进行开平方然后看所得到的结
果是否与所提供的缓和曲线参数A值相等。
2.完整缓和曲线与不完整缓和曲线起点终点的曲率半径的判断与计算:线路设计上的缓和曲线一般不会单独存在的,连续的缓和曲线起点或终点必定有一端都是要接圆曲线的,那么缓和曲线一端的半径值必定就是圆曲线的半径值了,求半径的问题就变成只需求出另外一端半径就可以了.上面说过首先判断出该缓和曲线是否是完整的办法,那么当是完整缓和曲线时候,起点或终点两端的半径,必定一端是无穷大,一端就是圆曲线半径了;那么当判断是不完整缓和曲线时,一端半径就是圆曲线半径,另一端的半径就绝对不能是无穷大了的,理论上应该是该端点的半径值要小于无穷大而大于所接圆曲线的半径值,那么该怎么求出来呢此时就牵涉到了不完整缓和曲线的参数方程:
A^2=[(R大-R小)÷(R大*R小)]*Ls
由上方程可以看出,R大就是我们所需要求的这端半径了,R小自然就是该不完整缓和曲线所接的圆曲线半径了。
A为该不完整缓和曲线参数,R小为所接圆曲线半径,Ls为该不完整缓和曲线的长度,这些图纸都提供的有了,只需按照上面的不完整缓和曲线的参数方程进行解方程就可得到另一端的半径值了,只要是正值那就OK了!!!
2.很有必要再说说不完整缓和曲线中的一个特例------卵形曲线
卵形曲线是不完整缓和曲线中的一种特殊情况,对于卵形曲线的定义是:两端同转向圆曲线中间所夹的那段同转向不完整缓和曲线就叫卵形曲线,也就是指那段缓和曲线前后各有个圆曲线相接,并且三段曲线的转向相同用上述判断复核是那么这段缓和曲线一般都是不完整的那么符合这样特征的就是卵形曲线,那么此时卵形曲线必定要复核上述的不完整缓
和曲线的参数方程:
A^2=[(R大-R小)÷(R大*R小)]*Ls
那么此时卵形曲线的两端半径就分别是所接两个圆曲线的半径值!也就是R大和R小.半径值就是无需求的,直接用卵形曲线所接前后两个圆曲线的半径值就可了.
其实关于不完整缓和曲线一端半径求算方法这点,在夏夜的“轻松测量系统软件电脑版”的菜单上也就有这个工具,懒得列方程解算的,不妨直接用软件计算也可嘛,我上述只是
讲述了下手工计算的方法.
至此,对于缓和曲线的特征判断与半径计算应该有个清晰的眉目了吧,那么在使用程序计算线路坐标的时候,遇见缓和曲线就先判断是否完整,然后用上述方法很快就可判断到起点或终点的曲率半径了。
最后解释下,说曲率其实就是半径的倒数,程序中经常见到这个概念,千万不要把曲率和半径混为一谈导致程序计算错误了!
以上所述是本人愚见,欢迎各位不吝赐教,共同学习交流,将课本理论与现实实践相结合,正确顺利使用线元法(积木法)坐标计算程序,为坐标计算做好数据准备,从而正确快速的计算出线路坐标,当然也欢迎测友与本人联系共同进步!。
