不等长缓和曲线计算示例

合集下载

缓和曲线的计算方法(三种)

偏角 l2 l
2 s
0
距离：用曲线长l来代替弦长。放样出第1点后，放样第2点时，用偏角和距离l交会得到。
（2）当点位于圆曲线上方法：架仪HY (或YH)，后视ZH(或HZ)，拨角b0，即找
到了切线方向，再按单圆曲线偏角法进行。
b0 2 0
ls 3R
此外还有极坐标法、弦线支距法、长弦偏角法。
3 ls 10 .00 m x0 l s 2 40 R 2 ls y 0 .17 m 0 6R
TH ( R p )tg
L H R ( 2 0 )

180

2l s 41 .96 m
E H ( R p ) sec
（2）当点位于圆曲线上，有：
x R sin q y R (1 cos ) p
2、偏角法（整桩距、短弦偏角法）要注意：点是位于缓和曲线，还是位于圆曲线。
位于圆曲线
位于缓和曲线
2、偏角法（整桩距、短弦偏角法）
（1）当点位于缓和曲线上，有：
总偏角 (常量 ) 0 ls 6R
（3）缓和曲线的参数方程:
（4）圆曲线终点的坐标:
二．主点(major point)的测设
1、测设元素的计算
（1）内移距p 和切线增长q的计算：
24 R ls l s3 q 2 240 R 2
p
l s2
2、主点的测设
（1）里程的计算
ZH=JD-TH；HY=ZH+ls；
QZ=ZH+LH/2；HZ=ZH+LH；YH=HZ-ls
三、带有缓和曲线的圆曲线详细测设 1、切线支距法 (tangent off-set method)

不等长缓和曲线与圆曲线的连接过程与计算公式

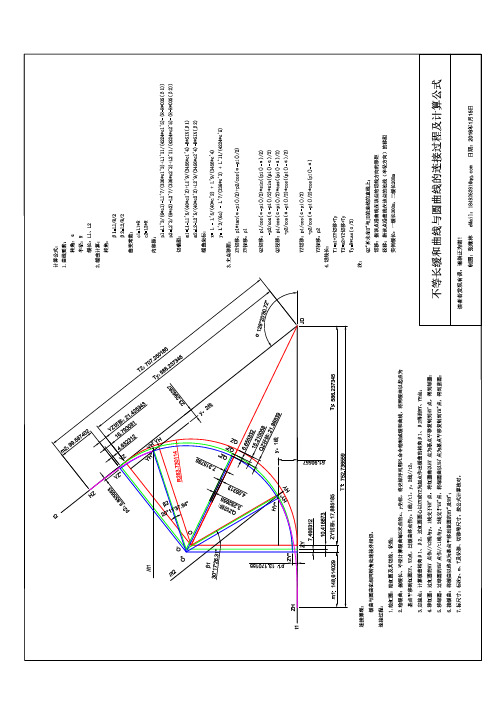
14.4677204 15.6036514 16.7967753 18.0483661 19.3596799 20.7319541 22.1664064 23.6642342 25.2266137 26.8546990 28.5496220 30.3124916 32.1443931 34.0463885 36.0195162 38.0647910 40.1832049 42.3757272 44.6433061 46.9868694 49.4073265 51.9055703
195
194.0293662
200
198.8986505
205
203.7542556
210
208.5951442
215
213.4202296
220
218.2283751
225
223.0183931
230
227.7890445
235
232.5390380
0
237.2670295
245
241.9716214
CAD的PL命令坐标序列 RDO(UCN1D6(,B61)6,6)&","&ROUN 1111111111111111122334455667788911119500001122334455664949494949494949477889,,,49494949494949.................4949.000..............99999999999999999....9..99998888776655999999999999988774321600543197417393719999999887541849334545005404415488188099998639239286663493750194617935915557986114626190199205063,2974163453887602796697323761241740969145,2789296679467,,,,,,,,,,,,,,,,,9182.582,,,,,,,,,,,,,00000000000001111,,,,9.2233445567889.................111152.............00000112345680246012376693828396207601358274223720027....560782916608070650235845271522784333605612837201790665893477975943146968026708588112820696512562068128490271157080699834844714522449568280265626925373179595882

缓和曲线）计算公式

高速公路的线路(缓和曲线)计算公式一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：x Z，y Z计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z，y Z为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：x Z，y Z计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z，y Z为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：S Z④变坡点高程：H Z⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x 求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：x,y ②待求点的切线方位角：αT计算过程：。

关于公路测量中圆曲线、缓和曲线(完整缓和曲线和非完整缓和曲线)的计算示例

关于公路测量圆曲线、缓和曲线（完整缓和曲线和非完整缓和曲线）的计算示例新浪微博：爱疯记录仪例：某道路桥梁中，A匝道线路。

已知交点桩号及坐标：SP，K9+000（2957714.490，485768.924）；JD1，K9+154.745（2957811.298，485889.647）；EP，K9+408.993（2957786.391，486158.713）。

SP—JD1方位角：51°16′25″；转角：右44°00′54.06″；JD1—EP方位角：95°17′20″。

由图纸上“A匝道直线、曲线及转角表”得知：K9+000—K9+116.282处于第一段圆曲线上，半径为385.75m；K9+116.282—K9+151.282处于第一段缓和曲线上，K9+151.282的半径为300m，缓和曲线要素A1=217.335，Ls1=35m；K9+151.282—K9+216.134处于第二段圆曲线上，半径为300m；K9+216.134—K9+251.134处于第二段缓和曲线上，K9+251.134的半径为1979.5，缓和曲线要素A2=111.245，Ls2=35m；K9+251.134—K9+408.933处于第三段圆曲线上，半径为1979.5m。

求：K9+130、K9+200、K9+230、K9+300的中桩坐标，切线方位角，左5米边桩的坐标，右10米边桩的坐标。

解：首先，我们知道要求一个未知点的坐标，必须知道起算点坐标，起算点至未知点的方位角，起算点至未知点的直线距离，然后利用坐标正算的计算公式，就可以直接求出未知点的坐标。

那么，关于圆曲线和缓和曲线（包括完整缓和曲线和非完整缓和曲线）的计算，我们需要知道如何求出起算点至圆曲线或缓和曲线上某点的方位角和直线距离。

下面，先列出关于圆曲线和缓和曲线中角度和距离计算的相关公式。

附：A匝道直线、曲线及转角表。

】下载地址：/view/f0677e38cdbff121dd36a32d7375a417866fc18f1 / 102 / 10y 轴。

缓和曲线的计算

缓和曲线的计算随着公路交通事业的发展,高等级公路将成为未来公路发展的主流。

在高等级公路中勘测和设计人员为了提高线型标准,普遍采用了以曲线为主的平面线型,设计图一般只给出了路线的有关参数和施工图,测量人员需要根据具体的路线里程和施工图进行再计算,计算出坐标用仪器放样,因此本文首先讨论缓和曲线任一点坐标的计算工地的施工放样。

1．缓和曲线的作用1）便于驾驶员操纵方向盘2）乘客的舒适与稳定，减小离心力变化3）满足超高、加宽缓和段的过渡，利于平稳行车4）与圆曲线配合得当，增加线形美观2．回旋线基本方程:即用回旋线作为缓和曲线的数学模型。

令：ρ=R，Ls=s 则 Ls=A2/R3．直角坐标及要素计算1）回旋线切线角（1）缓和曲线上任意点的切线角缓和曲线上任一点的切线与该缓和曲线起点的切线所成夹角。

βx=L2/2RL s（2）缓和曲线的总切线角β=L s /2R.180/л2）缓和曲线直角坐标任意一点P 处取一微分弧段ds ，其所对应的中心角为d βxdx=dscos βxdy=dssin βx3）缓和曲线常数（1）主曲线的内移值p 及切线增长值q内移值：p=Y h -R(1-cosβh )=Ls 2/24R切线增长值：q=X h -Rsinβh =Ls/2-Ls 3/240R 2（2）缓和曲线的总偏角及总弦长总偏角：βh =Ls/2R总弦长：C h =Ls-Ls 3/90R 24）缓和曲线要素计算《公路工程技术标准》规定，当R<R 免时，必须设置缓和曲线。

切线长()q a p R q T T h ++=+=2tan 外距 ()R a p R p E E h -+=+=2sec 曲线长 ()s s 18022180l aR l a R L h +=+-=πβπ圆曲线长 s 2l L L h y -=切线差 h h h L T D -=2平曲线五个基本桩号：ZH——HY——QZ——YH——HZ5、坐标计算1)如图1建立以ZH为坐标原点,过ZH点的缓和曲线切线为X轴, ZH点上缓和曲线的半径为Y轴的直角坐标系。

不等长缓和曲线坐标计算

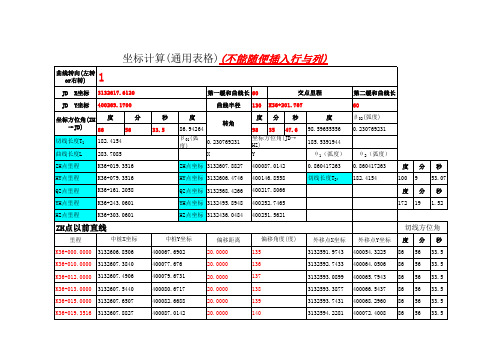
54.92 54.92 54.92 54.92 54.92 54.92 54.92 54.92 6.25
YH点至ZH点段缓和曲线
里程 K36+250.0000 K36+300.0000 K36+303.0601 K36+303.0601 K36+303.0601 K36+303.0601 K36+303.0601 K36+303.0601 K36+303.0601 K36+303.0601 中桩X坐标 3132488.9963 3132439.0942 3132436.0484 3132436.0484 3132436.0484 3132436.0484 3132436.0484 3132436.0484 3132436.0484 3132436.0484 中桩Y坐标 400253.4974 400251.8568 400251.5620 400251.5620 400251.5620 400251.5620 400251.5620 400251.5620 400251.5620 400251.5620 偏移距离 25.0000 25.0000 25.0000 25.0000 25.0000 25.0000 25.0000 25.0000 25.0000 25.0000 90 91 92 93 94 95 96 97 98 99 偏移角度外移点X坐标 3132486.9039 3132441.9264 3132439.3285 3132439.7605 3132440.1914 3132440.6211 3132441.0493 3132441.4760 3132441.9011 3132442.3244 外移点Y坐标 400228.5852 400227.0178 400226.7782 400226.8392 400226.9077 400226.9838 400227.0673 400227.1584 400227.2568 400227.3626

不对称缓和曲线要数的计算方法

精心整理不对称缓和曲线要数的计算方法????????? 发布日期：2012-02-12??浏览次数：52圆曲线两端缓和曲线不等长的测设方法，圆曲线起始端缓和曲线的长度为L1终端的缓和曲线长度为L2圆曲线半径为R,所测转角为a切线角切线增量内移值切线长曲线长或者外矢距Goto 1 ↙(注：↙表示按EXE键即可)2. XLZBZB使用说明：K? 正算时所求点的里程：L(-Z+Y) 正算时所求点距该里程中线的边距（左侧取负值，右侧取正值，在中线上取零（即数字0））3. 正算子程序程序名：SUB14→DimZ ↙(注：↙表示按EXE键即可)↙(注：↙表示按EXE键即可)I+J(Acos(G+QCJ(1÷P+CJD)×180÷π)+Bcos(G+QEJ(1÷P+EJD)×180÷π)+Z[4]cos(G+QZ[1]J(1÷P+Z[1]JD)×180÷π)+Bcos(G+Q(1-E)J(1÷P+(1-E)JD)×180÷π)+A cos(G+Q(1-C)J(1÷P+(1-C)JD) ×180÷π)) →X ↙段线元起点切线方位角→G: 二段线元终点里程→H: 二段线元起点曲率半径→P：二段线元终点曲率半径→R：二段线元左右偏标志→Q：…………………（注：如有多个曲线元要素，还要继续添加到数据库DAT中）I= 线元起点的X坐标：S= 线元起点的Y坐标: O= 线元起点里程:G= 线元起点切线方位角: H= 线元终点里程P= 线元起点曲率半径R= 线元终点曲率半径Q= 线元左右偏标志（注：左偏为-1，右偏为+1 ）（注：如有多个曲线元要素，还要继续添加到数据库DAT中,曲率半径直径输入半径值）5. 坐标反算程序名：ZBFS“U=”:S÷666.667→U ▲ 亩Goto 1（注：0表示数字零）说明：点位必须按顺序输入成封闭形图型！A B C D 为第一，二两点坐标（常量），X Y……为第三，四，五，六点坐标（变量）。

公路工程测量放线圆曲线、缓和曲线(完整缓和曲线、非完整缓和曲线)计算解析

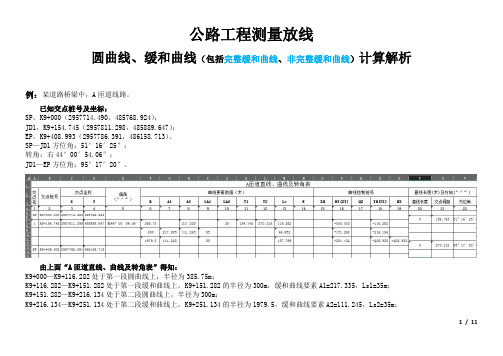
公路工程测量放线圆曲线、缓和曲线（包括完整缓和曲线、非完整缓和曲线）计算解析例：某道路桥梁中，A匝道线路。

已知交点桩号及坐标：SP，K9+000（2957714.490，485768.924）；JD1，K9+154.745（2957811.298，485889.647）；EP，K9+408.993（2957786.391，486158.713）。

SP—JD1方位角：51°16′25″；转角：右44°00′54.06″；JD1—EP方位角：95°17′20″。

由上面“A匝道直线、曲线及转角表”得知：K9+000—K9+116.282处于第一段圆曲线上，半径为385.75m；K9+116.282—K9+151.282处于第一段缓和曲线上，K9+151.282的半径为300m，缓和曲线要素A1=217.335，Ls1=35m；K9+151.282—K9+216.134处于第二段圆曲线上，半径为300m；K9+216.134—K9+251.134处于第二段缓和曲线上，K9+251.134的半径为1979.5，缓和曲线要素A2=111.245，Ls2=35m；1 / 11K9+251.134—K9+408.933处于第三段圆曲线上，半径为1979.5m。

求：K9+130、K9+200、K9+230、K9+300的中桩坐标，切线方位角，左5米边桩的坐标，右10米边桩的坐标。

下面，先列出关于圆曲线和缓和曲线中角度和距离计算的相关公式。

2 / 113 / 11y 轴。

过圆曲线上任意点P 的切线与ZY —JD 相交，夹角（切线角）为β，ZY —P 与ZY —JD 的夹角（弦切角）为α，ZY —P 的弧长为L ，ZY —P 的直线距离为d ，圆曲线的半径为R 。

5800不等长缓和曲线计算

5800不等长缓和曲线计算“XLZBJSCX” ◢LB1 1 ↙CLS : FIX 4 : 30→DIM Z ↙“K=”?K ◢（计算里程）IF K<本段曲线终点里程 AND K≥上段曲线终点里程：THEN 本段终点里程→Z[1] : 上段曲线终点里程→Z[2] ：曲线偏角→A : 1→I （注：左偏曲线输入-1→I,右偏曲线输入1→I）: 半径→R : 第一缓和曲线→Z[6] : 第二缓和曲线→Z[7] : T1切线→Z[12]: T2切线→Z[13]: 交点X→B :交点Y→C : 小里程向交点方位角→E : 交点向大里程方位角→F : GOTO 2 : IFEND↙…………LB1 2 ↙（曲线要素计算）Z[6]/2- Z[6]^3/(240*R^2)+ Z[6]^5/(34560*R^4) →Z[8] ↙（M1）Z[7]/2- Z[7]^3/(240*R^2)+ Z[7]^5/(34560*R^4) →Z[9] ↙（M2）Z[6]^2/(24*R)- Z[6]^4/(2688*R^3) →Z[10] ↙（P1）Z[7]^2/(24*R)- Z[7]^4/(2688*R^3) →Z[11] ↙（M2）π*A*R/180+0.5*( Z[6]+ Z[7])→S ↙（曲线长）90* Z[6]/(R*π) →Z[14] ↙（第一缓和曲线总偏角）90* Z[7]/(R*π) →Z[15] ↙（第二缓和曲线总偏角）B+ Z[12]*COS (E+180)→ Z[16] ↙（ZH点X）C+ Z[12]*SIN(E+180)→ Z[17] ↙（ZH点Y）Z[1]-S→Z[3] ↙(ZH点里程)Z[1]-S+ Z[6]→Z[4] ↙(HY点里程)Z[1]- Z[7]→Z[5] ↙(YH点里程)GOTO 3 ↙LB1 3 ↙(判断里程点与曲线关系)IF K≤Z[3] AND K> Z[2] : THEN GOTO 4 : IFEND ↙IF K≤Z[4] AND K> Z[3] : THEN GOTO 5 : IFEND ↙IF K≤Z[5] AND K> Z[4] : THEN GOTO 6 : IFEND ↙IF K≤Z[1] AND K> Z[5] : THEN GOTO 7 : IFEND ↙LB1 4 ↙（里程小于直缓点直线独立坐标）K- Z[3] →X : 0→Y : E→T : PROG“TYZBCX” ：GOTO 1 ↙LB1 5 ↙（第一缓和曲线独立坐标）K- Z[3] →H ↙H-H^5/(40*R^2* Z[6]^2)+H^9/(3456*R^4* Z[6]^4) →X ↙H^3/(6*R* Z[6])-H^7/(336*R^3* Z[6]^3) →Y ↙90*H^2/( R*π* Z[6]) →T ↙IF I>0 ：THEN T +E→T : ELSE E-T →T : T<0=>360+T→T : IFEND ↙PROG“TYZBCX” ：GOTO 1 ↙LB1 6 ↙（圆曲线独立坐标）K- Z[4] →H ↙H*180/( R*π)+ Z[14]→T ↙R*SIN T+ Z[8]→X ↙R*(1-COS T)+ Z[10]→Y ↙IF I>0 ：THEN T +E→T : ELSE E-T →T : T<0=>360+T→T : IFEND ↙PROG“TYZBCX” ：GOTO 1 ↙LB1 7 ↙（第二缓和曲线独立坐标）Z[1] -K →H ↙H-H^5/(40*R^2* Z[7]^2)+H^9/(3456*R^4* Z[7]^4) →U↙H^3/(6*R* Z[7])-H^7/(336*R^3* Z[7]^3) →V ↙90*H^2/( R*π* Z[7]) →T ↙Z[13]COS A+ Z[12]-U*COS A-V*SIN A→X ↙Z[13]*SIN A-U*SIN A+V*COS A→Y ↙IF I>0 ：THEN F-T→T : T<0=>360+T→T : ELSE F+T →T : IFEND ↙PROG“TYZBCX” ：GOTO 1 ↙子程序：“TYZBCX” ↙（统一坐标计算）IF I<0 : THEN -Y→Y : IFEND ↙“QXJ=” :T◢（切线方位角）Z[16]+X*COS E-Y*SIN E→Z[18] ↙Z[17]+X*SIN E+Y*COS E→Z[19] ↙“XI=” : Z[18] ◢（中线X）“YI=” : Z[19] ◢（中线Y）“PJ=”?J◢(输入边桩与线路夹角，左-右+)“PD=”?D◢（输入边桩距）Z[18]+D*COS(T+J) →Z[20] ↙Z[19]+D*SIN(T+J) →Z[21] ↙“XP=”: Z[20] ◢（边桩X）“YP=”: Z[21] ◢（边桩Y）RETURN↙4850程序转换成5800的方法4850程序转换成5800的方法好多同行有了4800或者4850的程序还要到处找5800的程序，不如自己搞定不求人，当然你想使用5800的其他功能，另当别论！1、赋值命令变化：如X=X＋R×cos（J－90V）变成X＋R×cos（J－90V）→X;N=1变成1→N2、sin、cos等变化：如sinA变成sin(A),cosA变成cos(A)3、运算顺序变化：如A=C^2/24B变成C^2/（24B）→A4、条件格式变化:如 N＜8=>Goto 2△变成N＜8=>Goto 2或者If N＜8:Then Goto 2:If End5、变量命令变化：如{A}变成?A或者?→A6、变量扩展命令变化:如Defm 10变成10 →DimZ7、在子程序末尾一定要加上Return你只要把4850的程序按以上进行变换，在5800上完全可以正常使用4850路线坐标计算路线坐标计算主程序LUYONG XLZBLbl 0{K}:K:M“X(ZJD)”:N“Y(ZJD)”放样时为置镜点坐标，也可以不输入；已知道路外一点反求中心线里程时，输入此点坐标。

缓和曲线计算过程

计算过程1、假定JD204坐标为（11562.569，7812.231）JD204 ZD204-1的坐标方位角为160°33′13″2、根据控制桩表，计算ZH点坐标。

计算公式为X1=X0+L×COSα，Y1=Y0+L×SINα。

式中：X0，Y0—JD204的坐标X1，Y1—HZ点的坐标L—JD204到HZ点的距离α—JD204到HZ点的方位角(即JD204 ZD204-1的坐标方位角160°33′13″)3、在缓和曲线上，利用公式β=180×S2/(6πRL0),T=(S-S5/(40R2L02))/COSβX2=X1+T×COSβ,Y2=Y1+T×SINβW=α-3β-180式中：X2，Y2—缓和曲线上任意一点的坐标S—缓和曲线上一点到ZH点的曲线距离β—缓和曲线任意一点到ZH点直线与切线的夹角。

T—缓和曲线任意一点到ZH点直线距离W—缓和曲线上任意一点的切线方位角L0—缓和曲线长度4、在圆曲线上，利用公式γ=90×M/（πR），I=2R×SINγX3=X（HY）+I×COS（W（HY）-γ），Y3=Y（HY）+I×SIN（W（HY）-γ）U=W（HY）-2γ式中：X3，Y3—圆曲线上任意点的坐标M—圆曲线上任意一点到HY点的曲线长度γ—HY点的切线方位角与圆曲线上任意一点到YH点连线的夹角。

I—圆曲线上任意一点到HY点的距离U—圆曲线上任意一点的切线方位角X（HY），Y（HY）—HY点的坐标，通过缓和曲线计算公式确定W（HY）—HY点的切线方位角根据缓和曲线的计算公式，计算HY点的切线方位角、坐标。

以HY点为坐标原点，HY点的切线方位角为X轴，HY点的法线方向为Y轴。

坐标原点为HY点的坐标。

5、根据设计图纸给定的E值、预偏心值和计算得到的切线方位角计算桥梁工作线交点、墩中心坐标。

桥梁工作线交点坐标计算公式为：X=X0+E×COS（α+90）Y=Y0+E×SIN（α+90）墩中心坐标计算公式为：X=X0+（F+E）×COS（α+90）Y=Y0+（F+E）×SIN（α+90）式中：X，Y—要计算的点的坐标E—曲线外距F—预偏心值X0，Y0—线路中心某点坐标α—线路中心某点切线方位角。

非完整缓和曲线计算实例

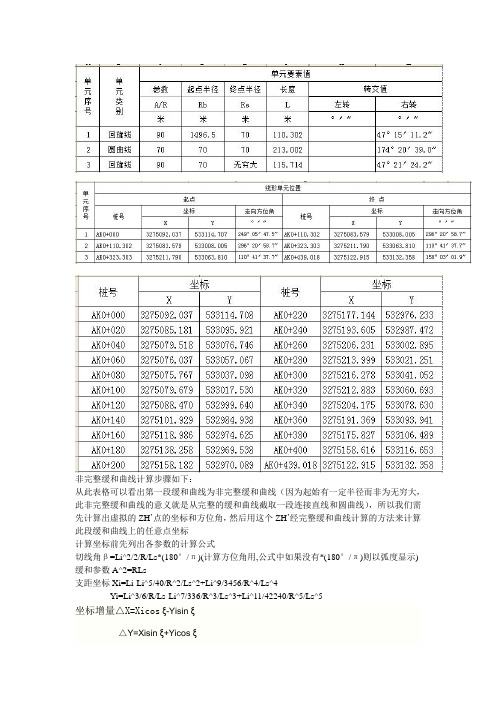
非完整缓和曲线计算步骤如下：从此表格可以看出第一段缓和曲线为非完整缓和曲线（因为起始有一定半径而非为无穷大，此非完整缓和曲线的意义就是从完整的缓和曲线截取一段连接直线和圆曲线），所以我们需先计算出虚拟的ZH’点的坐标和方位角，然后用这个ZH’经完整缓和曲线计算的方法来计算此段缓和曲线上的任意点坐标计算坐标前先列出各参数的计算公式切线角β=Li^2/2/R/Ls*(180°/π)(计算方位角用,公式中如果没有*(180°/π)则以弧度显示) 缓和参数A^2=RLs支距坐标Xi=Li-Li^5/40/R^2/Ls^2+Li^9/3456/R^4/Ls^4Yi=Li^3/6/R/Ls-Li^7/336/R^3/Ls^3+Li^11/42240/R^5/Ls^5坐标增量△X=Xicosξ-Yisin ξ△Y=Xisin ξ+Yicos ξ在第一缓和曲线时，ξ为ZH到JD的方位角，曲线左转时Yi为负号带入，右转时以正号代入在第二缓和曲线时，ξ为HZ到JD的方位角，曲线左转时Yi为正号带入，右转时以负号代入备注：Li:所求点弧长（此点至ZH‘的里程距离）R：曲线半径（以接圆曲线的半径为准）Ls:缓和曲线长（此为非完整缓和曲线，以计算出的完整缓和曲线长为准，而不是截取的缓和曲线长）开始计算：1. 先计算出虚拟的ZH’点桩号，因为根据缓和参数公式A^2=RLs,表格中已知缓和参数为90，半径为70所以求得缓和曲线长Ls=A^2/R=90^2/70=115.714,而根据表格知道实际缓和曲线长为110.302，则在起点里程AK0+000之前还有115.714-110.302=5.412M，所以此段缓和曲线的起点里程应为AK -5.4122. 计算切线角根据公式β=Li^2/2/R/Ls*（180°/π）=5.412^2/2/70/115.714*（180°/π）=0°6′12.93″3. 计算虚拟起点ZH‘方位角α，因为此线路为右转，从起点计算曲线任意点方位角时应为加，现在倒过来计算方位角所以为减，由已知条件得知AK0+000方位角为249°5′47.5″，所以虚拟ZH‘的方位角ξ为249°5′47.5″-0°6′12.93″=248°59′34.57″4. 计算虚拟起点ZH‘坐标，Xi=Li-Li^5/40/R^2/Ls^2+Li^9/3456/R^4/Ls^4=5.412-5.412^5/40/70^2/115.714^2+5.412^9/3456/70^4/115.714^4=5.412Yi=Li^3/6/R/Ls-Li^7/336/R^3/Ls^3+Li^11/42240/R^5/Ls^5=5.412^3/6/70 /115.714-5.412^11/42240/70^5/115.714^5=0.0033线路右转，在第一缓和曲线上，则Yi以正号代入△X=Xicosξ-Yisin ξ=5.412*cos(248°59′34.57″)-0.0033*sin(248°59′34.57″)=-1.937△Y=Xisin ξ+Yicosξ=5.412*sin(248°59′34.57″)+0.0033*cos(248°59′34.57″)=-5.0535虚拟起点ZH‘的坐标为（由于虚拟点在线元起点的前面（如果是在第二缓和曲线时虚拟点再线元终点的后面，则还是正常计算，为加上坐标增量）所以计算时应倒过来计算，所以为减去坐标增量）XZH‘=XZH-△X=3275092.037-（-1.937）=3275093.974YZH‘=YZH-△Y=533114.707-(-5.0535)=533119.7615. 现在可以开始由于虚拟点ZH‘来计算此段缓和曲线上的任意点，这里先计算缓和曲线终点HY点的坐标（HY点里程为ZH‘+115.714=AK0+110.302）Xi=Li-Li^5/40/R^2/Ls^2+Li^9/3456/R^4/Ls^4=115.714-115.714^5/40/70^ 2/115.714^2+115.714^9/3456/70^4/115.714^4=108.059Yi=Li^3/6/R/Ls-Li^7/336/R^3/Ls^3+Li^11/42240/R^5/Ls^5=115.714^3/6/ 70/115.714-115.714^7/336/70^3/115.714^3+115.714^11/42240/70^5/115.714 ^5=30.359线路右转，在第一缓和曲线上，则Yi以正号代入△X=Xicosξ-Yisin ξ=108.059*cos(248°59′34.57″)-30.359*sin(248°59′34.57″)=-10.396△Y=Xisin ξ+Yicosξ=108.059*sin(248°59′34.57″)+30.359*cos(248°59′34.57″)=-111.760XHY=XZH‘+△X=3275093.974+（-10.396）=3275083.578YHY=YZH‘+△Y=533119.761 +(-111.760)=533008.001切线角β= Li^2/2/R/Ls*(180°/π)=115.714^2/2/70/115.714*(180°/π)=47°21′23.76″所以HY点方位角为虚拟点ZH’加上（因为线路右转）47°21′23.76″=248°59′34.57″+47°21′23.76″=296°20′58.33″6.接着计算曲线上任意点坐标，方法同上，比如计算AK0+020的坐标（这里的AK0+020实际为AK0+025.412）曲线长Li为25.412，半径R为70，计算如下：Xi=Li-Li^5/40/R^2/Ls^2+Li^9/3456/R^4/Ls^4=25.412-25.412^5/40/70^2/ 115.714^2+25.412^9/3456/70^4/115.714^4=25.408Yi=Li^3/6/R/Ls-Li^7/336/R^3/Ls^3+Li^11/42240/R^5/Ls^5=25.412^3/6/7 0/115.714-25.412^7/336/70^3/115.714^3+25.412^11/42240/70^5/115.714^5= 0.3376线路右转，在第一缓和曲线上，则Yi以正号代入△X=Xicosξ-Yisin ξ=25.408*cos(248°59′34.57″)-0.3376*sin(248°59′34.57″)=-8.7932△Y=Xisin ξ+Yicosξ=25.408*sin(248°59′34.57″)+0.3376*cos(248°59′34.57″)=-23.840X=XZH‘+△X=3275093.974+（-8.7932）=3275085.181Y=YZH‘+△Y=533119.761 +(-23.840)=533095.921切线角β= Li^2/2/R/Ls*(180°/π)=25.412^2/2/70/115.714*(180°/π)=2°17′2.22″所以HY点方位角为虚拟点ZH’加上（因为线路右转）2°17′2.22″=248°59′34.57″+2°17′2.22″=251°16′36.79″。

缓和曲线公式(仅供参考)

缓和曲线计算(仅供参考)一、概念曲率半径从某一个值连续匀变为另一个值的曲线称为缓和曲线。

二、缓和曲线的已知参数和特征参数1、已知参数(1) 转角α(2) 圆曲线半径R(3) 缓和曲线长度l s2、缓和曲线特征参数与表达式为了便于说明缓圆曲线特征参数，预先建立直角坐标系ZH点是坐标系原点，ZH至JD点为X轴，过ZH点作X轴的垂直方向为Y轴，形成一个直角坐标系，ZH-HY、HY-ZH是缓圆曲线如图所示。

图、对称缓圆曲线(1) 回旋曲线参数：取图一部分放大如图中，曲线段ZH-HY是缓圆曲线。

回旋曲线是我国应用缓圆曲线的常用线型。

根据一般曲线曲率半径的表达特征，回旋曲线曲率半径表达式为ρ＝c／l （3-01）而半径的表达式为 c ＝Rl s （3-02）(2) 切线角：过缓圆曲线上P 点的切线与缓圆曲线ZH 点切线夹角，称为切线角用β表示。

设P 点附近存在dl 对应的d β为dβ＝dl/ρ整理得d β＝dl/Rl s积分上式得切线角表达式β=l 2／2Rl s (3-03)角度表达式 β=l 290°／Rl s (3-04)当l=ls 时，有 βs =l s ／2R (3-05)角度表达式 βs=l s 90°／R(3-06) (3) 缓圆曲线HY 点的点位坐标：图中，把过ZH 点的切线设为X 轴，过ZH 点作X 轴的垂直方向的直线设为Y 轴，形成缓圆曲线直角坐标系。

在P 点处相对于dl 的变化引起P 点的坐标变化，即dx=dl , dy=dl (3-07)积分处理，舍高次项得缓和曲线上任一点点坐标为x=l-l 5/40R 2l 2s +l 9/3456R 4l 4s -l 13/599040R 6l 6s +l 17/175472640R 8l 8s -l 21/78033715200R 10l10s (3-13) y=l 3/6Rl s -l 7/336R 3l 3s +l 11/42240R 5l 5s -l 15/9676800R 7l 7s +l 19/3530096640R 9l 9s -l 23/1880240947200R 11l11s (3-14)舍去第4项以后各项,有 x=l-l 5/40R 2l 2 s +l 9/3456R 4l 4 sy=l 3/6Rl s -l 7/336R 3l 3s +l 11/42240R 5l 5s (3-15)当l=l s 时,缓圆曲线HY 点的坐标为x s =l s -l 3 s /40R 2+l 5 s /3456R 4,y s =l 2 s /6R-l 4 s /336R 3+l 6 s /42240R 5(3-18) (4) 缓圆曲线内移参数p 与切线增值参数q:图中,在路线中线转弯处如果只设计缓圆曲线,路线中线的F,G 点分别是缓圆曲线(虚线)的ZY,YZ 点.在这种情况下, 车辆沿AF 直线段运行后在F 处处转入圆曲线,这时的线型必须有相应的变化。

公路缓和曲线段原理及缓和曲线计算公式Word版

公路缓和曲线段原理及缓和曲线计算公式一、缓和曲线缓和曲线是设置在直线与圆曲线之间或大圆曲线与小圆曲线之间，由较大圆曲线向较小圆曲线过渡的线形,是道路平面线形要素之一。

1．缓和曲线的作用1）便于驾驶员操纵方向盘2）乘客的舒适与稳定，减小离心力变化3）满足超高、加宽缓和段的过渡，利于平稳行车4）与圆曲线配合得当，增加线形美观2．缓和曲线的性质为简便可作两个假定：一是汽车作匀速行驶；二是驾驶员操作方向盘作匀角速转动，即汽车的前轮转向角从直线上的0°均匀地增加到圆曲线上。

S=A2/ρ（A：与汽车有关的参数）ρ=C/sC=A2由上式可以看出，汽车行驶轨迹半径随其行驶距离递减，即轨迹线上任一点的半径与其离开轨迹线起点的距离成反比，此方程即回旋线方程。

3．回旋线基本方程即用回旋线作为缓和曲线的数学模型。

令：ρ=R，l h=s 则 l h=A2/R4．缓和曲线最小长度缓和曲线越长，其缓和效果就越好；但太长的缓和曲线也是没有必要的，因此这会给测设和施工带来不便。

缓和曲线的最小长度应按发挥其作用的要求来确定：1）根据离心加速度变化率求缓和曲线最小长度为了保证乘客的舒适性，就需控制离心力的变化率。

a1=0,a2=v2/ρ,a s=Δa/t≤0.62）依驾驶员操纵方向盘所需时间求缓和曲线长度(t=3s)3）根据超高附加纵坡不宜过陡来确定缓和曲线最小长度超高附加纵坡（即超高渐变率）是指在缓和曲线上设置超高缓和段后，因路基外侧由双向横坡逐渐变成单向超高横坡，所产生的附加纵坡。

4）从视觉上应有平顺感的要求计算缓和曲线最小长度缓和曲线的起点和终点的切线角β最好在3°——29°之间，视觉效果好。

《公路工程技术标准》规定：按行车速度来求缓和曲线最小长度，同时考虑行车时间和附加纵坡的要求。

5．直角坐标及要素计算1）回旋线切线角（1）缓和曲线上任意点的切线角缓和曲线上任一点的切线与该缓和曲线起点的切线所成夹角。

圆曲线、缓和曲线计算例题《精选》

圆曲线坐标计算公式β=180°/π×L/R（L= βπ R/180°）弧长公式β为圆心角△X=sinβ×R△Y=(1-cosβ)×RC= 弦长X=X1+cos (α ±β/2)×CY=Y1+sin (α ±β/2)×Cβ代表偏角,（既弧上任一点所对的圆心角）。

β/2是所谓的偏角（弦长与切线的夹角）△X、△Y代表增量值。

X、Y代表准备求的坐标。

X1、Y1代表起算点坐标值。

α代表起算点的方位角。

R 代表曲线半径缓和曲线坐标计算公式β= L2/2RLS ×180°/πC= L - L5/90R2LS2X=X1+cos (α ±β/3)×CY=Y1+sin (α ±β/3)×CL代表起算点到准备算的距离。

LS代表缓和曲线总长。

X1、Y1代表起算点坐标值。

直线坐标计算公式X=X1+cosα×L Y=Y1+sinα×LX1、Y1代表起算点坐标值α代表直线段方位角。

L代表起算点到准备算的距离。

左右边桩计算方法X边=X中+cos（α±90°)×LY边=Y中+sin（α±90°)×L在计算左右边桩时，先求出中桩坐标，在用此公式求左右边桩。

如果在线路方向左侧用中桩方位角减去90°，线路右侧加90°，乘以准备算的左右宽度。

例题:直线坐标计算方法α(方位角)=18°21′47″X1=84817.831 Y1=352.177 起始里程DK184+714.029求DK186+421.02里程坐标解:根据公式X=X1+cosα×LX=84817.831+COS18°21′47″×(86421.02—84714.029)=86437.901Y=Y1+sinα×LY=352.177+sin18°21′47″×(86421.02—84714.029)=889.943求DK186+421.02里程左右边桩,左侧3.75m,右侧7.05m.解:根据公式线路左侧计算:X边=X中+cos（α±90°)×LX边=86437.901+cos(18°21′47″- 90°)×3.75=86439.082Y边=Y中+sin（α±90°)×LY边=889.943+sin(18°21′47″- 90°)×3.75=886.384线路右侧计算: X边=X中+cos（α±90°)×LX边=86437.901+cos(18°21′47″+ 90°)×7.05=86435.680 Y边=Y中+sin（α±90°)×L Y边=889.943+sin(18°21′47″+90°)×7.05=896.634例题:缓和曲线坐标计算方法α(ZH点起始方位角)=18°21′47″X1=86437.901 Y1=889.941起始里程DK186+421.02曲线半径2500缓和曲线长120m求HY点坐标,也可以求ZH点到HY点任意坐标解:根据公式β=L2/2RLS×180°/πβ=｛1202/(2×2500×120)｝×(180°/π)= 1°22′30.36″C=L-L5/90R2LS2C=120-1205/(90×25002×1202)=119.997X=X1+cos(α±β/3)×CX=86437.901+cos(18°21′47″-1°22′30.36″/3)×119.997=86552.086Y=Y1+sin(α±β/3)×CY=889.941+sin(18°21′47″-1°22′30.36″/3)×119.997=926.832求DK186+541.02里程左右边桩,左侧3.75m,右侧7.05m.解:根据公式线路左侧计算:X边=X中+cos（α±90°)×LX边=86552.086+cos｛(18°21′47″-1°22′30.36″)- 90°｝×3.75=86553.182Y边=Y中+sin（α±90°)×LY边=926.832+sin｛(18°21′47″-1°22′30.36″)- 90°｝×3.75=923.246线路右侧计算: X边=X中+cos（α±90°)×LX边=86552.086+cos｛(18°21′47″-1°22′30.36″)+ 90°｝×7.05=86550.026Y边=Y中+sin（α±90°)×LY边=926.832+sin｛(18°21′47″-1°22′30.36″)+ 90°｝×7.05=933.574缓和曲线方位角计算方法α=(起始方位角±β偏角)= 18°21′47″-1°22′30.36″=16°59′16.64″注:缓和曲线在计算坐标时,此公式只能从两头往中间推,只能从ZH点往HY点推,HZ点往YH 点推算,如果YH往HZ点推算坐标,公式里的β为β2/3.例题:圆曲线坐标计算方法α(HY点起始方位角)= 16°59′16.64″X1=86552.086Y1=926.832 曲线半径2500曲线长748.75起始里程DK186+541.02求YH点坐标,也可以求QZ点坐标或任意圆曲线一点坐标.解:根据公式β=180°/π×L/Rβ= 180°/π×748.75/2500=17°09′36.31″△X=sinβ×R△X=sin17°09′36.31″×2500=737.606△Y=(1-cosβ)×R△Y=(1-cos17°09′36.31″)×2500=111.290C=弦长C=745.954X=X1+cos(α±β/2)×CX= 86552.086 +cos(16°59′16.64″+360°-17°09′36.31″/2) ×745.954=87290.023Y=Y1+sin(α±β/2)×CY=926.832+ sin(16°59′16.64″+360°-17°09′36.31″/2) ×745.954=1035.905圆曲线方位角计算方法α=(起始方位角±β偏角)= 16°59′16.64″+360°-17°09′36.31″=359°49′40.33″求DK187+289.77里程左右边桩,左侧3.75m,右侧7.05m.解:根据公式线路左侧计算: X边=X中+cos（α±90°)×LX边=87290.023+cos(359°49′40.33″-90°)×3.75=87290.012Y边=Y中+sin（α±90°)×LY边=1035.905+sin(359°49′40.33″-90°)×3.75=1032.155线路右侧计算: X边=X中+cos（α±90°)×LX边=87290.023+cos(359°49′40.33″+90°)×7.05=87290.044Y边=Y中+sin（α±90°)×LY边=1035.905+sin(359°49′40.33″+90°)×7.05=1042.955。

不等长缓和曲线的平曲线计算

文章编号:1004-051X (2002)03-0032-02不等长缓和曲线的平曲线计算刘　洁1,粟卫国2(11桂林市市政综合设计院,广西　桂林　541001;21桂林公路管理局　广西　桂林　541002)摘　要:讨论公路与城市道路设计中常用不等长缓和曲线的平曲线,以及利用不等长缓和曲线平曲线要素的坐标计算方法。

关键词:不等长缓和曲线;平曲线;计算;方法中图分类号:U4121351 文献标识码:BC alculation on H orizontal Curve of the T ransitionCurve with Differed LengthL IU Jie 1,S U Wei -guo 2(11Guilin City Planning Design Institute ,Guilin ,Guangxi 541001,China ;21Guilin Highway Administration Bureau ,Guilin ,Guangxi 541002,China )Abstract :The paper discuss about the horizontal curve of the transition curve with differed length frequent 2ly used in the design of highway and city road construction ,and it also states the coordinate calculation method by using the horizontal curve basis of the transition curve with differed length.K ey Words :transition curve with differed length ;horizontal curve ;calculation ;method收稿日期:2002-07-9作者简介:刘　洁(1970-),女,广西桂林市人,工程师,主要从事路桥市政项目设计管理与研究;栗卫国(1968-),男,广西龙胜人,副总,高工,从事公路工程施工设计、管理与研究。

(完整版)缓和曲线、圆曲线测设计算例题

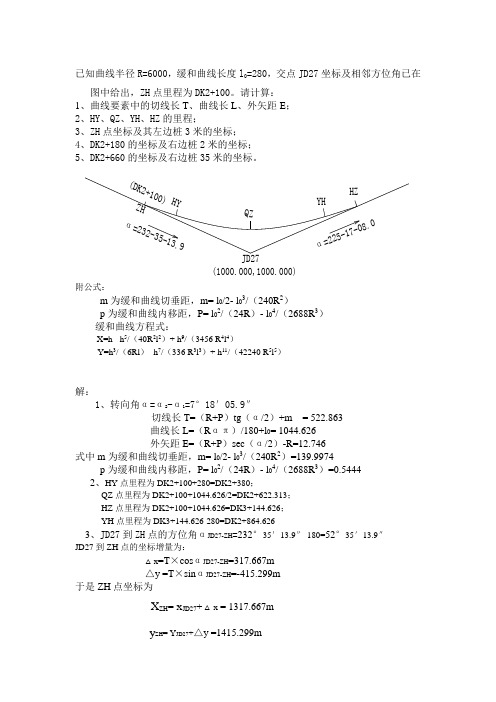
已知曲线半径R=6000，缓和曲线长度l 0=280，交点JD27坐标及相邻方位角已在图中给出，ZH 点里程为DK2+100。

请计算：1、曲线要素中的切线长T 、曲线长L 、外矢距E ；2、HY 、QZ 、YH 、HZ 的里程；3、ZH 点坐标及其左边桩3米的坐标；4、DK2+180的坐标及右边桩2米的坐标；5、DK2+660的坐标及右边桩35米的坐标。

永州α=225-17-08.0JD27(D K 2+100)(1000.000,1000.000)α=232-35-13.9H Z Q ZHZ H Y YH附公式：m 为缓和曲线切垂距，m= l 0/2- l 03/（240R 2）p 为缓和曲线内移距，P= l 02/（24R ）- l 04/（2688R 3）缓和曲线方程式：X=h - h 5/（40R 2l 2）+ h 9/（3456 R 4l 4）Y=h 3/（6Rl ）- h 7/（336 R 3l 3）+ h 11/（42240 R 5l 5）解：1、转向角α=α2-α1=7°18′05.9″切线长T=（R+P ）tg （α/2）+m = 522.863曲线长L=（R απ）/180+l 0= 1044.626外矢距E=（R+P ）sec （α/2）-R=12.746式中m 为缓和曲线切垂距，m= l 0/2- l 03/（240R 2）=139.9974p 为缓和曲线内移距，P= l 02/（24R ）- l 04/（2688R 3）=0.54442、HY 点里程为DK2+100+280=DK2+380；QZ 点里程为DK2+100+1044.626/2=DK2+622.313；HZ 点里程为DK2+100+1044.626=DK3+144.626；YH 点里程为DK3+144.626-280=DK2+864.6263、JD27到ZH 点的方位角αJD27-ZH =232°35′13.9″-180=52°35′13.9″ JD27到ZH 点的坐标增量为：△x =T ×cos αJD27-ZH =317.667m△y =T ×sin αJD27-ZH =-415.299m于是ZH 点坐标为X ZH = x JD27+ △x = 1317.667my ZH = Y JD27+△y =1415.299mZH点到左边桩3米的方位角αZH-左边桩= 232°35′13.9″-90=142°35′13.9″左边桩3米的坐标为：X左= x ZH+ 3×cosαZH-左边桩= 1315.284mY左= y ZH +3×sinαZH-左边桩=1417.122m4、DK2+180的坐标及右边桩2米的坐标:DK2+180在缓和曲线上，计算过程为：ZH点到JD27的方位角αZH-JD1= =232°35′13.9″DK2+180到ZH点的缓和曲线长度h为180-100=80根据缓和曲线方程式：X=h - h5/（40R2l2）+ h9/（3456 R4l4）=80.000Y=h3/（6Rl）- h7/（336 R3l3）+ h11/（42240 R5l5）=0.0508由X和Y可以求出DK5+900与ZH的距离D和它的偏角δ：D=√（X2+ Y2）=80.000δ=arctg（Y/ X）=0°02′11.0″于是DK2+180的坐标（X1，Y1）为：X1= 1317.667+Dcos（232°35′13.9″-δ）=1269.022Y1 = 1415.299+Dsin（232°35′13.9″-δ）=1351.788DK2+300右边桩2米的坐标（X2，Y2）为：X2= 1269.022+2×cos（232°35′13.9″-3δ+90）=1270.608Y2= 1351.788+2×sin（232°35′13.9″-3δ+90）=1350.5705、圆曲线点DK2+660计算过程为：曲中点QZ的里程推算为DK2+622.313, DK2+660到QZ的圆曲线长度为660-622.313=37.687,所对应的圆心角为O′=（180*37.687）/（πR）=0°21′35.6″， JD27到圆心O的方位角αJD27-O=225°17′08.0″-（180-7°18′05.9″）/2=138°56′10.95″圆心O的坐标为：X3 =1000+（E+R）cos（138°56′10.95″）=-3533.494Y3= 1000+（E+R）sin（138°56′10.95″）=4949.753DK2+660的坐标（X4，Y4）为：X4= X3++ R cos（138°56′10.95″+180- O′）=965.544Y4 = Y3+Rsin（138°56′10.95″+180- O′）=980.035DK2+660右边桩35米的坐标（X5，Y5）为：X5= X3++ （R+35）×cos（138°56′10.95″+180- O′）=991.788Y5= Y3+（R+35）×sin（138°56′10.95″+180- O′）=956.878。