模糊控制器的设计与MATLAB仿真
模糊控制及其MATLAB仿真教学设计 (2)

模糊控制及其MATLAB仿真教学设计一、模糊控制简介1.1 模糊控制的概念模糊控制是一种基于模糊逻辑思想的控制方法。
与传统的精确控制方法不同,它允许在处理不确定性和模糊性时采用一种定性的方法。
在模糊控制中,运用了模糊集合论的理论和方法,能很好地解决那些传统方法难以解决的非线性、时变、模糊等问题。
1.2 模糊控制的原理模糊控制的基本原理是将问题抽象为一些模糊集合,然后通过模糊推理和模糊逻辑运算实现模糊控制。
模糊控制的输入是经过模糊化后的模糊变量,输出是某个或某些经过去模糊化的控制变量。
1.3 模糊控制的优点模糊控制在面对复杂、非线性的控制问题时往往比传统控制方法更为有效。
其主要优点有: - 基于定性的知识 - 可以有效处理模糊、不确定性问题 - 快速响应和适应性强二、MATLAB仿真教学设计2.1 MATLAB仿真工具MATLAB是一种强大、多功能的科学计算软件,可以在其中进行模拟仿真实验。
在仿真实验中,MATLAB提供了多种工具来方便用户模拟不同的控制算法。
其中,使用Simulink可以创建模型,在其中加入不同的模块来构建模拟仿真实验。
2.2 模糊控制仿真实验可以使用Simulink在MATLAB中创建一个模糊控制的仿真实验。
具体步骤如下:1. 打开MATLAB,点击Simulink新建一个模型; 2. 在Simulink中选择Fuzzy Logic Toolbox,并将Fuzzy Logic Controller加入模型; 3. 加入Fuzzy Logic Controller后,可以进入FIS Editor编辑器,设置输入和输出变量,构建模糊控制规则; 4. 设置好规则之后,添加输入信号源和输出信号源; 5. 进行仿真和调试。
2.3 仿真教学设计为了更好地进行模糊控制的MATLAB仿真教学,可以采用以下设计方案: - 设计实验1:基础概念实验,通过模拟一个简单的控制过程,让学生了解模糊控制基本概念和原理。
基于Matlab的模糊控制系统的设计与仿真

编辑该系统得到仿真框如图 A 所示。对图 A 进行仿真, 需 要用鼠标双击其中的 $4VVK7W9;)?7F98*395563 模块, 打开它, 写 然后选择 &)L45)8M中的 &*@3* , 启 入事先已建好的 $%& 的名字, 动仿真过程, 就可通过 &?9X6 观察系统的仿真输出结果。结果 如图 E 所示。
!" 引言
模 糊 理 论 是 在 美 国 伯 克 莱 加 州 大 学 电 气 工 程 系 #$ % $&
的 任 意 一 个 对 BO= 的 修 改 将 影 响 任 何 其 它 已 打 开 的 NGO 中 的 显示结果。
’()*+ 教 授 于 !,-. 年 创 立 的 模 糊 集 合 理 论 的 数 学 基 础 上 发 展
E2,曲面观察器
规则观察器以非常详细的方式在任意时刻显示 计 算 过 程 , 从这个意义上看, 它给出了模糊推理系统一种微观的 视 角 。 如 果想看系统的整个输出曲面观察器, 即基于整个输入 集 的 输 出 级的变化范围, 需要打开曲面观察器。 看 曲 面 观 察 器 可 以 从 C)6D, 菜 单 选 择 &43.@?6 1 1 1来 打 开 它 , 到表示从 FGH 模糊控制系统映射的三维曲面观察器窗口如图 由这一个双输入、 单输出情况, 可以在图 " 中看到整个 " 所示, 映射。在图的下半部曲面观察器配备了初始菜单, 可以选择用 于绘图的两个输入量 ’ 、 ’F 和一个输出量 I 。弹出式菜单正下 方是两个文本输入域,可以确定在 J 轴和 K 轴包含多少网格 线。这为复杂的问题提供了合理的计算时间。 图 E77系统的仿真输出结果 图 A77系统的仿真框
・ E- ・
模糊控制Matlab仿真
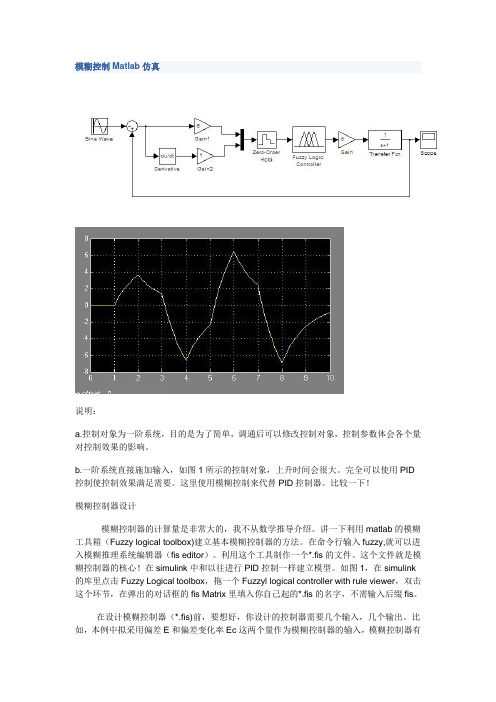
模糊控制Matlab仿真说明:a.控制对象为一阶系统,目的是为了简单,调通后可以修改控制对象,控制参数体会各个量对控制效果的影响。
b.一阶系统直接施加输入,如图1所示的控制对象,上升时间会很大。
完全可以使用PID 控制使控制效果满足需要。
这里使用模糊控制来代替PID控制器。
比较一下!模糊控制器设计模糊控制器的计算量是非常大的,我不从数学推导介绍。
讲一下利用matlab的模糊工具箱(Fuzzy logical toolbox)建立基本模糊控制器的方法。
在命令行输入fuzzy,就可以进入模糊推理系统编辑器(fis editor)。
利用这个工具制作一个*.fis的文件。
这个文件就是模糊控制器的核心!在simulink中和以往进行PID控制一样建立模型。
如图1,在simulink 的库里点击Fuzzy Logical toolbox,拖一个Fuzzyl logical controller with rule viewer,双击这个环节,在弹出的对话框的fis Matrix里填入你自己起的*.fis的名字,不需输入后缀fis。
在设计模糊控制器(*.fis)前,要想好,你设计的控制器需要几个输入,几个输出。
比如,本例中拟采用偏差E和偏差变化率Ec这两个量作为模糊控制器的输入,模糊控制器有一个输出。
很明显,这是利用模糊控制器代替PD控制的。
对应的模糊控制器的设计也要具有两个输入一个输出。
利用matlab的Fuzzy logical toolbox 设计模糊控制器(生成*.fis文件)的关键步骤:a.添加输入输出。
图3.fis编辑器默认的具有一个输出,添加第二个输入,并且分别命名为E,Ec,U。
b.确定隶属函数。
双击黄色和绿色的方框就可以进入隶属函数编辑对话框了。
设置E,Ec 的range为[-6,6],u的range为[-1,1]。
然后每一个变量再添加4个输入隶属函数,总共7个。
matlab提供了11种隶属函数,第一次用选择常用的三角形trimf,区别不大的。
简易模糊控制器设计及MATLAB仿真

简易模糊控制器的设计及仿真摘要:模糊控制(Fuzzy Control )是以模糊集理论、模糊语言和模糊逻辑推理 为基础的一种控制方法,它从行为上模仿人的模糊推理和决策过程。
本文利用MATLAB/SIMULIN 与FUZZYTOOLBO 对给定的二阶动态系统,确定模糊控制器的 结构,输入和输出语言变量、语言值及隶属函数,模糊控制规则,比较其与常规 控制器的控制效果,用MATLA 实现模糊控制的仿真。
关键词:模糊控制参数整定MATLAB 仿真二阶动态系统模型:120 30s 1 140s 1采用simulink 图库,实现常规PID 和模糊自整定PID 一.确定模糊控制器结构模糊自整定PID 为2输入3输出的模糊控制器。
在MATLAB 勺命令窗口中键 入fuzzy 即可打开FIS 编辑器,其界面如下图所示。
此时编辑器里面还没有FIS系统,其文件名为Un titled ,且被默认为Man da ni 型系统。
默认的有一个输入, 一个输出,还有中间的规则处理器。
在FIS 编辑器界面上需要做一下几步工作。
Ready首先,模糊自整定PID 为2输入3输出的模糊控制器,因此需要增加一个输入两个输出,进行的操作为:选择 Edit 菜单下的Add Variable/Input菜单项<F1S Name: Untitled FIS Type: And method Or method implicertionAggregationDefuzzificatiorHelpJ{ Close ]File S.A11¥j. ez:Unt it leduntitled (mamdani)output 1Current VariableType Rangeoutputloutput [01]最后,保存系统。
单击File 菜单,选择Export 下的To Disk 项 建的系统命名为PID_auot.fi•定义输入、输出模糊集及隶属函数如下图-FIS Editor: UntitledFile Edit Vie*FJS Mame:Anci mrthod Or method Implication AggregationDetuzzificatioroutputsoutput[01]. dose IReady其次,给输入输出变量命名。
基于matlab的模糊控制器的设计与仿真

基于MATLAB的模糊控制器的设计与仿真摘要:本文对模糊控制器进行了主要介绍。
提出了一种模糊控制器的设计与仿真的实现方法,该方法利用MA TLB模糊控制工具箱中模糊控制器的控制规则和隶属度函数,建立模型,并进行模糊控制器设计与仿真。
关键词:模糊控制,隶属度函数,仿真,MA TLAB1 引言模糊控制是一种特别适用于模拟专家对数学模型未知的较复杂系统的控制,是一种对模型要求不高但又有良好控制效果的控制新策略。
与经典控制和现代控制相比,模糊控制器的主要优点是它不需要建立精确的数学模型。
因此,对一些无法建立数学模型或难以建立精确数学模型的被控对象,采用模糊控制方法,往往能获得较满意的控制效果。
模糊控制器的设计比一般的经典控制器如PID控制器要复杂,但如果借助MATLAB则系统动态特性良好并有较高的稳态控制精度,可提高模糊控制器的设计效率。
本文在MATLAB环境下针对某个控制环节对模糊控制系统进行了设计与仿真。
2 模糊控制器简介模糊控制器是一种以模糊集合论,模糊语言变量以及模糊推理为数学基础的新型计算机控制方法。
显然,模糊控制的基础是模糊数学,模糊控制的实现手段是计算机。
本章着重介绍模糊控制的基本思想,模糊控制的基本原理,模糊控制器的基本设计原理和模糊控制系统的性能分析。
随着科学技术的飞速发展,在那些复杂的,多因素影响的严重非线性、不确定性、多变性的大系统中,传统的控制理论和控制方法越来越显示出局限性。
长期以来,人们期望以人类思维的控制方案为基础,创造出一种能反映人类经验的控制过程知识,并可以达到控制目的,能够利用某种形式表现出来。
而且这种形式既能够取代那种精密、反复、有错误倾向的模型建造过程,又能避免精密的估计模型方程中各种方程的过程。
同时还很容易被实现的,简单而灵活的控制方式。
于是模糊控制理论极其技术应运而生。
3 模糊控制的特点模糊控制是以模仿人类人工控制特点而提出的,虽然带有一定的模糊性和主观性,但往往是简单易行,而且是行之有效的。
模糊控制器的设计与MATLAB仿真

模糊控制器的设计与MATLAB仿真模糊控制器的设计与MATLAB仿真王桥( 安庆师范学院物理与电气工程学院安徽安庆246011)指导教师:吴文进摘要:随着现代科学技术的迅速发展,生产系统的规模越来越大,形成了复杂的大系统,导致了控制对象与控制器以及控制任务和目的的日益复杂化。
系统的复杂性主要表现在,被控对象模型的不确定性、系统信息的模糊性、高度非线性、输入信息多样化、多层次和多目标的控制要求、计算复杂性和庞大的数据处理以及严格的性能指标。
该设计分析了模糊控制理论原理,给出了常规模糊控制器的设计方法,并在MATLAB中进行仿真实验,实验结果验证了控制器的有效性。
关键词:模糊控制,PID控制,MATLAB仿真1引言智能控制是当前国内外人工智能,自动化,计算机技术领域中的热门话题,受到学术界、工程界和企业界的广泛关注。
正在积极进行有关智能控制的理论方法和应用技术的研究与开发工作,取得了许多新进展和新成果。
智能控制系统的发展,为智能自动化提供了理论基础,必将推动自动化向前发展。
智能控制主要包括以下几个方面,基于知识系统的专家控制、基于模糊系统的智能控制、基于学习及适应性的智能控制、基于神经网络的智能控制系统。
模糊控制指的是应用模糊集合理论统筹考虑控制的一种控制方式。
模糊控制的基本思想是把人类专家对特定的被控对象或过程的控制策略总结成一系列以:“IF(条件)…THEN(作用)”形式表示的控制规则,通过模糊推理得到控制作用集,作用于被控对象或过程。
控制作用集为一组条件语句,状态条件和控制作用均为一组被量化了的模糊语言集,如”正大”、”负大”、”高”等。
它们共同构成控制过程的模糊算法,定义模糊子集与建立模糊控制规则、由基本论域转变为模糊集合论域、模糊关系矩阵运算、模糊推理合成与求出控制输出模糊子集、进行清晰化运算,得到精确控制量。
本论文主要是对基于模糊系统的智能控制器中的常规模糊控制器和模糊自整定PID控制器进行设计。
模糊控制的Matlab仿真实例

其他例子
模型Shower.mdl―淋浴温度调节模糊控制系统仿真; 模型slcp.mdl―单级小车倒摆模糊控制系统仿真; 模型 slcp1.mdl―变长度倒摆小车模糊控制系统仿
真; 模型 slcpp1.mdl—定长、变长二倒摆模糊控制系
统仿真; 模型slbb.mdl―球棒模糊控制系统仿真; 模型sltbu.mdl―卡车智能模糊控制倒车系统仿真; 模型sltank2.mdl ― 用子系统封装的水箱控制仿
为简单起见,我们直接利用系统里已经编辑好的 模糊推理系统,在它的基础上进行修改。这里我 们采用与tank . fis中输入输出变量模糊集合完 全相同的集合隶属度函数定义,只是对模糊规则 进行一些改动,来学习模糊工具箱与仿真工具的 结合运用。对于这个问题,根据经验和直觉很显 然可以得到如下的模糊度示 波器
冷水阀子系统
这个仿真模型的输出是用示波器来表示的,如 图所示。通过示波器上的图形我们可以清楚地 看到温度和水流量跟踪目标要求的性能。
水温示波器
水流示波器
水温偏差区间模糊划分及隶属度函数
水流量偏差区间模糊划分及隶属度函数
输出对冷水阀控制策略的模糊化分及隶属度函数
选Edit菜单,选择Rules, 弹出一新界面Rule Editor. 在底部的选择框内,选择相应的 IF…AND…THEN 规则,点击Add rule 键,上部 框内将显示相应的规则。本例中用9条左右的规 则,依次加入。如下图所示:
模糊逻辑工具箱仿真结果
模糊规则浏览器用于显示各条模糊控制规则对 应的输入量和输出量的隶属度函数。通过指定 输入量,可以直接的显示所采用的控制规则, 以及通过模糊推理得到相应输出量的全过程, 以便对模糊规则进行修改和优化。
这样的结果与实际情况还是有些不符。通常顾客都是给15%的 小费,只有服务特别好或特别不好的时候才有改变,也就是说, 希望在图形中间部分的响应平坦些,而在两端(服务好或坏) 有凸起或凹陷。这时服务与小费是分段线性的关系。例如,用 下面 MATLAB 语句绘出的下图的情况。
模糊控制设计及仿真实例--智能控制作业

课程名称:智能控制理论与技术授课老师:徐华中学院:自动化学院专业名称:控制科学与控制工程姓名:廖桂潘学号:班级:自研0902班导师姓名:刘教瑜2010年9月1.一个三阶系统201232123b b ba a as ss s s+++++,其中a,b的值由自己设定,该系统具有非线性环节,如下图所示:依据上述条件设计一个模糊控制器:①用MATLAB仿真,得出仿真结果,②并通过改变a、b值对仿真结果的影响;③改变隶属度函数,从仿真结果图分析隶属度函数,模糊化对系统的影响;解:①(1)取b0=0,b1=0,b2=1.5,a1=4,a2=2,a3=0,在SIMULINK里建模如下图所示(2)用GUI建立FISE和EC分别为系统输出误差和误差的变化量,U为控制输出,编辑其隶属度函数如下编辑模糊推理规则如下(3)仿真结果如下2自己选定一个对象,设计一个神经网络控制系统。
解:被控对象为y(k)=0.3y(k-1)+0.2y(k-2)+0.1u(k-1)+0.6u(k-2),采用单神经元PID 控制,控制结构如下图所示:采用有监督的Hebb 学习规则,控制算法及学习算法如下:3131111222333()(1)()()()()/()()(1)()()()()(1)()()()()(1)()()()i i i i i i i I P D u k u k K w k x k w k w k w k w k w k z k u k x k w k w k z k u k x k w k w k z k u k x k ηηη=='=-+'==-+=-+=-+∑∑式中,2123()();()()(1);()()()2(1)(2);x k e k x k e k e k x k e k e k e k e k ==--=∆=--+-K K>0I P D ηηη﹑﹑分别为积分﹑比例﹑微分的学习速率,为神经元比例系数,。
基于MATLAB的模糊PID-Smith控制器的设计与仿真

基于MATLAB的模糊PID-Smith控制器的设计与仿真摘要:针对工业控制中大惯性、纯滞后、参数时变非线性受控对象难于控制问题,结合Smith预估算法能有效克服纯滞后、模糊控制鲁棒性较强以及PID控制稳态精度高这三者的优点,提出了一种模糊PID Smith控制器的设计方法,并将其应用于电机网络控制系统中。
MATLAB仿真结果表明,新的控制方案与传统的Smith控制器、Fuzzy PID控制器相比,不仅具有满意的控制性能,而且具有较强鲁棒性和抗干扰性能,稳态精度高,对时变滞后对象具有良好的控制效果。
关键词:网络控制系统;纯滞后;模糊PID;Smith控制;模糊PID Smith控制器0 引言PID控制是一种典型的传统反馈控制器,具有结构简单、鲁棒性好和易于实现等优点,被广泛地应用于工业过程控制。
在网络化控制系统中,传统PID控制器的参数的调整对被控对象的数学模型依赖较大,并且控制过程中的滞后性、控制参数的非线性和高阶性也增加了对控制参数的调整难度。
而模糊控制系统正是由于它不依赖于工业对象模型,具有较强的鲁棒性,近年来被广泛的应用到网络化控制系统领域。
本文在模糊PID控制的基础上,结合传统的Smith控制对时滞过程控制的有效性,提出了模糊PID Smith控制方案,并对直流伺服电机控制系统进行实例仿真分析,证明了该方案的有效性。
1 模糊PID控制器的设计1.1 模糊PID控制器PID参数模糊自整定是在常规PID控制的基础上,应用模糊集合理论建立参数K\-p、K\-i、K\-d与偏差e和偏差变化率ec 间的函数关系。
其结构图如图1所示。
参数K\-p、K\-i、K\-d与偏差e和偏差变化率ec间的函数关系如下:K\-p= K′\- p+ΔK\-p= K′\-p+{e,ec }\-pK\-i = K′\-i+ΔK\-i= K′\-i+{e,ec }\-iK\-d= K ′\-d+ΔK\-d= K′\-d+{e,ec }\-d其中,K′\-p,K′\-i,K′\-dΔK\-pΔK\-iΔK\-d为参数的修正值。
参数自调整模糊控制器设计及其Matlab仿真

基 础 上 增 添 了 一 个 功 能 模 块 一一 参 数 调 整 器 。 数 参 调 整 器 主 要 由两 部 分 组 成 : 是 系统 性 能测 量 模 块 , 一
焊 缝 自动 跟 踪 系 统 在 焊 接 过 程 中 , 尔 电 流 传 霍
值的变化量 ; 被控对 象的输入 , u是 即驱 动 步 进 电 机
真确性 和其对 系统性 能的提 高。
1 弧 焊 焊 缝 跟 踪 系 统 的 结 构 设 计
弧 焊 焊缝 自动 跟踪 系 统 采 用 电 弧 传 感 器 获 取 焊
运 转 的 脉 冲个 数 和 方 向 信 号 。
缝 跟 踪 信 号 , 体 结 构 如 图 1 示 , 要 由五 个 部 分 整 所 主
感 器不 断 检测 焊 接 电流信 号并 通 过 A D转 换 电路 /
传 人 D P控 制 器 。 S S D P控 制 器 内部 含 有 以软 件 形 式 实 现 的 参 数 自调 整 模 糊 控 制 器 。 数 自调 整 模 糊 控 参
制 器 中 的 系 统 性 能 测 量 模 块 根 据 检 测 到 的 焊 接 电
2 参 数 自调 整 模 糊 控 制 器 设 计
与 常 规 模 糊 控 制 器 相 比 , 设 计 的 参 数 自调 整 所
模 糊 控 制 器 的优 点 在 于 : 当焊 枪 远 离 焊缝 中 心 时 , 焊
差 值 的 作用 使 得 系 统 快速 响 应 , 快 减 小 焊 枪 的 位 尽 置误差 。 当焊 枪 靠 近焊 缝 中 心 时 , 积分 差值 的 绝 对 调 整 。
情 况 下 , 制 系 统 仍 能 保 持 较 好 的 性 能 。 时 利 用 控 同 Ma a t b仿 真 辅 助 设 计 软 件 的 Sm l k仿 真 库 优 化 l i ui n
实验一 模糊控制器的MATLAB仿真

实验一模糊控制器的MATLAB仿真一、实验目的本实验要求利用MATLAB/SIMULINK与FUZZYTOOLBOX对给定的二阶动态系统,确定模糊控制器的结构,输入和输出语言变量、语言值及隶属函数,模糊控制规则;比较其与常规控制器的控制效果;研究改变模糊控制器参数时,系统响应的变化情况;掌握用 MATLAB 实现模糊控制系统仿真的方法。
二、实验设备:计算机系统、Matlab 仿真软件三、实验原理For personal use only in study and research; not for commercial use模糊控制器它包含有模糊化接口、规则库、模糊推理、清晰化接口等部分,输人变量是过程实测变量与系统设定值之差值。
输出变量是系统的实时控制修正变量。
模糊控制的核心部分是包含语言规则的规则库和模糊推理。
模糊推理就是一种模糊变换,它将输入变量模糊集变换为输出变量的模糊集,实现论域的转换。
工程上为了便于微机实现,通常采用“或”运算处理这种较为简单的推理方法。
Mamdani推理方法是一种广泛采用的方法。
它包含三个过程:隶属度聚集、规则激活和输出总合。
模糊控制器的体系结构如图1所示。
For personal use only in study and research; not for commercial use图1 模糊控制器的体系结构四、实验步骤(1)对循环流化床锅炉床温,对象模型为()()1140130120++s s采用simulink 图库,实现常规PID 和模糊自整定PID 。
(2)确定模糊语言变量及其论域:模糊自整定PID 为2输入3输出的模糊控制器。
该模糊控制器是以|e|和|ec|为输入语言变量,Kp 、Ki 、Kd 为输出语言变量,其各语言变量的论域如下:误差绝对值:e={0,3,6,10}; 误差变化率绝对值:ec={0,2,4,6}; 输出Kp :Up={0,0.5,1.0,1.5}; 输出Ki :Ui={0,0.002,0.004,0.006};输出Kd :Ud={0,3,6,9}。
Matlab模糊控制器的设计以及simulink下对模糊控制器系统的仿真(word文档良心出品)
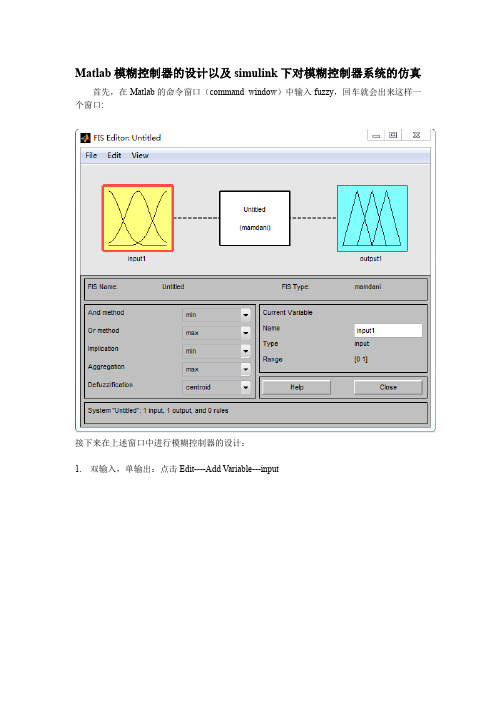
Matlab模糊控制器的设计以及simulink下对模糊控制器系统的仿真首先,在Matlab的命令窗口(command window)中输入fuzzy,回车就会出来这样一个窗口:接下来在上述窗口中进行模糊控制器的设计:1.双输入,单输出:点击Edit----Add Variable---input2.为E添加隶属度函数,E的论域为{-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6},E的模糊集合为{NB,NM,NS,NZ,PZ,PS,PM,PB},Edit—Membership Function edit,如下图所示:3.为EB添加隶属度函数,EB的论域为{-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6},EB的模糊集合为{NB,NM,NS,ZE,PS,PM,PB},Edit—Membership Function edit,如下图所示:4.为U添加隶属度函数,U的论域为{-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6},U的模糊集合为{NB,NM,NS,ZE,PS,PM,PB},Edit—Membership Function edit,如下图所示:其中E,EB,U均为模糊量。
5.为模糊控制器设计模糊规则,由于E的语言变量有8个,EB的语言变量有7个,所以模糊控制器的模糊规则总共有8*7=56条,接下来为模糊控制器添加规则:双击untitled,则有下面的表格:制定完成后,会形成模糊规则矩阵,系统会根据模糊输入量E,EB,经过模糊控制规则[56条],进而确定输出量U。
6.对输入量模糊化以及对输出量清晰化,我们采取最小最大重心法。
7.点击export—to file. ***#$.fis文件就是所设计的控制器。
8.下面对我们设计的模糊控制器进行检验,所构建的系统如下:系统分析:模糊控制器:双输入单输出,输入为误差以及误差的变化率的模糊量,输出为控制量的模糊量,模糊控制器中有56条规则。
matlab模糊控制器的设计

matlab模糊控制器的设计
设计模糊控制器的步骤如下:
1. 确定系统的输入和输出变量:确定系统要控制的输入和输出变量,以及它们的范围和取值。
2. 设计模糊集:根据系统的输入和输出变量的范围,在输入和输出空间中设计一组模糊集。
可以使用三角形、梯形等形状的模糊集。
3. 确定模糊规则:根据经验或专家知识,确定一组模糊规则。
每个模糊规则对应一个输入模糊集与一个输出模糊集的匹配。
4. 确定模糊推理方法:确定使用哪种模糊推理方法,如Mamdani或者Sugeno等。
5. 设计模糊控制器的模糊化和解模糊化方法:确定如何将输入变量模糊化为模糊集,以及如何将输出变量的模糊集解模糊化为具体的输出值。
6. 确定模糊控制器的参数:根据系统的实际需求和性能要求,调整模糊控制器的模糊规则和参数,以达到最佳控制效果。
7. 实现模糊控制器:使用MATLAB等工具实现设计好的模糊控制器,并进行模拟和实验验证。
以上是一般的模糊控制器设计步骤,具体的设计过程还需要根据具体的系统和控制需求进行调整和优化。
模糊pid控制matlab程序

模糊pid控制matlab程序
模糊PID控制是一种结合模糊控制和PID控制的方法,它可以
在控制系统中应对非线性和不确定性。
在MATLAB中,实现模糊PID
控制可以分为以下几个步骤:
1. 定义模糊系统,首先,需要使用MATLAB中的Fuzzy Logic Toolbox来定义模糊系统。
可以使用fuzzy函数来创建一个模糊系
统对象,并定义输入、输出和隶属函数等参数。
2. 设计模糊控制器,接下来,需要设计模糊控制器。
可以使用fisedit函数来打开模糊逻辑编辑器,通过编辑器来定义模糊控制
器的输入、输出和规则等。
3. 整合PID控制器,在MATLAB中,可以使用pid函数来创建
一个PID控制器对象。
然后,将模糊控制器和PID控制器整合在一起,可以通过串联、并联或级联的方式来实现模糊PID控制。
4. 闭环控制,最后,将设计好的模糊PID控制器应用于闭环控
制系统中。
可以使用sim函数来进行仿真,观察系统的响应和性能。
需要注意的是,模糊PID控制的设计涉及到模糊集合的定义、隶属函数的选择、规则的设置等,需要根据具体的控制对象和要求来进行调整和优化。
同时,对于PID控制器的参数调节也需要谨慎处理,可以使用MATLAB中的工具箱来进行参数整定和性能分析。
总的来说,实现模糊PID控制的MATLAB程序需要综合运用模糊逻辑工具箱和控制系统工具箱,通过适当的建模和调节来实现模糊PID控制器的设计和应用。
模糊控制器的matlab设计步骤

模糊PID控制器设计和仿真步骤:各变量隶属度函数的确定第一步:各变量隶属度函数的确定1、 用于PID 参数调整的模糊控制器采用二输入三输出的形式。
该控制器是以误差E 和误差变化率EC 作为输入,PID 控制器的三个参数P、I、D 的修正△KP、△KI、△KD 作为输出,如图1;2、 取输入E 和EC 和输出△KP、 △KI、△KD 模糊子集为{NB,NM,NS,ZO,PS,PM,PB},其论域为[-6,6],量化等级为{-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6};如图23、 在模糊逻辑工具箱的隶属度函数编辑器中,选择输入量E,EC 隶属函数为高斯型(gaussmf),输出△KP、△KI、△KD 的隶属函数为三角形(trimf),如图2和3。
图1图2图3第二步:根据图4规则建立模糊规则表,如图5:图4图5第三步:设置参数:与方式与方式 (And method)为min ;或方式(Or method)为max ;推理推理 (Implication)为min ;合成;合成 (Aggregation)为max ;去模糊(Defuzzification)为重心平均法(centroid )。
)。
第四步:保存该FIS 文件,取名为FuzzyPID.fis第五步:在MA MATLABTLAB 的M 文件编辑器里建立一个名为FuzzyPID.m 的文件,其内容为:martrix=readfis (‘Fuzzypid.fis ’),并运行。
,并运行。
第六步:打开SIMULINK ,新建一个Model ,选择一个Subsystem ,在其中编辑模块,如图6,并设置模糊化因子KE=KEC=0.01,解模糊因子KP=0.5,KI=KD=0.01,并在Fuzzy Logic Controller 模块的Parameters 中输入readfis('FuzzyPID.fis'):图6第七步:返回到新建的Model 中,按照如图7所示建立模糊PID 控制器,其中,控制器,其中,PID PID 初始值为KP0=20,KI0=1.35,KD0=3.7,传递函数为:图7第八步:保存为FuzzyPID.mdl 并运行。
使用Matlab进行模糊控制系统设计

使用Matlab进行模糊控制系统设计引言:近年来,随着科学技术的快速发展和应用场景的不断扩展,控制系统设计成为众多领域中的热点问题之一。
而模糊控制作为一种有效的控制方法,在自动化领域得到了广泛的应用。
本文将介绍如何使用Matlab进行模糊控制系统设计,旨在帮助读者更好地理解和运用这一方法。
一、模糊控制基础1.1 模糊理论概述模糊理论是由日本学者庵功雄于1965年提出的一种描述不确定性问题的数学工具。
模糊控制是指在系统建模和控制设计过程中,使用模糊集合和模糊规则进行推理和决策,从而实现对复杂、非线性和不确定系统的控制。
1.2 模糊控制的优势相比于传统的控制方法,模糊控制具有以下优势:- 模糊控制能够处理复杂、非线性和不确定系统,适用范围广。
- 模糊控制不需要精确的系统数学模型,对系统环境的变化较为鲁棒。
- 模糊控制方法简单易懂,易于实现和调试。
二、Matlab在模糊控制系统设计中的应用2.1 Matlab模糊工具箱的介绍Matlab提供了一个专门用于模糊逻辑和模糊控制设计的工具箱,该工具箱提供了丰富的函数和命令,使得模糊控制系统的设计过程更加简单和高效。
2.2 Matlab模糊控制系统设计流程在使用Matlab进行模糊控制系统设计时,可以按照以下步骤进行:1) 确定模糊控制系统的输入和输出变量;2) 设计模糊集合和决策规则;3) 确定模糊推理的方法和模糊控制器的类型;4) 设计模糊控制器的输出解模糊方法;5) 对设计好的模糊控制系统进行仿真和调试。
2.3 Matlab中常用的模糊控制函数和命令为方便读者进行模糊控制系统的设计和实现,Matlab提供了一系列常用的函数和命令,如:- newfis:用于创建新的模糊推理系统;- evalfis:用于对输入样本进行推理和解模糊;- gensurf:用于绘制模糊控制系统的输出曲面;- ruleview:用于直观地查看和编辑模糊规则等。
三、使用Matlab进行模糊控制系统设计的案例分析为了帮助读者更好地理解和运用Matlab进行模糊控制系统设计,本节将以一个实际案例进行分析。
模糊PID控制系统设计及MATLAB仿真

相比传统的PID控制系统,基于Matlab的模糊PID控制系统具有更好的适应性 和鲁棒性。在面对具有非线性、时变等特点的被控对象时,模糊PID控制系统可 以更好地实现精确控制。仿真结果表明,该方法在改善系统的动态性能和稳态精 度方面均具有显著的优势。
然而,基于Matlab的模糊PID控制系统仍然存在一些问题需要进一步研究和 解决。例如,针对不同的被控对象,如何自适应地调整模糊PID控制器的参数仍 然是一个亟待解决的问题。此外,如何进一步提高模糊PID控制系统的鲁棒性和 自适应性也是未来研究的重要方向。
模糊PID控制系统设计及MATLAB仿 真
01 引言
03 参考内容
目录
02
模糊PID控制系统设 计
摘要:本次演示主要介绍了模糊PID控制系统的设计方法及其在MATLAB环境 下的仿真过程。首先,阐述了模糊PID控制系统的基本原理和设计流程,并通过 一个实际案例加以说明。接下来,介绍了MATLAB仿真的基本原理和实施步骤,并 展示了仿真结果。最后,总结了本次演示的主要内容,并指出了未来的研究方向。
(4)设计控制表:根据模糊规则和控制要求,计算出各模糊变量的控制表。
(5)设计去模糊化器:去模糊化器的作用是将模糊量转换为精确量,以便 输出到被控对象。
3、设计案例
以一个简单的温度控制系统为例,介绍模糊PID控制系统的设计应用。该系 统的输入为温度误差和温度变化率,输出为加热器的控制信号。首先,确定输入 输出变量,定义相应的模糊变量。然后,根据控制要求和系统特性制定模糊规则, 并计算出各模糊变量的控制表。最后,设计去模糊化器,将模糊量转换为精确量, 输出加热器的控制信号。通过这样的设计流程,可以实现对该温度控制系统的数学计算软件,它可以用于各种控制系统仿真的工 具。在MATLAB中,可以使用Simulink模块进行系统建模和仿真。Simulink提供 了丰富的库和工具箱,可以方便地构建各种类型的控制系统模型,并对系统进行 仿真和分析。
模糊控制的Matlab仿真实例

THANK YOU
中心平均值去模糊化
去模糊化过程
04
Matlab仿真实例
输入输出变量定义
根据被控对象的特性,定义模糊控制系统的输入输出变量,如温度、湿度、压力等。
模糊化函数设计
为每个输入输出变量设计对应的模糊化函数,将实际值映射到模糊集合上。
模糊规则制定
根据专家知识和实际经验,制定模糊控制规则,如“如果温度过高,则调整冷却阀”。
输入输出关系
基于模糊逻辑运算和模糊集合的性质,建立输入和输出之间的映射关系。
推理规则
基于专家知识和经验,制定一系列的推理规则,用于指导模糊推理过程。
推理方法
常用的模糊推理方法包括最大值推理、最小值推理和中心平均值推理等。
模糊推理系统
02
Matlab模糊逻辑工具箱简介
模糊逻辑工具箱的功能
为了将模糊输出转换为实际输出,工具箱提供了多种去模糊化方法,如最大值去模糊化、最小值去模糊化和中心平均值去模糊化等。
性能指标选择
根据所选性能指标,采用合适的方法对模糊控制系统的性能进行评估,如极差分析法、方差分析法等。
性能评估方法
将模糊控制系统的性能与其他控制方法进行比较,如PID控制、神经网络控制等,以验证其优越性。
性能比较
01
02
03
模糊控制系统的性能评估
05
结论与展望
模糊控制对模型误差和参数变化具有较强的鲁棒性,能够适应不确定性和非线性系统。
输出模糊化
将模糊集合的输出映射到实际输出量上,同样采用隶属函数进行模糊化处理。
模糊化过程
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(10) (11)
(12) (13) (14) (15)
⑦模糊蕴含的标准法运算
R A B A B y/x, y
其中 y 为 1(当 y)或 y ( 当y)
(17)
(2)多输入模糊推理
以上讨论的都是模糊推理关系的前件部为一个输入的情况,但在模糊控制系统中经常遇到的问题往
往是多输入的,特别是两输入的情况,例如“如果压力偏高且还在继续升高,那么停止加热”这样的规
则。其一般形式为
如果 A 且 B,那么 C
现在 A’且 B’
结论:那么 C’
这里假设 A 和 A’,B 和 B’,C 和 C’分别是不同论域 X,Y,Z 上的模糊集合。
这是常用的一种合成方法。
(2)模糊语言变量
定义:带有模糊性的语言称为模糊语言。模糊语言变量用一个有五个元素的集合(X,T(X),U,G,M)
表示,其中 X 是语言变量名;T(X)是语言变量名的集合,且每个值都是在 U 上定义的模糊数 Xi;U 为语
言变量 X 的论域;G 为产生 X 数值名的语言值规则,是用于产生语言变量值的;M 为与每个语言变量含
整定 PID 控制器进行设计。
2 MATLAB 语言简介
MATLAB 是 math works 公司推出的一套高性能的数值计算和可视化软件,它集数值分析、矩阵运算、
信号处理和图形显示于一体,构成了一个方便的、界面友好的用户环境。MATLAB 含有丰富的工具箱,
其中主要有信号处理、控制系统、神经网络、通信、图像处理、鲁棒控制,非线性系统控制设计、系统
智能控制主要包括以下几个方面,基于知识系统的专家控制、基于模糊系统的智能控制、基于学习
及适应性的智能控制、基于神经网络的智能控制系统。模糊控制指的是应用模糊集合理论统筹考虑控制
的一种控制方式。模糊控制的基本思想是把人类专家对特定的被控对象或过程的控制策略总结成一系列
以:“IF(条件)…THEN(作用)”形式表示的控制规则,通过模糊推理得到控制作用集,作用于被控对
Rb A B A B (1 A( X ) B(Y ) /(x, y) X Y
⑥模糊蕴含的标准法运算
Rs A B A B Ay/x, y X Y
其中 y 为 1(当 y )或 0(当 y )
③模糊蕴含算术运算
Ra A B A B 1 (1 A( X ) B( y)) /(x, y) X Y
④模糊蕴含的最大最小运算
Rm A B A B (A( X ) B( y)) 1 A( X )) /(x, y) X Y
⑤模糊蕴含的布尔运算
情况下其隶属度函数曲线一定是凸模糊集合。如果该曲线是梯形平顶的,那么具有最大隶属度的元素可
能不止一个,这时就要所有取最大隶属度的元素求平均值。
(3)系数加权平均法
系数加权平均法的输出由下式决定:
象或过程。控制作用集为一组条件语句,状态条件和控制作用均为一组被量化了的模糊语言集,如”正
大”、”负大”、”高”等。它们共同构成控制过程的模糊算法,定义模糊子集与建立模糊控制规则、
由基本论域转变为模糊集合论域、模糊关系矩阵运算、模糊推理合成与求出控制输出模糊子集、进行清
晰化运算,得到精确控制量。本论文主要是对基于模糊系统的智能控制器中的常规模糊控制器和模糊自
关键词:模糊控制,PID 控制,MATLAB 仿真
1 引言
智能控制是当前国内外人工智能,自动化,计算机技术领域中的热门话题,受到学术界、工程界和
企业界的广泛关注。正在积极进行有关智能控制的理论方法和应用技术的研究与开发工作,取得了许多
新进展和新成果。智能控制系统的发展,为智能自动化提供了理论基础,必将推动自动化向前发展。
(16)
3.3 模糊逻辑推理 (1)模糊条件推理
在模糊逻辑控制中,经常用到模糊条件推理。其形式是: 如果什么什么,那么怎么怎么,否则怎么怎么。 用语言规则表示为:如果是 A,那么是 B,否则是 C 。
3
模糊控制器的设计与 MATLAB 仿真
第 4 页 共 14 页
其逻辑表达式是: ( A B) ((1 A) C)
能,得到了广泛的应用,成为当今国际领域中应用最广、最受人们喜爱的一种软件环境。本论文的软件
部分是在 MATLAB6.5 下编写完成的。
3 模糊逻辑控制理论
3.1 模糊集合
ቤተ መጻሕፍቲ ባይዱ
定义:给定论域 X,A={x}是 X 中的模糊集合的含义是
A : X 0,1
(1)
1
模糊控制器的设计与 MATLAB 仿真
论那么 C’。这里假设 Ai 和 A’,Bi 和 B’,Ci 和 C’分别是不同论域 X,Y,Z 上的模糊集合。 “Ai 且 Bi,那么 Ci”的隶属度表达式为
Ai( X ) Bi( y) Ci(z)
若用定义蕴含关系 A→B=A∧B,则上式变成
Ai( X ) Bi( y) Ci(z)
推理结果为
C' ( A' ANDB')( A1ANDB1) C1 ( AnANDBn) Cn C1'C2' Cn' 其中 Ci' ( Ai' ANDBi')( AiANDBi) Ci
(4)模糊推理的性质
(19) (20) (21)
性质 1: 若合成运算符“Ο”采用最大-最小法或最大-积法,连接词“also”采用并法,则“Ο”
第 2 页 共 14 页
这样的隶属度函数表示其特征的集合。若μA(x)接近 1,表示 X 属于 A 的程度高,μA(x)接近于 0,
表示 X 属于 A 的程度低。
表示方法:模糊集合有很多表示方法,最根本的是将它所包含的元素及相应的隶属度函数表示出来。
因此它可用如下的形式来表示:
A {(x, A(x)) | x X }
和 “also”的运算次序可以交换,即
( A' ANDB') Ri ( A' ANDB')Ri
(22)
性质 2:若模糊蕴含关系采用 Rc 和 Rp 时,则有
( A' ANDB')( AiANDBi) Ci A'( Ai Ci) B'(Bi Ci)
(23)
3.4 模糊化运算
(1)单点模糊集合
如果输入量数据 x。是准确的,则通常将其模糊化为单点模糊集合。设模糊集合用 A 表示。
(24)
4
模糊控制器的设计与 MATLAB 仿真
第 5 页 共 14 页
图 3 隶属度函数 (2)三角模糊集合 如果输入量数据存在随机噪声,这时模糊运算相当于随机变量为模糊量。对于这种情况可以取模糊 量的隶属度函数为等腰三角形,如图 4 所示。三角形的顶点相应于该随机数的均值,底边的长度等 2δ, δ表示随机数据的标准差。由于本设计的输入量是准确的,因此采用单点模糊集合进行模糊化运算。
“A 且 B,那么 C”的隶属度度表达为
A( X ) B( y) C(z)
(18)
(3)多输入多规则模糊推理
以上介绍的是多输入的情况,下面讨论是多输入又是多推理规则的情况。
以两输入多规则情况为例,若有 n 条规则,其一般形式为:如果 A1 且 B1,那么 C1;否则如果 A2 且 B2,那么 C2;否则如果 A3 且 B3,那么 C3……………否则如果 An 且 Bn,那么 Cn;现在 A’且 B’结
也是一个模糊关系,记为 T=RΟS,它具有隶属度
RS(x, z) (R(x, y) * s( y, z))
(5)
其中,∨是并的符号,它表示对所有取最大值或上界值,*是二项积的符号。因此,上面的合成称
为最大-星合成。其中二项算子“*”可以定义为以下几种运算,其中 x,y∈[0,1]
交积:
x y min{x, y}
(6)
代数积:
x y xy
(7)
有界积:
x y max{0, x y 1}
(8)
强制积:
xy x( y 1)ory(x 1)or0(x, y 1)
(9)
若二项积采用求交运算,则 RS RS (x, z) (R(x, y) * s( y, z)) 称为最大-最小合成。
(2)
也可表示成如下的形式
x x xi xi
(3)
模糊集合的隶属度函数定义:在经典集合中,特征函数只能取 0 和 1 两个值,即特征函数与{0,1} 相对应;而在模糊集合中,其特征函数的取值范围从两个元素的集合扩大到在[0,1]区间连续取值。为 了把两者区分开来,就把模糊集合的特征函数称作隶属度函数。图 1 表示了这两种函数的关系。
性质 3:对于 Ci' ( Ai' ANDBi)( AiANDBi) Ci 的推理结果可以用如下简洁的形式表示
ci'(z) ai ci(z) 当模糊蕴含运算采用 Rc 时
ci'(z) aici(z) 当模糊蕴含运算采用 Rp 时
其中 i max(A'( X ) Ai( X )) max(B'( y) Bi( y))
中系数加权平均法用的较多。
(1)重心法
所谓重心法就是取隶属度函数曲线与横坐标轴围成面积作为代表点。理论上说应该计算输出范围内
一系列连续点的重心,但实际上是通过计算输出范围内整个点的重心,这是一种折衷方案。即
u xi N (xi) / N (xi)
(22)
(2)最大隶属度法
这种方法最简单,只要在推理结论的模糊集合中取最大的那个元素作为输出量即可。不过要求这种
图 4 隶属度函数
3.5 清晰化方法
清晰化方法又叫解模糊化方法。通过模糊推理得到的结果是一个模糊集合或隶属度函数,但在实际
