哈希表的查询程序(50单词查询)
哈希表查找(散列表查找)c++实现HashMap

哈希表查找(散列表查找)c++实现HashMap算法思想:哈希表什么是哈希表在前⾯讨论的各种结构(线性表、树等)中,记录在结构中的相对位置是随机的,和记录的关键字之间不存在确定的关系,因此,在结构中查找记录时需进⾏⼀系列和关键字的⽐较。
这⼀类查找⽅法建⽴在“⽐较”的基础上。
在顺序查找时,⽐较的结果为“="与“!=”两种可能;在折半查找、⼆叉排序树查找和B树查找时,⽐较的结果为“<"、"="和“>"3种可能。
查找的效率依赖于查找过程中所进⾏的⽐较次数。
理想的情况是希望不经过任何⽐较,⼀次存取便能得到所查记录,那就必须在记录的存储位置和它的关键字之间建⽴⼀个确定的对应关系f,使每个关键字和结构中⼀个惟⼀的存储位置相对应。
因⽽在查找时,只要根据这个对应关系f找到给定值K的像f(K)。
若结构中存在关键字和K相等的记录,则必定在f(K)的存储位置上,由此,不需要进⾏⽐较便可直接取得所查记录。
在此,我们称这个对应关系f为哈希( Hash)函数,按这个思想建⽴的表为哈希表。
哈希函数的构造⽅法哈希函数是从关键字集合到地址集合的映像。
通常,关键字集合⽐较⼤,它的元素包括所有可能的关键字,⽽地址集合的元素仅为哈希表中的地址值。
哈希函数其实是⼀个压缩映像,那么这种情况就不可避免的产⽣冲突,那么在建造哈希表时不仅要设定⼀个好的哈希函数,还要设定⼀种处理冲突的⽅法。
(设定的哈希函数H(key)和处理冲突的⽅法将⼀组关键字映像到⼀个有限的连续的地址集上,并以关键字在地址集中的“像”作为记录在表中的存储位置,这种表就是哈希表,映像的过程为哈希造表或散列,所得的存储位置称哈希地址或散列地址)(1)直接定址法取关键字或关键字的某个线性函数值为哈希地址。
即H(key)=key 或 H(key)=a*key+b (a,b为常数)。
举例1:统计1-100岁的⼈⼝,其中年龄作为关键字,哈希函数取关键字⾃⾝。
哈希表(Hash)的查找

哈希表(Hash)的查找一、哈希表相关概念1、哈希函数的基本概念哈希表又称散列表。
哈希表存储的基本思想是:以数据表中的每个记录的关键字 k为自变量,通过一种函数H(k)计算出函数值。
把这个值解释为一块连续存储空间(即数组空间)的单元地址(即下标),将该记录存储到这个单元中。
在此称该函数H为哈希函数或散列函数。
按这种方法建立的表称为哈希表或散列表。
理想情况下,哈希函数在关键字和地址之间建立了一个一一对应关系,从而使得查找只需一次计算即可完成。
由于关键字值的某种随机性,使得这种一一对应关系难以发现或构造。
因而可能会出现不同的关键字对应一个存储地址。
即k1≠k2,但H(k1)=H(k2),这种现象称为冲突。
把这种具有不同关键字值而具有相同哈希地址的对象称“同义词”。
在大多数情况下,冲突是不能完全避免的。
这是因为所有可能的关键字的集合可能比较大,而对应的地址数则可能比较少。
对于哈希技术,主要研究两个问题:(1)如何设计哈希函数以使冲突尽可能少地发生。
(2)发生冲突后如何解决。
2、哈希函数的构造方法常见的构造方法有很多种,如直接定址法,数字分析法,平方取中法等。
接下来,我们介绍其中的几种:(1)除留余数法取关键字k被某个不大于表长m的数p除后所得余数作为哈希函数地址的方法。
即:H(k)=k mod p这种方法的关键是选择好p。
使得数据集合中的每一个关键字通过该函数转化后映射到哈希表的任意地址上的概率相等。
理论研究表明,一般取p为小于m的最大质数或不包含小于20的质因素的合数。
(2)平方取中法先将关键字平方,然后取其中间几位作为散列地址。
所取位数由地址空间范围决定。
若地址空间小于所取位数值决定的范围,可通过乘以一比例因子来解决。
(3)折叠法把关键字分割成位数相等(最后一部分的位数可以不同)的几部分,然后通过折叠后将几部分进行相加,丢掉进位位,所得值即为散列地址。
散列的位数由地址空间的位数而定。
分割方法:从右至左相加方法有两种:移位叠加:将分割后的各部分低位对齐相加。
哈希表

123456789101112131415161718123456789101112131415161718 // HashTableInitializeTable(int TableSize) {HashTable H;int i;// 為散列表分配空間// 有些编譯器不支持為struct HashTable 分配空間,聲稱這是一個不完全的結構,// 可使用一个指向HashTable的指針為之分配空間。
// 如:sizeof(Probe),Probe作为HashTable在typedef定義的指針。
H = malloc(sizeof(struct HashTable));// 散列表大小为一个質数H->TableSize = Prime;// 分配表所有地址的空間H->Cells = malloc(sizeof(Cell) * H->TableSize);// 地址初始為空for (i =0; i < H->TableSize; i++)H->Cells[i].info = Empty;return H;}查找空单元并插入:// PositionFind(ElementType Key, HashTable H) {Position Current;int CollisionNum;// 冲突次数初始为0// 通過表的大小對關鍵字進行處理CollisionNum =0;Current = Hash( Key, H->TableSize );// 不為空時進行查詢while (H->Cells[Current].info != Empty &&H->Cells[Current].Element != Key) {Current =++CollosionNum *++CollisionNum;// 向下查找超過表範圍時回到表的開頭if (Current >= H->TableSize)Current -= H->TableSize;}return Current;}分離連接法散列表的查找过程基本上和造表过程相同。
哈希表查找方法原理(一)

哈希表查找方法原理(一)哈希表查找方法简介什么是哈希表?•哈希表是一种用于存储键值对(key-value)数据的数据结构。
•哈希表的本质是一个数组,每个数组元素称为一个桶(bucket)或槽(slot)。
•每个桶可以存储一个或多个键值对,通过使用哈希函数将键映射为桶的索引。
哈希函数的作用•哈希函数将任意大小的数据映射到固定大小的值。
•这个值作为索引用于访问哈希表中特定桶的位置。
•好的哈希函数应该具备以下特点:–确定性:对于相同的输入,哈希函数应始终返回相同的哈希值。
–均匀性:哈希值应尽可能地分布均匀,避免冲突。
–高效性:哈希函数应具备高效计算的特点,以提高查找效率。
哈希表的查找方法1.哈希表查找的基本过程:–通过哈希函数计算出要查找元素的哈希值。
–使用哈希值作为索引,在哈希表中访问对应的桶。
–检查桶中的元素,进行比较以确定是否找到目标元素。
2.根据桶内元素的存储方式,哈希表的查找方法可分为两种基本类型:a.链地址法(拉链法)–桶中的每个位置都是一个链表,用于存储哈希值相同的键值对。
–查找时,首先计算哈希值,然后在相应的链表中顺序查找目标元素。
–链地址法适合处理冲突较多的情况,但链表过长会影响查找效率。
b.开放地址法(线性探测法、二次探测法等)–桶中的每个位置都可以存储一个键值对。
–当发生冲突时,通过一定的方法找到下一个可用的桶来存储冲突的元素。
–常用的探测方法包括线性探测、二次探测等。
–开放地址法适合处理冲突较少的情况,但可能会造成桶的利用率低下。
哈希表查找的时间复杂度•在理想情况下,哈希表的查找时间复杂度为O(1)。
•但在最坏情况下,查找时间复杂度可能会达到O(n),其中n为待查找元素的总数。
•好的哈希函数和适当的处理冲突方法可以尽量降低冲突的发生,提高查找效率。
总结•哈希表通过哈希函数将键映射为桶的索引,实现了高效的查找操作。
•哈希表的查找方法主要有链地址法和开放地址法,根据具体情况选择合适的方法。
详解哈希表的查找

详解哈希表的查找哈希表和哈希函数在记录的存储位置和它的关键字之间是建立一个确定的对应关系(映射函数),使每个关键字和一个存储位置能唯一对应。
这个映射函数称为哈希函数,根据这个原则建立的表称为哈希表(Hash Table),也叫散列表。
以上描述,如果通过数学形式来描述就是:若查找关键字为key,则其值存放在f(key) 的存储位置上。
由此,不需比较便可直接取得所查记录。
注:哈希查找与线性表查找和树表查找最大的区别在于,不用数值比较。
冲突若key1 ≠ key2 ,而f(key1) = f(key2),这种情况称为冲突(Collision)。
根据哈希函数f(key)和处理冲突的方法将一组关键字映射到一个有限的连续的地址集(区间)上,并以关键字在地址集中的“像”作为记录在表中的存储位置,这一映射过程称为构造哈希表。
构造哈希表这个场景就像汽车找停车位,如果车位被人占了,只能找空的地方停。
构造哈希表由以上内容可知,哈希查找本身其实不费吹灰之力,问题的关键在于如何构造哈希表和处理冲突。
常见的构造哈希表的方法有 5 种:(1)直接定址法说白了,就是小学时学过的一元一次方程。
即 f(key) = a * key + b。
其中,a和b 是常数。
(2)数字分析法假设关键字是R进制数(如十进制)。
并且哈希表中可能出现的关键字都是事先知道的,则可选取关键字的若干数位组成哈希地址。
选取的原则是使得到的哈希地址尽量避免冲突,即所选数位上的数字尽可能是随机的。
(3)平方取中法取关键字平方后的中间几位为哈希地址。
通常在选定哈希函数时不一定能知道关键字的全部情况,仅取其中的几位为地址不一定合适;而一个数平方后的中间几位数和数的每一位都相关,由此得到的哈希地址随机性更大。
取的位数由表长决定。
(4)除留余数法取关键字被某个不大于哈希表表长 m 的数 p 除后所得的余数为哈希地址。
即f(key) = key % p (p ≤ m)这是一种最简单、最常用的方法,它不仅可以对关键字直接取模,也可在折叠、平方取中等运算之后取模。
哈希表的定义查找及分析bklt

一、直接地址法
:
取关键字或关键字的某个线性函值为哈希地址
即: H(key) = key 或: H(key) = a* key + b
其中,a, b为常数。
二、数字分析法
假设关键字集合中的每个关键字都是由 s 位 数字组成 (u1, u2, …, us),分析关键字集中的全 体, 并从中提取分布均匀的若干位或它们的组 合作为地址。
查找不成功时的ASL
ASLunsucc=( )/11
= /11
10
11
3
8
线性探测再散列的优点:
只要哈希表未满,总能找到一个空地址。
缺点:会产生二次聚集。
01…
70 19 33 18
5678 9
… 12
9
二、 链地址法
在哈希表的每一个单元中存放一个指针,将所 有的同义词连成一个链表。 假设哈希地址在区间[0 .. m-1]上,则哈希表为
一个指针数组。
typedef struct node{ //定义链表中结点 KeyType key; 其它成员 ; struct node *next;
} Node,*Nodeptr; typedef Nodeptr chainhash[m];// 定义指针数组10
例1: 关键字集合 { 19, 01, 23, 14, 55, 68, 11, 82, 36 }
若采用线性探测再散列处理冲突
0 1 2 3 4 5 6 7 8 9 10
55 01 23 14 68 11 82 36 19
11 21 3 62 5 1
若采用二次探测再散列处理冲突
0 1 2 3 4 5 6 7 8 9 10
第9章-查找第4讲-哈希表
3、数字分析法
关键字
92317602 92326875 92739628 92343634 92706816 92774638 92381262 92394220
希 地 址
位 作 为 哈
取 最 后 两
02 75 28 34 16 38 62 20
哈希地址的集合为(2,75,28,34,16,38,62,20)。
77
54 16 43 31 29 46 60 74 88
90
共探查2次 哈希表创建完毕
17/35
成功查找的情况
查找关键字为29的记录:
h(29)=29%13=3:16≠29; d0=3,d1=(3+1)=4:43≠29; d2=(4+1)=5:31≠29; d3=(5+1)=6:29=29。成功!
9/35
关键字:16 74 60 43 54 90 46 31 29 88 77
hh((917645320640319))==139842752
0 1 2 3 4 5 6 7 8 9 10 11 12
54 16 43 31
46 60 74
90
注意:存在哈希冲突。
解:n=11,m=13,设计除留余数法的哈希函数为: h(k)=k mod p p应为小于等于m的素数,设p=13。
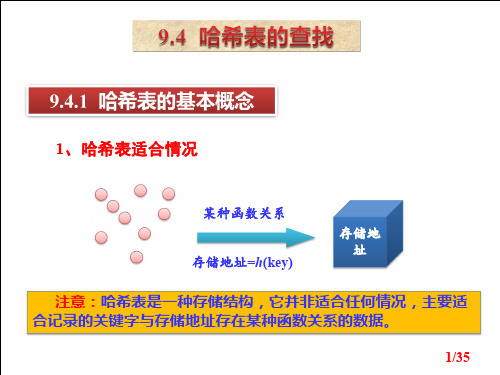
1、哈希表适合情况
某种函数关系 存储地址=h(key)
存储地 址
注意:哈希表是一种存储结构,它并非适合任何情况,主要适 合记录的关键字与存储地址存在某种函数关系的数据。
1/35
示例
学号 姓名
201001001 张三 201001003 李四 … 201001025 王五
记录数n=20,无序
哈希表

示例:设给定的关键字为 key = 23938587841,若存储空间限定 3 位, 则 划分结果为每段 3 位. 上述关键字可划分为 4段: 239 385 878 41 把超出地址位数的最高位删去, 仅保留最低 的3位,做为可用的哈希地址。 移 位 法 分 界 法
13
除留余数法
设哈希表中允许的地址数为 m, 取一个不大 于 m,但最接近于或等于 m 的质数 p 作为 除数,利用以下公式把关键字转换成哈希地 址。哈希函数为:
一子集中的关键字互为同义词。
• 同义词通过一个单链表链接起来。各链表的表头
结点组成一个向量。
23
• 示例:给出一组表项关键字{ Burke, Ekers, Broad, Blum, Attlee, Alton, Hecht, Ederly }。哈希函数为: Hash (x)=ord (x)-ord („A‟)。x为首字母。 • 用它计算可得: Hash (Burke) = 1 Hash (Broad) = 1 Hash (Attlee) = 0 Hash (Alton) = 0 Hash (Ekers) = 4 Hash (Blum) = 1 Hash (Hecht) = 7 Hash (Ederly) = 4
5
直接定址法
此类函数取关键字的某个线性函数值作 为哈希地址:
Hash ( key ) = a * key + b
常数 } { a, b为
这类哈希函数是一对一的映射,一般不会产生 冲突。但是,它要求哈希地址空间的大小与关键 字集合的大小相同。实际中可应用情况很少。
6
数字分析法
设有 n 个 d 位数,每一位可能有 r 种不 同的符号。这 r 种不同的符号在各位上出现 的频率不一定相同,可能在某些位上分布均 匀些;在某些位上分布不均匀,只有某几种 符号经常出现。可根据哈希表的大小,选取 其中各种符号分布均匀的若干位作为哈希地 址。
哈希查找的流程

哈希查找的流程Hash lookup is a fundamental algorithm used in computer science to quickly retrieve data from a large dataset. The process involves using a hash function to map data to a unique key, which is then used to store and retrieve the data efficiently.哈希查找是计算机科学中使用的基本算法,用于从大型数据集中快速检索数据。
该过程涉及使用哈希函数将数据映射到唯一键,然后使用该键来高效地存储和检索数据。
From a technical perspective, the first step in a hash lookup process is to apply a hash function to the search key. This generates a unique hash value that is used as an index to access the corresponding data in a hash table. The hash table is a data structure that stores key-value pairs and allows for constant-time retrieval of data.从技术角度来看,哈希查找过程中的第一步是对搜索键应用哈希函数。
这将生成一个唯一的哈希值,该值用作索引来访问哈希表中的相应数据。
哈希表是一种存储键值对的数据结构,可以实现数据的常数时间检索。
One of the key advantages of hash lookup is its efficiency in retrieving data, especially in large datasets. This is because the use of a hash function allows for constant-time access to data, regardless of the size of the dataset. As a result, hash lookup is commonly used in applications where quick data retrieval is crucial, such as database systems and information retrieval systems.哈希查找的一个关键优势是它在检索数据方面的效率,特别是在大型数据集中。
数据结构 第9章 查找4-哈希表

6个元素用7个 地址应该足够!
1
2
23 9
3
4
39 25 11
5
6
H(25)=25%7=4 H(11)=11%7=4
有冲突!
在哈希查找方法中,冲突是不可能避免的,只能 尽可能减少。
所以,哈希方法必须解决以下两个问题:
1)构造好的哈希函数
(a)所选函数尽可能简单,以便提高转换速度; (b)所选函数对关键码计算出的地址,应在哈希地址集中 大致均匀分布,以减少空间浪费。
4、数字分析法
特点:某关键字的某几位组合成哈希地址。所选的位应当 是:各种符号在该位上出现的频率大致相同。 例:有一组(例如80个)关键码,其样式如下: 讨论: 3 4 7 0 5 2 4 ① 第1、2位均是“3和4”,第3位也 3 4 9 1 4 8 7 只有“ 7、8、9”,因此,这几位不 3 4 8 2 6 9 6 能用,余下四位分布较均匀,可作 3 4 8 5 2 7 0 为哈希地址选用。 3 4 8 6 3 0 5 3 4 9 8 0 5 8 ② 若哈希地址取两位(因元素仅80 3 4 7 9 6 7 1 个),则可取这四位中的任意两位组 3 4 7 3 9 1 9 合成哈希地址,也可以取其中两位与 位号:① ② ③ ④ ⑤ ⑥ ⑦ 其它两位叠加求和后,取低两位作哈 希地址。
11 22
△
47 92 16
3
▲
7
29
△
8
△
解释:
① 47、7(以及11、16、92)均是由哈希函数得到的没有冲突 的哈希地址; ② Hash(29)=7,哈希地址有冲突,需寻找下一个空的哈希地址: 由H1=(Hash(29)+1) mod 11=8,哈希地址8为空,因此将29存入。 ③ 另外,22、8、3同样在哈希地址上有冲突,也是由H1找到空 的哈希地址的。
4-哈希查找过程

| 哈希查找过程哈希表查找在哈希表上查找的过程和哈希造表的构造过程基本一致。
1)给定K值,根据构造表时所用的哈希函数求哈希地址j,2)若此位置无记录, 则查找不成功;否则比较关键字,若和给定的关键字相等则成功;否则根据构造表时设定的冲突处理的方法计算“下一地址”,重复2)1. 哈希表查找算法Status SearchHash(HashTable H, KeyType key, int&p, int&c){ /*在开放定址哈希表H中查找关键字为key的数据*//*用c记录发生冲突的次数,初值为0*/p=Hash(k);/*求哈希地址*/while(H.data[p].key!=NULL && H.data[p].key!=key)/*该位置填有数据且与所查关键字不同*/collision(p, ++c);/*求下一探查地址p*/if(H.data[p].key==key )return SUCCESS; /*查找成功,p返回待查数据元素位置*/else return UNSUCCESS;/*查找不成功,p返回插入位置*/}2. 哈希表插入算法Status InsertHash(HashTable&H, DataType e){/*查找不成功时在H中插入数据元素e,并返回SUCCESS*//*若冲突次数过大,则重建哈希表*/c=0;if(SearchHash(H, e.key, p, c))return UN SUCCESS;/*数据已在哈希表中,不需插入*/else if(c<hashsize[H.sizeindex]/2){H.data[p]=e; ++H.count;/*次数c还未达到上限,插入e*/return SUCCESS;}else {RecreatHashTable(H); /*重建哈希表*/return SUCCESS;}哈希表查找与插入算法举例•关键字序列为:•{19,14,23,01,68,20,84,27,55,11,10,79}•哈希函数为H(key)= key mod 13•采用线性探测处理冲突建立哈希查找表如下:请查找关键字为84的记录0 1 2 3 4 5 6 7 8 9 10 11 12140168275519208479231110Key=84哈希地址H(84)=6,因为e.data[6]不空,且e.data[6].key=19≠84,冲突冲突处理H1=(6+1)MOD13=7,e.data[7]不空,且e.data[7].key=20≠84, 冲突冲突处理H2=(6+2)MOD13=8,e.data[8]不空,且e.elem[8].key=84,查找成功,返回数据在哈希表中的序号8。
哈希表的查找

1
2 3
4
2)算法思想: 设n 个记录存放在一个有序顺序表 L 中,并按其关键 码从小到大排好了序。查找范围为l=0, r=n-1; 求区间中间位置mid=(l+r)/2; 比较: L[mid].Key = x,查找成功,返回mid,结束; L[mid].Key > x,r=mid-1; L[mid].Key < x,l=mid+1; 若l<=r 转2,否则查找失败,返回 0;
对查找表常用的操作有哪些?
查询某个“特定的”数据元素是否在表中; 查询某个“特定的”数据元素的各种属性; 在查找表中插入一元素; 从查找表中删除一元素。
9.1 基本概念
如何评估查找方法的优劣? 查找的过程就是将给定的值与文件中各记录的关 键字逐项进行比较的过程。所以用比较次数的平均值 来评估算法的优劣,称为平均查找长度(ASL: average search length)。i 1 i Ci ASL P
考虑对单链表结构如何折半查找? ——无法实现!
2)算法实现:
int Search_Bin ( SSTable ST, KeyType key ) { // 在有序表ST中折半查找其关键字等于key的数据元素。 // 若找到,则函数值为该元素在表中的位置,否则为0。 low = 1; high = ST.length; // 置区间初值 while (low <= high) { mid = (low + high) / 2; if (key == ST.elem[mid].key) return mid; // 找到待查元素 else if ( key < ST.elem[mid].key) high = mid - 1; // 继续在前半区间进行查找 else low = mid + 1; // 继续在后半区间进行查找 } return 0; // 顺序表中不存在待查元素 } // Search_Bin
哈希表查找课件

解决以下二个问题:
1)构造“好”的哈希函数 所选函数尽可能简单,以便提高转换效率。 所选函数对关键码计算出的地址,应在哈希地址中大致均匀分布,以 减少空间浪费。 2)选择一种好的处理冲突方法
9.3.2 哈希函数的构造方法
常用的哈希函数有: 1.直接定址法 2.数字分析法(略) 3.平方取中法 (略) 4. 折叠法 (略) 5.除留余数法 6. 随机数法(略)
作业:
∧
01 14 27 79
∧
∧
55 68
∧
∧ ∧
19 20 84
∧
∧
∧ ∧
10 11 23
∧
∧
∧
9.3.4哈希表的查找及其分析
查找过程和造表过程一致。由于“冲突”的产生,使得哈希表的查找
过程仍然是一个给定值和关键字进行比较的过程。因此,仍需以ASL作为 衡量哈希表查找效率的量度。决定哈希表查找的ASL的因素: 1.选用的哈希函数; 2.选用的处理冲突的方法; 3.哈希表饱和的程度,装载因子α =n/m 值的大小 一般情况,可认为选用的哈希函数是“均匀”的,则在讨论ASL时,
可以不考虑它的因素。哈希表的ASL是处理冲突方法和装载因子的函数。
可以证明查找成功时有下列结果(见P261) 线性探测再散列平均查找长度为Snl= 随机探测再散列平均查找长度为 Snr= 链地址法平均查找长度为Snc=
总结:本堂课我们首先学习了哈希表的构造方法
及与其相关的几个概念(如,哈希表、哈希函数、 同义词、冲突、二次聚集等);然后学习了几个最 常用的哈希函数及处理冲突的方法。其中,除留余 数法和开放定地址处理冲突的方法是本堂课重点要 掌握的知识。
1.直接定址法
哈希函数为关键码的线性函数,即:
python哈希查找

python哈希查找import randomINDEXBOX=7 #哈希表元素个数MAXNUM=13 #数据个数class Node: #声明链表结构def __init__(self,val):self.val=valself.next=Noneglobal indextableindextable=[Node]*INDEXBOX #声明动态数组def create_table(val): #建⽴哈希表⼦程序global indextablenewnode=Node(val)myhash=val%7 #哈希函数除以7取余数current=indextable[myhash]if current.next==None:indextable[myhash].next=newnodeelse:while current.next!=None:current=current.nextcurrent.next=newnode #将节点加⼊链表def print_data(val): #打印哈希表⼦程序global indextablepos=0head=indextable[val].next #起始指针print(' %2d:\t' %val,end='') #索引地址while head!=None:print('[%2d]-' %head.val,end='')pos+=1if pos % 8==7:print('\t')head=head.nextprint()def findnum(num): #哈希查找⼦程序i=0myhash =num%7ptr=indextable[myhash].nextwhile ptr!=None:i+=1if ptr.val==num:return ielse:ptr=ptr.nextreturn0#主程序data=[0]*MAXNUMindex=[0]*INDEXBOXfor i in range(INDEXBOX): #清除哈希表indextable[i]=Node(-1)print('原始数据:')for i in range(MAXNUM):data[i]=random.randint(1,30) #随机数建⽴原始数据print('[%2d] ' %data[i],end='') #并打印出来if i%8==7:print()for i in range(MAXNUM):create_table(data[i]) #建⽴哈希表print()while True:num=int(input('请输⼊查找数据(1-30),结束请输⼊-1:'))if num==-1:breaki=findnum(num)if i==0:print('#####没有找到 %d #####' %num) else:print('找到 %d,共找了 %d 次!' %(num,i)) print('\n哈希表:')for i in range(INDEXBOX):print_data(i) #打印哈希表print()。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
#include <conio.h>
#include <memory.h>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define szNAME 100
#define HASH_ROOT 74 /*用于计算哈希地址的随机数*/
#define szHASH 80 /*哈希表总长度*/
#define COUNT 50 /*单词总数*/
/*哈希表结构体*/
struct THash {
int key; /*钥匙码*/
char word[20]; /*单词*/
int depth; /*检索深度*/
};
/*根据钥匙码和哈希根计算哈希地址*/
int GetHashAddress(int key, int root)
{
return key % root;
}/*end GetHashAddress*/
/*冲突地址计算,如果发现地址冲突,则用当前地址和钥匙码、哈希根重新生成一个新地址*/
int GetConflictAddress(int key, int address, int root)
{
int addr = address + key % 5 + 1;
return addr % root;
}/*end GetConflictAddress*/
/*根据字符串生成哈希钥匙码,这里的方法是将串内所有字符以数值形式求累加和*/
int CreateKey(char * word)
{
int key = 0;
unsigned char * n = (unsigned char *)word;
while(*n) key += *n++;
return key;
}/*end CreateKey*/
/*输入一个单词,并返回哈希钥匙码*/
int GetName(char * word)
{
scanf("%s", word);
return CreateKey(word);
}/*end CreateKey*/
/*根据单词个数、长度和哈希根构造哈希表*/
struct THash * CreateNames(int size, int root, int count)
{
int i =0, key = 0, addr = 0, depth = 0; char word[20];
struct THash * h = 0, *hash = 0;
/*哈希根和长度不能太小*/
if(size < root || root < 2) return 0;
/*根据哈希表长度构造一个空的哈希表*/
hash = (struct THash *)malloc(sizeof(struct THash) * size);
/*将整个表清空*/
memset(hash, 0, sizeof(struct THash) * size);
for(i = 0; i < count; i++) {
/*首先产生一个随机的单词,并根据单词计算哈希钥匙码,再根据钥匙码计算地址*/ key = GetName(word);
addr = GetHashAddress(key, root);
h = hash + addr;
if (h->depth == 0) { /*如果当前哈希地址没有被占用,则存入数据*/
h->key = key;
strcpy(h->word , word);
h->depth ++;
continue;
}/*end if*/
/*如果哈希地址已经被占用了,就是说有冲突,则寻找一个新地址,直到没有被占用*/ depth = 0;
while(h->depth ) {
addr = GetConflictAddress(key, addr, root);
h = hash + addr;
depth ++;
}/*end while*/
/*按照新地址存放数据,同时记录检索深度*/
h->key = key;
strcpy(h->word , word);
h->depth = depth + 1;
}/*next*/
return hash;
}/*end CreateNames*/
/*在哈希表中以特定哈希根查找一个单词的记录*/
struct THash * Lookup(struct THash * hash, char * word, int root)
{
int key = 0, addr = 0; struct THash * h = 0;
/*不接受空表和空名称*/
if(!word || !hash) return 0;
key = CreateKey(word);
addr = GetHashAddress(key, root);
h = hash + addr;
/*如果结果不正确表示按照冲突规则继续寻找*/
while(strcmp(h->word , word)) {
addr = GetConflictAddress(key, addr, root);
h = hash + addr;
if(h->key == 0) return 0;
}/*end while*/
return hash + addr;
}/*end Lookup*/
/*根据一条哈希表记录打印该单词的信息*/
void Print(struct THash * record)
{
if (!record) {
printf("【查无单词】\n");
return ;
}/*end if*/
if(record->depth)
printf("【单词】%s\t【检索深度】%d\n", record->key, record->word, record->depth ); else
printf("【空记录】\n");
/*end if*/
}/*end Print*/
/*打印单词表*/
void Display(struct THash * hash, int size)
{
struct THash * h = 0;
if (!hash || size < 1) return ;
printf("单词表:\n");
printf("--------------------\n");
for(h = hash; h < hash + size; h++) {
printf("【地址】%d\t", h - hash);
Print(h);
}/*next*/
printf("--------------------\n");
}/*end Display*/
/*主函数,程序入口*/
int main(void)
{
/*哈希表变量声明*/
struct THash * hash = 0, * h = 0;
int cmd = 0; /*命令*/
char word[10]; /*单词单词*/
/*生成50个单词用的哈希表*/
hash = CreateNames(szHASH, HASH_ROOT, COUNT);
for(;;) {
printf("哈希表展示:1-显示哈希表;2-检索单词;其他任意键退出:\n"); cmd = getch();
cmd -= '0';
switch(cmd) {
case 1: Display(hash, szHASH); break;
case 2:
printf("请输入要检索的单词:");
scanf("%s", word);
h = Lookup(hash, word, HASH_ROOT);
printf("【地址】%d\t", h - hash);
Print(h);
break;
default:
free(hash);
return 0;
}/*end case*/
}/*next*/
return 0;
}/*end main*/。
