高一数学必修 立体几何证明题
高中数学立体几何证明题汇总

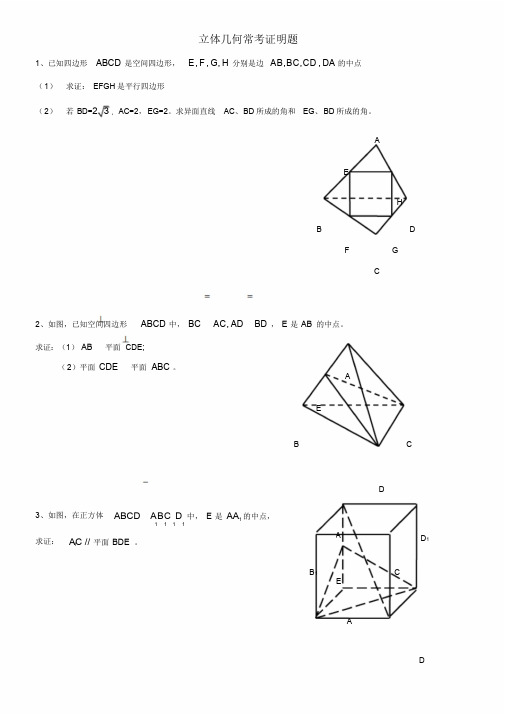
立体几何常考证明题1、已知四边形ABCD 是空间四边形,,,,E F G H 分别是边,,,AB BC CD DA 的中点 (1) 求证:EFGH 是平行四边形(2) 若BD=AC=2,EG=2。
求异面直线AC 、BD 所成的角和EG 、BD 所成的角。
2、如图,已知空间四边形ABCD 中,,BC AC AD BD ==,E 是AB 的中点。
求证:(1)⊥AB 平面CDE;(2)平面CDE ⊥平面ABC 。
3、如图,在正方体1111ABCD A B C D -中,E 是1AA 的中点, 求证: 1//A C 平面BDE 。
AED 1CB 1D CBAAH GFEDCBAEDBC4、已知ABC ∆中90ACB ∠=,SA ⊥面ABC ,AD SC ⊥,求证:AD ⊥面SBC .5、已知正方体1111ABCD A B C D -,O 是底ABCD 对角线的交点.求证:(1) C 1O ∥面11AB D ;(2)1AC ⊥面11AB D .6、正方体''''ABCD A B C D -中,求证:(1)''AC B D DB ⊥平面;(2)''BD ACB ⊥平面.7、正方体ABCD —A 1B 1C 1D 1中.(1)求证:平面A 1BD ∥平面B 1D 1C ;SDCBAD 1ODB AC 1B 1A 1CA 1B 1C 1D 1NMPCBA(2)若E 、F 分别是AA 1,CC 1的中点,求证:平面EB 1D 1∥平面FBD .8、四面体ABCD 中,,,AC BD E F =分别为,AD BC 的中点,且2EF AC =, 90BDC ∠=,求证:BD ⊥平面ACD9、如图P 是ABC ∆所在平面外一点,,PA PB CB =⊥平面PAB ,M 是PC 的中点,N 是AB 上的点,3AN NB =(1)求证:MN AB ⊥;(2)当90APB ∠=,24AB BC ==时,求MN 的长。
高一数学立体几何解答题与答案详解

高一数学立体几何解答题与答案详解1.在正方体ABCD -A 1B 1C 1D 1中,E 、F 为棱AD 、AB 的中点. (1)求证:EF ∥平面CB 1D 1;(2)求证:平面CAA 1C 1⊥平面CB 1D 1. (1)证明:连结BD .在长方体1AC 中,对角线11//BD B D .又E 、F 为棱AD 、AB 的中点, //EF BD ∴. 11//EF B D ∴.又B 1D 1⊂≠ 平面11CB D ,EF ⊄平面11CB D ,∴ EF ∥平面CB 1D 1. (2) 在长方体1AC 中,AA 1⊥平面A 1B 1C 1D 1,而B 1D 1⊂≠ 平面A 1B 1C 1D 1, ∴ AA 1⊥B 1D 1.又在正方形A 1B 1C 1D 1中,A 1C 1⊥B 1D 1,∴ B 1D 1⊥平面CAA 1C 1. 又 B 1D 1⊂≠ 平面CB 1D 1,∴平面CAA 1C 1⊥平面CB 1D 1.2.如图,长方体1111D C B A ABCD -中,1==AD AB ,21=AA ,点P 为1DD 的中点。
(1)求三棱锥D PAC -的体积;(2)求证:直线1BD ∥平面PAC ; (3)求证:直线1PB ⊥平面PAC . 解:(1)11113326D PAC P DAC DAC V V S PD DA DC PD --∆==⋅=⨯⨯⨯⨯= (2)证明:设O 为AC 、BD 的交点,连接PO 在1D DB ∆,PO 是中位线,1//PO D B ∴ 又1D B ⊄平面PAC ,PO ⊂平面PAC 1//D B ∴平面PAC (3)证明:1AB AD == ∴四边形ABCD 是正方形∴AC BD ⊥又1B B ⊥平面ABCD ,AC ⊂平面ABCD ∴1B B ⊥AC 而1ACBB B = ∴ AC ⊥平面11BB D D又1B P ⊂平面11BB D D ∴AC ⊥1B P 连接1B O ,由条件知22211113B P D P B D =+=,22232PO DP DO =+=2221192B O BB BO =+=, 显然 22211B O B P PO =+ ∴1B P PO ⊥ 又1B PAC O =PD 1C 1B 1A 1DC BA图6CCA B A1C1B1D∴1B P ⊥平面PAC3.在 正三棱柱C B A ABC 111-中,底面边长为2 (1)设侧棱长为1,求证C B B A 11⊥;(2)设B A 1与C B 1成600角,求侧棱长。
高中数学立体几何证明题汇总

高中数学立体几何证明题汇总立体几何常考证明题1.已知四边形ABCD是空间四边形,E,F,G,H分别是边AB,BC,CD,DA的中点。
1)证明EFGH是平行四边形。
2)已知BD=23,AC=2,EG=2,求异面直线AC、BD所成的角和EG、BD所成的角。
2.如图,已知空间四边形ABCD中,BC=AC,AD=BD,E 是AB的中点。
1)证明AB垂直于平面CDE。
2)证明平面CDE垂直于平面ABC。
3.如图,在正方体ABCD-A1B1C1D1中,E是AA1的中点。
证明A1C平行于平面BDE。
4.已知三角形ABC中∠ACB=90,SA垂直于面ABC,AD垂直于SC。
证明AD垂直于面SBC。
5.已知正方体ABCD-A1B1C1D1,O是底面ABCD对角线的交点。
1)证明C1O平行于面AB1D1.2)证明AC1垂直于面AB1D1.6.正方体ABCD-A1B1C1D1中。
1)证明AC垂直于平面B1D1D。
2)证明BD1垂直于平面ACB1.7.正方体ABCD-A1B1C1D1中。
1)证明平面A1BD平行于平面B1DC。
2)已知E、F分别是AA1、CC1的中点,证明平面EB1D1平行于平面FBD。
8.四面体ABCD中,AC=BD,E、F分别为AD、BC的中点,且EF=AC/2,∠XXX。
证明BD垂直于平面ACD。
9.如图P是△ABC所在平面外一点,PA=PB,CB垂直于平面PAB,M是PC的中点,N是AB上的点,AN=3NB。
1)证明XXX垂直于AB。
2)当∠APB=90,AB=2BC=4时,求MN的长度。
10.如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是AB、AD、C1D1的中点。
证明平面D1EF平行于平面BDG。
11.如图,在正方体ABCD-A1B1C1D1中,E是AA1的中点。
1)证明A1C平行于平面BDE。
2)证明平面A1AC垂直于平面BDE。
12、已知矩形ABCD,PA垂直于平面ABCD,AB=2,PA=AD=4,E为BC的中点。
高中数学立体几何常考证明题汇总

新课标立体几何常考证明题汇总令狐采学1、已知四边形ABCD 是空间四边形,,,,E F G H分别是边,,,AB BC CD DA 的中点(1) 求证:EFGH 是平行四边形 (2)若BD=AC=2,EG=2。
求异面直线AC 、BD 所成的角和EG 、BD 所成的角。
证明:在ABD ∆中,∵,E H 分别是,AB AD 的中点∴1//,2EH BD EH BD = 同理,1//,2FG BD FG BD =∴//,EH FG EH FG =∴四边形EFGH 是平行四边形。
(2) 90° 30 °考点:证平行(利用三角形中位线),异面直线所成的角 2、如图,已知空间四边形ABCD 中,,BC AC AD BD ==,E 是AB 的中点。
求证:(1)⊥AB 平面CDE;(2)平面CDE ⊥平面ABC 。
证明:(1)BC AC CE AB AE BE =⎫⇒⊥⎬=⎭同理,AD BD DE AB AE BE =⎫⇒⊥⎬=⎭又∵CE DE E ⋂=∴AB ⊥平面CDE (2)由(1)有AB ⊥平面CDE又∵AB ⊆平面ABC ,∴平面CDE ⊥平面ABCAH GF E D CB AEDBC考点:线面垂直,面面垂直的判定3、如图,在正方体1111ABCD A B C D -中,E 是1AA 的中点, 求证:1//A C 平面BDE 。
证明:连接AC 交BD 于O ,连接EO , ∵E 为1AA 的中点,O 为AC 的中点 ∴EO 为三角形1A AC 的中位线∴1//EO AC 又EO 在平面BDE 内,1A C 在平面BDE 外 ∴1//A C 平面BDE 。
考点:线面平行的判定4、已知ABC ∆中90ACB ∠=,SA ⊥面ABC ,AD SC ⊥,求证:AD ⊥面SBC . 证明:90ACB ∠=∵°BC AC ∴⊥又SA ⊥面ABC SA BC ∴⊥ BC ∴⊥面SAC又,SC AD SC BC C ⊥⋂=AD ∴⊥面SBC 考点:线面垂直的判定5、已知正方体1111ABCD A B C D -,O 是底ABCD 对角线的交点.求证:(1)C1O∥面11AB D ;(2)1AC ⊥面11AB D . 证明:(1)连结11A C ,设11111A CB D O ⋂=,连结1AO∵1111ABCD A B C D -是正方体 11A ACC ∴是平行四边形 ∴A1C1∥AC 且 11A C AC =又1,O O 分别是11,A C AC 的中点,∴O1C1∥AO 且11O C AO =11AOC O ∴是平行四边形 111,C O AO AO ∴⊂∥面11AB D ,1C O ⊄面11AB D ∴C1O∥面11AB D(2)1CC ⊥面1111A B C D 11!CC B D ∴⊥又1111A C B D ⊥∵, 1111B D AC C ∴⊥面111AC B D ⊥即 同理可证11A C AD ⊥, 又1111D B AD D ⋂=AED 1CB 1DCBASDCB AD 1ODBA C 1B 1A 1C∴1A C ⊥面11AB D考点:线面平行的判定(利用平行四边形),线面垂直的判定 6、正方体''''ABCD A B C D -中,求证:(1)''AC B D DB ⊥平面;(2)''BD ACB ⊥平面.考点:线面垂直的判定7、正方体ABCD —A1B1C1D1中.(1)求证:平面B1D1C ;(2)若E 、F 分别是AA1,CC1的中点,求证:平面EB1D1∥平面FBD .证明:(1)由B1B∥DD1,得四边形BB1D1D 是平行四边形,∴B1D1∥BD,又BD 平面B1D1C ,B1D1⊂平面B1D1C ,∴BD∥平面B1D1C . 同理A1D∥平面B1D1C .而A1D∩BD=D ,∴平面A1BD∥平面B1CD .(2)由BD∥B1D1,得BD∥平面EB1D1.取BB1中点G ,∴AE∥B1G. 从而得B1E∥AG,同理GF∥AD.∴AG∥DF.∴B1E∥DF.∴DF∥平面EB1D1.∴平面EB1D1∥平面FBD .考点:线面平行的判定(利用平行四边形)8、四面体ABCD 中,,,AC BD E F =分别为,AD BC 的中点,且22EF AC =, A 1AB 1C 1C D 1D GE FNMPCB A90BDC ∠=,求证:BD ⊥平面ACD证明:取CD 的中点G ,连结,EG FG ,∵,E F 分别为,AD BC 的中点,∴EG 12//AC =12//FG BD =,又,AC BD =∴12FG AC =,∴在EFG ∆中,222212EG FG AC EF +== ∴EG FG ⊥,∴BD AC ⊥,又90BDC ∠=,即BD CD ⊥,AC CD C ⋂= ∴BD ⊥平面ACD考点:线面垂直的判定,三角形中位线,构造直角三角形9、如图P 是ABC ∆所在平面外一点,,PA PB CB =⊥平面PAB ,M 是PC 的中点,N 是AB 上的点,3AN NB = (1)求证:MN AB ⊥;(2)当90APB ∠=,24AB BC ==时,求MN 的长。
高中立体几何证明题

高中立体几何证明题一、线面平行的证明题1已知正方体ABCD - A_{1}B_{1}C_{1}D_{1},E,F分别是AB,BC的中点,求证:EF∥平面A_{1}C_{1}D。
解析1. 连接AC。
- 在 ABC中,因为E,F分别是AB,BC的中点,所以EF∥ AC。
2. 正方体ABCD - A_{1}B_{1}C_{1}D_{1}中:- AC∥ A_{1}C_{1}。
- 由EF∥ AC和AC∥ A_{1}C_{1}可得EF∥ A_{1}C_{1}。
- 又A_{1}C_{1}⊂平面A_{1}C_{1}D,EFnot⊂平面A_{1}C_{1}D。
- 根据线面平行的判定定理,所以EF∥平面A_{1}C_{1}D。
题2在三棱柱ABC - A_{1}B_{1}C_{1}中,D是AB的中点,求证:AC_{1}∥平面CDB_{1}。
解析1. 连接BC_{1},交B_{1}C于点E。
- 在三棱柱ABC - A_{1}B_{1}C_{1}中,E为BC_{1}的中点。
2. 因为D是AB的中点:- 所以在 ABC_{1}中,DE∥ AC_{1}。
- 又DE⊂平面CDB_{1},AC_{1}not⊂平面CDB_{1}。
- 根据线面平行的判定定理,可得AC_{1}∥平面CDB_{1}。
二、线面垂直的证明题3在四棱锥P - ABCD中,底面ABCD是正方形,PA = PB = PC = PD,求证:PA⊥平面ABCD。
解析1. 连接AC,BD交于点O,连接PO。
- 因为底面ABCD是正方形,所以O为AC,BD中点。
- 又PA = PC,PB = PD,根据等腰三角形三线合一的性质:- 可得PO⊥ AC,PO⊥ BD。
- 而AC∩ BD = O,AC⊂平面ABCD,BD⊂平面ABCD。
- 根据直线与平面垂直的判定定理,所以PO⊥平面ABCD。
- 又PA = PB = PC = PD,AO = BO = CO = DO,所以 PAO≅ PBO≅ PCO ≅ PDO。
高中数学立体几何常考证明题汇总版

⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯最新料介绍⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯新课标立体几何常考据明题汇总1、已知四边形ABCD 是空间四边形,E, F , G , H 分别是边 AB, BC , CD, DA 的中点( 1)求证:EFGH是平行四边形( 2)若BD=2 3 ,AC=2,EG=2。
求异面直线A C、BD所成的角和EG、 BD所成的角。
AE HB DF GC证明:在ABD 中,∵ E, H 分别是 AB, AD 的中点∴ EH // BD , EH 1BD 2同理, FG // BD , FG 1BD ∴ EH // FG , EH FG ∴四边形EFGH是平行四边形。
2(2) 90 ° 30°考点:证平行(利用三角形中位线),异面直线所成的角2、如图,已知空间四边形ABCD 中,BC AC , AD BD ,E是AB的中点。
求证:( 1)AB平面 CDE;( 2)平面CDE平面 ABC 。
ABC ACCE AB E证明:( 1)BEAEAD BDB C 同理,DE ABAE BE又∵ CE DE E∴ AB平面 CDED( 2)由( 1)有AB平面CDE又∵ AB平面 ABC ,∴平面 CDE平面 ABC考点:线面垂直,面面垂直的判断3、如图,在正方体 ABCD A 1B 1C 1D 1 中, E 是 AA 1 的中点,求证: A 1C // 平面 BDE 。
AD 1证明:连结 AC 交 BD 于 O ,连结 EO ,B 1CE∵ E 为 AA 1 的中点, O 为 AC 的中点∴ EO 为三角形 A 1 AC 的中位线 ∴ EO // AC 1AD又 EO 在平面 BDE∴ AC // 平面 BDE1内, AC 在平面 BDE 外 1 BC。
考点:线面平行的判断4、已知ABC 中 ACB 90 , SA 面ABC , AD SC ,求证: AD面 SBC .证明: ∵ ACB90 °BC ACS又 SA 面 ABCSAB CBC 面 SACDBC ADAB 又 SCAD, SC BCCAD 面 SBCC考点:线面垂直的判断5、已知正方体 ABCDA 1B 1C 1D 1 , O 是底 ABCD 对角线的交点 .D 1C 1求证: (1 ) C 1O ∥面 AB D; (2) AC面 AB D .B 11 111 1A 1证明:( 1)连结 A 1C 1 ,设 A 1C 1B 1D 1O 1,连结 AO 1∵ ABCDA 1B 1C 1D 1 是正方体 A 1 ACC 1 是平行四边形D∴ A 1C 1∥ AC 且 A 1C 1ACCO又 O 1 ,O 分别是 A 1C 1, AC 的中点,∴ O 1C 1∥ AO 且 O 1C 1 AOABAOC 1O 1 是平行四边形C 1O ∥ AO 1 , AO 1 面 AB 1D 1 , C 1O 面 AB 1D 1 ∴C 1O ∥面 AB 1D 1( 2) CC 1面 A 1B 1C 1D 1C C 1 B 1D !又∵ A 1C1B 1D1 ,B 1 D 1 面 A 1C 1 C即 A 1 C B 1 D 1 同理可证A 1CAD1,又D 1B1AD 1D 1A 1C 面 AB 1D 1考点:线面平行的判断(利用平行四边形) ,线面垂直的判断6、正方体 ABCD A' B 'C ' D '中,求证:(1)AC平面B ' D ' DB;(2)BD '平面ACB '.考点:线面垂直的判断7、正方体 ABCD —A1B1C1D1中. (1)求证:平面 A1BD ∥平面 B1D 1C;D 1C1(2) 若 E、 F 分别是 AA1, CC1的中点,求证:平面EB1D1∥平面 FBD .B1A1证明: (1)由 B1B∥ DD 1,得四边形 BB1D 1D 是平行四边形,∴B1D 1∥ BD ,F 又 BD 平面 B1D 1C, B1D1平面 B1D1C,E GDC ∴ BD∥平面 B1D1C.A B同理 A1D ∥平面 B1D1C.而A1D ∩ BD= D,∴平面 A1BD ∥平面 B1CD.(2)由 BD∥ B1D 1,得 BD ∥平面 EB 1D1.取 BB1中点 G,∴ AE ∥B1G.进而得 B1E∥AG,同理 GF ∥ AD.∴ AG∥ DF .∴ B1E∥ DF .∴DF ∥平面 EB1D1.∴平面 EB1D1∥平面 FBD .考点:线面平行的判断(利用平行四边形)8、四周体ABCD中,AC BD , E, F 分别为 AD, BC 的中点,且 EF 2AC ,2BDC 90 ,求证:BD平面 ACD证明:取 CD 的中点 G ,连结EG, FG,∵E, F分别为AD, BC的中点,∴ EG //1 AC 2FG //1BD ,又AC BD ,∴ FG1AC ,∴在EFG 中, EG2FG 2 1 AC2EF 2 222∴ EG FG ,∴ BD AC ,又BDC 90,即 BD CD ,ACCD C∴ BD平面 ACD考点:线面垂直的判断, 三角形中位线,结构直角三角形9、如图P是ABC 所在平面外一点,PA PB, CB平面PAB,M是PC的中点,N是AB P上的点,AN 3NB( 1)求证:MN AB ;(2)当APB 90 ,AB2BC 4 时,求 MN 的长。
高一数学必修2立体几何证明题汇总.

2、如图,在正方体1111ABCD A B C D 中,E 是1AA 的中点,求证: 1//AC 平面BDE 。
A E D 1 CB 1 DC B A8、如图,在正方体1111ABCD A B C D 中,E 、F 、G 分别是AB 、AD 、11C D 的中点.求证:平面1D EF ∥平面BDG .15.(12分)已知正方体ABCD —A 1B 1C 1D 1的棱长为a ,M 、N 分别为A 1B 和AC 上的点,A 1M =AN =23a ,如图.(1)求证:MN ∥面BB 1C 1C ;(2)求MN 的长.16.(12分)(2009·浙江高考)如图,DC ⊥平面ABC ,EB ∥DC ,AC =BC =EB =2DC =2,∠ACB =120°,P ,Q 分别为AE ,AB 的中点.(1)证明:PQ ∥平面ACD ;(2)求AD 与平面ABE 所成角的正弦值.生物练习1.由细胞膜的成分推知,构成细胞膜所必须的化学元素是()A.C、H、O、N B.C、H、O、N、PC.C、H、O、S、P D.C、H、O、Mg、Fe2.在制备细胞膜的实验中常用新鲜成熟的哺乳动物的红细胞作材料是因为()A.哺乳动物红细胞在水中容易胀破B.哺乳动物红细胞容易收集C.哺乳动物红细胞内没有核膜、线粒体膜等细胞器膜D.哺乳动物红细胞的细胞膜在分离时容易沉淀在下面3.任何系统都有边界,边界对系统的稳定至关重要。
细胞作为一个基本的生命系统,它的边界是()A.细胞壁B.细胞膜C.细胞核D.细胞膜表面的蛋白质4.科学上鉴别死细胞和活细胞,常用“染色排除法”,例如,用台盼蓝染色,死的动物细胞会被染成蓝色,而活的动物细胞不着色,从而判断细胞是否死亡。
所利用的是细胞膜的哪种功能()A.保护细胞内部结构的功能B.进行细胞间的信息交流C.控制物质进出功能D.免疫功能5.经研究发现,动物的唾液腺细胞内高尔基体含量较多。
高中数学立体几何常考证明题汇总

立体几何常考证明题汇总考点1:证平行利用三角形中位线;异面直线所成的角已知四边形ABCD 是空间四边形;,,,E F G H 分别是边,,,AB BC CD DA 的中点 (1) 求证:EFGH 是平行四边形(2) 若BD=23;AC=2;EG=2..求异面直线AC 、BD 所成的角和EG 、BD 所成的角.. 考点2:线面垂直;面面垂直的判定如图;已知空间四边形ABCD 中;,BC AC AD BD ==;E 是AB 的中点.. 求证:1⊥AB 平面CDE;2平面CDE ⊥平面ABC .. 考点3:线面平行的判定如图;在正方体1111ABCD A B C D -中;E 是1AA 的中点;求证: 1//A C 平面BDE 考点4:线面垂直的判定已知ABC ∆中90ACB ∠=;SA ⊥面ABC ;AD SC ⊥;求证:AD ⊥面SBC .考点5:线面平行的判定利用平行四边形;线面垂直的判定 已知正方体1111-ABCD A B C D ;O 是底ABCD 对角线的交点.求证:1 C 1O ∥面11AB D ;21AC ⊥面11AB D . 考点6:线面垂直的判定正方体''''ABCD A B C D -中;求证:1''AC B D DB ⊥平面;2''BD ACB ⊥平面.考点7:线面平行的判定利用平行四边形正方体ABCD —A 1B 1C 1D 1中.1求证:平面A 1BD ∥平面B 1D 1C ; 2若E 、F 分别是AA 1;CC 1的中点;求证:平面EB 1D 1∥平面FBD .考点8:线面垂直的判定;三角形中位线;构造直角三角形 四面体ABCD 中;,,AC BD E F =分别为,AD BC 的中点;且22EF AC =; AE D CBDCBAAH GFE DCBAEDBCSDCB AD 1ODBAC 1B 1A 1CA 1ABBC 1D 1DG EFNMP CBA90BDC ∠=;求证:BD ⊥平面ACD考点9:三垂线定理如图P 是ABC ∆所在平面外一点;,PA PB CB =⊥平面PAB ;M 是PC 的中点;N 是AB 上的点;3AN NB =1求证:MN AB ⊥;2当90APB ∠=;24AB BC ==时;求MN 的长..考点10:线面平行的判定利用三角形中位线的如图;在正方体1111ABCD A B C D -中;E 、F 、G 分别是AB 、AD 、11C D 中点.求证:平面1D EF ∥平面BDG .考点11:线面平行的判定利用三角形中位线;面面垂直的判定 如图;在正方体1111ABCD A B C D -中;E 是1AA 的中点.1求证:1//A C 平面BDE ; 2求证:平面1A AC ⊥平面BDE .考点12:线面垂直的判定;构造直角三角形已知ABCD 是矩形;PA ⊥平面ABCD ;2AB =;4PA AD ==;E 为BC 的中点.(1) 求证:DE ⊥平面PAE ;2求直线DP 与平面PAE 所成的角.考点13:线面垂直的判定;构造直角三角形;面面垂直的性质定理;二面角的求法定义法如图;在四棱锥P ABCD -中;底面ABCD 是060DAB ∠=且边长为a 的菱形;侧面PAD 是等边三角形;且平面PAD 垂直于底面ABCD . 1若G 为AD 的中点;求证:BG ⊥平面PAD ; 2求证:AD PB ⊥;3求二面角A BC P --的大小.考点14:线面垂直的判定;运用勾股定理寻求线线垂直如图1;在正方体1111ABCD A B C D -中;M 为1CC 的中点;AC 交BD 于点O ;求证:1AO ⊥平面MBD .考点15:线面垂直的判定如图2;在三棱锥A-BCD 中;BC =AC ;AD =BD ;作BE ⊥CD ;E为垂足;作AH ⊥BE 于H.求证:AH ⊥平面BCD .考点16:线面垂直的判定;三垂线定理证明:在正方体ABCD -A 1B 1C 1D 1中;A 1C ⊥平面BC 1D 考点17:面面垂直的判定证二面角是直二面角如图;过S 引三条长度相等但不共面的线段SA 、SB 、SC;且∠ASB=∠ASC=60°;∠BSC=90°;求证:平面ABC ⊥平面BSC .参考答案1.证明:在ABD ∆中;∵,E H 分别是,AB AD 的中点∴1//,2EH BD EH BD = 同理;1//,2FG BD FG BD =∴//,EH FG EH FG =∴四边形EFGH 是平行四边形.. 2 90° 30 ° 2. 证明:1BC AC CE AB AE BE =⎫⇒⊥⎬=⎭同理;AD BD DE AB AE BE =⎫⇒⊥⎬=⎭又∵CE DE E ⋂= ∴AB ⊥平面CDE 2由1有AB ⊥平面CDE又∵AB ⊆平面ABC ; ∴平面CDE ⊥平面ABC 3. 证明:连接AC 交BD 于O ;连接EO ; ∵E 为1AA 的中点;O 为AC 的中点 ∴EO 为三角形1A AC 的中位线 ∴1//EO AC 又EO 在平面BDE 内;1A C 在平面BDE 外 ∴1//A C 平面BDE ..4. 证明:90ACB ∠=∵° BC AC ∴⊥又SA ⊥面ABC SA BC ∴⊥ BC ∴⊥面SAC又,SC AD SC BC C ⊥⋂=AD ∴⊥面SBC5. 证明:1连结11A C ;设11111A C B D O ⋂=;连结1AO∵ 1111ABCD A B C D -是正方体 11A ACC ∴是平行四边形∴A 1C 1∥AC 且 11A C AC = 又1,O O 分别是11,A C AC 的中点;∴O 1C 1∥AO 且11O C AO =11AOC O ∴是平行四边形 111,C O AO AO ∴⊂∥面11AB D ;1C O ⊄面11AB D ∴C 1O ∥面11AB D21CC ⊥面1111A B C D 11!CC B D ∴⊥又1111A C B D ⊥∵; 1111B D AC C ∴⊥面 111AC B D ⊥即 同理可证11A C AD ⊥; 又1111D B AD D ⋂=∴1AC ⊥面11AB D 7. 证明:1由B 1B ∥DD 1;得四边形BB 1D 1D 是平行四边形;∴B 1D 1∥BD ; 又BD 平面B 1D 1C ;B 1D 1⊂平面B 1D 1C ; ∴BD ∥平面B 1D 1C . 同理A 1D ∥平面B 1D 1C .而A 1D ∩BD =D ;∴平面A 1BD ∥平面B 1CD .2由BD ∥B 1D 1;得BD ∥平面EB 1D 1.取BB 1中点G ;∴AE ∥B 1G .从而得B 1E ∥AG ;同理GF ∥AD .∴AG ∥DF .∴B 1E ∥DF .∴DF ∥平面EB 1D 1.∴平面EB 1D 1∥平面FBD .8. 证明:取CD 的中点G ;连结,EG FG ;∵,E F 分别为,AD BC 的中点;∴EG 12//AC = 12//FG BD =;又,AC BD =∴12FG AC =;∴在EFG ∆中;222212EG FG AC EF +== ∴EG FG ⊥;∴BD AC ⊥;又90BDC ∠=;即BD CD ⊥;AC CD C ⋂=∴BD ⊥平面ACD9. 证明:1取PA 的中点Q ;连结,MQ NQ ;∵M 是PB 的中点;∴//MQ BC ;∵ CB ⊥平面PAB ;∴ MQ ⊥平面PAB ∴QN 是MN 在平面PAB 内的射影 ;取 AB 的中点D ;连结 PD ;∵,PA PB =∴PD AB ⊥;又3AN NB =;∴BN ND = ∴//QN PD ;∴QN AB ⊥;由三垂线定理得MN AB ⊥2∵90APB ∠=;,PA PB =∴122PD AB ==;∴1QN =;∵MQ ⊥平面PAB .∴MQ NQ ⊥;且112MQ BC ==;∴2MN = 10. 证明:∵E 、F 分别是AB 、AD 的中点;∴EF ∥BD又EF ⊄平面BDG ;BD ⊂平面BDG ∴EF ∥平面BDG ∵1D GEB ∴四边形1D GBE 为平行四边形;1D E ∥GB又1D E ⊄平面BDG ;GB ⊂平面BDG ∴1D E ∥平面BDG ;1EF D E E ⋂=;∴平面1D EF ∥平面BDG11. 证明:1设AC BD O ⋂=;∵E 、O 分别是1AA 、AC 的中点;∴1A C ∥EO又1AC ⊄平面BDE ;EO ⊂平面BDE ;∴1A C ∥平面BDE 2∵1AA ⊥平面ABCD ;BD ⊂平面ABCD ;1AA BD ⊥又BD AC ⊥;1AC AA A ⋂=;∴BD ⊥平面1A AC ;BD ⊂平面BDE ;∴平面BDE ⊥平面1A AC 12. 证明:在ADE ∆中;222AD AE DE =+;∴AE DE ⊥∵PA ⊥平面ABCD ;DE ⊂平面ABCD ;∴PA DE ⊥又PA AE A ⋂=;∴DE ⊥平面PAE 2DPE ∠为DP 与平面PAE 所成的角在Rt PAD ∆;42PD =;在Rt DCE ∆中;22DE =在Rt DEP ∆中;2PD DE =;∴030DPE ∠=13. 证明:1ABD ∆为等边三角形且G 为AD 的中点;∴BG AD ⊥ 又平面PAD ⊥平面ABCD ;∴BG ⊥平面PAD 2PAD 是等边三角形且G 为AD 的中点;∴AD PG ⊥ 且AD BG ⊥;PG BG G ⋂=;∴AD ⊥平面PBG ;PB ⊂平面PBG ;∴AD PB ⊥3由AD PB ⊥;AD ∥BC ;∴BC PB ⊥ 又BG AD ⊥;AD ∥BC ;∴BG BC ⊥ ∴PBG ∠为二面角A BC P --的平面角在Rt PBG ∆中;PG BG =;∴045PBG ∠=14. 证明:连结MO ;1A M ;∵DB ⊥1A A ;DB ⊥AC ;1A A AC A ⋂=;∴DB ⊥平面11A ACC ;而1AO ⊂平面11A ACC ∴DB ⊥1A O . 设正方体棱长为a ;则22132A O a =;2234MO a =.在Rt △11A C M 中;22194A M a =.∵22211A O MO A M +=;∴1AO OM ⊥. ∵OM ∩DB =O ;∴ 1A O ⊥平面MBD . 15. 证明:取AB 的中点F;连结CF ;DF .∵AC BC =;∴CF AB ⊥.∵AD BD =;∴DF AB ⊥. 又CF DF F =;∴AB ⊥平面CDF . ∵CD ⊂平面CDF ;∴CD AB ⊥. 又CD BE ⊥;BE AB B ⋂=; ∴CD ⊥平面ABE ;CD AH ⊥. ∵AH CD ⊥;AH BE ⊥;CD BE E ⋂=;∴ AH ⊥平面BCD . 16. 证明:连结ACBD AC ∵⊥∴ AC 为A 1C 在平面AC 上的射影17证明∵SB=SA=SC;∠ASB=∠ASC=60°∴AB=SA=AC 取BC 的中点O;连AO 、SO;则AO ⊥BC;SO ⊥BC;∴∠AOS 为二面角的平面角;设SA=SB=SC=a;又∠BSC=90°;∴BC=2a;SO=22a;AO 2=AC 2-OC 2=a 2-21a 2=21a 2;∴SA 2=AO 2+OS 2;∴∠AOS=90°;从而平面ABC ⊥平面BSC .。
高中数学立体几何证明题汇总
立体几何常考证明题1、已知四边形ABCD 是空间四边形,E, F,G, H 分别是边AB,BC,CD , DA 的中点(1)求证:EFGH是平行四边形(2)若BD=2 3 ,AC=2,EG=2。
求异面直线AC、BD所成的角和EG、BD所成的角。
AEHB DF GC2、如图,已知空间四边形ABCD 中,BC AC, AD BD ,E 是AB 的中点。
求证:(1)AB 平面CDE;(2)平面CDE 平面ABC 。
AEB CD3、如图,在正方体A BCD ABC D 中,E 是AA1 的中点,1 1 1 1求证:A1C // 平面BDE 。
A D1B1 CEADBC 14、已知ABC 中ACB 90 , SA 面ABC , AD SC ,求证:AD 面SBC .SDBAC5、已知正方体ABCD A1B1C1D1,O是底ABCD 对角线的交点. D1C1B1求证:(1) C1O∥面AB1D1 ;(2) A1C 面AB1D1 .A1DCOA B6、正方体ABCD A'B'C 'D'中,求证:(1)AC 平面B'D 'DB ;(2)BD ' 平面ACB '.27、正方体ABCD —A1B1C1D1 中.(1)求证:平面A1BD∥平面B1D1C;D 1C1 (2)若E、F 分别是AA1,CC1 的中点,求证:平面EB1D1∥平面FBD .A1B1FEGCDAB8、四面体ABCD 中,AC BD,E, F 分别为AD, BC 的中点,且BDC 90 ,求证:BD 平面ACD2EF AC ,29、如图P 是ABC 所在平面外一点,PA PB, CB 平面PAB ,M 是PC 的中点,N 是AB 上的点,AN 3NBP(1)求证:MN AB ;(2)当APB 90 ,AB 2BC 4 时,求MN 的长。
MCANB310、如图,在正方体ABCD A1B1C1D1 中,E 、F 、G 分别是AB 、AD 、C1D1 的中点. 求证:平面D1EF ∥平面BDG .11、如图,在正方体A BCD ABC D 中,E 是1 1 1 1 AA 的中点.1(1)求证:A1C // 平面BDE ;(2)求证:平面A AC 平面BDE .112、已知ABCD 是矩形,PA 平面ABCD ,AB 2 ,PA AD 4 ,E 为BC 的中点.(1)求证:DE 平面PAE ;(2)求直线DP 与平面PAE 所成的角.413 、如图,在四棱锥P ABCD 中,底面ABCD 是DAB 600 且边长为a的菱形,侧面PAD 是等边三角形,且平面PAD 垂直于底面ABCD .(1)若G 为AD 的中点,求证:BG 平面PAD ;(2)求证:AD PB ;(3)求二面角 A BC P 的大小.14、如图1,在正方体ABCD A1B1C1D1 中,M 为CC1 的中点,AC 交BD 于点O,求证:A1O 平面MBD .15、如图2,在三棱锥A-BCD中,BC=AC,AD=BD,作BE⊥CD,E为垂足,作AH⊥BE于H.求证:AH⊥平面BCD.516、证明:在正方体ABCD -A1B1C1D1 中,A 1C⊥平面BC1DD1 C1A 1B 1D CA B17、如图,过S 引三条长度相等但不共面的线段SA、SB、SC,且∠ASB= ∠ASC=60 °,∠BSC=90°,求证:平面ABC ⊥平面BSC.WORD文档6专业资料。
(完整版)高一数学常考立体几何证明的题目及答案

1、如图,已知空间四边形ABCD 中,,BCAC ADBD ,E 是AB 的中点。
求证:(1)AB平面CDE; (2)平面CDE 平面ABC 。
2、如图,在正方体1111ABCDA B C D 中,E 是1AA 的中点,求证:1//AC 平面BDE 。
3、已知ABC 中90ACB o,SA面ABC ,AD SC ,求证:AD面SBC .4、已知正方体1111ABCDA B C D ,O 是底ABCD 对角线的交点.求证:(1) C 1O ∥面11AB D ;(2)1AC 面11AB D .5、正方体''''ABCD A B C D 中,求证:(1)''AC B D DB 平面;(2)''BD ACB 平面.6、正方体ABCD —A 1B 1C 1D 1中.(1)求证:平面A 1BD ∥平面B 1D 1C ;(2)若E 、F 分别是AA 1,CC 1的中点,求证:平面EB 1D 1∥平面FBD .AED BCAED 1CB 1DCBASDCBAD 1ODBAC 1B 1A 1CA 1B 1C 1C D 1DGEF7、四面体ABCD 中,,,ACBD E F 分别为,AD BC 的中点,且22EFAC ,90BDCo,求证:BD平面ACD8、如图,在正方体1111ABCDA B C D 中,E 、F 、G 分别是AB 、AD 、11C D 的中点.求证:平面1D EF ∥平面BDG .9、如图,在正方体1111ABCDA B C D 中,E 是1AA 的中点.(1)求证:1//A C 平面BDE ;(2)求证:平面1A AC 平面BDE .10、已知ABCD 是矩形,PA 平面ABCD ,2AB,4PA AD ,E 为BC 的中点.(1)求证:DE 平面PAE ;(2)求直线DP 与平面PAE 所成的角.11、如图,在四棱锥P ABCD 中,底面ABCD 是60DAB且边长为a 的菱形,侧面PAD 是等边三角形,且平面PAD 垂直于底面ABCD .(1)若G 为AD 的中点,求证:BG 平面PAD ;(2)求证:AD PB .12、如图1,在正方体1111ABCDA B C D 中,M 为1CC 的中点,AC 交BD 于点O ,求证:1AO 平面MBD .13、如图2,在三棱锥A-BCD 中,BC =AC ,AD =BD ,作BE ⊥CD ,E为垂足,作AH ⊥BE 于H.求证:AH ⊥平面BCD .14.(12分)求证平行于三棱锥的两条相对棱的平面截三棱锥所得的截面是平行四边形.已知:如图,三棱锥S—ABC,SC∥截面EFGH,AB∥截面EFGH.求证:截面EFGH是平行四边形.15.(12分)已知正方体ABCD—A1B1C1D1的棱长为a,M、N分别为A1B和AC上的点,A1M=AN=23a,如图.(1)求证:MN∥面BB1C1C;(2)求MN的长.16.(12分)(2009·浙江高考)如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q分别为AE,AB的中点.(1)证明:PQ∥平面ACD;(2)求AD与平面ABE所成角的正弦值.17.(12分)如图,在四面体ABCD中,CB=CD,AD⊥BD,点E、F分别是AB、BD的中点.求证:(1)直线EF∥面ACD.(2)平面EFC ⊥平面BCD.1、如图,已知空间四边形ABCD 中,,BC AC AD BD ,E 是AB 的中点。
高中数学立体几何常考证明题汇总(不含答案)

立体几何常考证明题汇总考点:证平行(利用三角形中位线),异面直线所成的角1、已知四边形ABCD 是空间四边形,,,,E F G H 分别是边,,,AB BC CD DA 的中点 (1) 求证:EFGH 是平行四边形(2) 若BD=AC=2,EG=2.求异面直线AC 、BD 所成的角和EG 、BD 所成的角.考点:线面垂直,面面垂直的判定2、如图,已知空间四边形ABCD 中,,BC AC AD BD ==,E 是AB 的中点. 求证:(1)⊥AB 平面CDE;(2)平面CDE ⊥平面ABC .考点:线面平行的判定3、如图,在正方体1111ABCD A B C D -中,E 是1AA 的中点,求证: 1//AC 平面BDE .AED 1CB 1DCB AAHGFEDCBAEDBC考点:线面垂直的判定4、已知ABC ∆中90ACB ∠=,SA ⊥面ABC ,AD SC ⊥,求证:AD ⊥面SBC .考点:线面平行的判定(利用平行四边形),线面垂直的判定5、已知正方体1111ABCD A BC D -,O 是底ABCD 对角线的交点. 求证:(1) C 1O ∥面11AB D ;(2)1AC ⊥面11AB D .考点:线面垂直的判定6、正方体''''ABCD A B C D -中,求证:(1)''AC B D DB ⊥平面;(2)''BD ACB ⊥平面.SDCBAD 1ODB AC 1B 1A 1CNMPCBA考点:线面平行的判定(利用平行四边形)7、正方体ABCD —A 1B 1C 1D 1中.(1)求证:平面A 1BD ∥平面B 1D 1C ; (2)若E 、F 分别是AA 1,CC 1的中点,求证:平面EB 1D 1∥平面FBD .考点:线面垂直的判定,三角形中位线,构造直角三角形8、四面体ABCD 中,,,AC BD E F =分别为,AD BC 的中点,且22EF AC =, 90BDC ∠= ,求证:BD ⊥平面ACD考点:三垂线定理9、如图P 是ABC ∆所在平面外一点,,PA PB CB =⊥平面PAB ,M 是PC 的中点,N 是AB 上的点,3AN NB =A1考点:线面平行的判定(利用三角形中位线)10、如图,在正方体1111ABCD A B C D -中,E 、F 、G 分别是AB 、AD 、11C D 的中点.求证:平面1D EF ∥平面BDG .考点:线面平行的判定(利用三角形中位线),面面垂直的判定11、如图,在正方体1111ABCD A B C D -中,E 是1AA 的中点.(1)求证:1//AC 平面BDE ; (2)求证:平面1A AC ⊥平面BDE .考点:线面垂直的判定,构造直角三角形12、已知ABCD 是矩形,PA ⊥平面ABCD ,2AB =,4PA AD ==,E为BC 的中点.(1)求证:DE ⊥平面PAE ;(2)求直线DP 与平面PAE 所成的角.考点:线面垂直的判定,构造直角三角形,面面垂直的性质定理,二面角的求法(定义法)13、如图,在四棱锥P ABCD -中,底面ABCD 是060DAB ∠=且边长为a 的菱形,侧面PAD 是等边三角形,且平面PAD 垂直于底面ABCD .(1)若G 为AD 的中点,求证:BG ⊥平面PAD ; (2)求证:AD PB ⊥;(3)求二面角A BC P --的大小.考点:线面垂直的判定,运用勾股定理寻求线线垂直14、如图1,在正方体1111ABCD A B C D -中,M 为1CC 的中点,AC 交BD 于点O ,求证:1AO ⊥平面MBD .考点:线面垂直的判定15、如图2,在三棱锥A-BCD 中,BC =AC ,AD =BD ,作BE ⊥CD ,E为垂足,作AH ⊥BE 于H.求证:AH ⊥平面BCD .考点:线面垂直的判定,三垂线定理16、证明:在正方体ABCD -A 1B 1C 1D 1中,A 1C ⊥平面BC 1D考点:面面垂直的判定(证二面角是直二面角)17、如图,过S 引三条长度相等但不共面的线段SA 、SB 、SC ,且∠ASB=∠ASC=60°,∠BSC=90°,求证:平面ABC ⊥平面BSC .AC。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2、如图,在正方体1111ABCD A B C D 中,E 是1AA 的中点,求证: 1//AC 平面BDE 。
A E D 1 CB 1 DC B A8、如图,在正方体1111ABCD A B C D 中,E 、F 、G 分别是AB 、AD 、11C D 的中点.求证:平面1D EF ∥平面BDG .15.(12分)已知正方体ABCD —A 1B 1C 1D 1的棱长为a ,M 、N 分别为A 1B 和AC 上的点,A 1M =AN =23a ,如图.(1)求证:MN ∥面BB 1C 1C ;(2)求MN 的长.16.(12分)(2009·浙江高考)如图,DC ⊥平面ABC ,EB ∥DC ,AC =BC =EB =2DC =2,∠ACB =120°,P ,Q 分别为AE ,AB 的中点.(1)证明:PQ ∥平面ACD ;(2)求AD 与平面ABE 所成角的正弦值.生物练习1.由细胞膜的成分推知,构成细胞膜所必须的化学元素是()A.C、H、O、N B.C、H、O、N、PC.C、H、O、S、P D.C、H、O、Mg、Fe2.在制备细胞膜的实验中常用新鲜成熟的哺乳动物的红细胞作材料是因为()A.哺乳动物红细胞在水中容易胀破B.哺乳动物红细胞容易收集C.哺乳动物红细胞内没有核膜、线粒体膜等细胞器膜D.哺乳动物红细胞的细胞膜在分离时容易沉淀在下面3.任何系统都有边界,边界对系统的稳定至关重要。
细胞作为一个基本的生命系统,它的边界是()A.细胞壁B.细胞膜C.细胞核D.细胞膜表面的蛋白质4.科学上鉴别死细胞和活细胞,常用“染色排除法”,例如,用台盼蓝染色,死的动物细胞会被染成蓝色,而活的动物细胞不着色,从而判断细胞是否死亡。
所利用的是细胞膜的哪种功能()A.保护细胞内部结构的功能B.进行细胞间的信息交流C.控制物质进出功能D.免疫功能5.经研究发现,动物的唾液腺细胞内高尔基体含量较多。
其原因是()A.腺细胞的生命活动需要较多的能量B.腺细胞要合成大量的蛋白质C.高尔基体可加工和运输蛋白质D.高尔基体与细胞膜的主动运输有关6.某物质是动植物细胞中普遍存在的一种由104个氨基酸组成的化合物,在能量代谢过程中起重要作用,那么该物质生成的场所以及它发挥生理作用的场所分别是()A.高尔基体和叶绿体B.核糖体和细胞核C.核糖体和线粒体D.细胞核和线粒体7.信使RNA在细胞核内合成,它从细胞核中出来与细胞质中的核糖体结合的过程中,通过几层的生物膜()。
A.4层B.3层C.2层D.0层8、细胞核的主要功能是()()A.进行能量转换B.合成蛋白质C.储存和复制遗传物质D.储存能量物质9.下列对生物膜的叙述,正确的是()①各种生物膜在结构和化学组成上完全相同②生物膜把细胞质分隔成一个个小的区室,使细胞内同时进行多种化学反应,而互不干扰③各种生物膜在结构、功能上各自独立④细胞内广阔的膜面积为酶提供了附着位点,为多种化学反应的进行创造了有利条件A.①②B.①④C.②③D.②④10.下图是根据细胞器的相似或不同点进行分类的,下列选项中不是此图分类依据的是()液泡高尔基体叶绿体线粒体A.无膜结构B.单层膜还是双层膜C.有色素D.是否普遍存在于动植物细胞中11.下列有关生物膜的叙述,不正确的是()A.各种生物膜的化学组成大致相同,结构相似B.细胞内的许多重要的化学反应都在生物膜上进行C.与蛋白质的合成和分泌密切相关的生物膜结构有核糖体、内质网、高尔基体、细胞膜等D.一种细胞器的部分生物膜是通过形成具有膜的小泡转移到另一种细胞器的12.细胞核中易被碱性染料染成深色的结构是()A.核膜B.核仁C.染色质D.核质13、下列各项中,不具有膜结构的细胞器是( ) A.染色体与核糖体B.中心体与核糖体C.线粒体与高尔基体D.中心体与线粒体14、将一黑色公绵羊的体细胞核移入到一白色母绵羊去除细胞核的卵细胞中,再将此细胞植入一黑色母绵羊的子宫内发育,生出的小绵羊即是“克隆绵羊”。
那么此“克隆绵羊”为()A.黑色公绵羊B.黑色母绵羊C.白色公绵羊D.白色母绵羊15、胰岛细胞中和合成胰岛素有关的一组细胞器是()A.核糖体、内质网、高尔基体、中心体 B.核糖体、内质网、高尔基体、线粒体C.核糖体、内质网、高尔基体、叶绿体 D.内质网、中心体、高尔基体、线粒体16、荠菜根的分生区细胞的能量转换场所是 ( )A.叶绿体B.线粒体 C.核糖体 D.叶绿体和线粒体17 、下列关于细胞核的说法,不正确的是()A.细胞核是遗传物质存储和复制的场所B细胞核控制细胞的代谢和遗传C.细胞核位于细胞的正中央,所以是细胞的控制中心D.DNA主要存储于细胞核中18.下列现象中,不属于渗透作用的是()A.水分子通过半透膜 B.水通过细胞膜C.水通过原生质层 D.水通过细胞壁19.植物细胞中被称为“养料制造车间”的是( )A.线粒体 B.叶绿体 C.高尔基体 D.内质网20.当把紫色的洋葱鳞片叶的表皮置于浓度为0.3 g/mL的蔗糖溶液中后,原生质层和细胞壁之间将 ( )A.紧紧贴在一起 B.充满细胞液 C.充满蔗糖溶液 D.充满清水21.下列物质属于分泌蛋白的是()①肠肽酶②抗体③载体④线粒体氧化酶⑤性激素⑥胰岛素A.①②③④ B.②③④⑥ C.①②⑥ D.①⑥22以“出芽”方式相互转换的膜结构是()A.核膜与内质网膜 B.线粒体膜与细胞膜C.内质网膜与高尔基体膜 D.内质网膜与细胞膜23.在细胞的生物膜系统中,联系最广,功能较多的细胞器是()A.细胞膜 B.内质网 C.核膜 D.线粒体24.对染色体和染色质叙述错误的是()A.染色质是细胞内易被碱性染料染成深色的物质B.染色质和染色体组要是由DNA和蛋白质组成C.染色质和染色体是不同物质在同一时期的两种物质D.染色质和染色体只存在于真核细胞中25.人的红细胞和精子的寿命都很短,从细胞结构考虑,这一事实说明了()A.环境因素的影响 B.功能决定寿命的长短C.细胞核和细胞质相互依存 D.核遗传决定细胞寿命26.将哺乳动物的红细胞分别浸入a,b,c 三个装有不同浓度溶液的烧杯中,一段时间以后,a中的红细胞吸水涨破,b中的红细胞失水皱缩,c中的红细胞维持正常形态,则abc溶液浓度的大小关系是()A.a>b>c B.a<b<c C.a<c<b D.a>c>b27.细胞核内行使遗传功能的结构是()A.核膜 B.核孔 C.染色质 D.核仁28.细胞作为最基本的生命系统,其控制中心是()A.细胞壁 B.细胞膜 C.细胞核 D.细胞质29.下列关于原生质层的说法,正确的是 ( )A.原生质层是由细胞膜、液泡膜构成的B.原生质层是由细胞壁、细胞质和液泡膜组成的C.原生质层是选择透过性膜 D.动、植物细胞均有原生质层30.甜菜根细胞的液泡中有花青素,使块根为红色。
将块根切成小块放在蒸馏水中,水无明显的颜色变化,但用盐酸处理这些块根后再放人蒸馏水中,则能使水变红。
其原因是( )A.花青素不溶于水而溶于盐酸 B.盐酸破坏了细胞膜的选择透过性C.盐酸破坏了原生质层的选择透过性 D.细胞壁被盐酸破坏31.下列有关叙述错误的是A.一切生物的生命活动都是在细胞内或在细胞的参与下完成的B.SARS病毒没有细胞结构,也能独立完成生命活动C.除病毒外,一切生物体都是由细胞构成的,细胞是构成有机体的基本单位D.单细胞生物依靠单个细胞就能完成各种生命活动,多细胞生物依赖各种分化的细胞密切合作,共同完成生命活动32. 下列有机物和它们水解产物的配对,哪项是错误的A.淀粉→葡萄糖B.蛋白质→氨基酸C.脂肪→甘油、脂肪酸D.DNA→磷酸、核糖、含氮碱基33.蛋白质稀释液中加入双缩脲试剂后,颜色是()A.浅蓝色B.砖红色C.绿色D.紫色34.仙人掌生活在缺水的沙漠中,在仙人掌的细胞中含量最多的化合物是()A.水B.蛋白质C.脂质D.糖类35.下列健康人的4种液体样本中,能与双缩脲试剂发生紫色反应的是()①尿液②胃液③汗液④唾液A.①③B.①④C.②③D.②④36.下列化合物中,主要以离子形式存在于细胞中的是()A.水B.糖类C.核酸D.无机盐37.下列物质中,动物细胞内不具有的是( )A.葡萄糖B.糖元C.核糖D.纤维素38.胰岛素和性激素都是生物激素,它们的化学本质分别是()A.蛋白质和脂肪B.脂质和蛋白质C.蛋白质和固醇D.磷脂和蛋白质39.种氨基酸的平均相对分子质量为128,现有一蛋白质分子由两条多肽链组成,具有肽键98个,此蛋白质的相对分子质量是()A.12800 B.12544 C.11036 D.1228840、植物体内和动物体内都有的单糖是( )A.葡萄糖B.乳糖C.蔗糖D.麦芽糖41.白细胞能吞噬绿脓杆菌,与这一现象有关的是A.主动扩散B.协助扩散C.具有渗透性D.细胞膜的流动性42、信使RNA在细胞核中合成,它从细胞核中出来与核糖体结合的过程中,直接通过了几层选择透过性膜?A、0层B、1层C、2层D、3层43.细胞膜的结构特点是具有一定的流动性,能够反映该特点的实例有①白细胞吞噬病菌②蛋白质不能吸收③变形虫的变形运动④水分子能自由进出细胞⑤细胞融合A.①②③B.①③⑤C.②④⑤D.③④⑤44.在下列结构中,其成分不含磷脂分子的一组细胞器是①线粒体②核糖体③叶绿体④细胞核⑤内质网⑥中心体⑦高尔基体A.①③B.④⑤C.⑤⑦D.②⑥45.下列细胞结构中含有遗传物质的是A.液泡和线粒体B.线粒体和中心体C.中心体和叶绿体D.叶绿体和线粒体46.细菌细胞与玉米细胞的结构相比,哪一项只存在玉米细胞内A.蛋白质B.DNAC.核膜D.细胞壁47.蚕豆根尖的分生区细胞中与能量转换有关的是①叶绿体②线粒体③中心体④细胞质基质A.①②B.②③C.②④D.①②④48.某毒素侵入人体后,妨碍了细胞呼吸而影响人体的正常生理活动,这种毒素可能作用于A.核糖体B.细胞核C.线粒体D.细胞膜49.下列试管中各注入10mL过氧化氢溶液,实验中产生气泡最多的是()50.关于蛋白酶的叙述,不正确的是()A.蛋白酶是蛋白质B.蛋白酶可以作为药品治疗某些疾病C.蛋白酶可以水解所有的肽键D.利用酶工程可以提高蛋白酶的稳定性51.酶在经0°C和100°C温度处理后,都没有活性,因为()A.经过0°C处理的酶的活性不能恢复B.经过100°C处理的酶的活性不能恢复C.经过0°C处理的酶其空间结构被破坏D.经过100°C处理的酶被氧化分解。
