化教例题习题上学生版
二年级上教案-第六单元第九课9的乘法口诀练习(一)-人教版

二年级上教案-第六单元第九课9的乘法口诀练习(一)-人教版教学内容:本节课为二年级上册数学课,教学内容为第六单元第九课“9的乘法口诀练习(一)”。
学生将在教师的指导下,通过练习和巩固,熟练掌握9的乘法口诀。
教学目标:1. 让学生熟练掌握9的乘法口诀。
2. 培养学生运用乘法口诀解决问题的能力。
3. 培养学生合作交流、积极参与的学习态度。
教学难点:1. 9的乘法口诀的记忆和应用。
2. 学生在计算过程中容易出现的错误。
教具学具准备:1. 乘法口诀表。
2. 练习题。
3. 白板、白板笔。
4. 学生自备乘法口诀表。
教学过程:1. 导入新课:教师简要回顾上一节课的内容,引导学生进入本节课的学习。
2. 讲解新课:教师讲解9的乘法口诀,强调记忆方法和注意事项。
同时,通过典型例题,展示乘法口诀的应用。
3. 练习环节:学生分小组进行练习,教师巡回指导,解答学生疑问。
练习内容主要包括9的乘法口诀的记忆和应用。
4. 小组竞赛:组织学生进行小组竞赛,提高学生的积极性和参与度。
竞赛内容为9的乘法口诀的抢答。
5. 课堂小结:教师对本节课的学习内容进行总结,强调重点和难点。
6. 课后作业布置:教师布置课后作业,要求学生加强对9的乘法口诀的记忆和应用。
板书设计:1. 二年级上教案-第六单元第九课9的乘法口诀练习(一)-人教版2. 正文:教学内容、教学目标、教学难点、教具学具准备、教学过程、板书设计、作业设计、课后反思作业设计:1. 课后作业:完成练习题,加强9的乘法口诀的记忆和应用。
2. 家庭作业:家长协助孩子,用9的乘法口诀解决实际问题。
课后反思:1. 教师应关注学生在学习过程中遇到的问题,及时调整教学方法,提高教学效果。
2. 注重培养学生的合作意识和团队精神,提高学生的综合素质。
3. 加强对学生的个别辅导,关注学困生,提高他们的学习兴趣和成绩。
总之,本节课的教学内容、教学目标、教学难点、教具学具准备、教学过程、板书设计、作业设计和课后反思均围绕9的乘法口诀练习展开,旨在提高学生熟练掌握9的乘法口诀,培养学生的合作意识和团队精神,提高学生的综合素质。
相交线与平行线典型例题分析和提高类型题(学生版)
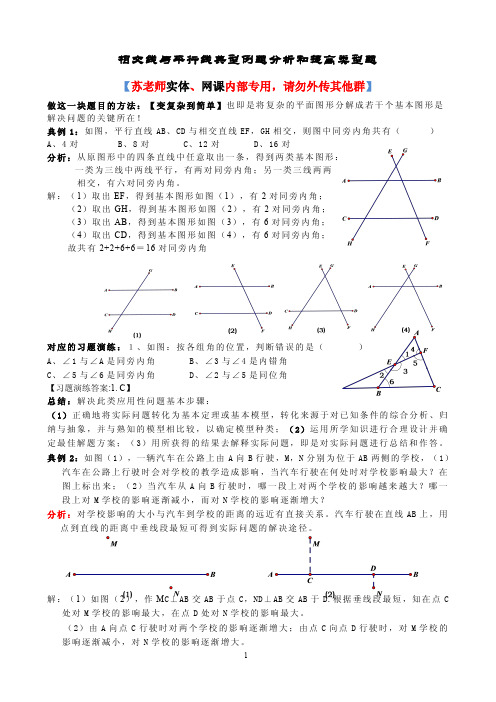
相交线与平行线典型例题分析和提高类型题【苏老师实体、网课内部专用,请勿外传其他群】做这一块题目的方法:【变复杂到简单】也即是将复杂的平面图形分解成若干个基本图形是解决问题的关键所在!典例1:如图,平行直线AB、CD与相交直线EF,GH相交,则图中同旁内角共有()A、4对B、8对C、12对D、16对分析:从原图形中的四条直线中任意取出一条,得到两类基本图形:一类为三线中两线平行,有两对同旁内角;另一类三线两两相交,有六对同旁内角。
解:(1)取出EF,得到基本图形如图(1),有2对同旁内角;(2)取出GH,得到基本图形如图(2),有2对同旁内角;(3)取出AB,得到基本图形如图(3),有6对同旁内角;(4)取出CD,得到基本图形如图(4),有6对同旁内角;故共有2+2+6+6=16对同旁内角对应的习题演练:1、如图:按各组角的位置,判断错误的是()A、∠1与∠A是同旁内角B、∠3与∠4是内错角C、∠5与∠6是同旁内角D、∠2与∠5是同位角【习题演练答案:1.C】总结:解决此类应用性问题基本步骤:(1)正确地将实际问题转化为基本定理或基本模型,转化来源于对已知条件的综合分析、归纳与抽象,并与熟知的模型相比较,以确定模型种类;(2)运用所学知识进行合理设计并确定最佳解题方案;(3)用所获得的结果去解释实际问题,即是对实际问题进行总结和作答。
典例2:如图(1),一辆汽车在公路上由A向B行驶,M,N分别为位于AB两侧的学校,(1)汽车在公路上行驶时会对学校的教学造成影响,当汽车行驶在何处时对学校影响最大?在图上标出来;(2)当汽车从A向B行驶时,哪一段上对两个学校的影响越来越大?哪一段上对M学校的影响逐渐减小,而对N学校的影响逐渐增大?分析:对学校影响的大小与汽车到学校的距离的远近有直接关系。
汽车行驶在直线AB上,用点到直线的距离中垂线段最短可得到实际问题的解决途径。
解:(1)如图(2),作M C⊥AB交AB于点C,ND⊥AB交AB于D.根据垂线段最短,知在点C 处对M学校的影响最大,在点D处对N学校的影响最大。
六年级上册数学教案-第3单元:第5课时 列方程解答分数的简单实际问题练习-苏教版

六年级上册数学教案第3单元:第5课时列方程解答分数的简单实际问题练习苏教版教案:六年级上册数学教案第3单元:第5课时列方程解答分数的简单实际问题练习苏教版一、教学内容本节课的教学内容为苏教版六年级上册第3单元分数的简单实际问题练习。
本节课主要让学生通过解决实际问题,掌握列方程解答分数问题的方法,提高学生的数学应用能力。
二、教学目标1. 让学生掌握列方程解答分数问题的基本方法。
2. 培养学生解决实际问题的能力,提高学生的数学思维。
3. 培养学生合作学习、积极思考的良好学习习惯。
三、教学难点与重点重点:掌握列方程解答分数问题的方法。
难点:如何将实际问题转化为方程,求解分数问题。
四、教具与学具准备教具:黑板、粉笔、多媒体课件学具:练习本、笔五、教学过程1. 实践情景引入教师出示情景:小明有2/3的苹果,小红有3/4的苹果,两人一共有多少苹果?学生思考,引导学生在黑板上画出苹果的示意图,并提出问题:如何求两人一共有多少苹果?2. 例题讲解教师出示例题:小明有2/3的苹果,小红有3/4的苹果,两人一共有多少苹果?教师引导学生将问题转化为方程,并讲解方程的解法。
步骤1:设两人一共有x个苹果。
步骤2:根据题意,列出方程2/3x + 3/4x = x。
步骤3:解方程,求出x的值。
3. 随堂练习教师出示随堂练习题:小华有1/5的糖果,小明有2/7的糖果,两人一共有多少糖果?学生独立完成练习题,教师巡回指导。
4. 学生自主练习教师出示自主练习题:请你选取一个分数实际问题,列方程解答。
学生自主练习,教师巡回指导。
5. 板书设计板书题目:小明有2/3的苹果,小红有3/4的苹果,两人一共有多少苹果?板书解题步骤:步骤1:设两人一共有x个苹果。
步骤2:列出方程2/3x + 3/4x = x。
步骤3:解方程,求出x的值。
六、作业设计(1)小华有1/5的糖果,小明有2/7的糖果,两人一共有多少糖果?答案:14/35(2)小明的成绩是全班的2/5,小红的成绩是全班的3/8,小明比小红多几分之几?答案:1/242. 课后反思及拓展延伸本节课学生掌握了列方程解答分数实际问题的方法,但在解方程的过程中,部分学生对分数的运算仍存在困难。
学生版 高中数学必修2直线与圆的位置关系知识点总结经典例题与习题

高中数学必修2 直线与圆的位置关系【一】、圆的定义及其方程.(1)圆的定义:平面内与定点距离等于定长的点的集合(轨迹)叫做圆,定点叫做圆心,定长就是半径;(圆心是定位条件,半径是定型条件) (2)圆的标准方程: ;圆心),(b a圆的一般方程:)04(02222>-+=++++F E D F Ey Dx y x ;圆心 ,半径为 ;【二】、点与圆的位置关系(仅以标准方程为例,其他形式,则可化为标准式后按同样方法处理)设),(00y x P 与圆222)()(r b y a x =-+-;若P 到圆心之距为d ; ①P 在在圆C 外 ; ②P 在在圆C 内 ; ③P 在在圆C 上 ; 【三】、直线与圆的位置关系:设直线0:=++C By Ax l 和圆222)()(:r b y a x C =-+-,圆心C 到直线l 之距为d ,由直线l 和圆C 联立方程组消去x (或y )后,所得一元二次方程的判别式为∆,则它们的位置关系如下:相离 ;相切 ;相交 ; 注意:这里用d 与r 的关系来判定,称为几何法,只有对圆才实用,也是最简便的方法;利用∆判定称为代数法,对讨论直线和二次曲线的位置关系都适应。
【四】、两圆的位置关系:(1)代数法:解两个圆的方程所组成的二元二次方程组;若方程组有两组不同的实数解,则两圆相交;若方程组有两组相同的实数解,则两圆相切;若无实数解,两圆相离。
(2)几何法:设圆1O 的半径为1r ,圆2O 的半径为2r①两圆外离 ; ②两圆外切 ; ③两圆相交 ; ④两圆内切 ⑤两圆内含 ;(五)已知圆C :(x-a)2+(y-b)2=r 2(r>0),直线L :Ax+By+C=01.位置关系的判定:判定方法1:联立方程组得到关于x(或y)的方程(1)△>0相交;(2)△=0相切;(3)△<0相离。
判定方法2:若圆心(a,b)到直线L的距离为d(1)d<r相交;(2)d=r相切;(3)d>r相离。
梯形“小题狂练”-2024-2025学年五年级数学上册典型例题系列(学生版)苏教版

第二单元专练篇·08:梯形“小题狂练”一、填空题。
1.一个梯形的上底是18分米,是高的3倍,又比下底短8分米,梯形的面积是()平方分米。
2.如图一个梯形,高和上底都是7厘米,如果把上底再延长7厘米就能成为一个平行四边形,原来梯形的面积是()平方厘米,如果上底缩短为0厘米,那么新图形的面积()平方厘米。
3.一个梯形的面积是20平方米,如果它的上底乘2、下底乘2、高也乘2,现在它的面积是()平方米。
4.一个梯形的上底是3米,下底是5米,面积是28平方米,它的高是()米。
5.梯形的上底增加4cm,下底减少4cm,高不变,面积()。
(填“增加”“减少”或“不变”。
)6.一个平行四边形的底是10厘米,高是8厘米,如果将它剪成两个完全一样的梯形。
其中一个梯形的高是8厘米,那么上下底之和是()厘米,面积是()平方厘米。
7.《九章算术》卷一记载这样一道数学题:今有邪田一头广三十步,一头广四十二步,正从六十四步,问为田几何?意思是:今有直角梯形田,上底长30步,下底长42步,底边上的高长64步。
这块田的面积是()平方步。
8.一个梯形,上底与下底的和是12dm,高是3dm,面积是()dm2。
9.一个直角梯形的下底是9厘米,如果把上底增加4厘米,它就变成了一个正方形。
这个梯形的面积是()。
10.若一条线段把长方形(如图)分成了一个最大的等腰直角三角形和一个梯形。
那么,梯形的面积是()2cm,三角形的面积是()2cm。
11.一个直角梯形的上底是6cm,如果把下底减少4cm,它就变成一个正方形,这个直角梯形的面积是()cm2;从梯形中截取一个最大的三角形,这个三角形的面积是()cm2。
12.如图,两条平行线之间有三个图形,其中图②面积()图③面积(填“大于”“小于”或“等于”)。
如果想让图①与图③面积相等,在不改变其它条件的情况下,图①的底需要增加()厘米。
13.在扶贫工作队的帮扶下,李大爷用75m长的篱笆围了一块一面靠墙的梯形苗圃(如图所示),这块苗圃占地()m2。
《化简含有字母的式子(第4课时)》(教案)-五年级上册数学苏教版

教案:《化简含有字母的式子(第4课时)》一、教学目标1. 让学生理解并掌握化简含有字母的式子的方法。
2. 培养学生运用数学语言表达思维过程的能力。
3. 培养学生合作交流、解决问题的能力。
二、教学重点与难点1. 教学重点:化简含有字母的式子的方法。
2. 教学难点:如何引导学生运用数学语言表达思维过程。
三、教学过程1. 导入新课利用复习导入法,引导学生回顾已学的有关含有字母的式子的知识,为新课的学习做好铺垫。
2. 探究新知(1)教师出示例题,引导学生观察并发现式子中的规律。
例题:化简下列式子。
a. 2x xb. 3a - ac. 4b 2b - b(2)学生独立思考,尝试化简上述式子。
(3)学生交流自己的化简过程,教师点评并总结化简方法。
(4)教师引导学生总结含有字母的式子的化简规律。
3. 巩固练习(1)教师出示练习题,学生独立完成。
练习题:化简下列式子。
a. 5y - 2yb. 4c c - 2cc. 3x 2x x - x(2)学生交流自己的答案,教师点评并总结。
4. 小结教师引导学生回顾本节课所学内容,总结化简含有字母的式子的方法。
5. 作业布置(1)课后自主完成练习题。
(2)预习下一节课的内容。
四、教学反思1. 教师要关注学生在课堂上的表现,及时调整教学策略,提高教学效果。
2. 注重培养学生的数学语言表达能力,提高学生的合作交流能力。
3. 加强对学生的个别辅导,关注学困生,提高他们的学习兴趣和自信心。
五、板书设计1. 化简含有字母的式子的方法。
2. 例题及解答过程。
3. 练习题及答案。
六、课后评价1. 学生对化简含有字母的式子的方法的掌握程度。
2. 学生在课堂上的参与度,合作交流能力。
3. 学生作业完成情况。
重点关注的细节:化简含有字母的式子的方法及其教学过程在数学教学中,化简含有字母的式子是一个重要的内容。
对于五年级的学生来说,他们已经接触过一些基本的代数知识,如字母表示数、等式的基本性质等。
生物化学教程(上)复习题(王镜岩--朱圣庚-徐长发-版-高等教育出版社)

二十种基本氨基酸简写符号丙氨酸Ala 精氨酸Arg 天冬氨酸Asp 半胱氨酸Cys 谷氨酰胺Gln 谷氨酸Glu 组氨酸His 异亮氨酸 Ile 甘氨酸 Gly 天冬酰胺 Asn 亮氨酸 Leu 赖氨酸 Lys 甲硫氨酸 Met 苯丙氨酸Phe 脯氨酸Pro 丝氨酸Ser 苏氨酸Thr 色氨酸Trp 酪氨酸Tyr 缬氨酸Val1.等电点:在某一特定pH值溶液时,氨基酸主要以两性离子形式存在,净电荷为零,在电场中不向电场的正极或负极移动,这时的溶液pH值称为该氨基酸的等电点。
2.杂多糖:水解时产生一种以上的单糖或和单糖衍生物,例如果胶物质、半纤维素、肽聚糖和糖胺聚糖等3.复合糖:糖类的还原端和蛋白质或脂质结合的产物。
4.蛋白多糖:又称黏多糖,为基质的主要成分,是多糖分子与蛋白质结合而成的复合。
5.糖蛋白:糖蛋白是一类复合糖或一类缀合蛋白质,糖链作为缀合蛋白质的辅基,一般少于是15个单糖单位,也称寡糖链或聚糖链。
6.糖胺聚糖:曾称粘多糖,氨基多糖和酸性多糖。
糖胺聚糖是一类由重复的二糖单位构成的杂多糖,其通式为:【己糖醛酸-己糖胺】n,n随种类而异,一般在20到60之间。
7.复合脂:除含脂肪酸和醇外,尚有所谓非脂分子成分(磷酸、糖和含氮碱等),如甘油磷脂、鞘磷脂、甘油糖脂和鞘糖脂,其中鞘磷脂和鞘糖脂又合称为鞘脂。
8.必需脂肪酸:体内不能合成或合成速度不能满足机体需要,必须通过食物供给。
9.脂蛋白:是由脂质和蛋白质以非共价键结合的复合体。
10.活化能:指在一定温度下,1mol底物全部进入活化态所需要的自由能11.过渡态:在酶催化反应中,酶与底物或底物类似物间瞬时生成的复合物,是具有高自由能的不稳定状态。
12.全酶:(1)由蛋白质组分(即酶蛋白)和非蛋白质组分(一般为辅酶或激活物)组成的一种结合酶。
(2)含有表达全部酶活性和调节活性所需的所有亚基的一种全寡聚酶。
13.反馈抑制:是指最终产物抑制作用,即在合成过程中有生物合成途径的终点产物对该途径的酶的活性调节,所引起的抑制作用。
《逻辑的力量 》教材例题习题解答+强化巩固-高二语文(统编版选择性必修上册)

习题解答 二 逻辑推理相关问题
习题解答
1.阅读下面的故事,分析运用了什么样的推理形式,其推理过程是怎样的。 唐代有一个农夫耕田时挖到一瓮马蹄形黄金,乡里立刻派人送到县衙去,县官
担心公库防护不严,就放到自己家里。隔夜打开检验,发现都是土块。瓮金出土时, 乡里人都曾去见证。县官无法辩白,最终承认将黄金掉包的罪名。就在快要定案的 时候,事情传到了一个叫袁滋的官员耳里。袁滋说:“我怀疑这案子里有冤情。”州 府长官就让他重新调查。他点验出瓮中马蹄金共二百五十多块。请金铺铸造同样形 状和大小的马蹄金,才造出一半数目,总重就达三百斤了。又了解到当初是两个农 夫用竹扁担抬着瓮到县府的。算一下,如果这二百五十多块是真金,就不是两个人 抬得动的。这说明在运送的过程中,金子就被换成土块了。至此案情大白,县官洗 清冤屈。
答 案 :两难推理。如果我去林妹妹处则足以致疾;如果我不去林妹妹处也足以 致疾;我或者去林妹妹处,或者不去林妹妹处总之都足以致疾。
习题解答
5.以下选段均出自教材所学课文,分析他们各自运用了什么样的推理形式? (2)大概是物以希为贵罢。北京的白菜运往浙江,便用红头绳系住菜根,倒挂在水 果店头,尊为“胶菜”;福建野生着的芦荟,一到北京就请进温室,且美其名曰“龙 舌兰”。(鲁迅《藤里野先生》)
分析:鲁迅的《祝福》中,鲁四老爷的这句话存在两个错误捆绑:一是把祥林 嫂的死和祝福捆绑,二是把死和“谬种”捆绑。祥林嫂的死与年关的祝福活 动,只是时间上接近的两件事,并无因果关系--不是祥林嫂自主选择或命中 注定。明明没有因果关系的事件,因为发生的时间相近等表面联系,就把它 们看成是因果事件,叫作强加因果,违反了充足理由律。
习题解答
运用逻辑规律分析下列语段中的结论,各自违反了什么样的逻辑规律? 3.“服务员同志,请当心,你的手指浸到我的汤里去了。” “没有关系,汤不烫,我不痛。”
鲁教版九年级化学例题解析:性质决定用途

性质决定用途物质的性质决定物质的用途,物质的用途体现物质的性质。
课后习题 1. 为了飞艇的安全,艇内充入的气体最好是()。
A. 空气B. 氧气C. 氦气D. 二氧化碳解析要使飞艇飞起,充入气体的密度一定要比空气小,而且该气体的性质要稳定。
氦气是属于稀有气体的一种,化学性质稳定,不易发生爆炸,且密度比空气小很多。
故答案为C。
2. 夏天从冰箱里拿出来的饮料,放置片刻后,饮料瓶外壁会潮湿,说明空气中含有()。
A. 氮气B. 氧气C. 水蒸气D. 二氧化碳解析因为从冰箱中拿出来的饮料温度比较低,空气中的水蒸气遇冷液化为液态水,使饮料瓶外壁变得潮湿。
故答案为C。
请根据空气中有关成分的特性和用途,在下表中填空。
保护气、制化肥解析本题考查的是空气中各成分的性质与用途,氧气能支持燃烧和供给呼吸;氮气常温下化学性质稳定,可作保护气,高温、高能量条件下能与某些物质发生化学反应,可用于制化肥;稀有气体通电会发出不同颜色的光(氩气——蓝紫色光;氦气——粉红色光;氖气——红光;氙气——特强白光),可用于霓虹灯和激光技术;氦气密度小,且化学性质很稳定,可用于填充探空气球。
答案氧气常温下化学性质稳定,高温、高能量条件下可与某些物质发生化学反应氩气用于霓虹灯、激光技术氦气点拨上述三道题从不同角度考查了空气中各成分的性质和用途,准确掌握各成分的性质,并能根据这些性质了解其相应的用途是解答此类试题的关键。
变式训练题 1.以下关于氮气用途的说法中不正确的是()。
A. 利用氮气化学性质稳定的特点,可用于充氮灯泡B. 氮气是一种重要的化工原料,可用来制取多种化肥和炸药C. 空气中约78%是氮气,氮气能供给呼吸D. 可利用液氮给手术刀降温,作制冷剂2. 相信你能“举一反三”。
“举一”:空气可用于制氮肥的原料,说明空气中含有。
“反三”:请你举出实例,说明空气中含有下列成分。
(1)空气中含有氧气:。
(2)空气中含有水蒸气:。
(1)空气中含有二氧化碳:。
鲁教版九年级化学例题解析:化学式的意义

化学式的意义课后习题 1.“H2SO4”表示的意义是:(1)表示物质。
(2)表示该物质的1个。
(3)表示该物质由、和元素结合而形成的。
(4)表示该物质的每个分子中含有个、个、个。
(5)该物质的相对分子质量是。
(6)该物质中、、元素的质量比为。
(7)该物质中几种元素的质量分数分别为、、。
解析本题考查了化学式的意义及相关计算。
化学式不仅可以表示一种纯净物,也可以表示该纯净物的元素组成;对于由分子构成的纯净物,化学式还可以表示该纯净物的一个分子。
根据物质的化学式可以计算相对分子质量(化合物中各原子的相对原子质量总和)、化合物中各元素的质量比(各原子相对原子质量与原子个数乘积的比值)、某元素的质量分数(某元素相对原子质量和与该物质相对分子质量的比值)。
本题中,“H2SO4”可以表示硫酸这种物质,还可以表示1个硫酸分子。
从该化学式可知,硫酸由氢、硫、氧三种元素组成;每个硫酸分子中含有2个氢原子、1个硫原子和4个氧原子。
硫酸的相对分子质量等于1×2+32+16×4=98;氢、硫、氧三种元素的质量比为1×2∶32∶16×4=1∶16∶32;氢元素的质量分数为1×2/98×100%=2.04%、硫元素的质量分数为32/98×100%=32.65%、氧元素的质量分数为16×4/98×100%=65.31%。
答案(1)硫酸(2)分子(3)氢硫氧(4) 2 氢原子 1 硫原子 4 氧原子(5) 98 (6)氢硫氧 1∶16∶32(7) 2.04% 32.65% 65.31%点评对化学式意义的理解,重点是对化学式中的符号、数字意义的理解。
注意:当化学式前面出现数字时,只具有微观含义,表示几个分子,如“3H2SO4”只能表示3个硫酸分子。
变式训练题 1.下列有关说法正确的是()。
A.2O表示两个氧分子 B.钠离子的符号为Na+C.一氧化碳的化学式为Co D.H2O中含有氧分子2. 以下化学符号表示意义最多的是()。
第二单元多边形的面积平行四边形篇-2024-2025学年五年级数学上册典型例题系列(学生版)苏教版

篇首寄语我们每位老师都希望把最好的教学资料留给学生使用,所以在平时教学时,能够快速找到高质量、高效率、高标准的资料显得十分重要。
编者以前常常游走于各大学习网站寻找自己所需的资料,可却总在花费大量时间与精力后才能找到自己心仪的那份,这样费时费力不讨好,实在有些苦恼。
正因如此,每次在寻找资料时,编者就会想,如果是自己来创作一份资料那又该如何呢?那么这份资料应该首先满足自身教学需要,并达到我的高标准要求,然后才能为他人提供参考。
于是,本着这样的想法,在结合自身教学需求和学生实际情况后,最终酝酿出了一个既适宜课堂教学,又适应课后作业,还适合阶段复习的大综合系列。
《2024-2025学年四年级数学上册典型例题系列》,它基于教材知识和常年真题进行总结与编辑,该系列主要分为典型例题篇、专项练习篇、单元复习篇、思维素养篇、分层试卷篇等五个部分。
1.典型例题篇,按照单元顺序进行编辑,主要分为计算和应用两大部分,其优点在于考题典型,考点丰富,变式多样。
2.专项练习篇,从高频考题和期末真题中选取专项练习,其优点在于选题经典,题型多样,题量适中。
3.单元复习篇,汇集系列精华,高效助力单元复习,其优点在于综合全面,精练高效,实用性强。
4.思维素养篇,新的学年,新的篇章,从课本到奥数,从方法到思维,从基础技能到核心素养,其优点在于由浅入深,思维核心,方法易懂。
5.分层试卷篇,根据试题难度和水平,主要分为A卷·基础巩固卷、B卷·素养提高卷、C卷·思维拓展卷,其优点在于考点广泛,分层明显,适应性广。
时光荏苒,转眼之间,《典型例题系列》已经历三个学年三个版本,在过去,它扬长补短,去粗取精,日臻完善;在未来,它承前启后,不断发展,未有竟时。
黄金无足色,白璧有微瑕,如果您在使用资料的过程中有任何宝贵意见,请留言于我,欢迎您的使用,感谢您的支持!101数学创作社2024年9月13日2024-2025学年五年级数学上册典型例题系列第二单元多边形的面积·平行四边形篇【十一大考点】【第一篇】专题解读篇专题名称第二单元多边形的面积·平行四边形篇专题内容本专题以平行四边形的面积及实际应用为主。
化学补充习题答案上教版

化学补充习题答案上教版化学是一门研究物质的组成、结构、性质以及变化规律的基础自然科学。
在高中化学教学中,补充习题是帮助学生巩固和深化课堂所学知识的重要手段。
以下是一些化学补充习题的答案,供参考:习题一:化学计量学基础1. 计算1摩尔氢氧化钠(NaOH)的质量。
- 解答:根据摩尔质量的定义,1摩尔氢氧化钠的质量等于其摩尔质量,即23(Na)+ 16(O)+ 1(H)= 40g。
2. 确定1升0.5摩尔/升的硫酸(H2SO4)溶液中硫酸根离子(SO4^2-)的摩尔数。
- 解答:硫酸根离子的摩尔数等于溶液的摩尔浓度乘以体积,即0.5摩尔/升× 1升 = 0.5摩尔。
习题二:化学反应类型1. 判断下列反应类型:- a) 2H2 + O2 → 2H2O- b) NaOH + HCl → NaCl + H2O- 解答:a) 合成反应;b) 中和反应。
2. 描述氧化还原反应的特征。
- 解答:氧化还原反应的特征是反应过程中至少有一个元素的氧化态发生变化。
习题三:化学平衡1. 描述勒夏特列原理。
- 解答:勒夏特列原理指出,如果一个处于平衡状态的系统受到外部条件(如压力、温度或浓度)的改变,系统将调整自身以抵消这种改变,从而重新达到平衡。
2. 解释如何通过改变条件来影响化学平衡。
- 解答:增加反应物浓度或减少生成物浓度可以推动平衡向生成物方向移动;增加压力或温度(对于吸热反应)也可以促使平衡向生成物方向移动。
习题四:有机化学基础1. 写出甲烷(CH4)的燃烧反应方程式。
- 解答:CH4 + 2O2 → CO2 + 2H2O。
2. 判断下列化合物是否为同分异构体:- a) 乙醇(C2H5OH)和二甲醚(CH3OCH3)- 解答:是的,它们具有相同的分子式(C2H6O),但结构不同。
习题五:化学实验操作1. 描述如何使用滴定法测定溶液的酸碱度。
- 解答:滴定法是通过将已知浓度的标准溶液逐滴加入待测溶液中,直到反应完成,通过计算消耗的标准溶液体积来确定待测溶液的浓度。
初一【平方差公式和完全平方公式例题】习题版

个性化备课笔记教学主题:平方差和完全平方公式例题(学生版)教学重难点:重点·1.掌握平方差公式和完全平方公式;2.能够基本识别应用此类公式;3.能够正向运用两个公式并且能够正确计算难点·1.应用平方差公式和完全平方公式解决实际问题;2.能够逆向灵活使用平方差和完全平方公式授 课 内 容例题精讲:专题一:平方差公式例1:计算下列各整式乘法①位置变化(73)(37)x y y x +-②符号变化(27)(27)m n m n ---③数字变化98102⨯④系数变化(4)(2)24n n m m +-⑤项数变化(32)(32)x y z x y z ++-+ ⑥公式变化2(2)(2)(4)m m m +-+◆变式拓展训练◆【变式1】2244()()()()y x x y x y x y ---+++【变式2】22(2)(4)33b b a a ---【变式3】22222210099989721-+-++-…专题二:平方差公式的应用例2:计算22004200420052003-⨯的值为多少?◆变式拓展训练◆【变式1】22()()x y z x y z -+-+- 【变式2】2301(3021)(3021)⨯+⨯+【变式3】(25)(25)x y z x y z +-+-++ 【变式4】已知a 、b 为自然数,且40a b +=,(1)求22a b +的最大值;(2)求ab 的最大值。
专题三:完全平方公式例3:计算下列各整式乘法①位置变化:22()()x y y x --+②符号变化:2(32)a b --③数字变化:2197④方向变化:2(32)a -+⑤项数变化:2(1)x y +-⑥公式变化22(23)(46)(23)(23)x y x y x y x y -+-+++◆变式拓展训练◆ 【变式1】224,2a b a ab b +=++则的值为( )A.8B.16C.2D.4 【变式2】已知221() 4.,()_____2a b ab a b -==+=则 【变式3】已知225.6,x y xy x y +=-=+则的值为( )A.1B.13C.17D.25 【变式4】已知222(1)()32x x x y x y xy ---=-+-,求的值专题四:完全平方公式的运用例4:已知:4,2x y xy +==,求:①22x y +;②44x y +; ③2()x y -◆变式拓展训练◆【变式1】2242411310,;x x x x x x -+=++已知求①②【变式2】225,2,4xy x y x y x y x y ++=++已知满足求的值。
鲁教版九年级化学例题解析:如何区分燃烧现象

如何区分燃烧现象课后习题 1. 以下有关物质在氧气中燃烧现象的叙述中,不准确的是()。
A.物质在氧气中燃烧都会发光发热B.物质在氧气中燃烧比在空气中燃烧激烈C.碳在氧气中燃烧时,伴有蓝色火焰和火星四射D.铁丝在氧气中燃烧有黑色固体生成解析本题考查同学们对碳、铁丝等物质在氧气、空气中燃烧现象的理解和区分。
下面将不同物质在空气中和在氧气中燃烧的现象进行比较,以期帮助同学们理解记忆。
黑色木炭,空气燃烧,持续红热,无烟无焰;红热木炭,见氧复燃,发出白光,温度很高。
淡黄硫黄,空气燃烧,火焰淡蓝,放出热量;燃硫入氧,燃烧更旺,火焰蓝紫,美丽漂亮,生成气体,气味够呛。
铁丝见空气不燃,灼烧红热离火冷;伸入纯氧剧烈燃,火星四射成黑色,瓶底铺沙(水)防炸裂。
[:学,科,]碳在氧气中燃烧发出白光,放出热量,生成一种使澄清石灰水变浑浊的气体,没有蓝色火焰和火星四射的现象,故答案为C。
2. 在你观察过的①碳、②铁、③石蜡在氧气里燃烧的实验中,有火焰出现的是;火星四射的是;放出热量的是;集气瓶里事先垫一层沙或倒少量水的是,这是因为。
解析在观察实验现象时,要注意“烟”、“雾”、“光”、“火焰”的区别。
“烟“是固体小颗粒悬浮在空气中产生的,如红磷在氧气中燃烧产生白烟,它是生成物五氧化二磷的固体小颗粒。
“雾”是液体小液滴悬浮在空气中产生的,如天气寒冷时我们常看到下雾现象。
“光”一般是固体直接燃烧产生的现象,如镁在空气中燃烧看到的耀眼强光。
“火焰”一般是气体或液体燃烧产生的现象,如蜡烛在氧气中燃烧时,会由固态转换为液态,再由液态转换为气态,最后燃烧的是石蜡蒸气。
碳(固体)在氧气中燃烧火星四射、发出白光,放出大量的热,生成一种能使澄清石灰水变浑浊的气体。
铁丝在氧气中剧烈燃烧,火星四射,放出大量的热,生成一种黑色固体。
石蜡在氧气里燃烧发出白光,放出大量的热,瓶壁上形成水雾,生成能使澄清石灰水变浑浊的气体。
所以有火焰出现的是石蜡,火星四射的是铁和碳,且这三种物质燃烧都放出热量;做碳、铁在氧气中燃烧的实验时,需要事先在集气瓶底部铺一层细沙或装少量水,能防止溅落下来的灼热碳粉或熔化灼烧的铁和四氧化三铁把瓶底炸裂。
鲁教版九年级化学例题解析:氯酸钾制氧计算变式

氯酸钾制氧计算变式根据化学方程式进行的计算,是化学计算的重要内容之一。
下面由一道例题谈谈根据化学方程式的简单计算,并对该题变形和拓展,以帮助同学们更好地掌握该部分内容。
例题 把氯酸钾和二氧化锰的混合物15.5 g 放入大试管中加热,充分反应后冷却、称量,剩余固体质量为10.7 g 。
剩余固体中存在哪些物质?各为多少?解析 二氧化锰催化氯酸钾制取氧气,是我们非常熟悉的一个反应。
根据题给信息可知,该反应为“充分反应”,故剩余的固体里没有氯酸钾,只有生成的氯化钾和催化剂二氧化锰。
二氧化锰是催化剂,其质量在化学反应前后不变。
因此,根据质量守恒定律,反应前氯酸钾与反应后氯化钾的质量之差就是氧气的质量。
根据氧气的质量,结合反应的化学方程式可计算出氯化钾的质量,最后求二氧化锰的质量。
答案 根据质量守恒定律可知,生成氧气的质量为:15.5 g-10.7 g=4.8 g 。
设:剩余固体中含氯化钾质量为x 。
二氧化锰的质量为:10.7 g -7.45 g =3.25 g答:剩余固体中含氯化钾的质量为7.45 g ,含二氧化锰的质量为3.25 g 。
点拨 本题是对教材练习题的一个变式,利用的原理和所求的问题是相同的,但给出的反应进行程度不同,本题中明确指出“充分反应”,计算较为简单。
因此,同学们在学习时,要特别重视教材习题的练习和掌握。
根据化学方程式进行计算,关键是找准相关纯净物质量代入计算,当题目中未给出纯净物质量时,我们就应换种思维思考:根据质量守恒定律看物质的总质量是否发生变化,从而进一步分析解题。
变式题 为了测定实验室中氯酸钾样品的纯度,某学习小组取2.5 g 该样品与0.8 g 二氧化锰混合。
加热该混合物t 1时间后(假设杂质不参加反应),冷却,称量剩余固体混合物的质量,重复以上操作,依次称得加热t 1、t 2、t 3、t 4时间后剩余固体的质量,记录数据如下表所示:加热时间 t 1 t 2 t 3 t 4 剩余固体质量/g 2.48 2.41 2.34 2.34请仔细分析实验数据,回答下列问题:(1)在_________时间,该样品中氯酸钾已反应完全。
整数、假分数和带分数的互化-学生版
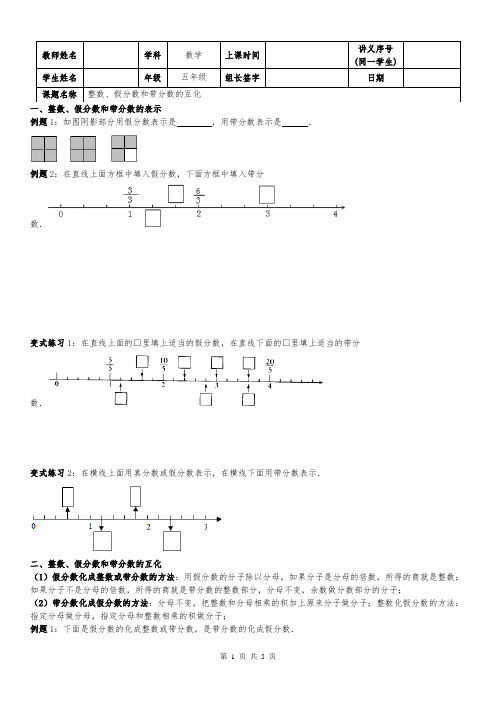
讲义序号教师姓名学科数学上课时间(同一学生) 学生姓名年级五年级组长签字日期课题名称整数、假分数和带分数的互化一、整数、假分数和带分数的表示例题1:如图阴影部分用假分数表示是,用带分数表示是.例题2:在直线上面方框中填入假分数,下面方框中填入带分数.变式练习1:在直线上面的□里填上适当的假分数,在直线下面的□里填上适当的带分数.变式练习2:在横线上面用真分数或假分数表示,在横线下面用带分数表示.二、整数、假分数和带分数的互化(1)假分数化成整数或带分数的方法:用假分数的分子除以分母,如果分子是分母的倍数,所得的商就是整数;如果分子不是分母的倍数,所得的商就是带分数的整数部分,分母不变,余数做分数部分的分子;(2)带分数化成假分数的方法:分母不变,把整数和分母相乘的积加上原来分子做分子;整数化假分数的方法:指定分母做分母,指定分母和整数相乘的积做分子;例题1:下面是假分数的化成整数或带分数,是带分数的化成假分数.35.例题2:把下面的假分数化成带分数或整数,把带分数化成假分数:= = 8= 7= 3=变式练习1:把下面的假分数化成带分数或整数.(1)= (2)= (3)= (4)= .变式练习2:2=====.=;;.变式练习3:变式练习4:把化成带分数是()A.B.C.变式练习5:把下面的分数约分,是假分数的要化成带分数或整数1.例题3:下列说法正确的有()①整数可以化作任意自然数为分母的分数;②真分数一定小于1,假分数一定大于1;③与相等的分数有无数个;④数a的倒数为. A. 1个 B. 2个 C. 3个 D. 4个变式练习1:要使是假分数,是真分数,未知数x的值应该是()A. 7 B. 6 C. 8变式练习2:一个分数,它的分子除以分母商1余1,这个分数是()A.真分数B.假分数C.带分数D.无法确定变式练习3:任何一个整数都可以写成分数形式..变式练习4:一个假分数不能化成整数就一定能化成带分数..变式练习5:把化成带分数是1..(判断对错)变式练习6:2化成假分数是..(判断对错)是能化成整数的假分数,那么a是8的因数..变式练习7:变式练习8:一个带分数,分子是3,把它化成假分数后分子是28,则这个带分数最小是.例题4:假分数的倒数一定比这个假分数小..(判断对错)变式练习1:假分数的倒数是真分数..(判断对错)拓展提升:的分数单位是,它至少添上个这样的分数单位就是假分数;1的分数单位是,再添上个这样的分数单位就与最小的质数相等.三、小数、分数、百分数的互化例题1:= ÷2= %变式练习1:1用假分数表示是,用百分数表示是,用小数表示是.四、分数大小的比较例题1:下列分数中介于整数5与6之间的是()A .B.C.D.例题2:下面的几个分数中,()与2不相等.A .B.C.D.变式练习1:在横线里添上适当的数 <0.2=0.6=2时15分= 时8.26平方米= 平方米 平方分米假分数与带分数的互化习题1、173 =2、274 =3、314 =4、335 =5、 237 =6、133 =7、112 =8、3114 =9、3113 = 10、114 = 11、95 = 12、193 = 13、174 = 14、156 = 15、136 = 16、232 = 17、158 = 18、195 = 19、496 = 20、467 = 21、247 = 22、435 = 23、338 = 24、537 = 25、334 = 26、513 = 27、3311 = 28、2317 =29、6512 = 30、256 = 31、312 = 32、51121 = 33、315 = 34、249 = 35、513 = 36、625 = 37、618 = 38、2213 = 39、2314 = 40、116 =。
12.地表雕刻师(教学设计含练习)五年级科学上册苏教版
再次,在案例分析部分,我选择了几个典型的案例进行分析,但感觉学生参与度不够高。我应该更加注重学生的参与,例如通过小组讨论、角色扮演等方式,让学生更加主动地参与到案例分析中来。
核心素养目标
本节课的核心素养目标为培养学生的地理观察能力、科学思维能力和实践创新能力。通过学习地表雕刻师的相关知识,学生能够运用科学的方法观察和分析地表形态的改变,培养地理观察能力;在学习过程中,学生需要运用科学思维,理解侵蚀和沉积的作用,以及地表雕刻师在地球演变过程中的角色,提升科学思维能力;同时,通过实践活动,让学生结合自己的生活经验,运用所学知识解释周围的地表形态,培养实践创新能力。
5.课堂展示与点评(15分钟)
目标:锻炼学生的表达能力,同时加深全班对地表雕刻师的认识和理解。
过程:
各组代表依次上台展示讨论成果,包括主题的现状、挑战及解决方案。
其他学生和教师对展示内容进行提问和点评,促进互动交流。
教师总结各组的亮点和不足,并提出进一步的建议和改进方向。
6.课堂小结(5分钟)
目标:回顾本节课的主要内容,强调地表雕刻师的重要性和意义。
典型例题讲解
例题1:地表雕刻师的主要作用是什么?请举例说明。
答案:地表雕刻师的主要作用是改变地表形态。例如,流水侵蚀作用可以形成峡谷、河流等地形,风力侵蚀作用可以形成沙丘、戈壁等地形,冰川侵蚀作用可以形成冰川谷、冰斗等地形。
例题2:侵蚀作用和沉积作用有什么区别?请举例说明。
答案:侵蚀作用是指地表雕刻师对地表进行破坏和侵蚀的过程,如流水侵蚀、风力侵蚀、冰川侵蚀等。沉积作用是指地表雕刻师将侵蚀过程中产生的物质沉积下来,形成新的地表形态,如河流沉积、风力沉积、冰川沉积等。
小数综合应用-2024-2025学年五年级数学上册典型例题系列(学生版)苏教版

第三单元专练篇·08:小数综合应用一、填空题。
1.0.9米可以看成把1米平均分成()份,表示这样的()份。
它写成分数是()米。
2.一个数由6个十,8个百分之一,3个0.001组成,这个数是(),读作()。
3.7.89中的“9”所在数位是()位,它的计数单位是()。
4.当3.62<3.□3时,□里能填的数字有()。
5.在“2.5、12、10.1、60”这4个数中,如果在末尾添上“0”,()大小不变,()大小有变化。
6.在6.309、6.390、69.73、69.03这几个小数中,最大的数是();去掉各数中的“0”后大小不变的数是()。
7.把0.072扩大到原来的()倍是72,把870缩小到原数的()是0.87。
8.在括号里填上合适的数。
1.38米=()分米=()厘米8元9角=()元38.65公顷=()平方米 6.42吨=()吨()千克9.截至到6月3日全球累计确诊新冠肺炎人数达到五亿三千零九万五千七百人,这个数改写成用“万”作单位的数是()万人,省略亿位后面的尾数的近似数是()亿人。
10.按照“四舍五入”法,近似数是4.40的最大三位小数是(),最小三位小数是()。
二、选择题。
11.下面各数中,读出的“零”的个数与其他三个不同的是()。
A.200108B.600.30C.502.09D.401.7012.一个小数由两个8、两个0和小数点组成,且去掉其中一个0,而不改变原数的大小。
这个小数是()。
A.8.008B.0.880C.0.088D.0.80813.将2.508、2.58、2.518、2.581这四个数按从小到大的顺序排列,排在第三位的数是()。
A.2.508B.2.58C.2.518D.2.58114.把2.88的小数点向右移动三位,再缩小到所得数的1100,得到()。
A.0.288B.28.8C.288D.288015.把5.6千克、5.6吨、5.06吨、5000千克按从小到大排列,排在第二的是()。
梯形的面积与实际应用-2024-2025学年五年级数学上册典型例题系列(学生版)苏教版

第二单元专练篇·10:梯形的面积与实际应用1.如图所示,小花爷爷用30米长的篱笆靠着墙围个菜地,求这个菜地的面积。
2.为改善居民的生活环境,全面提升居民的舒适感、幸福度、满意率,凤凰小区在门口的梯形空地上建个“小花园”,种植了一片花卉。
同时为了便于居民观赏,修建了两条3米宽的小路(如图),花卉的种植面积是多少平方米?3.一个梯形原来上底与下底的和是18厘米,如果上底延长3厘米,下底延长5厘米,高不变,那么面积增加24平方厘米。
原来梯形的面积是多少平方厘米?4.王老伯家用85米长的竹篱笆在一块靠墙的空地上围了一个菜地(如图)。
(1)这个菜地的面积是多少平方米?(2)如果每平方米可以收西红柿30千克,这块菜地可以收西红柿多少千克?5.一块梯形装饰板,上底5分米,下底11分米,高1米,两面都要涂油漆,需要涂油漆的面积是多少平方分米?6.一个平行四边形的面积是90平方厘米,把它分成两个完全相同的梯形,每个梯形的上底是8厘米,下底是10厘米。
这个平行四边形的高是多少厘米?7.一堆钢管,从上往下数,第一层有5根,第二层有7根,下面每一层都比上一层多2根,一共有10层,这堆钢管一共有多少根?8.在一块梯形草坪(如下图)中修了一条平行四边形的小路,求草坪的实际面积是多少平方米?9.为建设美丽广州,向绿而行,某区要设计一个长方形绿化用地,如下图。
(1)请在图上画一条线段,将长方形分成一个等腰三角形(种木棉树)和一个梯形(种洋紫荆)。
(2)种木棉树的面积是多少平方米?种洋紫荆的面积是多少平方米?10.有一个梯形花园(如图,单位米),每平方米种花6棵,这个花园一共能种多少棵花?11.学校有一块梯形的地,上底长10米,下底长12米,高为9米,要平均分给两个班种花,你认为怎样分配才合理呢?画一画、算一算,来尝试说出自己的理由。
12.王大伯利用一面墙围成一个鸡舍(如图)。
已知所用篱笆全长11.8米。
这个鸡舍的面积是多少平方米?13.爷爷用65米的篱笆把老家的鸭塘围了三面(如图),正好和岸边围成了一个直角梯形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、热力学1(例题)某一化学反应若在定温定压下(298K 、P 0)进行,放热40.0KJ ,若使反应通过可逆电池来完成,则吸热4.0KJ 。
计算: (1)计算该化学反应的∆r S m 。
(2)当该反应自发进行时(即不做功时),环境的熵变及总熵变。
(3)反应体系可能做的最大功为多少? 解:(1)11400013.42298.151r r r m S Q JS J K mol T K mol ξξ--∆∆====⋅⋅⋅⨯ (2)114000--=-134.2298.151r Q Q JS J K mol T T K molξξ--+∆===⋅⋅⋅⋅⨯实P 环1113.42134.2147.6S S S J K mol --∆=∆+∆=+=⋅⋅环总系(3)40000400044000R G H T S H Q J J J ∆=∆-∆=∆-=--=- f ,max 44000W G J ∴=+∆=-2、(习题)1mol 理想气体从300K ,100kPa 下等压加热到600K ,求此过程的Q 、W 、U 、H 、S 、G 。
已知此理想气体300K 时的S m =150.0J·K -1·mol -1,c p ,m =30.00 J·K -1·mol -1。
3、(例题)在K 15.298的等温情况下,两个瓶子中间有旋塞相通,开始时,一放2m olO 2.0,压力为KPa 325.1012.0⨯,另一放2m olN 8.0,压力为KPa 325.1018.0⨯,打开旋塞后,两气互相混合,计算:(1)终了时瓶中的压力;(2)混合过程中的Q 、W 、U ∆、S ∆(3)如等温下可逆地使气体回到原状,计算过程中的Q 和W 。
解:(1)222222320.02447,50663O N O N O N n RT n RT n RTV V V m P Pa P P V =+=+=⨯==总总终总(2)以二球气体为体系,w=0,0u =V ,则Q=0222222221N ln n ln n ln 2n ln 2 5.763mix O N O O N O N V V S S S n R R R R J K V V -=+=+=+=⋅V V V 总总 (3)1mix 5.763S S J K -=-=-⋅V V 分离 而RS Q T =V 分离∴1mix298.2 5.7631719R S Q T T S K J K J -==-=-⨯⋅=-V V 分离 又∵0U =V ,∴1719R W Q J =-=+3、 (习题)液态Br 2在331.4K 时沸腾,Br 2(l )在282.5K 时的蒸气压为13.33KPa ,计算298.2K 时Br 2(g )的标准摩尔生成吉布斯自由能 。
已知 △f Gm θ(Br 2,l,Φ)=0。
设Br 2(l )→Br 2(g )的θ∆m H ,θm S ∆与T 无关。
4、(例题)已知Br 2(g )的标准生成热△f Hm θ(Φ)和标准生成自由能△f Gm θ(Φ)分别为30.71和3.14 KJ mol -1。
(1)计算液态溴在298K 时的蒸气压 (2)近似计算溴在323K 时的蒸气压(3)近似计算标准压力下液态溴的沸点已知 △f Gm θ(Br 2,l,Φ)=0, △f Hm θ(Br 2,l,Φ)=0 解: Br 2(l )Br 2(g ) (1)()()2ln lnBr r m pP G RT K RT P θθθΦ=-Φ-V∴()()22g 3140ln1.26748.314298Br f m r m P G G Rr P RTRT θθθΦΦ=-=-=-=-⨯V V 、、2(298)0.2816Br P P K K P θθ==,∴20.281628.53Br P P kPa θ=⨯= (2) 近似计算,可认为v m H θV 为常数.211(323)(,,)11113071011ln 0.9594(298)2983238.3142983238.314298323p f m v m p K K H Br g H K K R J K mol θθθθ--Φ⎛⎫⎛⎫⎛⎫=-=-=-= ⎪ ⎪ ⎪⋅⋅⎝⎭⎝⎭⎝⎭V V (323) 2.610(298)p p K K K K θθ=,(323) 2.6100.28610.7350p K K θ=⨯=2(323)0.7350Br p P K K P θθ==,20.735074.47Br P P kPa θ=⨯=(3)沸点时,2Br P P θ=,2()1Br P P P K T P Pθθθθ===(323)11ln ()()323v m P P b H K K K T R T θθθ=-V ,3071011ln 0.735()8.314323b T =- ∴ 332b T K =5、(例题)双原子分子理想气体 B 从初态 300K 、100KPa 分别经可逆及不可逆绝热膨胀至压力均为10KPa 的终态。
如果不可逆过程所作的功仅为可逆过程的 10%,请计算不可逆过程的终态温度、ΔU 、ΔH 、Q 、W 。
6(习题)在298.1K ,101.325Pa 时,反应)l (O H )l (Hg )s (O H )g (H 2g 2+=+θ∆m rH 的为1mol .J 8.195-。
若设计为可逆电池,在电池)kg .m ol 1.0(KOH |)P (H 12-θ )l (Hg )s (HgO +中进行上述反应,电池的电动势为V 9265.0,试求上述反应的θθ∆∆m m rG rS 和。
7、(习题)(1)轮胎中压力为506.5kPa 的100dm 3空气泄漏于大气中(P 0=101.3kPa),问对大气做功多少?(假定温度恒定不变)(2)1kg 的水在正常沸点100度时汽化为同温度的水蒸汽,吸热2259.2 kJ 。
计算汽化过程中的W及体系能的变化ΔU。
8(例题) 苯在正常沸点353K 下的∆vap H m 0=30.77KJ.mol -1,今将353K 及P 0下的1molC 6H 6(l)向真空等温蒸发为同温同压的苯蒸气(设为理想气体)。
试求:(1)此过程中苯吸收的热量Q 和作的功W ;(2)苯的摩尔气化滴∆vap S m 0及摩尔气化吉布斯自由能∆vap G m 0; (3)环境的熵变∆S 环;(4)应用有关原理,判断上述过程是否自发? (5)298K 时苯的蒸气压为多大?解:(1)0,W = ()()()()P vap m m m Q U W U Q W n H P V g V l θ=∆-=∆=+=∆--⎡⎤⎣⎦P P 外 ()111130770mo 18.314mo 353vap m m vap m n H P V g n H nRTmol J l mol J K l K θθ---=∆-=∆-=⨯⋅-⨯⋅⋅⨯外=27835J (2)11130770mo 87.2mo 353vap mvap m H J l S J K l TKθθ---∆⋅∆===⋅⋅0vap m vap m vap m G H T S θθθ∆=∆-∆=(3)127835=78.9353Q Q J S J K T T K-∆=-=-=-⋅环环(4)()1111==187.278.98.30vap m S S S n S S mol J K mol J K J K θ----∆∆+∆∆+∆=⨯⋅⋅+-⋅=⋅>环环隔体故真空蒸发为不可逆过程 由克—克方程1122111121130770mo 11ln ,ln 1013258.314mo 353298vap m H P P J K l P R T T Pa J K l K K θ----∆⎛⎫⋅⋅⎛⎫=-=- ⎪ ⎪⋅⋅⎝⎭⎝⎭ 214633P Pa =9、(例题)(1)如果房间的一电冰箱的箱门打开,并保持致冷机运转,能否降低全室温度,为什么?(2)设该电冰箱在0℃与室温(25℃)作理想可逆循环每小时能冻出1 kg 的冰,如房间的总热容为150 kJ·K -1,估算电冰箱工作10小时后室温度的变化? 已知水的比热为4.184 J·K -1,1克水的凝固热为339 J·g -1(9分)解:(1)不能。
因为,冰箱门打开,箱与室空气流通,使高低两个热源温度相等。
致冷机工作,致冷机消耗的电功以及冰箱冷却器 (低温热源)吸的热都以热的形式放到室 (高温热源),当冰箱门打开时,室空气又流入箱,使室气温升高。
这样,总的效果是致冷机消耗电能转化为室空气的能,反使室温度升高。
因而使室温度非但不降低反而升高。
(2) Q'=1000×(4.184×25+339)×10=4436 kJ β=T 1/(T 2-T 1)= 273/25 = 10.92 β=Q'/WW =Q'/10.92=4436/10.92=406.23 kJ Q 2=W +Q'=4842 kJ ΔT=4842/150=32 KT 3=298+32=330 K ,房间温度变为330 K 。
10(例题)已知水的正常熔化热1fus 3347J g .H -=⋅ΘΔ。
()11p,m 2H O,753J K mol .C l --=⋅⋅,()11p,m 2H O,354J K mol .C s --=⋅。
计算5mol 1-度水在p Ө下凝固为同温同压下的冰的熵变,并判断是否自发过程。
解:设计路径ΔS 268K =ΔS 1+ΔS 2+ΔS 273K ()()fus mp,m p,m fre273268lnln 268273H C l C s T Δ=+- 11273268334.71875.3ln35.4ln 21.33J K mol 268273273--⨯=⨯+⨯-=-⋅⋅ ()()()()268K 273K p,m p,m 1334.718135.475.32682735825J mol H H n C s C l TΔΔΔ-⎡⎤=+-⎣⎦=-⨯+⨯-⨯-=-⋅ 1p 2685825J mol Q H Δ-==-⋅,11582521.74J K mol 268Q S T Δ---===⋅⋅环 1121.3321.740.42J K mol 0S S S ΔΔΔ--=+=-+=⋅⋅>隔离系环 ∴是自发过程。
11(例题)在298.15K 时,有0.01Kg 的N 2O 4(g ),压力为202.65KPa 现把它全部转变成NO 2(g ),压力为30.40KPa ,求过程的△r G 。
