优化问题实例解析 共41页PPT资料
合集下载
生活中的优化问题举例课件

综上,当 v0≥16 时,v=16 km/h 全程燃料费最省, 为 32 000 元;当 v0<16,即 v=v0 时全程燃料费最省,为 1 000v20元.(12 分) v0-8
归纳升华 本题是用料最省问题.先根据特殊情况求出比例系 数,进而求出解析式,再利用导数求最值是常用方法.需 要注意的对参数的讨论.
综上每月生产 200 吨产品时利润达到最大,最大利润 为 315 万元.
归纳升华 (1)经济生活中优化问题的解法:经济生活中要分析 生产的成本与利润及利润增减的快慢,以产量或单价为自 变量很容易建立函数关系,从而可以利用导数来分析、研 究、指导生产活动.
(2)关于利润问题常用的两个等量关系: ①利润=收入-成本; ②利润=每节产品的利润×销售件数.
2.解决优化问题的一般步骤
[思考尝试·夯基] 1.思考判断(正确的打“√”,错误的打“×”). (1)磁盘的最大存储量问题是优化问题.( ) (2)求某长方体容器的容积问题是优化问题.( ) (3)汽油的使用效率的提高问题是优化问题.( ) 解析:(1)(2)是优化问题,(3)不是优化问题.
答案: (1)√ (2)√ (3)×
答案:5
类型 1 用导数解决面积、容积最大问题(自主 研析)
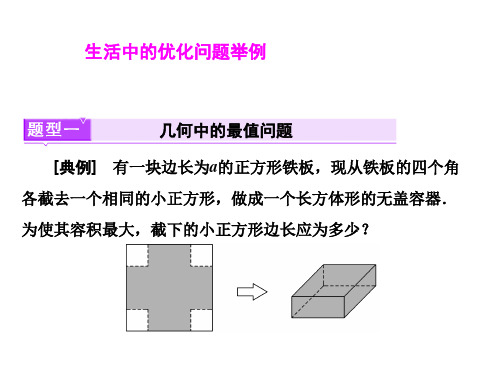
[典例 1] 有一块边长为 a 的正方形铁板,现从铁板的四个 角各截去一个相同的小正方形,做成一个长方体形的无盖 容器.为使其容积最大,截下的小正方形边长应为多少?
解:设截下的小正方形边长为 x,容器容积为 V(x),
则做成的长方体形无盖容器底面边长为 a-2x,高为 x, V(x)=(a-2x)2x,0<x<a2. 即 V(x)=4x3-4ax2+a2x,0<x<a2. 实际问题归结为求 V(x)在区间0,a2上的最大值
生活中的优化问题举例一幻灯片PPT

的尺,才 寸能使四周空小白?面积最
分析:〔1〕建模关系式
四 周 空 海 白 报 面 总 版 积 面 心积 面 积
〔2〕函数关系式:
x
128
S (x)(x4 )( 2 )12(x8 0 )
〔3〕解模: x
如何求函数S (x)(x4 )1 ( 2 2 )8 12(x8 0 )最小值
x
方法一:根本均值不等式法:“一正二定三相等〞
团结守纪、笃学上进
生活中的优化问题举例(一〕
生活中经常遇到求利润最大、用料
最省、效率最高等问题, 这些问题 通常称为优化问题 .通 过 前面的学
习, 我们知道,导数是求函数最大小
值的有力工具 .本节我们运用导 数, 解决一些生活中的优化问题.
一、根底知识链接
1 、y 函 2 x 3 数 3 x 2 1x 2 5 在 0 ,3 上的
审题 —— 建模—— 解模 —— 作答
变例:在边 60c长 m的为正方形铁片的 去四 相角 等切 小正
余下一个边 x的长正为方形,再把 沿它 虚的 线边 折起(
做成一个无盖的 子方 ,底 箱箱 底的边长 时是 ,多 箱少 底
容积最大?最大 多容 少积 ?是 x
分析:
60 x
x x
1、如何箱子容积与箱底边长关系?
2
最大存储量为 R2
2mn
例4:某种圆柱形的饮料罐的容积一定时,如何确定它的 高与底半径,使得所用材料最省?
解 设圆柱的高为h,底面半径为R.
h
那么外表积为 S(R)=2πRh+2πR2.
又V=πR2h(定值), 则h V .
R
R2
S(R)2RV R22R2
2V R
生活中的优化问题举例PPT(人教A版选修2-2)

1.4《生活中的优化 问题举例》
问题背景:饮料瓶大小对饮料公司利润的影响
下面是某品牌饮料的三种规格不同的产品,若它们 的价格如下表所示,则 (1)对消费者而言,选择哪一种更合算呢? (2)对制造商而言,哪一种的利润更大?
规格(L)
2
1.25
0.6
价格(元)
5.1
4.5
2.5
例1、某制造商制造并出售球形瓶装的某种饮料,瓶子的制造
解析:依题意可设每月土地占用费y1=
k1 x
,每月
库存货物的运费y2=k2x,其中x是仓库到车站的距
离,于是由2=1k01 ,得k1=20;8=10k2,得k2=45.
因此两项费用之和为y=2x0+45x,
y′=-2x02 +45, 令y′=0,得x=5(x=-5舍去),此点即为最小 值点. 故当仓库建在离车站5千米处时,两项费用之和 最小.
16
0
极小值
(16,+∞)
+
增函数↗
∵S(x)在(0,+∞)上只有一个极值点 ∴由上表可知,当x=16,即当版心高为16dm,dm,宽为8dm时,海报四周的 空白面积最小。
新知视界
• 1.优化问题 • 生活中经常遇到求利润最大、用料最省、
效率最高等问题,这些问题通常称为优化 问题.
∴S2=16π2(r2x2-x4), (S2)′=16π2(2r2x-4x3), 由(S2)′=0,得x= 22r(x=0舍去), ∴Smax=2πr2,故选A. 答案:A
• 3.某商品一件的成本为30元,在某段时间 内,若以每件x元出售,可卖出(200-x)件, 当 每 件 商 品 的 定 价 为 ________ 元 时 , 利 润 最大.
问题背景:饮料瓶大小对饮料公司利润的影响
下面是某品牌饮料的三种规格不同的产品,若它们 的价格如下表所示,则 (1)对消费者而言,选择哪一种更合算呢? (2)对制造商而言,哪一种的利润更大?
规格(L)
2
1.25
0.6
价格(元)
5.1
4.5
2.5
例1、某制造商制造并出售球形瓶装的某种饮料,瓶子的制造
解析:依题意可设每月土地占用费y1=
k1 x
,每月
库存货物的运费y2=k2x,其中x是仓库到车站的距
离,于是由2=1k01 ,得k1=20;8=10k2,得k2=45.
因此两项费用之和为y=2x0+45x,
y′=-2x02 +45, 令y′=0,得x=5(x=-5舍去),此点即为最小 值点. 故当仓库建在离车站5千米处时,两项费用之和 最小.
16
0
极小值
(16,+∞)
+
增函数↗
∵S(x)在(0,+∞)上只有一个极值点 ∴由上表可知,当x=16,即当版心高为16dm,dm,宽为8dm时,海报四周的 空白面积最小。
新知视界
• 1.优化问题 • 生活中经常遇到求利润最大、用料最省、
效率最高等问题,这些问题通常称为优化 问题.
∴S2=16π2(r2x2-x4), (S2)′=16π2(2r2x-4x3), 由(S2)′=0,得x= 22r(x=0舍去), ∴Smax=2πr2,故选A. 答案:A
• 3.某商品一件的成本为30元,在某段时间 内,若以每件x元出售,可卖出(200-x)件, 当 每 件 商 品 的 定 价 为 ________ 元 时 , 利 润 最大.
1.4生活中的优化问题举例课件人教新课标

2.利用导数解决生活中优化问题的一般步骤是什么? 剖析:利用导数解决生活中优化问题的一般步骤如下:
重难聚焦
名师点拨1.在求实际问题的最大(小)值时,一定要考虑实际问题的 意义,不符合实际意义的值应舍去. 2.在实际问题中,有时会遇到函数在区间内只有一个点使f'(x)=0的 情形,如果函数在这点有极大(小)值,那么不与端点值比较,也可以知 道这就是最大(小)值. 3.在解决实际优化问题时,不仅要注意将问题中涉及的变量关系用 函数关系表示,还应确定出函数关系中自变量的定义区间.
题型一
题型二
题型三
题型四
典例透析
利润最大问题 【例3】 某分公司经销某品牌产品,每件产品的成本为3元,并且每 件产品需向总公司交a(3≤a≤5)元的管理费,估计当每件产品的售 价为x(9≤x≤11)元时,一年的销售量为(12-x)2万件. (1)求分公司一年的利润L(单位:万元)与每件产品的售价x的函数关 系式; (2)当每件产品的售价为多少元时,分公司一年的利润L最大?并求出 L的最大值Q(a). 分析:(1)利用题中等量关系找出L与x的函数关系式;(2)求出(1)中函 数关系式的导函数,再利用导数求最值.
当x=140时,y=175,即当x=140,y=175时,S取得最小值24 500. 故当广告的高为140 cm,宽为175 cm时,可使矩形广告的面积最小.
题型一
题型二
题型三
题型四
典例透析
典例透析
题型一
题型二
题型三
题型四
解:(1)隔热层厚度为 x cm,
由题意知每年能源消耗费用为 C(x)= 3xk+5, 再由 C(0)=8,得 k=40,因此 C(x)= 3x4+05. 而建造费用为 C1(x)=6x.
重难聚焦
名师点拨1.在求实际问题的最大(小)值时,一定要考虑实际问题的 意义,不符合实际意义的值应舍去. 2.在实际问题中,有时会遇到函数在区间内只有一个点使f'(x)=0的 情形,如果函数在这点有极大(小)值,那么不与端点值比较,也可以知 道这就是最大(小)值. 3.在解决实际优化问题时,不仅要注意将问题中涉及的变量关系用 函数关系表示,还应确定出函数关系中自变量的定义区间.
题型一
题型二
题型三
题型四
典例透析
利润最大问题 【例3】 某分公司经销某品牌产品,每件产品的成本为3元,并且每 件产品需向总公司交a(3≤a≤5)元的管理费,估计当每件产品的售 价为x(9≤x≤11)元时,一年的销售量为(12-x)2万件. (1)求分公司一年的利润L(单位:万元)与每件产品的售价x的函数关 系式; (2)当每件产品的售价为多少元时,分公司一年的利润L最大?并求出 L的最大值Q(a). 分析:(1)利用题中等量关系找出L与x的函数关系式;(2)求出(1)中函 数关系式的导函数,再利用导数求最值.
当x=140时,y=175,即当x=140,y=175时,S取得最小值24 500. 故当广告的高为140 cm,宽为175 cm时,可使矩形广告的面积最小.
题型一
题型二
题型三
题型四
典例透析
典例透析
题型一
题型二
题型三
题型四
解:(1)隔热层厚度为 x cm,
由题意知每年能源消耗费用为 C(x)= 3xk+5, 再由 C(0)=8,得 k=40,因此 C(x)= 3x4+05. 而建造费用为 C1(x)=6x.
生活中的优化问题举例课件
=972(9x-5)(x-3). 令 f′(x)=0,解得 x=59或 x=3(舍去). 当 0<x<59时,f′(x)>0,当59<x<1 时,f′(x)<0, 所以 x=59时,f(x)有最大值 f 59=20 000. 所以当 x=59时,本年度的年利润最大,最大年利润为 20 000 万元.
生活中的优化问题举例
几何中的最值问题 [典例] 有一块边长为a的正方形铁板,现从铁板的四个角 各截去一个相同的小正方形,做成一个长方体形的无盖容器. 为使其容积最大,截下的小正方形边长应为多少?
[解] 设截下的小正方形边长为x,容器容积为V(x),则做 成的长方体形无盖容器底面边长为a-2x,高为x,
y′=2-1x228,令y′=0,∵x>0,∴x=8. 因为当0<x<8时,y′<0;当x>8时,y′>0, 所以当x=8时,y取最小值,此时宽为8 m,长为16 m. 即当堆料场的长为16 m,宽为8 m时,可使砌墙所用材料最省.
利润最大问题
[典例] 某汽车生产企业上年度生产一品牌汽车的投入成 本为10万元/辆,出厂价为13万元/辆,年销售量为5 000辆,本 年度为适应市场需求,计划提高产品档次,适当增加投入成 本,若每辆车投入成本增加的比例为x(0<x<1),则出厂价相 应提高的比例为0.7x,年销售量也相应增加.已知年利润= (每辆车的出厂价-每辆车的投入成本)×年销售量.
1.经济生活中优化问题的解法 经济生活中要分析生产的成本与利润及利润增减的快 慢,以产量或单价为自变量很容易建立函数关系,从而可 以利用导数来分析、研究、指导生产活动. 2.关于利润问题常用的两个等量关系 (1)利润=收入-成本. (2)利润=每件产品的利润×销售件数.
[活学活用] 工厂生产某种产品,次品率p与日产量x(万件)间的关系为p=
人教版-生活中的优化问题举例优秀课件

将包装盒捏成球状,因为小包装的半径小, 其利润低,生产商就提高销售价格来平衡与 大包装的利润.
人教版-生活中的优化问题举例优秀课 件
探究(三):磁盘的最大存储量问题 人教版-生活中的优化问题举例优秀课件
【背景材料】计算机把信息存储在磁盘上, 磁盘是带有磁性介质的圆盘,并由操作系统 将其格式化成磁道和扇区.磁道是指不同半径 所构成的同心圆轨道,扇区是指被圆心角分 割成的扇形区域.磁道上的定长的弧可作为基 本存储单元,根据其磁化与否可分别记录数 据0或1,这个基本单元通常称为比特,磁盘 的构造如图所示.
思考3:要使磁盘的存储量达到最大,那
么最内一条磁道上的比特数为多少?
R
2r
n
r
思考4:这张磁盘的存储量最大可达到多
少比特? R r 2 r mn
人教版-生活中的优化问题举例优秀课 件
人教版-生活中的优化问题举例优秀课 件
思考5:若R为定值,r为变量,那么这张
磁盘的存储量 f(r) m 2nr(Rr)(0 r R )
思考1:现有一张半径为R的磁盘,它的存储
区是半径介于r与R的环形区域,且最外面的
磁道不存储任何信息,那么这张磁盘的磁道
数最多可达多少?
R
Rr m
最内一条磁道.
r
思考2:由于每条磁道上的比特数相同, 那么这张磁盘存储量的大小取决于哪条 磁道上的比特数?
人教版-生活中的优化问题举例优秀课 件
人教版-生活中的优化问题举例优秀课 件
2 r 2 (r m)
2 (R m)
n
n
n
(R r m)(R r) mn
理论迁移 人教版-生活中的优化问题举例优秀课件
例 某汽车制造厂有一条价值为60万元
人教版-生活中的优化问题举例优秀课 件
探究(三):磁盘的最大存储量问题 人教版-生活中的优化问题举例优秀课件
【背景材料】计算机把信息存储在磁盘上, 磁盘是带有磁性介质的圆盘,并由操作系统 将其格式化成磁道和扇区.磁道是指不同半径 所构成的同心圆轨道,扇区是指被圆心角分 割成的扇形区域.磁道上的定长的弧可作为基 本存储单元,根据其磁化与否可分别记录数 据0或1,这个基本单元通常称为比特,磁盘 的构造如图所示.
思考3:要使磁盘的存储量达到最大,那
么最内一条磁道上的比特数为多少?
R
2r
n
r
思考4:这张磁盘的存储量最大可达到多
少比特? R r 2 r mn
人教版-生活中的优化问题举例优秀课 件
人教版-生活中的优化问题举例优秀课 件
思考5:若R为定值,r为变量,那么这张
磁盘的存储量 f(r) m 2nr(Rr)(0 r R )
思考1:现有一张半径为R的磁盘,它的存储
区是半径介于r与R的环形区域,且最外面的
磁道不存储任何信息,那么这张磁盘的磁道
数最多可达多少?
R
Rr m
最内一条磁道.
r
思考2:由于每条磁道上的比特数相同, 那么这张磁盘存储量的大小取决于哪条 磁道上的比特数?
人教版-生活中的优化问题举例优秀课 件
人教版-生活中的优化问题举例优秀课 件
2 r 2 (r m)
2 (R m)
n
n
n
(R r m)(R r) mn
理论迁移 人教版-生活中的优化问题举例优秀课件
例 某汽车制造厂有一条价值为60万元
生活中的优化问题举例 课件

练一练 1.请你设计一个包装盒.如图所示,ABCD 是边长 为 60 cm 的正方形硬纸片,切去阴影部分所示的四个全 等的等腰直角三角形,再沿虚线折起,使得 A,B,C, D 四个点重合于图中的点 P,正好形成一个正四棱柱形 状的包装盒.E、F 在 AB 上,是被切去的一个等腰直角 三角形斜边的两个端点.设 AE=FB=x(cm).
令 S′=0 得 v=20, 当 v∈(0,20)时,S′<0;当 v∈(20,+∞)时,S′>0. ∴v=20 km/h 是 S 的极小值点,也是最小值点, ∴v=20 km/h 时,每千米的费用总和最少.
讲一讲 3.某厂生产某种电子元件,如果生产出一件正品,可 获利 200 元,如果生产出一件次品,则损失 100 元.已知 该厂制造电子元件过程中,次品率 p 与日产量 x 的函数关 系是:p=4x+3x32(x∈N*). (1)将该厂的日盈利额 T(元)表示为日产量 x(件)的函数; (2)为获最大盈利,该厂的日产量应定为多少件?
(1)求 k 的值及 f(x)的表达式; (2)隔热层修建多厚时,总费用 f(x)达到最小,并 求最小值.
[尝试解答] (1)由题设,隔热层厚度为 x cm,每年
能源消耗费用为 C(x)=3x+k 5,
再由 C(0)=8,得 k=40,
因此 C(x)=3x4+0 5.
而建造费用为 C1(x)=6x. 最后得隔热层建造费用与 20 年的能源消耗费用之
(1)若广告商要求包装盒的侧面积 S(cm2)最大,试问 x 应 取何值?
(2)某厂商要求包装盒的容积 V(cm3)最大,试问 x 应取何 值?并求出此时包装盒的高与底面边长的比值.
解:设包装盒的高为 h(cm),底面边长为 a(cm). 由已知得 a= 2x,h=60-22x= 2(30-x),0<x<30. (1)S=4ah=8x(30-x)=-8(x-15)2+1 800, 所以当 x=15 时,S 取得最大值.
生活中的优化问题举例PPT精品课件_2

不可能解脱人
范 民的灾难,反
缜
而大大加重了 人民的负担。
因此,不断有
人反对佛教,
其中最著名的
是齐、梁间杰
出的无神论者
范缜。
大放光彩的艺术
书法 绘画 雕塑 音乐 舞蹈
王 羲 之
《 兰
亭
序 》
帖 卷
三国两晋南北朝 时期的石窟寺艺 术(点击)
优化问题的答案
用导数解决数学问题
问题4:无盖方盒的最大容积问题
一边长为a的正方形铁片,铁片的四 角截去四个边长都是x的小正方形,然 后做成一个无盖方盒,x 多大时,方盒的 容积V最大?
作业:
• P114 4、7。
科学技术的进步
范缜(450—约510年)是南阳舞阴人,年轻时 家境贫寒,学习十分刻苦。他在湖北某地任太 守时,当地寺庙很多,民间迷信活动频繁。他 劝导人们不要迷信,并下令封闭了寺庙。针对 佛教宣扬神不灭的谬论,他发表了《神灭论》。 齐朝竟陵王萧子良,发动僧侣和文士同范缜辩 论,谁也驳不倒他;又以做中书郎为诱饵,劝 他放弃神灭论的主张。范缜听了大笑说:“假 如我是个卖论取官的人,早就官至尚书令了, 还用你说什么中书郎?”后来,梁武帝又发动 60多名达官贵人,写了70多篇文章来反驳范缜, 也没有将他驳倒。
• 汽油的使用效率G=汽油的消耗量w/汽车行 使路程s,
即:G=w/s
• 求G的最小值问题.
问题2:如何使一个圆形磁盘储存更多信息?
例2 磁盘的最大存储量问题:
问题3:饮料瓶大小对饮料公司利润有影响 吗?
• 你是否注意过,市场上等量的小包装的物品 一般比大包装的要贵些?你想从数学上知道 它的道理吗?
• 是不是饮料瓶越大,饮料公司的利润越大?
( 人教A版生活中的优化问题举例课件 (共37张PPT)

当 x∈(0,20)时,V′>0; 当 x∈(20,30)时,V′<0. 所以当 x=20 时,V 取得极大值,也是最大值. 此时ha=12,即包装盒的高与底面边长的比值为12.
解决面积、容积的最值问题的思路: 1.解决长度、面积、容积的最值问题,要正确引入变量,将面积或容积表示 为变量的函数,结合实际问题的定义域,利用导数求解函数的最值. 2.必要时,可选择建立适当的坐标系,利用点的坐标建立函数关系或曲线方 程,以利于解决问题.
解析:设矩形场地的长为 x,则宽为 8-x,
面积为 S=x(8-x)(0<x<8),
令 S′=8-2x=0,得 x=4.
此时 S 最大值=42=16(m2).
答案:C
2.要做一个圆锥形的漏斗,其母线长为 20 cm,要使其体积最大,则高为( )
3 A. 3 cm
10 3 B. 3 cm
16 C. 3 3 cm
l=2x+2y+2( 22x)=(32+ 2)x+1x6. 所以 l′=32+ 2-1x62.令 l′=0,即32+ 2-1x62=0, 解得 x1=8-4 2,x2=4 2-8(舍去). 当 0<x<8-4 2时,l′<0; 当 8-4 2<x<4 2时,l′>0. 所以当 x=8-4 2时,l 取得最小值. 此时,x=8-4 2≈2.343 (m),y≈2.828 (m). 即当 x 为 2.343 m,y 为 2.828 m 时,用料最省.
探究一 长度、面积、容积的最值问题
[典例 1] 请你设计一个包装盒,如图所示,四边形 ABCD 是边长为 60 cm 的正方形硬纸片,切去阴影部分所示的 四个全等的等腰直角三角形,再沿虚线折起,使得 A,B, C,D 四个点重合于图中的点 P,正好形成一个正四棱柱 形状的包装盒,E,F 在 AB 上,是被切去的一个等腰直 角三角形斜边的两个端点,设 AE=FB=x cm.
生活中的优化问题举例-课件

• (1)阅读理解,认真审题.就是读懂题中的 文字叙述,理解叙述所反映的实际背景, 领悟实际背景中的数学本质,写出题中的 数量关系,实现应用问题向数学问题转 化.
• (2)引入数学符号,建立数学模型.一般地, 设自变量为x,函数为y,并用x表示相关的 量,运用已掌握的数学知识、物理知识及 其他相关的知识,将问题中的数量关系表 示为一个数学关系式,实现问题的数学化, 即建立数学模型.
• [解析] 设圆柱的底面半径为r,高为h, • 则S圆柱底=2πr2,S圆柱侧=2πrh,
∴圆柱的表面积 S=2πr2+2πrh.∴h=S-2π2rπr2, 又圆柱的体积 V=πr2h=rS-22πr3,V′=S-26πr2, 令 V′=0 得 S=6πr2,∴h=2r,
又 r=
6Sπ,∴h=2
• 1.解决实际应用问题时,要把问题中所 涉及的几个变量转化成函数关系式,这需 要通过分析、联想、抽象和转化完成,函 数的最值要由 极值 和 端点的函数值 确定,当定义域是开区间 且 函 数 只 有 一 个 极值时,这个极值也就是它的 最值 .
• 2.生活中经常遇到求利润最大、用料最 省、效率最高等问题,这些问题通常称为 优化问题 .通过前面的学习,我们知道导数 是求函数最大(小)值的有力工具,运用导数 可以解决一些生活中的 优化问题 .
• 现该公司准备共投入3百万元,分别用于广 告投入和技术改造投入,请设计一种资金 分配方案,使得该公司获得最大收益.
• (注:收益=销售额-投入,答案数据精确 到0.01)
(参考数据: 2≈1.414, 3≈1.732)
• [解析] 设3百万元中技术改造投入为x百 万元,广告费投入为(3-x)百万元,
∴f′(θ) =40a·(5-3cosθ)′·sinθs-in(25θ-3cosθ)·(sinθ)′ =40a·3-si5nc2θosθ. 令 f′(θ)=0,得 cosθ=35.
• (2)引入数学符号,建立数学模型.一般地, 设自变量为x,函数为y,并用x表示相关的 量,运用已掌握的数学知识、物理知识及 其他相关的知识,将问题中的数量关系表 示为一个数学关系式,实现问题的数学化, 即建立数学模型.
• [解析] 设圆柱的底面半径为r,高为h, • 则S圆柱底=2πr2,S圆柱侧=2πrh,
∴圆柱的表面积 S=2πr2+2πrh.∴h=S-2π2rπr2, 又圆柱的体积 V=πr2h=rS-22πr3,V′=S-26πr2, 令 V′=0 得 S=6πr2,∴h=2r,
又 r=
6Sπ,∴h=2
• 1.解决实际应用问题时,要把问题中所 涉及的几个变量转化成函数关系式,这需 要通过分析、联想、抽象和转化完成,函 数的最值要由 极值 和 端点的函数值 确定,当定义域是开区间 且 函 数 只 有 一 个 极值时,这个极值也就是它的 最值 .
• 2.生活中经常遇到求利润最大、用料最 省、效率最高等问题,这些问题通常称为 优化问题 .通过前面的学习,我们知道导数 是求函数最大(小)值的有力工具,运用导数 可以解决一些生活中的 优化问题 .
• 现该公司准备共投入3百万元,分别用于广 告投入和技术改造投入,请设计一种资金 分配方案,使得该公司获得最大收益.
• (注:收益=销售额-投入,答案数据精确 到0.01)
(参考数据: 2≈1.414, 3≈1.732)
• [解析] 设3百万元中技术改造投入为x百 万元,广告费投入为(3-x)百万元,
∴f′(θ) =40a·(5-3cosθ)′·sinθs-in(25θ-3cosθ)·(sinθ)′ =40a·3-si5nc2θosθ. 令 f′(θ)=0,得 cosθ=35.
生活中的优化问题举例课件

跨部门协作
加强部门间的沟通和协作 ,打破信息孤岛,提高整 体工作效率。
合理分配工作任务
任务分配原则
根据员工的能力、经验和专长, 合理分配工作任务,确保工作量
均衡和高效。
优先级排序
根据任务的重要性和紧急性,指导 员工对工作任务进行优先级排序, 确保高优先级任务得到优先处理。
激励与考核机制
建立有效的激励和考核机制,鼓励 员工积极承担工作任务,提高工作 积极性和满意度。
在此添加您的文本16字
优先处理重要和紧急的任务,避免拖延和浪费时间。
在此添加您的文本16字
学习一些时间管理技巧,如番茄工作法等。
在此添加您的文本16字
避免多任务处理,尽量专注于单一任务,以提高工作效率 。
04
工作中的优化问题
பைடு நூலகம்
提高工作效率
制定合理的工作计划
减少干扰因素
根据工作优先级和任务量,制定每日 、每周和每月的工作计划,确保工作 有序进行。
生活中的优化问题举例课件
• 购物中的优化问题 • 旅行中的优化问题 • 日常生活中的优化问题 • 工作中的优化问题 • 学习中的优化问题
01
购物中的优化问题
寻找最优惠的价格
01
在购物时,消费者通常会寻找最 优惠的价格,以节省开支。
02
比较不同商家的价格,考虑商品 的质量、品牌、售后服务等因素 ,权衡性价比,选择最优惠的价 格。
02
旅行中的优化问题
选择最佳的旅行路线
总结词
选择最佳的旅行路线是旅行中的重要优化问题,可以减少时间和金钱的浪费。
详细描述
在旅行前,我们需要根据目的地、交通工具、时间等因素,选择一条最佳的旅行 路线。这需要考虑路线的长度、所需时间、交通工具的舒适度、费用等因素,以 便在有限的时间内尽可能多地游览景点,并减少不必要的花费。
最新2019-23生活中的优化问题-PPT课件

r2),(0rR)
3
3
V2
2
(R2r4
r6)
9
(V2)'r
2
9
(4R2r36r5)
令(V2)'r 0,得r=
2 3R
0<r< 32R时, (V2)'r 0, 32RrR时, (V2)'r 0,
例2在半径为R的圆上取一个圆心角为α(弧度)的扇形 卷成的圆锥,问α为多大时,圆锥的体积最大?
耗油量y(升)关于行驶速度x(千米/小时)的函数解析式
可表示为y=1281000x383x8(0x120),已知甲乙两地 相距100千米
1. (2)当汽车以多大的速度匀速行驶时,从甲地到乙地耗 油量最少,最少为多少升?
( 2 ) 当 速 度 为 x 千 米 / 小 时 , 汽 车 从 甲 地 到 乙 地 行 驶 了 1 0 x 0 小 时 1. 设耗油量为h(x)升,依题意得
例5:在边长为60cm的正 方形铁皮的四角切去相等
的正方形,再把它的边沿虚 线折起(如图),做成一个无 盖的方底箱子,箱底边长为 多少时,箱子的容积最大?最大容积是多少?
解:设箱底边长为x cm,则箱高h=(60-x)/2 cm.箱子容积
V(x)=x2h=(60x2-x3)/2 (0<x<60). 令 V(x)60x3x2 0,解得x=0(舍去),x=40. 由题意可知,当x2过小(接近0)或过大(接近60)时,箱子 的容积很小,因此,且V(40)=16000 是最大值. 答:当x=40cm时,箱子容积最大,最大容积是16000cm3. 注意:题中有单位时在假设和答中均要写单位,在说
1. 因为h(x)在(0,120]上只有一个极小值,所以它是最小值
3
3
V2
2
(R2r4
r6)
9
(V2)'r
2
9
(4R2r36r5)
令(V2)'r 0,得r=
2 3R
0<r< 32R时, (V2)'r 0, 32RrR时, (V2)'r 0,
例2在半径为R的圆上取一个圆心角为α(弧度)的扇形 卷成的圆锥,问α为多大时,圆锥的体积最大?
耗油量y(升)关于行驶速度x(千米/小时)的函数解析式
可表示为y=1281000x383x8(0x120),已知甲乙两地 相距100千米
1. (2)当汽车以多大的速度匀速行驶时,从甲地到乙地耗 油量最少,最少为多少升?
( 2 ) 当 速 度 为 x 千 米 / 小 时 , 汽 车 从 甲 地 到 乙 地 行 驶 了 1 0 x 0 小 时 1. 设耗油量为h(x)升,依题意得
例5:在边长为60cm的正 方形铁皮的四角切去相等
的正方形,再把它的边沿虚 线折起(如图),做成一个无 盖的方底箱子,箱底边长为 多少时,箱子的容积最大?最大容积是多少?
解:设箱底边长为x cm,则箱高h=(60-x)/2 cm.箱子容积
V(x)=x2h=(60x2-x3)/2 (0<x<60). 令 V(x)60x3x2 0,解得x=0(舍去),x=40. 由题意可知,当x2过小(接近0)或过大(接近60)时,箱子 的容积很小,因此,且V(40)=16000 是最大值. 答:当x=40cm时,箱子容积最大,最大容积是16000cm3. 注意:题中有单位时在假设和答中均要写单位,在说
1. 因为h(x)在(0,120]上只有一个极小值,所以它是最小值
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
example_11_4_2.m
【例11-5】求解humps()函数在区间[0,1]内的
极小值。
• 解:为显示该优化问题的每一步的迭代过程,先编写优化方法的输出 函数myoutput.m并在优化参数中进行设置。
• function stop = myoutput(x,optimvalues,state); % 优化方法的输出函数 • history = []; • stop = false; • if state == 'iter' • history=[history;x]; • end • fplot(humps,[0,2]) • hold on • plot(history,humps(history),'r.',... • 'MarkerSize',14) % 绘制迭代点 • pause(1) % 暂停1秒
• 【例11-1】有两种液体产品P1和P2,每件产品P1在第一车间的处理时 间为1小时,在第二车间的处理时间为1.25小时;每件产品P2在第一车 间的处理时间为1小时,在第二车间的处理时间为0.75小时。每个车间 每月有200小时的时间可以利用,而且P2产品的市场需求量最大为150 件,假定P1产品和P2产品的利润每件分别为4美元和5美元,问P1产品 和P2产品的生产量分别为多少时生产商所获得的利润最大。
200
1.25 0
0.75 1
x1 x2
1程序:
• f=[-4;-5];
• A=[1,1;1.25,0.75;0,1];b=[200;200;150];
• lb=[0 0]; • [x,fval,exitflag]=linprog(f,A,b,[],[],lb) % 线性规划问题求解 • 为更直观地理解线性规划的几何意义,这里又编写了LP_demo.m函数
x0 (1.9,2)
• 解:首先绘制出Banana函数的曲面图。
• 下面进行优化求解,为获得更好的效果,这里采用动态图形来显示每 一步迭代的过程,这里首先介绍一个专门绘制“Banana”函数优化求 解迭代点的函数bandemoutfcn()。
• 调用函数fminsearch()求解上述优化问题,在原绘图程序的基础上输入 如下代码:
文运件行结。果:
x = 50.0000 150.0000 fval =-950.0000 exitflag =1
【例11-3】计算下面函数在 x,y[3,3]上的极值。
z f ( x ,y ) 3 ( 1 x ) 2 e x 2 ( y 1 ) 2 1 0 ( x x 3 y 5 ) e x 2 y 2 1 e ( x 1 ) 2 y 2
'OutputFcn' • [x,fval,exitflag,output]=fminsearch(f,x0,OPTIONS)
example_11_4_1.m
• 下面再利用fminunc()函数求解上述优化问题,编写如下程序代码: • x0=[-1.9,2]; • OPTIONS=optimset('LargeScale','off','OutputFcn',bandemoutfcn); % 设置
• plot3(-1.9,2,267.62,'ko','markersize',12,'linewidth',1,'erasemode','none') • text(-1.9,2.3,267.62,'\fontname{隶书}\fontsize{16}开始','color',[0,0,0]) • plot3(1,1,0,'ko','markersize',12,'linewidth',1,'erasemode','none') • text(1,1.3,100,'\fontname{隶书}\fontsize{16}结束','color',[0,0,0]) • set(gcf,'Color','w') • x0=[-1.9,2]; • f='100*(x(2)-x(1)^2)^2+(1-x(1))^2'; % 利用字符串定义函数表达式 • OPTIONS=optimset('OutputFcn',bandemoutfcn); % 设置优化控制参数
vals',200, 'InitialHessType','scaled-identity','LineSearchType','quadcubic'); % 更新优化参数 • [x,fval,exitflag,output]=fminunc({f,grad},x0,OPTIONS) % 优化问题求解
• 解:设P1产品和P2产品的生产量分别为x1和x2时生产商所获得的利润 最大,则目标函数和约束条件可以写为:
min
4x1 5x2
x1 x2 200 x s.t. 1.25x1 0.75x2 200
x1 0, 0 x2 150
f [4,5]T
1 1
5
3
• 解:首先绘制该二元函数在z=0上下两部分的曲面图,
• 下面编写求极值的主函数,这里由于不知道初始点,所以借助ginput() 函数在等高线图形上取点作为初始点的横纵坐标,得到的结果如图:
▲
3 ▲: 极大值点 : 极小值点
2
10
15
最 优 值 :8.1062
0
0
-5
-1
-10 3
-2
-3 -3
最优值:-3.0498 最优值:-0.064936 最 优 值 :3.5925
最 优 值 :3.7766
2 1
-2
0 -1
-1
最 优 值 :-6.5511
-1
-2
-2
-3 -3
0
1
1 0
2
3 2
pea3 ks_jizhi.m
【例11-4】Banana函数优化。
f(x ,y ) 1 0 0 (y x 2 )2 (1 x )2
优化参数 • grad='[100*(4*x(1)^3-4*x(1)*x(2))+2*x(1)-2;100*(2*x(2)-2*x(1)^2)]'; %
梯度表达式描述 • f='100*(x(2)-x(1)^2)^2+(1-x(1))^2'; % 函数表达式 • OPTIONS=optimset(OPTIONS,'HessUpdate','bfgs','gradobj','on','MaxFunE
【例11-5】求解humps()函数在区间[0,1]内的
极小值。
• 解:为显示该优化问题的每一步的迭代过程,先编写优化方法的输出 函数myoutput.m并在优化参数中进行设置。
• function stop = myoutput(x,optimvalues,state); % 优化方法的输出函数 • history = []; • stop = false; • if state == 'iter' • history=[history;x]; • end • fplot(humps,[0,2]) • hold on • plot(history,humps(history),'r.',... • 'MarkerSize',14) % 绘制迭代点 • pause(1) % 暂停1秒
• 【例11-1】有两种液体产品P1和P2,每件产品P1在第一车间的处理时 间为1小时,在第二车间的处理时间为1.25小时;每件产品P2在第一车 间的处理时间为1小时,在第二车间的处理时间为0.75小时。每个车间 每月有200小时的时间可以利用,而且P2产品的市场需求量最大为150 件,假定P1产品和P2产品的利润每件分别为4美元和5美元,问P1产品 和P2产品的生产量分别为多少时生产商所获得的利润最大。
200
1.25 0
0.75 1
x1 x2
1程序:
• f=[-4;-5];
• A=[1,1;1.25,0.75;0,1];b=[200;200;150];
• lb=[0 0]; • [x,fval,exitflag]=linprog(f,A,b,[],[],lb) % 线性规划问题求解 • 为更直观地理解线性规划的几何意义,这里又编写了LP_demo.m函数
x0 (1.9,2)
• 解:首先绘制出Banana函数的曲面图。
• 下面进行优化求解,为获得更好的效果,这里采用动态图形来显示每 一步迭代的过程,这里首先介绍一个专门绘制“Banana”函数优化求 解迭代点的函数bandemoutfcn()。
• 调用函数fminsearch()求解上述优化问题,在原绘图程序的基础上输入 如下代码:
文运件行结。果:
x = 50.0000 150.0000 fval =-950.0000 exitflag =1
【例11-3】计算下面函数在 x,y[3,3]上的极值。
z f ( x ,y ) 3 ( 1 x ) 2 e x 2 ( y 1 ) 2 1 0 ( x x 3 y 5 ) e x 2 y 2 1 e ( x 1 ) 2 y 2
'OutputFcn' • [x,fval,exitflag,output]=fminsearch(f,x0,OPTIONS)
example_11_4_1.m
• 下面再利用fminunc()函数求解上述优化问题,编写如下程序代码: • x0=[-1.9,2]; • OPTIONS=optimset('LargeScale','off','OutputFcn',bandemoutfcn); % 设置
• plot3(-1.9,2,267.62,'ko','markersize',12,'linewidth',1,'erasemode','none') • text(-1.9,2.3,267.62,'\fontname{隶书}\fontsize{16}开始','color',[0,0,0]) • plot3(1,1,0,'ko','markersize',12,'linewidth',1,'erasemode','none') • text(1,1.3,100,'\fontname{隶书}\fontsize{16}结束','color',[0,0,0]) • set(gcf,'Color','w') • x0=[-1.9,2]; • f='100*(x(2)-x(1)^2)^2+(1-x(1))^2'; % 利用字符串定义函数表达式 • OPTIONS=optimset('OutputFcn',bandemoutfcn); % 设置优化控制参数
vals',200, 'InitialHessType','scaled-identity','LineSearchType','quadcubic'); % 更新优化参数 • [x,fval,exitflag,output]=fminunc({f,grad},x0,OPTIONS) % 优化问题求解
• 解:设P1产品和P2产品的生产量分别为x1和x2时生产商所获得的利润 最大,则目标函数和约束条件可以写为:
min
4x1 5x2
x1 x2 200 x s.t. 1.25x1 0.75x2 200
x1 0, 0 x2 150
f [4,5]T
1 1
5
3
• 解:首先绘制该二元函数在z=0上下两部分的曲面图,
• 下面编写求极值的主函数,这里由于不知道初始点,所以借助ginput() 函数在等高线图形上取点作为初始点的横纵坐标,得到的结果如图:
▲
3 ▲: 极大值点 : 极小值点
2
10
15
最 优 值 :8.1062
0
0
-5
-1
-10 3
-2
-3 -3
最优值:-3.0498 最优值:-0.064936 最 优 值 :3.5925
最 优 值 :3.7766
2 1
-2
0 -1
-1
最 优 值 :-6.5511
-1
-2
-2
-3 -3
0
1
1 0
2
3 2
pea3 ks_jizhi.m
【例11-4】Banana函数优化。
f(x ,y ) 1 0 0 (y x 2 )2 (1 x )2
优化参数 • grad='[100*(4*x(1)^3-4*x(1)*x(2))+2*x(1)-2;100*(2*x(2)-2*x(1)^2)]'; %
梯度表达式描述 • f='100*(x(2)-x(1)^2)^2+(1-x(1))^2'; % 函数表达式 • OPTIONS=optimset(OPTIONS,'HessUpdate','bfgs','gradobj','on','MaxFunE
