CT图像重建(X线成像系统)
ct重建算法

CT重建算法1. 介绍计算机断层扫描(Computed Tomography, CT)是一种通过旋转式X射线扫描来获取物体内部详细结构的成像技术。
CT重建算法是将获得的一系列投影数据转化为图像的过程。
本文将介绍CT重建算法的原理、常见算法以及应用。
2. 原理CT重建算法的原理基于X射线的相对吸收特性。
当X射线通过物体时,被吸收的程度与物体的密度有关。
通过在不同角度上获得物体的吸收投影数据,可以得到物体的密度分布。
CT重建算法将这些投影数据转换为物体的二维或三维图像。
3. 常见算法3.1 过滤回投影算法(Filtered Backprojection)过滤回投影算法是最常用的CT重建算法之一。
它在重建过程中使用反投影和滤波两个步骤。
反投影(Backprojection)是将投影数据沿着投影路径反向投射到图像平面上。
滤波(Filtering)是为了抵消投影数据中带来的伪影,通常使用高通滤波器来增强边缘。
过滤回投影算法的优点是简单、快速,适用于大部分CT重建应用。
然而,它对数据质量要求较高,容易受到噪声的影响。
3.2 代数重建技术(Algebraic Reconstruction Technique,ART)代数重建技术是一种迭代重建算法。
它通过假设一个初始图像,然后通过反复调整该图像,使其产生的投影数据与实际投影数据越来越接近。
ART算法的优点是对噪声更加稳健,并且可以提供更好的图像质量。
然而,它的计算量较大,需要更长的重建时间。
3.3 迭代重建算法除了ART算法,还有其他一些迭代重建算法,如最小二乘迭代算法、最小均方偏差迭代算法等。
这些算法的思想都是通过迭代过程逐步调整图像,使其产生的投影数据与实际投影数据更接近。
迭代重建算法的优点是能够处理高噪声情况下的重建问题,并且可以提供更好的图像质量。
然而,它的计算量较大,需要更长的重建时间。
4. 应用CT重建算法在医学领域有着广泛的应用。
它可以用于诊断与鉴别诊断,如放射影像学、肿瘤检测和血管成像等。
医学成像系统

医学成像系统
目 录
• 医学成像系统概述 • CT(计算机断层扫描)成像系统 • MRI(核磁共振成像)系统 • X光成像系统
01
医学成像系统概述
定义与特点
定义
医学成像系统是一种用于医学诊断和治疗的技术,通过图像呈现人体内部结 构和功能。
特点
高分辨率、高灵敏度、高对比度、无创性、实时性。
医学成像系统的历史与发展
历史
医学成像技术自19世纪初以来不断发展,经历了从早期的X光成像到现代的核磁 共振、超声和内窥镜等技术的发展过程。
发展
随着科技的不断进步,医学成像系统的技术和设备不断升级,成像质量、速度和 精度不断提高,为临床诊断和治疗提供了更多可能性。
医学成像系统的类型
X光成像
CT(计算机断 层扫…
X光图像质量与临床应用
X光图像质量
影响X光图像质量的因素包括曝光时间、管电压、焦距和对比 度等。通过对这些参数的调整,可以获得高质量的X光图像。
X光临床应用
X光广泛应用于骨折、关节脱位等骨骼疾病的检查,以及胸部 、腹部等内脏疾病的检查。同时,在牙科和口腔科等领域,X 光也被用于检查牙齿和颌骨等硬组织疾病。
THANK YOU.
产生射频脉冲,并接收回波信号。
计算机系统
进行数据处理和图像重建。
其他辅助设备
如病人床、射频屏蔽室等。
MRI图像质量与临床应用
1
图像质量因素:包括分辨率、对比度、信噪比 等。
2
临床应用广泛:如神经系统、肌肉骨骼、肿瘤 等疾病的诊断。
3
MRI与其他成像技术比较:如CT、X光、超声 等。
04
X光成像系统
X光设备结构与功能
X光设备结构
医学图像处理-第3章-X射线计算机体层成像
3.灰度
灰度:指图像面黑白或明暗的程度。 从全黑到全白可有无数个不同的灰度。 CT 影像是以灰度分布的形式显示的图像 。
CT图像的本质是μ成像。
若CT值按2000个计算,相应的灰度值也有 2000个,即从全黑(CT值为-l000)到全白 (CT值为+1000)有2000个不同的黑白或明 暗等级(灰度),CT像是一个灰度不同、且 灰度变化不连续的图像。
造成CT图像的不均匀性。
22
2.CT值
μ是一个物理量,CT值表达人体组织对X线
衰减的量值 。
CT值定义:CT影像中每个像素对应的物质 对X线线性平均衰减量大小的表示。应用中 CT值:人体被测组织的吸收系数与水的吸收
系数的相对值: CT值x wK w
CT值单位“HU” 。μw为73keV能量X线在水
解出180×180个单元体所对应的μ 。 32
3.2.2 数据采集基本原则
CT成像数据采集是利用X线管和检测器等的 同步扫描来完成。 检测器是一种X线光子转换为电流信号的换 能器。 1.须按空间位置有规律地进行 X线束经被测人体层面吸收的投影是X线束 扫描位置的函数。 数据采集须按照被测人体层面的空间位置有 规律地进行。
主要内容 3.1 CT成像技术发展 3.2 CT成像原理 3.3 数据采集与扫描方法 3.4 CT图像重建 3.5 CT图像处理 3.6 图像重建方法
4
第一节 CT成像技术发展
5
3.1 CT成像技术发展
1917年,雷登(J.Radon) 指出对二维或三 维的物体,可以从各个不同方向上的投影,用 数学方法计算出唯一的一张重建图像。称之谓 雷登变换。
7
1967年,豪斯菲尔德(Godfrey Hounsfield)制成了 第一台可用于临床的CT。1971年9月第一台头扫 描CT机安装在英国的一所医院中。
CT技术的图像重建

CT(计算机断层成像,Computed Tomography 的缩写)技术是20世纪50至70年代由美国科学家A. M. Cormark和英国科学家G. N. Hounsfield通过核物理、核医学等领域的一系列研究和实验发明的,他们因此共同获得1979年诺贝尔医学奖。
从1971年第一代供临床应用的CT设备问世以来,随着电子技术的飞速发展,CT技术不断改进,诸如螺旋式CT机、电子束扫描机等新型设备逐渐被医疗机构普遍采用。
此外,CT技术在工业无损探测、资源勘探、生态监测等领域也得到了广泛的应用(参考文献)。
什么是CT,它与传统的X射线成像(如人们在医院拍的X光片)有什么区别?让我们看一个一般的概念图示,如图一。
假定有一个半透明物体,其中嵌入5个不同透明度的球。
如果按照照片1(a)那样单方向地观察,因为有2个球被前面的球遮挡,我们可能错误地认为只有3个球,尽管重叠球的透明度较低,任无法确定球的数目,更不要说各个球的透明度了。
而如果按照图1(b)那样让物体旋转起来,从多角度观察,就能够分辨出5个球以及他们各自的透明度。
到医院作射线检查时,人体的内脏就像上面的半透明物体,传统的X射线成像原理就像图1(a),X 射线和胶片相当于光源和人眼;CT技术原理就像图1(b),只不过旋转的不是人体,而是X 光管和探测器。
概括地说,传统的X射线成像将人体器官和组织前后重叠地直接投影到胶片上,呈现出具有一定分辨率、但仍不够清晰的图像,CT则在不同深度的断面上,从各个角度用探测器接收旋转的X光管发出、并由于穿过人体而使强度衰减的射线,再经过测量和计算,将人体器官和组织的影像重新构建出来,称为图像重建。
X射线强度衰减与图像重建的数学原理X射线在穿过均匀材料的物质时,其强度的衰减率与强度本身成正比,即其中I为射线强度,l为物质在射线方向的厚度,u为物质对射线的衰减系数。
由此可得其中I0为入射强度,当X射线的能量一定时,衰减系数u随射线穿过的材料不同而改变,如骨骼的u比软组织的大,X射线的强度在骨骼中衰减得更快。
2.225.2CT系统结构医学影像设备学
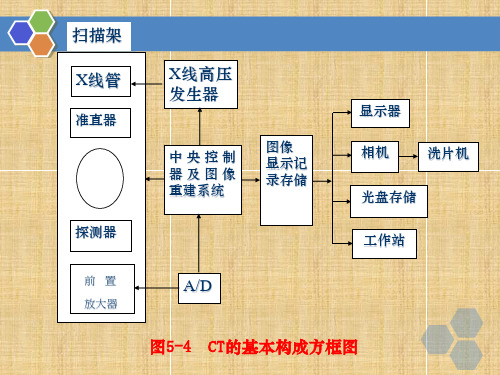
❖ 作用:探测器是将X线能量转换为电信号的装 置。
256排探测器
(三)探测器 探测器类型有两种: ❖ 一种是气体探测器; ❖ 另一种是荧光固体探测器。 荧光固体探测器又分为两种:
▪ 闪烁探测器 ▪ 稀土陶瓷探测器 稀土陶瓷探测器X线吸收利用率可达99% 。
(四)数据采集系统 数据处理主要由前置放大器、对数放大器、积分
器、多路转换器、模/数转换器、接口电路等构成。 作用:将探测器输出的微弱电信号经放大后,再
经ADC转换为计算机能够识别的数字信号,并经接 口电路将此数字信号输入计算机。
(五)扫描机架 一是旋转部分,主要由X线管
及其冷却系统、准直器及其控制 系统、滤过器、探测器、数据处 理装置、滑环部分、高压发生器 (低压滑环式SCT)等组成。
2.CT X线管 CT X线管也有固定阳极X线管和旋转阳极X线
管两种。 固定阳极管的长轴与探测器平行; 旋转阳极X线管的长轴则与探测器垂直。
CT 管及冷却外形
电子束控金属球管
(二)准直器(collimator)与滤过器(filter) 1.X线准直器 (collimator)
(1)限定成像的空间范围(限定断层层厚) (2)降低受检者的表面辐射剂量 (3)减少进入探测器的散射线
❖ 准直器可决定扫描层的厚度。常见CT扫描层的 厚度为1mm、2mm、3mm、5mm、7mm、8mm、10mm。 准直器结构简单,但要求非常精确 。
2.X线滤过器
(1)
(2)
CT的滤过器
❖ 数据采集系统简称DAS,是扫描系统的重要 组成部分。它由探测器(detector)和数据处理 装置组成。
X线计算机体层成像设备XCT

X线计算机体层成像设备XCT
第36页
1
2
I0是入射前X线强度 I是入射后X线强度
μ是均匀介质线性衰减系数
d为物质厚度
X线计算机体层成像设备XCT
第37页
X线计算机体层成像设备XCT
第38页
❖ 公式1中所用介质是均匀一致介质,人体能够看成 全部组织衰减系数加权平均。
❖ 公式2是测定物质衰减系数基本关系式和基本依据 。经过它,得到投影值和二维分布矩阵,由此重 建出图像。
X线计算机体层成像设备XCT
第39页
❖ (二)CT图像重建基本方法
❖ 图像重建方法是图像矩阵求解方法。如有N×N 图像矩阵,有N×N个独立线性方程组,而且求解 N×N个矩阵中体素吸收系数 μij 。
X线计算机体层成像设备XCT
第52页
❖ (三)滤过器
❖ ①吸收低能X线,这些低能射线对CT图像形成没 有任何作用,不过却增加了病人照射剂量。
❖ ②使穿过滤过器和受检者投射线束能量分布到达 均匀硬化。
X线计算机体层成像设备XCT
第53页
❖ (四)探测器
❖X 射线探测器(Detector)是一个将 X 射线能量转 换为可供统计电信号装置。 它接收到射线照射, 然后产生与辐射强度成正比电信号。通常,探测 器所接收到射线信号强弱,取决于该部位人体截 面内组织密度。密度高组织,比如骨骼吸收 X 射 线较多,探测器接收到信号较弱;密度较低组织 ,比如脂肪等吸收 X 射线较少,探测器取得信号 较强。这种不一样组织对 X 射线吸收值不一样性 质可用组织吸收系数 m 来表示,所以探测器所接 收到信号强弱所反应是人体组织不一样 m值,从 而对组织性质作出判断。
CT图像重建技术

CT图像重建技术CT图像重建技术000计算机层析成像(Computed Tomography,CT)是通过对物体进行不同角度的射线投影测量而获取物体横截面信息的成像技术,涉及到放射物理学、数学、计算机学、图形图像学和机械学等多个学科领域。
CT技术不但给诊断医学带来革命性的影响.还成功地应用于无损检测、产品反求和材料组织分析等工业领域。
CT技术的核心是由投影重建图像的理论,其实质是由扫描所得到的投影数据反求出成像平面上每个点的衰减系数值。
图像重建的算法有很多,本文根据CT扫描机的发展对不同时期CT所采用重建算法分别进行介绍。
第一代和第二代CT机获取一个单独投影的采样数据是从一组平行射线获取的,这种采样类型叫平行投影。
平行投影重建算法一般分为直接法与间接法两大类。
直接法是直接计算线性方程系数的方法,如矩阵法、迭代法等。
间接法是先计算投影的傅立叶变换,再导出吸收系数的方法,如反投影法、二维傅立叶重建法和滤波反投影法等[1]。
2.1 直接法2.1.1 矩阵法设一个物体的内部吸收系数矩阵为:(1)为了求得该矩阵中的元素值,我们可以先计算该矩阵在T个角度下的T组投影值 ,如设水平方向时 ,则:(2)同样其它角度下也有类似方程,把所有方程联立得到求解,即可求得所有u值。
通常情况下,由于联立方程组的数目往往不同于未知数个数,且可能有不少重复的方程,这样形成的不是方阵,所以一般不满秩,此时需要利用广义逆矩阵法进行求解。
2.1.2 迭代法实际应用中,由于图像尺寸较大,联立的方程个数较多,采用直接采用解析法难度较大,因此提出了迭代重建方法。
迭代法的主要思想是:从一个假设的初始图像出发,采用迭代的方法,将根据人为设定并经理论计算得到的投影值同实验测得的投影值比较,不断进行逼近,按照某种最优化准则寻找最优解[2]。
通常有两种迭代公式,一种是加法迭代公式[2]:(3)另一种是乘法迭代公式[2]:(4)两式中是相邻两次迭代的结果;是某一角度的实测投影值,是计算过程的计算投影值, 是投影的某一射线穿过点的点数,即计算投影值的射线所经过的像素的数目,是松弛因子。
CT图像重建

昆明理工大学信息工程与自动化学院学生实验报告(2009 —2010学年第一学期)课程名称:医学成像系统与放射治疗装置开课实验室:3208 2008 年12月24日、实验目的与意义医学成像技术是生物医学工程专业的一门重要的专业课程,课程主要涉及X光仪器,CT仪器,MRI仪器和核医学仪器的工作原理及成像方法。
其中CT算法的出现又为后来数字化医学成像技术的发展提供了基础。
该门课程为生物医学工程专业的专业基础课。
CT技术是医学成像系统中的一种重要手段。
它通过特定的算法,利用计算机的高速运算功能,可以在短时间内快速呈现人体断层图像。
让学生练习CT图像的重建有助于学生理解CT算法的内容,熟悉数字图像重建的过程。
同时也能培养学生的团队精神和解决实际问题的能力。
二、实验算法原理1、M ATLA处理数字图像的基本函数;2、X-CT三维图像重建的基本算法。
CT图象重建有四种基本的算法:矩阵法,迭代法,傅立叶算法,反投影算法.我们采用的方法为卷积反投影•卷积反投影有:平行光束投影的卷积反投影算法,等角扇形光来投影的重建算法•1).平行光束投影的卷积反投影算法从投影重建三维物体的图像,就是重建一个个横断面。
这样三堆图像的重建就归结为二维图象的重建。
二维图像的重建问题可以从数学上描述如下。
假定g(x,y)表示一个二维的未知函数,通过g(x,y)的直线称为光钱(见图2. 1)。
沿光线g(x,y)的积分称作光线积分。
沿相同方向的一组光线积分,就构成一个投影。
图2. 1中垂直于直线CC'(与X轴夹角为)的光线所形成。
图2.1 g(x, y)在方向的投影P (t)的投影P(t),称之为g(x,y)在方向的投影。
光线积分和投影在数学上可以定义如下:在图2.1中直线AB的方程为:X cos Ysin t i (2.1)其中t i是AE到原点的距离,g(x,y)沿AB的积分为:P (t i) AB g(x, y)ds g(x, y) (xcos ysin tjdxdy (22)对于给定的,g(x, y)在方向的投影P (t)是t的函数。
CT成像原理介绍PPT课件

CT成像与其他医学影像技术的比较
与传统的X射线相比,CT成像能够提供 更准确的内部结构信息,并且能够通过
三维重建技术展示物体的立体图像。
MRI(磁共振成像)与CT成像有类似 的成像原理,但MRI使用磁场而非X射 线,适用于某些类型的检查,如神经系
统和关节。
Ultrasound(超声成像)是一种无创 、无辐射的成像技术,适用于观察软组 织,但在观察骨结构和肺部等方面不如
放射治疗计划制定
靶区勾画
放射治疗前,医生通过CT图像精 确勾画出肿瘤的位置和大小,作
为制定放疗计划的依据。
剂量计算
基于CT图像,可以对放疗剂量进 行精确计算,确保肿瘤得到足够 照射而周围正常组织不受损伤。
放疗验证
通过比较放疗前后的CT图像,可 以验证放疗效果,及时调整治疗
方案。
科研和教学
医学研究
通过傅里叶变换,可以将投影数据从空间域转换到频率域,从而更好地突出物体 的边缘和细节。
滤波反投影算法
滤波反投影算法是CT成像中最常用的算法之一。它通过滤波和反投影两个步骤来重 建图像。
滤波是为了去除噪声和伪影,提高图像质量。反投影则是将滤波后的数据还原成图 像的过程。
滤波反投影算法具有快速、稳定和易于实现的特点,因此在现代CT成像中得到了广 泛应用。
02
CT成像能够提供物体内部结构的 二维或三维图像,广泛应用于医 学、工业和科研等领域。
CT成像的发明和发展
1960年代初,英国工程师Godfrey Hounsfield发明了第一台CT扫描仪 ,并获得了1979年的诺贝尔生理学 或医学奖。
随着技术的不断发展,CT成像的扫描 速度、分辨率和图像质量得到了显著 提高,同时出现了多种不同类型的CT 扫描仪,如多排螺旋CT、双源CT等。
医学影像图像重建

举例:
12
99
12
A D
B E
C F
6 15
0o
C A
D B
E F
12
9
60o
A B
F C
E D
ቤተ መጻሕፍቲ ባይዱ
12
9
120o
A 1
B
2
C 3
D
4
E 5
F 6
B
6
A
C
F
D
E
15
0o 得6
15
60o 120o 12 12 99
❖ 每进行一次扫描,X线束将沿某一方向进行投影,从 而得到一个断层面上各个体元的线积分。假设将一
现
▪ 在每一次迭代过程中,将近似重建得到的图像的投影 同实测的投影进行比较,然后将比较得到的差值反投 到图像上,每一次反投影之后得到一幅新的近似图像
▪ 当对所有的投影方向都进行上述处理后,一次迭代便 完成,用前一次迭代的结果作为下一次迭代的初始值, 继续上述步骤
▪ 直到做了一定次数的迭代后,认为迭代的结果已经足 够准确,则重建过程结束
回去,得到各个反投影图像gθ(x)
g (r ) (r cos( ))
再将各个方向上的反投影相加
b(r )
g
(r )
1
0
(r
c os (
))
求得各个方向上的反投影累加b(r)
❖ 重建步骤:
求出各方向上的投影
求得对应的反投影累计
进行傅里叶变换
用滤波窗卷积的办法进行滤波
解析法重建
反傅里叶变换
❖FBP法:先在频率空间对投影数据进行滤波,再将滤 波后的投影数据反投影得到重建断层图像
CT图像重建(CT Image Reconstruction)

Shepp-Logan体模
S-L体模是CT图像重建领域用于仿真计算的经典头部模型, 于1974年由L.A.Shepp和B.F.Logan首次提出,可生成2D或者 3D的标准投影数据。S-L体模通过椭圆来表征不同的形状, 不同的灰度用来模拟不同组织的衰减系数,例如最外层的椭 圆模拟头骨,内部的两个小椭圆模拟大脑内部特征或者肿瘤。
CT图像重建 (CT Image Reconstruction)
学习内容(Learning objects)
❖ CT图像重建的历史( A brief history ) ❖ 基本术语(Some basic terms) ❖ 图像重建思想(Reconstruction ideas) ❖ 图像重建算法(Reconstruction algorithms)
Johann Radon entered the University of Vienna where he was awarded a doctorate in 1910 for a dissertation on the calculus of variations. The year 1911 he spent in Göttingen, became assistant professor at the University of Brünn (now Brno) for a year and then moved to the Technische Hochschule in Vienna. In 1919 Radon became assistant professor at Hamburg becoming a full professor in Greifswald in 1922. He was appointed to the University of Vienna in 1947 and he remained there for the rest of his life.
医学成像系统实验-X-CT图像重建

医学成像系统实验:X-CT图像重建实验目的:Sheep-Logan模型是由10个位置、大小、方向、密度各异的椭圆组成,用来模拟一个脑断层的图像。
通过该模型,可以获得各个投影方向上数据的解析表达式。
利用matlab产生Sheep-Logan模型的仿真投影数据,重建X-CT图像,从而理解图像重建算法。
实验内容:基本要求部分1.利用Sheep-Logan头部模型生成平行束投影。
本部分要求:写出平行束投影表达式,根据Sheep-Logan模型自行编程生成各个方向上投影离散数据,与matlab函数所生成的数据加以比较,充分理解X-CT 投影数据获得的过程。
2.根据平行束投影数据重建图像。
本部分要求:自行编写利用滤波反投影法、R-L函数卷积反投影法、S-L函数重建图像的程序,比较重建的效果,并与matlab提供的函数相比较,充分的理解平行束投影重建算法。
3.在重建过程中,引入噪声、检测器损坏、旋转中心偏移等问题,对重建的结果加以比较和探讨。
可获得免试资格的选做部分(仍选其一即可获得免试资格,根据完成的水平给与相当于期末考试的分数,多选多得分)1.扇形束重建:利用Sheep-Logan模型,根据扇形束投影的原理自行编程生成投影数据,与matlab函数比较;利用数据重排方法和直接加权反投影方法重建图像,比较效果;在重建过程中,同样引入一些误差来源加以分析;理解共轭采样对,分析重建所需的最小数据集。
2.三维螺旋X-CT仿真:自行生成一组重叠或者相套的椭球模型作为体数据,设计一组螺旋X-CT的参数(多排/单排、p=d/W),根据投影原理,生成一套投影数据,利用360°差值和180°差值重建若干个断面的图像,与仿真数据比较,分析重建效果;改变一些配置的参数,比较重建效果。
3.迭代重建算法:自行查阅文献,理解迭代中间算法的基本原理,根据投影数据实现迭代重建算法,与各类反投影算法加以比较,分析优、缺点。
CT图像重建

二、问题引入
• 复杂投影问题
如果断层成像问题再复杂一点我们怎么办呢? 比如说,公园里有很 多很多树。仅靠两张照片就能画出一张公园地图吗? 如果我们考虑 的矩阵远远大于两行两列,仅仅靠知道每一行的和及每一列的和, 我们能解出原矩阵吗? 一般来说,不能。
二、问题引入
• 复杂投影问题
我们需要更多的数据。这些数据从何而来呢? 我们需要从更多不同 的角度来采集数据。类似于上面谈到的“猜猜矩阵”的问题,我们 需要从不同的角度对矩阵求和。这样一来,就需要用到更复杂的数 学来解决一个实际的断层成像问题。
统计迭代重建算法:统计迭代重建质量被普遍认为要优于 FBP 算法,但其 仍未得到推广,一个原因是由于统计迭代自身仍然存在不足,主要是重建时 间较长和适应性较差。
四、图像重建的数学方法
X-CT图像重建方法总结
代数重建法 ( ART )
迭代法
联合迭代重建法 (SIRT )
图像重建方法
基于统计学的优化方法
四、图像重建的数学方法
1、联立方程式法
2、迭代法
2、反投影法
断层平面中某一点的密度值可以看作是这一平面内所有经过该 点的射线的投影值之和(的均值)
• 设x1=5,x2=0,x3=2,x4=18
(3)
(4)
• p1=x1+x2=5, p2=x3+x4=20 • p3=x1+x4=7, p4=x2+x4=18 • p5=x3=2, p6=x1+x4=23,p7=x2=0
5 3.3 4.1 8.7
3、滤波反投影法(Filtered back projection) 也称为卷积反投影法(convolution back projection,CBP)
CT图像重建(X线成像系统)

ED=D×Wr
当辐射有多个种类和能量时,在一个组织或器官的 当量剂量就是各个辐射所致的当量剂量的和。
CT剂量
ED给出了不同辐射条件下人体发生生物效应的定量描述,但 人体不同组织或器官对辐射的敏感性和给人体造成的危害是 不同的。 因此又提出组织权重因子Wt(tissue weighting factor) 对上述的ED进行进一步修正。由Wr 和Wt两个因子修正后的 吸收剂量称为有效剂量(effective dose,ED)
伦琴表达照射量只用于能量低于3MeV的X线或 射线辐射,不 适合粒子辐射或能量高于3MeV的光子。 只适用于描述射线对空气的照射,并不能准确表达患者对辐射 的吸收。
பைடு நூலகம்
CT剂量
吸收剂量
描述组织吸收的射线能量 国际单位为:戈瑞(Gy) 1Gy=1J/kg 定义:1kg物质(人体组织)吸收1焦耳能量时的辐射量 吸收剂量D:质量为m(kg)的物质在辐射中吸收的能量 为E(J)时,其吸收剂量 D=E/m (Gy)
CT图像重建
直接反投影法的局限:
容易产生星形伪影
产生原因:反投影法把取 自有限物体空间的投影均 匀地回抹(反投影)到了 射线所及的无限空间的各 个像素上,包括原来像素 值为0的点。
CT图像重建
中心切片定理
CT图像重建
中心切片定理:某断层(或它对应的图像)f(x,y)在视角为 时 得到的平行投影(函数)的一维傅里叶变换,等于f(x,y)二维傅 里叶变换F(w1,w2 )过原点的一个垂直切片,且切片与轴w1相交成
CT剂量
CT剂量
CT剂量
CT剂量
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
DE=D×QF
DE单位:希沃特(Sv),D:戈瑞(Gy),QF:无量纲
DE常用于辐射防护的定量计算。
CT剂量
当量剂量和有效剂量
综合以人类为对象的研究结果,专家们对QF进行 了适当的调整,确定了辐射权重因子Wr (radiation weighting factor)的值,并提出了 当量剂量ED( equivalent dose)的概念。
CT图像重建
p即为CT扫描过程中采集到的投影数据
P是输入射线与输出射线强度比值的对数,在数值上等于沿射线 方向上物质的衰减系数的线积分。
CT重建问题:已知物质的X线衰减系数的线积分,如何求解它的 线性衰减系数分布?
数据预处理
投影数据测量误差:
假设X线束是单能的
散射线问题:假定所有到达探测器的都是初级X线光子
CT图像重建
直接反投影法
CT图像重建
反投影法的基本思想
在对某一层面一个方向的扫描完成后,用得到的投影值沿着 扫描路径回抹到体素对应的像素上。改变方向后的多次扫描 形成多次回抹,同一像素上多次回抹的灰度累加即完成图像 重建。
反投影法示例
CT图像重建
第一次运算:水平照射后,将射线和放入图像单元
CT图像重建
直接反投影法的局限:
容易产生星形伪影
产生原因:反投影法把取 自有限物体空间的投影均 匀地回抹(反投影)到了 射线所及的无限空间的各 个像素上,包括原来像素 值为0的点。
CT图像重建
中心切片定理
CT图像重建
中心切片定理:某断层(或它对应的图像)f(x,y)在视角为 时 得到的平行投影(函数)的一维傅里叶变换,等于f(x,y)二维傅 里叶变换F(w1,w2 )过原点的一个垂直切片,且切片与轴w1相交成
CT图像重建
概述 直接矩阵变换法 直接反投影法 中心切片定理 滤波反投影法
CT图像重建
概述
CT图像重建
投影重建图像理论的提出
1917年,奥地利数学家Radon提出了投影重建图像的理论 Radon的观点解决了从函数的线积分求解原函数的问题,即由 物体的一组横断面的投影来重建其横断面图像。
CT图像重建
工程可实现的滤波反投影法的重建步骤:
在某个投射方向上(设角度为 )对物体进行平行束扫描, p(t , ) 获得离散的投影数据 对投影数据 p(t , ) 填补足够多的0以避免“周期间”的干
扰,得到 p ' (t , ) 对补零后的投影 p' (t , ) 进行傅里叶变换,得到 P' (, ) 给频域的投影 P' (, ) 乘以一个滤波函数 H ' ( ) ,得到滤 波后投影的傅里叶变换 G ( , )
CT图像重建
反投影法图解
假设位于扫描范围内只有 一个钉子,则经过钉子进 行一个方向扫描的投影是 一个脉冲函数。 将测得的脉冲信号反投影 到矩阵中去,就得到第一 次反投影。
CT二次线性扫描,将测到的 脉冲信号再反投影到矩阵中去, 得到第二次反投影。 系统每旋转一次,便构成一次 新的反投影。 所有反投影的叠加形成了一个 带有星形伪影的图像,即一个 扩散的圆形区域。
ED=D×Wr×Wt
ED(有效剂量)考虑了人体具体组织器官承受辐射的能力和 危险系数,能更准确地反映不同类型的辐射对人体造成的危 害。
CT剂量
CT剂量分布曲线
CT剂量
CT剂量和普通放射剂量的区别
普通放射过程中剂量接受面积大,剂量一般集中在皮肤表面,而 CT的射线源在不停地旋转,剂量分布比较均匀。 CT采用窄束X线,普通放射检查采用宽束射线。在同样照射条件 下,宽束线散射线多。 CT检查的射线能量高,线质硬,穿透性强,被人体吸收少。 CT的探测器转换效率高,射线利用率高。 CT辐射能量不仅照射了所选择的层面,在层面附近也被能量照 射。 CT剂量不能用常规X线机的病人入射表面剂量(ESD)来表示。
CT剂量
轴向剂量分布曲线
在理想状态下,轴向剂 量分布曲线和灵敏度剖 面线SSP(Section sensitivity profile)重 叠,均呈高斯形状,其 全值半高宽(FWHM) 等于层厚。
CT剂量
在实际中,SSP比剂量分布曲线略窄,尤 其是在探测器侧使用准直器时。
CT剂量
X线的剂量基础 CT剂量分布曲线
CT剂量表示方法
剂量的影响因素
剂量的测量
CT剂量
X线的剂量基础
CT剂量
照射量
用来描述传递给患者的辐射总量。 单位为:伦琴(R) 1R=2.58×10-4C/kg
定义:在1kg空气中产生2.58×10-4C(库仑)静电荷所需要 的X线或 射线的能量。
若用P5=u2+u4…⑤ 式代替④式联立方程组,
∵ ⑤可由①+ ② -③得到 ∴由⑤、①、 ② 、③组成的方程组只有三个独立方 程,方程数少于未知数,方程组无唯一解。
假如把物质的扫描面分成N×N矩阵,只要投影数 据即方程数量足够多,同样可解得每一像素的X线 衰减系数。 在求解方程组时有多种方法,其中之一是直接矩阵 变换法。
CT图像重建
直接矩阵变换法
CT图像重建
假定某物质在扫描面上由4个均匀的部分组成,且衰 减系数分别为u1、 u2、 u3、 u4,并已知它们在水平、 竖直和对角方向的积分。
选择其中四个方程组成独立方 程组: P1=u1+u2 ①
P2=u3+u4
P3=u1+u3 P4=u1+u4
②
③ ④
CT图像重建
第二次运算:垂直照射后,再将射线和加到图像单 元中
CT图像重建
第三次运算:取对角线方向(右上)的照射,将射 线和再加到图像单元中
第四次运算:取左上方向的对角线照射,并将射线 和加到前面的图像单元中
CT图像重建
最后的运算:从每个图像单元中减去背景值(背景 强度等于某投射角情况下各投影值之和),再将各 吸收系数除以最大公约数,得到最后结果。 其他资料的最后运算:在求出累加值后,再给累加 得到的各个像素除以反投影的次数,也就是除以经 过像素的射线数。
CT剂量
CT剂量
CT剂量
CT剂量
英国1989年CT检查仅占X线诊断的2%,而导致 的国民集体剂量约占总剂量的20%。 1998年,英国CT检查占X线诊断的4%,检查所 致国民集体剂量已上升至40%。 常规X线正位胸片的有效剂量约0.03mSv,而做 CT胸部扫描时,有效剂量最高可达6~7mSv, 是X线正位胸片的200倍。 CT辐射剂量问题越来越受到关注。
CT剂量指数并不直接表征各种扫描所致受检者的剂量, 但与受检者所受剂量密切相关。 与吸收剂量的单位相同:戈瑞(Gy)或mGy
CT剂量
CT剂量指数100(CTDI100)
X线CT旋转一周,将平行于旋转轴Z轴(垂直于横断面)的剂 量分布D(z)沿Z轴从-50mm到+50mm积分,除以层厚T 的商 CTDI100=
ED=D×Wr
当辐射有多个种类和能量时,在一个组织或器官的 当量剂量就是各个辐射所致的当量剂量的和。
CT剂量
ED给出了不同辐射条件下人体发生生物效应的定量描述,但 人体不同组织或器官对辐射的敏感性和给人体造成的危害是 不同的。 因此又提出组织权重因子Wt(tissue weighting factor) 对上述的ED进行进一步修正。由Wr 和Wt两个因子修正后的 吸收剂量称为有效剂量(effective dose,ED)
CT图像重建
对 G ( , ) 进行傅里叶反变换,得到被滤波的时 域投影 g (t , ) 将时域投影 g (t , )反投影并累加到二维离散图像 矩阵。为了提高空间分辨率,经常在反投影前进 行预插值 改变一个投射方向对物体进行扫描,对所得投影 重复上述过程,直到所有投射角度扫描完毕
CT图像重建
探测器和数据采集系统的非线性:探测器的输出 有赖于其之前受到的辐射情况 与扫描物体有关:患者在扫描过程中并非完全静 止不动 焦点外的X线辐射、扫描物质中金属的存在、机 架未对准、球管焦点漂移、机械稳定性、球管转 子颤动等。 数据的预处理和后处理与重建算法同样重要。
CT图像重建
散射辐射使剂量曲线的尾部拉得很长。
轴向剂量分布曲线在很大程度上由焦点尺 寸、CT的几何参数、准直器宽度决定。
CT剂量
CT剂量表示方法
CT剂量
CT剂量指数(CTDI)
CTDI(CT dose index)是CT设备辐射剂量特征的实用 表征量。 迄今得到公认使用的CTDI: CT剂量指数100(CTDI100) 加权CT剂量指数(CTDIw) 容积CT剂量指数(CTDIvol)
CT图像重建
1967年CT研发时所采用的图像重建方法即联立方程组法。
联立方程组法的局限性:
当方程组的规模越来越大时,即便在计算机上编程实现, 其工作量也很大。 需采集远远多于N2个投影数据,因为许多方程是相关的。 当方程的数量超过未知数数量时,方程组的解未必收敛, 因为投影值的测量存在误差。
CT图像重建需解决的问题
就是希望用检测到的投影数据,设法求出该断层的每个像素的线 性衰减系数或其等效值(如密度)后,再以其灰度值绘出图像。 我们求解的是:一个二维分布函数,该函数表示物质的X线衰减 系数。
