matlab第4章
第4章-MATLAB符号运算

simplify与simple命令
• simplify普遍使用于表达式化简。此外,还可以 使用simple函数进行化简; • simplify 函数可以对包含和式、根式、分数、 乘方、指数、对数、三角函数等的表达式化简; • 而simple 函数的目标是寻找最少字符的表达式。 • 例:Jacobi矩阵的Jacobian行列式。
findsym函数的例
syms a b c x >> f=sym('a*x^2+b*x+c'); >> findsym(f,1) %确定符号表达式首选的一个 变量 ans = x >> findsym(f,2) %确定符号表达式首选、次选 的2个变量 ans = x,c
符号微积分运算
• diff(f) 对符号表达式f进行微分运算,符号变量由前面 的规则确定; • diff(f,a) f对指定变量a进行微分运算; • diff(f,n)或diff(f,a,n) 计算f对默认变量或指定变量a 的n 阶导数,n是正整数; • int(f) 对于符号变量f代表的符号表达式,求f关于默认 变量的不定积分; • int(f,v) 计算f关于变量v的不定积分; • int(f,a,b)或int(f,v,a,b) 量v从a到b的定积分。 计算f关于默认变量或指定变
符号变量的定义
使用符号变量之前,应先对其予以声明,命令格式如下: • syms 变量名列表(其中各个变量名用空格分隔,不能 用逗号分隔) 如: syms x a • sym (‘变量名’) • 随后输入的 y = ax和y = a*sin(x) 就成了符号函数; f= ' sin(y)^2 ' 则定义了f为一个符号表达式; eq = ' a-y^2 =0 ' 定义了eq为一个符号方程。 如: sym(' y ' ) 经上述定义后,x, y, a已成为符号变量。
MATLAB-第4章

v
i 1
n
2 i
。
max { vi } 。
1 ≤i ≤n
设 A 是一个 m ×n 的矩阵,矩阵的 3 种常用范数如下。 1-范数: A 1 max { aij } 。
1 ≤ j ≤n i 1 m
2-范数: A 2 1 ,其中 λ 1 为 A'A 最大特征值。 ∞-范数: A max { aij } 。
【例4.6】先建立5 × 5矩阵A,然后将A的第一行元素乘以1, 第二行乘以2,…,第五行乘以5。 用一个对角矩阵左乘一个矩阵时,相当于用对角阵的第一个 元素乘以该矩阵的第一行,用对角阵的第二个元素乘以该 矩阵的第二行……依此类推,因此,只需按要求构造一个 对角矩阵D,并用D左乘A即可。命令如下: A=[1:5;2:6;3:7;4:8;5:9] D=diag(1:5); D*A %用D左乘A,对A的每行乘以一个指定常数
(2)构造对角矩阵 设V为具有m个元素的向量,diag(V,k)的功能是产生一个 n × n(n = m + k|)对角阵,其第k条对角线的元素即为 向量V的元素。 例如: diag(1:3,-1) ans = 0 0 0 0 1 0 0 0 0 2 0 0 0 0 3 0 省略k时,相当于k为0,其主对角线元素即为向量V的元素。
2.矩阵的秩与迹 (1)矩阵的秩 rank(A) (2)矩阵的迹 矩阵的迹即矩阵的对角线元素之和。 trace(A)。
3.向量和矩阵的范数
设向量 V = (v1 ,v2 ,…,vn ),向量的 3 种常用范数如下。 1-范数: V 2-范数: V ? -范数: V
1
vi 。
i 1
n
2
3.矩阵的转置 所谓转置,即把源矩阵的第一行变成目标矩阵第一列,第二 行变成第二列……依此类推。显然,一个m行n列的矩阵 经过转置运算后,变成一个n行m列的矩阵。MATLAB中, 转置运算符是单撇号(')。
Matlab学习教程 第四章(4)上机练习

第4章图形处理功能1 内容简介基本内容主要包括:(1)二维图形(2)三维图形(3)图形处理的基本技术2 达到的目标(1)掌握二维图形的绘制。
(2)掌握三维图形的绘制。
(3)掌握图形处理的基本技术3 具体内容3.1 二维图形3.1.1 基本绘图命令(1)当plot函数仅有一个输入变量例4-1y=[5 2 3 8 5]; %y 行矩阵plot(y) %一条线例4-2y=[5 2 3 8 5;2 4 3 1 5;1 1 1 1 1]; %y 矩阵plot(y) %5条线,等于矩阵的列数(2)当plot函数有两个输人变量例4-3x=0:0.01*pi:pi;y=sin(x).*cos(x);plot(x,y)例4-3x=0:0.01*pi:pi;y=[sin(x);cos(x); sin(x).*cos(x)];plot(x,y)例4-4x1=0:0.01*pi:pi;x2=pi:0.01*pi:2*pi;x=[x1' x2'];y=[sin(x1') cos(x2')];plot(x,y)例4-5x1=1:5;x2=6:10;y1=x1;y2=2*x2;plot([x1;x2],[y1;y2])%plot([x1' x2'],[y1' y2'])(3)当plot函数有三个输入变量时MATLAB语言中提供的对曲线的线型、颜色以及标识的控制符如表4.l所示。
例4-6 绘制带有显示属性设置的二维图形。
x=0.5*pi: 0.1*pi:2*pi;y=sin(x);z=cos(x);plot (x, y, '--ko', x, z, '-. r*')3.1.2 特殊的二维图形函数(1)特殊坐标系的二维图形函数(a)对数坐标例4-7 绘制X坐标为对数坐标的二维图形。
x=0.5*pi: 0.1*pi:2*pi;y=sin(x);semilogx (x, y, '-ro')(b)极坐标例4-8绘制极坐标下的二维图形。
第4章 MATLAB文件操作

2.写文本文件 fprintf 函数的调用格式为: COUNT= fprintf(fid, format, A) 其中A存放要写入文件的数据。先按format指定 的格式将数据矩阵A格式化,然后写入到fid所指 定的文件。格式符与fscanf函数相同。
4.3 数据文件定位 MATLAB提供了与文件定位操作有关的函数 fseek和ftell。fseek函数用于定位文件位置指针, 其调用格式为: status=fseek(fid, offset, origin) 其中fid为文件句柄,offset表示位置指针相对 移动的字节数,origin表示位置指针移动的参 照位置。若定位成功,status返回值为0,否则 返回值为–1。
文件数据格式有两种形式,一是二进制文件,二是 文本文件。在打开文件时需要进一步指定文件格 式类型,即指定是二进制文件还是文本文件。
4.1.2 文件的关闭 文件在进行完读、写等操作后,应及时关闭。关 闭文件用fclose函数,调用格式为: sta=fclose(fid) 该函数关闭fid所表示的文件。sta表示关闭文件操 作的返回代码,若关闭成功,返回0,否则返回–1。
4.2 文件的读写操作 4.2.1 二进制文件的读写操作 1.读二进制文件 fread 函数可以读取二进制文件的数据,并将数据 存入矩阵。其调用格式为: [A,COUNT]=fread(fid,size, precision) 其中A用于存放读取的数据,COUNT返回所读取 的数据元素个数,fid为文件句柄,size为可选项, 若不选用则读取整个文件内容,若选用则它的值 可以是下列值:
例4-1 建立一数据文件magic5.dat,用于存放5阶 魔方阵。 程序如下: fid=fopen(‘magic5.dat’,‘w’); cnt=fwrite(fid,magic(5),‘int32’); fclose(fid);
第4章MATLAB程序流程控制-习题答案

第4章M A T L A B程序流程控制-习题答案第4章MATLAB程序流程控制习题4一、选择题1.下列关于脚本文件和函数文件的描述中不正确的是()。
AA.函数文件可以在命令行窗口直接运行B.去掉函数文件第一行的定义行可转变成脚本文件C.脚本文件可以调用函数文件D.函数文件中的第一行必须以function开始2.下列程序的输出结果是()。
Dy=10;ify==10y=20;elseify>0y=30enddisp(y)A.1B.30C.10D.203.有以下语句:a=eye(5);forn=a(2:end,:)for循环的循环次数是()。
CA.3B.4C.5D.104.设有程序段k=10;whilekk=k-1end则下面描述中正确的是()。
AA.while循环执行10次B.循环是无限循环C.循环体语句一次也不执行D.循环体语句执行一次5.有以下程序段:x=reshape(1:12,3,4);m=0;n=0; fork=1:4ifx(:,k)<=6m=m+1; elsen=n+1; end end则m 和n 的值分别是()。
CA .66B .21C .22D .126.调用函数时,如果函数文件名与函数名不一致用()。
A A .函数文件名B .函数名 C .函数文件名或函数名均可D .@函数名 7.如果有函数声明行为“f unction[x,y,z]=f1(a,b,c)”,则下述函数调用格式中错误的是 ()。
B A .x=f1(a,b,c)B .[x,y,z,w]=f1(a,b,c) C .[x,b,z]=f1(a,y,c)D .[a,b]=f1(x,y,z) 8.执行语句“f n=@(x)10*x;”,则fn 是()。
A A .匿名函数B .函数句柄C .字符串D .普通函数 9.执行下列语句后,变量A 的值是()。
D >>f=@(x,y)log(exp(x+y)); >>A=f(22,3); A .22,3B .22C .3D .25 10.程序调试时用于设置断点的函数是()。
matlab课后习题答案第四章
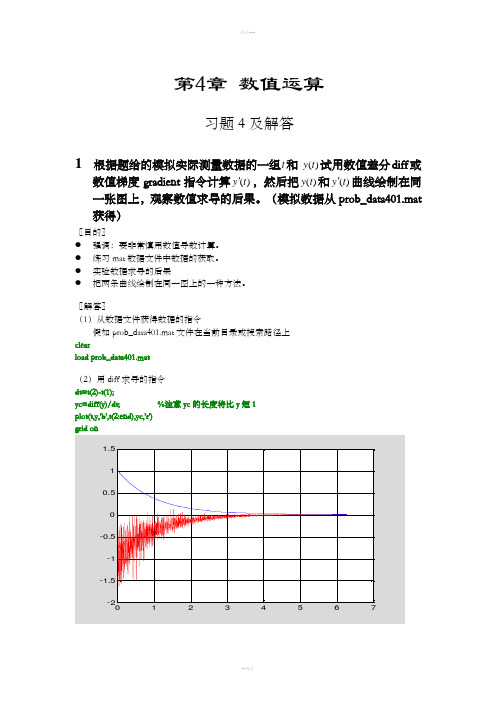
第4章数值运算习题 4 及解答1 根据题给的模拟实际测量数据的一组t和)(t y试用数值差分diff或数值梯度gradient指令计算)(t y',然后把)(t y和)(t y'曲线绘制在同一张图上,观察数值求导的后果。
(模拟数据从prob_data401.mat 获得)〖目的〗●强调:要非常慎用数值导数计算。
●练习mat数据文件中数据的获取。
●实验数据求导的后果●把两条曲线绘制在同一图上的一种方法。
〖解答〗(1)从数据文件获得数据的指令假如prob_data401.mat文件在当前目录或搜索路径上clearload prob_data401.mat(2)用diff求导的指令dt=t(2)-t(1);yc=diff(y)/dt; %注意yc的长度将比y短1plot(t,y,'b',t(2:end),yc,'r')grid on(3)用gradent 求导的指令(图形与上相似)dt=t(2)-t(1);yc=gradient(y)/dt;plot(t,y,'b',t,yc,'r')grid on〖说明〗● 不到万不得已,不要进行数值求导。
● 假若一定要计算数值导数,自变量增量dt 要取得比原有数据相对误差高1、2个量级以上。
● 求导会使数据中原有的噪声放大。
2 采用数值计算方法,画出dt tt x y x ⎰=0sin )(在]10 ,0[区间曲线,并计算)5.4(y 。
〖提示〗● 指定区间内的积分函数可用cumtrapz 指令给出。
● )5.4(y 在计算要求不太高的地方可用find 指令算得。
〖目的〗● 指定区间内的积分函数的数值计算法和cumtrapz 指令。
● find 指令的应用。
〖解答〗dt=1e-4;t=0:dt:10;t=t+(t==0)*eps;f=sin(t)./t;s=cumtrapz(f)*dt;plot(t,s,'LineWidth',3)ii=find(t==4.5);s45=s(ii)s45 =1.65413 求函数x ex f 3sin )(=的数值积分⎰=π0 )(dx x f s ,并请采用符号计算尝试复算。
第4章 MATLAB 非线性方程(组)的求解

x*k
=
g(x* ),即x* 是 g 的不动点,也就是f 的根。
fixpt.m
逐次逼近: 将隐式方程归结为显式计 算
y
y=x
p1 p0
y=g(x)
✓
x
x0
x1 x*
y
y=x
y=g(x)
p0
p1
x x1 x0 x*
y p0
y=x
✓
y=g(x) p1
x0
x*
y
y=g(x) p0
x x1
y=x
是函数表达式中附加的参数x是返回的根fval是根x处的目标函数的值exitflag表明解存在的情况正数表明解存在负数表示解不存在遇到复数nan或者无穷大等
第4章 非线性方程(组)的求解
本章目标:求 f (x) = 0 的根
4.1 二分法 4.2 简单迭代法 4.3 Newton法 4.4 抛物线法 4.5 非线性方程组的求解 4.6 实例解析
p1
x x0 x* x1
4.3 Newton法
原理:将非线性方程线性化 —— Taylor 展开
取 x0 x*,将 f (x)在 x0 做一阶Taylor展开:
f (x)
f ( x0 )
f ( x0 )(x x0 )
f
(
2!
)
(
x
x0
)2,
在
x0
和
x
之间.
将 (x* x0)2 看成高阶小量,则有:
x = g (x)
f (x) 的根
g (x) 的不动点
从一个初值 x0 出发,计算 x1 = g(x0), x2 = g(x1), …,
第4章 MATLAB程序流程控制

第4章 MATLAB程序流程控制
2.switch语句 switch语句根据表达式的取值不同,分别执行不 同的语句,其语句格式为:
第4章 MATLAB程序流程控制
(3) 多分支if语句: if 条件1 语句组1 elseif 条件2 语句组2 …… elseif 条件m 语句组m else 语句组n end
第4章 MATLAB程序流程控制
第4章 MATLAB程序流程控制
例4-4 输入一个字符,若为大写字母,则输出其对应 的小写字母;若为小写字母,则输出其对应的大写 字母;若为数字字符则输出其对应的数值,若为其 他字符则原样输出。
age is 17>> >> fprintf('age is %d\n',17); age is 17
第4章 MATLAB程序流程控制
例4-2 求一元二次方程ax2 +bx+c=0的根。 程序如下: a=input('a=?'); b=input('b=?'); c=input('c=?'); delta=b*b-4*a*c; x=[(-b+sqrt(delta))/(2*a),(-b-sqrt(delta))/(2*a)]; disp(['x1=',num2str(x(1)),',x2=',num2str(x(2))]);
M文件的扩展名为.mFra bibliotek第4章 MATLAB程序流程控制
1.建立新的M文件 为建立新的M文件,启动MATLAB编辑器有3种方法。 ① 在MATLAB主窗口选择“主页”选项卡,在“文件” 命令组中单击“新建脚本”命令按钮。 ② 在MATLAB命令行窗口输入命令: edit 文件名 启动MATLAB编辑器后,输入M文件的内容并存盘。 ③ 在命令历史窗口选中一些命令(按住Ctrl可同时选 择多条命令),然后从右键快捷菜单中选择“创建 脚本”命令,将会启动MATLAB编辑器,并在编辑 区中加入所选中的命令。
MATLAB程序设计基础教程(刘国良)-第4章

函数
体
第4章 M脚本与M函数
2.脚本M文件 脚本文件也叫命令文件,是独立执行的文件,它不接受输 入参数,不返回任何值,而是代码的结合,该方法允许用户将 一系列MATLAB命令输入到一个简单的脚本“.m”文件中,只 要在MATLAB命令窗口中执行该文件,则会依次执行该文件中 的命令。 脚本M文件中包含一族由MATLAB语言所支持的语句,它类 似于DOS下的批处理文件,它的执行方式很简单,用户只需在 MATLAB 的提示符“>>”下键入该M文件的文件名,这样 MATLAB就会自动执行该M文件中的各条语句,并将结果直接返 回到MATLAB 的工作空间。
第4章 M脚本与M函数
3.块注释 在 MATLAB 5以前的版本中,注释是逐行进行的,采用百 分号(%)进行标记。逐行注释不利于用户增加和修改注释内容。 在MATLAB 5及以后的版本中,用户可以使用“%{”和“%}” 符号进行块注释,“%{”和“%}”分别代表注释块的起始和 结束。
第4章 M脚本与M函数
第4章 M脚本与M函数
在使用脚本文件时需要注意一点:如果当前工作区中存在 与该脚本同名的变量,则当输入该文件名时,系统将其作为变 量名执行。
MATLAB中有一个专门用于寻找“.m”文件的路径搜索器。 “.m”文件是以目录和文件夹的方式分布于文件系统中的,一 部分“.m”文件的目录是MATLAB的子目录,由于MATLAB的一 切操作都是在它的搜索路径,包括当前路径中进行的,因此如 果调用的函数在搜索路径之外,MATLAB就会认为此函数不存 在。
第4章 M脚本与M函数
4.1.2 M文件的建立、运行与命名规则 M文件的语法类似于一般高级语言,是一种程序化的编程
语言,但是与传统的高级语言相比,M文件又有其特点。它只 是一个简单的ASCII码型文本文件,因此,它的语法比一般的 高级语言要简单,程序也容易调试,并具有很好的交互性。
第4章 MATLAB编程基础

(3)使用C-MEX文件:在必须使用for或 while循环体时,为了提高执行效率,可以将 循环部分的代码转化为C-MEX文件。 (4)尽量使用函数文件:在MATLAB中,函 数文件的效率一般比脚本文件的效率要高, 这是由于函数文件有自己的工作空间,执行 一次后仅保存程序运行必需的变量,并将函 数编译成伪代码,下次调用时提高了效率。
例:根据用户要求找出数组x中的最大值、最 小值或所有元素的和。
t=[0:100];x=exp(-t).*sin(t); %给定数组x require=input('Type min,max,or sum.','s') %用户输入要求 require=lower(require); switch require case 'min' %分支判断通过比较字符串完 成 minimum=min(x) case 'max' maximum=max(x) case 'sum' total=sum(x) otherwise disp('You have not entered a proper requirement') end
例:利用for循环求1!+2!+3!+ +5!的值
sum=0; for i=1:5 pdr=1; for k=1:i pdr=pdr*k; end sum=sum+pdr; end
e x 1 x x 2 2 x3 6 例:找出近似级数 中误差大于1%之前的最大的x值(精确到小数点后两
垂直条形图 水平条形图
误差条形图 y轴对数刻度 坐标
commet stairs
rose compass
《MATLAB程序设计》第4章数组及应用

0x0012FF68 a[0] 0x0012FF6C a[1] 0x0012FF70 a[2] 0x0012FF74 a[3]
数组元素
0x0012FF78 a[4]
0x0012FF7C a[5]
8
一维数组在内存中的存储形式
说明:
(1)数组名a表示内存首地址,是地址常量。
(2)数组a中每个数组元素占的内存空间根据 数组类型确定,整个数组占的内存为:数组元 素个数乘以每个元素所占内存空间如: int a[10]; 4×10=40 float b[20]; 4×20=80 double c[5]; 8×5=40 char d[8]; 1×8=8
第4章 数组
教学内容
数组的定义及应用
字符串处理函数
几个常用算法:排序算法(选择排序、
冒泡排序)
1
第4章 数组
重点、难点
数组的定义及应用
常用算法的设计(选择排序、
冒泡排序)
2
第4章 数组
教学目标
熟练掌握数组的定义及应用
掌握字符数组的定义及应用
掌握常用的字符串处理函数
熟练掌握几个常用算法:排序
算法(选择排序、冒泡排序)
分析:所谓转置就是将矩阵的行列互换,即将 a矩阵 的a[i][j]元素变成b矩阵的b[j][i]。
24
#include <iostream> using namespace std; int main() { int a[3][4] ={{1,2,3,4},{3,4,5,6},{5,6,7,8}}; int b[4][3],i,j; for(i=0;i<3;i++) //输出二维数组a[3][4] { for(j=0;j<4;j++) cout<<a[i][j]<<" "; cout<<endl; } for(i=0;i<4;i++) //将矩阵a转置给矩阵b for(j=0;j<3;j++) b[i][j]=a[j][i]; for(i=0;i<4;i++) //输出二维数组b[4][3] { for(j=0;j<3;j++) cout<<b[i][j]<<" "; cout<<endl; } return 0;}
第4章MATLAB程序设计

例 求一个值n,使n!最大但小于1050。 MATLAB程序如下: %初始化 r=1;k=1; 执行后结果如下: %做循环 The 41!Is while r<1e50 3.345253e+049 r=r*k; k=k+1; end k=k-1;r=r/k;k=k-1; % 输出结果 disp(['The',num2str(k),'!is',num2str(r)])
4.2.3 循环结构 for 循环:可完成指定次重复的循环,且在循环开 始之前,就知道代码重复的次数。
while 循环:while语句可完成不定次重复的循 环,与for语句不同,每次循环前要先判断条件 是否满足,再决定循环是否进行。
例 利用rand函数产生10个随机数,然后利用嵌套 for循环进行从小到大排序。
2 1.5 1 0.5 0 150 100 50
然后通过调用函数fun计算出z, 并利用mesh绘制出网格线。 编写的脚本文件如下: % 坐标系准备 x=[0:.02:2]; y=[-2:.02:0]; % 调用函数计算函数值 z=fun(x,y); % 绘图 figure mesh(z)
150 100 50
4.3.2 函数的调用 函数调用的一般格式如下: [输出实参表] = 函数名(输入实参表) 要注意的是,函数调用时各实参出现的顺 序、个数,应与函数定义时形参的顺序、 个数一致,否则会出错。函数调用时,先 将实参传递给相应的形参,从而实现参数 传递,然后再执行函数的功能。
例 对于函数
z ( x 1)2 ( y 1)2
fprintf函数中,format字符中常常会使用到一些特 殊字符来灵活的实现一些显示功能 format string 结果 %d %e %f %g 把值作为整数来处理 用科学记数法来显示数据 用于格式化浮点数,并显示这个 数 用科学记数格式,或浮点数格式, 根据那个表示的数位短,显示那 个 转到新的一行
(完整版)第4章MATLAB程序流程控制_习题答案

第4章 MATLAB程序流程控制习题4一、选择题1.下列关于脚本文件和函数文件的描述中不正确的是()。
AA.函数文件可以在命令行窗口直接运行B.去掉函数文件第一行的定义行可转变成脚本文件C.脚本文件可以调用函数文件D.函数文件中的第一行必须以function开始2.下列程序的输出结果是()。
Dy=10;if y==10y=20;elseif y>0y=30enddisp(y)A.1 B.30 C.10 D.203.有以下语句:a=eye(5);for n=a(2:end,:)for循环的循环次数是()。
CA.3 B.4 C.5 D.104.设有程序段k=10;while kk=k-1end则下面描述中正确的是()。
AA.while循环执行10次B.循环是无限循环C.循环体语句一次也不执行D.循环体语句执行一次5.有以下程序段:x=reshape(1:12,3,4);m=0;n=0;for k=1:4if x(:,k)<=6m=m+1;elsen=n+1;endend则m和n的值分别是()。
CA.6 6 B.2 1 C.2 2 D.1 26.调用函数时,如果函数文件名与函数名不一致,则使用()。
A A.函数文件名B.函数名C.函数文件名或函数名均可D.@函数名7.如果有函数声明行为“function [x,y,z]=f1(a,b,c)”,则下述函数调用格式中错误的是()。
BA.x=f1(a,b,c) B.[x,y,z,w]=f1(a,b,c)C.[x,b,z]=f1(a,y,c) D.[a,b]=f1(x,y,z)8.执行语句“fn=@(x) 10*x;”,则fn是()。
AA.匿名函数B.函数句柄C.字符串D.普通函数9.执行下列语句后,变量A的值是()。
D>> f=@(x,y) log(exp(x+y));>> A=f(22,3);A.22,3B.22 C.3 D.2510.程序调试时用于设置断点的函数是()。
MATLAB教程-第4章

4.6 稀疏矩阵
本小节的主要内容包括: 稀疏矩阵与全矩阵 创建与转换稀疏矩阵 操作稀疏矩阵
4.7 小结
本章主要讲解如何在MATLAB中进行矩阵分析。矩阵运算 和分析是MATLAB的基础应用,几乎所有的高等应用都 需要使用到矩阵分析的内容。矩阵分析包括的范围很广 ,本章讲解最基本的内容
本章讲解的知识点包括: 矩阵运算 线性方程组 特征值和特征向量 矩阵分解 矩阵函数 稀疏矩阵
4.1 矩阵运算
本小节的主要内容包括: 矩阵加减运算 矩阵乘法 矩阵除法 矩阵的幂 矩阵的按位运算
4.2 线性方程组
本小节的主要内容包括: 线性方程的形式 计算矩阵行列式 计算矩阵的逆 计算条件数 计算范数 计算矩阵的秩
EVD分解 Schur分解 Cholesky分解 LU分解 QR分解 SVD分解
MATLAB函数 eig、eigs schur chol、cholinc lu、luinc qr svd、svds
4.5 矩阵函数
矩阵函数是以矩阵为参变量的函数。虽然MATLAB中有很 多函数都支持矩阵作为输入参数,但是这其中大部分是 对矩阵进行按位运算。
4.3 特征值和特征向量
MATLAB中的eig函数用于求矩阵特征值和特征向量,其调 用格式为:
D = eig(A) [V, D] = eig(A)
4.4 矩阵分解
矩阵分解通过将复杂矩阵表示成形式简单矩阵的组合,以进 行理论分析或数值计算。通常矩阵分解将复杂矩阵分解 为几个简单矩阵的乘积。下表列出了一些常用的矩阵分 解及其对应的MATLAB实现函数。
第4章 MATLAB 绘图

4.图例标注
菜单Insert---legend 命令legend('string1','string2',...)
4.1.6 一个图形窗口多个子图的绘制
subplot(m,n,i)把图形窗口分为m*n个子图,并在第i个子图 中画图 例 4-11 在同一坐标系中画出两个函数,y=cos2x,y=sinxsin6x 的图形,自变量的范围为0≤ x ≤π,函数y=cos2x用红色星号,函数 y=sinxsin6x用蓝色实线,并加图名、坐标轴、图形、图例标注 解 MATLAB命令为: x=0:pi/50:pi; y1=cos(2*x);y2=sin(x).*sin(6*x); plot(x,y1,'r*',x,y2,'b-'),grid on title(‘曲线y1=cos(2x)曲线y2=sin(x)sin(6x)') xlabel('x轴'),ylabel('y轴') gtext('y1=cos(2x)'),gtext('y2=sin(x)sin(6x)') legend('y1=cos(2x)','y2=sin(x)sin(6x)')
group 8 6 4 2 0 10 30 20
stack
1
2
3
4 stack
5
6
0
1
2
3
4 stack
5
6
8 6 5 4 3 2 1 0 10 20 30 6 4 2 0
其它特殊绘图略(见教科书 )
1
2
3
4
5
6
4.3 三维曲线绘图
第四章 MATLAB符号计算

Ezpolar函数实现极坐标中二维曲 线图象的绘制,它的调用格式:
ezpolar(f,[a,b])
说明: 绘图表达式为rho=f(theta)极坐标曲线,
theta的取值范围为,缺省时为[0,2*pi]
例:p83
4.5.2三维绘图函数
ezplot3是实现三维绘图的函数,它的 调用格式:
ezplot3(x,y,z,[tmin,tmax]) ezplot3(x,y,z,[tmin,tmax ],'animate')
3.符号表达式的提取分子和分母运算
在matlab中可利用numden函数来提取符号表达式 中的分子或分母。其一般调用格式为:
[n,d]=numden(s)
说明:
参数s是符号表达式是一个 有理分式或可以展开为有理
例: s=sym('2/5+3/7')
n= 29
分式,numden函数把有理分 式的分子返回给n,分母返回
dsolve在求常微分方程组时 的调用格式为:
dsolve('eq1,eq2,...','cond1,cond2...','v')
说明: 该函数求解常微分方程组eq1,…,eqn在初值条件或边界 条件为cond1,…,condn下的符号特解,若不给出初值 条件,则求方程组的通解,v为指定的返回值中的变量 表示。
例4-9解超越方程组
sin(x+y)-y*exp(x)=0 x^2-y=2
syms x y
[x,y]=solve('sin(x+y)-y*exp(x)=0','x^2-y=2')
x =-.66870120500236202933135901833637
第四章 MATLAB程序设计

第二节 选择结构
2.1 if 语句
在MATLAB中,if 语句有三种格式
1、单分支if 语句
语句格式为: if 条件 语句组 end 当逻辑表达式的值为真时,执行该结 构中的执行语句,执行完之后继续向 下进行;若为假,则跳过结构中的内 容,向下执行。
实例分析
例4.4 当x是整数矩阵时,输出x的值。
程序3:
x=input('输入x='); y=cos(x+1)+sqrt(x*x+1);
u=cos(x+1);
v= sqrt(x*x+1); y=u+v end if x~=10
if x~=10
y=x*sqrt(x+sqrt(x));
end
y
y=x*sqrt(x+sqrt(x))
end
第二节 选择结构
if 条件1 语句组1 elseif 条件2 语句组2 …… elseif 条件m 语句组m else if-elseif的执行方式为:如果逻辑表达式1 的值为真,则执行语句1;如果为假,则判 语句组m+1 断逻辑表达式2,如果为真,则执行语句2, end 否则向下执行。
3、多分支if语句
实例分析
y
实例分析
例4.11 求
ye
0.5 x
sin( x
6
)
定积分。
a=0;b=3*pi;n=1000; h=(b-a)/n; x=a:h:b; f=exp(-0.5*x).*sin(x+pi/6);
for i=1:n
s(i)= (f(i)+f(i+1))*h/2; end s=sum(s)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
行向量元素为按降幂排列的多项式系数。
1.多项式乘法函数 conv ( )
格式:C= conv (A, B) %求多项式A和B的乘积
A、B是两个多项式的系数向量,按降幂排列。 conv( ) 把两个多项式相乘合并成一个多项式。
2
p1 2s 3;
2
p2 s 2 4
3 2
A (2s 3)(s 4) 2s 3s 8s 12
x:操作点处的状态向量
u:操作点处的输入向量
x,u缺省值为0。
20
( s 1)(s 2 2s 6) 2 【例4.4】 求传递函数 G(s) 2 s (s 3)(s 3 2s 2 3s 4)
的分子和分母多项式,并求传递函数的特征 根。
21
% num 分子多项式 % conv( ) 采用嵌套形式
G (s)
5s 3 s 3 6 s 2 11s 6
13
3.部分分式展开函数residue ( ) 功能:对两个多项式的比进行部分展开。 格式:[r, p, k]=residue(b, a) 求B(s)/A(s)的部分分式展开式 向量b和a是按s降幂排列的多项式系数。
14
B( s) bn s n bn1s n1 ...b0 F ( s) A( s) an s n an1s n1 ...a0
38
2.并联 G(s)=G1(s)+G2(s) 模型并联函数 parallel 格式:[num, den]=parallel(num1, den1, num2, den2) num1, den1:G1(s) 的分子、分母多项式 num2, den2:G2(s)的分子、分母多项式 num, den:G(s) 的分子、分母多项式
第4章 控制系统数学模型
控制系统常用的数学模型有: 传递函数模型、状态方程模型、零极点增益模型 等。 这些模型之间可以相互转换。 本章主要介绍如何利用MATLAB/Simulink建模和 对模型进行转换。
1
4.5 MATLAB/Simulink在模型中的应用
4.5.1 与多项式相关的函数
MATLAB中多项式用行向量表示,
3
注意:一个conv 只能用于两个多项式的运算。 如果有多个多项式,则要用多个conv。 用多个conv嵌套使用,记得加括号。
B (s 3)(2s 5)(2s 5) 4s3 32s 2 85s 75
4
2.多项式求根函数 roots( ) 格式为: r= roots (p) 其中,p为多项式,r为所求的根。 可对传递函数分子和分母求根,求出系统的零极点。
图4.7 simulink中的传递函数模型
29
2、利用零极点模型建立系统模型 系统开环传递函数零极点形式为 G ( s) 2( s 5)
s( s 3)
零点为-5;极点为0和-3,增益为2。
步骤1:新建一个模型窗口
步骤2:为模型添加所需模块
零极点模型: continuous →Zero-Pole
图4.8 simulink中的零极点表示模型
31
4.6 系统模型转换及连接
4.6.1 模型转换 线性时不变系统(LTI)的模型包括 传递函数(Transfer Function)模型TF 零极点增益(ZPK)模型ZPK 状态空间(State Space)模型SS 在一些场合需要某种模型,在另一些场合可能需 要另外一种模型,这就需要进行模型的转换。
[z,p k]=tf2zp(num,den) 从传递函数模型获取零极点增益
[num,den]=zp2tf(z,p,k)从零极点模型获取分子分母多项式
34
6( s 2) 【例4.10】系统的零极点模型G(s) ( s 1)(s 3)(s 5)
求其传递函数模型。
解:MATLAB程序代码:
num [bn , bn1,...b0 ] den [an , an1,...a0 ]
执行命令 [r,p,k]=residue(num,den),
给出部分分式展开式的留数r、极点p和余数k:
15
s 4 11s 3 39s 2 52s 26 F ( s) s 4 10s 3 35s 24
s 4 11s 3 39s 2 52s 26 1 2.5 3 0.5 F ( s) 1 4 3 s 10s 35s 24 s 4 s 3 s 2 s 1
16
4.5.4 建立状态空间模型相关的函数
状态空间表达式
X AX Bu Y CX Du
Derivative
Integrator Transfer Fcn Zero-Pole State Space Transport Delay
输入信号微分
输入信号积分 传递函数模型 零极点模型 状态空间系统模型 固定时间传输延迟
19
4.5.6 Simulink 模型与状态空间模型的转化
以状态空间形式线性化模型的函数linmod 格式为:[A,B,C,D]=linmod(„sys‟,x,u) sys: 需要进行线性化的simulink模型的名称 linmod命令返回sys系统在操作点处的状态空间矩阵。
s 5 5s 4 20s 3 40s 2 60s 36
%den分母多项式
s 6 5s 5 9s 4 13s 3 12s 2
22
% r为分母多项式的根
23
【例4.5】 一系统微分方程如下:
y (3) 11y ( 2) 11y (1) 10y u ( 2) 4u (1) 8u
建立常规系统的传递函数。
8
【例】用MATLAB建立系统传递函数模型。
s2 G (s) 2 s s 10
方法1:
方法2:
9
2.从传递函数模型中提取分子分母多项式 系数的函数tfdata( )
格式:[num,den]=tfdata(sys, „v‟)
sys:传递函数 v功能:返回分子分母多项式系数向量。
10
4.5.3 建立零极点形式的数学模型相关函数
单输入单输出系统的零 极点模型表示为: ( s z1 )(s z 2 ) ( s zm ) G(s) K ( s p1 )(s p2 ) ( s pn ) 其中z i为系统的零点,]为系统的零点向量; [z p i为系统的极点, ]为系统的极点向量; [p K为系统增益,]为系统的增益向量。 [k
输出口模块:ports&subsystems→out1
28
步骤3:将模块连接好 步骤4:打开相加器参数设置对话框,设置为“+-” 步骤5:打开传递函数Transfer Fcn参数设置对话框, numerator设置为“[2 10]”,denominator设置为“[1 3 0]”。 步骤6:将模型存为“untitled1.mdl”文件。
11
1.建立零极点数学模型的函数 zpk( )
格式:sys= zpk (z, p, k) 【例】用MATLAB建立系统零极点增益模型。
G( s) 18( s 2) ( s 4)(s 15)(s 25)
12
2.提取模型零极点增益向量的函数zpkdata ( ) 格式:[z, p, k]=zpkdata(sys, „v‟) v功能:返回零极点和增益向量。
对线性定常系统,s的系数均为常数,且a0不等于0。
MATLAB中,传递函数由分子多项式系数向量num 和分母多项式系数向量den构成。 num=[bm,bm-1, …,b0], den=[an,an-1, …,a0]
则传递函数表示为: G ( s) num( s)
den( s)
7
1.建立传递函数模型的函数 tf( ) 格式:sys= tf (num, den) % sys是建立的传递函数
32
图4.9 模型转换关系图
33
表4.4 模型转换函数
函数名 ss2tf 功能 状态空间模型转换为传递函数模型
ss2zp
tf2zp tf2ss zp2tf
状态空间模型转换为零极点模型
传递函数模型转换为零极点模型 传递函数模型转换为状态空间模型 零极点模型转换为传递函数模型
zp2ss
零极点模型转换为状态空间模型
使用MATLAB建立传递函数模型。
解:建立模型的MATLAB程序代码:
%分子、分母多项式系数
%建立传递函数模型
24
s 4s 8 【例4.6】 传递函数 G ( s) 3 s 11s 2 11s 10
2
求其分子分母多项式,零极点。
25
%建立传递函数模型 %提取分子、分母多项式
26
%提取零极点和增益
1
27
【例4.9】单位负反馈系统的开环传递函数为 2s 10 G( s) 2 s 3s 分别利用simulink中的传递函数 模型和零极点模型建立系统模型。 1、利用传递函数模型建立系统模型
步骤1:新建一个模型窗口
步骤2:为模型添加所需模块 传递函数: continuous →transfer Fcn 相加器: math operations →sum 输入口模块:ports&subsystems→in1
3.反馈函数feedback
格式:
[num, den]=feedback(num1, den1, num2, den2, sign) num1, den1:G(s)的分子、分母多项式 num2, den2:H(s)的分子、分母多项式 sign= -1为负反馈(默认值),sign=1为正反馈
在MATLAB中,系统状态空间用[A,B,C,D]矩阵 组表示,即系统表示为ss(A,B,C,D)
