机器人运动分析中矩阵变换

合集下载

机器人雅可比矩阵

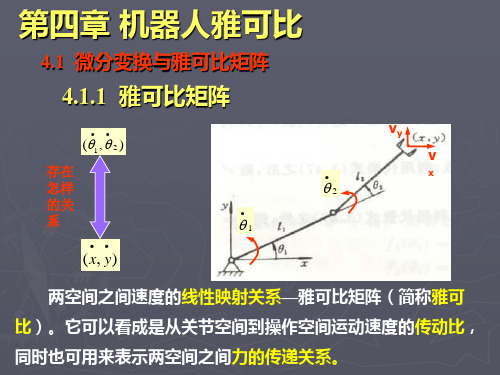
两自由度机器人
对于一个两自由度的机器人，其雅可比矩阵是一个2x2矩阵，其中包含了机器人的两个关节角度和两个关节速度之间的线性关系
。
矩阵形式
雅可比矩阵的矩阵形式为：J = [[a, b], [c, d]]，其中a、b、c、d 是机器人关节角度和关节速度之
间的线性关系系数。
计算方法
对于两自由度机器人，可以通过已知的关节角度和关节速度，以及机器人运动学方程，计算得到
解析机器人模型
计算偏导数
雅可比矩阵描述了机器人末端与控制输入之间的关系，通过直接计算机器人关节变量对末端位置和姿态的偏导数得到。
根据机器人的几何模型和关节类型，解析机器人的运动学模型，得到末端位置和姿态与关节变量的关系。
利用解析得到的运动学模型，计算机器人末端位置和姿态对关节变量的偏导数，得到雅可比矩阵的元素。
参数优化
调整雅可比矩阵的参数
通过对雅可比矩阵的参数进行调整，如增加或减少矩阵的行或列，能够优化矩阵的计算过程，提高计算效率。
优化迭代算法的参数
对于使用迭代算法计算雅可比矩阵的情形，通过调整迭代算法的参数，如增加迭代次数、改变收敛准则等，能够提高计算精度和速度。
控制策略改进
引入新的控制策略
针对具体应用场景，引入新的控制策略，如采用模糊控制、神经网络等，能够更好地解决机器人控制问题，进而改进雅可比矩阵的计算效果。
计算方法
对于四自由度机器人，可以通过已知的关节角度和关节速度，以及机器人运动学方程，计算得到雅可比矩阵。
05
雅可比矩阵的优化与改进
优化算法选择
选用高效算法
对于雅可比矩阵的计算，选用高效的算法能够显著提升计算速度和精度，例如采用数值差分法、有限元法等。

齐次变换矩阵在机器人运动学中的应用

LIU Feng
（Hunan Institute of Technology，Hengyang Hunan 421002）
Abstract: Matrix is an important mathematical tool for robotics. In this paper, homogeneous transformation matrix was introduced to represent the pose of robot. To be specific, researchers established a proper coordinate system for each joint of the robot, and then used homogeneous coordinates to establish the transformation relationship between two adjacent coordinate systems, and then the kinematics equation of the robot was obtained. Keywords: robot；kinematics；rotation martrix；homogeneous transformation matrix
1 所示，则机械手（工具）的位姿可以由坐标系 {B} 的坐标
原点 o′ 在坐标系 {A} 中的坐标 ( px ,py ,pz)′ 和与 o′x′,o′y′,o′ z′ 正向同方向的单位向量在坐标系 {A} 中的坐标表示。
若记 i′,j′,k′ 表示与 o′x′,o′y′,o′ z′ 正向同方向的单位向
（6）
为了得到 P 在 {A} 坐标系中的坐标，要将 P 在 {B}

机器人学_机器人雅可比矩阵

0 0 0 1
若Rot（δx，δy，δz）和Rot（δx‘，δy’，δz‘）表示两
个不同的微分旋转，则两次连续转动的结果为：
1 (z z ' ) y y ' z z ' 1 (x x' ) Rot(x, y, z ) Rot(x' , y ' , z ' ) (y y ' ) x x' 1 0 0 0 0 0 0 1
Trans(d x , d y , d z )Rot(k , d ) I 44
于是得微分算子Δ
0 k d z k y d 0
k z d 0 k x d 0
k y d k x d 0 0
dx dy dz 0
四. 微分旋转的无序性当θ→0 时，有sinθ→dθ，cosθ→1．若令δx=dθx，δy=dθy， δz=dθz，则绕三个坐标轴(p16)的微分旋转矩阵分别为
0 0 1 0
0 0 0 1
略去高阶无穷小量
0 y 1 xy 1 x Rot( x, x) Rot( y, y ) y x 1 0 0 0 1 xy y 0 1 x Rot( y, y ) Rot( x, x) y x 1 0 0 0

令 Trans(d x , d y , d z )Rot(k , d ) I 44 为微分算子
则相对基系有dT=Δ0T，相对i系有dT=TΔi 。这里Δ的下标不同是由于微运动相对不同坐标系进行的。
三.微分平移和微分旋转微分平移变换与一般平移变换一样，其变换矩阵为:
1 0 Trans(dx, dy, dz) 0 0 0 1 0 0 0 dx 0 dy 1 dz 0 1

机器人运动学雅克比矩阵第8讲机器人的微分运动与速度

? 对于有n个关节的机器人，其雅可比矩阵是6×n矩阵，其
前三行称为位置雅可比矩阵，代表对手爪线速度V 的传递比；后三行称为方位矩阵，代表相应的关节速度 q?i 对手爪
角速度 ? 的传递比，因此将 J 分块为：
?V?
??? ??
?
?J i1 ??J a1
Ji2 Ja2
? ?
?q?1 ?
J in Ja2
三逆雅可比矩阵及奇异性雅可比矩阵的奇异性由此可见当雅可比矩阵的行列式为0时既使手爪的速度为一个定值关节速度也将趋于无穷大最终结果会导致关节及该关节的驱动装置损坏
第八讲机器人的雅可比矩阵与速度分析
（一）雅可比矩阵的定义（二）雅可比矩阵的构造法（三）逆雅可比矩阵（四）力雅可比（五）加速度关系
（一）雅可比矩阵的定义
? 把机器人关节速度向量 q?i 定义为：
q? ? ?q?1 q?2 ? ? q?n T
式中，q?i (1,2,? , n) 为连杆 i 相对于
i ? 1的角速度或线速度。
? 手爪在基坐标系中的广义速度向量为：
? ? V
?
?v?
???
? ?
?
x?
y?
z? ? x
?y
?z T
? q? 与 V之间的线性映射关系称为
比矩阵来确定关节速度向量。
? 当 J 是方阵时，可对J 直接求逆，得到 J ?1?q?，但比较困
难。
? 通常直接对机器人的逆解进行微分来求 J ?1?q?。
（三）逆雅可比矩阵及奇异性
例题：图中所示二自由度机械手，手部沿固定坐标系 X正向以1.0m/s 的速度移动，杆长均为0.5m。设在某瞬时θ 1＝ 30°，θ 2＝60°，求相应瞬时的关节速度。

机器人的数学基础齐次变换矩阵及其运算

令上面两式相等，则得变换方程
W BTW TTB STG STG TT
上海电机学院机械学院
变换方程中的任一变换矩阵都可用其余的变换矩阵来表
示。例如，为了对目标物进行有效操作，工具坐标系{T}相对于
目标坐标系{G}的位姿 GTT
是预先规定的，需要改变
B W
T
以达到
这一目的，即通常规定
G T
T
，求
B W
上海电机学院机械学院
下面我们写出变换矩阵的一般表达形式
nx ox ax px ny oy ay py T = nz oz az pz 0001
式中 n, o, a 是旋转变换列向量，p 是平移向量，其逆是
T-1 =
nx ny nz - p.n ox oy oz - p.o ax ay az - p.a 000 1
若手臂绕Z0轴旋转90°，则手臂到达G2；若手臂不动，仅手部绕手腕Z1轴转90°，则手部到达 G3.写出手部坐标系G2、G3表达式。
上海电机学院机械学院
上海电机学院机械学院
3．复合齐次变换
复合变换是由固定参考坐标系或当前运动坐标系的一系列沿轴平移和绕轴旋转变换所组成的。任何变换都可以分解为按一定顺序的一组平移和旋转变换。
ky
sin
cos
0 ny
oy
ky
nz oz kz 0
0 1nz oz kz
nx ny
ox oy
kx cos
ky
sin
sin cos
0 0
onxx
ny oy
nz oz
nz oz kz 0
0 1kx ky kz
把上式右端三矩阵相乘，并运用旋转矩阵的正交性质：

机器人学变换矩阵-概述说明以及解释

机器人学变换矩阵-概述说明以及解释1.引言1.1 概述机器人学是研究机器人的机械结构、运动规划、感知与控制等方面的学科。

作为人工智能和自动化领域的重要分支，机器人学在工业、医疗、农业、航空航天等领域有着广泛的应用。

本文旨在介绍机器人学中的一个重要概念——变换矩阵。

变换矩阵能够描述机器人在三维空间中的位置和姿态，是机器人学中的核心概念之一。

通过对变换矩阵的研究，可以帮助我们更好地理解机器人的运动规划、姿态表示以及感知与控制等问题。

在本文中，我们将从机器人学基础开始，介绍机器人学的概述和机器人的运动学知识。

然后，我们将详细讨论变换矩阵的应用，包括机器人姿态表示、运动规划以及感知与控制等方面。

最后，我们将介绍变换矩阵的计算方法，包括坐标系变换、旋转矩阵与平移矩阵以及变换矩阵的乘法与逆矩阵等内容。

通过本文的阅读，读者将能够了解机器人学中的变换矩阵的概念、应用和计算方法。

同时，我们也将对变换矩阵的未来发展进行展望，并总结本文的内容。

机器人学的研究对于推动自动化技术的发展具有重要的意义，希望本文能够为读者对机器人学的研究和应用提供一定的帮助和启示。

*（请注意，以上内容仅为示例，具体内容需要根据文章内容和结构进行编写）*文章结构是指文章按照一定的组织方式和逻辑顺序来呈现内容的方式。

本文的结构如下：1. 引言1.1 概述1.2 文章结构1.3 目的2. 正文2.1 机器人学基础2.1.1 机器人学概述2.1.2 机器人运动学2.1.3 机器人学中的变换矩阵2.2 变换矩阵的应用2.2.1 机器人姿态表示2.2.2 机器人运动规划2.2.3 机器人感知与控制2.3 变换矩阵的计算方法2.3.1 坐标系变换2.3.2 旋转矩阵与平移矩阵2.3.3 变换矩阵的乘法与逆矩阵3. 结论3.1 总结3.2 对变换矩阵的展望3.3 结束语本文的结构按照从前到后的逻辑顺序组织，首先通过引言部分引入了文章的背景和目的，然后在正文部分逐步介绍了机器人学的基础知识、变换矩阵的应用以及计算方法，最后在结论部分进行总结，并对变换矩阵的未来发展进行展望，并以结束语作为文章的结尾。

雅可比矩阵在机器人运动中的应用

雅可比矩阵在机器人运动中的应用
1、什么是离散雅可比矩阵
离散雅可比矩阵(Discrete Jacobian Matrix)是一种矩阵，它可以用来在机器人运动中表征机器人关节的变化。

它的各元素表示的是每个关节的误差，当关节变动时它们之间以特定的函数或将坐标变换。

它是一个多列多行的矩阵，是一种具有变换性质的矩阵，具有不好求解的变换能力。

2、雅可比矩阵在机器人运动中的应用
a. 雅可比矩阵可用于机器人运动的运动规划。

例如，对于一个六轴机器人，可以利用雅可比矩阵计算出一组关节变换，实现机器人从起始点移动到目标点的运动规划。

b. 雅可比矩阵可以用来计算每个关节的变化，这有助于机器人可编程实现直线和曲线运动。

c. 雅可比矩阵可用于分析转动角速度和角度变化。

d. 雅可比矩阵可用于计算相关度，判断机械臂移动是否稳定。

e. 雅可比矩阵可用于某些运动学算法中，用来计算机器人关节的运动学参数，例如机械臂的位置，速度，加速度以及操纵力和力矩。

f. 雅可比矩阵可用于计算右手法则，以计算机器人操纵力和力矩及其变化。

3、雅可比矩阵的优缺点
a. 优点：雅可比矩阵具有变换性，可以用来计算任意一个关节变动所带来的影响，可实现微小调节以改变机器人空间位姿，有助于更好地控制和定位机器人，并为机器人运动规划提供可靠的参考值；
b. 缺点：离散雅可比矩阵的求解速度较慢，而且有时由于机器人17极空间非线性特征而造成求解精度偏差。

ur5 末端变换矩阵t

ur5 末端变换矩阵t
UR5是一种常见的工业机器人，其末端变换矩阵T用于描述机器人末端执行器的位置和姿态。

末端变换矩阵T通常表示为一个
4x4的矩阵，可以将末端执行器的坐标系与基坐标系进行转换。

末端变换矩阵T可以通过机器人的正运动学方程来计算。

正运动学方程描述了机器人各个关节的位置与末端执行器的位置之间的关系。

具体而言，UR5的正运动学方程可以表示为：
T = T_base T_1 T_2 T_3 T_4 T_5 T_6 T_tool.
其中，T_base是机器人基坐标系到第一个关节坐标系的变换矩阵，T_1到T_6分别是各个关节之间的变换矩阵，T_tool是末端执行器坐标系到末端工具的变换矩阵。

每个变换矩阵T_i都可以表示为一个4x4的矩阵，其中包含了平移和旋转信息。

一般来说，平移部分表示为一个3维向量，旋转部分表示为一个3x3的旋转矩阵。

通过将各个变换矩阵相乘，可以得到整个机器人的末端变换矩
阵T，它描述了末端执行器在基坐标系中的位置和姿态。

需要注意的是，具体的末端变换矩阵T的数值是根据机器人的几何结构和关节参数确定的。

对于UR5机器人而言，这些参数已经通过机器人的设计和制造确定，并且可以在相关的文档或者官方网站上找到。

总结起来，UR5机器人的末端变换矩阵T是一个4x4的矩阵，用于描述机器人末端执行器的位置和姿态。

它可以通过机器人的正运动学方程计算得到，具体的数值是根据机器人的几何结构和关节参数确定的。

机器人旋转变换矩阵和平移变换矩阵物理意义

机器人旋转变换矩阵和平移变换矩阵物理意义机器人旋转变换矩阵和平移变换矩阵的物理意义机器人旋转变换矩阵和平移变换矩阵是机器人控制中的重要概念，它们描述的是机器人在关节空间内的变换关系，是机器人形状变换的基础。

本文将从物理意义和数学推导这两个方面来详细阐述旋转变换矩阵和平移变换矩阵的意义。

一、旋转变换矩阵的物理意义旋转变换矩阵是机器人运动学中的重要概念，它主要用于描述机器人各关节之间在关节空间内的相对旋转关系，并能有效地表示机器人关节的空间位置和姿态。

旋转变换矩阵是一个3×3矩阵，它可以用以下公式表示：R= [Ri] = [a1 a2 a3]其中Ri就是机器人每个关节之间的相对旋转矩阵，它表示关节之间绕着指定轴的旋转角度。

特别地，旋转变换矩阵还可以用来表示机器人关节的空间位置和姿态。

如果将3 x 3矩阵R视为一个向量，它便可以描述机器人末端的一个三维坐标系。

旋转变换矩阵由四个矩阵元素a,b,c和d构成，a,b和c分别表示x,y,z轴的旋转角度，而d为一个称为“偏转”的矩阵元素，被用来描述“坐标系间的偏移”，也表示机器人末端的空间位置。

旋转变换矩阵还可以用来表示机器人末端的姿态。

机器人末端有两种姿态，一种是末端朝向、即末端的三维空间位置和方向，另一种是机器人轴向、即机器人末端的转向角。

这两种姿态都可以用旋转变换矩阵来描述，a,b,c三个元素表示末端朝向，而d表示机器人轴向。

二、平移变换矩阵的物理意义平移变换矩阵也是机器人运动学中重要的概念，它用来描述机器人各关节之间在关节空间内的相对位移关系，有效能实现机器人从一个空间点移动到另一个空间点的轨迹设计。

同样，平移变换矩阵也是一个3×3矩阵，可以用以下公式表示：T= [Tj] = [q1 q2 q3]其中Tj为机器人每个关节之间的相对位移矩阵，它表示关节之间的位移距离。

特别地，平移变换矩阵可以用来描述机器人末端关节的位移关系，也可以用来表示机器人关节的空间位置和运动轨迹。

机器人运动分析中矩阵变换

(Pa)z nz
dz
x
oz
y
az z
简写为：
Td RT RTS(P)d
T0
RT
其中，R是旋转矩阵
nx ox ax
R
n
y
oy
a
y
.
n z o z a z
S(P)为矢量P的反对称矩阵 S(P)矩阵具有以下性质：
0
S(P)
pz
p 0
py px
.
py px 0
S ( P ) P , S ( P ) P .
B BB A 0R B ARTB A SR (APBO)A A
4.3 雅可比矩阵的构造法
构造雅可比矩阵的方法有矢量积法和微分变换法，雅可比矩阵J(q)既可当成是从关节空间向操作空间的速度传递的线性关系，也可看成是微分运动转换的线性关系，即：
VJ(q)q
DJ(q)dq
对于有n个关节的机器人，其雅可比矩阵J(q) 是
T S ( P ) ( P ) T , T S ( P ) ( P ) T
RTS(P)((P P on))xx (Pa)x
(Pn)y (Po)y (Pa)y
((P P on))zz (Pa)z
相应的，广义速度V的坐标变换为：
T RT RTS(P)
T0
RT
任意两坐标系A和B之间广义速度的坐标变换为：
线性关系称为雅可比矩阵，记为J，即：
x
y
z
x
y
J
q1
q
2
q n
4-3
z
在数学上，机器人终端手抓的广义位置
（位姿）矢量P可写成：
x(q1, ,qn)

浅析工业机器人的坐标转换矩阵算法

浅析工业机器人的坐标转换矩阵算法工业机器人是一种广泛应用于生产自动化领域的设备，它可以代替人工完成重复性、繁琐、危险的工作任务。

在工业机器人的运动控制中，坐标转换矩阵算法是其中的核心问题之一、本文将对工业机器人的坐标转换矩阵算法进行浅析。

坐标转换矩阵算法是工业机器人运动控制的核心，它主要涉及到机器人末端执行器的位置和姿态的描述。

工业机器人通常采用笛卡尔坐标系来描述物体的位置和姿态，而关节坐标系用来描述机器人关节角度。

坐标转换矩阵算法就是将笛卡尔坐标系中的位置和姿态转换为关节坐标系的角度。

在工业机器人中，常见的坐标系包括世界坐标系、基坐标系、工具坐标系和末端执行器坐标系。

世界坐标系是一个固定的参考坐标系，通常以机器人基座为原点，用来描述整个机器人工作空间中物体的位置和姿态。

基坐标系是机器人控制系统中的一个坐标系，以机器人基座为原点，用来描述机器人关节的位置。

工具坐标系是描述机器人末端工具的位置和姿态的坐标系，通常以末端工具的夹持点为原点。

末端执行器坐标系是描述机器人末端执行器的位置和姿态的坐标系，也就是通常所说的工具坐标系。

在进行坐标转换时，首先需要将工具坐标系中的位置和姿态转换到基坐标系中，然后再将基坐标系中的位置和姿态转换到世界坐标系中。

这涉及到从工具坐标系到基坐标系的平移和旋转变换。

平移变换通常通过将工具坐标系的原点相对于基坐标系的原点进行平移得到。

旋转变换通常通过工具坐标系的坐标轴相对于基坐标系的坐标轴进行旋转得到。

根据旋转变换的不同方式，常见的旋转表示方法有欧拉角表示法和四元数表示法。

在坐标转换矩阵算法中，最常用的方法是使用齐次变换矩阵。

齐次变换矩阵可以同时表示位移和旋转变换，因此非常适合实现坐标转换。

齐次变换矩阵是一个4x4的矩阵，其中前三行表示旋转变换，第四行表示平移变换，最后一行是(0,0,0,1)。

通过矩阵乘法的方式，可以将工具坐标系的位置和姿态转换到基坐标系中。

值得注意的是，在进行坐标转换时，需要考虑到物体的姿态描述方式。

mdh的连杆变换矩阵的一般形式

mdh的连杆变换矩阵的一般形式MDH（Modified Denavit-Hartenberg）方法是一种常用的机器人运动学建模方法，用于描述机器人的连杆变换关系。

连杆变换矩阵是MDH方法的核心概念，通过矩阵形式表达了机器人各个连杆之间的位置和姿态关系。

本文将介绍MDH的连杆变换矩阵的一般形式，并解释其含义和应用。

连杆变换矩阵的一般形式可以表示为：T(i-1, i) = Rot(z,θ(i-1)) * Trans(z,d(i-1)) * Trans(x,a(i-1)) * Rot(x,α(i))其中，T(i-1, i)表示第i-1个坐标系到第i个坐标系的变换矩阵；Rot(z,θ(i-1))表示绕z轴旋转θ(i-1)角度的旋转矩阵；Trans(z,d(i-1))表示沿z轴平移d(i-1)距离的平移矩阵；Trans(x,a(i-1))表示沿x轴平移a(i-1)距离的平移矩阵；Rot(x,α(i))表示绕x轴旋转α(i)角度的旋转矩阵。

这些矩阵的乘积表示了从第i-1个坐标系到第i个坐标系的总体变换关系。

连杆变换矩阵的一般形式中的参数θ(i-1)、d(i-1)、a(i-1)和α(i)分别表示了机器人各个连杆的旋转角度和平移距离。

这些参数可以通过机器人的几何结构和运动学特性来确定。

通过将这些参数代入连杆变换矩阵的一般形式，可以得到具体的变换矩阵。

连杆变换矩阵的一般形式可以用来描述机器人的运动学模型。

通过将各个连杆变换矩阵的乘积相乘，可以得到机器人末端执行器的坐标变换关系。

这个变换关系可以用来计算机器人末端执行器在工作空间中的位置和姿态，从而实现机器人的正向和逆向运动学分析。

在机器人的正向运动学分析中，已知机器人的关节角度，可以通过连杆变换矩阵的一般形式来计算机器人末端执行器的位置和姿态。

这个过程涉及到了连杆变换矩阵的乘积和矩阵运算，需要注意矩阵的顺序和运算规则，以确保计算结果的准确性。

在机器人的逆向运动学分析中，已知机器人末端执行器的位置和姿态，需要求解机器人的关节角度。

机器人运动学建模旋转矩阵

机器人运动学建模旋转矩阵机器人运动学建模旋转矩阵随着科技的不断进步和人工智能的快速发展，越来越多的机器人被引入到工业生产和日常生活中。

机器人在工业生产中的使用很多时候需要执行精确的动作和运动，因此需要对机器人进行运动学建模，以便更好地控制其动作和轨迹。

而机器人运动学建模的核心就是旋转矩阵。

一、机器人运动学机器人运动学又称为机器人空间运动学，是研究机器人在运动中各个部位位置与时间变化关系的学科。

机器人运动学分为正运动学和逆运动学两种，前者是由给定各个部位的运动状态，通过正演得到机械臂末端的位置和姿态，所谓的末端位置和姿态，通常是以笛卡尔坐标系下的三个空间位置变量和三个空间角姿态变量︰ [X, Y, Z,., , , ],其中 , , 分别代表绕笛卡尔坐标系中的X、Y、Z轴转到目标末端姿态的角度，即为姿态变量（也称欧拉角变量）。

后者是已知机械臂末端的位置和姿态，要求求出各个部位的运动状态，所谓的逆运动学问题。

二、旋转矩阵机器人运动学建模的核心之一就是旋转矩阵。

旋转矩阵是指是用来描述刚体的旋转变换的一个正交矩阵。

矩阵的每一列就是描述坐标系中一个基向量，它们互相垂直，必须统一长度，且每个向量应该 be 一个标准正交基向量，既应该具有单位长度又应该互相垂直。

矩阵中的每一个元素是基向量在另一坐标系中的投影（点积）。

因此，三维空间中的旋转变换可以通过一个 3X3 的旋转矩阵来表示，其中某一列就是描述坐标系中一个基向量。

考虑到二维空间中的旋转变换可以通过一个2x2的旋转矩阵(cos, sin、-sin, cos)来表示，我们可以将三维的旋转矩阵写成：cos(a)cos(b) cos(a)sin(b)sin(c)-sin(a)cos(c) sin(a)sin(b)cos(c)+cos(a)sin(c)-sin(a)cos(b) sin(a)sin(b)sin(c)+cos(a)cos(c) cos(a)sin(b)cos(c)-sin(a)sin(c)-sin(b) cos(b)sin(c) cos(b)cos(c)其中a,b,c是三个角度，表示绕X，Y，Z轴的旋转角度。

机器人运动学中变换矩阵左乘右乘的理解

机器人运动学中变换矩阵左乘右乘的理解机器人运动学中变换矩阵的左乘和右乘的理解1.引言机器人运动学是机器人学中的重要分支，研究机器人在空间中的运动及其相关变换。

其中，变换矩阵的理解和运用在机器人运动学中起到关键作用。

在机器人的位姿变换中，变换矩阵的左乘和右乘是我们需要理解和掌握的概念。

本文将深入探讨机器人运动学中变换矩阵左乘和右乘的理解及其应用，并分享个人观点和理解。

2.变换矩阵的基本概念在机器人运动学中，变换矩阵是描述机器人位姿变换的一种方式。

它通过矩阵的形式，将初始坐标系中的点映射到目标坐标系中。

在机器人运动学中，我们通常使用齐次变换矩阵来表示位姿变换，即4x4的矩阵。

3.变换矩阵的左乘和右乘在机器人运动学中，变换矩阵可以通过左乘和右乘来实现坐标系的变换。

左乘是指将变换矩阵放在被变换点的左边，而右乘是指将变换矩阵放在右边。

两者的区别在于坐标系变换的次序不同。

3.1 左乘的理解和应用左乘表示先进行变换矩阵的操作，再对被变换点进行坐标系的变换。

这种方式常用于描述从物体坐标系到参考坐标系的变换。

在机器人运动学中，我们通常使用齐次变换矩阵的左乘来描述机械臂末端执行器的位姿变换。

通过左乘变换矩阵，我们可以将机械臂末端执行器的位姿从机械臂坐标系变换到参考坐标系中。

3.2 右乘的理解和应用右乘表示先对被变换点进行坐标系的变换，再进行变换矩阵的操作。

这种方式常用于描述从参考坐标系到物体坐标系的变换。

在机器人运动学中，我们通常使用齐次变换矩阵的右乘来描述相机与物体之间的位姿关系。

通过右乘变换矩阵，我们可以将物体的位姿从参考坐标系变换到相机坐标系中。

4.变换矩阵左乘和右乘的对比相比而言，左乘和右乘的区别在于变换的次序不同，即坐标系变换与矩阵操作的顺序不同。

左乘更适用于描述物体坐标系到参考坐标系的变换，而右乘更适用于描述参考坐标系到物体坐标系的变换。

在实际应用中，根据不同的问题和需求，我们可以灵活运用左乘和右乘的方式来描述机器人的位姿变换。

机器人运动学中变换矩阵左乘右乘的理解

机器人运动学中变换矩阵左乘右乘的理解1. 引言在机器人运动学中，变换矩阵是一个核心概念，它用于描述机器人末端执行器相对于基座的位置和姿态。

而在进行变换矩阵的计算过程中，左乘和右乘往往是容易引起混淆的地方。

本文将深入探讨机器人运动学中变换矩阵左乘右乘的理解，帮助读者更加深入地理解这一重要概念。

2. 左乘和右乘的概念在机器人运动学中，一个坐标系相对于另一个坐标系的变换通常是通过一个4x4的变换矩阵来表示的。

假设我们有两个变换矩阵A和B，它们分别表示两个坐标系之间的变换关系。

当我们想要对某个向量或点进行这两个变换的组合时，就涉及到了左乘和右乘的操作。

•左乘：表示在原有变换的基础上进行相对位移或旋转。

即先进行左边的变换，再进行右边的变换。

•右乘：表示在原有变换的基础上进行绝对位移或旋转。

即先进行右边的变换，再进行左边的变换。

3. 左乘和右乘的比喻我们可以用日常生活中的例子来更好地理解左乘和右乘的概念。

想象一辆汽车在高速公路上行驶，这辆汽车可以进行前进和转向的操作。

•左乘：相当于在车身自身坐标系上进行操作，比如车辆自身转向或者车辆自身前进。

•右乘：相当于在世界坐标系上进行操作，比如在道路上的绝对位置调整或者全局导航的位移。

通过这个比喻，我们可以更清晰地理解左乘和右乘的区别，以及它们在机器人运动学中的应用。

4. 变换矩阵的左乘和右乘计算方法在机器人运动学中，变换矩阵的左乘和右乘的具体计算方法也是至关重要的。

在实际操作中，我们需要根据特定的场景和问题，选择合适的左乘和右乘的顺序，才能得到准确的结果。

假设有两个变换矩阵A和B，它们的表示如下： A = [[R1, p1], [0, 1 ]] B = [[R2, p2], [0, 1 ]]其中R表示旋转矩阵，p表示平移向量。

•左乘(A左乘B)的计算方法：先将A和B相乘，得到新的变换矩阵C，即C = A * B。

•右乘(B右乘A)的计算方法：先将B和A相乘，得到新的变换矩阵D，即D = B * A。

举例说明运用齐次变换矩阵求解机器人正运动学的方法

举例说明运用齐次变换矩阵求解机器人正运动学的方法齐次变换矩阵用于描述刚体在空间中的位姿（位置和方向）。

在机器人正运动学问题中，运用齐次变换矩阵可以求解机器人末端执行器的位姿。

我们以一个简单的2R（两个旋转关节）机械臂为例进行说明。

假设2R机械臂有两个关节q1和q2，臂长分别为L1和L2。

我们的目标是求解两个关节角度q1和q2下，末端执行器的位置坐标(x, y)和方向theta。

首先，我们需确定两个坐标系。

通常将基坐标系（frame0）放在第一个关节处，frame1放在第二个关节处，frame2放在末端执行器处。

然后，我们需要分别计算从frame0到frame1的齐次变换矩阵T01和从frame1到frame2的齐次变换矩阵T12。

T01表示frame1相对于frame0的位姿，其旋转角度为q1，平移距离为L1。

矩阵形式如下：```T01 = | cos(q1) -sin(q1) 0 L1*cos(q1) || sin(q1) cos(q1) 0 L1*sin(q1) || 0 0 1 0 || 0 0 0 1 |```同理，T12表示frame2相对于frame1的位姿，其旋转角度为q2，平移距离为L2。

矩阵形式如下：```T12 = | cos(q2) -sin(q2) 0 L2*cos(q2) || sin(q2) cos(q2) 0 L2*sin(q2) || 0 0 1 0 || 0 0 0 1 |```接下来，我们需要计算从frame0到frame2的齐次变换矩阵T02。

通过矩阵乘法，我们可以得到：```T02 = T01 * T12```最后，我们从T02矩阵中提取机器人末端执行器的位置和方向。

位置坐标(x, y)就是T02矩阵中的平移部分，即：```x = T02[0][3]y = T02[1][3]```方向theta可以通过以下公式计算：```theta = atan2(T02[1][0], T02[0][0])```所以，通过齐次变换矩阵，我们可以求解出机器人末端执行器的位置和方向，从而解决2R机械臂的正运动学问题。

举例说明运用齐次变换矩阵求解机器人正运动学的方法

举例说明运用齐次变换矩阵求解机器人正运动学的方法运用齐次变换矩阵求解机器人正运动学是机器人学中重要的一个应用。

在机器人学中，正运动学问题是指根据机器人各关节的运动参数，求解机器人末端执行器的位置和姿态。

齐次变换矩阵是一种用来描述从一个坐标系到另一个坐标系的变换关系的方法，它可以将平移和旋转变换统一起来，因此非常适用于机器人的运动学描述。

下面我们以一个简单的二自由度机械臂为例，详细说明如何运用齐次变换矩阵求解机器人正运动学。

1.机器人几何参数的定义我们首先需要定义机器人的几何参数，包括各关节的长度、原点位置和旋转轴方向等。

假设我们的机器人臂长分别为L1和L2，关节1的旋转轴在z轴上，关节2相对于关节1的旋转轴在y轴上。

2.齐次变换矩阵的构建根据机器人的几何参数，我们可以构建各关节相对于前一关节的齐次变换矩阵。

对于本例中的二自由度机械臂，我们需要构建两个齐次变换矩阵，分别表示关节1和关节2相对于机器人基座的变换关系。

假设关节1的变换矩阵为T1，关节2的变换矩阵为T2，机器人基座的变换矩阵为Tbase。

根据机器人几何参数的定义，我们可以得到如下变换矩阵的表达式：T1 = [cos(θ1) -sin(θ1) 0 L1*cos(θ1)sin(θ1) cos(θ1) 0 L1*sin(θ1)00100001]T2 = [cos(θ2) 0 sin(θ2) L2*cos(θ2)0100-sin(θ2) 0 cos(θ2) L2*sin(θ2)0001]Tbase = [1 0 0 001000 0 1 d_base0001]其中θ1和θ2分别表示关节1和关节2的旋转角度，d_base表示机器人基座的高度。

3.机器人末端执行器的正运动学求解对于机器人末端执行器的正运动学问题，我们需要根据机器人各关节的运动参数，如各关节的旋转角度，通过乘法计算得到末端执行器的位置和姿态。

具体过程如下：a)首先，将各关节的变换矩阵相乘，得到机器人末端执行器相对于基座的变换矩阵。

机构学和机器人学3运动学中的矩阵法

5
若二定、长绕矢直量角r坐随标刚轴体的旋一转组，旋旋转转次序为：
先绕z转α→绕y轴转β角→绕x轴转γ角达到终点，则：
r2 R ,x R , y R ,z r1
（3-9）
r2 R r1
（3-10）
cc
R sc css
ss csc
sc cc sss cs ssc
轴转回原先的位置，这种方法可用五次转动来实现。
8
r2 R , y R ,x R,z R ,x R , y r1
即为绕任意轴 u 旋转φ角， r 前后位置的关系式。
r2
R
,u
r1
（3-13）
(3-12)中五只矩阵连乘即得
R
,u
的表达式。
由图：
sin uy
sin ux
p1 y
cos1
j
q1
y
1
1
（3—23）
qjx
写成简单形式：q jy 1
R1 j 00
p j R1 j 1
p1
q1x q1y （3—24） 1
或：
q 1
j
D1 j
q1
1
（3—25）
则3×3矩阵 D1j 称为平面位移矩阵。
18
二、空间位移矩阵
刚体空间位移矩阵，类似以上（3-20）、（3-22）、（3-25）方式的描述，图仍然适用于空间机构，只要用三维旋转矩阵
R R , ,
、 R
,
u
或
R , ,
代替
即可。
为了方便，现用
R
,u
代替R
于是相应表达式
（3—20）成： q j p j R ,u q1 p1 （3—26）

机器人的数学基础齐次变换矩阵及其运算

相对于固定坐标系
算子左乘
相对于动坐标系
算子右乘
上海电机学院机械学院
❖ 已知坐标系中点U的位置矢量 u 7 3 2 1，T 将此点绕Z轴旋转90°，再绕Y轴旋转90°，如图所示，求旋转变换后所得的点W。
W Rot(Y,90)Rot(Z,90)U
0 0 1 0 0 1 0 0 7
0Leabharlann 1000 0
0 1 0 0
0 0 1 0
x
y
z
1
cos
Rot(
z,
)
sin 0
0
sin cos
0 0
0 0 1 0
0 0 0 1
上海电机学院机械学院
CAT ABT CBT
4．变换矩阵相乘
对于给定的坐标系｛A｝、｛B｝、｛C｝，已知｛B｝相对｛A｝的描述为 ABT ，｛C｝相对｛B｝的描述为 CBT ，则
x' x cos y sin
y'
x
sin
y
c os
z' z
x' cos sin 0 0 x
y'
sin
cos
0
0
y
z' 0
0 1 0 z
1
0
0
0
1
1
记为: a′=Rot(z, θ)a
旋转算子
上海电机学院机械学院
绕Z轴旋转算子内容为：
cos sin 0 0
Rot(z,
)
sin
1
0
0
0
3
1 0 0 0 0 0 1 0 2
0
0
0
1 0
0

举例说明运用齐次变换矩阵求解机器人正运动学的方法

举例说明运用齐次变换矩阵求解机器人正运动学的方法机器人正运动学是指根据机器人关节角度，求出机器人末端执行器的位置和姿态。

运用齐次变换矩阵的方法可以方便地求解机器人正运动学。

齐次变换矩阵是一种描述机器人移动和旋转的数学工具，它能够将机器人的位置和姿态用一个矩阵表示出来。

在机器人正运动学中，我们需要根据机器人各个关节的角度来求出机器人的位置和姿态。

假设机器人有n个关节，每个关节的旋转角度分别为θ1,θ2,...,θn。

我们可以用齐次变换矩阵来表示机器人每个关节的旋转和移动。

假设第i个关节的齐次变换矩阵为Ti，则Ti = [cosθi -sinθi 0 ai;sinθi cosθi 0 bi;0 0 1 ci;0 0 0 1];其中ai, bi, ci分别表示第i个关节的位置坐标，θi表示第i个关节的旋转角度。

机器人的末端执行器的位置和姿态可以通过将所有关节的齐次变换矩阵相乘得到。

即T0n = T1 * T2 * ... * Tn;其中T0n表示机器人的末端执行器的齐次变换矩阵。

通过分析T0n的各个元素，我们可以得到机器人末端执行器的位置和姿态信息。

举例说明，假设有一个二自由度机器人，其第一个关节的旋转角度为θ1，第二个关节的旋转角度为θ2。

假设机器人的关节长度均为1，且第二个关节相对于第一个关节的位置偏移为1。

则第一个关节的齐次变换矩阵为T1 = [cosθ1 -sinθ1 0 0;sinθ1 cosθ1 0 0;0 0 1 0;0 0 0 1];第二个关节相对于第一个关节的位置偏移为1，因此第二个关节的位置坐标为(1,0,0)。

其齐次变换矩阵为T2 = [cosθ2 -sinθ2 0 1;sinθ2 cosθ2 0 0;0 0 1 0;0 0 0 1];将两个齐次变换矩阵相乘得到机器人的末端执行器的齐次变换矩阵为T0n = T1 * T2= [cosθ1cosθ2-sinθ1sinθ2 -cosθ1sinθ2-sinθ1cosθ2 0 cosθ1;sinθ1cosθ2+cosθ1sinθ2 -sinθ1sinθ2+cosθ1cosθ2 0 sinθ1;0 0 1 0;0 0 01];通过分析T0n的各个元素，我们可以得到机器人末端执行器的位置和姿态信息。