数学物理方法傅里叶变换法
数学物理方法 复变函数 第五章 傅立叶变换

∫
ρ (x) d x = m......(4)
ቤተ መጻሕፍቲ ባይዱ
也即
-∞
∫
∞
-∞
lim ρ l (x) d x = m
l→ 0
由 (3) 、( 4)可以看出质点线密度
分布函数的直观图像。
它在
x ≠ 0时 , 为 0; 在 x = 0时,为 ∞ 。它的积分值为 m. 也即由 (3) 、 共 (4) 同来描述。
因此 , 在 Dirac 首次引入 δ 函数时,曾遭到许多数 学家的非难 但它在近代物理学中有 许多重要的应用 , 它可以用来描述物 理学中的一切点量 (点质量 \ 点电荷 \ 瞬时源 )且物理图象清 晰 .这样迫使数学家对 δ 函数的性质等进行研究 和解释 .
下一页 上一页 返回
第5章
傅里叶变换(Fourier transforms)
-∞
第5章
傅里叶变换(Fourier transforms)
第5节 δ函数
五 δ函数的性质
2 δ 函数具有挑选性
若 a = 0, 则有
这 一 性 质 表 明 , 虽 然 δ (x) 是 广 义 函 数 , 但 它 和 任 何 连 续 函 数 的 乘 积 在 ( - ∞, + ∞) 内 的 积 分 都 有 明 确 的 意 义 。 这 使 得 它在近代物理和工程技术中有广泛的应用。
..........
...(1)
下一页 上一页 返回
第5章
傅里叶变换(Fourier transforms)
第5节 δ函数
引入δ 一 引入δ函数的物理背景
注意 rect() 的写法 : 即保证 rect() 中的量的绝对值 >
傅里叶变换及其应用

傅里叶变换及其应用傅里叶变换(Fourier Transform)是一种重要的数学工具和数学分析方法,广泛应用于信号处理、图像处理、通信系统、量子力学等领域。
通过将一个函数表示成一组正弦和余弦函数的叠加,傅里叶变换能够将时域中的信号转化为频域中的信号,从而使得复杂的信号处理问题变得更加简单。
本文将介绍傅里叶变换的原理、性质以及其在实际应用中的几个重要方面。
一、傅里叶变换的原理和基本定义傅里叶变换是将一个函数f(x)表示成指数函数的叠加的过程。
设f(x)在时域上是以周期T为基本周期的连续函数,那么其傅里叶变换F(k)在频域上将成为以1/T为基本周期的连续函数。
傅里叶变换的基本定义如下:F(k) = ∫[f(x) * e^(-i2πkx/T)]dx其中,i是虚数单位,k是频率变量。
通过这样的变换,我们可以将时域上的函数转换为频域上的函数,从而可以更加清晰地分析信号的频谱特征。
二、傅里叶变换的性质傅里叶变换具有一些重要的性质,这些性质使得傅里叶变换成为一种强大的工具。
1. 线性性质:傅里叶变换具有线性性质,即若f(x)和g(x)的傅里叶变换分别为F(k)和G(k),则对应线性组合的傅里叶变换为aF(k) +bG(k),其中a和b为常数。
2. 时移性质:若f(x)的傅里叶变换为F(k),则f(x - a)的傅里叶变换为e^(-i2πak/T)F(k),即时域上的平移将对频域上的函数进行相位调制。
3. 频移性质:若f(x)的傅里叶变换为F(k),则e^(i2πax/T)f(x)的傅里叶变换为F(k - a),即频域上的平移将对时域上的函数进行相位调制。
4. 尺度变换性质:若f(x)的傅里叶变换为F(k),则f(ax)的傅里叶变换为1/|a|F(k/a),即函数在时域上的尺度变换会对频域上的函数进行缩放。
5. 卷积定理:若f(x)和g(x)的傅里叶变换分别为F(k)和G(k),则f(x) * g(x)的傅里叶变换为F(k)G(k),即在频域上的乘积等于时域上的卷积。
数学与物理学中的傅里叶变换及其应用

数学与物理学中的傅里叶变换及其应用傅里叶变换(Fourier Transform)是一种在数学和物理学中广泛应用的数学转换。
它是将一个时域信号(即随时间变化的函数)转换成一个频域信号(即随频率变化的函数)。
这种转换可以有很多应用,在数学和物理学中都非常重要。
最初,傅里叶变换是由法国数学家约瑟夫·傅里叶(Joseph Fourier)于19世纪发明的。
当时,他在研究热传导方程时发现,任何一个周期性函数都可以表示为一些正弦及余弦波的线性组合。
而这种线性组合就可以通过傅里叶变换得到。
傅里叶变换可以将连续时域信号(如音频信号、电信号等)表示成为连续频域信号。
例如,一段时间内的声音可以通过傅里叶变换变成不同频率的声音组合。
同时,傅里叶变换也可以将离散时域信号(如数字信号)表示为离散频域信号。
例如,在数字图像处理中,离散傅里叶变换可以将图像转换为一组频谱信息,从而方便进行图像的处理和分析。
傅里叶变换不仅可以用于信号分析,也可以广泛应用于物理学中的波动问题。
例如,光波、声波、电磁波等都可以通过傅里叶变换进行分析,并可以显示出不同波长和频率的成分。
在量子力学中,傅里叶变换也被广泛用于波函数的计算。
傅里叶变换在实际应用中是非常常见的。
例如,人们通过在电视上观看一部电影时,所看到的影像和声音都是通过傅里叶变换来得到的。
当人们在各种应用中收听音乐、观看电影、处理图像时,傅里叶变换都会被广泛应用。
此外,傅里叶变换在通信技术中也有着非常重要的应用。
通过傅里叶变换可以将信号分解成不同的频率成分,然后通过信号加密、压缩等方式对信号进行处理。
最后,需要指出的是,傅里叶变换并不是万能解决方案。
它只是一种将时域信号转换为频域信号的方法,而不是一种能够解决所有问题的黑盒子。
因此,在应用傅里叶变换时,需要对其能解决的范围进行了解,并针对不同的问题进行处理。
总的来说,傅里叶变换是一种非常重要的数学转换,在数学和物理学的研究和应用中占据着重要的位置。
简述傅里叶变换

简述傅里叶变换傅里叶变换是现代数学、物理及工程学的基石之一,它能将一个时间域信号转换成一个频域信号,为各种信号处理、控制、通信、图像处理等领域提供了有力的工具,是第一次把两个物理量之间的变换相结合,并在证明中使用了一些非常复杂的数学方法以及接近两个世纪的科学发展而发明的。
一、傅里叶变换的定义傅里叶变换是指将一个时间域函数f(x)转换成一个频域函数F(u)的过程。
其定义是:$$F(u) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{+\infty}f(x)e^{-jux}dx$$其中,j为虚数单位,u为频率,f(x)为原信号,F(u)为转换后的频率信号。
该公式中,积分的上下限为负无穷到正无穷。
分析以上公式,可以发现傅里叶变换有以下几个特点:1. 将原信号f(x)从时域转换到频域;2. 傅里叶变换公式是一个积分表达式,波形的具体形式决定了计算的难度;3. 积分变量是虚数u,表示频率;4. 傅里叶变换是线性的。
二、傅里叶变换的性质1. 时间移位性质该性质指的是如果将函数f(x)向右移动a单位,则傅里叶变换的频域函数F(u)将乘以e^-j2πau:$$FT(f(x-a)) = F(u) \cdot e^{-j2\pi ua}$$2. 频率移位性质该性质是当函数f(t)乘以一个复指数时,经傅里叶变换后,其频率也将发生移位。
$$FT(e^{j2\pi Tu}f(t)) = F(u-T) $$其中T是一个常数,表示频域移位的量。
3. 线性性质傅里叶变换是线性的,即对于任何两个函数f1(t)和f2(t),有:$$FT(af_1(t)+bf_2(t)) = aF_1(u)+bF_2(u)$$其中a和b是任何常数。
4. 傅里叶变换的共轭对称性傅里叶变换具有共轭对称性,即:$$F^*(u) = F(-u)$$5. 卷积定理该性质的表述是:f和g的卷积时f和g的傅里叶变换的乘积。
即:$$FT(f*g) = FT(f)\cdot FT(g)$$其中“*”表示卷积操作。
数学物理方法 第5章 傅里叶变换

0 xl l x 0 x l
-l 0
F(x)
l
x
图5.7(a)
1 l 1 l 1 l l a0 F ( x)dx f ( x) xdx l 0 l 0 l 0 2
2 l kx 2 l kx 2 l kx ak F ( x) cos dx f ( x) cos dx x cos dx 0 0 0 l l l l l l
k 1
a0 E (t )dt 2 2
1
0
E0 cost E 0 sin tdt 2
0
E0
E0 a k E0 sin t cos ktdt 0 2
0
[sin(k 1)t sin(k 1)t ]dt
解:
l 2 l kx 2 l kx l bk x sin dx x( ) cos 0 l l l k l 0 k
l 2 l l 2 kx 2l l ( )( 1) k ( ) sin (1) k 1 l k k l 0 k
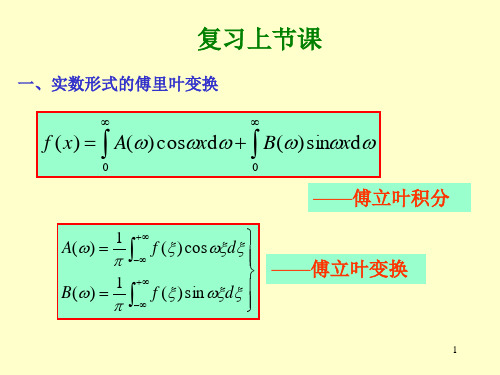
f ( x)
0
A( ) cosxd
0
B( ) sin xd
(称为傅里叶积分式)
A( )
B( )
1
1
f ( x) cosxdx
f ( x) sin xdx
(称为傅里叶变换式)
在 f (x) 的间断点,傅里叶积分的值
1 [ f ( x 0) f ( x 0)] 2
例4:定义在区间 (0, l ) 上的函数 f ( x) x ,试把它 展开为傅里叶级数。 解:方法一:偶延拓法,所找的周期函数 F (x)为偶 函数,如图5.7(a)所示。
傅里叶变换公式

傅里叶变换公式傅里叶变换是数学中一种重要的变换方法,用于将一个函数从时域表示(函数在时间上的表示)转换为频域表示(函数在频率上的表示)。
它是由法国数学家约瑟夫·傅里叶于19世纪提出的,广泛应用于信号处理、图像处理、通信、音频处理等领域。
F(ω) = ∫f(t)e^(-jωt)dt其中,F(ω)表示频率为ω的正弦波在函数f(t)中的振幅,即将函数f(t)分解为振幅谱F(ω)。
e代表自然对数的底数,j表示虚数单位,ω为频率。
这个公式的意义在于将一个函数f(t)转换成一系列振幅谱F(ω),表示不同频率正弦波在函数中所占的比重。
由于函数f(t)是由无数个不同频率的正弦波叠加而成的,因此通过傅里叶变换,我们可以分析一个函数中不同频率的成分。
这个过程也被称为频域分析。
傅里叶变换公式中的积分符号表示对整个时域进行积分,求出对应频率的振幅谱。
e^(-jωt)表示频率为ω的正弦波,振幅谱F(ω)表示频率为ω的正弦波在函数f(t)中的振幅。
通过在不同频率上进行积分,我们可以得到整个函数在频域上的表示。
傅里叶变换公式的应用非常广泛。
在信号处理领域,我们经常需要对信号进行频谱分析,以了解信号的频率成分。
例如,通过分析音频信号的频谱,我们可以分辨出不同乐器在音乐中的音高,从而实现音乐的识别和分类。
在图像处理领域,傅里叶变换可用于图像滤波、边缘检测等任务,提取图像中不同频率的特征。
此外,傅里叶变换还具有一些重要的性质,如线性性、位移性、尺度性等,这些性质使得傅里叶变换成为一种强大的工具。
例如,线性性质使得我们可以将傅里叶变换应用于信号的线性叠加,通过对不同频率的信号进行叠加,得到整体信号的频域表示。
总之,傅里叶变换是一种重要的数学工具,它能够将函数从时域表示转换为频域表示,帮助我们更好地理解信号和图像。
通过傅里叶变换,我们可以分析信号中不同频率的成分,实现信号处理、图像处理、通信等领域中的一系列任务。
傅里叶变换方法

傅里叶变换方法一、傅里叶变换方法简介傅里叶变换是一种分析信号的数学工具,可以将一个时间域函数转换成一个频率域函数。
它是由法国数学家约瑟夫·傅里叶在19世纪初提出的,并且在现代通信、图像处理、声音处理等领域有广泛应用。
二、离散傅里叶变换(DFT)方法1. 离散傅里叶变换的定义离散傅里叶变换(DFT)是一种将有限长度序列转换为具有相同长度的离散频率序列的算法。
它可以用于数字信号处理中,例如数字滤波器设计、频谱分析等。
2. DFT算法步骤DFT算法步骤如下:a. 将输入序列拆分成偶数和奇数部分。
b. 对偶数和奇数部分进行递归计算DFT。
c. 将两个部分合并为一个序列,并进行后续计算。
d. 重复上述步骤,直到得到最终结果。
3. DFT算法实现DFT算法可以使用FFT(快速傅里叶变换)来实现。
FFT是一种高效的计算DFT的方法,可以大大提高计算速度。
FFT算法的实现可以使用C语言、Python等编程语言。
三、傅里叶变换在信号处理中的应用1. 信号滤波傅里叶变换可以将时域信号转换为频域信号,从而可以进行滤波操作。
例如,对于一段音频信号,我们可以使用傅里叶变换将其转换为频谱图,并通过滤波器来过滤掉不需要的频率成分。
2. 图像处理在图像处理中,傅里叶变换可以用于图像增强、去噪等操作。
例如,在图像增强中,我们可以对原始图像进行傅里叶变换,然后通过调整频率域的值来增强图像的对比度和清晰度。
3. 声音处理在声音处理中,傅里叶变换可以用于声音压缩、降噪等操作。
例如,在声音压缩中,我们可以对原始声音进行傅里叶变换,并通过删除一些低幅度的频率成分来减小文件大小。
四、总结以上是关于傅里叶变换方法的简介以及在信号处理中的应用。
DFT是一种常见的计算离散频谱的方法,并且可以使用FFT算法来提高计算速度。
在实际应用中,傅里叶变换可以用于信号滤波、图像处理、声音处理等领域,具有广泛的应用前景。
数学物理方法2019傅里叶变换

Em, Em,
0t t
Em
o
t
将其展开为傅立叶级数.
Em
解 所给函数满足狄利克雷充分条件.
在点x n(n 0,±1,±2, )处不连续.
收敛于 Em Em Em(Em) 0,
2
2
当x n时, 收敛于f ( x). 和函数图象为
ak
1
u(t)cos ktdt
1
0
(
Em
的拉氏逆变换.
5.1 傅里叶级数
1807年12月21日,Fourier向法国科学院宣布:任意的 周期函数都能展开成正弦及余弦的无穷级数。当时整个科学院, 包括拉格朗日等,都认为他的结果是荒谬的。
傅立叶的两个最主要的贡献:
• “周期信号都可表示为谐波关 系的正弦信号的加权和”—— 傅里叶的第一个主要论点
数学物理方法2019傅里叶变换
所谓积分变换,就是把某函数类A中的任意一个函数 f ( t )
,经过某种可逆的积分方法(即为通过含参变量 的积分)
b
F() f (t)K(t,)dt a
变为另一函数类 B中的函数 F ( ) , 这里 K (t, ) 是一个确
定的二元函数,通常称为该积分变换的核.F ( ) 称为 f ( t )
的傅里叶逆变换.
(2)特别当核函数 K(t,p)ept(注意已将积分参变量
改写为变量 p ),当 a0,b,则
F(p) f(t)eptdt 0
称函数 F ( p ) 为函数 f ( t ) 的拉普拉斯 (Laplace)变换,简称
F ( p ) 为函数 f ( t ) 的拉氏变换.同时我们称 f ( t ) 为 F ( p )
记
a0 2
数学物理方法第五章傅里叶变换

l
l
l
l kx nx
sin cos dx0
l
l
l
l
1 2 dx 2 l
l
l
sin
2 k x dx
l
l
l
cos
2 k x dx
l
l
2、可以由函数的正交性求出傅立叶级数中的系数;
a f 1 l
0 2l l
xdx
a f 1l n l l
xconsxdx
l
(n1,2,3, )
b f 1l n l l
( a k cos
kπx l
b k sin
kπx )
l
k 1
2
2l l
说明 1、三角函数族是两两正交的
l kx
cos d x 0
l
l
(k 0),
l kx
sin d x 0
l
l
l kx nx
cos cos d x 0 (k n)
l
l
l
l kx nx
sin sin dx0 (kn),
f (x)
a
x
l
延拓到(- l,l)后再周期延拓,如图做偶延拓:
f (x)
a
l 0 l
x
所以
1l
x
a
a0
l
a(1
0
l
)dx 2
ak2 l0 la(1x l)co k lx sd x 2(2 4 n a 0 1 )2(k (k 2n )2n1 )
如图做奇延拓: f (x)
a
l
0l
x
2l x kx 2a
An 2cn
A n 称为f ( x)的振幅频谱(简称为频谱).它描述了各次谐波 的振幅随频率变化的分布情况。它清楚地表明了一个非正旋 周期函数包含了哪些频率分量及各分量所占的比重(如振幅 的大小)。因此频谱图在工程技术中应用比较广泛.所谓频谱 图,通常是指频率和振幅的关系图。
数学物理方法5傅里叶变换

图像增强
通过改变图像的频率成分,傅里叶 变换可以帮助增强图像的某些特征, 如边缘和纹理。
图像去噪
傅里叶变换可以帮助识别和去除图 像中的噪声,从而提高图像的质量。
量子力学
波函数分析
在量子力学中,波函数是一个描述粒子状态的函数。傅里叶变换 可以用来分析波函数的性质和行为。
量子纠缠
傅里叶变换在量子纠缠的研究中也有应用,可以帮助我们更好地理 解这种神秘的现象。
时间-频率分析
傅里叶变换将时间域的信号转换 为频率域的信号,通过分析信号 在不同频率下的强度和相位,可 以揭示信号的频率结构和变化规
律。
周期信号分析
对于周期信号,傅里叶变换可以 将其表示为一系列正弦波和余弦 波的叠加,从而方便地分析其频
率成分和振幅。
非周期信号分析
对于非周期信号,傅里叶变换将 其表示为无穷多个不同频率的正 弦波和余弦波的叠加,可以揭示
振动系统分析
在振动系统的分析中,傅里叶变换可以用于将时间域的振动信号转换为角频率域的信号, 从而方便地计算系统的固有频率、阻尼比等参数。
热传导分析
在热传导现象的分析中,傅里叶变换可以用于将时间域的温度分布转换为角频率域的温度 分布,从而方便地分析热传导的频率特性和变化规律。
05结果 具有共轭对称性,即F(-ω)=F*(ω)。
傅里叶变换的应用
01
02
03
信号处理
傅里叶变换在信号处理中 应用广泛,如频谱分析、 滤波、调制解调等。
图像处理
傅里叶变换在图像处理中 用于图像的频域分析,如 图像增强、去噪、特征提 取等。
数值分析
傅里叶变换在数值分析中 用于求解偏微分方程、积 分方程等数学问题。
数学物理方法chp5-3 傅里叶变换delta函数
a
11
5.函数的
( x ) 0 的实根 xk (k 1,2,3,) 全为单根 ( ' ( x) 0) 有 ( x xk ) ( x ) k | ' ( xk ) |
0, ( x ) 0 ( x) , ( x ) 0
1/l -l/2
o
l/2
x
15
(2)sinc 函数序列:
1 sin Kx ( x ) lim K x
6 5 4 3
K=8
K=16
sinKt/(pi*t)
2 1 0 -1 -2 -2
K=4Leabharlann -1.5-1-0.5
0 t
0.5
1
1.5
2
16
(3) 函数序列: ( x )
60
lim
m x 0, ( x 0) ( x) lim l ( x) lim rect , ( x 0) l 0 l 0 l l
( x)dx lim l ( x)dx m
l 0
引入δ函数:
0, ( x 0) ( x) , ( x 0) 0, a ( x)dx 1
(一)δ函数概念
– 问题 • 质点的密度函数如何表示? • 一般函数无法描写物理上的“点源”,如“点电荷”、 “质点”的密度,以及“瞬时力”等概念。 – 思路 • 质点是物体在尺度趋于零时的理想模型; • 一个位于原点、长度l、质量为m的线,线密度为 l(x)=m/l rect(x/l)的物体,当l->0时,可以看成质点;
( x ) C ( )eix d
数学物理方法傅里叶变换法

2
积分公式: e 2k2ekd k( /a )e2/4 2
e dk e e dk 2 k 2 k
2 4 2
2 (k 2 2 )2
2 e e dk 2 4 2
2 (k 2 2 )2
0
2
2e 4 2
e d 2 2
0
2
2 e 4 2
e x 2 dx
k2d
3k
41a
(r)[
4a2(eik
at eik
a)etik(rr)d1kd2kd3k]dV
16
41a
(r)[
1
42
1(eik ik
ateik a)etik(rr)d1kd2kd3k]dV
41at
(r)[
412i1k(eik
ateik
)aetik(rr)d1kd2kd3k]dV
41a
数学物理方法傅里叶 变换法
傅里叶变换
F (1)导数定理 ftiFf t iF()
(2)积分定理
F F
t
f
t
dt
1 i
ft
(3)相似性定理
Ff(ax)
1 a
F
(
a
)
2
(4)延迟性定理
F fx x0 e i x0 F( )
(5)位移性定理
F ei x0 fx F( 0 )
出现 (|rr|a)t对 r的积分只要在球面
S
r at
上进行
S
r at
以r为球心(矢径r),半径为at
U (r,t)1 (r)d S 1 (r)d S 4a tS a r t at 4aS a r t at
dS
为球面
数学物理方法1课件——第五章 傅里叶变换

∑ ∑ ∞ sin (2n −1) x
m sin (2n −1) x
f (x) =
= lim
n=1 2n −1
m→∞ n=1 2n −1
(−π < x < π )
m=1 1
0.5
-3 -2 -1 -0.5 -1
1
2
3
m=2 0.75
0.5 0.25
-3 -2 -1 -0.25 -0.5 -0.75
第五章傅里叶变换51傅里叶级数52傅里叶变换53傅里叶变换的性质54函数约瑟夫傅里叶傅立叶早在1807年就写成关于热传导的基本论文热的传播在论文中推导出著名的热传导方程并在求解该方程时发现函数可以由三角函数构成的级数形式表示从而提出任一函数都可以展成三角函数的无穷级数
第五章 傅里叶变换
§ 5.1 傅里叶级数 § 5.2 傅里叶变换 § 5.3 傅里叶变换的性质 § 5.4 δ函数
其中傅里叶变换系数为:
∫ A(k) = 1
∞
f (x) cos(kx)dx
π −∞
∫ B(k) = 1
∞
f (x) sin(kx)dx
π −∞
傅里叶变换存在的条件:
¾
函数
f (x) 在 (−∞, ∞) 区间内绝对可积,即积分
∞
∫−∞
f (x) dx 收敛
¾ 函数 f (x) 在任意有限区间内满足狄里希利条件,即 f (x) 分段
3. 展开式中的波数kn或频率ωn,取值是不连续的,
即 n = 0,1, 2,... (实数形式的展开) 或 n = 0, ±1, ±2,... (复数形式的展开)。
§ 5.2 傅里叶变换
1、实数形式的傅里叶积分变换
傅里叶积分定理:设函数f(x)是区间[-∞, ∞]上的非周期函数,
傅里叶变换详细解释

傅里叶变换详细解释傅里叶变换是一种数学工具,可以将一个函数分解成一系列正弦和余弦函数的和。
它在信号处理、图像处理、通信和物理学等领域中广泛应用。
傅里叶变换的详细解释包括其定义、数学表达式、性质和应用等方面。
首先,傅里叶变换可以将一个连续函数f(t) 分解成一系列正弦和余弦函数的和。
这些正弦和余弦函数的频率是连续的,可以覆盖整个频谱。
傅里叶变换的定义如下:F(ω) = ∫f(t) e^(-jωt) dt其中,F(ω) 是傅里叶变换后的函数,f(t) 是原始函数,ω 是频率,e 是自然常数。
傅里叶变换的数学表达式可以用复数的形式来表示。
当函数 f(t) 是实函数时,傅里叶变换F(ω) 是一个复函数,具有实部和虚部。
实部表示函数在频域中的振幅,虚部表示函数在频域中的相位。
傅里叶变换有一些重要的性质。
首先,傅里叶变换具有线性性质,即对于常数a 和 b,有 F(a*f(t) + b*g(t)) = a*F(f(t)) + b*F(g(t))。
这使得傅里叶变换在信号处理中非常有用,可以将多个信号叠加在一起进行分析。
其次,傅里叶变换具有平移性质。
如果将函数 f(t) 在时间域上平移 t0,那么它的傅里叶变换F(ω) 在频域上也会相应地平移 e^(-jωt0)。
这个性质使得我们可以通过平移信号来改变其频谱。
另外,傅里叶变换还具有对称性质。
当函数 f(t) 是实函数时,其傅里叶变换F(ω) 的实部是偶函数,虚部是奇函数。
这个对称性质使得我们可以通过傅里叶变换将实函数分解成实部和虚部的和。
傅里叶变换在许多领域中有广泛的应用。
在信号处理中,傅里叶变换可以将时域上的信号转换成频域上的信号,从而可以分析信号的频谱特性。
例如,通过傅里叶变换,我们可以将音频信号转换成频谱图,可以分析音频信号中不同频率的成分。
在图像处理中,傅里叶变换可以将图像转换成频域上的图像,从而可以对图像进行频域滤波和增强处理。
例如,通过傅里叶变换,我们可以将模糊的图像恢复成清晰的图像,或者将图像中的噪声去除。
傅里叶变换算法详细介绍.

从头到尾彻底理解傅里叶变换算法、上前言第一部分、DFT第一章、傅立叶变换的由来第二章、实数形式离散傅立叶变换(Real DFT)从头到尾彻底理解傅里叶变换算法、下第三章、复数第四章、复数形式离散傅立叶变换/***************************************************************************************************/这一片的傅里叶变换算法,讲解透彻,希望对大家会有所帮助。
感谢原作者们(July、dznlong)的精心编写。
/**************************************************************************************************/前言:“关于傅立叶变换,无论是书本还是在网上可以很容易找到关于傅立叶变换的描述,但是大都是些故弄玄虚的文章,太过抽象,尽是一些让人看了就望而生畏的公式的罗列,让人很难能够从感性上得到理解”---dznlong,那么,到底什么是傅里叶变换算法列?傅里叶变换所涉及到的公式具体有多复杂列?傅里叶变换(Fourier transform)是一种线性的积分变换。
因其基本思想首先由法国学者傅里叶系统地提出,所以以其名字来命名以示纪念。
哦,傅里叶变换原来就是一种变换而已,只是这种变换是从时间转换为频率的变化。
这下,你就知道了,傅里叶就是一种变换,一种什么变换列?就是一种从时间到频率的变化或其相互转化。
ok,咱们再来总体了解下傅里叶变换,让各位对其有个总体大概的印象,也顺便看看傅里叶变换所涉及到的公式,究竟有多复杂:以下就是傅里叶变换的4种变体(摘自,维基百科)连续傅里叶变换一般情况下,若“傅里叶变换”一词不加任何限定语,则指的是“连续傅里叶变换”。
连续傅里叶变换将平方可积的函数f(t)表示成复指数函数的积分或级数形式。
北京大学数学物理方法经典课件第五章-傅里叶变换

逆变换的概念
详细介绍傅里叶变换的逆变换 以及其作用。
逆变换公式
掌握逆变换的常用公式,理解 如何从频域还原原始信号。
信号重构
通过逆变换实现原始信号的还 原,并研究其重构误差。
时频分析和不确定性原理
时域分析 频域分析 不确定性原理
在时间域上分析信号的时变特性,研究信号的 时序行为。
将信号转换到频域,揭示信号的频谱分布和频 域行为。
学习如何使用傅里叶级数分析周期性信号, 揭示其频域特性。
实际案例
探索傅里叶级数在音频、图像和通信等实际 应用中的作用。
傅里叶变换的定义和性质
1
线性性质
2
学习傅里叶变换的线性性质及其意义。
3
定义
介绍傅里叶变换的基本定义和公式。
频域解释
了解傅里叶变换的频域解释,研究信 号的频谱特征。
傅里叶变换的逆变换
北京大学数学物理方法经 典课件第五章-傅里叶变 换 本课件是北京大学数学物理方法经典课件的第五章,深入讲解了傅里叶变换
的概念和性质,以及在不同领域中的广泛应用。
傅里叶级数
数学基础
了解傅里叶级数的定义和性质,掌握其在数 学领域中的应用。
信号重建
通过傅里叶级数的逆变换,实现信号的还原 和重建。
周期信号分析
探索时频分析中的不确定性原理,分析信号在 时频平面上的限制条件。
傅里叶变换的应用
信号滤波
利用傅里叶变换对信号进行滤波处理,去除 干扰或提取感兴趣的频率成分。
通信技术
研究傅里叶变换在调制、解调和频谱分析等 通信技术中的应用。
图像处理
探索傅里叶变换在图像处理中的应用,如图 像增强和去噪。
量子力学
了解傅里叶变换在量子力学研究中的重要作 用,如波函数的变换和量子力学运算符的表 示。
《数学物理方法》第十二章--11级-2012解析

将C(k,t) 代入式(12.2.17) 可得
在式(12.2.18)中令 t = 0 得 再与式(12.2.16)联立得 代入式(12.2.18)即有
(12.2.18)
60
(3)作像函数的傅里叶逆变换
61
利用奇,偶函数的性质及定积分公式(例4.2.7)p90
62
本题不利用卷积定理,在傅里叶的逆变换公式中对 指数作配方运算后,再利用定积分公式计算也可以 得到相同的结果。
上两式称为傅里叶余弦变换及其逆变换.
18
3. 三维傅里叶变换
正如由式(12.1.7)可以得到式(12.1.14),式 (12.1.15)一样,由式(12.1.10)可得
19
【例12.1.1】求 的傅里叶变换
解
20
【例12.1.2】求f(x)=exp[2ax2] 的傅里叶变换, 其中a为正数 解 由傅里叶变换的定义出发,并利用4.2节
耐心+坚持+努力 ≈成功
第十二章 积分变换法
积分变换法是物理学与其他应用科学中 求解数学物理方程的一种重要方法, 它适用于求解无界区域及半无界区域的 定解问题。
积分变换法是
通过对数理方程的积分变换,减少自变量的个数, 直至化为常微分方程,使求解问题大为简化。
此外,积分变换法还可以用来计算定积分,求解常 微分方程和积分方程.
49
§12.2 傅里叶变换法
傅里叶变换法广泛地应用于求解无界区 域的定解问题中.求解步骤为 ①对定解问题作傅里叶变换; ②求像函数; ③对像函数作傅里叶逆变换, 得解
对于半无界区域的定解问题
可采用傅里叶正弦变换(第一类边界条件),或傅里 叶余弦变换(第二类边界条件);也可将边界条件齐 次化后,采用延拓法,最后用傅里叶变换求解.
数学物理方法傅里叶变换法

数学物理方法傅里叶变换法傅里叶变换法是一种将一个函数表示为一系列正弦和余弦函数的叠加的方法。
这种方法在数学和物理学中广泛应用,在信号处理、图像处理、调制和解调等领域具有重要意义。
本文将详细介绍傅里叶变换法及其在数学和物理学中的应用。
傅里叶变换法的基本原理是基于傅里叶级数展开的思想。
傅里叶级数展开是将一个周期函数表示为一系列正弦和余弦函数的线性组合。
这种展开的思想被扩展到了非周期函数,即傅里叶变换。
傅里叶变换可以将一个函数表示为连续的正弦和余弦函数的积分形式。
傅里叶变换的定义公式如下:\[F(\omega)=\int_{-\infty}^{\infty}f(t)e^{-i\omega t}dt\]傅里叶变换的逆变换公式如下:\[f(t)=\frac{1}{2\pi}\int_{-\infty}^{\infty}F(\omega)e^{i\omega t}d\omega\]傅里叶变换法在数学中有广泛的应用。
它可以用于求解偏微分方程和积分方程等问题。
傅里叶变换法可以将微分方程转化为代数方程,简化求解过程。
例如,在热传导方程中,傅里叶变换法可以将其转化为常微分方程来求解。
在物理学中,傅里叶变换法用于分析和解释各种物理现象。
例如,在波动现象中,傅里叶变换法可以将一个周期信号分解为不同频率的正弦和余弦函数,从而可以分析波的频谱特性。
在光学中,傅里叶变换法可以用于分析光的传播和衍射现象。
在量子力学中,傅里叶变换法被广泛用于求解薛定谔方程。
傅里叶变换还具有信号处理和图像处理方面的重要应用。
在信号处理中,傅里叶变换可以将一个信号从时域转换到频域,从而可以方便地进行滤波、降噪等处理。
在图像处理中,傅里叶变换可以将一个图像从空域转换到频域,并可以进行图像增强、去噪等操作。
此外,傅里叶变换还有一些与之相关的变换方法,如离散傅里叶变换(DFT)和快速傅里叶变换(FFT)。
离散傅里叶变换是一种将离散信号转换到频域的方法,而快速傅里叶变换是一种计算傅里叶变换的高效算法。
傅里叶变换方法

傅里叶变换方法1. 傅里叶变换的概念傅里叶变换是一种数学工具,用于将一个函数或信号表示为一系列振幅和相位的复指数函数的和。
它可以将时域中的信号转换为频域中的信号,从而揭示出信号包含的频率成分和它们之间的关系。
傅里叶变换方法是由法国数学家约瑟夫·傅里叶在19世纪初提出的,他认为任何周期性函数都可以用一组正弦和余弦函数来表示。
这个思想被广泛应用于物理、工程、计算机科学等领域,成为了现代科学研究中不可或缺的工具。
2. 傅里叶级数与傅里叶变换傅里叶级数是指将一个周期函数表示为正弦和余弦函数的无穷级数。
它在周期性信号处理中得到广泛应用。
对于一个周期为T、连续可积的函数f(t),其傅里叶级数定义如下:f(t)=a02+∑(a n cos(2πnTt)+b n sin(2πnTt))∞n=1其中,a0、a n和b n是系数,可以通过函数f(t)的积分计算得到。
而傅里叶变换则是将非周期函数表示为连续频谱的积分形式。
对于一个连续可积的函数f(t),其傅里叶变换定义如下:F(ω)=∫f∞−∞(t)e−jωt dt其中,ω是频率,F(ω)表示函数f(t)在频率域中的表示。
3. 傅里叶变换的性质傅里叶变换具有许多重要的性质,这些性质使得它成为一种强大而灵活的工具。
以下是一些常见的傅里叶变换性质:•线性性质:傅里叶变换具有线性性质,即对于任意常数a和b以及两个函数f(t)和g(t),有F(af(t)+bg(t))=aF(f(t))+bF(g(t))。
•平移性质:如果将函数在时域上平移,则其在频域上也会相应平移。
具体而言,如果f(t)经过时移得到ℎ(t)=f(t−t0),那么它们的傅里叶变换满足H(ω)=F(ω)e−jωt0。
•尺度性质:如果将函数在时域上进行尺度变换,则其在频域上也会相应进行尺度变换。
具体而言,如果f(t)经过尺度变换得到ℎ(t)=f(at),那么它们的傅里叶变换满足H(ω)=1|a|F(ωa)。
傅里叶变换用法

傅里叶变换是一种在数学、工程学和物理学中广泛应用的数学工具。
它可以用于将一个具有周期性的信号从时域转换到频域,以便更方便地分析。
以下是傅里叶变换的基本用法:一、傅里叶变换的定义傅里叶变换是一种函数空间到另一个函数空间的线性映射,具体定义为:给定一个连续时间信号x(t),它表示一个随时间变化的函数。
对于任意x(t)及其傅里叶变换X(ω),它们的关系可以表示为X(ω) = ∫t*x(t)e^(-jωt) dt,其中ω为频率变量,t为时间变量。
这种关系就是著名的傅里叶级数或傅里叶变换定理。
二、傅里叶变换的基本性质傅里叶变换具有一些基本性质,这些性质为信号分析提供了强大的工具。
以下是其中一些基本性质:1. 线性性质:傅里叶变换是线性的,这意味着如果将两个信号相加或进行任何形式的线性操作,傅里叶变换的结果将是这两个信号的傅里叶变换的和或线性组合。
2. 时移性质:如果信号x(t)关于时间有恒定的移动,那么傅里叶变换X(ω)在相应位置会有相应的频率移位。
这是因为在时域和频域中,频率的定义是不同的。
3. 频移性质:傅里叶变换有一个性质,即在改变ω的取值时,傅里叶变换的结果将会相应地改变相位。
4. 频域尺度变换:通过改变ω的值,可以对频域中的数据在尺度上变化。
这使得频域分析成为一种强大的工具,可以对信号进行各种尺度比较。
三、傅里叶变换的应用傅里叶变换在许多领域都有应用,包括但不限于工程、物理和生物医学工程。
以下是一些具体的应用:1. 信号处理:傅里叶变换可以将信号从时域转换到频域,这使得各种信号处理任务变得更容易。
例如,通过傅里叶变换,可以找到信号中的主要频率成分,以便对其进行滤波、压缩等操作。
2. 图像处理:傅里叶变换在图像处理中也有应用。
可以将图像从空间域转换到频域,以便进行各种操作,如滤波、噪声消除等。
还可以通过反变换将处理后的频域图像转换回空间域。
3. 调频信号分析:在无线通信中,调频信号是常见的。
通过傅里叶变换,可以分析这些信号的频谱,从而了解信号的传输特性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
有的杂质向硅片内扩散,但不让新的杂质穿过硅片表面进入
硅片,这里求解的是半无界空间x>0中的定解问题:
uutx
a2uxx |x0 0
0
u |t0 0 (x 0) (x 0)
0是单位面积硅片 表层原有杂质总量.
10
解: 没有杂质穿过硅片表面,即: ux |x0 0 第二类齐次边界条件
积分变换法
积分变换在数学物理方程中也有广泛的用途,变换后, 方程得以化简,偏微分方程变成常微分方程,求解常微 方程后,再进行逆变换就得到原来偏微分方程的解, 同时,积分变换还可能得到有限形式的解,分离变数 法或者傅里叶级数发往往不能。 本章主要介绍傅里叶变换法在求解偏微分方程中的应用。
1
傅里叶变换
e dk e e dk 2k2 k
2 4 2
2 (k 2 2 )2
2e e dk 2 4 2
2 (k 2 2 )2
0
2
2e 4 2
e d 2 2
0
2
2 e 4 2
ex2 dx
uut|x0a2uNxx0 0
u |t0 0
12
解 首先把非齐次边界条件化为齐次边界条件,令 u(x,t) N0 w(x,t)
则化为关于w的定解问题:
wt w |
a2 x0
wxx u |x
0
0 N0
0
w |t0 u |t0 N0 N0
0
2
2 e 4 2
2
e 4 2
2
7
令 a t , i(x ) 利用上述公式可得
u(x,t) ( )
1
( x )2
e 4a2t d
2a t
例3 求解无限长细杆的有源热传导问题
ut a2uxx f (x, t)( x ) u |t0 0
N0 x/ 2a t ez2 dz
x/2a t
被积函数是偶函数,故
w(x,t) N0
2
x/ 2a t ez2 dz
0
误差函数
记做erfx,则w可写为:
x
w(x,t) N0erf ( 2a
) t
所求的解如下:
14
u( x, t )
N0
w(x,t)
N0 1 erf
引用例2结果可得
u(x,t)
20
( )
1
2a t
e
(
x ) 4a2t
2
d
0 2 ex2 /4a2t
高斯函数
2a t
11
右图描述了杂质浓度u(x,t)在硅片中
u( x, t )
硅1
的分布情况,曲线1对应于较早的时刻
片 表
2
2,3依次对应越来越晚的时刻,杂质浓 面
例6 泊松公式 求解三维无界空间中的波动问题
utt u |t
0
a23u 0
(r),Ut
|t
0
(r
)
15
解 做傅里叶变换,问题变换为常微分方程的初始值问题
U k 2a2U 0 U |t0 (k),U |t0 (k)
这个方程的解为
U (t, k) 1 (k)(eikat eikat ) 1 1 (k)(eikat eikat )
13
第一个积分中令 z (x ) / 2a t , dz d / 2a t
第二个积分中令 z ( x) / 2a t , dz d / 2a t
则有 w(x, t) N0 x/2a t ez2 dz N0
ez2 dz
x/2a t
dV
1
4a
(r)
17
1 r
(r
at
)eik
(
r
r
)
dk1dk2
dk3
dV
应用延迟定理
U (r,t)
1
4a
t
(r) (| r r | at)dV
| r r |
1
4a
(r) (| r r | at)dV
| r r |
出现 (| r r | at)
对
r 的积分只要在球面
S
r at
上进行
S
r at
以r为球心(矢径r),半径为at
U (r,t) 1 (r) dS 1 (r) dS
4a t Sart at
4 a Sart at
dS
为球面
S
2
2a ik
对U作逆傅里叶变换,可得最后的结果如下:
5
u( x, t) 1 [( x at) ( x at)] 1
x at
( )d
达朗贝尔公式
2
2a xat
例2 求解无限长细杆的热传导问题
uut|t0a2ux(xx) 0( x )
[
(
)e
ik
d
]e
k
2
a
2t
e
ik
x
dk
2
6
交换积分次序
u(x,t) 1
( )[
ek 2a2teik (x )dk]d
2
积分公式: e 2k2 ek dk ( / a)e 2 / 4 2
F F (1)导数定理 f t i f t iF()
(2)积分定理
F F
t
f
t
dt
1
i
ft
(3)相似性定理
F f(ax )
1 F( )
aa
2
(4)延迟性定理
F f x x0 eix0F()
连续的,所求的解可表示为对连续本征值求积分的傅里叶积
分,对于无界空间的定解问题,适用于傅里叶变换法求解。
例1 求解无限长弦的自由振动
utt u |t
0
a2u
xx (x),
0( x )
ut |t0 (x)
解: 应用傅里叶变换,即用 eikx / 2 同乘方程和定解条件
r at
的面积元,此即泊松公式.
18
三维无界空间中的波动,只要知道初始状况,就可以用泊松公式
求以后任一时刻的状况,具体说,为求时刻t在r的u(r,t),应以r为
球心,以at为半径作球面
S
r at
然后拿初始扰动 (r), (r)
按泊松公式在球面
S
r at
上积分
,波动以速度a传播,只有跟点r
相距at的那些点的初始扰动恰好在时刻t传到r
代入初始条件可得:A(k) 1 (k) 1 1 (k)
2
2a ik
B(k) 1 (k) 1 1 (k)
2
2a ik
故 U (t, k) 1 (k)eikat 1 1 (k)eikat
2
2a ik
1 (k )eikat 1 1 (k )eikat
2
2a ik
再进行傅里叶逆变换
U (r, t) [ (k) 1 (eikat eikat )
2
(k)
1 2a
1 ik
(eikat
e ik at
)]eikr dk1dk2dk3
1
4a
Байду номын сангаас(r)[
a
4
2
(eikat
eikat )eik(rr)dk1dk2dk3 ]dV
解: 作傅里叶变换,定解问题变为:
U k 2a2U 0
U |t0 (k) 此常微分方程的初始问题的解为 U(t, k) (k)ek2a2t
进行傅里叶逆变换可得:
u(x, t) F 1[U (t, k )] (k )ek2a2teikxdk
1
)
dk
dd
9
并利用积分公式可得最后的结果为:
u(x,t)
t
f
(
,
)
1
e
( x )2 4a2 (t
)
dd
0
2a (t )
例4 限定源扩散
在半导体扩散工艺中,杂质扩散深度远远小于硅片厚度,可
以把硅片看成无限厚,在限定源扩散中,是只让硅片表层已
16
1
4a
(r)[
1
4 2
1 ik
(eikat
eikat )eik(rr)dk1dk2dk3 ]dV
1
4a t
(r)[
1
4 2
1 ik
(eikat
eikat )eik(rr)dk1dk2dk3 ]dV
进行傅里叶逆变换
u(x,t) 1
2
t 0
f
(
,
