高等代数习题解答(第一章)
高等代数__课后答案__高等教育出版社

高等代数习题答案(一至四章)第一章 多项式 习题解答1、(1)由带余除法,得17(),39q x x =-262()99r x =--(2)2()1q x x x =+-,()57r x x =-+2、(1)2100p m q m ⎧++=⎨-=⎩ , (2)由22(2)010m p m q p m ⎧--=⎪⎨+--=⎪⎩得01m p q =⎧⎨=+⎩或212q p m =⎧⎨+=⎩。
3、(1)432()261339109,q x x x x x =-+-+()327r x =- (2)q (x )=22(52)x ix i --+,()98r x i =--4、(1)有综合除法:2345()15(1)10(1)10(1)5(1)(1)f x x x x x x =+-+-+-+-+- (2)234()1124(2)22(2)8(2)(2)f x x x x x =-+++-+++(3)234()24(75)5()(1)()2()()f x i x i i x i i x i x i =+-++--+-+++5、(1)x+1 (2)1 (3)21x -- 6、(1)u (x )=-x-1 ,v (x )=x+2 (2)11()33u x x =-+,222()133v x x x =-- (3)u (x )=-x-1, 32()32v x x x x =+--7、02u t =⎧⎨=⎩或23u t =-⎧⎨=⎩8、思路:根具定义证明证:易见d (x )是f (x )与g (x )的公因式。
另设()x ϕ是f (x )与g (x )的任意公因式,下证()()x d x ϕ。
由于d (x )是f (x )与g (x )的一个组合,这就是说存在多项式s (x )与t (x ),使 d (x )=s (x )f (x )+t (x )g (x )。
从而()()x f x ϕ,()()x g x ϕ,可得()()x d x ϕ。
高等代数(王萼芳石生明著)课后答案高等教育出版社

高等代数习题答案(一至四章)第一章 多项式 习题解答1、(1)由带余除法,得17(),39q x x =-262()99r x =--(2)2()1q x x x =+-,()57r x x =-+2、(1)2100p m q m ⎧++=⎨-=⎩ , (2)由22(2)010m p m q p m ⎧--=⎪⎨+--=⎪⎩得01m p q =⎧⎨=+⎩或212q p m =⎧⎨+=⎩。
3、(1)432()261339109,q x x x x x =-+-+()327r x =- (2)q (x )=22(52)x ix i --+,()98r x i =--4、(1)有综合除法:2345()15(1)10(1)10(1)5(1)(1)f x x x x x x =+-+-+-+-+- (2)234()1124(2)22(2)8(2)(2)f x x x x x =-+++-+++ (3)234()24(75)5()(1)()2()()f x i x i i x i i x i x i =+-++--+-+++5、(1)x+1 (2)1 (3)21x --6、(1)u (x )=-x-1 ,v (x )=x+2 (2)11()33u x x =-+,222()133v x x x =-- (3)u (x )=-x-1, 32()32v x x x x =+-- 7、02u t =⎧⎨=⎩或23u t =-⎧⎨=⎩ 8、思路:根具定义证明证:易见d (x )是f (x )与g (x )的公因式。
另设()x ϕ是f (x )与g (x )的任意公因式,下证()()x d x ϕ。
由于d (x )是f (x )与g (x )的一个组合,这就是说存在多项式s (x )与t (x ),使 d (x )=s (x )f (x )+t (x )g (x )。
从而()()x f x ϕ,()()x g x ϕ,可得()()x d x ϕ。
高等代数习题 北大第四版 答案一到四章

上式说明 ( f ( x), g( x)) h( x) 是 f (x)h(x) 与 g( x)h( x) 的一个组合。
另一方面,由 ( f (x), g( x)) | f ( x) 知 ( f (x), g(x))h(x) | f ( x)h( x) ,
同理可得 ( f ( x), g( x)) h( x) | g( x) h( x) ,
于是 u(x) = −q2 (x) = −x −1
。
v(x) = 1+ q1 (x )q2 (x ) = 1+1i(x + 1) = x + 2
2)仿上面方法,可得 ( f (x), g( x)) = x−1,且 u(x) = − 1 x + 1 ,v(x) = 2 x 2 − 2 x −1。
33
33
10.如果 f (x), g( x) 不全为零,证明:
⎛ ⎜ ⎝
(
f
f ( x) ( x), g( x))
, (
f(
g( x) x), g(
x))
⎞ ⎟ ⎠
=1。
证 存在 u(x), v( x) 使 ( f ( x), g( x)) = u( x) f ( x) + v( x) g( x) ,
又因为 f (x), g(x) 不全为0,所以 ( f (x), g(x)) ≠ 0 ,
39
99
2)同理可得 q(x) = x 2 + x −1, r( x) = −5x + 7 。
2. m, p, q 适合什么条件时,有
1) x 2 + mx −1 | x3 + px + q ,
2) x 2 + mx + 1| x4 + px2 + q 。
高等代数习题解答(第一章)(完整资料).doc

【最新整理,下载后即可编辑】高等代数习题解答第一章 多项式补充题1.当,,a b c取何值时,多项式()5f x x =-与2()(2)(1)g x a x b x =-++ 2(2)c x x +-+相等?提示:比较系数得6136,,555a b c =-=-=. 补充题2.设(),(),()[]f x g x h x x ∈,2232()()()f x xg x x h x =+,证明:()()()0f x g x h x ===.证明 假设()()()0f x g x h x ===不成立.若()0f x ≠,则2(())f x ∂为偶数,又22(),()g x h x 等于0或次数为偶数,由于22(),()[]g x h x x ∈,首项系数(如果有的话)为正数,从而232()()xg x x h x +等于0或次数为奇数,矛盾.若()0g x ≠或()0h x ≠则232(()())xg x x h x ∂+为奇数,而2()0f x =或2(())f x ∂为偶数,矛盾.综上所证,()()()0f x g x h x ===.1.用g (x ) 除 f (x ),求商q (x )与余式r (x ): 1)f (x ) = x 3- 3x 2 -x -1,g (x ) =3x 2 -2x +1; 2)f (x ) = x 4 -2x +5,g (x ) = x 2 -x +2. 1)解法一 待定系数法.由于f (x )是首项系数为1的3次多项式,而g (x )是首项系数为3的2次多项式,所以商q (x )必是首项系数为13的1次多项式,而余式的次数小于 2.于是可设q (x ) =13x +a , r (x ) =bx +c 根据 f (x ) = q (x ) g (x ) + r (x ),即x 3-3x 2 -x -1 = (13x +a )( 3x 2 -2x +1)+bx +c 右边展开,合并同类项,再比较两边同次幂的系数,得 2333a -=-,1123a b -=-++,1a c -=+解得79a =-,269b =-,29c =-,故得17(),39q x x =- 262().99r x x =--解法二 带余除法.3 -2 1 1 -3 -1 -1 1379-1 23- 1373-43- -173-14979- 269- 29-得17(),39q x x =- 262().99r x x =--2)2()1,()57.q x x x r x x =+-=-+ 262().99r x x =--2.,,m p q 适合什么条件时,有1)231;x mx x px q +-++ 2)2421.x mx x px q ++++ 1)解21x mx +-除3x px q++得余式为:2()(1)()r x p m x q m =+++-,令()0r x =,即210;0.p m q m ⎧++=⎨-=⎩故231x mx x px q +-++的充要条件是2;10.m q p m =⎧⎨++=⎩2)解21x mx ++除42x px q++得余式为:22()(2)(1)r x m p m x q p m =-+-+--+,令()0r x =,即22(2)0;10.m p m q p m ⎧-+-=⎪⎨--+=⎪⎩解得2421x mx x px q ++++的充要条件是0;1m p q =⎧⎨=+⎩ 或 21;2.q p m =⎧⎨=-⎩ 3.求()g x 除()f x 的商()q x 与余式()r x : 1)53()258,()3;f x x x x g x x =--=+2)32(),()12.f x x x x g x x i =--=-+1)解法一 用带余除法(略).解法二 用综合除法.写出按降幂排列的系数,缺项的系数为0: -3 2 0 -5 0 -8 0 + -6 18 -39 117 -3272 -6 13 -39 109 -327 所以432()261339109,()327.q x x x x x r x =-+-+=-2)解法一 用带余除法(略).解法二 用综合除法.写出按降幂排列的系数,缺项的系数为0:()f x1-2i 1 -1 -1 0 + 1-2i -4-2i -9+8i 1 -2i -5-2i -9+8i 所以2()2(52),()98.q x x ix i r x i =--+=-+4.把()f x 表成0x x -的方幂和,即表成 201020()()c c x x c x x +-+-+的形式:1)50(),1;f x x x == 2)420()23,2;f x x x x =-+=-3)4320()2(1)37,.f x x ix i x x i x i =--+-++=-注 设()f x 表成201020()()c c x x c x x +-+-+的形式,则0c 就是()f x 被x x -除所得的余数,1c 就是()f x 被x x -除所得的商式212030()()c c x x c x x +-+-+再被0x x -除所得的余数,逐次进行综合除法即可得到01,,,.n c c c1)解用综合除法进行计算1 1 0 0 0 0 0+ 1 1 1 1 11 1 1 1 1 1 1+ 1 2 3 41 2 3 4 51 + 1 3 61 3 6 101 + 1 41 4 101 + 11 5所以5234515(1)10(1)10(1)5(1)(1).x x x x x x=+-+-+-+-+-2)3)略5.求()f x与()g x的最大公因式:1)43232()341,()1;f x x x x xg x x x x=+---=+--2)4332()41,()31;f x x xg x x x=-+=-+3)42432()101,()6 1.f x x xg x x x=-+=-+++1)解用辗转相除法()g x()f x2()q x12-141 1 -1 -1 1 1 -3 -4 -11 1 3212 1 1 -1 -112-32- -1 1()r x-2 -3 -13()q x834312- 34- 14- -2 -22()r x34-34--1 -1-1 -13()r x所以((),()) 1.f x g x x =+2)((),()) 1.f x g x = 3)2((),()) 1.f x g x x =--6.求(),()u x v x 使()()()()((),()):u x f x v x g x f x g x += 1)432432()242,()22f x x x x x g x x x x x =+---=+---; 2)43232()421659,()254f x x x x x g x x x x =--++=--+; 3)4322()441,()1f x x x x x g x x x =--++=--. 1)解 用辗转相除法()g x ()f x2()q x1 1 1 1 -1 -2 -2 1 2 -1 -4 -21 1 0 -2 0 1 1 -1 -2 -2 1 1 -2 -21()r x1 0 -2 03()q x1 01 0 -2 0 1 0 -22()r x1 0 -23()r x由以上计算得11()()()(),f x q x g x r x =+ 212()()()(),g x q x r x r x =+ 132()()(),r x q x r x =因此22((),())()2f x g x r x x ==-,且2((),())()f x g x r x =21()()()g x q x r x =-21()()[()()()]g x q x f x q x g x =-- 212()()[1()()]()q x f x q x q x g x =-++所以212()()1,()1()()2u x q x x v x q x q x x =-=--=+=+.2)((),())1f x g x x =-,21122(),()13333u x x v x x x =-+=--. 3)((),())1f x g x =,32()1,()32u x x v x x x x =--=+--.7.设323()(1)22,()f x x t x x u g x x tx u =++++=++的最大公因式是一个二次多项式,求,t u 的值.解 略.8.证明:如果()(),()()d x f x d x g x 且()d x 为()f x 与()g x 的一个组合,那么()d x 是()f x 与()g x 的一个最大公因式.证明 由于()(),()()d x f x d x g x ,所以()d x 为()f x 与()g x 的一个公因式.任取()f x 与()g x 的一个公因式()h x ,由已知()d x 为()f x 与()g x 的一个组合,所以()()h x d x .因此,()d x 是()f x 与()g x 的一个最大公因式.9.证明:(()(),()())((),())()f x h x g x h x f x g x h x =,(()h x 的首项系数为 1). 证明 因为存在多项式()u x 和()v x 使 ((),())()()()()f x g x u x f x v x g x =+,所以((),())()()()()()()()f x g x h x u x f x h x v x g x h x =+,这表明((),())()f x g x h x 是()()f x h x 与()()g x h x 的一个组合,又因为 ((),())(),((),())()f x g x f x f x g x g x , 从而((),())()()(),((),())()()()f x g x h x f x h x f x g x h x g x h x ,故由第8题结论,((),())()f x g x h x 是()()f x h x 与()()g x h x 的一个最大公因式.注意到((),())()f x g x h x 的首项系数为1,于是(()(),()())((),())()f x h x g x h x f x g x h x =.10.如果(),()f x g x 不全为零,证明:()()(,)1((),())((),())f xg x f x g x f x g x =.证明 存在多项式()u x 和()v x 使((),())()()()()f x g x u x f x v x g x =+,因为(),()f x g x 不全为零,所以((),())0f x g x ≠,故由消去律得()()1()()((),())((),())f xg x u x v x f x g x f x g x =+,所以()()(,)1((),())((),())f xg x f x g x f x g x =.11.证明:如果(),()f x g x 不全为零,且()()()()((),())u x f x v x g x f x g x +=,那么((),())1u x v x =.证明 因为(),()f x g x 不全为零,故 ((),())0f x g x ≠,从而由消去律得()()1()()((),())((),())f xg x u x v x f x g x f x g x =+,所以((),())1u x v x =.12.证明:如果((),())1f x g x = ,((),())1f x h x =,那么((),()())1f x g x h x =. 证法一 用反证法.假设()((),()())1d x f x g x h x =≠,则(())0d x ∂>,从而()d x 有不可约因式()p x ,于是()(),()()()p x f x p x g x h x ,但因为((),())1f x g x =,所以()p x 不整除()g x ,所以()()p x h x ,这与((),())1f x h x =矛盾.因此((),()())1f x g x h x =.证法二 由题设知,存在多项式1122(),(),(),()u x v x u x v x ,使得11()()()()1u x f x v x g x +=,22()()()()1u x f x v x h x +=,两式相乘得12121212[()()()()()()()()()]()[()()]()()1u x u x f x v x u x g x u x v x h x f x v x v x g x h x +++=,所以((),()())1f x g x h x =.13.设11(),,(),(),,()m n f x f x g x g x 都是多项式,而且((),())1(1,2,,;1,2,,).i j f x g x i m j n ===求证:1212(()()(),()()()) 1.m n f x f x f x g x g x g x =证法一 反复应用第12题的结果 证法二 反证法14.证明:如果((),())1f x g x =,那么(()(),()())1f x g x f x g x +=. 证明 由于((),())1f x g x =,所以存在多项式()u x 和()v x 使 ()()()()1u x f x v x g x +=,由此可得()()()()()()()()1,u x f x v x f x v x f x v x g x -++= ()()()()()()()()1,u x f x u x g x u x g x v x g x +-+=即[][]()()()()()()1,u x v x f x v x f x g x -++=[][]()()()()()()1,v x u x g x u x f x g x -++= 于是((),()())1f x f x g x +=,((),()())1g x f x g x +=,应用第12题的结论可得(()(),()())1f x g x f x g x +=.注 也可以用反证法.15.求下列多项式的公共根:32432()221;()22 1.f x x x x g x x x x x =+++=++++提示 用辗转相除法求出2((),()) 1.f x g x x x =++于是得两多项式的公共根为1.2-± 16.判别下列多项式有无重因式: 1)5432()57248f x x x x x x =-+-+-; 2)42()443f x x x x =+--1)解 由于432'()5202144f x x x x x =-+-+,用辗转相除法可求得2((),'())(2)f x f x x =-,故()f x 有重因式,且2x -是它的一个 3 重因式.2)解 由于3'()484f x x x =+-,用辗转相除法可求得((),'())1f x f x =,故()f x 无重因式.17.求t 值使32()31f x x x tx =-+-有重根. 解2'()36f x x x t =-+.先用'()f x 除()f x 得余式 1263()33t t r x x --=+.当3t =时,1()0r x =.此时'()()f x f x ,所以21((),'())'()(1)3f x f x f x x ==-,所以1是()f x 的3重根.当3t ≠时,1()0r x ≠.再用1()r x 除'()f x 得余式215()4r x t =+.故当154t =-时,2()0r x =.此时,121((),'())()92f x f x r x x =-=+,所以12-是()f x 的2重根.当3t ≠且154t ≠-时,2()0r x ≠,则((),'())1f x f x =,此时()f x 无重根.综上,当3t =时,()f x 有3重根1;当154t =-时,()f x 有2重根12-.18.求多项式3x px q ++有重根的条件. 解 略.19.如果242(1)1x Ax Bx -++ ,求,A B .解法一 设42()1f x Ax Bx =++,则3'()42f x Ax Bx =+.因为242(1)1x Ax Bx -++,所以1是()f x 的重根,从而1也是'()f x 的根.于是(1)0f =且'(1)0f =,即10;420.A B A B ++=⎧⎨+=⎩解得1,2A B ==-.解法二 用2(1)x -除421Ax Bx ++得余式为(42)(31)A B x A B ++--+,因为242(1)1x Ax Bx -++,所以(42)(31)0A B x A B ++--+=,故420;310.A B A B +=⎧⎨--+=⎩ 解得1,2A B ==-.20.证明:212!!nx x x n ++++没有重根.证法一 设2()12!!n x x f x x n =++++ ,则21'()12!(1)!n x x f x x n -=++++-. 因为()'()!nx f x f x n -=,所以((),'())((),)1!nx f x f x f x n ==.于是212!!nx x x n ++++没有重根. 证法二 设2()12!!n x x f x x n =++++ ,则21'()12!(1)!n x x f x x n -=++++-. 假设()f x 有重根α,则()0f α=且'()0f α=,从而0!nn α=,得0α=,但0α=不是()f x 的根,矛盾.所以212!!nx x x n ++++没有重根. 21.略. 22.证明:x 是()f x 的k 重根的充分必要条件是(1)000()'()()0k f x f x f x -====,而()0()0k f x ≠.证明 (必要性)设0x 是()f x 的k 重根,从而0x 是'()f x 的1k -重根,是''()f x 的2k -重根,…,是(1)()k f x -的单根,不是()()k f x 的根,于是(1)000()'()()0k f x f x f x -====,而()0()0k f x ≠.(充分性)设(1)000()'()()0k f x f x f x -====,而()0()0k f x ≠,则0x 是(1)()k f x -的单根,是(2)()k f x -的2重根,…,是()f x 的k 重根.23.举例说明断语“如果α是'()f x 的m 重根,那么α是()f x 的m +1重根”是不对的.解 取1()()1m f x x α+=-+,则()'()1()m f x m x α=+-.α是'()f x 的m 重根,但α不是()f x 的m +1重根.注:也可以取具体的,如0,1m α==.24.证明:如果(1)()n x f x -,那么(1)()n n x f x -. 证明 略.25.证明:如果23312(1)()()x x f x xf x +++,那么12(1)(),(1)()x f x x f x --.证明2121()()x x x x ωω++=--,其中12ωω==.由于23312(1)()()x x f x xf x +++,故存在多项式()h x 使得33212()()(1)()f x xf x x x h x +=++,因此112122(1)(1)0;(1)(1)0.f f f f ωω+=⎧⎨+=⎩ 解得12(1)(1)0f f ==,从而12(1)(),(1)()x f x x f x --.26.求多项式1n x -在复数范围内和实数范围内的因式分解. 解 多项式1n x -的n 个复根为 22cossin ,0,1,2,,1kk k i k n n nππω=+=-,所以1n x -在复数范围内的分解式为1211(1)()()()n n x x x x x ωωω--=----.在实数范围内,当n 为奇数时:222112211221(1)[()1][()1][()1]n n n n n x x x x x x x x ωωωωωω---+-=--++-++-++,当n 为偶数时:222112222221(1)(1)[()1][()1][()1]n n n n n x x x x x x x x x ωωωωωω---+-=-+-++-++-++.27.求下列多项式的有理根: 1)3261514x x x -+-; 2)424751x x x ---;3)5432614113x x x x x +----.1)解 多项式可能的有理根是1,2,7,14±±±±. (1)40f =-≠,(1)360f -=-≠.由于44444,,,,1(2)171(7)1141(14)-------------都不是整数,所以多项式可能的有理根只有2.用综合除法判别:2 1 -6 15 -14 + 2 -8 14 2 1 -4 7 0 + 2 -4 1 -2 3≠0 所以2是多项式的有理根(单根).注:一般要求指出有理根的重数.计算量较小的话,也可以直接计算,如本题可直接算得(2)0f =,说明2是()f x 的有理根,再由'(2)0f ≠知.2是单根.用综合除法一般比较简单.2)答12-(2重根).3)答 1-(4重根),3(单根). 28.下列多项式在有理数域上是否可约? 1)21x -;2)4328122x x x -++; 3)631x x ++;4)1p x px ++,p 为奇素数; 5)441x kx ++,k 为整数. 1)解21x -可能的有理根是1±,直接检验知,都不是它的根,故21x -不可约.2)解 用艾森斯坦判别法,取2p =. 3)解 令1x y =+,则原多项式变为6365432(1)(1)1615211893y y y y y y y y ++++=++++++,取3p =,则由艾森斯坦判别法知多项式65432615211893y y y y y y ++++++不可约,从而多项式631x x ++也不可约.4)提示:令1x y =-,取素数p . 5)提示:令1x y =+,取2p =.。
(完整版)高等代数多项式习题解答
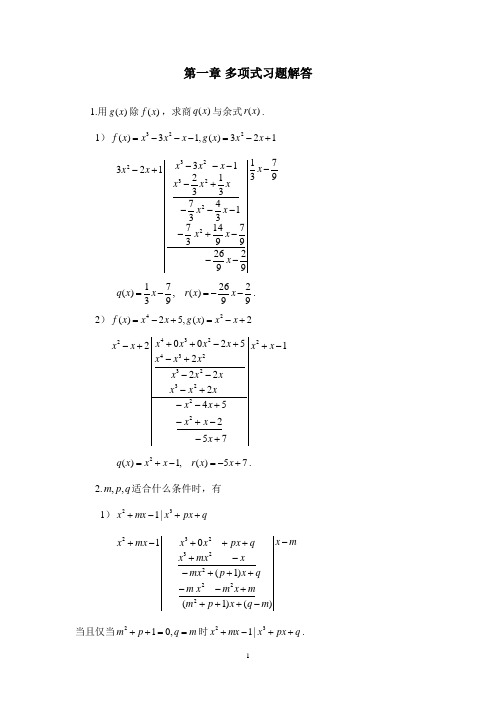
第一章 多项式习题解答1.用)(x g 除)(x f ,求商)(x q 与余式)(x r .1)123)(,13)(223+-=---=x x x g x x x x f9731929269791437134373132131232223232----+----+----+-x x x x x x x x x x x x x x 92926)(,9731)(--=-=x x r x x q . 2)2)(,52)(24+-=+-=x x x g x x x f17525422225200222223232342342-++--+-+--+---+-+-+++-x x x x x x x xx x x x x x x x x x x x x x75)(,1)(2+-=-+=x x r x x x q .2.q p m ,,适合什么条件时,有1)q px x mx x ++-+32|1m x m q x p m mx m x m qx p mx x mx x q px x x mx x --++++--+++--++++-+)()1()1(01222223232 当且仅当m q p m ==++,012时q px x mx x ++-+32|1.本题也可用待定系数法求解.当q px x mx x ++-+32|1时,用12-+mx x 去除q px x ++3,余式为零,比较首项系数及常数项可得其商为q x -.于是有q x mq x q m x mx x q x q px x ++--+=-+-=++)1()()1)((2323.因此有m q p m ==++,012.2)q px x mx x ++++242|1由带余除法可得)1()2()1)(1(2222224m p q x m p m m p mx x mx x q px x --++--++-+-++=++ 当且仅当0)1()2()(22=--++--=m p q x m p m x r 时q px x mx x ++++242|1.即⎩⎨⎧=--+=--010)2(22m p q m p m ,即⎩⎨⎧=+=,1,0p q m 或⎩⎨⎧==+.1,22q m p 本题也可用待定系数法求解.当q px x mx x ++++242|1时,用12++mx x 去除q px x ++24,余式为零,比较首项系数及常数项可得其商可设为q ax x ++2.于是有)1)((2224++++=++mx x q ax x q px x.)()1()(234q x mq a x q ma x a m x ++++++++=比较系数可得.0,1,0=+=++=+mq a p q ma a m 消去a 可得⎩⎨⎧=+=,1,0p q m 或⎩⎨⎧==+.1,22q m p 3.求)(x g 除)(x f 的商)(x q 与余式)(x r .1);3)(,852)(35+=--=x x g x x x x f解:运用综合除法可得327109391362327117083918605023---------商为109391362)(234+-+-=x x x x x q ,余式为.327)(-=x r2)i x x g x x x x f 21)(,)(23+-=--=.解:运用综合除法得:ii ii i i i 892521892421011121+----+-------商为)25(22i ix x +--,余式为i 89+-. 4.把)(x f 表成0x x -的方幂和,即表示成 +-+-+202010)()(x x c x x c c 的形式.1)1,)(05==x x x f ;2);2,32)(024-=+-=x x x x f3).1,73)1(2)(0234-=++-+-+=x i x x i ix x x f分析:假设)(x f 为n 次多项式,令])()()[()()()()(10021000202010--++-+-+=-++-+-+=n n nn x x c x x c c x x c x x c x x c x x c c x f0c 即为0x x -除)(x f 所得的余式,商为10021)()()(--++-+=n n x x c x x c c x q .类似可得1c 为0x x -除商)(x q 所得的余式,依次继续即可求得展开式的各项系数.解:1)解法一:应用综合除法得.5110141110416311563143211143211111111111100000115)(x x f =1)1(5)1(10)1(10)1(5)1(2345+-+-+-+-+-=x x x x x .解法二:把x 表示成1)1(+-x ,然后用二项式展开1)1(5)1(10)1(10)1(5)1(]1)1[(234555+-+-+-+-+-=+-=x x x x x x x2)仿上可得812226122412210412112082422128442302012-----------------432)2()2(8)2(22)2(2411)(+++-+++-=x x x x x f . 3)因为i iii i i i i i i i i i ii ii i i 2111510157104141173121-----------+-------+---- .)()(2))(1()(5)57(73)1(2)(432234i x i x i i x i i x i ix x i ix x x f +++-++-+-+=++-+-+=5.求)(x f 与)(x g 的最大公因式1)1)(,143)(23234--+=---+=x x x x g x x x x x f解法一:利用因式分解),13)(1(143)(3234--+=---+=x x x x x x x x f).1()1(1)(223-+=--+=x x x x x x g因此最大公因式为1+x .解法二:运用辗转相除法得)(3438)(01122132)(1434343)(41432112321212314121)(3122123423422223232x q x x q x x x x x x x x r x x x x x x x x x x r x x x x x x x x x x x x q =+=---------=--+---+--=------++--++-= 因此最大公因式为1+x .2)13)(,14)(2334+-=+-=x x x g x x x f .解:运用辗转相除法得(注意缺项系数补零)2564411627)(125627)(2565391649216491633323)(10310031004911916)(920910310132310323110391031)(13221232323423422223232--=--=+-+-+-+--=-++-+-+-++-+++--=+--++--+++-+-=x x q x x r x x x x x x x r x x x x x x x x x x x x x x x x r x x x x x x x x x x x x q .1))(),((=x g x f3).124624)(,110)(23424+++-=+-=x x x x x g x x x f)()()22(24)()(123x r x f x x x x f x g +=---=,),()22)((241)122()22)(22()(21223x r x x r x x x x x x x f ++-=---+--= ,)()122(22)(24122231x x r x x x x x x x r -=--=--=- 因此.122))(),((2--=x x x g x f6.求)(),(x v x u 使:))(),(()()()()(x g x f x g x v x f x u =+1);22)(,242)(234234---+=---+=x x x x x g x x x x x f解:运用辗转相除法得:)()(1022)(222422)(222221)(3133123423422323242342x q x x q x x xx x r x x x x x x x x x x r xx x x x x x x x x x x x q ==--=---+---+-=--+----++= 因此2)())(),((22-==x x r x g x f .且有 )()()()(11x r x q x g x f +=,),()()()(221x r x q x r x g +=).()()(321x q x r x r =于是)()]()()([)()()()()(21212x q x q x g x f x g x q x r x g x r --=-=)()]()(1[)()(212x g x q x q x f x q ++-=..2)()(1)(,1)()(212+=+=--=-=x x q x q x v x x q x u2);452)(,951624)(23234+--=++--=x x x x g x x x x x f解:运用辗转相除法得:)(96)(20999966936)(810249516241)(32422324523131)(3122123423422223232x q x x q x x x xx x x x r xx x x x x x x x x r x x x x x x x x x x x x q =+=+-+-+-+--=+--++--+-=+--+---++--+-= 因此1)())(),((2-=-=x x r x g x f .且有)()()()(11x r x q x g x f +=,),()()()(221x r x q x r x g +=).()()(321x q x r x r =于是)()]()()([)()()()()(21212x q x q x g x f x g x q x r x g x r --=-=)()]()(1[)()(212x g x q x q x f x q ++-=..13232)3131(21)()(1)(,3131)()(2212--=+---=--=+-==x x x x x q x q x v x x q x u 3).1)(,144)(2234--=++--=x x x g x x x x x f解:运用辗转相除法得:)(32)(3331431441)(21211)(121222342342222x q x x x r x x x x x x x x x x x x r x x xx x x x x q =--=++-++---++--=-----+= 因此.1)())(),((2==x r x g x f 且有)()()()(11x r x q x g x f +=,),()()()(221x r x q x r x g +=).()()(321x q x r x r =于是)()]()()([)()()()()(21212x q x q x g x f x g x q x r x g x r --=-=)()]()(1[)()(212x g x q x q x f x q ++-=..23)1)(3(1)()(1)(,1)()(232212--+=+-+=+=--=-=x x x x x x q x q x v x x q x u7.设u tx x x g u x x t x x f ++=++++=323)(,22)1()(的最大公因式是一个二次多项式,求u t ,的值.解:运用带余除法有),()()2()1(1)(22)1()(12323x r x g u x t x t u tx x u x x t x x f +=+--++⋅++=++++= 由题意可得,)(1x r 即为)(),(x g x f 的最大公因式.因此有01≠+t .进一步),(])1(211)[()(221x r t t x t x r x g ++-++= ])1(21[)1()2()1()1()(22222t t u x t t t u t t x r +--++-++-+=. 要使)(1x r 为)(),(x g x f 的最大公因式的充要条件是.0)(2=x r 即⎩⎨⎧=--+=-++-+,0)]2()1[(,0)2()1()1(222t t u t t u t t 解得⎪⎩⎪⎨⎧--=+-=⎪⎩⎪⎨⎧+-=--=⎪⎩⎪⎨⎧±==⎩⎨⎧-==.2111,117;2111,117;231,0;4,0i t i u i t i u i t u t u 8.证明:如果),(|)(),(|)(x g x d x f x d 且)(x d 为)(x f 与)(x g 的一个组合,那么)(x d 是)(x f 与)(x g 的一个最大公因式.证明:由)(|)(),(|)(x g x d x f x d 可知)(x d 是)(x f 与)(x g 的一个公因式.下证)(x f 与)(x g 的任意一个公因式是)(x d 的因式.由)(x d 为)(x f 与)(x g 的一个组合可知,存在多项式)(),(x v x u ,使得)()()()()(x g x v x f x u x d +=.设)(x ϕ是)(x f 与)(x g 的任意一个公因式,则)(|)(),(|)(x g x x f x ϕϕ.故)()()()(|)(x g x v x f x u x +ϕ即).(|)(x d x ϕ因此)(x d 是)(x f 与)(x g 的一个最大公因式.9.证明:)()(())(),(())()(),()((x h x h x g x f x h x g x h x f =的首项系数为1). 证明:存在多项式)(),(x v x u ,使得)()()()())(),((x g x v x f x u x g x f +=.所以有)()()()()()()())(),((x h x g x v x h x f x u x h x g x f +=.即)())(),((x h x g x f 是 )()(x h x f 与)()(x h x g 的一个组合.显然有)(|))(),((),(|))(),((x g x g x f x f x g x f .从而)()(|)())(),((),()(|)())(),((x h x g x h x g x f x h x f x h x g x f .由第8题结果)())(),((x h x g x f 是)()(x h x f 与)()(x h x g 的一个最大公因式.又)(x h 是首项系数为1的,因此).())(),(())()(),()((x h x g x f x h x g x h x f =10.如果)(x f ,)(x g 不全为零,证明1))(),(()(,)(),(()((=x g x f x g x g x f x f . 证明:由)(x f ,)(x g 不全为零可得其最大公因式不为零多项式,即.0))(),((≠x g x f 又存在多项式)(),(x v x u ,使得)()()()())(),((x g x v x f x u x g x f +=.于是))(),(()()())(),(()()(1x g x f x g x v x g x f x f x u +=. 因此1))(),(()(,)(),(()((=x g x f x g x g x f x f . 11.如果)(x f ,)(x g 不全为零,且))(),(()()()()(x g x f x g x v x f x u =+,那么1))(),((=x v x u .证明:由)(x f ,)(x g 不全为零可得.0))(),((≠x g x f 由))(),(()()()()(x g x f x g x v x f x u =+有.1))(),(()()())(),(()()(=+x g x f x g x v x g x f x f x u 于是1))(),((=x v x u .12.证明:如果,1))(),((,1))(),((==x h x f x g x f 那么.1))()(),((=x h x g x f 证法一、由条件1))(),((,1))(),((==x h x f x g x f 可得存在多项式)(),(11x v x u ; )(),(22x v x u 使得1)()()()(11=+x g x v x f x u ,1)()()()(22=+x h x v x f x u .两式相乘得1)()()()()()]()()()()()()()()([21211221=+++x h x g x v x v x f x h x v x u x g x v x u x f x u x u . 因此有.1))()(),((=x h x g x f证法二、反证法证明.显然.0))()(),((≠x h x g x f 若,1))()(),((≠x h x g x f 则存在不可约多项式)(x p ,使得)(x p 为)(x f 与)()(x h x g 的公因式.因此有)(|)(x f x p 且)()(|)(x h x g x p .由)(x p 的不可约性有)(|)(x g x p 或)(|)(x h x p .若)(|)(x g x p ,则)(x p 为)(x f 与)(x g 的一个公因式,与1))(),((=x g x f 相矛盾.若)(|)(x h x p ,则)(x p 为)(x f 与)(x h 的一个公因式,与1))(),((=x h x f 相矛盾.因此1))()(),((≠x h x g x f 不成立,即有.1))()(),((=x h x g x f13.设)(),(),(),(,),(),(2121x g x g x g x f x f x f n m 都是多项式,而且).,,2,1;,,2,1(,1))(),((n j m i x g x f j i ===求证:1))()()(),()()((2121=x g x g x g x f x f x f n m .证明:由),,2,1(1))(),((1n j x g x f j ==,反复利用第12题结果可得1))()()(),((211=x g x g x g x f n .类似可得.,,2,1))()()(),((21m i x g x g x g x f n i ==再反复利用12题结果可得1))()()(),()()((2121=x g x g x g x f x f x f n m .14.证明:如果,1))(),((=x g x f 那么.1))()(),()((=+x g x f x g x f 证明:方法一.由,1))(),((=x g x f 存在多项式)(),(x v x u 使得1)()()()(=+x g x v x f x u .从而有,1)())()(())()()((,1))()()(()())()((111111=+-++=++-x g x v x u x g x f x u x g x f x v x f x v x u 因此有.1))()(),((,1))()(),((=+=+x g x f x g x g x f x f 由12题结果结论成立.方法二:用反证法.若.1))()(),()((≠+x g x f x g x f 则存在不可约多项式)(x p ,使得)(x p 为)()(x g x f 与)()(x g x f +的公因式.即)()(|)(x g x f x p 且)()(|)(x g x f x p +.由)(x p 的不可约性及)()(|)(x g x f x p ,有)(|)(x f x p 或)(|)(x g x p .若)(|)(x f x p ,又)()(|)(x g x f x p +,因此有)]())()([(|)(x f x g x f x p -+,即)(|)(x g x p ,也即)(x p 为)(x f 与)(x g 的一个公因式,与1))(),((=x g x f 相矛盾.类似可得当)(|)(x g x p 时也与已知1))(),((=x g x f 矛盾.所以.1))()(),()((=+x g x f x g x f15.求下列多项式的公共根:.12)(;122)(23423++++=+++=x x x x x g x x x x f解法一:利用因式分解可得);1)(1(122)(223+++=+++=x x x x x x x f ).1)(1(12)(22234+++=++++=x x x x x x x x g因此1))(),((2++=x x x g x f .)(x f 与)(x g 的公共根为.2321i ±- 解法二:运用辗转相除法求出)(x f 与)(x g 的最大公因式,最大公因式的根即为所求的公共根.),1(2)1)(()(2++--=x x x x f x g ).1)(1()(2+++=x x x x f因此1))(),((2++=x x x g x f .)(x f 与)(x g 的公共根为.2321i ±- 16.判别下列多项式有无重因式: 1);84275)(2345-+-+-=x x x x x x f 解:,4421205)('234+-+-=x x x x x f运用辗转相除法可得.)2(44))('),((22-=+-=x x x x f x f 因此2-x 为)(x f 的三重因式.解法二:试根可得2为)(x f 的根)1()2()2()2()43)(2()(23232234++-=----=++--=x x x x x x x x x x x x f .因此2-x 为)(x f 的三重因式. 2).344)(24--+=x x x x f解:).12(4484)('33-+=-+=x x x x x f 1))('),((=x f x f .故)(x f 无重因式. 17.求t 值使13)(23-+-=tx x x x f 有重根.解法一:要使)(x f 有重根,则1))('),((≠x f x f ..63)('2t x x x f +-=),12(33)(')3131(13)(23+-+-=-+-=x t x f x tx x x x f .415)41523)(12(63)('2++-+=+-=t x x t x x x f当,033=-t 即3=t 时),(|)(',)1(3363)('22x f x f x x x x f -=+-=2)1())('),((-=x x f x f ,因此1为)(x f 的三重根. 当0415=+t ,即415-=t 时,21))('),((+=x x f x f ,21-为)(x f 的二重根.解法二:设b a x ab a x b a x b x a x x f 22232)2()2()()()(-+++-=--=. 因此有⎪⎩⎪⎨⎧==+=+.1,2,3222b a t ab a b a 由第一个方程有a b 26-=,代人第三个方程有,0132,1)23(232=+-=-a a a a 即0)12()1(2=+-a a .因此有⎪⎩⎪⎨⎧===,3,1,1t b a 或⎪⎪⎩⎪⎪⎨⎧-==-=.415,4,21t b a即当3=t 时1为)(x f 的三重根;当415-=t 时,21-为)(x f 的二重根.18.求多项式q px x ++3有重根的条件.解:令q px x x f ++=3)(.显然当0==q p 时,0为)(x f 的三重根.当0≠p 时, p x x f +=23)(',q x px xf q px x x f ++=++=32)('31)(3,)427()42729)(32()('222p q p p q x p q x p x f ++-+=. 要使)(x f 有重根,则1))('),((≠x f x f .即,042722=+pq p 即.027423=+q p 显然 0==q p 也满足.027423=+q p 因此)(x f 有重根的条件是.027423=+q p19.如果,1|)1(242++-Bx Ax x 求.,B A解法一:利用整除判定方法,1|)1(242++-Bx Ax x 的充要条件是用2)1(-x 除124++Bx Ax ,余式为零.)31()42()32()1(12224B A x A B A B Ax Ax x Bx Ax --++++++-=++.因此有0)31()42(=--++B A x A B ,即⎩⎨⎧-==⎩⎨⎧=--=+.2,1.031,042B A B A A B 解法二:要使1|)1(242++-Bx Ax x 成立,则1至少是124++Bx Ax 的二重根.因此1既是124++Bx Ax 的根,也是其导数的根.而Bx Ax Bx Ax 24)'1(324+=++.故有⎩⎨⎧-==⎩⎨⎧=+=++.2,1.024,01B A B A B A 解法三:利用待定系数法.令Dx D C x D C A x A C Ax D Cx Ax x Bx Ax +-++-+-+=++-=++)2()2()2()()1(12342224因此有⎪⎪⎩⎪⎪⎨⎧==-=+-=-.1,02,2,02D D C B D C A A C 解得⎪⎪⎩⎪⎪⎨⎧==-==.1,2,2,1D C B A 20.证明:!!212n x x x n++++ 不能有重根.证明:令,!!21)(2n x x x x f n++++= 则,)!1(!21)('12-++++=-n x x x x f n因此有,!)(')(n x x f x f n +=从而有)!),('())('),((n x x f x f x f n =.!n x n因式只有)0(≠c c 及)1,0(n k c cx k ≤≤≠.而)1,0(n k c cx k ≤≤≠显然不是)('x f 的因式.因此有1)!),('())('),((==n x x f x f x f n.所以)(x f 没有重根.21.如果a 是)('''x f 的一个k 重根,证明a 是)()()](')('[2)(a f x f a f x f ax x g +-+-=的一个3+k 重根. 证明:)],(')('[21)(''2)(')(''2)](')('[21)('a f x f x f a x x f x f a x a f x f x g ---=--++=).('''2)(''21)('''2)(''21)(''x f ax x f x f a x x f x g -=--+=显然有0)(")(')(===a g a g a g .由a 是)('''x f 的一个k 重根可得a 是)(''x g 的一个1+k 重根,设a 是)(x g 的s 重根,则3,12+=+=-k s k s .本题常见错误证法.错误证法一:由a 是)('''x f 的一个k 重根就得出a 是)(''x f 的一个1+k 重根,a 是)('x f 的一个2+k 重根,a 是)(x f 的一个3+k 重根,于是)(2)()()()](')('[2)(3x h a x a f x f a f x f a x x g k +-=+-+-=从而a 是)(x g 的3+k 重根.事实上,由a 是)('''x f 的一个k 重根推不出a 是)(''x f 的一个1+k 重根,a 是)('x f 的一个2+k 重根,a 是)(x f 的一个3+k 重根. 如3)()()()(23+-+-+-=+a x a x a x x f k ,则1)(2))(3()('2+-+-+=+a x a x k x f k ,2))(2)(3()(''1+-++=+k a x k k x f .a 既不是)(x f 的根,也不是)('x f 与)(''x f 的根.错误证法二:由)],(')('[21)(''2)(')(''2)](')('[21)('a f x f x f a x x f x f a x a f x f x g ---=--++=)('''2)(''21)('''2)(''21)(''x f ax x f x f a x x f x g -=--+=得出a 是)(''x g 的1+k 重根,直接得出a 是)(x g 的3+k 重根,缺了a 是)(x g 与)('x g 的根验证.22.证明:0x 是)(x f 的k 重根的充分必要条件是,0)()(')(0)1(00====-x f x f x f k 而.0)(0)(≠x f k证明:必要性.设0x 是)(x f 的k 重根,从而0x x -是)(x f 的k 重因式,从而是)('x f 的1-k 重因式,是)(''x f 的2-k 重因式,...,是)()1(x f k -的单因式,而不是)()(x f k 的因式.因此0x 是)(x f ,)('x f ,)(''x f ,...,)()1(x f k -的根,而不是)()(x f k 的根.故有,0)()(')(0)1(00====-x f x f x f k 而.0)(0)(≠x f k充分性.由,0)()(')(0)1(00====-x f x f x f k 而0)(0)(≠x f k 可知0x 是)(x f ,)('x f ,)(''x f ,...,)()1(x f k -的根,而不是)()(x f k 的根.因此0x 是)()1(x f k -的单根,是)()2(x f k -二重根,依此类推,是)(x f 的k 重根.23.举例说明断语“如果α是)('x f 的m 重根,那么α是)(x f 的1+m 重根”是不对的.解:例如2)()(1+-=+m x x f α,m x m x f ))(1()('α-+=.α是)('x f 的m 重根,但α不是)(x f 的根.24.证明:如果),(|)1(n x f x -那么)(|)1(n n x f x -.证明:由)(|)1(n x f x -可得)()1()(x g x x f n -=.从而.0)1(=f 因此有),()1()(x h x x f -=从而有).()1()(n n n x h x x f -=即)(|)1(n n x f x -.证法二:要证)(|)1(n n x f x -,只要证1-n x 在复数域上的各个根都是)(n x f 的根.1-n x 的根为.1,,2,1,0,2sin 2cos-=+=n k nk i n k x k ππ由)(|)1(n x f x -可得)()1()(x g x x f n -=.从而.0)1(=f 从而0)1()(==f x f nk .即,2sin 2cos nk i n k x k ππ+=1,,2,1,0-=n k 都是)(n x f 的根.因此有)(|)1(n n x f x -.25.证明:如果)()(|)1(32312x xf x f x x +++,那么).(|)1(),(|)1(21x f x x f x --证明:要证)(|)1(),(|)1(21x f x x f x --成立,只要证1是)(1x f 和)(2x f 的根.12++x x 的两个根为231,23121ii --=+-=εε.由)()(|)1(32312x xf x f x x +++可得)()1()()(23231x g x x x xf x f ++=+.于是,0)()1()()(,0)()1()()(2223222321112312131121=++=+=++=+εεεεεεεεεεεεg f f g f f即0)1(231)1(,0)1(231)1(2121=+-=--f if f i f .故有.0)1()1(21==f f 所以 )(|)1(),(|)1(21x f x x f x --.26.求多项式1-n x 在复数范围内和在实数范围内的因式分解. 解:1-n x 的根为.1,,2,1,0,2sin 2cos -=+=n k nk i n k k ππε故在复数范围内的分解式为)())()(1(112-----=-n n x x x x x εεε .在实数范围内,因k n k -=εε,)0(n k <<.当n 为奇数时,1-n x 的根中一个为实根,其余为虚根,其分解式为]1)([]1)(][1)()[1(12121222212++-++-++--=-+---x x x x x x x x n n n n nεεεεεε .当n 为偶数时,1-n x 的根中二个为实根,即,1±其余为虚根,其分解式为].1)([]1)(][1)()[1)(1(11212222212++-++-++-+-=-+---x x x x x x x x x n n n n nεεεεεε27.求下列多项式的有理根. 1);1415623-+-x x x解:多项式可能的有理根为.14,7,2,1±±±±由系数取值可知,x 取负数时,多项式的值均为负的,故该多项式没有负根.检验得2为其根,进一步运用综合除法可得074114821415612-----即)74)(2(14156223+--=-+-x x x x x x ,显然742+-x x 没有有理根.因此1415623-+-x x x 仅有一个有理根2,且为单根.2);157424---x x x解:多项式可能的有理根为.41,21,1±±±444222026242113121570421------------因此有)1()12()444()21(1574222224--+=--+=---x x x x x x x x x ,显然12--x x 没有有理根.因此21-为157424---x x x 的二重根.3).3111462345----+x x x x x解:多项式可能的有理根为.3,1±±检验得1-为其根,进一步运用综合除法可得1213630351133511038601138601311146111--------------故)3()1()12)(3()1(3111464222345-+=++-+=----+x x x x x x x x x x x .即1-为其四重跟,3为单根.28.下列多项式在有理数域上是否可约? 1);12+x解:显然12+x 无有理根,又为二次的,故在有理数域上不可约. 2);2128234++-x x x解:取素数2=p ,满足艾森斯坦判别法的条件,因此在有理数域上不可约. 3);136++x x 解:令,1+=y x).(3918211561)1()1(1)(234563636y g y y y y y y y y x x x f =++++++=++++=++=取素数,3=p )(y g 满足艾森斯坦判别法条件,因此在有理数域上不可约,从而)(x f 在有理数域上不可约.4)p px x p ,1++为奇素数;解:令1-=y x ,由p 为奇数可得1)1()1(1)(+-+-=++=y p y px x x f p p).()(1222211y g p y p C y C y C yC y p p p p p p p p p =-++--+-=---- 由组合数定义)11(-≤≤p k C kp 均为整数,且12)1()1()1(⋅-+--= k k k p p p C k p,分子中有因子p ,分母个各数均小于p ,又p 为素数,因此约分时p 不会被约去,因此有kpC p |,取素数为p ,)(y g 满足艾森斯坦判别式条件,因此)(y g 在有理数域上不可约,从而)(x f 在有理数域上不可约. 5)k kx x ,144++为整数. 解:令,1+=y x 则有).(2)1(4641)1(4)1(1423444y g y k y y y y k y kx x =+++++=++++=++取素数,2=p )(y g 满足艾森斯坦判别法条件,因此在有理数域上不可约,从而)(x f 在有理数域上不可约.。
高等代数-第1章习题及解答

习题1.11. 判断以下数集是否作成数环。
1)S={}Z ∈; 2) S={}0a a Q ≠∈; 3)S={},a b Z +∈;4)S={},a a b Q +∈.解: 1)错误。
不能包含除0以外的整数。
2)错误。
对差不封闭。
3)正确。
4)正确。
{}{},5,13a bi ab Q a bi a b Q Q +∈+∈2. 填空:1) 包含5i 的最小数域是或 2) 包含的最小数域是⎭⎬⎫⎩⎨⎧∈Q a a 31或{}{}{}0.,0,,,,0,1,2,3,,-l S a S a S ka S a S k l a bi a b Q F c di c di ≠≠∈≠∈∈=+∈⋅∈≠≠ 3.证明:如果一个数环S ,那么含有无限多个数。
证明:S 0可设是数环于是 其中 故含有无限多个数。
4.证明:S=是一个数环,是不是数域?证明: S 为数环,则S 对于数的加、减、乘封闭,且1=1+0i S 设+0,那么0222222220000,()()()()(),d c c di d c di c Q a bi a bi c di ac bd bc ad ic di c di c di cd ac bd bc adi c d c dac bd bc adQ c d ==+≠≠=∈++-++-==++-++-=++++-∈+否则 在的情形下,,与矛盾 在的情形下,与矛盾因此 又由于 22,Q c d a biS S c di∈++∴∈+ 故是数域。
121212,F F F F F F 5.设均为数域,证明也是数域,一定是数域吗?举例说明。
{}121222112,,,F F F F R F a bi a b Q F F F F ==+∈⊄⊄ 112证明:是数域,不一定是数域 反例:设F 因 F F 所以 不是数域()21,5(5,2)(2,3)(1)112;12(-1)(-2)12123455234125341n n k k k k +=+++++++−−−→−−−→− 习题1.21.计算下列排列的反序数: 1)75231468; 2)n(n-1)21;3)(2k)1(2k-1)2(k+1)k.解: ) ; 2) 3)2.利用对换把排列12345变成35241。
高等代数第一章答案(多项式)

若()()()x m x l x h +=,且()()x m x p |,()()x l x p |/,则()()x h x p |/。
证法1: 由()()x m x p |/有 ()()()x p x m x m 1=。
由()()x l x p |/有()()()()()0,1≠+=x r x r x p x l x l 。
于是 ()()()()()()()()x r x p x l x m x m x l x h ++=+=11。
因()0≠x r ,故()()x h x p |/。
证明2:用反证法。
若()()x h x p |,即()()()()x m x l x p +|, 又()()x m x p |,故()()()()()x m x m x l x p -+|,即()()x l x p |,矛盾。
问:若()()()()x g x h x f x h |,|//, 则()()()()x g x f x h +|成立吗?试举例说明。
答:不一定。
例如 ()()()1,1,+=-==x x g x x f x x h ,则()()()()x g x h x f x h |,|//,但()()()()x g x f x h +|。
例如 ()()()2,1,+=-==x x g x x f x x h , 则()()()()x g x h x f x h |,|//,且()()()()x g x f x h +/|。
例 求m l ,, 使()2523+++=x lx x x f 能被()12++=mx x x g 整除。
解法1:因()()3=∂x f ,()()2=∂x g ,故商()x q 满足()()1=∂x q ,且设()p x x q +=,则由 ()()()x g x q x f =,可得()()p x pm x p m x x lx x +++++=+++1252323,l m p pm p =+=+=,51,2,从而 4,2,2===l m p 。
高等代数北大编第1章习题参考答案

第一章多项式一、习题及参考解答1 .用g(x)除了(x),求商g(x)与余式r(x):1 ) f (x) = x3 - 3x2 - x -1, g(x) = 3x2 - 2x +1;2 ) f(x) = x4 -2x + 5,g(x) = x2 - x + 2。
解1)由带余除法,可得q(x) =L-Z,“x) =-竺x-2 ;2)同理可得g(x) = / +x-l,r(x) = -5x + 7。
2. 〃?,PM适合什么条件时,有1 ) X2 +/?1¥-1 I X3 + px + c/ 92) x2 + nix + 11 x4 + px2 +q。
解1 )由假设,所得余式为0,即(〃 + l + 〃?2)x + (q-〃?) = O,所以当 1 + 。
时有 /+〃a-11 X* + px +g 0q _ in = 0 .2)类似可得= 于是当〃? = 0时,代入(2)可得〃=夕+ 1;q + 1 —〃一" = 0而当2- 〃 -J = 0时,代入(2)可得4 = 1 04 = ] _, 时,皆有 / + + 1 I X,+ px2 + 9。
综上所诉,当p + nr = 23 .求g(x)除f(x)的商q(x)与余式:1 ) /(x) = 2«?-5x3-8x,g(x) = x + 3 ;2) f(x) = x3-x2 - xg(x) = x-l + 2i o解[)q(x) = 2x4 - 6x3 +13x2 - 39A+ 109 ,r(x) = -327 '2)= x2 -2LV-(5+2/)r(x) = -9 + 8/ °4 .把/1(X)表示成x-%的方幕和,即表成c()+ G(X —“0)+。
2(X — X。
)~ + …+ C n(X — X。
)” + …的形式:1)/(x) = x',x()= 1 ;2) /(X)= X4-2X2+3,X0 =-2 ;3) f (x) = x4 + 2汉3 -(1 + i)x2 -3x + 7 + i,x0 =-i o解 1 ) 由综合除法,可得f(x) = l + 5(x-l) + 10(x-l)2 + 10(x-1)3+5(X-1)4 + (x-1)5 ;2 ) 由综合除法,可得X4-2X2+3=11-24(X + 2) + 22* + 2)2 -8(.r + 2)3 + (x + 2),;3)由综合除法,可得『+2立3_(1 +82_3工+ (7 +,)= (7 + 5i)-5(x + i) + (-l-i)(x + i)2 -2i(x + i)3 + (x + i),。
《高等代数》第一章习题及答案

习题1.1解答1.下列数集哪些是数域?哪些是数环?哪些既非数域也非数环?1)所有正实数所成的集合.2)所有偶数(或奇数)构成的集合. 3)某个整数a 的所有整数倍所成的集合.4)F={Q b a b a ∈+,23}.解 1)所有正实数所成的集合对减法不封闭,所以不是数环,当然也非数域.2)所有偶数构成的集合对加、减、乘均封闭,所以是数环;但对除法不封闭,所以不是数域.3)某个整数a 的所有整数倍所成的集合对加、减、乘均封闭,所以是数环;但对除法不封闭,所以不是数域.4)在F={Q b a b a ∈+,23} 中取32,显然32×32∉F ,即对乘法不封闭,所以F 不是数环,当然也非数域.2.证明:两个数域的交是一个数域.解 设A ,B 是两个数域,则0,1∈A ,0,1∈B ,从而0,1∈A ∩B ;对任意x,y ∈A ∩B ,有x,y ∈A 和x,y ∈B ,从而x+y ∈A ,x-y ∈A ,x ×y ∈A ,x ÷y ∈A (对y ≠0),同样也有x+y ∈B ,x-y ∈B ,x ×y ∈B ,x ÷y ∈B (对y ≠0),所以x+y ∈A ∩B ,x-y ∈A ∩B ,x ×y ∈A ∩B ,x ÷y ∈A ∩B (对y ≠0),故A ∩B 是数域.3*.证明:F={a+bi|a,b ∈Q}(i 是虚单位)是一个数域.解 显然0=0+0i ∈F ,1=1+0i ∈F ;对任意a+bi,c+di ∈F ,有(a+bi)+(c+di)=(a+c)+(b+d)i ∈F ,(a+bi)-(c+di)=(a-c)+(b-d)i ∈F ,(a+bi)×(c+di)=(ac-bd)+(ad+bc)i ∈F ,若c+di ≠0,则(a+bi)÷(c+di)=F i d c ad cb d c bd ac d c di c bi a ∈+-+++=+-+222222)())((.所以F 是数域.4*.证明:G={a+bi|a,b ∈Z}是数环而不是数域.解 对任意a+bi,c+di ∈G ,有(a+bi)+(c+di)=(a+c)+(b+d)i ∈G ,(a+bi)-(c+di)=(a-c)+(b-d)i∈G ,(a+bi)×(c+di)=(ac-bd)+(ad+bc)i ∈G ,所以G 是数环.数1=1+0i ∈G ,2=2+0i ∈G ,2≠0,但1÷2∉G ,所以G 不是数域.习题1.2解答1.用行的初等变换,将下列矩阵化为行最简形.①⎪⎪⎪⎭⎫⎝⎛-213312011 ②⎪⎪⎪⎪⎪⎭⎫⎝⎛-2605573314122321③⎪⎪⎪⎭⎫⎝⎛---443112110013 ④⎪⎪⎪⎪⎪⎭⎫⎝⎛-----133331241246104210521 解 ①⎪⎪⎪⎭⎫ ⎝⎛-213312011→⎪⎪⎪⎭⎫ ⎝⎛-240330011→⎪⎪⎪⎭⎫ ⎝⎛--200110011→⎪⎪⎪⎭⎫⎝⎛100010001 ②⎪⎪⎪⎪⎪⎭⎫⎝⎛-2605573314122321→⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---------129100123032302321→⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---------129100123032302321→⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----23/700200032302321→⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----200023/70032302321→⎪⎪⎪⎪⎪⎭⎫⎝⎛1000010000100001 ③⎪⎪⎪⎭⎫ ⎝⎛---443112110013→⎪⎪⎪⎭⎫ ⎝⎛---443100131211→⎪⎪⎪⎭⎫ ⎝⎛----564036401211 →⎪⎪⎪⎭⎫ ⎝⎛---200036401211→⎪⎪⎪⎭⎫ ⎝⎛--100006400211→⎪⎪⎪⎭⎫ ⎝⎛-100002/31002/101 ④⎪⎪⎪⎪⎪⎭⎫⎝⎛-----133331241246104210521→⎪⎪⎪⎪⎪⎭⎫⎝⎛----231890126306600010521→⎪⎪⎪⎪⎪⎭⎫⎝⎛----660002318901263010521 ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----11000130001263010521→⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---40000110001263010521→⎪⎪⎪⎪⎪⎭⎫⎝⎛--10000010000063000521 →⎪⎪⎪⎪⎪⎭⎫⎝⎛100000100000310001012*.用行的与列的初等变换,将上题中的③化成形为⎪⎪⎭⎫ ⎝⎛000sE 的矩阵. 解 接上题中的③的行最简形⎪⎪⎪⎭⎫ ⎝⎛-100004/61002/101→⎪⎪⎪⎭⎫ ⎝⎛100000100001→⎪⎪⎪⎭⎫⎝⎛010*********习题1.3解答1.写出以下列行最简形矩阵为增广矩阵的线性方程组的全部解.①⎪⎪⎪⎭⎫ ⎝⎛-000032100301 ②⎪⎪⎪⎭⎫ ⎝⎛110000010010011 解 ①对应的线性方程组可写为⎩⎨⎧+=-=32312330x x x x令x 3=c ,得x 1=-3c ,x 2=3+2c ,全部解可表示为⎪⎩⎪⎨⎧=+=-=c x c x c x 321233 其中c 为任意数.② 对应的线性方程组可写为⎪⎩⎪⎨⎧==-=1014321x x x x令x 2=c ,得⎪⎪⎩⎪⎪⎨⎧===-=1014321x x c x c x 其中c 为任意数.2.解下列线性方程组:①⎪⎩⎪⎨⎧=+=+-=-+8311102322421321321x x x x x x x x ②⎪⎪⎩⎪⎪⎨⎧-=+-=-+-=+-=++69413283542432321321321321x x x x x x x x x x x x③⎪⎩⎪⎨⎧=--+=+-+=+-+12222412432143214321x x x x x x x x x x x x ④⎪⎩⎪⎨⎧-=+-+=-+-=+-+2534432312432143214321x x x x x x x x x x x x 解 ① 对应的增广矩阵为⎪⎪⎪⎭⎫ ⎝⎛--80311102132124~⎪⎪⎪⎭⎫ ⎝⎛---2/54/112/502/174/112/502124~⎪⎪⎪⎭⎫ ⎝⎛---101110034111002124~⎪⎪⎪⎭⎫ ⎝⎛---2400034111002124 由于系数矩阵的秩不等于增广矩阵的秩,所以原方程组无解.② 对应的增广矩阵为⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----69141328354214132~⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----69141328341325421~⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----147702814140147705421~⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---0000000021105421 对应的同解方程组可写为⎩⎨⎧+=--=-323212452x x x x x令x 3=c ,全部解可表示为⎪⎩⎪⎨⎧=+=--=cx c x cx 321221 其中c 为任意数.③对应的增广矩阵为⎪⎪⎪⎭⎫ ⎝⎛----111122122411112~⎪⎪⎪⎭⎫⎝⎛---020000100011112 ~⎪⎪⎪⎭⎫⎝⎛-00000010002/102/12/11 对应的同解线性方程组可写为⎩⎨⎧=+-=02/12/12/14321x x x x令x 2=c 1,x 3=c 2,得⎪⎪⎩⎪⎪⎨⎧===+-=021212142312211x c x cx c c x 其中c 1,c 2为任意数.④ 对应的增广矩阵为⎪⎪⎪⎭⎫ ⎝⎛-----253414312311112~⎪⎪⎪⎭⎫ ⎝⎛-----111124312325341~⎪⎪⎪⎭⎫ ⎝⎛------5957010181014025341~⎪⎪⎪⎭⎫ ⎝⎛----000005957025341 对应的同解线性方程组可写为⎩⎨⎧+-=--+-=+432432195575324x x x x x x x令x 3=c 1,x 4=c 2,得⎪⎪⎩⎪⎪⎨⎧==-+-=++=24132122117/97/57/57/7/7/6c x c x c c x c c x 其中c 为任意数.3.解下列齐次线性方程组:①⎪⎩⎪⎨⎧=+++=-++=-++02220202432143214321x x x x x x x x x x x x ②⎪⎩⎪⎨⎧=-++=--+=-++05105036302432143214321x x x x x x x x x x x x ③⎪⎪⎩⎪⎪⎨⎧=-+-=+-+=-++=+-+07420634072305324321432143214321x x x x x x x x x x x x x x x x 解 ① 对应的系数矩阵为⎪⎪⎪⎭⎫ ⎝⎛--212211121211~⎪⎪⎪⎭⎫ ⎝⎛----430013101211~⎪⎪⎪⎭⎫ ⎝⎛---430030103/4001 令x 4=c ,得⎪⎪⎩⎪⎪⎨⎧==-=-=cx c x c x c x 43213/433/4 中c 为任意数.② 对应的系数矩阵为⎪⎪⎪⎭⎫ ⎝⎛----5110531631121~⎪⎪⎪⎭⎫ ⎝⎛---040004001121~⎪⎪⎪⎭⎫⎝⎛--000004001121对应的同解方程为⎩⎨⎧=-+-=+04234231x x x x x令x 2=c 1,x 4=c 2,得⎪⎪⎩⎪⎪⎨⎧===+-=2431221102c x x c x c c x ③ 对应的系数矩阵为⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----7421631472135132~⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----5132631472137421~⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----199703419901410707421 ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----51007/1127/43001410707421~⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----510011243001410707421~⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---100051001410707421 系数矩阵的秩为4,对应的齐次线性方程组只有零解⎪⎪⎩⎪⎪⎨⎧====00004321x x x x4.讨论a,b 取什么值时下面的线性方程组无解,有唯一解,有无穷多解?①⎪⎩⎪⎨⎧=-++=++=-+b x a x x x x x x x x 3221321321)5(322 ②⎪⎩⎪⎨⎧=++=++=++4234321321321x bx x x bx x ax x x 解 ①系数矩阵的行列式为5111211112--a =400211112--a =(a-2)(a+2)当a ≠2且a ≠-2时,方程组有唯一解。
1983年版本张禾瑞高等代数第1章习题解答

1习 题 一1. 设f (x )=xx x 010010-,求f (x )=0的根.解 因)1()(2+=x x x f , 所以,在R 上)(x f 有一个根0=x ,在C 上)(x f 有三个根01=x ,i x =2,i x -=3.2.排列1 (k +1) 2 (k +2) … (k -1) (2k -1) k (2k )的反序数是多少?解 )1(21-k k . 3. 若π (i 1i 2 … i n )=k ,则π (i n i n -1 …i 2 i 1)=? 解 k n n i i i i n n --=-)1(21)(121 π. 4. 讨论排列n (n -1) … 21的奇偶性.解 因为 )1(21)21)1((-=-n n n n π,所以当 k n 4=时为偶排列; 当14+=k n 时为偶排列; 当 24+=k n 时为奇排列; 当34+=k n 时为奇排列. 5. 若n 阶行列式| a ij |=-a ,则| -a ij |=?解 a a n ij 1)1(+-=-.6. 用行列式定义计算2 (1) 0002000000199900030002000000001(2) 0000021n a a a --- (3) nnn n n n n na a a a a a 1,121,21000--解 ⑴ 2000-! ⑵ n n n a a a 21)1(21)1(+- ⑶ 11,21)1(21)1(n n n n n a a a ---7. 构造一个三阶行列式D =| a ij |,其中a ij 全不为零,但D =1.解 提示:利用行列式的性质,可将行列式100010001 化为每个元素都不等于零,比如 D=111121122.8. 设3f (x ) =1211123111211x x x x - 不计算行列式,求展开式中x 3的系数.解 1- .9. 若n (>2)阶行列式D 的元素都是1或-1,证明D 是一个偶数. 证明 该n (>2)阶行列式的每个项(连同符号)等于1或者-1, 且一共有偶数个项, 故等于1的项的个数与等于-1的项的个数之差是偶数.因此D 是一个偶数.10. 根据性质计算下面的行列式(1) n 001030100211111(2) a x a aa a a x aa a a ax a a a a a x ----(3) x y y x y xyx 0 00000 0000004 (4) n n n n a a a a a a a a a a a a a a a a ++++1111321321321321解 ⑴ )11(!2∑=-n i i n .(提示:将第i 列的元素乘以i 1-后加到第1列的对应元素上(n i ,,3,2 =)) . ⑵[]1)2()2(---+n a x a n x .⑶n n n y x 1)1(+-+.⑷ )1(1∑=+n i ia . 11. 设n 阶行列式D =nnn n n n a a a a a a a a a212222111211中元素a ij 都是整数,证明D 也是整数.证明 因为D=∑-n n nj j j j j j a a a 212121)()1(π 且每个元素ij a 都是整数, 所以D 为整数.12. 已知143,247,325都是13的倍数,不用计算,证明523742341也是13的倍数.证明 将第1列乘100 加到第3列对应的元素上;第2列各元5素乘以10 加到第3列对应的元素上,再按第3列展开, 可知结论成立.13. 把行列式D =dc b a 011111101101------ 依第四行展开加以计算解 D=d c b a --+-23.14. 设阶行列式D =nnn n n n a a a a a a a a a212222111211中元素都是整数,且D =1,证明D 的每一列元素,每一行元素都是互素的.证明 用反证法. 假设第i 行的元素不互素, 则可设)1(≠k 是第i 行的公因数,于是 11==kD D . 其中1D 的元素全为整数. 所以 kD 11= .这与1D 是整数矛盾. 15. 用数学归纳法证明 D n =n n a a a a ++++-11111111111111111216 =a 1a 2 …a n ⎪⎪⎭⎫ ⎝⎛+∑=n i i a 111 证明 用数学归纳法可证. 略.16. 设n 阶行列式D =n n 00103010021321求第1行元素的代数余子式之和:A 11+A 12+ … +A 1n .解 第1行元素的代数余子式之和等于第10题的习题(1)的行列式, 即为)11(!211211∑=-=+++n i n i n A A A . 17. 根据行列式 D =111111111=0 证明,n 个数码1, 2, …, n 构成的n !个排列中,奇偶排列各占一半.证明 因为 ∑=-=n n j j j j j j D 21210)1()(π, 所以n 个数码1,2,…,n 构成的!n 个排列中,奇偶排列各占一半.18. 用Cramer 法则解方程组。
高等代数习题(北大第四版)答案一到四章.docx

高等代数答案第一章多项式1 •用 g{x)除 /(.r),求商 </(.r)与余式 r(.r):1) /*(.r) = .r 3 - 3.r 2 - x-1,= 3.r 2 - 2.r +1: 2) f(x} = x 4 — 2.r+ 5,烈A ) = H -才+ 2 •解1)由带余除法,可得彳(才)=丄x--,/(.r) = - —.r--; 3 9 99 2 )同理可得久工)=X 2 + X- 1,心=-5.V+ 1 .2. m 、p 、q 适介什么条件时,冇1) x 1 + w.r-11 .t 3 + px+ q 、2) .r 2 + 7//.V+ 11 x 4 + + q o解I)由假设,所得余式为0,即(P+1 +〃小才+(0-刃) = 0,所以当+ 1 + - ° 时有才2 + my-11 x 3 + px*q° q- m- 02)类似可得(劝(2 — Q -刃?=0, j :是当加=o 时,代入(2)可得〃=夕+ 1:而当 [乡+ 1-p- ftl・=02-p-nr =0 时,代入(2〉可得0 = 1。
了 时,皆有 f + 〃/・丫+11 x 4 + pf + q o p + 〃厂=23. 求g(.x)除/(X )的商0⑴与余式:1) /*(.r) = Zr 5 - 5-r 3 - 8.i ,g(.r) = .r+ 3 :2) f(x) = 一 , 一 不 g(.v)=才一 l + 2/ o0(・丫) = 2r 4 - +13” 一 39才 +109解1);心)=-327°).(.丫) = '-2灯-(5+2/)。
/// = 0综上所诉,当 □攵.;p=q+\ -心)=-9 + 8/4. 把/(才)表示成才一兀的方幕和,即表成C Q +q(・Y-旺)+Q(才一・®)2 + ... + C…(X -X Q y+ …的形式:1) /(才)",兀 T;2) /*(.r) = .r4 - 2.x2 + 3,x0 = -2;3) /(r) = x + 2/x一(l + /).r2一3x+ 7 + /,兀=-/«解1)由综合除法,可得/(x) = 1+ 5(x-1) + 10(r -1)2 +10(x-l)3^5(x -l)4+(r-l)5;2) 由综合除法,可得x4 -21^ + 3 = 11 - 24(.r+ 2) + 22(.r+ 2)2 -8(.r+ 2)3 + (.r+ 2)4:3) 由综介除法,可得.r4 + 2/:? - (1 + /).? -3x + (7 + z)= (7+5/)-5(x+/)4- (- 1一/比+/予-2«+/)+ (r+ // o5. 求/(貯与肌工)的最大公因式:1) /(才)=.r4 + .r5 -3, - 4才- 1£(才)=,+ , -.丫-1 ;2) /(.r) = .r4 -4.? + l,^(.r) =.? -3,r +1 :3) f .r) - .r4 - lO.r2 + l,g(") - .r4 -心力 + 6A2 + 4/2r+ 1。
高等代数(北大版第三版)习题答案

高等代数(北大*第三版)答案目录第一章多项式第二章行列式第三章线性方程组第四章矩阵第五章二次型第六章线性空间第七章线性变换第八章 —矩阵第九章欧氏空间第十章双线性函数与辛空间注:答案分三部分,该为第一部分,其他请搜索,谢谢!第一章 多项式1. 用)(x g 除)(x f ,求商)(x q 与余式)(x r : 1)123)(,13)(223+-=---=x x x g x x x x f ; 2)2)(,52)(24+-=+-=x x x g x x x f 。
解 1)由带余除法,可得92926)(,9731)(--=-=x x r x x q ; 2)同理可得75)(,1)(2+-=-+=x x r x x x q 。
2.q p m ,,适合什么条件时,有 1)q px x mx x ++-+32|1, 2)q px x mx x ++++242|1。
解 1)由假设,所得余式为0,即0)()1(2=-+++m q x m p ,所以当⎩⎨⎧=-=++0012m q m p 时有q px x mx x ++-+32|1。
2)类似可得⎩⎨⎧=--+=--010)2(22m p q m p m ,于是当0=m 时,代入(2)可得1+=q p ;而当022=--m p 时,代入(2)可得1=q 。
综上所诉,当⎩⎨⎧+==10q p m 或⎩⎨⎧=+=212m p q 时,皆有q px x mx x ++++242|1。
3.求()g x 除()f x 的商()q x 与余式:1)53()258,()3f x x x x g x x =--=+; 2)32(),()12f x x x x g x x i =--=-+。
解 1)432()261339109()327q x x x x x r x =-+-+=-;2)2()2(52)()98q x x ix i r x i=--+=-+。
4.把()f x 表示成0x x -的方幂和,即表成2010200()()...()n n c c x x c x x c x x +-+-++-+的形式:1)50(),1f x x x ==;2)420()23,2f x x x x =-+=-;3)4320()2(1)37,f x x ix i x x i x i =+-+-++=-。
高等代数__课后答案__高等教育出版社

高等代数习题答案(一至四章)第一章 多项式 习题解答1、(1)由带余除法,得17(),39q x x =-262()99r x =--(2)2()1q x x x =+-,()57r x x =-+2、(1)2100p m q m ⎧++=⎨-=⎩ , (2)由22(2)010m p m q p m ⎧--=⎪⎨+--=⎪⎩得01m p q =⎧⎨=+⎩或212q p m =⎧⎨+=⎩。
3、(1)432()261339109,q x x x x x =-+-+()327r x =- (2)q (x )=22(52)x ix i --+,()98r x i =--4、(1)有综合除法:2345()15(1)10(1)10(1)5(1)(1)f x x x x x x =+-+-+-+-+- (2)234()1124(2)22(2)8(2)(2)f x x x x x =-+++-+++(3)234()24(75)5()(1)()2()()f x i x i i x i i x i x i =+-++--+-+++5、(1)x+1 (2)1 (3)21x -- 6、(1)u (x )=-x-1 ,v (x )=x+2 (2)11()33u x x =-+,222()133v x x x =-- (3)u (x )=-x-1, 32()32v x x x x =+--7、02u t =⎧⎨=⎩或23u t =-⎧⎨=⎩8、思路:根具定义证明证:易见d (x )是f (x )与g (x )的公因式。
另设()x ϕ是f (x )与g (x )的任意公因式,下证()()x d x ϕ。
由于d (x )是f (x )与g (x )的一个组合,这就是说存在多项式s (x )与t (x ),使 d (x )=s (x )f (x )+t (x )g (x )。
从而()()x f x ϕ,()()x g x ϕ,可得()()x d x ϕ。
完整版高等代数习题解答(第一章)

完整版高等代数习题解答(第一章)高等代数题解答第一章多项式补充题1.当a,b,c取何值时,多项式f(x)=x-5与g(x)=a(x-2)^2+b(x+1)+c(x^2-x+2)相等?提示:比较系数得a=-1,b=-1,c=6.补充题2.设f(x),g(x),h(x)∈[x],f^2(x)=xg^2(x)+x^3h^2(x),证明:假设f(x)=g(x)=h(x)不成立。
若f(x)≠0,则∂(f^2(x))为偶数,又g^2(x),h^2(x)等于或次数为偶数,由于g^2(x),h^2(x)∈[x],首项系数(如果有的话)为正数,从而xg^2(x)+x^3h^2(x)等于或次数为奇数,矛盾。
若g(x)≠0或h(x)≠0,则∂(xg^2(x)+x^3h^2(x))为奇数,而f^2(x)为偶数,矛盾。
综上所证,f(x)≠g(x)或f(x)≠h(x)。
1.用g(x)除f(x),求商q(x)与余式r(x):1)f(x) =x^3-3x^2-x-1,g(x) =3x^2-2x+1;2)f(x) =x^4-2x+5,g(x) =x^2-x+2.1)解法一:待定系数法。
由于f(x)是首项系数为1的3次多项式,而g(x)是首项系数为3的2次多项式,所以商q(x)必是首项系数为1的1次多项式,而余式的次数小于2.于是可设q(x)=x+a,r(x)=bx+c。
根据f(x)=q(x)g(x)+r(x),即x^3-3x^2-x-1=(x+a)(3x^2-2x+1)+bx+c,右边展开,合并同类项,再比较两边同次幂的系数,得a=-1/3,b=-2/3,c=-1,故得q(x)=x-1/3,r(x)=-x-1/3.2)解法二:带余除法。
用长除法得商q(x)=x^2+x-1,余式r(x)=-5x+7.2.m,p,q适合什么条件时,有1)x^2+mx-1/x^3+px+q;2)x^2+mx+1/x^4+px^2+q.解:1)将x^3+px+q除以x^2+mx-1得商为x+m+1/(x+m-1),所以当m≠1时有解。
(完整word版)高等代数多项式习题解答

第一章多项式习题解答1. 用g(x)除f(x),求商q(x)与余式r(x).5x2. m, p,q 适合什么条件时,有 1) x 2 mx 11 x 3 px qq(x)x 2 x 1, r(x)5x 7.x 3 0x 2 px q xp 10,q m 时 x 2 mx 11 x 3 px1) f(x)x 3 3x 2 2x3x 232x 3xx 1 3 2 2 1x —x -x3 3 7 24 1 x x 3 37 2 14 7 —x ■ x — 3 9 926 2 —x9 9q(x) £ r (x )26 x92) f(x)2x 5, g(x)4 x 4x0x 3 0x 2 x 3 2x 2 x 3 2x 22x 32x x 2xx2x2x 54x 5 x 2 mx 1当且仅当m 2 i,g(x)x 2x 1 1—x 3 3x 2本题也可用待定系数法求解 .当X 2 mx 1| x 3 px q 时,用x 2 mx 1去除x 3 px q ,余式为零,比较首项系数及常数项可得其商为 x q.于是有因此有m 2 p 1 0, q m .2) x 2 mx 11 x 4 2px q由带余除法可得42/ 2x px q (x mx1)( x2mx 2p 1 m ) m(2pm 2)x (q 1 pm 2) 当且仅当r(x) m(2 p 2m )x (q 1 p m 2) 0 时2x 42mx 11 x pxq .即m(2 p m 2) 2m,即 mQ 或 p 2小m 2,q 1p 0q 1 p,q 1.本题也可用待定系数法求解.当x 2 mx 1|x 4px 2 q 时,用x 2 mx 1去除x 4 px 2 q ,余式为零,比较首项系数及常数项可得其商可设为 x 2 ax q .于是 有3. 求 g(x)除 f (x)的商 q(x)与余式 r(x). 531) f (x) 2x 5x 8x, g(x) x 3; 解:运用综合除法可得 32580 6 18 39 1173272 6 1339 109 327商为 q(x) 2x 4 6x 3 13x 2 39x 109,余式为 r(x) 327.4 2x pxq (x 2ax q)( 2x mx 1)(m a)x 3 (ma2q 1)x(a mq)x q.ma q 1 p,a mq 0.消去a 可得m 0,或2p m 2,q 1 p,q 1.x 4 比较系数可得m a 0,2px q (x q)(x mx 1)x 3 (m q)x 2(mq 1)x q .2) f(x) x 3 x 2x,g(x) x 1 2i .解:运用综合除法得:1 2i 11 1 0 1 2i4 2i 9 8i 1 2i5 2i9 8i商为x 2 2ix (5 2i),余式为9 8i .c 0即为x X o 除f (x)所得的余式,商为q(x) q 可得C 1为x x o 除商q(x)所得的余式,依次继续即可求得展开式的各项系数 解:1)解法一:应用综合除法得•1 1 o o o o o11111 111111 112 3 4 1 1 2 3 4 51 3 6 1 1 3 6 1o1 4 1 1 4 1o 14.把 f(; x)表成x X °的方幂和,即表示成CoC 1(X X o ) C 2(X X o )2的形1) f(x) 5x12) f(x) 4x 2x 23, xo2;3) f(x) 4x2ix 3 (1 i)x 2 3x 7 i,x o1分析: 假设 f(x) 为n 次多项式,令f(x)C o G (x X o ) C 2(X X o )2C n (x X o )n式.x o )n1]C o (x X o )[G C 2(x x o )C n (x C 2(x X 。
高等代数[北大版]第1章习题参考答案解析
![高等代数[北大版]第1章习题参考答案解析](https://img.taocdn.com/s3/m/9f49e8bcf8c75fbfc77db2ad.png)
第一章 多项式1. 用)(x g 除)(x f ,求商)(x q 与余式)(x r : 1)123)(,13)(223+-=---=x x x g x x x x f ; 2)2)(,52)(24+-=+-=x x x g x x x f 。
解 1)由带余除法,可得92926)(,9731)(--=-=x x r x x q ; 2)同理可得75)(,1)(2+-=-+=x x r x x x q 。
2.q p m ,,适合什么条件时,有 1)q px x mx x ++-+32|1, 2)q px x mx x ++++242|1。
解 1)由假设,所得余式为0,即0)()1(2=-+++m q x m p ,所以当⎩⎨⎧=-=++0012m q m p 时有q px x mx x ++-+32|1。
2)类似可得⎩⎨⎧=--+=--010)2(22m p q m p m ,于是当0=m 时,代入(2)可得1+=q p ;而当022=--m p 时,代入(2)可得1=q 。
综上所诉,当⎩⎨⎧+==10q p m 或⎩⎨⎧=+=212m p q 时,皆有q px x mx x ++++242|1。
3.求()g x 除()f x 的商()q x 与余式:1)53()258,()3f x x x x g x x =--=+; 2)32(),()12f x x x x g x x i =--=-+。
解 1)432()261339109()327q x x x x x r x =-+-+=-;2)2()2(52)()98q x x ix i r x i=--+=-+。
4.把()f x 表示成0x x -的方幂和,即表成2010200()()...()n n c c x x c x x c x x +-+-++-+L 的形式:1)50(),1f x x x ==;2)420()23,2f x x x x =-+=-;3)4320()2(1)37,f x x ix i x x i x i =+-+-++=-。
高等代数第1章习题解

第一章习题解4902411=+,490911411388=⋅+41138823=+,而233881(,)=,所以(9405,5313)=12.设12,,, n a a a Z ∈,证明12121(,,,)((,,,),) n n n a a a a a a a -= 证明:令112(,,,), n d a a a = 2121((,,,),)n n d a a a a -= 由112(,,,), n d a a a =11121,,,,; i n d a i n d a ⇒=-11211112112(,,,),()((,,,),) n n n n d a a a d a d a a a a d d --⇒⇒⇒由212111211((,,,),)(,,,), n n n n d a a a a d a a a d a --=⇒1112112(,,,),(,,,) i n i d a i n d a d a i n ⇒=-⇒=21221(,,,) n d a a a d d ⇒⇒所以12d d =(630,504)=1264536=2·1764+1008, 1764=1008+756,1008=756+252,756=252·3→(1764,4536)=252 252=126·2所以(504, 630, 1764, 4536)=12622;()a b b aq a c c ap bc a pq a bc ⇒=⇒=⇒=⇒1;()a b b aq b a a bp b bp q pq ⇒=⇒=⇒=⇒=1p a b =±⇒=±若a x 对任意整数x 成立,那么取1x =,有11a a ⇒=±;反之,若1a =±,a x 显然成立;若x a 对任意整数x 成立,即a xp =对任意整数x 成立,取00x a =⇒=;反之,若0a =,x a 显然成立.7.设,,a b d Z ∈, 且(,)d a b =, 证明存在,u v Z ∈, 使得d au bv =+如果0a b ==,则000(,)a b a b ==⋅+⋅,所以结论成立; 如果,a b 不全为零,那么一定存在整数,s t 使0as bt +>,令所有这样的正整数组成的集合为D,即:0{|,}D as bt s t Z =+>∈, 由于D 是正整数组成的集合,故必有一个最小整数, 设这个正整数为d ',即有整数,u v 使d au bv '=+ 我们说d '就是,a b 的最大公因数.事实上,对于,a b 的任意公因数h ,显然有h au bv +h d '⇒;如果d '不是,a b 的公因数,不妨设d '不是a 的因数,那么由带余除法,有0,a d q r r d ''=+<<于是 1()()()a au bv q r r a qu b qv r D =++⇒=-+-⇒∈ 这与d '是D 中最小数的假设矛盾.如果P 不是质数,那么有两个大于1的整数,s t 使11,,p st s p t p =<<<< 显然有p st ,按题设,应有p s 或p t ,但这显然不可能..9.设12,S S 都是数环,请问12S S 与12S S 是否是数环,为什么?12S S 是数环,而12S S 未必是数环.事实上:1211,,,,a b S S a b S a b a b ab S ∀∈⇒∈⇒+-∈ 同理: 21,,,a b S a b a b ab S ∈⇒+-∈ 所以12,,a b a b ab S S +-∈ ,即12S S 是数环.取1257{|},{|}S k k Z S k k Z =∈=∈,这时1257,S S ∈∈,但121257121212,S S S S +=∉∉⇒∉所以12S S 未必是数环.,()()()(a c S a c a c b d S ∀++∈⇒+++=+++∈()()()(a c a c b d S +-+=-+-∈2()()()(a c ac bd ad bc S ++=-++∈所以{|,}S a a b Z =+∈是数环;但110S S =+∈=+∈=,而12Z ∉,所以2i S ∉,所以{|,}S a a b Z =+∈不是数域;{,}S a a b Q =+∈ 1.2一元多项式1.若43232231321(),()f x x x x x g x x x x =-+-+=-+-,求()(),()(),f x g x f x g x +-和()()f x g x4324325522()(),()()f x g x x x x f x g x x x x x +=++-=-+-+765432314141210621()()f x g x x x x x x x x =-+-+-+-2.求,,a b c 使22432211251()()x bx x ax x x cx x +--+=++--224322112211()()()()()x bx x ax x b a x ab x a b x +--+=+-+-++-432251x x cx x =++--所以: 2511,,b a ab c a b -=-=+=-213,,a b c ⇒=-==3.,,,a b c d 取何值时,多项式32322()()()f x a b c x a b c x dx =+-++-++与322()()()()g x a c x a d x c a x b =++-+++相等.1234,,,a b c d ====4.将多项式4323223()f x x x ax x =-++-化成2x +的方幂形式43232262852122261()()()()()f x x x x x =+-+++-++ 5.设多项式00(),()f x g x ≠≠,问(),()f x g x 的系数满足什么条件时,公式(()())max{(),()}f x g x f x g x ∂+≤∂∂等号成立?满足什么条件时,小于号成立?1110()n n n n f x a x a x a x a --=++++ ,1110()n n n n g x b x b x b x b --=++++ 当0n n a b +≠时,公式中的等号成立; 当0n n a b +=时,公式中的小于号成立;6.设(),(),()[]f x g x h x R x ∈,若222()()()f x xg x xh x =+,则0()()()f x g x h x ===(),()g x h x 至少有一个不是零多项式.由于(),()[]g x h x R x ∈,所以2222(()())max{(),()}g x h x g x h x ∂+=∂∂于是等式222()()()f x xg x xh x =+右边的的次数为奇数,而左边的次数为偶数,这导致矛盾,所以必然有0()()()f x g x h x ===7. .设(),()[]f x g x R x ∈,若00(),()f x g x ≠≠,证明则220()()f x g x +≠11100(),n n n n n f x a x a x a x a a --=++++≠ ,11100(),m m m m m g x b x b x b x b b --=++++≠ ,并且m n ≤于是22()()f x g x +的最高次项的系数为22,()n m a b m n +=或2,()n a m n <,不论是哪种情形,22()()f x g x +的最高次项的系数都不为零,所以220()()f x g x +≠(但这个结论对复数域上的多项式不成立,例如22(),(),f x ix g x x ==但22440()()f x g x x x +=-+=1.3多项式的整除性1.用()g x 除()f x ,求商式()q x 和余式()r x : (1) 322432123(),()f x x x x g x x x =-+-=-+ (2) 4322323(),()f x x x x g x x x =-+-=-+(1) 45164516()()(),(),()f x g x x q x x r x =+-=+=-(2) 221391731391732488824888()()(),(),()f x g x x x x q x x x r x x =--++=--=+ 2.确定,a b 的值,使223()g x x x =-+能整除43236()f x x x x ax b =-+++,得2153()()()()f x g x x x a x b =-++++-,所以53,a b =-=3.下列命题是否成立,为什么?(1)成立,否则由()(),()|()()h x f x h x f x g x +,则()|[()()]()()h x f x g x f x g x +-=导致矛盾;(2)不成立,例如11(),(),()h x x f x x g x x ==+=-,但2|x x ,即()|()()h x f x g x +(3) 不成立,例如22(),(),()h x x f x x g x x ===,但222|x x ,即()|()()h x f x g x(4)成立,由于()(),()()f xg x f x g x ∂=∂,所以(),()f x g x 只相差一个常数因子,所以()|()g x f x 成立.(),()f x g x 被()h x 除得的余式相等.()⇒设1122()()()(),()()()()f x h x q x r x g x h x q x r x =+=+,其中1100()()()r x or r x h x =≤∂<∂和2200()()()r x or r x h x =≤∂<∂于是1212()()()[()()][()()]f x g x h x q x q x r x r x -=-+-,由()[()()]h x f x g x -⇒12()()()h x r x r x -但1212[()()]max{(),()}()r x r x r x r x h x ∂-≤∂∂<∂,这显然不可能,除非120()()r x r x -=,即12()()r x r x =()⇐设12()()()(),()()()()f x h x q x r x g x h x q x r x =+=+,其中00()()()r x or r x h x =≤∂<∂于是12()()()[()()]f x g x h x q x q x -=-()[()()]h x f x g x ⇒-5.常数,,a b c 满足什么条件时,21()g x x ax =++能整除4()f x x bx c =++?2222121()()()()f x g x x ax a b a a x c a =-+-++-++- 所以222010,b a a c a +-=+-=所以221a b c a +=+=1()()()()()g x h x f x q x p x =,2()()()f x h x p x = 所以2112()()()()()()()()()()g x h x h x p x q x p x g x q x p x p x =⇒=()()q x g x ⇒7.证明:对任意非负整数n,都有222111|()n n x x x x ++++++n 用数学归纳法: 当0时,结论显然成立;假设结论在一切不大于n 的非负整数成立,那么在1n +时,3232212121111()[()]()[()]n n n n n x x x x x x x x +++++++=+++++- 221212111[()]()()n n n x x x x x x +++=++++++由归纳假设有222111|()n n x x x x ++++++,同时2212111|()()n x x x x x ++++++所以232311|()n n x x xx ++++++8.设k 是任意正整数,证明|()|()kx f x x f x ⇔,下面证明必要性用反证法:若|()x f x ,则10()(),f x xf x c c =+≠,那么1()[()]()k k k f x xf x c xg x c =+=+,由|()|k k x f x x c ⇒矛盾.9.证明:|()()x f x f x ⇔的常数项为011100(),nn n n n f x a x a xa x a a --=++++≠ 于是由于111|n n n n x a x a x a x --+++ ,1110|()n n n n x f x a x a x a x a --=++++所以111000|()()|n n n n x f x a x a x a x x a a ---+++⇒⇒= 反过来,若00a =,显然有|()x f x 10.证明:11||d n x x d n --⇔()⇐设n dq =,则1211111()()[()()]n dq d q d d q d q x x x x x x ---=-=-=-+++11|d n x x ⇒--()⇒若|d n ,设0,n dq r r d =+<<,于是11111()()n dq r dq r r r r dq r x x x x x x x x x +-=-=-+-=-+-由于111111|,|[()]|d n d r d q d r x x x x x x x ----⇒--,但0r d <<,这显然不可能.所以,必然有0r =,即|d n . 1.4最大公因式 1.求((),())f x g x(1)433234123(),()f x x x x g x x x =+--=+- (2) 32264530(),()f x x x x g x x x =-++=+- (3) 543243211(),()f x x x x x g x x x x =++-+=+++(4) 543257248(),f x x x x x x =-+-+-4325202144()g x x x x x =-+-+(1)2223422155()()()(),()()()f x g x x x x g x x x x x =+-+-=+--+-21212()()()r x x x x x =+-=-+所以1((),())f x g x x =-;(2) 741556()()()(),()()()f x g x x x g x x x =-+-=-+ 所以5((),())f x g x x =-; (3) 1((),())f x g x =(4)322221251()()(),()()()f x x x x g x x x =-++=-+所以22((),())()f x g x x =-2.设111()n n n n f x x a x a x a --=++++ 12121()n n n n g x x a x a x a ----=++++ ,1n >,求((),())f x g x由于10()()()()()()((),())n n n n g x a xg x f x a f x g x x a f x g x a =⎧=-⇒+-=⇒=⎨≠⎩3.设212(),(),m n m n m m f x x x x g x x x m n +-=---=--> ,求((),())f x gx4.对下列各题的(),()f x g x ,求(),()u x v x ,使((),())()()()()f x g x f x u x g x v x =+ (1)432421563()f x x x x x =+-++,3253()g x x x =-+ (2)432242(),f x x x x x =+---43222()g x x x x x =+--- (3)432442(),f x x x x x =--+-321()g x x x x =+--1)2215()()()()f x g x x x x =+--,22231()()()()g x x x x x =-+--21()x x x x -=-所以1((),())f x g x x =-15121225()[()()()])()()x g x x f x x f x -=+-+-所以222421115151555()()x x f x x x g x ⎛⎫⎛⎫-=--++- ⎪ ⎪⎝⎭⎝⎭221515()u x x =--,24211555()v x x x =+- (2)32()()f x g x x x =+-,32212()()()g x x x x x =-++-3222()x x x x -=-,所以22((),())f x g x x =-23221112()()()()[()()]()()()()()x g x x x x g x f x g x x x f x x g x -=--+=--+=--++所以:1()u x x =--,2()v x x =+(3)2234()()()()f x g x x x x =---+,2344717()()()g x x x x x =-+++-2493471774128()()()x x x x -+=--+,所以1((),())f x g x =22222212849341717747173443427179241284929245351107()()()()()()()()()()()()()[()()()][()()()()]()()()()x x x x g x x x x x x g x x f x x g x x x x f x g x x f x g x x x x f x x f x x x g x =-+----=--++-+=---=--++=-----++=--++-所以253511074949(),()x x x u x v x --+-== 5.令()f x 与()g x 是[]F x 中的多项式,而,,,a b c d是F中的数,并且满足0ad bc -≠,证明(()(),()())((),())af x bg x cf x dg x f x g x ++=12()((),()),()(()(),()())d x f x g x d x af x bg x cf x dg x ==++ 令 ()()(),()()())u x af x bg x v x cf x dg x =+=+ 那么 ()()(),()()())du x adf x bdg x bv x bcf x bdg x =+=+两式相减整理得:()()()d b f x u x v x ad bc ad bc=---同理:()()(),()()())cu x acf x bcg x av x acf x adg x =+=+()()()c ag x u x v x bc ad bc ad=---由于 111()((),())()|(),()|()d x f x g x d x f x d x g x =⇒11()|()(),()|()()d x af x bg x d x cf x dg x ⇒++ 12()|()d x d x ⇒反过来:2()(()(),()())((),())d x af x bg x cf x dg x u x v x =++=22()|(),()|()d x u x d x v x ⇒22()|()()()()|()()()d b d x u x v x f x ad bc ad bc c a d x u x v x g x bc ad bc ad ⎧-=⎪⎪--⇒⎨⎪-=⎪--⎩21()|()d x d x ⇒所以 12()()d x d x =6.证明定理1.4.7的逆:若1((),()())f x g x h x =,那么1((),())f x g x =与1((),())f x h x =都成立。
高等代数第三版习题答案

高等代数第三版习题答案高等代数是一门研究线性代数、多项式、群、环、域等代数结构及其性质的数学分支。
第三版的高等代数教材通常会包含大量的习题,旨在帮助学生更好地理解和掌握代数的基本概念和技巧。
以下是一些习题的答案示例,请注意,这些答案仅为示例,具体习题的答案需要根据实际的题目来确定。
第一章:线性空间习题1:判断下列集合是否构成线性空间,并说明理由。
- 解:集合\{(x, y) ∈ R^2 | x + y = 1\}不构成线性空间,因为它不满足加法封闭性。
例如,取两个元素(1, 0)和(0, 1),它们的和(1, 1)不在集合中。
习题2:证明线性空间的基具有唯一性。
- 解:设{v1, v2, ..., vn}和{w1, w2, ..., wm}是线性空间V的两个基。
根据基的定义,任何向量v ∈ V都可以唯一地表示为v =c1*v1 + c2*v2 + ... + cn*vn和v = d1*w1 + d2*w2 + ... + dm*wm。
由于表示是唯一的,我们可以得出n = m,并且存在一个可逆矩阵P,使得[v1, v2, ..., vn] = [w1, w2, ..., wn]P。
这意味着两个基是等价的,从而证明了基的唯一性。
第二章:线性变换习题1:确定线性变换T: R^3 → R^3,定义为T(x, y, z) = (x + y, x - y, z)的核和像。
- 解:核N(T)是所有满足T(v) = 0的向量的集合。
设(x, y, z) ∈ N(T),则(x + y, x - y, z) = (0, 0, 0)。
解这个方程组,我们得到x = 0,y = 0,z可以是任意实数。
因此,核是一维的,由向量(0, 0, 1)生成。
习题2:证明线性变换的复合是线性的。
- 解:设T: V → W和S: W → X是两个线性变换。
对于任意的v1, v2 ∈ V和任意的标量c,我们需要证明(S ∘ T)(cv1 + v2) = c(S∘ T)(v1) + (S ∘ T)(v2)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高等代数习题解答第一章 多项式补充题1.当,,a b c 取何值时,多项式()5f x x =-与2()(2)(1)g x a x b x =-++ 2(2)c x x +-+相等?提示:比较系数得6136,,555a b c =-=-=. 补充题2.设(),(),()[]f x g x h x x ∈¡,2232()()()f x xg x x h x =+,证明: ()()()0f x g x h x ===.证明 假设()()()0f x g x h x ===不成立.若()0f x ≠,则2(())f x ∂为偶数,又22(),()g x h x 等于0或次数为偶数,由于22(),()[]g x h x x ∈¡,首项系数(如果有的话)为正数,从而232()()xg x x h x +等于0或次数为奇数,矛盾.若()0g x ≠或()0h x ≠则232(()())xg x x h x ∂+为奇数,而2()0f x =或2(())f x ∂为偶数,矛盾.综上所证,()()()0f x g x h x ===.1.用g (x ) 除 f (x ),求商q (x )与余式r (x ):1)f (x ) = x 3- 3x 2 -x -1,g (x ) =3x 2 -2x +1;2)f (x ) = x 4 -2x +5,g (x ) = x 2 -x +2.1)解法一 待定系数法.由于f (x )是首项系数为1的3次多项式,而g (x )是首项系数为3的2次多项式,所以商q (x )必是首项系数为13的1次多项式,而余式的次数小于 2.于是可设 q (x ) =13x +a , r (x ) =bx +c 根据 f (x ) = q (x ) g (x ) + r (x ),即x 3-3x 2 -x -1 = (13x +a )( 3x 2 -2x +1)+bx +c 右边展开,合并同类项,再比较两边同次幂的系数,得2333a -=-, 1123a b -=-++, 1a c -=+ 解得 79a =- , 269b =- , 29c =- ,故得17(),39q x x =- 262().99r x x =-- 解法二 带余除法.3 -2 1 1 -3 -1 -113 79- 1 23- 13 73- 43- -1 73- 149 79- 269-29- 得 17(),39q x x =- 262().99r x x =-- 2) 2()1,()57.q x x x r x x =+-=-+ 262().99r x x =-- 2.,,m p q 适合什么条件时,有1)231;x mx x px q +-++2)2421.x mx x px q ++++1)解 21x mx +-除3x px q ++得余式为:2()(1)()r x p m x q m =+++-, 令()0r x =,即 210;0.p m q m ⎧++=⎨-=⎩ 故231x mx x px q +-++的充要条件是2;10.m q p m =⎧⎨++=⎩2)解 21x mx ++除42x px q ++得余式为:22()(2)(1)r x m p m x q p m =-+-+--+,令()0r x =,即 22(2)0;10.m p m q p m ⎧-+-=⎪⎨--+=⎪⎩ 解得2421x mx x px q ++++的充要条件是0;1m p q =⎧⎨=+⎩ 或 21;2.q p m =⎧⎨=-⎩ 3.求()g x 除()f x 的商()q x 与余式()r x :1)53()258,()3;f x x x x g x x =--=+2)32(),()12.f x x x x g x x i =--=-+1)解法一 用带余除法(略).解法二 用综合除法.写出按降幂排列的系数,缺项的系数为0:-3 2 0 -5 0 -8 0+ -6 18 -39 117 -3272 -6 13 -39 109 -327所以432()261339109,()327.q x x x x x r x =-+-+=-2)解法一 用带余除法(略).解法二 用综合除法.写出按降幂排列的系数,缺项的系数为0:()f x1-2i 1 -1 -1 0+ 1-2i -4-2i -9+8i1 -2i -5-2i -9+8i所以2()2(52),()98.q x x ix i r x i =--+=-+4.把()f x 表成0x x -的方幂和,即表成201020()()c c x x c x x +-+-+L的形式:1)50(),1;f x x x ==2)420()23,2;f x x x x =-+=-3)4320()2(1)37,.f x x ix i x x i x i =--+-++=-注 设()f x 表成201020()()c c x x c x x +-+-+L 的形式,则0c 就是()f x 被0x x -除所得的余数,1c 就是()f x 被0x x -除所得的商式212030()()c c x x c x x +-+-+L 再被0x x -除所得的余数,逐次进行综合除法即可得到01,,,.n c c c L1)解 用综合除法进行计算1 1 0 0 0 0 0+ 1 1 1 1 11 1 1 1 1 1 1+ 1 2 3 41 2 3 4 51 + 1 3 61 3 6 101 + 1 41 4 101 + 11 5所以 5234515(1)10(1)10(1)5(1)(1).x x x x x x =+-+-+-+-+-2)3)略5.求()f x 与()g x 的最大公因式:1)43232()341,()1;f x x x x x g x x x x =+---=+--2)4332()41,()31;f x x x g x x x =-+=-+3)42432()101,()6 1.f x x x g x x x =-+=-+++1)解 用辗转相除法()g x ()f x2()q x 12- 141 1 -1 -1 1 1 -3 -4 -1 1()q x 1 0 1 32 121 1 -1 -1 12- 32- -1 1()r x -2 -3 -1 3()q x 83 43 12- 34- 14- -2 -22()r x 34- 34- -1 -1-1 -13()r x 0所以((),()) 1.f x g x x =+2)((),()) 1.f x g x =3)2((),()) 1.f x g x x =--6.求(),()u x v x 使()()()()((),()):u x f x v x g x f x g x +=1)432432()242,()22f x x x x x g x x x x x =+---=+---;2)43232()421659,()254f x x x x x g x x x x =--++=--+;3)4322()441,()1f x x x x x g x x x =--++=--.1)解 用辗转相除法()g x ()f x2()q x 1 1 1 1 -1 -2 -2 1 2 -1 -4 -2 1()q x 11 0 -2 0 1 1 -1 -2 -21 1 -2 -2 1()r x 1 0 -2 0 3()q x 10 1 0 -2 0 1 0 -22()r x 1 0 -2 3()r x 0由以上计算得11()()()(),f x q x g x r x =+212()()()(),g x q x r x r x =+132()()(),r x q x r x =因此22((),())()2f x g x r x x ==-,且2((),())()f x g x r x =21()()()g x q x r x =-21()()[()()()]g x q x f x q x g x =--212()()[1()()]()q x f x q x q x g x =-++所以212()()1,()1()()2u x q x x v x q x q x x =-=--=+=+.2)((),())1f x g x x =-,21122(),()13333u x x v x x x =-+=--. 3)((),())1f x g x =,32()1,()32u x x v x x x x =--=+--.7.设323()(1)22,()f x x t x x u g x x tx u =++++=++的最大公因式是一个二次多项式,求,t u 的值.解 略.8.证明:如果()(),()()d x f x d x g x 且()d x 为()f x 与()g x 的一个组合,那么()d x 是()f x 与()g x 的一个最大公因式.证明 由于()(),()()d x f x d x g x ,所以()d x 为()f x 与()g x 的一个公因式.任取()f x 与()g x 的一个公因式()h x ,由已知()d x 为()f x 与()g x 的一个组合,所以()()h x d x .因此,()d x 是()f x 与()g x 的一个最大公因式.9.证明:(()(),()())((),())()f x h x g x h x f x g x h x =,(()h x 的首项系数为 1). 证明 因为存在多项式()u x 和()v x 使((),())()()()()f x g x u x f x v x g x =+,所以((),())()()()()()()()f x g x h x u x f x h x v x g x h x =+,这表明((),())()f x g x h x 是()()f x h x 与()()g x h x 的一个组合,又因为((),())(),((),())()f x g x f x f x g x g x ,从而((),())()()(),((),())()()()f x g x h x f x h x f x g x h x g x h x ,故由第8题结论,((),())()f x g x h x 是()()f x h x 与()()g x h x 的一个最大公因式.注意到((),())()f x g x h x 的首项系数为1,于是(()(),()())((),())()f x h x g x h x f x g x h x =.10.如果(),()f x g x 不全为零,证明:()()(,)1((),())((),())f xg x f x g x f x g x =.证明 存在多项式()u x 和()v x 使((),())()()()()f x g x u x f x v x g x =+,因为(),()f x g x 不全为零,所以((),())0f x g x ≠,故由消去律得()()1()()((),())((),())f xg x u x v x f x g x f x g x =+, 所以()()(,)1((),())((),())f xg x f x g x f x g x =. 11.证明:如果(),()f x g x 不全为零,且()()()()((),())u x f x v x g x f x g x +=,那么((),())1u x v x =.证明 因为(),()f x g x 不全为零,故 ((),())0f x g x ≠,从而由消去律得()()1()()((),())((),())f xg x u x v x f x g x f x g x =+, 所以((),())1u x v x =.12.证明:如果((),())1f x g x = ,((),())1f x h x =,那么((),()())1f x g x h x =. 证法一 用反证法.假设()((),()())1d x f x g x h x =≠,则(())0d x ∂>,从而()d x 有不可约因式()p x ,于是()(),()()()p x f x p x g x h x ,但因为((),())1f x g x =,所以()p x 不整除()g x ,所以()()p x h x ,这与((),())1f x h x =矛盾.因此((),()())1f x g x h x =.证法二 由题设知,存在多项式1122(),(),(),()u x v x u x v x ,使得11()()()()1u x f x v x g x +=,22()()()()1u x f x v x h x +=,两式相乘得12121212[()()()()()()()()()]()[()()]()()1u x u x f x v x u x g x u x v x h x f x v x v x g x h x +++=, 所以((),()())1f x g x h x =.13.设11(),,(),(),,()m n f x f x g x g x L L 都是多项式,而且((),())1(1,2,,;1,2,,).i j f x g x i m j n ===L L求证:1212(()()(),()()()) 1.m n f x f x f x g x g x g x =L L证法一 反复应用第12题的结果证法二 反证法14.证明:如果((),())1f x g x =,那么(()(),()())1f x g x f x g x +=.证明 由于((),())1f x g x =,所以存在多项式()u x 和()v x 使()()()()1u x f x v x g x +=,由此可得()()()()()()()()1,u x f x v x f x v x f x v x g x -++=()()()()()()()()1,u x f x u x g x u x g x v x g x +-+=即[][]()()()()()()1,u x v x f x v x f x g x -++=[][]()()()()()()1,v x u x g x u x f x g x -++=于是((),()())1f x f x g x +=,((),()())1g x f x g x +=,应用第12题的结论可得(()(),()())1f x g x f x g x +=.注 也可以用反证法.15.求下列多项式的公共根:32432()221;()22 1.f x x x x g x x x x x =+++=++++提示 用辗转相除法求出2((),()) 1.f x g x x x =++于是得两多项式的公共根为1.2- 16.判别下列多项式有无重因式:1)5432()57248f x x x x x x =-+-+-;2) 42()443f x x x x =+--1)解 由于432'()5202144f x x x x x =-+-+,用辗转相除法可求得2((),'())(2)f x f x x =-,故()f x 有重因式,且2x -是它的一个 3 重因式.2)解 由于3'()484f x x x =+-,用辗转相除法可求得((),'())1f x f x =,故()f x 无重因式.17.求t 值使32()31f x x x tx =-+-有重根.解 2'()36f x x x t =-+.先用'()f x 除()f x 得余式 1263()33t t r x x --=+. 当3t =时,1()0r x =.此时'()()f x f x ,所以21((),'())'()(1)3f x f x f x x ==-,所以1是()f x 的3重根.当3t ≠时,1()0r x ≠.再用1()r x 除'()f x 得余式215()4r x t =+.故当154t =-时,2()0r x =.此时,121((),'())()92f x f x r x x =-=+,所以12-是()f x 的2重根.当3t ≠且154t ≠-时,2()0r x ≠,则((),'())1f x f x =,此时()f x 无重根. 综上,当3t =时,()f x 有3重根1;当154t =-时,()f x 有2重根12-. 18.求多项式3x px q ++有重根的条件.解 略. 19.如果242(1)1x Ax Bx -++ ,求,A B .解法一 设42()1f x Ax Bx =++,则3'()42f x Ax Bx =+. 因为242(1)1x Ax Bx -++,所以1是()f x 的重根,从而1也是'()f x 的根.于是(1)0f =且'(1)0f =,即10;420.A B A B ++=⎧⎨+=⎩解得1,2A B ==-.解法二 用2(1)x -除421Ax Bx ++得余式为(42)(31)A B x A B ++--+,因为242(1)1x Ax Bx -++,所以(42)(31)0A B x A B ++--+=,故420;310.A B A B +=⎧⎨--+=⎩解得1,2A B ==-.20.证明:212!!nx x x n ++++L 没有重根. 证法一 设2()12!!nx x f x x n =++++L ,则21'()12!(1)!n x x f x x n -=++++-L . 因为()'()!nx f x f x n -=,所以 ((),'())((),)1!nx f x f x f x n ==. 于是212!!nx x x n ++++L 没有重根. 证法二 设2()12!!nx x f x x n =++++L ,则21'()12!(1)!n x x f x x n -=++++-L . 假设()f x 有重根α,则()0f α=且'()0f α=,从而0!nn α=,得0α=,但0α=不是()f x 的根,矛盾.所以212!!nx x x n ++++L 没有重根. 21.略.22.证明:0x 是()f x 的k 重根的充分必要条件是 (1)000()'()()0k f x f x f x -====L ,而()0()0k f x ≠.证明 (必要性)设0x 是()f x 的k 重根,从而0x 是'()f x 的1k -重根,是''()f x 的2k -重根,…,是(1)()k f x -的单根,不是()()k f x 的根,于是(1)000()'()()0k f x f x f x -====L ,而()0()0k f x ≠.(充分性)设(1)000()'()()0k f x f x f x -====L ,而()0()0k f x ≠,则0x 是(1)()k f x -的单根,是(2)()k f x -的2重根,…,是()f x 的k 重根.23.举例说明断语“如果α是'()f x 的m 重根,那么α是()f x 的m +1重根”是不对的.解 取1()()1m f x x α+=-+,则()'()1()m f x m x α=+-.α是'()f x 的m 重根,但α不是()f x 的m +1重根.注:也可以取具体的,如0,1m α==.24.证明:如果(1)()n x f x -,那么(1)()n n x f x -.证明 略.25.证明:如果23312(1)()()x x f x xf x +++,那么12(1)(),(1)()x f x x f x --.证明 2121()()x x x x ωω++=--,其中12ωω==. 由于23312(1)()()x x f x xf x +++,故存在多项式()h x 使得33212()()(1)()f x xf x x x h x +=++,因此112122(1)(1)0;(1)(1)0.f f f f ωω+=⎧⎨+=⎩ 解得12(1)(1)0f f ==,从而12(1)(),(1)()x f x x f x --.26.求多项式1n x -在复数范围内和实数范围内的因式分解.解 多项式1n x -的n 个复根为22cos sin ,0,1,2,,1k k k i k n n nππω=+=-L , 所以1n x -在复数范围内的分解式为1211(1)()()()n n x x x x x ωωω--=----L .在实数范围内,当n 为奇数时:222112211221(1)[()1][()1][()1]n n n n n x x x x x x x x ωωωωωω---+-=--++-++-++L ,当n 为偶数时:222112222221(1)(1)[()1][()1][()1]n n n n n x x x x x x x x x ωωωωωω---+-=-+-++-++-++L .27.求下列多项式的有理根:1)3261514x x x -+-;2)424751x x x ---;3)5432614113x x x x x +----.1)解 多项式可能的有理根是1,2,7,14±±±±.(1)40f =-≠,(1)360f -=-≠. 由于44444,,,,1(2)171(7)1141(14)-------------都不是整数,所以多项式可能的有理根只有2.用综合除法判别:2 1 -6 15 -14+ 2 -8 142 1 -4 7 0+ 2 -41 -2 3≠0所以2是多项式的有理根(单根).注:一般要求指出有理根的重数.计算量较小的话,也可以直接计算,如本题可直接算得(2)0f =,说明2是()f x 的有理根,再由'(2)0f ≠知. 2是单根.用综合除法一般比较简单.2)答 12-(2重根). 3)答 1-(4重根),3(单根).28.下列多项式在有理数域上是否可约?1)21x -;2)4328122x x x -++;3)631x x ++;4)1p x px ++,p 为奇素数;5)441x kx ++,k 为整数.1)解 21x -可能的有理根是1±,直接检验知,都不是它的根,故21x -不可约.2)解 用艾森斯坦判别法,取2p =.3)解 令1x y =+,则原多项式变为6365432(1)(1)1615211893y y y y y y y y ++++=++++++,取3p =,则由艾森斯坦判别法知多项式65432615211893y y y y y y ++++++不可约,从而多项式631x x ++也不可约.4)提示:令1x y =-,取素数p .5)提示:令1=+,取x yp=.2。
