建造师培训讲义单代号搭接网络计划时间参数计算
网络计划计算简易方法及技巧速成

双代号时标网络计划是以时间坐标为尺度编制的网络计划,以实箭线表示工作,以虚箭线 表示虚工作,以波形线表示工作的自由时差。 双代号时标网络图
1、关键线路 在时标双代号网络图上逆方向看,没有出现波形线的线路为关键线路(包括虚工作)。 如图中①→②→⑥→⑧
双代号时标网络图时间参数计算技巧
[例题]
1.3按节点法计算时间参数
说明 标注 定义
1.3按节点法计算时间参数
1.节点最早时间的计算 2.网络计划工期的计算 3.节点最迟时间的计算
1.3按节点法计算时间参数
4.节点法和工作法时间参数的对应关系 可以推知 及
[例题]
2 双代号时标网络计划
2.1双代号时标网络计划的概念 2.2双代号时标网络计划的时间参数计算
[例题]
3
解析:总时差 =实际进度拖延的天数-影响总工期的天பைடு நூலகம் 本题中:该工作原来的总时差=5-2=3
[例题]
3.在工程网络计划中,工作M的最迟完成时间为第25天,其持续时间为6天。该工作有三项紧前工作,他们的最早完成时间分别为第10天、第12天和第13天,则工作M的总时差为____。
6
解析:总时差=LS-ES=LF-EF EF=ES+D ES等于各紧前工作的最早完成时间的最大值(对于有紧前工作而言) 本题中:EF=13+6=19 M的总时差=LF-EF=25-19=6
10
解:总时差=min{紧后工作的总时差+两者的工作间隔 对I工作:3+8=11 对J工作:4+6=10
4 单代号搭接网络计划
4.1单代号搭接网络计划概述 4.2单代号搭接网络计划的计算
4.1单代号搭接网络计划概述
一级建造师《建设工程项目管理》 建设工程项目进度控制(4)单代号网络计划时间参数计算及关键线路的判定

(三)单代号网络计划时间参数计算及关键线路的判定1.单代号网络计划时间参数的计算(7个参数)参数标注及计算过程例根据下列单代号网络计划,用图算法计算时间参数、工期,标出关键线路●工作的最早开始时间(从起点顺着计算)网络计划起点节点ES=0其它节点ES=该工作的各个紧前工作的最早完成时间的最大值●工作的最早完成时间EF=该工作的最早开始时间+持续时间计算工期Tc=网络计划的终点的最早完成时间EFn●相邻两项工作的时间间隔(LAG)LAG=紧后工作的最早开始时间-本工作的最早完成时间●总时差TF(从终点逆着计算)网络计划终点节点,如果计划工期等于计算工期,则TF=0其它工作TF=TF i=min{LAG i,j+TF j}●工作自由时差FF工作无紧后工作FF=计划工期-该工作的最早完成时间工作有紧后工作,FF=FF i=min{LAG i,j}●工作最迟开始时间LSLS=该工作的最早开始时间+总时差●工作最迟完成时间LFLF=该工作的最早完成时间+总时差2.单代号网络计划的关键工作和关键线路的确定●关键工作单代号网络计划中,工作总时差最小的工作是关键工作●关键线路从起点节点开始到终点节点均为关键工作,且所有工作之间的时间间隔均为零的线路为关键线路不计算时间参数的情况下,由开始节点到终点节点形成的路线上各项工作持续时间之和最大值所对应的路线称为关键路线。
4.总结——网络计划时间参数计算步骤的比较双代号网络计划时间参数的计算步骤单代号网络计划时间参数的计算步骤(1)计算工作的最早开始时间和最早完成时间(1)计算工作的最早开始时间和最早完成时间(2)确定网络计划的计划工期(2)计算相邻两项工作之间的时间间隔(3)计算工作的最迟完成时间和最迟开始时间(3)确定网络计划的计划工期(4)计算工作的总时差(4)计算工作的总时差(5)计算工作的自由时差(5)计算工作的自由时差(6)确定关键工作和关键线路(6)计算工作的最迟完成时间和最迟开始时间(7)确定网络计划的关键线路计算的内容一致(除单代号的相邻两项工作之间的时间间隔)。
10-单代号搭接网络计划、双代号时标网络计划计算

10 网络图计算 10.1 单代号搭接网络计划计算
搭接网络计划具有如下几个特点: ①直接反映工作之间各种可能出现的顺序关系; ②大大简化了网络计划的图形和计算,尤其适合重复性工作和许多工作同时进行的
情况; ③丰富了网络计划的内容,极大地扩展了应用范围; ④可用多种方法手算,也可以采用计算机计算,方便灵活,适应性强。 因此,它作为一种严格的科学计划方法,借助于计算机手段,得到了广泛的应用和推广
16
10 网络图计算
绘制具体方法
2)间接绘图法 间接绘图法即先算后画。根据先绘制好的无时标网络计划,算出各个节点的最早时间,
确定关键线路,然后,再在时标表上确定节点位置,用箭线标出工作持续时间,某些工作 箭线长度不足以达到该工作的完成节点时,用波形线补足。绘图时一般宜先绘制关键线路 上的工作,再绘制非关键工作。 步骤如下: (1)绘制一般双代号网络计划草图。 (2)计算节点的最早时间,确定关键线路(用双线表示)。 (3)在时标表上,按最早开始时间确定每项工作的起点节点位置(图形尽量与草图一致)。 (4)按各工作的时间长度绘制相应工作的实线部分,使其在时间坐标上的水平投影长度等于 工作时间。虚工作因为不占时间,故只能以垂直虚线表示,其水平段以波形线表示。 (5)用波形线把实线部分与其紧后工作的起点节点连接起来,以表示自由时差。
17
10 网络图计算
(3) 关键线路和时间参数的确定
关键线路——自始至终不出现波形线的线路。 时间参数: (1) 工作最早时间 (2) 工作自由时差 (3) 工作总时差 (4) 工作最迟时间
18
12
10 网络图计算
10.2双代号时间坐标网络参数识别
表示方法 时标网络计划的工作以实箭线表示,虚工作以虚箭线表示,以波形线表示本工作与其紧
网络计划的时间参数计算

网络计划的时间参数计算一、双代号网络计划时间参数的计算(一)、按工作计算法1、以网络计划的起点为开始节点的工作,如果没有规定最早开始时间,那么最早开始时间为0,最早完成时间为最早开始时间加上持续时间。
其它工作的最早开始时间为其紧前工作的最早完成时间的最大值,其它工作最早完成时间为最早开始时间加上持续时间。
2、计算工期,以网络计划的终点为完成节点的工作的最早完成时间的最大值为计算工期。
3、计划工期,如果没有要求工期,那么计划工期就等于计算工作。
4、以网络计划的终点为完成节点的工作的最迟完成时间等于网络计划的计划工期,最迟开始时间等于最迟完成时间减去持续时间。
其它工作的最迟完成时间等于其紧后工作的最迟开始时间的最小值,其它工作的最迟开始时间等于最迟完成时间减去持续时间。
5、总时差,总时差等于应该工作的最迟开始时间减去最早开始时间,或者最迟完成时间减去最早完成时间。
6、对于有紧后工作的工作,自由时差等于该工作的紧后工作的最早开始时间减去本工作的最早完成时间的最小值。
对于没有紧后工作的工作,就是以网络计划的终点为完成节点的工作,自由时差等于网络计划的计划工期减去本工作的最早完成时间。
7、网络计划中总时差最小的工作为关键工作,当网络计划的计划工期与计算工期相等时,总时差为0的工作是关键工作。
8、将这些关键工作的首尾相连。
便至少形成一条从起点到终点节点的通路,通路上各项工作持续时间总和最大的就是关键线路。
(二)按节点计算法1、网络计划的起点节点如果未规定最早时间,其最早时间为0。
其它节点的最早时间等于开始节点的最早时间加上持续时间和的最大值。
2、网络计划的计算工期等于终点节点的最早时间。
3、假设未规定要求工期,计划工期等于计算工期。
4、网络计划的终点的最迟时间等于网络计划的计划工期,其它节点的最迟时间等于完成节点的最迟时间减去持续时间差的最小值。
5、工作的最早开始时间等于该工作的开始节点的最早时间。
6、工作的最早完成时间等于该工作的开始节点的最早时间加上持续时间。
工程网络计划有关时间参数的计算——一级建造师考试辅导《建设工程项目管理》第三章第三节讲义

正保远程教育旗下品牌网站美国纽交所上市公司(NYSE:DL)
建设工程教育网
/
一级建造师考试辅导《建设工程项目管理》第三章第三节讲义
工程网络计划有关时间参数的计算
1Z203033 工程网络计划有关时间参数的计算(P126~139)
第八个考点:工期
工期泛指完成任务所需要的时间,一般有以下三种:
(1)计算工期,根据网络计划时间参数计算出来的工期,用T C表示。
(2)要求工期,任务委托人所要求的工期,用T r表示。
(3)计划工期,根据要求工期和计算工期所确定的作为实施目标的工期,用T P表示。
第九个考点:双代号网络时间参数
一、六个时间参数
(1)最早开始时间(ES i-j),是指在各紧前工作全部完成后,工作 i-j有可能开始的最早时刻。
(2)最早完成时间(EF i-j),是指在各紧前工作全部完成后,工作i-j有可能完成的最早时刻。
(3)最迟开始时间(LS i-j),是指在不影响整个任务按期完成的前提下,工作i-j必须开始的最迟时刻。
(4)最迟完成时间(F i-j),是指在不影响整个任务按期完成的前提下,工作i-j必须完成的最迟时刻。
(5)总时差(TF i-j),是指在不影响总工期的前提下,工作i-j可以利用的机动时间。
1Z203035单代号搭接网络计划、关键工作和时差(一级建造师-2021版)

1Z203035单代号搭接网络计划、关键工作和时差Jacky老师3.3进度计划的编制和调整方法(五)-考点单代号搭接网络计划图关键工作、关键路线和时差进度计划调整的方法单代号搭接网络计划•普通网络计划,任一工作须在其紧前工作全部完成后才开始。
•为缩短工期,许多工作采用平行搭接的方式,即搭接网络计划。
单代号搭接网络计划图单代号搭接网络图箭线的表示方法箭线及上面的时距符号表示相邻工作间的逻辑关系。
•工作搭接顺序关系用前项工作的开始或完成时间与其紧后工作开始或完成时间之间的间距表示,具体有四类。
•FTS i,j——工作i完成时间与其紧后工作j开始时间的时间间距。
•两项工作之间可同时由四种基本连接关系中两种以上限制工作间的逻辑关系。
•完成到开始时距(FTS i,j):如修一条堤坝护坡时,一定要等土堤自然沉降后才能修护坡,这种等待的时间就是FTS时距。
•完成到完成时距(FTF i,j):如相邻两工作,当紧前工作的施工速度小于紧后工作时,则必须考虑为紧后工作留有充分的工作面,这种结束工作时间之间的间隔就是FTF时距。
•开始到开始时距(STS i,j):如道路工程中铺设路基和浇筑路面,待路基开始工作一定时间为路面工程创造一定工作条件之后,路面工程即可开始工作,这种开始工作时间之间的间隔就是STS时距。
•开始到完成时距(STF i,j):如挖掘带有部分地下水的土壤,地下水位以上的土壤可以在降低地下水位工作完成之前开始,但地下水位以下的土壤则必须要等降低地下水位之后才能开始。
降低地下水位工作的完成与何时挖地下水位以下的土壤有关,至于降低地下水位何时开始,则与挖土没有直接联系,这种开始到结束的限时时间就是STF时距。
单代号搭接出现负值的处理方法当某中间工作的ES i为负值时,将该工作用虚线与起点联系起来。
单代号搭接出现大于完成时间的处理方法当中间工作的完成时间大于最后工作的完成时间,将该工作与终点节点用虚箭线联系起来。
单代号网络计划时间参数计算
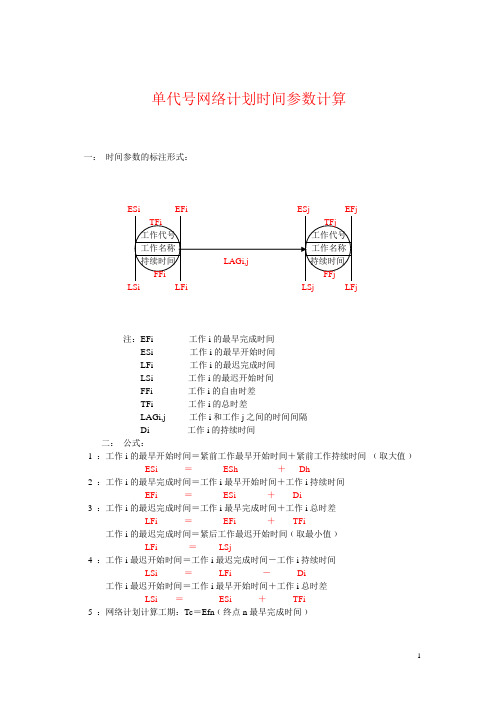
单代号网络计划时间参数计算一:时间参数的标注形式:LSi LFi LSj LFj注:EFi ---------- 工作i的最早完成时间ESi----------- 工作i的最早开始时间LFi----------- 工作i的最迟完成时间LSi------------工作i的最迟开始时间FFi------------工作i的自由时差TFi------------工作i的总时差LAGi,j--------工作i和工作j之间的时间间隔Di-------------工作i的持续时间二:公式:1 :工作i的最早开始时间=紧前工作最早开始时间+紧前工作持续时间﹙取大值﹚ESi =ESh +Dh2 :工作i的最早完成时间=工作i最早开始时间+工作i持续时间EFi =ESi +Di3 :工作i的最迟完成时间=工作i最早完成时间+工作i总时差LFi =EFi +TFi工作i的最迟完成时间=紧后工作最迟开始时间﹙取最小值﹚LFi =LSj4 :工作i最迟开始时间=工作i最迟完成时间-工作i持续时间LSi =LFi -Di工作i最迟开始时间=工作i最早开始时间+工作i总时差LSi =ESi +TFi5 :网络计划计算工期:Tc=Efn﹙终点n最早完成时间﹚6 :总时差:终点节点n的总时差=计划工期-工作n最早完成时间TFn =Tp -EFn工作i的总时差=紧后工j总时差+工作i-j时间间隔TFi =TFj +LAGi,j7 :自由时差:终点n的自由时差=计划工期-工作n的最早完成时间FFn =Tp -EFn工作i的自由时差=工作i-j时间间隔﹙取最小值﹚FFi =IAGi-j8:时间间隔:终点节点为虚拟节点时其时间间隔:i-n时间间隔=计算工期-工作i的最早完成时间LAGi,n =Tp -EFi其他节点﹙i-j﹚的时间间隔i-j 时间间隔=工作j最早开始时间-工作i最早完成时间LAGi,j =ESj -EFi三:计算程序:1:最早开始时间-------ES2:最早完成时间-------EF3:总时差----------------TF4:最迟开始时间-------LS5:最迟完成时间-------LF6:自由时差-----------FF。
考点4:单代号网络计划时间参数的计算

内ቤተ መጻሕፍቲ ባይዱ精编
1.计算最早开始时间和最早完成时间 网络计划中各项工作的最早开始时间和最早完成时间的计算应从网络计划 的起点节点开始,顺着箭线方向依次逐项计算。 2.网络计划的计算工期Tc Tc等于网络计划的终点节点行的最早完成时间EFn。 3.计算相邻两项工作之间的时间间隔LAGij相邻两项工作主和j之间的时 间间隔LAGi-j等于紧后工作j的最早开始时间ESj和本工作的最早完成时 间EFi之差。 4.计算工作总时差TFi: 工作i的总时差TFi应从网络计划的终点节点开始,逆着箭线方向依次逐项 计算。 5.计算工作自由时差: 工作i若无紧后工作,其自由时差FFj等于计划工期Tp减该工作的最早完成 时间EFn。 6.计算工作的最迟开始时间和最迟完成时间 7.关键工作和关键线路的确定 (1)关键工作:总时差最小的工作是关键工作。 (2)关键线路的确定按以下规定:从起点节点开始到终点节点均为关键 工作,且所有工作的时间间隔为零的线路为关键线路。
p
单代号网络计划的时间参数计算

3 . 1 各工作 的最 早 时间 参数
( 1 ) 最早 开始 时 间 E S i : 各 紧前 工 作 均 完成 后 , 本 工作 最早
有 可 能 开 始 的 时刻 它反 映 了作 业 队 最早 可 以在 该 时 刻投 入
( 2 ) 最早完成 时间 E F . : 本 工 作 的 最 早 开 始 时 刻 与其 持 续 时间 D 之和 , 即 EF i = E S , + D. , 它反 映 了施 工 作 业 队 最 早 可 以退 出本 施 工 段 施 工 的 时 刻 与 最 早 开 始 时 间概 念 相 对 应 . 某项 工
最早 开始时 间, 所 以有 L ≥E S , 则T F 。 ≥F F . , 可见 , 自 由时 差
是 总时 差 的 一 部 分
4 结 论
通 过 以 上 对 单 代 号 网络 图 的基 本 构 成 和 各 时 间参 数 计 算
的推 导 分 析 . 可得 出 以 下结 论 :
作 的 最早 开始 时间 E F j = Ma x { E F . } 。 单 代 号 网络 图终 点 节点 的最 早 完成 时 间 E F 就是该项 目
因为 若 干 紧前 工作 的 最早 完 成 时 间 的 最 大值 ,是 后 续 工
作 的 最早 开始 时 问 , 那 么 当某 些 工 作 存 在 自由时 差 时 , 也 意味 着 这 些 工作 的 最迟 开始 ( 完成) 时 间 一 定 大 于或 等 于 其 最 早 开 始( 完成 ) 工作 时间 , 即 L S ≥E S ( 或 L F . ≥E F 。 ) , 两者相差 的 时
单代号网络计划时间参数的计算方法
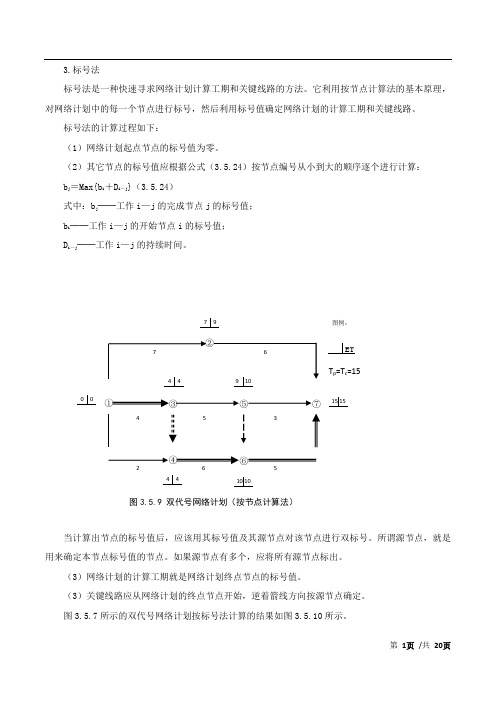
3.标号法标号法是一种快速寻求网络计划计算工期和关键线路的方法。
它利用按节点计算法的基本原理,对网络计划中的每一个节点进行标号,然后利用标号值确定网络计划的计算工期和关键线路。
标号法的计算过程如下:(1)网络计划起点节点的标号值为零。
(2)其它节点的标号值应根据公式(3.5.24)按节点编号从小到大的顺序逐个进行计算:b j=Max{b i+D i—j}(3.5.24)式中:b j──工作i—j的完成节点j的标号值;b i──工作i—j的开始节点i的标号值;D i—j──工作i—j的持续时间。
图3.5.9 双代号网络计划(按节点计算法)当计算出节点的标号值后,应该用其标号值及其源节点对该节点进行双标号。
所谓源节点,就是用来确定本节点标号值的节点。
如果源节点有多个,应将所有源节点标出。
(3)网络计划的计算工期就是网络计划终点节点的标号值。
(3)关键线路应从网络计划的终点节点开始,逆着箭线方向按源节点确定。
图3.5.7所示的双代号网络计划按标号法计算的结果如图3.5.10所示。
例题1. 计划工期与计算工期相等的双代号网络计划中,某工作的开始节点和完成节点均为关键节点时,说明该工作()。
【2015】A.一定是关键工作B.总时差为零C.总是差等于自由时差D.自由时差为零 【答案】C【解析】依据题干给出的条件,假设某工作的开始节点最早时间和和最迟时间为X ,某工作的完成节点最早时间和和最迟时间为Y ,该工作的持续时间为Z ;该工作的总时差是某工作的完成节点最迟时间Y 减某工作的开始节点(最早时间X+Z ); 该工作的自由时差是某工作的完成节点最早时间Y 减某工作的开始节点(最早时间X+Z );所以该工作总时差和自由时差=Y-(X+Z ),则总是差等于自由时差。
(三)单代号网络计划时间参数的计算方法单代号网络计划与双代号网络计划只是表现形式不同,它们所表达的内容则完全一样。
其时间参数的计算过程如下:1.计算工作的最早开始时间和最早完成时间工作最早开始时间和最早完成时间的计算应从网络计划的起点节点开始,顺着箭线方向按节点编④ ⑥ 图3.5.10 双代号网络计划(标号法)652(④,10)(③,4)(①,7)号从小到大的顺序依次进行。
单代号网络计划时间参数的计算方法

单代号网络计划时间参数的计算方法第一篇:单代号网络计划时间参数的计算方法单代号网络计划时间参数的计算方法1、计算最早开始时间和最早完成时间网络计划的起点节点的最早开始时间为0。
如起点节点的编号为1,则:ESi=0(i=1)工作最早完成时间=该工作最早开始时间加上其持续时间,即:EFi=ESi+Di工作最早开始时间=该工作的各个紧前工作的最早完成时间的最大值,如工作j的紧前工作的代号为i,则:ESj=max{EFi}或ESj=max{ESi+Di}。
式中ESi——工作j的各紧前工作的最早开始时间。
2、网络计划的计算工期TcTc等于网络计划的终点节点n的最早完成时间EFn,即:Tc=EFn3、计算相邻两项工作之间时间间隔LAGi-j相邻两项工作i和j之间的时间间隔LAGi-j=紧后工作j的最早开始时间ESj和本工作的最早完成时间EFi之差,即:LAGi-j=ES j-EF i4、计算工作总时差TFi工作i的总时差TFi应从网络计划的终点节点开始,逆着箭线方向依次逐项计算。
网络计划终点节点的总时差TFn,如计划工期=计算工期,其值为0,即:TFn=0其他工作i的总时差TFi=该工作的各个紧后工作j的总时差TF j +该工作与其紧后工作之间的时间间隔LAGi-j之和的最小值,即:TFi=min{TF j+LAGi-j}5、计算工作自由时差工作i若无紧后工作,其自由时差FFj=计划工期Tp-该工作的最早完成时间EFn,即:FFn=Tp-EFn当工作i有紧后工作j时,其自由时差FFi =该工作与其紧后工作j 之间的时间间隔LAGi-j的最小值,即:FFi=min{LAGi-j}6、计算工作的最迟开始时间和最迟完成时间工作i的最迟开始时间LSi等于该工作的最早开始时间ESi与其总时差TFi之和,即:LSi=ESi+TFi。
工作i的最迟完成时间LFi等于该工作的最早完成时间EFi与其总时差TFi之和,即:LFi=EFi+TFi。
单代号网络计划时间参数计算

单代号网络计划时间参数计算网络计划时间参数是指在网络计划中,根据活动的紧前关系和持续时间,计算出每个活动的最早开始时间(ES)、最晚开始时间(LS)、最早完成时间(EF)和最晚完成时间(LF),以及活动的总时差(TF)和自由时差(FF)。
这些参数对于实施项目的时间管理非常重要,帮助项目经理和团队成员掌握项目进度,并进行必要的调整和优化。
计算网络计划时间参数主要需要以下步骤:1.确定每个活动的紧前活动和持续时间。
紧前活动是指在开始该活动之前必须完成的活动,持续时间是指完成该活动所需的时间。
2.确定每个活动的最早开始时间(ES)。
对于没有紧前活动的活动,其最早开始时间为0,对于有紧前活动的活动,其最早开始时间为其紧前活动的最早完成时间。
3.确定每个活动的最早完成时间(EF)。
最早完成时间等于最早开始时间加上活动持续时间。
4.确定每个活动的最晚完成时间(LF)。
最晚完成时间等于其紧后活动中最早开始时间减去1、也就是说,其紧后活动的最早开始时间减去1就是该活动的最晚完成时间。
5.确定每个活动的最晚开始时间(LS)。
最晚开始时间等于最晚完成时间减去持续时间。
6.计算活动的总时差(TF)。
总时差等于最晚开始时间减去最早开始时间。
如果总时差为负数,表示该活动的实际完成时间不能延迟,否则会影响整个项目的进度。
7.计算活动的自由时差(FF)。
自由时差等于紧后活动的最早开始时间减去最早完成时间减去持续时间。
自由时差表示在不影响整个项目进度的情况下,该活动可以延迟的时间。
以上就是计算网络计划时间参数的基本步骤。
在实际项目管理中,可以使用专门的项目管理软件或Excel等工具进行计算。
通过合理地计算和调整网络计划时间参数,可以帮助项目经理和团队成员合理安排时间,保证项目的顺利实施。
单代号搭接网络计划

0天
基坑 回填土
基坑 或
排水
FTF=0天
A
B
(a)
(b)
整图理8课-件6
6
(二)单代号搭接网络的绘制
1.基本形式
单代号搭接网络以工程活动为节点,以带箭杆表示逻辑 关系。活动之间存在各种形式的搭接 关系(如 FTS、 FTF、STS、STF)。例如图8-23。
一个活动的自由时差是指这个活动不影 响其它活动的机动余地,则必须按该活动与 其它活动的搭接关系来确定自由时差。
当 i 活动有几个紧后活动时,必可以得到几个自由时 差 FFi,最终取其中的最小值
整理课件
return
27
2. 其他活动的最迟时间计算(从后向前传递)
A
B
A
B
A
B
FTS关系 :FFi=ESj-EFi-FTSij STS关系 :FFi=ESj-ESi-STSij FTF关系 :FFi=EFj-EFi-FTFij
同理C:ESc=4,EFc=10,
D:ESD=4,EFD=4十10=14,
E:ESE=4,EFE=4十4=8。
整理课件
return
15
对于F:
F有两个紧前活动,则ESF必有两个 计算结果。
由 B-F关系定义得:
ESF1=EFB十FTS BF=14十2=16, EFF1=ES F1十DF=16十2=18 由C-F关系定义得:
FTS=10天
A
B
=
10天
A
B
5天
FTF=5天
单代号网络图时间参数计算

单代号网络图时间参数计算1.计算工作的最早开始时间和最早完成时间工作i的最早开始时间ESiT应从网络图的起点节点开始,顺着箭线方向依次逐个计算。
起点节点的最早开始时间EST1如无规定时,其值等于零,即其它工作的最早开始时间等于该工作的紧前工作的最早完成时间的最大值,即式中,EFhT──工作i的紧前工作h的最早完成时间;EShT──工作i的紧前工作h的最早开始时间;hD──工作i的紧前工作h的工作持续时间。
工作的最早完成时间EFiT等于工作的最早开始时间加该工作的持续时间,即2.计算网络计划计算工期c T式中,T n EF──终点节点n的最早完成时间。
3.计算相邻两项工作之间的时间间隔工作i→工作j之间的时间间隔T i,j LAG是工作j的最早开始时间与工作i的最早完成时间的差值,其大小按下式计算:4.计算工作最迟开始时间和最迟完成时间工作的最迟完成时间应从网络图的终点节点开始,逆着箭线方向依次逐项计算。
终点节点所代表的工作n的最迟完成时间LFnT,应按网络计划的计划工期p T或计算工期cT确定,即1=EST{}{}m axm axhEShEFhESiDTTT+==iESiEFiDTT+=EFncTT=,EFiESjLAGjiTTT-=(1-1)(1-2)(1-3)(1-4)(1-5)工作的最迟完成时间等于该工作的紧后工作的最迟开始时间的最小值,即式中,LSj T ──工作i 的紧后工作j 的最迟开始时间; LFj T ──工作i 的紧后工作j 的最迟完成时间; i D ──工作i 的紧后工作j 的持续时间。
工作的最迟开始时间等于该工作的最迟完成减去工作持续时间,即5.计算工作的总时差工作总时差应从网络图的终点节点开始,逆着箭线方向依次逐项计算。
终点节点所代表的工作n 的总时差T n F 为零,即 其他工作的总时差等于该工作与其紧后工作之间的时间间隔加该紧后工作的总时差所得之和的最小值,即 式中,T j F ──工作i 的紧后工作j 的总时差。
单代号搭接网络计划时间参数的计算

四、单代号搭接网络计划时间参数的计算与前述单代号网络计划和双代号网络计划时间参数的计算原理基本相同。
现说明其计算方法。
1.计算工作的最早开始时间和最早完成时间工作最早开始时间和最早完成时间的计算应从网络计划的起点节点开始,顺着箭线方向依次进行。
(1)由于在单代号搭接网络计划中的起点节点一般都代表虚拟工作,故其最早开始时间和最早完成时间均为零,即:ESs=EFs=0(2)凡是与网络计划起点节点相联系的工作,其最早开始时间为零。
即:ES1=0(3)凡是与网络计划起点节点相联系的工作,其最早完成时间应等于其最早开始时间与持续时间之和。
(4)其他工作的最早开始时间和最早完成时间应根据时距按下列公式计算:①相邻时距为FTS时,ESj=EFi+FTSi,j(3—45)②相邻时距为STS时,ESj=ESi+STSi,j(3—46)③相邻时距为FTF时,EFj=EFi+FTFi,j(3—47)④相邻时距为STF时,EFj=ESi+STFi,j(3—48)EFj=ESj+Dj(3—49)ESj=EFj—Dj(3—50)(5)终点节点所代表的工作,其最早开始时间按理应等于该工作紧前工作最早完成时间的最大值。
由于在搭接网络计划中,终点节点一般都表示虚拟工作(其持续时间为零),故其最早完成时间与最早开始时间相等,且一般为网络计划的计算工期。
但是,由于在搭接网络计划中,决定工期的工作不一定是最后进行的工作,因此,在用上述方法完成计算之后,还应检查网络计划中其他工作的最早完成时间是否超过已算出的计算工期。
如其他工作的最早完成时间超过已算出的计算工期应由其它工作的最早完成时间决定的。
同时,应将该工作与虚拟工作(终点节点)用虚箭线相连2.计算相邻两项工作之间的时间间隔3.计算工作的时差搭接网络计划同前述简单的网络计划一样,其工作的时差也有总时差和自由时差两种。
(1)工作的总时差搭接网络计划中工作的总时差可以利用公式(3—30)和公式(3—31)计算。
单代号搭接网络计划时间参数计算(精)
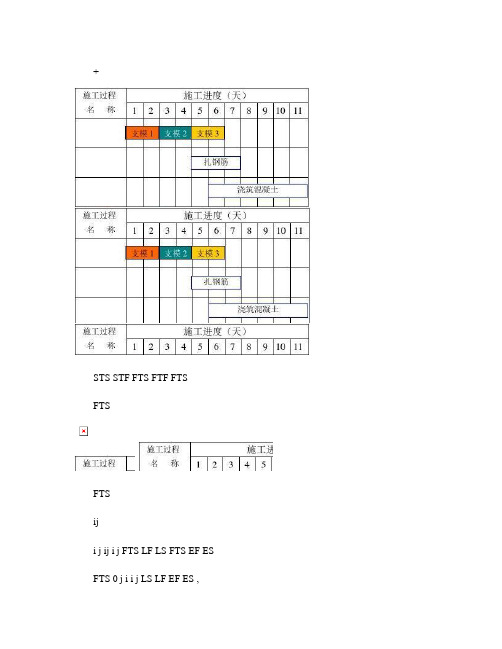
+STS STF FTS FTF FTSFTSFTSiji j ij i j FTS LF LS FTS EF ES FTS 0 j i i j LS LF EF ES ,STSSTS , i STS jSTSiji j ij i j STS LS LS STS ES ES STSFTFFTF , i FTF jFTFiji j ij i j FTF LF LF FTF EF EFSTFSTF i STF jSTFiji j ij i j STF LS LF STF ES EFSTS FTFj ESj EFSTSij i j ij i j STS LS LS STS ES ESFTF iji j ij i j FTF LF LF FTF EF EFi j STS=4 FTF=2j ES j EFSTS1284440 j j j ij i j D ES EF STS ES ESFTF1081818216 j j j ij i j D EF ES FTF EF EF 10 j ES 18 j EF 311 A101000 A A EF ES2 B25151010010 B AB A B EF FTS EF ES8 d3 D7221515510D AD A D ES FTF EF EFD0 STS222200 D D EF ES4 C21622515510660 c BC B C BC B C AC A C D FTF EF ES STS ES ES STS ES ES 2762121 C C EF ES5 F15202510110 F BF B F DF D F D STF ES ES STS ES ES35201515 F F EF ES0 FTF6 G3302051524321 DG D G FC F G CG C G STS ES ES STS ES ES STS ES ES34102424 G G EF ESE G 34 G EF , E F 35 F EF , 35 F E1 F G LFG LFF2 D 35 35 , , LS G LS F 35 10 25 35 20 15 LS D LS D LS F STS DF LS G STS DG 15 1 14 253 22 LS D 14 LFD D D E LS D DD 14 22 36 LFD 35 LFD DD 35 22 13 LFD LS D 3 C LS C LFC 4 B LS G STS CG LS C DC 25 3 22 226 28 LS B LS B LS B LS B LFB 5 A LFF STF BF LS C STS BC 35 25 10 22 5 17 28 2 15 11 LFC FTF BC D B 10 LS B LS B LS C LFD 0 LS A DA DB 10 15 25 D A 10 0 10 0 22 6 16 DA 35 5 10 20 LS A LS A LS A LS A LFA FTS AB STS AC FTFAD 0 10 10 LAGLAGij LAGij 1 FTS i EFi ESj LAGij j i ESj LAGij 2 STS ES j ( EFi FTS ij ESi FTSij LAGij 3 FTF ES j ( ES i STS ij j STSij LAGij EFi i FTSij LAGij LAGij 4 STF EF j ( EFi FTFij j j EFi FTSij i j LAGij EFj LAGij EF j ( ES i STFij EFj j LAGij 5 ES j LAGij min ES j EFj EFj LAGGE LAGFG LAGBF LAG AC LAG AD 35 34 1 , EFi ESi ES i EFi FTS ij STS ij STFij FTFij LAGij LAGFE 35 35 0 , LAGDE 24 0 3 21 , 15 0 1 14 35 22 13 LAGCG 24 21 3 0 24 15 5 4 , 35 10 25 0 , 21 0 6 15 , 22 10 5 7 LAGDG LAGDF LAGBC min( 21 10 5 6;27 25 2 0 0 12 LAGi-j LAGi-j D LAGi-j LAGDG FFD min LAGDF LAGDE 21 14 13 13 LAGi-j 0 STS=6 LAG=15 6 15 21 1 12 21 27 0 S A B F E C 6 22 0 28 STS=3 LAG=0 ESi TF EFi i Di LSi 15 0 35 24 STS=5 FTF=2 0 0 0 0 0 10 10 0 25 LAG=0 STF=25 LAG=0 25 15 h LF i 35 0 35 S 0 0 0 0 LAG=0 A 10 0 0 10 FTS=0 LAG=0 10 B 15 0 F 20 0 STS=5 LAG=4 35 25 1 34 G 10 1 LAG=1 35 35 E 0 0 35 STS=1 0 13 LAG=14 FTF=0 LAG=022 FTF=5 LAG=7 LAG=0 STS=0 2 LAG=21 STS=3 LAG=13 FTF=0 D 22 13 35 13 0B 8 8 FTF=10 3 E 15 18 STF=6 FTS=3 STS=3 FTF=2 S 0 0 A 5 5 11 D 12 23 14 15 7 G10 24 25 17 T 0 STS=7 7 STF=10 C 10 17 FTF=15 7 F 25 320 LAG=0 STF=6 LAG=2 0 0 5 LAG=0 0 0 A 5 0 5 STS=7 LAG=0 7 4 B 8 8FTF=10 12 LAG=0 3 4 E 15 18 ESi TF EFi i Di 22 LAG=0 4 G 10 28 LAG=4 32 0 T 0 32 0 32 32 LSi FFi LFi 4 0 0 0 S 0 0 FTS=3 LAG=0 11 7 23 D 12 18 3 30 7 0 STS=3 18 FTF=2 LAG=3 LAG=6 0 0 0 C 10 17 FTF=15 LAG=0 17 7 0 F 25 22 4 32 STF=10 LAG=11 32 LAG=0 32 7 0 7 0。
单代号搭接网络计划

(a)混合搭接关系
(b)网络计划中的表达方式
图5-36 STS和FTF混合搭接关系及其在网络计划中的表达方式
(a)混合搭接关系
(b)网络计划中的表达方式
图5-37 STF和FTS混合搭接关系及其在网络计划中的表达方式
2.单代号搭接网络计划时间参数的计算 1)工作最早开始时间和最早完成时间
凡与起点节点i相连的工作,其最早开始时间都应为零,即
(a)从横道图看STF时距
(b)用单代号搭接网络计划方法表示
图5-35 时距STF的表示方法
5)混合时距的搭接方法
在搭接网络计划中,相邻两项工作之间有时还会同时出现两种以上的 基本搭接关系。例如,工作i和j之间可能同时存在STS时距和FTF时距,或 同时存在STF时距和FTS时距等,如图5-36和图5-37所示。
3)开始到开始(STS)
从开始到开始的搭接关系如图5-34(a)所示,这种搭接关 系在网络计划的表示方法如图5-34(b)所示。
(a)从横道图看STS时距
(b)用单代号搭接网络计划方法表示
图5-34 时距STS的表示方法
4)开始到完成(STF)
从开始到完成的搭接关系如图5-35(a)所示,这种搭接关 系在网络计划的表示方法如图5-35(b)所示。
2)相邻两项工作之间的时间间隔
① 相邻时距为 STS i, j时, LAGi,j ES j ESi STSi,j
(5-33)
② 相邻时距为 FTF i, j时, LAGi,j EFj EFi FTFi,j
(5-34)
③ 相邻时距为 FTF i, j时, LAGi,j EFj ESi STFi,j
(5-39)
其他工作 i 的自由时差等于本工作与其紧后工作之间时间 间隔的最小值,即
(一)单代号搭接网络时间参数的计算与关键线路的确定

(一)单代号搭接网络时间参数的计算与关键线路的确定一、上机目的:1、理解、掌握单代号搭接网络在计算机中的存贮方法;2、掌握计算单代号搭接网络时间参数的算法思想;3、学会编制与调试较复杂的应用程序。
二、上机内容与步骤:长永高速公路第九标段某装配式砼板桥网络图其中:D1=0;D2=17;D3=18;D4=1;D5=3;D6=4;D7=1;D8=3;D9=2;D10=2;D11=18;D12=17;D13=28;D14=2;D15=3;D16=0。
网络图另给上机步骤:1、建立工作关系数据(D1KN.DBF)、工作资源消耗数据库(D2KN.DBF)及工作时间参数输出结果数据库文件(D3KN.DBF);2、编制最早开始时间与最早完成时间计算程序;3、编制最迟开始时间与最迟完成时间计算程序;4、编制确定关键线路的程序。
三、上机要求:1、认真复习工程进度管理相关知识;2、在理解网络图的存贮方法及时间参数计算的算法思想的前提下编制好程序步骤,准备好数据;3、按步骤建立数据库、输入程序、调试通过并与手算结果比较,直至得到正确结果;最早开始与最早结束时间的计算算法步骤:step1:输入已建立的相关数据库文件名称(D1KN、D2KN、D3KN);step2:为每个数据库开辟工作区;step3:输入开始工作的最早开始时间,并存入变量ES中;step4:第一个节点,最早开始时间=最早结束时间=ES;step5:令N1=2;step6:对于第N1个节点,判断N1是否超过终节点号?是,则转step12;否,则从D2KN 中提取节点N1的持续时间,存入变量D2中;step7:使D1KN数据库的记录指针指向其首记录;step8:判断D1KN的记录指针是否指向其结束标志?是,则转step10;否,再判断当前记录的终点号是否等于N1?否,则转step9;是,则找到N1的紧前节点,并从D3KN中提取N1的紧前节点的最早开始时间和最早结束时间,存于ES、EF中,计算ES3=max{ES+STS,EF+FTS},并将ES3与前一次计算的结果相比较,大者存入ES4中;step9:下移D1KN库中的记录指针,转step8;step10:N1号节点的最早开始时间ES=ES4,而最早结束时间EF=ES+D2,将ES、EF的值存入D3KN数据库中N1节点对应的“最早开始”、“最早结束”字段中;step11:N1加1(处理下一个节点),转step6;step12:结束。
单代号搭接网络计划的时间参数计算

单代号搭接网络计划的时间参数计算单代号搭接网络计划的时间参数计算摘要:在项目管理的实施过程中,网络计划的各工作之间往往受到工艺、组织等因素的限制,影响网络计划工期。
将这些限制条件如实地反映在单代号网络图中,就产生了单代号搭接网络计划。
本文介绍了单代号搭接网络图的时间参数、归纳了时间参数计算的全过程,指导单代号搭接网络计划在实际项目管理中的应用。
关键词:单代号搭接计划计算参数一、单代号搭接网络图的应用意义流水施工中各工作前后衔接,这样可以保证整个施工段都空闲下来,为后续工作提供工作面。
显而易见,这种只能等待施工段完全空闲下来后,后续工作才投入工作的方式,不能保证工期最短。
而在实际工作中,往往很多工作都是平行搭接的,即前专业队在某施工段作业一定时间后,如果已给后续工作可以投入工作的足够工作面,那么后续施工过程作业队就可投入工作,这样前后施工过程的施工段是搭接关系,两施工过程平行施工,可以缩短工期。
在单代号网络图中,将上述提到的各工作平行搭接关系也表达在网络图上,所形成的网络图即为单代号搭接网络图。
比起横道图、双代号即单代号网络图,这种网络计划表达最为简化。
实质上,搭接关系的存在起到限制各工作何时开始和何时结束的作用,在网络上这种关系一目了然。
二、单代号搭接网络图的搭接关系单代号搭接网络图与单代号网络图的基本构成方式完全相同。
网络图由节点和箭线构成,节点表示工作,箭线反映前后工作的逻辑关系,网络图上的线路用该线路上的节点编号从小到大依次表示。
与单代号网络图不同的是单代号搭接网络计划图中,增加了各工作间的搭接关系:1.以开始时间为时距原点(1)紧前工作的开始时间到紧后工作的开始时间的时间距离,用STSi,j表示,如图(a)。
这种搭接关系强调了紧前工作开始一段时间后,后续工作就可以开始进行了。
这是因为特定的施工活动完成到一定程度后,经过了STSi,j 时间,它已给后续工作投入施工提供了足够的工作面。
(2)紧前工作的开始时间到紧后工作的完成时间的时间距离,用STFi,j表示,如图(b)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
单代号搭接网络计划时间参数计算在一般的网络计划(单代号或双代号)中,工作之间的关系只能表示成依次衔接的关系,即任何一项工作都必须在它的紧前工作全部结束后才能开始,也就是必须按照施工工艺顺序和施工组织的先后顺序进行施工。
但是在实际施工过程中,有时为了缩短工期,许多工作需要采取平行搭接的方式进行。
对于这种情况,如果用双代号网络图来表示这种搭接关系,使用起来将非常不方便,需要增加很多工作数量和虚箭线。
不仅会增加绘图和计算的工作量,而且还会使图面复杂,不易看懂和控制。
例如,浇筑钢筋混凝土柱子施工作业之间的关系分别用横道图、双代号网络图和搭接网络图表示,如下图所示。
一.搭接关系的种类及表达方式单代号网络计划的搭接关系主要是通过两项工作之间的时距来表示的,时距的含义,表示时间的重叠和间歇,时距的产生和大小取决于工艺的要求和施工组织上的需要。
用以表示搭接关系的时距有五种,分别是STS (开始到开始)、STF (开始到结束)、FTS (结束到开始)、FTF (结束到结束)和混合搭接关系。
(一)FTS (结束到开始)关系结束到开始关系是通过前项工作结束到后项工作开始之间的时距(FTS )来表达的。
如下图所示。
FTS 搭接关系的时间参数计算式为:iji j ij i j FTS LF LS FTS EF ES +=+=当FTS =0时,则表示两项工作之间没有时距,j i i j LS LF EF ES ==,,即为普通网络图中的逻辑关系。
又如混凝土沉箱码头工程,沉箱在岸上预制后,要求静置一段养护存放的时间,然后才可下水沉放。
(二)STS (开始到开始)关系开始到开始关系是通过前项工作开始到后项工作开始之间的时距(STS )来表达的,表示在i 工作开始经过一个规定的时距(STS )后,j 工作才能开始进行。
STS 搭接关系的时间参数计算式为:iji j ij i j STS LS LS STS ES ES +=+=如道路工程中的铺设路基和浇筑路面,当路基工作开始一定时间且为路面工作创造一定条件后,路面工程才可以开始进行。
铺路基与浇路面之间的搭接关系就是STS (开始到开始)关系。
(三)FTF (结束到结束)关系结束到结束关系是通过前项工作结束到后项工作结束之间的时距(FTF )来表达的, 表示在i 工作结束(FTF )后,j 工作才可结束。
iji j ij i j FTF LF LF FTF EF EF +=+=如,基坑排水工作结束一定时间后,浇注砼工作才能结束。
(四)STF (开始到结束)关系开始到结束关系是通过前项工作开始到后项工作结束之间的时距(STF )来表达的,它表示i 工作开始一段时间(STF )后,j 工作才可结束。
STF 搭接关系的时间参数计算式为:iji j ij i j STF LS LF STF ES EF +=+=如,当基坑开挖工作进行到一定时间后,就应开始进行降低地下水的工作,一直进行到地下水水位降到设计位置。
(五)混合搭接关系混合搭接关系是指两项工作之间的相互关系是通过前项工作的开始到后项工作开始(STS )和前项工作结束到后项工作结束(FTF )双重时距来控制的。
即两项工作的开始时间必须保持一定的时距要求,而且两者结束时间也必须保持一定的时距要求。
混合搭接关系中的j ES 和j EF 应分别计算,然后在选取其中最大者。
挖槽10 d 降低地下水5 d按STS 关系:ij i j ij i j STS LS LS STS ES ES +=+=按FTF 关系: iji j ij i j FTF LF LF FTF EF EF +=+=如,某修筑道路工程,工作i 是修筑路肩,工作j 是修筑路面层,在组织这两项工作时,要求路肩工作至少开始一定时距STS=4以后,才能开始修筑路面层;而且面层工作不允许在路肩工作完成之前结束,必须延后于路肩完成一个时距FTF=2才能结束。
问路面工作的j ES 和j EF 。
按STS 关系:1284440=+=+==+=+=j j j ij i j D ES EF STS ES ES按FTF 关系:1081818216=-=-==+=+=j j j ij i j D EF ES FTF EF EF故要同时满足上述两者关系,必须选择其中的最大值,即10=j ES 和18=j EF 。
注:对于混合搭接关系,由于工作之间的制约关系,可能会出现工作不能连续工作,这时,要按间断型算法来计算(详见例题3)。
三.搭接网络计划时间参数的计算单代号搭接网络计划的时间参数的计算与前述原理基本相同,现以算例说明。
例1.已知某工程搭接网络计划如上图所示,试计算其时间参数。
(一)工作最早时间计算工作最早时间应从虚拟的起点节点开始,沿箭线方向自左向右,参照已知的时距关系,选用相应的搭接关系计算式计算。
(1)工作A101000=+==A A EF ES(2)工作B25151010010=+==+=+=B AB A B EF FTS EF ES(3)工作D7221515510-=-==+=+=D AD A D ES FTF EF EF显然,最早时间出现负值是不合理的,应将工作D 与虚拟起点节点相连,则注:在计算工作最早时,如果出现某工作最早开始时间为负值(不合理),应将该工作与起点节点用虚箭线相连接,并确定其时距为0=STS 。
222200=+==D D EF ES(4)工作C21622515510660=-+=-+==+=+==+=+=c BC B C BC B C AC A C D FTF EF ES STS ES ES STS ES ES在上式中,取最大者,则2762121=+==C C EF ES(5)工作F15202510110=-+=-+==+=+=F BF B F DF D F D STF ES ES STS ES ES在上式中,取最大者,则35201515=+==F F EF ES注:在计算工作最早时,如果出现有工作最早完成时间为最大值的中间节点,则应将该节点的最早完成时间作为网络计划的结束时间,并将该节点与结束节点用虚箭线相连接,并确定其时距为0=FTF 。
(6)工作G3302051524321=+=+==+=+==+=+=DG D G FC F G CG C G STS ES ES STS ES ES STS ES ES 在上式中,取最大者,则34102424=+==G G EF ES(二)总工期的确定应取各项工作的最早完成时间的最大值作为总工期,从上面计算结果可以看出,与虚拟终点节点E 相连的工作G 的34=G EF ,而不与E 相连的工作F 的35=F EF ,显然,总工期应取35,所以,应将F 与E 用虚箭线相连,形成工期控制通路。
(三)工作最迟时间的计算以总工期为最后时间限制,自虚拟终点节点开始,逆箭线方向由右向左,参照已知的时距关系,选择相应计算关系计算。
(1)工作F 和G 。
与虚拟终节点相连的工作的最迟结束时间就是总工期值。
152035,35251035,35=-===-==F F G G LS LF LS LF (2)工作D2232514115=-=-==-=-=DG G D DF F D STS LS LS STS LS LS在上式中,取最小者,则36221414=+=+==D D D D D LS LF LS由于工作D 的最迟结束时间大于总工期,显然是不合理的,所以,D LF 应取总工期的值,并将D 点与终节点E 用虚箭线相连,即13223535=-=-==D D D D D LF LS LF(3)工作C2862222325=+=+==-=-=C C C CG G C D LS LF STS LS LS(4)工作B111522817522102535=--=--==-=-==-=-=B BC C B BC C B BF F B D FTF LF LS STS LS LS STF LF LS在上式中,取最小者,则25151010=+=+==B B B B D LS LF LS(5)工作A201053516622010010=--=--==-=-==--=--=A AD D A AC C A A AB B A D FTF LF LS STS LS LS D FTS LS LS在上式中,取最小者,则101000=+=+==A A A A D LS LF LS(四)间隔时间LAG 的计算在搭接网络计划中,相邻两项工作之间的搭接关系除了要满足时距要求之外,还有一段多余的空闲时间,称之为间隔时间,通常用LAG ij 表示。
由于各个工作之间的搭接关系不同,LAG ij 必须要根据相应的搭接关系和不同的时距来计算。
(1)FTS (结束到开始)关系 )(ij i j ij FTS EF ES LAG +-=(2)STS (开始到开始)关系)(ij i j ij STS ES ES LAG +-=(3)FTF (结束到结束)关系)(ij i j ij FTF EF EF LAG +-=(4)STF (开始到结束)关系)(ij i j ij STF ES EF LAG +-=(5)混合搭接关系当相邻两工序之间是由两种时距以上的关系连接时,则应分别计算出其LAG ij ,然后取其中的最小值。
⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧--------=ij i j ij i j ij i jij i j ij FTF EF EF STF ES EF STS ES ES FTS EF ES LAG min在该例中,各工作之间的时间间隔LAG ij 为:7510220)022527;651021min(,156021141015,0251035032124,213024,451524132235,03535,13435=--===--=--==--==--==--==--==--==--==-==-==-=AD BC AC DF BF CG DG FG DE FE GE LAG LAG LAG LAG LAG LAG LAG LAG LAG LAG LAG(五)计算工作时差(1)工作总时差即为最迟开始时间与最早开始时间之差,或最迟结束时间与最早结束时间之差。
EF ijESiES jEFjEF j(2)工作自由时差如果一项工作只有一项紧后工作,则该工作与紧后工作之间的LAG i-j 即为该工作的自由时差;如果一项工作有多项紧后工作,则该工作的自由时差为其与紧后工作之间的LAG i-j 的最小值。
如该例中,工作D 之后有三个LAG i-j ,则13131421min =⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧====DE DF DG D LAG LAG LAG FF(六)关键线路判别单代号搭接网络计划的关键线路为自起点节点到终点节点总时差为0的节点及其间的LAG i-j 为0的通路连接起来形成的路线。
