自动控制原理及其应用(第二版)答案-黄坚.
《自动控制原理》黄坚课后习题答案解析

2-1试建立图所示电路的动态微分方程-u o+u o解:u 1=u i -u oi 2=C du 1dt i 1=i-i 2u o i=R 2u 1i 1=R 1=u i -u oR1dtd (u i -u o )=C(a)u C d (u i -u o )dtu o -R 2=i -u o R 1i=i 1+i 2i 2=C du 1dt u o i 1=R 2u 1-u o =L R2du odtR 1i=(u i -u 1)(b)解:du )-R 2(u i -u o )=R 1u 0-CR 1R 2(idt dt du oCR 1R 2du o dt du idt +R 1u o +R 2u 0=CR 1R 2+R 2u iu o+C R 2du 1dt o +L R 2du odtu du o dt R 1R 2L du o dt +CL R 2d 2u o dt 2=--i R 1u o R 1u oR 2+C )u o R 1R 2L du o dt ) CL R 2d 2u o dt 2=++(u i R 11R 11R 2+(C+2-2 求下列函数的拉氏变换。
(1) f(t)=sin4t+cos4tL [sin ωt ]= ωω2+s 2=s+4s 2+16L [sin4t+cos4t ]= 4s 2+16s s 2+16+s ω2+s 2L [cos ωt ]=解:解:L [t 3+e 4t ]= 3!s 41s-4+6s+24+s 4s 4(s+4)=(3) f(t)=t n e atL [t n e at ]=n!(s-a)n+1解:(4) f(t)=(t-1)2e 2tL [(t-1)2e 2t ]=e -(s-2)2(s-2)3解:2-3求下列函数的拉氏反变换。
A 1=(s+2)s+1(s+2)(s+3)s=-2=-1=2f(t)=2e -3t -e -2t(1) F(s)=s+1(s+2)(s+3)解:A 2=(s+3)s+1(s+2)(s+3)s=-3F(s)= 2s+31s+2-= A 1s+2s+3+ A 2(2) F(s)=s (s+1)2(s+2)f(t)=-2e -2t -te -t +2e -t解:= A 2s+1s+2+A 3+ A 1(s+1)2A 1=(s+1)2s (s+1)2(s+2)s=-1A 3=(s+2)s (s+1)2(s+2)s=-2d ds ss+2][A 2= s=-1=-1=2=-2(3) F(s)=2s 2-5s+1s(s 2+1)F(s)(s 2+1)s=+j =A 1s+A 2s=+jA 2=-5A 3=F(s)s s=0f(t)=1+cost-5sint解:= s + A 3s 2+1A 1s+A 2=12s s 2-5s+1=A 1s+A2 s=j s=jj -2-5j+1=jA 1+A 2-5j-1=-A 1+jA 2A 1=1F(s)= 1s s 2+1s -5s 2+1++解:=+s+1A 1s+3A 2(s+1)2+s A 3+A 4-12A 1= 23A 3= 112A 4= A 2= d [s=-1ds ](s+2)s(s+3) -34= -34A 2= +-43+f(t)=e -t 32e -3t 2-t e -t 121= s=-1 [s(s+3)]2[s(s+3)-(s+2)(2s+3)](2-4)求解下列微分方程。
自动控制原理 黄坚 第二版 课后答案第五章

5-1设单位负反馈系统的开环传递函数110)(+=s s G ,当把下列输入信号作用在闭环系统输入端时,试求系统的稳态输出。
(1))30sin()( +=t t r (2) )452cos(2)( -=t t r(s+1)1解: (s+11)1 )A ω 112+()2 1ω √ =0.905 = 112+1 1√ = 122 1√ =-5.2o φ ( ω ) ω 11 =-tg -1 1 11=-tg -1 c s (t)=0.9sin(t+24.8o) (1)计算的最后结果: (1))83.24sin(905.0)(+=t t c ; (2))3.532cos(785.1)(-=t t c ;5-2设控制系统的开环传递函数如下,试绘制各系统的开环幅相频率特性曲线和开环对数频率特性曲线。
(1))15)(5(750)(++=s s s s G (2))1110)(1(200)(2++=s s s s G(3))18)(12(10)(++=s s s G (4))1008()1(1000)(2+++=s s s s s G (5))1(10)(-=s s s G (6)13110)(++=s s s G(7))15)(1.0()2.0(10)(2+++=s s s s s G (8)13110)(+-=s s s G绘制各系统的开环幅相频率特性曲线:s(s+5)(s+15)(1) G(s)=750解:n-m=3I 型系统ω=0A()=∞ωφ-90o (ω)=-270o φ(ω)=0)=A(ω(2s+1)(8s+1)(3) G(s)=10解:n-m=20型系统ω=0)=10 A(ω-180φ)=-180o (ω)=0A()=ω0)=0o φ(ω)=s(s-1)(5) G(s)=10解:n-m=2I 型系统ω=0ω=∞)=∞A(ω-270)=-270o φ(ω)=-180φ)=-180o (ω)=0A()=ω10(s+0.2)s 2(s+0.1)(s+15)(7) G(s)=解:n-m=3II 型系统ω=0ω=∞)=∞A(ω-180o φ(ω)=-270oφ(ω)=0A()= ωω绘制各系统的开环对数频率特性曲线:s(s+5)(s+15)(1) G(s)=750解:s(G(s)=1051s+1)s+1)(151ω1=5ω2=15低频段曲线:20lgK=20dBω=0ω=∞-90)=-90o φ(ω)=-270)=-270o φ(ω)=相频特性曲线:(2s+1)(8s+1)(3) G(s)=10解:低频段曲线:20lgK=20dB ω1=0.125ω2=0.5相频特性曲线:ω=0ω=∞0)=0o φ(ω)=-180)=-180o φ(ω)=s(s-1)(5) G(s)=10解:低频段曲线:20lgK=20dB ω1=1ω=0ω=∞-270oφ(ω)=-180)=-180oφ(ω)=相频特性曲线:5-3已知电路如图所示,设R 1=19k Ω,R 2=1 k Ω,C=10μF 。
自动控制原理及其应用(第2版)黄坚第二章习题课

第二章习题课
(2-9)
2-9 若系统在单位阶跃输入作用时,已知初 若系统在单位阶跃输入作用时, 始条件为零的条件下系统的输出响应, 始条件为零的条件下系统的输出响应,求 系统的传递函数和脉冲响应。 系统的传递函数和脉冲响应。 -t 1 -2t R(s)= s c(t)=1-e +e r(t)=I(t) 1 - 1 + 1 = (s2+4s+2) 解: C(s)= s s+2 s+1 s(s+1)(s+2) (s2+4s+2) G(s)=C(s)/R(s)= (s+1)(s+2) (s2+4s+2) =1+ 2 - 1 脉冲响应: 脉冲响应 C(s)= (s+1)(s+2) s+2 s+1 c(t)= (t)+2e-2t-e-t δ
第二章习题课
(2) dy(t) 2 dt +y(t)=t
(2-4)
y(0)=0
第二章习题课
(2-5)
2-5 试画题图所示电路的动态结构图, 试画题图所示电路的动态结构图, c 并求传递函数。 并求传递函数。 i1 (1) 解: + R
Ur(s)
Cs _
I1(s)
+ +
i2
1
+
I(s)
R2
Uc(s)
+ i uo -
第二章习题课
(b) 解: (ui-u1) i=i1+i2 i= R
1
(2-1)
u1 L i
R1 C
+
ui
i1 i2
R2
+ uo -
自动控制原理黄坚 第二版 第三章习题答案

第三章习题课 (3-13)
3-13 已知系统结构如图,试确定系统稳 定时τ值范围。 R(s) 10 C(s) 1 解: 10(1+ 1 ) s G(s)=s2+s+10 s τ 10(s+1) =s(s2+s+10 s) τ 10(s+1) Φ(s)= s3 +s2+10 s2+10s+10 τ 10(1+10 )-10 τ b31= 1+10 >0 τ
e
-1.8
第三章习题课 (3-6)
3-6 已知系统的单位阶跃响应: -60t -10t c(t)=1+0.2e -1.2e (1) 求系统的闭环传递函数。 (2) 求系统的阻尼比和无阻尼振荡频率。 1 + 0.2 - 1.2 = 600 解: C(s)= s s+60 s+10 s(s+60)(s+10) 1 C(s)= 600 R(s)= s R(s) s2+70s+600 ω n=24.5 ζ 2 ω n=70 ω n2 =600 ζ=1.43
第三章习题课 (3-17)
1 r(t)=I(t), t , 2 t2 (2) 求系统的稳态误差: 1 K1 τ = 1 G(s)= 2 解: s +Kτ s s( 1 Kτ s+1)
1
1 R(s)= s υ=1
Kp=∞ K =K υ
ess1=0 τ ess2= =0.24 ess3=∞
R(s)= s1 2 R(s)= s1 3
(3) 求d1(t)作用下的稳态误差. 1 K F(s)= Js G(s)=Kp + s -F(s) 1 essd= lim s1+G(s)F(s) s s→0 - 1 1 =0 Js = lim s K) 1 s s→0 1+(Kp+ s Js
《自动控制原理》黄坚课后习题答案教学提纲

《自动控制原理》黄坚课后习题答案2-1试建立图所示电路的动态微分方程u o+u o解:u 1=u i -u oi 2=C du 1dt i 1=i-i 2u o i=R 2u 1i 1=R 1=u i -u oR1dtd (u i -u o )=C(a)u C d (u i -u o )dtu o -R 2=i -u o R 1i=i 1+i 2i 2=C du 1dt u o i 1=R 2u 1-u o =L R2du odtR 1i=(u i -u 1)(b)解:)-R 2(u i -u o )=R 1u 0-CR 1R 2(du idt dt duo CR 1R 2du o dt du idt +R 1u o +R 2u 0=CR 1R 2+R 2u iu o+C R 2du 1dt o +L R 2du odtu du o dt R 1R 2L du o dt +CL R 2d 2u o dt 2=--i R 1u o R 1u oR 2+C )u o R 1R 2L du o dt ) CL R 2d 2u o dt 2=++(u i R 11R 11R 2+(C+2-2 求下列函数的拉氏变换。
(1) f(t)=sin4t+cos4tL [sin ωt ]= ωω2+s 2=s+4s 2+16L [sin4t+cos4t ]= 4s 2+16s s 2+16+s ω2+s 2L [cos ωt ]=解:(2) f(t)=t 3+e 4t解:L [t 3+e 4t ]= 3!s 41s-4+6s+24+s 4s 4(s+4)=(3) f(t)=t n e atL [t n e at ]=n!(s-a)n+1解:(4) f(t)=(t-1)2e 2tL [(t-1)2e 2t ]=e -(s-2)2(s-2)3解:2-3求下列函数的拉氏反变换。
A 1=(s+2)s+1(s+2)(s+3)s=-2=-1=2f(t)=2e -3t -e -2t(1) F(s)=s+1(s+2)(s+3)解:A 2=(s+3)s+1(s+2)(s+3)s=-3F(s)= 2s+31s+2-= A 1s+2s+3+ A 2(2) F(s)=s (s+1)2(s+2)f(t)=-2e -2t -te -t +2e -t解:= A 2s+1s+2+ A 3+A 1(s+1)2A 1=(s+1)2s (s+1)2(s+2)s=-1A 3=(s+2)s (s+1)2(s+2)s=-2d ds ss+2][A 2= s=-1=-1=2=-2(3) F(s)=2s 2-5s+1s(s 2+1)F(s)(s 2+1)s=+j =A 1s+A 2s=+jA 2=-5A 3=F(s)s s=0f(t)=1+cost-5sint解:= s + A 3s 2+1A 1s+A 2=12s s 2-5s+1=A 1s+A2 s=j s=jj -2-5j+1=jA 1+A 2-5j-1=-A 1+jA 2A 1=1F(s)= 1s s 2+1s -5s 2+1++(4) F(s)=s+2s(s+1)2(s+3)解:=+s+1A 1s+3A 2(s+1)2+s A 3+A 4-12A 1= 23A 3= 112A 4= A 2= d [s=-1ds ](s+2)s(s+3) -34= -34A 2= +-43+f(t)=e -t 32e -3t 2-t e -t 121= s=-1 [s(s+3)]2[s(s+3)-(s+2)(2s+3)](2-4)求解下列微分方程。
《自动控制原理》黄坚课后习题答案

2-1试建立图所示电路的动态微分方程-u o+u o解:u 1=u i -u oi 2=C du 1dt i 1=i-i 2u o i=R 2u 1i 1=R 1=u i -u oR1dtd (u i -u o )=C(a)u C d (u i -u o )dtu o -R 2=i -u o R 1i=i 1+i 2i 2=C du 1dt u o i 1=R 2u 1-u o =L R2du odtR 1i=(u i -u 1)(b)解:)-R 2(u i -u o )=R 1u 0-CR 1R 2(dui dt dt duo CR 1R 2du o dt du idt +R 1u o +R 2u 0=CR 1R 2+R 2u iu o+C R 2du 1dt o +L R 2du odtu du o dt R 1R 2L du o dt +CL R 2d 2u o dt 2=--i R 1u o R 1u oR 2+C )u o R 1R 2L du o dt ) CL R 2d 2u o dt 2=++(u i R 11R 11R 2+(C+2-2 求下列函数的拉氏变换。
(1) f(t)=sin4t+cos4tL [sin ωt ]= ωω2+s 2=s+4s 2+16L [sin4t+cos4t ]= 4s 2+16s s 2+16+s ω2+s 2L [cos ωt ]=解:(2) f(t)=t 3+e 4t解:L [t 3+e 4t ]= 3!s 41s-4+6s+24+s 4s 4(s+4)=(3) f(t)=t n e atL [t n e at ]=n!(s-a)n+1解:(4) f(t)=(t-1)2e 2tL [(t-1)2e 2t ]=e -(s-2)2(s-2)3解:2-3求下列函数的拉氏反变换。
A 1=(s+2)s+1(s+2)(s+3)s=-2=-1=2f(t)=2e -3t -e -2t(1) F(s)=s+1(s+2)(s+3)解:A 2=(s+3)s+1(s+2)(s+3)s=-3F(s)= 2s+31s+2-= A 1s+2s+3+ A 2(2) F(s)=s (s+1)2(s+2)f(t)=-2e -2t -te -t +2e -t解:= A 2s+1s+2+ A 3+A 1(s+1)2A 1=(s+1)2s (s+1)2(s+2)s=-1A 3=(s+2)s (s+1)2(s+2)s=-2d ds ss+2][A 2= s=-1=-1=2=-2(3) F(s)=2s 2-5s+1s(s 2+1)F(s)(s 2+1)s=+j =A 1s+A 2s=+jA 2=-5A 3=F(s)s s=0f(t)=1+cost-5sint解:= s + A 3s 2+1A 1s+A 2=12s s 2-5s+1=A 1s+A2 s=j s=jj -2-5j+1=jA 1+A 2-5j-1=-A 1+jA 2A 1=1F(s)= 1s s 2+1s -5s 2+1++(4) F(s)=s+2s(s+1)2(s+3)解:=+s+1A 1s+3A 2(s+1)2+s A 3+A 4-12A 1= 23A 3= 112A 4= A 2= d [s=-1ds ](s+2)s(s+3) -34= -34A 2= +-43+f(t)=e -t 32e -3t 2-t e -t 121= s=-1 [s(s+3)]2[s(s+3)-(s+2)(2s+3)](2-4)求解下列微分方程。
自动控制原理及其应用第二版课后答案

自动控制原理及其应用第二版课后答案【篇一:《自动控制原理》黄坚课后习题答案】ss=txt>uo-u+o(a)解:i1=i-i2u1=ui-uouuu-ui=i1==211dud(u-u)i2=c=c(b)解:(u-u)i=i1+i2i=udui1=i2=c2duu1-uo=21u-uud(u-u)-c=12dudur2(ui-uo )=r1u0-cr1r2(-)duducr1r2+r1uo+r2u0=cr1r2+r2uidud2uuuduu--21112=2+cud2udu+(c+=12+(1+2)uo12duu+c2duo+22-2 求下列函数的拉氏变换。
(1) f(t)=sin4t+cos4t(2) f(t)=t3+e4t434t解:l[t+e](3) f(t)=tneat解:l[tneat]=(4) f(t)=(t-1)2e2t解:l[(t-1)2e2t]=e-(s-2)2-3求下列函数的拉氏反变换。
(1) f(s)=aa解:a1=(s+2)=-1a2=2 -f(t)=2e-3t-e-2t(2) f(s)=aaa解:a1=(s+1)=-1a2[=2a3s=-2=-2f(t)=-2e-2t-te-t+2e-t(3) f(s)=2as+aa解:f(s)(s2=a1s+a2j=a1s+aj-2-5j+1=ja1+a2-5j-1=-a1+ja2a1=1a2=-5a3=f(s)s=1++f(t)=1+cost-5sint(4) f(s)=解:=a+a+a+aa1a3a4a2ad[2]s=-1f(t)=e-t-e-t++e-3t(2-4)求解下列微分方程。
a2=5 a3=-4y(t)=1+5e-2t-4e-3t并求传递函数。
2-5试画题图所示电路的动态结构图,c+sc)r2r+rrscu(s)==c1+(+sc)r212121(2)cl1=-r2 /lsl2=-/lcs2l3=-1/scr1l1l3=r2/lcr1s2c112122-8 设有一个初始条件为零的系统,系统的输入、输出曲线如图,求g(s)。
《自动控制原理》黄坚课后习题答案

2-1试建立图所示电路的动态微分方程-u o+u o解:u 1=u i -u oi 2=C du 1dt i 1=i-i 2u o i=R 2u 1i 1=R 1=u i -u oR1dtd (u i -u o )=C(a)u C d (u i -u o )dtu o -R 2=i -u o R 1i=i 1+i 2i 2=C du 1dt u o i 1=R 2u 1-u o =L R2du odtR 1i=(u i -u 1)(b)解:)-R 2(u i -u o )=R 1u 0-CR 1R 2(dui dt dt duo CR 1R 2du o dt du idt +R 1u o +R 2u 0=CR 1R 2+R 2u iu o+C R 2du 1dt o +L R 2du odtu du o dt R 1R 2L du o dt +CL R 2d 2u o dt 2=--i R 1u o R 1u oR 2+C )u o R 1R 2L du o dt ) CL R 2d 2u o dt 2=++(u i R 11R 11R 2+(C+2-2 求下列函数的拉氏变换。
(1) f(t)=sin4t+cos4tL [sin ωt ]= ωω2+s 2=s+4s 2+16L [sin4t+cos4t ]= 4s 2+16s s 2+16+s ω2+s 2L [cos ωt ]=解:(2) f(t)=t 3+e 4t解:L [t 3+e 4t ]= 3!s 41s-4+6s+24+s 4s 4(s+4)=(3) f(t)=t n e atL [t n e at ]=n!(s-a)n+1解:(4) f(t)=(t-1)2e 2tL [(t-1)2e 2t ]=e -(s-2)2(s-2)3解:2-3求下列函数的拉氏反变换。
A 1=(s+2)s+1(s+2)(s+3)s=-2=-1=2f(t)=2e -3t -e -2t(1) F(s)=s+1(s+2)(s+3)解:A 2=(s+3)s+1(s+2)(s+3)s=-3F(s)= 2s+31s+2-= A 1s+2s+3+ A 2(2) F(s)=s (s+1)2(s+2)f(t)=-2e -2t -te -t +2e -t解:= A 2s+1s+2+ A 3+A 1(s+1)2A 1=(s+1)2s (s+1)2(s+2)s=-1A 3=(s+2)s (s+1)2(s+2)s=-2d ds ss+2][A 2= s=-1=-1=2=-2(3) F(s)=2s 2-5s+1s(s 2+1)F(s)(s 2+1)s=+j =A 1s+A 2s=+jA 2=-5A 3=F(s)s s=0f(t)=1+cost-5sint解:= s + A 3s 2+1A 1s+A 2=12s s 2-5s+1=A 1s+A2 s=j s=jj -2-5j+1=jA 1+A 2-5j-1=-A 1+jA 2A 1=1F(s)= 1s s 2+1s -5s 2+1++(4) F(s)=s+2s(s+1)2(s+3)解:=+s+1A 1s+3A 2(s+1)2+s A 3+A 4-12A 1= 23A 3= 112A 4= A 2= d [s=-1ds ](s+2)s(s+3) -34= -34A 2= +-43+f(t)=e -t 32e -3t 2-t e -t 121= s=-1 [s(s+3)]2[s(s+3)-(s+2)(2s+3)](2-4)求解下列微分方程。
《自动控制原理》黄坚课后习题答案解析

2-1试建立图所示电路的动态微分方程-u o+u o解:u 1=u i -u oi 2=C du 1dt i 1=i-i 2u o i=R 2u 1i 1=R 1=u i -u oR1dtd (u i -u o )=C(a)u C d (u i -u o )dtu o -R 2=i -u o R 1i=i 1+i 2i 2=C du 1dt u o i 1=R 2u 1-u o =L R2du odtR 1i=(u i -u 1)(b)解:)-R 2(u i -u o )=R 1u 0-CR 1R 2(du idt dt duo CR 1R 2du o dt du idt +R 1u o +R 2u 0=CR 1R 2+R 2u iu o+C R 2du 1dt o +L R 2du odtu du o dt R 1R 2L du o dt +CL R 2d 2u o dt 2=--i R 1u o R 1u oR 2+C )u o R 1R 2L du o dt ) CL R 2d 2u o dt 2=++(u i R 11R 11R 2+(C+2-2 求下列函数的拉氏变换。
(1) f(t)=sin4t+cos4tL [sin ωt ]= ωω2+s 2=s+4s 2+16L [sin4t+cos4t ]= 4s 2+16s s 2+16+s ω2+s 2L [cos ωt ]=解:(2) f(t)=t 3+e 4t解:L [t 3+e 4t ]= 3!s 41s-4+6s+24+s 4s 4(s+4)=(3) f(t)=t n e atL [t n e at ]=n!(s-a)n+1解:(4) f(t)=(t-1)2e 2tL [(t-1)2e 2t ]=e -(s-2)2(s-2)3解:2-3求下列函数的拉氏反变换。
A 1=(s+2)s+1(s+2)(s+3)s=-2=-1=2f(t)=2e -3t -e -2t(1) F(s)=s+1(s+2)(s+3)解:A 2=(s+3)s+1(s+2)(s+3)s=-3F(s)= 2s+31s+2-= A 1s+2s+3+ A 2(2) F(s)=s (s+1)2(s+2)f(t)=-2e -2t -te -t +2e -t解:= A 2s+1s+2+A 3+ A 1(s+1)2A 1=(s+1)2s (s+1)2(s+2)s=-1A 3=(s+2)s (s+1)2(s+2)s=-2d ds ss+2][A 2= s=-1=-1=2=-2(3) F(s)=2s 2-5s+1s(s 2+1)F(s)(s 2+1)s=+j =A 1s+A 2s=+jA 2=-5A 3=F(s)s s=0f(t)=1+cost-5sint解:= s + A 3s 2+1A 1s+A 2=12s s 2-5s+1=A 1s+A2 s=j s=jj -2-5j+1=jA 1+A 2-5j-1=-A 1+jA 2A 1=1F(s)= 1s s 2+1s -5s 2+1++(4) F(s)=s+2s(s+1)2(s+3)解:=+s+1A 1s+3A 2(s+1)2+s A 3+A 4-12A 1= 23A 3= 112A 4= A 2= d [s=-1ds ](s+2)s(s+3) -34= -34A 2= +-43+f(t)=e -t 32e -3t 2-t e -t 121= s=-1 [s(s+3)]2[s(s+3)-(s+2)(2s+3)](2-4)求解下列微分方程。
自动控制原理及其应用(第二版黄坚)课后习题答案
n
P2=G3G2 Δ2 =1
C(s) R(s)
=
Σk=1PkΔk
Δ
=1+GG22HG11++GG12GG23H2
第二章习题课 (2-11b)
2-11(b) 求系统的 传递函RC数(s()s)
R(s)
解:
G3(s) G3(s)
R=(sG_) 1G11+2+G+_GG4GH1 12GGGG112(3Hs+) G++G1G1G2GG42+(GH3sG)4(CsG4)(2Hs()s)
(s+1s)+22(s+3)est
+
s=0
s(ss++21)2est s=-3
+
lsim-1
d[
s(ss++23)est ds
]
=
2 3
+
1 12
e-3t+slim-1[
(-s(2s-24+s3-6)2)est+
(s+2)test s2+3s ]
(2-4-1) 求下列微分方程。
A2=(s+2)Y(s) s=-2 A3=(s+3)Y(s) s=-3
力所示,试采用复数阻抗法写出它们的传
递函数。
C
R2
R3
ui R1
-
∞ +
uo
+
R4
R5
UR1I==--UU(ROIR=4=2-++-RRR4(RR5+R1R)3+SR5R(2RR4CRRR5+325(2RU13R5R+SR1O33RC(5SSUR3+CC)O3R(+S+(RRR2CR1+-232)+2+RSR+1RRC3R3))32+R+S(3RR1C54R)4R+++315RRSR)C535U)+O1
《自动控制原理》黄坚课后习题答案解析

2-1试建立图所示电路的动态微分方程-u o+u o解:u 1=u i -u oi 2=C du 1dt i 1=i-i 2u o i=R 2u 1i 1=R 1=u i -u oR1dtd (u i -u o )=C(a)u C d (u i -u o )dtu o -R 2=i -u o R 1i=i 1+i 2i 2=C du 1dt u o i 1=R 2u 1-u o =L R2du odtR 1i=(u i -u 1)(b)解:du )-R 2(u i -u o )=R 1u 0-CR 1R 2(idt dt du oCR 1R 2du o dt du idt +R 1u o +R 2u 0=CR 1R 2+R 2u iu o+C R 2du 1dt o +L R 2du odtu du o dt R 1R 2L du o dt +CL R 2d 2u o dt 2=--i R 1u o R 1u oR 2+C )u o R 1R 2L du o dt ) CL R 2d 2u o dt 2=++(u i R 11R 11R 2+(C+2-2 求下列函数的拉氏变换。
(1) f(t)=sin4t+cos4tL [sin ωt ]= ωω2+s 2=s+4s 2+16L [sin4t+cos4t ]= 4s 2+16s s 2+16+s ω2+s 2L [cos ωt ]=解:解:L [t 3+e 4t ]= 3!s 41s-4+6s+24+s 4s 4(s+4)=(3) f(t)=t n e atL [t n e at ]=n!(s-a)n+1解:(4) f(t)=(t-1)2e 2tL [(t-1)2e 2t ]=e -(s-2)2(s-2)3解:2-3求下列函数的拉氏反变换。
A 1=(s+2)s+1(s+2)(s+3)s=-2=-1=2f(t)=2e -3t -e -2t(1) F(s)=s+1(s+2)(s+3)解:A 2=(s+3)s+1(s+2)(s+3)s=-3F(s)= 2s+31s+2-= A 1s+2s+3+ A 2(2) F(s)=s (s+1)2(s+2)f(t)=-2e -2t -te -t +2e -t解:= A 2s+1s+2+A 3+ A 1(s+1)2A 1=(s+1)2s (s+1)2(s+2)s=-1A 3=(s+2)s (s+1)2(s+2)s=-2d ds ss+2][A 2= s=-1=-1=2=-2(3) F(s)=2s 2-5s+1s(s 2+1)F(s)(s 2+1)s=+j =A 1s+A 2s=+jA 2=-5A 3=F(s)s s=0f(t)=1+cost-5sint解:= s + A 3s 2+1A 1s+A 2=12s s 2-5s+1=A 1s+A2 s=j s=jj -2-5j+1=jA 1+A 2-5j-1=-A 1+jA 2A 1=1F(s)= 1s s 2+1s -5s 2+1++解:=+s+1A 1s+3A 2(s+1)2+s A 3+A 4-12A 1= 23A 3= 112A 4= A 2= d [s=-1ds ](s+2)s(s+3) -34= -34A 2= +-43+f(t)=e -t 32e -3t 2-t e -t 121= s=-1 [s(s+3)]2[s(s+3)-(s+2)(2s+3)](2-4)求解下列微分方程。
自动控制原理黄坚课后习题答案

自动控制原理黄坚课后习题答案第一题题目:请简要说明自动控制系统的基本组成部分。
答案:自动控制系统的基本组成部分包括:1.被控对象(Plant):被控对象是指系统中需要被控制的实际物理过程或设备,可以是机械、电气、化工或其他领域的设备。
被控对象接收输入信号并产生相应的输出响应。
2.传感器(Sensor):传感器用于测量被控对象的某些状态或物理量,并将这些信息转换成适合控制器处理的电信号。
传感器的信号反映了被控对象的实际状态,如温度、压力、速度等。
3.控制器(Controller):控制器接收传感器提供的信息,并通过执行算法来生成适当的控制策略。
控制器的输出作为被控对象的输入信号,用于调节被控对象的状态或物理量。
4.执行器(Actuator):执行器接收来自控制器的控制信号,并将其转换为适合被控对象的输入形式。
执行器能够执行动作,例如打开或关闭阀门,调节电机速度等。
5.参考信号(Reference Signal):参考信号是用于指导控制系统工作的期望值或目标值。
控制系统通过与参考信号进行比较,并调节控制策略以使输出达到期望值。
6.反馈信号(Feedback Signal):反馈信号是被控对象产生的响应信号,可用于评估控制系统的性能。
控制系统可以根据反馈信号进行修正和调整,以实现更精确的控制。
第二题题目:请简要说明比例控制器、积分控制器和微分控制器的工作原理及特点。
答案:•比例控制器:比例控制器是通过比较被控对象的实际值与期望值之间的差异,并将该差异乘以比例增益系数来生成控制信号的。
比例控制器的输出正比于误差信号,可以快速响应系统的变化,但可能会导致稳定性问题。
•积分控制器:积分控制器是对误差信号进行积分,并将积分结果乘以积分增益系数后生成控制信号的。
积分控制器的作用是消除稳态误差,提高系统的稳定性和精度,但可能会引入超调和振荡问题。
•微分控制器:微分控制器是对误差信号进行微分,并将微分结果乘以微分增益系数后生成控制信号的。
《自动控制原理》黄坚课后习题答案解析

2-1试建立图所示电路的动态微分方程-u o+u o解:u 1=u i -u oi 2=C du 1dt i 1=i-i 2u o i=R 2u 1i 1=R 1=u i -u oR1dtd (u i -u o )=C(a)u C d (u i -u o )dtu o -R 2=i -u o R 1i=i 1+i 2i 2=C du 1dt u o i 1=R 2u 1-u o =L R2du odtR 1i=(u i -u 1)(b)解:du )-R 2(u i -u o )=R 1u 0-CR 1R 2(idt dt du oCR 1R 2du o dt du idt +R 1u o +R 2u 0=CR 1R 2+R 2u iu o+C R 2du 1dt o +L R 2du odtu du o dt R 1R 2L du o dt +CL R 2d 2u o dt 2=--i R 1u o R 1u oR 2+C )u o R 1R 2L du o dt ) CL R 2d 2u o dt 2=++(u i R 11R 11R 2+(C+2-2 求下列函数的拉氏变换。
(1) f(t)=sin4t+cos4tL [sin ωt ]= ωω2+s 2=s+4s 2+16L [sin4t+cos4t ]= 4s 2+16s s 2+16+s ω2+s 2L [cos ωt ]=解:解:L [t 3+e 4t ]= 3!s 41s-4+6s+24+s 4s 4(s+4)=(3) f(t)=t n e atL [t n e at ]=n!(s-a)n+1解:(4) f(t)=(t-1)2e 2tL [(t-1)2e 2t ]=e -(s-2)2(s-2)3解:2-3求下列函数的拉氏反变换。
A 1=(s+2)s+1(s+2)(s+3)s=-2=-1=2f(t)=2e -3t -e -2t(1) F(s)=s+1(s+2)(s+3)解:A 2=(s+3)s+1(s+2)(s+3)s=-3F(s)= 2s+31s+2-= A 1s+2s+3+ A 2(2) F(s)=s (s+1)2(s+2)f(t)=-2e -2t -te -t +2e -t解:= A 2s+1s+2+A 3+ A 1(s+1)2A 1=(s+1)2s (s+1)2(s+2)s=-1A 3=(s+2)s (s+1)2(s+2)s=-2d ds ss+2][A 2= s=-1=-1=2=-2(3) F(s)=2s 2-5s+1s(s 2+1)F(s)(s 2+1)s=+j =A 1s+A 2s=+jA 2=-5A 3=F(s)s s=0f(t)=1+cost-5sint解:= s + A 3s 2+1A 1s+A 2=12s s 2-5s+1=A 1s+A2 s=j s=jj -2-5j+1=jA 1+A 2-5j-1=-A 1+jA 2A 1=1F(s)= 1s s 2+1s -5s 2+1++解:=+s+1A 1s+3A 2(s+1)2+s A 3+A 4-12A 1= 23A 3= 112A 4= A 2= d [s=-1ds ](s+2)s(s+3) -34= -34A 2= +-43+f(t)=e -t 32e -3t 2-t e -t 121= s=-1 [s(s+3)]2[s(s+3)-(s+2)(2s+3)](2-4)求解下列微分方程。
《自动控制原理》黄坚课后习题答案

2-1试建立图所示电路的动态微分方程-u o+u o解:u 1=u i -u oi 2=C du 1dt i 1=i-i 2u o i=R 2u 1i 1=R 1=u i -u oR 1dtd (u i -u o )=C(a)u C d (u i -u o )dtu o -R 2=i -u o R 1i=i 1+i 2i 2=C du 1dt u o i 1=R 2u 1-u o =L R2du odtR 1i=(u i -u 1)(b)解:du )-R 2(u i -u o )=R 1u 0-CR 1R 2(idt dt du oCR 1R 2du o dt du idt +R 1u o +R 2u 0=CR 1R 2+R 2u iu o+C R 2du 1dt o +L R 2du odtu du o dt R 1R 2L du o dt +CL R 2d 2u o dt 2=--i R 1u o R 1u oR 2+C )u o R 1R 2L du o dt ) CL R 2d 2u o dt2=++(u i R 11R 11R 2+(C+2-2 求下列函数的拉氏变换。
(1) f(t)=sin4t+cos4tL [sin ωt ]= ωω2+s 2=s+4s 2+16L [sin4t+cos4t ]= 4s 2+16s s 2+16+s ω2+s 2L [cos ωt ]=解:(2) f(t)=t 3+e 4t解:L [t 3+e 4t ]= 3!s 41s-4+6s+24+s 4s 4(s+4)=(3) f(t)=t n e atL [t n e at ]=n!(s-a)n+1解:(4) f(t)=(t-1)2e 2tL [(t-1)2e 2t ]=e -(s-2)2(s-2)3解:2-3求下列函数的拉氏反变换。
A 1=(s+2)s+1(s+2)(s+3)s=-2=-1=2f(t)=2e -3t -e -2t(1) F(s)=s+1(s+2)(s+3)解:A 2=(s+3)s+1(s+2)(s+3)s=-3F(s)= 2s+31s+2-= A 1s+2s+3+ A 2(2) F(s)=s (s+1)2(s+2)f(t)=-2e -2t -te -t +2e -t解:= A 2s+1s+2+ A 3+A 1(s+1)2A 1=(s+1)2s (s+1)2(s+2)s=-1A 3=(s+2)s (s+1)2(s+2)s=-2d ds ss+2][A 2= s=-1=-1=2=-2(3) F(s)=2s 2-5s+1s(s 2+1)F(s)(s 2+1)s=+j =A 1s+A 2s=+jA 2=-5A 3=F(s)s s=0f(t)=1+cost-5sint解:= s + A 3s 2+1A 1s+A 2=12s s 2-5s+1=A 1s+A2 s=j s=jj -2-5j+1=jA 1+A 2-5j-1=-A 1+jA 2A 1=1F(s)= 1s s 2+1s -5s 2+1++(4) F(s)=s+2s(s+1)2(s+3)解:=+s+1A 1s+3A 2(s+1)2+s A 3+A 4-12A 1= 23A 3= 112A 4= A 2= d [s=-1ds ](s+2)s(s+3) -34= -34A 2= +-43+f(t)=e -t 32e -3t 2-t e -t 121= s=-1 [s(s+3)]2[s(s+3)-(s+2)(2s+3)](2-4)求解下列微分方程。
自动控制原理黄坚第二版第五章习题答案

5-4 已知系统的开环幅频率特性曲线, 写出传递函数并画出对数相频特性曲线。
(a) 20lgK=20 K=10
G(s)=(0.11s0+1)
L(ω ) dB
20
20lgK
0
10
-20dB/dec
ωc ω
(b) 20lgK=-20 K=0.1
G(s)=(0.0150ss+1)
L(ω ) dB
01
10 20
(e)
p=0
Im υ=1
-1
ω=0
0
Re
ω=0+
系统稳定
p=0
(e)
Im -1 0
υ=1
ω=0 Re
(f)
ω=0 -1
Im p=1 υ=0
0 Re
系统稳定
(a) p=1
-1
Im υ=0
ω=0
0
Re
系统稳定 ω=0+
系统不稳定
第五章习题课 (5-17)
5-17 已知系统开环幅频率特性曲线(1)写出
传递函数。(2)利用相位裕量判断稳定性(3)
ω1=0.1 ω2=0.2 ω3=15
相频特性曲线:
-40dB/dec
40
-60dB/dec
20
0 0.1 0.2 1 -20
-40dB/dec
φ (ω )
ω=0
φ (ω )=-180o
0 -90
15
ω
-60dB/dec
ω
ω=∞ φ (ω )=-270o -180 -270
第五章习题课 (5-4)
0
1 10 50 100ω
G(s)=(s+1)(0.12s+511)(0.01s+1)
《自动控制原理》黄坚课后习题答案解析

2-1试建立图所示电路的动态微分方程-u o+u o解:u 1=u i -u oi 2=C du 1dt i 1=i-i 2u o i=R 2u 1i 1=R 1=u i -u oR1dtd (u i -u o )=C(a)u C d (u i -u o )dtu o -R 2=i -u o R 1i=i 1+i 2i 2=C du 1dt u o i 1=R 2u 1-u o =L R2du odtR 1i=(u i -u 1)(b)解:)-R 2(u i -u o )=R 1u 0-CR 1R 2(dui dt dt duo CR 1R 2du o dt du idt +R 1u o +R 2u 0=CR 1R 2+R 2u iu o+C R 2du 1dt o +L R 2du odtu du o dt R 1R 2L du o dt +CL R 2d 2u o dt 2=--i R 1u o R 1u oR 2+C )u o R 1R 2L du o dt ) CL R 2d 2u o dt 2=++(u i R 11R 11R 2+(C+2-2 求下列函数的拉氏变换。
(1) f(t)=sin4t+cos4tL [sin ωt ]= ωω2+s 2=s+4s 2+16L [sin4t+cos4t ]= 4s 2+16s s 2+16+s ω2+s 2L [cos ωt ]=解:(2) f(t)=t 3+e 4t解:L [t 3+e 4t ]= 3!s 41s-4+6s+24+s 4s 4(s+4)=(3) f(t)=t n e atL [t n e at ]=n!(s-a)n+1解:(4) f(t)=(t-1)2e 2tL [(t-1)2e 2t ]=e -(s-2)2(s-2)3解:2-3求下列函数的拉氏反变换。
A 1=(s+2)s+1(s+2)(s+3)s=-2=-1=2f(t)=2e -3t -e -2t(1) F(s)=s+1(s+2)(s+3)解:A 2=(s+3)s+1(s+2)(s+3)s=-3F(s)= 2s+31s+2-= A 1s+2s+3+ A 2(2) F(s)=s (s+1)2(s+2)f(t)=-2e -2t -te -t +2e -t解:= A 2s+1s+2+ A 3+A 1(s+1)2A 1=(s+1)2s (s+1)2(s+2)s=-1A 3=(s+2)s (s+1)2(s+2)s=-2d ds ss+2][A 2= s=-1=-1=2=-2(3) F(s)=2s 2-5s+1s(s 2+1)F(s)(s 2+1)s=+j =A 1s+A 2s=+jA 2=-5A 3=F(s)s s=0f(t)=1+cost-5sint解:= s + A 3s 2+1A 1s+A 2=12s s 2-5s+1=A 1s+A2 s=j s=jj -2-5j+1=jA 1+A 2-5j-1=-A 1+jA 2A 1=1F(s)= 1s s 2+1s -5s 2+1++(4) F(s)=s+2s(s+1)2(s+3)解:=+s+1A 1s+3A 2(s+1)2+s A 3+A 4-12A 1= 23A 3= 112A 4= A 2= d [s=-1ds ](s+2)s(s+3) -34= -34A 2= +-43+f(t)=e -t 32e -3t 2-t e -t 121= s=-1 [s(s+3)]2[s(s+3)-(s+2)(2s+3)](2-4)求解下列微分方程。
自动控制原理黄坚第二版第四章习题答案

σ根 s=3-K+ω轨4r3--s+p14迹32ω13-+~3ω的3p2==s2=+-分001K.离p3r=3~KK点0θrr-===:012+ωω6012o=,,3+=01±810.7o
ζ=AK0sss(2.3rs1没5====)3B|--s有4.03系3'2+(得|.s|64s位s20统)×5+3.=+23s8于A根.171s2=|'×+根|6(轨s-23s×03=s)=+0轨.B2迹3-.0=332(7迹|-s.6+22)=j.6上201..8,9 舍s去3 p-33。
第四章习题课 (4-1)
4-1 已知系统的零、极点分布如图,大 致绘制出系统的根轨迹。
解: (1)
jω (2)
jω
600
0σ
0σ
(3)
jω
(4)
jω
900
0σ
600
0σ
第四章习题课 (4-1)
(5)
jω
(6)
jω
600
0σ
0σ
(7)
jω
1350
450
0σ
(8)
jω
1080
360
0σ
第四章习题课 (4-2)
p4
5)p4分=-离15点和z1会=-8合点
pp z13 -5.672
p
01 σ
2A)(s实)=轴s4+上25根s3轨+1迹71段s2+3p115~sp2 p3~z1
-6.2
3A)(s根)'=轨4s迹3+的75渐s2+近3线42s+315p4~-∞
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
s=-3 s=-2
= -1
=2
2 - 1 F(s)= s+3 s+2
f(t)=2e-3t-e-2t
2-3-2 函数的拉氏变换。 s F(s)= (s+1)2(s+2) s d [ s est] st 解:f(t)= e +lim (s+1)2 s=-2 s -1 ds s+2 st st 2 -2t st) =-2e +lim( e + e s -1 s+2 (s+2)2 =-2e-2t-te-t+2e-t =(2-t)e-t-2e-2t
解:L[t3+e4t]= (3) f(t)=tneat 解:L[tneat]= n! (s-a)n+1 3! 1 3! 1 + s-4 = 4 + s-4 3+1 s s
(4) f(t)=(t-1)2e2t 2 2 2t -(s-2) 解:L[(t-1) e ]=e (s-2)3
2-3-1 函数的拉氏变换。 s+1 F(s)=(s+1)(s+3) s+1 解:A1=(s+2) (s+1)(s+3) A2=(s+3) s+1 (s+1)(s+3)
第二章习题课
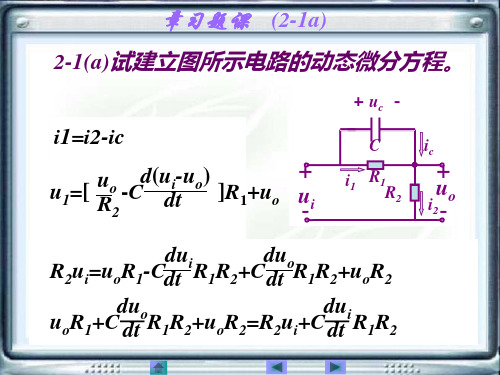
(2-1a)
2-1(a) 试建立图所示电路的动态微分方 程。 u
+
c
-
i1=i2-ic
+ d1(ui-uo+ ) + uo R u1u =[ -C R2 ]R1+uo ui u dt i R2 o - - -
C
解:
C C i1 R1 R2
ic
+ uo i2 -
dui du。 o 输入量为 u ,输出量为 u i=u 1+uo i o R2ui=uoR1-Cdt R1R2+C dt R1R2u +u R o 2 duc d(ui-uo) uo u1=i1R1 duo ic=C dui dt = dt i2= R uoR1+C dt R1R2+uoR 2 2=R2ui+C dt R1R2
(2-4-1) 求下列微分方程。 A3=(s+3)Y(s) A2=(s+2)Y(s) s=-2
s=-3
d2y(t) dy(t) +5 dt +6y(t)=6 ,初始条件: 2 dt · y(0)=y(0)=2 。 A1=1 , A2=5 , A3=-4 ∴ y(t)=1+5e-2t-4e-3t
′ 解:s2Y(s)-sY(0)-Y(0)+5sY(s)-5Y(0)+6Y(s)=
UC(s)=UO(s)+UL(s) I1(s)=IL(s)+IC(s)
UO(s) I2(s)= R2 UI(s)+UC(S) I1(s)= 即: R1 IL(s)=I1(s)-IC(s)
Ui 1 R1 I1
2-3-3 函数的拉氏变换。
∴ f(t)=1+cost-5sint
2s2-5s+1 F(s)= s(s2+1) 解:F(s)(s2+1) s=+j =A1s+A2 A1=1, A2=-5
s=+j s=0
A3=F(s)s
=1
s -5 1 F(s)= s + 2 + 2 s +1 s +1
2-3-4 函数的拉氏变换。
2-5-b 试画出题 2-1图所示的电路 的动态结构图,并 求传递函数。 解:ui=R1I1+uc uo ∴ iL= R2 UL(s)=sLIL(s)
+ ui -
R1 C
L
R2
+ uo -
uc=uo+uL i1=iL+ic
diL uL=L dt duc ic=C dt
Ui(s)=R1I1(s)+UC(s)
6+2s2+12s ∴ Y(s)= 2 s(s +5s+6) A1=sY(s)
s=0
1 s
(2-4-2)
求下列微分方程。
d3y(t) d2y(t) dy(t) 初始条件: +4 2 +29 =29, 3 dt dt dt · · y(0)=0 , y(0)=17 , · y(0)=-122 解:
2-5-a 试画题2-1图所示电路的动态结构图,并 求传递函数。 + uc - 解:ui=R1i1+uo ,i2=ic+i1 duc ic=C dt UI(s)=R1I1(s)+UO(s) I2(s)=IC(s)+I1(s) UI(s)-UO(s) 即: =I1(s) R1
第二章习题课
(2-1b)
2-1(b) 试建立图所示电路的动态微分方 程。 duc CL d2uo duo du L ic= = +C o L 2 R 1 uL= dt R2 dt dt R2 dt + + 2 uo C CL d uoR2 duo uo u u + +C i1= i o i2= R ui=u1+uo 2 dt - R2 R2 dt - 2 输入量为ui,输出量为uo。 duc d(ui-uo) u1=i1R1 ic=C dt = dt diL uo u =L L dt iL=i2= i1=iL+ic R2
求下列函数的拉氏变换。 (1) f(t)=sin4t+cos4t w 解:∵L[sinwt]= 2 2 w +s s L[coswt]= 2 2 w +s
习题课一 (2-2)
4 + s ∴L[sin4t+cos4t]= s2+16 s2+16 s+4 = 2 s +16
(2) f(t)=t3+e4t
C C ic
+ ui -
i1 R1 R2
+ uo i2 -
IC(s)=CsUC(s)[UI(s)-UO(s)]Cs= NhomakorabeaC(s)
UI(s)
UI(s) sC
1+ sC )R2 (R 1 IC(s) + I2(s) + I1(s)
UO(s)
-
1 R1
R2
UO(s)
1 ( +sC)R2 UO(s) R1 R2+R1R2sC = = 1 UI(s) R1+R2+R1R2sC ( sC)R + 1+ R 2 1
