第一次考试题高二

合集下载

2022-2023学年江苏省泰州市高二年级上册学期第一次教学质量调研考试数学试题

2022-2023学年江苏泰州教学质量第一次调研考试高二（数学）一、单选题（本大题共8小题，共40.0分.在每小题列出的选项中，选出符合题目的一项）1.经过两点，的直线的斜率为（）()0,1A -()2,4B A. B. C. D.322552232.直线与圆的位置关系是（）3480x y -+=()()221116x y -++=A.相离B.相交C.相切D.不确定3.已知椭圆的两个焦点的坐标分别是和，且椭圆经过点，则该()-()()4,0椭圆的标准方程是（）A. B. C.D.221168x y +=221168y x +=2212416x y +=221249x y +=4.已知椭圆上一点到椭圆一个焦点的距离是7，则点到另一个焦点的距离221259x y +=P P 为（）A.5B.3C.2D.75.若方程表示圆，则实数的取值范围为（）2220x y y m +--=m A. B. C. D.(),1-∞()1,+∞(),1-∞-()1,-+∞6.直线与圆相切，则的值是（）40x y -+=222x y r +=rA. B.27.已知椭圆（）的一条弦所在的直线方程是，弦的中22221x y a b +=0a b >>250x y -+=点坐标是，则椭圆的离心率是（）()4,1M -A.128.国家体育场“鸟巢”的钢结构鸟瞰图如图1所示，内外两圈的钢骨架是离心率相同的椭圆；某校体育馆的钢结构与“鸟巢”相同，其平面图如图2所示，若由外层椭圆长轴一端点和短轴一端点分别向内层椭圆引切线，，且两切线斜率之积等于，则A B AC BD 34-椭圆的离心率为（）A. B. C.345812二、多选题（本大题共4小题，共20.0分.在每小题有多项符合题目要求）9.已知圆：与圆：有四条公切线，则实数的1C ()229x y ++=2C ()221x a y-+=a 取值可能是（）A. B.1C. D.34-10.若直线：，：，：不能围成三角形，则的取1l 34x y +=2l 0x y -=3l 234x my -=m 值可能为（）A. B. C. D.2323-2929-11.已知椭圆：，，分别为它的左右焦点，，分别为它的左右顶C 2212516x y +=1F 2F A B 点，点是椭圆上的一个动点，下列结论中正确的有（）P A.存在使得P 12π2F PF ∠=B.的最小值为12cos F PF ∠725C.，则12π3F PF ∠=12F PF △D.直线与直线斜率乘积为定值PA PB 162512.已知圆：，直线：，点在直线上运动，直线，M ()2222x y ++=20x y +-=P PA 分别与圆相切于点，.则下列说法正确的是（）PB M A BA.四边形的面积的最小值为PAMBB.最小时，弦PA ABC.最小时，弦所在直线方程为PA AB 10x y +-=D.直线过定点AB 31,22⎛⎫- ⎪⎝⎭三、填空题（本大题共4小题，共20.0分）13.两圆与的公共弦所在直线的方程为______.22230x y y +--=2230x y x ++=14.已知过点的直线与以点，为端点的线段相交，则直线的斜()0,1-()4,2A ()3,1B -AB 率的取值范围为______.15.点在圆：上，，，则最小时，P C ()()22449x y -+-=()3,0A ()0,1B PBA ∠______.PB =16.如图，焦点在轴上的椭圆（）的左、右焦点分别为，，是x 22213x y a +=0a >1F 2F P 椭圆上位于第一象限内的一点，且直线与轴的正半轴交于点，的内切圆2F P y A 1APF △在边上的切点为，若，则该椭圆的离心率为______.1PF Q 14F Q =四、解答题（本大题共6小题，共70.0分.解答应写出文字说明，证明过程或演算步骤）17.（本小题10.0分）已知直线：和直线：，求分别满足下列条件的，1l 60ax by ++=2l ()120a x y -++=a 的值.b （1）直线过点，且直线和垂直；1l ()3,0-1l 2l （2）若直线和平行，且直线在轴上的截距为.1l 2l 1l y 3-18.（本小题12.0分）已知椭圆：斜率为1的直线与椭圆G 22221x y a b +=()交于，两点，以为底边作等腰三角形，顶点为.G A B AB ()3,2P -（1）求椭圆的方程；G （2）求直线的方程.AB 19.（本小题12.0分）已知圆过点，，且圆心在直线：上.C ()4,0A ()0,4B C 60x y +-=（1）若从点发出的光线经过直线反射，反射光线恰好平分圆的圆周，()4,1M y x =-1l C 求反射光线所在直线的一般式方程；1l （2）若点在直线上运动，求的最小值.Q 223QA QB +20.（本小题12.0分）已知圆内：有一点，为过点且倾斜角为的弦.O 228x y +=()1,2P -AB P α（1）当时，求弦的长；135α=︒AB （2）当弦被点平分时，求直线的方程；AB P AB（3）求过点的弦的中点的轨迹.P Q21.（本小题12.0分）在平面直角坐标系中，椭圆：（，点xOy C 22 221x ya b+=a b>>在椭圆上.12⎛⎫⎪⎝⎭C（1）求椭圆的方程；C（2）设椭圆的左、右顶点分别为，，点，为椭圆上异于，的两动点，记C A B P Q A B直线的斜率为，直线的斜率为，已知.求证：直线恒过轴上一AP1k QB2k127k k=PQ x定点.22.（本小题12.0分）如图，圆：.C()2210x a x y ay a-++-+=（1）若圆与轴相切，求圆的方程；C y C（2）当时，圆与轴相交于两点，（点在点的左侧）.问：是否存在4a=C x M N M N圆：，使得过点的任一条直线与该圆的交点，都满足O222x y r+=M A B若存在，求出圆的方程；若不存在，请说明理由.ANM BNM∠=∠O答案和解析1.【答案】C 【解析】解：经过两点，的直线的斜率是，()0,1A -()2,4B 415202+=-故选C.2.【答案】B【解析】解：圆的圆心坐标为，半径为4，()()221116x y -++=()1,1-圆心到直线的距离，15345d =<所以直线与圆的位置关系是相交.3480x y -+=()()221116x y -++=3.【答案】A【解析】解：由题意得，椭圆的长半轴，半焦距轴上，4a=c =x ，28b ∴==即椭圆的标准方程为.221168x y +=故选A.4.【答案】B 【解析】解：由知长半轴长，，221259x y +=5a =210a ∴=点到另一个焦点的距离为.∴P 271073a -=-=故选B.5.【答案】D 【解析】解：方程可变形为，2220x y y m +--=()2211x y m +-=+因为方程表示圆，则，所以.10m +>1m >-故选D.6.【答案】A 【解析】解：根据题意，得圆的圆心为，半径为，由直线与圆相切，得圆心到直线的距离，222x y r +=()0,0r d r =r =故选A.7.【答案】B 【解析】解：设直线与椭圆相交于，两点，弦的中点坐标是250x y -+=()11,A x y ()22,B x y ，()4,1M -则，，直线的斜率.128x x +=-122y y +=AB 12122y y k x x -==-由，得，2211222222221,1,x y a b x y a b ⎧+=⎪⎪⎨⎪+=⎪⎩()()()()12121212220x x x x y y y y a b +-+-+=，，21212212122yy x x b x x a y y -+∴=-⨯=-+2212b a∴=故椭圆的离心率.e c a ===故选B.8.【答案】C【解析】解：设内层椭圆方程为（），因为内、外层椭圆离心率相同，22221x y a b +=0a b >>所以外层椭圆方程可设成（），()()22221x y ma mb +=1m >设切线方程为，与联立得，AC ()1y k x ma =+22221x y a b +=，()2222322422211120ba k x ma k x m a k ab +++-=由，则，Δ0=()2212211b k a m =⋅-设切线方程为，BD 2y k x mb =+同理可求得，()222221b k m a =-所以，，242212434b k k a ⎛⎫==- ⎪⎝⎭2222222314b a c c a a a -==-=所以，因此.2214c a=12c e a ==故选C.9.【答案】ACD.【解析】解：由圆和的方程可知，1C 2C圆的圆心，半径，1C ()1C 13r =圆的圆心，半径，2C ()2,0C a 21r =因为两圆有四条公切线，所以两圆外离，两圆圆心距，则，2d a ==231a >+解得或，2a <-2a >所以实数的取值可以是，，3，不能是1.a 4-故选ACD.10.【答案】ABD 【解析】解：因为直线：，：，：不能围成三角形，1l 34x y +=2l 0x y -=3l 234x my -=所以存在或或过与的交点三种情况，13l l ∥23l l ∥3l 1l 2l 当时，有，解得；13l l ∥314234m =≠-29m =-当时，有，解得；23l l ∥110234m =≠-23m =当过与的交点时，则联立，解得3l 1l 2l 340x y x y +=⎧⎨-=⎩11x y =⎧⎨=⎩代入的方程，得，解得；3l 21314m ⨯-⨯=23m =-综上：或或.29m =-23m =23m =-故选ABD.11.【答案】BC【解析】解：设椭圆短轴上下顶点分别为，，C D E 由题知椭圆：中，，，，C 2212516x y +=5a =4b =3c =所以，，，，，，()13,0F -()23,0F ()5,0A -()5,0B ()0,4D ()0,4E -对于A 选项，由于，，，()13,4DF =-- ()23,4DF =- 1291670DF DF ⋅=-+=>所以的最大角为锐角，故不存在使得，错误；12F PF ∠P 12π2F PF ∠=对于B 选项，记，，则，1PF m =2PF n =10m n +=由余弦定理：()2221223636cos 22m n mn m n F PF mn mn +--+-∠==，264232327112252mn mn mn m n -==-≥-=+⎛⎫⎪⎝⎭当且仅当时取“＝”，B 正确；12PF PF =对于C 选项，由于，12π3F PF ∠=由焦点三角形面积公式得到，C 正确；122121πtan 16tan 26F PF S b F PF =∠=⨯=△对于D 选项，设（），，(),P x y 5x ≠±()5,0A -()5,0B 则，，，2212516x y +=5PA y k x =+5PB yk x =-于是，故错误.2222161251655252525PA PBx y y y k k x x x x ⎛⎫- ⎪⎝⎭⋅=⋅===-+---故选：BC12.【答案】AD【解析】解：由圆的方程知：圆心，半径()2,0M -r =对于，，四边形的面积A B PAMB 1222PAM S S PA r ==⨯⋅=△则当最小时，四边形的面积最小，PA PAMB 点到直线的距离，，Mdmin PA∴==此时A 正确；min S =又，此时，B 错误；111222PAMS PA r PM AB =⋅=⋅△∴AB ==对于C ，设，，，()11,A x y ()22,B x y ()00,P x y 则过作圆的切线，切线方程为：过作圆的切线，A ()()11222x x y y +++=B 切线方程为：，()()22222x x y y +++=又为两切线交点，，P ()()()()10102020222222x x y y x x y y +++=⎧⎪∴⎨+++=⎪⎩则，两点坐标满足方程：，A B ()()00222x x y y +++=即方程为：；AB ()()00222x x y y +++=当最小时，，直线方程为：，PA PM l ⊥∴PM 2y x =+由得：，即，220y x x y =+⎧⎨+-=⎩02x y =⎧⎨=⎩()0,2P方程为：，即，C 错误AB ∴()2222x y ++=10x y ++=对于D ，由C 知：方程为：；AB ()()00222x x y y +++=又，即，0020x y +-=002y x =-方程可整理为：，AB ∴()022220x y x x y -++++=由得：，过定点，D 正确.202220x y x y -+=⎧⎨++=⎩3212x y ⎧=-⎪⎪⎨⎪=⎪⎩AB ∴31,22⎛⎫- ⎪⎝⎭故选AD.13.【答案】3230x y ++=【解析】解：因为两圆方程为与，22230x y y +--=2230x y x ++=相减得：，即为公共弦所在直线的方程.3230x y ++=故答案为：.3230x y ++=14.【答案】23,,34⎛⎤⎡⎫-∞-⋃+∞ ⎪⎥⎢⎝⎦⎣⎭【解析】解：设，，，()0,1P -()4,2A ()3,1B -可得，，()213404PA k --==-()112303PB k --==---要使得直线与以点，为端点的线段相交，()4,2A ()3,1B -AB 则直线的斜率或，PB k k ≤PA k k ≥所以直线的斜率的取值范围为.23,,34⎛⎤⎡⎫-∞-⋃+∞ ⎪⎥⎢⎝⎦⎣⎭故答案为：.23,,34⎛⎤⎡⎫-∞-⋃+∞ ⎪⎥⎢⎝⎦⎣⎭15.【答案】4【解析】解：如图所示，由题意：圆：的圆心，半径，C ()()22449x y -+-=()4,4C 3r =当直线与圆相切时，为切点，且当与轴平行时最小，PB C P PB x PBA ∠.4=故答案为：4.16.【解析】解：设内切圆与的切点为，与的切点为，1AF M 2AF N 由切线长定理可得，，，，114MF QF ==PQ PN =AM AN =由对称性可得，12AF AF =由椭圆的定义可得()12122a PF PF PQ QF AF AP =+=++-，()()11128PN MF AM MF AP MF PN AN AP =+++-=++-=即有，所以，4a =213c =则双曲线的离心率为c e a ==.17.【答案】解：（1）由于直线和垂直，故，1l 2l ()110a a b ⋅-+⋅=又直线过点，故，1l ()3,0-360a -+=联立两式，解得，.2a =2b =-故有，.2a =2b =-（2）由于直线和平行，故，1l 2l ()11261a a b b ⋅=-⋅⎧⎪⎨⋅≠⨯⎪⎩直线在轴上的截距为，则，1l y 3-063b b ≠⎧⎪⎨-=-⎪⎩联立解得，.2a =2b =故有，.2a =2b =18.【答案】解：（1）由椭圆：（）焦点在轴上，且右焦点为G 22221x y a b+=0a b >>x，()则c =又，解得：，c e a ==a =又，2224b a c =-=椭圆的方程为；∴G 221124x y +=（2）设直线的方程为，设，的坐标分别为，（AB y x m =+A B ()11,x y ()22,x y ），12x x <中点为，AB ()00,E x y 由，整理得：，①221124y x m x y =+⎧⎪⎨+=⎪⎩22463120x mx m ++-=由韦达定理可知：，1232mx x +=-由中点坐标公式可知：，所以，120324x x m x +==-004m y x m =+=是等腰的底边，.AB PAB △PE AB ∴⊥的斜率，解得：，PE ∴241334m k m -==--+2m =直线的方程是：.∴AB 20x y -+=19.【答案】本题考查了直线方程的求解，考查了圆的性质，考查了二次函数的性质及两点间的距离公式，属于一般题.（1）求出直线的垂直平分线方程，与直线的方程联立可求圆心的坐标，求出点AB C 关于直线的对称点的坐标，根据反射光线必经过点和点，由()4,1M y x =-1M 1l 1M C 两点式方程可求解；（2）设点，则，利用两点间的距离公式及二次函数的性质可求()00,Q x y 0060x y +-=解.【解析】解：（1）圆过点，，故，的中点为，C ()4,0A ()0,4B A B ()2,2直线的方程为，即，AB 144x y +=4x y +=所以直线的垂直平分线为，即.AB 22y x -=-y x =因为圆心在直线：：上，且经过圆心，C 60x y +-=y x =C 由，得，即圆的圆心.60x y y x +-=⎧⎨=⎩33x y =⎧⎨=⎩C ()3,3C 设点关于直线的对称点为，()4,1M y x =-()1,M a b ，解得，，则，11141422MM b K a b a -⎧==⎪⎪-⎨++⎪=-⎪⎩1a =-4b =-()11,4M --则反射光线必经过点和点，1l 1M C 所以直线的方程为，即.1l 413431y x ++=++7490x y --=（2）设点，则.()00,Q x y 0060x y +-=又()()()()()2222222222000000003433446332QA QB x y x y x x x x +=-+++-=-+-++-，()()22000848824x x x ⎡⎤=-+=-+⎣⎦当时，的最小值为32.02x =223QA QB +20.【答案】解：（1）过点作于，连接，当时，O OG AB ⊥G OA 135α=︒直线的斜率为，故直线的方程为，即，AB 1-AB ()21y x -=-+10x y +-=OG ∴圆：的半径O 228x y +=r =，AG ∴===；2AB AG ∴==（2）当弦被平分时，，此时，AB P OP AB ⊥2OP k =-，12AB k ∴=的点斜式方程为，即直线的方程为；AB ∴()1212y x -=+AB 250x y -+=（3）设的中点，当的斜率存在时，设的斜率为，AB (),Q x y AB AB k 则点在直线上且，则点坐标满足Q AB OQ AB ⊥Q ()211y k x y x k -=+⎧⎪⎨=-⎪⎩消去，得，k 2220x y y x +-+=当的斜率不存在时，的中点的坐标为，也满足，AB AB Q ()1,0-2220x y y x +-+=故过点的弦的中点的轨迹方程为，即，P Q 2220x y y x +-+=()2215124x y ⎛⎫++-= ⎪⎝⎭故过点的弦的中点的轨迹是以.P Q 1,12⎛⎫-⎪⎝⎭21.【答案】解：（1）由题意得：，解得，222223114c aa b a b c ⎧=⎪⎪⎪+=⎨⎪⎪-=⎪⎩2241a b ⎧=⎪⎨=⎪⎩所以椭圆的方程为.C 2214x y +=（2）证明：依题意，点，，设，，()2,0A -()2,0B ()11,P x y ()22,Q x y 因为若直线的斜率为0，则点，关于轴对称，必有，不合题意.PQ P Q y AP BQ k k =-所以直线斜率必不为0，设其方程为（），与椭圆方程联立得PQ x ty n =+2n ≠±C ，2244x y x ty n ⎧+=⎨=+⎩整理得，()2224240t y nty n +++-=所以，且，()()2222Δ44440t n t n =-+->12221222444tn y y t n y y t ⎧+=-⎪⎪+⎨-⎪=⎪+⎩因为点是椭圆上一点，即，()11,P x y 221114x y +=所以，21211122111111422444AP BP x y y y k k x x x x -⋅=⋅===-+---所以，即，174AP BQBPk k k =-=281BP BQ k k ⋅=-因为()()()()121212122828282222BP BQ y y y y k k x x ty n ty n ⋅==--+-+-()()()()()2212222221212222284284(2)(2)422244n y y t t y y t n y y n t n t n n n t t -+==+-++----+-++，()()()()()()22228228271414222224n n n n n t n t n n t +++====---+-+-+所以，此时，32n =-()2Δ4470t =+>故直线：恒过轴上一定点.PQ 32x ty =-x 3,02D ⎛⎫- ⎪⎝⎭22.【答案】解：（1）因为由，可得，()22010x x a x y ay a =⎧⎨-++-+=⎩20y ay a -+=由题意得，所以或，()2Δ40a a =--=4a =0a =故所求圆的方程为或.C 225440x x y y -+-+=220x x y -+=（2）当时，令，得，即，4a =0y =2540x x -+=()()140x x --=求得或，所以，.1x =4x =()1,0M ()4,0N 假设存在圆：，当直线与轴不垂直时，O 222x y r +=AB x 设直线的方程为，代入，AB ()1y k x =-222x y r +=得，()22222120k x k x k r +-+-=设，，()11,A x y ()22,B x y 从而，，212221k x x k +=+221221k r x x k -=+因为、的斜率之和为，NA NB ()()()()()()122112121214144444k x x x x y y x x x x --+--⎡⎤⎣⎦+=----而()()()()()122112211414258x x x x x x x x --+--=-++，2222222282258111k r k r k k k --=⨯-⨯+=+++因为，所以，、的斜率互为相反数，即，ANM BNM ∠=∠NA NB 1212044y yx x +=--所以，即.228201r k -=+24r =当直线与轴垂直时，仍然满足，即、的斜率互为相反数，AB x ANM BNM ∠=∠NA NB 综上，存在圆：，使得O 224x y +=ANM BNM ∠=∠。

广东省揭阳市惠来县第一中学2024-2025学年高二上学期第一次阶段考试数学试题

广东省揭阳市惠来县第一中学2024-2025学年高二上学期第一次阶段考试数学试题一、单选题1．已知集合{0,2,5}M =，集合{}*N 05N x x =∈≤<∣，则M N = （）A ．{}0,2,5B ．{}0,2C ．{}2,5D ．{}22．复数z 满足1i 1zz =+-，则z =（）A ．1B ．2C D ．43．设,,x y z 的平均数为,M x 与y 的平均数为,N N 与z 的平均数为P .若x y z <<，则M 与P 的大小关系是（）A ．M P =B ．M P <C ．M P>D ．不能确定4，轴截面面积为1，则该圆锥的母线与底面所成的角为（）A ．15︒B ．30︒C ．45︒D ．60︒5．小刚参与一种答题游戏，需要解答A ，B ，C 三道题.已知他答对这三道题的概率分别为a ，a ，12，且各题答对与否互不影响，若他恰好能答对两道题的概率为14，则他三道题都答错的概率为（）A ．12B ．13C ．14D ．166．已知0a b >>，114a b a b+=-+，且54a b m -≥恒成立，则m 的取值范围为（）A ．5,2⎛⎤-∞ ⎥⎝⎦B ．(],2-∞C ．9,8⎛⎤-∞ ⎥⎝⎦D ．(],4∞-7．如图，边长为2的正方形ABCD 沿对角线AC 折叠，使1AD BC ⋅=，则三棱锥D ABC -的体积为（）A ．3B C ．3D ．48．()f x 是定义在R 上的函数，若()01f =，且对任意x ∈R ，满足()()22f x f x +≤+，()()88f x f x +≥+，则()2024f =（）A ．2023B ．2024C ．2025D ．2026二、多选题9．已知向量()1,1,0a = ，()0,1,1b = ，()1,2,1c =，则下列结论正确的是（）A ．向量a 与向量b 的夹角为π3B ．()c a b ⊥- C ．向量a 在向量b 上的投影向量为11,0,22⎛⎫ ⎪⎝⎭D ．向量c 与向量a ，b共面10．把函数()()π14sin cos 0π6f x x x ωωω⎛⎫=+⋅+<< ⎪⎝⎭的图象向右平移π12个单位长度，得到的函数是一个奇函数，则下列说法正确的是（）A ．()f x 的最小正周期为2πB ．()π3f x f x ⎛⎫-= ⎪⎝⎭C ．当π0,3x ⎡⎤∈⎢⎥⎣⎦时，()f x 的值域为[]1,2D ．若方程()1f x =在区间()π,m -上恰有六个不等实根，则实数m 的取值范围为7π2π,3⎛⎤ ⎥⎝⎦11．如图，点P 是棱长为2的正方体1111ABCD A B C D -的表面上一个动点，则（）A ．当P 在平面11BCCB 上运动时，四棱锥11P AA D D -的体积不变B ．当P 在线段AC 上运动时，1D P 与11A C 所成角的取值范围是ππ,32⎡⎤⎢⎥⎣⎦C ．若F 是11A B 的中点，当P 在底面ABCD 上运动，且满足PF ∥平面11B CD 时，PF 长D ．使直线AP 与平面ABCD 所成的角为45︒的点P的轨迹长度为π+三、填空题12．电影《孤注一掷》的上映引发了电信诈骗问题热议，也加大了各个社区反电信诈骗的宣传力度.已知某社区共有居民480人，其中老年人200人，中年人200人，青少年80人，若按年龄进行等比例的分层随机抽样，共抽取36人作为代表，则中年人比青少年多人13．邢台一中高二年级研究性学习小组为了实地测量某塔的高度，选取与塔底中心O 在同一个水平面内的两个测量基点A 与B ，在A 点测得：塔顶P 的仰角为45°，O 在A 的北偏东60°处，B 在A 的正东方向36米处，且在B 点测得O 与A 的张角为45°，则此塔的高度约为米（四舍五入，保留整数.1.414≈1.732≈）.14．已知函数()()2ln 1,1,21,1,x x f x x x x ⎧->⎪=⎨++≤⎪⎩若关于x 的方程()()1f x m m =≠有4个解，分别为1x ，2x ，3x ，4x ，其中1234x x x x <<<，则3411x x +=，12341111x x x x +++的取值范围是．四、解答题15．已知空间中三点()()()2,0,2,1,1,2,3,0,4A B C ----，设,a AB b AC ==(1)已知()a kb b +⊥ ，求k 的值；(2)若6c = ，且c BC λ= ，求c 的坐标.16．已知ABC V 的内角,,A B C 所对的边分别是sin sin ,,,sin a c A Ba b c a b C--=+.(1)求角B ；(2)若ABC V 外接圆的面积为12π，且ABC V 为锐角三角形，求ABC V 周长的取值范围.17．某年级数学兴趣小组组织游戏闯关活动，共设置了20道数学问题，满分100分.结束后在所有的答卷中随机抽取100份作为样本，将样本的成绩分成六段：()40,50，()50,60，……，90,100，得到如图所示的频率分布直方图.(1)求频率分布直方图中a 的值，并估计该年级全体学生这次数学成绩的中位数；(2)活动中，甲、乙两位同学独立参加竞赛，已知甲同学答对了12道，乙同学答对了8道，假设每道数学问题难度相当，被答对的可能性都相同.任选一道数学问题，求甲、乙两位同学恰有一人答对的概率.18．《九章算术》是我国古代的一部数学经典著作，在其中一篇《商功》中有如下描述：“斜解立方，得两堑堵”，堑堵是底面为直角三角形的直三棱柱．如图，在堑堵111ABC A B C -中，AB BC ⊥，1BC =，AB =12CC =，P 为棱AC 的中点，Q 为棱11A C 的中点．(1)证明：平面1//PBC 平面1AB Q ；(2)求二面角11Q AB A --的正切值；(3)求1CC 与平面1PBC 所成角的正弦值．19．已知()f x 是指数函数，且过点()()()1,23a f x g x f x b -⎛= +⎝是定义域为R 的奇函数(1)求,a b 的值；(2)若存在[]1,2c ∈-，使不等式()21206g c c m --+<成立，求实数m 的取值范围；(3)若函数()()()2412x x h x g g t +=++⨯恰有2个零点，求实数t 的取值范围．。

2022-2023学年甘肃省陕西师范大学平凉实验中学高二下学期第一次考试地理试题

2022-2023学年甘肃省陕西师范大学平凉实验中学高二下学期第一次考试地理试题1. 浮来山因山顶岩石类型在东西两侧30千米内绝无仅有，被古人称为浮来峰、飞来峰，有人用推覆构造来解释其成因。

推覆构造是一种岩层位移很大的断层构造，其上盘岩层自远处推移而来，上覆于相对停留在原地的岩块之上。

读推覆构造示意图，完成下列各题。

1．图中岩层按照年龄由新到老排列正确的是( )A．①②③④B．③②④①C．②④③①D．①④③②2．据题干材料推断浮来山的形成过程是( )A．外力侵蚀—水平挤压—断裂下陷—推移上覆B．水平挤压—岩层断裂—推移上覆—外力侵蚀C．水平挤压—断裂下陷—推移上覆—地壳上升D．推移上覆—水平挤压—岩层断裂—断块抬升2. 下图为世界局部图。

完成下面小题。

1．M半岛火山活动频繁的原因（）A．太平洋板块与美洲板块分离张裂B．太平洋板块与欧亚板块分离张裂C．太平洋板块与欧亚板块挤压碰撞D．太平洋板块与美洲板块挤压碰撞2．图中边界相关的宏观地形有（）①海岭②裂谷③山脉④岛弧A．①②B．②③C．③④D．①④3. 某河流流经滑坡集中分布区，该区域历史上发生过一次规模较大的滑坡，下图示意滑坡发生前后当地河谷地貌演化过程中的3个阶段（未分先后）。

据此完成下面小题。

1．该河谷地貌按时间演化的先后顺序是（）A．Ⅰ、Ⅱ、ⅢB．Ⅱ、Ⅰ、ⅢC．Ⅲ、Ⅱ、ⅠD．Ⅲ、Ⅰ、Ⅱ2．Ⅱ阶段，该河流部分河段河面变宽的主要原因是（）A．河流的侧蚀拓展B．滑坡体堵塞的作用C．上游来水量加大D．河床泥沙淤积增多3．Ⅰ阶段，新形成在河流左岸的河漫滩（）A．在洪水期不会被淹没B．由河流快速下切而成C．在河流凹岸侵蚀而成D．由坡面径流侵蚀而成4. 东北黑土区近年来因融雪侵蚀黑土而退化严重，有机质明显下降。

融雪期表层解冻土壤是融雪侵蚀发生的物质条件。

左图为2019年3月16日～21日东北地区某小流域融雪径流量与泥沙含量的变化过程。

采取“横坡垄作+垄沟秸秆覆盖”的农耕方式（右图），可有效减轻黑土退化。

高二语文下册第一次段考试题(附答案)

高二语文下册第一次段考试题（附答案）一、基础知识（12分,每小题3分）1．对下列加点字的解释，有错误的一组（）A．枪(触、碰)榆枋丰稔（庄稼成熟）锱铢（很小的重量单位）必较B．酒馔（饭食）门衰祚（福分）薄得鱼忘筌（捕鱼的竹器）C．形影相吊（安慰）夙婴（缠绕）疾病穷（囊中羞涩）且益坚D．只顾将（拿）来不矜（自夸）名节命途多舛(不顺)2．下列各句中，加点的成语使用恰当的—项是（）A．这是一个脏、乱、差的居住小区，物业管理人员不负责任，小区内非常混乱，闲杂人员随便出入，楼道里贴的像牛皮癣一样的各类小广告琳琅满目．．．．，业主们怨声载道。

B．两位阔别多年的老同学意外地在杭州西湖畔萍水相逢．．．．，两人又是握手又是拥抱，说起话来没完没了，别提多高兴了。

C．今年的厄尔尼诺现象将可能是自有记载以来最强的，预计将在圣诞节前后达到顶峰，并延续到2016年的一至二季度。

澳洲气象官员上午10:00举行发布会，各路媒体记者在大厅里严阵以待．．．．。

D．这些年来，随着人们接触的新事物越来越多，观念越来越开放，再加上经济水平的不断提高，中国人的自驾游活动搞得风生水起．．．．。

3．下列句子，没有语病的一句是（）A.父母对孩子监护管理的缺失是造成青少年流浪乞讨的根本原因。

所以，能否进一步完善未成年人的监护制度，是解决青少年流浪乞讨问题的重要途径。

B.我国将建立以公民身份证号码和组织机构代码为基础的统一社会信用代码制度，以后，每个公民一生都将有一个也是唯一的信用账号。

C.中央电视台新台址园区文化中心发生特别重大火灾，事故发生原因之一是工程中使用不合格保温板问题监管不力。

D. 不仅韩剧《来自星星的你》有爱情的美好，有穿越时空的奇思妙想，也有诚实守信、谦恭礼让的传统美德，而且充满了时尚文化元素，给中国观众留下了深刻印象。

4．填入下面一段文字横线处的语句，衔接最恰当的一句是（）传说中“中国最美的云和梯田”，隐匿于浙西南括苍山脉雾气迷蒙的群峰深处，弯弯绕绕的盘山公路，倏然甩出一角空地。

江西省部分学校2023-2024学年高二下学期第一次阶段性考试语文试题

江西省部分学校2023-2024学年高二下学期第一次阶段性考试语文试题试卷共8页，23小题，满分150分。

考试用时150分钟。

注意事项：1．答卷前，考生务必将自己的姓名、考场号、座位号、准考证号填写在答题卡指定位置上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3．考生必须保持答题卡的整洁。

考试结束后，请将答题卡交回。

一、现代文阅读（35分）（一）现代文阅读Ⅰ（本题共5小题，18分）阅读下面的文字，完成1~5题。

微观空间的科幻想象如何“化险为夷”，其实也就是人如何在微观空间中存在的问题。

既然“险”意味着不确定性和未知性，那么“化险为夷”就是依靠一种机制的建构，从而实现人在微观空间中的确定性。

机制的想象某种程度上也是实现微观空间的日常性。

首先，“化险为夷”基于对“险”的认识。

在微观空间的科幻想象中，其“险”的转换在于对微观科学的认识。

对于微观科学的认识建立在微观“感知体验”的基础上。

日常生活中我们所接触的宏观世界的科技，如航空航天、深海潜水、汽车、高铁和机器人等，都展现出宏观空间中的技术，可谓“触目”即认识，认识即“惊心”。

我们日常所接触的微观元素有纳米、量子、神经元以及微生物等，但它们对于大多数人来说只是停留于观念层面。

我们几乎很少对此有“触目”式的具体感知，也就难以有真实的体验了。

而对于科幻创作者来说，这种“真实”则是必需的，只有深刻的认识，才会有对“险”的深刻理解以及“化险为夷”的手段。

其次，“化险为夷”在于对“险”的掌控。

人在微观世界中将如何存在？这种掌控意味着什么？笔者认为，掌控首先是可以自如地出入微观世界。

如果我们进去而回不来，便会陷入一种困局，仍是充满未知性的焦虑。

从《奇异的旅程》中我们可以看到，影片的框架已建构了一套可进可出的规则：人物的缩小时间只有60分钟，之后会自动变回原形。

2021-2022学年安徽省蒙城县第八中学高二上学期第一次考试地理试题(Word版)

蒙城县第八中学2021—2022年度高二年级第一学期第一次考试地理试卷一、单选题（每题2分，共40分。

）陕北延安至榆林间的森林草原区（图左）黄土丘陵沟壑地貌发育，图右为该区自沟壑底部到丘陵顶部自然植被分布的典型剖面示意图。

当地水土流失严重，1999年以来，该地区实施了大规模退耕还林还草工程。

据此完成下面小题。

1．导致图右所示区域自然植被产生空间分异的根本因素是（）A．热量B．地形C．降水D．土壤肥力2．图右中最容易发生水土流失的部位是（）A．沟丘陵B．顶部C．坡面D．沟壑底部3．该地区退耕还林还草过程中，植被建设的有效途径是（）A．培育耐旱特色树种B．采用植被自然恢复C．营造大面积人工林D．人工促进自然恢复4．城市群的经济集中度可以作为衡量城市群内部协调程度的基本指标，集中度越低表明内部协调程度越高。

下表为某年长江经济带三大城市群经济集中度和产业集聚度统计数据。

据表可知（）长江三角洲城市群长江中游城市群成渝城市群中心城市GDP占比（%）37.4 47.9 60.4中心城市一产占比（%）18.1 25.1 35.8中心城市二产占比（%）31.1 48.6 55.2中心城市三产占比（%）44.0 53.8 72.0A．长江三角洲城市群经济集中度最高B．成渝城市群内部协调发展程度最高C．三大城市群产业集聚度最高的均为第三产业D．长江中游城市群中心城市经济辐射能力最强潮塌是在表层土壤迅速解冻，而下层土壤尚未解冻的情况下形成的一种自然灾害，具有很强的地域性和季节性，主要危害春小麦的生产。

据此完成下面小题。

5．推测容易出现潮塌灾害的时间是（）A．初春B．盛夏C．深秋D．隆冬6．潮塌不利于春小麦播种的主要原因是（）A．蒸发较微弱，空气缺水B．土壤解冻慢，冻害严重C．土壤冰层厚，气温过低D．水分难下渗，土壤过湿读“田纳西河流域的综合开发与治理图”，完成下面小题。

7．田纳西河从防洪入手，综合开发利用的核心资源是（）A．水资源B．煤炭资源C．铅锌资源D．土地资源8．田纳西河流域目前构成了美国最大的电力供应基地，优先开发的电能为（）A．火电B．水电C．核电D．风力发电总部设在上海的H公司是一家以精品服装为导向，手工高级定制为核心的服饰企业。

高二第一次月考(物理)试卷含答案解析

高二第一次月考（物理）（考试总分：100 分）一、单选题（本题共计5小题，总分30分）1.（6分）19世纪30年代,法拉第提出一种观点,认为在电荷周围存在电场,电荷之间通过电场传递相互作用力.对于电荷A 和电荷B 之间的电场,下列说法中正确的是( )A. 电荷B 在电荷A 的电场中受静电力的作用,自身并不产生电场B. B.撤去电荷B,电荷A 激发的电场就不存在了C. C.空间某点的电场强度等于两电荷在该点激发电场的场强的矢量和D.电场是法拉第假想的,实际上并不存在2.（6分）真空中有两个点电荷,它们之间的静电力为F,如果使它们间的距离增大到原来的2倍,将其中之一的电量也增大到原来的2倍,则它们间的作用力将变为( ) A.4F B.2F C.2F D.F 3.（6分）A 为已知电场中的一固定点,在A 点放一电量为q 的电荷,所受电场力为F ，A 点的场强为E,则( )A.若在A 点换上-q,A 点场强方向发生变化B.若在A 点换上电量为2q 的电荷,A 点的场强将变为2EC.若在A 点移去电荷q,A 点的场强变为零D.A 点场强的大小、方向与q 的大小、正负、有无均无关4.（6分）图示为等量异种的点电荷所形成的电场线分布,以下说法正确的是（）A.a 点的电势低于b 点的电势B.a 点的场强大于b 点的场强，方向相同C.将一负电荷从a 点移到b 点静电力做负功D.负电荷在a 点的电势能大于b 点的电势能5.（6分）A 、B 是一条电场线上的两个点,一带负电的微粒仅在电场力作用下以一定的初速度从A 点沿电场线运动到B 点,其速度v 与时间t 的关系图象如图甲所示,则此电场的电场线分布可能是图乙中（）二、多选题（本题共计3小题，总分18分）6.（6分）两个相同的负电荷和一个正电荷附近的电场线分布如图所示，c 是两负电荷连线的中点，d 是在正电荷的正上方，c 、d 到正电荷的距离相等，则（）A. a 点的电场强度比b 点的大B. a 点的电势比b 点的高C. c 点的电场强度比d 点的大D. c 点的电势比d 点的低7.（6分）真空中有两个完全相同的金属小球,所带电荷量分别为1q -和2q ,相距为r 时相互作用力为F ；今将两球接触后再放回原处,相互作用力为，F 31由此可判断两球原来的电荷量的关系是( )A.2:1:21=q qB.1:4:21=q qC.1:3:21=q qD.3:1:21=q q8.（6分）图中实线是一簇未标明方向的由点电荷产生的电场线。

高二地理第一次月考试题

三立高级中学2021-2022学年度上学期10月考试题高二地理时间：90分钟满分： 100分命题人：张伟 2021.10一、单项选择题（每小题2分，共48分）1．如下图所示，当太阳直射点位于P 点时，下列叙述正确的是（）A ．A 点所在纬度地区昼短夜长B ．C 点所在纬度地区昼长夜短 C ．B 点所在纬度地区昼短夜长D ．P 点所在纬度地区昼长夜短2．北京（40°N，116°E）是我国首都，我国全国统一使用北京时间。

一天中茂名某地（22°N，111°E）太阳高度最大时，北京时间为（） A ．12：00 B ．12：20C ．12：36D ．无法确定3．下图为“某半球俯视图”。

读图与a 点角速度相等的点有（）①b ②c ③d ④e姓名：班级：考场：座位号：A．①B．①②C．①②③D．①②③④4．夏至日（6.22日前后）这一天，下列各地白昼最长的是（）A．太原B．哈尔滨C．北京D．广东下图是“地球赤道与公转轨道的示意图”。

读图完成下面小题。

5．图中能表示黄赤交角的是（）A．①B．②C．③D．④6．确定南北回归线的度数是依据（）A．日地距离B．黄赤交角C．地球自转周期D．地球公转速度读下图“地球自转的线速度和角速度图”，A点位于北纬30°，B点位于南纬30°。

据此完成下列小题。

7．对图中A、B、C、D四点的叙述不正确的是（）A．A、B两点线速度相等B．B、C两点线速度相同C．A、B两点角速度不相等D．A、B两点角速度相同8．若∠AOC＝45°，对A、B、C三点叙述正确的是（）A．B、C两点地方时相同B．A、C两点地方时相同C．B、C两点昼长相同D．A、C两点的昼长不同9．地球公转产生了四季五带，其中关于五带内发生的天文现象，正确的是（）①热带每年太阳直射一次②北温带每年太阳直射一次③南温带无直射、无极昼与极夜现象④寒带有极昼与极夜现象A．①② B．①③C．③④ D．①③④10．下表是地球表面四地的线速度统计(假设地球是正球体)。

江苏省无锡市普通高中2024_2025学年高二政治上学期期末第一次学业水平模拟考试试题含解析

江苏省无锡市一般中学2024-2025学年高二政治上学期期末（第一次学业水平模拟）考试试题（含解析）一、单项选择题:下列各题的四个选项中,只有一项是最符合题意的。

本部分共30小题,每小题2分,共60分。

1.共享单车、共享充电宝等共享物品的出现,使消费者能通过合作的方式来和他人共同运用产品和服务,而无需持有产品与服务的全部权。

这些共享物品A. 是商品,是运用价值和价值的统一体B. 不是商品,因为没有用于交换C. 是商品,因为有运用价值D. 不是商品,因为它不是劳动产品【答案】A【解析】这些共享物品也是用于交换的劳动产品，是商品，是运用价值与价值的统一体，A项正确；这些共享物品是商品，B、D项不选；这些共享物品是商品，但不是因为其有运用价值，C项不选，故本题答案应为A。

【点睛】物品在以下四种状况下不是商品：（1）本身不是劳动产品，如自然状态的空气。

（2）是劳动产品，没有用于交换。

如农夫自产自用的粮食。

（3）没有运用价值，或失去了相应的运用价值。

如变质的食品、假冒的伪劣产品等。

（4）已经退出流通领域，进入消费领域。

如学生正在运用的学习用品。

2.2024年“双11”期间,各大商家通过降价促销来增加商品的销售量。

在不考虑其他条件的前提下,下列能精确反映这种促销活动带来的变更的是A.B.C.D.【答案】A【解析】各大商家通过降价促销来增加商品的销售量，这会使商品的价格下降，商品的需求量增加。

A 图像符合这一变更特征，正确；B图像表明商品价格上涨，商品需求量增加，这与题意不符；C、D图像表明商品价格不变，商品需求量增加，与题意不符，故本题答案应为A。

【点睛】正确区分需求曲线与供应曲线图像上的点移动与线移动：点移动表示需求曲线和供应曲线不变，由于价格的变动而引起需求或供应数量的变更，在图像上表现为曲线不动，曲线上的点在动。

图像上是点移动时，表明商品价格本身变动；线移动表示由于其他因素的变更而引起的需求或供应量的变更，在图像上表现为曲线的平移，这种状况表明商品价格本身不变动。

甘肃省天水市田家炳中学(原：天水四中)2022-2023学年高二上学期第一阶段考试物理试题(含答案)

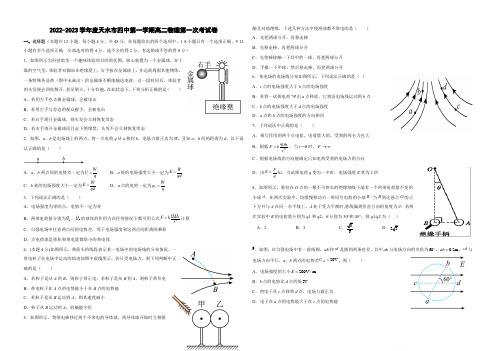
2022-2023学年度天水市四中第一学期高二物理第一次考试卷一、选择题（本题共12小题，每小题4分，共48分．在每题给出的四个选项中，1-8小题只有一个选项正确，9-12小题有多个选项正确．全部选对的得4分，选不全的得2分，有选错或不答的得0分） 1．如图所示为科技馆里一个趣味体验项目的简化图，核心装置为一个金属球，在干燥的空气里，体验者双脚站在绝缘凳上，右手按在金属球上，并远离周围其他物体。

一条特殊传送带（图中未画出）给金属球不断地输送电荷，过一段时间后，体验者的头发便会四处散开，甚至倒立，十分有趣，在此状态下，下列分析正确的是（） A ．若用左手也去摸金属球，会被电击 B ．若用左手与旁边的观众握手，会被电击 C ．若右手离开金属球，则头发会立刻恢复常态D ．若右手离开金属球而且走下绝缘凳，头发不会立刻恢复常态2．如图，a 、b 是电场线上的两点，将一点电荷q 从a 移到b ，电场力做正功为W ，且知a 、b 间的距离为d ，以下说法正确的是（）A ．a 、b 两点间的电势差一定为W U q= B ．a 处的电场强度大小一定为W E qd= C ．b 处的电场强度大小一定为W E qd = D ．a 点的电势一定为a W qϕ=3．下列说法正确的是（）A ．电场强度为零的点，电势不一定为零B ．两带电荷量分别为1Q 、2Q 的球体的作用力在任何情况下都可用公式122Q Q F k r =计算 C ．匀强电场中任意两点间的电势差，等于电场强度和这两点间距离的乘积 D ．点电荷就是体积和带电量都很小的带电体4．(本题4分)如图所示，带箭头的线段表示某一电场中的电场线的分布情况。

一带电粒子在电场中运动的轨迹如图中虚线所示。

若只受电场力，则下列判断中正确的是（）A ．若粒子是从A 到B ，则粒子带正电；若粒子是从B 到A ，则粒子带负电 B ．带电粒子在A 点的电势能小于在B 点的电势能C ．若粒子是从B 运动到A ，则其速度减小D ．粒子从B 运动到A ，机械能守恒5．如图所示，将带电棒移近两个不带电的导体球，两导体球开始时互相接触且对地绝缘，下述几种方法中使两球都不带电的是（） A ．先把两球分开，再移走棒 B ．先移走棒，再把两球分开C ．先将棒接触一下其中的一球，再把两球分开D ．手摸一下甲球，然后移走棒，再把两球分开6．某电场的电场线分布如图所示，下列说法正确的是（） A ．c 点的电场强度大于b 点的电场强度B ．若将一试探电荷q +由a 点释放，它将沿电场线运动到b 点C ．b 点的电场强度大于d 点的电场强度D ．a 点和b 点的电场强度的方向相同 7．下列说法中正确的是（）A ．相互作用的两个点电荷，电荷量大的，受到的库仑力也大B ．根据122q q F kr =，当r →0时，F →∞ C ．根据电场线的方向能确定已知电荷受到的电场力的方向D ．由FE q=知，当试探电荷q 变为一半时，电场强度E 变为2倍 8．如图所示，悬挂在O 点的一根不可伸长的绝缘细线下端有一个所带电荷量不变的小球A ．在两次实验中，均缓慢移动另一带同号电荷的小球B，当B 到达悬点O 的正下方并与A 在同一水平线上，A 处于受力平衡时,悬线偏离竖直方向的角度为θ．若两次实验中B 的电荷量分别为q 1和q 2，θ分别为30°和45°，则q 1/q 2为（） A ．2 B ．3C ．36D ．339．如图，在匀强电场中有一虚线圆，ab 和cd 是圆的两条直径，其中ab 与电场方向的夹角为60︒，0.2m ab =，cd 与电场方向平行，a 、b 两点的电势差20V ab U =。

北京市第一次普通高中2023-2024学年高二上学期学业水平合格性考试数学试题

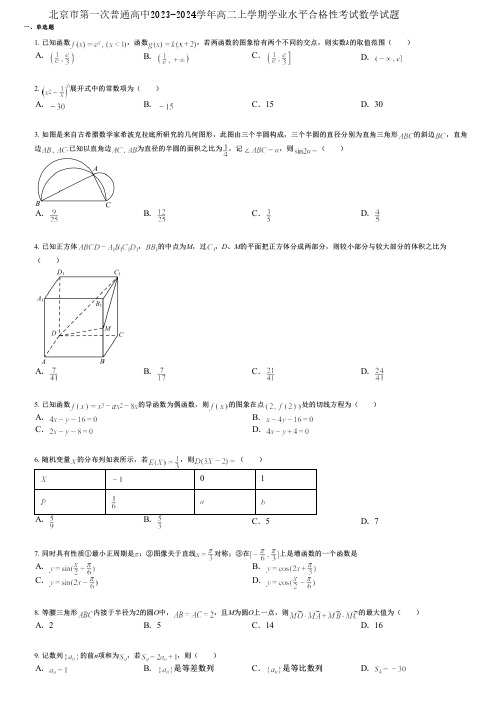
一、单选题1.已知函数，函数，若两函数的图象恰有两个不同的交点，则实数k 的取值范围（）A．B．C．D．2.展开式中的常数项为（）A．B．C ．15D ．303. 如图是来自古希腊数学家希波克拉底所研究的几何图形，此图由三个半圆构成，三个半圆的直径分别为直角三角形的斜边，直角边.已知以直角边为直径的半圆的面积之比为，记，则（）A．B．C．D．4. 已知正方体，的中点为M ，过，D 、M 的平面把正方体分成两部分，则较小部分与较大部分的体积之比为（）A．B．C．D．5. 已知函数的导函数为偶函数，则的图象在点处的切线方程为（）A．B．C．D．6. 随机变量的分布列如表所示，若，则（）1A．B．C ．5D ．77. 同时具有性质①最小正周期是；②图像关于直线对称；③在上是增函数的一个函数是A．B．C．D．8. 等腰三角形内接于半径为2的圆O 中，，且M 为圆O 上一点，则的最大值为（）A ．2B ．5C ．14D ．169. 记数列的前n项和为，若，则（）A．B ．是等差数列C ．是等比数列D．北京市第一次普通高中2023-2024学年高二上学期学业水平合格性考试数学试题二、多选题三、填空题10. 已知，，则的值等于A．B．C．D．11. 如图，长方体中，，若直线与平面所成的角为，则直线与直线所成的角为（）A．B．C．D．12. 设点，则且是点在直线上的（）A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件13. 已知正实数、满足，则（）A．的最大值为B ．的最小值为C．的最小值为D ．的最大值为14. 下列结论正确的有（）A．若随机变量，满足，则B．若随机变量，且，则C ．若线性相关系数越接近1，则两个变量的线性相关性越强D ．按从小到大顺序排列的两组数据：甲组：27，30，37，m ，40，50；乙组：24，n ，33，44．48，52，若这两组数据的第30百分位数、第50百分位数都分别对应相等，则15. 高中学生要从必选科目（物理和历史）中选一门，再在化学、生物、政治、地理这4个科目中，依照个人兴趣、未来职业规划等要素，任选2个科目构成“1＋2选考科目组合”参加高考.已知某班48名学生关于选考科目的结果统计如下：选考科目名称物理化学生物历史地理政治选考该科人数36392412a b下面给出关于该班学生选考科目的四个结论中，正确的是（）A．B ．选考科目组合为“历史＋地理＋政治”的学生可能超过9人C ．在选考化学的所有学生中，最多出现6种不同的选考科目组合D ．选考科目组合为“历史＋生物＋地理”的学生人数一定是所有选考科目组合中人数最少的16. 已知函数，是函数的极值点，以下几个结论中正确的是（）A．B．C．D．17. 过定点的直线与曲线交于不同的两点，则直线的斜率的取值范围是__________．18.有一个上、下底面半径分别为，的圆台，高为，则它的体积为______．四、填空题五、解答题六、解答题七、解答题19.已知的图象在处的切线与与函数的图象也相切，则该切线的斜率__________.20.已知，为常数，若，则___________，___________.21. 过抛物线焦点F 的直线l 交C 于点A ，B ，线段AB 中点M 的纵坐标为1，则直线AB 的斜率k 的值为__________；线段AB 的长度为__________．22. 已知函数，，.若，，且的最小值为，，求解下列问题.(1)化简的表达式并求的单调递增区间；(2)请完善表格并利用五点作图法绘制该函数在一个周期内的图象，并求在区间上的最值.23.已知函数.从下面的两个条件中任选其中一个：①；②若，且的最小值为，，求解下列问题：(1)化简的表达式并求的单调递增区间；(2)已知，求的值.24. 把函数的图象向左平移个单位，得到函数的图象，函数的图象关于直线对称，记函数.（1）求函数的最小正周期和单调增区间；（2）画出函数在区间上的大致图象.25.如图，在四棱锥中，四边形是边长为2的菱形，是边长为2的等边三角形，，.(1)求证：平面平面；(2)求平面和平面所成锐二面角的大小.八、解答题九、解答题26. 已知椭圆，右焦点为，动直线与圆相切于点，与椭圆交于、两点，其中点在轴右侧.（1）若直线过点，求椭圆方程；（2）求证：为定值.27. 海水养殖场使用网箱养殖的方法，收获时随机抽取了 100个网箱，测量各箱水产品的产量(单位:)，其频率分布直方图如图：定义箱产量在(单位:)的网箱为“稳产网箱”，箱产量在区间之外的网箱为“非稳产网箱”.（1）从该养殖场（该养殖场中的网箱数量是巨大的）中随机抽取3个网箱.将频率视为概率，设其中稳产网箱的个数为，求的分布列与期望；（2）从样本中随机抽取3个网箱，设其中稳产网箱的个数为，试比较的期望与的大小.28. 某县对高一年级学生进行体质测试（简称体测），现随机抽取了800名学生的体测结果等级（“良好以下”或“良好及以上”）进行分析，并制成下图所示的列联表.良好以下良好及以上合计男400550女50合计600800(1)将列联表补充完整；计算并判断是否有的把握认为本次体测结果等级与性别有关系；(2)将频率视为概率，用样本估计总体.若从全县高一所有学生中，采取随机抽样的方法次抽取1名学生成绩进行具体指标分析，连续抽取4次，且每次抽取的结果相互独立，记被抽取的4名学生的体测等级为“良好及以上”的人数为，求的分布列和数学期望.附表及公式：0.150.100.050.0250.0100.0050.0012.0722.7063.8415.0246.6357.87910.828其中，.。

2022-2023学年河北省衡水阳光中学高二上学期第一次阶段考试化学试题

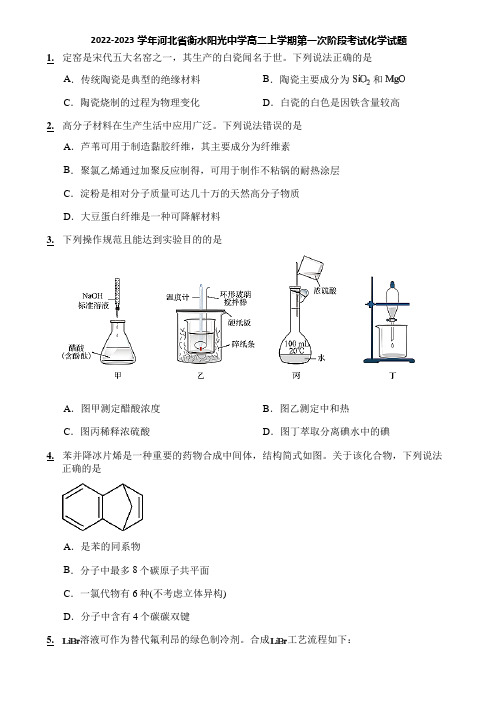
2022-2023学年河北省衡水阳光中学高二上学期第一次阶段考试化学试题1.定窑是宋代五大名窑之一，其生产的白瓷闻名于世。

下列说法正确的是A．传统陶瓷是典型的绝缘材料B．陶瓷主要成分为和C．陶瓷烧制的过程为物理变化D．白瓷的白色是因铁含量较高2.高分子材料在生产生活中应用广泛。

下列说法错误的是A．芦苇可用于制造黏胶纤维，其主要成分为纤维素B．聚氯乙烯通过加聚反应制得，可用于制作不粘锅的耐热涂层C．淀粉是相对分子质量可达几十万的天然高分子物质D．大豆蛋白纤维是一种可降解材料3.下列操作规范且能达到实验目的的是A．图甲测定醋酸浓度B．图乙测定中和热C．图丙稀释浓硫酸D．图丁萃取分离碘水中的碘4.苯并降冰片烯是一种重要的药物合成中间体，结构简式如图。

关于该化合物，下列说法正确的是A．是苯的同系物B．分子中最多8个碳原子共平面C．一氯代物有6种(不考虑立体异构)D．分子中含有4个碳碳双键5.溶液可作为替代氟利昂的绿色制冷剂。

合成工艺流程如下：下列说法错误的是A．还原工序逸出的用溶液吸收，吸收液直接返回还原工序B．除杂工序中产生的滤渣可用煤油进行组分分离C．中和工序中的化学反应为D．参与反应的为1∶1∶16.硫和氮及其化合物对人类生存和社会发展意义重大，但硫氧化物和氮氧化物造成的环境问题也日益受到关注，下列说法正确的是A．NO 2和SO 2均为红棕色且有刺激性气味的气体，是酸雨的主要成因B．汽车尾气中的主要大气污染物为NO、SO 2和PM2.5C．植物直接吸收利用空气中的NO和NO 2作为肥料，实现氮的固定D．工业废气中的SO 2可采用石灰法进行脱除7.用中子轰击X原子产生α粒子(即氦核He)的核反应为：X+n→Y+He。

已知元素Y在化合物中呈+1价。

下列说法正确的是A．H 3 XO 3可用于中和溅在皮肤上的NaOH溶液B．Y单质在空气中燃烧的产物是Y 2 O 2C．X和氢元素形成离子化合物D．6 Y和7 Y互为同素异形体8.茯苓新酸DM是从中药茯苓中提取的一种化学物质，具有一定生理活性，其结构简式如图。

广东省惠州市第一中学2021-2023学年高二上学期9月第一次月考语文试题及答案统编版高二

广东省惠州市第一中学2021-2023学年高二上学期9月第一次月考语文试题及答案统编版高二惠州一中2023届高二上学期第一次考试语文试卷卷面总分：150分考试时长：150分钟一、课内基础知识（本题共8小题，16分）1.下列各组句子中，加点词语的含义相同的一项是（2分）A.微夫人之力不及此微斯人，吾谁与归B.仲尼之徒无道桓文之事臣之所好者道也C.举所佩玉玦以示之者三杀人如不能举，刑人如恐不胜D.如或知尔，则何以哉纵一苇之所如，凌万顷之茫然2.下列各句中加点的词语，按词类活用现象归类正确的一项是（2分）①浴乎沂，风乎舞雩②赤也为之小，孰能为之大③无以，则王乎④为肥甘不足于口与⑤齐桓、晋文之事可得闻乎⑥谨庠序之教⑦吾得兄事之⑧素善留侯张良⑨良庖岁更刀，割也⑩交戟之卫士欲止不内A.①③/②④⑥/⑦⑨/⑧/⑤⑩B.①③/②④/⑤⑩/⑥⑧/⑦⑨C.①⑦/②⑧/③⑨/④⑥/⑤⑩D.①⑦/②④/⑥⑧/⑨/③⑤⑩3.对下列文化常识判断不正确的一项是（2分）A.宗庙，天子、诸侯供奉祖宗牌位的处所。

宗庙之事，在古代是国家重要的政事。

B.冠者，也称“弱冠”，指成年男子。

古代男子在二十岁是行加冠礼，表示成年。

C.庠序，古代泛指学校，殷代叫庠，周代叫序，与《送东阳马生序》中的“太学”一样。

D.参乘，即“骖乘”，古时站在车右陪乘或担任警卫的人。

乘，兵车，包括一车四马。

4.对下列加点词语的解释，不正确的一项是（2分）A.傲物则骨肉为行路行路：走路B.一日之内，一宫之间，而气候不齐气候：天气C.思厥先祖父祖父：泛指祖辈、父辈D.下而从六国破亡之故事故事：旧事5.从句式特征看，与“而今安在哉”一句相同的一项是（2分）A.架梁之椽，多于机上之工女B.夫晋，何厌之有C.戍卒叫，函谷举D.燕雀安知鸿鹄之志哉某启：昨日蒙教，窃以为与君实游处相好之日久，而议事每不合，所操之术多异故也。

虽欲强聒，终必不蒙见察，故略上报，不复一一自辨。

重念蒙君实视遇厚，于反覆不宜卤莽，故今具道所以，冀君实或见恕也。

高二数学第一次月考试卷理科试题

卜人入州八九几市潮王学校2021年地区高二数学第一次月考试卷(理科)说明：本套试卷分第一卷(选择题)和第二卷(非选择题)两局部。

试卷总分值是150，考试时间是是120分钟。

第Ⅰ卷(选择题一共60分)一、选择题：本大题一一共12小题，每一小题5分，一共60分。

在每一小题给出的四个选项里面，有一项为哪一项哪一项符合题目要求的，请将所选答案填在指定的答题栏内。

1．函数f(x)=2x+5，当x 从2变化到4时，函数的平均变化率是〔〕A2B4 C2D-2 2．以下求导运算正确的选项是〔〕 A 、3211)1(x x x -='+B 、2ln 1)(log '2x x =C 、'2)cos (x x =-2xsinxD 、e xx 3'log 3)3(= 3．一个物体的运动方程为21s tt 其中S 的单位是米，t 的单位是秒，那么物体在3秒末的瞬时速度是〔〕A 、7米/秒B 、6米/秒C 、5米/秒D 、8米/秒4．设f(x)在[a,b]上连续，将[a,b]n 等分，在每个小区间上任取i ξ，那么dx x f b a)(⎰是〔〕A 、∑=∞→ni i n f 1)(lim ξB 、∑=∞→-•ni i n n ab f 1)(lim ξC 、∑=∞→•n i i i n f 1)(lim ξξD 、∑=∞→ni i n f 1)(lim ξ•-i ξ()1-i ξ 5．函数2mnymx 的导数为3'4x y =，那么〔〕A 、m=－1,n=－2B 、m=－1,n=2C 、m=1,n=－2D 、m=1,n=2 6．函数)(x f y =在一点的导数值为0是函数)(x f y =在这点取极值的〔〕A 、充要条件B 、即不充分又不必要条件C 、充分非必要条件D 、必要非充分条件7．函数1ln 1ln xyx的导数为〔〕A 、2')ln 1(2x y +-=B 、2')ln 1(2x x y +=C 、2')ln 1(1x x y +-=D 、2')ln 1(2x x y +-=8、以下积分不正确的选项是〔〕A 、3ln 131=⎰dx x B 、xdx sin 0⎰π=-2 C 、31210=⎰dx x D 、23ln 29)1(232+=+⎰dx xx9．函数5224+-=x x y 的单调减区间是〔〕A 、[-1,1]B 、[-1，0]，[1，+∞]C 、〔-∞，-1〕，〔0，1〕D 、(-∞,-1),[1,+∞] 10．曲线y=ln(2x-1)上的点到直线2x-y+3=0的最短间隔是〔〕 A 、5B 、25C 、35D 、011．方程076223=+-x x在〔0，2〕内根的个数有〔〕A ．0B ．1C ．2D ．312、设P 点是曲线3233+-=x x y 上的任意一点，P 点处切线倾斜角为α，那么角α的取值范围是 A ．2[0,)[,)23πππ⋃B ．5[0,)[,)26πππ⋃C ．),32[ππD ．)65,2(ππ第二卷(非选择题一共90分)二、填空题：本大题一一共4小题，每一小题4分，一共16分.把答案填在题中的横线上． 13、定积分cdx b a⎰〔c 为常数〕的几何意义是：。

福建省高二下学期第一次月考数学试题(Word版)

高二下学期第一次月考数学试题（考试时间：120分钟满分：150分）、、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知函数在处的导数为，则（）()f x 1x =6()()11lim 3x f x f x∆→+∆-=∆A ．1B ．2C ．D ．6232．如图所示是函数的图象，其中为的导函数，则下列大小关系正确()y f x =()f x '()f x 的是（）A ．B ． ()()()213f f f ''>>'-()()()231f f f ''>>'-C ．D ．()()()312f f f >>''-'()()()321f f f >->'''3．已知某物体在平面上作变速直线运动，且位移（单位：米）与时间（单位：秒）之s t 间的关系可用函数：表示，则该物体在秒时的瞬时速度为（）()2ln 1s t t t =++-3t =A ．米/秒 B ．米/秒C ．米/秒 D ．米秒214()62ln2+212()4ln2+4．函数的图象大致为（）sin x xx xy e e --=+A ．B ．C ．D ．5．若对任意的，，且，都有，则m 的最小值是1x ()2,x m ∈+∞12x x <122121ln ln 2x x x x x x -<-（） A ．B ．C ．1D ．1ee 3e6．已函数及其导函数定义域均为，且，，则关于()f x ()f x 'R ()()0f x f x '->()01f =x的不等式的解集()e xf x >为（） A ． B ．C ．D ．{}0x x >{}0x x <{}1x x <{}1x x >7．在数学中，布劳威尔不动点定理是拓扑学里一个非常重要的不动点定理，它可应用到有限维空间，并且是构成一般不动点定理的基石．简单地讲就是对于满足一定条件的连续函数，存在点，使得，那么我们称该函数为“不动点”函数．若函数()f x 0x ()00f x x =为“不动点”函数，则实数的取值范围是（） ()()e ln xf x x a x =-a A ． B ．C ．D ．(],0-∞1,e ⎛⎤-∞ ⎝⎦(],1-∞(],e -∞8．已知,则（） 1ln1.1,,11a b c ===A ．B ．C ．D ．a b c >>a c b >>c b a >>c a b >>二、选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.9．下列函数的求导正确的是（）A ．B ．C ．D ．211x x '⎛⎫= ⎪⎝⎭()sin cos x x '=()()'e 1e x x x x =+()1ln 22'=x x10．已知，下列说法正确的是（） ()ln xf x x=A ．在处的切线方程为B ．若方程有两个不相等的实数()f x 1x =1y x =+()f x a =根，则 10a e<<C ．的极大值为D ．的极小值点为()f x 1e()f x e x =11．若函数在区间上存在最小值，则整数可以取（）()321233f x x x =+-()1,4a a -+a A ．-3B ．-2C ．-1D ．012．若存在实常数k 和b ，使得函数和对其公共定义域上的任意实数x 都满足：()F x ()G x 和恒成立，则称此直线为和的“隔离直线”，已()F x kx b ≥+()G x kx b ≤+y kx b =+()F x ()G x 知函数，，（e 为自然对数的底数），则下列结2()()f x x x R =∈1()(0)g x x x=<()2ln h x e x =论正确的是（）．A ．函数在区间上单递减()()()m x f x g x =-,⎛-∞ ⎝B ．和之间存在“隔离直线”，且k 的最小值为 ()f x ()g x 4-C ．和之间存在“隔离直线”，且b 的取值范围是 ()f x ()g x [4,0]-D ．和之间存在“隔离直线”，且“隔离直线”不唯一()f x ()h x 三、填空题：本题共4小题，每小题5分，共20分.13．函数在点处的切线方程为____________． 1()ln f x x x=-(1,1)-14．函数，则________． ()2(1)21xf x f x x '=+-()0f '=15．不等式对任意恒成立，则正实数的取值范围为________． 1e ln 0a x x a x --≥()1,x ∈+∞a 16．若函数在区间D 上有定义，且均可作为一个三角形的()g x ,,,(),(),()a b c D g a g b g c ∀∈三边长，则称在区间D 上为“M 函数”．已知函数在区间为()g x ()1ln x f x x k x -=-+1,e e ⎡⎤⎢⎥⎣⎦“M 函数”，则实数k 的取值范围为_________________．四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.17．（10分）已知函数，，且．求：()32f x x ax =-a ∈R ()11f '=(1)a 的值及曲线在点处的切线方程； ()y f x =()()1,1f (2)函数在区间上的最大值． ()f x []0,218. （12分）已知函数在及处取得极值．()32f x x ax bx c =+++13x =-1x =(1)求a ，b 的值；(2)若方程有三个不同的实根，求c 的取值范围． ()0f x =19．（12分）已知函数．()2211ln 2a f x x x x a +=-+(1)当时，求函数的单调增区间． 2a =()f x (2)讨论函数的单调性． ()f x20.（12分）2022年2月4日，第二十四届冬季奥林匹克运动会开幕式在北京国家体育场举行，拉开了冬奥会的帷幕．冬奥会发布的吉祥物“冰墩墩”、“雪容融”得到了大家的广泛喜爱，达到一墩难求的地步．当地某旅游用品商店获批经销此次奥运会纪念品，其中某个挂件纪念品每件的成本为5元，并且每件纪念品需向税务部门上交元的税收，预计5a +(58)a ≤≤当每件产品的售价定为元时，一年的销售量为万件，x (1317)x ≤≤2(18)x -(1)求该商店一年的利润(万元)与每件纪念品的售价的函数关系式； L x (2)求出的最大值． L ()Q a21．（12分）已知函数为的导数.()e cos 2,()x f x x f x '=+-()f x (1)当时，求的最小值；0x ≥()f x '(2)当时，恒成立，求的取值范围.π2x ≥-2e cos 20xx x x ax x +--≥a22．（12分）已知函数.2()e (e 2.718)=-= x f x ax (1)若在有两个零点，求实数的取值范围；()f x ()0,∞+a (2)设函数，证明：存在唯一的极大值点，且2()e [()1]x g x f x ax x =+--()g x 0x . 0321()e 4<<g x龙岩一中2024届高二下学期第一次月考数学试题参考答案题号1 2 3 4 5 6 7 8 9 10 11 12 答案BAABABBDBCBCBC DAB C13．14． 1 15． 16．23y x =-(],e -∞()2e 4,-+∞17．解:（1），解得：()32f x x ax =-Q ()'232f x x ax ∴=-()'1321f a ∴=-=1a =故，()32f x x x =-(1)0f =曲线在点处的斜率为，切线方程即 ...........5()y f x =()()1,1f 1k =(1)(1)y f k x -=-1y x =-分（2）由（1）可知：，令，解得()32f x x x =-()'232f x x x =-()'2320f x x x =-= 1220,3x x ==故当时，，所以单调递减；当时，，所以2[0,)3x ∈()'0f x <()f x 2[,2]3x ∈()'0f x >()f x 单调递增；区间内，当时取最大值，最大值为 ...........10分()f x []0,22x =(2)4f =18．解:（1）由题意得，函数在及处取得极值， ()232f x x ax b '=++()f x 13x =-1x =得，解得 .()11203331320af b f a b ⎧⎛⎫-=-+=⎪ ⎪⎝'⎭⎨⎪=++'=⎩11a b =-⎧⎨=-⎩此时，.()()()2321311x x x x f x --=+'-=当时，，函数在上单调递增； 13x <-()0f x ¢>()f x 1,3⎛⎫-∞- ⎪⎝⎭当时，，函数在上单调递减；113-<<x ()0f x '<()f x 1,13⎛⎫- ⎪⎝⎭当时，，函数在上单调递增. 1x >()0f x ¢>()f x ()1,+∞所以，在处取得极大值，在处取得极小值，满足题意. ...........6分 ()f x 13x =-1x =（2）由（1）知，在处取得极大值，在处取得极小值．又有三()f x 13x =-1x =()0f x =个不同的实根，由图象知，解得，所以实数c 的取值范围是()150327110fc f c ⎧⎛⎫-=+>⎪ ⎪⎝⎭⎨⎪=-+<⎩5127c -<<5,127⎛⎫- ⎪⎝⎭．...........12分19．解:（1）函数的定义域为，()2211ln 2a f x x x x a+=-+()0,∞+当时，，所以. 2a =()215ln 22f x x x x =-+()()221251252()22x x x x f x x x x x---+'=-+==故当时，，函数在上单调递增；10,2x ⎛⎫∈ ⎪⎝⎭()0f x ¢>()f x 10,2⎛⎫ ⎪⎝⎭当时，，函数在上单调递减；1,22x ⎛⎫∈ ⎪⎝⎭()0f x '<()f x 1,22⎛⎫ ⎪⎝⎭当时，，函数在上单调递增；()2,x ∈+∞()0f x ¢>()f x ()2,+∞所以函数的单调递增区间有和；...........4分()f x 10,2⎛⎫⎪⎝⎭()2,+∞（2）由可得：()2211ln 2a f x x x x a+=-+. ()2221()11(1)()ax x a a ax a x a f x x a x ax ax--+-++'=-+==①当时，，在上单调递增；...........6分 a<0()0f x ¢>()f x ()0,∞+②当时，时，时，在上单调递增；01a <<()0,x a ∈()0f x ¢>()f x ()0,a 时，时，在上单调递减； 1,x a a ⎛⎫∈ ⎪⎝⎭()0f x '<()f x 1,a a ⎛⎫⎪⎝⎭时，，在上单调递增；............8分 1,x a ⎛⎫∈+∞ ⎪⎝⎭()0f x ¢>()f x 1,a ⎛⎫+∞ ⎪⎝⎭③当时，，且仅在时，，所以函数在上单调递增1a =()0f x '≥1x =()0f x '=()f x ()0,∞+；...........9分④当时，时，时，在上单调递增；1a >10,x a ⎛⎫∈ ⎪⎝⎭()0f x '>()f x 10,a ⎛⎫⎪⎝⎭时，时，在上单调递减； 1,x a a ⎛⎫∈ ⎪⎝⎭()0f x '<()f x 1,a a ⎛⎫⎪⎝⎭时，，在上单调递增；............11分(),x a ∈+∞()0f x ¢>()f x (),a +∞综上所述，当时，函数在上单调递增；a<0()f x ()0,∞+当时，函数在和上单调递增，在上单调递减；01a <<()f x ()0,a 1,a ⎛⎫+∞ ⎪⎝⎭1,a a ⎛⎫⎪⎝⎭当时，函数在上单调递增；1a =()f x ()0,∞+当时，函数在和上单调递增，在上单调递减；...........12分1a >()f x 10,a ⎛⎫ ⎪⎝⎭(),a +∞1,a a ⎛⎫⎪⎝⎭20．解（1）由题意，预计当每件产品的售价为元，而每件产品的成本为5x (1317)x ≤≤元，且每件产品需向税务部门上交元，(5)a +(58)a ≤≤所以商店一年的利润(万元)与售价的函数关系式为：L x 2(10)(18),[13,17]L x a x x =---∈．...........5分（2）∵，∴， 2(10)(18),[13,17]L x a x x =---∈(3823)(18)L a x x =+--'令，解得：或，而，则，...........7分 0L '=3823a x +=18x =58a ≤≤38216183a+≤≤①当，即时，当时，，单调递38216173a +≤<5 6.5a ≤<38213,3a x +⎛⎫∈ ⎪⎝⎭0L >'A A A A L 增，当时，，单调递减，∴当时，取最大值382,173a x +⎛⎫∈ ⎪⎝⎭0L '<L 3823a x +=L 34(8)27a -；...........9分 ②当，即时，当时，，单调递增， 38217183a+≤≤ 6.58a ≤≤()13,17x ∈0L >'A A A A L ∴当时，取最大值，...........11分17x =L 7a -综上， ...........12分 ()()348,5 6.5277,6.58a a Q a a a ⎧-≤<⎪=⎨⎪-≤≤⎩21．（1）由题意，，令，则， ()e sin x f x x '=-()e sin x g x x =-()e cos x g x x '=-当时，，，所以，从而在上单调递增， 0x ≥e 1x ≥cos 1≤x ()0g x '≥()g x [0,)+∞则的最小值为，故的最小值1；...........4分()g x (0)1g =()f x '（2）由已知得当时，恒成立，令，π2x ≥-()e cos 20xx x ax +--≥()e cos 2x h x x ax =+--，...........5分()e sin x h x x a '=--①当时，若时，由（1）可知，∴为增函数， 1a ≤0x ≥()10h x a '≥-≥()h x ∴恒成立，∴恒成立，即恒成立，()()00h x h ≥=()0x h x ⋅≥()e cos 20x x x ax +--≥若，令则，令，则π,02x ⎡⎫∈-⎪⎢⎣⎭()e sin x m x x a =--()e cos x m x x '=-()e cos xn x x =-，()e sin x n x x '=+令，则，∵在在内大于零恒成立，()e sin x p x x =+()e cos x p x x '=+()p x 'π,02x ⎡⎫∈-⎪⎢⎣⎭∴函数在区间为单调递增，又∵，，，()p x π,02⎡⎫-⎪⎢⎣⎭π2πe 102p -⎛⎫-=-< ⎪⎝⎭()01p =∴上存在唯一的使得，∴当时，，此时()p x 0π,02x ⎛⎫∈- ⎪⎝⎭()00p x =0π,2x x ⎡⎫∈-⎪⎢⎣⎭()0n x '<为减函数，()n x 当时，，此时为增函数，又∵，，()0,0x x ∈()0h x '>()n x π2πe 02n -⎛⎫-=> ⎪⎝⎭()00n =∴存在，使得，∴当时，，为增函数，10π,2x x ⎛⎫∈- ⎪⎝⎭()10n x =1π,2x x ⎡⎫∈-⎪⎢⎣⎭()0m x '>()m x 当时，，为减函数，又∵，，()1,0x x ∈()0m x '<()m x π2πe 102m a -⎛⎫-=+-> ⎪⎝⎭()010m a =-≥∴时，，则为增函数，∴，∴π,02x ⎡⎫∈-⎪⎢⎣⎭()0h x '>()h x ()()00h x h ≤=()e cos 20x x x ax +--≥恒成立，..........9分②当时，在上恒成立，则在上为增函数， 1a >()e cos 0x m x x '=-≥[0,)+∞()m x [0,)+∞∵，， ()010m a =-<ln(1)(ln(1))e sin(ln(1))1sin(ln(1))0a m a a a a ++=-+-=-+≥∴存在唯一的使，()20,x ∈+∞()20h x '=∴当时，，从而在上单调递减，∴，20x x ≤<()0h x '<()h x [)20,x ()()00h x h <=∴，与矛盾，...........11分()e cos 20xx x ax +--<2e cos 20x x x x ax x +--≥综上所述，实数的取值范围为. ...........12分 a (,1]-∞22．(1)解：令，，则，2()0xf x e ax =-=()0,x ∈+∞2e xa x=23．因为在有两个零点，所以函数与的图象有两个不同的交点，()f x ()0,∞+y a =2ex y x=令，则， ()22e (),0,h x x x =∈+∞()()23e 2e (),0,xx x h x x x x -'==∈+∞当时，；当时，． (0,2)x ∈()0h x '<(2,)x ∈+∞()0h x '>所以在单调递减，在单调递增，所以，()h x (0,2)(2,)+∞()()2mine 24h x h ==又当时，，当时，，所以；...........4分0x +→()h x →+∞x →+∞()h x →+∞2e4a >(2) 证明：，故，()e (e 1)x x g x =x --()e (2e 2)x xg x =x '--令，， ()2e 2x m x =x --()2e 1x m x ='-当时，，当时，， 1ln2x <()0m x '<1ln 2x >()0m x '>所以在上单调递减，在上单调递增， ()m x 1(,ln )2-∞1(ln +)2∞，又，，，(0)0m =1ln 211(ln )2e ln 2ln 21022m =--=-<22(2)2e (2)20e 2m ==----->由零点存在性定理及的单调性知，方程在上有唯一根，...........6分()h x ()0m x =1(2,ln )2-设为且，从而有两个零点和，0x 002e 20xx =--()m x 0x 0当或时，，当时，，0x x <0x >()0g x '>00x x <<()0g x '<所以在单调递增，在上单调递减，在单调递增， ()g x 0(,)x -∞0(0)x ，(0+)∞，从而存在唯一的极大值点，由，得， ...........8分 ()g x 0x 002e 20x x =--002e 2xx +=，2000000000222111()e (e 1)(1)()(2)=224444x x x x x x g x x x x x ++-++∴=--=--=-+≤（）当且仅当，即时，取等号，002x x -=+01x =-若，则，与题意矛盾，01x =-0102e 22e 10x x =----≠故，所以取等不成立，所以得证，...........10分 01x ≠-01()4g x <又，在单调递增，012ln2x -<< ()g x 0,x -∞（）所以得证，...........11分 2242032()(2)e e (2)1e e e g x g ----⎡⎤>-=---=+>⎣⎦所以............12分 0321()e 4g x <<。

北京市第一次普通高中2023-2024学年高二上学期学业水平合格性考试数学试题

③ k R ，使曲线 y f x 与 y kx 恰有两个交点.
其中所有正确结论的序号是
.
试卷第 3页，共 7页
三、解答题
25．已知函数 f x 2cos2x .
(1)求 f x 的最小正周期；
(2)求
f
x
在区间
0,
π 2
上的最大值和最小值.
26．阅读下面题目及其解答过程.
已知函数 f x 2x 2x .
北京市第一次普通高中 2023-2024 学年高二上学期学业水平合格性考试数学试题
学校:___________姓名：___________班级：___________考号：___________
一、单选题
1．已知集合 A 1, 0,1, B 1, 2 ，则 A B （）
A． 1
B． 2
C．1, 2
1 2
试卷第 2页，共 7页
D． 1 6
18． sin15 cos15 2 （）
A．
1 2
B．1
C． 3 2
19．已知 a 0,b 0 ，且 a b 1，则 a b 的取值范围是（）
A．1, 0
B． 0,1
C． 1,1
D．2
D． 2,2
20．某校组织全校 1850 名学生赴山东曲阜、陕西西安和河南洛阳三地开展研究性学习
D．1,0,1, 2
2．复数 i2 （）
A．i
B． i
3．函数 f x x x2 1 的零点为（）
C．1
D． 1
A． 1
B．0
C．1
4．已知向量
a
0,1
,
b
2,1
，则
a
b

2020-2021学年北京市高二第一次普通高中学业水平合格性考试数学试题(解析版)

2020-2021学年北京市高二第一次普通高中学业水平合格性考试数学试题一、单选题1．已知集合{1,0,2},{0,1,2}A B =-=，则A B ＝（） A ．{－1，0，2} B ．{0，1，2} C ．{－1，0，1} D ．{－1，0，1，2} 【答案】D【分析】由集合并集概念求得结果即可. 【详解】由题知，{}1,0,1,2A B ⋃=-. 故选：D.2．已知复数134i z =-，223i z =-+，则12z z +=（） A ．1i - B ．5i - C ．17i - D ．5i +【答案】A【分析】根据复数加法运算求得结果.【详解】由题知，()()123243i 1i z z +=-+-+=- 故选：A3．函数2()log f x x =的定义域是（） A ．(1,)-+∞ B ．(0,)+∞ C ．(1,)+∞ D ．(2,)+∞【答案】B【分析】利用真数大于直接求解【详解】由题意0x >，故函数2()log f x x =的定义域是(0,)+∞ 故选：B4．下列函数中，在区间()0,∞+上单调递减的是（）A ．2y x B ．y =C ．2xy =D ．12xy ⎛⎫= ⎪⎝⎭【答案】D【分析】根据基本初等函数的单调性判断可得出结论.【详解】函数2y x 、y x =、2xy =在()0,∞+上均为增函数，函数12xy ⎛⎫= ⎪⎝⎭在()0,∞+上为减函数. 故选：D.5．下列各点中，在函数()21x f x =-的图象上的点是（） A ．（0，0） B ．（0，1） C ．（1，0） D ．（1，2）【答案】A【分析】直接代入计算可得.【详解】解：因为()21xf x =-，所以()00210f =-=，故函数过点()0,0.故选：A.6．某校为了解学生关于校本课程的选课意向，计划从高一、高二这两个年级共500名学生中，采用分层抽样的方法抽取50人进行调査．已知高一年级共有300名学生，那么应抽取高一年级学生的人数为（） A ．10 B ．20C ．30D ．40【答案】C【分析】根据分层抽样的定义求出相应比例，进而得出结果.【详解】解：因为高一年级共有300名学生，占高一、高二这两个年级共500名的30035005=，则采用分层抽样的方法抽取50人中，应抽取高一年级学生的人数为350305⨯=人.故选：C.7．如图，四边形ABCD 是平行四边形，则AB BC +=（）A ．ACB ．CAC ．BD D ．DB【答案】A【分析】根据向量加法的三角形法则计算可得；【详解】解： AB BC AC故选：A8．在平面直角坐标系xOy 中，角α以Ox 为始边，它的终边经过点()4,3，则cos α=（）A ．45-B ．45 C ．34-D ．34【答案】B【分析】由任意角的三角函数的定义即可求得结果. 【详解】解：角α以Ox 为始边，终边经过点()4,3，∴4cos 5α==. 故选：B.9．函数()||1f x x =-的零点个数是（） A ．0 B ．1 C ．2 D ．3【答案】C【分析】令()||10f x x =-=求解. 【详解】令()||10f x x =-=，解得 1x =±，所以函数()||1f x x =-的零点个数是2，故选：C10．已知a R ∈，则“1a >”是“0a >”的（） A ．充分而不必要条件 B ．必要而不充分条件 C ．充要条件 D ．既不充分也不必要条件【答案】A【分析】根据两者的推出关系，结合充要条件的概念分析即可．【详解】若1a >，则0a >成立，若0a >，无法推出1a >，故1a >是0a >的充分不必要条件，故选：A ．【点睛】本题考查了充分条件必要条件的判断，考查逻辑思维能力，属于基础题． 11．sin20°cos10°＋cos20°sin10°＝（）A ．12 B C D ．1【答案】A【分析】逆用两角和的正弦公式求值. 【详解】原式()1sin 2010sin 302=︒+︒=︒=故选：A12．如图，在长方体1111ABCD A B C D -中，AB ＝AD ＝2，13AA =，则四棱锥1D ABCD -的体积为（）A ．3B ．4C ．6D ．9【答案】B【分析】根据长方体的特殊线面关系，结合棱锥体积公式求得结果. 【详解】在长方体中，1DD ⊥底面ABCD ，则四棱锥1D ABCD -的体积为122343⨯⨯⨯=.故选：B13．已知篮球运动员甲、乙的罚球命中率分别为0.9，0.8，且两人罚球是否命中相互独立．若甲、乙各罚球一次，则两人都命中的概率为（） A ．0.08 B ．0.18 C ．0.25 D ．0.72【答案】D【分析】根据独立事件乘法公式求解【详解】由题意，根据独立事件乘法两人都命中的概率为0.90.80.72⨯= 故选：D14．在△ABC 中，a ＝4，A ＝45°，B ＝60°，则b ＝（） A ．22B ．23C ．6D ．42【答案】C【分析】利用正弦定理直接求解【详解】由正弦定理34sin 226sin sin sin 2a b a Bb A B A=∴===故选：C15．不等式x （x －1）＜0的解集为（） A ．{01}xx <<∣ B ．{10}xx -<<∣C ．{0x x <∣或1}x >D ．{1xx <-∣或0}x > 【答案】A【分析】根据一元二次方程的两个根，解得一元二次不等式的解集. 【详解】方程()10x x -=有两个根0,1，则不等式()10x x -<的解集为{}01x x << 故选：A16．在△ABC 中，a ＝2，b ＝4，C ＝60°，则c ＝（）A ．2B ．C ．4D ．6【答案】B【分析】直接利用余弦定理求解即可. 【详解】2222cos 416812c a b ab C =+-=+-=∵，c ∴=故选：B17．函数()3sin cos f x x x =的最大值为（） A ．1 B ．12C ．2D ．32【答案】D【分析】由二倍角公式可得()3sin 22f x x =，结合正弦函数的值域即可得结果【详解】∵()33sin cos sin 22f x x x x ==，∴函数()3sin cos f x x x =的最大值是32.故选：D.18．已知224a b >>，则（） A ．a ＞b ＞2 B ．b ＞a ＞2C ．a ＜b ＜2D ．b ＜a ＜2【答案】A【分析】利用指数函数单调性解不等式即可【详解】222422a b a b >>=∴>> 故选：A19．已知向量,a b 在正方形网格中的位置如图所示．若网格中每个小正方形的边长均为1，则·a b ＝（）A ．3B ．32C ．6D ．12【答案】C【分析】从图中读出向量模长和夹角，按照数量积运算公式求得结果. 【详解】由图知，322a b ==，，两向量的夹角为45°，则2··cos ,3226a b a b a b ==⨯⨯= 故选：C20．在信息论中，设某随机事件发生的概率为p ，称21log p为该随机事件的自信息．若随机抛一枚均匀的硬币1次，则“正面朝上”这一事件的自信息为（） A ．0 B ．12C ．1D ．2【答案】C【分析】首先求出“正面朝上”的概率，再代入计算可得；【详解】解：随机抛一枚均匀的硬币1次，则“正面朝上”的概率12p =，所以22211log log log 2112p===，故“正面朝上”这一事件的自信息为1；故选：C二、填空题21．已知a ，b 是实数，且a ＞b ，则－a ________－b （填“＞”或“＜”）．【答案】＜【分析】根据不等式的性质计算可得；【详解】解：因为a b >，所以a b -<- 故答案为：<22．已知向量a ＝（1，m ），b ＝（2，4）．若//a b ，则实数m ＝________．【答案】2【分析】根据向量平行关系求得参数.【详解】由//a b 知，124m=，解得m =2. 故答案为：223．设m ，n 是两条不同的直线，,αβ是两个不同的平面．给出下列三个命题： ①如果m ∥n ，m ⊥α，那么n ⊥α； ②如果m ⊥α，m ⊥β，那么α//β； ③如果α⊥β，m ∥β，那么m ⊥α．其中所有真命题的序号是________．【答案】①②【分析】由线面垂直的判定定理可判断①；由线面垂直的性质可判断②；由面面垂直的性质可判断③【详解】解：对于①，由m ∥n ，m ⊥α，可得n ⊥α，所以①正确；对于②，由m ⊥α，m ⊥β，可得α//β，所以②正确；对于③，由α⊥β，m ∥β，可得直线m 与平面α可平行，可能相交但不垂直，可能垂直，还有可能直线m 在平面α内，所以③错误，故答案为：①②三、双空题24．已知函数1()f x x x=+，则f (x )是________函数（填“奇”或“偶”）；f (x )在区间（0，＋∞）上的最小值是________．【答案】奇 2【分析】根据奇函数定义判断函数奇偶性；利用基本不等关系求得最小值.【详解】由题知，1()()f x x f x x-=--=-，故()f x 是奇函数；(0,)x ∈+∞时，1()2f x x x =+≥=，当且仅当1x =时，等号成立，则()f x 的最小值为2. 故答案为：奇；2.四、解答题25．已知函数()sin 4f x x π⎛⎫=- ⎪⎝⎭．（1）写出f (x )的最小正周期；（2）求f (x )在区间0,2π⎡⎤⎢⎥⎣⎦上的最小值和最大值．【答案】（1）2π ；（2）最小值为．【分析】（1）根据函数解析式写出最小正周期；（2）根据正弦函数单调性判断函数在区间上的单调性，从而求得最值.【详解】解：（1）f (x )的最小正周期为2π．（2）因为02x π，所以444x πππ--．所以函数在0,2π⎡⎤⎢⎥⎣⎦上单调递增，当44x ππ-=-，即x ＝0时，f (x )取得最小值2-；当44x ππ-=，即2x π=时，f (x )所以f (x )在区间0,2π⎡⎤⎢⎥⎣⎦上的最小值为26．阅读下面题目及其解答过程．已知函数23,0()2,0x x f x x x x +⎧=⎨-+>⎩，（1）求f （－2）与f （2）的值；（2）求f (x )的最大值．解：（1）因为－2＜0，所以f （－2）＝ ① ．因为2＞0，所以f （2）＝ ② ．（2）因为x ≤0时，有f (x )＝x ＋3≤3，而且f （0）＝3，所以f (x )在(,0]-∞上的最大值为 ③ ．又因为x ＞0时，有22()2(1)11f x x x x =-+=--+，而且 ④ ，所以f (x )在（0，＋∞）上的最大值为1．综上，f (x )的最大值为 ⑤ ．以上题目的解答过程中，设置了①~⑤五个空格，如下的表格中为每个空格给出了两个选项，其中只有一个正确，请选出你认为正确的选项，并填写在答题卡的指定位置（只需填写“A ”或“B ”）．④ A ．f （1）＝1 B ．f （1）＝0 ⑤ A ．1 B ．3【答案】（1）①A ； ②B ；（2）③A ； ④A ； ⑤B ．【分析】依题意按照步骤写出完整的解答步骤，即可得解；【详解】解：因为23,0()2,0x x f x x x x +⎧=⎨-+>⎩，（1）因为20-<，所以()2231f -=-+=，因为20>，所以()222220f =-+⨯=（2）因为0x ≤时，有()33f x x =+≤，而且()03f =，所以()f x 在(,0]-∞上的最大值为3．又因为0x >时，有22()2(1)11f x x x x =-+=--+，而且()11f =，所以()f x 在()0,∞+上的最大值为1．综上，()f x 的最大值为3．27．如图，在三棱锥O －ABC 中，OA ，OB ，OC 两两互相垂直，OA ＝OB ，且D ，E ，F 分别为AC ，BC ，AB 的中点．（1）求证：DE ∕∕平面AOB ；（2）求证：AB ⊥平面OCF ．【答案】（1）见解析；（2）见解析．【分析】（1）D ，E 分别为AC ，BC 的中点，得DE AB ∕∕，从而证明DE ∕∕平面AOB ；（2）OA ，OB ，OC 两两互相垂直，得：OC ⊥平面AOB ，从而得出OC AB ⊥，由题易知AB OF ⊥从而证明AB ⊥平面OCF ．【详解】解：（1）在△ABC 中，D ，E 分别为AC ，BC 的中点，所以DE ∥AB ．又因为DE⊄平面AOB，所以DE∥平面AOB．（2）因为OA＝OB，F为AB的中点，所以AB⊥OF．因为OC⊥OA，OC⊥OB，所以OC⊥平面AOB．所以AB⊥OC．所以AB⊥平面OCF．28．为确定传染病的感染者，医学上可采用“二分检测方案”．假设待检测的总人数是2m（m为正整数）．将这2m个人的样本混合在一起做第1轮检测（检测1次），如果检测结果是阴性，可确定这些人都未感染；如果检测结果是阳性，可确定其中有感染者，则将这些人平均分成两组，每组12m-个人的样本混合在一起做第2轮检测，每组检测1次．依此类推：每轮检测后，排除结果为阴性的组，而将每个结果为阳性的组再平均分成两组，做下一轮检测，直至确定所有的感染者．例如，当待检测的总人数为8，且标记为“x”的人是唯一感染者时，“二分检测方案”可用下图表示．从图中可以看出，需要经过4轮共n次检测后，才能确定标记为“x”的人是唯一感染者．（1）写出n的值；（2）若待检测的总人数为8，采用“二分检测方案”，经过4轮共9次检测后确定了所有的感染者，写出感染者人数的所有可能值；（3）若待检测的总人数为102，且其中不超过2人感染，写出采用“二分检测方案”所需总检测次数的最大值．【答案】（1）7n =；（2）感染者人数可能的取值为2，3，4；（3）39．【分析】（1）由图可计算得到n 的取值；（2）当经过4轮共9次检测后确定所有感染者，只需第3轮对两组都进行检查，由此所有可能的结果；（3）当所需检测次数最大时，需有2名感染者，并在第2轮检测时分居两组当中，从而将问题转化为待检测人数为92的组，每组1个感染者，共需的检测次数，由此可计算求得结果.【详解】（1）由题意知：第1轮需检测1次；第2轮需检测2次；第3轮需检测2次；第4轮需检测2次；12227n ∴=+++=；（2）由（1）可知：若只有1个感染者，则只需7次检测即可；经过4轮共9次检测查出所有感染者，比只有1个感染者多2次检测，则只需第3轮时，对两组都都进行检查，即对最后4个人进行检查，可能结果如下图所示：∴感染者人数可能的取值为2，3，4.（3）若没有感染者，则只需1次检测即可；若只有1个感染者，则只需121021+⨯=次检测即可；若有2个感染者，若要检测次数最多，则第2轮检测时，2个感染者不位于同一组中；此时相当于两个待检测人数均为92的组，每组1个感染者，此时每组需要12919+⨯=次检测；∴此时两组共需21938⨯=次检测；∴若有2个感染者，且检测次数最多，共需38139+=次检测. 综上所述：所需总检测次数的最大值为39.。

第一次考试题高二

2022-2023学年江苏省泰州市高二年级上册学期第一次教学质量调研考试数学试题

广东省揭阳市惠来县第一中学2024-2025学年高二上学期第一次阶段考试数学试题

2022-2023学年甘肃省陕西师范大学平凉实验中学高二下学期第一次考试地理试题

高二语文下册第一次段考试题(附答案)

江西省部分学校2023-2024学年高二下学期第一次阶段性考试语文试题

2021-2022学年安徽省蒙城县第八中学高二上学期第一次考试地理试题(Word版)

高二第一次月考(物理)试卷含答案解析

高二地理第一次月考试题

江苏省无锡市普通高中2024_2025学年高二政治上学期期末第一次学业水平模拟考试试题含解析

甘肃省天水市田家炳中学(原：天水四中)2022-2023学年高二上学期第一阶段考试物理试题(含答案)

北京市第一次普通高中2023-2024学年高二上学期学业水平合格性考试数学试题

2022-2023学年河北省衡水阳光中学高二上学期第一次阶段考试化学试题

广东省惠州市第一中学2021-2023学年高二上学期9月第一次月考语文试题及答案 统编版高二

高二数学第一次月考试卷理科 试题

福建省高二下学期第一次月考数学试题(Word版)

北京市第一次普通高中2023-2024学年高二上学期学业水平合格性考试数学试题

2020-2021学年北京市高二第一次普通高中学业水平合格性考试数学试题(解析版)

广东省惠州市第一中学2021-2023学年高二上学期9月第一次月考语文试题及答案统编版高二

高二数学第一次月考试卷理科试题