高职《高等数学》教学中融入数学建模思想的几个案例
高等数学教学中的数学建模思想运用研究

高等数学教学中的数学建模思想运用研究高等数学在我国高质量人才培养中的作用不可替代。
但是,其中一些抽象的概念和定理,往往令学生望而生畏。
研究数学建模思想在高中数学教学中的应用,实际问题不仅比教材上的概念、定理更加具体,而且,可以培养学生数学的应用能力和创新能力。
高等数学数学建模思想创新能力数学应用能力一、引言高等数学教学是我国高等学校非数学专业学生培养计划中的一门非常重要的基础课。
在我国高质量人才培养过程中具有不可替代的作用。
通过对高等代数的学习,可以为其它专业课或者是基础课打下非常坚实的数学基础,并且提供必要的数学概念,培养学生的数学素质和修养。
在高等数学教学过程中,在向学生传授知识的同时,还应该利用教学过程中的各种环节来培养学生的逻辑推理能力、抽象思维能力、空间想象能力以及预算能力;培养学生利用已经掌握的知识综合运用去分析问题、解决问题的能力;培养学生的自主学习能力;以及培养学生的创新能力和创新精神。
数学建模的过程,就是一个对问题进行分析、提炼、演绎推理、归纳总结的过程,改变了传统仅重视推理的数学教学模式,突出了对数学知识的深入理解和实践应用,能够将抽象的数学思想具体化、复杂的推理简单化,强调对数学知识的直观说明和解释。
将数学建模思想融入到高等数学建模过程中,可以让学生不仅能够掌握表面的数学知识,而且有助于学生学会如何“使用数学”,学会将实际问题进行数学模型化,利用所学的数学知识来解决实际问题。
因此,将数学建模思想融入到高等数学教学过程中是十分必要的。
二、高等数学教学中的数学建模思想运用的基本思路1.在概念讲授中的应用高等数学中的极限、函数、积分、级数等概念,其本质上都是从客观事物中抽象出来的数学模型。
在对这些概念进行讲授时,应该自然而然的引入生活中的一些,来让学生将抽象的数学概念与客观世界向联系。
教师应该尽可能的结合实际,在观察、操作、猜想、实验、归纳以及验证等方面为学生提供更加直观、更加丰富的背景材料,从而引导学生自主到参加到教学活动中来。
[在高职数学教学中融入数学建模的探讨]大学数学建模经典例题
![[在高职数学教学中融入数学建模的探讨]大学数学建模经典例题](https://img.taocdn.com/s3/m/f81405fa5f0e7cd1842536f7.png)
[在高职数学教学中融入数学建模的探讨]大学数学建模经典例题高等职业教育是普通高等教育的重要组成部分,也是高等教育发展的一个新类型。
近几年来我国高等职业教育飞速发展,规模不断扩张,职教理念也不断成熟。
高职教育模式也由传统的学科教育模式向就业导向模式转变。
但是在高职教育飞速发展的同时,也逐渐暴露出一些问题。
在教学方面主要体现为课程结构不合理、基础课程不能体现实用性等。
高等数学作为高职院校一门重要的基础课程,一直没有真正摆脱普通高校教学模式的影响,从来没有真正体现出自己的高职特色。
因此我们必须在高职数学的教学中注重数学的实用性,而将数学建模融入到我们的数学教学中,是我们高职数学教学改革的主要方向。
1、高职数学教学的教学现状分析高职教育的培养目标是培养高素质的技能型人才。
我们必须转变传统的人才培养观念,主动适应社会需求,加强与行业、企业的结合,深化改革,加快发展,增强培养高技能人才的能力。
高等数学课程是高职教育必不可少的基础课程,它不仅为学生的后续学习奠定了基础,而且对学生科学思维的培养和形成具有重要意义。
受传统高校教学模式的影响,目前高等数学的教学在教学过程重理论轻应用,与高职教育的目标有些偏离,从而导致数学教学枯燥无味。
另外教材的建设与高职的发展有些脱节,目前大部分高职教材在教学内容上仍是按照原有的教学体系进行设计,不能有效的指导学生在专业课程的实质性应用。
我们高职学生学习数学的主要目的不仅为了掌握更多的数学知识,为专业课程打下基础,更重要的是培养他们的思维能力,并解决工作中遇到的具体问题。
传统的数学教学虽然有效的培养了学生的逻辑思维能力,但是这种教学方法在也扼杀了学生的创造性思维,学生不知道如何将自己所学的数学知识应用到生产实践中。
面对以上的问题,我们的高职数学教学亟需改革,以适应目前高职教育的人才培养目标。
2、高职数学教学中融入数学建模的作用数学在经济、军事、科技等各个领域均有着广泛的应用,比如电子计算机的发明和应用等。
数学建模案例在高等数学教学中的应用
经 过 一 些 合 理 假 设 后 , 到 如 图 2 2坐 标 系 , 中 A, , D正 方 形 A D 的 中 心 为 坐 标 原 点 . BC 0为 A 连 线 与 轴 的 夹 角 , ( C 厂 0)
首 先 , 们 把 易 拉 罐 近 似 看 成 一 个 正 圆 柱 形 进 行 建 模 是 有 一 定 合 理 性 的 . 一 步 观 察 我 们 发 现 罐 体 的侧 边 我 进
材 料 很 薄 , 顶 盖 材 料 很 硬 ( , 为 要 使 劲 拉 ); 说 明 实 际 建 模 必 须 考 虑 不 同 部 位 的 体 积 ( 同 部 位 材 料 不 而 厚 因 这 不 同 , 应 的 价 格 也 不 同 ) 因此 , 们 可 简 化 为 如 下 模 型 : 拉 罐 内 部 体 积 一 定 , 盖 厚 度 为 其 余 部 分 厚 度 的 相 . 我 易 顶 倍 时 , 易 拉罐 材料 的体 积最 小 的罐体 内部 的尺寸 为 多少 ? 使 设 饮 料 罐 的 半 径 为 r 因 此 , 径 为 d=2 ), 的 高 为 h, 内 体 积 为 ; 盖 外 的 材 料 的 厚 度 为 b 项 盖 的 厚 ( 直 r 罐 罐 顶 ,
.
为 A, c两 脚 与 地 面 距 离 之 和 , ) g( 为 , 两 脚 与 地 面 距 离 之 和 , 0) 0, D f( g ( 0 ) .由假 设 ( ) g都 是 连 续 函 数 . 假 设 ( ), 于 任 意 0 厂 ) g( )中 2 ,, 由 3 对 ( 和 0
案 例 2: 点 存 在 定 理 与 椅 子 放 平 问 题 零
在 介 绍 闭 区 问 上 连 续 函 数 的 零 点 存 在 定 理 时 , 们 可 以 给 出 下 面 来 自 日常 生 活 中 的 问 题 : 把 四 条 腿 长 我 一
高职高专数学建模思想融入高等数学教学的探索

高职高专数学建模思想融入高等数学教学的探索【摘要】高职高专数学建模是培养学生综合运用知识解决实际问题的重要手段,而高等数学教学存在着理论与实践脱节、缺乏应用意识等问题。
将数学建模思想融入高等数学教学具有重要意义。
本文探讨了数学建模思想在高等数学教学中的必要性和具体运用方法,并通过实践案例分析展示了其在教学中的实际效果。
通过本文的研究可以启示教师在教学中要注重培养学生的实际应用能力,展望未来数学建模思想将更广泛地融入高等数学教学,促进学生综合能力的提升。
【关键词】高职高专、数学建模、高等数学教学、思想融入、问题、必要性、具体运用、实践案例、教学启示、展望未来。
1. 引言1.1 背景介绍为了解决这些问题,将数学建模思想融入高等数学教学中变得尤为重要。
通过将数学建模思想和方法引入高等数学教学中,可以更好地激发学生学习兴趣,提高其数学实践能力和解决实际问题的能力。
数学建模思想在教学中的具体运用也将有助于提升教育教学的质量,培养学生的创新思维和实践能力。
本文将探讨高职高专数学建模思想融入高等数学教学的意义和必要性,分析数学建模思想在教学中的具体运用,并通过实践案例分析来论证该教学模式的有效性。
结合这些内容,对教学的启示和未来的发展进行展望。
2. 正文2.1 高职高专数学建模的意义高职高专数学建模的意义在于引导学生运用数学知识解决实际问题,培养学生的实践能力和创新思维。
通过数学建模,学生能够了解数学在现实生活中的应用,增强数学知识的实用性和可操作性。
数学建模还可以培养学生的团队合作能力和综合分析能力,让他们在解决复杂问题时能够更好地合作、思考和创新。
数学建模还能够帮助学生培养问题意识和解决问题的能力,使他们具备更强的实践能力和探索精神。
高职高专数学建模的意义在于提高学生的综合素质,增强他们的数学实践能力和创新能力,为他们未来的学习和工作打下坚实的基础。
2.2 高等数学教学存在的问题传统的高等数学教学注重理论的讲解和公式的推导,缺乏实际问题的引入和应用,导致学生对数学的兴趣不高,学习动力不足。
数学建模案例在高等数学教学中的应用

高等数学是高等院校理工科 和经管类学生必修的一门数学基础课 程, 直接关系到学生后续数学课程和专业课程 的学习。然而 , 现在 的 教学模式 过分强调数 学知识 的理 论性和技巧 性 ,忽略 了数学的应用 性。而数 学建模在提高学生学习数学的兴趣 ,提高学生主动获取 知识 的能力 ,培养学生应用知识解决实际问题的能力等方面体现 了重要 的 作用。因此, 将数学建模的思想融人日常的高等数学的课程教学中是 当今高等数学课程教学改革 的主要趋势。 1 在高等t学教学过程中啊入救掌t■思想 的必要性 传 统 的数 学课程体 系偏重理 论 、注 重推理 ,淡 化知识 的实际背 景 ,使教学与实际割裂开来 ,导致学生 即使学了很多的公式 、定理 , 也不能用其解决实际问题。而数学建模就为我们提供了这一平 台,使 学 生在熟练掌握数学基本知识的同时 , 增强 了分析 、解决实际问题 的
教学文件教学业务部门的管理教学理论教育和研究活动等方面构成保管文件材料这是一种间接的教学活动的原始记录包括教师的教学价值结果的分析分析的论文研究项目教案反思在教学理论以及其他活动间接声像档案如教学实践视频等这些图像表达并辅以简短的文字澄清历史纪录纪录片直观典型的特点学校档案馆协助完成任务中占据重要地位的教育活动知识和信息的方式因为他们是存储详细真实地反映了大学的教学历史图片审查后传送的文件如教师教学教案实验报告研究论文毕业设计论论文等可以快速了解高等教育教学情境的基本使命而且还作为一种教学管理评估的基础上基本参考
证 明 :将 椅 子 旋 转 9 0 。 ,对 角 线 A c和 B D互 换 , 由
g ( o J = 0 , - 厂 【 0 ) > 0可知 g (  ̄ / 2 ) > 0 , , 2 ) = 0。令 ^ ) = g ( a ) - f ( o )
数学建模在高中数学教学中的应用案例

数学建模在高中数学教学中的应用案例数学建模是一种将现实问题转化为数学问题,并通过数学方法进行求解的过程。
它不仅能提高学生的数学思维能力和解决实际问题的能力,还能激发学生对数学的兴趣。
在高中数学教学中,数学建模已经逐渐得到应用。
本文将以几个实际案例来探讨数学建模在高中数学教学中的应用。
案例一:城市交通流量优化城市交通拥堵一直是人们头疼的问题。
如何合理规划城市道路,优化交通流量,成为了城市规划师们的重要任务。
在高中数学课堂中,可以通过数学建模来让学生了解交通流量优化的原理和方法。
首先,学生可以通过观察城市道路交通流量的数据,了解不同时间段和不同道路的交通流量情况。
然后,他们可以使用数学模型,如线性规划模型,来分析交通流量的变化规律,并提出相应的优化方案。
通过这种方式,学生不仅能够学习到线性规划的基本原理,还能将其应用到实际问题中。
案例二:环境污染治理环境污染是当前社会面临的严重问题之一。
在高中数学教学中,可以通过数学建模来让学生了解环境污染治理的方法和效果。
学生可以通过收集环境污染数据,了解不同因素对环境污染的影响。
然后,他们可以使用数学模型,如微分方程模型,来模拟环境污染的传播和变化过程,并提出相应的治理方案。
通过这种方式,学生不仅能够学习到微分方程的基本原理,还能将其应用到实际问题中。
案例三:金融风险评估金融风险评估是金融领域的重要工作之一。
在高中数学教学中,可以通过数学建模来让学生了解金融风险评估的方法和意义。
学生可以通过收集金融市场数据,了解不同金融产品的风险情况。
然后,他们可以使用数学模型,如概率模型,来评估金融产品的风险水平,并提出相应的风险控制方案。
通过这种方式,学生不仅能够学习到概率论的基本原理,还能将其应用到实际问题中。
通过以上几个案例,我们可以看到数学建模在高中数学教学中的应用是非常广泛的。
通过数学建模,学生不仅能够学习到数学的基本知识和技能,还能培养他们的实际问题解决能力和创新精神。
把数学建模融入高等数学教学中的两个案例

CUIHa ・ i iyng,H OU e y W n—u, L n s n ILi —ha
( ai C ussD p r e t f e igU i n es y B in 1 0 0 , hn ) B s o r e a m n o B i n no U i ri , e i c e t j n v t j g 0 1 1 C ia
象 、 化 、 用数 学 的语 言 和 方 法 , 立 数 学模 型 , 简 运 建
边 , 且 能够 加 深 学生 对 许 多 重要 的数 学概 念 、 而 方
法 的理解 , 高他们学 习高等数 学 的兴 趣 、 心 , 提 信 甚
至有 可能造 成 “ 而后 知 不 足 ” 用 的进 一步 学 习 更多
o ih rmah mai si u o wa d.T a e fh g e t e t sp tf r r c wo c s s:t e c i cde c ewe n mi u e h n n o rh n h on i n e b t e n t a d a d h u a d,t e s a e h h p
第2 4卷第 1 总 7 期 9期
把数学建模融人高等数学教学 中的两个 案例
崔 海英 , 文 字 , 林 杉 侯 李
( 京 联 合 大 学 基 础部 , 京 北 北 10 0 ) 0 1 1
[ 摘 要 ] 简单介 绍 了数 学建模 , 出 了可 以将 数 学建模 融入到 高等数 学教 学 中去 , 出ai a o e ig i n r d c d,a d a d a o r i g ma h m ai a o ei g i t e c i g ta t e m t e tc lm d l si to u e n n n ie fme gn t e tc lm d l n o ta h n n
将数学建模引入高等数学教学中的典型案例

实验室管理人员实验课程的开课计划、实验课程二次选课;实验药品、低值品的申请与采购;实验设备的采购与管理;实验档案的管理;实验室开放的管理等等。
3实验室实验教学队伍建设的核心实验室实验教学队伍建设的核心首先是满足实验室对各层次人才的需求,其次是满足相关专业的人员需求,再就是尽可能提高上述人员的工作紧密度,特别是实验教学一线人员。
高校人员的条块与系列的差异,涉及到分配与利益不同,不可能一蹴而就。
但有一点大家是共识的,即:提高教学质量是教学改革的方向,任何阻碍终将都会被去除。
参考文献:[1]吴志强.全面提高本科实验室条件建设质量之举措[J].实验室研究与探索,2012(7):1-4.[2]刘树郁.高校实践教育的探索与思考[J].实验室研究与探索,2012,31(6):103-105.[3]时铭显.面向21世纪的美国工程教育改革[J].中国大学教育,2002,3.0引言高等数学课程[1]是数学类主干课程的核心,长期以来,在高等数学的教学中,教材大部分内容讲解概念、定理、推论及公式,教学上一味强调数学的严密性和逻辑性、抽象性,让学生感到似乎数学离我们很远,甚至有学了也没有什么用的错误想法,而数学建模正是联系数学理论知识与实际应用问题的桥梁,反映数学知识在各个领域的广泛应用,所以我们教师在高等数学教学过程中要不断渗透数学建模思想。
中国科学院院士李大潜曾提出“将数学建模的思想和方法融入大学数学类主干课程教学中”[2]。
合理安排数学建模案例是数学建模的思想与方法融入到高等数学中的具体实践[3,4],譬如,减肥模型、销售模型、人口模型、传染病模型等,让学生带着较愉悦的心情实实在在体会到所学数学知识与日常生活与现代科学技术的密不可分性,使学生在分析实际数学建模案例过程中体会数学的乐趣与应用价值,以培养学生解决实际应用问题能力。
因此,将数学建模案例融入在高等数学教学中有着十分重要的意义。
究竟如何将数学建模与高等数学相融合呢?1在高等数学的概念引入中渗透数学建模思想高等数学的概念一般都是从客观事物的某种数量关系或空间形式中抽象出来的数学模型,本身这一过程就是数学建模的过程,因此,我们在引入概念时,借助概念产生的来源背景和实际生活中的实际例子,对其抽象、概括、归纳求解自然而然引出概念,使学生实实在在感受到数学的作用,数学就在我们身边。
在高等数学中融入数学建模的教学案例分析

第27卷㊀第3期河南教育学院学报(自然科学版)Vol.27㊀No.32018年9月JournalofHenanInstituteofEducation(NaturalScienceEdition)Sep.2018收稿日期:2018-05-17基金项目:河南省高等学校重点科研项目(18B110018)ꎻ商丘学院教改项目(KYC-2017-24)作者简介:仝㊀伟(1985 )ꎬ男ꎬ河南信阳人ꎬ商丘学院计算机工程学院讲师.doi:10.3969/j.issn.1007-0834.2018.03.014在高等数学中融入数学建模的教学案例分析仝㊀伟(商丘学院计算机工程学院ꎬ河南商丘476000)㊀㊀摘要:结合高等数学课堂教学实践ꎬ以问题为导向ꎬ通过实际案例剖析如何将数学建模的思想融入高等数学的教学中ꎬ并对教学效果进行分析和评价ꎬ促使教师改变教学模式ꎬ从而提高学生学习兴趣和课堂教学质量ꎬ进而提高学生解决实际问题的数学素养.关键词:高等数学ꎻ数学建模ꎻ案例研究ꎻ教学模型ꎻ教学方法中图分类号:G642.4㊀㊀㊀㊀文献标志码:A㊀㊀㊀㊀文章编号:1007-0834(2018)03-0058-040㊀引言随着信息多元化的快速发展ꎬ各种新事物不断涌现ꎬ大学生对数学的学习重视程度有不断下降的趋势ꎬ他们很少有人能够认识到当今社会如此受崇拜的高科技技术其本质上是数学技术ꎬ比如医学上的CT(com ̄putedtomography)技术㊁图像模糊处理技术㊁指纹存储识别㊁数据分析处理㊁金融风险预测㊁人工智能机器人的设计㊁导弹的轨迹追踪以及火箭的可靠性试验等.当今的数学知识不再是一个辅助作用ꎬ而是更广泛地直接应用到各技术领域中ꎬ数学正在向一切领域渗透.作为一名高校教师的迫切任务是如何使学生认识到数学的重要性ꎬ把数学的思想㊁方法等轻松愉快地传授给他们ꎬ使他们能够用数学思维方式去思考问题.在教学中笔者感触最深的是ꎬ学生学完数学课程ꎬ只会完成一些设定好的简单计算ꎬ而对一些实际问题ꎬ不会利用数学方法去处理ꎬ比如说和我们的生活息息相关的贷款利息的计算问题.贷款买房ꎬ如果采用等额本息还款方式ꎬ如何选择贷款年限以及清楚地计算出每月的还款额ꎬ很多学生甚至身边的同事都感到茫然ꎬ感觉这应该是很高深的算法.其实学过数列的相关知识ꎬ就很容易解决这样的问题.这种现象也从侧面反映了应试教育的缺陷ꎬ应该引起高校教师的重视.为了改变这种现象ꎬ在教学中应该把数学建模的思想融入数学类主干课程中[1]ꎬ利用它引入数学中的概念㊁方法㊁思维ꎬ使数学课堂更加贴近实际生活ꎬ让学生感觉到高等数学不再是那么虚无缥缈的东西ꎬ不仅体会到了数学知识的魅力ꎬ还提高了学生分析解决实际问题的能力ꎬ使学生更有兴趣主动地思考问题.高等数学是一门比较抽象的学科ꎬ也是大部分同学进入大学都要学习的一门公共课程.但是教学模式跟不上时代发展的需要ꎬ教材编写规范化㊁严谨化ꎬ导致学生看到的都是概念㊁定理㊁抽象符号ꎬ实例又比较陈旧ꎬ和生活脱节ꎬ所以限制了学生学习的主动性和积极性.这就要求教师要充分备课ꎬ收集一些与生活密切相关㊁同学们又比较关心的数学模型引入数学课堂教学.数学模型一定要简单易懂ꎬ与生活联系紧密ꎬ引起学生的关注和兴趣ꎬ这样调动了学生积极思考的主动性ꎬ从而顺利地切入数学专业知识讲解中来.1㊀如何将数学建模思想融入高等数学教学中高等数学教学内容较多ꎬ而教学课时有限ꎬ因此如何讲好高等数学课程对数学教师提出了严峻的挑战[2].不能再像以前一样满堂课全面讲解系统的理论知识ꎬ教会学生如何解题ꎬ而应该尽快改变这种教学模式ꎬ认识上要把数学当做一种工具去解决实际问题作为学习的出发点ꎬ从而提高数学的地位ꎬ满足社会发展的需要.如何快速恰当地将数学模型思想融入要讲的数学知识中ꎬ这就要求教师备课不能仅仅局限于教材ꎬ要查找文献素材或者创新实例ꎬ把与生活密切相关又恰到好处的实例模型融入要讲解的课堂内容中.这种教学模式对教师提出了较高的要求ꎬ不仅要求教师具有较强的专业知识ꎬ同时还要求教师开阔视野ꎬ拓宽自己㊀第3期仝㊀伟:在高等数学中融入数学建模的教学案例分析59的知识面ꎬ尽可能多地了解和涉及数学在其他科学领域中的应用.比如ꎬ教经济类的学生㊁计算机类的学生㊁土木工程和通信工程的学生ꎬ他们对数学的偏重点不同ꎬ讲课尽可能收集到和专业相近的数学模型ꎬ补充到教材中去.教师是学生获得知识的主要来源ꎬ因此要求教师要向双师型转变ꎬ在注重理论知识的同时ꎬ还要有丰富的企业实践经验ꎬ从而更好地给学生传道㊁授业㊁解惑.高等数学中的许多概念㊁定理并不是 无源之水 ꎬ它们都是来源于实际问题ꎬ通过某一类实际问题ꎬ抽象出数学中的符号和工具ꎬ从而更好地解决此类问题ꎬ所以在大学的数学课堂中ꎬ我们的教学不能仅仅讲解抽象概念㊁符号ꎬ应该以问题为导向ꎬ引导学生在观察一些现象中主动去思考总结ꎬ下面举一些实际案例讲解如何把数学建模思想融入高等数学的教学中去.比如教师在讲解导数的概念时ꎬ不要仅仅局限于直接讲导数的定义㊁导数代表切线的斜率等ꎬ而要给学生灌输一种数学思想ꎬ把导数直接表述为变化率ꎬ让学生直观地去接触㊁理解一个未知的概念ꎬ然后ꎬ让同学们思考变化率代表什么样的现象ꎬ如生活中见到物体冷却时温度随时间变化的快慢ꎬ物体位移随时间变化的快慢等ꎬ让学生体会变化率贴近生活的含义ꎬ让学生真正理解原来导数是描述这种现象的.例如ꎬ在讲解定积分的概念时ꎬ一定要让学生了解其产生的实际背景及涉及的故事情节ꎬ了解其用途ꎬ真正体会定积分的含义ꎬ并用其解决实际生活中的问题ꎬ拉近数学与生活的距离.可以提问学生各种几何图形面积的求法ꎬ比如如何求椭圆的面积.给大家一点时间思考ꎬ通过讨论发现它们和规则图形的区别ꎬ由常量到变量如何处理这种问题.大家还能想到哪些变量数学问题ꎬ比如物理上恒力做功到变力做功ꎬ匀速直线运动到变速直线运动等.通过分析发现解决这类问题的共同点ꎬ不同背景下的问题最终归结成一类问题ꎬ那能不能用更好的方法或工具解决呢?从而避免了很多重复的工作ꎬ这样就水到渠成地引出了概念定理的核心内容.由具体到抽象ꎬ顺理成章地给出了定积分的概念ꎬ同学们知道定积分原来是解决这一类问题而产生的ꎬ比先讲概念再举例子效果更好.在讲解高等数学中的微分中值定理时ꎬ大部分教师只是讲解如何构造辅助函数ꎬ从几何角度出发证明定理.其实还可以按照它的物理实际意义去讲解ꎬ如平均速度等于某一时刻的瞬时速度.对于拉格朗日中值定理可举例:某个游客9点从山脚下出发ꎬ到14点爬到山顶ꎻ第二天上午9点从山顶出发ꎬ到14点到达山脚.问题:上山和下山过程中能否找到某一时刻的速度相同?这样通俗易懂的实例很容易激发同学们的思考.两者对学生能力培养有着不同的价值ꎬ前者突出对定理证明的理解和证明能力的提高ꎬ后者则突出对定理内涵的理解和应用能力的提高ꎬ应针对学生实际ꎬ有侧重采用不同的讲法ꎬ以通俗易懂的方式㊁素材㊁实例㊁讲解微积分ꎬ前提要求教师要充分备课.上例还可以用于讲解一元函数的介值定理ꎬ例如:某人第一天早上8点从山下出发ꎬ14点到达山顶.第二天早上8点由山顶出发按照原路线返回ꎬ并于14点到达山下原出发点.问题:在两天的行程中是否存在这样一个位置ꎬ该人经过这个位置的时刻相同[3]?针对该实际问题可建立数学模型:已知连续函数f(x)和g(x)ꎬ其中xɪ[aꎬb]ꎬ且有f(a)=8ꎬf(b)=14和g(a)=14ꎬg(b)=8ꎬ求证存在一点x0ɪ[aꎬb]ꎬ使得f(x0)=g(x0).高等数学作为基础学科ꎬ要弱化定理的证明过程ꎬ教会学生用直观的几何解释理解定理的内容ꎬ这样就减轻了学生的思维负担.比如在讲解微分方程的齐次方程时ꎬ向同学们提问探照灯或者汽车车灯的镜面是什么样的形状ꎬ为什么要这样去设计呢ꎬ改成其他形状好不好?这些都是现实中的实际问题ꎬ能够引起学生强烈的好奇心ꎬ活跃课堂气氛.比如在讲解极限时ꎬ可以提出这样的问题:一天之中分针和时针重合的时间有多少次?这种问题同学们在生活中经常遇到ꎬ教师可以先把它留下来给学生课下思考ꎬ大家经常见到这种现象ꎬ所以他们应该会感兴趣ꎬ思考解决此类问题的办法.在课堂教学中融入数学建模思想ꎬ可以有效解决数学教学的枯燥无味ꎬ因为通过数学建模的问题往往都是来源于实际生活ꎬ我们为了改变和创造世界ꎬ就不得不面临着做出各种合理的假设ꎬ收集各种数据ꎬ再利用数学方法建立各种变量之间的关系ꎬ即数学模型.复杂的模型求解还需要借助计算机软件处理ꎬ用得到的结果验证实际效果ꎬ整个过程就是一个不断探索创新㊁不断改进㊁不断优化的过程ꎬ让学生成为主体ꎬ锻炼学生观察事物㊁团结合作的能力.2 教学中融入数学建模案例分析案例选取要精巧适度㊁实际应用性强㊁学生比较感兴趣ꎬ同时具备人文气息.通过通俗易懂的语言描述出来ꎬ上课语言幽默和风趣ꎬ内容充满生活性和文化性ꎬ这样会给学生带来耳目一新的感觉ꎬ使数学恢复原本所具有的人文色彩和生活色彩.下面举几个教学中的实例进行分析ꎬ例如在讲解一阶常微分方程时引入 物体60㊀河南教育学院学报(自然科学版)2018年冷却模型 .案例1㊀把一杯100ħ开水放到周围环境温度20ħ中ꎬ观察水的温度在冷却过程中的变化规律.分析㊀根据牛顿冷却定律ꎬ物体温度T(t)的变化率与物体T和环境的温度之差成正比的关系.设T=T(t)ꎬ则dTdt=-k(T-20)(k>0)ꎬ这就是物体冷却过程的数学模型.得到了含有温度T关于时间t的导数的方程ꎬ可以请学生观察这个方程与之前学习过的方程有什么异同.通过这个方程我们能解出关于T(t)的函数关系吗?如果能解出来ꎬ方程的解是什么呢?如何解呢?通过这个问题我们可以首先引入微分方程的概念:含有未知函数T及它的一阶导数dTdt的方程ꎬ称为一阶微分方程.模型求解:确定T和时间t的关系ꎬ需要从方程中解出Tꎬ如何求解该微分方程呢?将方程改写成1T-20dT=-kdtꎬ这样变量T和t就分离出来了ꎬ两边同时积分ʏ1T-20dT=ʏ-kdtꎬ即lnT-20=-kt+lnCꎬ则T=Ce-kt+20.从而不需要测量就可以得到任意时刻水在冷却过程中的温度.然后让同学们思考:这个模型可以应用到哪些方面?比如说侦探小说里面的法医鉴定某人死亡的时间大致在几小时之前.还可以给同学们布置课外作业 请你破案 [4]ꎬ这样的模型选取简单易懂ꎬ同学们经常在电视剧和小说中看到这种情景.所以很容易让同学们产生共振ꎬ激发学生探索思考ꎬ从而让学生既体会到用数学理论解决实际问题的乐趣ꎬ又巩固了数学建模思想和方法ꎬ同时也培养了他们以后遇到疑难问题时理性思考问题的思维方式.案例2㊀探照灯的形状[5].上课时可以给学生提出这样的问题:汽车头上车灯的镜面是什么形状?为什么要这样设计呢?大家能否利用所学的微积分的知识去解释呢?探照灯的优点是:由点光源发出去的光线经过镜面时都能平行地反射出去ꎬ所以照射得更远.如图1探照灯的聚光镜的镜面是由图中的曲线L绕x轴旋转一周而成ꎬ设点光源为Oꎬ曲线L:y=y(x)ꎬ设M(xꎬy)是曲线上任一点ꎬMT为切线ꎬ斜率为yᶄ.分析探照灯的镜面形状如下ꎬ因为图1㊀聚光灯镜面Fig.1㊀CurveofmirrorsurfaceofspotlightøOMN=øNMRꎬ所以tanøOMN=tanøNMRꎬ则由正切的夹角公式可得ꎬyyᶄ2+2xyᶄ-y=0ꎬyᶄ=-xyʃ1+(xy)2ꎬ解得y2=2C(x+C2).则镜面的方程为y2+z2=2C(x+C2).此图形为典型的抛物线绕x轴旋转一周而形成的旋转抛物面ꎬ代表了探照灯形状的方程.通过这一案例的讲解ꎬ不仅可以使学生对抽象的微分方程建立直观的印象ꎬ而且又可以使学生认识到微分方程与实际联系比较密切的教学内容ꎬ因此学生就更容易理解并掌握住学习的内容ꎬ并把它转化到实际中去.案例3㊀饿狼追兔问题[6].现有一只兔子㊁一匹狼ꎬ兔子位于狼的正西100m处ꎬ假设兔子与狼同时发现对方并一起起跑ꎬ兔子往正北60m处的巢穴跑ꎬ而狼在追兔子.已知兔子㊁狼是匀速跑且狼的速度是兔子的两倍.问狼能追杀兔子美餐一顿吗?分析㊀假设狼始终沿着兔子的方向追击ꎬ为了研究狼能否追上兔子ꎬ可以先考虑狼追击兔子的曲线轨迹.建立直角参考系ꎬ以兔子为原点Oꎬ东西㊁南北方向为x轴㊁y轴ꎬA为狼的初始位置ꎬB为兔子的巢穴.设兔子的速度为vꎬ狼的追击曲线为y=y(x).则根据狼在某一点P(xꎬy)的切线方向指向兔子和相同时间内狼跑的距离是兔子的两倍ꎬ从而列出两个方程式ꎬyᶄ=-vt-yxꎬ2vt=ʏ100x1+yᶄ2dx.可得:2(y-xyᶄ)=ʏ100x1+yᶄ2dx.即2xyᵡ=1+yᶄ2ꎬ又初始条件为y(100)=0ꎬyᶄ(100)=0.结合计算机利用数学软件MATLAB求解ꎬy=130x32-10x12+2003ꎬ当x=0时ꎬy=2003>60ꎬ说明狼追不上兔子ꎬ只能铩羽而归.这个问题若改为狼的速度是兔子的3倍又是什么样?或者r倍会是什么样?让同学们课下分析讨论ꎬ这个例子不仅可以了解高阶微分方程ꎬ还融入了数学建模的思想ꎬ同时可以把它推广到军事上的导弹追击拦截问题等.表第3期仝㊀伟:在高等数学中融入数学建模的教学案例分析61㊀1是常见的教学模型案例.表1㊀教学模型案例Tab.1㊀Teachingmodelcases教学内容教学模型案例函数的极限割圆术求圆的面积㊁时针和分针重合的次数㊁连续复利(助学贷款㊁住房贷款)㊁植物生长㊁人口增长㊁细菌繁殖㊁经济增长㊁环境污染指标等模型ꎬ饮酒驾车问题ꎬ非法传销的 魅力 问题ꎬ合理避税问题导数易拉罐的外形设计㊁手机生产商的定价问题㊁最优化模型(商品存储费用优化ꎬ批量进货的周转周期ꎬ磁盘最大存储量ꎬ交通管理中的红㊁黄㊁绿灯亮的时间问题ꎬ洗衣机的节水问题)微分传染病模型㊁药物成分在体内的分布积分第二宇宙速度的计算㊁通信卫星的覆盖面积问题㊁行星轨道问题㊁交通信息黄灯闪烁时间的设定问题㊁天然气产量预测问题常微分方程探照灯镜面的形状㊁水的冷却模型(法医鉴定)㊁雪融化过程体积变化过程㊁降落伞下落运动规律㊁假画的鉴定㊁核废料处理㊁放射性元素衰变㊁传染病的流行㊁抵押贷款问题㊁饿狼追兔问题㊁导弹追踪问题级数龟兔赛跑悖论㊁投资费用问题3㊀小结面对目前的高等数学教学中出现的各种问题和困境ꎬ高等数学的教学改革刻不容缓ꎬ要想把高度抽象难懂的数学知识面向大众ꎬ必须把数学建模思想及案例融入教学中去ꎬ让学生体会到数学中的乐趣ꎬ同时也感受到数学的力量.这样学生学过高等数学后才能把它变成一种强有力的工具ꎬ解决生活中遇到的各种问题.总之ꎬ高校教师应该把数学建模思想和案例完美地融入数学教学中作为自己追求的目标.在 互联网+ 的信息化时代大背景环境下ꎬ我们顺应时代发展的步伐ꎬ在高等数学教学过程中从教学内容㊁教学方法和授课方式等方面融入数学建模思想ꎬ使学生不再机械地学习高等数学ꎬ而是由实际问题联想到高等数学的知识ꎬ从实际案例中学习数学知识ꎬ从精心设计的微课资源上学习数学知识ꎬ把传统教学和微课资源以及多媒体结合起来ꎬ理解和领会本门课程的核心思想ꎬ全面提高学生的数学素养ꎬ不断推动高等数学教学的改革和发展.参考文献[1]㊀李大潜.将数学建模思想融入数学类主干课程[J].中国大学教学ꎬ2006(1):9-11.[2]㊀王金华.数学建模思想融入高等数学教学的研究与实践[J].湘南学院学报ꎬ2010ꎬ31(4):31-33.[3]㊀唐小峰.数学建模思想融入高等数学教学的研究与探讨[J].佳木斯教育学院学报ꎬ2013(2):125-127.[4]㊀朱长青.将数学建模引入高等数学中的典型案例[J].价值工程ꎬ2014(3):258-259.[5]㊀同济大学数学系.高等数学:上册[M].北京:高等教育出版社ꎬ2014:306-307.[6]㊀洪清.高等数学教学中引入生活实训的实践与思考[J].九江学院学报(自然科学版)ꎬ2014(3):121-123.ResearchonTeachingCasesofMathematicalModelingAppliedinAdvancedMathematicsTONGWei(SchoolofComputerEngineeringꎬShangqiuCollegeꎬShangqiu476000ꎬChina)Abstract:Basedonadvancedmathematicsteachingpracticeandguidanceofproblemorientedꎬintroducedhowtopermeatethethinkingofmathematicalmodelingintoadvancedmathematicalteaching.Tochangethemodeofteachingꎬanalyzedandevaluatedtheteachingeffect.Itimprovedstudents learninginterestandthequalityofteachingꎬandfurtherimprovedstudents mathematicalliteracytosolvepracticalproblems.Keywords:advancedmathematicsꎻmathematicalmodelingꎻcasesstudyꎻteachingmodelꎻteachingmethod。
数学建模思想方法融入高等数学课堂的教学实例

1 引言
长 期 以来 , 高等 数学 教 学 和 培养 学 生 解 决实 例 问题 能力相 脱节 的 现象 比较严 重 , 统 教 学模 式 所 传 导致 的教学 内容 和体 系一成 不变 、 教学 手段单 一 、 教 学 以考 试 为 目的等 问题 已经严 重地 影 响到高 等数学 的教学 效果 。为改 变 这 一 现状 , 克服 传 统 教 学模 式
2 2 模 型建 立与 分析 . 看到 这个 问 题 , 先 , 指 导 学 生 查 阅 相 关 文 首 要
所带来 的种种弊端, 我们尝试着将数学建模思想方 法融人 到 高等数 学 的实 际 教学 过 程 中 , 以培养 学 生 解 决实 际 问题 的能力 , 动 学 生 学 习高 等 数 学 的积 调 极 性 和主 动性 。下面 以一类 变质性 物 品的生 产一库 存 问题 作为应 用 实例 , 以数 学建模思 想 方法为 指导 , 尝试着 应用 高等数 学知识 去解 决这 一应 用实例 。
【 e od 】 m te ai o en ;dacdmahmai ;e r rt gosivnoyss m;pldea l K yw rs ah m t a m dl gavne te t sdt i ae od; etr yt ap e xmp c l i c eo n e i e [ 中图分类号]0 2 27 [ 文献标识码]A [ 文章编 号]17 6 4—32 (0 2 0 2 9 2 1 )3—0 9 0 0 8— 4
类变质性物品的生产一 库存 问题为例 , 以数 学建模 思想方 法为指导 , 应用高等数学知识 去解决应用 实例 , 对于 强 化学 以致用的 目的、 培养学生的创新意识和创 新能力有很 大的启发性 。 【 关键词】 数学建模 ; 高等数学; 变质物 品; 库存 系统 ; 应用 实例
新工科背景下数学建模融入“高等数学”课程教学典型案例王于琴

新工科背景下数学建模融入“高等数学”课程教学典型案例王于琴发布时间:2023-06-15T08:40:19.669Z 来源:《教学与研究》2023年7期作者:王于琴[导读] 本文针对传统数学课堂教学中存在的问题,结合“新工科”背景下对人才的需求,改革教学方法,提出将数学建模思想融入课堂教学。
数学建模思想的引入,使抽象的理论变得更直观、生动,大大激发学生的学习兴趣,同时也提高了学生分析问题和解决问题的能力。
通过典型案例的实施过程探索教学成效以及教学反思,进而不断的改进教学方法。
重庆机电职业技术大学重庆 402760摘要:本文针对传统数学课堂教学中存在的问题,结合“新工科”背景下对人才的需求,改革教学方法,提出将数学建模思想融入课堂教学。
数学建模思想的引入,使抽象的理论变得更直观、生动,大大激发学生的学习兴趣,同时也提高了学生分析问题和解决问题的能力。
通过典型案例的实施过程探索教学成效以及教学反思,进而不断的改进教学方法。
关键字:新工科;数学建模;高等数学本案例针对传统数学课堂教学中存在的问题,结合“新工科”背景下对人才的需求,提出将数学建模思想融入课堂教学,通过具体的案例、数学建模思想的引入,使抽象的理论变得更直观、生动,大大激发学生的学习兴趣,同时达到提高学生分析问题和解决问题的能力。
一、改革背景2017年2月18日,教育部提出“新工科建设”,要求培养工程实践能力强、学科交叉融合和跨界整合的人才。
这对数学类课程建设提出了新的要求。
“新工科”是培养适应未来工程发展的应用型人才。
“新工科”人才培养理念是用成果导向替代学科导向,成果导向又由以学生为中心、反向设计和持续改进三个理念组成。
数学课程是所有高校工科专业的基础课程,而目前数学课程的课堂绝大多数都是教师在满堂灌,未体现出学生的主体地位,并且讲授的知识是纯理论知识较多,与实际问题相结合较少,因此未能达到“新工科”对应用型人才的培养。
通过在数学课堂中引入数学建模思想,一方面使学生能够认到专业知识与数学知识之间密不可分的关系;另一方面通过对具体问题分析、求解的过程,充分体现出学生的主体地位。
高等数学在数学建模中科学应用举例

室
设玻璃的热传导系数 为k1,空气的热传导系数 为k2,
内
单位时间通过单位面积由温度高的一侧流向温度低的
室
一侧的热量为θ
外
T1 Ta
T2
Tb
由热传导公式 θ=kΔT/d
d
l
解得:
d
k1
T1
d
Ta
k2 Ta
Tb l
k1
Tb
T2 d
Ta
1 k1l k2d T1 T2
R 线速 度v显然也是常数,否则图象声音必然会失真。此外,计数器的读 数n与转
ωvt 积分得到过的圈数有θ关,从而与转t 过的角
度θ成正比2 。
1 2
dθ v( π r ) dt 0
0
即
θ
2π ω
( ωv t π
r
2
)
1 2
t 0
2π ω
( ωπv t
再一步深入考虑
还应考虑回声传回来所需要的时间。为此,令石块下落 的真正时间 为t1,声音传回来 的时间记 为t2,还得解一个方程组:
h
g k
( t1
1 k
e kt1
)
g k2
h 340t2
这一方程组是非线性 的,求解不太容易, 为了估算崖高竟要去 解一个非线性主程组 似乎不合情理
t1 t2 3.9 相对于石块速度,声音速度要快得多,我们可 用方法二先求一次 h,令
令k=K/m,解得
F m dv mg Kv
v
dt
cekt
g
k
代入初始条件 v(0)=0,得c=-g/k,故有
再积分一次,得:
v g g ekt kk h g t g ekt c k k2
高职数学教学中融入数学建模思想的探讨

高职数学教学中融入数学建模思想的探讨引言当前,高考第五批和中专对口升学学生成为高职院校的主要生源,高等数学在高职院校不仅是工科学生公共必修课,同时也为经济类的专业基础课,对学生学习后续专业课程非常重要。
但学生数学基础相对薄弱,对学习不感兴趣,自制力差。
而学生对线性代数抽象的概念定理及其冗繁的计算难以接受成为线性代数教学的突出表现,因此,在线性代数教学中融入数学建模思想方法是解决学生理解困难和实现教学目标的有效途径。
一、高职院校线性代数教学情况与建模发展概况1.线性代数教学情况。
行列式、矩阵和线性方程组是目前高职院校线性代数部分教学的主要内容,所用的教材是以理论计算为主体,教学偏重其基本定义和定理,过分强调理论学习,忽视其方法和应用,有关线性代数应用实例几乎不涉及。
再者高职院校高等数学总体课时少,因此线性代数部分课时也非常有限,但其理论抽象,内容较多,教师在课堂上大多采用填鸭式的教学方式,导致该课程与实际应用严重脱离,造成了学生感觉线性代数知识枯燥,计算繁杂,学习它无用处,大大降低了学生的学习热情。
2.数学建模及其发展概况。
数学建模的基本思想就是利用数学知识化解实际问题,就是对问题展开调查、观测和分析,明确提出假设,经过抽象化精简,创建充分反映实际问题的数量关系;并利用数学知识和matlab、lingo、mathematics等数学软件解所获得的模型;再用税金结论表述实际问题,结合实际信息去检验结果,最后根据检验情况去对模型展开改良和应用领域,它并使学数学与用数学获得统一。
数学建模大专组竞赛积极开展尚无15年,参赛的高职院校逐年减少,我院在多年的参赛中获得了一定的成果,但因数学建模难度小和学生数学基础薄弱以及高职院校学制的原因,出席数学建模培训的学生基本为小一新生,而且只有大部分,显著受惠面小。
二、数学建模思想融人线性代数教学中的具体实施线性代数因其理论抽象,逻辑严密,计算繁琐,让人对其现实意义感受不到,使高职学生学习起来有困难,也就很难激发学生的学习兴趣,因此,线性代数教学过程中就要求教师介绍应用案例应体现科学性、通俗性和实用性。
高职数学教学中如何融入数学建模思想

高职数学教学中如何融入数学建模思想摘要:在当前高职院校中,数学作为一门比较基础的必修课程,它具有一定的重要性。
但是由于多方面因素的影响,大部分学生在学习的过程中感觉很困惑,这也使得高职院校数学教学暴露出较多的问题。
因此,应当及时的对数学教学内容进行改善与创新,将数学建模融入高职数学教学中有利于提升学生的思维逻辑。
本文首先分析高职数学教学中融入数学建模的重要性,随后提出对应的教学方法,以供参考。
关键词:高职数学;教学策略;数学建模1 前言高职数学教学是培养学生掌握适当的理论知识,应用所掌握的数学知识解决实际问题的能力。
高职数学教学过程中,应注重学生应用数学能力的培养,使数学变为解决生活实际问题的工具,不断提高学生的数学素养。
数学建模是实现应用数学知识解决生活实际问题的有效途径,在高职数学教学过程中,最迫切、最主要的问题就是如何将建模思想方法融入高职数学教学中,有效提高高职数学的教学质量,使学生成为应用型人才。
2 建模思想的相关概述数学建模可以从字面意思上理解为对真实世界存在的一种特定的对象做出的一些重要的假设,通过合理的数学工具,得到一个正确的数学结构。
借助于数学建模,我们可以理解一些特定现象的真实性,同时,借助于数学建模,还能够准确预测目标的未来发展趋势,在处理某些数据的过程当中,可以采用更准确的方法控制它的方向和走向,进而设计出符合人们所需求的相关产品。
在数学建模的过程当中我们首先需要分析问题,再根据问题的分析提出一个科学的模型假设,最后再进行求解。
根据所得的数据进行验证和分析,这样就可以很好地将模型应用到实际生活当中。
3 数学建模思想的作用3.1锻炼学生分析问题的能力构建数学模型的一个很重要的步骤就是进行模型假设。
要求大学生能够根据实际对象的特征和建立模型的目的,对所提出的问题进行必要的合理的简化,不同的假设会得到不同的模型。
从某种程度上说,构建的假设对数学建模是否成功发挥着十分重要的作用,这就要求学生能够分析清楚题目的特点,根据题目的特征联想相关的数学知识,进而建立合理的数学模型。
将数学建模思想融入高数课堂的案例分析-2019年教育文档

将数学建模思想融入高数课堂的案例分析1.引言高职院校开设公共基础课高等数学,强调数学知识的应用性.而采用传统单一的“填鸭式”的理论教学方法很难达到目的.很多高数教师可能都被学生问过这样一个问题:“学高数有什么用?”这说明通过我们的课堂教学,没有让学生感受到他们学到的东西能解决广泛的实际问题.数学建模是一种数学的思考方法,是通过抽象、简化,运用数学的语言和方法,建立数学模型,求解模型并得到结论及验证结论是否正确、合理的全过程,是解决传统教学活动中学生缺乏运用数学知识解决实际问题能力的有效途径[1].本文用数学建模的思想和方法,应用所学的高数相关的知识详细分析解答了“除雪机除雪问题”,是将数学建模思想融入高等数学教学一个案例.2.案例分析微积分是高数的核心内容,是解决实际问题强有力的数学工具,下面我们就尝试用学过的定积分解决一个日常生活问题.冬天的大雪常使公路上积起厚雪影响交通,有条10公里的公路积雪有一台除雪机负责清扫.每当路面积雪平均厚度达到0.5m时,除雪机就开始工作.但问题是开始除雪后,大雪仍下个不停,使路面上积雪越来越厚,除雪机工作速度逐渐减慢,直到继续工作.降雪的大小直接影响除雪机的工作速度,那么除雪机能否完成这10km路程的除雪任务,当雪下多大时除雪机无法工作[2]?相关情况和部分数据:(1)降雪持续下了一个小时;(2)降雪速度随时间变化,但下得最大时,积雪厚度的增量是每秒0.1cm;(3)当积雪厚度达到1.5m时,除雪机将无法工作;(4)除雪机在没有雪路上行驶速度为10m/s.问题分析:首先考虑与除雪机除雪有关的因素,其主要因素有:下雪的速度,积雪的厚度,除雪机工作速度及下雪持续的时间.为使问题简化,假设(1)下雪速度保持不变;(2)除雪机工作速度与积雪厚度成反比.设置变量,记下雪速度为R(cm/s),积雪厚度为d(m),除雪机工作速度为v(m/s).建立模型:(1)下雪厚度模型.在下雪速度保持不变的情况下,积雪在t秒内厚度增量△d=■Rt,因此t秒内积雪厚度为:d(t)=0.5+■(2.1)(2)除雪机工作速度模型.由问题的假设,并注意到当d=0时,v=10;d=1.5时,v=0,可建立关系式v(t)=10(1-■d(t)),0.5≤d(t)≤1.5,将(2.1)式带入得t秒时除雪机工作速度公式v(t)=■(2-■)(2.2)利用上述公式,可确定除雪机被迫停止工作的时间,由v(t)=0,得t■=■(2.3)除雪机工作t秒时的行驶距离S(t)=?蘩■■v(u)du=■?蘩■■(2-■)du=■t-■t■(2.4)情形1:大雪以每秒0.1cm的速度持续1h.积雪新增的厚度是■=3.6(m),再加上原来雪深0.5m,已经超过1.5m.只能考虑除雪机从雪厚0.5m到雪厚1.5m时的工作时间和除雪距离.由(2.3)可得:t■=■=■=1000(s)≈16.67(min),即除雪机只能工作16.67min就得停止工作,其行驶的距离由(2.4)得:S(t■)=S(1000)=■-■≈3.3(km).情形2:大雪以每秒0.025cm的速度持续1h.图1下雪速度速度变化图积雪新增的厚度恰好是情形1的■,为0.9m,再加上原来雪深0.5m,雪深不超过1.5m,除雪机始终可以工作.除雪机除雪10km所需时间,将S=10×1000m带入(2.4)得:10000=■t-■t■,t=2000(s)≈33.33(min),即只雪33.33(min)除雪机就可以清除完10km的积雪.模型改进:上述模型假设下雪速度保持不变,实际上,持续下1h雪,下雪的速度不可能恒定不变.现从实际出发把假设做得更合理些.假设下雪的速度在前30min均匀增大到最大值0.1cm/s,在后30min逐渐减小到零.如图1所示.用r(t)表示t时刻的下雪速度,则r(t)=■?摇?摇0≤t≤1800a-■?摇?摇1800≤t≤3600(2.5)r(t)的单位为cm/s.利用在t=1800处r(t)的连续性,可知参数a=0.2.积雪厚度函数:当0≤t≤1800时,d(t)=0.5+■?蘩■■■du=0.5+■t■(2.6)计算得d(1800)=0.5■=0.5+0.9=1.4(m),即除雪机工作30min时,积雪厚度达到1.4m.当1800≤t≤3600时,d(t)=1.4+■?蘩■■(0.2-■)du=0.01(0.2t-■t■)-1.3(2.7)计算得d(3600)=0.01(0.2×3600-■-1.3=2.3(m),说明雪还在下时除雪机已经停止工作.工作时间利用(2.7),取d(t)=1.5m可得t≈35(min).若考虑更复杂些,则还可以建立与实际更接近的数学模型.3.结语高职院校学生的数学基础相对较弱,学习高数有些吃力,利用传统的教学方法给他们“满堂灌”抽象的理论知识只会使他们对这门课望而生畏.在教学过程中引进数学模型,渗透数学建模的思想和方法,不仅能大大激发学生学习数学的兴趣,而且能提高他们应用数学的能力,还能够提升教师的教学水平,完善现有的教学方法,从而有效提高高等数学的教学质量.。
将数学建模融入高职经济数学中的教学案例

关键词: 经济数学;数学建模;数学教学
K ey w ords : economic mathematics; mathematical modeling; mathematical education
中图分类号:O 141.4;G712
文献标识码:A
文章编号=1006-4311(2017)13-0207-02 个交叉路□车辆进出数量相等。
〇 引言 经济数学是高职院校财经类专业设置的核心课程之 一, 是经管类各专业的一门重要基础课, 而使数学建模的 知识融入到高职经济数学这门基础课程教学中, 以更好地 为高素质、 高技能型人才培养目标服务, 一直是高职院校 数学教学改革的难点。 数学建模是通过调查研究、 了解信息、 简化假设、 抽象 分析、 运用数学的符号和程序, 以此建立数学模型, 以求解 模型得到结果并解决实际问题, 最后实际检验结论是否正 确的全过程。 目前数学建模课程的教学实验虽取得了一些 成效, 但也存在着不足。 究其原因, 其一数学建模主要针对 本科教学而高职类较少, 特别是经济数学建模教学和辅导 的教材缺乏; 其二重理论教学而轻实践应用, 很难得到有 实际应用的数学模型,缺乏所研究问题的知识和背景; 其 三没有明确的数学建模教学方法的指导。所 以 , 要推动高 职院校数学建模教学活动的有效开展, 必须进一步对数学 建模在高职院校教学中的作用进行探索与研究。 最近几年数学建模的竞赛活动在全国高职院校蓬勃 开展, 广州大学市政技术学院积极探索将数学建模的内容 融入数学或专业教学之中。下面作者结合自身的教学经 验, 给出三个把数学建模融入高职经济数学教学的案例。 i 交通网络流量分析问题 i. i 模型准备广东某城市单行线的交通流量如下图 所示, 以每小时通过的汽车数量来度量, 数字则表示该路
数学建模案例在高等数学教学中的应用探讨

数学建模案例在高等数学教学中的应用探讨高等数学是大学本科数学的一门基础课程,它主要涵盖微积分、线性代数和概率论等内容。
数学建模是将实际问题抽象为数学模型,并运用数学方法进行求解和分析的过程。
在高等数学教学中,数学建模可以帮助学生理解和应用数学知识,提高解决实际问题的能力。
下面将列举十个数学建模在高等数学教学中的应用案例。
1. 空气动力学模型:通过建立空气动力学模型,可以分析飞机的升力、阻力等特性,帮助学生理解微积分中的导数和积分概念,并应用这些概念解决实际问题。
2. 生物动力学模型:生物动力学模型可以描述生物体内的物质转化和能量转移过程,帮助学生理解微积分中的微分方程概念,并应用微分方程求解生物动力学问题。
3. 优化模型:通过建立优化模型,可以求解最大值、最小值等优化问题,帮助学生理解微积分中的极值问题,并应用优化方法解决实际问题,如最佳生产方案、最优投资策略等。
4. 随机模型:随机模型可以描述随机事件的发生规律,帮助学生理解概率论中的随机变量、概率分布等概念,并应用概率论方法分析和预测实际问题,如风险评估、统计调查等。
5. 线性回归模型:线性回归模型可以描述变量之间的线性关系,帮助学生理解线性代数中的矩阵和向量运算,并应用线性回归方法进行数据拟合和预测,如经济增长预测、市场需求分析等。
6. 系统动力学模型:系统动力学模型可以描述复杂系统的动态演化过程,帮助学生理解微分方程和线性代数的综合应用,并应用系统动力学方法分析系统稳定性和优化控制,如交通流量控制、环境污染管理等。
7. 物理建模:物理建模可以将物理现象转化为数学模型,帮助学生理解微积分中的物理应用,并应用物理建模方法解决实际问题,如物体运动轨迹预测、力学系统分析等。
8. 金融建模:金融建模可以描述金融市场的波动和风险特征,帮助学生理解概率论和统计学在金融领域的应用,并应用金融建模方法进行风险评估和投资决策,如股票价格预测、期权定价等。
9. 网络建模:网络建模可以描述网络中节点和连接的关系,帮助学生理解图论和线性代数在网络分析中的应用,并应用网络建模方法解决实际问题,如社交网络分析、电力系统优化等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高职《高等数学》教学中融入数学建模思想的几个案例摘要:本文就高职高专高等数学课程在微分学的教学过程中,融入数学建模思想给出了若干个案例,旨在加强数学建模向高等数学渗透,增进学生对数学建模的了解,提高学生学习数学的兴趣,并使其感受数学应用的广泛性。
关键词:高职高等数学数学建模案例
近年来,我国高等职业教育蓬勃发展,高等职业教育肩负着培养面向生产、建设、服务和管理第一线需要的高技能人才的使命。
高等职业教育的培养目标决定了高职培养的是高技能专门应用型人才,不要求学生的理论水平多高,但实践能力、动手能力要强。
数学建模在国民经济和社会活动的诸多方面都有非常具体的应用。
数学建模是用数学方法解决实际问题的第一步,许多模型的求解要借助计算机软件求解。
数学建模是把数学与计算机技术相结合解决各领域实际问题的一门学科。
现在的高职院校开设的数学课课时较少,而数学建模侧重数学应用,内容贴近实际,丰富多彩,是很好的培养应用能力的载体,很有必要把数学建模案例有机融入高等数学课程教学中,一方面培养学生的能力,提高素质,另一方面让学生体会到所学的数学是有用的,而且贴近实际的鲜活案例还能提高学生学习的兴趣,一举几得何乐不为。
下面就高等数学课中可融入数学建模的地方给出几个案例。
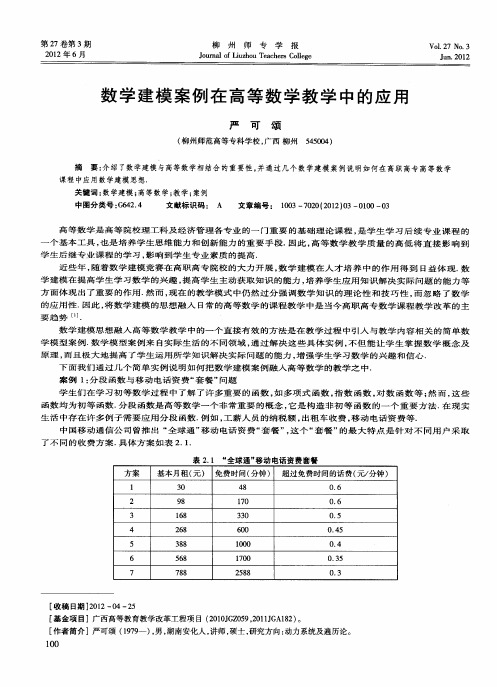
一、函数部分,可融入建立函数关系的几个案例
案例1某单位要建造一个容积为v(m3)的长方形水池,
它的底为正方形,如果池底的单位面积造价为a元,侧面单位面积造价b元,试建立总造价与底面边长之间的函数关系.
案例2 某种品牌的电视机,销售价为1500元时,每月可销售2000台,每台销价为1000元时,每月可多销售400台.试求该电视机的线性需求函数.
案例3某工厂生产某型号车床,年产量为a台,分若干批进行生产,每批生产准备费为b元,设产品均匀投入市场,且上一批用完后立即生产下一批,即平均库存量为批量的一半.设每年每台库存费为c元.显然,生产批量大则库存费高;生产批量少则批数增多,因而生产准备费高.为了选择最优批量,试求出一年中库存费和生产准备费之和与批量的函数关系.
案例4有一块边长为l(cm)的正方形铁皮,它的四角剪去四块边长都是x的小正方形,形成一只没有盖的容器,求这容器的容积v 与高x的函数关系.5某单位有汽车一辆,一年中的税款、保险费及司机工资等支出共a(元),另外,行驶单位路程需油费b (元),试写出一年中该车总费用y与行驶路程x的函数关系式.案例6一物体由静止开始作直线运动,前10s内作匀加速运动,加速度为2m/s2,10s后作匀速运动,运动开始时路程为零,试建立路程s与时间t之间的函数关系.7某地区上年度电价为0.8元/kw.h.,年用电量为a/kw.h.,本年度将电价降到0.55元/kw.h至0.75元/kw.h.之间.而用户期望电价为0.4元/kw.h..经测算,下调后新增的用电量与实际电价和用户期望电价的差成反
比(比例系数为k),该地区电力的成本价为0.3元/kw.h,写出本年度电价下调后,电力部门的收益y与实际电价x的函数关系式(提示:收益=实际用电量×(实际电价-成本价)).8 1982年底,我国人口为10.3亿,如果不实行计划生育政策,按照年均2%的自然增长率,那么到2000年底,我国人口将是多少?若人口基数为p0,人口自然增长率为r,试建立人口模型。
9
用铝板制作一个容积为v的直圆柱形易拉罐,求其表面积与底面半径的函数关系。
学习内容做好了铺垫。
涉及到简单的最优化模型,存储模型,人口模型等。
可作为例题或课后习题。
二、极限与连续部分的数列极限部分可融入房贷问题
案例1(等额本金贷款还是等额本息贷款合适?)
贷款买房与我们的生活息息相关,2009年10月李先生购房缺资金15万元,决定向某银行贷款,贷款期限10年,当时的年利率5.94%,但李先生没贷过款,利率可打9折,如果采用等额本息还款法,计算他每月的还款额是多少?若采用利随本清的等本不等息递减还款法,计算他每月的还款额是多少?比较两种贷款的优劣?
两种方式总还款差额为4215.745元,等额本金贷款总还款额少,但前期还款压力大。
如果你当时资金特别紧张,可采用等额本息贷款,如果你想总还款额少,你可选择等额本金贷款。
三、导数部分可融入简单的最优化问题和边际与弹性分析案例
案例1:降价能增收吗?
在市场竞争中,商品价格大战随处可见。
如手机价格大战、电视价格大战、空调价格大战……那么,降价能增收吗?下面通过数
学建模及微积分的方法来揭开其中的神秘面纱。
结果分析:上述结果说明价格下降1%,需求上涨幅度大于1%时,收益才会增加,否则降价将不增收或反而减收,这是符合实际情况的。
在实际教学中,由于课时及学生程度不同,可适当选择案例,让学生了解数学建模及数学的应用的广泛性。
参考文献:
[1]王振吉,封梅.经济应用数学基础.北京交通大学出版社,2010.
[2]叶其孝.可以融入高等数学课程的数学建模教学单元.。
