计算材料学(第一性原理_密度泛函理论_分子动力学)-md
计算材料-第一性原理

第三章 计算材料学-第一性原理及应用
材料计算模拟的尺度
计算机在材料科学与工程中的应用
第三章 计算材料学-第一性原理及应用
典型模拟方法及所对应的模拟尺度
材料电子结构模拟-第一性原理 材料原子层次模拟-分子动力学 材料介观层次模拟-相场动力学 材料宏观层次模拟-有限元法
计算机在材料科学与工程中的应用
第三章 计算材料学-第一性原理及应用
多粒子体系的第一性原理
材料的性质(如硬度、电磁和光学性质)和发生在固体内 的物理和化学过程是由它所包含的原子核及其电子的行为 决定的。
理论上,给定一块固体化学成分(即所含原子核的电荷和 质量),我们就可以计算这些固体的性质。因为一块固体 实际上是一个多粒子体系。决定这个体系性质的波函数可 以通过解薛定谔(Schrödinger)波动方程来获得。
计算机在材料科学与工程中的应用
第三章 计算材料学-第一性原理及应用
计算材料学用途
曾庆丰说,迈海材料基因组国际研究院是在华夏幸福、清华产业 园、陕西金控等产业资本支持下成立的,预计到2020年形成初具 规模的产业链布局,主要包括材料基因组软件、新能源材料、低 维材料与器件、石墨烯、生物3D打印和特色专科医院等,将形 成超过10亿元人民币规模的材料基因组产业集群。
1964年,P.Hohenberg和W.Kohn在非均匀电子气理论的基础上,提出两个基本 定理,奠定了密度泛函理论的基础。
定理1:对于一个共同的外部势v(r), 相互作用的多粒子系统的所有基态性质都由
(非简并)基态的电子密度分布n(r)唯一地决定。
计算机在材料科学与工程中的应用
第三章 计算材料学-第一性原理及应用
1965年柯恩又和沈吕九证明(W. Kohn and L. J. Shan, Physical Review 140, All33):一个多粒子体系的粒子密度函数可以通过一个 简单的单粒子波动方程获得。这个单粒子波动方程现在被称作柯恩 -沈(Kohn-Sham)方程。 Hohenberg,Kohn和Shan的理论就是诺贝尔化学奖颁词所指的密 度泛函理论。显然,密度泛函理论大大简化了应用量子力学探讨材 料物理性质所涉及的数学问题。
密度泛函理论描述材料基态性质和反应动力学

密度泛函理论描述材料基态性质和反应动力学密度泛函理论(DFT)是一种量子力学计算方法,用于描述材料的基态性质和反应动力学。
它基于量子力学的基本原理,通过对材料中所有电子的波函数进行统计,得到电子的密度分布,并据此计算材料的物理性质和化学反应。
在密度泛函理论中,我们利用了一种名为“泛函”的数学函数,该函数将系统的电子密度作为输入,并输出能量、力和其他相关性质。
泛函理论的核心思想是将复杂的多体问题简化为单一的电子密度问题,从而降低了计算的复杂性。
这使得DFT成为材料科学和化学研究中的重要工具。
首先,DFT可以用来预测材料的基态性质。
通过计算材料的晶体结构和电子能带结构,可以得到材料的基态能量、键长、晶格参数和电子分布等重要性质。
这些性质对于了解材料的稳定性、机械性质、光学性质等至关重要。
例如,我们可以利用DFT方法预测某种材料的晶体结构和稳定性,以优化材料的性能,例如改善导电性、光电性和磁性。
此外,DFT还可以用于分子模拟,研究分子的结构和物性,例如预测分子的电荷分布、光学吸收和化学反应。
其次,DFT能够描述材料的反应动力学。
通过DFT计算材料和分子之间的反应势能垒和反应速率常数,可以预测化学反应的速率和选择性。
这对于理解材料的催化性能和催化反应机制至关重要。
催化剂在许多工业过程中起着关键作用,例如水的电解、颗粒的合成和废气的处理。
通过DFT计算,我们可以优化催化剂的活性、选择性和稳定性,从而提高催化反应的效率。
在应用DFT进行密度泛函理论计算时,需要选择合适的泛函近似和基组。
泛函近似是用于计算电子相关性的数学函数,而基组则是用于展开电子波函数的一组基本函数。
不同的泛函和基组对于计算结果的精度和可靠性有重要影响。
因此,在选择泛函和基组时,需要根据具体问题和所研究的材料性质进行合理的折衷和优化。
尽管DFT在理论和实际应用中取得了巨大成功,但它仍然存在一些局限性。
首先,DFT是基于密度的近似,无法直接处理强关联和强关联效应,因此在处理过渡金属催化反应、磁性材料和强关联电子体系等问题时可能存在误差。
计算材料学(第一性原理_密度泛函理论_分子动力学)-md(课堂课资)

• 其中, • 根据定理一, • 根据变分原理有:
因此,基态电荷密度所对应的总能值,总是比其他任何密
广义梯度近似泛函不仅是电荷密度的函数而且和这点电荷密度随空间的变化有关轨道泛函范德瓦尔斯泛函95章节内容均匀电子气体系的定义均匀电子气体系完全由其电荷密度来表示同时也可定义一个只包含一个电子的球体的半径96章节内容excn与交换关联项的关系excn是由于电子间交换和关联相互作用带来的能量变化空间某点的excn值通过对其周围空间的各点积分得到在每个电子周围会产生所谓的xchole即在其周围其他电子密度将减少电子间的相互作用包括泡利排斥简并能库仑能等97章节内容蒙特卡罗方法得到的si的xchole98章节内容三种方法lcao利用分子和原子轨道展开波函数99章节内容
在
的区域内的通解是:
利用边界条件:
得:
章节内容
12
简单例子二:一维无限深势阱(1)
解:A=0, cos =0, B=0, sin =0,
能级(能量本征值) :
波函数:
(n 为奇数)
(n 为偶数)
分立能级!!! n= 1, 2,3, 。。。
章节内容
13
简单例子三:库仑场(中心力场)中的电子(1)
• 原子核产生的库仑场是一种特殊的中心力场, 如果原子核外只有一个 电子:质量为m, 带电量-e, 取原子核为坐标原点,电子受原子核吸
电子的动能项
原子核的动能项
核与核的相互作用项
电子与电子相互作用项
电子与原子核的相互作用项
-- 每立方米物质对应的求和指标i, j 是 的数量级。想要求解这样的系统,必 须做一系列的合理简化
【豆丁推荐】-》一种基于第一性原理的4H_SiC结构缺陷计算模型

0.引言SiC 材料具有宽禁带、高临界击穿电场、高饱和电子漂移速度和高的热导率等各种优秀特性。
目前,SiC 外延生长技术的主要问题是外延层中高密度的缺陷。
主要包括螺旋位错(TSDS)、刃型位错(TEDS)和基面位错(BPDS)等,其密度分别为104,104~105,104~105cm -2[1]。
在4H-SiC 外延生长工艺中,衬底上的基面位错能够转化成外延层中的刃型位错。
这种转化降低了外延层中基面位错的密度,也就减小了外延层中缺陷对SiC 器件的损害。
通过对基面位错的模拟,可以计算位错的密度和分布,态密度,能带结构,基面位错的转化等[2]。
将结构缺陷模拟应用于PIN 二极管的优化,在实验无法勘察位错外貌和结构,或者研究自然条件下很难出现位错的界面时,用计算机模拟位错可以为位错研究提供依据。
基于计算模拟,人们对碳化硅材料特性进行了广泛的研究。
1986年Bacon ,Liang 等人采用Linnard-Jones 势模拟了多种六角密集结构的金属位错结构;1994年MeijieTang [3]等通过修正Tersoff 势函数,延长粒子之间作用的范围,对晶体SiC 材料的力学性质进行了模拟。
Chang K J [4]等,利用abinitio 分子动力学模拟对SiC 的结构、电子云密度进行了模拟。
目前对于4H-SiC 位错的模拟还很少,它的结构及模型还待于探索和研究。
本文主要介绍了一种4H-SiC 结构位错模型及计算模拟过程中的主要技术细节。
1.4H-SiC 的计算模拟基本模拟过程是在一定系统及已知分子势能函数下,从计算分子间作用力着手,求解牛顿运动方程,来计算作用在原子集团上每个原子的力[5]。
准确确定位错芯原子组态的合理方法是采用半离散模型,即把晶体划分为两个区域:靠近位错芯(包含位错芯)的区域I ,在次以外的区域为区域II 。
在区域I 中引入一缺陷,此时要根据弹性理论所预计的位移来改变原子坐标,然后原子同时弛豫,通过反复迭代方程,使系统中每个原子逐步位移到势能最低位置,从而确定出最小势能的原子组态。
第一性原理分子动力学

3
理论基础
1、从头计算分子动力学 实际上很难直接求解多电子体系分子或固体的方程 式,因而早在量子力学发展初期就曾提出将电子运动与 原子核的运动分开处理的方案,这就是著名的波恩-奥 本海默绝热近似。
4
理论基础
1、从头计算分子动力学
波恩-奥本海默绝热近似
物理思想: 原子核的质量比电子大1840倍以上,电子的运动速 度远远快于核的速度。对于分子或固体中的电子系统, 总的电子波函数取决于做热振动的离子的瞬时相对位置。 • 电子运动很快,以至于绝热近似地来适应缓慢运 动着的离子的影响; • 离子缓慢运动,快速运动的电子可以看成一个均 匀的背景; • 电子和离子可以看成两个独立的子系统。
i (r , t ) i (r , t t ) 2 i (r , t ) i (r , t t ) t 2 t 2 1 E 2 i (r , t ) i (r , t t ) ij j (r , t ) * i (r , t ) j 2
26
共轭梯度算法
最速下降方法
F g x
1
x x1
假设最速降落的方向可以通过该点的负梯度得到,则
g1 Gx1
那么,沿此方向移动就可到达该方向的最小值,即
x b g
1
1 1
27
共轭梯度算法
最速下降方法
F (x b g )min
1 1 1
g G(x b g ) 0
9
Hellmann-Feynman定理
E H RI RI H H H RI RI RI E H E RI RI RI E H RI RI H RI
第一节第一性原理计算方法综述

第一性原理计算的理论方法随着科技的发展,计算机性能也得到了飞速的提高,人们对物理理论的认识也更加的深入,利用计算机模拟对材料进行设计已经成为现代科学研究不可缺少的研究手段。
这主要是因为在许多情况下计算机模拟比实验更快、更省,还得意于计算机模拟可以预测一些当前实验水平难以达到的情况。
然而在众多的模拟方法中,第一性原理计算凭借其独特的精度和无需经验参数而得到众多研究人员的青睐,成为计算材料学的重要基础和核心计算。
本章将介绍第一性原理计算的理论基础,研究方法和ABINIT软件包。
1.1 第一性原理第一性原理计算( 简称从头计算,the abinitio calculation),指从所要研究的材料的原子组分出发,运用量子力学及其它物理规律,通过自洽计算来确定指定材料的几何结构、电子结构、热力学性质和光学性质等材料物性的方法。
基本思想是将多原子构成的实际体系理解成为只有电子和原子核组成的多粒子系统,运用量子力学等最基本的物理原理最大限度的对问题进行”非经验”处理。
【1】第一性原理计算就只需要用到五个最基本的物理常量即( m o.e.h.c.k b ) 和元素周期表中各组分元素的电子结构,就可以合理地预测材料的许多物理性质。
用第一性原理计算的晶胞大小和实验值相比误差只有几个百分点,其他性质也和实验结果比较吻合,体现了该理论的正确性。
第一性原理计算按照如下三个基本假设把问题简化:1.利用Born-Oppenheimer 绝热近似把包含原子核和电子的多粒子问题转化为多电子问题。
2.利用密度泛函理论的单电子近似把多电子薛定谔方程简化为比较容易求解的单电子方程。
3.利用自洽迭代法求解单电子方程得到系统基态和其他性质。
以下我将简单介绍这些第一性原理计算的理论基础和实现方法:绝热近似、密度泛函理论、局域密度近似(LDA)和广义梯度近似(GGA)、平面波及赝势方法、密度泛函的微扰理论、热力学计算方法和第一性原理计算程序包ABINIT。
计算材料学:第一性原理计算及其应用

波粒二象性
Louis de Broglie (1924) 2
波粒二象性
Louis de Broglie (1924)
M. Bron (1926) 2
薛定谔方程
Schrödinger(1926)
3
薛定谔方程
Schrödinger(1926) Heisenberg(1926)
3
薛定谔方程
Schrödinger(1926)
13
V. Zolyomi and J. Kurti, Physical Review B 70, 085403 (2004).
14
Never End ……
15
spin
ቤተ መጻሕፍቲ ባይዱ
Never End ……
External Field Temperature Time-dependent Excited States Transport
15
参考文献
[1] Kohanoff J 2006 Electronic Structure Calculations for Solids and Molecules (Cambridge:Cambridge University Press) [2] Martin R M 2004 Electronic Structure (Cambridge:Cambridge University Press) [3] Ouyang M, Huang J L, Cheung C L and Lieber C M 2001 Science 292 702 [4] Zolyomi V and Kurti J 2004 Physical Review B 70 085403 [5] Rakitin A, Papadopoulos C and Xu J M 2003 Phys. Rev. B 67 03341
计算材料学-第5章 分子动力学性能分析及其应用

cxy
M 1iM 1xixyiy
M 1iM 1xix
2M 1iM ቤተ መጻሕፍቲ ባይዱyiy
2
x-xyiy
2
2
x- x yiy
(5.2)9
cxy也可以写为
cxy
M i 1xi
yi
M 1iM 1xiiM 1yi
iM 1xi2M 1iM 1xi2iM 1yi2M 1iM 1y22
(5.3)0
热力学性质,如温度、压力、热容。这些量可由 体系的坐标和动量的统计平均得到,称为静态性 能。
有一类热力学性质不能在一次模拟中直接得到。 也就是说,这些性质不能表达为体系中所有粒子 坐标和动量的一些函数的简单平均,称为动态性 能。
物性参量可以根据原子的坐标和速度通过统计处理得出, 在统计物理中可以利用系综微观量的统计平均值来计算物 性参量值,即
分子动力学模拟可以提供特定时刻的值,这样使得我 们可以计算一个时刻的物理量与同一时刻或另一时刻(时 间t以后) 的另一物理量的关联函数,这个值被称为时间关 联系数,关联函数可以写为
(5.31)
上式用到了lim t→0时,Cxy=〈xy〉和 lim t→ 时, Cxy=<x><y>
如果<x>和<y>是不同的物理量,则关联函数称为交叉关联 函数(cross-correlation function)。
热力学量关于平均值的分布应该是高斯分布,即
发现一个特定值 A 的几率为
p(A)=
(5.1)
式中,为方差, =〈 的平方根。
〉。标准偏差为方差
微观领域往往研究单个粒子的行为,
宏观性质是大量粒子的综合行为。
分子动力学(MD)方法可以研究由热力学统计物 理能够给出的各种性能参数。统计力学将系统的 微观量与宏观量通过统计物理联系起来。
计算材料学
摘要:本文通过第一性原理方法,从理论角度研究掺杂ZnO的电子结构(包括能带结构、电子态密度)。
氧化锌(ZnO是一种有着广泛的应用前景的宽带隙半导体材料,属II-VI 族,在光电和压电等方面有着优越的价值。
在室温下禁带宽度为 3.37eV,束缚激子能高达60meV 关键词:ZnO第一性原理能带结构态密度ZnO是一种有着十分广泛的应用前景宽带隙半导体材料。
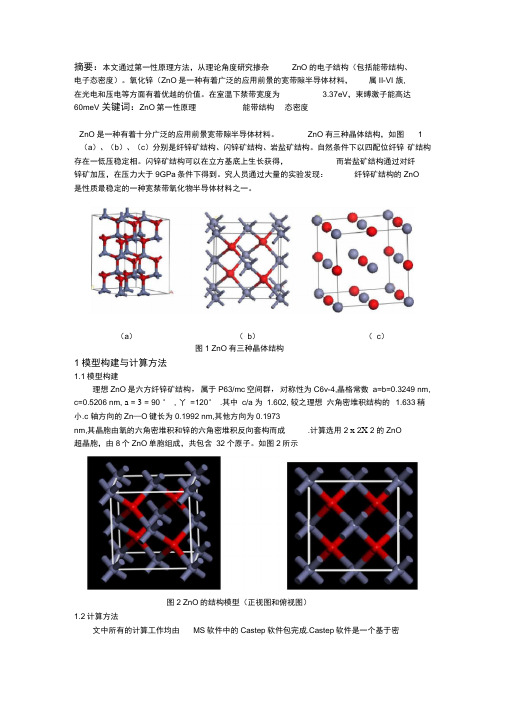
ZnO有三种晶体结构,如图1(a)、(b)、(c)分别是纤锌矿结构、闪锌矿结构、岩盐矿结构。
自然条件下以四配位纤锌矿结构存在一低压稳定相。
闪锌矿结构可以在立方基底上生长获得,而岩盐矿结构通过对纤锌矿加压,在压力大于9GPa条件下得到。
究人员通过大量的实验发现:纤锌矿结构的ZnO是性质最稳定的一种宽禁带氧化物半导体材料之一。
(a)(b)(c)图1 ZnO有三种晶体结构1模型构建与计算方法1.1模型构建理想ZnO是六方纤锌矿结构,属于P63/mc空间群,对称性为C6v-4,晶格常数a=b=0.3249 nm, c=0.5206 nm, a = 3 = 90 ° , 丫=120° .其中c/a 为1.602, 较之理想六角密堆积结构的 1.633稍小.c 轴方向的Zn—O键长为0.1992 nm,其他方向为0.1973nm,其晶胞由氧的六角密堆积和锌的六角密堆积反向套构而成.计算选用2 x 2X 2的ZnO超晶胞,由8个ZnO单胞组成,共包含32个原子。
如图2所示图2 ZnO的结构模型(正视图和俯视图)1.2计算方法文中所有的计算工作均由MS软件中的Castep软件包完成.Castep软件是一个基于密度泛函方法的从头算量子力学程序:利用总能量平面波赝势方法,将粒子势用赝势替代,电子波函数用平面波基组展开,电子-电子相互作用的交换和相关势由局域密度近似(LDA)或广义梯度近似(GGA)进行校正,它是目前较为准确的电子结构计算的理论方法。
纳米材料的模拟与计算方法介绍

纳米材料的模拟与计算方法介绍导言在纳米科技的快速发展下,纳米材料成为了当前科学研究领域的一个热门话题。
然而,由于其微观结构的特殊性,研究和理解纳米材料的性质和行为是一项极具挑战性的任务。
为了更好地理解纳米材料,科学家们使用了许多不同的方法,其中模拟与计算方法起到了重要作用。
本文将介绍纳米材料模拟与计算方法的相关内容,希望能为读者提供一些基础的知识。
一、分子动力学模拟分子动力学模拟是研究纳米材料中原子和分子运动的一种常用方法。
通过对粒子之间相互作用势能和动力学方程的数值求解,可以得到纳米材料中原子和分子的运动轨迹和相关性质。
分子动力学模拟广泛应用于研究纳米材料的力学性质、热学性质、电学性质和输运性质等方面。
二、密度泛函理论密度泛函理论是一种用于计算材料性质的强大方法,尤其适用于纳米材料的研究。
该理论通过求解电子的波函数和电荷密度,可以得到纳米材料的能带结构、电子结构和电荷分布等重要信息。
密度泛函理论已经在纳米材料的构造优化、电荷转移、光学性质等方面取得了许多重要成果。
三、格林函数方法格林函数方法是处理纳米材料中电子传输问题的一种强大工具。
通过求解电子传输方程,可以得到纳米材料中电子在能带中的行为以及电导率等重要性质。
此外,格林函数方法还可用于研究纳米材料中的谷极化、量子霍尔效应和自旋输运等现象。
四、量子力学计算方法对于纳米材料中的原子和分子级别的问题,量子力学计算方法是非常重要的。
量子力学计算方法可以通过解质点的薛定谔方程来研究纳米材料中微观粒子的行为。
其中,常用的方法包括密度泛函理论、哈特里-福克近似、量子化学方法等。
这些方法可以用于研究纳米材料的电子结构、化学反应和光学性质等。
五、多尺度模拟方法纳米材料的尺度范围很广,从纳米级到宏观级都涵盖其中。
为了研究纳米材料在不同尺度下的行为,多尺度模拟方法应运而生。
多尺度模拟方法可以将不同尺度下的模型和方法相互关联,使得研究者可以在不同尺度下进行模拟和计算。
计算材料学PPT课件

15
x[c (r ) ]x [(r ) ]c [(r )]
交换能
关联能
Ex LcS[D A]d3r(r)x(c(r),(r)) d3r(r)[x((r),(r) )c((r),(r))]
精选ppt课件考20虑21 了自旋
16
➢ Local Density Methods
假设局域电子密度可以被认为是均匀电子气,或等效地说,电子密度是随空间缓慢 变化的函数。 交换项
精选ppt课件2021
10
• Hohenberg-Kohn定理说明了粒子数密度 是确定多粒子系统基态物理性质的基本变 量以及能量泛函对粒子数密度函数的变分 是确定系统基态的途径。但是仍然存在三 个问题未解决:
• (1) 如何确定粒子数密度函数;
• (2) 如何确定动能泛函;
• (3) 如何确定交换关联能泛函。
6
• 将多电子问题变为了单电子问题,但是没 有考虑电子的交换反对称性 。为了研究电 子的交换反对称性的影响,采用Slater行 列式来求能量,经过合适的变换,得到了 如式所示方程:
2 V ( r ) i'( i)d '||r r i''( r 'r )||2 i( r ) i'( i)||,d ' i * 'r |( r r '') r i( |r ') E i i( r )
精选ppt课件2021
11
• 为了解决这三个问题,Kohn W与 Sham L.J共同合作,提出了Kohn- Sham方程 。
2 V K [( S r )i ( ] r ) E ii ( r )
N
2
(r) |i(r)|
i1
计算材料学

分子动力学理论及其模拟方法摘要:本文阐述了分子动力学的基本理论以及分子动力学模拟的方法,清楚地解释了从头计算理论、自洽场理论,然后对一些基本概念比如力场、牛顿运动方程及其数值解法、系综、周期性边界条件、积分步长作了一些阐述。
分析和总结了分子动力学模拟的基本步骤,并且在材料科中的应用情况进行了简要概述。
接着对分子动力学模拟的发展及应用前景作了一些论述关键词:分子动力学;模拟;从头计算;自洽场;牛顿动力学正文:分子动力学是一门结合物理,数学和化学的综合技术。
分子动力学是一套分子模拟方法,该方法主要是依靠牛顿力学来模拟分子体系的运动,以在由分子体系的不同状态构成的系综中抽取样本,从而计算体系的构型积分,并以构型积分的结果为基础进一步计算体系的热力学量和其他宏观性质。
分子动力学模拟(moleculardynamics simulation , MD) [1]是在评估和预测材料结构和性质方面模拟原子和分子的一种物质微观领域的重要模拟方法,通过计算机对原子核和电子所构成的多体体系中的微观粒子之间相互作用和运动进行模拟,在此期间把每一原子核视为在全部其他的原子核和电子所构成的经验势场的作用下按照牛顿定律进行运动,进而得到体系中粒子的运动轨迹,再按照统计物理的方法计算得出物质的结构和性质等宏观性能。
简而言之即是应用力场及根据牛顿运动力学原理所发展的一种计算机模拟方法。
分子动力学模拟是一种非常有效的计算机技术已成为重要的科学研究的方法之一。
1分子动力学的基本理论1.1从头计算理论原则上讲,有了HFR方程(不论是RHF方程或是UHF方程),就可以计算任何多原子体系的电子结构和性质。
真正严格的计算称之为从头计算法。
RHF方程的极限能量与非相对论薛定谔方程的严格解之差称为相关能。
对于某些目的,还需要考虑体系的相关能。
UHF方程考虑了相关能的一小部分,更精密的作法则须取多斯莱特行列式的线性组合形式的波函数,由变分法求得这些斯莱特行列式的组合系数。
【国家自然科学基金】_计算材料学_基金支持热词逐年推荐_【万方软件创新助手】_20140730
推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
科研热词 第一性原理 电子结构 数值模拟 第一原理 高频电磁场 高应变速率 预热 银一氧化物触头 铝锂合金 铜管 钛铌合金 钛-氢体系 遗传算法 递归统计 质量扩散方程 计算模型 计算材料学 计算机仿真 结构稳定性 结合能 细观结构 组装技术 第一原理计算 立体形貌观察 空拔 稳定性 程氏理论 离子聚合物胶体 界面 电磁软接触连铸 电弧参数 电子理论 电化学-力学耦合 球磨 玻恩有效电荷 熔池接触面积 热源模型 热分解 溶解热 溶剂/非溶剂 温热变形 温度场 温度 流变方程 氧化物性质 残余应力 残余变形 正交实验法 枝晶生长 材料科学 材料学 机械感度
科研热词 复合材料 高分子材料学 非等温结晶 铺丝路径 误差回转神经网络 自由基二聚体 自动铺丝 聚3,3-二叠氮甲基氧杂丁环(pbamo) 等参线 热处理 正离子吸引 正交投影 梯度下降算法 材料学 曲率 应变诱导析出 差示扫描量热仪(dsc) 回复 分子间相互作用 再结晶 位错密度 仿真 π /π 键 ttf nb微合金钢 b样条 7003铝合金
2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
计算材料学概述

计算材料学概述计算材料学是基于物理建模与数值计算方法,通过理论计算主动对材料-器件-微系统的本征特性、结构与组分、使用性能以及合成与制备工艺进行综合设计,达到对材料结构与功能的调控,并提供优化设计和协同制造技术的一门交叉边缘学科。
1 密度泛函理论密度泛函理论是一种研究多电子体系电子结构的量子力学方法。
密度泛函理论在物理和化学上都有广泛的应用,特别是用来研究分子和凝聚态的性质,是凝聚态物理和计算化学领域最常用的方法之一。
在通常的多体问题电子结构的计算中,原子核可以看作静止不动的(波恩-奥本海默近似),这样电子可看作在原子核产生的静电势中运动。
电子的定态可由满足多体薛定谔方程的波函数描述:其中为电子数目,为电子间的相互作用势。
算符和称为普适算符,它们在所有系统中都相同,而算符则依赖于系统,为非普适的。
可以看出,单粒子问题和比较复杂的多粒子问题的区别在于交换作用项。
目前有很多成熟的方法来解多体薛定谔方程,例如:物理学里使用的图形微扰理论和量子化学里使用的基于斯莱特行列式中波函数系统展开的组态相互作用(CI)方法。
然而,这些方法的问题在于较大的计算量,很难用于大规模复杂系统的计算。
相比之下,密度函理论将含的多体问题转化为不含的单体问题上,成为解决此类问题的一个有效方法。
在密度泛函理论中,最关键的变量为粒子密度,它由下式给出霍恩伯格和沃尔特·科恩在1964年提出 [1],上面的关系可以反过来,即给出基态电子密度,原则上可以计算出对应的基态波函数。
也就是说,是的唯一泛函,即对应地,所有其它基态可观测量均为的泛函进而可以得出,基态能量也是的泛函,其中外势场的贡献可以用密度表示成泛函和称为普适泛函,而显然不是普适的,它取决于所考虑的系统。
对于确定的系统,即已知,需要将泛函对于求极小值。
这里假定能够得出和的表达式。
对能量泛函求极值可以得到基态能量,进而求得所有基态可观测量。
对能量泛函求变分极值可以用不定算子的拉格朗日方法,这由科恩和沈吕久在1965年完成 [2]。
密度泛函

E[ ,V ] i
多电子体系的基态能
N
i 1
N
1 e2 E[ ,V ] i i j ji EXC [ ] d 3rVXC (r) (r) 2 i, j r12 i 1
23
交换关联泛函
要求解Kohn-Sham方程,必须给出Kohn-Sham函数各项 的具体表达式,由于交换关联能没有经典对应量,因此无 法直接得到它的密度泛函形式,所以要进行一定的假设。 目前最常用的假设就是局域密度近似(Local Density Approximation,LDA)
Vext V (ri ) d 3rV (r) (r ri )
单个电子的定域外势, 描述电子在离子实的晶 格周期势场中运动。
V (r) v(r Rl )
l
8
证明
H Hint Vext
(r) (r1 ,..., rN )
i
(r r ) (r ,..., r
LDA E d XC [ (r)] ( LDA) XC [ ] VXC (r) XC [ (r)] (r) (r) d (r)
在LDA情形下,多体系统的基态能简化为
E ( LDA)
1 3 3 e2 i d rd r (r ) (r) 2 r r i d XC ( (r )) d r (r ) (r) d (r )
因此,定理一得证。(互为逆否命题同真同假)
12
(r) Vext H
13
定理二是密度泛函框架下的变分原理,此定理与波函数形 势下的能量变分原理相同。
因为根据定理一,粒子数密度能唯一的确定波函数,从而 使变分原理在以密度为变量的情况下仍然存在。 定理二为用变分法处理实际问题指出了一条途径。
材料设计与计算机模拟第一性原理与密度泛函理论

• 第一原理的基本思想:
将多原子构成的体系理解为由电子和原子核组成的多粒子系统,在 解体系Schrődinger方程的过程中,最大限度地进行“非经验性”处理, 即不涉及任何经验参数,所要输入的只是原子的核电荷数和一些模拟 环境参量。
• 在密度泛函理论中,将电子密度作为描述体系状态的基本变量,可追 溯到Thomas和Fermi用简并的非均匀电子气来描述单个原子的多电子 结构。
• 直到Hohenberg和Kohn提出了两个基本定理才奠定了密度泛函理论的 基石。
• 随后Kohn和Sham的工作使密度泛函理论成为实际可行的理论方法。
✓ 猜测试探波函数 ✓ 构造所有算符 ✓ 求解单粒子赝薛定谔方程
✓ 对于解出的新的波函数,重新构造Hartree-Fock算符
✓ 重复以上循环,直到收敛(即前后叠代的结果相同)
自恰场(SCF)方法是求解材料电子结构问题的常用方
对处理原子数较少的系统来说,Hartree-Fock近似是一种 很方便的近似方法。
• 多粒子系统的Schrődinger方程
其中ψ 和H分别对应于多粒子系统的波函数和哈密顿量。
原则上只要对上式进行求解即可得出所有物理性质,然而由于电子之间的相 互作用的复杂性,要严格求出多电子体系的Schrődinger方程解是不可能的, 必须在物理模型上进一步作一系列的近似。
• 换句话说,做第一原理计算(ab initio calculation)便可知道一块固体
但用于原子数大的系统,问题就变得非常复杂,此计算 方法的计算量随着电子数的增多呈指数增加,这种计算对计 算机的内存大小和CPU的运算速度有着非常苛刻的要求,它 使得对具有较多电子数的计算变得不可能。同时Hartree-Fock 近似方法给出的一些金属费米能和半导体能带的计算结果和 实验结果偏差较大。
第一性原理及密度泛函理论

引
的理论。
言
l 量力力学是反映微观粒子(分子、原子、原子核、基本粒子)运动规律
Байду номын сангаас
l 以量子力学为基础,结合高速发展的计算技术分别建立起来的计算材 料科学、计算物理、量子化学等分枝学科,促进了物理学、化学和材 料科学的发展,为发展和设计新型材料提供了理论基础和新的研究方 法。 l 在理论上最具诱惑力,且在将来最有可能开展真正意义上的材料设计 的计算就是解体系的Schrődinger方程,即为计算材料学中的第一原理 计算。
密度泛函理论
• 在密度泛函理论中,将电子密度作为描述体系状态的基本变量,可追 溯到Thomas和Fermi用简并的非均匀电子气来描述单个原子的多电子 结构。
• 直到Hohenberg和Kohn提出了两个基本定理才奠定了密度泛函理论的 基石。 • 随后Kohn和Sham的工作使密度泛函理论成为实际可行的理论方法。
多粒子体系的第一原理
• 第一原理的基本思想:
将多原子构成的体系理解为由电子和原子核组成的多粒子系统,在 解体系Schrődinger方程的过程中,最大限度地进行“非经验性”处理, 即不涉及任何经验参数,所要输入的只是原子的核电荷数和一些模拟环 境参量。 计算所求得的结果是体系Schrődinger方程的本征值和本征函数(波 函数),有了这两项结果,就可研究体系的基本物理性质。
多粒子体系的第一原理
l 价电子近似
在原子模型中,近核电子可被紧紧束缚在核的周围,这些束缚电子 是定域的,比较稳定,因而对固体性质的贡献很小。而在外层轨道的 价电子可以是离域的,当原子结合在一起组成固体时,这些电子的状 态变化很大,对固体的电学和光学性质有决定性的影响。因此,可将 固体看作是由原子核-束缚电子构成的离子核和价电子组合而成。
第一性原理与密度泛函理论PPT课件

4
• 多粒子系统的Schrődinger方程
其中ψ 和H分别对应于多粒子系统的波函数和哈密顿量。
原则上只要对上式进行求解即可得出所有物理性质,然而由于电子之间的相 互作用的复杂性,要严格求出多电子体系的Schrődinger方程解是不可能的, 必须在物理模型上进一步作一系列的近似。
5
+ 换句话说,做第一原理计算(ab initio calculation)便可知道一块固体
猜测试探波函数 构造所有算符 求解单粒子赝薛定谔方程
对于解出的新的波函数,重新构造Hartree-Fock算符
重复以上循环,直到收敛(即前后叠代的结果相同)
自恰场(SCF)方法是求解材料电子结构问题的常用方法
11
对处理原子数较少的系统来说,Hartree-Fock近似是一种 很方便的近似方法。
决定的。
20世纪初量子力学的出现,原则上提出
了像原子核和电子这样的微观粒子运动
和交互作用的定律。
理论上,给定一块固体化学成分(即所 含原子核的电荷和质量),我们就可以 计算这些固体的性质。因为一块固体实 际上是一个多粒子体系。决定这个体系 性质的波函数可以通过解薛定谔 (Schrödinger)波动方程来获得。
的性质。
可 是 , 这 个 薛 定 谔 波 动 方 程 有 3×N 个 变 量
(N是粒子总数),极其复杂,假使我们把
目前世界上的所有电脑都用上,让它跑千年、
万年都不可能算出来。正如1929年量子物理
大师狄拉克(Dirac)所言:处理大部分物理
学和全部化学问题的基本定理已经完全知道。
困难在於这些定律的应用所引出的数学方程
动能可以写为
25Leabharlann 库仑能可具体表达为:此时总能量 Et的表达式可写为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
求解条件:用来构造有效势的 电荷密度与解Kohn-Sham方程 得来的电荷密度一致。 解Kohn-Sham方程,这一步 计算量最大,里面需要用到许 多技巧,比如平面波展开,赝 势等。
SCF:自洽求解
交换关联函数, LDA
• 交换关联势在意义上是非局域的,我们前面提到这一部分包含两部分 交换相互作用和关联作用(即是有相互作用粒子和无相互作用粒子的
力学量的取值
• 经典力学中,物体任何力学量的取值都是确定的,可以用力学量来完 全描述。 • 对于微观粒子,只有当它处于某力学量算符的本征态时,该力学量才 有确定值,这个值就是该本征态下算符的本征值。当粒子处于任意波 函数描述的状态时,力学量取值不是确定的,而是存在统计分布。 • 与厄密算符对于得本征函数系是一套正交归一完全系,任意波函数都 可以通过这一套完备基来展开。而任意波函数的力学量取值必为本征 谱中的一个值。 其概率为本征值对应的波函数的因子
LDA与GGA近似的效果
• LDA计算原子游离能、分子解离能误差在10-20%;对于 分子键长、晶体结构可以准确到1%左右。 • 与LDA近似计算结果比较,GGA近似有以下的特点: --能更好的描述轻原子、分子、团簇以及碳氢化合物;对 3d过渡金属性质的描述更准确; --对某些半导体性质的过渡金属氧化物基态的描述更准确; --GGA近似给出的3d过渡金属磁性较大; --与实验结果和LDA近似计算结果比较,GGA近似给出的 晶格参数较大。
非自旋极化系统,
自旋极化系统,
电子气关联能的表达式,
交换关联函数, GGA
• 在L(S)DA的基础上,人们又进一步发展了广义梯度近似(GGA)。 GGA在L(S)DA的基础上,认为交换关联能 不但是电子密度的函数, 而且还是其梯度的函数。其表达式为:
--到此为止,整个过程就只有一次近似,即局域密度近似;那么这个计算 结果的正确与否就决定了LDA(GGA)的合理与否。
解:A=0, cos =0,
(n 为奇数)
B=0, sin =0,
能级(能量本征值) : 波函数:
(n 为偶数)
分立能级!!! n= 1, 2,3, 。。。
简单例子三:库仑场(中心力场)中的电子(1)
• 原子核产生的库仑场是一种特殊的中心力场, 如果原子核外只有一个 电子:质量为m, 带电量-e, 取原子核为坐标原点,电子受原子核吸 引的势能为:
厄密算符:对任意函数
则
如果满足 为厄密算符。
两种写法等价
厄密算符与力学量
• 厄密算符有以下基本性质: 1、厄密算符的本征值是实数,实际观察值必为厄米算符某一本征值 2、厄密算符属于不同本征值的本征函数相互正交 3、厄密算符的本征函数组成完全系 4 平均值
• 力学量的表示 -在量子力学中,表示力学量的都是线性厄密算符。 坐标算符: r 动量算符: p 动能算符: T 能量算符: E • 在量子力学基本假设中,只要将经典力学量F中的对应的力学量中的 动量和位置,分别换成动量算符和位置算符就可以得到相应力学量的 算符。
按照几率求平均值的法则可以求出力学量的平均值:
简单例子一:自由粒子
• 薛定谔方程:自由粒子势函数,V=0
自由粒子的能量为常数,其解当定态,通解为:
因此自由粒子有着平面波的形式
简单例子二:一维无限深势阱(1)
• 势函数 • 薛定谔方程将可以写成:
在
的区域内的通解是: 得:
利用边界条件:
简单例子二:一维无限深势阱(1)
数学运算符号。
式子中,
在量子力学中我们通常接触的都为线性算符:
为算符。
刻画可观测量的都是线性算符,这是由态叠加原理造成的。
• 运算规则
1、算符之和满足交换律结合律 2、算符之积交换律并不普遍满足
算符运算规则
• 算符之和满足交换律和结合
• 算符之积
交换律并不普遍满足,所以分对易算子和非对易算子。因此量子力 学中算符和函数在式子中的顺序很重要。
多电子体系的薛定谔方程
• 材料的许多性质都与材料的电子性质有着很大的关联,求解电子态是 量子领域一个重要的问题。通常的物质可以看成是原子核与其周围的
电子组成,量子力学里面它的薛定谔方程通常可以表述为:
电子的动能项
原子核的动能项
核与核的相互作用项 电子与电子相互作用项 电子与原子核的相互作用项
-- 每立方米物质对应的求和指标i, j 是 须做一系列的合理简化
哈密顿量:
Thomas-Fermi-Dirac近似
• 最初量子系统的密度泛函理论是由Thomas和fermi在1926年提出。 Thomas和fermi的理论中,忽略了电子的相互作用,将电子系统理想 地看作没有相互作用的均匀电子气, 并将电子系统的动能近似为是电 子密度的函数。1930年Dirac对此理论进行拓展,他利用局域密度近似 来处理电子间的关联效应。那么,外场下的能量方程可以表示为:
的数量级。想要求解这样的系统,必
波恩-奥本海默近似
• 因为原子核的质量为电子的1000倍左右,因此其速度比电子慢得多; 那么,可以将电子运动分为两个部分:考虑电子运动时,原子核处于 其瞬时的位置,而考虑核的运动时不考虑电子在空间的具体分布。这
样可以将原子核与电子分离求解。
将上式代人薛定谔方程,电子部分:
对于密度的变分可以用对单电子波函数的变分代替,
变分得到Kohn-Sham 方程(2)
• 单电子形式的方程
• 上面三个方程被统称为Kohn-Sham方程
-- Kohn-Sham方程的核心是用无相互作用粒子模型代替有相互作用 粒子哈密顿量中的相应项,而将有相互作用粒子的全部复杂性归于 交换关联相互作用泛函数中EXC -- EXC包含有两部分,一部分为相互作用电子体系与假定无相互作 用电子体系的动能之差,另一部分为相互作用电子体系与假定无相 互作用电子体系的相互作用能之差。
第一章 密度泛函理论
第一节:量子力学基本知识
引言: 密度泛函理论是通过计算电子体系的性质来描述物 质的性质。而电子的运动遵循自己的法则,量子力学。而 量子力学对电子的描述与计算有一套法则。
• • • • • •
物质的波粒二象性 波函数以及态叠加原理 薛定谔方程 算符 简单体系电子行为求解 变分法—求解基态波函数的一种方法
• 其中,
• 根据定理一,
• 根据变分原理有:
因此,基态电荷密度所对应的总能值,总是比其他任何密 度给出的低。
Kohn-Sham方程
• H-K定理一,
~
-- Kohn和Sham, 1965年提出的方法,将有相 互作用多电子 系统转换为单电子问题: 用假定的无相互作用电子系统来 代替有相互作用的电子系统。 --这个方法的关键点有二: 一,将无相互作用动能项和长程库仑项单独列出来; 二,剩下的交换关联能项利用局域函数或者近局域函数进行 处理。
求基态波函数的一种方法:
设体系波函数:
, q代表全体坐标, C1,C2,C3为特定参数 那么 ,则
i=1,2,3….. 求方程组得到Ci,得到基态和基态波函数。
• 思考: 那么,如果有多个电子构成的体系, 其波函数如何求解?
第二节 密度泛函理论
• • • • • 多体系统的困难 波恩-奥本海默近似(绝热近似) Hohenberg-Kohn 定理 局域密度近似(LDA) Kohn-Sham方程的求解流程
Kohn-Sham能量泛函形式
• 无相互作用系统的哈密顿量由动能项和有效作用势能项组成
电荷密度等每个自旋轨道的平方总和
系统的动能,
库仑相互作用,
变分得到Kohn-Sham 方程(1)
• 根据H-K定理二,基态能量和电子密度泛函可以变分得到:
加上粒子数不变的条件 ,
:
用N个单粒子波函数 构成密度函数,
证明:
• • 对于多电子体系 假设有两个不同外势 将对应两个不同哈密顿量 不是 的基态,则: 给出了相同的基态电荷密度 ,那么它们 以及不同基态波函数 。因为
同时,
那么, 同样,
最后推出:
定理二
• 定理二: 在粒子数不变条件下能量泛函对 密度函数的变分就得到系统基态的能量 --对于任何给定的外场,都可以将系统的能量定
•
也是这个体系可能的状态
对于A的测量结果可能是a1, 也可能是a2, 而且测得的相应几率是确定的。
薛定谔方程
• 波函数怎么随着时间变化,各种具体情况下怎么找出相应的波函数?
这个方程为1926年薛定谔提出的一个假说。但是,正确性已经得到了验证。
• 定态薛定谔方程
1 粒子子在空间几率密度不随着时间变 2 任何力学量都不随时间变化 3 任何力学量测量值的几率不随时间变化
物质的波粒二象性
• 光具有波动性和粒子性的双重特性 -20世纪初,爱因斯坦(Einstein)提出光子学说解释了光电效应(photoemission) • 物质也具有波粒二象性。 - 1924年,法国科学家L.de Broglie认为:既然光具有二象性,则电子等微观粒子 也可有波动性 - 1927年,Davisson和Germer应用Ni晶体进行的电子衍射实验证实了de Broglie 的假设:电子具有波动性。将一束电子流经一定电压加速后通过金属单晶体,像 单色光通过小圆孔一样发生衍射现象,在感光底片的屏幕上,得到一系列明暗相 间的衍射环(图9-1)
为主量子数, 为角动量量子数, m 称为磁量子数
氢原子各轨道电子密度分布
径向分布
电子角分布
s p d电子的电荷密度
s电子
理想
p电子
晶体能级重排 d电子
变分法
• 设体系哈密顿算符 H的本征值由小到大的顺序排列为: E0, E1, E2, E3, …. • 与这些本征值对应的本征函数为 , , ….. • 则任意波函数 下,函数所描述的状态中,体系能量的平均值一定大 于或等于基态能量,即:
