Matlab模糊控制器的设计以及simulink下对模糊控制器系统的仿真

Simulink模糊控制教程

给出复杂模糊控制器设计实例和结果展示
实战演练三：模糊控制器优化与改进
模糊控制器优化方法：遗传算法、粒子群算法等改进模糊控制器性能的措施：调整隶属度函数、增加模糊规则数量等实际应用中模糊控制器的调试与测试案例分析：某工业过程控制中模糊控制器的应用与优化
实战演练四：模糊控制器在实时系统中的应用
更多可能性。
模糊控制理论的研究将更加注重实际应用，与工程实践的结合将更加紧密，推动工业自动化领域的进步与发展。
模糊控制在工业自动化领域的应用前景
工业自动化领域的现状和趋势
模糊控制技术的优势和特点
模糊控制在工业自动化领域的应用案例
模糊控制在工业自动化领域的未来发展前景
感谢观看
汇报人：XX
控制器性能评估
评估指标：准确性、稳定性、鲁棒性评估方法：仿真实验、实际测试评估工具：Simulink、Matlab/Simulink 评估步骤：设计控制器、搭建仿真模型、进行实验测试、分析实验结果
05
Simulink模糊控制应用实例
模糊控制在电机控制系统中的应用
模糊控制原理简介
模糊控制在电机控制中的应用实例
练
01
添加章节标题
02
Simulink模糊控制简介
模糊控制基本概念
模糊控制是一种基于模糊集合理论的控制方法，通过将输入变量模糊化，将模糊逻辑应用于控制
系统。
模糊控制的基本原理是通过模糊化、模糊推理和去模糊化三个步骤实
现控制。
模糊集合理论是模糊控制的基础，它通过模糊集合来表示输入和输出变量，并使用模糊逻辑规则进
去模糊化操作
定义：将模糊逻辑系统输出的模糊集合转换为清晰值的过程

模糊控制Matlab仿真

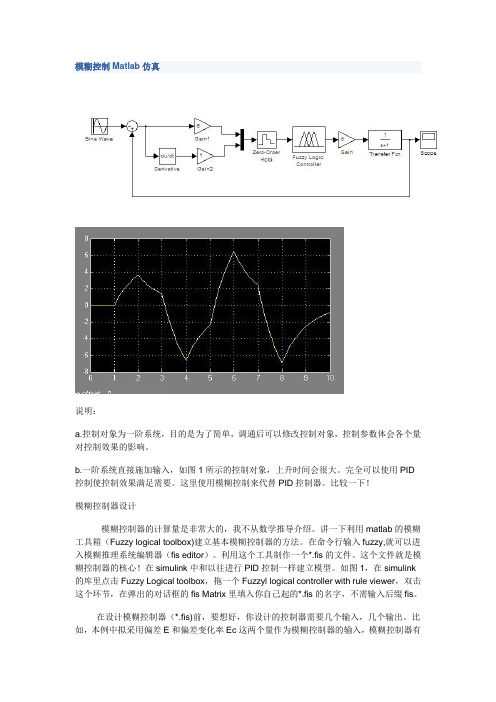
模糊控制Matlab仿真说明：a.控制对象为一阶系统，目的是为了简单，调通后可以修改控制对象，控制参数体会各个量对控制效果的影响。

b.一阶系统直接施加输入，如图1所示的控制对象，上升时间会很大。

完全可以使用PID 控制使控制效果满足需要。

这里使用模糊控制来代替PID控制器。

比较一下！模糊控制器设计模糊控制器的计算量是非常大的，我不从数学推导介绍。

讲一下利用matlab的模糊工具箱（Fuzzy logical toolbox)建立基本模糊控制器的方法。

在命令行输入fuzzy,就可以进入模糊推理系统编辑器（fis editor）。

利用这个工具制作一个*.fis的文件。

这个文件就是模糊控制器的核心！在simulink中和以往进行PID控制一样建立模型。

如图1，在simulink 的库里点击Fuzzy Logical toolbox，拖一个Fuzzyl logical controller with rule viewer，双击这个环节，在弹出的对话框的fis Matrix里填入你自己起的*.fis的名字，不需输入后缀fis。

在设计模糊控制器（*.fis)前，要想好，你设计的控制器需要几个输入，几个输出。

比如，本例中拟采用偏差E和偏差变化率Ec这两个量作为模糊控制器的输入，模糊控制器有一个输出。

很明显，这是利用模糊控制器代替PD控制的。

对应的模糊控制器的设计也要具有两个输入一个输出。

利用matlab的Fuzzy logical toolbox 设计模糊控制器(生成*.fis文件）的关键步骤：a.添加输入输出。

图3.fis编辑器默认的具有一个输出，添加第二个输入，并且分别命名为E，Ec，U。

b.确定隶属函数。

双击黄色和绿色的方框就可以进入隶属函数编辑对话框了。

设置E,Ec 的range为[-6,6]，u的range为[-1,1]。

然后每一个变量再添加4个输入隶属函数，总共7个。

matlab提供了11种隶属函数，第一次用选择常用的三角形trimf，区别不大的。

模糊控制simulink实例

模糊控制simulink实例一、模糊控制概述模糊控制是一种基于人工智能的控制方法，它模拟人类的思维方式进行控制决策。

模糊控制的核心思想是将模糊语言和模糊推理应用于控制系统中，通过建立模糊规则和模糊集合来实现对系统的控制。

模糊控制具有适应性强、处理非线性和复杂系统能力强等优点，在工业控制领域得到了广泛应用。

二、Simulink简介Simulink是MathWorks公司开发的一款基于MATLAB的通用仿真平台。

Simulink提供了一个直观的图形化界面，可以用于设计、模拟和实现各种系统模型。

Simulink 支持多领域的仿真，包括控制系统、信号处理、通信系统等，同时也提供了丰富的库函数和工具箱，方便用户进行系统建模与仿真。

三、模糊控制在Simulink中的应用模糊控制在Simulink中的应用可以通过Fuzzy Logic Toolbox来实现，该工具箱提供了一系列用于模糊控制设计和仿真的函数和模块。

下面介绍一个简单的模糊控制实例来说明模糊控制在Simulink中的应用。

3.1 系统建模首先，我们需要确定模糊控制系统的输入、输出和控制规则。

假设我们要设计一个小型的温度控制系统，系统的输入是环境温度（T），输出是加热器的电压（V）。

根据经验，我们可以定义几个模糊集合来描述温度和电压的状态，例如”冷”、“适中”和”热”。

然后，我们可以根据这些模糊集合定义一些模糊规则，例如”当温度冷时，增加电压”等。

3.2 模糊控制器设计在Simulink中，我们可以使用Fuzzy Logic Controller模块来设计模糊控制器。

该模块提供了一种快速且简单的方法来创建模糊控制器。

首先，我们需要定义输入和输出的模糊集合，以及模糊规则。

然后，我们可以将这些参数传递给Fuzzy Logic Controller模块，并设置输入输出的信号传递方式。

3.3 系统仿真在完成模糊控制器的设计后，我们可以进行系统的仿真。

在Simulink中，我们可以通过连接输入信号和模拟环境来模拟系统的行为。

基于matlab的模糊控制器的设计与仿真

基于MATLAB的模糊控制器的设计与仿真摘要：本文对模糊控制器进行了主要介绍。

提出了一种模糊控制器的设计与仿真的实现方法，该方法利用MA TLB模糊控制工具箱中模糊控制器的控制规则和隶属度函数，建立模型，并进行模糊控制器设计与仿真。

关键词：模糊控制，隶属度函数，仿真，MA TLAB1 引言模糊控制是一种特别适用于模拟专家对数学模型未知的较复杂系统的控制，是一种对模型要求不高但又有良好控制效果的控制新策略。

与经典控制和现代控制相比，模糊控制器的主要优点是它不需要建立精确的数学模型。

因此，对一些无法建立数学模型或难以建立精确数学模型的被控对象，采用模糊控制方法，往往能获得较满意的控制效果。

模糊控制器的设计比一般的经典控制器如PID控制器要复杂，但如果借助MATLAB则系统动态特性良好并有较高的稳态控制精度，可提高模糊控制器的设计效率。

本文在MATLAB环境下针对某个控制环节对模糊控制系统进行了设计与仿真。

2 模糊控制器简介模糊控制器是一种以模糊集合论，模糊语言变量以及模糊推理为数学基础的新型计算机控制方法。

显然，模糊控制的基础是模糊数学，模糊控制的实现手段是计算机。

本章着重介绍模糊控制的基本思想，模糊控制的基本原理，模糊控制器的基本设计原理和模糊控制系统的性能分析。

随着科学技术的飞速发展，在那些复杂的，多因素影响的严重非线性、不确定性、多变性的大系统中，传统的控制理论和控制方法越来越显示出局限性。

长期以来，人们期望以人类思维的控制方案为基础，创造出一种能反映人类经验的控制过程知识，并可以达到控制目的，能够利用某种形式表现出来。

而且这种形式既能够取代那种精密、反复、有错误倾向的模型建造过程，又能避免精密的估计模型方程中各种方程的过程。

同时还很容易被实现的，简单而灵活的控制方式。

于是模糊控制理论极其技术应运而生。

3 模糊控制的特点模糊控制是以模仿人类人工控制特点而提出的，虽然带有一定的模糊性和主观性，但往往是简单易行，而且是行之有效的。

模糊控制实例及simulink仿真实验报告

模糊控制实例及simulink仿真实验报告
一、背景介绍
模糊控制是一种基于模糊逻辑的控制方法，其优点在于可以很好地处理复杂的非线性和不确定性系统，而且不需要精确的数学模型和计算，能够快速实现控制的优化。

二、实例介绍
本次实例采用一个双轮小车为对象，实现小车在平面上向指定位置运动的控制。

通过小车的速度和转向角两个输入变量，输出一个模糊控制信号，控制小车前进和转向。

三、实验过程
1. 建立模糊控制系统模型
打开Simulink软件，建立一个新模型，模型中包括输入变量、输出变量和控制器。

2. 设计输入变量和输出变量
（1）设计输入变量
本实例选择小车速度和转向角两个输入变量，每个变量包含三个模糊集合，速度变量分别为“慢速”、“中速”、“快速”，转向角变量分别为“左转”、“直行”、“右转”。

（2）设计输出变量
模糊控制信号输出变量选择小车的前进和转向，每个变量包含三个模糊集合，分别为“慢行”、“中行”、“快行”、“左转”、“直行”、“右转”。

3. 建立控制器
建立模糊控制器，包含输入变量和输出变量的关系，建立控制规则库和模糊关系。

4. 仿真实验
在Simulink下进行仿真实验，调整控制器参数，观察小车运动状态，对比试验。

四、实验结果
经过多次试验和调整，得到最优的小车模糊控制参数，可以实现小车的平滑运动
和准确转向。

五、实验结论
本实验通过建立一个小车的模糊控制系统，可以有效实现小车的平滑运动和准确转向，控制效果优于传统的PID控制方法。

模糊控制可以很好地处理非线性、不确定性和模糊性的系统，适合许多需要快速优化控制的场合。

模糊PID控制器设计及MATLAB仿真_李健

图 1 模糊 PID 控制结构图
PID 参数模糊自整定是先找出 PID 控制器的 3 个参数 Kp、 Ki 和 Kd 与偏差 e 和偏差变化率 ec 之间的模糊关系，在运行中通过不断检测 e 和 ec，根据模糊控制规则来对 3 个参量进行在
线修改，以满足不同 e 和 ec 对控制器参数的不同要求，从而使
起较大的超调。微分系数 Kd 影响系统的动态特性，Kd 越大，越
能抑制偏差变化，但过大会延长调节时间，降低抗干扰能力。
根据参数 Kp、Ki、Kd 对系统输出特性的影响情况，可归纳出系统在被控过程中对于不同的偏差和偏差变化率，参数 Kp、Ki、 Kd 的自整定原则：
摘要将模糊控制器和 PID 控制器结合在一起，构造了一个模糊 PID 控制器，利用模糊推理的方法调整 PID 控制器的参数，并利用 MATLAB 的 SUMLINK 工具箱，对系统进行仿真，仿真结果表明模糊 PID 控制器能使系统达到满意的控制效果。关键词：PID 控制器，模糊控制，MATLAB，SIMULINK，系统仿真
1．3 模糊控制算法的确立
PID 参数的整定必须考虑到在不同时刻 3 个参数的作用以
及相互之间的互联关系。模糊自整定 PID 是在 PID 算法的基础
上通过计算当前系统误差 e 和误差变化 ec，利用模糊规则进行
模糊推理，查询模糊矩阵表进行参数调整。参数修正公式：
＇
Kp ＝Kp ＋（e，ec）p
被控对象具有良好的动、静态性能。
1．2 PID 控制器的确立
通常，PID 控制器的控制算式为：

模糊pidmatlab(simulink)仿真详细步骤

下面用一个简单的例子作介绍：（本例不是特别针对实现什么功能，只是为了介绍方便）第一部分创建一个模糊逻辑（.fis文件）第一步：打开模糊推理系统编辑器步骤：在Commond Window 键入fuzzy回车打开如下窗口，既模糊推理系统编辑器第二步：使用模糊推理系统编辑器本例用到两个输入，两个输出，但默认是一个输人，一个输出步骤：1、添加一个输入添加一个输出得如下图2、选择Input、output(选中为红框)，在Name框里修改各输入的名称并将And method 改为prod，将Or method 改为probor提示：在命名时’_’在显示时为下标，可从上图看出。

第三步：使用隶属函数编辑器该编辑器提供一个友好的人机图形交互环境，用来设计和修改模糊推理系中各语言变量对应的隶属度函数的相关参数，如隶属度函数的形状、范围、论域大小等，系统提供的隶属度函数有三角、梯形、高斯形、钟形等，也可用户自行定义。

步骤：1、双击任何一个输入量（In_x、In_y）或输出量打开隶属度函数编辑器。

2、在左下处Range和Display Range处添加取值范围，本例中In_x和In_y的取值范围均为[0 10], Out_x和Out_y的取值范围均为[0 1]3、默认每个输入输出参数中都只有3个隶属度函数，本例中每个输入输出参数都需要用到五个，其余几个需要自己添加：选中其中一个输入输出参数点击Edit菜单，选Add MFS…打开下列对话框将MF type设置为trimf(三角形隶属度函数曲线，当然你也需要选择其他类型) 将Number of MFs设置为2点击OK按钮同样给其他三个加入隶属度函数4、选中任何一个隶属度函数（选中为红色），在Name中键入名称，在Type 中选择形状，在Params中键入范围，然后回车如下图：5、关闭隶属函数编辑器第四步：使用规则编辑器通过隶规则编辑器来设计和修改“IF...THEN”形式的模糊控制规则。

模糊控制simulink实例

模糊控制simulink实例模糊控制是一种基于人类智能的控制方法，其能够克服传统控制方法中的困难和不足，使得控制系统能够更加稳定和灵活地进行控制。

在模糊控制中，模糊规则和模糊推理是非常关键的，而Simulink正是一款非常适合模拟和控制系统的MATLAB工具箱。

现在，我们就来看一个基于Simulink的模糊控制实例。

假设我们有一个小车可以沿着一条直线上下运动，并且需要通过模糊控制来控制小车的运动。

我们将小车的速度和位置分别作为系统的输入和输出，其中小车的速度可以在0-10m/s之间变化，而小车的位置则可以在0-50m之间变化。

需要注意的是，在这个系统中，小车的速度和位置都是模糊的，我们需要通过模糊规则和推理来确定小车应该如何移动。

首先，我们需要确定一组模糊规则来描述小车的运动。

这里我们设定了三个模糊规则，分别是：1. 如果小车位置很靠近上限，那么小车速度应该减缓。

2. 如果小车位置中间，那么小车速度应该保持不变。

3. 如果小车位置很靠近下限，那么小车速度应该加速。

然后，我们需要建立一组模糊推理机制来根据当前状态来确定小车的下一个状态。

这里我们选择了三个模糊推理机制：模糊最小性、模糊加法和模糊乘法。

其中，模糊最小性是用来确定模糊集合之间的交集，模糊加法是用来确定两个模糊集合之间的并集，而模糊乘法则是用来确定两个模糊集合之间的乘积。

最后，我们需要使用Simulink建立一个模糊控制系统，并将上述规则和推理机制应用到这个系统中。

在Simulink中，我们可以使用Fuzzy Logic Controller来实现这个过程。

首先，我们需要将输入和输出变量添加到Fuzzy Logic Controller中。

然后，我们需要为每个变量设置一个模糊集合，以便能够将当前状态转换为模糊状态。

接下来，我们需要将模糊规则添加到Fuzzy Logic Controller中，并为每个规则设置一些权重，以便能够决定规则的优先级。

基于MATLABSIMULINK仿真模糊PID控制效果研究

第28卷第1期2021年3月天津农学院学报Journal of Tianjin Agricultural UniversityVol.28,No.1March,2021文章编号：1008-5394(2021)01-0049-04DOI：10.19640/ki.jtau.2021.01.010基于MATLAB/SIMULINK仿真模糊PID控制效果研究曹督尊，刘国彦砒作者，甘敏，赵金才(天津农学院工程技术学院，天津300392)摘要：本文提出一种模糊逻辑控制方案来提升传统PID型控制器的控制效果。

使用MATLAB/SIMULINK软件对高阶非时滞控制系统与二阶时滞系统分别采用传统PID型控制和添加模糊PID控制参数进行了阶跃输入响应仿真对比，发现对于高阶非时滞系统的参数加入模糊变量控制后控制效果有显著提升。

关键词：模糊逻辑控制；PID控制；SIMULINK模型中图分类号：TM921文献标识码：AStudy of fuzzy logic PID controller based on MATLAB/SIMULINKCao Duzun,Liu Guoyan Correspondin8Author;Gan Min,Zhao Jincai(College of Engineering and Technology,Tianjin Agricultural University,Tianjin300392,China)Abstract:This paper proposed a fuzzy logic controlling method which can improve the effect of PID type controller.The MATLAB/SIMULINK software was used to simulate comparison of step input response between the high-order non-delay control system and the second-order delay system,with the second-order delay system using traditional PID control and fuzzy PID control parameters respectively.As a result,it is found that the control effect of the parameters of high-order non-delayed system was significantly improved by adding fuzzy variable control.Key words：fuzzy logic controller;PID control;SIMULINK models目前自动控制研究领域中传统PID型控制方面具有结构简单实现、控制效果好等特点，被广泛应用于工业过程控制叫然而传统PID型控制方法依旧存留着控制精度不高、超调量过大、有一定的调节时间等问题駕通过对PID型控制系统的比例参数因子进行模糊逻辑控制即可有效提高控制系统的控制性能。

MATLAB控制系统各种仿真例题(包括simulink解法)

一、控制系统的模型与转换1．请将下面的传递函数模型输入到matlab 环境。

]52)1)[(2(24)(32233++++++=s s s s s s s G )99.02.0)(1(568.0)(22+--+=z z z z z H ，T=0.1s >> s=tf('s');G=(s^3+4*s+2)/(s^3*(s^2+2)*((s^2+1)^3+2*s+5)); GTransfer function:s^3 + 4 s + 2 ------------------------------------------------------ s^11 + 5 s^9 + 9 s^7 + 2 s^6 + 12 s^5 + 4 s^4 + 12 s^3>> num=[1 0 0.56];den=conv([1 -1],[1 -0.2 0.99]); H=tf(num,den,'Ts',0.1)Transfer function: z^2 + 0.56 ----------------------------- z^3 - 1.2 z^2 + 1.19 z - 0.992．请将下面的零极点模型输入到matlab 环境。

请求出上述模型的零极点，并绘制其位置。

)1)(6)(5()1)(1(8)(22+++-+++=s s s s j s j s s G )2.8()6.2)(2.3()(1511-++=----z z z z z H ，T=0.05s>>z=[-1-j -1+j]; p=[0 0 -5 -6 -j j];G=zpk(z,p,8)Zero/pole/gain: 8 (s^2 + 2s + 2) -------------------------- s^2 (s+5) (s+6) (s^2 + 1)>>pzmap(G)>> z=[0 0 0 0 0 -1/3.2 -1/2.6]; p=[1/8.2];H=zpk(z,p,1,'Ts',0.05)Zero/pole/gain:z^5 (z+0.3125) (z+0.3846) ------------------------- (z-0.122)Sampling time: 0.05>>pzmap （H ）二、线性系统分析1. 请分析下面传递函数模型的稳定性。

基于MATLAB的温度模糊控制系统的设计

基于MATLAB的温度模糊控制系统的设计MATLAB是一种强大的数学计算软件，用于科学与工程领域的数据处理、分析和可视化等应用。

在温度控制系统设计中，模糊控制是一种常用的控制方法。

本文将介绍基于MATLAB的温度模糊控制系统的设计。

温度模糊控制系统的设计包括四个主要步骤：建立模糊控制器，设计模糊推理规则，模糊化与去模糊化以及系统仿真。

首先，建立模糊控制器。

在MATLAB中，可以使用Fuzzy Logic Toolbox工具箱来创建和管理模糊逻辑系统。

可以使用命令fuzzy，创建一个模糊逻辑系统对象。

在创建模糊控制器对象后，需要定义输入和输出变量。

输入变量可以是温度偏差，输出变量可以是控制信号。

然后，可以使用addInput和addOutput命令来添加输入和输出变量。

接下来，设计模糊推理规则。

在模糊推理中，需要定义一组规则来描述输入变量和输出变量之间的关系。

可以使用addRule命令来添加规则。

规则的数量和形式可以根据实际需求进行调整。

然后，进行模糊化与去模糊化。

模糊化是将模糊输入变量转换为模糊集，而去模糊化是将模糊输出变量转换为具体的控制信号。

可以使用evalfis命令进行模糊化和去模糊化。

模糊化使用模糊逻辑系统对象对输入变量进行处理，而去模糊化使用模糊逻辑系统对象对输出变量进行处理。

最后，进行系统仿真。

可以使用Simulink工具箱来进行系统仿真。

在仿真过程中，将温度控制系统与模糊控制器进行连接，然后通过给定的输入条件观察系统的响应。

可以利用Simulink中的Scope来显示温度的变化，并且可以通过模糊控制器来调整温度。

在设计温度模糊控制系统时，还需要考虑参数调节和性能评估等问题。

可以使用MATLAB中的优化工具箱对模糊控制器的参数进行调节，以获得更好的控制性能。

还可以使用MATLAB中的性能评估工具来评估系统的性能，例如稳定性、精度和鲁棒性等。

综上所述，基于MATLAB的温度模糊控制系统的设计包括建立模糊控制器、设计模糊推理规则、模糊化与去模糊化以及系统仿真等步骤。

基于MATLAB／SIMULINK直流电机调速系统模糊控制的建模与仿真

式中：Ｔ＝Ｌ／为电枢回路电磁时问；Ｒ
Ｅ＝Ｃｎ为额定励磁下电动机的反电动势；，在零初始条件下对（）式进行拉氏变换得１
ＧＤ。２４＝２．５；ＣⅣ一３／ｏＰＩ＊ｅ
固定转矩为６。７３１电机模型的实现．
（）电机数学模型１额定励直流电机电枢回路电压平衡方程式为：
Ｕｄ。一Ｅ — ＲＩｄ十Ｉ，
围３直流电机仿真模型
标器在模型窗口上 “ ”出所需的控画
直流电机模糊控制系统结构图如图１所示。
图１模糊控制直流电机系统框图
由图１可见，机直流调速系统的过程为：测速电由
发电机输出电压中取出转速负反馈电压，与给定电压进行比较得到的偏差和偏差变化率送给模糊控制器。由模糊控能器计算出电机控制量，送给电机，实现电
２ＳＭＵＩＫ下直流调速系统仿真模型的实现ＩＬＮ
计算机仿真技术是应用电子计算机对研究对象的数学模型进行计算和分析的方法。对于从事控制系统研究与设计的技术人员而言，ＭＡＴＩＢ是目前控制Ａ系统计算机辅助设计实用且有救的工具。这不仅是因为它能解决控制论中大量存在的矩阵运算问题，更因为它提供了强有力的工具箱支持。与控制系统直接相关的工具箱有控制系统、系统辨识、信息处理、优化等还有一些先进和流行的控制策略工具箱，如鲁棒控制、ｕ一分析与综台、神经网络、模糊预测控制、非线性控制设计、模糊逻辑等。可以说目前理论界和工业界广泛应用和研究的控制算法，几乎都可以在ＭＡＴＩＡＢ中找到相应的工具箱。同时，ＭＡＴＩＡＢ软件中还提供了新的控制系统模型输人与仿真工具ＳＭＵＩＮＫ，它具有构造模型简单、ＩＩ动态修改参数实现系统控制容易、界面友好、功能强大等优点，成为动态建模与仿真方面应用最广泛的软件包之一。它可以利用鼠

matlab模糊控制器的设计

matlab模糊控制器的设计
设计模糊控制器的步骤如下：
1. 确定系统的输入和输出变量：确定系统要控制的输入和输出变量，以及它们的范围和取值。

2. 设计模糊集：根据系统的输入和输出变量的范围，在输入和输出空间中设计一组模糊集。

可以使用三角形、梯形等形状的模糊集。

3. 确定模糊规则：根据经验或专家知识，确定一组模糊规则。

每个模糊规则对应一个输入模糊集与一个输出模糊集的匹配。

4. 确定模糊推理方法：确定使用哪种模糊推理方法，如Mamdani或者Sugeno等。

5. 设计模糊控制器的模糊化和解模糊化方法：确定如何将输入变量模糊化为模糊集，以及如何将输出变量的模糊集解模糊化为具体的输出值。

6. 确定模糊控制器的参数：根据系统的实际需求和性能要求，调整模糊控制器的模糊规则和参数，以达到最佳控制效果。

7. 实现模糊控制器：使用MATLAB等工具实现设计好的模糊控制器，并进行模拟和实验验证。

以上是一般的模糊控制器设计步骤，具体的设计过程还需要根据具体的系统和控制需求进行调整和优化。

模糊控制器的matlab设计步骤

模糊PID控制器设计和仿真步骤：各变量隶属度函数的确定第一步：各变量隶属度函数的确定1、用于PID 参数调整的模糊控制器采用二输入三输出的形式。

该控制器是以误差E 和误差变化率EC 作为输入，PID 控制器的三个参数P、I、D 的修正△KP、△KI、△KD 作为输出，如图1；2、取输入E 和EC 和输出△KP、 △KI、△KD 模糊子集为{NB,NM,NS,ZO,PS,PM,PB}，其论域为[-6,6],量化等级为{-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6}；如图23、在模糊逻辑工具箱的隶属度函数编辑器中，选择输入量E，EC 隶属函数为高斯型（gaussmf）,输出△KP、△KI、△KD 的隶属函数为三角形（trimf），如图2和3。

图1图2图3第二步：根据图4规则建立模糊规则表，如图5：图4图5第三步：设置参数：与方式与方式 (And method)为min ；或方式（Or method)为max ；推理推理 (Implication)为min ；合成；合成 (Aggregation)为max ；去模糊（Defuzzification)为重心平均法（centroid ）。

）。

第四步：保存该FIS 文件，取名为FuzzyPID.fis第五步：在MA MATLABTLAB 的M 文件编辑器里建立一个名为FuzzyPID.m 的文件，其内容为：martrix=readfis （‘Fuzzypid.fis ’），并运行。

，并运行。

第六步：打开SIMULINK ，新建一个Model ，选择一个Subsystem ，在其中编辑模块，如图6，并设置模糊化因子KE=KEC=0.01，解模糊因子KP=0.5，KI=KD=0.01，并在Fuzzy Logic Controller 模块的Parameters 中输入readfis('FuzzyPID.fis')：图6第七步：返回到新建的Model 中，按照如图7所示建立模糊PID 控制器，其中，控制器，其中，PID PID 初始值为KP0=20，KI0=1.35，KD0=3.7，传递函数为：图7第八步：保存为FuzzyPID.mdl 并运行。

Simulink模糊控制教程

发展
在20世纪70年代和80年代，模糊控制的理论框架逐渐形成，模糊集合、模糊逻辑和模糊推理等基本概念得到深入研究和应用。
应用
随着计算机技术的发展，模糊控制的应用领域不断扩大，涉及工业控制、智能家居、医疗等领域。
模糊控制的应用领域
01
工业控制
模糊控制在工业控制领域中得到了广泛应用，例如温度控制、压力控制、
最小值清晰化
将最小值推理得到的输出模糊集合映射到清晰输出上，通常采用中心平均法或中心最大值法。
04
模糊控制系统的仿真与实现
模糊控制系统的仿真
模糊逻辑工具箱
使用Simulink的模糊逻辑工具箱进行模糊控制系统的仿真，可以方便地创建模糊控制器并进行仿真分析。
模糊化与去模糊化
在仿真过程中，需要将输入信号模糊化，将输出信号去模糊化，以模拟实际模糊控制器的行为。
使用这个工具箱，用户可以轻松地构建和测试各种类型的模糊控制系统，包括单输入单输出（SISO）系统
和多输入多输出（MIMO）系统。
03
模糊控制器设计
模糊化方法
输入模糊化
将输入信号映射到对应的模糊集合上，通常采用三角形、梯形或任何可用的形状来表示模糊集合。
输出模糊化
根据系统输出和期望输出的偏差，调整模糊集合的中心和宽度，以实现输出模糊化。
模糊控制在液位控制系统中的应用
总结词
液位控制系统要求精确控制液位高度，同时要考虑到液体的流动性和容器的形状等因素，模糊控制能够实现高精度的液位控制。
详细描述
在液位控制系统中，模糊控制器可以根据液位传感器的实时数据和设定值，通过模糊逻辑推理快速调整进液或出液阀门的开度，实现液位的精确控制。同时，模糊控制器还可以根据液体的物理特性和容器的大小等因素对液位变化进行预测和控制。

智能控制实验报告1

智能控制实验报告实验题目: 模糊控制器设计学院: 电气工程学院班级:姓名:学号:实验题目: 模糊控制器设计实验目的: 1.熟悉和掌握模糊控制器的结构、原理及应用；2、熟练应用MATLAB软件, 进行模糊控制的Matlab仿真。

实验原理：在Simulink环境下对PID控制系统进行建模：对模糊控制系统的建模关键是对模糊控制器的建模。

Matlab软件提供了一个模糊推理系统（FIS）编辑器, 只要在Matlab命令窗口键入Fuzzy就可进入模糊控制器编辑环境。

模糊推理系统编辑器用于设计和显示模糊推理系统的一些基本信息, 如推理系统的名称, 输入、输出变量的个数与名称,模糊推理系统的类型、解模糊方法等。

实验仪器: 计算机MATLAB软件实验步骤：打开模糊推理系统编辑器, 在MATLAB的命令窗（command window）内键入：fuzzy命令, 弹出模糊推理系统编辑器界面, 如下图所示：在FIS编辑器界面上, 执行菜单命令“Edit”-> “Add Variable”->“Input”, 加入新的输入input, 如下图所示:选择input（选中为红框）, 在界面右边文字输入处键入相应的输入名称, 例如温度输入用tmp-input, 磁能输入用mag-input, 如下图所示:双击所选input, 弹出一新界面, 在左下Range处和Display Range处, 填入取值范围, 例如0至9（代表0至90）；在右边文字输入Name处, 填写隶属函数的名称, 例如lt或LT（代表低温）；在Type处选择trimf（意为: 三角形隶属函数曲线, triangle member function）在Params（参数）处, 选择三角形涵盖的区间, 填写三个数值, 分别为三角形底边的左端点、中点和右端点在横线上的值如下图中所示:用鼠标左键双击输入变量, 弹出输入变量的隶属函数编辑器, 执行菜单命令“Edit”-> “Remove All MFs”, 然后执行菜单命令“Edit”-> “Add MFs”, 弹出“Membership Function”对话框, 将隶属函数的类型设置为“trimf”,并修改隶属函数的数目为3, 如图所示, 单击“OK”按钮返回。