通用2019年中考数学总复习第四章第五节相似三角形课件
微专题16 相似三角形之五大模型++++课件+2025年九年级中考数学总复习人教版(山东)

过一个直角顶点向两边作垂线,得到△PGE∽△PHF
29
【针对训练】
14.如图,在Rt△ABC中,∠ABC=90°,AB=3,BC=4,在Rt△MPN中,∠MPN=90°,点P在AC
3
上,PM交AB于点E,PN交BC于点F,当PE=2PF时,AP=_______.
30
15.如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,直角∠MON的顶点O在AB上,OM,
微专题16
相似三角形
之五大模型
2
模型1
特点
A字型(公共顶角)
两个三角形有一个公共角∠BAC,或者有DE∥BC,或者DE与BC不平行,
有∠ABC=∠AED
示例
思路 △ADE∽△ABC或△AED∽△ABC.如果没有明确说明对应关系,就应分
结论 以上两种情况讨论
3
【针对训练】
1.如图,在Rt△ABC中,∠ABC=90°,E,F分别为AC,BC的中点,连接EF,H为AE的中点,
1
ON分别交CA,CB于点P,Q,∠MON绕点O任意旋转.当 = 时, 的值为______;当
2
1
= 时, 的值为______.(用含n的式子表示)
31
16.(2024·青岛市南区二模)如图,点F在四边形ABCD的边AB上,
(1)如图1,当四边形ABCD是正方形时,过点B作BE⊥CF,垂足为O,交AD于点E.则BE
∴∠PBG=180°-∠ABC=90°,
∴∠PBG=∠POC=90°,
∵∠BPG=∠OPC,
∴△BPG∽△OPC,
∴ = ,
人教版中考数学专题课件:相似三角形及其应用

皖考解读
考点聚焦
皖考探究
当堂检测
相似三角形及其应用
考点3 平行线分线段成比例定理
三条平行线截两条直线,所得的对应线段 定理 成比例 ________. 平行于三角形一边的直线截其他两边 (或两边的延 推论 长线),所得的对应线段________. 成比例
皖考解读
考点聚焦
皖考探究
当堂检测
相似三角形及其应用
皖考解读 考点聚焦 皖考探究 当堂检测
相似三角形及其应用
考点7 相似三角形的应用
几何图 形的证 明与计算 相似三角 形在实际 生活中的 应用
证明线段的数量关系,求线段的长度,图形的 面积等. 首先根据题中的条件,找出相似三角形,再利 用相似三角形的性质解答. (1)利用投影、平行线、标杆等构造相似三角形 求解; (2)测量底部可以到达的物体的高度; (3)测量底部不可以到达的物体的高度; (4)测量河的宽度.
皖考解读
考点聚焦
皖考探究
当堂检测
相似三角形及其应用
考点2 比例线段
定义 对于四条线段 a、b、c、d,如果其中两条线段的长度的 线段 比与另两条线段的长度的比相等,即_____________ a∶b=c∶d ,那 么,这四条线段叫做成比例线段,简称比例线段. 在线段 AB 上, 点 C 把线段 5-1 AB 分成两条线段 AC 和 BC(AC = AB 黄金 >BC),如果AC ____________ ,那么称线段 AB 被点 C 黄金 2 分割 分割,点 C 叫做线段 AB 的黄金分割点,AC 与 AB 的比 0.618 叫做黄金比,黄金比约为________.
皖考解读
考点聚焦
皖考探究
当堂检测
相似三角形及其应用
山东省2022年中考数学(五四制)一轮课件:第四章 第5课时 相似三角形

1.相似三角形对应高的比、对应角平分线的比、对应中线 的比都等于__相__似__比___; 2.相似三角形的周长比等于__相__似__比___,面积比等于 __相__似__比__的__平__方___
状元笔记:在利用“两边成比例且夹角相等的两个三角形相似”判定两个 三角形相似时,一定要确保成比例的两边的夹角为相等角
3.如图,已知∠BAC=∠EAD,AB=20.4,AC=48,AE=17,AD=40.求 证:△ABC∽△AED.
证明:∵AB=20.4,AC=48,AE=17,AD=40,
AB 20.4
AC 48
AB AC
∴AE= 17 =1.2,AD=40=1.2,∴AE=AD.
∵∠BAC=∠EAD,∴△ABC∽△AED.
(一线三垂直平移变形)
∠B=∠AGE=∠D=90°,则 △ABC∽△FDE
1.(2019·淄博)如图,在△ABC中,AC=2,BC=4,D为BC边上的一点, 且∠CAD=∠B.若△ADC的面积为a,则△ABD的面积为( C )
A.2a
5 B.2a
C.3a
7 D.2a
2.(2021·威海乳山模拟)如图,在△ABC中,AB=9,AC=6,点M在边 AB上,且AM=3,点N在边AC上.当AN= 2或4.5 时,△AMN与原三角形 相似.
【思路分析】 (1)利用三角形全等的性质、等腰三角形的性质、三角形内角和定理可 得; (2)同(1)的证明方法;
AB BD (3)证明△ABD∽△DCF,根据相似三角形的性质可得 CD = CF ,求出CF的最 大值.
【规范解答】 (1)∠ADE=30°. (2)(1)中结论仍成立. 理由:∵AB=AC,∴∠B=∠ACB. ∵∠ACB=∠ACE, ∴∠B=∠ACE.∵AB=AC,BD=CE, ∴△ABD≌△ACE(SAS), ∴AD=AE,∠BAD=∠CAE,∴∠DAE=∠BAC=120°, ∴∠ADE=30°. (3)CF的最大值为 9 .
中考数学复习·图形的相似+相似三角形专题(位似、相似、相似三角形证明及应用)名校名师全解全练精品课件

A.12.36 cm C.32.36 cm
5-1 【解析】∵黄金比为 ≈0.618 , ∴ 它 的 宽 约 为 2 0.618×20≈12.36 cm.
【答案】A
上一页
下一页
宇轩图书
考
点
训
a
练
首页
2 . (2010 中考变式题 )已知 = = ,且 a + b+ c≠0 ,则 2 5 7 2a+3b-2c 的值为( a+b+c 5 A. 14 )
的周长与五边形 A′B′C′D′E′的周长的比值为
上一页
下一页
宇轩图书
中考典例精析
(2011·河北)如图所示,在6×8网格图中,每 个小正方形边长均为1.点O和△ABC的顶点均为小正方形
首页
的顶点.
(1)以O为位似中心,在网格图中作△A′B′C′,使△A′B′C′和 △ABC位似,且位似比为1∶2. (2)连接(1)中的AA′,求四边形AA′C′C的周长.(结果保留根号) 【点拨】位似图形一定是相似图形,可以利用相似图形的性质计算或 证明. 【 解 答 】 (1) 如 图 所 示. (2)AA′ =CC′ = 2. 在
目录
第六章 图形的相似与解直角三角形 第23讲 图形的相似与位似
考点知识精讲
中考典例精析
举一反三
考点训练
宇轩图书
考点知识精讲
考点一 成比例线段与比例的定义及性质
首页
1.对于四条线段 a、b、c、d,如果 做成比例线段,简称比例线段.
那么这四条线段叫
2.表示两个比相等的式子叫做比例式,简称比例. 3.连比:连在一起的三个数的比,叫做连比. a c 4.比例的基本性质:如果 = ,那么 ad=bc ,反之也成立.其中 b d a b a 与 d 叫做比例外项,b 与 c 叫做比例内项.特殊地 = ⇔b2=ac. b c
2019年中考数学专题复习资料--全等三角形含答案(共11页).docx
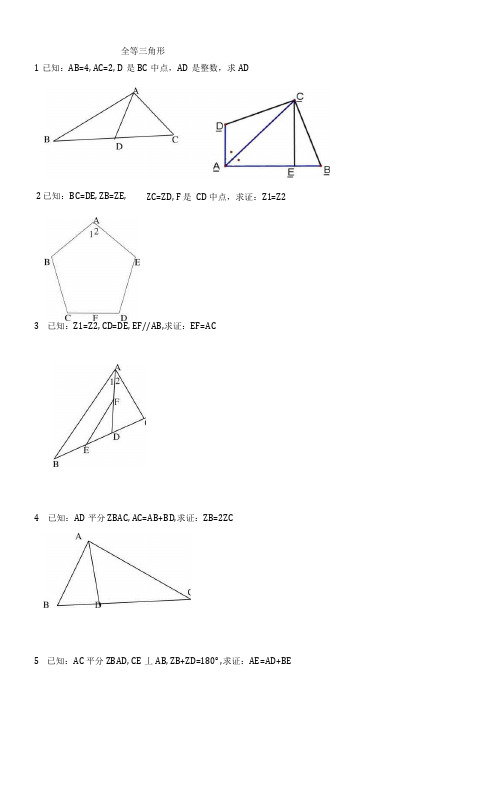
全等三角形1已知:AB=4, AC=2, D 是BC 中点,AD 是整数,求AD3 已知:Z1=Z2, CD=DE, EF//AB,求证:EF=AC4 已知:AD 平分ZBAC, AC=AB+BD,求证:ZB=2ZC5 已知:AC 平分ZBAD, CE 丄AB, ZB+ZD=180° ,求证:AE=AD+BEZC=ZD, F 是 CD 中点,求证:Z1=Z22 已知:BC=DE, ZB=ZE,6如图,四边形ABCD中,AB〃DC, BE、CE分别平分ZABC、ZBCD,且点E在AD上。
求证:BC=AB+DC。
7 已知:AB=CD, ZA=ZD,求证:ZB=ZC&P 是ZBAC 平分线AD 上一点,AC>AB,求证:PC-PB<AC-AB9 已知,E 是AB 中点,AF=BD, BD=5, AC=7,求DC13已知:如BD1AC ,分别为D、E, BD、CE相交于点F。
求证:BE=CD. 图,AB=AC, CEXAB,垂足10.如图,已知AD/7BC, ZPAB的平分线与ZCBA的平分线相交于E, CE的连线交AP于D.求证:AD+BC=AB. 11如图,AABC中,AD是ZCAB的平分线,且AB=AC+CD,求证:ZC=2ZB12 如图:AE、BC 交于点M, F 点在AM 上,BE/7CF, BE=CF。
求证:AM是△ABC的中线。
14 在AABC 中,ZACB = 90°, AC = BC ,直线MV 经过点C ,且AD 丄MZV 于D , BE L MN 于E . (1) 当直线MN绕点C旋转到图1的位置时,求证:① ^ADC竺ACEB;② DE = AD + BE ;(2)当直线MV绕点C旋转到图2的位置时,(1)中的结论还成立吗?若成立,请给出证明; 若不成立,说明理由.15如图所示,已知AE丄AB, AF丄AC, AE=AB, AF=AC。
求证:16.如图,已知AC〃BD, EA、EB分别平分ZCAB和ZE,则AB与AC+BD相等吗?请说明理由DBA, CD过点(1) EC=BF; (2) EC丄BFB C17.如图9所示,AABC是等腰直角三角形,ZACB=90° , AD是BC边上的中线,过C作AD的垂线,交AB于点E,交AD于点F,求证:ZADC=ZBDE.图9全等三角形证明经典(答案)1. 延长AD到E,使DE=AD,则三角形ADC全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE即:10-2<2AD<10+2 4<AD<6又AD是整数,则AD=52证明:连接BF和EF。
第21讲 相似三角形-中考数学一轮复习知识考点习题课件

∵四边形ABCD是正方形,∴∠DCG=90°. ∵CF平分∠DCG,∴∠FCG=21(1)∠DCG=
2 45°.
∵∠EGF=90°,∴∠GCF=∠CFG=45°,
∴FG=CG,∴EG=CE+CG=2+FG.
由(1A)B知=,△BEBA,E∽△1G0EF,= 8 ,
EG FG 2 FG FG
∴
1
∴ CE FG
第四章 图形初步与三角形
第21讲 类似三角形
上一页 下一页
1.(202X·武威)生活中到处可见黄金分割的美.如图,在设计人体雕像时,使
雕像的腰部以下a与全身b的高度比值接近0.618,可以增加视觉美感.若图
中b为2米,则a约为A( ) A.1.24米 B.1.38米 C.1.42米 D.1.62米
A.14
B.15
C. 8 3 D.6 5
上一页 下一页
15.(202X·乐山)把两个含30°角的直角三角板按如图所示拼接在一起,点E
为AD的中点,连接BE,交AC于点F,则AF
3
=__5______.
AC
上一页 下一页
16.(202X·湖州)在每个小正方形的边长为1的网格图形中,每个小正方形的顶 点称为格点,顶点都是格点的三角形称为格点三角形.如图,已知 Rt△ABC是6×6网格图中的格点三角形,则该图中所有与Rt△ABC类似的 格点三角形中,面积最大的三角形的斜边长是___5__2___.
2,A′D′=3,则△ABC与△A′B′C′的面积比为( A )
A.4∶9
B.9∶4
C.2∶3
D.3∶2
上一页 下一页
4.(202X·雅安)如图,每个小正方形的边长均为1,则下列图形中的三角形(阴 影部分)与△A1B1C1类似的是( B )
2024年河北省中考数学一轮复习考点突破课件:相似三角形(含位似)

(2)AE=_______.
第六节 相似三角形(含位似)
突
破
子题衍生 △ACE 与△BDE 的周长比为 __2_∶__3__;△BDE 与△ACE 的面积比为
重 ___9_∶__4__. 难
题
型
第六节 相似三角形(含位似)
突
破
仿真再练一 [2023·石家庄 47 中模拟]如下图,在 Rt△ABC 中,
第六节 相似三角形(含位似)
■考点二 相似三角形(多边形)的性质与判定(8 年 5 考)
定义:对应角相等,对应边成比例的两个三角形叫做相似三角形,相似三
相 角形对应边的比叫做相似比.
似
三
1. 平行于三角形一边的直线和其他两边(或两边的延长线)相
角
交,所截得的三角形与原三角形⑨__相__似__.
形 2. ⑩___两__ 角对应相等的两个三角形相似.
相似三角形(含位似)
对接版本 人教 九下第二十七章 P23~59. 冀教 九上第二十五章 P57~102. 北师 九上第四章 P76~123.
第六节 相似三角形(含位似)
■考点一 比例线段的相关概念
线段的比:两条线段的比是两条线段的长度之比.
比例线段:在四条线段 a,b,c,d 中,如果 a 与 b 的比等于 c 与
突
破
5 如图,△ABC 中,∠A=78°,AB=4,AC=6.将△ABC 沿图示中的虚线剪开,剪下
重 的阴影三角形与原三角形不相似的是 ( C )
难
题
型
第六节 相似三角形(含位似)
突
破
仿真再练二 已知 Rt△ABC 中,∠BAC=90°,过点 A 作一条直线,使其将
重 △ABC 分成两个相似的三角形.观察下列图中尺规作图痕迹,作法错误的是 (
专题4.5锐角三角函数中考数学第一轮总复习课件

(3)sinA+cosA_>___1;sin2A+cos2A_=___1, sinα=cos(_9_0_º_-_α_);cosα=sin(_9_0_º_-_α_);
典例精讲
锐角三角函数
知识点一
【例1】(1)式子2cos30º-tan45º- (1 tan 60 )2 的值是__0__.
5.已知△ABC中,AB=10,AC= 2 7,∠B=30º,则△ABC的面积等于_1_5__3_或__1_0__3_.
6.四边形ABCD中,BD是对角线,∠ABC=90º,tan∠ABD=
3 4
,AB=20,
BC=10,AD=13,则线段CD=1_7__或___8_9__.
A
A A
E F
B
DC
B
C´
02
解直角三角形
精讲精练
03 解直角三角形应用
考点聚焦
解直角三角形的应用
知识点三
1.视角,2.方向角(方位角),3.坡度(坡比),坡角:i=tanα=h:l.
在测量高度,宽度,距离等问题中,常见的构造的基本图形如下:
③利用反射构造相似. ②同一地点看不同点 ①不同地点看同一点
典例精讲
直角三角形应用
A
K
I
H
N
M
D
A
K
I
NH M
D
A
K
I
H N
M
D
E
O
B 图1 G
FE O
CB 图2 G
FE
O
C B 图3 G
F C
B. 1
c os2
1
C.sin2α+1 D.cos2α+1
第五节 相似三角形(含位似) 【九年级 中考数学复习】

第2题图
A. 7
B. 7.5
C. 8
D. 8.5
命题点 2 相似三角形的性质及判定(均是在证明过程中涉及)
基础训练
3. (2019重庆A卷)如图,△ABO∽△CDO,若BO=6,DO=3,
CD=2,则AB的长是( C )
A. 2
B. 3
C. 4
D. 5
4. 如图,在△ABC中,点D,E分别在边AB、AC上,下列条
(不与端点重合),连接AD,DE,若∠ADE=45°.
(1)求证:△ABD∽△DCE;
(2)若AB=4 2,BD=1,求AE的长.
第7题图
【思维教练】(1)要证△ABD∽△DCE,由等腰直角三角形的性质可得一组角相
等且均为45°,由∠ADE=45°,结合一线三等角模型可得另一组角相等,即
可得证;(2)要求AE的长,可通过求CE的长求解.由AB、AC的长可得BC的长,
线段 成比例 . 平行线分线段成比例
推论:平行于三角形一边的直线截其他两边(或
两边的延长线)所得的对应线段 成比例 )
返回思维导图
1.相似三角形对应角 相等 ,对应边 成比例 . 相似三角形的性质 2.相似三角形的对应线段(高、中线、角平分线) 成比例 .
3.相似三角形的周长比等于 相似比 ,面积比等于相似比的平方)
2.相似三角形 对应线段成比例
3.相似三角形的周长比
等于相似比,面积
1.相似多边形对
相似
比等于相似比的平方
应角相等,对应边 相似多边 三角形 相似三角 一般三角形
的比等于相似比 形的性质(含位似) 形的判定 直角三角形
2.相似多边形的周
有平行截线--用
长比等于相似比,面
中考数学一轮复习专题解析—相似三角形

中考数学一轮复习专题解析—相似三角形复习目标1.了解相似图形和相似三角形的概念。
2.掌握三角形相似的判定方法和性质并学会运用。
考点梳理一、相似图形1.形状相同的图形叫相似图形,在相似多边形中,最简单的是相似三角形.2.比例线段的相关概念如果选用同一单位量得两条线段b a ,的长度分别为n m ,,那么就说这两条线段的比是nm b a =,或写成n m b a ::=. 注意:在求线段比时,线段单位要统一,单位不统一应先化成同一单位. 在四条线段d c b a ,,,中,如果b a 和的比等于d c 和的比,那么这四条线段d c b a ,,,叫做成比例线段,简称比例线段.注意:(1)当两个比例式的每一项都对应相同,两个比例式才是同一比例式.(2)比例线段是有顺序的,如果说a 是d c b ,,的第四比例项,那么应得比例式为:ad c b =. 3. 比例的性质基本性质:(1)bc ad d c b a =⇔=::;(2)b a c b c c a ⋅=⇔=2::.注意:由一个比例式只可化成一个等积式,而一个等积式共可化成八个比例式,如bc ad =,除了可化为d c b a ::=,还可化为d b c a ::=,b a d c ::=,c a d b ::=,c d a b ::=,b d a c ::=,a b c d ::=,a c b d ::=.更比性质(交换比例的内项或外项):()()()a b c d a c d c b d b ad b c a ⎧=⎪⎪⎪=⇒=⎨⎪⎪=⎪⎩,交换内项,交换外项.同时交换内外项 反比性质(把比的前项、后项交换):cd a b d c b a =⇒=. 合比性质:dd c b b a d c b a ±=±⇒=. 注意:实际上,比例的合比性质可扩展为:比例式中等号左右两个比的前项,后项之间 发生同样和差变化比例仍成立.如:⎪⎪⎩⎪⎪⎨⎧+-=+--=-⇒=d c d c b a b a c c d a a b d c b a 等等. 等比性质: 如果)0(≠++++====n f d b n m f e d c b a ,那么b a n f d b m e c a =++++++++ . 注意:(1)此性质的证明运用了“设k 法” ,这种方法是有关比例计算,变形中一种常用方法.(2)应用等比性质时,要考虑到分母是否为零.(3)可利用分式性质将连等式的每一个比的前项与后项同时乘以一个数,再利用等比性质也成立.4.比例线段的有关定理平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例.推论:(1)平行于三角形一边的直线截其它两边(或两边的延长线)所得的对应线段成比例.(2)平行于三角形一边并且和其它两边相交的直线,所截得的三角形的三边与原三角形三边对应成比例.定理:如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形第三边.5.黄金分割把线段AB 分成两条线段)(,BC AC BC AC >,且使AC 是BC AB 和的比例中项,叫做把线段AB 黄金分割,点C 叫做线段AB 的黄金分割点,其中AB AC 215-=≈0.618AB 例1.如果0ab cd =≠,则下列正确的是( )A .::a c b d =B .::a d c b =C .::a b c d =D .::d c b a = 【答案】B【分析】根据比例的基本性质,列出比例式即可.【详解】解:∵0ab cd =≠,∵::a d c b =,故选:B .例2.两个相似多边形的一组对应边的长分别为6cm ,9cm ,那么它们的相似比为( )A .23B C .49 D .94【答案】A【分析】根据相似多边形的性质求解即可;【详解】两个相似多边形一组对应边的长分别为6cm ,9cm ,∵它们的相似比为:6293=.故选A .二、相似三角形的概念对应角相等,对应边成比例的三角形,叫做相似三角形.相似用符号“∵”表示,读作“相似于” .相似三角形对应边的比叫做相似比(或相似系数).相似三角形对应角相等,对应边成比例.注意:∵对应性:即两个三角形相似时,通常把表示对应顶点的字母写在对应位置上,这样写比较容易找到相似三角形的对应角和对应边.∵顺序性:相似三角形的相似比是有顺序的.∵两个三角形形状一样,但大小不一定一样.∵全等三角形是相似比为1的相似三角形.二者的区别在于全等要求对应边相等,而相似要求对应边成比例.三、相似三角形的等价关系(1)反身性:对于任一ABC ∆有ABC ∆∵ABC ∆.(2)对称性:若ABC ∆∵'''C B A ∆,则'''C B A ∆∵ABC ∆.(3)传递性:若ABC ∆∵C B A '∆'',且C B A '∆''∵C B A ''''''∆,则ABC ∆∵C B A ''''''∆.四、相似三角形的基本定理定理:平行于三角形一边的直线和其它两边(或两边延长线)相交,所构成的三角形与原三角形相似.定理的基本图形:五、三角形相似的判定方法1、定义法:对应角相等,对应边成比例的两个三角形相似.2、平行法:平行于三角形一边的直线和其它两边(或两边的延长线)相交,所构成的三角形与原三角形相似.3、判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.简述为:两角对应相等,两三角形相似.4、判定定理2:如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似.简述为:两边对应成比例且夹角相等,两三角形相似.5、判定定理3:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似.简述为:三边对应成比例,两三角形相似.6、判定直角三角形相似的方法:(1)以上各种判定均适用.(2)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.(3)直角三角形被斜边上的高分成的两个直角三角形与原三角形相似.直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项。
中考数学基础复习第19课相似三角形及其性质课件

【考点剖析】 【考点1】比例线段 例1.如图,l1∥l2∥l3,AB=3,BC=5,DF=12,求DE和EF的长.
【解析】∵l1∥l2∥l3, ∴ AB DE (平行线分线段成比例),
AC DF
∵AB=3,BC=5,∴AC=AB+BC=8,
∵DF=12,∴ 3 DE .∴DE=4.5,
8 12
第19课 类似三角形及其性质
【知识清单】 一、平行线分线段成比例 两条直线被一组平行线所截,所得的对应线段____成__比__例___. 二、类似三角形的性质 性质1:类似三角形的对应角____相__等___,对应边的比____相__等___. 性质2:类似三角形周长的比等于____类__似__比___. 性质3:类似三角形对应高的比、对应中线的比、对应角平分线的比等于 ____类__似__比___. 性质4:类似三角形的面积的比等于类似比的____平__方___.
b b+2x
b(b+2x)
b(b+2x)
∵a>b>0,x>0,∴m-n= 2x(a-b)>0,
b(b+2x)
∴m>n.
若图中的两个矩形类似,则需m=n.
∴图中的两个矩形不类似.
反思:利用类似多边形的性质转化为比例式求解.
【学后检测】
1.如图l1∥l2∥l3,若
AB=3 BC 2
,DF=10,则DE=
3
则点C坐标为 ( B )
A.(-1,-1) C. (1, 4)
3
B.( 4 , 1)
3
D.(-2,-1)
3.(202X·吉林)如图,在△ABC中,D,E分别是边AB,AC的中点.若△ADE的面积
为1
2
3
第18节相似三角形-中考数学一轮知识复习课件

相似比为13 ,把线段 AB 缩短,则点 A 的对应 点 A'的坐标为__(_2_,_1_)_或_(_-__2,__-__1)__.
知识清单
线段的比和比例线段 1.线段的比:两条线段__长_度___的比叫做 两条线段的比. 注意:求两条线段的比,要求长度单位相 同;线段的比与选用的长度单位无关. 2.对于四条线段 a,b,c,d,如果其中 两条线段的比__等__于__另外两条线段的比,就 说这四条线段是成比例线段.
=6-6-32x -38 x2=-38 x2+32 x.
当 x≥2 时,S 随 x 增大而减少.
与 AC 交于点 G,则相似三角形共有( C )
A.3 对
B.5 对
C.6 对
D.8 对
针对训练 6.(2019·凉山州改编)如图,∠ABD=∠BCD= 90°,DB 平分∠ADC,过点 B 作 BM∥CD 交 AD 于 点 M.连接 CM 交 DB 于点 N.求证:BD2=AD·CD.
证明:∵DB 平分∠ADC, ∴∠ADB=∠CDB. 且∠ABD=∠BCD=90°. ∴△ABD∽△BCD. ∴ABDD =BCDD . ∴BD2=AD·CD.
4.(2020·宁夏)在平面直角坐标系中,△ ABC 的三个顶点的坐标分别是 A(1,3),B(4, 1),C(1,1).
(1)画出△ABC 关于 x 轴成轴对称的△A1B1C1; (2)画出△ABC 以点 O 为位似中心,位似比为 1∶2 的△A2B2C2.
解:(1)(2)如图所示,△A1B1C1,△A2B2C2即为所求.
(2)若AADC =37 ,求FAGF 的值.
