第二章节形式语言与自动机理论参考测试答案
形式语言与自动机理论-蒋宗礼-第二章参考答案

2.1回答下面的问题: (周期律 02282067)(1)在文法中,终极符号和非终极符号各起什么作用?✓ 终结符号是一个文法所产生的语言中句子的中出现的字符,他决定了一个文法的产生语言中字符的范围。
✓ 非终结符号又叫做一个语法变量,它表示一个语法范畴,文法中每一个产生式的左部至少要还有一个非终结符号,(二,三型文法要求更严,只允许左部为一个非终结符号)他是推导或归约的核心。
(2)文法的语法范畴有什么意义?开始符号所对应的语法范畴有什么特殊意义?✓ 文法的非终结符号A 所对应的语法范畴代表着一个集合L (A ),此集合由文法产生式中关于A 的产生式推导实现的✓ 开始符号所对应的语法范畴则为文法G = {V ,T ,P ,S}所产生的语言L (G )={w S T w w **|⇒∈且}(3)在文法中,除了的变量可以对应一个终极符号行的集合外,按照类似的对应方法,一个字符串也可以对应一个终极符号行集合,这个集合表达什么意义?✓ 字符串对应的终极符号行集合表示这个字符串所能推导到的终极字符串集合,为某个句型的语言。
(4)文法中的归约和推导有什么不同?✓ 推导:文法G = {V ,T ,P ,S},如果,)(,,*Y T VP ∈∈→δγβα则称γαδ在G 中推导出了γβδ。
✓ 归约:文法G = {V ,T ,P ,S},如果,)(,,*Y T VP ∈∈→δγβα则称γβδ在G 中归约到γαδ。
✓ 这他们的定义,我个人理解两个概念从不同角度看待文法中的产生式,推导是自上而下(从产生式的左边到右边),而归约是自下而上(从产生式的右边到左边),体现到具体实际中,如编译中语法分析时语法树的建立,递归下降,LL (1)等分析法采用自开始符号向下推导识别输入代码生成语法树,对应的LR (1),LALR 等分析法则是采用自输入代码(相当于文法中语言的句子)自底向上归约到开始符号建立语法树,各有优劣。
(5)为什么要求定义语言的字母表上的语言为一个非空有穷集合?✓ 非空:根据字母表幂的定义:εε,}{0∑=为字母表中0个字符组成的。
形式语言与自动机理论第二章蒋宗礼

2.2 形式定义
• P——为产生式(production)的非空有穷集合。P中的元素均具有 形式αβ,被称为产生式,读作:α定义为β。其中 α∈(V∪T)+,且α中至少有V中元素的一个出现。β∈(V∪T)*。 α称为产生式αβ的左部,β称为产生式αβ的右部。产生 式又叫做定义式或者语法规则。
A1A },A)。
第20页/共106页
2.2 形式定义
⑸ ({S , A , B , C , D},{a , b , c , d,#} , {SABCD , Sabc# , AaaA , ABaabbB , BCbbccC,cCcccC,CDccd# ,CDd#, CD#d},S)。
⑹ ({S},{a , b} , {S00S , S11S , S00 , S11},S)。
第32页/共106页
2.2 形式定义
• 例 2-5 设G=({S,A,B},{0,1},{SA|AB,A0|0A,B1|11},S)
对于n≥1,
A n 0n
首先连续n-1次使用产生式;A0A, 最后使用产生式A0;
A n 0nA
连续n次使用产生式A0A;
B1
使用产生式B1;
B 11
使用产生式B11。
• CFL
• CFG(CNF、GNF)、PDA、CFL的性质。
• TM
• 基本TM、构造技术、TM的修改。
• CSL
• CSG、LBA。
第4页/共106页
教材及主要参考书目
1.蒋宗礼,姜守旭. 形式语言与自动机理论. 北京:清华大学出版 社,2003年
2.John E Hopcroft, Rajeev Motwani, Jeffrey D Ullman. Introduction to Automata Theory, Languages, and Computation (2nd Edition). Addison-Wesley Publishing Company, 2001
《形式语言与自动机》(王柏、杨娟编著)课后习题答案-推荐下载

P2
9.对应图(a)(b)的状态转换图写出正则式。(图略) (1) 由图可知 q0=aq0+bq1+a+ε
q1=aq2+bq1 q0=aq0+bq1+a =>q1=abq1+bq1+aaq0+aa =(b+ab) q1+aaq0+aa =(b+ab) *( aaq0+aa)
=>q0=aq0+b(b+ab) *( aaq0+aa ) +a+ε
(2) 由生成式得:
S=aA+B ①
A=bB+cC ② B=a+bB ③ C=D+abB ④ D=dB ⑤ 由③得 B=b*a ⑥ 将⑤⑥代入④ C=d+abb*a=d+ab+a ⑦ 将⑥⑦代入② A=b+a+c(d+b+a) ⑧ 将⑥⑧代入① S=a(b+a+c(d+ab+a))+b*a
=ab+a+acd+acab+a+b*a
4.对下列文法的生成式,找出其正则式 (1) G=({S,A,B,C,D},{a,b,c,d},P,S),生成式 P 如下:
S→aA S→B
A→abS A→bB
B→b B→cC
C→D D→bB
D→d
(2) G=({S,A,B,C,D},{a,b,c,d},P,S),生成式 P 如下:
S→aA S→B
P: S→aS S→bS S→ε
(2) 右线性文法 G=({S},{a,b},P,S)
P: S→aS S→bS S→abb
自动机理论、语言和计算导论课后习题答案(中文版)

Solutions for Section 2.2Exercise 2.2.1(a)States correspond to the eight combinations of switch positions, and also must indicate whether the previous roll came out at D, i.e., whether the previous input was accepted. Let 0 represent a position to the left (as in the diagram) and 1 a position to the right. Each state can be represented by a sequence of three 0's or 1's, representing the directions of the three switches, in order from left to right. We follow these three bits by either a indicating it is an accepting state or r, indicating rejection. Of the 16 possible states, it turns out that only 13 are accessible from the initial state, 000r. Here is the transition table:杠杆可能出现8种情况,影响着最终状态。
并且也要说明,前面一个大理石球是否从D滚出,也就是说,前一个输入是否被接受。
令0 代表向左方的状态(如图表),1 代表向右方。
这三个杠杆的每一个状态都可以用三个数(0或1)组成的序列表示。
这个序列后面跟着字母a或者r。
形式语言与自动机答案蒋宗礼

形式语言与自动机答案蒋宗礼【篇一:形式语言第四章参考答案(蒋宗礼)】p> 解:所求正则表达式为:(0+1)*。
+⑵ {0, 1}。
解:所求正则表达式为:(0+1)+。
⑶ { x│x∈{0,1}且x中不含形如00的子串 }。
解:根据第三章构造的fa,可得所求正则表达式为:1*(01+)*(01+0+1)。
⑷ { x│x∈{0,1}*且x中不含形如00的子串 }。
++ +q1为终态时的正则表达式:0*1(1*(0(10)*111*1)*(0(10)*00*1)*)* q2为终态时的正则表达式:0*11*0((10)*(111*11*0)*(00*11*0)*)*q3为终态时的正则表达式:0*11*0(10)*1(11*11*0((10)*(00*11*0)*)*1)* q4为终态时的正则表达式:0*11*0(10)*11(1*(11*0((00*11*0)*(10)*)*11)*)*将以上5个正则表达式用“+”号相连,就得到所要求的正则表达式。
⑺ { x│x∈{0,1}且当把x看成二进制数时,x模5与3同余和x为0时,│x│=1且x≠0时,x的首字符为1}。
解:先画出状态转移图,设置5个状态q0、q1、q2、q3、q4,分别表示除5的余数是0、1、2、3、4的情形。
另外,设置一个开始状态q.由于要求x模5和3同余,而3模5余3,故只有q3可以作为终态。
由题设,x=0时,│x│=1,模5是1,不符合条件,所以不必增加关于它的状态。
下面对每一个状态考虑输入0和1时的状态转移。
q: 输入1,模5是1,进入q1。
+q0: 设x=5n。
输入0,x=5n*2=10n,模5是0,故进入q0输入1,x=5n*2+1=10n+1,模5是1,故进入q1q1:设x=5n+1。
输入0,x=(5n+1)*2=10n+2,模5是2,故进入q2输入1,x=(5n+1)*2+1=10n+3,模5是3,故进入q3 q2:设x=5n+2。
自动机习题中文解答全
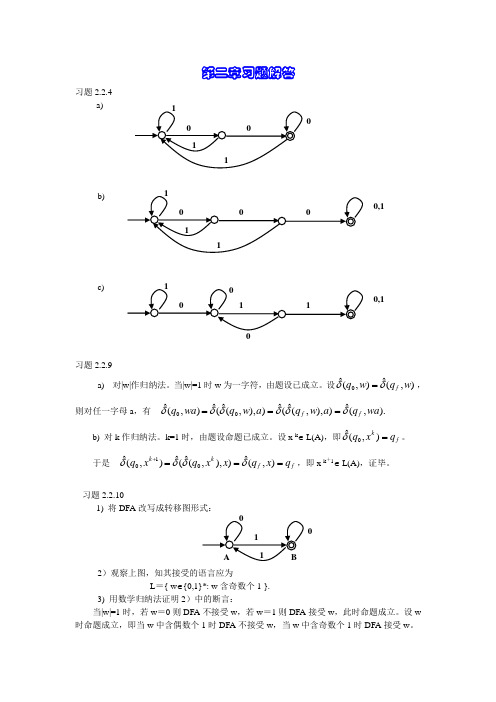
第二章习题解答习题2.2.4a) b) c) 习题2.2.9a) 对|w|作归纳法。
当|w|=1时w 为一字符,由题设已成立。
设),(ˆ),(ˆ0w q w q fδδ=, 则对任一字母a ,有 ).,(ˆ)),,(ˆ(ˆ)),,(ˆ(ˆ ),(ˆ00wa q a w q a w q wa q ff δδδδδδ=== b) 对k 作归纳法。
k=1时,由题设命题已成立。
设x k ∈ L(A),即f k q x q =),(ˆ0δ。
于是 ff k k q x q x x q x q ===+),(ˆ)),,(ˆ(ˆ ),(ˆ010δδδδ,即x k +1∈ L(A),证毕。
习题2.2.101) 将DFA 改写成转移图形式:2)观察上图,知其接受的语言应为L ={ w ∈{0,1}*: w 含奇数个1 }. 3) 用数学归纳法证明2)中的断言:当|w|=1时,若w =0则DFA 不接受w ,若w =1则DFA 接受w ,此时命题成立。
设w 时命题成立,即当w 中含偶数个1时DFA 不接受w ,当w 中含奇数个1时DFA 接受w 。
0,10,1对于任一字符c :若c=0,则当w 中含偶数个1时由于DFA 不接受w ,故A w q =),(ˆ0δ,从而A wc q =),(ˆ0δ;当w 中含奇数个1时由于DFA 接受w ,故B w q =),(ˆ0δ,从而B wc q =),(ˆ0δ。
若c=1,则当w 中含偶数个1时由于DFA 不接受w ,故A w q =),(ˆ0δ,从而B wc q =),(ˆ0δ;当w 中含奇数个1时由于DFA 接受w ,故B w q =),(ˆ0δ,从而A wc q =),(ˆ0δ。
总之,当wc 中含偶数个1时DFA 不接受wc ,当wc 中含奇数个1时DFA 接受wc 。
命题得证。
习题2.2.111) 将DFA 改写成转移图形式:2)观察上图,知其接受的语言应为L ={ w ∈{0,1}*: w 不含子串00 }.3) 用数学归纳法证明2)中的断言,过程与前题类似。
形式语言与自动机理论-蒋宗礼-第一章参考答案

第一章参考答案1.1请用列举法给出下列集合。
(吴贤珺02282047)⑴你知道的各种颜色。
解:{红,橙,黄,绿,青,蓝,紫}⑵大学教师中的各种职称。
解:{助教,讲师,副教授,教授}⑶你所学过的课程。
解:{语文,数学,英语,物理,化学,生物,历史,地理,政治}⑷你的家庭成员。
解:{父亲,母亲,妹妹,我}⑸你知道的所有交通工具。
解:{汽车,火车,飞机,轮船,马车}⑹字母表{a , b}上长度小于4的串的集合。
解:{a,b,aa,bb,ab,ba,aaa,aab,aba,abb,baa,bab,bba,bbb}⑺集合{1,2,3,4}的幂集。
解:{Φ,{1},{2},{3},{4},{1,2},{1,3},{1,4},{2,3},{2,4},{3,4},{1,2,3},{1,2,4},{1,3,4},{2,3,4},{1,2,3,4} }⑻所有的非负奇数。
解:{1,3,5,7,…}⑼0~100的所有正整数。
解:{1,2,3, (100)(10) 1~10之间的和为10的整数集合的集合。
解:设所求的集合为A,集合A中的元素为A i(i=1,2,3,…),A i也是集合,A i中的元素在1~10之间,并且和为10。
根据集合元素的彼此可区分性,可以计算出A i中元素的最多个数,方法是:把1开始的正整数逐个相加,直到等于10(即10=1+2+3+4),这样,A i中最多有4个元素。
原因是:从最小的1开始,每次加入新的元素都只依次增加1,这样相加的和最小,要加到10,元素个数就最多。
求出最大的∣A i∣=4后,再求出元素个数为3,2,1的集合就可以了。
故A={{10},{1,9},{2,8},{3,7},{4,6},{1,2,7},{1,3,6},{1,4,5},{2,3,5},{1,2,3,4}}1.2 请用命题法给出下列集合1.3 给出下列集合的幂集.(02282075 冯蕊)(1)Φ(2){Φ}(3){Φ,{Φ}}(4){ε,0,00}(5){0,1}解答:(1){Φ}(2){Φ,{Φ}}(3){Φ,{Φ},{{Φ}},{Φ,{Φ}}}(4){Φ,{ε},{0},{00},{ε,0},{ε,00},{0,00},{ε,0,00}}(5){Φ,{0},{1},{0,1}}1.4.列出集合{0,1,2,3,4}中(褚颖娜02282072)(1)所有基数为3的子集{0,1,2},{0,1,3},{0,1,4},{0,2,3,},{0,2,4},.{1,2,3},{1,2,4},{1,3,4},{0,3,4},{2,3,4}(2)所有基数不大于3的子集Ф,{0},{1},{2},{3},{4},{3,4},{2,4},{2,3},{1,4},{1,3},{0,4},{0,3},{0,2},{1,2},{0,1},{0,1,2},{0,1,3}{0,1,4},{0,2,3,},{0,2,4},.{1,2,3},{1,2,4},{1,3,4},{0,3,4},{2,3,4}1.5解答:1、3、8、10、11、12、16正确1.6证明下列各题目(02282081 刘秋雯)1)A=B,iff A是B的子集且B是A的子集证明:充分条件:∵A=B则由集合相等的定义知对于任何x∈A,有x∈B∴A为B的子集同理,B为A的子集必要条件:∵A为B的子集∴对于任何x∈A,都有x∈B又∵B为A的子集,∴对于任何x∈B有,x∈A由集合相等的定义知,A=B2)如果A为B的子集,则|A|〈=|B|证明:A为B的子集,则对于任何x∈A有x∈B,∴存在一个集合C 使B=A∪C 且A∩C为空集则|B|=|A|+|C||C|〉=0∴|A|〈=|B|3)如果A为B的真子集,则|A|〈=|B|证明:(1)当A为有穷集合时,因为A为B的真子集,且则对于任何x∈A有x∈B,且存在∈B的x,此x不∈A∴存在一个非空集合C ,使B=A∪C 且A∩C为空集则|B|=|A|+|C| 且|C|〉=1∴|A|〈|B|(2)当A为无穷集合,因为A为B的真子集,则B一定也为无穷集合,|A|=∞,|B|=∞∴|A|=|B|综合(1),(2)所述,|A|<=|B|4)如果A是有穷集且A为B的真子集则|A|〈|B|证明:见上题证明(1)5)如果A为B的子集,则对于任何x∈A,有x∈B证明:若A为B的子集,则由子集定义可知,对于任何x∈A,有x∈B6)如果A是B的真子集,则对于任何x∈A,有x∈B,并且存在x∈B,但x不∈A 证明:由真子集的定义可证7)如果A为B的子集,B为C的子集,则A为C的子集证明:A为B的子集,B为C的子集则对于任何x∈A,则x都∈B,且,又对于任何y∈B,则y∈C,∴对于任何x∈A,x∈C∴A为C的子集8)如果A为B的真子集,B为C的真子集,则A为C的真子集证明:A为B的真子集,B为C的真子集则对于任何x∈A,则x都∈B,且,存在x∈B但次x不∈A,又对于任何y∈B,则y∈C,存在y∈C但此y不∈B,∴对于任何x∈A,x∈C,存在x∈C.x不∈A∴A为C的真子集9)如果A为B的子集,B为C的真子集,则A为C的真子集证明:因为A为B的子集,B为C的真子集则对于任何x∈A,x都∈B,且x都∈C又对于任何y∈B,则y∈C,存在y∈C但此y不∈B,则y不∈A∴对于任何x∈A,x∈C,存在x∈C.x不∈A∴A为C的真子集10)如果A为B的真子集,B为C的子集,则A为C的真子集证明:A为B的真子集,B为C的子集则对于任何x∈A,则x都∈B,且存在x∈B但次x不∈A,又对于任何y∈B,则y∈C∴对于任何x∈A,x∈C,存在x∈C.x不∈A∴A为C的真子集11)如果A=B,则|A|=|B|证明:A=B,则A与B所含元素相同∴|A|=|B|12)如果A为B的子集,B为C的真子集,或如果A为B的真子集,B为C的子集,则A为C的真子集证明:证明见9,101.7 A = {1,2,3,4,5,6} B = {1,3,5} C = {2,4,6} U = {0,1,2,3,4,5,6,7,8,9}A(1). B= {1,3,5} = B(2). C B A )(= {1,3,5} }6,4,2{={1,2,3,4,5,6} = A (3). )()(C U B A - = {1,3,5} }9,8,7,5,3,1,0{ ={0,1,3,5,7,8,9} = C(4).A-B-C= {2,4,6} – {2,4,6}=Φ(5).A × B × C ×Φ=ΦA ×Φ = Φ (6). A C AB A )(= {1,3,5} {0,7,8,9} {0,7,8,9}= {0,1,3,5,7,8,9} = C(7). C AB A ⨯⨯ =C B A ⨯⨯ =)},(),(),(|),{(C b B a C b B a C b B a b a A ∈∈∈∈∈∈⨯或或 =)},,(),,(),,(|),,{(C c B b A a C c B b A a C c B b A a c b a ∈∈∈∈∈∈∈∈∈或或 (8). C B A B A)( = C A A= C A= A={1,2,3,4,5,6}1.8 对论域U 上的集合A 、B 、C ,证明以下结论成立。
编译原理-第2章 形式语言的基本知识-习题答案

第2章形式语言的基本知识习题答案第 1 题文法G=({A,B,S},{a,b,c},P,S)其中P 为:S→Ac|aBA→abB→bc写出L(G[S])的全部元素。
答案:L(G[S])={abc}第 2 题文法G[N]为:N→D|NDD→0|1|2|3|4|5|6|7|8|9G[N]的语言是什么?答案: 允许0 开头的非负整数或者G[N]的语言是V+。
V={0,1,2,3,4,5,6,7,8,9}第3题为只包含数字、加号和减号的表达式,例如9-2+5,3-1,7等构造一个文法。
答案:G[S]:S->S+D|S-D|DD->0|1|2|3|4|5|6|7|8|9第 4 题已知文法G[Z]:Z→aZb|ab写出L(G[Z])的全部元素。
答案:L(G[Z])={a n b n|n>=1}第 5 题(答案不唯一)写一文法,使其语言是偶正整数的集合。
要求:(1) 允许0 打头;(2)不允许0 打头。
答案:(1)允许 0 开头的偶正整数合的文法E→NT|DT→NT|DN→D|1|3|5|7|9D→0|2|4|6|8(2)不允许 0 开头的偶正整数集合的文法E→NT|DT→FT|GN→D|1|3|5|7|9D→2|4|6|8F→N|0G→D|0第 6 题已知文法G:<表达式>::=<项>|<表达式>+<项><项>::=<因子>|<项>*<因子><因子>::=(<表达式>)|i试给出下述表达式的最左推导及语法树。
(1)i+(i+i)(2)i+i*i答案:(1) <表达式>=><表达式>+<项>=><表达式>+<因子>=><表达式>+(<表达式>)=><表达式>+(<表达式>+<项>)=><表达式>+(<表达式>+<因子>)=><表达式>+(<表达式>+i)=><表达式>+(<项>+i)=><表达式>+(<因子>+i)=><表达式>+(i+i)=><项>+(i+i)=><因子>+(i+i)=>i+(i+i)(2) <表达式>=><表达式>+<项>=><表达式>+<项>*<因子>=><表达式>+<项>*i=><表达式>+<因子>*i=><表达式>+i*i=><项>+i*i=><因子>+i*i=>i+i*i第7 题为句子i+i*i 构造两棵语法树,从而证明下述文法G[〈表达式〉]是二义的。
《形式语言与自动机》期末复习题及答案(一)

形式语言与自动机期末复习题及答案(一)1.有图灵机 M=(Q, ∑, Γ, δ,q 0 , B , F) 接受语言{w t w│w ∈{a, b}*},按照下图说明其接受过程。
(本题15分 )[q 1[q 6,B]答:abtab 的分析过程:[q 1,B]abtab├a [q 2,a]btab├ab [q 2,a]tab├abt [q 3,a]ab├ ab [q 4,B]tab├a [q 5,B]btab├[q 6,B]abtab├a [q 1,B]btab ├ab [q 2,b]tab├abt [q 3,b]ab ├abta [q 3,b]b ├abt [q 4,B]ab├a [q 5,B]btab ├ab [q 7,B]tab ├abt [q 8,B]ab├abta [q 8,B]b ├abtab [q 8,B]B├abta [q 9,B]b 接受abtab√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√2.简述《形式语言与自动机》课程的主要内容。
(本题10分)答:语言的文法描述;RL (RG 、FA 、RE 、RL 的性质 );CFL (CFG(CNF 、GNF)、PDA 、CFL 的性质);TM (基本TM 、构造技术、TM 的修改);CSL (CSG 、LBA )。
3.简述《形式语言与自动机》课程的学习目的和基本要求。
(本题10分) 答:本专业人员4种基本的专业能力:计算思维能力、算法的设计与分析能力、程序设计和实现能力、计算机软硬件系统的认知、分析、设计与应用能力。
其中计算思维能力包括:逻辑思维能力和抽象思维能力、构造模型对问题进行形式化描述、理解和处理形式模型。
本课程应使学生掌握如下知识:正则语言、下文无关语言的文法、识别模型及其基本性质、图灵机的基本知识。
锻炼培养如下能力:形式化描述和抽象思维能力、了解和初步掌握“问题、形式化描述、自动化(计算机化)”这一最典型的计算机问题求解思路。
《形式语言与自动机》(王柏、杨娟编著)课后习题答案

形式语言与自动机课后习题答案第二章4.找出右线性文法,能构成长度为1至5个字符且以字母为首得字符串。
答:G={N,T,P,S}其中N={S,A,B,C,D} T={x,y} 其中x∈{所有字母} y∈{所有得字符} P如下: S→x S→xA A→y A→yBB→y B→yC C→y C→yD D→y6.构造上下文无关文法能够产生L={ω/ω∈{a,b}*且ω中a得个数就是b得两倍}答:G={N,T,P,S}其中N={S} T={a,b} P如下:S→aab S→aba S→baaS→aabS S→aaSb S→aSab S→SaabS→abaS S→abSa S→aSba S→SabaS→baaS S→baSa S→bSaa S→Sbaa7.找出由下列各组生成式产生得语言(起始符为S)(1)S→SaS S→b(2)S→aSb S→c(3)S→a S→aE E→aS答:(1)b(ab)n /n≥0}或者L={(ba)n b/n≥0}(2) L={a n cb n /n≥0}(3)L={a2n+1 /n≥0}第三章1.下列集合就是否为正则集,若就是正则集写出其正则式。
(1)含有偶数个a与奇数个b得{a,b}*上得字符串集合(2)含有相同个数a与b得字符串集合(3)不含子串aba得{a,b}*上得字符串集合答:(1)就是正则集,自动机如下题(2)。
(3) 就是正则集先瞧L’为包含子串aba得{a,b}*上得字符串集合显然这就是正则集,可以写出表达式与画出自动机。
(略)则不包含子串aba得{a,b}*上得字符串集合L就是L’得非。
根据正则集得性质,L也就是正则集。
4.对下列文法得生成式,找出其正则式(1)G=({S,A,B,C,D},{a,b,c,d},P,S),生成式P如下:S→aA S→BA→abS A→bBB→b B→cCC→D D→bBD→d(2)G=({S,A,B,C,D},{a,b,c,d},P,S),生成式P如下:S→aA S→BA→cC A→bBB→bB B→aC→D C→abBD→d答:(1) 由生成式得:S=aA+B ①A=abS+bB ②B=b+cC ③C=D ④D=d+bB ⑤③④⑤式化简消去CD,得到B=b+c(d+bB)即B=cbB+cd+b =>B=(cb)*(cd+b) ⑥将②⑥代入①S=aabS+ab(cb)*(cd+b)+(cb)*(cd+b) =>S=(aab)*(ab+ε)(cb)*(cd+b) (2) 由生成式得:S=aA+B ①A=bB+cC ②B=a+bB ③C=D+abB ④D=dB ⑤由③得 B=b*a ⑥将⑤⑥代入④ C=d+abb*a=d+ab+a ⑦将⑥⑦代入② A=b+a+c(d+b+a) ⑧将⑥⑧代入① S=a(b+a+c(d+ab+a))+b*a=ab+a+acd+acab+a+b*a5、为下列正则集,构造右线性文法:(1){a,b}*(2)以abb结尾得由a与b组成得所有字符串得集合(3)以b为首后跟若干个a得字符串得集合(4)含有两个相继a与两个相继b得由a与b组成得所有字符串集合答:(1)右线性文法G=({S},{a,b},P,S)P: S→aS S→bS S→ε(2) 右线性文法G=({S},{a,b},P,S)P: S→aS S→bS S→abb(3) 此正则集为{ba*}右线性文法G=({S,A},{a,b},P,S)P: S→bA A→aA A→ε(4) 此正则集为{{a,b}*aa{a,b}*bb{a,b}*, {a,b}*bb{a,b}*aa{a,b}*}右线性文法G=({S,A,B,C},{a,b},P,S)P: S→aS/bS/aaA/bbBA→aA/bA/bbCB→aB/bB/aaCC→aC/bC/ε7、设正则集为a(b a)*(1)构造右线性文法(2)找出(1)中文法得有限自b动机答:(1)右线性文法G=({S,A},{a,b},P,S)P: S→aA A→bS A→ε(2)自动机如下:)9、对应图(a)(b)得状态转换图写出正则式。
形容性格的词语及形式语言与自动机理论第二章参考答案

形容性格的词语性格:外向善良开朗活泼好动轻松愉快热情可亲豁达稳重幽默真诚豪爽耿直成熟独立果断健谈机敏深沉坚强兴奋热情率直毅力友爱风趣沉静谨慎忠诚友善严肃忠心乐观坦率勇敢自信自立沉著执著容忍体贴满足积极有趣知足勤劳和气无畏务实轻浮冲动幼稚自私依赖任性自负拜金暴躁倔强虚伪孤僻刻薄武断浮躁莽撞易怒轻率善变狡猾易怒多疑懒惰专横顽固猜疑挑衅冷漠虚荣冷淡反覆跋扈自负逆反怨恨鲁莽放任贫乏固执内向脆弱自卑害羞敏感迟钝柔弱畏缩顺从胆小安静寡言保守被动忍让抑郁谨慎胆怯温和老实平和顺服含蓄迁就羞涩忸怩缓慢乏味散漫迟缓罗嗦耐性悲观消极拖延烦躁妥协唠叨好交际善组织有韧性可依赖规范型好心肠善交际无异议竞争性自控性受尊重激励性重秩序有条理聆听者无拘束领导者受欢迎神经质糊涂虫有惰性易兴奋好批评不专注好争吵无目标不宽恕无热忱易激动难预测不合群不灵活喜操纵情绪化大嗓门统治欲强迫性好表现适应能力强工作有效率能克服困难办事认真细心严守秩序有条理善于体察别人常为小事而动感情完美主义者轻率不踏实易见异思迁易轻率作决定语言动作迟缓不易暴露内心活动执拗不灵活适应能力差显得落落寡合不圆滑老练不善言谈交际善解人意井井有条意志坚定自我牺牲考虑周到雷历风行适应力强喜好娱乐善于说服坚持不懈善于分析专心致志一丝不苟令人信服生气勃勃惹人喜爱外交手腕令人高兴瞻前顾后循规蹈矩善于社交不怕困难性情平和理想主义无攻击性感情外露勇敢正义聪明好学实事求是务实实际一本正经使人振作反应敏捷文化修养贯彻始终快言快语爱管闲事追求刺激豪放不羁积极负责埋头工作果敢坚持富有朝气表情丰富反应敏捷兴趣广泛随波逐流精力充沛喜交朋友活力充沛活泼开朗能说会道温柔体贴不拘小节交际广泛风趣幽默处事洒脱淡泊名利助人为乐瞻前顾后乐天达观成熟稳重幼稚调皮温柔体贴活泼可爱普普通通内向害羞外向开朗心地善良循规蹈矩聪明伶俐善解人意风趣幽默思想开放积极进取正义正直处事洒脱异想天开淡泊名利小心谨慎敢作敢当乐观向上诚实坦白圆滑老练急性子喋喋不休无同情心胆小怕事言语不清无安全感优柔寡断不善表达不受欢迎难以琢磨小肚鸡肠排斥异己不善交际不懂幽默慢条斯理婆婆妈妈重色轻友胆小怕事老实守旧老实巴交脾气暴躁贪小便宜见异思迁水性扬花多愁善感情绪多变狡猾善变悲观失意见利忘义情绪不佳暴力倾向损人利己附庸风雅时喜时悲患得患失沉默寡言生活紊乱小心翼翼逆来顺受悲观消极郁郁寡欢缺乏耐力按部就班过分敏感杂乱无章脾气暴躁情绪低落信心受挫烦躁粗心萎蘼不振犹豫不决缺乏自信忧心忡忡难于取悦慢条斯理好吃懒做疑神疑鬼形容个性:爱财如命,安分守己,安贫乐道,安如泰山,傲慢不逊,傲血欺霜,八面玲珑,白璧无瑕,百折不挠,饱食终日,暴殄天物,卑躬屈膝,表里如一,别具匠心,别具一格,彬彬有礼,冰清玉洁,博闻强识,博古通今,博学多才,不学无术,临危不惧......2.1回答下面的问题:(周期律02282067)(1)在文法中,终极符号和非终极符号各起什么作用?✓终结符号是一个文法所产生的语言中句子的中出现的字符,他决定了一个文法的产生语言中字符的范围。
形式语言与自动机理论蒋宗礼第一章参考复习资料

第一章参考答案1.1 请用列举法给出下列集合。
(吴贤珺02282047)⑴ 你知道的各种颜色。
解:{红,橙,黄,绿,青,蓝,紫}⑵ 大学教师中的各种职称。
解:{助教,讲师,副教授,教授}⑶ 你所学过的课程。
解:{语文,数学,英语,物理,化学,生物,历史,地理,政治}⑷ 你的家庭成员。
解:{ 父亲,母亲,妹妹,我}⑸ 你知道的所有交通工具。
解:{ 汽车,火车,飞机,轮船,马车}⑹ 字母表{a , b} 上长度小于 4 的串的集合。
解:{a,b,aa,bb,ab,ba,aaa,aab,aba,abb,baa,bab,bba,bbb}⑺ 集合{1,2,3,4} 的幂集。
解:{①,{1},{2},{3},{4},{1,2},{1,3},{1,4},{2,3},{2,4},{3,4},{1,2,3},{1,2,4}, {1,3,4},{2,3,4},{1,2,3,4} }⑻ 所有的非负奇数。
解: {135,7,…}⑼0〜100的所有正整数。
解: {1,2,3, (100)(10) 1〜10之间的和为10的整数集合的集合。
解:设所求的集合为A,集合A中的元素为A i (i=1,2,3,…),A i也是集合,A i中的元素在1〜10之间,并且和为10。
根据集合元素的彼此可区分性,可以计算出A i中元素的最多个数,方法是:把 1 开始的正整数逐个相加,直到等于10(即10=1+2+3+4),这样,A i中最多有4个元素。
原因是:从最小的1开始,每次加入新的元素都只依次增加1,这样相加的和最小,要加到10,元素个数就最多。
求出最大的I A i 1= 4后,再求出元素个数为3, 2, 1的集合就可以了。
故A={{10},{1,9},{2,8},{3,7},{4,6},{1,2,7},{1,3,6},{1,4,5},{2,3,5},{1,2,3,4}}1.2 请用命题法给出下列集合2.(1){x|0 x 100且x z}(2) {x|x {a,b}*且|x| 4}(3) {B|B {1,2,3,4}}(4) {L|L {a,b}*}(5) {x|x 2n 1,n N}(6) {(a,b)|a b 10且a,b [4,9]}⑺{x|x {0,*,且x中0的个数是1的个数的两倍}(8){x|x {0,*,且x中 1 的个数是10}(9){ x|x {0,1}*,且x中倒数第十个字符为1}|A||(10){A| x i A,x i [1,10],i [1,|A|], x i=10}i11.3 给出下列集合的幂集. ( 02282075 冯蕊)(1) ①⑵{①}(3) {①,{①}}⑷{ & ,0,00}(5) {0,1}解答:(1) {①}(2) {①,{①}}⑶{①,{①},{{①}},{①,{①}}}⑷{①,{ & },{0},{00},{ & ,0},{ & ,00},{0,00},{ & ,0,00}}①,{0},{1},{0,1}}1.4.列出集合{0,1 ,2,3,4}中(褚颖娜02282072)( 1) 所有基数为3 的子集{0,1,2},{0,1,3},{0,1,4},{0,2,3,} ,{0 ,2,4} ,.{1 ,2,3} ,{1 ,2,4},{1,3,4} ,{0,3,4},{2,3,4}(2) 所有基数不大于 3 的子集①,{0} , {1} , {2} , {3} , {4} , {3 , 4} , {2 , 4} , {2 , 3}, {1 , 4} , {1 , 3}, {0 , 4} ,{0 ,3} ,{0 ,2} ,{1 ,2} ,{0 ,1} ,{0 ,1,2} ,{0 ,1,3}{0,1,4},{0,2,3,},{0,2,4},.{1 ,2,3},{1 ,2,4},{1 ,3,4},{0,3,4},{2,3,4}1.5 解答:1、3、8、10、11、12、16正确1.6 证明下列各题目02282081 刘秋雯) 1) A=B iff A 是B的子集且B是A的子集证明:充分条件:•/ A=B则由集合相等的定义知对于任何x € A,有x € B••• A为B的子集同理, B 为 A 的子集必要条件:••• A为B的子集•对于任何x € A,都有x € B又••• B为A的子集,•对于任何x€ B 有,x€ A由集合相等的定义知,A=B2) 如果A为B的子集,则|A| 〈=|B|证明:A 为B 的子集,则对于任何x€ A 有x€ B,•存在一个集合C使B=A U C 且A n C为空集则|B|=|A|+|C| |C|〉=0• |A|〈=|B|3) 如果A为B的真子集,则|A| 〈=|B|证明:(1)当 A 为有穷集合时,因为 A 为B 的真子集,且则对于任何x€ A 有x€ B,且存在€ B的x,此x不€ A•存在一个非空集合 C ,使B=A U C 且A n C 为空集则|B|=|A|+|C| 且|C|> =1• |A|〈|B|(2)当A为无穷集合,因为A为B的真子集,则 B 一定也为无穷集合,|A| = s, |B|=m• |A|=|B|综合( 1),(2)所述,|A|<=|B|4) 如果A是有穷集且A为B的真子集则|A| 〈 |B|证明:见上题证明( 1 )5) 如果A为B的子集,则对于任何x € A,有x€ B证明:若A为B的子集,则由子集定义可知,对于任何x€ A,有x€ B6) 如果A是B的真子集,则对于任何x€ A,有x € B,并且存在x€ B,但x不€ A证明:由真子集的定义可证7)如果A为B的子集,B为C的子集,贝U A为C的子集证明:A为B的子集,B为C的子集则对于任何x € A,则x都€ B, 且,又对于任何y € B,贝Uy€ C,「.对于任何x€ A,x€ C••• A为C的子集8)如果A为B的真子集,B为C的真子集,贝U A为C的真子集证明:A为B的真子集,B为C的真子集则对于任何x € A,则x都€ B,且,存在x€ B 但次x 不€ A,又对于任何y€ B,则y€ C,存在y € C但此y不€ B,•••对于任何x€ A,x € C,存在x€ C.x不€ A• A为C的真子集9)如果A为B的子集,B为C的真子集,贝U A为C的真子集证明:因为 A 为 B 的子集, B 为 C 的真子集则对于任何x € A,x都€ B,且x都€ C又对于任何y€ B,则y€ C,存在y € C但此y不€ B,则y不€ A•••对于任何x€ A,x € C,存在x€ C.x不€ A• A为C的真子集10)如果A为B的真子集,B为C的子集,贝U A为C的真子集证明:A为B的真子集,B为C的子集则对于任何x € A,则x都€ B,且存在x€ B 但次x 不€ A,又对于任何y€ B,贝U y€ C•••对于任何x€ A,x € C,存在x€ C.x不€ A• A为C的真子集11)如果A=B 则|A| = |B|证明:A=B ,则A 与B 所含元素相同• |A|=|B|12)如果A为B的子集,B为C的真子集,或如果A为B的真子集集,为C的子则A为C的真子集证明:证明见9,101.7 A = {1,2,3,4,5,6} B = {1,3,5} C = {2,4,6} U = {0,1,2,3,4,5,6,7,8,9}(1). A B={1,3,5} = B(2) .(A B) C={1,3,5} {2,4,6}={1,2,3,4,5,6} = A(3) .(A B) (U C)={1,3,5} {0,135,7,8,9}={0,135,7,8,9} = C(4) .A-B-C={2,4,6} -{2,4,6}⑸.A X B X C XA X =⑹.(A B) A C A={1,3,5} {0,7,8,9} {0,7,8,9}={0,1,3,5,7,8,9} = C(7). ABAC=A B C=A {(a,b)|(a B,b C)或(a B,b C)或(a B,b C)}C)} ={(a,b,c)|(a A,b B,c C)或(a A,b B,c C)或(a A,b B,c(8). A B (A B) C=A A C=A C=A={1 , 2, 3, 4, 5, 6}1. 8对论域U上的集合A、B、C,证明以下结论成立。
《形式语言与自动机》期末测试题

《形式语言与自动机》期末测试题《形式语言与自动机》期末测试题(规定时间:2小时)学号姓名1. (12 pts)选择填空(多选):(a) 由正规表达式a*定义的语言;A,C(或只回答C)(b) 语言{a m b m∣m ≥0} ;B(c) 语言{a m b m c m∣m ≥0} ;D(d) 语言{a m b n c m∣m,n ≥0} ;B(e) 对角化(diagonalization)语言L d;F(f) 通用语言(universal)语言L u;E供选择的答案:A. 是某个有限状态自动机的语言;B. 是某个下推自动机的语言, 但不是任何有限状态自动机的语言;C. 是某个有限状态自动机的语言,但不是任何空栈接受方式的确定下推自动机的语言;D. 是某个可停机的图灵机的语言, 但不是任何下推自动机的语言;E. 是某个图灵机的语言, 但不是任何可停机的图灵机的语言;F. 不是任何图灵机的语言.2. (7 pts)图灵机({ q0, q1, q2, q3 }, { 0,1 }, { 0,1,B }, δ, q0, B, {q3 })有如下转移规则:δ(q0, 0)=(q1,1, R)δ(q1, 1)=(q2, 0, L)δ(q2, 1)=(q0, 1, R)δ(q1, B)=(q3, B, R)给出从初始ID q00110开始,该图灵机可以到达的完整的ID序列, 直到它停机.3. (12 pts)设有四个语言(或问题)A,B,C 和D. 这些语言可以是,也可以不是递归可枚举语言,但已知如下条件:(此题出得不好)i. A 可以归约到B(不一定是多项式时间归约,下同);ii. B 可以归约到C;iii. D 可以归约到C;对于以下6个命题,分别指出它们是“真”,或是“假”,或是“不能确定”:(a) A是递归可枚举的但不是递归的,而C 是递归的. 假(A 不是递归的与C是递归的不可能同时成立)(b) B不是递归的,而D 是递归可枚举的. 不能确定(c) A的补不是递归可枚举的,而B 的补是递归可枚举的. 不能确定(d) B的补不是递归的,而C 的补是递归的. 假(e) 如果 A 是递归的,那么 B 的补是递归的. 不能确定(f) 如果 C 是递归的,那么 D 的补是递归的. 真4. (11 pts) 文法 G 的产生式集合为:S →AS ∣b, A →BB ∣a ∣b,B →BA ∣a . 下面的左图表示对于文法 G 和字符串 ababb 应用 CYK 算法时所构造的表,各集合与表元素符号之间的对应关系可参照右边的图. 试问(a) 计算 X 15 时与哪几对表元素相关? (5 pts)(b) X 15 = ? (5 pts) {S,A,B}(c) 是否有ababb ∈ L(G)? (1 pt) Ye sX 15X 14X 13X 12X 11X 25X 24X 23X 22X 35X 34X 33X 45X 44X 55a 1a 2a 3a 4a 5a b a b b {S,B }{S,A,B }{S,A }{A,B }{S }{A,B }{S,B }φ {A,B }{S,B }{S,A }{S,A }{S }{S }X 155. (8 pts) 对于正规语言和上下文无关语言两类语言,分别指出下列四个问题是否可判定的:(a) 给定该语言类中的任一语言 L ,判定 L 是否为空?都可以(b) 给定该语言类中的任一语言 L 和任何字符串 w ,判定 w 是否属于 L ?. 都可以 (c) 给定该语言类中的语言 L 和 M ,判定 L 是否与M 相等?. 对正规语言可以,对上下文无关语言不可以对于递归语言和递归可枚举语言两类语言,分别指出上述问题(b )是否可判定的:对递归语言可以,对递归可枚举语言不可以6. (15 pts) 对下面描述每一对语言,指出以下 4 种选择中的哪一个正确表达了它们之间的关系:(1)?(2):语言(1)是语言(2)的真子集;(1)?(2):语言(2)是语言(1)的真子集;(1)=(2):语言(1)和语言(2)相等;(1)?(2):语言(1)和语言(2)之间没有包含关系,即(1)中的某些串不在(2)中,(2)中的某些串不在(1)中.(a) (1)产生式集为S →0S1∣1S0∣ε 的 CFG 的语言.(2)正规表达式 (0+1)* 的语言.(1)?(2). (2) generates all strings of 0's and 1's, while (1) doesn't generate strings like 11, or any odd-length string.(b)(1)以终态方式接受的PDA({ p,q },{ 0,1 },{ X,Z },δ,q,Z,{ p })的语言,其中δ转移包括:δ(q,0,Z)=(q,XZ), δ(q,0,X)=(q,XX), δ(q,1,X)=(p,ε), δ(p,1,X)=(p,ε).(2)产生式集为S→0S1∣0S∣ε的CFG的语言.(1)?(2). These almost look the same. (2) is the set of strings of the form 0n1m such that 0 ≤ m ≤ n. However, the PDA of (1) cannot reach state p without reading at least one 0 and one 1, so it accepts the set of strings of the form 0n1m such that 1 ≤ m ≤ n .(c) (1)产生式集为S→AS∣SB∣ε,A→0 和B→1 的CFG的语言.(2)正规表达式0*1* 的语言.(1)=(2)(d) (1)正规表达式(0+1)*11(0+1)* 的语言.(2)正规表达式(0*1*11)*0*110*1* 的语言.(1)?(2). (1) is all strings of 0's and 1's with two consecutive 1's. (2) misses some of these strings, e.g., something ending with 110101(e)(1)NFA({ p,q },{ 0,1 },δ,q,{ q })的语言,其中转移函数δ为:δ(q,0)={p }, δ(q,1)=φ, δ(p,0)={p,q}, δ(p,1)={p}.(2)产生式集为S→AS∣ε,A→0B 和B→ 0B∣1B ∣0 的CFG的语言.(1)=(2). Both define the language of regular expression (0(0+1)*0)*.7. (10 pts)利用上下文无关语言的闭包运算可以证明某些语言是或不是上下文无关语言.试证明{a n b n+2∣n ≥0} 为上下文无关语言,而{a n b n-i c i d n-j e j∣i,j≤n} 不是上下文无关语言(提示,已知{0n1n∣n ≥0} 为上下文无关语言,而{0n1n2n∣n ≥0} 不是上下文无关语言).前者可以用连接和同态运算;后者可以用同态运算。
形式语言与自动机理论--第三章参考答案
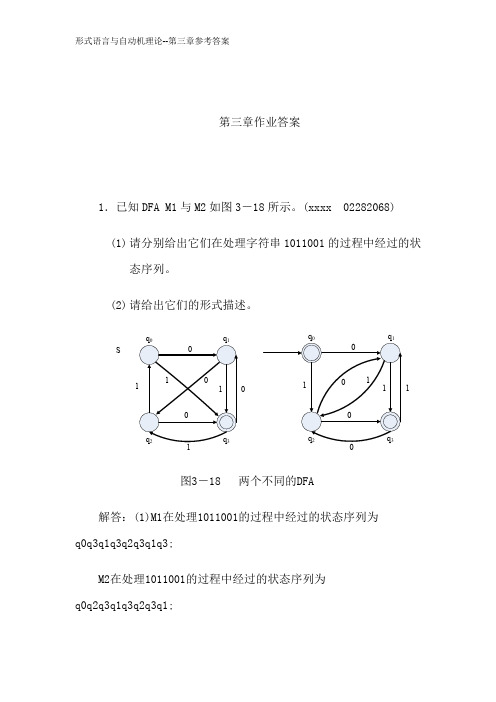
第三章作业答案1.已知DFA M1与M2如图3-18所示。
(xxxx 02282068) (1) 请分别给出它们在处理字符串1011001的过程中经过的状态序列。
(2) 请给出它们的形式描述。
Sq q1q q图3-18 两个不同的DFA解答:(1)M1在处理1011001的过程中经过的状态序列为q0q3q1q3q2q3q1q3;M2在处理1011001的过程中经过的状态序列为q0q2q3q1q3q2q3q1;(2)考虑到用形式语言表示,用自然语言似乎不是那么容易,所以用图上作业法把它们用正则表达式来描述:M1: [01+(00+1)(11+0)][11+(10+0)(11+0)]* M2: (01+1+000){(01)*+[(001+11)(01+1+000)]*} *******************************************************************************2.构造下列语言的DFA( xx02282085 ) (1){0,1}*,1(2){0,1}+,1(3){x|x{0,1}+且x 中不含00的串}(设置一个陷阱状态,一旦发现有00的子串,就进入陷阱状态)(4){ x|x{0,1}*且x中不含00的串}(可接受空字符串,所以初始状态也是接受状态)(5){x|x{0,1}+且x中含形如10110的子串}(6){x|x{0,1}+且x中不含形如10110的子串}(设置一个陷阱状态,一旦发现有00的子串,就进入陷阱状态)(7){x|x{0,1}+且当把x看成二进制时,x模5和3同余,要求当x为0时,|x|=1,且x0时,x的首字符为1 }1.以0开头的串不被接受,故设置陷阱状态,当DFA在启动状态读入的符号为0,则进入陷阱状态2.设置7个状态:开始状态qs,q0:除以5余0的等价类,q1:除以5余1的等价类,q2:除以5余2的等价类,q3:除以5余3的等价类,q4:除以5余4的等价类,接受状态qt3.状态转移表为(8){x|x{0,1}+且x的第十个字符为1}(设置一个陷阱状态,一旦发现x的第十个字符为0,进入陷阱状态)(9){x|x{0,1}+且x以0开头以1结尾}(设置陷阱状态,当第一个字符为1时,进入陷阱状态)(10){x|x{0,1}+且xxx至少含有两个1}(11){x|x{0,1}+且如果x以1结尾,则它的xx为偶数;如果x以0结尾,则它的xx为奇数}可将{0,1}+的字符串分为4个等价类。
编译原理期末复习

(8) E=E+F
(9) Write (E)
(10)Halt
(11)L1: E=B*
(12)F=F+2
(13)E=E+F
(14)Write (E)
(15)If E>100 goto L2
(16)halt
(17)L2:F=F-1
(18)goto L1
47
48
49
50
语句(1)—语句(5)、(6)—(10)、语句(11)— (15)、语句(16)、语句(17)和(18)分别是 一个基本块 设语句(1)—语句(5)为① 语句(6)—语句(10)为② 语句(11)—语句(15)为③ 语句(16)为④ 语句(17)和(18)为⑤、
A. S→Sx|xy
B. S→xy|xSy
C. S→xx|yxx
D. S→Sy|x
CH4 语法分析——自下而上分析
练习:
下列文法中 是LL(1)文法…………( )
A. S→aSb|ab
B. S→aS|b
C. S→ab|Sab
自动机理论、语言和计算导论课后习题答案(中文版)

自动机理论、语言和计算导论课后习题答案(中文版)Solutions for Section 2.2Exercise 2.2.1(a)States correspond to the eight combinations of switch positions, and also must indicate whether the previous roll came out at D, i.e., whether the previous input was accepted. Let 0 represent a position to the left (as in the diagram) and 1 a position to the right. Each state can be represented by a sequence of three 0's or 1's, representing the directions of the three switches, in order from left to right. We follow these three bits by eithera indicating it is an accepting state or r, indicating rejection. Of the16 possible states, it turns out that only 13 are accessible from the initial state, 000r. Here is the transition table: 杠杆可能出现8种情况,影响着最终状态。
并且也要说明,前面一个大理石球是否从D滚出,也就是说,前一个输入是否被接受。
令0 代表向左方的状态(如图表),1 代表向右方。
这三个杠杆的每一个状态都可以用三个数(0或1)组成的序列表示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.1回答下面的问题: (周期律 02282067) (1)在文法中,终极符号和非终极符号各起什么作用?✓ 终结符号是一个文法所产生的语言中句子的中出现的字符,他决定了一个文法的产生语言中字符的范围。
✓ 非终结符号又叫做一个语法变量,它表示一个语法范畴,文法中每一个产生式的左部至少要还有一个非终结符号,(二,三型文法要求更严,只允许左部为一个非终结符号)他是推导或归约的核心。
(2)文法的语法范畴有什么意义?开始符号所对应的语法范畴有什么特殊意义? ✓ 文法的非终结符号A 所对应的语法范畴代表着一个集合L (A ),此集合由文法产生式中关于A 的产生式推导实现的✓ 开始符号所对应的语法范畴则为文法G = {V ,T ,P ,S}所产生的语言L (G )={w S T w w **|⇒∈且}(3)在文法中,除了的变量可以对应一个终极符号行的集合外,按照类似的对应方法,一个字符串也可以对应一个终极符号行集合,这个集合表达什么意义?✓ 字符串对应的终极符号行集合表示这个字符串所能推导到的终极字符串集合,为某个句型的语言。
(4)文法中的归约和推导有什么不同?✓ 推导:文法G = {V ,T ,P ,S},如果,)(,,* T VP ∈∈→δγβα则称γαδ在G 中推导出了γβδ。
✓ 归约:文法G = {V ,T ,P ,S},如果,)(,,*T VP ∈∈→δγβα则称γβδ在G 中归约到γαδ。
✓ 这他们的定义,我个人理解两个概念从不同角度看待文法中的产生式,推导是自上而下(从产生式的左边到右边),而归约是自下而上(从产生式的右边到左边),体现到具体实际中,如编译中语法分析时语法树的建立,递归下降,LL (1)等分析法采用自开始符号向下推导识别输入代码生成语法树,对应的LR (1),LALR 等分析法则是采用自输入代码(相当于文法中语言的句子)自底向上归约到开始符号建立语法树,各有优劣。
(5)为什么要求定义语言的字母表上的语言为一个非空有穷集合? ✓ 非空:根据字母表幂的定义:εε,}{0∑=为字母表中0个字符组成的。
这样,当字母表中没有字符的情况,字母表也有一个元素,字母表为空就没有意义,而且,如果字母表为空,将无法定义其上的语言,使得理论体系不严密。
✓ 有穷:我们将语言抽象成形式语言的目的就是为了有穷的表示无限的语言,在此基础上我们才定义了字母表和语言,如果字母表为无穷的,他就违背了我们研究问题的初衷,这也使得研究失去意义(6)任意给定一个字母表∑,该字母表上的语言都具有有穷描述吗?为什么?✓ 错误,因为一个字母表上有不可数无穷多个语言,而有穷表示只可能是可数无穷多个,又因为不可数无穷集和可数无穷集不是一一对应的,所以存在这样的语言,他不存在有穷表示。
(7)请总结一下,在构造文法时,可以从哪几个方面入手? ✓ 我们可以将其类比于软件工程中的概念:-)✓ 首先,也是最重要的一点,需求分析,我们需要知道需要构造的语言的特点,具体表现形式,以及一些需要注意的细节,通过一些特例提炼特点。
✓ 其次,概要设计,将语言从具体中抽象到符号上,按照其特性将其划分类别。
✓ 再次,详细设计,将每一部分抽象的成果具体化,将所有细节符号化 ✓ 再次,编码,将详细设计的结果用文法符号的语言表示出来 ✓ 最后,测试,找出边缘数据,特殊数据进行测试。
(8)按照文法的乔姆斯基体系,文法被分为几类?各有什么样的特点? 分为四类:✓ 文法G = {V ,T ,P ,S},对应的L(G)则为0型文法或短语结果文法。
✓ 如果对于P ∈→∀βα,均有αβ≥成立,则称G为1型文法或上下文有关文法,对应的L(G)称为1型语言。
✓ 如果对于P ∈→∀βα,均有αβ≥成立,且V ∈α成立,则称G为2型文法,或上下文无关文法,对应的L(G)为2型语言。
✓ 如果对于P ∈→∀βα,所有βα→均有:wB A w A →→或成立,其中,,,+∈∈T w V B A 则称G为3型文法,或正则文法,对应的L(G)称3型语言。
(9)什么叫左线性文法?什么叫右线性文法?什么叫线性文法✓ 文法G = {V ,T ,P ,S},如果对于P ∈→∀βα,所有βα→均有:wBx A w A →→或成立,,,,,*T w x V B A ∈∈则称G为线性文法。
✓ 文法G = {V ,T ,P ,S},如果对于P ∈→∀βα,所有βα→均有:wBA w A →→或成立,其中,,,+∈∈T w VB A 则称G为右线性文法。
✓ 文法G = {V ,T ,P ,S},如果对于P ∈→∀βα,所有βα→均有:BwA w A →→或成立,其中,,,+∈∈T w VB A 则称G为左线性文法。
(10)既然已经定义2-10中允许RL 包含空语句ε,那么定理2-6和定理2-7还有什么意义?此为定义与定理的区别,定义2-10是针对文法G是RG的情况下,定义其产生式加上εS后仍为RG,G的语言仍为RL,而定理2-6和定理2-7针对的前提条件是如果→L为RL,他们都是通过定义2-10证明得到的,可以在以后的推论中直接应用的。
******************************************************************************* 2. 设L = { 0n | n ≥1 },试构造满足要求的文法G.(1)G是RG.(2)G是CFG, 但不是RG.(3)G是CSG, 但不是CFG.(4)G是短语结构文法,但不是CSG.解答:1:S→0|0S2:S→0|0S|SS3:S→0|0S|ASAS→SAAS→0A0A→S00AS→004:S→0|0S|ASAS→SA|ABBABB→ASAB→A|ε******************************************************************************* 3.设文法G的产生式集如下,试给出句子id+id*id的两个不同的推导和两个不同的归约E→id|c|+E|-E|E+E|E-E|E*E|E/E|E**E|Fun(E) (褚颖娜02282072)推导:(1)E=>E+E=>E+E*E=>E+E*id=> E+id*id=>id+id*id(2)E=>E*E=>E*id=>E+E*id=>E+id*id=>id+id*id归约:(1)id+id*id<= E+id*id<= E+E*id<= E+E*E <=E+E<=E(2)id+id*id<= E+id*id<= E+E*id<=E*id<= E*E<=E****************************************************************************** 2.4 设文法G的产生式集如下,试给出句子aaabbbccc的至少两个不同的推导和至少两个不同的归约(02282081刘秋雯)bB→bbCB→BCbC→bccC→cc解:推导一:S→aBC|aSBCaB→abS=>aSBC=>aaSBCBC=>aaaBCBCBC=>aaabCBCBC=>aaabBCCBC=>aaabbCCBC=>aaabbCBCC=>aaabbBCCC=>aaabbbCCC=>aaabbbcCC=>aaabbbccc推导二:S=>aSBC=>aaSBCBC=>aaaBCBCBC=>aaaBBCCBC=>aaaBBCBCC=>aaabbCBCC=>aaabbBCCC=>aaabbbCCC=>aaabbbcCC=>aaabbbccc归约一、归约二分别为推导一和推导二的逆过程******************************************************************************* 5 句子abeebbeeba的一个推导如下:(陈伟芳学号??)S=>aAa 使用产生式S→aAa=>aSSa 使用产生式A→SS=>abAbSa 使用产生式S→bAb=>abSSbSa 使用产生式A→SS=>abeSbSa 使用产生式S→e=>abeebSa 使用产生式S→e=>abeebbAba 使用产生式S→bAb=>abeebbSSba 使用产生式A→SS=>abeebbeSba 使用产生式S→e=>abeebbeeba 使用产生式S→e不能给出abeebbeeb的归约,因为由文法G中产生式推出的句子只有三种情况:头尾都是a,头尾都是b,或者只有一个e,而abeebbeeb上面三个条件都不符合,所以它不是文法G 的一个句子,当然也就不能给出它的一个归约了。
*******************************************************************************2.6 设文法G的产生式集如下,请给出G的每个语法范畴代表的集合.S→aSa|aaSaa|aAaA→bA|bbbA|bBB→cB|cCC→ccC|DDD→dD|d解:set(D)={d}+set(C)={ c2n d m|m≥2 n≥0}set(B)={ c n d m |m≥2 n≥1}set(A)={ b p c n d m | p≥1, m≥2, n≥1}set(S)={ a q b p c n d m a q| p≥1 ,m≥2, n≥1, q≥1}******************************************************************************* 7.给定如下文法,请用自然语言描述它们定义的语言。
(吴贤珺02282047)⑴A→aaA│aaBB→Bcc│D#ccD→bbbD│#解:该语言由四部分组成:第一部分是偶数个a(至少有两个),第二部分是3的倍数个b (可以是0个),第三部分是两个“#”号,第四部分是偶数个c(至少有两个)。
⑵A→0B│1B│2BB→0C│1C│2CC→0D│1D│2D│0│1│2D→0B│1B│2B解:该语言的句子是字母表∑={0,1,2}上所有长度为3的倍数的字符串,且非空。
⑶A→0B│1B│2BB→0C│1B│2BC→0E│1D│2D│0│1│2D→0C│1B│2BE→0E│1D│2D│0│1│2解:观察发现C和E所对应产生式右部是相同的。
