2020高考数学全国卷3理科答案
高考理科数学试题及答案2024

高考理科数学试题及答案(考试时间:120分钟试卷满分:150分)一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.31ii+=+() A .12i + B .12i - C .2i + D .2i -2. 设集合{}1,2,4A =,{}240x x x m B =-+=.若{}1AB =,则B =()A .{}1,3-B .{}1,0C .{}1,3D .{}1,53. 我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯()A .1盏B .3盏C .5盏D .9盏4. 如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部 分所得,则该几何体的体积为() A .90π B .63π C .42π D .36π5. 设x ,y 满足约束条件2330233030x y x y y +-≤⎧⎪-+≥⎨⎪+≥⎩,则2z x y =+的最小值是()A .15-B .9-C .1D .96. 安排3名志愿者完成4项工作,每人至少完成1项,每项工作由1人完成,则不同的安排方式共有()A .12种B .18种C .24种D .36种7. 甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩.老师说:你们四人中有2位优秀,2位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩.看后甲对大家说:我还是不知道我的成绩.根据以上信息,则()A .乙可以知道四人的成绩B .丁可以知道四人的成绩C .乙、丁可以知道对方的成绩D .乙、丁可以知道自己的成绩8. 执行右面的程序框图,如果输入的1a =-,则输出的S =()A .2 B .3 C .4 D .59. 若双曲线C:22221x y a b-=(0a >,0b >)的一条渐近线被圆()2224x y -+=所截得的弦长为2,则C 的 离心率为()A .2B .3C .2D .2310. 若2x =-是函数21`()(1)x f x x ax e -=+-的极值点,则()f x 的极小值为()A.1-B.32e --C.35e -D.111. 已知直三棱柱111C C AB -A B 中,C 120∠AB =,2AB =,1C CC 1B ==,则异面直线1AB与1C B 所成角的余弦值为()A .32 B .155 C .105D .33 12. 已知ABC ∆是边长为2的等边三角形,P 为平面ABC 内一点,则()PA PB PC ⋅+的最小值是()A.2-B.32-C. 43- D.1- 二、填空题:本题共4小题,每小题5分,共20分。
2020年高考理科数学全国卷2-答案

2020年普通高等学校招生全国统一考试·全国Ⅱ卷理科数学答案解析一、选择题 1.【答案】A【解析】由题意可得:{}1012AB =-,,,,则{2()3UA B =-},.故选:A .【考点】并集、补集的定义与应用 2.【答案】D【解析】当π6α=-时,πcos2cos 03α⎛⎫=- ⎪⎝⎭>,选项B 错误;当π3α=-时,2πcos 2cos 03α⎛⎫=- ⎪⎝⎭<,选项A 错误;由α在第四象限可得:sin 0cos 0αα,><,则sin22sin cos 0ααα=<,选项C 错误,选项D 正确;故选:D .【考点】三角函数的符号,二倍角公式,特殊角的三角函数值 3.【答案】B【解析】由题意,第二天新增订单数为50016001200900+-=,故需要志愿者9001850=名.故选:B . 【考点】函数模型的简单应用 4.【答案】C【解析】设第n 环天心石块数为n a ,第一层共有n 环,则{}n a 是以9为首项,9为公差的等差数列,9(1)99n a n n =+-⨯=,设n S 为{}n a 的前n 项和,则第一层、第二层、第三层的块数分别为232,,n n n n n S S S S S --,因为下层比中层多729块,所以322729n n n n S S S S -=-+,即3(927)2(918)2(918)(99)7292222n n n n n n n n ++++-=-+,即29729n =,解得9n =,所以32727(9927)34022n S S +⨯===.故选:C .【考点】等差数列前n 项和有关的计算5.【答案】B【解析】由于圆上的点()21,在第一象限,若圆心不在第一象限,则圆与至少与一条坐标轴相交,不合乎题意,所以圆心必第一象限,设圆心的坐标为()a a ,,则圆的半径为a ,圆的标准方程为()()222x a y a a -+-=.由题意可得()()22221a a a -+-=,可得2650a a -+=,解得1a =或5a =,所以圆心的坐标为()11,或()55,,圆心到直线230x y --=距离均为d ==;所以,圆心到直线230x y --=.故选:B .【考点】圆心到直线距离的计算 6.【答案】C【解析】在等式m n m n a a a +=中,令1m =,可得112n n n a a a a +==,12n na a +∴=. 所以,数列{}n a 是以2为首项,以2为公比的等比数列,则1222n nn a -=⨯=,()()()()1011011105101210122122212211212k k k k k k a a a a ++++++--∴+++===-=---,1522k +∴=,则15k +=,解得4k =.故选:C .【考点】利用等比数列求和求参数的值 7.【答案】A【解析】根据三视图,画出多面体立体图形,图中标出了根据三视图M 点所在位置,可知在侧视图中所对应的点为E ,故选:A .的【考点】根据三视图判断点的位置 8.【答案】B 【解析】22221(00)x y C a b a b-=:>,> ∴双曲线的渐近线方程是by x a=±直线x a =与双曲线22221(00)x yC a b a b-=:>,>的两条渐近线分别交于D ,E 两点不妨设D 为在第一象限,E 在第四象限联立x ab y x a =⎧⎪⎨=⎪⎩,解得x a y b =⎧⎨=⎩ 故()D a b ,联立x ab y x a =⎧⎪⎨=-⎪⎩,解得x a y b =⎧⎨=-⎩ 故()E a b -, ∴||2ED b =∴ODE △面积为:1282ODE S a b ab =⨯==△双曲线22221(00)x y C a b a b-=:>,>∴其焦距为2228cab ==当且仅当a b ==∴C 的焦距的最小值:8.故选:B .【考点】双曲线焦距的最值问题 9.【答案】D【解析】由()ln 21ln 21f x x x =+--得()f x 定义域为12x x ⎧⎫≠±⎨⎬⎩⎭,关于坐标原点对称,又()()ln 12ln 21ln 21ln 21f x x x x x f x -=----=--+=-,()f x ∴为定义域上的奇函数,可排除AC ;当1122x ⎛⎫∈- ⎪⎝⎭,时,()()()ln 21ln 12f x x x =+--,()ln 21y x =+在1122⎛⎫- ⎪⎝⎭,上单调递增,()ln 12y x =-在1122⎛⎫- ⎪⎝⎭,上单调递减,()f x ∴在1122⎛⎫- ⎪⎝⎭,上单调递增,排除B ;当12x ⎛⎫∈-∞- ⎪⎝⎭,时,()()()212ln 21ln 12lnln 12121x f x x x x x +⎛⎫=----==+ ⎪--⎝⎭,2121x μ=+-在12⎛⎫-∞- ⎪⎝⎭,上单调递减,()ln f μμ=在定义域内单调递增,根据复合函数单调性可知:()f x 在12⎛⎫-∞- ⎪⎝⎭,上单调递减,D 正确.故选:D .【考点】函数奇偶性和单调性的判断 10.【答案】C【解析】设球O 的半径为R ,则24π16πR =,解得:2R =.设ABC △外接圆半径为r ,边长为a ,ABC212a ∴=,解得:3a =,2233r ∴=∴球心O 到平面ABC 的距离1d ===.故选:C . 【考点】球的相关问题的求解 11.【答案】A【解析】由2233x y x y ----<得:2323x x y y ----<,令()23t tf t -=-,2x y =为R 上的增函数,3x y -=为R 上的减函数,()f t ∴为R 上的增函数,x y ∴<,0y x ->,11y x ∴-+>,()ln 10y x ∴-+>,则A 正确,B 错误;x y -与1的大小不确定,故CD 无法确定.故选:A .【考点】数式的大小的判断问题 12.【答案】C【解析】由i m i a a +=知,序列i a 的周期为m ,由已知,5m =,511()12345i i k i C k a a k +===∑,,,, 对于选项A ,511223344556111111(1)()(10000)55555i i i C a a a a a a a a a a a a +===++++=++++=∑≤52132435465711112(2)()(01010)5555i i i C a a a a a a a a a a a a +===++++=++++=∑,不满足;对于选项B ,51122334455611113(1)()(10011)5555i i i C a a a a a a a a a a a a +===++++=++++=∑,不满足;对于选项D ,51122334455611112(1)()(10001)5555i i i C a a a a a a a a a a a a +===++++=++++=∑,不满足;故选:C【考点】数列的新定义问题 二、填空题 13.【答案】2【解析】由题意可得:211cos45a b →→⋅=⨯⨯=0k a b a →→→⎛⎫-= ⎪⎝⎭,即:2202k a ab k →→→⨯-=-=,解得:2k =.故答案为:2. 【考点】平面向量的数量积定义与运算法则 14.【答案】36【解析】4名同学到3个小区参加垃圾分类宣传活动,每名同学只去1个小区,每个小区至少安排1名同学,∴先取2名同学看作一组,选法有:246C =.现在可看成是3组同学分配到3个小区,分法有:336A =.根据分步乘法原理,可得不同的安排方法6636⨯=种.故答案为:36.【考点】计数原理的实际应用15.【答案】【解析】122z z ==,可设12cos 2sin i z θθ=+,22cos 2sin i z αα=+,()()122cos cos 2sin sin i 3i z z θαθα∴+=+++=+,()()2cos cos 2sin sin 1θαθα⎧+⎪∴⎨+=⎪⎩()422cos cos 2sin sin 4θαθα++=,化简得:1cos cos sin sin 2θαθα+=-()()122cos cos 2sin sin iz z θαθα∴-=-+-==故答案为: 【考点】复数模长的求解 16.【答案】①③④【解析】对于命题1p ,可设1l 与2l 相交,这两条直线确定的平面为α;若3l 与1l 相交,则交点A 在平面α内,同理,3l 与2l 的交点B 也在平面α内,所以,AB α⊂,即3l α⊂,命题1p 为真命题;对于命题2p ,若三点共线,则过这三个点的平面有无数个,命题2p 为假命题;对于命题3p ,空间中两条直线相交、平行或异面,命题3p 为假命题;对于命题4p ,若直线m ⊥平面α,则m 垂直于平面α内所有直线,直线l ⊂平面α,∴直线m ⊥直线l ,命题4p 为真命题.综上可知,14p p ∧为真命题,12p p ∧为假命题,23p p ⌝∨为真命题,34p p ⌝∨⌝为真命题.故答案为:①③④.【考点】复合命题的真假,空间中线面关系有关命题真假的判断 三、解答题 17.【答案】(1)23π; (2)3+【解析】(1)由正弦定理可得:222BC AC AB AC AB --=⋅,2221cos 22AC AB BC A AC AB +-∴==-,()0πA ∈,,2π3A ∴=. (2)由余弦定理得:222222cos 9BC AC AB AC AB A AC AB AC AB =+-=++=,即()29AC AB AC AB +-=.22AC AB AC AB +⎛⎫⎪⎝⎭≤(当且仅当AC AB =时取等号),()()()22223924AC AB AC AB AC AB AC AB AC AB +⎛⎫∴=+-+-=+⎪⎝⎭,解得:AC AB +≤仅当AC AB=时取等号),ABC ∴△周长3L AC AB BC =+++≤,ABC ∴△周长的最大值为3+【考点】解三角形的相关知识,涉及到正弦定理角化边的应用、余弦定理的应用、三角形周长最大值的求解问题18.【答案】(1)12000; (2)0.94; (3)详见解析【解析】(1)样区野生动物平均数为201111200602020i i y ==⨯=∑,地块数为200,该地区这种野生动物的估计值为2006012000⨯=(2)样本(),i i x y的相关系数为20()()0.94ii xx y y r --===≈∑ (3)由于各地块间植物覆盖面积差异较大,为提高样本数据的代表性,应采用分层抽样,先将植物覆盖面积按优中差分成三层,在各层内按比例抽取样本,在每层内用简单随机抽样法抽取样本即可. 【考点】平均数的估计值、相关系数的计算,抽样方法的选取 19.【答案】(1)12;(2)22113627x y C +=:,2212C y x =:.【解析】(1)()0F c ,,AB x ⊥轴且与椭圆1C 相交于A 、B 两点,则直线AB 的方程为x c =,联立22222221x cx y a b a b c =⎧⎪⎪+=⎨⎪=+⎪⎩,解得2x c b y a =⎧⎪⎨=±⎪⎩,则22b AB a =,抛物线2C 的方程为24y cx =,联立24x c y cx =⎧⎨=⎩,解得2x c y c =⎧⎨=±⎩,4CD c ∴=,43CD AB =,即2843b c a=,223b ac =,即222320c ac a +-=,即22320e e +-=,01e <<,解得12e =,因此,椭圆1C 的离心率为12;(2)由(1)知2a c =,b =,椭圆1C 的方程为2222143x yc c +=,联立222224143y cx x y c c ⎧=⎪⎨+=⎪⎩,消去y 并整理得22316120x cx c +-=,解得23x c =或6x c =-(舍去),由抛物线的定义可得25533c MF c c =+==,解得3c =.因此,曲线1C 的标准方程为2213627x y +=,曲线2C 的标准方程为212y x =.【考点】椭圆离心率的求解,利用抛物线的定义求抛物线和椭圆的标准方程 20.【答案】(1)证明见解析; (2. 【解析】(1)M N ,分别为BC ,11B C 的中点,1//MN BB ∴又11//AA BB 1//MN AA ∴.在ABC △中,M 为BC 中点,则BC AM ⊥.又侧面11BB C C 为矩形,1BC BB ∴⊥,1//MN BB ,MN BC ⊥,由MN AM M =,,MN AM ⊂平面1A AMN ,∴BC ⊥平面1A AMN .又11//B C BC ,且11B C ⊄平面ABC ,BC ⊂平面ABC ,11//B C ∴平面ABC .又11B C ⊂平面11EB C F ,且平面11EB C F平面ABC EF =11//B C EF ∴//EF BC ∴又BC ⊥平面1A AMN ,∴EF ⊥平面1A AMN ,EF ⊂平面11EB C F ,∴平面11EB C F ⊥平面1A AMN .(2)连接NP//AO 平面11EB C F ,平面AONP 平面11EB C F NP =,∴//AO NP .根据三棱柱上下底面平行,其面1A NMA平面ABC AM =,面1A NMA平面1111A B C A N =,∴//ON AP .故:四边形ONPA是平行四边形.设ABC △边长是6m (0m >),可得:ON AP =,6NP AO AB m ===.O 为111A B C △的中心,且111A B C △边长为6m ,∴16sin 603ON =⨯⨯︒,故:ON AP ==.//EF BC ,∴AP EPAM BM=,∴3EP=.解得:EP m =.在11B C 截取1B Q EP m ==,故2QN m =,1B Q EP =且1//B Q EP ,∴四边形1B QPE 是平行四边形,∴1//B E PQ .由(1)11B C ⊥平面1A AMN ,故QPN ∠为1B E 与平面1A AMN 所成角.在Rt QPN △,根据勾股定理可得:PQ ,sinQN QPN PQ ∴∠===∴直线1B E 与平面1A AMN . 【考点】证明线线平行和面面垂直,线面角21.【答案】(1)当π03x ⎛⎫∈ ⎪⎝⎭,时,()()0f x f x '>,单调递增,当π2π33x ⎛⎫∈ ⎪⎝⎭,时,()()0f x f x '<,单调递减,当2ππ3x ⎛⎫∈ ⎪⎝⎭,时,()()0f x f x '>,单调递增.(2)证明见解析; (3)证明见解析.【解析】(1)由函数的解析式可得:()32sin cos f x x x =,则:()()22423sin cos sin f x x x x'=-()2222sin 3cos sin x x x =-()222sin 4cos 1x x =-()()22sin 2cos 12cos 1x x x =+-,()0f x '=在()0πx ∈,上的根为:12π2π33x x ==,,当π03x ⎛⎫∈ ⎪⎝⎭,时,()()0f x f x '>,单调递增,当π2π33x ⎛⎫∈ ⎪⎝⎭,时,()()0f x f x '<,单调递减,当2ππ3x ⎛⎫∈ ⎪⎝⎭,时,()()0f x f x '>,单调递增.(2)注意到()()()()22πsin πsin 2πsin sin2f x x x x x f x +=+⎡+⎤==⎣⎦,故函数()f x 是周期为π的函数,结合(1)的结论,计算可得:()()0π0f f ==,2π3228f ⎛⎛⎫=⨯= ⎪ ⎝⎭⎝⎭,223f π⎛⎛⎫=⨯= ⎪ ⎝⎭⎝⎭⎝⎭()max 8f x ⎡⎤=⎣⎦,()min 8f x ⎡⎤=-⎣⎦,即()f x ≤. (3)结合(2)的结论有:2222sin sin 2sin 4sin 2n x x x x 233333sin sin 2sin 4sin 2n x x xx ⎡⎤=⎣⎦ ()()()2222123sin sin sin 2sin 2sin 4sin 2sin 2sin 2n n n x x x x x x x x -⎡⎤=⎣⎦23233sin sin 2nx x ⎡⎤⨯⨯⎢⎥⎣⎦≤ 23n ⎡⎤⎢⎥⎢⎥⎝⎭⎣⎦≤34n ⎛⎫= ⎪⎝⎭. 【考点】导数的应用22.【答案】(1)14C x y +=:;2224C x y -=:;(2)17cos 5ρθ=. 【解析】(1)由22cos sin 1θθ+=得1C 的普通方程为:4x y +=; 由11x t t y t t ⎧=+⎪⎪⎨⎪=-⎪⎩得:2222221212x t t y t t ⎧=++⎪⎪⎨⎪=+-⎪⎩,两式作差可得2C 的普通方程为:224x y -=. (2)由2244x y x y +=⎧⎨-=⎩得:5232x y ⎧=⎪⎪⎨⎪=⎪⎩,即5322P ⎛⎫ ⎪⎝⎭,; 设所求圆圆心的直角坐标为()0a ,,其中0a >,则22253022a a ⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭,解得:1710a =,∴所求圆的半径1710r =,∴所求圆的直角坐标方程为:22217171010x y ⎛⎫⎛⎫-+= ⎪ ⎪⎝⎭⎝⎭,即22175x y x +=,∴所求圆的极坐标方程为cos 5ρθ=. 【考点】极坐标与参数方程的综合应用23.【答案】(1)32x x ⎧⎨⎩≤或112x ⎫⎬⎭; (2)(][)13-∞-+∞,,. 【解析】(1)当2a =时,()43f x x x =-+-.当3x ≤时,()43724f x x x x =-+-=-,解得:32x ≤;当34x <<时,()4314f x x x =-+-=,无解;当4x 时,()43274f x x x x =-+-=-,解得:112x ;综上所述:()4f x 的解集为32x x ⎧⎨⎩≤或112x ⎫⎬⎭. (2)()()()()22222121211f x x a x a x a x a a a a =-+-+---+=-+-=-(当且仅当221a x a -≤≤时取等号),()214a ∴-,解得:1a -≤或3a ,a ∴的取值范围为(][)13-∞-+∞,,. 【考点】绝对值不等式的求解,利用绝对值三角不等式求解最值。
2020年高考理科数学及答案解析(全国Ⅲ卷)

2020年普通高等学校招生全国统一考试理科数学(含答案解析)注意事项:1.答卷前,考生务必将自己的姓名和准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合2{1,0,1,2}{|1}A B x x =-=≤,,则A B = A .{}1,0,1-B .{}0,1C .{}1,1-D .{}0,1,2【答案】A 【难度】容易 【点评】本题考查集合之间的运算关系,即包含关系.在高一数学强化提高班上学期课程讲座1,第一章《集合》中有详细讲解,其中第02节中有完全相同类型题目的计算.在高考精品班数学(理)强化提高班中有对集合相关知识的总结讲解. 2.若(1i)2i z +=,则z = A .1i -- B .1+i -C .1i -D .1+i【答案】D 【难度】容易【点评】本题考查复数的计算。
在高二数学(理)强化提高班下学期,第四章《复数》中有详细讲解,其中第02节中有完全相同类型题目的计算。
在高考精品班数学(理)强化提高班中有对复数相关知识的总结讲解。
3.《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝,并称为中国古典小说四大名著.某中学为了解本校学生阅读四大名著的情况,随机调查了100位学生,其中阅读过《西游记》或《红楼梦》的学生共有90位,阅读过《红楼梦》的学生共有80位,阅读过《西游记》且阅读过《红楼梦》的学生共有60位,则该校阅读过《西游记》的学生人数与该校学生总数比值的估计值为A .0.5B .0.6C .0.7D .0.8【答案】C 【难度】容易【点评】本题在高考数学(理)提高班讲座 第十四章《概率》中有详细讲解,在寒假特训班、百日冲刺班中均有涉及。
2020年全国卷Ⅲ高考理科数学试题及答案

2020年全国卷Ⅲ高考理科数学试题及答案注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上.2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合,,则中元素的个数为 {(,)|,,}A x y x y y x =∈≥*N {(,)|8}B x y x y =+=A B A .2 B .3 C .4 D .62.复数的虚部是 113i -A . B . C .D .310-110-1103103.在一组样本数据中,1,2,3,4出现的频率分别为,且,则下面四种情形中,对1234,,,p p p p 411i i p ==∑应样本的标准差最大的一组是 A . B . 14230.1,0.4p p p p ====14230.4,0.1p p p p ====C .D .14230.2,0.3p p p p ====14230.3,0.2p p p p ====4.Logistic 模型是常用数学模型之一,可应用于流行病学领域.有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数(t 的单位:天)的Logistic 模型:,其中K 为最大确诊病()I t 0.23(53)()=1e t K I t --+例数.当时,标志着已初步遏制疫情,则t *约为 *()0.95I t K =(ln193)≈A .60B .63C .66D .695.设O 为坐标原点,直线x =2与抛物线C :交于D ,E 两点,若,则C 的焦点坐22(0)y px p =>OD OE ⊥标为 A .B .C .D .1(,0)41(,0)2(1,0)(2,0)6.已知向量a ,b 满足,,,则 ||5=a ||6=b 6⋅=-a b cos ,=+a a b A . B . C .D .3135-1935-173519357.在△ABC 中,cos C =,AC =4,BC =3,则cos B = 23A .B .C .D .191312238.下图为某几何体的三视图,则该几何体的表面积是A .B.C .D .9.已知2tan θ–tan(θ+)=7,则tan θ= π4A .–2B .–1C .1D .210.若直线l 与曲线y 和x 2+y 2=都相切,则l 的方程为 15A .y =2x +1B .y =2x +C .y =x +1 D .y =x + 1212121211.设双曲线C :(a >0,b >0)的左、右焦点分别为F 1,F 2.P 是C 上一点,且22221x y a b-=F 1P ⊥F 2P .若△PF 1F 2的面积为4,则a =A .1B .2C .4D .812.已知55<84,134<85.设a =log 53,b =log 85,c =log 138,则A .a <b <cB .b <a <cC .b <c <aD .c <a <b二、填空题:本题共4小题,每小题5分,共20分。
2020年高考理科数学(全国卷Ⅰ真题)——(含答案和解析)

(一)必考题:共60分.
17.设 是公比不为1的等比数列, 为 , 的等差中项.
(1)求 的公比;
(2)若 ,求数列 的前 项和.
18.如图, 为圆锥的顶点, 是圆锥底面的圆心, 为底面直径, . 是底面的内接正三角形, 为 上一点, .
【点睛】本题考查利用导数求解函图象的切线方程,考查计算能力,属于基础题
7.设函数 在 的图像大致如下图,则f(x)的最小正周期为()
A. B.
C. D.
【答案】C
【解析】
【分析】
由图可得:函数图象过点 ,即可得到 ,结合 是函数 图象与 轴负半轴的第一个交点即可得到 ,即可求得 ,再利用三角函数周期公式即可得解.
【详解】由图可得:函数图象过点 ,
将它代入函数 可得:
又 是函数 图象与 轴负半轴的第一个交点,
所以 ,解得:
所以函数 的最角函数的性质及转化能力,还考查了三角函数周期公式,属于中档题.
8. 的展开式中x3y3的系数为()
A.5B.10
C.15D.20
【答案】C
据此结合目标函数 几何意义可知目标函数在点A处取得最大值,
联立直线方程: ,可得点A的坐标为: ,
据此可知目标函数的最大值为: .
故答案为:1.
【点睛】求线性目标函数z=ax+by(ab≠0)的最值,当b>0时,直线过可行域且在y轴上截距最大时,z值最大,在y轴截距最小时,z值最小;当b<0时,直线过可行域且在y轴上截距最大时,z值最小,在y轴上截距最小时,z值最大.
A.0B.1C. D.2
高考理科数学试题全国卷

2015年普通高等学校招生全国统一考试理科数学 第Ⅰ卷一. 选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的. (1)设复数z 满足1+z1z-=i ,则|z |= (A )1 (B(C(D )2(2) 2010cos16010sin cos sin ︒︒︒︒-=(A) (B2 (C )12- (D )12(3) 设命题P :∃n ∈N ,2n >2n ,则⌝P 为(A )∀n ∈N , 2n >2n (B )∃ n ∈N , 2n ≤2n(C )∀n ∈N , 2n ≤2n (D )∃ n ∈N , 2n =2n(4)投篮测试中,每人投3次,至少投中2次才能通过测试.已知某同学每次投篮投中的概率为0.6,且各次投篮是否投中相互独立,则该同学通过测试的概率为 (A )0.648 (B )0.432(C )0.36 (D)0.312(5)已知M(x 0,y 0)是双曲线C :2212xy -= 上的一点,F 1、F 2是C 上的两个焦点,若12MF MF ⋅u u u u r u u uu r <0,则y 0的取值范围是(A )(-3,3) (B )(-6,6) (C )(3-,3) (D )() (6)《九章算术》是我国古代内容极为丰富的数学名着,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧度为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放斛的米约有 (A )14斛 (B )22斛 (C )36斛 (D )66斛(7)设D 为?ABC 所在平面内一点3BC CD =u u u r u u u r,则(A ) 1433AD AB AC =-+u u u r u u ur u u u r (B ) 1433AD AB AC =-u u u r u u u r u u u r(C ) 4133AD AB AC =+u u u r u u u r u u u r (D ) 4133AD AB AC =-u u u r u u u r u u u r(8)函数f (x )=cos (ωx +φ)的部分图像如图所示,则f (x )的单调递减区间为(A )(kπ−14,kπ+34,),k ∈z (b )(2kπ−14,2kπ+34),k ∈z(C )(k −14,k +34),k ∈z (D )(2k −14,2k +34),k ∈z(9)执行右面的程序框图,如果输入的t =0.01,则输出的n = (A )5 (B )6 (C )7 (D )8(10)25()x x y ++的展开式中,52x y 的系数为(A )10 (B )20 (C )30 (D )60(11)圆柱被一个平面截去一部分后与半球(半径为r )(12)该几何体三视图中的正视图和俯视图如图所示.(13)表面积为16 + 20π,则r =(A )1 (B )2 (C )4 (D )812.设函数f (x )=e x (2x -1)-ax +a ,其中a 1,若存在唯一的 整数x 0,使得f (x 0)0,则a 的取值范围是( ) A .[32e -,1) B . [33,24e -) C . [33,24e ) D . [32e,1) 第II 卷二、填空题:本大题共3小题,每小题5分(13)若函数2()()f x xln x a x +=+为偶函数,则a =(14)一个圆经过椭圆221164x y +=的三个顶点,且圆心在x 轴上,则该圆的标准方程为 . (15)若x ,y 满足约束条件10040x x y x y -≥⎧⎪-≤⎨⎪+-≤⎩,则y x 的最大值为 .(16)在平面四边形ABCD 中,∠A =∠B =∠C =75°,BC =2,则AB 的取值范围是 . 三.解答题:解答应写出文字说明,证明过程或演算步骤. (17)(本小题满分12分)S n 为数列{a n }的前n 项和.已知a n >0,a n 2+2a n =4S n +3 (Ⅰ)求{a n }的通项公式: (Ⅱ)设b n =1a n a n+1,求数列{b n }的前n 项和(18)如图,四边形ABCD 为菱形,∠ABC =120°,E ,F 是平面ABCD 同一侧的两点,BE ⊥平面ABCD , DF ⊥平面ABCD ,BE =2DF ,AE ⊥EC . (1)证明:平面AEC ⊥平面AFC(2)求直线AE 与直线CF 所成角的余弦值 (19)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x (单位:千元)对年销售量y (单位:t )和年利润z (单位:千元)的影响,对近8年的年宣传费x i 和年销售量y i (i =1,2,···,8)数据作了初步处理,得到下面的散点图及一些统计量的值.8i=1∑(x i -x r )28i=1∑(w i -w u r )28i=1∑(x i -x r)(y i -y u r )8i=1∑(w i -w u r )(y i -y u r )46.656.36.8289.81.61469108.8表中w i i x ,w u r =18i=1∑i w(Ⅰ)根据散点图判断,y =a +bx 与y =c +x y 关于年宣传费x 的回归方程类型?(给出判断即可,不必说明理由)(Ⅱ)根据(Ⅰ)的判断结果及表中数据,建立y 关于x 的回归方程;(Ⅲ)以知这种产品的年利率z 与x 、y 的关系为z =0.2y -x .根据(Ⅱ)的结果回答下列问题:(i ) 年宣传费x =49时,年销售量及年利润的预报值是多少? (ii ) 年宣传费x 为何值时,年利率的预报值最大?ABCF ED年宣传费(千元)年销售量/t附:对于一组数据(u 1 v 1),(u 2 v 2)…….. (u n v n ),其回归线v =αβ+u 的斜率和截距的最小二乘估计分别为:(20)(本小题满分12分)在直角坐标系xoy 中,曲线C :y =24x 与直线l:y =kx +a (a >0)交于M ,N 两点,(Ⅰ)当k =0时,分别求C 在点M 和N 处的切线方程;(Ⅱ)y 轴上是否存在点P ,使得当k 变动时,总有∠OPM =∠OPN ?说明理由. (21)(本小题满分12分)已知函数f (x )=31,()ln 4x ax g x x ++=- (Ⅰ)当a 为何值时,x 轴为曲线()y f x = 的切线;(Ⅱ)用min {},m n 表示m ,n 中的最小值,设函数}{()min (),()(0)h x f x g x x => ,讨论h (x )零点的个数请考生在(22)、(23)、(24)三题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做第一个题目计分,做答时,请用2B 铅笔在答题卡上将所选题号后的方框涂黑. (22)(本题满分10分)选修4-1:几何证明选讲是☉O 的切线,BC 交☉O 于点E (I ) 若D 为AC 的中点,证明:DE 是☉O 的切线;(II ) 若OA ,求∠ACB 的大小.?(23)(本小题满分10分)选修4-4:坐标系与参数方程在直角坐标系xOy 中.直线1C :x =-2,圆2C :(x -1)2+(y -2)2=1,以坐标原点为极点, x 轴的正半轴为极轴建立极坐标系.(I ) 求1C ,2C 的极坐标方程; (II ) 若直线3C 的极坐标方程为()4R πθρ=∈,设2C 与3C 的交点为M ,N ,求△C 2MN 的面积(24)(本小题满分10分)选修4—5:不等式选讲已知函数f (x )=|x +1|-2|x -a |,a >0.(Ⅰ)当a =1时,求不等式f (x )>1的解集;(Ⅱ)若f (x )的图像与x 轴围成的三角形面积大于6,求a 的取值范围2015年普通高等学校招生全国统一考试理科数学试题答案A 卷选择题答案 一、 选择题(1)A (2)D (3)C (4)A (5)A (6)B (7)A (8)D (9)C (10)C (11)B (12)D A 、B 卷非选择题答案 二、填空题(13)1 (14) 22325()24x y ±+= (15)3(16)二、 解答题 (17)解:(I )由2243n n n a a S +=+,可知211124 3.n n n a a S ++++=+可得221112()4n n n n a a a a a +++-+-= 即由于0n a >可得1 2.n n a a +-=又2111243a a a +=+,解得111()3a a =-=舍去,所以{}n a 是首相为3,公差为2的等差数列,通项公式为2 1.n a n =+ (II )由21n a n =+设数列{}n b 的前n 项和为n T ,则(18)解:(I )连结BD ,设BD I AC=G ,连结EG ,FG ,EF.在菱形ABCD 中不妨设GB=1.由∠ABC=120°,可得3由BE ⊥平面ABCD, AB=BC 可知AE=EC.又AE ⊥EC ,所以3EG ⊥AC.在Rt ∆EBG 中,可得2故DF=22.在Rt ∆FDG 中,可得FG=62在直角梯形BDFE 中,由BD=2,2,DF=22,可得FE=322.从而222,EG FG EF EG FG +=⊥所以又,.AC FG G EG AFC =⊥I 可得平面因为EG AEC ⊂平面 所以平面AEC AFC ⊥平面(III ) 如图,以G 为坐标原点,分别以GB ,GC 的方向为x 轴,y 轴正方向,GB u u u r为单位长,建立空间直角坐标系G-xyz.由(I )可得2(03,0),(102),(10(03,0)A E F C --,,,,,,所以 232),(13,2AE CF ==-u u u r u u u r ,,故3cos ,AE CF AE CF AE CF⋅==⋅u u u r u u u ru u u r u u u r u u u r u u u r所以直线AE 与直线CF 所成直角的余弦值为33. (19)解:(I )由散点图可以判断,y c x =+适宜作为年销售量y 关于年宣传费x 的回归方程类型。
2023年高考数学全真模拟(全国甲卷乙卷通用)理数03答案

2023年高考数学全真模拟卷三(全国卷)理科数学(考试时间:120分钟;试卷满分:150分)注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上第I 卷(选择题)一、单选题(本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项符合题目要求)1.已知集合{}31A x x =-<,{B y y ==,则A B = ()A .∅B .[)4,+∞C .()2,+∞D .[)0,2【答案】C【分析】根据一元一次不等式可解得集合A ,再根据函数值域求法可求得集合B ,由交集运算即可得出结果.【详解】由题意可得{}2A x x =>,由函数值域可得{}0B y y =≥,所以{}2A B x x ⋂=>.故选:C 2.某班40人一次外语测试的成绩如下表:其中中位数为()A .78B .80C .79D .78和89【答案】C【分析】根据中位数的概念即可求得.【详解】解:由题意得:所有成绩从小到大排列,第二十位是78,第二十一位是80,则中位数为7880792+=.故选:C 3.若复数z 满足()()1i i 4z -+=,其中i 为虚数单位,则z 的虚部为()A .2B .2-C .1D .1-【答案】C【分析】根据复数的除法运算与减法运算得2i z =+,进而根据复数的概念求解即可.【详解】解:由题意可知()()()41i 4i i 2i 1i 1i 1i z +=-=-=+--+,所以,z 的虚部为1.故选:C.4.双曲线22221(0,0)x y a b a b -=>>,焦点到渐近线的距离为1,则双曲线方程为()A .2214y x -=B .2214x y -=C .22123x y -=D .22132x y -=【答案】B【分析】由离心率可得12b a =,从而可得渐近线方程,根据焦点到渐近线的距离为1可得c ,从而可求a ,故可得双曲线的方程.【详解】由题可知c a =,222514b e a =+=,得12b a =,则渐近线方程为20x y ±=,焦点到渐近线的距离为1,1=,可解得c =,所以2a =,由222c a b =+得1b =.所以双曲线方程为2214x y -=.故选:B.5.“天圆地方”观反映了中国古代科学对宇宙的认识,后来发展成为中国传统文化的重要思想.中国古人将琮、璧、圭、璋、璜、琥六种玉制礼器谓之“六瑞”,玉琮内圆外方,表示天和地,中间的穿孔表示天地之间的沟通,可以说是中国古代世界观很好的象征物.下面是一玉琮图及其三视图,设规格如图所示(单位:cm ),则三视图中A ,B 两点在实物中对应的两点在实物玉璧上的最小距离约为()(3π≈ 1.4≈)A .8.4B .9.8C .10.4D .11.2【答案】A【分析】玉琮的中空部分看成一圆柱,A ,B 两点可看成是圆柱轴截面所对应矩形的对角线的端点,将圆柱侧面展开,线段AB 的长就是沿该圆柱表面由A 到B 的最短距离.【详解】本题考查传统文化与圆柱的侧面展开图.由题意,将玉琮的中空部分看成一圆柱,A ,B 两点可看成是圆柱轴截面所对应矩形的对角线的端点,现沿该圆柱表面由A到B ,如图,将圆柱侧面展开,可知()min 8.4AB =≈.故选:A .6.已知定义在R 上的函数()21x mf x -=-(m 为实数)是偶函数,记0.5log 3a =,()2log 5b f =,()c f m =,则a 、b 、c 的大小关系为()A .a b c <<B .a c b<<C .c<a<bD .c b a<<【答案】B【分析】由偶函数的性质可得m 的值,即可得函数()f x 的解析式,分析函数单调性,结合对数的运算性质比较大小.【详解】()21x mf x -=-(m 为实数)是R 上的偶函数,∴()()f x f x -=,即2121x m x m ----=-,∴--=-x m x m ,即()()22x m x m --=-,∴0mx =,则0m =,此时()21xf x =-,0.5log 30a =<,()2log 540b f ==>,()(0)0c f m f ===,则a c b <<.故选:B7.若某一几何体的三视图如图所示,则该几何体是()A .三棱柱B .四棱柱C .五棱柱D .六棱柱【答案】C【分析】根据三视图还原出立体图形即可得到答案.【详解】根据其三视图还原出其立体图形如下图所示,易得其为五棱柱,故选:C.8.已知,a b ∈R ,则“1ab ≥”是“222a b +≥”的()A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件【答案】A【分析】根据充分条件、必要条件及不等式的性质可得解.【详解】由22||12||||2ab a b a b ≥⇒+≥≥,而222a b +≥不一定能得到1ab ≥,例如,0,2a b ==,所以“1ab ≥”是“222a b +≥”的充分而不必要条件.故选:A 9.已知△ABC 满足22AB BA CA =⋅,则△ABC 的形状为()A .直角三角形B .等边三角形C .等腰直角三角形D .等腰三角形【答案】D【分析】根据已知得到22cos c bc A =,利用正弦定理可求得sin 2sin cos =C B A ,结合三角形内角和为π以及两角和的正弦公式可求得in 0()s A B -=,即可确定三角形形状.【详解】解:根据22AB BA CA =⋅得到:22cos c bc A =,由正弦定理2sin sin b cR B C==,可得2sin 2sin sin cos C B C A =,又C 为三角形的内角,得到sin 0C ≠,可得sin 2sin cos =C B A ,又[]sin sin ()sin()C A B A B π=-+=+,∴sin()sin cos cos sin 2sin cos A B A B A B B A +=+=,即sin cos cos sin 0A B A B -=,∴in 0()s A B -=,且A 和B 都为三角形的内角,∴A B =,则ABC 的形状为等腰三角形.故选:D .10.在新型冠状病毒肺炎疫情联防联控期间,社区有5名医务人员到某学校的高一、高二、高三3个年级协助防控和宣传工作.若每个年级至少分配1名医务人员,则不同的分配方法有()A .25种B .50种C .300种D .150种【答案】D【分析】首先分析将5个人分为三小组且每小组至少有一人,则可能分法有:(2,2,1),(3,1,1)两种情况,每种情况利用分步计数原理计算情况数,最后相加即可.【详解】当5个人分为2,2,1三小组,分别来自3个年级,共有2213531322C C C A 90A ⋅=种;②当5个人分为3,1,1三小组时,分别来自3个年级,共有3113521322C C C A 60A ⋅=种.综上,选法共有9060150+=.故选:D.11.已知函数()2tan sin tan 1xf x x x =++,则下列结论正确的是()A .()f x 在区间ππ,33⎛⎫- ⎪⎝⎭上单调递减B .()f x 在区间π0,2⎛⎫ ⎪⎝⎭上有极小值C .设()()2g x f x =-在区间ππ,22⎛⎫- ⎪⎝⎭上的最大值为M ,最小值为m ,则4M m +=D .()f x 在区间ππ,22⎛⎫- ⎪⎝⎭内有且只有一个零点【答案】D【分析】由商数关系化简函数,结合导数法可得函数性质及图象,即可逐个判断.【详解】因为()22sin tan cos sin sin tan 1sin 1cos xx x f x x x x x x =+=++⎛⎫+ ⎪⎝⎭πsin sin cos π,2x x x x k k ⎛⎫=+≠+∈ ⎪⎝⎭Z ,所以()()()22cos cos 12cos 1cos 1f x x x x x '=+-=-⋅+.当ππ,22x ⎛⎫∈- ⎪⎝⎭时,令()0f x '=,解得π3x =±,则当x 变化时,()f x ',()f x 的变化情况如下表所示.x ππ,23⎛⎫-- ⎪⎝⎭π3-ππ,33⎛⎫- ⎪⎝⎭π3ππ,32⎛⎫ ⎪⎝⎭()f x '-0+0-所以()f x 在区间ππ,22⎛⎫- ⎪⎝⎭上的图象如图所示.对A ,()f x 在区间ππ,33⎛⎫- ⎪⎝⎭上单调递增,A 错;对B ,()f x 在区间π0,2⎛⎫ ⎪⎝⎭上有极大值,无极小值,B 错;对C ,()()2g x f x =-在区间ππ,22⎛⎫- ⎪⎝⎭上的最大值为24M =-,最小值为24m =--,4M m +=-,C 错;对D ,()f x 在区间ππ,22⎛⎫- ⎪⎝⎭内有且只有一个零点,D 对.故选:D.12.已知函数()f x 的定义域为R ,且满足()()110f x f x -+-=,()()8f x f x +=,()11f =,()31f =-,()()21,021,24x a x f x x b x ⎧-++<≤⎪=⎨+-<≤⎪⎩,给出下列结论:①1a =-,3b =-;②()20231f =;③当[]4,6x ∈-时,()0f x <的解集为()()2,02,4- ;④若函数()f x 的图象与直线y mx m =-在y 轴右侧有3个交点,则实数m 的取值范围是111,16264⎛⎫⎛⎫--⋂- ⎪ ⎪⎝⎭⎝⎭.其中正确结论的个数为()A .4B .3C .2D .1【答案】C【分析】由()11f =,()31f =-解出,a b 的值可判断①;由周期和奇偶函数的性质计算()20231f =-可判断②;作出函数()f x 在[]0,4上的图象,根据图象可判断③;讨论当0m >和0m <,方程()mx m f x -=的解的个数可判断④.【详解】因为()()110f x f x -+-=,所以()()f x f x -=-,所以函数()f x 为奇函数,()00f =.因为()()8f x f x +=,所以()f x 的周期为8.又()()21111f a =-++=,所以10a +=,所以1a =-,()3311f b =+-=-,所以3b =-,故①正确.因为,()()()()202325381111f f f f =⨯-=-=-=-,故②错误.易知()()211,0231,24x x f x x x ⎧--+<≤⎪=⎨--<≤⎪⎩,作出函数()f x 在[]0,4上的图象,根据函数()f x 为奇函数,及其周期为8,得到函数()f x 在R 上的图象,如图所示,由()f x 的图象知,当[]4,6x ∈-时,()0f x <的解集为()()2,02,4- ,故③正确.由题意,知直线()1y mx m m x =-=-恒过点()1,0,与函数()f x 的图象在y 轴右侧有3个交点根据图象可知当0m >时,应有51m m ⨯-<,即14m <,且同时满足()mx m f x -=,[]8,10x ∈无解,即当[]8,10x ∈时,()()()108f x x x =--,()()108x x mx m --=-无解,所以Δ0<,解得1616m -<<+所以1164m -<<.当0m <时,应有31m m ⨯->-,即12m >-,且同时满足()mx m f x -=,[]6,8x ∈无解,即当[]6,8x ∈时,()()()68f x x x =--,()()58x x mx m --=-无解,所以Δ0<,解得1212m --<<-+1122m -<<-+综上,1164m -<或1122m -<<-+.故选:C.第II 卷(非选择题)二、填空题(本题共4小题,每小题5分,共20分)13.函数()12f x x x=+在1x =处切线的倾斜角为_______.【答案】45【分析】求导,求出斜率,进而可得倾斜角.【详解】()212f x x '=-+,则()11211f '=-+=,即函数()12f x x x=+在1x =处切线的斜率为1,则倾斜角为45 故答案为:45 14.已知平面向量(2,)a x =-,b = ,且()a b b -⊥,实数x 的值为_____.【答案】【分析】表示出(3,a b x -=- ,其与b =数量积为0,可算得出x .【详解】解:因为(2,)a x =-,b = ,所以(3,a b x -=-又()a b b -⊥,则()30a b b x -⋅=-= 故x =故答案为:15.设1F 、2F 分别为椭圆()222210x y a b a b+=>>的左右焦点,与直线y b =相切的圆2F 交椭圆于点E ,且E 是直线1EF 与圆2F 相切的切点,则椭圆焦距与长轴长之比为________.【答案】3【分析】根据题意可得12EF EF ⊥,利用椭圆性质可得()()22222a b b c -+=,结合222a b c =+,即可求得22c a .【详解】如图所示,连接2EF ,易得12EF EF ⊥,圆2F 的半径r b =,所以2EF b =,而122EF EF a +=,所以12EF a b =-,122F F c =,所以()()22222a b b c -+=,且有222a b c =+,化简可得23a b =,所以()22249a a c =-,所以2259a c =,可得22c a =.故答案为:16.已知函数()ln f x ax x x =-与函数()e 1xg x =-的图象上恰有两对关于x 轴对称的点,则实数a 的取值范围为__________.【答案】(),1e -∞-【分析】图象恰有两对关于x 轴对称的点,即0x ∃>,使得()()f x g x -=,即ln e 1xax x x -+=-有两解,对等式全分离,构造()ln e 1x x x h x x-+=,求导求单调性,求出值域,对图象进行判断,即可得出a 的取值范围.【详解】因为函数()f x 与()g x 的图象上恰有两对关于x 轴对称的点,所以0x >时()()f x g x -=有两解,即ln e 1x ax x x -+=-有两解,所以ln e 1x x x a x-+=有两解,令()ln e 1x x x h x x -+=,则()()()2e 11x x h x x --'=,所以当()0,1x ∈时,()0h x '>,函数()h x 单调递增;当()1,x ∈+∞时,()0h x '<,函数()h x 单调递减,所以()h x 在1x =处取得极大值,(11e h =-,且()0,1x ∈时,()h x 的值域为(),1e -∞-;()1,x ∈+∞时,()h x 的值域为(),1e -∞-,因此ln e 1x x x a x-+=有两解时,实数a 的取值范围为(),1e -∞-.故答案为:(),1e -∞-三、解答题(本题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答)(一)必考题:共60分17.已知公差不为0的等差数列{}n a 的前n 项和为n S ,2S 、4S 、55S +成等差数列,且2a 、7a 、22a 成等比数列.(1)求{}n a 的通项公式;(2)若11n n n b a a +=,数列{}n b 的前n 项和为n T ,证明:16n T <.【答案】(1)21n a n =+(2)证明见解析【分析】(1)公式法列方程组解决即可;(2)运用裂项相消解决即可.【详解】(1)由题知,设{}n a 的公差为d ,由题意得42527222250S S S a a a d =++⎧⎪=⎨⎪≠⎩,即11121112(46)(2)(510)5(6)()(21)0a d a d a d a d a d a d d +=++++⎧⎪+=++⎨⎪≠⎩,解得132a d =⎧⎨=⎩,所以1(1)3(1)221n a a n d n n =+-=+-⨯=+,所以{}n a 的通项公式为21n a n =+.(2)证明:由(1)得21n a n =+,所以111111(21)(23)22123n n n b a a n n n n +⎛⎫===- ⎪++++⎝⎭,所以1111111111123557212323236n T n n n ⎛⎫⎛⎫=-+-+⋅⋅⋅+-=-<⎪ ⎪+++⎝⎭⎝⎭.18.为促进新能源汽车的推广,某市逐渐加大充电基础设施的建设,该市统计了近五年新能源汽车充电站的数量(单位:个),得到如下表格:年份编号x 12345年份20162017201820192020新能源汽车充电站数量y /个37104147196226(1)已知可用线性回归模型拟合y 与x 的关系,请用相关系数加以说明;(2)求y 关于x 的线性回归方程,并预测2024年该市新能源汽车充电站的数量.参考数据:51710i i y ==∑,512600i i i x y ==∑,()521149.89i iy y =-=∑ 3.16≈.参考公式:相关系数()()niix x yyr --=∑回归方程ˆˆˆybx a =+中斜率和截距的最小二乘估计公式分别为;()()()121ˆniii nii x x y y b x x ==--=-∑∑,ˆˆay bx =-.【答案】(1)答案见解析;(2)ˆ471yx =+;预测2024年该市新能源汽车充电站的数量为424个.【分析】(1)利用相关系数的计算公式即可得解;(2)先利用已知数据和公式得到y 关于x 的线性回归方程,再将2024年所对应的年份编号代入线性回归方程即可得解.【详解】解:(1)由已知数据得()11234535x =⨯++++=,17101425y =⨯=,()()()2222152101210i i x x=-=-+-+++=∑,()()55115260053142470iii i i i x x yy x y x y ==--=-=-⨯⨯=∑∑,所以4700.993.16149.89r ≈≈⨯.因为y 与x 的相关系数近似为0.9,接近1,说明y 与x 的线性相关程度相当高,从而可以用线性回归模型拟合y 与x 的关系.(2)由(1)得()()()51215470ˆ4710iii ii x x y y bx x ==--===-∑∑,ˆˆ1424731ay bx =-=-⨯=,放所求线性回归方程为ˆ471yx =+.将2024年对应的年份编号9x =代人回归方程得ˆ4791424y=⨯+=,故预测2024年该市新能源汽车充电站的数量为424个.19.如图,在四棱锥P -ABCD 中,AB CD ∥,AB ⊥BC ,122BC CD PA PD AB =====,PC =E 为AB的中点.(1)证明:BD ⊥平面APD ;(2)求平面APD 和平面CEP 的夹角的余弦值.【答案】(1)证明见解析(2)22【分析】(1)已知条件求出AB ,BD ,AD 的长度,勾股定理证得BD AD ⊥,取AD 的中点O ,连接OP ,OC ,有PO AD ⊥,得PO ,勾股定理证得PO OC ⊥,从而PO ⊥平面ABCD ,有BD OP ⊥,所以BD ⊥平面APD .(2)建立空间直角坐标系,求相关点的坐标,求相关向量的坐标,求平面APD 和平面CEP 的一个法向量,利用向量夹角公式求平面APD 和平面CEP 的夹角的余弦值【详解】(1)在直角梯形ABCD 中,易得AB =4,BD =AD =,∴222AD BD AB +=,∴BD ⊥AD .取AD 的中点O ,连接OP ,OC ,易得PO ⊥AD ,PO =,如图所示,在△CDO 中,易得OC ==,又PC =,∴222OC PO PC +=,∴PO ⊥OC ,又PO ⊥AD ,AD OC O = ,,AD OC ⊂平面ABCD ,∴PO ⊥平面ABCD ,BD ⊂平面ABCD ,∴BD ⊥OP ,又BD ⊥AD ,AD OP O ⋂=,,AD OP ⊂平面APD ,∴BD ⊥平面APD .(2)如图,以D 为坐标原点,DA ,DB 所在直线分别为x ,y 轴,过点D 且与PO 平行的直线为z 轴建立空间直角坐标系,则D (0,0,0),()A ,()0,B ,)E,P,()C ,∴(CP =,()CE = ,∵BD ⊥平面APD ,∴平面APD 的一个法向量为()10,1,0n =.设平面CEP 的法向量为()2,,n x y z =u u r,则2200n CP n CE ⎧⋅=⎪⎨⋅=⎪⎩,得00⎧+=⎪⎨=⎪⎩,取y =1,得()20,1,1n = ,∴122cos ,2n n =,∴平面APD 和平面CEP 的夹角的余弦值为22.20.已知抛物线()2:20C x py p =>的焦点为F ,准线为l ,点P 是直线1:2l y x =-上一动点,直线l 与直线1l 交于点Q,QF =(1)求抛物线C 的方程;(2)过点P 作抛物线C 的两条切线,PA PB ,切点为,A B ,且95FA FB -≤⋅≤,求PAB 面积的取值范围.【答案】(1)24x y=(2)⎡⎣【分析】(1)计算2,22p p Q ⎛⎫-- ⎪⎝⎭,0,2p F⎛⎫⎪⎝⎭,根据距离公式计算得到2p =,得到抛物线方程.(2)求导得到导函数,计算切线方程得到AB 的直线方程为()002y y xx +=,联立方程,根据韦达定理得到根与系数的关系,根据向量运算得到034y -≤≤,再计算PAB S =△.【详解】(1)直线1:2l y x =-,当2p y =-时,22p x =-,即2,22p p Q ⎛⎫-- ⎪⎝⎭,0,2p F⎛⎫⎪⎝⎭,则QF ==,解得2p =或25p =-(舍去),故抛物线C 的方程为24x y =.(2)设()11,A x y ,()22,B x y ,()00,P x y ,24x y =,2x y '=,PA 的直线方程为:()1112x y x x y =-+,整理得到()112y y xx +=,同理可得:PB 方程为()222y y xx +=,故()()010*******y y x x y y x x ⎧+=⎪⎨+=⎪⎩,故AB 的直线方程为()002y y xx +=,()00224y y xx x y ⎧+=⎨=⎩,整理得到200240x x x y -+=,12012024 x x x x x y +=⎧⎨=⎩,()()()1122121212,1,11FA FB x y x y x x y y y y ⋅=-⋅-=+-++()02221212221212000216123164x x x x x x x x y x y y +-=+-+=-++=-,09235y -≤-≤,解得034y -≤≤,设P 到AB 的距离为d ,12PABS AB d =⋅=△,034y -≤≤,故[]2044,20y +∈,4,PAB S ⎡∈⎣△21.已知01a <<,函数()1x f x x a -=+,()1log a g x x x =++.(1)若()e e g =,求函数()f x 的极小值;(2)若函数()()y f x g x =-存在唯一的零点,求a 的取值范围.【答案】(1)2(2)1,1e ⎡⎫⎪⎢⎣⎭【分析】(1)由()e e g =可求出1ea =,则()1e xf x x -=+,然后对函数求导,由导数的正负可求出函数的单调区间,从而可求出函数的极小值;(2)令()1log 1x a F x ax -=--(0x >),则()111ln ln x F x xa a x a -⎛⎫'=- ⎪⎝⎭,令()11ln ln x x xaa a ϕ-=-,利用导数可求出其单调区间和最小值,然后分11ln 10ln a a a----≥和10ea <<讨论函数的零点即可.【详解】(1)由()1e e e 1log e e ea g a =⇒++=⇒=,所以()1e x f x x -=+,()11e xf x -'=-,令()01f x x '=⇒=,当1x <时,()0f x '<,当1x >时,()0f x ¢>,所以()f x 在(,1)-∞上递减,在(1,)+∞上递增,所以()f x 的极小值为()12f =;(2)()()1log 1x a f x g x a x --=--,令()1log 1x a F x a x -=--(0x >),()F x 存在唯—的零点,()11111ln ln ln ln x x F x a a xa a x a x a --⎛⎫'=-=- ⎪⎝⎭,令()11ln ln x x xaa a ϕ-=-,()()11ln ln x x a x a a ϕ-'=+,令()10ln x x aϕ'=⇒=-,当10ln x a<<-时,()0x ϕ'<;当1ln x a>-时,()0x ϕ'>,所以()x ϕ在10,ln a ⎛⎫- ⎪⎝⎭上递减,在1,ln a ⎛⎫-+∞ ⎪⎝⎭上递增,所以()11ln min 11ln ln ax a a a ϕϕ--⎛⎫=-=-- ⎪⎝⎭,①若11ln 10ln aa a----≥,即111ln ln ln ln a a a ⎛⎫⎛⎫--≤- ⎪ ⎪⎝⎭⎝⎭,令1ln t a-=,所以()111ln ln 10t t t t t ⎛⎫--≤⇒-+≥ ⎪⎝⎭,所以1t ≥,所以11ln a -≥,即11ea <时,()()min 00x F x ϕ'≥⇒≥,所以()F x 在()0,∞+上递增,注意到()10F =,所以()F x 存在唯一的零点,符合题意②当10e a <<时,()100ln aϕ=->,()min 0x ϕ<,()22213(ln )133ln ln ln a a a a a aϕ-=-=,令22()3(ln )1t a a a =-,10ea <<,则221()3[2(ln )2ln ]6ln (ln 1)t a a a a a a a a a'=+⋅⋅=+,因为10ea <<,所以ln 1a <-,所以()6ln (ln 1)0t a a a a '=+>,所以22()3(ln )1t a a a =-在10,e ⎛⎫⎪⎝⎭上单调递增,所以2221113()3(ln 110e e e e t a t ⎛⎫⎛⎫<=-=-< ⎪ ⎪⎝⎭⎝⎭,所以()22213(ln )133ln 0ln ln a a a a a aϕ-=-=>所以()x ϕ即()F x '在10,ln a ⎛⎫- ⎪⎝⎭和1,ln a ⎛⎫-+∞ ⎪⎝⎭上各有一个零点1x ,2x ,()F x 在()10,x 上递增,()12,x x 上递减,()2,0x 上递增,而()11ln 0ln F a a'=-<,所以121x x <<,()1log 1x a F x a x -=--,当110a x a -<<时,()111log 11(1)0a F a a x a x -------<-=<;当1x a >时,()10log 10a F x a>--=,而()()110F x F >=,()()210F x F <=,所以()F x 在()10,x ,()12,x x 和()2,x +∞上各有一个零点,共3个零点了,舍去.综上,a 的取值范围为1,1e ⎡⎫⎪⎢⎣⎭.(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.[选修4-4:坐标系与参数方程]22.在直角坐标系xOy 中,直线l的参数方程为cos sin x t y t αα⎧=⎪⎨=⎪⎩(t 为参数).以坐标原点为极点,x 轴的正半轴为极轴建立坐标系,曲线C 的极坐标方程为2853cos 2ρθ=-,直线l 与曲线C 相交于A ,B两点,)M .(1)求曲线C 的直角坐标方程;(2)若2AM MB =,求直线l 的斜率.【答案】(1)2214x y +=(2)【分析】(1)根据极坐标与直角坐标直角的转化222cos sin x y x y ρθρθρ=⎧⎪=⎨⎪=+⎩,运算求解;(2)联立直线l 的参数方程和曲线C 的直角坐标方程,根据参数的几何意义结合韦达定理运算求解.【详解】(1)∵()()222222288453cos 2cos 4sin 5cos sin 3cos sin ρθθθθθθθ===-++--,则2222cos 4sin 4ρθρθ+=,∴2244x y +=,即2214x y +=,故曲线C 的直角坐标方程为2214x y +=.(2)将直线l的参数方程为cos sin x t y t αα⎧=⎪⎨=⎪⎩(t 为参数)代入曲线C 的直角坐标方程为2214x y +=,得)()22cos sin 14t t αα+=,整理得()()222cos 4sin 10t t ααα++-=,设A ,B 两点所对应的参数为12,t t ,则121222221,cos 4sin cos 4sin t t t t ααααα+=-=-++,∵2AM MB =,则122t t =-,联立1212222cos 4sin t t t t ααα=-⎧⎪⎨+=-⎪+⎩,解得122222cos 4sin cos 4sin t t αααααα⎧=-⎪⎪+⎨⎪=⎪+⎩,将12,t t 代入12221cos 4sin t t αα=-+得2222221cos 4sin cos 4sin cos 4sin αααααααα⎛⎫⎛⎫-=- ⎪⎪ ⎪⎪+++⎝⎭⎝⎭,解得2223tan 4k α==,故直线l的斜率为2±.[选修4-5:不等式选讲]23.已知:()1f x x x m =+--,0m >.(1)若2m =,求不等式()2f x >的解集;(2)()()g x f x x m =--,若()g x 的图象与x 轴围成的三角形面积不大于54,求m 的取值范围.【答案】(1)3,2∞⎛⎫+ ⎪⎝⎭;(2)(]0,8.【分析】(1)利用零点分段法求解出绝对值不等式;(2)先求出()21,312,121,1x m x mg x x m x m x m x -++>⎧⎪=+--≤≤⎨⎪--<-⎩,由()0g x =,解得:122121,3m x m x -=+=,则()21444133m x x m ---==+,由函数单调性得到()()max 1g x g m m ==+,根据函数图象与x 轴围成的三角形面积不大于54,列出方程,求出m 的取值范围.【详解】(1)当2m =时,()3,21221,123,1x f x x x x x x >⎧⎪=+--=--≤≤⎨⎪-<-⎩,当2x >时,()32f x =>成立;当12x -≤≤时,()212f x x =->,则322x <≤;当1x <-时,()32f x =-<不合题意,综上,()2f x >的解集为3,2∞⎛⎫+ ⎪⎝⎭;(2)因为0m >,所以()21,12312,121,1x m x m g x x x m x m x m x m x -++>⎧⎪=+--=+--≤≤⎨⎪--<-⎩,由()0g x =,解得:122121,3m x m x -=+=,则()21444133m x x m ---==+,当1x <-时,()g x 单调递增,当1x m -≤≤时,()g x 单调递增,当x >m 时,()g x 单调递减,所以当x m =时,()g x 取得最大值,()()max 1g x g m m ==+,∴图象与x 轴围成的三角形面积为()()221421154233S m m =⨯+=+≤,解得:108m -≤≤,又0m >,则08m <≤,∴m 的取值范围是(]0,8.。
全国高考理科数学试题及答案全国卷3.pdf

E C
B A
学海无涯
ABCD 分成体积相等的两部分.求二面角 D- AE - C 的余弦值.
20.(12分)已知抛物线 C : y2 = 2x ,过点(2,0)的直线 l 交 C 于 A , B 两点,圆 M 是以
D.8
10.已知椭圆 C :
x2 a2
+
y2 b2
= 1 ( a b 0 )的左、右顶点分别为
A1, A2 ,且以线段
A1 A2 为直
径的圆与直线 bx − ay + 2ab = 0相切,则 C 的离心率为()
A. 6 3
B. 3 3
C. 2 3
11.已知函数 f (x) = x2 − 2x + a(ex−1 + e−x+1) 有唯一零点,则 a = ()
D. 1 3
A. − 1
B. 1
C. 1
D.1
2
3
2
12.在矩形 ABCD 中, AB =1, AD = 2 ,动点 P 在以点 C 为圆心且与 BD 相切的圆上.若
AP = AB + AD ,则 + 的最大值为
A.3
B. 2 2
C. 5
二、填空题:(本题共4小题,每小题5分,共20分)
D.2
A.月接待游客量逐月增加 B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月 D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
4. (x + y)(2x − y)5 的展开式中 x3 y3 的系数为()
A.-80
B.-40
C.40
D.80
5
.
已
2020年新高考(全国卷)数学试卷结构与评析
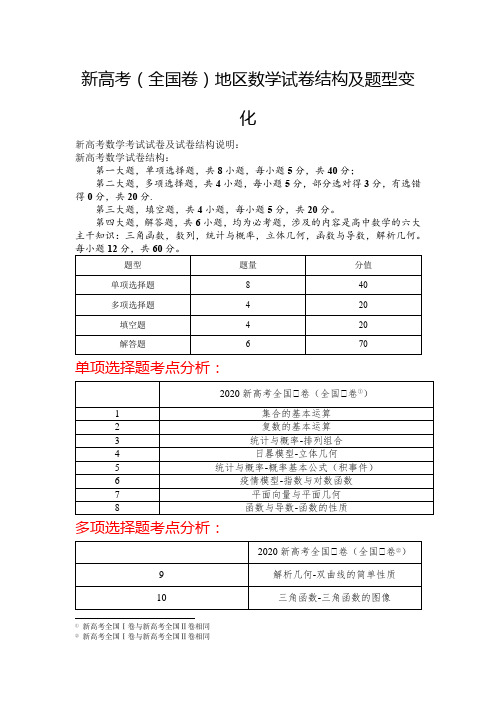
新高考(全国卷)地区数学试卷结构及题型变化新高考数学考试试卷及试卷结构说明:新高考数学试卷结构:第一大题,单项选择题,共8小题,每小题5分,共40分;第二大题,多项选择题,共4小题,每小题5分,部分选对得3分,有选错得0分,共20分.第三大题,填空题,共4小题,每小题5分,共20分。
第四大题,解答题,共6小题,均为必考题,涉及的内容是高中数学的六大主干知识:三角函数,数列,统计与概率,立体几何,函数与导数,解析几何。
单项选择题考点分析:多项选择题考点分析:①新高考全国Ⅰ卷与新高考全国Ⅱ卷相同新高考选择题部分分析:①新高考与之前相比,最大的不同就是增加了多项选择题部分,选择题部分由原来的12道单选题,变成了8道单选题与4道多选题。
这有利于缩小学生选择题部分成绩的差距,过去学生错一道单选题,可能就会丢掉5分,在新高考中,考生部分选对就可以得3分,在一定程度上保证了得分率。
②新高考的单项选择题部分主要考察学生的基础知识和基本运算能力,总体上难度不大,只要认真复习,一般都可以取得一个较好的成绩。
在多项选择题上,前两道较为基础,后两道难度较大,能够突出高考的选拔性功能,总体上来看,学生比以往来讲,更容易取得一个不错的成绩,但对于一些数学基础比较的好的同学来说,这些题比以往应该更有挑战性。
过去,只需要在四个选项中选一个正确答案,现在要在四个选项中,选出多个答案,比以往来说,要想准确的把正确答案全部选出来,确实有一定的难度、③新高考数学试卷的第4题,第6题和第12题都体现了创新性。
第4题,以古代知识为背景,考察同学们的立体几何知识,这体现了数学考试的价值观导向。
弘扬传统文化的同时也鼓励同学们走进传统文化。
近年来,对于这类题目也是屡见不鲜,平时也应该鼓励学生去关注一些古代的数学著作,如《九章算术》,《孙子算经》等等,通过对这些著作的了解,再遇到这类题目时,在一定程度上能够减少恐惧感与焦虑感。
第6题则体现了聚焦民生,关注社会热点。
2020年全国统一高考数学试卷(理科)(全国卷新课标1)

2020年全国统一高考数学试卷(理科)(新课标Ⅰ)一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(5分)已知集合M={x|﹣4<x<2},N={x|x2﹣x﹣6<0},则M∩N=()A.{x|﹣4<x<3} B.{x|﹣4<x<﹣2} C.{x|﹣2<x<2} D.{x|2<x<3} 2.(5分)设复数z满足|z﹣i|=1,z在复平面内对应的点为(x,y),则()A.(x+1)2+y2=1 B.(x﹣1)2+y2=1C.x2+(y﹣1)2=1 D.x2+(y+1)2=13.(5分)已知a=log20.2,b=20.2,c=0.20.3,则()A.a<b<c B.a<c<b C.c<a<b D.b<c<a4.(5分)古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是(≈0.618,称为黄金分割比例),著名的“断臂维纳斯”便是如此.此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是.若某人满足上述两个黄金分割比例,且腿长为105cm,头顶至脖子下端的长度为26cm,则其身高可能是()A.165cm B.175cm C.185cm D.190cm5.(5分)函数f(x)=在[﹣π,π]的图象大致为()A.B.C.D.6.(5分)我国古代典籍《周易》用“卦”描述万物的变化.每一“重卦”由从下到上排列的6个爻组成,爻分为阳爻“”和阴爻“”,如图就是一重卦.在所有重卦中随机取一重卦,则该重卦恰有3个阳爻的概率是()A.B.C.D.7.(5分)已知非零向量,满足||=2||,且(﹣)⊥,则与的夹角为()A.B.C.D.8.(5分)如图是求的程序框图,图中空白框中应填入()A.A=B.A=2+C.A=D.A=1+9.(5分)记S n为等差数列{a n}的前n项和.已知S4=0,a5=5,则()A.a n=2n﹣5 B.a n=3n﹣10 C.S n=2n2﹣8n D.S n=n2﹣2n 10.(5分)已知椭圆C的焦点为F1(﹣1,0),F2(1,0),过F2的直线与C交于A,B两点.若|AF2|=2|F2B|,|AB|=|BF1|,则C的方程为()A.+y2=1 B.+=1C.+=1 D.+=111.(5分)关于函数f(x)=sin|x|+|sin x|有下述四个结论:①f(x)是偶函数②f(x)在区间(,π)单调递增③f(x)在[﹣π,π]有4个零点④f(x)的最大值为2其中所有正确结论的编号是()A.①②④B.②④C.①④D.①③12.(5分)已知三棱锥P﹣ABC的四个顶点在球O的球面上,PA=PB=PC,△ABC是边长为2的正三角形,E,F分别是PA,AB的中点,∠CEF=90°,则球O的体积为()A.8πB.4πC.2πD.π二、填空题:本题共4小题,每小题5分,共20分。
2020年全国统一高考数学试卷(理科)(新课标Ⅲ)及答案解析

试题第1页,总21页绝密★启用前2020年全国统一高考数学试题(理科)(新课标Ⅲ)试题副标题注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)请点击修改第I 卷的文字说明 一、单选题1.已知集合{}{}21,0,1,21A B x x ,=-=≤,则A B ⋂=( )A .{}1,0,1-B .{}0,1C .{}1,1-D .{}0,1,2【答案】A 【解析】 【分析】先求出集合B 再求出交集. 【详解】21,x ≤∴11x -≤≤,∴{}11B x x =-≤≤,则{}1,0,1A B ⋂=-, 故选A . 【点睛】本题考查了集合交集的求法,是基础题. 2.若(1i)2i z +=,则z =( ) A .1i -- B .1+i - C .1i - D .1+i【答案】D 【解析】 【分析】根据复数运算法则求解即可.试题第2页,总21页…………○…………外…………○…………装…………○…………订…………○…………线…………○…………※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※…………○…………内…………○…………装…………○…………订…………○…………线…………○…………【详解】()(2i 2i 1i 1i 1i 1i 1i )()z -===+++-.故选D . 【点睛】本题考查复数的商的运算,渗透了数学运算素养.采取运算法则法,利用方程思想解题. 3.《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝,并称为中国古典小说四大名著.某中学为了解本校学生阅读四大名著的情况,随机调查了100学生,其中阅读过《西游记》或《红楼梦》的学生共有90位,阅读过《红楼梦》的学生共有80位,阅读过《西游记》且阅读过《红楼梦》的学生共有60位,则该校阅读过《西游记》的学生人数与该校学生总数比值的估计值为( ) A.B.C.D.【答案】C 【解析】 【分析】根据题先求出阅读过西游记的人数,进而得解. 【详解】由题意得,阅读过《西游记》的学生人数为90-80+60=70,则其与该校学生人数之比为70÷100=0.7.故选C . 【点睛】本题考查抽样数据的统计,渗透了数据处理和数学运算素养.采取去重法,利用转化与化归思想解题.4.(1+2x 2 )(1+x )4的展开式中x 3的系数为 A .12 B .16 C .20 D .24【答案】A 【解析】 【分析】本题利用二项展开式通项公式求展开式指定项的系数. 【详解】由题意得x 3的系数为314424812C C +=+=,故选A .【点睛】本题主要考查二项式定理,利用展开式通项公式求展开式指定项的系数.试题第3页,总21页…………○…………外…………○…………装…………○…………订…………○…………线…………○…………学校:___________姓名:___________班级:___________考号:___________…………○…………内…………○…………装…………○…………订…………○…………线…………○…………5.已知各项均为正数的等比数列{}n a 的前4项和为15,且53134a a a =+,则3a =( ) A .16 B .8C .4D .2【答案】C 【解析】 【分析】利用方程思想列出关于1,a q 的方程组,求出1,a q ,再利用通项公式即可求得3a 的值. 【详解】设正数的等比数列{a n }的公比为q ,则2311114211115,34a a q a q a q a q a q a ⎧+++=⎨=+⎩, 解得11,2a q =⎧⎨=⎩,2314a a q ∴==,故选C .【点睛】本题利用方程思想求解数列的基本量,熟练应用公式是解题的关键。
2020年高考文科数学全国卷3(附答案与解析)

数学试卷 第1页(共20页) 数学试卷 第2页(共20页)绝密★启用前2020年普通高等学校招生全国统一考试·全国Ⅲ卷文科数学注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}1235711A =,,,,,,{}|315B x x =<<,则A B 中元素的个数为 ( )A .2B .3C .4D .52.若()1i 1i z +=-,则z = A .1i -B .1i +C .i -D .i3.设一组样本数据1x ,2x ,…,n x 的方差为0.01,则数据110x ,210x ,…,10n x 的方差为( )A .0.01B .0.1C .1D .104.Logistic 模型是常用数学模型之一,可应用于流行病学领域.有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数()t I (t 的单位:天)的Logistic 模型:()()0.23531t K I t e --=+,其中K 为最大确诊病例数.当()0.95I t K *=时,标志着已初步遏制疫情,则t *约为(ln193≈)( ) A .60B .63C .66D .69 5.已知πsin sin 13θθ⎛⎫++= ⎪⎝⎭,则πsin 6θ⎛⎫+=⎪⎝⎭( )A .12BC .23D.2 6.在平面内,A ,B 是两个定点,C 是动点.若1AC BC ⋅=,则点C 的轨迹为( ) A .圆B .椭圆C .抛物线D .直线7.设O 为坐标原点,直线2x =与抛物线()2:20C y px p =>交于D ,E 两点,若OD OE ⊥,则C 的焦点坐标为( )A .104⎛⎫ ⎪⎝⎭,B .102⎛⎫ ⎪⎝⎭, C .()10,D .()20,8.点()01-,到直线()1y k x =+距离的最大值为( )A .1BCD .2 9.下图为某几何体的三视图,则该几何体的表面积是( )A. B.C.D.10.设3log 2a =,5log 3b =,23c =,则( )A .a c b <<B .a b c <<C .b c a <<D .c a b << 11.在ABC △中,2cos 3C =,4AC =,3BC =,则tan B =( )AB. C.D.12.已知函数()1sin sin f x x x=+,则( )A .()f x 的最小值为2B .()f x 的图像关于y 轴对称C .()f x 的图像关于直线πx =对称D .()f x 的图像关于直线π2x =对称毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------数学试卷 第3页(共20页) 数学试卷 第4页(共20页)二、填空题:本题共4小题,每小题5分,共20分.13.若x ,y 满足约束条件0201x y x y x +⎧⎪-⎨⎪⎩≥,≥,≤,则32z x y =+的最大值为________.14.设双曲线2222:1x y C a b-=()00a b >,>的一条渐近线为y =,则C 的离心率为________. 15.设函数()xe f x x a =+,若()14ef '=,则a =________. 16.已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的切球表面积为________. 三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答. (一)必考题:共60分. 17.(12分)设等比数列{}n a 满足124a a +=,318a a -=. (1)求{}n a 的通项公式;(2)记n S 为数列{}3log n a 的前n 项和.若13m m m S S S +++=,求m .18.(12分)某学生兴趣小组随机调查了某市100天中每天的空气质量等级和当天到某公园锻炼(1)分别估计该市一天的空气质量等级为1,2,3,4的概率;(2)求一天中到该公园锻炼的平均人次的估计值(同一组中的数据用该组区间的中点值为代表);(3)若某天的空气质量等级为1或2,则称这天“空气质量好”;若某天的空气质量等级为3或4,则称这天“空气质量不好”.根据所给数据,完成下面的22⨯列联表,并根据列联表,判断是否有95%的把握认为一天中到该公园锻炼的人次与该市当天空气质量不好附:()()()()2n ad bc a b c d a c K b d -=++++,.19.(12分)如图,在长方体1111ABCD A B C D -中,在E ,F 分别在棱1DD ,1BB 上,且12DE ED =,12BF FB =,证明:数学试卷 第5页(共20页) 数学试卷 第6页(共20页)(1)当AB BC =时,EF AC ⊥; (2)点1C 在平面AEF 内.20.(12分)已知函数()32f x x kx k =-+. (1)讨论()f x 的单调性;(2)若()f x 有三个零点,求k 的取值范围.21.(12分)已知椭圆()222:10525x y C m m+=<<,A ,B 分别为C 的左、右顶点.(1)求C 的方程;(2)若点P 在C 上,点Q 在直线6x =上,且BP BQ =,BP BQ ⊥,求APQ △的面积.(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.22.[选修4—4:坐标系与参数方程](10分)在直角坐标系xOy 中,曲线C 的参数方程为()222123x t tt t y t t ⎧=--⎪≠⎨=-+⎪⎩为参数且,C 与坐标轴交于A ,B 两点. (1)求AB ;(2)以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,求直线AB 的极坐标方程.23.[选修4—5:不等式选讲](10分) 设a ,b ,c ∈R ,0a b c ++=,1abc =. (1)证明:0ab bc ca ++<;(2)用{}max a b c ,,表示a ,b ,c 中的最大值,证明:{}max a b c ,,毕业学校_____________ 姓名________________ 考生号________________________________ _____________-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------数学试卷 第7页(共20页) 数学试卷 第8页(共20页)2020年普通高等学校招生全国统一考试·全国Ⅲ卷文科数学答案解析一、选择题 1.【答案】B【解析】采用列举法列举出AB 中元素的即可.由题意,{}5711AB =,,,故AB 中元素的个数为3. 故选:B【考点】集合的交集运算 2.【答案】D【解析】先利用除法运算求得z ,再利用共轭复数的概念得到z 即可.因为()()()21i 1i 2ii 1i 1i 1i 2z ---====-++-,所以i z =.故选:D . 【考点】复数的除法运算,共轭复数的概念 3.【答案】C【解析】根据新数据与原数据关系确定方差关系,即得结果.因为数据i ax b +,()12i n =,,…,的方差是数据i x ,()12i n =,,…,的方差的2a 倍,所以所求数据方差为2100.011⨯=,故选:C . 【考点】方差 4.【答案】C【解析】将t t *=代入函数()()0.23531t K I t e--=+结合()0.95I t K *=求得t *即可得解.()()0.23531t K I t e --=+,所以()()0.23530.951t KI tK e**--==+,则()0.235319t e*-=,所以,()0.2353ln193t *-=≈,解得353660.23t *+≈≈. 故选:C .【考点】对数的运算,指数与对数的互化 5.【答案】B【解析】将所给的三角函数式展开变形,然后再逆用两角和的正弦公式即可求得三角函数式的值.由题意可 得:1sin sin 12θθθ+=,则:3sin 12θθ=1cos 2θθ+,从而有:sin coscos sin663ππθθ+=,即πsin 6θ⎛⎫+= ⎪⎝⎭.故选:B .【考点】两角和与差的正余弦公式及其应用 6.【答案】A【解析】首先建立平面直角坐标系,然后结合数量积的定义求解其轨迹方程即可.设()20AB a a =>,以AB 中点为坐标原点建立如图所示的平面直角坐标系,则:()0A a -,,()0B a ,,设()C x y ,,可得:()AC x a y →=+,,()BC x a y →=-,,从而:()()2AC BC x a x a y →→⋅=+-+,结合题意可得:()()21x a x a y +-+=,整理可得:2221x y a +=+,即点C 的轨迹是以AB .故选:A .【考点】平面向量及其数量积的坐标运算,轨迹方程的求解 7.【答案】B【解析】根据题中所给的条件OD OE ⊥,结合抛物线的对称性,可知4DOx EOx π∠=∠=,从而可以确定出点D 的坐标,代入方程求得p 的值,进而求得其焦点坐标,得到结果.因为直线2x =与抛物线()220y px p =>交于E ,D 两点,且OD OE ⊥,根据抛物线的对称性可以确定4DOx EOx π∠=∠=,所以数学试卷 第9页(共20页) 数学试卷 第10页(共20页)()22D ,,代入抛物线方程44p =,求得1p =,所以其焦点坐标为102⎛⎫⎪⎝⎭,,故选:B . 【考点】圆锥曲线,直线与抛物线的交点,抛物线的对称性,点在抛物线上的条件,抛物线的焦点坐标 8.【答案】B【解析】首先根据直线方程判断出直线过定点()10P -,,设()01A -,,当直线()1y k x =+与AP 垂直时,点A 到直线()1y k x =+距离最大,即可求得结果.由()1y k x =+可知直线过定点()10P -,,设()01A -,,当直线()1y k x =+与AP 垂直时,点A 到直线()1y k x =+距离最大,即为AP =.故选:B . 【考点】解析几何初步的问题,直线过定点,利用几何性质 9.【答案】C【解析】根据三视图特征,在正方体中截取出符合题意的立体图形,求出每个面的面积,即可求得其表面积.根据三视图特征,在正方体中截取出符合题意的立体图形根据立体图形可得:12222ABC ADC CDBS S S ===⨯⨯=△△△,根据勾股定理可得:AB AD DB ===∴ADB △是边长为(2°11sin 6022ADB S AB AD =⋅⋅==△,∴该几何体的表面积是:632⨯++故选:C .【考点】根据三视图求立体图形的表面积,根据三视图画出立体图形 10.【答案】A【解析】分别将a ,b 改写为331log 23a =,351log 33b =,再利用单调性比较即可.因为333112log 2log 9333a c ===<,355112log 3log 25333b c ===>,所以a c b <<.故选:A .【考点】对数式大小的比较 11.【答案】C【解析】先根据余弦定理求c ,再根据余弦定理求cos B ,最后根据同角三角函数关系求tan B .设AB c =,BC a =,CA b =,22222cos 91623493c a b ab C =+-=+-⨯⨯⨯=,3c ∴=,2221cos9a c bB +-==,sinB ∴=tan B ∴=.故选:C . 【考点】余弦定理,同角三角函数关系 12.【答案】D【解析】根据基本不等式使用条件可判断A ;根据奇偶性可判断B ;根据对称性判断C ,D .sin x 可以为负,所以A 错;sin 0x ≠,()x k k π∴≠∈Z ,()()1sin sin f x x f x x-=--=-,()f x ∴关于原点对称;()()12sin sin f x x f x x π-=--≠,()()1sin sin f x x f x xπ-=+=,故B 错;()f x ∴关于直线2x π=对称,故C 错,D 对.故选:D .【考点】函数定义域与最值,奇偶性,对称性 二、填空题 13.【答案】7【解析】作出可行域,利用截距的几何意义解决.不等式组所表示的可行域如图.因为32z x y =+,所以322x z y =-+,易知截距2z 越大,则z 越大,平移直线32x y=-,当322x zy =-+经过A点时截距最大,此时数学试卷 第11页(共20页) 数学试卷 第12页(共20页)z 最大,由21y x x =⎧⎨=⎩,得12x y =⎧⎨=⎩,()12A ,,所以max 31227z =⨯+⨯=.故答案为:7.【考点】简单线性规划的应用,线性目标函数的最大值【解析】根据已知可得a=结合双曲线中a ,b ,c 的关系,即可求解.由双曲线方程22221x y a b -=可得 其焦点在x 轴上,因为其一条渐近线为y=,所以ba=c e a ===故【考点】双曲线性质 15.【答案】1【解析】由题意首先求得导函数的解析式,然后得到关于实数a 的方程,解方程即可确定实数a 的值.由函数的解析式可得:()()()()()221x xx e x a e e x a f x x a x a +-+-'==++,则:()()()()12211111e a aef a a ⨯+-'==++,据此可得:()241aeea =+,整理可得:2210a a -+=,解得:1a =.故答案为:1.【解析】与球有关的组合体问题,一种是内切,一种是外接.解题时要认真分析图形,明确切点和接点的位置,确定有关元素间的数量关系,并作出合适的截面图,如球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径;球外接于正方体,正方体的顶点均在球面上,正方体的体对角线长等于球的直径.将原问题转化为求解圆锥内切球的问题,然后结合截面确定其半径即可确定体积的值.易知半径最大球为圆锥的内切球,球与圆锥内切时的轴截面如图所示,其中2BC =,3AB AC ==,且点M 为BC边上的中点,设内切圆的圆心为O ,由于AM ==122S =⨯⨯=△ABC r,则: ()11113322222ABC AOB BOC AOCS S S S AB r BC r AC r r =++=⨯⨯+⨯⨯+⨯⨯=⨯++⨯=△△△△,解得:r =,其体积:343Vr π==.. 三、解答题17.【答案】(1)13n n a -= (2)6m =数学试卷 第13页(共20页) 数学试卷 第14页(共20页)【解析】(1)设等比数列{}n a 的公比为q ,根据题意,列出方程组,求得首项和公比,进而求得通项公式.设等比数列{}n a 的公比为q ,根据题意,有1121148a a q a q a +=-=⎧⎨⎩,解得113a q =⎧⎨=⎩,所以13n n a -=.(2)由(1)求出{}3log n a 的通项公式,利用等差数列求和公式求得n S ,根据已知列出关于m 的等量关系式,求得结果.令313log log 31n n n b a n -===-,所以()()01122n n n n n S +--==,根据13m m m S S S +++=,可得()()()()1123222m m m m m m -++++=,整理得2560m m --=,因为0m >,所以6m =.【考点】比数列通项公式基本量的计算,等差数列求和公式的应用18.【答案】(1)该市一天的空气质量等级分别为1、2、3、4的概率分别为0.43、0.27、0.21、0.09 (2)350锻炼的人次与该市 当天的空气质量有关.【解析】(1)根据频数分布表可计算出该市一天的空气质量等级分别为1、2、3、4的概率.由频数分布表可知,该市一天的空气质量等级为1的概率为216250.43100++=,等级为2的概率为510120.27100++=,等级为3的概率为6780.21100++=,等级为4的概率为7200.09100++=. (2)利用每组的中点值乘以频数,相加后除以100可得结果.由频数分布表可知,一天中到该公园锻炼的人次的平均数为100203003550045350100⨯+⨯+⨯=.(3)根据表格中的数据完善22⨯列联表,计算出2K 的观测值,再结合临界值表可得结()21003383722 5.820 3.84155457030K ⨯⨯-⨯=⨯⨯⨯≈>,因此,有95%的把握认为一天中到该公园锻炼的人次与该市 当天的空气质量有关.【考点】利用频数分布表计算频率和平均数,独立性检验的应用19.【答案】(1)因为长方体1111ABCD A B C D -,所以1BB ABCD ⊥平面,1AC BB ∴⊥,因为长方体1111ABCD A B C D -,AB BC =,所以四边形ABCD 为正方形,AC BD ∴⊥.因为1BB BD B =,111BB BD BB D D ⊂、平面,因此11AC BB D D ⊥平面,因为11EF BB D D ⊂平面,所以AC EF ⊥.(2)在1CC 上取点M 使得12CM MC =,连DM ,MF ,因为12D E ED =,11DD CC ∥,11DD CC =,所以1ED MC =,1ED MC ∥,所以四边形1DMC E 为平行四边形,1DM EC ∴∥.因为MF DA ∥,MF DA =,所以四边形MFAD 为平行四边形,DM AF ∴∥,1EC AF ∴∥,因此1C 在平面AEF 内. 【解析】(1)根据正方形性质得AC BD ⊥,根据长方体性质得1AC BB ⊥,进而可证数学试卷 第15页(共20页) 数学试卷 第16页(共20页)11AC BB D D ⊥平面,即得结果.因为长方体1111ABCD A B C D -,所以1BB ABCD ⊥平面,1AC BB ∴⊥,因为长方体1111ABCD A B C D -,AB BC =,所以四边形ABCD 为正方形,AC BD ∴⊥.因为1BB BD B =,111BB BD BB D D ⊂、平面,因此11AC BB D D ⊥平面,因为11EF BB D D ⊂平面,所以AC EF ⊥.(2)只需证明1EC AF ∥即可,在1CC 上取点M 使得12CM MC =,再通过平行四边形性质进行证明即可.在1CC 上取点M 使得12CM MC =,连DM ,MF ,因为12D E ED =,11DD CC ∥,11DD CC =,所以1ED MC =,1ED MC ∥,所以四边形1DMC E 为平行四边形,1DM EC ∴∥.因为MF DA ∥,MF DA =,所以四边形MFAD 为平行四边形,DM AF ∴∥,1EC AF ∴∥,因此1C 在平面AEF 内.【考点】线面垂直判定定理,线线平行判定20.【答案】(1)由题,()23f x x k '=-,当0k ≤时,()0f x '≥恒成立,所以()f x 在()-∞+∞,上单调递 增;当0k >时,令()0f x '=,得x =,令()0f x '<,得x ,令()0f x '>,得x -<x 所以()f x在⎛上单调递减,在⎛-∞ ,,⎫+∞⎪⎪上单调递增. 【解析】(1)()23f x x k '=-,对k 分0k ≤和0k >两种情况讨论即可.由题,()23f x x k '=-,当0k ≤时,()0f x '≥恒成立,所以()f x 在()-∞+∞,上单调递增;当0k >时,令()0f x '=,得x =,令()0f x'<, 得x ,令()0f x '>,得x -<x ()f x在⎛ ⎝上单调递减,在⎛-∞⎝,⎫+∞⎪⎪⎭上单调递增. (2)()f x 有三个零点,由(1)知0k >,且00ff ⎧⎛⎪ ⎪⎝⎨⎪⎪⎩><,解不等式组得到k 的范围,再利用零点存在性定理加以说明即可.由(1)知,()f x 有三个零点,则0k >,且00f f ⎧⎛⎪ ⎪⎝⎨⎪⎪⎩><,即22203203k k ⎧+⎪⎪⎨⎪-⎪⎩,解 得4027k <<,当4027k <<且20fk =>,所以()f x 在上有唯一一个零 点,同理1k --<()()23110f k k k --=--+<,所以()f x 在1k ⎛--⎝,上有唯一一个零点,又()f x 在⎛ ⎝上有唯一一个零点,所以()f x 有三个零点,综上可知k 的取值范数学试卷 第17页(共20页) 数学试卷 第18页(共20页)围为4027⎛⎫ ⎪⎝⎭,.【解析】(1)因为()2:10525x yC m m+=<<,可得5a =,b m =,根据离心率公式,结合已知,即可求得答案.()222:10525x y C m+=<<,5a ∴=,b m =,根据离心率c e a ====解得54m =或54m =-(舍),C ∴的方程为:22214255x y ⎛⎫ ⎪⎝⎭+=,即221612525x y +=. (2)点P 在C 上,点Q 在直线6x =上,且BP BQ =,BP BQ ⊥,过点P 作x 轴垂线,交点为M ,设6x =与x 轴交点为N ,可得PMB BNQ ≅△△,可求得P 点坐标,求出直线AQ 的直线方程,根据点到直线距离公式和两点距离公式,即可求得APQ △的面积.点P 在C 上,点Q 在直线6x =上,且BP BQ =,BP BQ ⊥,过点P 作x 轴垂线,交点为M ,设6x =与x 轴交点为N .根据题意画出图形,如图BP BQ =,BP BQ ⊥,90PMB QNB ∠=∠=,又90PBM QBN ∠+∠=,90BQN QBN ∠+∠=,PBM BQN ∴∠=∠,根据三角形全等条件“AAS ”,可得:PMB BNQ ≅△△,221612525x y +=, ()50B ∴,,651PM BN ∴==-=,设P 点为()P P x y ,,可得P 点纵坐标为1P y =,将其代入221612525x y +=,可得:21612525P x +=,解得:3P x =或3P x =-,P ∴点为()31,或()31-,, ①当P 点为()31,时,故532MB =-=,PMB BNQ ≅△△,2MB NQ ∴==,可得:Q 点为()62,,画 出图象,如图()50A -,,()62Q ,,可求得直线AQ 的直线方程为:211100xy -+=,根据点到直线距离公式可得P 到 直线AQ 的距离为:d ===,根据两点间距离公式可得:AQ =APQ ∴△面积为:15252⨯=;②当P 点为()31-,时,故5+38MB ==,PMB BNQ ≅△△,8MB NQ ∴==,可得:Q 点为()68,, 画出图象,如图()50A -,,()68Q ,,可求得直线AQ 的直线方程为:811400x y -+=,根据点到直线距离公式可得P数学试卷 第19页(共20页) 数学试卷 第20页(共20页)到直线AQ 的距离为:d ===根据两点间距离公式可得:AQ ==APQ ∴△面积为:1522=,综上所述,APQ △面积为:52.【考点】椭圆标准方程,三角形面积,椭圆的离心率定义,数形结合求三角形面积【解析】(1)由参数方程得出A ,B 的坐标,最后由两点间距离公式,即可得出AB 的值.令0x =,则220t t +-=,解得2t =-或1t =(舍),则26412y =++=,即()012A ,.令0y =,则2320t t -+=,解得2t =或1t =(舍),则2244x =--=-,即()40B -,.AB ∴=(2)由A ,B 的坐标得出直线AB 的直角坐标方程,再化为极坐标方程即可.由(1)可知()120304AB k -==--, 则直线AB 的方程为()34y x =+,即3120x y -+=.由cos x ρθ=,sin y ρθ=可得,直线AB 的极坐标方程 为3cos sin 120ρθρθ-+=.【考点】利用参数方程求点的坐标,直角坐标方程化极坐标方程 23.【答案】(1)()22222220a b c a b c ab ac bc ++=+++++=,()22212ab bc ca a b c ∴++=-++. a ,b ,c 均不为0,则2220a b c ++>,()222120ab bc ca a b c ∴++=-++<. (2)不妨设{}max a b c a =,,,由0a b c ++=,1abc =可知,0a >,0b <,0c <.a b c =--,1a bc=,()222322224b c b c bc bc bc a a a bc bc bc ++++∴=⋅===≥.当且仅当b c =时,取等号,a ∴{}3max 4a b c ,,.【解析】(1)由()22222220a b c a b c ab ac bc ++=+++++=结合不等式的性质,即可得出证明.()22222220a b c a b c ab ac bc ++=+++++=,()22212ab bc ca a b c ∴++=-++.a ,b ,c 均不为0,则2220a b c ++>,()222120ab bc ca a b c ∴++=-++<. (2)不妨设{}max a b c a =,,,由题意得出0a >,0b c ,<,由()222322b c b c bca aa bcbc+++=⋅==,结合基本不等式,即可得出证明.不妨设{}max a b c a =,,,由0a b c ++=,1abc =可知,0a >,0b <,0c <,a b c =--,1a bc=,()222322224b c b c bc bc bca a a bcbcbc++++∴=⋅===≥.当且仅当b c =时,取等号,a ∴{}3max 4a b c ,,.【考点】不等式的基本性质,基本不等式的应用。
2020年高考理科数学全国卷(全国ⅠⅡ Ⅲ卷)共三套试卷试题真题及答案

设an 是公比不为 1 的等比数列, a1为 a2 , a3 的等差中项. (1)求 an 的公比; (2)若 a1 1 ,求数列 nan 的前 n 项和.
18.(12 分) 如图, D 为圆锥的顶点, O 是圆锥底面的圆心, AE 为底面直径,
AE AD . △ABC 是 底 面 的 内 接 正 三 角 形 , P 为 DO 上 一 点 , PO 6 DO .
D. a<2
二、填空题:本题共 4 小题,每小题 5 分,共 20 分.
2x y 2≤0,
13.若
x
,
y
满足约束条件
x
y
1≥0,
则
z
x
7
y
的最大值为
.
y 1≥0,
14.设 a , b 为单位向量,且 a b 1,则 a b
.
15.已知 F
为双曲线
C
:
x2 a2
y2 b2
1a>0,b>0 的右焦点, A 为 C 的右顶点, B 为 C
6 (1)证明: PA 平面PBC ; (2)求二面角 B PC E 的余弦值.
19.(12 分) 甲、乙、丙三位同学进行羽毛球比赛,约定赛制如下: 累计负两场者被淘汰;比赛前抽签决定首先比赛的两人,另一人轮空;每场比赛的胜者与轮空者
进行下一场比赛,负者下一轮轮空,直至有一人被淘汰;当一人被淘汰后,剩余的两人继续比赛,直 至其中一人被淘汰,另一人最终获胜,比赛结束.
3.非选择题的作答:用黑色签字笔直接答在答题卡上对应的答题区域内。写在试卷,草稿纸和答
上
题卡上的非答题区域均无效。
4.选考题的作答:先把所选题目的题号在答题卡上指定的位置用 2B 铅笔涂黑。答案写在答题卡 上对应的答题区域内,写在试卷,草稿纸和答题卡上的非答题区域均无效。
2020届高考全国卷24省9月联考甲卷--数学(理)试卷(附答案)

以
ck+1 ck
=bbnn+2
=
9,所以数列{cn}是公比和首项均为 9的等比数列,即 Hn=9(9n8-1)=9n8+1 - 9 8.
17.【名师指导】本题考查线面垂直的判定定理和二面角 .
(Ⅰ)利用勾股定理得到 OA1⊥ OB,再利用面面垂直
判定定理即可证明;(Ⅱ)以 O为坐标原点,OB,OC,
有 72+36=108种购买方式,故选 D. 10.A 【解析】本题考查存在性问题 .由题意知 aea =m,
-b2
+kb-
2 e
=m,令
f(a)=aea,g(b)= -b2 +
kb- 2e,即存在实数 a,b,m,使得 f(a)=g(b)=m,
— 数学(理科)·答 1—
因为 f′(a)=(a+1)ea,所以 f(a)在(-∞,-1)上
6.B 【解析】本题考查函数的奇偶性及函数单调性.由题意
可知 f(x)为奇函数,因为对任意 x1,x2∈[0,+∞)时, 均有 g(x1x)1--g x2(x2)>0,可知函数 g(x)在[0,+∞)上 单调递增,所以 f(x)在 R上单调递增,又因为 g(1)=
2,所以 f(1)=2,f(-1)= -2,由 |f(m)|>2,可 得
左平移43π个单位长度,则 g(x)=-槡3cosx-槡23,D满 足条件;若 f(x)的图象向右平移 56π个单 位 长 度,则
( ) g(x)=槡3sin x-23π -槡23,不满足条件;若 f(x)的图
象向左平移56π个单位长度,则 g(x)=-槡3sinx-槡23,
不满足条件,C不满足条件,故选 C.
(Ⅰ)利用图表 1,2即可求解;(Ⅱ)根据条件列出甲的
月收入的可能取值,并计算符合要求的概率 .
2020年高考理科数学全国卷3(附答案与解析)

2020年普通高等学校招生全国统一考试·全国Ⅲ卷理科数学答案解析一、选择题 1.【答案】C【解析】采用列举法列举出A B 中元素的即可.由题意,A B 中的元素满足8y x x y ⎧⎨+=⎩≥,且x ,*y ∈N ,由82x y x +=≥,得4x ≤,所以满足8x y +=的有()17,,()26,,()35,,()44,,故A B 中元素的个数为4.故选:C .【考点】集合的交集运算,交集定义的理解 2.【答案】D【解析】利用复数的除法运算求出z 即可.因为()()113131313131010i z i i i i +===+--+,所以复数113z i=-的虚部为310.故选:D . 【考点】复数的除法运算,复数的虚部的定义 3.【答案】B【解析】计算出四个选项中对应数据的平均数和方差,由此可得出标准差最大的一组. 对于A 选项,该组数据的平均数为()()140.1230.4 2.5A x =+⨯++⨯=,方差为()()()()222221 2.50.12 2.50.43 2.50.44 2.50.10.65A s =-⨯+-⨯+-⨯+-⨯=;对于B 选项,该组数据的平均数为()()140.4230.1 2.5B x =+⨯++⨯=,方差为()()()()222221 2.50.42 2.50.13 2.50.14 2.50.4 1.85B s =-⨯+-⨯+-⨯+-⨯=;对于C 选项,该组数据的平均数为()()140.2230.3 2.5C x =+⨯++⨯=,方差为()()()()222221 2.50.22 2.50.33 2.50.34 2.50.2 1.05C s =-⨯+-⨯+-⨯+-⨯=;对于D 选项,该组数据的平均数为()()140.3230.2 2.5D x =+⨯++⨯=,方差为()()()()222221 2.50.32 2.50.23 2.50.24 2.50.3 1.45D s =-⨯+-⨯+-⨯+-⨯=.因此,B 选项这一组的标准差最大.故选:B . 【考点】标准差的大小比较,方差公式的应用 4.【答案】C【解析】将t t *=代入函数()()0.23531t K I t e --=+结合()0.95I t K *=求得t *即可得解.()()0.23531t K I t e --=+,所以()()0.23530.951t KI t K e**--==+,则()*0.235319t e -=,所以,()0.2353ln193t *-=≈,解得353660.23t *+≈≈.故选:C .【考点】对数的运算,指数与对数的互化 5.【答案】B【解析】根据题中所给的条件OD OE ⊥,结合抛物线的对称性,可知4DOx EOx π∠=∠=,从而可以确定出点D 的坐标,代入方程求得p 的值,进而求得其焦点坐标,得到结果.因为直线2x =与抛物线()220y px p =>交于E ,D 两点,且OD OE ⊥,根据抛物线的对称性可以确定4DOx EOx π∠=∠=,所以()22D ,,代入抛物线方程44p =,求得1p =,所以其焦点坐标为102⎛⎫⎪⎝⎭,,故选:B .【考点】圆锥曲线,直线与抛物线的交点,抛物线的对称性,点在抛物线上的条件,抛物线的焦点坐标 6.【答案】D【解析】计算出()a ab ⋅+、a b +的值,利用平面向量数量积可计算出cos a a b +,的值.5a =,6b =,6a b ⋅=-,()225619a a b a a b ∴⋅+=+⋅=-=.()2222257a b a ba ab b +=+=+⋅+=-,因此,()1919cos 5735a a ba ab a a b⋅++===⨯⋅+,.故选:D . 【考点】平面向量夹角余弦值的计算,平面向量数量积的计算,向量模的计算 7.【答案】A【解析】根据已知条件结合余弦定理求得AB ,再根据222cos 2AB BC AC B AB BC+-=⋅,即可求得答案.在ABC △中,2cos 3C =,4AC =,3BC =.根据余弦定理:2222cos AB AC BC AC BC C =+-⋅⋅,2224322433AB =+-⨯⨯⨯,可得29AB =,即3AB =.由22299161cos 22339AB BC AC B AB BC +-+-===⋅⨯⨯,故1cos 9B =.故选:A . 【考点】余弦定理解三角形8.【答案】C【解析】根据三视图特征,在正方体中截取出符合题意的立体图形,求出每个面的面积,即可求得其表面积.根据三视图特征,在正方体中截取出符合题意的立体图形根据立体图形可得:12222ABC ADC CDB S S S ===⨯⨯=△△△,根据勾股定理可得:AB AD DB ===ADB ∴△是边长为,根据三角形面积公式可得:(211sin 6022ADBS AB AD =⋅⋅==△∴该几何体的表面积是:632=⨯++ 故选:C .【考点】根据三视图求立体图形的表面积,根据三视图画出立体图形 9.【答案】D【解析】利用两角和的正切公式,结合换元法,解一元二次方程,即可得出答案.2tan tan 74πθθ⎛⎫-+= ⎪⎝⎭,tan 12tan 71tan θθθ+∴-=-,令tan t θ=,1t ≠,则1271tt t+-=-,整理得2440t t -+=,解得2t =,即tan 2θ=.故选:D .【考点】利用两角和的正切公式化简求值 10.【答案】D【解析】根据导数的几何意义设出直线l 的方程,再由直线与圆相切的性质,即可得出答案.设直线l 在曲线y =(0x,则00x >,函数y导数为y '=,则直线l 的斜率k =,设直线l 的方程为)0y x x =-,即00xx -+=,由于直线l 与圆2215x y +=相切,则=,两边平方并整理得2005410x x --=,解得01x=,015x =-(舍),则直线l 的方程为210x y -+=,即1122y x =+.故选:D .【考点】导数的几何意义的应用,直线与圆的位置的应用 11.【答案】A【解析】根据双曲线的定义,三角形面积公式,勾股定理,结合离心率公式,即可得出答案.5ca=,c ∴,根据双曲线的定义可得122PF PF a -=,1212142PF F PF S PF =⋅=△,即128PF PF ⋅=, 12F P F P ⊥,()222122PF PF c ∴+=,()22121224PF PF PF PF c ∴-+⋅=,即22540a a -+=,解得1a =,故选:A .【考点】双曲线的性质以及定义的应用,勾股定理,三角形面积公式的应用 12.【答案】A【解析】由题意可得a 、b 、()01c ∈,,利用作商法以及基本不等式可得出a 、b 的大小关系,由8log 5b =,得85b =,结合5458<可得出45b <,由13log 8c =,得138c =,结合45138<,可得出45c >,综合可得出a 、b 、c 的大小关系.由题意可知a 、b 、()01c ∈,, ()222528log 3lg3lg81lg3lg8lg3lg8lg 241log 5lg5lg522lg5lg 25lg5a b ⎛⎫⎛⎫++⎛⎫==⋅⋅==⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭<<,a b ∴<;由8log 5b =,得85b =,由5458<,得5488b <,54b ∴<,可得45b <;由13log 8c =,得138c =,由45138<,得451313c <,54c ∴>,可得45c >.综上所述,a b c <<.故选:A .【考点】对数式的大小比较,基本不等式、对数式与指数式的互化,指数函数单调性的应用 二、填空题 13.【答案】7【解析】作出可行域,利用截距的几何意义解决.不等式组所表示的可行域如图.因为32z x y =+,所以322x z y =-+,易知截距2z 越大,则z 越大,平移直线32x y =-,当322x zy =-+经过A 点时截距最大,此时z 最大,由21y x x =⎧⎨=⎩,得12x y =⎧⎨=⎩,()12A ,,所以max 31227z =⨯+⨯=.故答案为:7.【考点】简单线性规划的应用,求线性目标函数的最大值 14.【答案】240【解析】写出622x x ⎛⎫+ ⎪⎝⎭二项式展开通项,即可求得常数项.622x x ⎛⎫+ ⎪⎝⎭其二项式展开通项:()()()621221236661222rrr r r r r r r r r C xC x C x x T x ---+-⎛⎫⋅⋅⋅⋅=⋅⎭= ⎝=⎪,当1230r -=,解得4r =,622x x ⎛⎫∴+ ⎪⎝⎭的展开式中常数项是:664422161516240C C ⋅=⋅=⨯=.故答案为:240.【考点】二项式定理,利用通项公式求二项展开式中的指定项15. 【解析】与球有关的组合体问题,一种是内切,一种是外接.解题时要认真分析图形,明确切点和接点的位置,确定有关元素间的数量关系,并作出合适的截面图,如球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径;球外接于正方体,正方体的顶点均在球面上,正方体的体对角线长等于球的直径.将原问题转化为求解圆锥内切球的问题,然后结合截面确定其半径即可确定体积的值.易知半径最大球为圆锥的内切球,球与圆锥内切时的轴截面如图所示,其中2BC =,3AB AC ==,且点M 为BC 边上的中点,设内切圆的圆心为O ,由于AM ==122S =⨯⨯=△ABC r ,则:()11113322222ABC AOB BOC AOC S S S S AB r BC r AC r r =++=⨯⨯+⨯⨯+⨯⨯=⨯++⨯=△△△△r,其体积:343V r π=.. 16.【答案】②③【解析】利用特殊值法可判断命题①的正误;利用函数奇偶性的定义可判断命题②的正误;利用对称性的定义可判断命题③的正误;取0x π-<<可判断命题④的正误.综合可得出结论.对于命题①,152622f π⎛⎫=+= ⎪⎝⎭,152622fπ⎛⎫-=--=- ⎪⎝⎭,则66f f ππ⎛⎫⎛⎫-≠ ⎪ ⎪⎝⎭⎝⎭,所以,函数()f x 的图象不关于y 轴对称,命题①错误;对于命题②,函数()f x 的定义域为{}x x k k π≠∈Z ,,定义域关于原点对称,()()()()111sin sin sin sin sin sin f x x x x f x x x x ⎛⎫-=-+=--=-+=- ⎪-⎝⎭,所以,函数()f x 的图象关于原点对称,命题②正确;对于命题③,11sin cos 22cos sin 2f x x x x x πππ⎛⎫⎛⎫-=-+=+⎪ ⎪⎛⎫⎝⎭⎝⎭- ⎪⎝⎭, 11sin cos 22cos sin 2f x x x x x πππ⎛⎫⎛⎫+=++=+⎪ ⎪⎛⎫⎝⎭⎝⎭+ ⎪⎝⎭,则22f x f x ππ⎛⎫⎛⎫-=+ ⎪ ⎪⎝⎭⎝⎭,所以,函数()f x 的图象关于直线2x π=对称,命题③正确;对于命题④,当0x π-<<时,sin 0x <,()1sin 02sin f x x x=+<<,命题④错误.故答案为:②③.【考点】正弦型函数的奇偶性、对称性,最值的求解 三、解答题17.【答案】(1)25a =,37a =,21n a n =+,当1n =时,13a =成立;假设n k =时,21k a k =+成立.那么1n k =+时,()()134321423211k k a a k k k k k +=-=+-=+=++也成立.则对任意的*n ∈N ,都有21n a n =+成立.(2)()12122n n S n +=-⋅+【解析】(1)利用递推公式得出2a ,3a ,猜想得出{}n a 的通项公式,利用数学归纳法证明即可.由题意可得2134945a a =-=-=,32381587a a =-=-=,由数列{}n a 的前三项可猜想数列{}n a 是以3为首项,2为公差的等差数列,即21n a n =+,证明如下:当1n =时,13a =成立;假设n k =时,21k a k =+成立.那么1n k =+时,()()134321423211k k a a k k k k k +=-=+-=+=++也成立.则对任意的*n ∈N ,都有21n a n =+成立;(2)由错位相减法求解即可.由(1)可知,()2212n nn a n ⋅=+⋅,()()231325272212212n n n S n n -=⨯+⨯+⨯++-⋅++⋅,①()()23412325272212212n n n S n n +=⨯+⨯+⨯++-⋅++⋅,②,由-①②得:()()()()()21231112126222221262212122212n n n n n n S n n n -+++--=+⨯+++-+⋅=+⨯-+⋅=⋅⨯---,即()12122n n S n +=-⋅+.【考点】求等差数列的通项公式,利用错位相减法求数列的和18.【答案】(1)该市一天的空气质量等级分别为1、2、3、4的概率分别为0.43、0.27、0.21、0.09 (2)350(3()221003383722 5.820 3.84155457030K ⨯⨯-⨯=⨯⨯⨯≈>,因此,有95%的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关.【解析】(1)根据频数分布表可计算出该市一天的空气质量等级分别为1、2、3、4的概率.由频数分布表可知,该市一天的空气质量等级为1的概率为216250.43100++=,等级为2的概率为510120.27100++=,等级为3的概率为6780.21100++=,等级为4的概率为7200.09100++=. (2)利用每组的中点值乘以频数,相加后除以100可得结果.由频数分布表可知,一天中到该公园锻炼的人次的平均数为100203003550045350100⨯+⨯+⨯=.(3)根据表格中的数据完善22⨯列联表,计算出2K 的观测值,再结合临界值表可得结论.22⨯列联表如下:()221003383722 5.820 3.84155457030K ⨯⨯-⨯=⨯⨯⨯≈>,因此,有95%的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关.【考点】利用频数分布表计算频率和平均数,独立性检验的应用19.【答案】(1)在棱1CC 上取点G ,使得112C G CG =,连接DG 、FG 、1C E 、1C F ,长方体1111ABCD A B C D -中,AD BC ∥且AD BC =,11BB CC ∥且11BB CC =,112C G CG=12BF FB =,112233CG CC BB BF ∴===且CG BF =,所以,四边形BCGF 平行四边形,则AF DG∥且AF DG =,同理可证四边形1DEC G 为平行四边形,1C E DG ∴∥且1C E DG =,1C E AF ∴∥且1C E AF =,则四边形1AEC F 为平行四边形,因此,点1C 在平面AEF 内.(2)7【解析】(1)连接1C E 、1C F ,证明出四边形1AEC F 为平行四边形,进而可证得点1C 在平面AEF 内.在棱1CC 上取点G ,使得112C G CG =,连接DG 、FG 、1C E 、1C F ,长方体1111ABCD A B C D -中,AD BC ∥且AD BC =,11BB CC ∥且11BB CC =,112C G CG=12BF FB =,112233CG CC BB BF ∴===且CG BF =,所以,四边形BCGF 平行四边形,则AF DG∥且AF DG =,同理可证四边形1DEC G 为平行四边形,1C E DG ∴∥且1C E DG =,1C E AF ∴∥且1C E AF =,则四边形1AEC F 为平行四边形,因此,点1C 在平面AEF 内;(2)以点1C 为坐标原点,11C D 、11C B 、1C C 所在直线分别为x 、y 、z 轴建立空间直角坐标系1C xyz -,利用空间向量法可计算出二面角1A EF A --的余弦值,进而可求得二面角1A EF A --的正弦值.以点1C 为坐标原点,11C D 、11C B 、1C C 所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系1C xyz -,则()213A ,,、()1210A ,,、()202E ,,、()011F ,,,()011AE =--,,,()202AF =--,,,()1012A E =-,,,()1201A F =-,,,设平面AEF 的法向量为()111m x y z =,,,由00m AE m AF ⎧⋅⎪⎨⋅=⎪⎩=,得11110220y z x z --=⎧⎨--=⎩取11z =-,得111x y ==,则()111m =-,,,设平面1A EF 的法向量为()222n x y z =,,,由1100n A E n A F ⎧⋅=⎪⎨⋅=⎪⎩,得22222020y z x z -+=⎧⎨-+=⎩,取22z =,得21x =,24y =,则()142n =,,,3cos 3m n m n m n⋅===⨯⋅,,设二面角1A EF A--的平面角为θ,则cos θ=,sinθ∴==.因此,二面角1A EF A --.【考点】点在平面的证明,利用空间向量法求解二面角20.【答案】(1)221612525x y +=(2)52【解析】(1)因为()222:10525x y C m m+=<<,可得5a =,b m =,根据离心率公式,结合已知,即可求得答案.()222:10525x y C m m +=<<,5a∴=,b m =,根据离心率4c e a ====, 解得54m =或54m =-(舍),C ∴的方程为:22214255x y ⎛⎫ ⎪⎝⎭+=,即221612525x y +=. (2)点P 在C 上,点Q 在直线6x =上,且BP BQ =,BP BQ ⊥,过点P 作x 轴垂线,交点为M ,设6x =与x 轴交点为N ,可得PMB BNQ ≅△△,可求得P 点坐标,求出直线AQ 的直线方程,根据点到直线距离公式和两点距离公式,即可求得APQ △的面积.点P 在C 上,点Q 在直线6x =上,且BP BQ =,BP BQ ⊥,过点P 作x 轴垂线,交点为M ,设6x =与x 轴交点为N .根据题意画出图形,如图BP BQ =,BP BQ ⊥,90PMB QNB ∠=∠=,又90PBM QBN ∠+∠=,90BQN QBN ∠+∠=,PBM BQN ∴∠=∠,根据三角形全等条件“AAS ”,可得:PMB BNQ ≅△△,221612525x y +=, ()50B ∴,,651PM BN ∴==-=,设P 点为()P P x y ,,可得P 点纵坐标为1P y =,将其代入221612525x y +=,可得:21612525P x +=,解得:3P x =或3P x =-,P ∴点为()31,或()31-,, ①当P 点为()31,时,故532MB =-=,PMB BNQ ≅△△,2MB NQ ∴==,可得:Q 点为()62,,画 出图象,如图()50A -,,()62Q ,,可求得直线AQ 的直线方程为:211100x y -+=,根据点到直线距离公式可得P 到直线AQ 的距离为:d ===,根据两点间距离公式可得:AQ =,APQ ∴△面积为:1522⨯=;②当P 点为()31-,时,故5+38MB ==,PMB BNQ ≅△△,8MB NQ ∴==,可得:Q 点为()68,,画出图象,如图()50A -,,()68Q ,,可求得直线AQ 的直线方程为:811400x y -+=,根据点到直线距离公式可得P到直线AQ 的距离为:d ===AQ ==APQ ∴△面积为:1522=,综上所述,APQ △面积为:52. 【考点】椭圆标准方程,三角形面积,椭圆的离心率定义,数形结合求三角形面积 21.【答案】(1)34b =-(2)由(1)可得()334f x x x c =-+,()231133422f x x x x ⎛⎫⎛⎫'=-=+- ⎪⎪⎝⎭⎝⎭,令()0f x '>,得12x >或12x -<;令()0f x '<,得1122x -<<,所以()f x 在1122⎛⎫- ⎪⎝⎭,上单调递减,在12⎛⎫-∞- ⎪⎝⎭,,12⎛⎫+∞ ⎪⎝⎭,上单调递增,且()114f c -=-,1124f c ⎛⎫-=+ ⎪⎝⎭,1124f c ⎛⎫=- ⎪⎝⎭,()114f c =+,若()f x 所有零点中存在一个绝对值大于1的零点0x ,则()10f ->或()10f <,即14c >或14c -<.当14c >时,()1104f c -=->,11024f c ⎛⎫-=+ ⎪⎝⎭>,11024f c ⎛⎫=- ⎪⎝⎭>,()1104f c =+>,又()()32464341160f c c c c c c -=-++=-<,由零点存在性定理知()f x 在()41c --,上存在唯一一个零点0x ,即()f x 在()1-∞-,上存在唯一一个零点,在()1-+∞,上不存在零点,此时()f x 不存在绝对值不大于1的零点,与题设矛盾;当14c -<时,()1104f c -=-<,11024f c ⎛⎫-=+ ⎪⎝⎭<,11024f c ⎛⎫=- ⎪⎝⎭<,()1104f c =+<,又()()32464341160f c c c c c c -=++=->,由零点存在性定理知()f x 在()14c -,上存在唯一一个零点0x ',即()f x 在()1+∞,上存在唯一一个零点,在()1-∞,上不存在零点,此时()f x 不存在绝对值不大于1的零点,与题设矛盾;综上,()f x 所有零点的绝对值都不大于1.【解析】(1)利用导数的几何意义得到102f ⎛⎫'= ⎪⎝⎭,解方程即可.因为()23f x x b '=+,由题意,102f ⎛⎫'= ⎪⎝⎭,即21302b ⎛⎫⨯+= ⎪⎝⎭,则34b =-; (2)由(1)可得()231132422f x x x x ⎛⎫⎛⎫'=-=+- ⎪⎪⎝⎭⎝⎭,易知()f x 在1122⎛⎫- ⎪⎝⎭,上单调递减,在12⎛⎫-∞- ⎪⎝⎭,,12⎛⎫+∞ ⎪⎝⎭,上单调递增,且()114f c -=-,1124f c ⎛⎫-=+ ⎪⎝⎭,1124f c ⎛⎫=- ⎪⎝⎭,()114f c =+,采用反证法,推出矛盾即可.由(1)可得()334f x x x c =-+,()231133422f x x x x ⎛⎫⎛⎫'=-=+- ⎪⎪⎝⎭⎝⎭,令()0f x '>,得12x >或12x -<;令()0f x '<,得1122x -<<,所以()f x 在1122⎛⎫- ⎪⎝⎭,上单调递减,在12⎛⎫-∞- ⎪⎝⎭,,12⎛⎫+∞ ⎪⎝⎭,上单调递增,且()114f c -=-,1124f c ⎛⎫-=+ ⎪⎝⎭,1124f c ⎛⎫=- ⎪⎝⎭,()114f c =+,若()f x 所有零点中存在一个绝对值大于1的零点0x ,则()10f ->或()10f <,即14c >或14c -<.当14c >时,()1104f c -=->,11024f c ⎛⎫-=+ ⎪⎝⎭>,11024f c ⎛⎫=- ⎪⎝⎭>,()1104f c =+>,又()()32464341160f c c c c c c -=-++=-<,由零点存在性定理知()f x 在()41c --,上存在唯一一个零点0x ,即()f x 在()1-∞-,上存在唯一一个零点,在()1-+∞,上不存在零点,此时()f x 不存在绝对值不大于1的零点,与题设矛盾;当14c -<时,()1104f c -=-<,11024f c ⎛⎫-=+ ⎪⎝⎭<,11024f c ⎛⎫=- ⎪⎝⎭<,()1104f c =+<,又()()32464341160f c c c c c c -=++=->,由零点存在性定理知()f x 在()14c -,上存在唯一一个零点0x ',即()f x 在()1+∞,上存在唯一一个零点,在()1-∞,上不存在零点,此时()f x 不存在绝对值不大于1的零点,与题设矛盾;综上,()f x 所有零点的绝对值都不大于1. 【考点】利用导数研究函数的零点,导数的几何意义,反证法22.【答案】(1)(2)3cos sin 120ρθρθ-+=【解析】(1)由参数方程得出A ,B 的坐标,最后由两点间距离公式,即可得出AB 的值.令0x =,则220t t +-=,解得2t =-或1t =(舍),则26412y =++=,即()012A ,.令0y =,则2320t t -+=,解得2t =或1t =(舍),则2244x =--=-,即()40B -,.AB ∴=(2)由A ,B 的坐标得出直线AB 的直角坐标方程,再化为极坐标方程即可.由(1)可知()120304AB k -==--,则直线AB 的方程为()34y x =+,即3120x y -+=.由cos x ρθ=,sin y ρθ=可得,直线AB 的极坐标方程为3cos sin 120ρθρθ-+=.【考点】利用参数方程求点的坐标,直角坐标方程化极坐标方程 23.【答案】(1)()22222220a b c a b c ab ac bc ++=+++++=,()22212ab bc ca a b c ∴++=-++. a ,b ,c 均不为0,则2220a b c ++>,()222120ab bc ca a b c ∴++=-++<. (2)不妨设{}max a b c a =,,,由0a b c ++=,1abc =可知,0a >,0b <,0c <,a b c =--,1a bc=,()222322224b c b c bc bc bc a a a bc bc bc ++++∴=⋅===≥.当且仅当b c =时,取等号,a ∴ {}3max 4a b c ,,.【解析】(1)由()22222220a b c a b c ab ac bc ++=+++++=结合不等式的性质,即可得出证明.()22222220a b c a b c ab ac bc ++=+++++=,()22212ab bc ca a b c ∴++=-++.a ,b ,c 均不为0,则2220a b c ++>,()222120ab bc ca a b c ∴++=-++<. (2)不妨设{}max a b c a =,,,由题意得出0a >,b ,0c <,由()222322b c b c bca aa bcbc+++=⋅==,结合基本不等式,即可得出证明.不妨设{}max a b c a =,,,由0a b c ++=,1abc =可知,0a >,0b <,0c <,a b c =--,1a bc=,()222322224b c b c bc bc bc a a a bc bc bc ++++∴=⋅===≥.当且仅当b c =时,取等号,a ∴{}3max 4a b c ,,.【考点】不等式的基本性质,基本不等式的应用2020年普通高等学校招生全国统一考试·全国Ⅲ卷理科数学答案解析一、选择题 1.【答案】C【解析】采用列举法列举出A B 中元素的即可.由题意,A B 中的元素满足8y x x y ⎧⎨+=⎩≥,且x ,*y ∈N ,由82x y x +=≥,得4x ≤,所以满足8x y +=的有()17,,()26,,()35,,()44,,故A B 中元素的个数为4.故选:C .【考点】集合的交集运算,交集定义的理解 2.【答案】D【解析】利用复数的除法运算求出z 即可.因为()()113131313131010i z i i i i +===+--+,所以复数113z i=-的虚部为310.故选:D . 【考点】复数的除法运算,复数的虚部的定义 3.【答案】B【解析】计算出四个选项中对应数据的平均数和方差,由此可得出标准差最大的一组. 对于A 选项,该组数据的平均数为()()140.1230.4 2.5A x =+⨯++⨯=,方差为()()()()222221 2.50.12 2.50.43 2.50.44 2.50.10.65A s =-⨯+-⨯+-⨯+-⨯=;对于B 选项,该组数据的平均数为()()140.4230.1 2.5B x =+⨯++⨯=,方差为()()()()222221 2.50.42 2.50.13 2.50.14 2.50.4 1.85B s =-⨯+-⨯+-⨯+-⨯=;对于C 选项,该组数据的平均数为()()140.2230.3 2.5C x =+⨯++⨯=,方差为()()()()222221 2.50.22 2.50.33 2.50.34 2.50.2 1.05C s =-⨯+-⨯+-⨯+-⨯=;对于D 选项,该组数据的平均数为()()140.3230.2 2.5D x =+⨯++⨯=,方差为()()()()222221 2.50.32 2.50.23 2.50.24 2.50.3 1.45D s =-⨯+-⨯+-⨯+-⨯=.因此,B 选项这一组的标准差最大.故选:B . 【考点】标准差的大小比较,方差公式的应用 4.【答案】C【解析】将t t *=代入函数()()0.23531t K I t e --=+结合()0.95I t K *=求得t *即可得解.()()0.23531t K I t e --=+,所以()()0.23530.951t KI t K e**--==+,则()*0.235319t e -=,所以,()0.2353ln193t *-=≈,解得353660.23t *+≈≈.故选:C .【考点】对数的运算,指数与对数的互化 5.【答案】B【解析】根据题中所给的条件OD OE ⊥,结合抛物线的对称性,可知4DOx EOx π∠=∠=,从而可以确定出点D 的坐标,代入方程求得p 的值,进而求得其焦点坐标,得到结果.因为直线2x =与抛物线()220y px p =>交于E ,D 两点,且OD OE ⊥,根据抛物线的对称性可以确定4DOx EOx π∠=∠=,所以()22D ,,代入抛物线方程44p =,求得1p =,所以其焦点坐标为102⎛⎫⎪⎝⎭,,故选:B .【考点】圆锥曲线,直线与抛物线的交点,抛物线的对称性,点在抛物线上的条件,抛物线的焦点坐标 6.【答案】D【解析】计算出()a ab ⋅+、a b +的值,利用平面向量数量积可计算出cos a a b +,的值.5a =,6b =,6a b ⋅=-,()225619a a b a a b ∴⋅+=+⋅=-=.()2222257a b a ba ab b +=+=+⋅+=-,因此,()1919cos 5735a a ba ab a a b⋅++===⨯⋅+,.故选:D . 【考点】平面向量夹角余弦值的计算,平面向量数量积的计算,向量模的计算 7.【答案】A【解析】根据已知条件结合余弦定理求得AB ,再根据222cos 2AB BC AC B AB BC+-=⋅,即可求得答案.在ABC △中,2cos 3C =,4AC =,3BC =.根据余弦定理:2222cos AB AC BC AC BC C =+-⋅⋅,2224322433AB =+-⨯⨯⨯,可得29AB =,即3AB =.由22299161cos 22339AB BC AC B AB BC +-+-===⋅⨯⨯,故1cos 9B =.故选:A . 【考点】余弦定理解三角形8.【答案】C【解析】根据三视图特征,在正方体中截取出符合题意的立体图形,求出每个面的面积,即可求得其表面积.根据三视图特征,在正方体中截取出符合题意的立体图形根据立体图形可得:12222ABC ADC CDB S S S ===⨯⨯=△△△,根据勾股定理可得:AB AD DB ===ADB ∴△是边长为,根据三角形面积公式可得:(211sin 6022ADBS AB AD =⋅⋅==△∴该几何体的表面积是:632=⨯++ 故选:C .【考点】根据三视图求立体图形的表面积,根据三视图画出立体图形 9.【答案】D【解析】利用两角和的正切公式,结合换元法,解一元二次方程,即可得出答案.2tan tan 74πθθ⎛⎫-+= ⎪⎝⎭,tan 12tan 71tan θθθ+∴-=-,令tan t θ=,1t ≠,则1271tt t+-=-,整理得2440t t -+=,解得2t =,即tan 2θ=.故选:D .【考点】利用两角和的正切公式化简求值 10.【答案】D【解析】根据导数的几何意义设出直线l 的方程,再由直线与圆相切的性质,即可得出答案.设直线l 在曲线y =(0x,则00x >,函数y =导数为y '=l 的斜率k =,设直线l 的方程为)0y x x =-,即00xx -+=,由于直线l 与圆2215x y +=相切,则=,两边平方并整理得2005410x x --=,解得01x=,015x =-(舍),则直线l 的方程为210x y -+=,即1122y x =+.故选:D .【考点】导数的几何意义的应用,直线与圆的位置的应用 11.【答案】A【解析】根据双曲线的定义,三角形面积公式,勾股定理,结合离心率公式,即可得出答案.5ca=,c ∴,根据双曲线的定义可得122PF PF a -=,1212142PF F PF S PF =⋅=△,即128PF PF ⋅=, 12F P F P ⊥,()222122PF PF c ∴+=,()22121224PF PF PF PF c ∴-+⋅=,即22540a a -+=,解得1a =,故选:A .【考点】双曲线的性质以及定义的应用,勾股定理,三角形面积公式的应用 12.【答案】A【解析】由题意可得a 、b 、()01c ∈,,利用作商法以及基本不等式可得出a 、b 的大小关系,由8log 5b =,得85b =,结合5458<可得出45b <,由13log 8c =,得138c =,结合45138<,可得出45c >,综合可得出a 、b 、c 的大小关系.由题意可知a 、b 、()01c ∈,, ()222528log 3lg3lg81lg3lg8lg3lg8lg 241log 5lg5lg522lg5lg 25lg5a b ⎛⎫⎛⎫++⎛⎫==⋅⋅==⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭<<,a b ∴<;由8log 5b =,得85b =,由5458<,得5488b <,54b ∴<,可得45b <;由13log 8c =,得138c =,由45138<,得451313c <,54c ∴>,可得45c >.综上所述,a b c <<.故选:A .【考点】对数式的大小比较,基本不等式、对数式与指数式的互化,指数函数单调性的应用 二、填空题 13.【答案】7【解析】作出可行域,利用截距的几何意义解决.不等式组所表示的可行域如图.因为32z x y =+,所以322x z y =-+,易知截距2z 越大,则z 越大,平移直线32x y =-,当322x zy =-+经过A 点时截距最大,此时z 最大,由21y x x =⎧⎨=⎩,得12x y =⎧⎨=⎩,()12A ,,所以max 31227z =⨯+⨯=.故答案为:7.【考点】简单线性规划的应用,求线性目标函数的最大值 14.【答案】240【解析】写出622x x ⎛⎫+ ⎪⎝⎭二项式展开通项,即可求得常数项.622x x ⎛⎫+ ⎪⎝⎭其二项式展开通项:()()()621221236661222rrr r r r r r r r r C xC x C x x T x ---+-⎛⎫⋅⋅⋅⋅=⋅⎭= ⎝=⎪,当1230r -=,解得4r =,622x x ⎛⎫∴+ ⎪⎝⎭的展开式中常数项是:664422161516240C C ⋅=⋅=⨯=.故答案为:240.【考点】二项式定理,利用通项公式求二项展开式中的指定项15. 【解析】与球有关的组合体问题,一种是内切,一种是外接.解题时要认真分析图形,明确切点和接点的位置,确定有关元素间的数量关系,并作出合适的截面图,如球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径;球外接于正方体,正方体的顶点均在球面上,正方体的体对角线长等于球的直径.将原问题转化为求解圆锥内切球的问题,然后结合截面确定其半径即可确定体积的值.易知半径最大球为圆锥的内切球,球与圆锥内切时的轴截面如图所示,其中2BC =,3AB AC ==,且点M 为BC 边上的中点,设内切圆的圆心为O ,由于AM ==122S =⨯⨯=△ABC r ,则:()11113322222ABC AOB BOC AOC S S S S AB r BC r AC r r =++=⨯⨯+⨯⨯+⨯⨯=⨯++⨯=△△△△r,其体积:343V r π=.. 16.【答案】②③【解析】利用特殊值法可判断命题①的正误;利用函数奇偶性的定义可判断命题②的正误;利用对称性的定义可判断命题③的正误;取0x π-<<可判断命题④的正误.综合可得出结论.对于命题①,152622f π⎛⎫=+= ⎪⎝⎭,152622fπ⎛⎫-=--=- ⎪⎝⎭,则66f f ππ⎛⎫⎛⎫-≠ ⎪ ⎪⎝⎭⎝⎭,所以,函数()f x 的图象不关于y 轴对称,命题①错误;对于命题②,函数()f x 的定义域为{}x x k k π≠∈Z ,,定义域关于原点对称,()()()()111sin sin sin sin sin sin f x x x x f x x x x ⎛⎫-=-+=--=-+=- ⎪-⎝⎭,所以,函数()f x 的图象关于原点对称,命题②正确;对于命题③,11sin cos 22cos sin 2f x x x x x πππ⎛⎫⎛⎫-=-+=+⎪ ⎪⎛⎫⎝⎭⎝⎭- ⎪⎝⎭, 11sin cos 22cos sin 2f x x x x x πππ⎛⎫⎛⎫+=++=+⎪ ⎪⎛⎫⎝⎭⎝⎭+ ⎪⎝⎭,则22f x f x ππ⎛⎫⎛⎫-=+ ⎪ ⎪⎝⎭⎝⎭,所以,函数()f x 的图象关于直线2x π=对称,命题③正确;对于命题④,当0x π-<<时,sin 0x <,()1sin 02sin f x x x=+<<,命题④错误.故答案为:②③.【考点】正弦型函数的奇偶性、对称性,最值的求解 三、解答题17.【答案】(1)25a =,37a =,21n a n =+,当1n =时,13a =成立;假设n k =时,21k a k =+成立.那么1n k =+时,()()134321423211k k a a k k k k k +=-=+-=+=++也成立.则对任意的*n ∈N ,都有21n a n =+成立.(2)()12122n n S n +=-⋅+【解析】(1)利用递推公式得出2a ,3a ,猜想得出{}n a 的通项公式,利用数学归纳法证明即可.由题意可得2134945a a =-=-=,32381587a a =-=-=,由数列{}n a 的前三项可猜想数列{}n a 是以3为首项,2为公差的等差数列,即21n a n =+,证明如下:当1n =时,13a =成立;假设n k =时,21k a k =+成立.那么1n k =+时,()()134321423211k k a a k k k k k +=-=+-=+=++也成立.则对任意的*n ∈N ,都有21n a n =+成立;(2)由错位相减法求解即可.由(1)可知,()2212n nn a n ⋅=+⋅,()()231325272212212n n n S n n -=⨯+⨯+⨯++-⋅++⋅,①()()23412325272212212n n n S n n +=⨯+⨯+⨯++-⋅++⋅,②,由-①②得:()()()()()21231112126222221262212122212n n n n n n S n n n -+++--=+⨯+++-+⋅=+⨯-+⋅=⋅⨯---,即()12122n n S n +=-⋅+.【考点】求等差数列的通项公式,利用错位相减法求数列的和18.【答案】(1)该市一天的空气质量等级分别为1、2、3、4的概率分别为0.43、0.27、0.21、0.09 (2)350(3()221003383722 5.820 3.84155457030K ⨯⨯-⨯=⨯⨯⨯≈>,因此,有95%的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关.【解析】(1)根据频数分布表可计算出该市一天的空气质量等级分别为1、2、3、4的概率.由频数分布表可知,该市一天的空气质量等级为1的概率为216250.43100++=,等级为2的概率为510120.27100++=,等级为3的概率为6780.21100++=,等级为4的概率为7200.09100++=. (2)利用每组的中点值乘以频数,相加后除以100可得结果.由频数分布表可知,一天中到该公园锻炼的人次的平均数为100203003550045350100⨯+⨯+⨯=.(3)根据表格中的数据完善22⨯列联表,计算出2K 的观测值,再结合临界值表可得结论.22⨯列联表如下:()221003383722 5.820 3.84155457030K ⨯⨯-⨯=⨯⨯⨯≈>,因此,有95%的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关.【考点】利用频数分布表计算频率和平均数,独立性检验的应用19.【答案】(1)在棱1CC 上取点G ,使得112C G CG =,连接DG 、FG 、1C E 、1C F ,长方体1111ABCD A B C D -中,AD BC ∥且AD BC =,11BB CC ∥且11BB CC =,112C G CG=12BF FB =,112233CG CC BB BF ∴===且CG BF =,所以,四边形BCGF 平行四边形,则AF DG∥且AF DG =,同理可证四边形1DEC G 为平行四边形,1C E DG ∴∥且1C E DG =,1C E AF ∴∥且1C E AF =,则四边形1AEC F 为平行四边形,因此,点1C 在平面AEF 内.(2)7【解析】(1)连接1C E 、1C F ,证明出四边形1AEC F 为平行四边形,进而可证得点1C 在平面AEF 内.在棱1CC 上取点G ,使得112C G CG =,连接DG 、FG 、1C E 、1C F ,长方体1111ABCD A B C D -中,AD BC ∥且AD BC =,11BB CC ∥且11BB CC =,112C G CG=12BF FB =,112233CG CC BB BF ∴===且CG BF =,所以,四边形BCGF 平行四边形,则AF DG∥且AF DG =,同理可证四边形1DEC G 为平行四边形,1C E DG ∴∥且1C E DG =,1C E AF ∴∥且1C E AF =,则四边形1AEC F 为平行四边形,因此,点1C 在平面AEF 内;(2)以点1C 为坐标原点,11C D 、11C B 、1C C 所在直线分别为x 、y 、z 轴建立空间直角坐标系1C xyz -,利用空间向量法可计算出二面角1A EF A --的余弦值,进而可求得二面角1A EF A --的正弦值.以点1C 为坐标原点,11C D 、11C B 、1C C 所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系1C xyz -,则()213A ,,、()1210A ,,、()202E ,,、()011F ,,,()011AE =--,,,()202AF =--,,,()1012A E =-,,,()1201A F =-,,,设平面AEF 的法向量为()111m x y z =,,,由00m AE m AF ⎧⋅⎪⎨⋅=⎪⎩=,得11110220y z x z --=⎧⎨--=⎩取11z =-,得111x y ==,则()111m =-,,,设平面1A EF 的法向量为()222n x y z =,,,由1100n A E n A F ⎧⋅=⎪⎨⋅=⎪⎩,得22222020y z x z -+=⎧⎨-+=⎩,取22z =,得21x =,24y =,则()142n =,,,3cos 3m n m n m n⋅===⨯⋅,,设二面角1A EF A--的平面角为θ,则cos θ=,sinθ∴==.因此,二面角1A EF A --.【考点】点在平面的证明,利用空间向量法求解二面角20.【答案】(1)221612525x y +=(2)52【解析】(1)因为()222:10525x y C m m+=<<,可得5a =,b m =,根据离心率公式,结合已知,即可求得答案.()222:10525x y C m m +=<<,5a∴=,b m =,根据离心率4c e a ====, 解得54m =或54m =-(舍),C ∴的方程为:22214255x y ⎛⎫ ⎪⎝⎭+=,即221612525x y +=. (2)点P 在C 上,点Q 在直线6x =上,且BP BQ =,BP BQ ⊥,过点P 作x 轴垂线,交点为M ,设6x =与x 轴交点为N ,可得PMB BNQ ≅△△,可求得P 点坐标,求出直线AQ 的直线方程,根据点到直线距离公式和两点距离公式,即可求得APQ △的面积.点P 在C 上,点Q 在直线6x =上,且BP BQ =,BP BQ ⊥,过点P 作x 轴垂线,交点为M ,设6x =与x 轴交点为N .根据题意画出图形,如图BP BQ =,BP BQ ⊥,90PMB QNB ∠=∠=,又90PBM QBN ∠+∠=,90BQN QBN ∠+∠=,PBM BQN ∴∠=∠,根据三角形全等条件“AAS ”,可得:PMB BNQ ≅△△,221612525x y +=, ()50B ∴,,651PM BN ∴==-=,设P 点为()P P x y ,,可得P 点纵坐标为1P y =,将其代入221612525x y +=,可得:21612525P x +=,解得:3P x =或3P x =-,P ∴点为()31,或()31-,, ①当P 点为()31,时,故532MB =-=,PMB BNQ ≅△△,2MB NQ ∴==,可得:Q 点为()62,,画 出图象,如图()50A -,,()62Q ,,可求得直线AQ 的直线方程为:211100x y -+=,根据点到直线距离公式可得P 到直线AQ 的距离为:d ===,根据两点间距离公式可得:AQ =,APQ ∴△面积为:1522⨯=;②当P 点为()31-,时,故5+38MB ==,PMB BNQ ≅△△,8MB NQ ∴==,可得:Q 点为()68,,画出图象,如图()50A -,,()68Q ,,可求得直线AQ 的直线方程为:811400x y -+=,根据点到直线距离公式可得P到直线AQ 的距离为:d ===AQ ==APQ ∴△面积为:1522=,综上所述,APQ △面积为:52. 【考点】椭圆标准方程,三角形面积,椭圆的离心率定义,数形结合求三角形面积 21.【答案】(1)34b =-(2)由(1)可得()334f x x x c =-+,()231133422f x x x x ⎛⎫⎛⎫'=-=+- ⎪⎪⎝⎭⎝⎭,令()0f x '>,得12x >或12x -<;令()0f x '<,得1122x -<<,所以()f x 在1122⎛⎫- ⎪⎝⎭,上单调递减,在12⎛⎫-∞- ⎪⎝⎭,,12⎛⎫+∞ ⎪⎝⎭,上单调递增,且()114f c -=-,1124f c ⎛⎫-=+ ⎪⎝⎭,1124f c ⎛⎫=- ⎪⎝⎭,()114f c =+,若()f x 所有零点中存在一个绝对值大于1的零点0x ,则()10f ->或()10f <,即14c >或14c -<.当14c >时,()1104f c -=->,11024f c ⎛⎫-=+ ⎪⎝⎭>,11024f c ⎛⎫=- ⎪⎝⎭>,()1104f c =+>,又()()32464341160f c c c c c c -=-++=-<,由零点存在性定理知()f x 在()41c --,上存在唯一一个零点0x ,即()f x 在()1-∞-,上存在唯一一个零点,在()1-+∞,上不存在零点,此时()f x 不存在绝对值不大于1的零点,与题设矛盾;当14c -<时,()1104f c -=-<,11024f c ⎛⎫-=+ ⎪⎝⎭<,11024f c ⎛⎫=- ⎪⎝⎭<,()1104f c =+<,又()()32464341160f c c c c c c -=++=->,由零点存在性定理知()f x 在()14c -,上存在唯一一个零点0x ',即()f x 在()1+∞,上存在唯一一个零点,在()1-∞,上不存在零点,此时()f x 不存在绝对值不大于1的零点,与题设矛盾;综上,()f x 所有零点的绝对值都不大于1.【解析】(1)利用导数的几何意义得到102f ⎛⎫'= ⎪⎝⎭,解方程即可.因为()23f x x b '=+,由题意,102f ⎛⎫'= ⎪⎝⎭,即21302b ⎛⎫⨯+= ⎪⎝⎭,则34b =-; (2)由(1)可得()231132422f x x x x ⎛⎫⎛⎫'=-=+- ⎪⎪⎝⎭⎝⎭,易知()f x 在1122⎛⎫- ⎪⎝⎭,上单调递减,在12⎛⎫-∞- ⎪⎝⎭,,12⎛⎫+∞ ⎪⎝⎭,上单调递增,且()114f c -=-,1124f c ⎛⎫-=+ ⎪⎝⎭,1124f c ⎛⎫=- ⎪⎝⎭,()114f c =+,采用反证法,推出矛盾即可.由(1)可得()334f x x x c =-+,()231133422f x x x x ⎛⎫⎛⎫'=-=+- ⎪⎪⎝⎭⎝⎭,令()0f x '>,得12x >或12x -<;令()0f x '<,得1122x -<<,所以()f x 在1122⎛⎫- ⎪⎝⎭,上单调递减,在12⎛⎫-∞- ⎪⎝⎭,,12⎛⎫+∞ ⎪⎝⎭,上单调递增,且()114f c -=-,1124f c ⎛⎫-=+ ⎪⎝⎭,1124f c ⎛⎫=- ⎪⎝⎭,()114f c =+,若()f x 所有零点中存在一个绝对值大于1的零点0x ,则()10f ->或()10f <,即14c >或14c -<.当14c >时,()1104f c -=->,11024f c ⎛⎫-=+ ⎪⎝⎭>,11024f c ⎛⎫=- ⎪⎝⎭>,()1104f c =+>,又()()32464341160f c c c c c c -=-++=-<,由零点存在性定理知()f x 在()41c --,上存在唯一一个零点0x ,即()f x 在()1-∞-,上存在唯一一个零点,在()1-+∞,上不存在零点,此时()f x 不存在绝对值不大于1的零点,与题设矛盾;当14c -<时,()1104f c -=-<,11024f c ⎛⎫-=+ ⎪⎝⎭<,11024f c ⎛⎫=- ⎪⎝⎭<,()1104f c =+<,又()()32464341160f c c c c c c -=++=->,由零点存在性定理知()f x 在()14c -,上存在唯一一个零点0x ',即()f x 在()1+∞,上存在唯一一个零点,在()1-∞,上不存在零点,此时()f x 不存在绝对值不大于1的零点,与题设矛盾;综上,()f x 所有零点的绝对值都不大于1. 【考点】利用导数研究函数的零点,导数的几何意义,反证法22.【答案】(1)(2)3cos sin 120ρθρθ-+=【解析】(1)由参数方程得出A ,B 的坐标,最后由两点间距离公式,即可得出AB 的值.令0x =,则220t t +-=,解得2t =-或1t =(舍),则26412y =++=,即()012A ,.令0y =,则2320t t -+=,解得2t =或1t =(舍),则2244x =--=-,即()40B -,.AB ∴=(2)由A ,B 的坐标得出直线AB 的直角坐标方程,再化为极坐标方程即可.由(1)可知()120304AB k -==--,则直线AB 的方程为()34y x =+,即3120x y -+=.由cos x ρθ=,sin y ρθ=可得,直线AB 的极坐标方程为3cos sin 120ρθρθ-+=.【考点】利用参数方程求点的坐标,直角坐标方程化极坐标方程 23.【答案】(1)()22222220a b c a b c ab ac bc ++=+++++=,()22212ab bc ca a b c ∴++=-++. a ,b ,c 均不为0,则2220a b c ++>,()222120ab bc ca a b c ∴++=-++<. (2)不妨设{}max a b c a =,,,由0a b c ++=,1abc =可知,0a >,0b <,0c <,a b c =--,1a bc=,()222322224b c b c bc bc bc a a a bc bc bc ++++∴=⋅===≥.当且仅当b c =时,取等号,a ∴ {}3max 4a b c ,,.【解析】(1)由()22222220a b c a b c ab ac bc ++=+++++=结合不等式的性质,即可得出证明.()22222220a b c a b c ab ac bc ++=+++++=,()22212ab bc ca a b c ∴++=-++.a ,b ,c 均不为0,则2220a b c ++>,()222120ab bc ca a b c ∴++=-++<. (2)不妨设{}max a b c a =,,,由题意得出0a >,b ,0c <,由()222322b c b c bca aa bcbc+++=⋅==,结合基本不等式,即可得出证明.不妨设{}max a b c a =,,,由0a b c ++=,1abc =可知,0a >,0b <,0c <,a b c =--,1a bc=,()222322224b c b c bc bc bc a a a bc bc bc ++++∴=⋅===≥.当且仅当b c =时,取等号,a ∴{}3max 4a b c ,,.【考点】不等式的基本性质,基本不等式的应用。
